基于频率和模态保证准则的结构内部多缺陷反演 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

江守燕^,²⁾, 赵林鑫, 杜成斌河海大学工程力学系,南京 210098

IDENTIFICATION OF MULTIPLE FLAWS IN STRUCTURES BASED ON FREQUENCY AND MODAL ASSURANCE CRITERIA ¹⁾

Jiang Shouyan^,²⁾, Zhao Linxin, Du ChengbinDepartment of Engineering Mechanics, Hohai University, Nanjing 210098, China

通讯作者: 2) 江守燕,副教授,主要研究方向：计算力学与虚拟仿真. E-mail:syjiang@hhu.edu.cn

收稿日期:2019-03-31接受日期:2019-06-26网络出版日期:2019-07-18

基金资助:

1) 国家自然科学基金.51579084
中央高校基本科研业务费专项资金.2019B16314
中央高校基本科研业务费专项资金.2018B48514
浙江省水利科技重点项目.RB1703

Received:2019-03-31Accepted:2019-06-26Online:2019-07-18
作者简介 About authors

摘要
静响应(位移、应变等)在实际问题的反演分析中很难由安装在结构上的一组传感器记录得到,而结构的动力特性(频率、振型)和动力响应(加速度、速度、动位移)在实际问题中较易通过传感器采集得到. 文中基于频率残差和模态保证准则构建了反演分析模型的目标函数,并结合频域内动力扩展有限元法和人工蜂群智能优化算法的优点,扩展有限元法通过引入非连续位移模式在不重新划分网格的情况下通过改变水平集函数反映缺陷的数量、位置及大小, 避免了反演分析每次迭代过程中的网格重剖分,人工蜂群智能优化算法在每次迭代中都采用全局和局部搜索,找到最优解的概率大幅增大并可很好地避免局部最优,同时,通过引入拓扑变量,将缺陷的数量纳入到反演分析过程中,迭代过程中可智能反演出缺陷的数目,建立了结构内部多缺陷(孔洞、裂纹)的反演分析模型. 通过若干算例的分析表明：建立的反演分析模型能够较为准确地探测出结构内部圆形、椭圆形以及裂纹状缺陷的数量、位置及大小,且算法具有较好的鲁棒性.
关键词： 扩展有限元法;人工蜂群算法;多缺陷反演;频率;模态

Abstract
Static response (displacement, strain, etc.) can hardly be recorded by a group of sensors installed on the structure in the inversion analysis of practical problems, while the dynamic characteristics (frequency, mode) and dynamic response (acceleration, velocity, dynamic displacement) of the structure can be easily acquired by sensors in practical problems. In this paper, the objective function of the inversion analysis model is constructed based on frequency residuals and modal assurance criteria. Combining the advantages of dynamic extended finite element method in frequency domain and artificial bee colony intelligent optimization algorithm, the extended finite element method avoids re-meshing in each iteration by introducing discontinuous displacement approximation and can reflect the number, location and size of defects by changing the level set function. In each iteration, the artificial bee colony intelligent optimization algorithm uses global and local searches. The probability of finding the optimal solution increases greatly and avoids local optimum. At the same time, by introducing topological variables, the number of flaws is incorporated into the inversion analysis process. The number of flaws can be intelligently inverted in the iteration process. Then, the inversion analysis model of multiple flaws (voids, cracks) in the structure is established. The analysis of several examples shows that the inversion analysis model can accurately detect the number, location and size of circular flaws, elliptical flaws, or crack in the structure. The result also shows the good robustness of the algorithm.
Keywords：extended finite element methods;artificial bee colony algorithm;identification of multiple flaws;frequency;modal

PDF (3297KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
江守燕, 赵林鑫, 杜成斌. 基于频率和模态保证准则的结构内部多缺陷反演 ¹⁾. 力学学报[J], 2019, 51(4): 1091-1100 DOI:10.6052/0459-1879-19-078
Jiang Shouyan, Zhao Linxin, Du Chengbin. IDENTIFICATION OF MULTIPLE FLAWS IN STRUCTURES BASED ON FREQUENCY AND MODAL ASSURANCE CRITERIA ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(4): 1091-1100 DOI:10.6052/0459-1879-19-078

引言

结构内部的缺陷反演是一类典型的反分析问题,反分析问题由正分析过程和目标函数极小化迭代过程两部分组成. 基于数值方法的正分析过程为复杂结构内部的缺陷反演提供了一条有效途径,对于含缺陷的结构正分析问题是一类典型的不连续问题. 在数值方法中,有限元法(finite element methods, FEM)被广泛地用于科学和工程问题的数值分析中,也频繁地用于不连续问题的计算分析中^[1-3],但对于不连续问题,有限元法需要严格遵从不连续界面进行网格剖分,界面演化时还需要进行网格重剖分;此外,各种各样的新型数值方法也逐渐发展起来用于不连续问题的分析,如：无网格伽辽金法^[4],无网格破裂单元法^[5-7],比例边界有限元法^[8-11],数值流形法^[12-13], 扩展有限元法(extended finite element methods, XFEM)^[14-15];在这些数值方法中,XFEM是模拟不连续问题最有前景的一种数值方法,它与水平集法^[16]的结合避免了反演分析迭代过程中的网格重剖分.

XFEM和智能优化算法的结合已广泛用于缺陷的反演问题中^[17-22],文献^[17,18,19]将XFEM与遗传算法相结合进行缺陷反演,基本的遗传算法效率较低且容易陷入局部最优解,Nanthakumar等^[20]将XFEM与多级坐标搜索法相结合进行压电材料内部缺陷的反演,但这些研究均为单缺陷反演;Sun等^[21]将XFEM与人工蜂群算法、梯度优化算法相结合进行了结构内部多缺陷的反演,最近赵文虎等^[23]和马春平等^[24]将XFEM和人工蜂群、人工鱼群算法相结合,并通过聚类分析有效地提高了反演分析的收敛速度,能够较快速定位结构中缺陷的数量、位置及大小,但这些研究中实测的响应均考虑为静响应(位移、应变等),这在实际问题的反演中很难由安装在结构上的一组传感器记录得到,实际可操作性困难. 相比较而言,结构的动力特性(频率、振型)和动力响应(加速度、速度、动位移)等在实际问题中较易通过传感器采集得到,文献^[25,26,27]基于结构的动力响应构建目标函数进行了结构内部的缺陷反演. 结构的动力特性(频率、振型)和动力响应与结构物理参数(如质量、刚度、阻尼等)是紧密相关的,当结构产生损伤时,这些内在的物理参数将或多或少的发生变化,这就必将引起结构振动特性的改变^[28]. 基于结构振动特性,对结构内部的缺陷进行识别,与局部检测方法相比,可全面地对结构进行检测,且操作简单快捷,不影响结构正常使用^[29],其可行性已得到室内试验的验证^[30-32].

基于频率残差和模态保证准则构建目标函数,并结合XFEM和人工蜂群智能优化算法的优点,通过引入拓扑变量,将缺陷的数量纳入到反演分析过程中,重点研究结构内部多缺陷(孔洞、裂纹)的反演分析模型. 阐述利用频域内动力XFEM进行结构内部圆形、椭圆形以及裂纹状缺陷反演分析时XFEM位移模式的构建以及水平集函数的表征,给出基于频域内动力XFEM和人工蜂群智能优化算法的结构内部多缺陷的反演分析流程. 最后,通过若干算例验证建立的反演分析模型.

1 多缺陷检测的反分析法

缺陷检测的目标是通过正分析和目标函数最小化迭代过程找出描述物理缺陷的一组参数. 通过给定一系列不同的测量值响应(例如：加速度、应变、频率、振型),一般来说,测量结果是由安装在结构上的一组传感器记录得到的. 通常,使用最小化实测数据与每次正分析得到的预测数据差的迭代过程求解这类反分析问题,迭代过程不断更新描述物理缺陷的模型参数并最小化目标函数,直至优化收敛到缺陷区域.

多缺陷检测的反分析问题可以描述为：已知问题的弹性域$\varOmega \in {\pmb R}^2$、位移边界$\varGamma _{u} $、外力边界$\varGamma _{t} $、已知位移条件$\bar{\pmb u} $、已知外力条件$ \bar {\pmb t}$以及在结构边界测得的若干测点响应$ \tilde {\pmb \omega }$,寻找结构内部的若干缺陷边界$\varGamma _{{v1}} $, $\varGamma _{{v2}} $, $\varGamma _{{v3}} $, $\cdots$. 结构内部任一缺陷边界$\varGamma _{{v}i} $ ($i = 1,2,3, \cdots , n$,其中$n$为待反演的缺陷个数)可通过一组未知参数${\pmb \theta }_i $表示为

(1)$$ {\pmb \theta }_i = \left\{ \theta _{i1} , \ \ \theta _{i2} , \ \ \theta _{i3} ,\ \ \cdots , \ \ \theta _{im} \right\} \in R^m $$

式中,$m$为反演第$i$个缺陷所需的参数总数.

1.1 目标函数

基于智能优化算法的结构内部缺陷反演研究,也就是通过对测量和计算得到的响应参数进行比较来构建目标函数,并对目标函数进行寻优问题的求解. 通过频率残差和模态保证准则来构建目标函数$O\left( {\pmb \theta } \right)$,即

(2)$$ O\left( {\pmb \theta } \right) = \dfrac{\sqrt {\sum_{i = 1}^{ NF} {\left( {\omega _i^{c}-\omega _i^{m} } \right)^2} } }{\sqrt {\sum_{i = 1}^{ NF} {\left( {\omega _i^{m} } \right)^2} } } + \sum_{j = 1}^{ NM} {\dfrac{\left\| {{\pmb \varPhi }_j^{c}-{\pmb \varPhi }_j^{ m} } \right\|_2 }{\left\| {{\pmb \varPhi }_j^{m} } \right\|_2 }} $$

式中,$\left\| \ \cdot \ \right\|_2 $代表向量的2范数;$NF$和$NM$是用来计算目标函数值的频率阶数和模态数;$\omega _i^{c} $和$\omega _i^{m} $分别为第$i$阶频率的计算值和测量值;${\pmb \varPhi }_j^{c} $和${\pmb \varPhi }_j^{m} $分别为第$j$阶频率对应模态的计算值和测量值.

1.2 缺陷数目的反演

实际结构中缺陷的数目往往是未知的,因此所建立的多缺陷反分析模型必须要解决的一个问题就是：如何快速准确地反演缺陷的个数.

若结构中可能存在的最大缺陷数量为$n$,第$i$个缺陷待反演的参数为${\pmb \theta }_i $,则$n$个缺陷待反演的参数集合为

(3)$$ {\pmb \theta } = \left\{ {\pmb \theta }_1 , \ \ {\pmb \theta }_2 , \ \ {\pmb \theta }_3 , \ \ \cdots , \ \ {\pmb \theta }_n \right\} $$

通过引入拓扑变量$\kappa _i $(该变量的取值只能为0或1),将缺陷的数量纳入到反演分析过程之中,则待反演的参数集合为

(4)$$ {\pmb \theta } = \left\{ {\pmb \theta }_1 , \ \ \kappa _1 , \ \ {\pmb \theta }_2 , \ \ \kappa _2 , \ \ {\pmb \theta }_3 , \ \ \kappa _3 , \ \ \cdots , \ \ {\pmb \theta }_n , \ \ \kappa _n \right\} $$

其中

(5)$$ \left. \begin{array}{ll} {\pmb \theta }_i^{\min } \leqslant {\pmb \theta }_i \leqslant {\pmb \theta }_i^{\max } \\ \kappa _i = 0 \ \ {or} \ \ 1 \end{array} \!\! \right\} \ i = 1,2, \cdots ,n $$

式(4)给出的可能解所对应的实际缺陷为

(6)$$ {\pmb \theta } = \left\{ \tilde{\pmb \theta }_1 , \ \ \tilde {\pmb \theta }_2 , \ \ \tilde {\pmb \theta }_3 , \ \ \cdots , \ \ \tilde{\pmb \theta }_n \right\} $$

其中

(7)$$ \tilde{\pmb \theta }_i = \kappa _i {\pmb \theta }_i , \ \ i = 1,2, \cdots ,n $$

这种方法只需给出最终收敛准则,在反演过程中便能自动得到缺陷的数目、位置和大小. 变量$\kappa _i $仅是一个控制缺陷存在与否的变量,如果$\kappa _i = 0$,那么代表第$i$个缺陷不存在,即$\kappa _i {\pmb \theta }_i = {\bf 0}$,缺陷所对应的参数在反演过程中将不起作用;如果$\kappa _i = 1$,那么代表第$i$个缺陷是存在的,即$\kappa _i {\pmb \theta}_i = {\pmb \theta }_i $. 可以看出,拓扑变量$\kappa _i $只反映缺陷的存在与否,对反演过程中缺陷的位置、尺寸等参数没有影响. 反演分析时,假定结构中可能存在的缺陷数目$n$(即拓扑变量的个数)总是大于或等于结构中实际存在的缺陷数目$n_v $. 由于拓扑变量$\kappa _i $是一个离散变量,第$i$个缺陷待反演的其他参数为连续变量,拓扑变量$\kappa _i $可通过下式确定

(8)$$ \kappa _i = \left\{ \begin{array}{ll} {0,} & {\kappa _i < 0.5} \\ {1,} & {\kappa _i \geqslant 0.5} \end{array} \right., \ \ i = 1,2, \cdots ,n $$

2 动力问题的扩展有限元法

2.1 水平集法

水平集方法是一种处理移动界面的有效数值方法,它将界面的变化表示成比界面高一维的函数$\phi ({\pmb x},t)$. 例如, $R^2$中一维移动界面$\varGamma (t) \subset R^2$可表示成

(9)$$ \varGamma (t) = \{{\pmb x} \in R^2:\phi ({\pmb x},t) = 0\} $$

式中,函数$\phi ({\pmb x},t)$为水平集函数;${\pmb x}$为考察点的坐标;$t$为时间. 这里界面是静止的,不随时间变化.

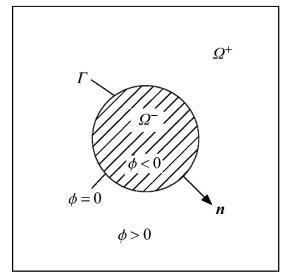
如图1所示,界面将求解域$\varOmega $分割成两个子域$\varOmega ^-$和$\varOmega ^ + $. 在界面上,水平集函数$\phi = 0$;在子域$\varOmega ^-$内,水平集函数$\phi < 0$;在子域$\varOmega ^ + $内,水平集函数$\phi > 0$.

图1

新窗口打开|下载原图ZIP|生成PPT
图1含圆形界面的求解域

Fig. 1Domain with circular discontinuous interfaces

结构内部任意形状的缺陷在反演分析时可采用规则的圆形或椭圆形缺陷进行近似拟合. 值得指出的是,对于实际问题,由于测试信号来自于含任意缺陷的结构,当采用规则的圆形或椭圆形缺陷进行近似拟合时,相当于测试信号增加了来自于缺陷形状的误差,可能会降低反演算法的有效性. 圆形缺陷的水平集函数可表示成

(10)$$ \phi ({\pmb x}) = \left\| {{\pmb x}-{\pmb x}_{c} } \right\|-r_{c} $$

式中,${\pmb x}_{c} $为圆心点的坐标向量;$r_{c} $为半径. 椭圆形缺陷的水平集函数可表示成

(11)$$ \phi ({\pmb x}) = \left\| \dfrac{\left[ {\left( {x-x_{c} } \right)\cos \theta + \left( {y-y_{c} } \right)\sin \theta } \right]^2}{a^2}+ \right.\\ \qquad \left.\dfrac{\left[ {\left( {y-y_{c} } \right)\cos \theta-\left( {x-x_{c} } \right)\sin \theta } \right]^2}{b^2} \right\|-1 $$

式中,$\left( {x_{c} ,y_{c} } \right)$为椭圆中心点坐标;$a$为椭圆的半长轴;$b$为椭圆的半短轴;$\theta $为椭圆的方向角,以逆时针为正,$\theta \in \left[ {- \pi , \pi } \right]$.

裂纹状缺陷采用两个水平集函数$\psi ({\pmb x},t)$和$\phi ^k({\pmb x},t) \ (k = 1,2)$描述^[32], $\psi ({\pmb x},t)$的零水平集$\psi ( {\pmb x},t) = 0$为裂纹面,波前水平集$\phi ^k({\pmb x},t)$与$\psi ({\pmb x},t)$是正交的. $\psi ({\pmb x},t)$取为符号距离函数,可表达为

(12)$$ \psi ({\pmb x},t) = \left\| {{\pmb x}-{\pmb x}^\ast } \right\| {sign}[({\pmb x}-{\pmb x}^\ast ) \cdot {\pmb n}] $$

波前水平集$\phi ^k({\pmb x},t)$为

(13)$$ \phi ^k({\pmb x},t) = ({\pmb x}-{\pmb x}_k ) \cdot {\pmb t} $$

式中,${\pmb x}$为考察点$P$的坐标;${\pmb x}^\ast $为考察点$P$在裂纹面上的投影点坐标;${\pmb n}$为裂纹面的单位外法向;$ {\pmb x}_k $为第$k$个裂尖坐标;${\pmb t}$为第$k$个裂纹尖端处的单位切向矢量.

反演圆形缺陷时,式(4)中待反演参数${\pmb \theta }_i $为

(14)$$ {\pmb \theta }_i = \left\{ x_{{c}i} , \ \ y_{{c}i} , \ \ r_{{c}i} \right\} $$

其中,$\left( {x_{{c}i} ,y_{{c}i} } \right)$为第$i$个圆形缺陷的圆心坐标,$r_{{c}i} $为第$i$个圆形缺陷的半径.

反演椭圆形缺陷时,式(4)中待反演参数${\pmb \theta }_i $为

(15)$$ {\pmb \theta }_i = \left\{ x_{{e}i} , \ \ y_{{e}i} , \ \ a_i , \ \ b_i , \ \ \beta _i \right\} $$

其中,$\left( x_{{e}i} ,y_{{e}i} \right)$为第$i$个椭圆形缺陷的中心点坐标;$a_i $为第$i$个椭圆形缺陷半长轴,$b_i $为第$i$个椭圆形缺陷的半短轴;$\beta $为第$i$个椭圆形缺陷的方位角,即整体坐标系与局部坐标系之间的夹角.

反演裂纹时,式(4)中待反演参数${\pmb \theta }_i $为

(16)$$ {\pmb \theta }_i = \left\{ x_{{s}i} , \ \ y_{{s}i} , \ \ x_{{e}i} , \ \ y_{{e}i} \right\} $$

其中,$\left( x_{{s}i} , \ \ y_{{s}i} \right)$为第$i$条裂纹的起点坐标;$\left( x_{{e}i} , \ \ y_{{e}i} \right)$为第$i$条裂纹的终点坐标.

数值计算时,仅仅储存单元结点的水平集值,即$\phi _i = \phi ({\pmb x}_i )$,单元内部的水平集函数通过下式插值得到

(17)$$ \phi ^{h}({\pmb x}) = \sum_i {N_i } ({\pmb x})\phi _i $$

式中,$N_i ({\pmb x})$为结点$i$对应的常规有限元的插值形函数.

2.2 扩展有限元位移模式

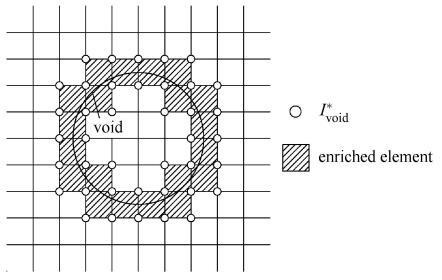
采用频域内动力XFEM计算含圆形或椭圆形缺陷结构频率和振型的估计值时,XFEM位移模式可表示为

(18)$$ {\pmb u}^{h}({\pmb x}) = \sum_{i \in I} N_i ( {\pmb x}) {\pmb u}_i + \sum_{i \in I_{void}^\ast } N_i^\ast ({\pmb x})[V({\pmb x})-V({\pmb x}_i )]{\pmb v}_i $$

式中,$N_i ({\pmb x})$为常规有限元结点$i$处的插值形函数;${\pmb u}_i $为结点$i$处的位移值;$V({\pmb x})$为改进函数;${\pmb v}_i $为改进结点$i$处的改进位移值;$N_i^\ast ({\pmb x})$为改进单元结点$i$处的单位分解函数,其形式可以和$N_i ({\pmb x})$相同,也可以不同,文中取二者相同;$I_{void}^\ast $为模型中改进结点集合,如图2所示. 通过改进函数$V({\pmb x})$对被缺陷边界切割的那些单元的结点(结点子集：$I_{void}^\ast $)进行改进,若结点位于缺陷内,$V({\pmb x}) = 0$,否则$V({\pmb x}) = 1$. 对于裂纹状缺陷,XFEM位移模式的构建可参见文献^[34].

图2

新窗口打开|下载原图ZIP|生成PPT
图2扩展有限元改进结点

Fig. 2Enrichment nodes for extended finite element

2.3 扩展有限元离散方程

根据扩展有限元法的位移模式式(18)并利用虚功原理,忽略阻尼的影响,可得离散系统的控制方程为

(19)$$ \left[ \!\!\begin{array}{cc} {\pmb M}_{uu} & {\pmb M}_{uv} \\ {\pmb M}_{vu} & {\pmb M}_{vv} \end{array}\!\! \right]\left\{ \!\!\begin{array}{c} \ddot{\pmb u} \\ \ddot{\pmb v} \end{array} \!\! \right\} + \left[\!\! \begin{array}{cc} {\pmb K}_{uu} & {\pmb K}_{uv} \\ {\pmb K}_{vu} & {\pmb K}_{vv} \end{array}\!\! \right]\left\{\!\! \begin{array}{c} {\pmb u} \\ {\pmb v} \end{array} \!\! \right\} = \left\{ \!\! \begin{array}{c} {\pmb F}_{u} \\ {\pmb F}_{v} \end{array}\!\! \right\} $$

式中,${\pmb M}_{ij} \left( {i,j = {u},{v}} \right)$, $ {\pmb K}_{ij} \ \left( {i,j ={u,v}} \right)$分别为整体质量矩阵和劲度矩阵;$ \ddot {\pmb u} $, $ \ddot{\pmb v} $为结点加速度列阵;$ {\pmb u} $, $ {\pmb v} $为结点位移列阵;${\pmb F}_i \ \left( {i = {u,v}} \right)$为整体荷载列阵.

单元刚度矩阵和单元质量矩阵通过下式表示

(20)$$ {\pmb k}^{e} = \left[ \!\! \begin{array}{cc} {\pmb k}^{uu} & {\pmb k}^{uv} \\ {\pmb k}^{vu} & {\pmb k}^{vv} \end{array}\!\! \right] , \quad {\pmb m}^{e} = \left[\!\! \begin{array}{cc} {\pmb m}^{uu} & {\pmb m}^{uv} \\ {\pmb m}^{vu} & {\pmb m}^{vv} \end{array} \!\! \right] $$

其中

(21)$ {\pmb k}^{rs} = \int_{\varOmega ^{\rm e}} ({\pmb B}^r)^{\rm T} {\pmb D \pmb B}^s d \varOmega =\\ \qquad \int_{\varOmega ^{e}} \left[ {\pmb B}_1^r \ \ {\pmb B}_2^r \ \ {\pmb B}_3^r \ \ {\pmb B}_4^r \right]^{T} \cdot \\ \qquad {\pmb D}\left[ {\pmb B}_1^s \ \ {\pmb B}_2^s \ \ {\pmb B}_3^s \ \ {\pmb B}_4^s \right] d\varOmega \ \ \ \ \ \ (r,s = { u,v}) $

(22)$ {\pmb B}_i^{u} = \left[\!\! \begin{array}{ccc} \dfrac{\partial N_i }{\partial x} & 0 & \dfrac{\partial N_i }{\partial y} \\ 0 & \dfrac{\partial N_i }{\partial y} & \dfrac{\partial N_i }{\partial x} \end{array} \!\! \right]^{T} , \ \ i = 1,2,3,4 $

(23)$ {\pmb B}_i^{v} = \left[ \!\! \begin{array}{ccc} \dfrac{\partial \left( {N_i^\ast \mathop{V}\limits^\frown } \right)}{\partial x} & 0 & \dfrac{\partial \left( {N_i^\ast \mathop{V}\limits^\frown } \right)}{\partial y} \\ 0 &\dfrac{\partial \left( {N_i^\ast \mathop{V}\limits^\frown } \right)}{\partial y} & \dfrac{\partial \left( {N_i^\ast \mathop{V}\limits^\frown } \right)}{\partial x} \end{array} \!\! \right]^{T} \\ \mathop{V}\limits^\frown = V({\pmb x})-V({\pmb x}_i ) , \ i = 1,2,3,4 $

(24)$ \left. \!\!\begin{array}{l} {\pmb m}^{uu} = \int_{\varOmega ^{e}} \rho \left( {\pmb N} \right)^{T } {\pmb N} d\varOmega \\ {\pmb m}^{uv} = \left( {\pmb m}^{vu} \right)^ {T} = \int_{\varOmega ^{e}} \rho \left( {\pmb N} \right)^ {T} \left( {\pmb N} \mathop{V}\limits^\frown \right) d\varOmega \\ {\pmb m}^{vv} = \int_{\varOmega ^{e}} \rho \left( {\pmb N} \mathop{V}\limits^\frown \right)^{T} \left( {\pmb N}\mathop{V}\limits^\frown \right) d\varOmega \end{array}\!\! \right\} $

(25)$\left.\!\!\begin{array}{l} {\pmb N} = \left[ {\pmb N}_1 \ \ {\pmb N}_2 \ \ {\pmb N}_3 \ \ {\pmb N}_4 \right] \ {\pmb N}_i = \left[\!\! \begin{array}{cc} {N_i } & 0 \\ 0 & {N_i } \end{array} \!\! \right] , \ \ \ i = 1,2,3,4 \end{array} \!\!\right\}$

式中,$\rho $为质量密度.

在动力平衡方程式(19)中,令等号右端项为0,便得到自由振动方程,在工程实际中,阻尼对结构自振频率和振型的影响极小,可略去其影响,故得到无阻尼系统的自由振动方程为

(26)$$ \left[ \!\!\begin{array}{cc} {\pmb M}_{uu} & {\pmb M}_{uv} \\ {\pmb M}_{vu} & {\pmb M}_{vv} \end{array} \!\!\right]\left\{ \!\! \begin{array}{c} \ddot{\pmb u} \\ \ddot{\pmb v} \end{array} \!\! \right\} + \left[\!\! \begin{array}{cc} {\pmb K}_{uu} & {\pmb K}_{uv} \\ {\pmb K}_{vu} & {\pmb K}_{vv} \end{array} \!\! \right]\left\{ \!\! \begin{array}{c} {\pmb u} \\ {\pmb v} \end{array}\!\! \right\} = {\bf 0} $$

对于裂纹状缺陷,单元质量矩阵及单元刚度矩阵的具体求解可参见文献^[34].

文中仅需求解结构若干阶低频率及其相应的振型,采用以迭代法为基础的"直接滤频法"进行频率和振型的求解.

3 多缺陷反演分析模型

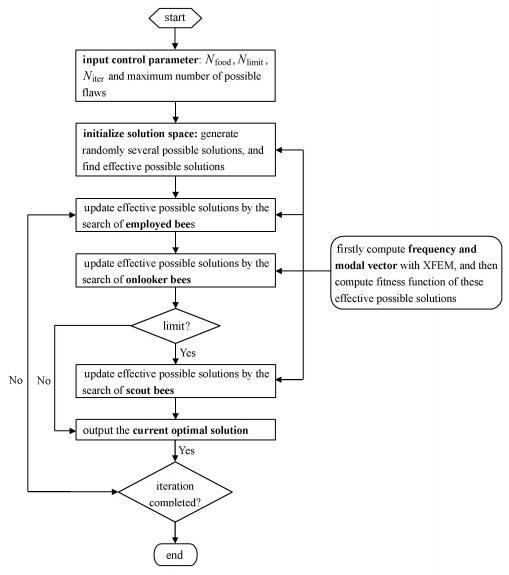
在频域内动力XFEM中扩充人工蜂群算法反演最佳的模型参数. 人工蜂群算法的适应度函数值$f\left( {\pmb \theta } \right)$取为目标函数$O\left( {\pmb \theta } \right)$的倒数,即

(27)$$ f\left( {\pmb \theta} \right) = 1 / {O\left( {\pmb \theta } \right)} $$

人工蜂群智能优化算法中主要有3个控制参数：蜜源的数量($N_{food}$)、优化极值不变的最大搜索限定次数($N_{ limit}$)和最大迭代次数($N_{iter}$),算法的具体流程可参见文献^[22]. 该优化算法首先在解空间生成大量的随机样本(可能解),在初始生成的可能解中,会有较多的无效可能解,主要包括下面3种类型的无效解：(1)可能解中拓扑变量均为0,相当于无缺陷情况,(2)可能解中有缺陷超出结构的边界,(3)可能解中缺陷有交叉,上述3种情况下的可能解均为无效解,无需计算其适应度函数,可直接排除;随后通过蜜蜂的搜索行为(采蜜蜂搜索阶段、观察蜂搜索阶段、侦察蜂搜索阶段)不断地更新有效可能解的质量,最终寻找到最优解. 在最优解的搜索过程中,利用XFEM计算适应度函数值来衡量有效可能解的质量. 多缺陷反演分析流程如图3所示.

图3

新窗口打开|下载原图ZIP|生成PPT
图3多缺陷反演分析流程图

Fig. 3Identified processes of multiple flaws

4 数值算例

4.1 两个圆形缺陷的反演

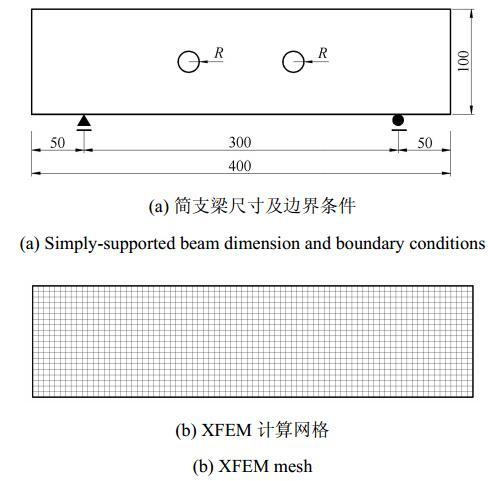
如图4(a)为含两个圆形缺陷的简支梁,梁的长度为400 mm,宽度100 mm. 数值计算时,假设简支梁处于平面应力状态,简支梁被离散成20$\times $80的均匀网格(图4(b)). 基体的弹性模量$E =22$ GPa,泊松比 $\nu =0.167$. 真实结构的前5阶频率值和对应的模态向量通过XFEM数值解得到.

图4

新窗口打开|下载原图ZIP|生成PPT
图4简支梁及XFEM计算网格

Fig. 4Simply-supported beam and XFEM mesh

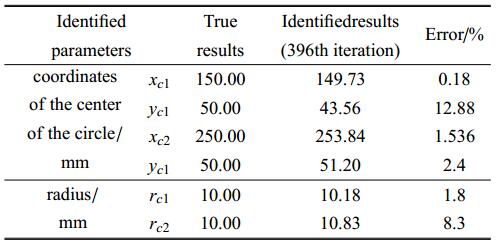
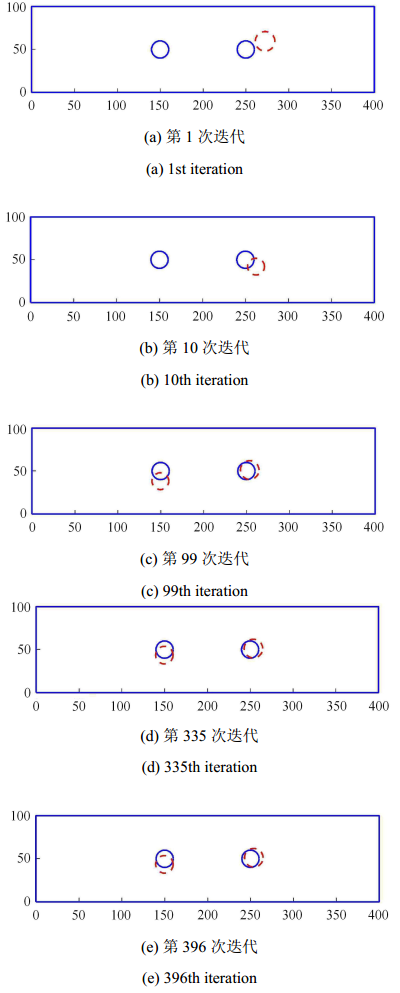
每个圆形缺陷有4个待反演参数,圆心坐标$\left( {x_{c} ,y_{c} } \right)$、圆的半径$r_{c}$及拓扑变量$\kappa $,则两个圆形缺陷共有8个待反演参数. 反演分析时,蜜源的数量$N_{ food}=100$,优化极值不变的最大搜索限定次数$N_{limit}=5$,最大迭代次数$N_{iter}=400$. 待反演参数的限值为$x_{c} \in \left[ {50} \ \ {350} \right]$,$y_{c} \in \left[ {10} \ \ {90} \right]$,$r_{c} \in \left[ 1 \ \ {20} \right]$,$\kappa \in \left[ 0 \ \ 1 \right]$,假定结构中可能存在的最大缺陷数目为4. 表1给出了迭代至396步时圆形缺陷的最终反演结果及相应的误差,图5给出了两个圆形缺陷的反演过程,从图中可以看出, 建立的反演分析模型能够较为准确地探测出圆形缺陷的数量、大小和位置.

Table 1
表1
表1两个圆形缺陷的反演结果
Table 1Identified results of two circular flaws

新窗口打开|下载CSV

图5

新窗口打开|下载原图ZIP|生成PPT
图5两个圆形缺陷的反演过程

Fig. 5Identified processes of two circular flaws

4.2 两个椭圆形缺陷的反演

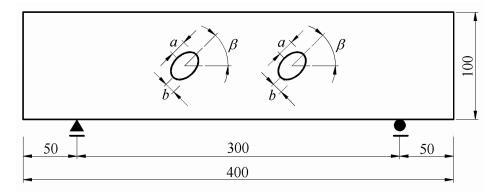
本算例简支梁的尺寸及边界条件同算例4.1,但梁内部含两个椭圆形缺陷,如图6所示. 数值计算时,梁的计算网格、材料参数等亦同算例4.1. 真实结构的前5阶频率值和对应的模态向量通过XFEM数值解得到.

图6

新窗口打开|下载原图ZIP|生成PPT
图6含两个椭圆形缺陷的简支梁

Fig. 6Simply-supported beam with two elliptical flaws

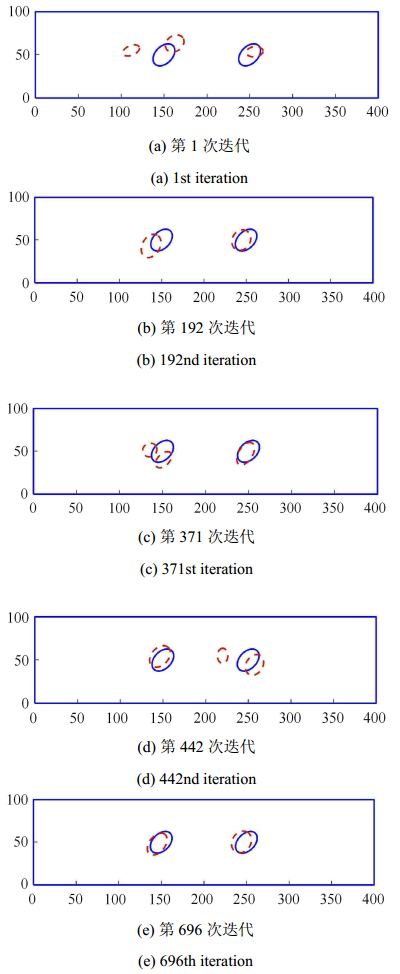
每个椭圆形缺陷有6个待反演参数,椭圆中心点坐标$\left( {x_{e} ,y_{e} } \right)$、椭圆长半轴$a$、椭圆短半轴$b$及椭圆倾角$\beta $及拓扑变量$\kappa $,则两个椭圆形缺陷共有12个待反演参数. 反演分析时,蜜源的数量$N_{ food}=100$,优化极值不变的最大搜索限定次数$N_{limit}=5$,最大迭代次数$N_{iter}=700$. 待反演参数的限值为$x_{e} \in \left[ {50} \ \ {350} \right]$,$y_{e} \in \left[ {10} \ \ {90} \right]$,$a \in \left[ 5 \ \ {20} \right]$,$b \in \left[ 5 \ \ {20} \right]$,$\beta \in \left[ 0 \ \ {90} \right]$,$\kappa \in \left[ 0 \ \ 1 \right]$,假定结构中可能存在的最大缺陷数目为4. 表2给出了迭代至696步时椭圆形缺陷的最终反演结果及相应的误差,图7给出了两个椭圆形缺陷的反演过程,从图中可以看出,建立的反演分析模型能够较为准确地探测出椭圆形缺陷的数量、大小和位置.

Table 2
表2
表2两个椭圆形缺陷的反演结果
Table 2Identified results of two elliptical flaws

新窗口打开|下载CSV

图7

新窗口打开|下载原图ZIP|生成PPT
图7两个椭圆形缺陷的反演过程

Fig. 7Identified processes of two elliptical flaws

4.3 两个裂纹的反演

本算例简支梁的尺寸及边界条件同算例4.1,但梁内部含两条裂纹状缺陷,如图8所示. 数值计算时,梁的计算网格、材料参数等亦同算例4.1. 真实结构的前5阶频率值和对应的模态向量通过XFEM数值解得到.

图8

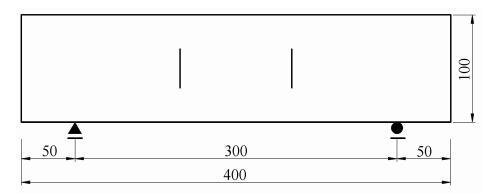
新窗口打开|下载原图ZIP|生成PPT
图8含两条裂纹状缺陷的简支梁

Fig. 8Simply-supported beam with two cracks

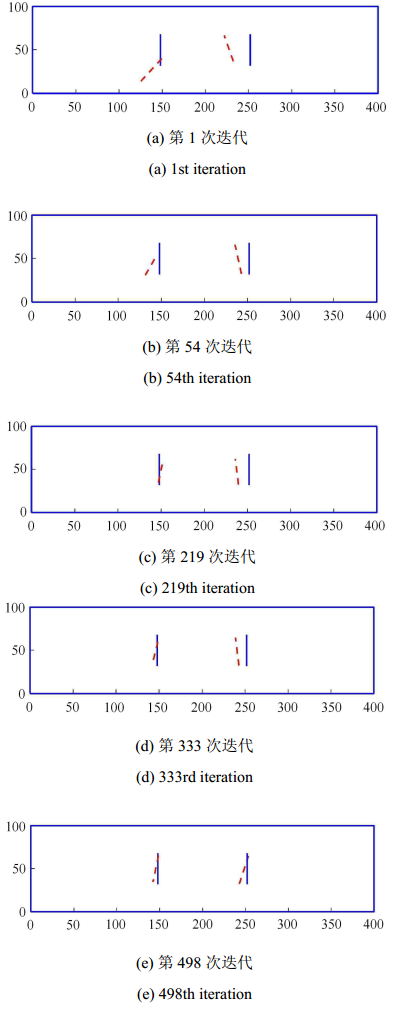
每个裂纹有5个待反演参数,裂纹起点坐标$\left( {x_{s} ,y_{s} } \right)$、裂纹终点坐标$\left( {x_{e} ,y_{e} } \right)$及拓扑变量$\kappa $,则两个裂纹共有10个待反演参数. 反演分析时,蜜源的数量$N_{ food}=100$,优化极值不变的最大搜索限定次数$N_{limit}=5$,最大迭代次数$N_{iter}=500$. 待反演参数限值为$x_{s} , x_{e} \in \left[ {20} \ \ {380} \right]$,$y_{s} , y_{e} \in \left[ {10} \ \ {90} \right]$,$\kappa \in \left[ 0 \ \ 1 \right]$,假定结构中可能存在的最大缺陷数目为4. 表3给出了迭代至498步时裂纹的最终反演结果及相应的误差, 图9给出了两个裂纹的反演过程,从图中可以看出,建立的反演分析模型能够较为准确地探测出结构内部裂纹的数量、大小和位置.

Table 3
表3
表3两个裂纹的反演结果
Table 3Identified results of two cracks

新窗口打开|下载CSV

图9

新窗口打开|下载原图ZIP|生成PPT
图9两个裂纹状缺陷的反演过程

Fig. 9Identified processes of two cracks

4.4 鲁棒性分析

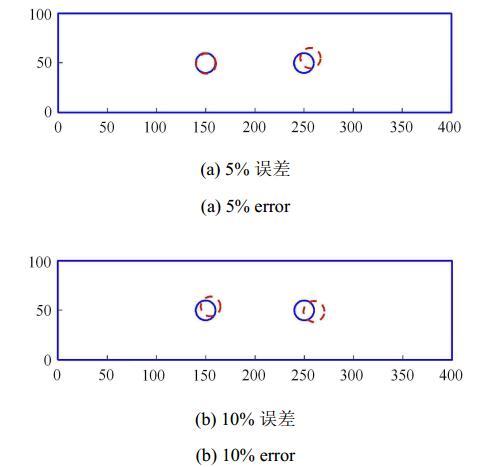
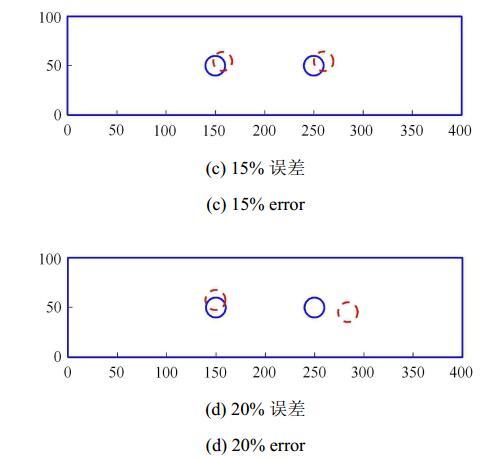
实际问题中,所测得的信号与真实值相比通常存在一定误差,本算例研究了算法在传感器测得值有一定误差情况下的适定性问题. 本算例同算例4.1,只是在通过XFEM数值解得到的结构实际响应值的基础上分别引入5%, 10%, 20%的人工测量误差,以探讨测量误差对反演结果的影响,验证算法的鲁棒性. 在相同迭代次数下,不同误差下的反演结果如图10所示,从图中可以得出,算法的鲁棒性较好,但是当误差过大(本算例为20%)时, 反演得到的缺陷位置将出现较大偏差.

图10

新窗口打开|下载原图ZIP|生成PPT
图10不同误差下的反演结果

Fig. 10Identified results under different degrees of error

图10

新窗口打开|下载原图ZIP|生成PPT
图10不同误差下的反演结果(续)

Fig. 10Identified results under different degrees of error (continued)

5 结论

相比于静响应,结构的动力特性(频率、振型)等在实际问题中较易通过传感器采集得到,文中基于频率残差和模态保证准则构建了反演分析模型的目标函数,并结合频域内动力扩展有限元法和人工蜂群智能优化算法的优点,同时,通过引入拓扑变量,将缺陷的数量纳入到反演分析过程中,建立了结构内部多缺陷的反演分析模型,为实际结构的无损检测技术提供了一条新的途径.

通过若干算例的分析表明：建立的反演分析模型能够较为准确地探测出结构内部圆形、椭圆形、裂纹状缺陷的数量、位置及大小. 文中反演的缺陷类型虽然为孔洞和裂纹,但相关理论可推广应用于夹杂问题的反演分析.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Ortiz

, Pandolfi

. Finite-deformation irreversible cohesive elements for three-dimensional crack-propagation analysis
International Journal for Numerical Methods in Engineering, 1999,44(9):1267-1282

DOI URL [本文引用: 1]

[2]

Nishioka

, Tokudome

, Kinoshita

. Dynamic fracture-path prediction in impact fracture phenomena using moving finite element method based on Delaunay automatic mesh generation
International Journal of Solids and Structures, 2001,38:5273-5301

DOI URL

[3]

Bouchard

, Bay

, Chastel

. Numerical modelling of crack propagation: Automatic remeshing and comparison of different criteria
Computer Methods in Applied Mechanics & Engineering, 2003,192:3887-3908

[本文引用: 1]

[4]

Belytschko

, Lu

, Gu

. Element-free Galerkin methods
International Journal for Numerical Methods in Engineering, 1994,37:229-256

DOI URL [本文引用: 1]

[5]

Rabczuk

, Belytschko

. Cracking particles: A simplified meshfree method for arbitrary evolving cracks
International Journal for Numerical Methods in Engineering, 2014,61:2316-2343

[本文引用: 1]

[6]

Rabczuk

, Areias

PMA

, Belytschko

. A simplified mesh-free method for shear bands with cohesive surfaces
International Journal for Numerical Methods in Engineering, 2007,69:993-1021

DOI URL

[7]

, Augarde

. An adaptive cracking particle method for 2D crack propagation
International Journal for Numerical Methods in Engineering, 2016,108(2):1626-1648

DOI URL [本文引用: 1]

[8]

江守燕, 李云, 杜成斌 . 改进型扩展比例边界有限元法
力学学报, 2019,51(1):278-288

[本文引用: 1]

( Jiang

Shouyan

, Li

Yun

, Du

Chengbin

. Improved extended scaled boundary finite element methods
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(61):278-288 (in Chinese))

[本文引用: 1]

[9]

陈楷, 邹德高, 孔宪京等. 多边形比例边界有限单元非线性化方法及应用
浙江大学学报(工学版), 2017,51(10):1996-2004

( Chen

Kai

, Zou

Degao

, Kong

Xianjing

, et al. Novel nonlinear polygon scaled boundary finite element method and its application
Journal of Zhejiang University (Engineering Science), 2017,51(10):1996-2004 (in Chinese))

[10]

章鹏, 杜成斌, 江守燕 . 比例边界有限元法求解裂纹面接触问题
力学学报, 2017,49(6):1335-1347

( Zhang

Peng

, Du

Chengbin

, Jiang

Shouyan

. Crack face contact problem analysis using the scaled boundary finite element method
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(6):1335-1347(in Chinese))

[11]

钟红, 暴艳利, 林皋 . 基于多边形比例边界有限元的重力坝裂缝扩展过程模拟
水利学报, 2014,45(S1):30-37

[本文引用: 1]

( Zhong

Hong

, Bao

Yanli

, Lin

Gao

. Modelling of crack propagation of gravity dams based on scaled boundary polygons
Journal of Hydraulic Engineering, 2014,45(S1):30-37 (in Chinese))

[本文引用: 1]

[12]

徐栋栋, 郑宏, 杨永涛等. 多裂纹扩展的数值流形法
力学学报, 2015,47(3):471-481

DOI Magsci [本文引用: 1]

数值流形法的求解体系建立在两套覆盖(包括数学覆盖和物理覆盖) 和接触环路的基础之上,实现了对连续和非连续问题的统一求解. 在处理裂纹问题时,数学覆盖无需与裂纹重合,方便岩体破坏过程的模拟. 通过在裂纹尖端影响区域内的物理片上增加用于模拟应力奇异性的增强位移函数,发展了扩展的数值流形法. 在此基础上,提出一种多裂纹扩展的控制算法,并给出了裂纹扩展过程中材料体的整体响应. 针对典型的线弹性断裂力学问题, 给出的数值算例表明所建议的方法是正确有效的.

( Xu

Dongdong

, Zheng

Hong

, Yang

Yongtao

. Multiple crack propagation based on the numerical manifold method
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(3):471-481 (in Chinese))

DOI Magsci [本文引用: 1]

杨永涛, 徐栋栋, 郑宏 . 动载下裂纹应力强度因子计算的数值流形元法
力学学报, 2014,46(5):730-738

DOI Magsci [本文引用: 1]

<p>相较于传统有限元，数值流形方法（numerical manifold method， NMM）的一个显著优点是在处理裂纹问题时网格无需与裂纹重合，这就方便了岩体破坏过程的模拟. 基于包含裂尖增强函数的NMM，采用Newmark 隐式动力学算法进行时间积分，重点研究了动力载荷条件下裂纹动态应力强度因子（dynamic stress intensity factor，DSIF）的求解方法. 针对典型的线弹性动力裂纹问题，给出了NMM 的数值算例. 结果表明NMM 能够准确计算动载荷条件下裂纹的DSIF，并且具有较好的收敛性.</p>

( Yang

Yongtao

, Xu

Dongdong

, Zheng

Hong

. Evaluation on stress intensity factor of crack under dynamic load using numerical manifold method
Chinese Journal of Theoretical and Applied Mechanics, 2014,46(5):730-738 (in Chinese))

DOI Magsci [本文引用: 1]

文龙飞, 王理想, 田荣 . 动载下裂纹应力强度因子计算的改进型扩展有限元法
力学学报, 2018,50(3):599-610

[本文引用: 1]

( Wen

Longfei

, Wang

Lixiang

, Tian

Rong

. Accrate computation on dynamic SIFs using improved XFEM
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):599-610 (in Chinese))

[本文引用: 1]

[15]

刘学聪, 章青, 夏晓舟 . 一种新型裂尖加强函数的显式动态扩展有限元法
工程力学, 2017,34(10):10-18

[本文引用: 1]

( Liu

Xuecong

, Zhang

Qing

, Xia

Xiaozhou

. A new enrichment function of crack tip in XFEM dynamics by explicit time algorithm
Engineering Mechanics, 2017,34(10):10-18 (in Chinese))

[本文引用: 1]

[16]

Osher

, Sethian

. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations
Journal of Computational Physics, 1988,79(1):12-49

DOI URL [本文引用: 1]

[17]

Rabinovich

, Givoli

, Vigdergauz

. Crack identification by 'arrival time' using XFEM and a genetic algorithm
International Journal for Numerical Methods in Engineering, 2009,77(3):337-359

DOI URL [本文引用: 2]

[18]

Waisman

, Chatzi

, Smyth

. Detection and quantification of flaws in structures by the extended finite element method and genetic algorithms
International Journal for Numerical Methods in Engineering, 2010,82(3):303-328

[本文引用: 1]

[19]

Chatzi

, Hiriyur

, Waisman

, et al. Experimental application and enhancement of the XFEM-GA algorithm for the detection of flaws in structures
Computers & Structures, 2011,89(7-8):556-570

[本文引用: 1]

[20]

Nanthakumar

, Lahmer

, Rabczuk

. Detection of flaws in piezoelectric structures using extended FEM
International Journal for Numerical Methods in Engineering, 2013,96:373-389

DOI URL [本文引用: 1]

[21]

Sun

, Waisman

, Betti

. A multiscale flaw detection algorithm based on XFEM
International Journal for Numerical Methods in Engineering, 2014,100:477-503

DOI URL [本文引用: 1]

[22]

江守燕, 杜成斌 . 基于扩展有限元的结构内部缺陷(夹杂)的反演分析模型
力学学报, 2015,47(6):1037-1045

DOI Magsci [本文引用: 2]

<p>传统的结构检测方法一般需要钻孔取样,对结构本身有一定的破坏作用,而无损检测方法在检测过程中不破坏结构本身,这项技术的重要性日益显著. 结合扩展有限元法和人工蜂群智能优化算法的优点,建立了结构内部缺陷(夹杂)的反演分析模型,为结构的无损检测技术提供了一条新的途径.扩展有限元法通过引入非连续位移模式可以在不重新划分网格的情况下通过改变水平集函数反映缺陷(夹杂)的位置及大小,避免了反演分析每次迭代过程中的网格重剖分,人工蜂群智能优化算法在每次迭代中都采用全局和局部搜索,找到最优解的概率大大增加并可很好地避免局部最优,因此,扩展有限元法与人工蜂群智能优化算法的结合有效地减少了反演分析的计算工作量. 通过若干算例的分析表明:建立的反演分析模型能准确地探测结构内部存在的单个缺陷(夹杂).</p>

( Jiang

Shouyan

, Du

Chengbin

. Numerical model for identification of internal defect or inclusion based on extended finite elememt methods
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(6):1037-1045 (in Chinese))

DOI Magsci [本文引用: 2]

Zhao

, Du

, Jiang

. An adaptive multiscale approach for identifying multiple flaws based on XFEM and a discrete artificial fish swarm algorithm
Computer Methods in Applied Mechanics & Engineering, 2018,339:341-357

[本文引用: 1]

[24]

, Yu

, Van Lich

, et al. An effective computational approach based on XFEM and a novel three-step detection algorithm for multiple complex flaw clusters
Computers & Structures, 2017,193:207-225

[本文引用: 1]

[25]

Jung

, Jeong

, Taciroglu

. Identification of a scatterer embedded in elastic heterogeneous media using dynamic XFEM
Computer Methods in Applied Mechanics & Engineering, 2013,259:50-63

[本文引用: 1]

[26]

Zhang

, Nanthakumar

, Lahmer

, et al. Multiple cracks identification for piezoelectric structures
International Journal of Fracture, 2017,206(2):151-169

DOI URL [本文引用: 1]

[27]

Zhang

, Wang

, Lahmer

, et al. A dynamic XFEM formulation for crack identification
International Journal of Mechanics & Materials in Design, 2016,12:427-448

[本文引用: 1]

[28]

朱宏平, 余璟, 张俊兵 . 结构损伤动力检测与健康监测研究现状与展望
工程力学, 2011,28(2):1-11

Magsci [本文引用: 1]

基于动力特性的结构损伤检测方法在过去几十年中得到了迅猛发展。该技术的核心思想在于结构的振动特性(比如频率、振型、模态阻尼等)是结构物理参数(如质量、阻尼和刚度)的函数，结构损伤即意味着结构物理参数的改变，而物理参数的改变必然引起结构振动特性的改变。该文介绍了结构健康监测与损伤动力检测方法的涵义、应用现状和分类方法。对基于动力特性的结构损伤检测方法和识别算法做了重点介绍，分析了各种方法的优点和不足之处。最后对有待进一步研究的问题和结构损伤检测方法发展趋势进行了展望。

( Zhu

Hongping

, Yu

Jing

, Zhang

Junbing

. A summary review and advantages of vibration-based damage identification methods in structural health monitoring
Engineering Mechanics, 2011,28(2):1-11 (in Chinese))

Magsci [本文引用: 1]

Wahalathantri

, Thambiratnam

, Chan

THT

, et al. Vibration based baseline updating method to localize crack formation and propagation in reinforced concrete members
Journal of Sound & Vibration, 2015,344:258-276

[本文引用: 1]

[30]

Bui

, Mommessin

, Perrotin

, et al. Assessing local-scale damage in reinforced concrete frame structures using dynamic measurements
Engineering Structures, 2014,79:22-31

DOI URL [本文引用: 1]

[31]

, Yang

, Loh

. A finite-element based damage detection technique for nonlinear reinforced concrete structures
Structural Control and Health Monitoring, 2015,22:1223-1239

DOI URL

[32]

Pesic

, Zivanovic

, Dennis

, et al. Experimental and finite element dynamic analysis of incrementally loaded reinforced concrete structures
Engineering Structures, 2015,103:15-27

DOI URL [本文引用: 2]

[33]

Stolarska

, Chopp

, Mo?s

, et al. Modelling crack growth by level sets in the extended finite element method
International Journal for Numerical Methods in Engineering, 2001,51:943-960

DOI URL

[34]

江守燕, 杜成斌 . 动载下缝端应力强度因子计算的扩展有限元法
应用数学和力学, 2013,34(6):586-597

[本文引用: 2]

( Jiang

Shouyan

, Du

Chengbin

. Evaluation on stress intensity factors at the crack tip under dynamic loads using extended finite element methods
Applied Mathematics and Mechanics, 2013,34(6):586-597 (in Chinese))

[本文引用: 2]