功能梯度球形水凝胶的化学力学耦合分析 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

杨健鹏^*^,^?, 王惠明^,^*^,^?^,²⁾

* 浙江大学工程力学系,杭州 310027

? 浙江大学浙江省软体机器人与智能器件研究重点实验室,杭州 310027

CHEMOMECHANICAL ANALYSIS OF A FUNCTIONALLY GRADED SPHERICAL HYDROGEL ¹⁾

Yang Jianpeng^*^,^?, Wang Huiming^,^*^,^?^,²⁾

* Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China

? Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, Zhejiang University, Hangzhou 310027, China

通讯作者: 2) 王惠明, 教授, 主要研究方向为智能软材料非线性力学等. E-mail:wanghuiming@zju.edu.cn

收稿日期:2019-01-14接受日期:2019-04-3网络出版日期:2019-07-18

基金资助:

1) 国家自然科学基金资助项目.11772296
国家自然科学基金资助项目.11621062

Received:2019-01-14Accepted:2019-04-3Online:2019-07-18
作者简介 About authors

摘要
作为一种新型智能材料,水凝胶具有特殊的化学力学耦合性能.采用功能梯度形式可使得水凝胶具有更好的适应性和可调控性.本研究中假设交联密度沿径向按幂函数规律变化,并基于水凝胶的大变形多场耦合一般理论,采用Flory-Huggins自由能函数,建立了功能梯度球形水凝胶在球对称情形的控制方程,并开展了功能梯度球形水凝胶在给定内压和化学势情行的非均匀大变形溶胀行为的理论研究.计算结果表明,不同梯度指数的球形水凝胶的内压、内孔半径曲线和内压、内表面径向伸长率曲线均呈现出一段稳定区间和另一段不稳定区间,说明内压超出某临界值会发生失稳并导致水凝胶的最终破坏.内压的临界值随梯度指数的增大而增大.研究表明,功能梯度球形水凝胶的材料参数(梯度指数、亲疏水特性、交联密度和溶剂分子的体积)和环境化学势对水凝胶溶胀行为具有重要的影响.在给定内表面压力的情况下,功能梯度球形水凝胶内表面的径向位移随梯度指数的改变接近为线性变化,而随其他参数的影响都呈现出明显的非线性.本研究有助于实现水凝胶智能结构和器件在复杂条件下的精准调控.}
关键词： 功能梯度水凝胶;化学力学耦合;溶胀行为;大变形;球对称

Abstract
As a kind of new smart materials, hydrogel has a special chemomechanical coupling effect. By using the functionally graded material, the adaptability and controllability of the hydrogel can be improved distinctly. In this analysis, the crosslink density of the hydrogel is assumed to be a power-law function of the radial position. By employing the general multi-field coupling large deformation theory and the Flory-Huggins free energy function, the governing equations of the functionally graded spherical hydrogel (FGSH) undergoing the spherically symmetric deformation are developed. The theoretical analysis of the swelling behavior accompanying the inhomogeneous large deformation is presented for the FGSH when subjected to the internal pressure and the prescribed chemical potential. Numerical results show that both the internal pressure-internal radius curve and the internal pressure-radial stretch curve exhibit a stable region and an unstable region, which means that if the internal pressure exceeds a certain critical value, the instability will occur and the hydrogel will finally be damaged. The critical value of the internal pressure increases with the increasing of gradient index. It is shown that the material parameters, such as gradient index, the interaction parameter between the polymer network and the solvent, the cross-link density and the volume of the solvent molecular, and the environmental chemical potential have a significant effect on the swelling behavior of the FGSH. If the internal pressure is fixed, the radial displacement of FGSH at the internal surface is nearly linear with respect to the gradient index, while it appears obvious nonlinear to other parameters. The investigation is helpful to realize the precise control of the hydrogel-based smart structures and devices under the complex environments.
Keywords：functionally graded hydrogel;chemomechanical coupling;swelling behavior;large deformation;spherical symmetry

PDF (4425KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
杨健鹏, 王惠明. 功能梯度球形水凝胶的化学力学耦合分析 ¹⁾. 力学学报[J], 2019, 51(4): 1054-1063 DOI:10.6052/0459-1879-19-019
Yang Jianpeng, Wang Huiming. CHEMOMECHANICAL ANALYSIS OF A FUNCTIONALLY GRADED SPHERICAL HYDROGEL ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(4): 1054-1063 DOI:10.6052/0459-1879-19-019

引言

水凝胶是由物理或者化学交联方式形成的高分子网络通过吸入外界环境中的水分子形成的^[1-2],表现为性质柔软且能对外部的刺激通过吸收或释放大量的水而产生显著的响应.水凝胶由于具有良好的刺激响应性、生物相容性、可降解性、成本低等特性^[2-4],已被应用到很多领域,比如药物运输、组织工程学、刺激敏感制动器、软体机器人以及微型阀等^[5-6].在诸多工程实际中,水凝胶的溶胀特性对器件功能起到了关键作用^[7-9],因此,发展能够描述水凝胶溶胀行为的理论和模拟方法,近年来已受到广泛关注^[10-12].

水凝胶的化学力学耦合行为可在不同的外界刺激下发生,如湿度^[13-14]、温度^[15-17]、机械载荷^[18-19]、离子浓度^[20]、电场^[21]等,这种响应宏观上表现为水凝胶的溶胀和收缩,且变形都比较大,属于非线性大变形问题.近年来,关于水凝胶溶胀行为的理论和数值研究都取得了很大的进展,代表性的工作有Hong等^[10]建立了用于描述高分子水凝胶中水分子输运和大变形的耦合行为的一般理论.基于水凝胶的有限变形理论,已取得不少研究成果,如内含刚性核的球型单层和双层凝胶的溶胀分析^[22-23],水凝胶内的空穴行为分析^[14,24]等.Dai和Song^[25]利用摄动法给出了水凝胶球壳在平衡态的半解析解.此外,Liu等^[26]建立了水凝胶在不同环境激励下的快速均匀扩散理论,并开展了实验研究.

功能梯度材料是一种内部组成成分呈梯度变化的复合材料,功能梯度的引入可显著增强材料的性能,以适应复杂的应用环境或满足特殊的应用,相关的研究得到了许多专家****的专注^[27-29].为了使水凝胶具有更好的性能,科研工作者将功能梯度结构引入到水凝胶中^[30-31].Guvendiren等^[32]实验研究了交联密度沿厚度方向变化的水凝胶薄膜表面失稳图案的动态演化.Wu等^[33]理论研究了交联密度沿厚度方向按指数函数规律变化的水凝胶薄层因溶胀引起的表面失稳.本文研究功能梯度水凝胶球壳在内压和化学势共同作用下的溶胀行为.功能梯度的形式假设为在干状态下,水凝胶的交联密度沿径向按幂函数规律变化^[34].建立了功能梯度球形水凝胶在球对称非均匀变形的控制方程,运用打靶法得到给定边值问题的解,并完成了参数分析.

1 力学模型及基本方程

球形水凝胶在内压和化学势共同作用下的力学模型如图1所示.在干的状态(化学势$\mu =-\infty)$,球形水凝胶的内外半径分别为$A$和$B$,如图1(a)所示.球形水凝胶在内压$p$和对应化学势为$\mu$的水溶剂环境中,溶胀至平衡状态,此时球形水凝胶的内外半径分别为$a$和$b$,如图1(b).对于均匀的水凝胶在自由溶胀情形,达到平衡状态时,水凝胶将发生均匀变形.而对于功能梯度水凝胶,由于材料的不均匀特性,将产生不均匀的溶胀.同时在水凝胶的球形空腔中施加压力$p$,达到平衡状态时,水凝胶将产生不均匀的球对称变形.

图1

新窗口打开|下载原图ZIP|生成PPT
图1球壳形水凝胶在内压和化学势共同作用下的力学模型

Fig. 1Mechanical model of a spherical hydrogel subjected to chemomechanical loadings

取干状态下的水凝胶为参考状态,考察距离中心为$R$的物质点,将随着水凝胶的变形而移动至距离中心为$r$的点处. 定义环向伸长率为\begin{equation} \label{eq1} \lambda _\theta = r / R(1) \end{equation}取径向两个相邻的物质点,参考状态下距中心距离分别为$R$与$R+{ d}R$,最终达到平衡状态之后的位置分别为$r(R)$与$r(R+{ d}R)$,则径向伸长率为 \begin{equation} \label{eq2} \lambda _r = \frac{r\left( {R + \mbox{d}R} \right)-r\left( R \right)}{\left( {R + \mbox{d}R} \right)-R} = \mbox{d}r\mbox{/d}R(2) \end{equation}

假设在溶胀的过程中,水分子和水凝胶高分子网络是不可压缩的,即有 \begin{equation} \label{eq3} 1 + \nu C = \lambda _r \lambda _\theta ^2(3) \end{equation} 其中,$v$是单个水分子的体积,$C$为平衡状态下水分子的浓度.

记$S_{\theta }(R)$和$ S_{r}(R)$分别为环向和径向的名义应力,则球对称问题的平衡方程为 \begin{equation} \label{eq4} \frac{\mbox{d}S_r }{\mbox{d}R} + 2\frac{S_r -S_\theta }{R} = 0(4) \end{equation}

功能梯度材料的力学性能在空间上呈连续变化. 本研究中,假设单位体积的聚合物分子链的数量沿半径方向按幂函数规律变化^[30],即 \begin{equation} \label{eq5} N = N_0 \left( {R / A} \right)^\alpha(5) \end{equation} 式中$\alpha $为梯度指数. 特别地,当$\alpha =0$时即为均匀水凝胶. $N_{0}$为内表面层的单位体积聚合物分子链的数量.

采用Flory和Rehner的自由能^[10,35],可写出状态方程为

(6)$$ \left.\begin{array}{l} \frac{S_r }{N_0 kT} = \left ( {R/A} \right)^\alpha \left( {\lambda _r-\lambda _r^{-1} } \right) + \frac{\lambda _\theta ^2 }{\nu N_0 }\cdot \left[ {\mbox{ln}\left( {\frac{\nu C}{1 + \nu C}} \right)} \right. + \\ \qquad \left. {\frac{1}{1 + \nu C} + \frac{\chi }{\left( {1 + \nu C} \right)^2}-\frac{\mu }{kT}} \right] \\ \frac{S_\theta }{N_0 kT} = \left( {R/A} \right)^\alpha \left( {\lambda _\theta -\lambda _\theta ^{-1} } \right)+ \frac{\lambda _\theta \lambda _r }{\nu N_0 }\cdot \left[ {\mbox{ln}\left( {\frac{\nu C}{1+\nu C}} \right)} \right. + \\ \qquad \left. {\frac{1}{1 + \nu C} + \frac{\chi }{\left( {1 + \nu C} \right)^2}-\frac{\mu }{kT}} \right] \end{array}\right\}$$

其中,$k$是玻尔兹曼常数,$T$是绝对温度. $\chi$是关于混合焓的无量纲参数,表征水凝胶高分子网络的亲疏水特征.对于好的溶剂,$\chi $的取值范围为0.1~0.5^[22].$N_{0}\nu$是关于聚合物网络弹性性能的无量纲参数,通常取值范围为^[22]10$^{-2}\sim10^{-5}$. $\mu$为化学势,与环境相对湿度$RH$间的关系为$\mu =kT\ln(RH)$^[13].

记环向和径向的真实应力为$\sigma_{\theta }(R)$和$\sigma _{r}(R)$,有

(7)$$ \left.\begin{array}{l} \frac{\sigma _r }{N_0 kT} = \left ( {R/A} \right)^\alpha \left( {\frac{\lambda _r }{\lambda _\theta ^2 }-\frac{1}{\lambda _r \lambda _\theta ^2 }} \right)+\frac{1}{\nu N_0 }\cdot \\[4mm] \qquad \left[ {\mbox{ln}\left( {\frac{\nu C}{1+\nu C}} \right)+\frac{1}{1+\nu C}+\frac{\chi }{\left( {1+\nu C} \right)^2}-\frac{\mu }{kT}} \right] \\[4mm] \frac{\sigma _\theta }{N_0 kT} = \left( {R/A} \right)^\alpha \left( {\lambda _r^{-1} -\frac{1}{\lambda _r \lambda _\theta ^2 }} \right) + \frac{1}{\nu N_0 }\cdot \\[4mm] \qquad \left[ {\mbox{ln}\left( {\frac{\nu C}{1+\nu C}} \right)+\frac{1}{1+\nu C}+\frac{\chi }{\left( {1+\nu C} \right)^2}-\frac{\mu }{kT}} \right] \\ \end{array}\right\}$$

当外表面自由,受内压$p$作用情形,边界条件为

(8)$$ \left.\begin{array}{ll} R = A: & \sigma _r =-p\\ R = B: & \sigma _r = 0\\ \end{array}\right\} $$

2 求解方法

为方便起见,引入以下无量纲参数

(9)$$ \left.\begin{array}{l} r^\ast =\frac{r}{A},\mu ^\ast =\frac{\mu }{kT},p^\ast =\frac{p}{N_0 kT},\zeta =\frac{R}{A},R_t =\frac{B}{A}\\[4mm] S_\theta ^\ast =\frac{S_\theta }{N_0 kT},S_r^\ast =\frac{S_r }{N_0 kT},\sigma _\theta ^\ast =\frac{\sigma _\theta }{N_0 kT},\sigma _r^\ast =\frac{\sigma _r }{N_0 kT}\end{array}\right\} $$

利用式(9),式(1)、式(2)和式(4)可改写为

$$\begin{align*} &\lambda _\theta = \frac{r^\ast }{\zeta }(10)\\ &\frac{\mbox{d}r^\ast }{\mbox{d}\zeta } = \lambda _r(11)\\ &\frac{\mbox{d}S_r^\ast }{\mbox{d}\zeta } + 2\frac{S_r^\ast-S_\theta ^\ast }{\zeta } = 0(12)\end{align*} $$

利用式(3)和式(9),式(6)~式(8)可改写为

(13)$$ \left.\begin{array}{l} S_r^\ast = \zeta ^\alpha \left ( {\lambda _r -\lambda _r^{-1} } \right)+\frac{\lambda _\theta ^2 }{\nu N_0 }\cdot \\[4mm] \qquad \left[ {\mbox{ln}\left( {\frac{\lambda _r \lambda _\theta ^2 -1}{\lambda _r \lambda _\theta ^2 }} \right)+\frac{1}{\lambda _r \lambda _\theta ^2 }+\frac{\chi }{\lambda _r ^2\lambda _\theta ^4 }-\mu ^\ast } \right] \\[4mm] S_\theta ^\ast = \zeta ^\alpha \left( {\lambda _\theta -\lambda _\theta ^{-1} } \right)+\frac{\lambda _\theta \lambda _r }{\nu N_0 }\cdot \\[4mm] \qquad \left[ {\mbox{ln}\left( {\frac{\lambda _r \lambda _\theta ^2 -1}{\lambda _r \lambda _\theta ^2 }} \right)+\frac{1}{\lambda _r \lambda _\theta ^2 }+\frac{\chi }{\lambda _r ^2\lambda _\theta ^4 }-\mu ^\ast } \right] \\ \end{array}\right\}$$

$$ \begin{align*} &\left.{\begin{array}{l} \sigma _r^\ast = \zeta ^\alpha \left( {\frac{\lambda _r }{\lambda _\theta ^2 }-\frac{1}{\lambda _r \lambda _\theta ^2 }} \right)+\frac{1}{\nu N_0 }\cdot \\ \qquad \left[ {\mbox{ln}\left( {\frac{\lambda _r \lambda _\theta ^2 -1}{\lambda _r \lambda _\theta ^2 }} \right)+\frac{1}{\lambda _r \lambda _\theta ^2 }+\frac{\chi }{\lambda _r ^2\lambda _\theta ^4 }-\mu ^\ast } \right] \\ \sigma _\theta ^\ast = \zeta ^\alpha \left( {\lambda _r^{-1} -\frac{1}{\lambda _r \lambda _\theta ^2 }} \right)+\frac{1}{\nu N_0 }\cdot \\ \qquad \left[ {\mbox{ln}\left( {\frac{\lambda _r \lambda _\theta ^2 -1}{\lambda _r \lambda _\theta ^2 }} \right)+\frac{1}{\lambda _r \lambda _\theta ^2 }+\frac{\chi }{\lambda _r ^2\lambda _\theta ^4 }-\mu ^\ast } \right] \end{array}}\right\}(14) \\ & \zeta = 1: \quad \sigma _r^\ast =-p^\ast(15a) \\ & \zeta = R_t : \quad \sigma _r^\ast = 0(15b)\end{align*} $$

利用式(13),可由平衡方程(12)导出如下方程 \begin{equation} \label{eq9} \mbox{d}\lambda _r \mbox{ / d}\zeta = F\left( {\zeta ,r^\ast ,\lambda _r } \right)(16) \end{equation} 式中

$$ \left.\begin{array}{l} F\left( {\zeta ,r^\ast ,\lambda _r } \right) = {\left[ {F_1 \left( {\zeta ,r^\ast ,\lambda _r } \right)-F_2 \left( {\zeta ,r^\ast ,\lambda _r } \right)} \right]} /{F_3 \left( {\zeta ,r^\ast ,\lambda _r } \right)} \\ F_1 \left( {\zeta ,r^\ast ,\lambda _r } \right)= 2\zeta ^{\alpha-1}\left(\frac{r^\ast }{\zeta }-\frac{\zeta }{r^\ast }-\lambda _r + \lambda _{_r }^{-1} \right)+ \\ \qquad 2\frac{r^\ast (\lambda _r-{r^\ast }/ \zeta )}{\zeta ^2vN_0 }G_1 \left( {\zeta ,r^\ast ,\lambda _r } \right)\\ F_2 \left( {\zeta ,r^\ast ,\lambda _r } \right)= \alpha \zeta ^{\alpha-1}\left( {\lambda _r-\lambda _r^{-1} } \right) + \\ \qquad \frac{2r^\ast (\zeta \lambda _r-r^\ast )}{\zeta ^3\nu N_0 }G_2 \left( {\zeta ,r^\ast ,\lambda _r } \right)\\ F_3 \left( {\zeta ,r^\ast ,\lambda _r } \right)= \zeta ^\alpha (1 + \lambda _r^{-2} ) + \frac{1}{\nu N_0 }\cdot \\ \qquad \left[ {\frac{(r^\ast )^2}{(r^\ast )^2\lambda _r^2-\lambda _r \zeta ^2}-\frac{1}{\lambda _r^2 }-\frac{2\chi \zeta ^2}{(r^\ast )^2\lambda _r^3 }} \right] \\ G_1 \left( {\zeta ,r^\ast ,\lambda _r } \right) = \ln \left[ {1 - \frac{\zeta ^2}{(r^\ast )^2\lambda _r }} \right] + \frac{\zeta ^2}{(r^\ast )^2\lambda _r } + \frac{\chi \zeta ^4}{(r^\ast )^4\lambda _r^2 } - \mu ^\ast \\ G_2 \left( {\zeta ,r^\ast ,\lambda _r } \right) = \ln \left[ {1-\frac{\zeta ^2}{(r^\ast )^2\lambda _r }} \right] + \frac{\zeta ^2}{(r^\ast )^2\lambda _r-\zeta ^2} - \\ \qquad \frac{\chi \zeta ^4}{(r^\ast )^4\lambda _r^2 }-\mu ^\ast \end{array}\!\!\right\}(17) $$

联立式(11)和式(16),得到关于$r^{\ast }$和$\lambda _{r}$的一阶非线性常微分方程组,可采用打靶法求解. 求解方法如下：先猜想一个内表面的径向位移$r^{\ast }\vert _{\zeta = 1}$,并由式(10)求得内表面的$\lambda _{\theta }\vert _{\zeta = 1}$. 再由内表面应力边界条件,即式(15a),结合径向真实应力的表达式,见式(14)的第一式,采用二分法, 可求得内表面的$\lambda _{r}\vert _{\zeta = 1}$. 在内表面的径向位移$r^{\ast }\vert _{\zeta = 1}$和$\lambda _{r}\vert _{\zeta = 1}$均已知时,可用Matlab软件的ODE45函数对关于$r^{\ast }$和$\lambda $$_{r}$的一阶非线性常微分方程组进行求解. 最后利用外表面的应力边界条件,即式(15b),进行判断,若满足指定的数值精度,即得到原问题的数值解. 否则,调整内表面的径向位移$r^{\ast }\vert _{\zeta = 1}$,重复上述计算,最终求得不同内压$p^{\ast }$作用下的一系列解.

需要指出的是,若内表面不受内压作用,即$p^{\ast }=0$,此时即为内外表面都是应力自由的溶胀问题. 由于功能梯度材料的不均匀特性,凝胶各部分的溶胀程度不相同,属于非均匀溶胀, 因此这种情形仍需采用打靶法进行求解. 特别地,若进一步有梯度指数$\alpha =0$,即退化为均匀水凝胶的情形,此时若内外表面都是应力自由的,则溶胀是均匀的,属于自由溶胀. 在溶胀达到平衡状态时,凝胶内部将保持零应力状态. 若此时记$\lambda _{\theta }=\lambda _{r}=\lambda _{0}$,结合零应力的条件,即$\sigma _{r}^{\ast}=0$或$\sigma _{\theta }^{\ast }=0$,可得到关于$\lambda _{0}$的非线性为代数方程^[18],可用二分法进行求解,得到自由溶胀情形的伸长率$\lambda _{0}$和水凝胶中水分子的无量纲浓度$\nu C_0 = \lambda _0^3-1$.

3 数值结果与分析

3.1 梯度指数$\alpha $的影响

取水凝胶的计算参数为$N_0v=0.001$, $\mu^\ast=0$, $\chi=0.5$和$Rt=5$. 图2给出了梯度指数分别为$\alpha=0.2$, 0和$-0.2$三种情形在内压作用下水凝胶球壳内表面径向位移和伸长率的响应曲线. 由于受内压作用,水凝胶内表面的变形比外表面大, 这里给出了功能梯度水凝胶内表面位移和伸长率随内压$p^\ast$变化的响应曲线.

图2(a)实线部分画出了梯度指数为$\alpha =0.2$时功能梯度水凝胶内表面无量纲径向位移(也即球壳的无量纲内半径$a/A)$对内压的响应曲线. 图中可以看到,曲线会出现一个极值点,即在内压小于某一临界值时,同一内压值会对应有两个$a/A$值. 梯度指数$\alpha =0$和$-0.2$的$p^{\ast }-a/A$曲线也同样存在一个极值点,这是因为本文采用的是neo-Hookean模型, 因此给出的曲线会呈现一段稳定区间和另一段不稳定区间. 当内表面径向位移小于极值点对应的临界值时,是稳定的,而当内表面径向位移大于极值点对应的临界值时, 是不稳定的. 当梯度指数$\alpha =0.2$时,如图2(a)实线所示,达到溶胀平衡状态($\mu ^{\ast }=0$)时,当$p^{\ast }=0$时,内表面无量纲径向位移$a/A=2.086$;当达到临界内压$p^{\ast }=0.875$时,内表面位移$a/A=6.743$. 即当内压的变化范围为$p^{\ast } \in [0, 0.875]$,稳定区间为$a/A \in [2.086, 6.743]$. 当内压超过临界值时,水凝胶的高分子网络会因为发生跃变失稳而最终导致破坏^[36-37].

图2

新窗口打开|下载原图ZIP|生成PPT
图2梯度指数$\alpha$对内压作用下功能梯度水凝胶球壳内表面响应的影响

Fig. 2Effect of the gradient index $\alpha $ on the responses at the internal surface for the internally pressurized, functionally graded spherical hydrogel

图2(b)实线部分画出了梯度指数$\alpha =0.2$时水凝胶径向伸长率对内压的响应曲线. 图中可以看到,在稳定区间内,内表面的径向伸长率$\lambda _{ra}$随内压的增大而减小. 由于$\lambda _{r}={d}r/{ d}R$,说明在内表面附近,当$R$增大时,$r$增大的量越来越小, 间接体现了更大的压力会使内表面附近的高分子网络受压更严重. 当内压为零时,内表面的径向伸长率$\lambda _{ra}=2.214$,环向伸长率$\lambda _{\theta a}=2.087$,两者的值并不相同,这一结果也证实了由于功能梯度材料的不均匀特性, 导致即使是在内外表面都是应力自由的情形,功能梯度水凝胶溶胀时的变形也是不均匀的.

当$\alpha >0$时,为正梯度指数的功能梯度水凝胶,当$\alpha =0$时,为均匀水凝胶,当$\alpha <0$时,为负梯度指数的功能梯度水凝胶. 从图2(a)和图2(b)可以看出,随着梯度指数的增大,临界内压值也随着增大,而且稳定区间有所扩大. 在给定内压$p$的情况下,梯度指数越大,稳定状态下水凝胶内表面的位移越小, 而径向伸长率的变化规律则正好相反. 梯度指数$\alpha $与单位体积聚合物链的数量有关. 当$\alpha $增大时,与弹性模量和剪切模量相关的两个参数：$\nu N_{0}(R/A)^{\alpha }$和$N_{0}(R/A)^{\alpha }kT$,都会沿径向方向梯度增大,这会使聚合物网络更不易发生变形.

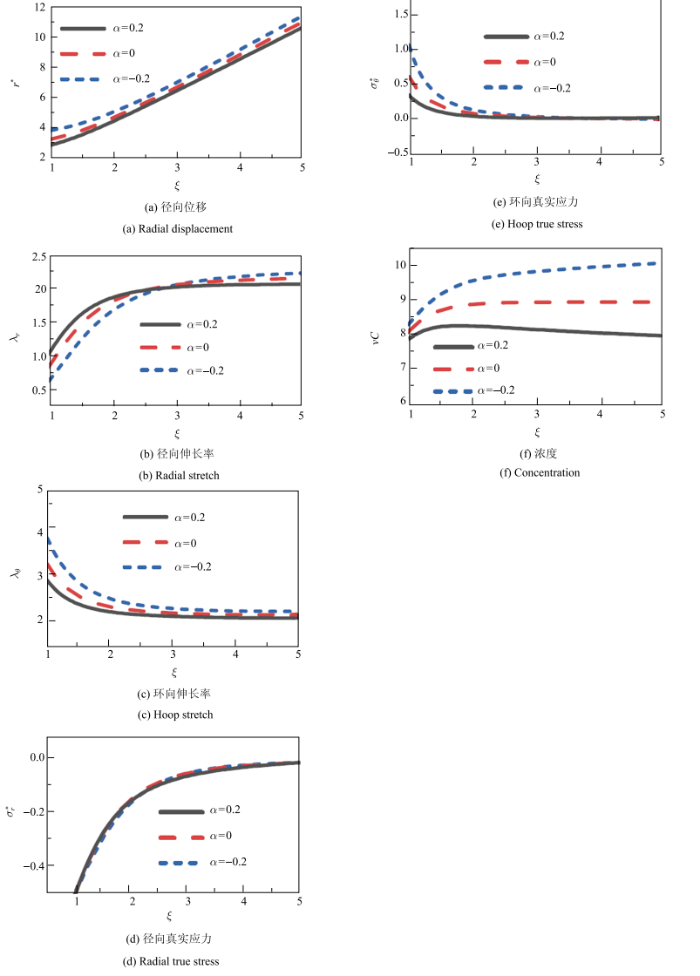
图3给出了在给定内压$p$情况下功能梯度水凝胶球壳内的弹性场和浓度场的分布图. 计算参数取为$p^{\ast }=0.5$, $N_{0}\nu =0.001$, $\mu^{\ast }=0$, $\chi =0.5$和$R_t=5$. 从图3(a)给出的不同梯度指数功能梯度水凝胶内部的位移分布曲线可以看出,在内压和化学势的共同作用下, 水凝胶内各点处的径向位移从内到外是不断增大的,且梯度指数越小,相应位置点的径向位移越大.

图3

新窗口打开|下载原图ZIP|生成PPT
图3功能梯度水凝胶球壳内的弹性场和浓度场的分布图

Fig. 3Distributions of the elastic and concentration fields of the internally pressurized, functionally graded spherical hydrogel

图3(b)和图3(c)分别给出了不同梯度指数下功能梯度水凝胶径向和环向的伸长率分布图. 图中可以看出,同一点处的径向伸长率小于环向伸长率. 对于三种给定的梯度指数和$\alpha =0.2$, 0和$-0.2$,径向伸长率沿径向方向从里向外不断增大,而环向伸长率沿径向方向从里向外不断减小, 当接近外表面即$\zeta $接近5时,径向和环向伸长率的值趋于相等,这是由于外表面接近自由溶胀, 这一现象也与Zhao 等^[22]给出的结果相一致. 对比不同梯度指数下的径向和环向的伸长率图,环向的伸长率随梯度指数的增大而减小, 内表面的径向伸长率随梯度指数的增大而增大,而外表面的径向伸长率随梯度指数的增大而略有减小. 还可以看出内表面的环向伸长率为最大伸长率,因此增大梯度指数可以降低最大伸长率的值.

不同梯度指数功能梯度水凝胶径向和环向真实应力的分布图分别见图3(d)和图3(e). 可以看出,由于内表面径向受压,所以径向应力$\sigma _{r}^{\ast }$为负值,且数值等于$-0.5$,即给定的内表面应力边界条件. 而内表面环向应力$\sigma _{\theta }^{\ast }$为正值,即环向受拉,且环向应力值在绝对值上比径向应力值大. 在接近外表面处,由于外表面自由,环向和径向的应力都趋于零. 对比不同梯度指数下的径向和环向的真实应力分布图,可以看出改变梯度指数对径向真实应力的影响很小, 但增大梯度指数能明显减小环向真实应力,即增大梯度指数有利于改善内压作用下溶胀水凝胶的力学性能.

图3(f)给出了水凝胶中的水分子浓度的分布图. 可以看到由于内压的作用,内表面的浓度低于外表面的浓度. 对比不同梯度指数下的浓度曲线,可以看到增大梯度指数能降低水凝胶内的水分子浓度. 另外,由于梯度指数的影响,正梯度指数($\alpha =0.2$)的功能梯度水凝胶内的水分子浓度由里到外先升高后又缓慢降低,而负梯度指数($\alpha = -0.2$)的功能梯度水凝胶内的水分子浓度则是由里到外一直升高,不过浓度的升高逐渐变缓,相比之下, 均匀水凝胶($\alpha =0$)中的水分子浓度只在内表面附近有升高,之后浓度便趋于平稳.

3.2 材料参数$N_{0v}$的影响

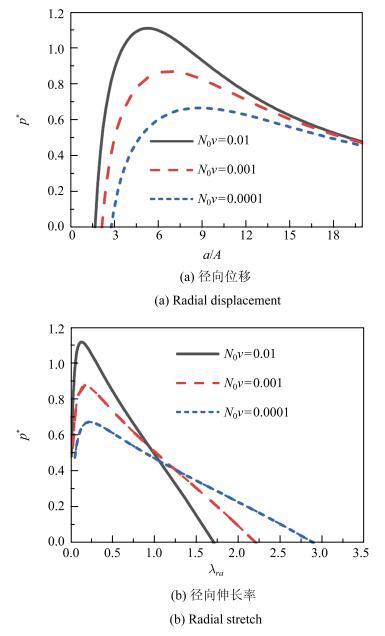
水凝胶材料参数$N_{0}v$的不同,对溶胀性能有直接的影响. 图4给出了当$N_{0}v$分别取0.01,0.001和0.000 1时,梯度指数$\alpha =0.2$的功能梯度水凝胶内表面无量纲径向位移和径向伸长率对内压的响应曲线. 仅考虑稳定区间内的部分,图4(a)中曲线表明,$N_{0}v$越大,内压$p$的稳定区间越大, 相同内压对应的内表面的径向位移越小. $N_{0}v$的大小与弹性模量有关,它是聚合物网络弹性模量的无量纲测量值,说明当$N_{0}v$越大时, 聚合物网络的弹性模量越大,水凝胶的溶胀变形会越小. 图4(b)所示的内表面径向伸长率对内压的响应曲线表明,增大$N_{0}v$可以使内压为零时内表面处的径向伸长率变小, 这是因为增大$N_{0}v$使得水凝胶整体的聚合物网络弹性模量升高的缘故.

图4

新窗口打开|下载原图ZIP|生成PPT
图4材料参数$N_{0}v$对内压作用下功能梯度水凝胶球壳内表面响应的影响

Fig. 4Effect of the material property $N_{0}v$ on the responses at the internal surface for the internally pressurized, functionally graded spherical hydrogel

3.3 材料参数$\chi$的影响

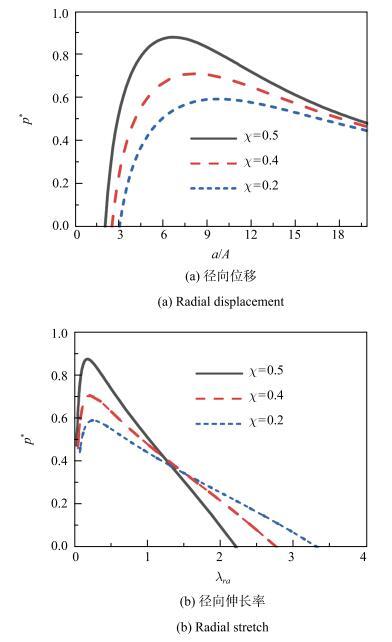
图5给出了当$\chi $分别取0.2,0.4和0.5时,功能梯度水凝胶($\alpha =0.2$)内表面无量纲径向位移和径向伸长率对内压的响应曲线. 仅考虑稳定区间内的曲线,图5(a)中曲线表明,$\chi $越大,稳定区间越大,相同内压对应的内表面的径向位移越小. 图5(b)表明,增大$\chi $可以使内压为零时内表面处的径向伸长率减小,但将增大峰值内压值. $\chi $是混合焓的无量纲测量值,当$\chi >0$且不断增大时,表示水凝胶的疏水性越来越高,所以吸水能力会降低,导致吸水时的溶胀变形相应变小.

图5

新窗口打开|下载原图ZIP|生成PPT
图5材料参数$\chi$对内压作用下功能梯度水凝胶球壳内表面响应的影响

Fig. 5Effect of the material property $\chi $ on the responses at the internal surface for the internally pressurized, functionally graded spherical hydrogel

3.4 环境参数$\mu^{\ast}$的影响

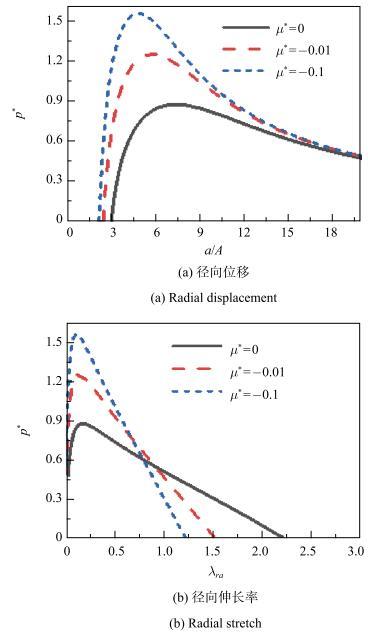
6给出了当化学势$\mu^{\ast }$分别取0,$-0.01$和$-0.1$时,功能梯度水凝胶($\alpha =0.2$)内表面无量纲径向位移和径向伸长率对内压的响应曲线. 仅考虑稳定区间内的曲线,图6(a)中曲线显示,当$\mu ^{\ast }$越小时,相同内压对应的内表面的径向位移越小. $\mu $表示的是环境中水的化学势,与相对湿度间的关系可以描述为$\mu =kT\ln(RH)$^[13]. 当$\mu^{\ast}=0~(\mu ^{\ast}=\mu /kT)$时,表示外界相对湿度为100%,即饱和状态,此时水凝胶容易吸水,所以溶胀达到稳定时的位移也就比较大, 当$\mu ^{\ast }$取负值时,表示外界相对湿度小于100%(其中$\mu ^{\ast }=-0.01$表示环境相对湿度约为99.0%,$\mu ^{\ast }=-0.1$表示环境相对湿度约为90.5%),这时吸水能力较弱. $\mu ^{\ast }$越小,表示湿度越低,吸水能力也就越弱,水凝胶的溶胀变形也就会越小. 还可以注意到,相对湿度从饱和到不饱和转变时对响应曲线的影响很明显,相对湿度只从100%降低到99%, 便使水凝胶内压的稳定区间明显增大. 图6(b)所示的水凝胶内表面径向伸长率对内压的响应曲线,考虑内压为零的情形,因为减小$\mu ^{\ast }$使得水凝胶整体的吸水能力减弱,从而使得变形减小,也就减小了平衡时的内表面的径向伸长率.

图6

新窗口打开|下载原图ZIP|生成PPT
图6化学势$\mu ^{\ast }$对内压作用下功能梯度水凝胶球壳内表面响应的影响

Fig. 6Effect of the chemical potential $\mu ^{\ast }$ on the responses at the internal surface for the internally pressurized, functionally graded spherical hydrogel

材料参数$\mu ^{\ast }$和$\chi $都与水凝胶的溶胀性能直接相关,增大$\chi $的值和减小$\mu ^{\ast }$的值都可以显著提高内压的峰值,而相对湿度从饱和到不饱和转变时对响应曲线的影响尤其明显, 为了探究这和水凝胶吸水能力的关系,表1列出当改变$\mu ^{\ast }$和$\chi $时均匀水凝胶(梯度指数$\alpha =0$)自由溶胀达到平衡状态时的水浓度. 可以看出,当$\chi =0.5$,$\mu ^{\ast }$从0改变到$-0.01$时,虽然湿度变化很小,但自由溶胀达到平衡时的水浓度从8.965 8减小到2.455 2, 变化很大,说明环境相对湿度不饱和时对水凝胶的溶胀性能影响很大. 相应的,图6中当$\mu ^{\ast }$从0改变到$-0.01$时,稳定区间变化也很大,结合表中其他数据以及图5和图6中的响应曲线, 可以看出内压作用的功能梯度水凝胶的稳定区间与其溶胀性能有很大关系.

Table 1
表1
表1均匀${(\alpha =0)}$水凝胶自由溶胀至平衡状态时的水分子浓度${(N_{0}\nu =0.001)}$
Table 1Concentration of water molecular in the free swelling homogeneous ($\alpha =0$) hydrogel at the equilibrium state ($N_{0}\nu =0.001$)

新窗口打开|下载CSV

3.5 参数对内外表面位移响应的影响

在本算例中,设定球形凝胶的外径与内径之$R_t=5$以及无量纲内压$p^{\ast }=0.4$. 图7给出了在给定内压情况下水凝胶内外表面无量纲位移$a/A$和$b/A$随计算参数变化的响应曲线, 其中图7(b)的横坐标采用了对数坐标. 图7(a)~图7(d)的计算参数分别设定如下：$N_{0}\nu =0.001$, $\mu ^{\ast }=0$, $\chi =0.5$~(图7(a));$\alpha =0$, $\mu ^{\ast }=0$, $\chi =0.5$~(图7(b));$\alpha =0$, $ N_{0}\nu =0.001$, $\chi =0.5$~(图7(c));$\alpha =0$, $ N_{0}\nu =0.001$, $\mu ^{\ast }=0$~(图7(d)). 图中可以看到,在内给定的计算区间内,水凝胶内外表面的位移随梯度指数$\alpha $的变化是接近为线性的,而材料参数$N_{0}\nu $、化学势$\mu ^{\ast }$以及材料参数$\chi $对水凝胶内外表面位移的影响则表现为非线性的.

图7

新窗口打开|下载原图ZIP|生成PPT
图7给定内压情况下各参数变化对水凝胶内外表面径向位移的影响

Fig. 7Effect of the material parameters on the radial displacement at the internal and external surface for the internally pressurized hydrogel

4 结论

基于大变形多场耦合一般理论,研究了功能梯度球形水凝胶在内压和化学势共同作用下的化学力学耦合行为,分析了材料参数$\alpha$,$N_{0}\nu $和$\chi $以及化学势$\mu ^{\ast}$对水凝胶溶胀性能的影响.研究表明,内压作用下的不同梯度指数的功能梯度球形水凝胶均存在跃变失稳的现象,且临界内压值与材料参数$\alpha$,$N_{0}\nu $和$\chi $以及化学势$\mu^{\ast}$均有关.本文研究对于高性能水凝胶结构的设计以及水凝胶智能器件在复杂化学力学应用条件下驱动性能的精准调控,具有积极的意义.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Hoffman

. Hydrogels for biomedical applications
Advanced Drug Delivery Reviews, 2002,54(1):3-12

DOI URL [本文引用: 1]

[2]

Zhang

, Khademhosseini

. Advances in engineering hydrogels
Science, 2017, 356(6337):eaaf3627

DOI URL [本文引用: 2]

[3]

, Xu

, Feng

. Tissue-growth model for the swelling analysis of core-shell hydrogels
Soft Materials, 2013,11(2):117-124

DOI URL

[4]

Mredha

MTI

, Kitamura

, Nonoyama

, et al. Anisotropic tough double network hydrogel from fish collagen and its spontaneous in vivo bonding to bone
Biomaterials, 2017,132:85-95

DOI URL [本文引用: 1]

[5]

Carpi

, Smela

. Biomedical Applications of Electroactive Polymer Actuators.
Chichester: John Wiley & Sons Ltd., 2009

[本文引用: 1]

[6]

李铁风, 李国瑞, 梁艺鸣等. 软体机器人结构机理与驱动材料研究综述
力学学报, 2016,48(4):756-766

DOI Magsci [本文引用: 1]

<p>软体机器人是一类新型机器人，具有结构柔软度高，环境适应性好，亲和性强，功能多样等特点，有着十分广阔的研究和应用前景. 智能材料在软体机器人结构设计及实际应用中扮演了重要的角色，其特殊的驱动机制极大拓展了软体机器人的功能. 介绍了软体机器人的发展和研究现状，按其应用场合及功能总结了几种典型的软体机器人. 从仿生机理的角度，介绍了蠕虫、弯曲爬行虫、鱼类游动等几类仿生运动机理以及其相应的软体机器人. 还按不同驱动类型将软体机器人归纳为气动、形状记忆合金、离子交换聚合物金属复合材料、介电高弹体、响应水凝胶、化学燃烧驱动等类型. 介绍了软体机器人的制作方法与工艺，分析了目前软体机器人研究的主要挑战，提出对未来研究的展望.</p>

( Li

Tiefeng

, Li

Guorui

, Liang

Yiming

, et al. Review of materials and structures in soft robotics
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(4):756-766 (in Chinese))

DOI Magsci [本文引用: 1]

, Guan

, Lee

. An oral delivery device based on self-folding hydrogels
Journal of Controlled Release, 2006,110(2):339-346

DOI URL [本文引用: 1]

[8]

Zalachas

, Cai

, Suo

, et al. Crease in a ring of a PH-sensitive hydrogel swelling under constraint
International Journal of Solids and Structures, 2013,50(6):920-927

DOI URL

[9]

卢同庆, 孙丹琪, 王继堃等. 高韧温敏复合水凝胶仿生变色鱼
中国科学:技术科学, 2018,48(12):1288-1294

[本文引用: 1]

( Lu

Tongqing

, Sun

Danqi

, Wang

Jikun

, et al. Hydrogel based biomimetic chameleon fish with super high toughness
Scientia Sinica Technologica, 2018,48(12):1288-1294 (in Chinese))

[本文引用: 1]

[10]

Hong

, Zhao

, Zhou

, et al. A theory of coupled diffusion and large deformation in polymeric gels
Journal of the Mechanics and Physics of Solids, 2008,56(5):1779-1793

DOI URL [本文引用: 3]

[11]

Bouklas

, Landis

, Huang

. A nonlinear, transient finite element method for coupled solvent diffusion and large deformation of hydrogels
Journal of the Mechanics and Physics of Solids, 2015,79:21-43

DOI URL

[12]

Liu

, Toh

, Ng

. Advances in mechanics of soft materials: A review of large deformation behavior of hydrogels
International Journal of Applied Mechanics, 2015,7(5):1530001

DOI URL [本文引用: 1]

[13]

Hong

, Zhao

, Suo

. Drying-induced bifurcation in a hydrogel-actuated nanostructure
Journal of Applied Physics, 2008,104(8):084905

DOI URL [本文引用: 3]

[14]

Wang

, Cai

. Cavitation in a swollen elastomer constrained by a non-swellable shell
Journal of Applied Physics, 2015,117(15):103535

[本文引用: 2]

[15]

Cai

, Suo

. Mechanics and chemical thermodynamics of phase transition in temperature-sensitive hydrogels
Journal of the Mechanics and Physics of Solids, 2011,59(11):2259-2278

DOI URL [本文引用: 1]

[16]

Guo

, Li

, Zhou

. Modeling programmable deformation of self-folding all-polymer structures with temperature-sensitive hydrogels
Smart Materials and Structures, 2013,22(11):115028

DOI URL

[17]

Zheng

, Liu

. Phase transition of temperature-sensitive hydrogel under mechanical constraint
ASME Journal of Applied Mechanics, 2018,85(2):021002

[本文引用: 1]

[18]

Hong

, Liu

, Suo

. Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load
International Journal of Solids and Structures, 2009,46(17):3282-3289

DOI URL [本文引用: 2]

[19]

Zhang

, Hu

, Tang

, et al. Fracture toughness and fatigue threshold of tough hydrogels
ACS Macro Letters, 2018,8(1):17-23

[本文引用: 1]

[20]

Lai

, Li

. Modeling of effect of initial fixed charge density on smart hydrogel response to ionic strength of environmental solution
Soft Matter, 2010,6(2):311-320

DOI URL [本文引用: 1]

[21]

Attaran

, Brummund

, Wallmersperger

. Modeling and simulation of the bending behavior of electrically-stimulated cantilevered hydrogels
Smart Materials and Structures, 2015,24(3):035021

DOI URL [本文引用: 1]

[22]

Zhao

, Hong

, Suo

. Inhomogeneous and anisotropic equilibrium state of a swollen hydrogel containing a hard core
Applied Physics Letters, 2008,92(5):051904

DOI URL [本文引用: 4]

[23]

, Zhong

. Inhomogeneous equilibrium swelling of core-shell-coating gels
Soft Materials, 2013,11(2):215-220

DOI URL [本文引用: 1]

[24]

Wang

, Cai

. Drying-induced cavitation in a constrained hydrogel
Soft Matter, 2015,11(6):1058-1061

DOI URL [本文引用: 1]

[25]

Dai

, Song

. Some analytical formulas for the equilibrium states of a swollen hydrogel shell
Soft Matter, 2011,7(18):8473-8483

DOI URL [本文引用: 1]

[26]

Zheng

, Li

, Liu

. The fast homogeneous diffusion of hydrogel under different stimuli
International Journal of Mechanical Sciences, 2018,137:263-270

DOI URL [本文引用: 1]

[27]

郑保敬, 梁钰, 高效伟等. 功能梯度材料动力学问题的POD模型降阶分析
力学学报, 2018,50(4):787-797

[本文引用: 1]

( Zheng

Baojing

, Liang

, Gao

Xiaowei

, et al. Analysis for dynamic response of functionally graded materials using pod based reduced order model
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(4):787-797 (in Chinese))

[本文引用: 1]

[28]

许新, 李世荣 . 功能梯度材料微梁的热弹性阻尼研究
力学学报, 2017,49(2):308-316

( Xu

Xin

, Li

Shirong

. Analysis of thermoelastic damping for functionally graded material micro-beam
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(2):308-316 (in Chinese))

[29]

马强, 周凤玺, 刘杰 . 梯度波阻板的地基振动控制研究
力学学报, 2017,49(6):1360-1369

[本文引用: 1]

( Ma

Qiang

, Zhou

Fengxi

, Liu

Jie

. Analysis of ground vibration control by graded wave impeding block
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(6):1360-1369 (in Chinese))

[本文引用: 1]

[30]

Guvendiren

, Yang

, Burdick

. Swelling-induced surface patterns in hydrogels with gradient crosslinking density
Advanced Functional Materials, 2009,19(19):3038-3045

DOI URL [本文引用: 2]

[31]

Bakarich

, Gorkin III

, Gately

, et al. 3D printing of tough hydrogel composites with spatially varying materials properties
Additive Manufacturing, 2017,14:24-30

DOI URL [本文引用: 1]

[32]

Guvendiren

, Burdick

, Yang

. Kinetic study of swelling-induced surface pattern formation and ordering in hydrogel films with depth-wise crosslinking gradient
Soft Matter, 2010,6(9):2044-2049

DOI URL [本文引用: 1]

[33]

, Bouklas

, Huang

. Swell-induced surface instability of hydrogel layers with material properties varying in thickness direction
International Journal of Solids and Structures, 2013,50(3-4):578-587

DOI URL [本文引用: 1]

[34]

Anani

, Rahimi

. Stress analysis of thick pressure vessel composed of functionally graded incompressible hyperelastic materials
International Journal of Mechanical Sciences, 2015,104(3):1-7

DOI URL [本文引用: 1]

[35]

Flory

, Rehner

. Statistical mechanics of cross-linked polymer networks II. Swelling
Journal of Chemical Physics, 1943,11(11):521-526

DOI URL [本文引用: 1]

[36]

Zamani

, Pence

. Swelling, inflation, and a swelling-burst instability in hyperelastic spherical shells
International Journal of Solids and Structures, 2017,125:134-149

DOI URL [本文引用: 1]

[37]

Cheng

, Jia

, Guo

, et al. Delayed burst of a gel balloon
Journal of the Mechanics and Physics of Solids, 2019,124:143-158

DOI URL [本文引用: 1]