张洁皓, 段玥晨, 侯玉亮, 铁瑛, 李成^,2)郑州大学机械工程学院, 郑州 450001

MULTI-SCALE METHOD OF PLAIN WOVEN COMPOSITES SUBJECTED TO LOW VELOCITY IMPACT BASED ON ASYMPTOTIC HOMOGENIZATION¹⁾

Zhang Jiehao, Duan Yuechen, Hou Yuliang, Tie Ying, Li Cheng^,2)School of Mechanical Engineering, Zhengzhou University, Zhengzhou 450001, China

通讯作者: 2) 李成, 教授, 主要研究方向：复合材料力学. E-mail:chengli@zzu.edu.cn

收稿日期:2019-05-22网络出版日期:2019-09-18

基金资助:

1) 国家自然科学基金资助项目.U1333201 国家自然科学基金资助项目.U1833116 国家自然科学基金资助项目.11402234

Received:2019-05-22Online:2019-09-18
作者简介 About authors


摘要
针对平纹编织复合材料低速冲击响应和损伤问题,提出了一种多尺度分析方法. 首先, 建立微观尺度单胞模型,引入周期性边界条件,采用最大主应力失效准则和直接刚度退化模型表征纤维丝和基体的损伤起始与演化,预测了纤维束的弹性性能和强度性能. 其次,将这些性能参数代入介观尺度单胞模型,基于Hashin和Hou的混合失效准则以及连续介质损伤模型对介观尺度单胞进行6种边界条件下的渐进损伤模拟.然后采用渐进均匀化方法,以介观尺度单胞为媒介预测了0$^\circ$和90$^\circ$子胞的性能参数,并建立平纹编织复合材料的子胞模型,进而扩展成为材料的宏观尺度低速冲击模型. 在此基础上,研究了平纹编织复合材料低速冲击下的力学响应与损伤特征.结果表明：宏观冲击仿真和试验吻合较好, 验证了多尺度方法的正确性;最大接触力、材料吸能和分层面积均随冲击能量的增大而增大,分层损伤轮廓逐渐从椭圆形向圆形转化;基体拉伸和压缩损伤的长轴方向分别与子胞材料主方向正交和一致,损伤面积前者远大于后者.
关键词： 平纹编织复合材料;渐进均匀化;低速冲击;多尺度

Abstract
A multi-scale approach was presented to analyze low velocity impact response and damage of plain woven composites. Firstly, by using the maximum principal stress failure criterion and direct stiffness degradation model to characterize the damage initiation and damage evolution of fiber and matrix, micro-scale unit cell under the periodical boundary condition was established to predict the elastic and strength properties of fiber bundles, which were substituted into the meso-scale unit cell. After that, the progressive damage simulation of meso-scale unit cell under six boundary conditions was carried out based on the mixed failure criteria of Hashin and Hou, and continuum damage model. Then the effective properties of 0$^\circ$and 90$^\circ$subcell were predicted based on the asymptotic homogenization method by using meso-scale unit cell as the media, and the subcell model of plain woven composites was established. The subcell model was then extended into a macro-scale low velocity impact model. Based on the above methods, the mechanical response and damage characteristics of plain woven composites under low velocity impact were studied. The results show that macro-scale impact simulation results agree well with experimental results, which verifies the correctness of multi-scale approach. The maximum contact force, absorbed energy and delamination area increase with the increasing impact energy, and the delamination damage morphology gradually transforms from ellipse to circle.The long axis direction of matrix tensile damage and matrix compressive damage are orthogonal and consistent with the material principal direction of subcell respectively, and the damage area of the former is much larger than that of the latter.
Keywords：plain woven composites;asymptotic homogenization;low velocity impact;multi-scale


PDF (40088KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张洁皓, 段玥晨, 侯玉亮, 铁瑛, 李成. 基于渐进均匀化的平纹编织复合材料低速冲击多尺度方法¹⁾. 力学学报[J], 2019, 51(5): 1411-1423 DOI:10.6052/0459-1879-19-133
Zhang Jiehao, Duan Yuechen, Hou Yuliang, Tie Ying, Li Cheng. MULTI-SCALE METHOD OF PLAIN WOVEN COMPOSITES SUBJECTED TO LOW VELOCITY IMPACT BASED ON ASYMPTOTIC HOMOGENIZATION¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(5): 1411-1423 DOI:10.6052/0459-1879-19-133

引言

相对于传统层合复合材料和合金材料,编织复合材料具有更高的比强度、比模量和不易分层、抗疲劳等优点^[1-2]. 平纹编织复合材料作为工业上最常用的一种编织复合材料,被广泛地用在航空航天和军用器械的结构件上^[3-6]. 然而,由于平纹编织复合材料在使用过程中不可避免地会受到低能量水平的冲击,这些冲击极易在材料内部产生目视不可见的损伤,进而严重地降低材料的使用寿命和力学性 能^[7-8]. 因此,研究平纹编织复合材料在低速冲击下的力学响应和损伤特征是十分有必要的.

目前,国内外对编织复合材料抗冲击性能研究的数值模型可分为两大类：介观模型^[9-12]和宏观模型^[13-16].Wang等^[9]研究了纱线间摩擦对平纹编织复合材料冲击响应的影响,发现摩擦系数增大会导致纵波速度变慢和更长的冲击历程.Palta等^[10]提出了一种改进的多尺度有限元模型,并研究了多层编织复合材料的抗冲击性能,发现多尺度模型在计算准确性和效率方面均优于纯介观模型.Carpenter等^[11]基于应变率相关的介观尺度模型模拟了平纹和三维编织复合材料的高速冲击过程,分析了材料复杂的破坏机制.李裕春等^[12]研究了平头弹冲击作用下平纹织物的动态响应,发现纱线的应变能和动能以及摩擦是主要的吸能方式.Cousigné等^[13]建立了包含材料非线性和塑性的本构模型,利用LS-DYNA软件模拟了编织复合材料的低速冲击过程,仿真和试验取得了很好的一致性.Yang等^[14]利用试验和宏观有限元模型研究了编织混杂层合复合材料的混杂效应对材料抗低速冲击性能的影响,发现当混杂质量比为37:63时材料有最高的吸能和穿孔阈值.Kinvi-Dossou等^[15]考虑了应变率效应以及温度对编织复合材料弹性性能的影响,利用二步渐进均匀化方法建立了材料的宏观低速冲击有限元模型.杨扬等^[16]基于Autodyn软件模拟了平纹编织C/SiC复合材料低速冲击过程,根据碎片云的结构和轴向速度验证了模拟的合理性,并推导出了材料的极限侵彻深度预测公式.这些研究采用的介观模型虽然可以准确地再现纤维束之间复杂的空间构型,但是有模型过大、计算成本太高等缺点.而宏观模型大都将编织复合材料直接等效为正交各向异性材料,并未考虑织物细观结构, 不可避免地造成一定的误差.

针对上述问题,本文提出了一种针对平纹编织复合材料低速冲击的多尺度分析方法,兼顾了计算精度与效率. 首先,利用微观尺度单胞模型预测了纤维束的弹性和强度性能. 然后,基于三维Hashin失效准则和连续介质损伤模型,对介观尺度单胞进行6种边界条件下的渐进损伤模拟. 其次,采用渐进均匀化方法建立材料子胞模型,进而搭建了平纹编织复合材料的宏观低速冲击模型,仿真和试验结果吻合良好,并研究了低速冲击下材料的力学响应和损伤 特征.

1 微观和介观尺度单胞几何模型

1.1 微观尺度单胞几何模型

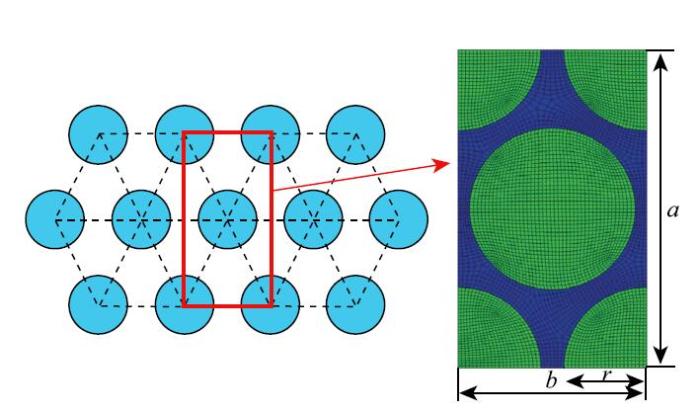
由于进行介观尺度单胞的数值分析需要纤维束的性能参数,故建立如图1所示的微观尺度单胞模型,通过数值模拟来获得纤维束的力学性能. 模型中E-玻璃纤维丝呈六方分布,其中$a$和$b$分别为单胞的长度和宽度, $r$为纤维丝半径,满足关系式2$\pi r^{2}$(ab)=0.7,表示纤维束中纤维丝体积分数为70%.

图1

新窗口打开|下载原图ZIP|生成PPT
图1微观尺度单胞几何模型

Fig. 1Geometrical model of micro-scale unit cell

1.2 介观尺度单胞几何模型

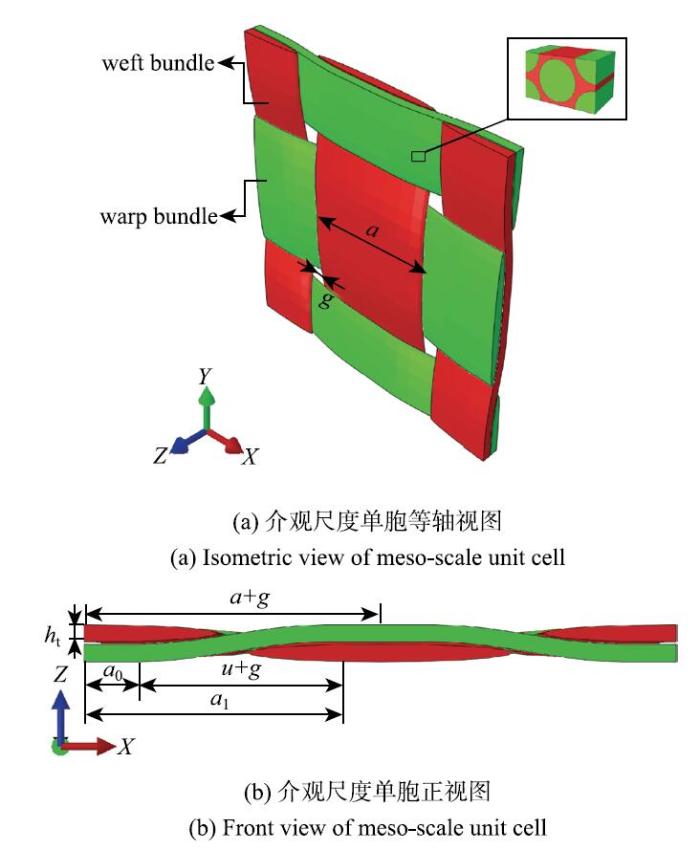
平纹编织复合材料的细观结构特征对材料力学性能有着显著的影响^[17-18]. 费庆国等^[19]将纤维束的波动角简化为恒定的角度,导致纤维束存在明显的转折, 与实际情况不符.Dixit等^[20]利用像素法建立了材料的单胞模型,但该模型不能准确地再现纤维束光滑的表面形态. 经比较分析,本文采用文 献^[21]提出的三维卷曲模型,介观尺度单胞几何模型如图2所示, 为便于显示隐去基体部分,其中微观尺度单胞代表介观尺度单胞纤维束的一个微元, 模型参数见表1.纤维束走向方程可以表示为

(1)$$z = \left\{ {{\begin{array}{*{20}l} - h_{\rm t} / 2,& 0 \le x \le a_{\rm 0} \\[3mm] \sin \left[ {\left( {x - \dfrac{w + g}{2}} \right)\dfrac{{\pi }}{u + g}} \right]\dfrac{h_{\rm t} }{2},& a_{\rm 0} \le x \le a_{\rm l} \\[3mm] h_{\rm t} / 2, &a_{\rm l} \le x \le w + g \end{array} }} \right. $$

其中, $h_{\rm t}$为纤维束的厚度, $w$为纤维束的宽度, $g$为相邻经纬纤维束的间隙长度, $u$为纤维束弯曲部分的直线长度.

Table 1
表1
表1介观尺度单胞几何参数
Table 1Geometric parameter of meso-scale unit cell

新窗口打开|下载CSV

图2

新窗口打开|下载原图ZIP|生成PPT
图2介观尺度单胞几何模型

Fig. 2Geometric model of meso-scale unit cell



模型中纤维束占单胞体积的62.5%,由纱线填充系数为0.7可得纤维体积分数为43.75%,其中纤维束的材料主方向通过离散坐标系指定.

1.3 周期性边界条件

对于一个周期性单胞,必须施加周期性边界条件以此来保证数值分析的正确性.两个相对面的位移场可以分别表示为^[22]

(2)\begin{equation} \label{eq1} u_i^{\rm k - } = \overline{\varepsilon}_{ij} x_j^{\rm k - } + u_i^\ast \end{equation}

(3)\begin{equation} \label{eq2} u_i^{\rm k + } = \overline{\varepsilon}_{ij} x_j^{\rm k + } + u_i^\ast\end{equation}

其中, 上标k+和k-\!代表单胞的两个相对面,两式相减可以得到相对面的位移差为

(4)\begin{equation} \label{eq3} u_i^{\rm k + } - u_i^{\rm k - } =\overline{\varepsilon}_{ij} (x_j^{\rm k + } - x_j^{k - } ) = \overline{\varepsilon}_{ij} \varDelta _j^k \end{equation}

由于$\varDelta ^{\rm k}_j$为定值, 一旦给定$\overline{\varepsilon}_{ij}$, 位移差即为常数.

在软件ABAQUS中可以使用Equation语句来约束主从节点的相对位移,从而实现周期性边界条件的施加.

2 渐进损伤模型

2.1 微观尺度渐进损伤模型

E-玻璃纤维丝和树脂基体都可视为各向同性材料,均可用最大主应力准则判定损伤起始^[21]. 纤维丝一旦发生失效,表现为彻底地丧失承载能力, 基体表现为弹塑性, 失效后仍有一定的强度,所以纤维和基体失效后分别将其模量折减为原来的0.1%和40%^[23].

最大主应力准则可表示为

(5a)$$\sigma _{\rm I} \le X_{\rm t} $$

(5b)$$\sigma _{{\rm I}{\rm I}{\rm I}} \le X_{\rm c} $$

(5c)$$\tau _{\max } \ge S $$

其中, $\sigma $$_{\rm I}$和$\sigma $$_{\rm III}$为第一主应力和第三主应力, $X_{\rm t}$, $X_{\rm c}$和$S$分别为拉伸、压缩和剪切强度.

2.2 介观尺度渐进损伤模型

介观尺度单胞中的基体仍采用最大主应力准则和直接刚度退化作为损伤起始和退化准则.

纤维束可以视为纤维增强复合材料,结合Hashin^[24]和Hou^[25]的失效准则并引入表征剪切应力影响程度的剪切修正因子判断纤维束的损伤起始,表达式如式(6)$\sim$式(9)所示.

纤维拉伸失效($\sigma $$_{\rm 11} \ge $0)

(6)\begin{equation} \label{eq7} \left( {\frac{\sigma _{\rm 11} }{X_{\rm T} }} \right)^2 + \alpha (\frac{\tau _{12} + \tau _{13} }{S_{12} }) \ge 1 \end{equation}

纤维压缩失效($\sigma $$_{11}<0$)

(7)\begin{equation} \label{eq8} \left( {\frac{\sigma _{11} }{X_{\rm C} }} \right)^2 \ge 1 \end{equation}

基体拉伸失效($\sigma $$_{22}$+$\sigma $$_{33}$0)

(8)\begin{equation} \label{eq9} \left( {\frac{\sigma _{22} }{Y_{\rm T} }} \right)^2 + \left( {\frac{\sigma _{12} }{S_{12} }} \right)^2 + \left( {\frac{\sigma _{23} }{S_{23} }} \right)^2 \ge 1 \end{equation}

基体压缩失效($\sigma _{22}+\sigma _{33}<0)$

(9)\begin{equation} \label{eq10} \frac{1}{4}\left( {\frac{ - \sigma _{22} }{S_{12} }} \right)^2 + \frac{Y_{\rm c}^2 \sigma _{22} }{4S_{12}^2 Y_{\rm c} } - \frac{\sigma _{22} }{Y_{\rm c} } + \left( {\frac{\sigma _{12} }{S_{23} }} \right)^2 \ge 1 \end{equation}

其中, $\sigma $$_{ij}(i,j$=1,2,3)为各个方向主应力张量,$\alpha $为剪切修正因子, $X_{\rm T}$和$X_{\rm C}$为纵向拉压强度, $Y_{\rm T}$和$Y_{\rm C}$为横向拉压强度,$S_{ij}(i$, $j$=1,2,3)为各个方向剪切强度.

采用文献^[26]中的基于连续损伤力学的损伤演化方法,通过引入随应变变化的损伤变量$D_{\rm f}$和$D_{\rm m}$来表征纤维和基体的损伤程度, 可表示为

(10)\begin{equation} \label{eq11} D_{\rm f} = 1 - (1 - d_{\rm ft} )(1 - d_{\rm fc} ) \end{equation}

(11)$$D_{\rm m} = 1 - (1 - d_{\rm mt} )(1 - d_{\rm mc} )$$

其中, 损伤变量分量$d_{\rm ft}$, $d_{\rm fc}$, $d_{\rm mt}$和$d_{\rm mc}$可分别表示为

(12)$$d_{\rm ft} =\frac{\varepsilon _{\rm f,1}^{\rm t} }{\varepsilon _{\rm f,1}^{\rm t} - \varepsilon _{\rm o,1}^{\rm t} }\Bigg( {1 - \frac{\varepsilon _{\rm o,1}^{\rm t} }{\varepsilon _{\rm 11} }} \Bigg) $$

(13)$$d_{\rm fc} =\frac{\varepsilon _{\rm f,1}^{\rm c} }{\varepsilon _{\rm f,1}^{\rm c} - \varepsilon _{\rm o,1}^{\rm t} }\left( {1 - \frac{\varepsilon _{\rm o,1}^{\rm c} }{\varepsilon _{\rm 11} }} \right) $$

(14)$$d_{\rm mt} =\frac{\varepsilon _{\rm f,2}^{\rm t} }{\varepsilon _{\rm f,2}^{\rm t} - \varepsilon _{\rm o,2}^{\rm t} }\Bigg( {1 - \frac{\varepsilon _{\rm o,2}^{\rm t} }{\varepsilon _{\rm 22} }} \Bigg) $$

(15)$$d_{\rm mc} =\frac{\varepsilon _{\rm f,2}^{\rm c} }{\varepsilon _{\rm f,2}^{\rm c} - \varepsilon _{\rm o,2}^{\rm c} }\left( {1 - \frac{\varepsilon _{\rm o,2}^{\rm c} }{\varepsilon _{\rm 22} }} \right) $$

式中, $\varepsilon ^{\rm t}_{\rm o,1}$和$\varepsilon^{\rm c} _{\rm o,1}$为纤维拉伸和压缩起始破坏应变, $\varepsilon^{\rm t} _{\rm o,2}$和$\varepsilon ^{\rm c} _{\rm o,2}$为基体拉伸和压缩起始破坏应变, $\varepsilon^{\rm t} _{\rm f,1}$和$\varepsilon^{\rm c} _{\rm f,1}$为纤维拉伸和压缩最终破坏应变, $\varepsilon^{\rm t} _{\rm f,2}$和$\varepsilon ^{\rm c}_{\rm f,2}$为基体拉伸和压缩最终破坏应变.

当材料某处满足初始损伤准则时, 表现为此处刚度的减小,损伤后的材料刚度矩阵为

(16)$$C_{\rm d}\!=\! \left[\!\!{\begin{array}{cccccc} {{D_{\rm f} }C_{11}^0}&\hspace{-2mm}{{D_{\rm f} }{D_m}C_{12}^0}&\hspace{-2mm}{{D_{\rm f} }C_{13}^0}&\hspace{-2mm}0&\hspace{-2mm}0&\hspace{-2mm}0 \\ {}&\hspace{-2mm}{{D_{\rm m} }C_{22}^0}&\hspace{-2mm}{{D_{\rm m} }C_{23}^0}&\hspace{-2mm}0&\hspace{-2mm}0&\hspace{-2mm}0 \\ {}&\hspace{-2mm}{}&\hspace{-2mm}{C_{33}^0}&\hspace{-2mm}0&\hspace{-2mm}0&\hspace{-2mm}0 \\ {}&\hspace{-2mm}{{\rm sym} }&\hspace{-2mm}{}&\hspace{-2mm}{{D_m}C_{44}^0}&\hspace{-2mm}0&\hspace{-2mm}0 \\ {}&\hspace{-2mm}{}&\hspace{-2mm}{}&\hspace{-2mm}{}&\hspace{-2mm}{{D_{\rm f} }C_{55}^0}&\hspace{-2mm}0 \\ {}&\hspace{-2mm}{}&\hspace{-2mm}{}&\hspace{-2mm}{}&\hspace{-2mm}{}&\hspace{-2mm}{{D_{\rm f} }{D_{\rm m} }C_{66}^0} \end{array}} \!\!\right] $$

其中, $C^0_{ ij}(i,j=1,2,\cdots ,6)$为未损伤刚度矩阵分量.

2.3 渐进损伤模拟实现流程

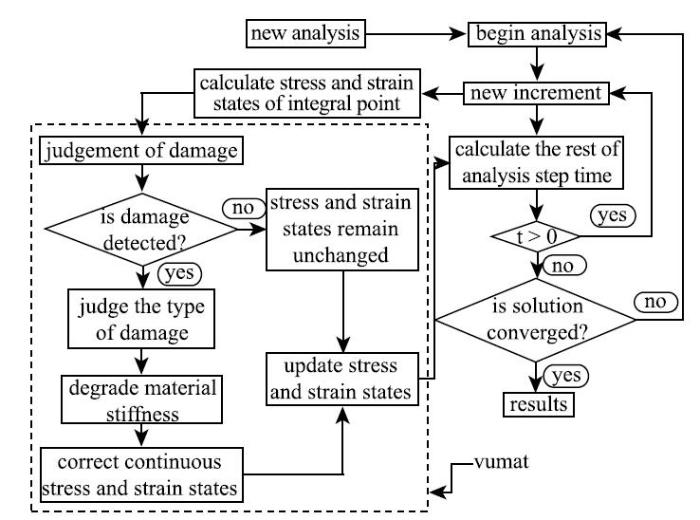
编写软件ABAQUS用户定义材料子程序VUMAT,利用损伤准则对材料积分点进行损伤判断, 损伤发生后,根据刚度退化模型对材料刚度进行折减, 并更新单元应力,最后由子程序返回给主程序当前增量步的应力和损伤状态变量.渐进损伤模拟具体流程如图3所示.

图3

新窗口打开|下载原图ZIP|生成PPT
图3渐进损伤模拟实现流程图

Fig. 3The flow chart of progressive damage simulation^[27]

3 介观尺度到宏观尺度的均匀化和宏观冲击模型的建立

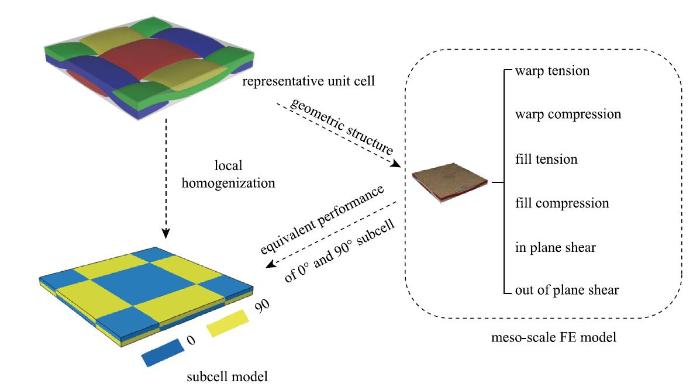
平纹编织复合材料可看做由0$^\circ$和90$^\circ$复合材料层合板上下正交铺设而成^[28],这两种层合板在本文中统称为子胞. 介观到宏观的均匀化过程如图4所示,即通过对介观尺度单胞进行6种边界条件的渐进损伤模拟,包括：经向拉伸、经向压缩、纬向拉伸、纬向压缩、面内剪切和面外剪切,然后利用体积平均法从模拟结果中获得0$^\circ$和90$^\circ$子胞的等效力学性能,并建立平纹编织复合材料的子胞模型, 进而由子胞模型扩展成为宏观模型.

图4

新窗口打开|下载原图ZIP|生成PPT
图4介观到宏观均匀化过程

Fig. 4The process of meso-macro homogenization



体积平均法的公式如下

(17a)$$\label{eq14} \mathop \sigma \limits^\_ \mbox{ = }\frac{1}{V}\int_V {\sigma _{ij} } {\rm d}V $$

(17b)$$\mathop \varepsilon \limits^\_ \mbox{ = }\frac{1}{V}\int_V {\varepsilon _{ij} } {\rm d}V $$

其中, $\sigma $$_{ij}$, $\varepsilon $$_{ij}(i$,$j$=1,2,3)为子胞中单元的应力、应变分量, $V$为子胞的体积,$\overline{\sigma} $为子胞的等效平均应力,$\overline{\varepsilon} $为子胞的等效平均应变.

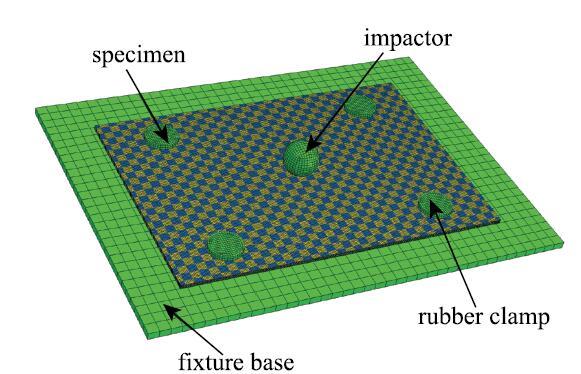
根据文献^[29]的实验条件搭建的平纹编织复合材料宏观尺度低速冲击有限元模型如图5所示,其中靶板由子胞模型阵列而成, 尺寸为148 mm$\times $101 mm$\times$1.96 mm, 在每层之间加入0.01mm的内聚力(cohesive)单元用来模拟冲击过程中的层间分层. 冲头为直径16mm的球体, 质量为5.632 kg, 在模拟过程中视为刚体.其中胶层的单元类型为COH3D8, 其余部分用C3D8R单元离散,材料的本构模型与纤维束相同. 当单元中发生纤维失效时,即认为此单元完全丧失了承载能力并从模型中删除^[14].

图5

新窗口打开|下载原图ZIP|生成PPT
图5平纹编织复合材料宏观尺度低速冲击有限元模型

Fig. 5The macro-scale low velocity impact FE model for plai woven composite

4 结果与分析

4.1 微观尺度结果与分析

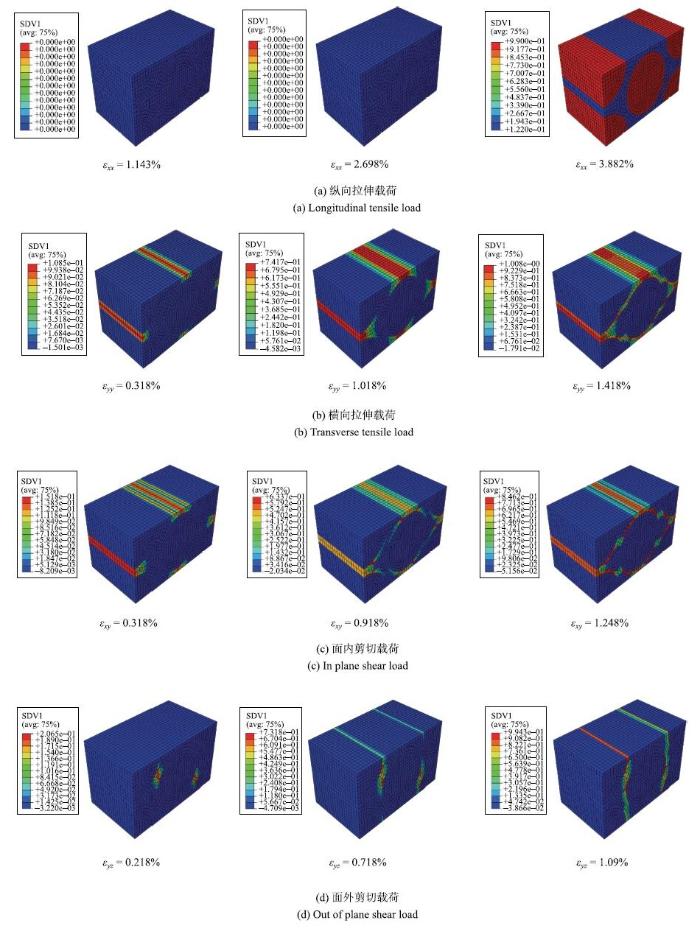
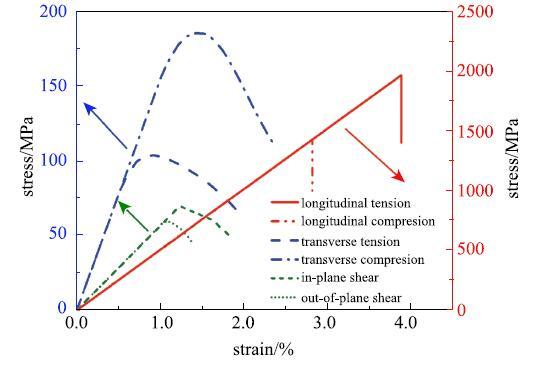
采用文献^[21]提供的E-玻璃纤维和树脂基体的性能参数作为微观尺度计算的输入参数,如表2所示. 通过对微观尺度单胞施加周期性边界条件,进行不同载荷下的渐进损伤模拟, 图6给出了渐进损伤扩展云图,仿真所得的应力--应变曲线见图7,其中纤维束的弹性模量和强度分别由曲线的初始斜率和峰值应力决定.表3给出了有限元模拟得到的纤维束性能参数与利用Chamis细观力学公式^[30]计算的结果对比情况,从表中可以看出, 两者的最大偏差不超过15%,表明了数值计算结果的合理性. 如图6所示,纵向拉伸时纤维丝最先发生损伤, 并引起整体材料的破坏;纤维束的横向拉伸破坏主要是由于基体开裂引起的,而纤维丝在失效过程中一直保持完好;纤维束的剪切损伤最先发生在基纤界面处,随着载荷的增大向基体其他部分扩展. 从图7可以看出,纵向拉伸和压缩曲线从加载到破坏一直呈线性,并最终由于纤维丝的轴向断裂引发失效;而预测得到的纤维束横向性能远远低于纵向性能,这是因为横向加载时纤维丝不再作为主承载组分.

Table 2
表2
表2纤维束组分材料性能参数^[21]
Table 2Mechanical properties of fiber bundle component^[21]

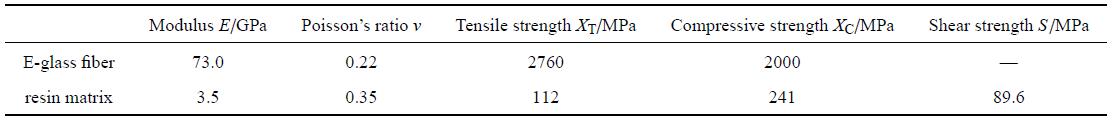新窗口打开|下载CSV

Table 3
表3
表3纤维束性能参数
Table 3Mechanical properties of fiber bundle

新窗口打开|下载CSV

图6

新窗口打开|下载原图ZIP|生成PPT
图6纤维束不同载荷下的渐进损伤扩展

Fig. 6Damage expansion for fiber bundle under different loadings

图7

新窗口打开|下载原图ZIP|生成PPT
图7纤维束不同载荷下的应力--应变曲线

Fig. 7Stress-strain curves for fiber bundle under different loadings

4.2 介观尺度结果与分析

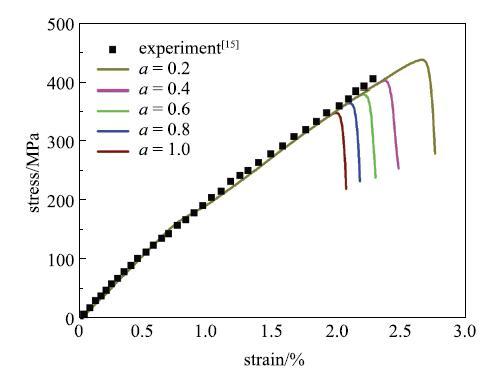
剪切修正因子$\alpha $表征剪切应力对材料损伤的贡献程度,图8给出了$\alpha$对平纹编织复合材料拉伸应力--应变曲线的影响规律.从图中可以看出, $\alpha $从0.2增长到1.0时, 峰值应力由439MPa下降到351 MPa, 但$\alpha$不会影响材料损伤前的模量大小. 当$\alpha$=0.4时模拟结果与试验^[15]最为接近,弹性模量和强度的相对误差分别为3.05%和0.74%.

图8

新窗口打开|下载原图ZIP|生成PPT
图8$\alpha $对平纹编织复合材料拉伸应力--应变曲线的影响规律

Fig. 8Effect of $a $on tensile stress-strain curve of plain woven composite



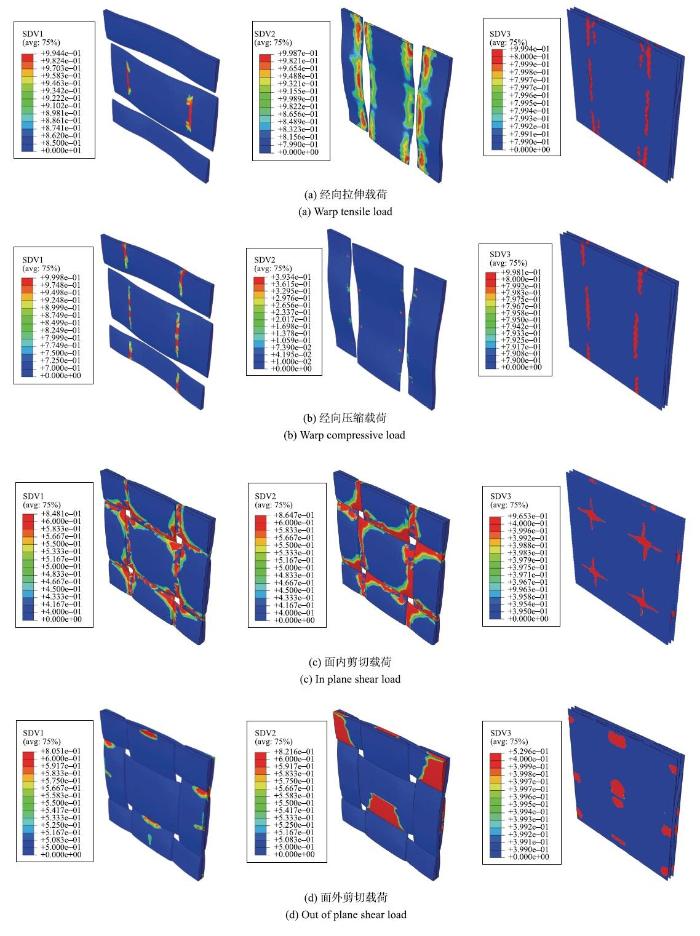
基于上述模型验证结果,对介观尺度单胞分别进行6种边界条件下的渐进损伤模拟,图9给出剪切修正因子取值$\alpha $=0.4时,4种典型载荷下峰值应力处的损伤形式.其中状态变量SDV1和SDV2分别代表纤维束单元的纤维和基体损伤;SDV3代表基体单元的损伤.

如图9(a)所示, 在经向拉伸载荷下, 各种损伤均发生在纤维束交错区域,这是因为纤维束波动效应引起此处剪切应力集中. 对于经向压缩的情况,如图9(b)所示, 经向压缩损伤的分布与经向拉伸较为类似,不同的是由于基体的压缩强度高于拉伸强度,纬向纤维束上并未出现明显的基体损伤. 如图9(c)所示,在面内剪切载荷下,各种损伤主要集中在经、纬纤维束交错形成的4个矩形区域处.如图9(d)所示,面外剪切时的基体单元损伤分布在基体边界的角点和中心点处;纤维束的基体和纤维损伤分别出现在经、纬向纤维束上,且都集中在纤维束波动角最大的区域,这是由于此处的轴向剪切应力 最大.

图9

新窗口打开|下载原图ZIP|生成PPT
图9典型载荷下介观单胞损伤形貌

Fig. 9Damage morphology of meso-scale unit cell under typical loads

4.3 介观到宏观尺度均匀化结果与分析

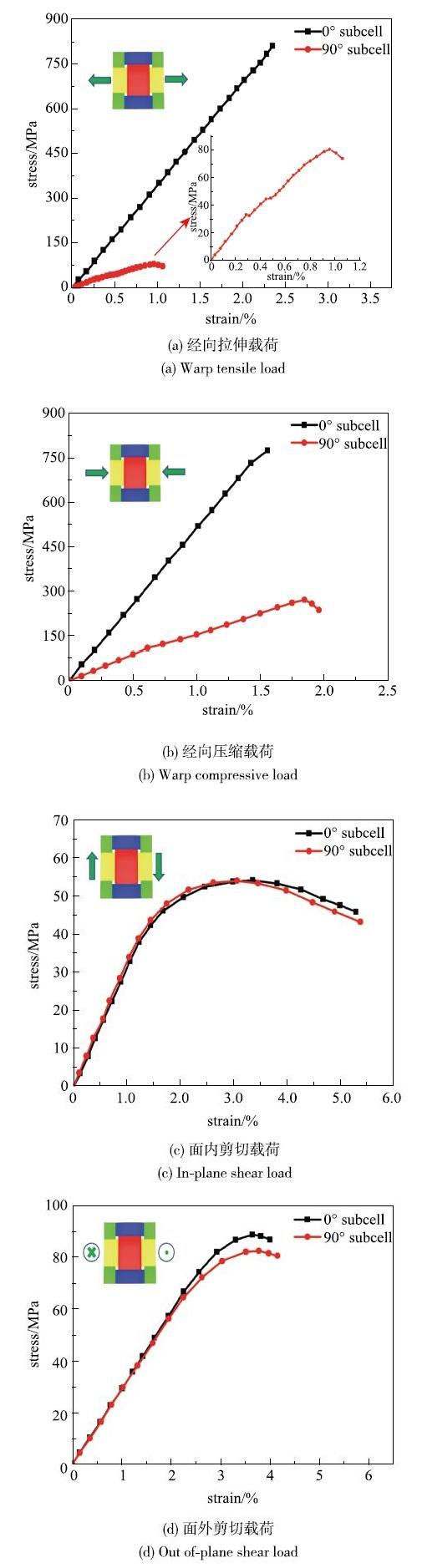
从介观尺度单胞在6种边界条件下的渐进损伤模拟结果中提取0$^\circ$和90$^\circ$子胞的等效应力--应变曲线如图10所示.当施加经向载荷, 如图10(a)和 图10(b)所示,由于0$^\circ$子胞的材料主方向与载荷方向一致, 曲线表现出良好的线性;而90$^\circ$子胞承受着偏轴载荷,基体裂纹的不断增长造成曲线的非线性,曲线的峰值应力和斜率明显低于0$^\circ$子胞. 由于介观单胞的对称性,经向和纬向加载所得的结论几乎完全相同, 为节省篇幅,将不再讨论纬向加载的情况. 如图10(c)和图10(d)所示,0$^\circ$和90$^\circ$子胞的面外及面内剪切的峰值应力均较低,这是因为首先纤维束的剪切强度很小,另一方面纤维束交错区域的剪切应力集中导致纤维束迅速达到剪切强度而丧失承载能力,且0$^\circ$和90$^\circ$子胞的受力状态相同,造成两者的剪切应力应变曲线极为接近.

图10

新窗口打开|下载原图ZIP|生成PPT
图10子胞不同载荷下的应力--应变曲线

Fig. 10Stress-strain curves for subcell under different loadings



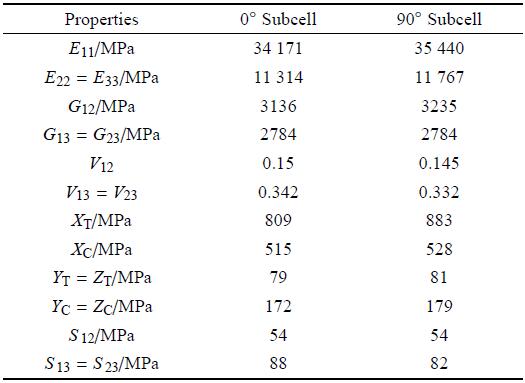
从图10的应力--应变曲线提取0$^\circ$和90$^\circ$子胞的力性能参数如表4所示,其中模量和强度分别由曲线的斜率和最高点决定,可以看出0$^\circ$和90$^\circ$子胞的性能非常接近,这可由介观尺度单胞的对称性 解释.

Table 4
表4
表40$^\circ$和90$^\circ$子胞性能参数
Table 4Mechanical properties of 0$^\circ$and 90$^\circ$subcell

新窗口打开|下载CSV

通过将所得的0$^\circ$和90$^\circ$子胞的性能参数代入平纹编织复合材料子胞模型,进而将子胞模型阵列扩展成为材料的宏观尺度低速冲击模型,实现介观尺度到宏观尺度的均匀化.

4.4 宏观尺度结果与分析

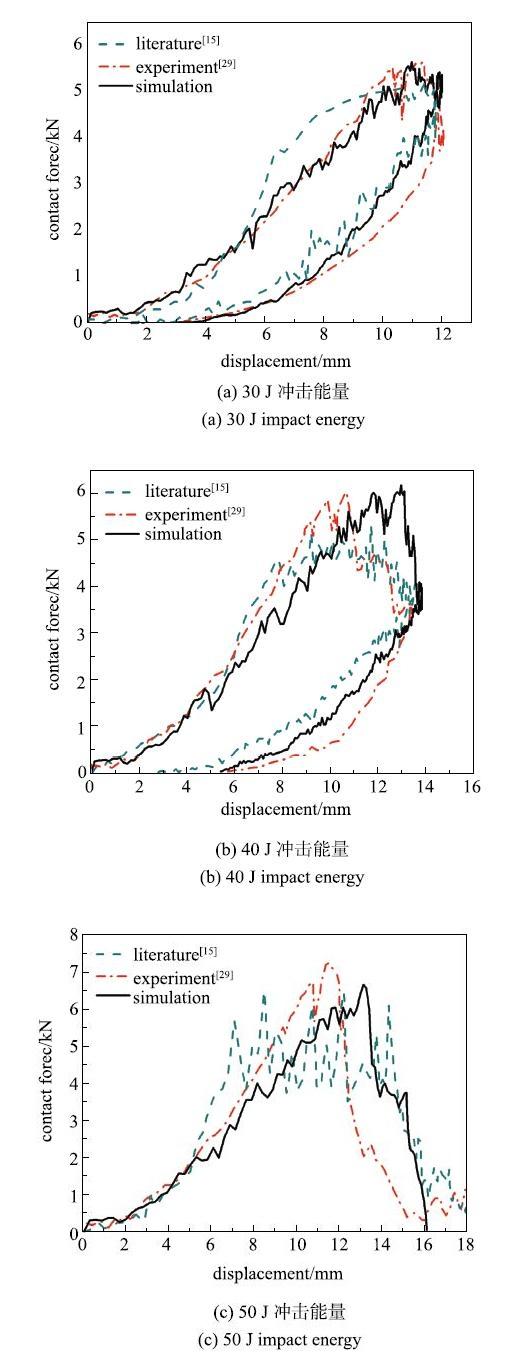
基于上文子胞模型扩展而成的宏观尺度低速冲击模型, 分别进行30 J, 40J和50 J的低速冲击模拟,图11给出了仿真和试验的冲击力--位移曲线对比图. 从图中可以看出,冲击能量为30 J和40 J时的曲线呈闭环样式, 靶板均未被穿透,冲头发生了回弹. 冲击能量为50 J时的曲线呈开环样式, 冲头穿透了靶板,这与文献^[29]的实验现象一致. 在冲击开始阶段没有单元的损伤,接触仅仅发生在冲头和靶板的表面,有限元模型能够充分地反映冲击过程中层合板的弹性变形.由于冲头在模拟中被视为刚体导致在冲头回弹阶段仿真的冲击力要略微地大于试验.表5和表6分别为最大冲击力和吸收能量的对比分析, 从表中可以看出,相较于文献^[15], 本文的预测结果与试验更为吻合.

Table 5
表5
表5仿真最大冲击力与试验最大冲击力对比
Table 5Comparisons of simulation and experiment results of peak contact force

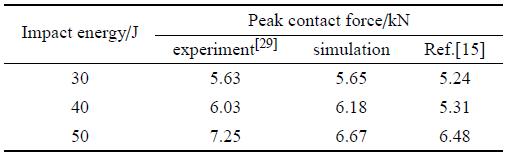新窗口打开|下载CSV

Table 6
表6
表6仿真吸收能量与试验吸收能量对比
Table 6Comparisons of simulation and experiment results of absorbrd energy

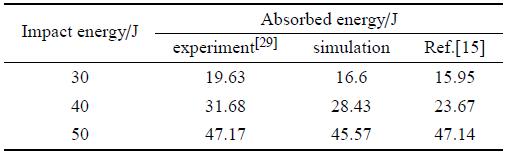新窗口打开|下载CSV

图11

新窗口打开|下载原图ZIP|生成PPT
图11数值模拟和试验冲击力--位移曲线对比

Fig. 11Comparisons of simulation and experiment results of impact force-displacement curves



图12给出了冲击能量为40 J时的仿真和试验^[29]损伤形貌图, 从图中可以看出仿真和试验的损伤形貌非常相似,均在靶板背面出现了严重的纤维断裂,在冲击中心区域周围发生了大量的基体开裂和层间分层.

图12

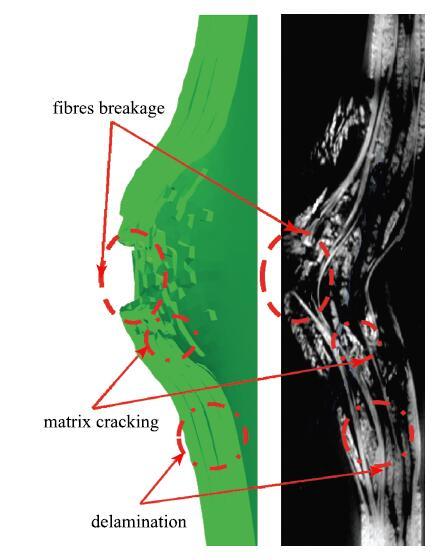新窗口打开|下载原图ZIP|生成PPT
图1240 J 冲击能量下数值模拟和试验^[29]损伤形貌对比

Fig. 12Comparisons of simulation and experiment results^[29] of damage morphology under 40 J impact energy



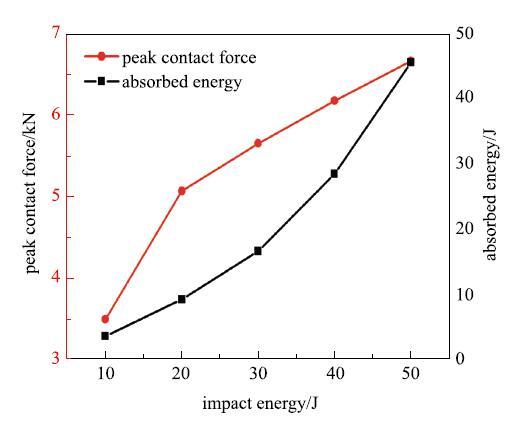
图13给出了冲击能量为10 J$\sim $50 J的冲击响应结果. 从图中可以看出,最大冲击力和吸能与冲击能量基本上呈线性关系; 冲击能量从10 J增加到20J时, 最大冲击力从3.49 kN增加到5.07 kN, 增长了近45.3%,这是因为10 J冲击能量下的冲头并未侵彻靶板,靶板正面和背面均未发生明显的纤维断裂损伤. 而当冲击能量为20 J时,冲头已经部分侵彻靶板, 可以明显地发现纤维断裂损伤后的单元删除;随着冲击能量增大吸能曲线的斜率在不断地增大,表明靶板的吸能效果越来越好, 这是因为在冲击能量较小的情况下基体损伤是主要的失效模式,靶板通过基体损伤的吸能效果要远远小于纤维损伤.另一个原因是随着冲击能量的提高, 靶板的塑性变形程度大幅度提高,吸收了更多来自冲头的动能.

图13

新窗口打开|下载原图ZIP|生成PPT
图13平纹编织复合材料冲击响应

Fig. 13Impact response of plain woven composite



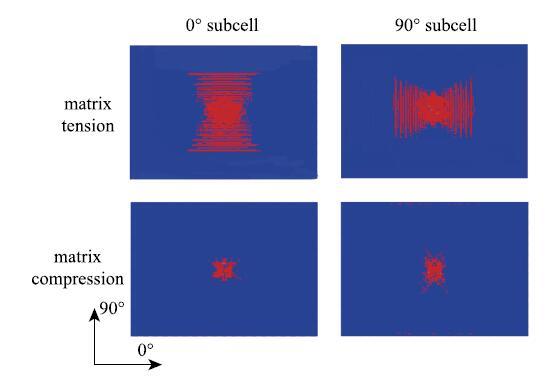
由于单元发生纤维失效后即删除, 无法进行纤维损伤的定量分析,故本文仅研究平纹编织复合材料低速冲击下的基体损伤和分层损伤.图14给出了40J冲击能量下平纹编织复合材料0$^\circ$和90$^\circ$子胞的基体损伤分布情况.可见, 基体拉伸损伤的长轴方向与子胞材料主方向正交,基体压缩损伤的长轴方向与子胞材料主方向一致.基体压缩强度远高于基体拉伸强度,导致基体拉伸损伤面积明显大于基体压缩损伤面积.

图14

新窗口打开|下载原图ZIP|生成PPT
图1440 J 冲击能量下基体损伤示意图

Fig. 14Schematic diagram of matrix damage under 40J impact energy



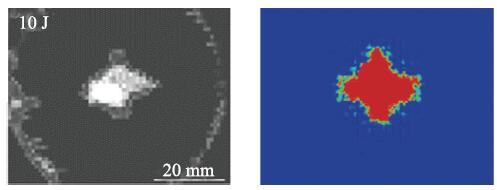
图15给出冲击能量为10 J时数值模拟和试验^[29]分层损伤图的对比, 可以看出两者的分层损伤轮廓非常接近,均近似呈椭圆形分布. 其中试验和仿真的分层损伤面积分别为219mm$^{2}$和240 mm$^{2}$.

图15

新窗口打开|下载原图ZIP|生成PPT
图1510 J 冲击能量下数值模拟和试验^[29]分层损伤图对比

Fig. 15Comparison of simulation and experiment results^[29]of delamination images under 10 J impact energy



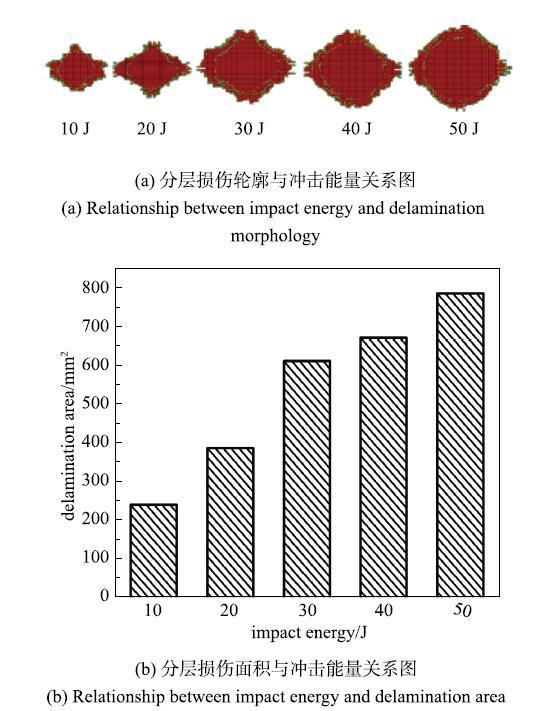
图16给出了10$\sim $50 J冲击能量下的分层损伤数值模拟结果.从图中可以看出, 随着冲击能量的增加,分层损伤轮廓逐渐从椭圆形向圆形转化;分层损伤面积与冲击能量呈正相关, 在冲击能量大于30J时增长速度变缓.

图16

新窗口打开|下载原图ZIP|生成PPT
图16分层损伤数值模拟结果

Fig. 16Numerical simulation results of delamination damage

5 结论

本文首先建立微观尺度单胞得到纤维束的性能参数,并对介观尺度单胞进行6种边界条件下的渐进损伤模拟,采用渐进均匀化方法从介观单胞提取0$^\circ$和90$^\circ$子胞的力学性能,最后搭建平纹编织复合材料的宏观模型进行了不同冲击能量下的低速冲击模拟,得出以下结论.

(1)拉伸载荷下,平纹编织复合材料的纤维和基体损伤主要集中在纤维束交错区域;压缩载荷下, 纤维束上几乎无基体损伤发生; 剪切载荷下,纤维束波动角大的区域极易出现损伤.

(2)平纹编织复合材料可以简化为由0$^\circ$和90$^\circ$子胞上下正交铺设而成,0$^\circ$和90$^\circ$子胞均匀化后的力学性能可近似为完全相同.

(3)宏观低速冲击模拟预测的力学响应和损伤特征与试验结果吻合较好,验证了方法的可行性; 随着冲击能量增大,最大冲击力、材料吸能和分层损伤均增大,分层损伤轮廓逐渐从椭圆形过渡到圆形;基体拉伸和压缩损伤的长轴方向分别与子胞材料主方向正交和一致,损伤面积前者远大于后者.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Zhao ZQ, Dang HY, Zhang C , et al. A multi-scale modeling framework for impact damage simulation of triaxially braided composites
Composites Part A : Applied Science and Manufacturing, 2018,110:113-125
[本文引用: 1]

[2] 马丕波, 蒋高明, 高哲 等. 纺织结构复合材料冲击拉伸研究进展
力学进展, 2013,43(3):329-357
[本文引用: 1]

( Ma Pibo, Jiang Gaoming, Gao Zhe , et al. Advances in impact tensile properties of 3-D textile structural composites
Advances in Mechanics, 2013,43(3):329-357(in Chinese))
[本文引用: 1]

[3] 郭洪宝, 王波, 贾普荣 等. 平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
力学学报, 2016,48(2):361-368
[本文引用: 1]

( Guo Hongbao, Wang Bo, Jia Purong , et al. Mesoscopic danage behaviors of plain woven ceramic composite under in-plane shear loading
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(2):361-368(in Chinese))
[本文引用: 1]

[4] Zhou Y, Lu ZX, Yang ZY . Progressive damage analysis and strength prediction of 2D plain weave composites
Composites Part B : Engineering, 2013,47:220-229


[5] 郭洪宝, 贾普荣, 王波 等. 基于迟滞行为的2D-SiC/SiC复合材料组份力学性能分析
力学学报, 2015,47(2):260-269


( Guo Hongbao , JiaPurong, Wang Bo, et al. Study on constituent properties of a 2D-SiC/SiC composite by hysteresis measurments
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(2):260-269(in Chinese))


[6] 杨成鹏, 矫桂琼, 王波 等. 2D-C/SiC复合材料的单轴拉伸力学行为及其强度
力学学报, 2011,43(2):330-337
[本文引用: 1]

( Yang Chengpeng, Jiao Guiqiong, Wang Bo , et al. Uniaxial tensile stress-strain behavior and strength of plain woven C/SiC composite
Chinese Journal of Theoretical and Applied Mechanics, 2011,42(2):330-337(in Chinese))
[本文引用: 1]

[7] Bandaru AK, Chavan VV, Ahmad S , et al. Low velocity impact response of 2d and 3d kevlar/polypropylene composites
International Journal of Impact Engineering, 2016,93:136-143.
[本文引用: 1]

[8] Grasso M, Xu YG, Ramji A , et al. Low-velocity impact behaviour of woven laminate plates with fire retardant resin,
Composites Part B: Engineering, 2019,171:1-8
[本文引用: 1]

[9] Wang Y, Chen XG, Young R , et al. Finite element analysis of effect of inter-yarn friction on ballistic impact response of woven fabrics
Composite Structures, 2016,135:8-16
[本文引用: 2]

[10] Palta E, Fang H . On a multi-scale finite element model for evaluating ballistic performance of multi-ply woven fabrics
Composite Structures, 2019,207:488-508
[本文引用: 1]

[11] Carpenter AJ, Anderson CE, Chocron S . Mesoscale simulations of high-velocity impact on plain-weave and 3-D weave S-2 glass targets
Procedia Engineering, 2015,103:60-67
[本文引用: 1]

[12] 李裕春, 徐全军, 刘强 等. 平头弹冲击作用下平纹织物的动态响应分析
材料科学与工程学报, 2010,28(3):379-384
[本文引用: 2]

( Li Yuchun, Xu Quanjun , Liu qiang, et al. Dynamic response of plain-woven fabricsubjected to ballistic impact of a flat-nosed projectile
Journal of Materials Science & Engineering, 2010,28(3):379-384(in Chinese))
[本文引用: 2]

[13] Cousigné O, Moncayo D, Coutellier D , et al. Numerical modeling of nonlinearity, plasticity and damage in CFRP-woven composites for crash simulations
Composite Structures, 2014,115:75-88
[本文引用: 2]

[14] Yang B, Wang ZQ, Zhou LM , et al. Experimental and numerical investigation of interply hybrid composites based on woven fabricsand PCBT resin subjected to low-velocity impact
Composite Structures, 2015,132:464-476
[本文引用: 2]

[15] Kinvi-Dossou G, Matadi BR, Bonfoh N , et al. A numerical homogenization of E-glass/acrylic woven composite laminates: Application to low velocity impact
Composite Structures, 2018,200:540-554
[本文引用: 3]

[16] 杨扬, 徐绯, 张岳青 等. 平纹编织C/SiC复合材料低速冲击数值模拟
爆炸与冲击, 2015,35(1):22-28
[本文引用: 2]

( Yang Yang, Xu Fei, Zhang Yueqing , et al. Numerical simulation on low-speed impact responseof 2D plain-woven C/SiC composite
Explosion and Shock Waves, 2015,35(1):22-28(in Chinese))
[本文引用: 2]

[17] Wang H, Wang ZW . Quantification of effects of stochastic feature parameters of yarn on elastic properties of plain-weave composite---Part 1: Theoretical modeling
Composites Part A : Applied Science and Manufacturing, 2015,78:84-94
[本文引用: 1]

[18] Wang H, Wang ZW . Quantification of effects of stochastic feature parameters of yarn on elastic properties of plain-weave composite---Part 2: Statistical predictions vs. mechanical experiments
Composites Part A : Applied Science and Manufacturing, 2016,84:147-157
[本文引用: 1]

[19] 费庆国, 姜东, 陈素芳 等. 高温下编织复合材料热相关参数识别方法研究
力学学报, 2018,50(3):53-63
[本文引用: 1]

( Fei Qingguo, Jiang Dong, Chen Sufang , et al. Thermal-related parameter identification of braided composites at high temperature
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):53-63(in Chinese))
[本文引用: 1]

[20] Dixit A, Mali HS, Misra RK . Unit cell model of woven fabric textile composite for multiscale analysis
Procedia Engineering, 2013,68:352-358
[本文引用: 1]

[21] 王新峰 . 机织复合材料多尺度渐进损伤研究. [博士论文]
南京:南京航空航天大学, 2007
[本文引用: 5]

( Wang Xinfeng . Multi-scale analyses of damage evolution in woven composite materials. [PhD Thesis]
Nanjing: Nanjing University of Aeronautics and Astronautics, 2007(in Chinese))
[本文引用: 5]

[22] Xia ZH, Zhou CW, Yong QL , et al. On selection of repeated unitcell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites
International Journal of Solids and Structures, 2006,43(2):266-278.
[本文引用: 1]

[23] Wang C, Zhong YC, Adaikalaraj PF , et al. Strength prediction for bi-axial braided composites by a multi-scale modelling approach
Journal of Materials Science, 2016,51(12):6002-6018
[本文引用: 1]

[24] Hashin Z . Failure criteria for unidirectional fiber composites
Journal of Applied Mechanics, 1980,47(2):329-334
[本文引用: 1]

[25] Hou JP, Petrinic N, Ruiz C , et al. Prediction of impact damage incomposite plates
Composites Science and Technology, 2000,60(2):273-281
[本文引用: 1]

[26] Tie Y, Hou YL, LI C , et al. An insight into the low-velocity impact behavior of patch-repaired CFRP laminates using numerical and experimental approaches
Composite Structures, 2018,190:179-188
[本文引用: 1]

[27] 孙振辉, 铁瑛, 侯玉亮 等. 相对冲击位置和补片层数对胶接修理CFRP复合材料层合板抗冲击性能的影响
复合材料学报, 2019,36(5):1114-1123
[本文引用: 1]

( Sun Zhenhui, Tie Ying, Hou Yuliang , et al. Effect of relative impact location and patch layer number on impact resistance of adhesive repaired CFRP composite laminates
Acta Materiae Compositae Sinica, 2019,36(5):1114-1123(in Chinese))
[本文引用: 1]

[28] Mulay SS , Udhayaraman R. On the constitutive modelling and damage behaviour of plain woven textile composite
International Journal of Solids and Structures, 2019, 156- 157:73-86
[本文引用: 1]

[29] Matadi BR, Coulibaly M, Khabouchi A , et al. Glass fibres reinforced acrylic thermoplastic resin-based tri-block copolymers composites: low velocity impact response at various temperatures
Composite Structures, 2017,160:939-951
[本文引用: 8]

[30] Chamis CC . Mechanics of composites materials: past,present and future
Journal of Composites Technology and Research, 1989,11(1):3-14
[本文引用: 1]