,2)北京航空航天大学生物医学工程高精尖创新中心, 生物与医学工程学院,北京 100083A RESONANCE FREQUENCY EXTRACTION METHOD FROM LOW Q-FACTOR MATERIALS BASED ON RESONANT ULTRASOUND SPECTROSCOPY1)
Zhang Qiang, Fan Fan, Wang FeiNiu, Shen Fei, Niu Haijun,2)Beijing Advanced Innovation Center for Biomedical Engineering, School of Biological Science and Medical Engineering, Beihang University, Beijing 100083, China通讯作者: 2) 牛海军, 教授, 主要研究方向：生物力学, 医学超声,生物医学信号处理等. E-mail:hjniu@buaa.edu.cn
收稿日期:2019-03-2网络出版日期:2019-09-18
| 基金资助: |
Received:2019-03-2Online:2019-09-18
作者简介 About authors
摘要
超声共振谱技术通过测量样本在超声激励下产生的固有共振频率来计算弹性参数,而共振频率的提取是整个测量过程的关键.低$Q$值(品质因数)材料由于其衰减特性,导致共振谱平缓并无法直观地从谱图上观察得到共振频率,为从中提取更为有效的共振频率, 本文提出了一种新的共振频率提取方法.采用经验模态分解法将材料频率响应自适应分解为有限个具有特殊振荡特性的固有模态函数分量,根据材料的超声共振谱先验信息选择具有共振频率特性的固有模态函数分量,并从中提取共振频率. 以短切纤维环氧树脂材料(仿骨材料, $Q \approx$25)为例, 通过实验与传统线性预测方法进行对比,计算弹性系数和工程模量. 实验结果表明新方法的计算效率高,对弱激发模态更为敏感,共振频率的匹配数量(26)多于传统方法(21)且满足5倍于弹性系数的估计要求,优化后的弹性模量更接近标准值.新方法可从低$Q$值材料平缓的频谱中提取数量足够且有效的共振频率,不仅有效提升了力学参数估计的可靠性,而且拓展了超声共振谱技术的应用范围.
关键词：
Abstract
Resonant ultrasound spectroscopy (RUS) allows identification of the elastic coefficients of solid materials vibrating under an ultrasonic excitation from the measurement of their inherent frequencies. Retrieving the resonant frequencies is therefore a key signal processing step in RUS. However, according to the attenuation characteristics of low $Q$-factor (quality factor) materials, the resonance spectrum obtained by the experiment is flat and the resonance frequencies can not be directly observed from the spectrum. Therefore, in order to retrieve more effective resonance frequencies than traditional approach from the low $Q$-factor materials, a new extraction method of resonance frequencies was proposed to solve the limitation in this paper. The empirical mode decomposition method was used to decompose the frequency response of the specimen into finite Intrinsic Mode Function (IMF) components with special oscillation characteristics. According to the prior information of resonant ultrasound spectroscopy (RUS),the relevant IMF component was selected to retrieve reliable resonance frequencies from the resonance spectrum. The short fiber filled epoxy (a kind of bone-like materials, $Q \approx $25) was adopted as the specimen to calculate the elastic coefficients and engineering moduli compared with the traditional linear prediction method. The experimental results show that the new method has high computational efficiency and is more sensitive to the weak excitation modes of low $Q$-factor materials. The number of effective resonance frequencies (26) are more than traditional linear prediction methods (21), which also satisfied 5 times estimation requirement of elastic constants. In addition, the optimized elastic moduli are closer to the standard values of the short fiber filled epoxy. In conclusion, the EMD-based method can retrieve a sufficient quantity and effective resonance frequencies from the flat spectrum of low $Q$-factor materials, which can not only improve the reliability of the estimation of mechanical parameters, but also extend the application range of resonant ultrasound spectroscopy.
Keywords：
PDF (3928KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张强, 樊璠, 王蕊, 沈飞, 牛海军. 一种基于超声共振谱的低Q值材料共振频率提取方法1). 力学学报[J], 2019, 51(5): 1500-1506 DOI:10.6052/0459-1879-19-049
Zhang Qiang, Fan Fan, Wang FeiNiu, Shen Fei, Niu Haijun.
引言
超声共振谱[1-3](resonant ultrasound spectroscopy,RUS)是二十世纪九十年代发展起来的一种材料力学特性测量方法,被物理学家认为是测量高$Q$值(品质因数)固体材料弹性系数最准确的方法.基本原理是运用超声激励样本产生自由振动,根据测得的多个固有共振频率频谱,利用反演方法计算材料的弹性系数[2].方法的独特之处在于可用于尺寸极小[4]($<$1mm)材料样本的无损检测,一次实验能够估计样本的全部弹性系数和力学参数,且具有高度可重 复性.品质因数[5-7]$Q$是材料在拉伸、剪切、体积压缩、纵向压缩中测量得到的储能模量与损耗模量之比,是弹性材料的一个重要参数. $Q$值愈大, 说明材料变形中储能占比愈大,材料愈接近理想弹性.低$Q$值材料(通常$Q<50$)包括生物硬组织材料[8-9](牙齿、骨骼)和一些合成材料,其力学特性的准确测量对深刻理解其功能,选择力学相容性材料和研究内部结构变化等方面具有重要的理论研究意义和实际应用价值.然而, RUS在用于低$Q$值材料测量时存在天然缺陷.主要原因在于材料的高衰减特性[10]导致了共振谱的谱峰平缓,无法直观地从谱图上观察得到共振频率. 为了能够获取共振频率,Lebedev等[11-13]研究者结合线性预测法,提出了平缓共振谱中的共振频率提取技术,并在内含缺陷的低$Q$值岩石样本的固有共振频率提取研究中得到了良好结果.随后,Kinney等[14-15]通过洛伦兹线性拟合方法提取了干湿状态下牙本质的固有共振频率,研究了牙组织的弹性系数与力学特性. 近年来Pascal的研究小组[16-18]利用线性预测法成功测量了$Q$值更低的皮质骨的弹性系数,打破了RUS对于低$Q$值材料弹性常数测量的限制.Niu的研究小组[19]同样运用上述方法提取牙本质的共振频率,结合RUS测量估计了多个弹性系数, 并计算了弹性模量与泊松比,得到了一致性较好的重复测量结果.
目前, 线性预测法仍是提取低$Q$值材料共振频率主流方法,并在生物材料中得到了广泛应用. 但是,该方法在提取共振频率时存在3个问题[11,16]： (1)方法假设谱线是由多个洛伦兹线型叠加而成的,而拟合叠加后的曲线与原谱线存在着差异,很可能导致共振频率的信息损失; (2) 为降低拟合的复杂度,传统方法须人为对共振频谱分段,但重叠频段中提取的共振频率往往存在不一致的情况,导致频率的筛选较为困难; (3)在拟合过程中,线性预测滤波器的阶数会影响提取效果, 缺乏相应的标准,需反复多次试验或人为确定阶数.
针对上述问题,本文提出了一种针对平缓共振峰中共振频率提取的自适应方法,基于经验模态分解和RUS先验条件,提高低$Q$值材料共振频率提取的数量和有效性,从而有助于提升RUS对力学参数估计的可靠性.
1 实验和方法
1.1 共振频率提取算法
本文将引入经验模态分解[20](empirical mode decomposition,EMD)方法对低$Q$值材料平缓的共振谱进行分解和研究,EMD作为一种非平稳信号处理方法, 可根据信号自身的特征进行平稳化处理,将复杂的信号序列分解为有限平稳的固有模态函数(intrinsic mode function, IMF), IMF需满足两个条件, 一是在整个数据段内,局部极值点和过零点的数目必须相等, 或最多相差1个; 二是在任意时刻,有局部极大值点形成的上包络线和局部极小值点形成的下包络线的平均值为零.因此, 任何一个信号可以分解成若干有限个IMF分量之和,其筛选步骤如下：步骤 1 找出数据序列的$x(n)$中所有极大值和极小值,利用三次样条插值函数拟合出上下包络线, 得到第一个均值记为 $p_1(n)$, $x(n)$与均值的差值记为 $h_1 (n)$
步骤 2 $h_1 (n)$作为新的数据序列,检查其是否满足IMF成立的条件. 如果不符合, 返回第一步将$h_1 (n)$替换$x(n)$, 再次进行筛选至满足条件, 例如进行了$k$次筛选
步骤 将满足条件的 $h_k (n)$作为第一阶分量IMF分量 $c_1(n)$, 用原始信号 $x(n)$减去 $c_1 (n)$得到残余数据 $r_1(n)$
步骤 4 将$r_1 (n)$作为新的原始信号重复上述筛选步骤,直到筛选得到的差值数据 $r_{m + 1} (n)$单调时终止
步骤 5 还原信号, 原始信号
$x(n)$可以表示成IMF分量与残余项和形式
式中, 残余项$r_{m + 1} (n)$代表了信号中的平均趋势, 而各个IMF分量$c_i(n)$则表征了信号从高频到低频的分布.这种方法高效、简便且具有完备性.相比传统线性预测方法,信号经过EMD分解后得到的IMF分量能够将原始信号完全重构,不损失原始信号的任何信号特性. 将 $r_{m + 1} (n)$作为第$m+$1个IMF 分量, 频率响应 FR可看作
将式(5)两边分别平方得
原始信号的正交指数$OI$定义为
若 OI为0, 则表明IMF分量具有正交特性.Huang等[20]通过大量的试验发现,一般信号的正交性指标通常不会超过1%,因此认为各IMF分量是近似正交的, 且具有特殊的物理意义,即每个IMF分量代表原始信号在不同尺度上的振荡特性.基于IMF分量的正交特性, 我们假设实验材料的共振谱信号经EMD分解后,存在某一IMF分量具有与共振频率相一致的振荡特性,其局部极大值即为对应的共振频率值.
在存在噪声等干扰时, EMD分解很可能出现模式混叠问题[21-23], 导致IMF包含不同的振荡模式或单个振荡模式分布于多个IMF中.本文进一步采用集成的方法[24-25](ensemble empirical mode decomposition, EEMD)解决该问题,EEMD是一种噪声辅助数据分析方法, 在目标数据$x(n)$中依次加入多组高斯白噪声序列 $s(n)$,通过取平均的方式消除模式混叠, 使各IMF分量更具独有的物理特性.至此,我们将低$Q$值材料中共振频率的提取问题转化为识别具有共振频率特性的IMF分量,并从中提取所需的共振频率.频率响应FR经EEMD分解得到具有完备性和正交性的IMF分量,从材料先验信息[16]中得到理论共振频率的数量$N_{\rm cal}$,目标IMF的波峰数量$N_{\rm imf}$最接近且小于$N_{\rm cal}$,具体实现过程如图1所示.
图 1
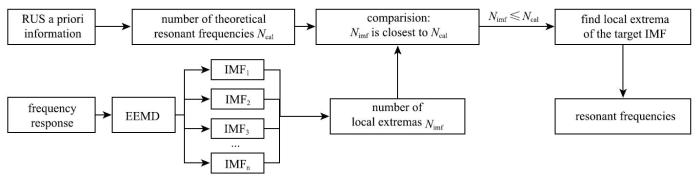新窗口打开|下载原图ZIP|生成PPT图 1共振频率提取算法流程图
Fig. 1Flow chart of resonance frequency extraction method
图 2
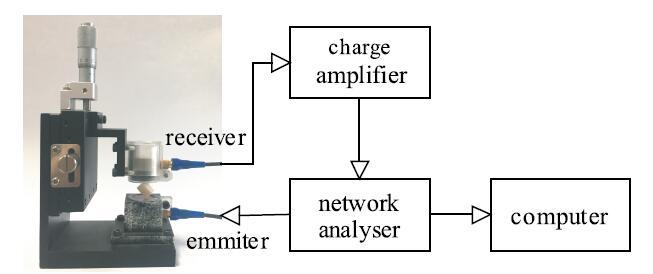新窗口打开|下载原图ZIP|生成PPT图 2超声共振测量实验平台
Fig. 2Experiment platform of resonant ultrasound spectroscopy
1.2 实验系统
本文选用已知工程模量的短切纤维环氧树脂[17](常用仿骨材料, Sawbone公司产品, $Q<30$) 为实验对象,样本呈立方体状, 采用低速金刚石切割机(SYJ-150,沈阳科晶自动化设备有限公司, 精度0.01 mm)和全烧结金刚石锯片(厚0.3mm), 在喷水状态下切割样本, 然后分别使用 500, 800,2000目砂纸对切割后的样本进行打磨. 测得尺寸40 mm$\times $50 mm $\times $60 mm, 重量为196.3 mg.实验系统由一组超声探头、信号发生与接收器和计算机组成(如图3).样本的两个对角夹在两个剪切波接触式超声探头(V154RM, Panametrics Inc., US)之间, 其超声探头频率为2.25 MHz, 分辨率约为26 Hz.矢量分析仪(Bode 100, Omicron electronics GmbH, AT)为激励探头提供70$\sim$400 kHz的扫频信号, 频率响应由上方的探头接收,由电荷放大器(HQA-15M-10T, Femto Messtechnik GmbH,DE)放大后送回矢量分析仪记录,共振谱分析和力学参数计算在计算机中进行[26].图 3
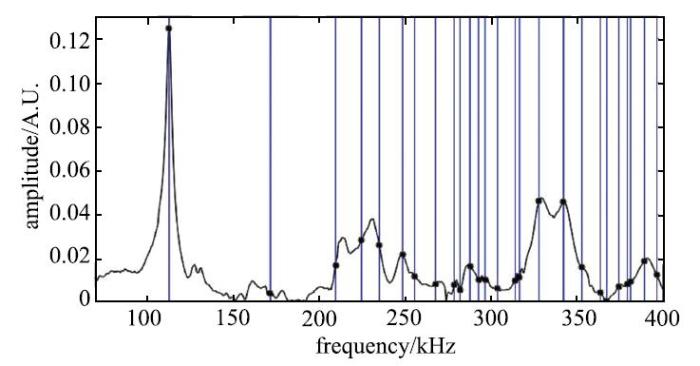新窗口打开|下载原图ZIP|生成PPT图 3样本在70$\sim$400 kHz范围中一次频率响应和用新方法提取的26个共振频率(*标出的位置为6次实验中出现3以上的共振峰位置, 直线表示共振峰均值)
Fig. 3One of 6 frequency response of the specimen between 70 and 400 kHz and 26 resonant frequencies distributions by new method (*: The calculated resonant frequencies presented in at least 3 times; vertical line: the mean values of the resonant frequencies)
1.3 理论共振频率计算
假设样本为横观各向同性[27]材料, 其有5个独立的弹性常数,如式(9)所示. 由于短切纤维环氧树脂常用作仿骨材料,这里采用一组皮质骨弹性系数作为初始值[17], $C_{11} = 15.0$GPa, $C_{12} $=7.6 GPa, $C_{13} = 8.4$GPa, $C_{33} = 23.1$GPa,$C_{44} = 4.3$GPa.根据弹性常数 $C_{ij}$初值, 利用寻找拉格朗日方程$L$驻点的方法可以计算样本理论共振频率
其中, $\rho $和$V$分别为样本密度和体积, $c$为材料初始弹性常数,$u_i $为位移场.采用瑞利里兹法[8](Rayleigh-Ritz)进行式(10)的求解,通过定义目标函数$F(C)$
其中, $f_i^{\rm cal}$为第$i$个理论共振频率, $f_i^{\exp }$为第$i$个实验共振频率, $N$为实验共振频率个数, $w_i$为权重.采用莱文贝格--马夸特方法[2](Levenberg-Marquardt)计算,在收敛条件下, $F(C)$达到最小时的$C$即为所测量样本的弹性常数.
2 结果
如图3所示, 样本频谱除了有几个明显的波峰外, 大部分谱线相对平缓.为更多激发某些不敏感的共振模式, 需多次调整样本与超声探头的位置,我们对样本共测量6次, 标准差阈值设为0.5%[28].新方法提取的共振频率如图3所示, 通过比较发现新方法计算更为高效,相同条件下提取效率约为线性预测法的15倍.根据样本的密度及尺寸, 计算样本的理论共振频率并选取前50阶,作为超声共振实验的扫频范围参考. 如表2所示,单个共振频率的匹配以相对误差Err%为阈值,而样本整体的弹性系数估计以均方根误差RMS为筛选标准.Ulrich等[29]认为在测量低$Q$值材料(如含缺陷岩石)时,RMS小于1%即为有效, 短切纤维环氧树脂材料的Q值约为25,这里将 Err %设置为1%,通过试错法[16]分别匹配了26和21个共振频率, 验证了假设,最终得到的RMS分别为0.44%和0.45%.
Table 2
表2
表2弹性系数与工程模量的优化结果
Table 2
 |
新窗口打开|下载CSV
迭代优化后的弹性系数和工程模量如表2所示, $E_\tau$表示横向的工程模量, $E_\alpha$表示纵向拉伸和压缩的工程模量[30-31],样本标准值由拉压实验得到,新方法提取的共振频率得到的工程模量更为准确.
3 讨论与总结
本文提出了一种从低$Q$值材料中提取固有共振频率的新方法,采用经验模态分解法将材料频率响应自适应分解成多个具有独立物理特性的IMF分量,根据材料的超声共振谱先验信息选择具有共振峰特性的IMF分量,提取相应的共振频率和品质因子.以已知工程模量的短切纤维环氧树脂样本为例,比较两种方法提取的共振频率在RUS应用中的计算效果,验证所提方法的有效性.Migliori等[2]认为可靠的弹性系数估计要求共振频率为弹性系数的5倍以上(最优是8$\sim$10倍),但在低$Q$值材料中很难实现. 我们假设样本为横观各向同性材料,即需25个有效实验共振频率,表1表明仅有新方法可以实现共振频率的提取数量要求. 从表2中不难发现,采用传统线性预测法得到的工程模量$E_\alpha$严重失真(误差约为20%), 而采用新方法提取的共振频率,能够估计得到更为准确的工程模量,表明方法能够从平缓的频谱中准确识别出有效的固有共振频率,为RUS测量低$Q$值材料的力学性质提供保障.主要原因在于新方法在假设和算法特点方面更适用于低$Q$值材料：第一,经验模态分解具有完备性, 各IMF分量合成后的曲线与原曲线一致,避免了信息丢失的问题; 第二, 新方法可自适应提取共振频率,无需设定参数和划分频段, 所得共振频率具有全局特征; 第三,通过集成后的IMF分量更具独特的振荡特性,有助于提高共振频率的识别率和提取精度.
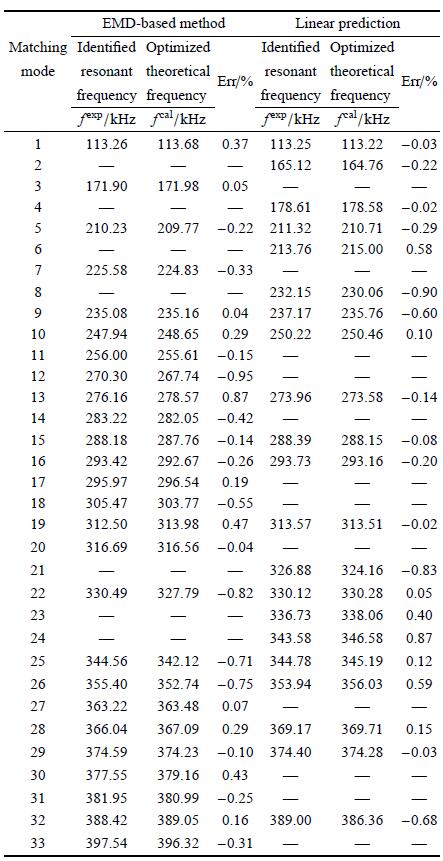
Table 1
表1
表1优化后的理论共振频率与实验共振频率配对结果
Table 1
 |
新窗口打开|下载CSV
本文采用的短切纤维环氧树脂材料($Q \approx $25)属于高衰减材料,RUS应用于低$Q$值材料的局限性主要在于共振谱相对平缓,导致难以准确提取共振频率. 实际过程中仅能提取部分共振频率,在后续的匹配过程中还将剔除误差较大的共振频率,导致实际匹配数量远低于理论值. 对比两种方法的共振频率匹配结果,不仅证明了低$Q$值材料共振频率的提取难度, 而且反映出新方法的有效性.从表1中发现新方法在低幅值的高频区域(360$\sim$400 kHz)提取效果更好,表明目标IMF能够更好地识别弱激发模态.表2中由新方法计算得到的工程模量较传统线性预测法更接近样本标准值,但二者均低于且不在其标准值范围内,原因可能是某些共振频率缺失导致的计算偏差,也侧面印证了RUS应用于测量低$Q$值材料弹性系数的难度.
RUS中弹性系数估计是一个多参数并行优化的问题,误差较大的共振频率容易导致整体估计出现严重错误,这对共振峰提取提出了更高的要求. 根据表1匹配结果发现,传统线性预测法提取的某些共振频率间隔过于接近,可能是仅为满足洛伦兹拟合结果而并不真实存在的共振峰,代入RUS计算后导致整体计算结果出现严重偏差,而表2结果从侧面印证了基于经验模态分解的共振频率提取算法能够得到更丰富且有效的共振频率,从而为后续的弹性系数准确估计提供了保障. 与此同时,我们采用了不同样本进行实验, 并得到了一致的结论.
综上所述, 本文提出的新方法计算效率较高,能够从低$Q$值材料的平缓共振谱中识别更多且有效的共振频率,满足RUS方法对共振峰的数量要求, 对弱激发振动模态更为敏感,提取结果与理论共振频率匹配效果更好,比传统线性预测方法有着明显的优势, 拓宽了RUS的应用范围,使其能够更为有效地测量低$Q$值材料的力学性质.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 4]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
