,*,2), 刘仓理,?,3), 蔡灵仓?, 胡昌明*, 俞宇颖*, 胡凌*A MODEL OF NEUTRON IRRADIATION EMBRITTLEMENT FOR METALS1)
Ye Xiangping,*,2), Liu Cangli,?,3), Cai Lingcang?, Hu Changming*, Yu Yuying*, Hu Ling*通讯作者: 2)叶想平,助研,主要研究方向：辐照金属材料的本构关系与断裂特性. E-mail:yxpxiaogao13@163.com3)刘仓理,研究员,主要研究方向：冲击动力学. E-mail:cangliliu@sohu.com
收稿日期:2019-01-18网络出版日期:2019-09-18
| 基金资助: |
Received:2019-01-18Online:2019-09-18
作者简介 About authors
摘要
金属材料的辐照脆化问题一直以来都是核能安全领域亟待解决的关键问题之一.为了更准确地预测金属材料的辐照脆化行为,基于Johnson-Cook本构模型,将未辐照金属材料的断裂真应力取作辐照材料的断裂真应力,建立了通过辐照退火态金属材料屈服强度就能够预测其整个真应力$\!$-$\!$-$\!$应变曲线,以及断裂真应变的辐照脆化模型.实验研究了不同中子剂量辐照退火态高纯铝的准静态拉伸真应力$\!$-$\!$-$\!$应变曲线、断裂真应力和断裂真应变随辐照剂量的变化规律.结果表明,辐照剂量越高,高纯铝的屈服强度越高,断裂真应变越低,但断裂真应力几乎不变.通过TEM显微分析获得了高纯铝内部辐照缺陷的尺寸和数密度随辐照剂量的变化规律,结果表明,辐照剂量越高,孔洞的尺寸和数密度越高,但位错环尺寸和数密度始终很小,难以准确统计.由辐照高纯铝实验数据拟合得到了辐照脆化模型所需参数,并检验了该模型的预测效果.结果表明,无论是通过实验还是显微分析得到辐照高纯铝的屈服强度,模型的预测结果均能够与实验结果较好地吻合,且模型对退火态高纯铝临界中子剂量的预测值也与文献结果一致.
关键词：
Abstract
Irradiation embrittlement of metals is very important in the field of nuclear energy safety. In order to describe the irradiation embrittlement behavior of metals, a neutron irradiation embrittlement model for annealed metals was proposed based on Johnson-Cook constitutive model. The fracture true stress of the irradiated samples was taken as the same as the unirradiated sample. This model can predict the whole true stress-strain curve, and the fracture true strain of the irradiated annealed materials by using the yield strength only. The tensile true stress-strain curves, the fracture true stress, and the fracture true strain of high-purity aluminum with different doses were measured by quasi-static tensile tests. The results showed that a higher dose results in a higher yield strength and a lower fracture true strain. However, the fracture true stress is almost unchangeable. The size and number density of irradiation-induced defects for high-purity aluminum with different doses were mearsured by TEM microscope. The results showed that a higher dose results in a higher size and a higher number density of voids, but the size and the number density of dislocation loops were difficult to measure accurately due to their size and number density are too small. The parameters of this model were fitted by experimental data of high-purity aluminum, and the application effect of this model was checked. The predicted results of this model agree well with the experimental data, regardless wtether the yield was obtained by quasi-static tensile tests or by the size and number density of irradiation-induced defects. The critical irradiation dose of annealed high-purity aluminum predicted by this model also agrees well with literature.
Keywords：
PDF (16534KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
叶想平, 刘仓理, 蔡灵仓, 胡昌明, 俞宇颖, 胡凌. 中子辐照金属材料的脆化模型研究1). 力学学报[J], 2019, 51(5): 1538-1544 DOI:10.6052/0459-1879-19-025
Ye Xiangping, Liu Cangli, Cai Lingcang, Hu Changming, Yu Yuying, Hu Ling.
引言
核能具有资源丰富,环境友好等优势,使得人类有望在不久的将来终极解决能源问题[1-2]. 核反应堆防护结构材料在服役过程中接受中子辐照发生脆化,使其在外部载荷作用下更容易发生断裂,降低反应堆的安全可靠性能. 因此,金属材料的辐照脆化一直是核能安全领域亟待解决的关键问题之一[3-8].辐照脆化模型是评估和预测反应堆防护结构材料脆化性能的关键.目前,世界各核大国在工程中应用的辐照脆化模型均是基于大 数据统计的半经验唯象模型[1,9].这些唯象模型的形式也很简单,各国均每隔数年从反应堆内取出预先放置的与反应堆防护结构材质相同的监测试样,并对试样开展不同温度的断裂韧性测试实验,获得不同中子剂量监测试样的参考零塑性转变温度增量($\Delta RT_{\rm NDT} $)统计数据.通过不断积累实验数据,拟合得到$\Delta RT_{\rm NDT} $随中子剂量和实验温度的变化趋势,由此拟合出$\Delta RT_{\rm NDT} $随中子剂量和实验温度的变化规律,再引入一定的安全系数,便建立了各自防护结构材料所特有的半经验辐照脆化模型[1,9-11].除中子剂量外,部分元素(尤其是Cu和P)在辐照过程中发生偏析也能够显著降低材料韧性,各国使用的防护结构材料不同,因此,各自关注的元素种类也不尽相同,例如：法国、俄罗斯只关注Cu,P元素[12-14],欧盟和美国比较关注Cu, P, Ni元素[15-17],而日本则关注Cu, P/Si,Ni元素[9]. 这类半经验的辐照脆化模型研究较早,已经积累了大量实验数据,长期以来也保障了反应堆的安全运行.但该类模型的预测结果普遍偏保守,安全裕值大,不利于进一步提高核能效益;缺乏对材料辐照脆化物理机制的描述能力,也缺乏描述辐照材料其它断裂性能参量的能力(如：断裂应变等)[10,18].因此,为了更准确预测辐照材料的脆化行为,发展基于材料自身形变和断裂特性,不依赖特定材料,且具有更广泛的断裂性能描述能力的辐照脆化模型就显得十分必要[10,18-20].
近年来,Byun等[21-25]总结分析了大量辐照退火态金属材料的准静态拉伸应力$\!$-$\!$-$\!$应变曲线数据,发现不同中子剂量辐照材料的真应力$\!$-$\!$-$\!$应变曲线在应变轴正向上平移适当应变量,能够使其塑性段与未辐照材料的真应力$\!$-$\!$-$\!$应变曲线重合, 表明相同真应力条件下,材料的应变硬化率与辐照剂量无关.Byun等[21-22,25]进一步研究发现,辐照剂量低于临界剂量$D_{\rm c}$(退火态金属材料发生完全脆性断裂所需最小中子剂量值)时,退火态金属材料的准静态拉伸断裂真应力与辐照剂量无关,可将未辐照材料的断裂真应力取作辐照材料的断裂真应力,且以上现象普遍存在于退火态BCC, FCC和HCP金属材料中.因此,只要能够获得辐照退火态金属材料的屈服强度,以及相应未辐照材料的准静态拉伸真应力$\!$-$\!$-$\!$应变关系和断裂真应力,就能够预测辐照材料的断裂真应变. 这就将预测辐照材料的断裂真应变转变为预测其屈服强度(将辐照脆化问题转化为辐照硬化问题).无论是精确控制实验加载条件,无损(避免材料进入塑性,卸载后弹性形变能够完全恢复)获得材料的屈服强度实测值;还是通过显微分析统计得到辐照材料内部孔洞尺寸和数密度,结合辐照硬化理论模型计算获得辐照材料的屈服强度,都将极大地降低实验难度[26-27]. 这对于建立更加通用和普适的辐照脆化模型具有非常重要的意义.本文基于Johnson-Cook(J-C)本构关系[28],建立能够预测中子辐照退火态金属材料真应力应变曲线和断裂真应变的量化分析模型.以退火态高纯铝为研究对象,研究了中子辐照高纯铝的准静态拉伸形变和断裂特性随辐照剂量的变化规律,检验了该辐照脆化模型的预测能力,结果表明,模型预测结果与实验结果吻合较好.
1 辐照脆化理论模型
首先基于J-C本构关系建立了中子辐照退火态金属材料的本构模型[28].由于相同真应力条件下,大量中子辐照退火态金属材料的应变硬化系数与辐照剂量无关,因此,可将辐照剂量对材料真应力$\!$-$\!$-$\!$应变关系的影响转换为平移真应变量,进而添加到整体真应变中[21-25].同时,准静态加载条件下,可忽略应变率效应以及绝热温升效应,常温实验条件又可忽略温度软化效应.因此,改进的J-C模型为式中,$\varepsilon _{\rm dpa} = \beta \sqrt[{}^{^n}]{\dfrac{\Delta \sigma _{\rm dpa}}{B}}$为辐照材料真应力$\!$-$\!$-$\!$应变曲线塑性段与未辐照材料的真应力$\!$-$\!$-$\!$应变曲线重合所需的真应变平移量,$\Delta\sigma _{\rm dpa} $为辐照引起的屈服强度增加量,$\beta $为拟合参数. $A$,$B$和$n$分别为未辐照金属材料的准静态拉伸屈服强度、应变硬化系数和硬化指数,$\sigma $和$\varepsilon $分别为真应力和真应变.通过少数几个剂量点辐照材料的实验数据,拟合得到式(1)所需参数,以及确定材料的断裂真应力后,只需获得其他剂量点材料的屈服强度就能够预测其整个塑性段的真应力$\!$-$\!$-$\!$应变关系,及其断裂真应变.
辐照缺陷引起的金属材料屈服强度增加量与缺陷尺寸和数密度的关系为
式中,$M=3.06$和2.6分别对应FCC和BCC金属,$G$和$b$分别为材料剪切模量和伯格矢量,$N$和$d$分别为辐照缺陷的数密度和平均直径,$\alpha $为强化系数.因此,只需通过显微分析获取辐照退火态金属材料内部辐照缺陷尺寸和数密度,结合式(1)就能够预测其整个真应力$\!$-$\!$-$\!$应变曲线关系,以及断裂真应变.
2 中子辐照退火态高纯铝实验结果与分析
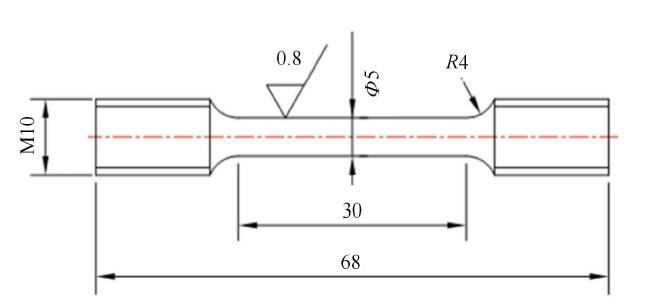
本实验所用材料为完全退火态高纯铝(纯度99.999,5%),能够避免其他金属材料的高中子活化率给后续实验研究带来的放射性问题[29-32]. 实验样品尺寸如图1所示.将原始样品放入研究堆中接受不同剂量的快中子辐照,辐照温度为40$^\circ$C,辐照剂量分别为0.01,dpa, 0.09,dpa, 0.22,dpa和0.83,dpa.准静态拉伸实验的横梁位移速度为2,mm/min,工程应变率为1.1$\times $10$^{-3}$,s$^{-1}$.图1
新窗口打开|下载原图ZIP|生成PPT图1实验样品尺寸图
Fig. 1Dimension of specimen
不同中子剂量高纯铝的准静态拉伸工程应力$\!$-$\!$-$\!$应变曲线如图2(a)所示,随着辐照剂量的增加,高纯铝屈服强度($\sigma_{0.2}$)和极限拉伸强度(及最大拉伸工程应力,UTS)不断增大,均匀延伸率(即材料发生颈缩前的均匀延伸率,取UTS对应的延伸率为均匀延伸率,ER)不断降低,表现出典型的辐照硬化和脆化效应.大量退火态金属材料在0.1,dpa附近时,其工程应变硬化系数就趋近于零,同时出现过屈服点的现象[3,5,21,24,33].然而,0.83,dpa的辐照高纯铝依然具有一定的工程应变硬化率,且未出现过屈服点现象,如图2(a)所示,表明高纯铝的$D_{\rm c}$更高,抗辐照脆化性能较强.将工程应力$\!$-$\!$-$\!$应变曲线转换为真应力$\!$-$\!$-$\!$应变曲线后,如图2(b)所示.高纯铝的断裂真应变(即真应力$\!$-$\!$-$\!$应变曲线应变硬化率为0时对应的真应变值,也称失稳真应变,$\varepsilon_{\rm PIS}$)随辐照剂量的增加而降低,其断裂真应力(即真应力$\!$-$\!$-$\!$应变曲线应变硬化率为0时对应的真应力值,也称失稳真应力,$\sigma_{\rm PIS} $)却基本恒定在60.5,MPa,表现出$\sigma _{\rm PIS}$与辐照剂量无关的特性,这与Byun等[21-22,25]总结的大量中子辐照退火态金属材料的断裂真应力与辐照剂量无关的结果一致.
图2
新窗口打开|下载原图ZIP|生成PPT图2不同剂量中子辐照退火态高纯铝的准静态拉伸应力$\!$-$\!$-$\!$应变曲线
Fig. 2Stress-strain curves of annealed high-purity aluminum with different neutron doses for tensile tests
将0.01,dpa, 0.09,dpa,0.22,dpa和0.83,dpa辐照高纯铝的真应力$\!$-$\!$-$\!$应变曲线分别向应变轴正向平移0.016, 0.095, 0.145和0.250应变量后发现,其塑性部分几乎与未辐照高纯铝的真应力$\!$-$\!$-$\!$应变曲线重合,如图2(c)所示.这表明相同真应力条件下,高纯铝的准静态拉伸应变硬化率与辐照剂量无关,这也与Byun等[21-22]的结果一致.平移真应变量($\varepsilon _{\rm shift}$)的选取依据是使得辐照材料的塑性段能够更好地与未辐照材料的真应力$\!$-$\!$-$\!$应变曲线重合[21-25].
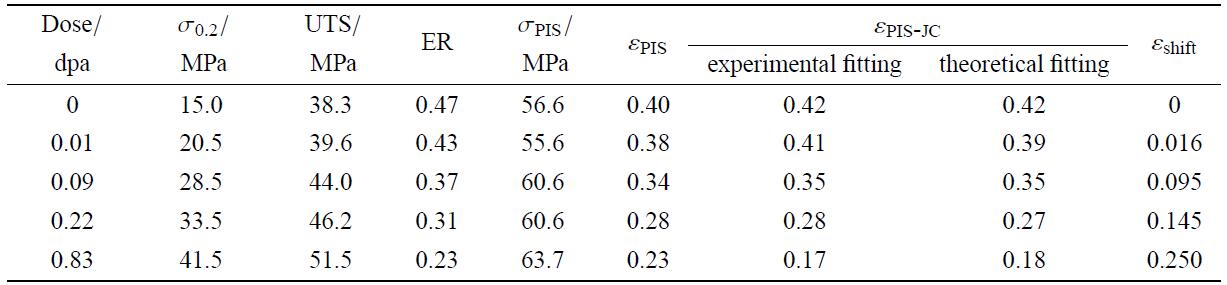
实验统计结果如表1所示.
Table 1
表1
表1退火态高纯铝准静态拉伸统计数据
Table 1
 |
新窗口打开|下载CSV
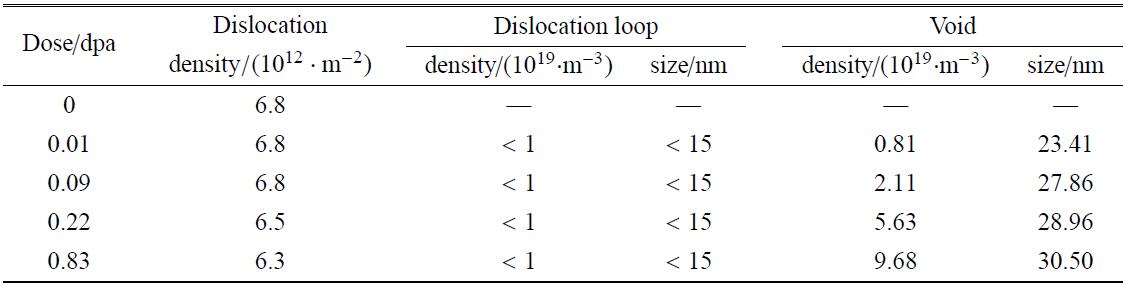
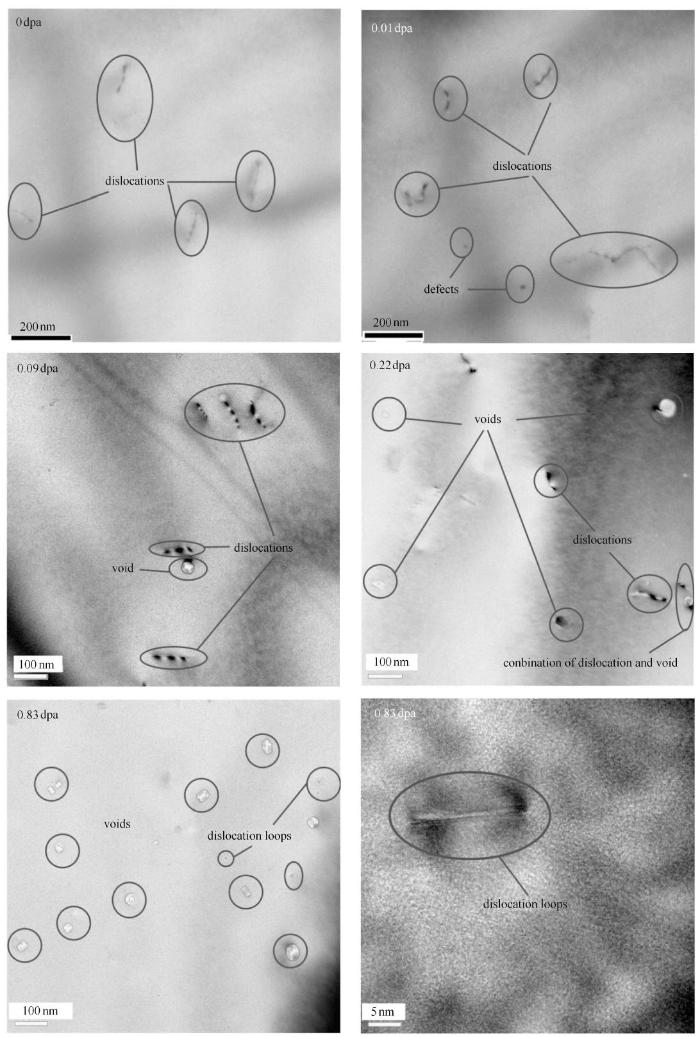
采用TEM显微技术分析了实验用平行样品内部微结构特性.结果表明,样品内部位错密度极低,均为10$^{12}$,m$^{-2}$量级,如图3和表2所示(0,dpa表示未辐照高纯铝);其准静态拉伸屈服强度($\sigma_{0.2}=15$,MPa)与文献[34]报道的完全退火太高纯铝实验结果也一致,再次表明材料确实为完全退火态. 随着辐照剂量的增加,高纯铝内部辐照孔洞的尺寸越来越大,数密度越来越高,,如图3和表2所示. 由于位错环尺寸和数密度均太小,即便是0.83,dpa样品内部都需要变换十几个视场才能够 找到一个位错环,如图3所示.因此,无法准确统计其具体数值,但根据0.83,dpa样品内部观察到的极少量位错环尺寸和数量信息,大致能够给出所有样品内部位错环尺寸上限值为15,nm,数密度上限值为10$^{19}$,m$^{-3}$,如表2所示.
Table 2
表2
表2退火态高纯铝内部缺陷尺寸和数密度数据统计结果
Table 2
 |
新窗口打开|下载CSV
图3
新窗口打开|下载原图ZIP|生成PPT图3不同剂量原始退火态高纯铝的典型TEM图
Fig. 3TEM micrographs of typical microstructures of undeformed annealed high-purity aluminum with different neutron doses
3 模型检验
由未辐照高纯铝拉伸真应力$\!$-$\!$-$\!$应变曲线数据拟合可得式(1)中$A = 15$,MPa,$B = 80$,MPa,$n =0.65$,再结合辐照高纯铝拉伸真应力$\!$-$\!$-$\!$应变曲线数据拟合可得式(1)中$\beta = 1.4$.如果采用实验方法准确获得式(1)中$\Delta \sigma _{\rm dpa}$值,则采用以上拟合参数的辐照高纯铝本构模型理论预测值与实验值的对比结果如图4(a)所示.图中相同颜色实线为实验结果,虚线为 理论预测结果,可以看出模型预测结果与实验结果吻合得非常好.取退火态高纯铝的$\sigma_{\rm PIS} = 60.5$,MPa,得到理论预测的断裂真应变值$\varepsilon _{\rm PIS\hbox{-}JC}$如表1所示(实验拟合),脆化模型预测的断裂真应变值与实验值同样吻合较好.
图4
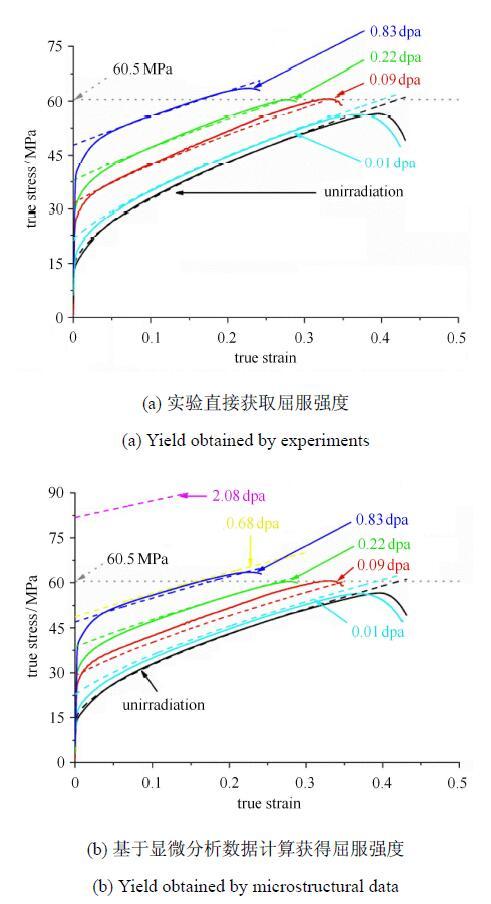新窗口打开|下载原图ZIP|生成PPT图4模型预测结果(虚线)与实验结果(实现)对比图
Fig. 4Comparison of experimental results (solid line)with calculated results(dash line) by model of irradiation embrittlement
如果采用半定量的式(2)理论计算得到式(1)中$\Delta \sigma _{\rm dpa}$值,则根据表1和表2实验数据拟合可得 式(2)中$\alpha = 0.66$.采用以上参数的辐照材料本构模型理论预测值与实验值的对比结果如图4(b)所示. 同样,图中相同颜色实线为实验结果,虚线为理论预测结果,可以看出模型预测结果依旧与实验结果吻合的较好. 同样取退火态高纯铝的$\sigma _{\rm PIS} =60.5$,MPa,得到理论预测的断裂应变值$\varepsilon _{\rm PIS\hbox{-}JC }$如表1所示(理论拟合),此时,脆化模型预测的断裂应变值与实验值仍然吻合较好.根据文献[35]中不同剂量退火态高纯铝内部空洞的尺寸和数密度显微数据,结合式(1)和式(2),以及本文拟合得到的相应参数,计算可得0.68,dpa和2.08,dpa高纯铝的屈服强度分别为42.2,MPa和68.8,MPa,且模型预测其真应力$\!$-$\!$-$\!$应变曲线如图4(b)中黄色和紫色虚线所示. 基于文献显微数据计算的0.68,dpa高纯铝的真应力$\!$-$\!$-$\!$应变曲线略高于本文显微数据计算的0.83,dpa高纯铝的真应力$\!$-$\!$-$\!$应变曲线,这主要可能是由于实验材质的略微差异和数据分散性所致. 2.08,dpa高纯铝的理论预测屈服强度已经超过了$\sigma _{\rm PIS} $(60.5,MPa),据此推测2.08,dpa时高纯铝将发生完全脆性断裂,因此,退火态高纯铝的临界中子剂量应在0.83,dpa$\sim$2.08,dpa之间. 如果采用两点差值拟合法,可得1.7,dpa时高纯铝屈服强度将与其$\sigma_{\rm PIS}$相同,均为60.5,MPa,据此判定高纯铝的临界中子剂量约为1.7,dpa,这与文献[23,24]的预测结果非常吻合.以上结果表明本文提出的辐照脆化理论模型能够较好的预测辐照退火态高纯铝的屈服强度,断裂应变,以及临界中子剂量.
4 结论
本文基于J-C本构模型,结合宏观断裂应力判据,建立了通过获取辐照退火态金属材料屈服强度就能够预测其整个真应力$\!$-$\!$-$\!$应变曲线、断裂真应变和临界中子剂量的辐照脆化理论模型.研究了不同中子剂量退火态高纯铝的形变和断裂特性随辐照剂量的变化规律,结果表明：(1) 高纯铝屈服强度随辐照剂量的增加而增大,断裂真应变随辐照剂量增加而降低,但断裂真应力基本稳定在60.5,MPa;
(2) 相同真应力条件下,退火态高纯铝的应变硬化系数与辐照剂量无关;
(3) 辐照孔洞尺寸和数密度均随辐照剂量增加而增大,但位错环尺寸和数密度均很小,难以准确统计其尺寸和数密度;
(4) 建立的辐照脆化理论模型对辐照退火态高纯铝的真应力$\!$-$\!$-$\!$应变曲线、断裂真应变和临界中子剂量的预测值均与实验值吻合较好.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 3]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 7]
[本文引用: 3]
[本文引用: 1]
[本文引用: 2]
[本文引用: 5]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
