,*,2), 伊兴睿*, 钟山?, 姜楠**, 张山鹰?EXPERIMENTAL STUDY ON QUANTITATIVE MEASUREMENT OF THREE-DIMENSIONAL STRUCTURE OF HAIRPIN VORTEX BY STEREO-PIV 1)
Tian Haiping,*,2), Yi Xingrui*, Zhong Shan?, Jiang Nan**, Zhang Shanying?通讯作者: 2) 田海平,讲师,主要研究方向：实验流体力学, 湍流相干结构,流动控制. E-mail:tianhaiping88@126.com
收稿日期:2020-06-17接受日期:2020-11-4网络出版日期:2020-11-18
| 基金资助: |
Received:2020-06-17Accepted:2020-11-4Online:2020-11-18
作者简介 About authors
摘要
发卡涡是湍流相干结构研究中最为关注的内容,实现发卡涡三维结构的定量测量并进行流体动力学分析,对深入研究湍流相干结构、实现湍流精准控制等具有重要意义.本研究通过对合成射流装置进行合理控制,使得层流边界层中产生了规则的人造发卡涡结构,进而用体视图像粒子测速仪(Stereo-PIV)锁相实验技术对发卡涡结构所在的三维空间流场进行了定量测量,并得到了一个完整周期内形成的发卡涡三维结构的空间流场. 结果发现,重构所得的三维发卡涡结构质量较高, 实验技术和方案具有可行性.发卡涡结构所在空间流场情况,符合目前人们对于发卡涡、高低速条带、喷射和扫掠事件的常规认识. 此外,对近壁二次流向涡、展向涡量集中区域的展向涡头和强剪切区域、与低速喷射流体相关的汇聚流动和发散流动等有了更细致的认识.同时, 也探讨了"基于二维脉动流场的相关特征去重构发卡涡三维流场"的可行性.为进一步定量探究发卡涡结构的形成演化、不同涡结构的融合及二次诱导等壁湍流相干结构问题提供思路.
关键词：
Abstract
Hairpin vortex is one of the most concerned paradigm in the study of turbulent coherent structures. The quantitative experimental measurement and hydrodynamic analysis of the three-dimensional hairpin vortex structures~is of great significance for further~applications in the turbulent flow control.~In this study, with an optimized arrangement of the synthetic jet device, a~series of~regular artificial hairpin vortex structures~are~produced in the laminar boundary layer, and then the three-dimensional shapes of~hairpin vortex structures are quantitatively revealed by stereoscopic particle image velocimetry (Stereo-PIV) using phase-locking technique. The three-dimensional flow field of the hairpin vortex within a complete period is obtained. The quality of the reconstructed three-dimensional hairpin vortex structure is reliable. The results are in line with the general knowledge of hairpin vortex, low/high~speed streaks and~ejection/sweeping~events. In addition, we acquire a more detailed understanding of the near-wall secondary vortex, the spanwise~vortex head and the area of strong shear in the spanwise~vorticity~concentration region, and the convergent/divergent flow related to the ejection~event. We also discuss the reconstruction of the three-dimensional flow field of hairpin vortice based on the fluctuating characteristics of two-dimensional flow field. It provides an idea for the quantitative study of wall turbulence coherent structure in the formation and evolution of the hairpin vortex structure, the fusion of adjacent vortex structures and the secondary induced vortex.
Keywords：
PDF (15144KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
田海平, 伊兴睿, 钟山, 姜楠, 张山鹰. 基于Stereo-PIV技术的三维发卡涡结构定量测量研究1). 力学学报[J], 2020, 52(6): 1666-1677 DOI:10.6052/0459-1879-20-203
Tian Haiping, Yi Xingrui, Zhong Shan, Jiang Nan, Zhang Shanying.
引言
相干结构的发现被认为是20世纪湍流研究的重大进展之一[1], 深入研究相干结构的组织形态、发展演化及其与周围流场的动力学特性规律[2], 是理解更复杂流动[3-4]及对湍流实现有效控制[5-7] 的基础. 在众多形式的相干结构中, 发卡涡[8-9]引起了人们极大的关注: 一是发卡涡的产生、发展和演化涉及壁湍流边界层的各个分区; 二是发卡涡与高低速条带、喷射扫掠等猝发事件、发卡涡涡包等不同尺度、不同类型相干结构间均存在紧密关联[10-11],从而对雷诺应力分布、摩擦阻力的产生起着重要作用.诚然, 在实验研究领域, 对发卡涡的组织形态和动力学机制的研究已经取得了丰硕的成果[12-15]. 但大部分实验结果是基于二维平面的瞬态结果经线性随机估计[15]、拓扑平均[4,16]等手段处理得到的,而直接通过实验手段在湍流边界层中定量地测量发卡涡的三维空间结构并分析其动力学特性仍然具有一定的挑战.目前通过3D-3C-PIV实验技术直接对真实湍流边界层流场进行测量并提取到发卡涡三维结构还不够成熟, 难度是普遍存在的,仅在湍斑[17]、人造发卡涡[18]的测量中观测到了发卡涡结构. 究其原因是复杂的: 一是, 目前测量三维流场的主流技术是3D-3C-PIV, 这类设备价格高昂, 对相机和测试过程要求较高, 且数据量大、分析处理耗时较长;二是, 湍流边界层流场近壁面速度梯度大, 现有PIV技术在精细重构湍流边界层的缓冲层及以下的区域的流场时存在较大难度[19-21];三是, 在真实壁湍流场中存在的某一个发卡涡结构的形状和尺度特征及流场特性均受很多因素的影响,完整的典型发卡涡实际很少, 更难以捕捉、提取和分析.
尽管发卡涡来自壁湍流, 但对其形态结构及流体动力学机制的研究, 并不是只有在壁湍流场中才有答案. 反而, 在层流边界层中生成完整、可控的发卡涡结构, 并通过控制发卡涡的产生位置、时间、频率、尺度、强度等, 用以研究发卡涡的演化过程、相邻发卡涡的耦合机制、二次涡的诱导生成机理及控制发卡涡以实现减小壁面摩阻[22]等更具可操作性,层流场中的研究结果对于评估湍流边界层中相关的流体动力学行为, 也具重要的借鉴价值.
用人工方式在边界层流动中制造发卡涡, 实质上就是要在边界层近壁局部区域产生有形的、无形的、或时有时无的阻碍,来达到流体在近壁面局部区域积聚或受到障碍、绕流卷曲成发卡涡的动力过程. 目前, 为实现这一过程主要有4种方式: 其一,通过在边界层壁面局部区域不断注入低速流体, 低速流体积聚震荡产生发卡涡结构[18,23],其特点是实验时需不断注入外界流体, 且产生发卡涡的频率、尺度均不可控; 其二, 通过绕流固定障碍物(半球[24-25]、球[26]、圆柱[27]、其他形状[28]等)诱导生成发卡涡结构,其特点是: 发卡涡的产生频率、形态和尺度与被绕流物体密切相关, 除非替换固定障碍物, 否则不可调节; 其三, 通过绕流可动结构(动粗糙元技术[29], 压电陶瓷片[30])诱导生成发卡涡结构,其特点是发卡涡的产生频率、形态和尺度与可动结构密切相关, 通过控制可动结构的频率、振幅等可实现对发卡涡结构的部分控制; 其四,合成射流装置(synthetic jet)产生涡环后在边界层横流流场中形成发卡涡结构[31-33], 其特点是发卡涡的产生频率、形态和尺度与合成射流参数密切相关, 容易控制. 综上所述, 合成射流技术生成发卡涡的过程可控程度最高,即便在无3D-3C-PIV的情况下, 只需与Stereo-PIV系统密切配合即可定量测量发卡涡的三维结构, 且该方法属于零质量射流技术, 对原有的边界层流场无流量进出、无结构性影响, 是一种较为理想的人造发卡涡方式, 且有利于系统化实验的开展. Koo和Kang[22]就是通过控制这种人造发卡涡来进行减小壁面摩擦阻力的研究的, 三维发卡涡结构的生成过程通过流动显示做了定性分析. Wen和Tang等[34-36]也在层流场中通过合成射流产生人造发卡涡的方式研究了不同相位、不同空间位置的两个发卡涡相互耦合的流体动力学特性, 以期发现壁湍流中发卡涡融合和诱导的机制, 研究中发卡涡的三维结构也用流动显示的方法呈现, 而定量分析只能采用2D-PIV数据或数值模拟的结果. 可见, 对可控发卡涡三维结构进行定量测量是壁湍流领域一个亟需突破的课题.
本文通过Stereo-PIV锁相实验技术定量测量了合成射流装置在层流边界层中所产生发卡涡的三维结构, 介绍了一套实验研究发卡涡的新方案, 对发卡涡结构特征和动力学行为进行了深入刻画, 以期为研究发卡涡发展演化、涡系融合、二次诱导等问题提供思路.
1 实验系统及数据处理方法
1.1 实验系统介绍
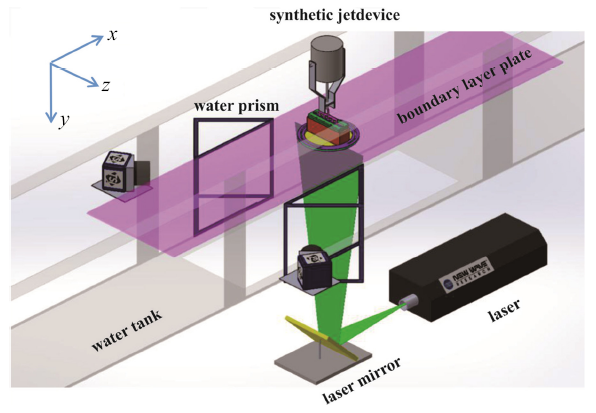
实验是在英国曼彻斯特大学机械航空与土木工程学院的低速循环水槽实验室进行的.实验系统主要由低速循环水槽、合成射流装置、Stereo-PIV系统等三大部分组成,实验平台布局如图1所示.图1
新窗口打开|下载原图ZIP|生成PPT图1实验平台布局示意图
Fig. 1Layout of experimental platform
1.1.1 低速循环水槽及边界层平板
实验用低速循环水槽长$3.64$ m, 实验段长$0.8$ m, 截面积为0.305 m $\times$0.305 m, 流速在0 $\sim$ 0.4 m/s内连续可调. 自由来流速度0.1 m/s时, 水槽湍流度为0.8%. 实验段侧壁和底部开有玻璃窗口, 便于开展流动显示和PIV实验. 实验时水的自由来流速度$U_{\infty } =0.12$ m/s, 水流方向为自左向右(图1).
在距离水槽底面$0.31$ m高度处, 放置一块长$1.38$ m, 宽$0.3$ m, 厚5 mm的铝合金板材, 倒扣在水槽中,其前缘进行椭圆形修型, 作层流边界层平板使用. 边界层平板上距离前缘$0.715$ m处, 开有圆孔,能与合成射流装置的射流出口圆盘平面完美配合. 平板和合成射流装置作为一个整体可沿流向在水槽上方实现平移. 平板前缘不加扰动、合成射流装置不工作时, 平板下表面自然发展成层流边界层.
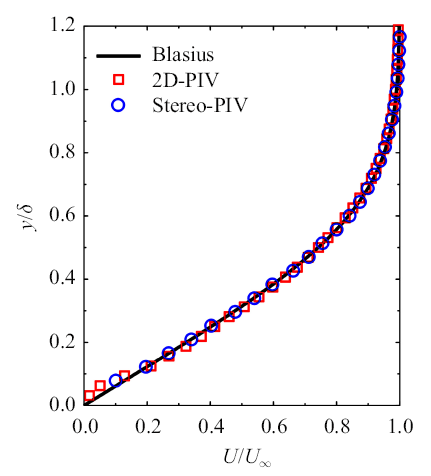
图2为分别用2D-PIV测量流法向平面和Stereo-PIV测量展法向平面获得的层流边界层外尺度无量纲化的平均速度剖面,二者与Blasisus曲线符合较好, 验证了流场和Stereo-PIV实验的可靠性.
图2
新窗口打开|下载原图ZIP|生成PPT图2层流边界层平均速度剖面
Fig. 2Mean velocity profile of the laminar boundary layer
1.1.2 合成射流装置及其控制系统
合成射流是一种由激励器振动导致空腔内交替吹吸外界流体而产生的非连续射流. 实验中用到的合成射流激励器可以在空腔中产生活塞运动,空腔通过孔口与外界流体连通. 吹出的流体由于孔口剪切作用形成射流涡环, 遇边界层后涡环沿流向拉伸并远离壁面向外抬升,进而形成具有展向涡涡头及两个反向旋转涡腿结构的发卡涡. 实验用到的合成射流装置主要包括合成射流腔体、电磁激振器和位移传感器3部分.
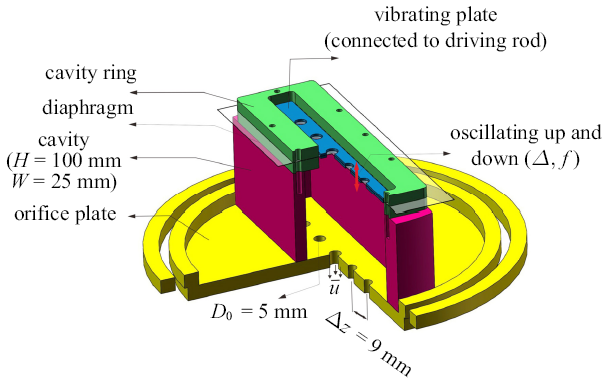
合成射流腔体是一个长方形腔体(如图3所示), 长$H=100$ mm,宽$W=25$ mm. 腔体上有流体进出的一端连接在一个圆盘平板上;而另一端是隔膜片, 可在电磁激振器的作用下,振动片使薄膜在腔体内上下做活塞运动, 带动流体进出腔体.圆盘上有$N=5$个沿展向整齐排列的圆形射流出口, 孔深$h=5$ mm (即圆板厚度),孔径为$D_{0} =5$ mm, 相邻两个射流出口的展向间距$\Delta z=9$ mm.圆盘恰好嵌入边界层平板的圆形开孔中, 且两者配合的表面光滑无台阶.
图3
新窗口打开|下载原图ZIP|生成PPT图3合成射流腔体结构
Fig. 3Schematic of synthetic jet cavity structure
在合成射流研究中, $\alpha_{A} $和$R_{V}$是两个非常重要的无量纲参量[31], 其中$\alpha_{A}$是空腔截面积与射流出口总截面积的比值, 定义为
式(1)中, $H$为射流腔体的长, $W$为腔体的宽, $N$为圆形射流出口的数目, $D_{0}$为孔径大小. 本实验中$\alpha_{A} \approx 25.5$. $R_{V}$是射流出口平均速度$\overline u $和来流速度$U_{\infty } $的比值,定义为
其中, $\varDelta $是电磁激励器的振幅, $f$是激励器振动频率. 实验中,电磁激励器振动的频率$f=2$ Hz, 通过调节激励器的振幅$\varDelta$, 使$R_{V}=0.1$, 此时合成射流产生的涡环在层流边界层横流运动中产生典型发卡涡结构.
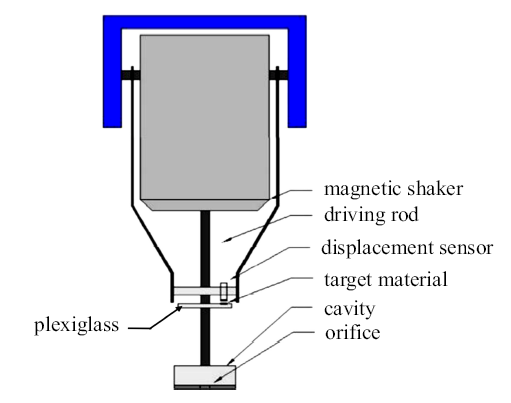
图4是合成射流激励装置, 展现了电磁激励器的结构模型及位移传感器的安装位置.电磁激励器的振幅$\varDelta $、频率$f$等振动参数由Labview软件控制,带动驱动连杆与射流空腔一端的隔膜片一起运动. 受射流腔体内压力变化影响,隔膜片的运动无法与激励器之间实现完全同步、同幅振动.位移传感器能把真实的振动信号及动作延迟参数及时回传到Labview软件界面上,用以实时监督实验过程及调整振动幅值、相位等信息, 以确保控制效果.
图4
新窗口打开|下载原图ZIP|生成PPT图4合成射流激励装置
Fig. 4Synthetic jet actuator
1.1.3 Stereo-PIV系统
实验中使用的是低频Stereo-PIV系统, 购自TSI公司, 最高采集频率15 Hz, 主要包括照明系统(Nd:YAG LASER,200 mJ/pulse)、双相机系统(2352 $\times$ 1768 pixels)及同步控制系统(TSI Synchronizer 610036). 如图1所示:激光片光经激光反射镜反射后, 从水槽底部窗口垂直入射, 照亮法展向($y-z)$平面. 两相机置于水槽两侧同一高度, 与被采集平面满足Scheimpflug成像原则, 为避免光在气液界面产生折射, 实验过程中在水槽两侧各加装了一个$45^{\circ}$的水棱镜,也间接确定了实验中两相机镜头光轴的夹角为$90^{\circ}$. 双相机、激光装置是安装在三维立体坐标架上的, 可对其移动产生精准控制. 标定时, 考虑标定靶放置和近壁面标定阻碍等实际情况, 先标定"目标待测平面"正下方的"虚待测平面", 标定完成后再将双相机同步竖直提升到"目标待测平面"进行数据采集. 实验时用的示踪粒子购自Dantec公司, 平均粒径5 $\mu$m.
实验过程中, Labview软件将空腔隔膜片与激励器振动的延迟情况通过数据采集卡传给PIV系统的同步控制器信号触发端,从而实现隔膜片振动、激光光源系统出光和相机采集等工作的协调同步,保证了锁相采集工作的精度.
为遍历发卡涡发展的整个周期, 低频Stereo-PIV系统相继采集了25个相位的数据, 相位间隔$15^{\circ}$. 实验中采样频率$f=2$ Hz,相机曝光时间间隔为1000 ns. 每个相位重构得到的2D-3C流场共有235 $\times$ 108 ($z-y)$个数据点, 物理空间大小为95.9 cm $\times$ 43.9 cm, 空间分辨率为0.41 mm. 每个相位采集的样本量为600个粒子图像对, 考虑实验中参数调节及恢复流场稳定等耗时, 采集整个周期所需的时间跨度约为3.5 h. 在控制参数$R_{V}=0.1$下,实验中选取了位于圆出口下游的多个不同的测量位置, 本文只对射流出口下游$x=D_{0}=5$ mm处的实验结果进行分析.
1.2 三维流场重构方法
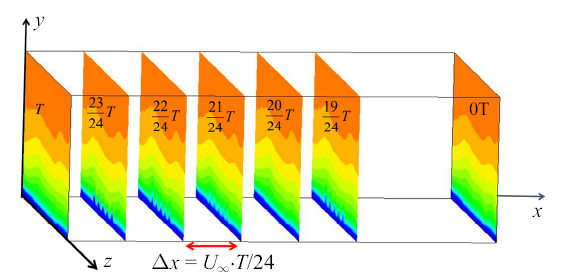
合成射流装置的运动周期为$T$, 相邻相位间的时间分辨率为$T/24$. 为得到一个完整周期内的三维流场, 流向坐标应当将时间参数转换为空间流向坐标, 遵循"泰勒冻结假设"的思想, 相位间隔时间与相干结构流向迁移速度的乘积可以看作流向上的空间分辨率.众所周知, 边界层流动近壁速度梯度大, 合成射流所产生流动结构的迁移速度随空间位置变化而变化. 本文主要探究Stereo-PIV锁相实验技术测量三维发卡涡结构的可行性, 并研究发卡涡的结构形态和动力学特性,而经时间坐标转化得到的空间流向长度对所关心的问题并不敏感. 为简便, 这里以来流速度$U_{\infty }$与相位时间间隔$T/24$的乘积作为流向上的空间分辨率, 即$\Delta x=U_{\infty } \cdot T/24$. 本文在重构发卡涡三维结构时,将25个相位的平均流场结果按照相位顺序进行倒序排列,得到一个周期$T$内的三维流场(见图5). 因为流向尺度问题,研究结果中未对结果进行无量纲化处理. 同时, 也应注意到:流向实质上是时间序列的反方向, $x$轴上的零点没有实际意义.图5
新窗口打开|下载原图ZIP|生成PPT图5三维流场重构方法示意图
Fig. 5Schematic diagram of 3D flow field reconstruction method
2 实验结果与分析
Stereo-PIV锁相实验数据, 先进行相位平均, 再按照图5方法重构三维流场. 最终获取的三维流场物理空间大小为62.5 mm $\times$ 43.9 mm $\times$ 95.9 mm,流向、法向和展向上的分辨率分别为2.5 mm、0.41 mm和0.41 mm,有$25 \times 108 \times 235$ $(x \times y \times z)$个速度矢量.2.1 全局流场结果及实验效果评估
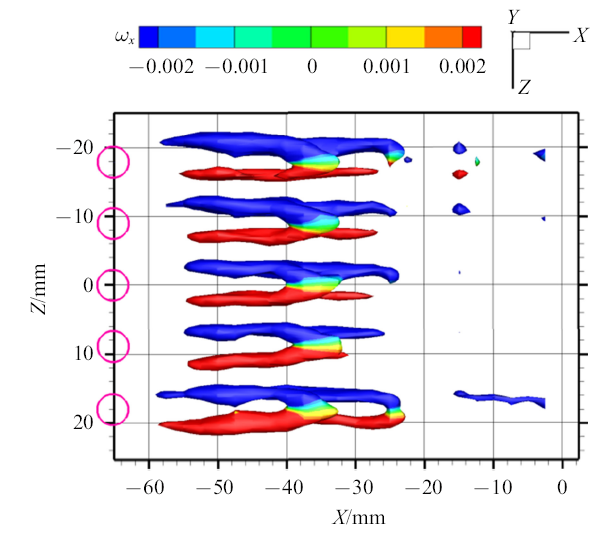
图6是一个完整的合成射流周期内由5个射流出口形成的发卡涡结构图,圆圈所代表的是射流出口的位置.将最中间的射流出口位置定义在展向上的零点($z=0)$和法向的零点($y=0)$.图中发卡涡三维结构是用$Q$值等值面显示的,等值面上彩色云图标识的是流向涡量$\omega_{x} $的大小. 尽管实验采集过程较长,但经重构得到的5个发卡涡在展向上整齐排列且具有相同结构, 发卡涡结构特征明显,规律性强. 在流向上比较光滑无台阶, 展向上亦无错位. 可见, 实验方案可行,合成射流装置运行平稳, 对相位和位置的控制也较为精确, 采集系统同步性良好,整套实验装置具有较高的可靠性.图6
新窗口打开|下载原图ZIP|生成PPT图6$Q$值等值面显示的发卡涡结构(等值面上是流向涡量$\omega_{x} $云图)
Fig. 6Iso-surfaces of $Q$-criterion color coded with streamwise vorticity $\omega_{x} $
2.2 单发卡涡结构所在流场的空间结构形态
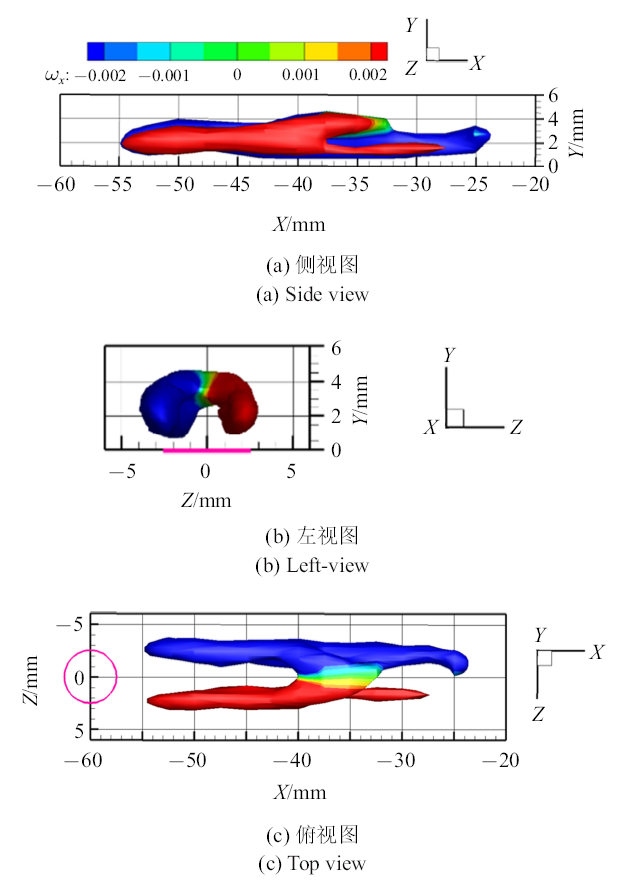
为了深入研究发卡涡的结构特征和周围流场的特性, 下面取最中间发卡涡所在的相位重构三维流场进行细致分析. 选定的空间范围为:$-60$ mm $<x<-20$ mm, $0<y<6$ mm, $-6$ mm $<z<6$ mm, 可提取到完整的单个发卡涡结构,射流出口中心位于($y=0$, $z=0$). 图7是单个发卡涡三维结构的三视图, 显示方法同图6. 可见, 射流出口的下游形成了一个完整的发卡涡结构, 在流向上大致位于$-55$ mm $<x<-35$ mm,约为$4D_{0}$.图7
新窗口打开|下载原图ZIP|生成PPT图7$Q$值等值面显示的单个发卡涡结构s(等值面上是流向涡量$\omega_{x}$云图)
Fig. 7Single hairpin vortex structure (iso-surfaces of $Q$-criterion color coded with streamwise vorticity $\omega_{x})$
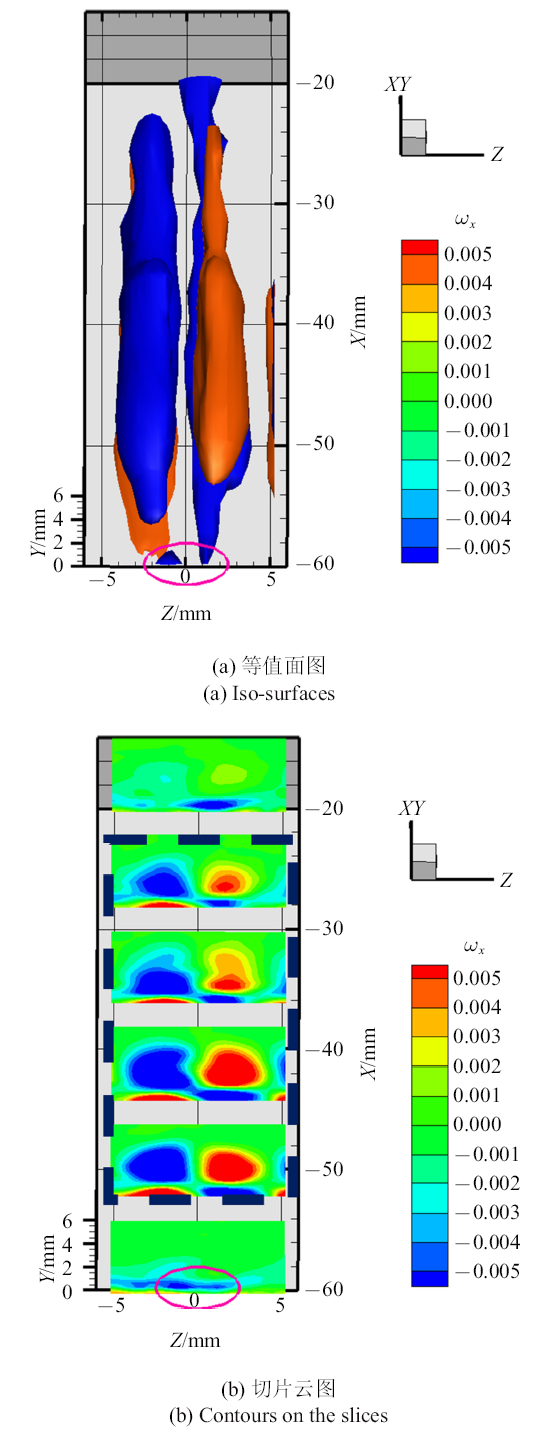
发卡涡结构上红色区域代表的是正向旋转的涡腿结构, 蓝色区域代表反向旋转的涡腿结构, 与流向涡量空间分布(图8(a))相吻合. 同时,涡腿结构位置与法向涡量分布高度一致(图9). 从流向涡量切片分布图(图8(b))中易知, 与一对反向旋转涡腿相对应的流向涡下面还诱导出一个与之符号相反的二次流向涡或壁面强剪切区域,其法向尺度非常小. 两对流向涡量结构呈双层分布, 其符号沿法向上下相反,在展向上左右相反. Chen[2,37]和 Li等[5]在数值模拟研究中也发现了相同结构. 与3D-3C PIV相比, 也体现出Stereo-PIV在近壁流场测量上的优势.
图8
新窗口打开|下载原图ZIP|生成PPT图8一个合成射流周期内相位平均的流向涡量$\omega_x$空间分布
Fig. 8Spatial distribution of phase-averaged streamwise vorticity $\omega_x$ during a synthetic jet actuation cycle
图9
新窗口打开|下载原图ZIP|生成PPT图9一个周期内相位平均的法向涡量$\omega_y$空间分布
Fig. 9Spatial distribution of phase-averaged wall-normal vorticity $\omega_y$ during a synthetic jet actuation cycle
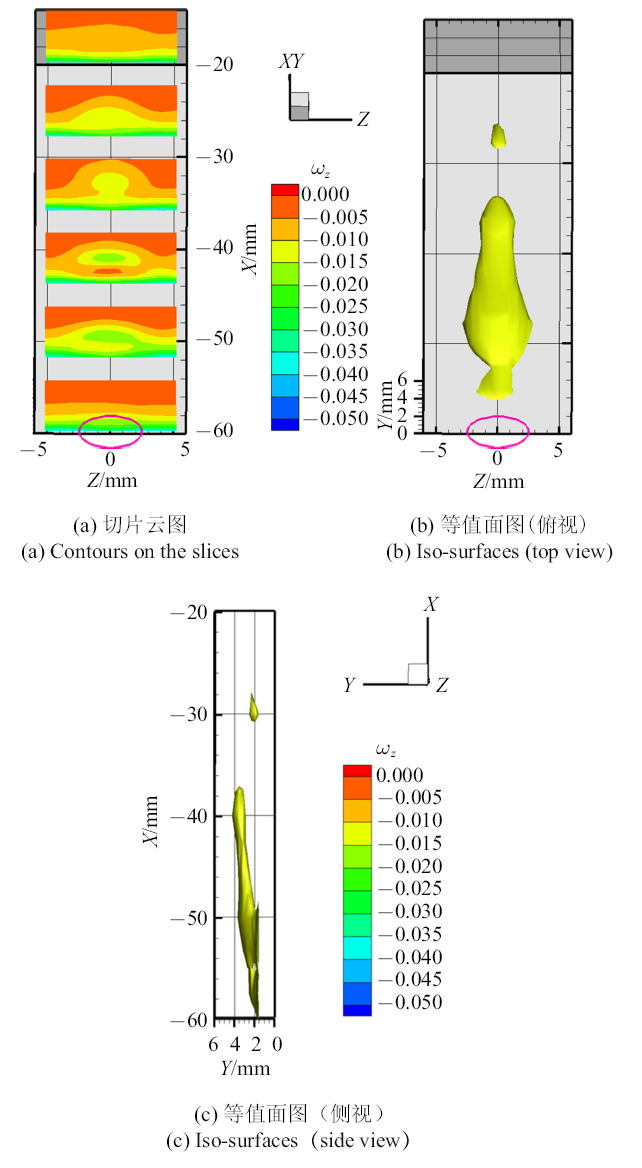
发卡涡的涡头结构位于俯视图(图7(c))中红蓝相间的位置, 结合左视图(图7(b)), 涡头中心位置坐标约为$(x=-38,y=4,z=0)$.从展向涡量的分布图(图10)看, 射流出口的下游存在一个负的展向涡量集中区域(图10(a)),且沿着流动方向逐渐远离壁面(图10(b)和图10(c)),形成倾斜结构(图10(c)).
图10
新窗口打开|下载原图ZIP|生成PPT图10一个周期内相位平均的展向涡量$\omega_z$空间分布
Fig. 10Spatial distribution of phase-averaged spanwise vorticity $\omega_z$ during a synthetic jet actuation cycle
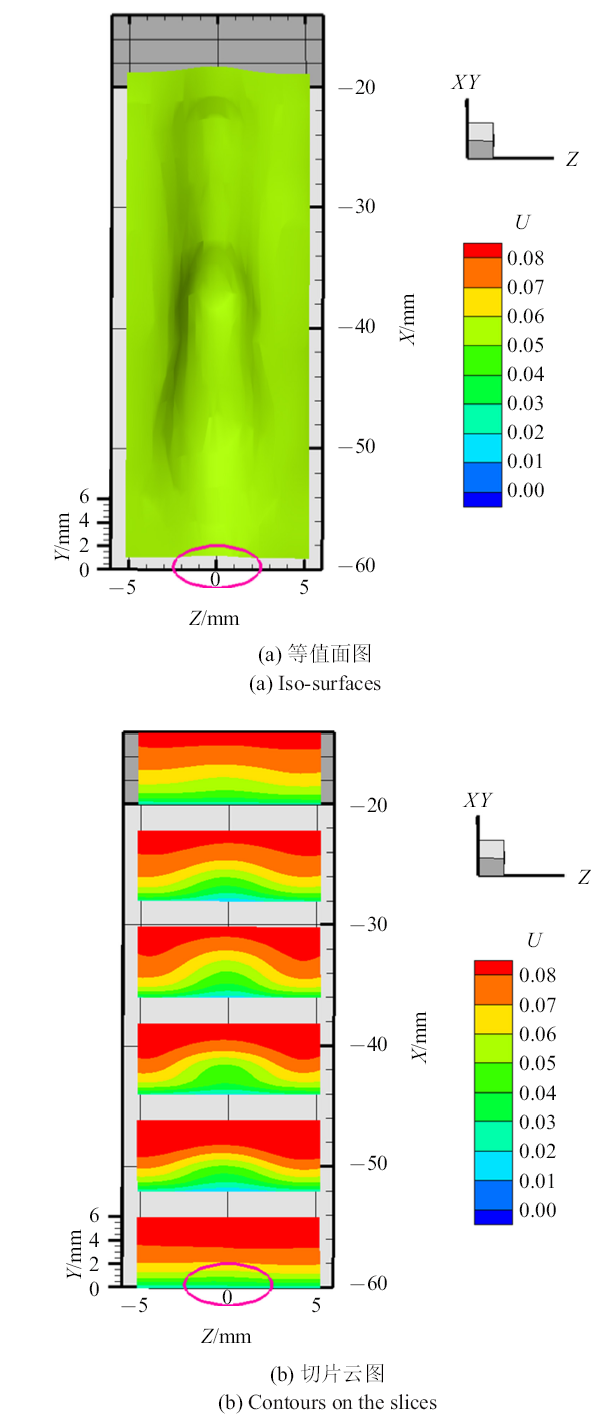
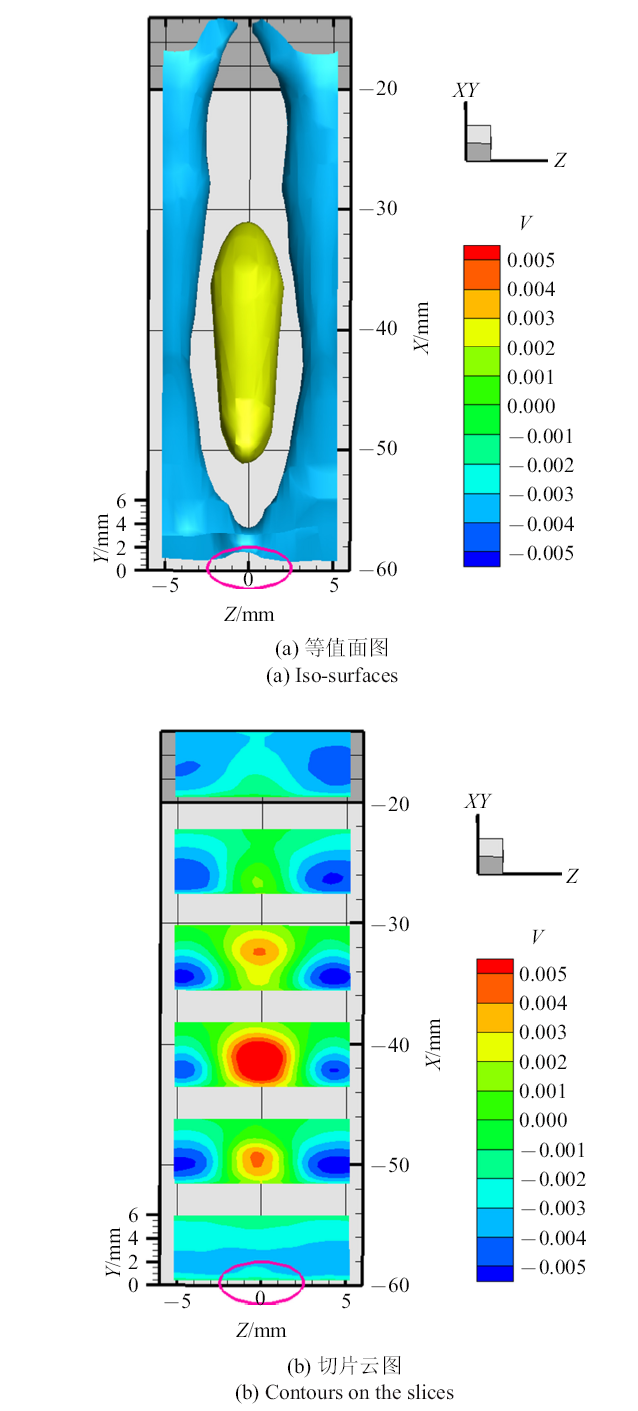
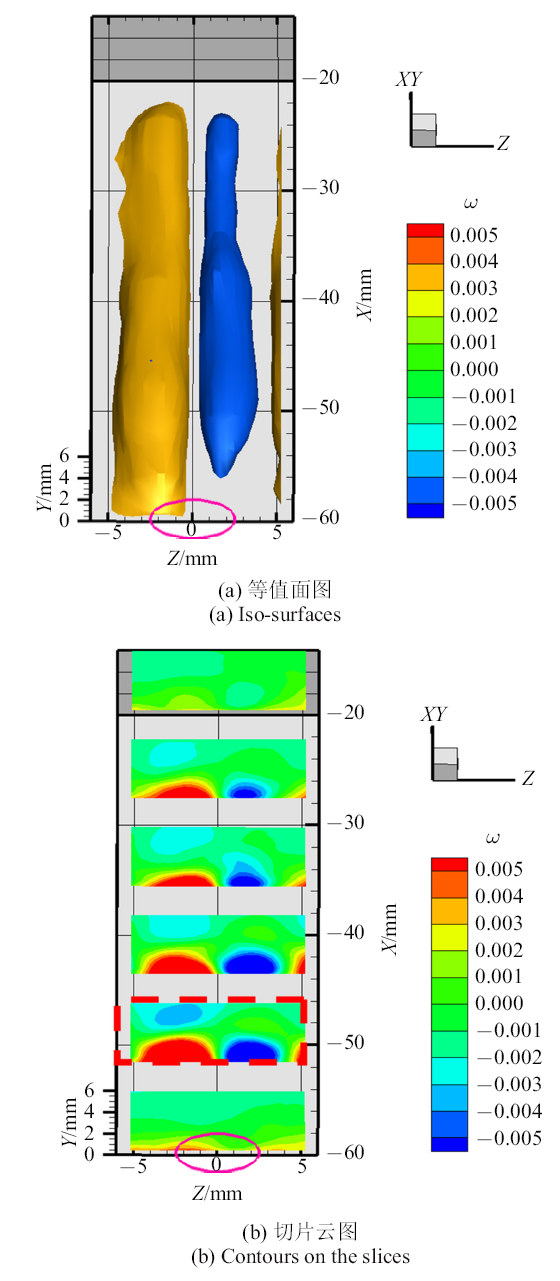
图11~图13分别展示了单个发卡涡所在三维流场中3个速度分量等值面的空间结构及法展向($y-z)$切平面速度云图的分布情况.在射流出口下游$-55$ mm $<x<-35$ mm的流场区域,即流向上发卡涡存在的位置(图7), 形成低速带状结构(图11(a)), 且该区域对应的法向速度为正(图12(a)), 两侧为负(图12(b)). 相比两个涡腿中间的对应的低速流体区域, 涡头位置的低速流体区域在展向上更窄、法向上更高. 而结合展向速度分布特征(图13), 展向速度的空间分布呈现双层分布特点(图13(b)).
图11
新窗口打开|下载原图ZIP|生成PPT图11一个周期内相位平均的流向速度$u$空间分布
Fig. 11Spatial distribution of phase-averaged streamwise velocity $u$ during a synthetic jet actuation cycle
图12
新窗口打开|下载原图ZIP|生成PPT图12一个周期内相位平均的法向速度$v$空间分布
Fig. 12Spatial distribution of phase-averaged wall-normal velocity $v$ during a synthetic jet actuation cycle
图13
新窗口打开|下载原图ZIP|生成PPT图13一个周期内相位平均的展向速度$w$空间分布
Fig. 13Spatial distribution of phase-averaged spanwise velocity $w$ during a synthetic jet actuation cycle
可见, 发卡涡的涡头及两个反向旋转的涡腿,使得低速流体在发卡涡涡头上游的中心区域产生积聚形成低速流体,同时低速流体还有远离壁面的趋势, 即形成"喷射流体区域", 发生"喷射"事件.从切片云图上看, 喷射流体区域两侧是高速流体(图11(b))、有向壁运动的趋势(图12(b)),即发生"扫掠"运动. 同时, 发卡涡的涡腿结构位置靠近壁面一侧,流体的展向运动指向发卡涡结构中心轴线, 较为强烈, 是主要运动(图13(a));而远离壁面一侧, 流体的展向运动趋势相反.
2.3 发卡涡及周围流场的运动规律
本节以发卡涡结构涡头中心处的法向速度和流向速度作为参考基准对三维重构流场进行了重建,着重分析平面上的流动规律及与空间分布之间的关联. 图14分析了$z=0$ mm处流法向$x-y$平面上带速度矢量的展向涡量云图.图中圆圈位置为展向涡头位置, 虚线所示区域是负的展向涡量集中的区域,两者没有明显界限. 从速度矢量上看,虚线区域上下两部分流体的运动方向发生明显变化,因此虚线所示区域是一个强剪切的区域, 该区域与图10(c)中展向涡量结构相对应.图中黑色圆点是流动滞止点的大致位置. 强剪切区域的右下方流体是低速流体,结合速度矢量看, 该区域发生喷射事件,这与图11和图12所呈现的关于发卡涡中心区域发生喷射事件的结果相同.而强剪切层外, 尤其是滞止点左上方流体区域, $u'>0$且$v'<0$, 发生扫掠事件.因而, 强剪切层是自由来流与涡结构产生的低速喷射流体共同作用的结果.图14
新窗口打开|下载原图ZIP|生成PPT图14流法向截面上($z=0$ mm)带速度矢量的展向涡量$\omega_z $云图
Fig. 14Contour of spanwise vorticity $\omega_z $ with velocity vectors on $x-y$ plane at $z=0$ mm
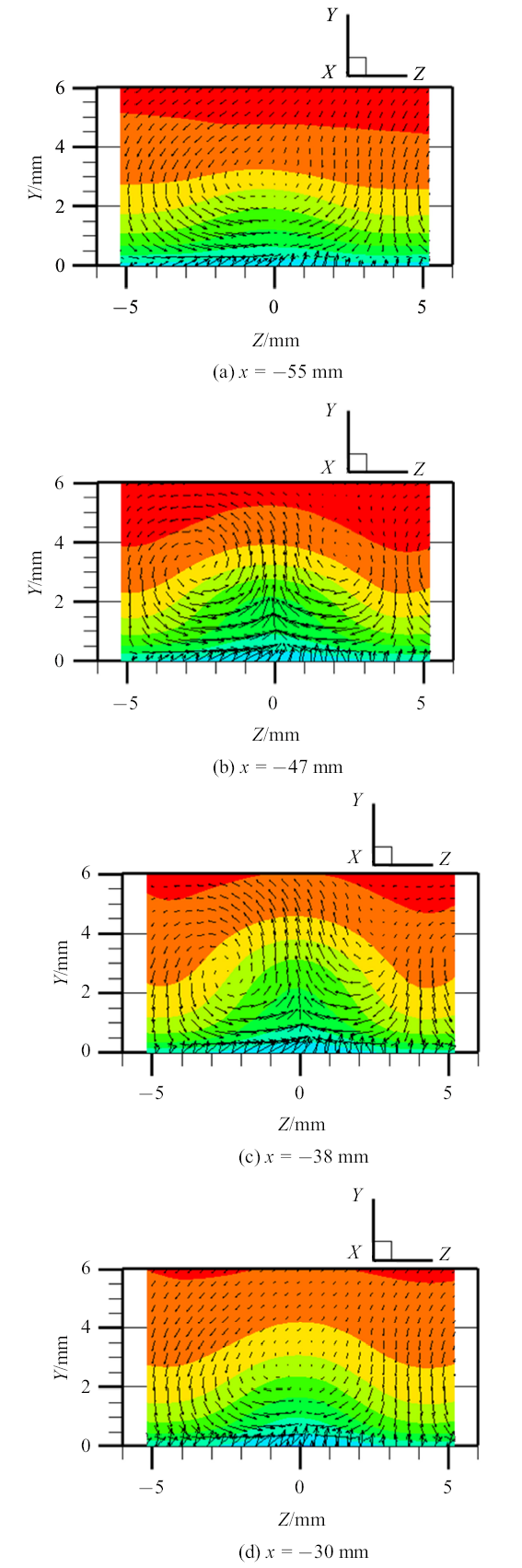
图15是4个带有速度矢量的流向速度云图, 分别位于$x=-55$ mm, $x=-47$ mm, $x=-38$ mm和$x=-30$ mm的法展向($y-z)$截面. 对图7的分析已知, $-55$ mm $<x<-35$ mm为发卡涡结构主要作用的区域,从图15(a)~图15(c)可以发现, 低速流体区域的外形轮廓逐渐向法向"凸起".截面流场展向中心线附近的流体向上运动的趋势以$x=-47$ mm的情况最为明显:近壁面上的低速流体($u'<0)$向中间汇聚并垂直壁面向上运动($v'>0)$,到达上部空间后向两侧缓缓流动. 这种流动在平面流场上形成了两个反向旋转的涡旋运动, 两个涡旋运动的外侧,流体向下运动($v'<0)$, 形成两个高速流体区域($u'>0)$. 这两个涡旋运动对应的就是发卡涡结构的两个反旋的涡腿结构. 再一次证明,发卡涡存在的区域, 展向中心内部发生喷射事件, 而两侧发生扫掠事件. 在发卡涡涡头位置$x=-38$ mm的平面流场仍有相似趋势,而发卡涡存在区域之外位于$x=-30$ mm的平面流场上则无此趋势.
图15
新窗口打开|下载原图ZIP|生成PPT图15法展向截面上带速度矢量的流向速度$u'$云图
Fig. 15Contour of streamwise velocity $u'$ with velocity vectors on $y-z$ plane
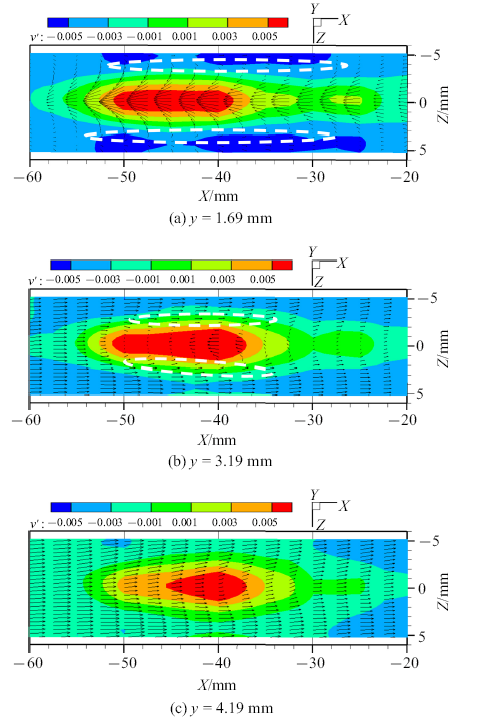
图16是3个带速度矢量的法向速度云图, 分别来自位于$y=1.69$ mm, $y=3.19$ mm和$y=4.19$ mm的流展向($x-z)$平面.从图16(a)上看, 发卡涡所在区域展向中心处的流体有正的法向速度分量($v'>0)$, 速度矢量显示流体从两侧汇聚, 并向上游运动($u'<0)$.而展向两侧位置具有两个明显的剪切层(图16(a)中白色虚线所示区域), 位置上与流向涡量集中的区域相对应, 因而它的形成与准流向涡或发卡涡涡腿结构密切相关. 剪切层外侧的流体有负的法向速度($v'<0)$, 速度矢量显示其向下游运动($u'>0)$.随着法向位置的增高, 剪切层逐渐向内收缩(图16(b)), 并消失(图16(c)). 同时, 发卡涡所在中心区域流体的喷射运动也逐渐减弱. 另外,也注意到同一流展向平面的低速流体区域沿着流向其展向的宽度是变化的, 在发卡涡涡头附近最窄.
图16
新窗口打开|下载原图ZIP|生成PPT图16流展向截面上带速度矢量的法向速度$v'$云图
Fig. 16Contours of wall-normal velocity $v'$ with velocity vectors on $x-z$ plane
经3个平面上的速度矢量分析, 可知以发卡涡涡头迁移运动速度为基准,流法向平面内展向涡量集中区域内速度矢量为零的坐标可指示发卡涡结构涡头的位置;法展向平面上两个反向旋转的旋涡中心(速度矢量为零)的坐标可以指示发卡涡涡腿的法向中心位置;流展向平面上剪切层的位置, 可指示发卡涡涡腿在该平面的投影. 因此,利用二维流场的相关特征来重构发卡涡三维流场, 在理论上具有可操作性.
2.4 关于主发卡涡下游的一对流向涡结构的讨论
从单个发卡涡三维结构的俯视图(图7(c))和侧视图(图7(a))上还可以看到发卡涡结构的下游,还有一对反向旋转的流向涡结构,位于发卡涡涡头的下方且未与主发卡涡结构完全分离,流向上大致位于$-40$ mm $<x<-25$ mm.这一对流向涡结构内部也有一个低速流体区域(图11(a)),但其强度明显弱于上游的低速流体. 在展向涡量剖面云图(图14)中,特别注意到$-32$ mm $<x<-26$ mm的区域内也存在一个集中的展向涡量区域,只是强度较低. 而在图6中显示的5个发卡涡结构看,这个低强度的展向涡量区域是不是发卡涡结构的涡头难以判断.Suponitsky等[38]对射流涡环横流运动的数值模拟工作中也发现了相同现象,并认为是涡环的在横流运动中会同时生成主、次两个发卡涡. 同时, 鉴于锁相技术,该位置产生的这对流向涡也有可能是下游发卡涡的近壁部分,因为发卡涡结构在近壁的迁移速度较慢,在法向上也可能与后一个发卡涡主体部分重叠. 因此, 它的成因需要进一步探究.
3 结论
本文得到以下几点主要结论:(1) 基于Stereo-PIV锁相实验技术可以在层流边界层中实现对合成射流装置所产生发卡涡三维结构的定量测量. 同时, 相较于3D-3C PIV, Stereo-PIV在流场近壁结构精细测量上占有优势.
(2) 所测发卡涡结构三维空间流场符合目前对发卡涡、高低速条带、喷射和扫掠事件的基本认知.
(3) 本文还对二次流向涡、展向涡量集中区域的展向涡头、与低速喷射流体相关的汇聚流动和发散流动等相关问题进行了深入的讨论. 特别注意到: (a)流向涡量和展向速度空间结构呈现双层分布特性; (b)展向涡量集中区域, 一部分是发卡涡展向涡头, 另一部分是边界层流场来流与发卡涡涡腿间的喷射流体相互作用形成的强剪切区域, 且二者无明显区分界限; (c)低速喷射流体的来源是两侧反向旋转涡腿带动近壁流体(涡腿下层流体)向中心产生的"汇聚"流动, 喷射流体遇到强剪切层后在展向上向两侧作"发散"流动, 经涡腿结构上方, 受涡腿旋转带动成为高速扫掠流体的主要来源.
(4) 以发卡涡涡头的迁移运动为基准的三维空间流场, 其各平面矢量图上呈现出与发卡涡结构有明显相关性的信息, 可作为"用二维脉动流场的相关特征实现重构三维发卡涡"的实验依据, 以期在有限的实验条件下得到质量更高、信息更全的发卡涡特征数据.
本文采用低频Stereo-PIV锁相实验方案定量测得的发卡涡三维结构,其流向尺度不够严谨. 因而严格意义上讲, 它仍不是真实的发卡涡结构. 尽管如此,该技术方案仍然为定量研究可控发卡涡、乃至进一步研究发卡涡发展演化、涡系融合、二次诱导等问题提供了一些思路.为实现严格意义上的发卡涡三维结构的定量测量,下一步考虑用更新颖的技术手段或更先进的测试设备完成对流向尺度的精确测量,以实现对结果进行无量纲化工作, 增加研究工作的普适性. 与此同时,通过改变无量纲化的控制参数, 按需实现对生成发卡涡结构的有效调控.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
The particle image velocimetry (PIV) and hydrogen-bubble visualization technique are used to investigate the flat-plate boundary layer transition induced by an array of roughness elements. The streamwise evolutions of the mean and fluctuation velocity are analyzed, and the critical Reynolds number Re(k,c) is determined between 339 and 443 under current experimental setup. The hairpin vortices shed from supercritical roughness elements are visualized by swirling strength, in which two pairs of counter-rotating vortices can be observed: one vortex pair is the manifestation of the neck of the hairpin vortices shed from the top of the roughness; the other vortex pair, which originates from the lower part of the roughness, comes from the streamwise vortices that are constantly perturbed by the hairpin vortex shedding.
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 2]
DOIURL
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
A new statistical coherent structure (CS), the velocity vorticity correlation structure (VVCS), using the two-point cross-correlation coefficient R-ij of velocity and vorticity components, u(i) and omega(j), (i, j = 1, 2, 3), is proposed as a useful descriptor of CS. For turbulent channel flow with the wall-normal direction y, a VVCS study consists of using u(i) at a fixed reference location y(r), and using vertical bar R-ij(Y-r; x, y, z)vertical bar R-0 to define a topologically invariant high-correlation region, called VVCSu. The method is applied to direct numerical simulation (DNS) data, and it is shown that the VVCSij qualitatively and quantitatively captures all known geometrical features of near-wall CS, including spanwise spacing, streamwise length and inclination angle of the quasi-streamwise vortices and streaks. A distinct feature of the VVCS11 is that its geometry continuously varies with y(r). A topological change of VVCSii from quadrupole (for smaller y(r)) to dipole (for larger y(r)) occurs at y(r)(+) = 110, giving a geometrical interpretation of the multilayer nature of wall-bounded turbulent shear flows. In conclusion, the VVCS provides a new robust method to quantify CS in wall-bounded flows, and is particularly suitable for extracting statistical geometrical measures using two-point simultaneous data from hotwire, particle image velocimetry/laser Doppler anemometry measurements or DNS/large eddy simulation data.
[本文引用: 1]
