连续纤维增强复合材料结构基频最大化设计 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

程长征^*^,^?, 卞光耀^*^,^?, 王选^,^*^,^?^,²⁾, 龙凯^**, 李景传^*^,^?, 吴乔国^*^,^?

^*合肥工业大学工程力学系, 合肥 230009

^?合肥工业大学土木工程结构与材料安徽省重点实验室, 合肥 230009

^**华北电力大学新能源电力系统国家重点实验室, 北京 102206

FUNDAMENTAL FREQUENCY MAXIMIZATION DESIGN FOR CONTINUOUS FIBER-REINFORCED COMPOSITE STRUCTURES ¹⁾

Cheng Changzheng^*^,^?, Bian Guangyao^*^,^?, Wang Xuan^,^*^,^?^,²⁾, Long Kai^**, Li Jingchuang^*^,^?, Wu Qiaoguo^*^,^?

^*Department of Engineering Mechanics, Hefei University of Technology, Hefei 230009, China

^?Anhui Key Laboratory of Civil Engineering Structures and Materials, Hefei University of Technology, Hefei 230009, China

^**State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China

通讯作者: 2)王选, 讲师, 主要研究方向: 结构拓扑优化. E-mail:xuanwang@hfut.edu.cn

收稿日期:2020-03-11接受日期:2020-03-11网络出版日期:2020-09-18

基金资助:

1)国家自然科学基金.11772114
安徽省自然科学基金.2008085QA21
中央高校基本科研业务费专项资金.PA2019GDQT0016
中央高校基本科研业务费专项资金.JZ2019HGBZ0127
中央高校基本科研业务费专项资金.PA2019GDPK0039
中央高校基本科研业务费专项资金.JZ2020HGTA0080

Received:2020-03-11Accepted:2020-03-11Online:2020-09-18
作者简介 About authors

摘要
与传统的金属材料相比, 纤维增强复合材料在强度、刚度、抗断裂等诸多方面具备更优良的性能, 目前纤维增强复合材料已在汽车、航空航天等工业领域得到了广泛应用. 本文提出一种求解连续纤维增强复合材料结构无阻尼自由振动下的基频最大化问题的拓扑优化方法. 为了实现结构拓扑构型与纤维角度的同步优化, 建立了以准许的材料用量体积分数为约束、以结构的一阶特征值为目标函数的动力学拓扑优化模型, 该模型包括表征结构拓扑构型的密度设计变量和表征纤维方向的角度设计变量. 详细推导了特征值目标函数关于密度设计变量和角度设计变量的解析灵敏度列式, 并采用移动渐进线方法 (method of moving asymptotes, MMA) 进行了优化求解; 最后通过3个数值算例验证本文方法的有效性, 其中包括一个以刚度最大化为目标的静力学优化算例, 和两个以一阶特征值为目标的动力学优化算例. 结果表明, 所提方法优化迭代过程稳健, 收敛快, 能够在实现结构拓扑构型与纤维角度的一体化优化的同时, 有效提高结构的频率.
关键词： 拓扑优化;连续纤维;动力学优化;SIMP方法

Abstract
Compared with traditional metal-materials, fiber-reinforced composite materials have better performance in many aspects such as strength, stiffness, and fracture resistance. At present, fiber-reinforced composite materials have been widely used in automotive, aerospace, and other industrial fields. This paper proposes a topology optimization method for solving the fundamental frequency maximization of undamped free vibration of continuous fiber-reinforced composite structures. To achieve the simultaneous optimization of the structural topological configuration and the fiber angle. A dynamic topological optimization model is established with the permitted material usage as the constraint and the structure's first-order eigenvalue as the objective function. The model includes density design variables that characterizes the topological configuration of the structure and angular design variables that characterizes the fiber orientation. The analytical sensitivity formulas of the objective function of eigenvalue with respect to density design variables and angle design variables are derived in detail, and the method of moving asymptotes (MMA) is used to solve the optimization problem. Finally, three numerical examples are performed to verify the effectiveness of the proposed method, which includes a static optimization example with the stiffness maximization as the goal and two dynamic optimization examples with the first-order eigenvalue maximization as the goal. The results show that the proposed method can achieve a stable iterative history and fast convergence, and can effectively improve the structural frequency while achieving the integrated optimization of the structural topological configuration and the fiber angle.
Keywords：topology optimization;continuous fiber;dynamic optimization;SIMP method

PDF (3732KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
程长征, 卞光耀, 王选, 龙凯, 李景传, 吴乔国. 连续纤维增强复合材料结构基频最大化设计 ¹⁾. 力学学报[J], 2020, 52(5): 1422-1430 DOI:10.6052/0459-1879-20-083
Cheng Changzheng, Bian Guangyao, Wang Xuan, Long Kai, Li Jingchuang, Wu Qiaoguo. FUNDAMENTAL FREQUENCY MAXIMIZATION DESIGN FOR CONTINUOUS FIBER-REINFORCED COMPOSITE STRUCTURES ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1422-1430 DOI:10.6052/0459-1879-20-083

引言

随着现代工业的发展, 很多新型材料被研制并成功应用于不同领域, 其中纤维增强复合材料就是最常用的一种, 已在汽车、建筑以及航空航天工业等领域得到广泛应用^[1]. 纤维增强复合材料由基体材料和增强材料两部分组成. 与单独组分材料和传统的金属材料相比, 纤维增强复合材料在强度、刚度、抗断裂、抗疲劳、热稳定性等诸多方面具备更优良的性能. 另一方面, 当结构所受的外激励频率与自身的固有频率接近时, 就会发生共振现象, 共振会导致机器破坏、桥梁倒塌等严重危害. 因此, 本文开展连续纤维增强复合材料结构基频最大化设计研究具有重要意义.

基频最大化是结构动力学拓扑优化中被广泛关注的优化问题之一. Ma等^[2]采用均匀化方法较早研究了动力学拓扑优化问题. Pedersen^[3]通过引入新的材料刚度插值格式避免了基于SIMP (solid isotropic material with penalization)方法的频率优化中在低密度区出现的局部模态现象. 为了适应实际制造工艺要求, Niu等^[4]采用均匀化方法实现了蜂窝材料结构在宏观和微观两个尺度上同步优化以最大化结构基频, Huang等^[5]基于BESO (Bi-directional evolutionary structural optimization)方法研究了体积约束下的结构一阶频率最大化问题. Xia等^[6]基于水平集方法研究了结构在无阻尼自由振动下的频率最大化问题, 得到了光滑的拓扑构型边界, 在此基础上, 他们进一步考虑了均匀边界腐蚀对动力学优化问题中基频的影响^[7]. 高兴军和马海涛^[8]提出了一种将移频与虚假模态识别相结合的通用方法, 以消去连续体结构动力拓扑优化中局部模态的不利影响. 动力学拓扑优化方面的研究还包括最大化高阶本征频率或最大化两阶本征频率的带宽^[9]、最大化受迫振动下的动柔度^[10-13]等. 此外, 还可以将上面度量结构的振动效应的指标作为约束函数来建模^[14-15]. 文献^[16]从不同优化方法角度对结构动力学拓扑优化问题做了较为全面的综述.

纤维增强复合材料结构的纤维角度优化问题也是被大家关注的热点问题之一. Pedersen^[17]基于OC准则方法(optimality criteria based method)实现了层压膜结构的厚度和纤维角度优化. Luo 和Gea^[18]基于能量的方法以应变能最小化或基频最大化为目标, 实现了三维板壳结构的纤维角度优化问题. Setoodeh等^[19]基于SIMP方法研究了单工况和多工况载荷作用下二维复合结构的拓扑构型和纤维角度的同步优化问题, 以最大化结构的刚度. Stegmann和Lund^[20]基于多相材料插值思想提出了一种新颖的DMO (discrete material optimization method)实现了一般的层压复合壳的纤维优化. Niu等^[21]将DMO法拓展到考虑最小声辐射的层压复合板结构的离散纤维角度优化问题中. Gao等^[22]将复合材料结构的离散纤维优化问题转化为可用连续体拓扑优化方法处理的材料选择问题, 提出了一种有效的二值参数化列式. 段尊义等^[23]将连续化惩罚策略与Heaviside惩罚函数引入传统DMO模型中, 提高了复合材料单层板结构的纤维角度优化的收敛率. 他们还将所提方法拓展到纤维角度和结构拓扑构型一体化优化问题中, 以最大化结构的刚度^[24]. Xia和Shi^[25]基于Shepard插值方法^[26]构造了一个连续分布的纤维场, 研究纤维增强复合材料结构的刚度最大化问题. Yan等^[27]以最大结构刚度为目标, 基于双向渐进结构优化法提出了一种实现正交材料纤维方向和结构拓扑构型的同步优化. Xu等^[28]实现了考虑载荷不确定性的纤维增强复合结构的纤维方向的鲁棒性优化. Papapetrou等^[29]将SIMP方法和水平集方法结合, 实现了纤维角度和结构拓扑的同步优化, 以最大化结构的刚度. Luo等^[30]针对纤维增强复合材料的刚度最大化问题, 提出了离散-连续的参数化列式, 可有效减小优化问题陷入局部优化解的风险.

可以看出, 现有文献大部分关注单一均质材料结构的动力学拓扑构型的优化、或单纯考虑纤维角度优化问题, 另外, 关于纤维增强复合材料结构的拓扑构型和纤维方向的同步优化方面的研究大部分关注刚度最大化优化问题, 而在动力学背景下考虑结构拓扑构型和纤维方向同步优化的研究较少. 因此, 本文旨在提出一种针对连续纤维增强复合材料结构无阻尼自由振动下的基频最大化问题的拓扑优化方法, 实现结构拓扑构型与纤维方向的同步优化, 以最大化结构的第一阶本征频率.

1 连续纤维增强复合材料结构优化模型

1.1 复合材料结构自由振动有限元分析

考虑二维正交各向异性材料线弹性结构无阻尼自由振动分析的离散型有限元方程表示如下

(1) $ \begin{eqnarray} \label{eq1} Ku_i =\omega _i^2 Mu_i \end{eqnarray} $

其中, $u_i $为第$i$阶特征频率$\omega _i $所对应的特征向量. $ K$和$ M$分别为结构的总体刚度阵和质量阵, 由对应的单元刚度阵$ K_e^0$和质量阵$ M_e^0 $组装形成. $ M_e^0 $和$ K_e^0 $分别由式(2)和式(3)确定

(2) $ \begin{eqnarray} \label{eq2} && M_e^0 =\iint_{\varOmega _e } { N^{\rm T}}\rho _0 Nh{\rm d}\varOmega _e \end{eqnarray}$

(3) $ \begin{eqnarray} \label{eq3} K_e^0 (\theta _e )=\iint_{\varOmega _e } { B^{\rm T}} C(\theta _e ) Bh{\rm d}\varOmega _e \end{eqnarray}$

其中, $h$为结构的厚度, $\rho _0 $为材料的质量密度, $ N$为双线性等参元形函数组成的矩阵. $ B$为应变位移矩阵. $ M_e^0$和$ K_e^0$分别为单元$e$所对应的单元质量阵和刚度阵. $\theta _e$为单元$e$所对应的表征纤维方向的角度设计变量, 即建立在单元$e$上的纤维主方向和垂直于纤维主方向上的局部坐标${X}'$-${Y}'$与全局坐标$X$-$Y$之间的旋转角度, 如图1所示.

图 1

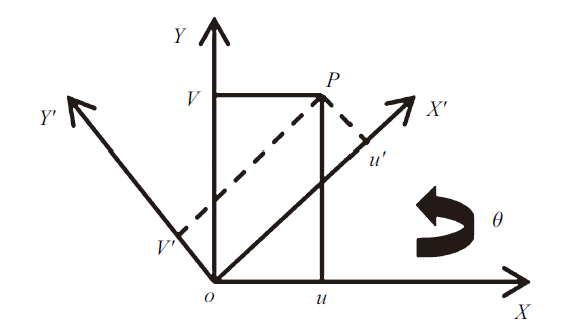新窗口打开|下载原图ZIP|生成PPT
图 1坐标转换示意图

Fig. 1Schematic illustration of coordinate transformation

式(3)中的$ C$为全局坐标下的正交本构材料矩阵, 其表达式为

(4) $ \begin{eqnarray} \label{eq4} C_e (\theta _e )= T(\theta _e ) C_0 T^{\rm T}(\theta _e ) \end{eqnarray}$

其中, $ C_0 $为局部坐标下的正交本构材料矩阵, 由沿纤维轴向的弹性刚度$E_x $, 纤维横向弹性刚度$E_y $, 剪切模量$G_{xy} $, 泊松比$V_{xy} $, $V_{yx} $五个材料常数组成, 其表达式为

(5) $ \begin{eqnarray} \label{eq5} C_0 =\frac{1}{1-V_{xy} V_{yx} }\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {E_x } & {V_{yx} E_x } & 0 \\ {V_{xy} E_y } & {E_y } & 0 \\ 0 & 0 & {G_{xy} \left( {1-V_{xy} V_{yx} } \right)} \\ \end{array} }} \right]\ \ \end{eqnarray}$

式中, $E_x $, $E_y $, $V_{xy} $, $V_{yx} $满足$V_{yx} E_x =V_{xy} E_y $.

式(4)中的$ T(\theta _e )$为$ C$与$ C_0 $之间的转换矩阵, 其表达式由下式定义

(6) $ \begin{eqnarray} \label{eq6} T=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} {\cos^2\theta } & {\sin^2\theta } & {-2\sin\theta \cos\theta } \\ {\sin^2\theta } & {\cos^2\theta } & {2\sin\theta \cos\theta } \\ {\sin\theta \cos\theta } & {-\sin\theta \cos\theta } & {\cos^2\theta -\sin^2\theta } \\ \end{array} }} \right] \end{eqnarray}$

1.2 材料插值格式

为了实现结构拓扑构型与纤维角度的同步优化, 这里采用SIMP方法来实现结构拓扑构型的优化, 即给每一个单元引入一个密度设计变量$x_e $, 然后采用SIMP材料插值模型建立单元刚度阵和质量阵与单元密度设计变量$x_e $之间的关系

(7) $ \begin{eqnarray} \label{eq7} && M_e (x_e)=x_e^q M_e^0 \end{eqnarray} $

(8) $ \begin{eqnarray} \label{eq8} K_e (x_e,\theta _e )=x_e^p K_e^0 (\theta _e ) \end{eqnarray}$

其中, $ M_e $和$ K_e $分别为引入表征拓扑构型的密度变量之后的单元质量阵和刚度阵, $p$和$q$分别为刚度阵和质量阵的惩罚因子, $ M_e^0 $和$ K_e^0$分别由式(2)和式(3)确定.

众所周知, 在用SIMP求解动力学优化问题时, 材料低密度区域通常会出现局部模态^[3,8-9,31], 这是由于在低密度区域(如$x_e\leqslant 0.1)$, 基于$q=1$惩罚之后的质量阵与基于$p=3$惩罚之后的刚度阵比值过高造成的^[3,9]. 避免局部模态的常用方法有: (1)修改刚度矩阵的惩罚方式^[3,5]; (2)修改质量矩阵的惩罚方式^[9-10,12]. 在这里, 为了避免低密度区域中的局部模态, 采用文献^[9]中的方法, 修改质量阵的惩罚方式

(9) $ \begin{eqnarray} \label{eq9} M_e (x_e)=\left\{ {{\begin{array}{l@{\ \ }l} x_e^q M_e^0, &x_e <0.1\\ x_e M_e^0, &x_e \geqslant 0.1\\ \end{array} }} \right. \end{eqnarray}$

这里设置刚度矩阵惩罚因子$p=3$,对于质量矩阵, 当单元密度$x_e \geqslant 0.1$时, 设置惩罚因子为1; 当单元密度$x_e <0.1$时, 设置惩罚因子$q=6$. 通过式(8)和式(9)可知, 通过修改质量阵的惩罚方式可以很好地避免底密度区域质量阵与刚度阵的比值过高的情况, 从而有效避免局部模态.

1.3 优化模型

结构拓扑优化旨在满足某些约束条件下寻找最优的材料分布, 以期获得最佳的结构性能. 与文献^[32,33,34]关注的优化问题不同, 本文研究连续纤维增强复合材料结构在无阻尼自由振动下的基频最大化优化问题, 以实现纤维方向角度与结构拓扑构型的同步优化, 其对应的数学列式可表示如下

(10) $ \begin{eqnarray} \label{eq10} \left. \begin{array}{ll} \mbox{find}:\left\{ {{\begin{array}{*{20}c} { x=\left\{ {x_1 ,x_2 ,\cdots ,x_{N_e } } \right\}} \\ { \theta =\left\{ {\theta _1 ,\theta _2 ,\cdots ,\theta _{N_e } } \right\}} \\ \end{array} }} \right. \\ \mbox{max}:\left\{ {\min \left\{ {\omega _i^2 } \right\}} \right\} \\ {\rm s.t.}\left\{ {{\begin{array}{*{20}c} { K( x, \theta )u_i =\omega _i^2 M(x)u_i } \\ { \sum\limits_{e=1}^{N_e } {x_e V_e \leqslant f_v V_0 } } \\ {0<x_{\min } \leqslant x_e \leqslant 1} \\ {-2\pi \leqslant \theta _e \leqslant 2\pi } \\ \end{array} }} \right. \\ \end{array} \right\} \end{eqnarray}$

在此优化模型中, 有两类设计变量, 其中$ x$为表征结构拓扑构型的密度设计变量集合, $ \theta $为表征纤维方向的角度设计变量集合, $N_e $为用来离散设计域的单元个数. $\omega _i $为第$i$阶特征频率, $u_i $为其对应的特征向量. $ K$和$ M$分别为引入两类设计变量之后结构的总体刚度阵和质量阵. $V_e $和$V_0 $分别为单元$e$和整个设计域的体积, $f_v $为设计领域中可用实体材料的体积分数比. $x_{\min } $为很小的正数, 作为密度设计变量的下限以防止刚度矩阵奇异, 本文取$x_{\min } =10^{-3}$. 本文设置每个纤维角度变量$\theta _e $的范围为$[-2\pi ,2\pi]$,宽的纤维角度范围允许角度旋转到最佳位置, 可以避免较窄的角度变量范围导致的潜在的局部解问题^[35].

2 灵敏度分析与灵敏度过滤

动力学优化问题可能存在重特征根问题, 特别是那些设计自由度多、依赖的设计参数多的结构, 在优化的过程中可能会出现两阶特征根相等的情况, 重特征根会导致优化问题不连续, 进而导致多重特征根关于设计变量的敏度难于计算的困难. 目前也有较多优秀工作讨论了这一问题, 并给出了有效的解决方案^[9,36]. 重特征根问题不是这篇文章的关注点, 因此, 这里假设所关注的特征根均为单根, 即特征根均互不相等, 这样可以推导单特征值关于两类设计变量的灵敏度.

2.1 特征值对密度设计变量的灵敏度

式(10)中无阻尼自由振动分析的有限元方程两边同时对密度设计变量$x_e $求导, 并化简可得

(11) $ \begin{eqnarray} \lt(\frac{\partial K}{\partial x_e }-\frac{\partial \omega _i^2 }{\partial x_e } M-\omega _i^2 \frac{\partial M}{\partial x_e } ) u_i =( K-\omega _i^2 M)\frac{\partial u_i }{\partial x_e } \end{eqnarray}$

对式(11)两边同时左乘$ u_i^{\rm T} $, 再经过简单化简可得特征值$\lambda _i =\omega_i^2 $关于设计变量$x_e $的灵敏度

(12) $ \begin{eqnarray} \label{eq12} \frac{\partial \lambda _i }{\partial x_e }=\frac{\partial \omega _i^2 }{\partial x_e }=\frac{ u_i^{\rm T} \lt(\dfrac{\partial K}{\partial x_e }-\omega _i^2 \dfrac{\partial M}{\partial x_e } ) u_i }{ u_i^{\rm T} M u_i } \end{eqnarray}$

其中, ${\partial K} / {\partial x_e }$和${\partial M} / {\partial x_e }$与材料插值格式有关, 具体表达式可根据式(8)和式(9)计算得到

(13) $ \begin{eqnarray} \label{eq13} &&\frac{\partial K}{\partial x_e }=\frac{\partial K_e }{\partial x_e }=px_e^{p-1} \frac{\partial K_e^0 }{\partial x_e } \end{eqnarray}$

(14) $ \begin{eqnarray} \label{eq14} \frac{\partial M}{\partial x_e }=\frac{\partial M_e }{\partial x_e }=\left\{ {{\begin{array}{ll} qx_e^{q-1} \dfrac{\partial M_e^0 }{\partial x_e }, & x_e <0.1\\[2mm] x_e \dfrac{\partial M_e^0 }{\partial x_e }, &x_e \geqslant 0.1\\ \end{array} }} \right. \end{eqnarray}$

2.2 特征值对角度设计变量的灵敏度

类似于求特征值关于密度设计变量的灵敏度, 可以推导特征值关于角度设计变量$\theta _e $的灵敏度, 其表达式如下

(15) $ \begin{eqnarray} \label{eq15} \frac{\partial \lambda _i }{\partial \theta _e }=\frac{\partial \omega _i^2 }{\partial \theta _e }=\frac{ u_i^{\rm T} \dfrac{\partial K}{\partial \theta _e } u_i }{ u_i^{\rm T} M u_i } \end{eqnarray}$

值得注意的是, 这里假设质量矩阵与纤维方向无关. 式(15)中刚度阵$ K$对角度设计变量$\theta _e $的导数${\partial K} / {\partial \theta _e }$可表示为

(16) $ \begin{eqnarray} \label{eq16} &&\frac{\partial K}{\partial \theta _e }=\frac{\partial K_e }{\partial \theta _e }=x_e^p \iint_{\varOmega _e } B^{\rm T}\lt(\frac{\partial T(\theta _e )}{\partial \theta _e } C_0 T^{\rm T}(\theta _e )+ . \\&&\qquad T(\theta _e ) C_0 \frac{\partial T^{\rm T}(\theta _e )}{\partial \theta _e } ) B h{\rm d}\varOmega _e \end{eqnarray}$

关于体积约束关于设计变量的敏度可直接求导获得, 这里省略其细节推导.

2.3 灵敏度过滤

由于有限元网格离散的影响, 基于单元密度的拓扑优化方法经常遭受棋盘格和网格依赖性等数值不稳定性问题. 为了获得清晰的黑白设计, 本文采用式(17)对式(12)中定义的第一阶特征值(最小特征值) $\lambda _1 $关于密度设计变量$x_e $的敏度进行过滤

(17) $ \begin{eqnarray} \label{eq17} \frac{\partial \hat{{\lambda }}_1 }{\partial x_e }=\frac{ \sum\limits_{i\in N_{ei} } {H_{ei} } \dfrac{\partial \lambda _1 }{\partial x_i }}{ \sum\limits_{i\in N_{ei} } {H_{ei} } } \end{eqnarray}$

其中权重函数$H_{ei} $定义为

(18) $ \begin{eqnarray} H_{ei} =\min \left\{ {0,r_{\min } -{\rm dist}(e,i)} \right\} \end{eqnarray}$

式中, dist$(e,i)$为单元$e$的中心和单元$i$的中心之间的欧式距离, $N_{ei} $是指单元中心落在以单元$e$为中心、半径为$r_{\min } $的圆形邻域内的单元集合. 以过滤后的敏度代替式(12)参入优化迭代.

上述优化问题可以用不同的优化算法来求解, 如序列线性规划法(SLP)^[37], 移动渐近线算法(MMA)^[38]等, 本文采用MMA算法求解上述优化问题. 数值测试表明角度设计变量灵敏度的绝对值相对于密度设计变量灵敏度的绝对值要小很多, 为了避免陷入局部解, 提高收敛效率, 本文采用式(19)定义的变步长策略, 即使设计变量移动步长随着迭代步数的增加逐渐减小

(19) $ \begin{eqnarray} \label{eq19} \left. {\begin{array}{l} {\rm move}\_x=0.995\ast {\rm move}\_x \\ {\rm move}\_\theta =0.95\ast {\rm move}\_\theta \\ \end{array}} \right\} \end{eqnarray}$

其中, ${\rm move}\_x$和${\rm move}\_\theta $分别为单元密度变量和角度设计变量的移动步长. 它们的初始值分别设置为${\rm move}\_x=0.5$, ${\rm move}\_\theta =0.1$.

当优化过程满足式(20)定义的收敛条件时, 停止迭代

(20) $ \begin{eqnarray} \left. {\begin{array}{l} \max \left| {x_k -x_{k-1} } \right|\leqslant \varepsilon \\ \max \left| {\theta _k -\theta _{k-1} } \right|\leqslant \varepsilon \\ \end{array}} \right\} \end{eqnarray} $

式中, $k $为当前迭代步数, $\varepsilon $为容许的收敛误差, 并取$\varepsilon =1.0\times10^{-3}$.

3 数值算例与讨论

本节通过一个静力学优化算例和两个算例动力学优化算例来展示本文方法的有效性. 若无特殊说明, 平板厚度设置为1 mm, 质量密度设置为1.6 g/cm$^3$; 本构材料阵中4个独立的物理参数取值为$E_x =385$ GPa, $E_y =118$ GPa, $V_{xy} =0.3$和$G_{xy} =84$ GPa. 假设初始结构为完全实体材料, 即所有密度设计变量$x_e $的初始值均为1. 本文所有的角度变量均以弧度制表示. 本文所有算例中MMA算法参数取值列于表1中.

Table 1
表1
表1MMA子程序中参数取值
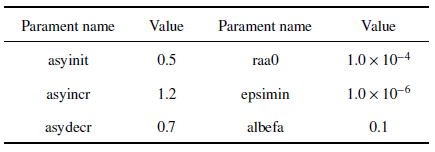Table 1Parameters needed for MMA subroutine

新窗口打开|下载CSV

3.1 算例一

算例一考虑短悬臂梁的刚度最大化优化问题. 几何尺寸为80 mm $\times$ 40 mm的设计域和边界条件如图2所示, 梁左端完全固支, 在右端中心点处受大小为30 N的横向拉力. 设计域由$80\times40$个平面应力单元来离散. 材料准许的体积分数设定为0.3.

图 2

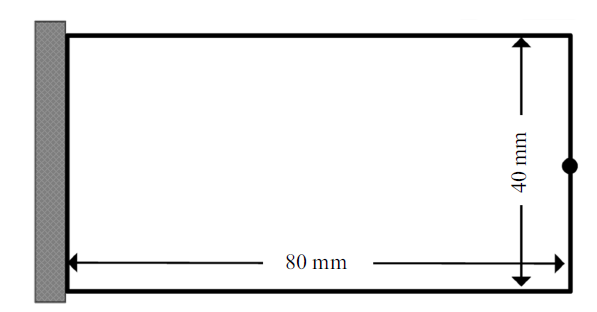新窗口打开|下载原图ZIP|生成PPT
图 2悬臂梁的设计域和边界条件

Fig. 2Design domain and boundary condition of cantilever beam

为了验证本文方法对静力学优化问题的有效性, 考虑以0, $\pi /6$, $\pi /2$, 及$[-2\pi ,2\pi ]$区间内产生的一个随机数为初始纤维方向. 图3显示了4种不同初始纤维方向所对应的优化结果. 从结果可以看出, 尽管初始纤维角度不同, 但优化后的纤维基本沿轴向拉伸方向分布, 增强了结构的刚度, 符合工程实际情况, 这验证了本文方法对静力学优化问题的有效性.

图 3

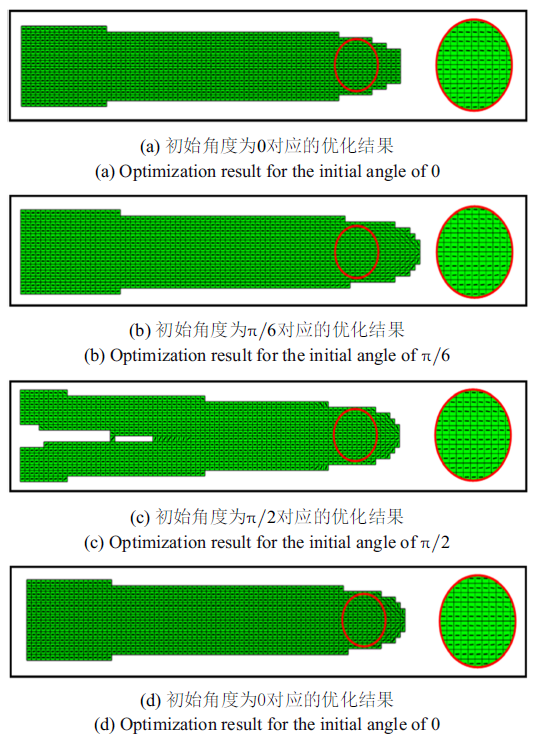新窗口打开|下载原图ZIP|生成PPT
图 3不同初始纤维方向对应的优化结果

Fig. 3Optimization results for different initial fiber orientations

3.2 算例二

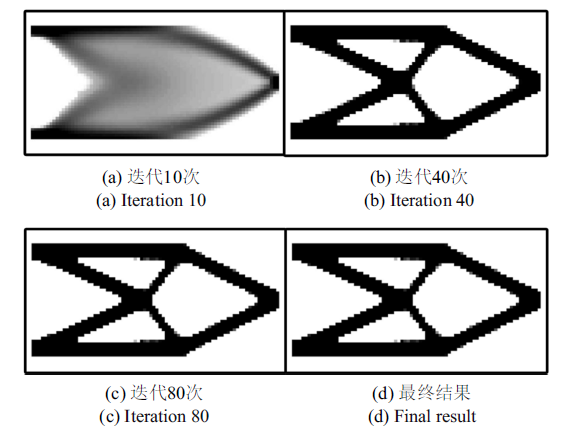
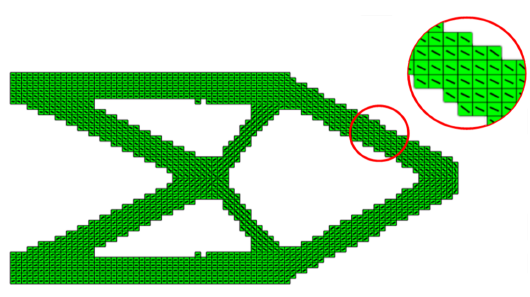
算例二考虑悬臂梁动力学优化问题. 设计域与算例一相同, 梁左端完全固支, 在右边中心点处附加一个大小为28.8 g的集中质量点. 设置纤维初始方向为水平方向, 即设置所有角度设计变量$\theta _e $的初始值为0. 材料准许的体积分数设定为0.4.

图4显示了连续纤维增强悬臂梁在无阻尼自由振动下结构拓扑构型的迭代过程. 优化算法在迭代87步之后收敛, 此时结构对应的最小特征值为188.76 Hz. 图5显示了悬臂梁的纤维分布情况. 可以看出, 本文方法可以获得清晰的拓扑构型, 优化后纤维方向基本沿悬臂梁横向中轴线呈对称分布.

图 4

新窗口打开|下载原图ZIP|生成PPT
图 4悬臂梁拓扑构型的迭代过程

Fig. 4Iterative process of topological configuration of cantilever beam

图 5

新窗口打开|下载原图ZIP|生成PPT
图 5悬臂梁纤维方向的优化结果

Fig. 5Optimization result of fiber orientation for cantilever beam

为了进一步验证所提方法的有效性, 在图5显示的最终纤维角度的优化结果基础上, 让所有单元对应的角度变量逆时针偏转角度$\beta $. 在几个典型的偏转角度$\pi/6$, $\pi/4$, $\pi/3$, $5\pi/12$, $\pi/2$下, 结构对应的最小特征值$\lambda _1$分别为128.96, 96.06, 75.41, 64.63, 61.32. 可以看出, 纤维方向偏转一定角度后结构对应的最小特征值均比通过本文优化方法获得的结果(188.76 Hz)要小, 这说明本文方法能够有效找到更优的纤维方向分布, 提高结构的频率.

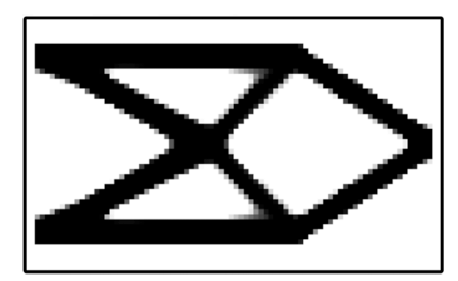
图6显示了各向同性材料悬臂梁在无阻尼自由振动下结构拓扑构型的优化结果, 其中材料本构阵中使用的独立物理参数为: 杨氏模量$E=385$ GPa, 泊松比$V=0.3$. 可以看出, 本文获得的拓扑构型与文献^[15]中的动力学优化结果类似, 优化算法在迭代61步之后收敛, 此时对应的最小特征值为188.87 Hz. 对于当前的悬臂梁优化算例, 各向同性材料拓扑优化结果与纤维增强的正交各向异性材料结构拓扑构型结果相似.

图 6

新窗口打开|下载原图ZIP|生成PPT
图 6各向同性材料悬臂梁的拓扑构型

Fig. 6Topological configuration of cantilever beam with isotropic material

3.3 算例三

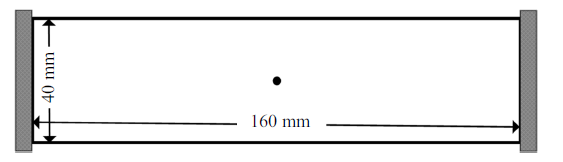
算例三考虑固支细长梁结构的动力学优化问题. 几何尺寸为160 mm $\times$ 40 mm的设计域和边界条件如图7示, 梁两端全固定, 平板中心处附加一个质量为51.2 g的质量点. 设计域由$160\times 40$个平面应力单元来离散. 设置纤维角度设计变量的初始值为$\theta _e =0$. 材料准许的体积分数为$0.4$.

图 7

新窗口打开|下载原图ZIP|生成PPT
图 7固支梁的设计域和边界条件

Fig. 7Design domain and boundary condition of clamped beam

图8显示了连续纤维增强固支细长梁在无阻尼自由振动下结构拓扑构型的迭代过程. 图9 显示了固支细长梁纤维方向的优化结果. 从优化结果可知, 本文方法可以获得清晰的拓扑构型, 纤维方向主要沿着杆件的方向分布. 图10显示了前两阶特征值的迭代历史. 从结果可以看出, 优化算法在迭代77步之后到达收敛, 此时结构对应的最小特征值为373.86 Hz, 第2阶特征值为22 869.56 Hz, 前两阶特征值在优化的过程中始终分离的, 第2阶特征值始终大于第1阶特征值, 未产生重特征根问题, 这验证了本文关注的特征值为单根的假定.

图 8

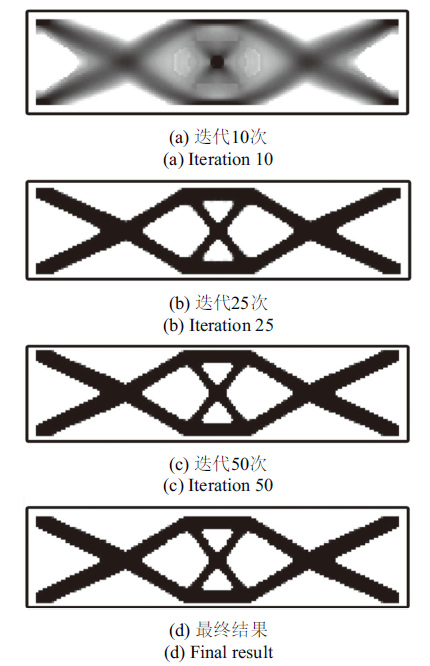新窗口打开|下载原图ZIP|生成PPT
图 8固支梁拓扑构型的迭代过程

Fig. 8Iterative process of topological configuration of clamped beam

图 9

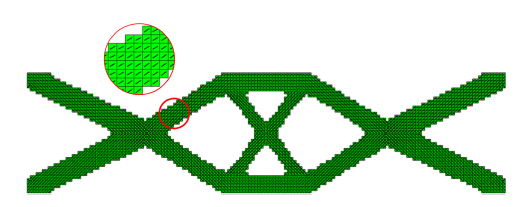新窗口打开|下载原图ZIP|生成PPT
图 9固支梁纤维方向的优化结果

Fig. 9Optimization result of fiber orientation for clamped beam

图 10

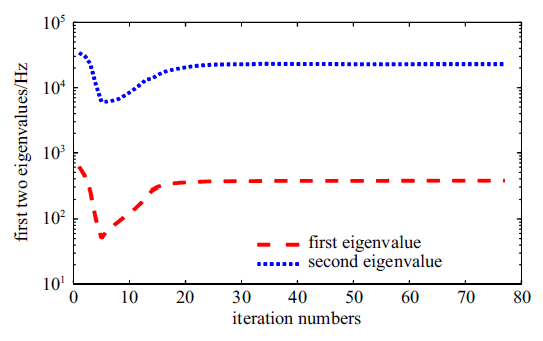新窗口打开|下载原图ZIP|生成PPT
图 10固支梁前2阶特征值的迭代历史

Fig. 10Iteration history of the first two eigenvalue of clamped beam

同样, 为了进一步验证本文方法的有效性, 在图9显示的最终纤维角度的优化结果基础上, 让所有单元对应的角度变量逆时针偏转角度$\beta$. 在几个典型的偏转角度$\pi/6$, $\pi/4$, $\pi/3$, $5\pi/12$, $\pi/2$下, 结构对应的最小特征值$\lambda _1 $的值分别为262.18, 198.32, 157.31, 135.58, 128.84. 由表3可知, 结果与悬臂梁相优化问题类似, 纤维方向偏转一定角度后所得结构的最小特征值均变小, 这进一步说明本文方法的有效性.

4 结论

针对连续纤维增强复合材料结构无阻尼自由振动下的基频最大化问题, 本文提出了一种有效实现拓扑构型和纤维方向同步优化的拓扑优化方法. 建立了以准许的材料用量体积分数为约束、以结构的一阶特征值为目标函数的动力学拓扑优化模型, 详细推导了目标函数关于密度设计变量和角度设计变量的解析灵敏度列式. 为了避免陷入局部最优解, 采用了变移动步长的策略. 最后, 通过一个静力学优化算例和两个动力学优化算例验证了本文方法的有效性. 结果表明, 本文方法在实现结构拓扑构型与纤维角度的一体化优化的同时, 可以有效改善结构的性能.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

沈观林, 胡更开. 复合材料力学II. 北京: 清华大学出版社, 2006,247

[本文引用: 1]

( Shen

Guanlin

, Hu

Gengkai

. Mechanics Composite Matierials II. Beijing: Tsinghua University Press, 2006,247(in Chinese))

[本文引用: 1]

[2]

, Kikuchi

, Cheng

. Topological design for vibrating structures
Computer Methods in Applied Mechanics and Engineering, 1995,121(1-4):259-280

[本文引用: 1]

[3]

Pedersen

. Maximization of eigenvalues using topology optimization
Structural and Multidisciplinary Optimization, 2000,20(1):2-11

DOI URL [本文引用: 4]

[4]

Niu

, Yan

, Cheng

. Optimum structure with homogeneous optimum cellular material for maximum fundamental frequency
Structural and Multidisciplinary Optimization, 2009,39(2):115-138

DOI URL [本文引用: 1]

Ultra-light cellular materials exhibit high stiffness/strength to weight ratios and bring opportunity for multifunctional performance. One of their potential applications is to build structure with optimum dynamic performance, which is extremely important for some structural parts in vehicle engineering and attracts a great attention. This paper presents a two-scale optimization method and aims at finding optimal configurations of macro structures and micro-structures of cellular material with maximum structural fundamental frequency. In this method macro and micro densities are introduced as independent design variables for macrostructure and microstructure. Optimizations at two scales are integrated into one system through homogenization theory and base material is distributed between the two scales automatically with optimization model. Microstructure of materials is assumed to be homogeneous at the macro scale to meet today’s manufacture practice and reduce manufacturing cost. Plane structure with homogeneous cellular material and perforated plate are studied. Numerical experiments validate the proposed method and computational model.

[5]

Huang

, Zuo

, Xie

. Evolutionary topological optimization of vibrating continuum structures for natural frequencies
Computers & Structures, 2010,88(5-6):357-364

[本文引用: 2]

[6]

Xia

, Shi

, Wang

. A level set based shape and topology optimization method for maximizing the simple or repeated first eigenvalue of structure vibration
Structural and Multidisciplinary Optimization, 2011,43(4):473-485

[本文引用: 1]

[7]

, Shi

, Xia

, et al. Maximizing the first eigenfrequency of structures subjected to uniform boundary erosion through the level set method
Engineering with Computers, 2019,35(1):21-33

[本文引用: 1]

[8]

高兴军, 马海涛. 连续体结构动力拓扑优化中局部模态处理的新方法
力学学报, 2014,46(5):739-746

DOI URL [本文引用: 2]

采用固体各向同性材料惩罚模型（solid isotropic material with penalization， SIMP）进行动力拓朴优化通常在优化过程中会出现虚假的局部振动模态，为消除这种虚假模态产生的不利影响，提出了移频与虚假模态识别相结合的通用方法. 研究中考虑以材料体积为约束、结构基频最大化为目标的优化模型，并采用节点设计变量描述设计域内材料分布. 基于虚假模态的特性，首先在特征值分析中应用移频方法排除特征值接近于零的低阶虚假模态，然后再依据虚假模态识别准则判定并剔除其他可能存在的虚假模态，从而可以高效可靠地确定结构真实的固有振动模态. 数值算例表明，提出的方法可以有效地消除动力拓扑优化中虚假模态可能产生的不利影响，并保证优化解的可靠性.

( Gao

Xingjun

, Ma

Haitao

. A New method for dealing with pseudo modes in topology optimization of continua for free vibration
Chinese Journal of Theoretical and Applied Mechanics, 2014,46(5):739-746 (in Chinese))

DOI URL [本文引用: 2]

, Olhoff

. Topological design of freely vibrating continuum structures for maximum values of simple and multiple eigenfrequencies and frequency gaps
Structural and Multidisciplinary Optimization, 2007,34(2):91-110

DOI URL [本文引用: 6]

A frequent goal of the design of vibrating structures is to avoid resonance of the structure in a given interval for external excitation frequencies. This can be achieved by, e.g., maximizing the fundamental eigenfrequency, an eigenfrequency of higher order, or the gap between two consecutive eigenfrequencies of given order. This problem is often complicated by the fact that the eigenfrequencies in question may be multiple, and this is particularly the case in topology optimization. In the present paper, different approaches are considered and discussed for topology optimization involving simple and multiple eigenfrequencies of linearly elastic structures without damping. The mathematical formulations of these topology optimization problems and several illustrative results are presented.

[10]

Olhoff

, Du

. Topological design for minimum dynamic compliance of continuum structures subjected to forced vibration
// 6th World Congresses of Structural and Multidisciplinary Optimization, 2010

[本文引用: 2]

[11]

Olhoff

, Niu

. Minimizing the vibrational response of a lightweight building by topology and volume optimization of a base plate for excitatory machinery
Structural and Multidisciplinary Optimization, 2016,53(3):567-588

DOI URL

[12]

Niu

, He

, Shan

, et al. On objective functions of minimizing the vibration response of continuum structures subjected to external harmonic excitation
Structural and Multidisciplinary Optimization, 2018,57(6):2291-2307

DOI URL [本文引用: 1]

[13]

刘虎, 张卫红, 朱继宏. 简谐力激励下结构拓扑优化与频率影响分析
力学学报, 2013,45(4):588-597

DOI URL [本文引用: 1]

研究了简谐力激励下以结构指定位置稳态阶段位移响应幅值为目标函数、结构体积为约束的拓扑优化设计问题. 通过在频域上使用模态叠加法求解简谐力激励下的位移响应, 分析了激励频率和作用方向对位移响应幅值及其优化结果的影响.引入材料属性的多项式插值惩罚模型, 有效消除了动力学拓扑优化局部模态现象.分析了高频激励下位移响应幅值拓扑优化存在的稳定性差、结构不连续等问题, 并通过引入附加静位移约束, 获得了清晰合理的结构形式.理论分析和算例结果揭示了位移响应幅值优化过程中结构模态的变化规律, 验证了该拓扑优化模型的有效性.

( Liu

, Zhang

Weihong

, Zhu

Jihong

. Structual topology optimization and frequency influence analsis under harmonic force excitation
Chinese Journal of Theoretical and Applied Mechanics, 2013,45(4):588-597 (in Chinese))

DOI URL [本文引用: 1]

叶红玲, 沈静娴, 隋允康. 频率约束的三维连续体结构动力拓扑优化设计
力学学报, 2012,44(6):1037-1045

DOI URL [本文引用: 1]

针对频率约束和结构重量最小的动力拓扑优化问题, 基于(independent continuous mapping, ICM)独立、连续、映射方法,建立了频率约束下的三维连续体拓扑优化模型. 利用瑞利商和一阶泰勒展式对频率约束进行了显式化处理,并采用幂函数与复合指数函数作为过滤函数,将优化模型进行了标准化转换, 利用对偶理论及数学规划法进行了求解. 另外,利用质量矩阵和刚度矩阵过滤函数比值与动态约束处理了局部模态和模态交换等数值问题. 最后,通过应用两类不同过滤函数的数值算例表明了文中模型及方法在处理动力拓扑优化问题上的合理性与有效性.

( Ye

Hongling

, Shen

Jingxian

, Sui

Yunkang

. Dynamic topological optimal design of three-dimensional contimuum structures with frequencies constraints
Chinese Journal of Theoretical and Applied Mechanics, 2012,44(6):1037-1045 (in Chinese))

DOI URL [本文引用: 1]

龙凯, 谷先广, 王选. 基于多相材料的连续体结构动态轻量化设计方法
航空学报, 2017,38(10):129-138

[本文引用: 2]

( Long

Kai

, Gu

Xianguuang

, Wang

Xuan

. Light weight design method for continuum structure under vibration using multiphase matierials
Acta Aeronauticaet Astronautica Sinica, 2017,38(10):129-138 (in Chinese))

[本文引用: 2]

[16]

Zargham

, Ward

, Ramli

, et al. Topology optimization: A review for structural designs under vibration problems
Structural and Multidisciplinary Optimization, 2016,53(6):1157-1177

[本文引用: 1]

[17]

Pedersen

. On thickness and orientational design with orthotropic materials
Structural Optimization, 1991,3(2):69-78

[本文引用: 1]

[18]

Luo

, Gea

. Optimal bead orientation of 3D shell/plate structures
Finite Elements in Analysis and Design, 1998,31(1):55-71

[本文引用: 1]

[19]

Setoodeh

, Abdalla

, Gürdal

. Combined topology and fiber path design of composite layers using cellular automata
Structural and Multidisciplinary Optimization, 2005,30(6):413-421

[本文引用: 1]

[20]

Stegmann

, Lund

. Discrete material optimization of general composite shell structures
International Journal for Numerical Methods in Engineering, 2005,62(14):2009-2027

[本文引用: 1]

[21]

Niu

, Olhoff

, Lund

, et al. Discrete material optimization of vibrating laminated composite plates for minimum sound radiation
International Journal of Solids and Structures, 2010,47(16):2097-2114

[本文引用: 1]

[22]

Gao

, Zhang

, Duysinx

. A bi-value coding parameterization scheme for the discrete optimal orientation design of the composite laminate
International Journal for Numerical Methods in Engineering, 2012,91(1):98-114

[本文引用: 1]

[23]

段尊义, 阎军, 牛斌等. 基于改进离散材料插值格式的复合材料结构优化设计
航空学报, 2012,33(12):2221-2229

[本文引用: 1]

( Duan

Zunyi

, Yan

Jun

, Niu

Bin

, etal. Design optimization of composite materials based on improved discrete matierials optimization model
Acta Aeronauticaet Astronautica Sinica, 2017, 2012,33(12):2221-2229 (in Chinese))

[本文引用: 1]

[24]

Duan

, Yan

, Zhao

. Integrated optimization of the material and structure of composites based on the Heaviside penalization of discrete material model
Structural and Multidisciplinary Optimization, 2015,51(3):721-732

[本文引用: 1]

[25]

Xia

, Shi

. Optimization of composite structures with continuous spatial variation of fiber angle through Shepard interpolation
Composite Structures, 2017,182:273-282

[本文引用: 1]

[26]

Kang

, Wang

. Structural topology optimization based on non-local Shepard interpolation of density field
Computer Methods in Applied Mechanics and Engineering, 2011,200(49-52):3515-3525

DOI URL [本文引用: 1]

This paper presents a non-local density interpolation strategy for topology optimization based on nodal design variables. In this method, design variable points can be positioned at any locations in the design domain and may not necessarily coincide with elemental nodes. By using the Shepard family of interpolants, the density value of any given computational point is interpolated by design variable values within a certain circular influence domain of the point. The employed interpolation scheme has an explicit form and satisfies non-negative and range-restricted properties required by a physically significant density interpolation. Since the discretizations of the density field and the displacement field are implemented on two independent sets of points, the method is well suited for a topology optimization problem with a design domain containing higher-order elements or non-quadrilateral elements. Moreover, it has the ability to yield mesh-independent solutions if the radius of the influence domain is reasonably specified. Numerical examples demonstrate the validity of the proposed formulation and numerical techniques. It is also confirmed that the method can successfully avoid checkerboard patterns as well as "islanding" phenomenon. (C) 2011 Elsevier B.V.

[27]

Yan

, Xu

, Hua

, et al. Concurrent topology optimization of structures and orientation of anisotropic materials
Engineering Optimization, 2019: 1-14

[本文引用: 1]

[28]

, Gao

, Wu

, et al. Robust topology optimization for multiple fiber-reinforced plastic (FRP) composites under loading uncertainties
Structural and Multidisciplinary Optimization, 2019,59(3):695-711

DOI URL [本文引用: 1]

[29]

Papapetrou

, Patel

, Tamijani

. Stiffness-based optimization framework for the topology and fiber paths of continuous fiber composites
Composites Part B$:$ Engineering, 2020,183:107681

[本文引用: 1]

[30]

Luo

, Chen

, Liu

, et al. A discrete-continuous parameterization (DCP) for concurrent optimization of structural topologies and continuous material orientations
Composite Structures, 2020: 111900

[本文引用: 1]

[31]

朱继宏, 张卫红, 邱克鹏. 结构动力学拓扑优化局部模态现象分析
航空学报, 2005,26(4):619-623

[本文引用: 1]

( Zhu

Jihong

, Zhang

Weihong

, Qiu

Kepeng

. Investigation of localized modes in topology optimization of dynamic structures
Acta Aeronautica et Astronautica Sinica, 2005,26(4):619-623 (in Chinese))

[本文引用: 1]

[32]

王选, 胡平, 龙凯. 考虑嵌入移动空洞的多相材料布局优化
力学学报, 2019,51(3):852-862

[本文引用: 1]

( Wang

Xuan

, Hu

Ping

, Long

Kai

. Multiphase material layout optimization considering embedding movable holes
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):852-862 (in Chinese))

[本文引用: 1]

[33]

胡俊, 亢战. 考虑可控性的压电作动器拓扑优化设计
力学学报, 2019,51(4):1073-1081

[本文引用: 1]

( Hu

Jun

, Kang

Zhan

. Topology optimization of piezoelectric actuator considering controllability
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(4):1073-1081 (in Chinese))

[本文引用: 1]

[34]

龙凯, 王选, 吉亮. 面向应力约束的独立连续映射方法
力学学报, 2019,51(2):620-629

[本文引用: 1]

( Long

Kai

, Wang

Xuan

, Ji

Liang

. Independent continuous mapping method for stress constraint
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):620-629 (in Chinese))

[本文引用: 1]

[35]

Jiang

, Hoglund

, Smith

. Continuous fiber angle topology optimization for polymer composite deposition additive manufacturing applications
Fibers, 2019,7:14

DOI URL [本文引用: 1]

[36]

Seyranian

, Lund

, Olhoff

. Multiple eigenvalues in structural optimization problems
Structural Optimization, 1994,8(4):207-227

DOI URL [本文引用: 1]

[37]

Fujii

, Kikuchi

. Improvement of numerical instabilities in topology optimization using the SLP method
Structural and Multidisciplinary Optimization, 2000,19(2):113-121

DOI URL [本文引用: 1]

In this paper, we present a method for preventing numerical instabilities such as checkerboards, mesh-dependencies and local minima occurring in the topology optimization which is formulated by the homogenization design method and in which the SLP method is used as optimizer. In the present method, a function based on the concept of gravity (which we named “the gravity control function”) is added to the objective function. The density distribution of the topology is concentrated by maximizing this function, and as a result, checkerboards and intermediate densities are eliminated. Some techniques are introduced in the optimization procedure for preventing the local minima. The validity of the present method is demonstrated by numerical examples of both the short cantilever beam and the MBB beam.

[38]

Svanberg

. The method of moving asymptotes—A new method for structural optimization
International Journal for Numerical Methods in Engineering, 1987,24(2):359-373

DOI URL [本文引用: 1]