曹明月^*, 张启^*, 吴建国^?, 葛敬冉^,*,2), 梁军^,*,3)*北京理工大学先进结构技术研究院, 北京 100081
^?北京强度环境研究所可靠性与环境工程技术重点实验室, 北京 100076

STUDY ON NONLINEAR CONSTITUTIVE RELATIONSHIP AND FRACTURE BEHAVIOR OF STITCHED C/SiC COMPOSITES$^{\bf 1)}$

Cao Mingyue^*, Zhang Qi^*, Wu Jianguo^?, Ge Jingran^,*,2), Liang Jun^,*,3)*Institute of Advanced Structure Technology, Beijing Institute of Technology, Beijing 100081, China
^?Key Laboratory of Reliability and Environment Engineering Technology, Beijing Institute of Structure and Environment Engineering, Beijing 100076, China

通讯作者: 2)葛敬冉, 副教授, 主要研究方向: 复合材料损伤与断裂. E-mail:gejingran@bit.edu.cn;3)梁军, 教授, 主要研究方向: 复合材料力学. E-mail:liangjun@bit.edu.cn

收稿日期:2020-04-25接受日期:2020-06-1网络出版日期:2020-07-18

基金资助:

1)国家自然科学基金.11802018 国家自然科学基金.111732002

Received:2020-04-25Accepted:2020-06-1Online:2020-07-18
作者简介 About authors


摘要
C/SiC复合材料具有高比强度、高比模量和优良的热稳定性能等一系列优点, 广泛应用于航空航天领域中. 裂纹扩展进而引起的脆性断裂是其主要失效形式之一, 因而材料的断裂性能分析对材料的结构设计和应用有重要的指导意义. 本文开展了缝合式C/SiC复合材料简单力学试验和断裂试验, 研究了材料在不同载荷下的力学响应及断裂特征. 基于缝合式C/SiC复合材料简单力学试验, 建立了材料宏观非线性损伤本构方程, 并模拟了缝合式C/SiC复合材料单边切口梁和双悬臂梁的断裂行为. 本构方程采用简单函数描述了材料在复杂应力状态下的非线性应力-应变曲线, 并考虑了反向加载过程中造成的裂纹闭合. 基于商业有限元软件ABAQUS, 通过编写UMAT子程序实现非线性损伤本构方程, 采用单个单元验证了建立的本构方程的有效性. 在此基础上, 采用线弹性损伤本构和非线性损伤本构分别模拟了缝合式C/SiC复合材料单边切口梁和双悬臂梁的断裂行为. 采用非线性损伤本构方程模拟的力-位移曲线结果与试验结果更为吻合, 非线性损伤本构预测的失效载荷与试验失效载荷更为接近, 验证了所建立的非线性损伤本构方程的准确性, 为C/SiC复合材料断裂行为的研究提供了借鉴, 为缝合式C/SiC复合材料结构的设计和应用提供了理论基础.
关键词： 缝合式C/SiC复合材料;非线性本构;断裂;损伤

Abstract
C/SiC composites have a series of advantages such as high specific strength, high specific modulus, excellent thermal stability, etc, being widely used in the aerospace field. Brittle fracture caused by crack propagation is one of its main failure forms. Therefore, the fracture performance analysis of the material has important guiding significance for the structural design and application of the material. Simple mechanical experiments and fracture experiments of stitched C/SiC composites are carried out, the mechanical response and fracture characteristics of the materials under different loads being studied in the paper. Based on simple mechanical experiments of stitched C/SiC composites, the macroscopic nonlinear damage constitutive equation is established, and the fracture behavior of stitched C/SiC composites with unilateral notched beam and double cantilever beam are simulated. The constitutive equation uses simple equations to describe the nonlinear stress-strain curve of the material under complex stress conditions, and considers the crack closure on the reverse loading process. Based on the commercial finite element software ABAQUS, the non-linear damage constitutive equations are realized by writing a UMAT subroutine. The validity of the established constitutive equation is verified by a single element. On this basis, the linear elastic damage constitutive model and the nonlinear damage constitutive model are used to simulate the fracture behavior of the stitched C/SiC composites with a single-side notched beam and a double cantilever beam, respectively. The force-displacement curves simulated by the nonlinear damage constitutive equation are more consistent with the test results, and the failure load predicted by the nonlinear damage constitutive are closer to the test failure load, which verifies the accuracy of the nonlinear damage constitutive equation established in this paper. The paper provides a reference for the study of the fracture behavior of C/SiC composites and provides a theoretical basis for the design and application of stitched C/SiC composites structures.
Keywords：stitched C/SiC composites;nonlinear constitutive;fracture;damage


PDF (1623KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
曹明月, 张启, 吴建国, 葛敬冉, 梁军. 缝合式C/SiC复合材料非线性本构关系及断裂行为研究$^{\bf 1)}$. 力学学报[J], 2020, 52(4): 1095-1105 DOI:10.6052/0459-1879-20-058
Cao Mingyue, Zhang Qi, Wu Jianguo, Ge Jingran, Liang Jun. STUDY ON NONLINEAR CONSTITUTIVE RELATIONSHIP AND FRACTURE BEHAVIOR OF STITCHED C/SiC COMPOSITES$^{\bf 1)}$. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(4): 1095-1105 DOI:10.6052/0459-1879-20-058

引言

C/SiC复合材料具有较高的比刚度、比强度及优良的高温性能, 在航空航天等领域有广阔的应用前景^[1-3]. 国内外****针对C/SiC复合材料的力学性能开展了广泛的试验研究^[4-8], 裂纹扩展进而引起的脆性断裂是其主要失效形式之一^[9-10]. C/SiC复合材料服役于航空航天飞行器的发动机、机翼等多个部位, 在材料的内部存在微小孔洞、微小裂纹等多种细观缺陷, 在受到外来载荷的作用时, 这些内部缺陷会进一步扩展形成宏观尺度上的裂纹, 表现为基体/纤维开裂、界面脱粘等, 最终可能会导致结构的破坏, 极大地影响了材料的使用寿命. 研究C/SiC复合材料的断裂行为对改善材料性能有重要的意义, 可以为结构设计和应用提供理论指导.

目前ABAQUS中常用的模拟裂纹扩展的方法有节点释放技术^[11-13]、内聚力单元法^[14-16]和扩展有限元法^[17-20]等. C/SiC复合材料虽然是脆性材料, 但却具有较好的韧性, 外观表现出明显的非线性行为. 单纯地使用ABAQUS中的裂纹扩展方法不足以描述材料断裂失效前的非线性行为. 建立材料的非线性损伤本构是描述其非线性力学行为的有效方法, 目前针对C/SiC类复合材料建立了多种本构方程^[21-25]. 如Din等^[21]基于PUCK准则和热力学损伤演化定律开发了弹塑性损伤模型, 可以描述开孔碳纤维增强聚合物层压板的非线性行为. Xie等^[22]提出了一个包含可变参数的塑性势函数, 并基于Weibull统计分布建立了损伤状态函数, 所开发的本构模型能够计算3D针刺C/C-SiC复合材料在偏轴拉伸载荷以及剪切载荷下的力学响应. Li等^[23]引入标量型损伤变量, 基于连续介质力学, 提出了新的热力学势能函数, 为C/SiC复合材料开发了一个弹塑性损伤本构, 可以描述材料在循环载荷下的力学行为. Wei等^[24]基于PUCK失效准则, 引入两种剪切变形模式及缩放函数, 开发了一个三维渐进损伤模型, 可以描述拉伸载荷下大孔碳纤维增强聚合物板的3种不同的破坏模式. 杨正茂等^[25]引入一组标量损伤变量, 建立了陶瓷基复合材料含循环热冲击预损伤材料的损伤演化模型, 可以描述陶瓷基复合材料在热机械载荷作用下的损伤演化特征. 国内外****在C/SiC类复合材料非线性本构方程上取得了重要的成果, 但大都参数确定复杂. 针对缝合式C/SiC复合材料可用于断裂计算的非线性本构方程还鲜有涉及.

本文为模拟缝合式C/SiC复合材料单边切口梁和双悬臂梁的断裂行为, 基于简单力学试验和CT扫描结果, 建立了宏观非线性损伤本构方程. 在有限元软件ABAQUS中, 将非线性本构方程编写成UMAT子程序, 应用到简单算例中, 验证本构方程有效性. 进而模拟缝合式C/SiC复合材料单边切口梁和双悬臂梁断裂的力学响应, 与试验结果进行对比. 为缝合式C/SiC复合材料的结构设计和进一步应用提供理论基础.

1 缝合式C/SiC复合材料力学试验

1.1 基础力学试验

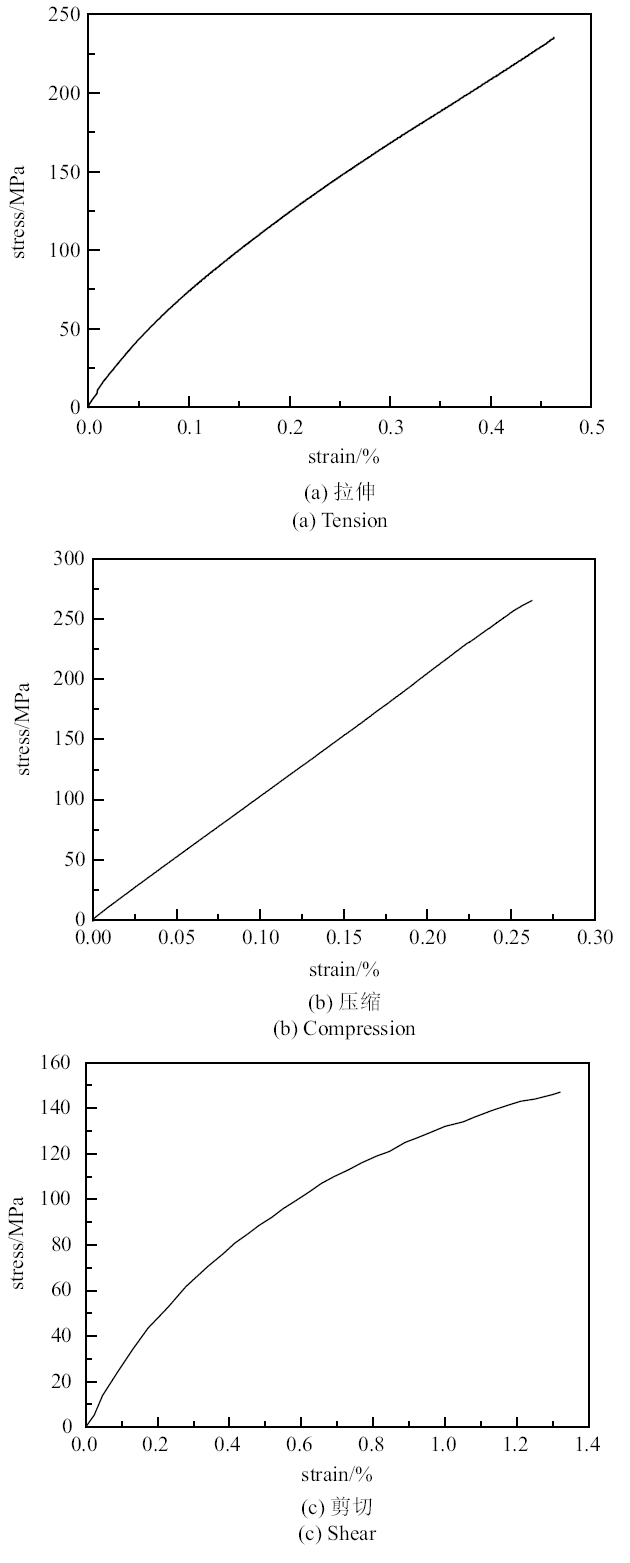
缝合式C/SiC复合材料, 在原有二维平纹编织C/SiC复合材料的基础上, 在厚度方向上引入了纱线缝合^[26], 采用CVI^[27]工艺制备而成. 其在不同的加载条件下表现出不同的力学特性, 但基础载荷状况是拉伸、压缩、剪切. 拉伸试验件参考标准ASTM C1275—2000. 压缩试验件参考标准ASTM C1358—2005. 剪切试验件参考标准ASTM C1292—2000(2005). 每种工况做3个试验件.

通过试验, 获得了0$^{\circ}$正轴向试件的平均拉伸、压缩和剪切应力-应变曲线. 由图1(a)可以看出缝合式C/SiC复合材料从开始加载就表现出明显的非线性特征, 模量随应变的增大而减小. 图1(b)显示在压缩载荷下, 材料表现出准脆性材料的力学行为. 失效前应力-应变曲线表现为近线性, 且压缩强度高于拉伸强度, 反映出材料的损伤行为具有显著的拉压异性特征. 由图1(c)可以看出, 在剪切载荷下材料也表现出明显的非线性. C/SiC材料内部存在大量微孔洞, 在加载过程中, 微细观损伤产生并累计, 宏观表现为刚度退化和非弹性应变的累积, 最终导致材料表现出非线性特征.

图1

新窗口打开|下载原图ZIP|生成PPT
图1基础力学试验曲线

Fig. 1Experimental curve of basic mechanics



缝合式C/SiC复合材料的细观结构包括纤维束、基体和初始缺陷. 以拉伸为例, 由图2拉伸试件的CT扫描结果可以看出, 基体中裂纹数量和缺陷面积远远大于纤维束中的裂纹数量和缺陷面积. 这可能是由于材料承受拉伸载荷时, 基体强度小于纤维束强度, 基体所受应力先达到开裂应力, 基体中缺陷萌生裂纹, 随着拉伸载荷的不断增大, 最终出现图2中的纤维开裂和界面脱粘现象. 在此过程中的微细观损伤的产生和累计是导致材料非线性的主要原因.

图2

新窗口打开|下载原图ZIP|生成PPT
图2拉伸应力下CT扫描照片

Fig. 2CT scan photos under tensile stress

1.2 单边切口梁试验

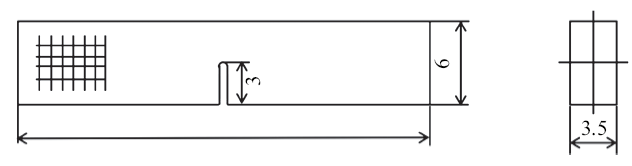
采用单边切口梁法(SENB), 对缝合式C/SiC复合材料的面内断裂性能进行测试, 测试标准参考ASTM E399-17. 如图3所示, 设计试样尺寸为30 mm$\times$6 mm$\times$3.5 mm, 裂纹长度为3 mm, 宽度为0.5 mm, 实验加载速度为0.1 mm/min. 共做3个试验件.

图3

新窗口打开|下载原图ZIP|生成PPT
图3单边切口梁(SENB)试件

Fig. 3Single side notched beam (SENB) test piece



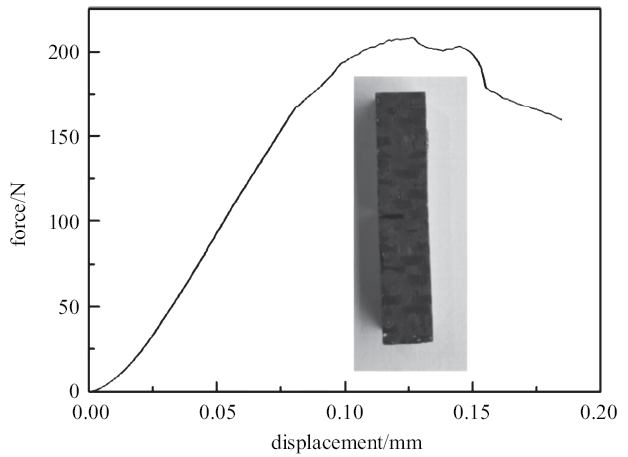
单边切口梁平均力-位移曲线如图4所示,力-位移曲线初始阶段有上凸尾迹存在, 这是由于夹具与试样件之间的滑移. 之后曲线呈现近似线性变化. 在接近最大载荷前, 有一小段曲线表现出短暂的非线性, 这可能是由于部分纤维断裂造成的. 达到最大载荷之后, 曲线呈现波动下降特征, 这可能是由于纤维趋向于相对较小的聚集状态, 有层次地发生断裂拔出. 图4中展示了单边切口梁试件破坏后的宏观形貌, 材料在试验前后几何外观并没有发生明显的形变, 未发现明显的裂纹扩展现象.

图4

新窗口打开|下载原图ZIP|生成PPT
图4单边切口梁力-位移曲线

Fig. 4Force-displacement curve of single-sided notched beam

1.3 双悬臂梁试验

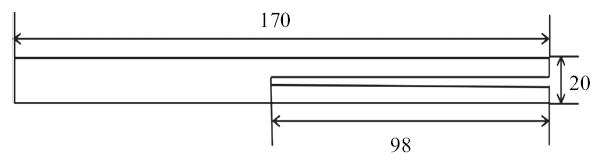
采用双悬臂梁试验, 对缝合式C/SiC复合材料的层间断裂性能进行测试, 测试标准参考ASTM D5528. 设计试样尺寸为170 mm$\times$20 mm$\times$6 mm, 初始裂纹长度98 mm, 缝宽为0.79 mm, 如图5所示. 共做3个试验件.

图5

新窗口打开|下载原图ZIP|生成PPT
图5双悬臂梁试件

Fig. 5Double cantilever beam test piece



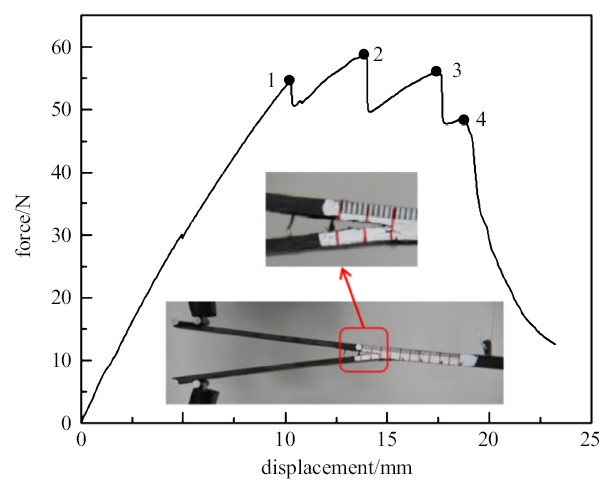
双悬臂梁平均力-位移曲线如图6所示, 由曲线可以看出材料在失效前表现出一定的非线性. 在图中从左到右出现4个突降点. 第一个突降点是由加工问题导致, 在试验件宽度中部产生了小面积的裂纹扩展; 第二个突降点对应的是力的最大值, 该时刻试验件边缘裂纹初次扩展; 第三个突降点对应试验件边缘的裂纹第二次较大扩展; 第四个突降点处, 裂纹已经缓慢扩展至最大值, 停止扩展, 并开始逐渐弯曲破坏. 图6中展示了双悬臂梁试件破坏后的宏观形貌, 可以看出层间裂纹扩展了较大距离.

图6

新窗口打开|下载原图ZIP|生成PPT
图6双悬臂梁力-位移曲线

Fig. 6Force-displacement curve of double cantilever beam

2 宏观非线性损伤本构

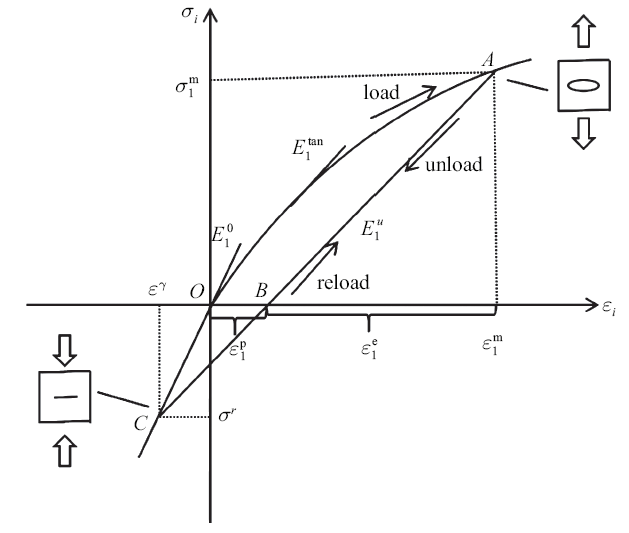
缝合式C/SiC复合材料在加载状态和卸载状态下有不同的应力-应变曲线. 以沿材料主方向上的拉伸加卸载下的应力-应变曲线为例进行分析, 忽略迟滞效应的影响, 可以得到一个理论化的模型, 如图7所示.

图7

新窗口打开|下载原图ZIP|生成PPT
图7拉伸加卸载材料的应力-应变曲线图^[28]

Fig. 7Stress-strain curve of materials under tensionloading and unloading^[28]



假设材料首先历经$OA$段承受拉伸载荷的过程, $\sigma _1^{\rm m}$和$\varepsilon _1^{\rm m}$对应$A$点的应力和应变. 图中$E_1^0$表示材料主方向上(1方向)的拉伸弹性模量, $E_1^{\tan}$为拉伸加载条件下的切线模量, $E_1^{\rm u}$表示卸载(或重新加载至卸载点前)阶段的卸载模量. 模型中假设$C$点($\varepsilon ^{\rm r}$, $\sigma ^{\rm r})$为"裂纹闭合点", 随着拉伸加载应力不断增大, 由于部分残余应力释放, 该裂纹闭合点的应力值会发生一定的变化.

从$O$点开始对材料进行加载, 初始模量为$E_1^0 $, 在拉伸载荷超过弹性极限后, 由于材料中产生基体开裂、界面脱粘等微观损伤, 材料的拉伸切线模量$E_1^{\tan }$随加载应力的增大而不断减小, 并形成非弹性应变$\varepsilon _1^{\rm p} $. 加载至$A$点后经历卸载过程, 卸载路径近似沿$A$点至$B$点所在直线, 卸载模量$E_1^{\rm u}$小于弹性模量. 当拉伸应力向压缩应力状态转换后, 由于基体微裂纹闭合等原因, 卸载模量在较高的压缩应力水平下近似恢复到初始弹性模量$E_1^0 $, 即表现出损伤钝化行为. 假设压缩应力超过$\sigma ^{\rm r}$后, 卸载模量$E_1^{\rm u}$完全恢复为初始弹性模量$E_1^0 $. 重加载时应力-应变路径则沿$C$点至$A$点所在直线, 过$A$点后再加载将产生新的拉伸损伤, 切线模量$E_1^{\tan}$和卸载模量$E_1^{\rm u}$继续减小, 直至材料最终破坏. 面内剪切加卸载条件下, 材料的应力-应变曲线形态与拉伸试验结果类似, 但是剪应力反向后不存在"裂纹闭合点".

以上分析表明, 材料在拉伸或剪切载荷下, 加载历史对力学行为有很大影响. 因此, 本构模型中描述复合材料的应力-应变行为时, 应把材料所经历的加载历史作为一个考虑点, 并区分加载和卸载两种不同状态下的应力-应变关系. 基于以上分析, 本文参考二维C/SiC复合材料的本构方程^[28-30], 建立了缝合式C/SiC复合材料的非线性损伤本构方程.

2.1 非线性应力应变关系

缝合式C/SiC复合材料的预制体为周期性平纹编织结构, 可将其视为正交各向异性材料, 其应力-应变关系为

(1)\begin{eqnarray} \left\{ {\begin{array}{l} \varepsilon _1 \\ \varepsilon _2 \\ \varepsilon _6 \\ \end{array}} \right\}=\left[ {{\begin{array}{*{20}c} {1/E_1^0 } & {-v_{21}^0 /E_2^0 } & 0 \\ {-v_{12}^0 /E_1^0 } & {1/E_2^0 } & 0 \\ 0 & 0 & {1/G_{12}^0 } \\ \end{array} }} \right]\left\{ {\begin{array}{l} \sigma _1 \\ \sigma _2 \\ \sigma _6 \\ \end{array}} \right\}= S_0 \sigma \end{eqnarray}
其中, $\varepsilon _i$和$\sigma _i$ ($i=1$, 2, 6)分别为材料主方向和剪切方向的应力和应变, $E_{1,2}^0 $, $G_{12}^0 $, $\upsilon _{12}^0 (\upsilon _{21}^0)$依次为初始弹性模量、剪切模量、泊松比. $S_0$为无损伤状态下的柔度矩阵.

在加载过程中, 缝合式C/SiC复合材料产生损伤, 模量、泊松比等性质都会有所变化, 但损伤后的材料仍可近似视为正交各向异性材料. 由于$\upsilon _{12}^0(\upsilon _{21}^0 )$数值非常小, $S_{12}^0 (S_{21}^0 )$可以近似视为常数, 同时满足$E_1^0 \upsilon _{21}^0=E_2^0 \upsilon _{12}^0 $. 据此对式(1)求逆, 得到损伤后材料应力-应变关系的增量表达式

(2)\begin{eqnarray} \left\{ {\begin{array}{l} {\rm d}\sigma _1 \\ {\rm d}\sigma _2 \\ {\rm d}\sigma _6 \\ \end{array}} \right\}=\left[ {{\begin{array}{*{20}c} {E_1 E_1^0 E_2^0 /t} & {v_{21}^0 E_1^0 E_1 E_2 /t} & 0 \\ {v_{12}^0 E_2^0 E_1 E_2 /t} & {E_2 E_1^0 E_2^0 /t} & 0\\ 0 & 0 & {G_{12}} \\ \end{array} }} \right]\cdot \left\{ {\begin{array}{l} {\rm d}\varepsilon _1 \\ {\rm d}\varepsilon _2 \\ {\rm d}\varepsilon _6 \\ \end{array}} \right\}=C{\rm d}\varepsilon \end{eqnarray}
式中, $t=E_1^0 E_2^0 -\nu _{12}^0 \nu _{21}^0 E_1 E_2 $, $C$为损伤后材料的刚度矩阵. $E_1 ,E_2 $和$G_{12}$为损伤后材料的拉伸模量和剪切模量, 随着加载状态的改变而改变, 可以描述材料的加卸载损伤状态.

由于缝合式C/SiC复合材料卸载存在残余应变, 表现出伪塑性行为; 加载过程中材料模量逐渐减小. 用函数^[29]描述单调加载条件下材料的拉伸和剪切应力-应变关系

(3)\begin{eqnarray} \left.\begin{array}{l} \sigma _i =A_1 \varepsilon _i +A_2 \varepsilon _i^2 +A_3 \varepsilon _i^3 +A_4 \varepsilon _i^4 +A_5 \varepsilon _i^5\\\qquad \left( {0\leqslant \varepsilon _i \leqslant \varepsilon _i^{\rm tb} ;i=1,2} \right) \\ \tau _{12} =B_1 \gamma _{12} +B_2 \gamma _{12}^2 +B_3 \gamma _{12}^3 +B_4 \gamma _{12}^4 +\\\qquad B_5 \gamma _{12}^5 \left( {\left| {\gamma _{12} } \right|\leqslant \gamma _{12}^{\rm b} } \right) \\ \end{array}\right\} \end{eqnarray}
式中, $A_i $和$B_i$ $(i = 1, 2, {\ldots}, 5)$为多项式函数的第$i$阶系数; $\varepsilon _i^{\rm tb} $为材料的拉伸断裂应变, $\gamma _{12}^{\rm b}$为面内剪切断裂应变.

式(3)对应变分量求导, 得到材料切线模量$E_i^{\tan } $和$G_{12}^{\tan } $的表达式

(4)\begin{eqnarray} \left.\begin{array}{l} E_i^{\tan } =A_1 +2A_2 \varepsilon _i +3A_3 \varepsilon _i^2 +4A_4\varepsilon _i^3 +5A_5 \varepsilon _i^4\\\qquad \left( {0\leqslant \varepsilon _i \leqslant \varepsilon _i^{\rm tb} ;i=1,2} \right) \\ G_{12}^{\tan } =B_1 +2B_2 \gamma _{12} +3B_3 \gamma _{12}^2 +4B_4 \gamma _{12}^3 +\\\qquad 5B_5 \gamma _{12}^4 \left( {\left| {\gamma _{12} } \right|\leqslant \gamma _{12}^{\rm b} } \right) \\ \end{array}\right\} \end{eqnarray}
式中, $A_1 $和$B_1 $的物理意义即为材料的拉伸和剪切初始弹性模量$E_1^0 $和$G_{12}^0 $.

材料压缩试验曲线中, 应力-应变曲线表示为近线性, 因此描述压缩状态下的应力-应变关系函数为

(5)\begin{eqnarray}\sigma _i =E_i^{\rm c} \varepsilon _i \left( {\varepsilon _i^{\rm cb} \leqslant \varepsilon _i \leqslant 0;i=1,2} \right)\end{eqnarray}
式中$\varepsilon _i^{\rm cb} $为材料的压缩断裂应变.

卸载和加载状态不同, 在卸载以及重加载至卸载点A($\varepsilon _1^{\rm m}$, $\sigma _1^{\rm m})$前, 材料的简化应力-应变曲表现为近线性. 随着载荷增大, 卸载模量逐渐减小; 拉伸出现裂纹之后反向加载裂纹闭合, 损伤存在拉压异性. 仍以沿面内材料主方向上的拉伸为例(如图7所示), 材料的拉伸卸载模量$E_i^{\rm u} $与拉伸卸载最大应变$\varepsilon _i^{\rm m}$之间的关系可以用逻辑函数^[30]描述

(6)\begin{eqnarray}E_i^{\rm u} =A_6 +\frac{A_7 -A_6 }{\lt[1+\lt(\dfrac{\varepsilon _i^{\rm m} }{y_0 })^{e_0}]}\ \ (\varepsilon _i \leqslant \varepsilon _i^{\rm m} ,\sigma _i \geqslant \sigma ^{\rm r},i=1,2)\quad\end{eqnarray}
式中, $A_{7}$, $A_{6}$, $y_{0}$和$e_{0}$为逻辑函数的形状参数, 由实验曲线拟合得到. $\sigma^{\rm r}$为裂纹闭合点应力, $\varepsilon _i^{\rm m} $为面内简单拉伸加载所达到的最大拉伸应变. 当无加载历史(即$\varepsilon _1^{\rm m}=0$)时, $E_i^{\rm u} =A_7 $. 参数$A_{7}$的物理意义为拉伸弹性模量$E_i^0 $.

类似的, 用逻辑函数描述材料的剪切卸载模量$G_{12}^{\rm u} $与剪切卸载最大应变$\gamma _{12}^{\rm m} $之间的关系

(7)\begin{eqnarray}G_{12}^{\rm u} =B_6 +\frac{B_7 -B_6 }{1+\lt(\dfrac{\gamma _{12}^{\rm m} }{y_1 })^{e_1}}\left( {\left| {\gamma _{12} } \right|\leqslant \gamma _{12}^{\rm m} } \right)\end{eqnarray}
式中, $B_{7}$, $B_{6}$, $y_{1}$和$e_{1}$为形状参数, 由实验曲线拟合得到.

目前国内外尚且没有统一的有关复合材料的失效准则, 本文采用考虑材料拉压强度不等的Hoffman失效准则^[31-32], 其表达式如下

(8)\begin{eqnarray}\frac{\sigma _1^2 }{X_{\rm t} X_{\rm c} }-\frac{\sigma _1 \sigma _2 }{X_{\rm t} X_{\rm c}}+\frac{\sigma _2^2 }{Y_{\rm t} Y_{\rm c} }+\frac{X_{\rm c} -X_{\rm t} }{X_{\rm t} X_{\rm c} }+\frac{Y_{\rm c} -Y_{\rm t}}{Y_{\rm t} Y_{\rm c} }+\frac{\tau _{12}^2 }{S^2}<1\quad\end{eqnarray}
式中, $X_{\rm t}$和$Y_{\rm t}$分别为1方向和2方向的拉伸强度, $X_{\rm c}$和$Y_{\rm c}$非别为1方向和2方向的压缩强度, $S$为剪切强度. 非线性本构方程中所使用的参数如表1所示.

Table 1
表 1
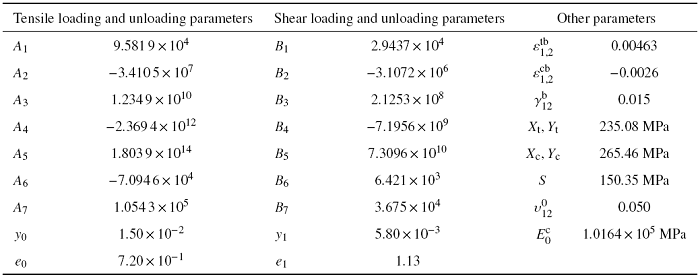
表 1缝合C/SiC复合材料本构模型参数
Table 1Parameters of stitched C/SiC composites constitutive model

新窗口打开|下载CSV

表1中$A_{6}$, $A_{7}$, $y_{0}$, $e_{0}$, $B_{6}$, $B_{7}$, $y_{1}$, $e_{1}$这8个和卸载相关的参数参考文献^[5]的实验数据.

2.2 数值实现

将非线性损伤本构模型编写成用户材料子程序UMAT. 为了更好地收敛, 需要计算材料的雅克比矩阵$D$, 即应力增量对应变增量的变化率. 其定义如下

(9)\begin{eqnarray}D=\frac{\partial \Delta \sigma }{\partial \Delta \varepsilon}\end{eqnarray}
当增量步的步长足够小, 即$\Delta t \to 0$时, 根据式(2), 近似有

(10)\begin{eqnarray} \left\{ {\begin{array}{l} \Delta \sigma _1 \\ \Delta \sigma _2 \\ \Delta \sigma _6 \\ \end{array}} \right\}_{n+1} =\left[ {{\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} }} \right]_{n+1} \left\{ {\begin{array}{l} \Delta \varepsilon _1 \\ \Delta \varepsilon _2 \\ \Delta \varepsilon _6 \\ \end{array}} \right\}_{n+1} \end{eqnarray}
UMAT程序中使用3个状态变量$\varepsilon _1^{\rm m} $, $\varepsilon _2^{\rm m} $和$\left|{\gamma _{12}^{\rm m} }\right|$分别记录材料在加卸载过程中所达到的最大拉伸应变和最大工程剪切应变. 通过比较应变分量与状态变量的大小判断材料的加卸载状态, 应变分量大于状态变量处于加载状态, 反之, 则处于卸载状态. 材料在反向压缩过程中, 压缩应力大于$\sigma ^{\rm r}$时, 保持为卸载模量, 反之, 模量变为$E_1^0 $. 最后进行单元失效检查, 当Hoffman失效判据满足时, 刚度矩阵折减为接近于零的数值, 材料破坏. UMAT具体流程如下所示:

(1)读取$n+1$步的应变张量 $\varepsilon _{n+1} =\varepsilon _n +\Delta \varepsilon _{n+1} $;

(2)判断加卸载状态 $\varepsilon _{i,n+1} \Leftrightarrow \varepsilon ^{\rm m}_i$, $\sigma _{i,n} \Leftrightarrow \sigma ^{\rm r}$;

(3)计算损伤模量 $E_{1}$, $E_{2}$, $G_{12}$;

(4)计算名义应力张量 $\left\{ {\sigma _i } \right\}_{n+1} =\left\{ {\sigma _i } \right\}_n +\left\{ {C_{ij} } \right\}_{n+1} \left\{ {\Delta \varepsilon _j } \right\}_{n+1} $;

(5)计算雅可比矩阵 $D=\dfrac{\partial \Delta \sigma}{\partial \Delta \varepsilon}$;

(6)失效判断.

2.3 单个单元验证

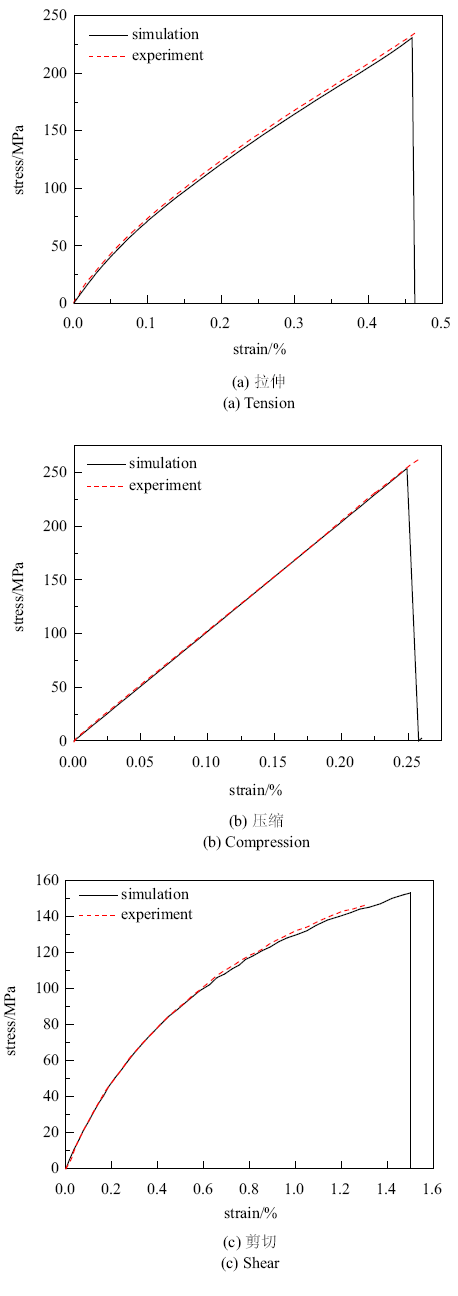
在ABAQUS中建立单个单元模型, 单元类型选取4节点减缩积分平面应力单元(CPS4R), 结合UMAT模拟简单加载条件下缝合式C/SiC复合材料的力学响应, 如图8所示. 由图8可以看出, 模拟结果与试验结果吻合良好. 图8中, 压缩强度在达到破坏强度以前, 先满足了UMAT中使用的Hoffman失效判据, 所以试验压缩强度大于模拟压缩强度. 剪切则与之相反, 所以试验剪切强度小于模拟剪切强度. 综上, 本文建立的本构方程可以很好地描述缝合式C/SiC复合材料的非线性.

图8

新窗口打开|下载原图ZIP|生成PPT
图8简单加载下材料的应力-应变曲线对比图

Fig. 8Comparison of stress-strain curves of materialsunder simple loading



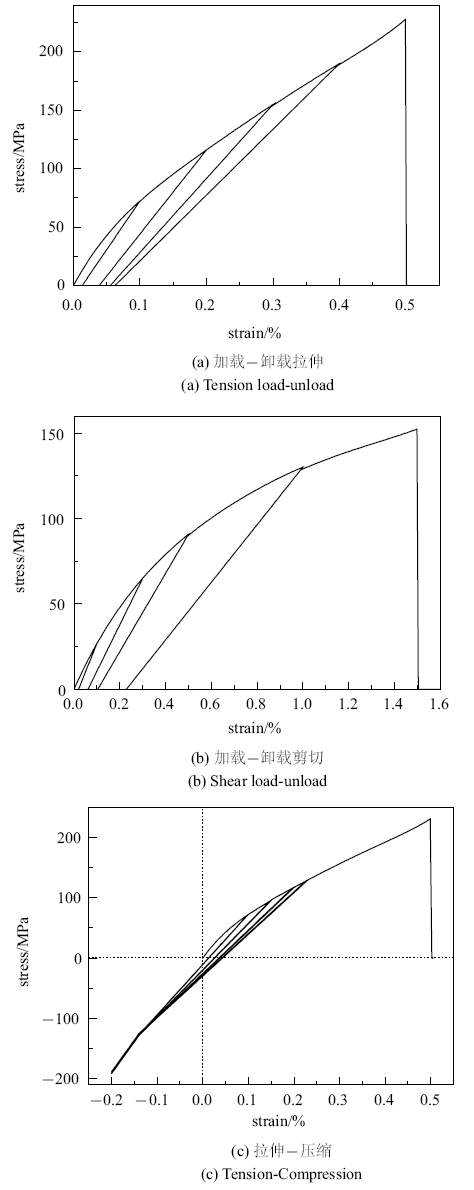
同样, 在ABAQUS中建立单个单元模型, 结合UMAT模拟复杂应力状态下缝合式C/SiC复合材料的力学响应, 如图9所示. 由图9(a)和图9(b)可以看出, 加载模量随应变增大而减小, 卸载模量随应变的增大而减小, 残余应变越来越大, 材料具有明显的非线性特征, 表现出伪塑性. 由图9(c)可以看出, 反向加载到一定程度时裂纹闭合, 材料模量恢复成初始模量. 当材料加载载荷达到相应的破坏强度时, 刚度矩阵取接近于零的数值, 模拟材料的破坏. 基于以上分析, 建立的非线性本构方程可以模拟重复使用下材料的力学行为, 为缝合式C/SiC复合材料结构的进一步应用提供借鉴.

图9

新窗口打开|下载原图ZIP|生成PPT
图9复杂应力下材料的应力-应变曲线图

Fig. 9Stress-strain curve of materials under complex stress

3 缝合式C/SiC复合材料断裂行为模拟

3.1 单边切口梁断裂行为模拟

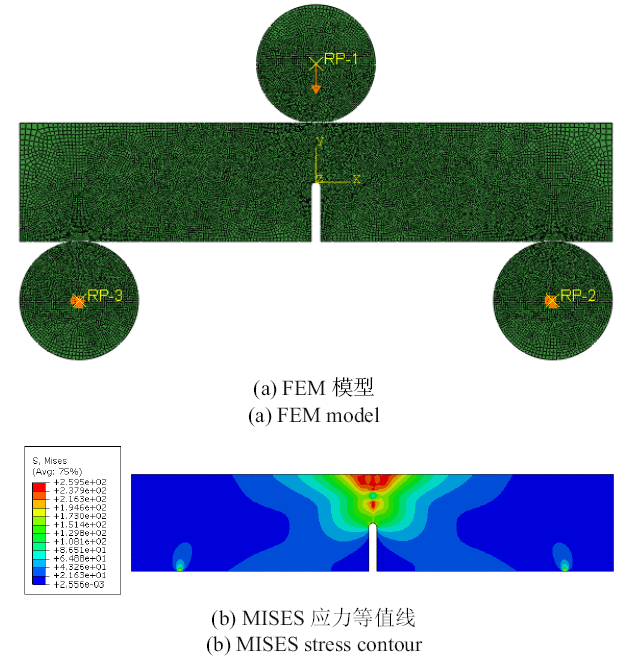
依据1.2节单边切口梁试件, 建立如图10(a)所示的模型, 单元类型为CPS4R, 模型共有21951个网格, 为验证网格无关性, 同时计算了所示模型1/4, 1/2, 2倍网格数量的模型, 综合考虑计算效率和精度, 选择了目前的模型. 边界条件如图10(a)所示, 两个支座和压头均为刚体, 在刚体和单边切口梁之间建立面面接触, 固定左右两个支座起支撑作用, 上方的压头施加向下的位移载荷. 并对裂纹周围的网格进行加密, 以便更好地捕捉断裂行为.

图10

新窗口打开|下载原图ZIP|生成PPT
图10单边切口梁模型

Fig. 10Single-sided notched beam model



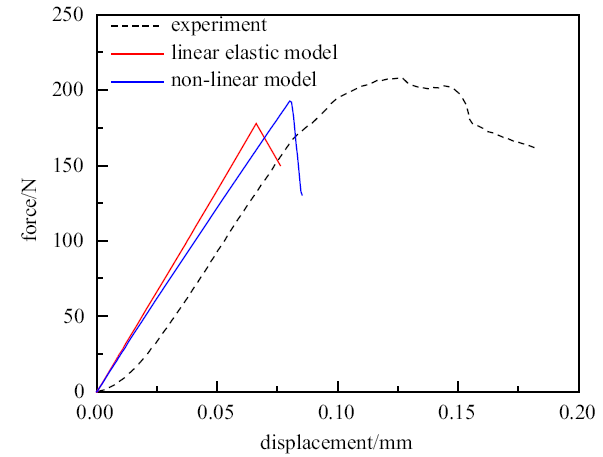
结合第2节所述宏观非线性本构的UMAT子程序进行模拟, 同时对比计算了线弹性本构下的单边切口梁断裂行为. 使用非线性模型计算得到的单边切口梁MISES应力云图如图10(b)所示, 数值计算结果同试验结果对比如图11所示. 由图11看出, 强度点前, 试验与模拟曲线接近平行却没有重合, 是由于SENB试验中, 夹具与试样件之间滑移导致上凸尾迹, 线弹性模型没有考虑材料的非线性行为, 所以更加偏离试验曲线. 强度点后, 试验与模拟结果存在一定差异, 是由于有限元模型对实际模型进行了简化, 没有区分出纤维和基体, 没有考虑缝合纱位置, 而基体纤维相继失效和缝合纱位置对强度点后的试验曲线有较大的影响. 由表2可以看出, 线弹性模型预测的失效载荷相对试验失效载荷误差为$-$14.625%, 而非线性模型误差为$-$7.448%, 线弹性模型的失效载荷误差是非线性模型的1.96倍, 非线性模型计算结果与实验结果较为接近.

图11

新窗口打开|下载原图ZIP|生成PPT
图11单边切口梁模拟与实验结果对比图

Fig. 11Comparison of simulation and experimentalresults of single-sided notched beam



Table 2
表2
表2单边切口梁有限元与实验结果的比较
Table 2Comparison of finite element and experimental results of single-sided notched beam

新窗口打开|下载CSV

3.2 双悬臂梁断裂行为模拟

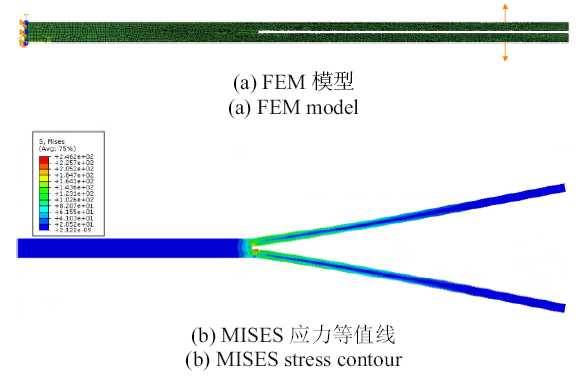
依据1.3节双悬臂梁试验, 建立如图12(a)所示的模型, 单元类型为CPS4R, 模型共有17590个网格, 为验证网格无关性, 同时计算了所示模型1/4, 1/2, 2倍网格数量的模型, 综合考虑计算效率和精度, 选择了目前的模型. 采用在左端固定, 在裂缝上下两侧施加位移载荷的边界条件, 如图12(a)所示. 对裂纹周边的网格进行加密.

图12

新窗口打开|下载原图ZIP|生成PPT
图12双悬臂梁模型

Fig. 12Double cantilever beam model



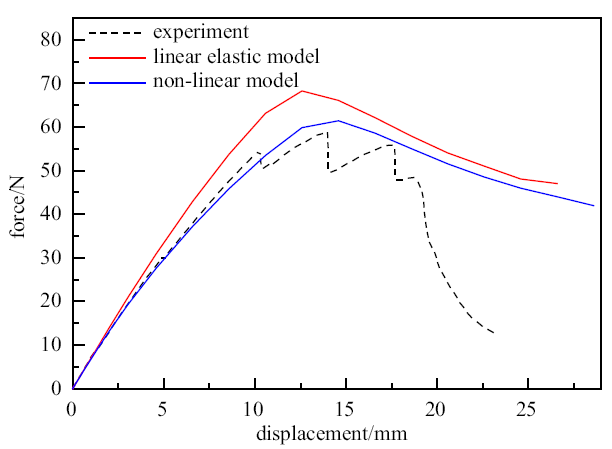
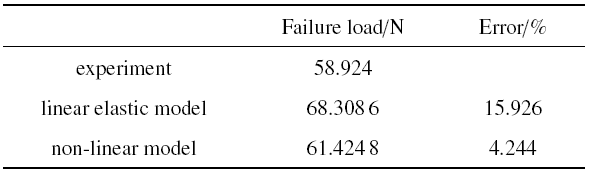
结合第2节所述宏观非线性本构的UMAT子程序进行模拟, 同时对比计算了线弹性本构下的双悬臂梁断裂行为. 使用非线性模型计算得到的双悬臂梁MISES应力云图如图12(b)所示, 数值计算结果同试验结果对比如图13所示. 由图13看出, 强度点前, 非线性模型曲线与实验曲线较为接近, 线弹性模型与实验曲线相差较大, 是由于线弹性模型没有考虑材料的非线性行为. 强度点后, 试验与模拟结果存在一定差异, 是由于有限元模型对实际模型进行了简化, 没有区分出纤维和基体, 没有考虑缝合纱的位置, 而基体纤维相继失效和缝合纱位置对强度点后的试验曲线有较大的影响. 由表3可以看出, 线弹性模型预测的失效载荷相对试验失效载荷误差为15.926%, 而非线性模型误差为4.244%, 线弹性模型的失效载荷误差是非线性模型的3.75倍, 非线性模型计算结果与实验结果较为接近. 本文提出的计算模型可以较好地模拟缝合式C/SiC复合材料的力-位移曲线.

图13

新窗口打开|下载原图ZIP|生成PPT
图13双悬臂梁模拟与试验结果对比图

Fig. 13Comparison of simulation and test results ofdouble cantilever beam



Table 3
表3
表3双悬壁梁有限元与实验结果的比较
Table 3Comparison of finite element and experimentalresults of double cantilever beams

新窗口打开|下载CSV

4 结论

(1)本文依据简单力学试验及CT扫描结果, 为缝合式C/SiC复合材料建立了宏观非线性本构方程. 本构方程中参数可以通过数量较少的简单加载及加卸载力学试验获得. 本构方程可以区别加载、卸载、重加载三种状态, 并考虑了反向加载过程中造成的裂纹闭合, 可以描述缝合式C/SiC复合材料在复杂应力状态下的力学行为.

(2)在ABAQUS中, 结合UMAT模拟缝合式C/SiC复合材料单边切口梁和双悬臂梁的断裂行为. 与线弹性本构对比, 非线性本构模拟结果与试验更加吻合. 说明本文建立的非线性本构可以较好地预测缝合式C/SiC复合材料单边切口梁和双悬臂梁的断裂行为.

(3)本文基于简单力学试验建立了缝合式C/SiC复合材料的宏观唯象本构方程, 未区分纤维、基体和缺陷, 在后续工作中将建立复合材料的细观模型, 把孔隙作为单独的因素考虑, 结合现有宏观模型, 实现对C/SiC复合材料的多尺度分析.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 陈倩, 张汉哲, 吴钦 等. 复合材料水翼水动力与结构强度特性数值研究
力学学报, 2019,51(5):1350-1362
[本文引用: 1]

( Chen Qian, Zhang Hanzhe, Wu Qin, et al. Numerical study on hydrodynamic and structural strength characteristics of composite hydrofoil
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(5):1350-1362 (in Chinese))
[本文引用: 1]

[2] 刘艮, 张伟. 亚音速气流中复合材料悬臂板的非线性振动响应研究
力学学报, 2019,51(3):912-921


( Liu Gen, Zhang Wei. Research on nonlinear vibration response of composite cantilever plate in subsonic airflow
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):912-921 (in Chinese))


[3] 李伟, 方国东, 李玮洁 等. 碳纤维增强复合材料微观烧蚀行为数值模拟
力学学报, 2019,51(3):835-844
[本文引用: 1]

( Li Wei, Fang Guodong, Li Weijie, et al. Numerical simulation of micro-ablation behavior of carbon fiber reinforced composites
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):835-844 (in Chinese))
[本文引用: 1]

[4] Nozawa T, Ozawa K, Choi YB, et al. Determination and prediction of axial/off-axial mechanical properties of SiC/SiC composites
Fusion Engineering and Design, 2012,87(5-6):803-807
DOIURL [本文引用: 1]
A SiC/SiC composite is a candidate material for a demonstration fusion power reactor (DEMO). Identifying the inherent anisotropy of composites is required to predict axial/off-axial mechanical properties for various failure modes. This study evaluated crack propagation behavior by the various modes to provide strength anisotropy maps and we discussed a method to analytically predict this trend. The strength anisotropy maps identified for various fabric orientations clearly indicate that the composites failed in the mixed modes. Specifically, due to the axial anisotropy, five individual mode strengths such as tensile/compressive strengths in the axial/transverse directions, respectively, as well as the in-plane shear strength, are identified to become essential input parameters. With the analytical criterion based on the Tsai-Wu model, the strength anisotropy could satisfactorily be described. (C) 2012 Elsevier B.V.

[5] Li J, Jiao G, Wang BD, et al. Damage characteristics and constitutive modeling of the 2D C/Si C composite: Part I-Experiment and analysis
Chinese Journal of Aeronautics, 2014,27(6):1586-1597
DOIURL [本文引用: 1]
This paper reports an experimental investigation on the macroscopic mechanical behaviors and damage mechanisms of the plain-woven (2D) C/SiC composite under in-plane on-and off-axis loading conditions. Specimens with 15 degrees, 30 degrees, and 45 degrees off-axis angles were prepared and tested under monotonic and incremental cyclic tension and compression loads. The obtained results were compared with those of uniaxial tension, compression, and shear specimens. The relationships between the damage modes and the stress state were analyzed based on scanning electronic microscopy (SEM) observations and acoustic emission (AE) data. The test results reveal the remarkable axial anisotropy and unilateral behavior of the material. The off-axis tension test results show that the material is fiber-dominant and the evolution rate of damage and inelastic strain is accelerated under the corresponding combined biaxial tension and shear loads. Due to the damage impediment effect of compression stress, compression specimens show higher mechanical properties and lower damage evolution rates than tension specimens with the same off-axis angle. Under cyclic tension-compression loadings, both on-axis and off-axis specimens exhibit progressive damage deactivation behaviors in the compression range, but with different deactivation rates. (C) 2014 Production and hosting by Elsevier Ltd. on behalf of CSAA & BUAA.

[6] Dassios KG, Kostopoulos V, Steen M. Intrinsic parameters in the fracture of carbon/carbon composites
Composites Science and Technology, 2005,65(6):883-897
DOIURL

Abstract

The R-curve, bridging stress profile and the corresponding bridging law of C/C woven composites were calculated for two different specimen configurations: compact tension (CT) and double-edge-notch (DEN). Monotonic tensile loading as well as cyclic loading was performed on CT specimens and the R-curve was evaluated from the change of specimen compliance in the presence and absence of the bridging zone by quantifying the total damage in the material through an effective crack length approach. The bridging stresses and laws for the DEN specimens tested under monotonic tension were calculated directly through the elastic correction of the measured displacement. The comparison of the R-curves and bridging laws between the two configurations was performed after identification of a common damage extent measure, the local crack opening displacement. The rising part of the R-curve was found similar for the two configurations, with the mean initiation and plateau values being R₀ ∼ 1.3 and R_∞ ∼ 9.5 kJ/m², respectively. In contrast, the bridging laws evaluated for the two configurations were in disagreement. It was concluded that the investigated material, although characterised as Class-III in the literature, exhibits crack growth and bridging, however of a Small rather of a large scale and that the calculated R-curve can serve as an intrinsic parameter that characterises the fracture behaviour of the material independently of configuration, and – thus – independently of dimensions and geometry.

[7] Xie D, Salvi A, Waas A, et al. Discrete cohesive zone model to simulate static fracture in carbon fiber composites
Journal of Composite Materials, 2005,40(22):2025-2046
DOIURL

[8] Liu MS, Li YL, Xu F, et al. Dynamic compressive mechanical properties and a new constitutive model of 2D-C/SiC composites
Materials Science and Engineering, 2008,489(1-2):120-126
[本文引用: 1]

[9] 卢广达, 陈建兵. 基于一类非局部宏-微观损伤模型的裂纹模拟
力学学报, 2020,52(3):749-762
[本文引用: 1]

( Lu Guangda, Chen Jianbing. Cracking simulation based on a nonlocal macro-meso-scale damage model
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(3):749-762 (in Chinese))
[本文引用: 1]

[10] 王勃, 张阳博, 左宏 等. 压应力对压剪裂纹扩展的影响研究
力学学报, 2019,51(3):845-851
[本文引用: 1]

( Wang Bo, Zhang Yangbo, Zuo Hong, et al. Study on the inflfluence of compressive stress on the compression shear crack propagation
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):845-851 (in Chinese))
[本文引用: 1]

[11] Di Stasio L, Ayadi Z. Finite element solution of the fiber/matrix interface crack problem: Convergence properties and mode mixity of the Virtual Crack Closure Technique
Finite Elements in Analysis and Design, 2019,167:103332
DOIURL [本文引用: 1]

[12] Shokrieh MM, Rajabpour-Shirazi H, Heidari-Rarani M. Simulation of mode I delamination propagation in multidirectional composites with R-curve effects using VCCT method
Computational Materials Science, 2012,65:66-73
DOIURL
In this investigation, a finite element formulation for Timoshenko beam element with only displacement degrees of freedom is first addressed for the laminated composite beams. The resulting continuous isoparametric quadrilateral element is simple to formulate and efficient through the convergence with coarse meshes along the crack tip. Afterwards, a finite element procedure is proposed for the simulation of mode I delamination growth in symmetric multidirectional double cantilever beam (DCB) specimens based on the fracture mechanics using the above-mentioned element. To take into account R-curve effects in DCB specimens, a variable strain energy release rate is utilized instead of constant initiation fracture toughness. The strain energy release rate is computed using virtual crack closure technique (VCCT) method. The results of the finite element simulation agree well with the experimental data available in the literature. It confirms that the proposed approach is reliable and feasible for modeling of mode I delamination growth in laminated composites with large-scale fiber bridging. (c) 2012 Elsevier B.V.

[13] Liu PF, Hou SJ, Chu JK, et al. Finite element analysis of postbuckling and delamination of composite laminates using virtual crack closure technique
Composite Structures, 2011,93(6):1549-1560
DOIURL [本文引用: 1]
The two-dimensional and three-dimensional parametric finite element analysis (FEA) of composite flat laminates with two through-the-width delamination types: 0(4)/(+/-theta)(6)//0(4) and 0(4)//(+/-theta)(6)//0(4) (theta = 0 degrees, 45 degrees, and "//" denotes the delaminated interface) under compressive load are performed to explore the effects of multiple delaminations on the postbuckling properties. The virtual crack closure technique which is employed to calculate the energy release rate (ERR) for crack propagation is used to deal with the delamination growth. Three typical failure criteria: B-K law, Reeder law and Power law are comparatively studied for predicting the crack propagation. Effects of different mesh sizes and pre-existing crack length on the delamination growth and postbuckling properties of composite laminates are discussed. Interaction between the delamination growth mechanisms for multiple cracks for 0(4)//(+/-theta)(6)//0(4) composite laminates is also investigated. Numerical results using FEA are also compared with those by existing models and experiments. (C) 2010 Elsevier Ltd.

[14] Aymerich F, Dore F, Priolo P. Prediction of impact-induced delamination in cross-ply composite laminates using cohesive interface elements
Composites Science and Technology, 2008,68(12):2383-2390
DOIURL [本文引用: 1]

Abstract

The paper investigates the potential of cohesive interface elements for damage prediction in laminates subjected to low-velocity impact. FE models with interface elements adopting a bilinear cohesive law were first calibrated and validated by simulation of standard fracture toughness tests and then employed to model the impact response of cross-ply graphite/epoxy laminated plates.
The developed model provided a correct simulation of the impact response of laminates in a wide range of energy values and successfully predicted size, shape and location of main damage mechanisms. The results of the analyses also pointed out the importance of employing a damage criterion capable of accounting for the constraining effect of out-of-plane compression on the initiation of the decohesion phase.

[15] Harper PW, Hallett SR. A fatigue degradation law for cohesive interface elements-Development and application to composite materials
International Journal of Fatigue, 2010,32(11):1774-1787
DOIURL

Abstract

A cohesive zone interface element degradation law is presented for analyzing delamination crack propagation under cyclic loading. Development of the law is based on a detailed study of the numerical cohesive zone and the extraction of strain energy release rate from this zone, enabling a direct link with experimental Paris Law data. The law is implemented using three-dimensional interface elements within the explicit finite element code LS-Dyna. Validation is presented by way of application to composite material fatigue fracture toughness tests; Double Cantilever Beam for Mode I, End Notch Flexure for mode II and Mixed Mode Bending for the mixed mode case. In all cases good agreement with experimental data available in the open literature and/or theoretical solutions was obtained.

[16] 王志凯, 陈志鹏, 杨娜娜 等. 初始缺陷对复合材料层合板力学性能影响研究
西北工业大学学报, 2019,37(4):730-736
DOIURL [本文引用: 1]

( Wang Zhikai, Chen Zhipeng, Yang Nana, et al. Study on the effect of initial defects on the mechanical properties of composite laminates
Journal of Northwestern Polytechnical University, 2019,37(4):730-736 (in Chinese))
DOIURL [本文引用: 1]

[17] Motamedi D, Mohammadi S. Fracture analysis of composites by time independent moving-crack orthotropic XFEM
International Journal of Mechanical Sciences, 2012,54(1):20-37
DOIURL [本文引用: 1]
Time-independent orthotropic enrichment functions are introduced for dynamic propagation analysis of moving cracks in composites by the extended finite element method (XFEM). The proposed enrichment functions are derived from the analytical solutions for a moving/propagating crack in orthotropic media, and can be considered as a new extension to the available XFEM techniques for dynamic analysis of stationary and moving cracks in orthotropic materials. They are included within the framework of partition of unity and XFEM to enhance the accuracy of basic FEM solution near a moving crack tip in orthotropic media. The method allows for analysis of the whole crack propagation pattern on an unaltered finite element mesh, which is independently defined from the existence of any predefined crack or its propagation path. A combination of dynamic crack initiation toughness and crack orientation along the maximum circumferential stress is used to design a relatively simple and efficient formulation. Dynamic stress intensity factors (DSIFs) are evaluated by means of the domain separation integral method and the dynamic energy release rate. The time dependent XFEM equations are constructed by discretizing the standard weak formulation of the governing elastodynamics equation. They are solved by the unconditionally stable Newmark time integration scheme. A number of benchmark and test problems are simulated and the results are compared with the available reference results to illustrate the accuracy and efficiency of the proposed scheme. (C) 2011 Elsevier Ltd.

[18] Baydoun M, Fries T P. Crack propagation criteria in three dimensions using the XFEM and an explicit-implicit crack description
International Journal of Fracture, 2012,178(1-2):51-70
DOIURL
This paper studies propagation criteria in three-dimensional fracture mechanics within the extended finite element framework (XFEM). The crack in this paper is described by a hybrid explicit-implicit approach as proposed in Fries and Baydoun (Int J Numer Methods Eng, 2011). In this approach, the crack update is realized based on an explicit crack surface mesh which allows an investigation of different propagation criteria. In contrast, for the computation of the displacements, stresses and strains by means of the XFEM, an implicit description by level set functions is employed. The maximum circumferential stress criterion, the maximum strain energy release rate criterion, the minimal strain energy density criterion and the material forces criterion are realized. The propagation paths from different criteria are studied and compared for asymmetric bending, torsion, and combined bending and torsion test cases. It is found that the maximum strain energy release rate and maximum circumferential stress criterion show the most favorable results.

[19] Chen C, Cai HY, Li JJ, et al. One-dimensional extended FEM based approach for predicting the tensile behavior of SHCC-FRP composites
Engineering Fracture Mechanics, 2020,225:106775
DOIURL

[20] Ma X, Bian K, Liu H, et al. Numerical and experimental investigation of the interface properties and failure strength of CFRP T-Stiffeners subjected to pull-off load
Materials & Design, 2020,185:108231
[本文引用: 1]

[21] I Ud Din, Hao P, Franz G, et al. Elastoplastic CDM model based on Puck's theory for the prediction of mechanical behavior of Fiber Reinforced Polymer (FRP) composites
Composite Structures, 2018(201):291-302
[本文引用: 2]

[22] Xie J, Fang G, Chen Z, et al. An anisotropic elastoplastic damage constitutive model for 3D needled C/C-SiC composites
Composite Structures, 2017,176:164-177
DOIURL [本文引用: 1]

[23] Li J, Jiao G, Wang B, et al. Damage characteristics and constitutive modeling of the 2D C/SiC composite: Part II-Material model and numerical implementation
Chinese Journal of Aeronautics, 2015,28(1):314-326
DOIURL [本文引用: 1]
In this work, a macroscopic non-linear constitutive model accounting for damage, inelastic strain and unilateral behavior is proposed for the 2D plain-woven C/SiC composite. A set of scalar damage variables and a new thermodynamic potential expression are introduced in the framework of continuum damage mechanics. In the deduced constitutive equations, the material's progressive damage deactivation behavior during the compression loading is described by a continuous function, and different deactivation rates under uniaxial and biaxial compression loadings are also considered. In damage evolution laws, the coupling effect among the damage modes and impediment effect of compression stress on the development of shear damage in different plane stress states are taken into account. Besides, the general plasticity theory is applied to describing the evolution of inelastic strain in tension and/or shear stress state. The Tsai-Wu failure criterion is adopted for strength analysis. Additionally, the material model is implemented as a user-defined material subroutine (UMAT) and linked to the ABAQUS finite element software, and its performance is demonstrated through several numerical examples.

[24] Wei L, Zhu W, Yu Z, et al. A new three-dimensional progressive damage model for fiber-reinforced polymer laminates and its applications to large open-hole panels
Composite Science and Technology, 2019,182:107757
DOIURL [本文引用: 1]

[25] 杨正茂, 刘晖, 杨俊杰. 含热冲击预损伤的陶瓷基复合材料损伤本构模型
力学学报, 2019,51(6):1797-1809
[本文引用: 2]

( Yang Zhengmao, Liu Hui, Yang Junjie. Damage constitutive model forthermal shocked-ceramic matrix composite
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(6):1797-1809 (in Chinese))
[本文引用: 2]

[26] 张根西, 张培伟, 李彦斌 等. 缝合式三维编织C/SiC复合材料拉伸加卸载力学行为
复合材料学报, 2019,36(12):2894-2901
[本文引用: 1]

( Zhang Genxi, Zhang Peiwei, Li Yanbin, et al. Tensile loading and unloading mechanical behavior of stitched three-dimensional braided C/SiC composites
Acta Materiae Compositae Sinica, 2019,36(12):2894-2901 (in Chinese))
[本文引用: 1]

[27] 李艳, 崔红, 王斌 等. 致密化工艺对厚壁针刺C/C复合材料性能的影响
复合材料学报, 2017,34(10):2337-2343
[本文引用: 1]

( Li Yan, Cui Hong, Wang Bin, et al. Influence of densification process on the properties of thick-wall needle-punched C/C composites
Acta Materiae Compositae Sinica, 2017,34(10):2337-2343 (in Chinese))
[本文引用: 1]

[28] 李俊, 矫桂琼, 王波 等. 二维编织 C/SiC 复合材料非线性损伤本构模型与应用
复合材料学报, 2013,30(1):165-171
URL [本文引用: 3]
Based on the fundamental mechanical tests of 2D woven C/SiC composite material, a macroscopic orthotropic non-linear damage constitutive model was established. In this model, the detectable strains were chosen as variables, and functions in simple form were used to demonstrate the stress-strain relationship of the material under damage evolution caused by uniaxial tension and shear loads, and besides the rule of stiffness change in unloading state respectively. Meanwhile, the unilateral effect and damage-deactivation behavior were also considered. The constitutive model was implemented into UMAT in ABAQUS finite element software, and it could describe the material’s non-linear and linear property of stress-strain relationship in loading and unloading state respectively, and also its load history. Through modeling the open hole plates in tension, strain distribution besides the hole agrees well with the experiment result, which proves the availability of the proposed constitutive model.
( Li Jun, Jiao Guiqiong, Wang Bo, et al. Nonlinear damage constitutive model of 2D braided C/SiC composites and its application
Acta Materiae Compositae Sinica, 2013,30(1):165-171 (in Chinese))
URL [本文引用: 3]
Based on the fundamental mechanical tests of 2D woven C/SiC composite material, a macroscopic orthotropic non-linear damage constitutive model was established. In this model, the detectable strains were chosen as variables, and functions in simple form were used to demonstrate the stress-strain relationship of the material under damage evolution caused by uniaxial tension and shear loads, and besides the rule of stiffness change in unloading state respectively. Meanwhile, the unilateral effect and damage-deactivation behavior were also considered. The constitutive model was implemented into UMAT in ABAQUS finite element software, and it could describe the material’s non-linear and linear property of stress-strain relationship in loading and unloading state respectively, and also its load history. Through modeling the open hole plates in tension, strain distribution besides the hole agrees well with the experiment result, which proves the availability of the proposed constitutive model.

[29] Mccarthy CT, O'Higgins RM, Frizzell RM. A cubic spline implementation of non-linear shear behaviour in three-dimensional progressive damage models for composite laminates
Composite Structures, 2010,92(1):173-181
DOIURL [本文引用: 1]

Abstract

An experimental study was carried out to characterise the constitutive response of carbon fibre-reinforced epoxy laminates. While maintaining essentially linear behaviour in the fibre and transverse directions, this material displays significant non-linear shear stress–strain behaviour to rupture. It is shown that the well known Hahn-Tsai non-linear shear model does not provide an acceptable fit for the strain range examined and so a novel approach was derived where a cubic spline interpolation method was used to capture the non-linear shear behaviour. The well known ply discount model, based on Hashin’s failure criteria, was also used to predict fibre and transverse matrix damage in the laminates. The spline approach is coupled with maximum strain failure criteria to predict the response in the in-plane and out-of-plane shear directions. The material Jacobian matrix is fully defined, thus allowing a full implicit material model to be implemented. Hence, the model is suitable for both implicit and explicit finite element codes. It is shown that the model accurately predicts the response of the material for load cases in which shear stresses dominate. The performance of the model is demonstrated by considering a number of laminate configurations and failure of an open-hole tension specimen.

[30] Elias N Eliopoulos, Theodore P Philippidis. A progressive damage simulation algorithm for GFRP composites under cyclic loading. Part I: Material constitutive model
Composite Science and Technology, 2001,71:742-749
DOIURL [本文引用: 2]

[31] 黄文超, 朱照泽. 飞机复合材料长桁面外拉伸失效分析
机械强度, 2019,41(3):248-252
[本文引用: 1]

( Huang Wenchao, Zhu Zhaoxi. Failure analysis of outer tension of aircraft composite long truss
Journal of Mechanical Strength, 2019,41(3):248-252 (in Chinese))
[本文引用: 1]

[32] Schellekens JCJ, Borst RD. The use of the Hoffman yield criterion in finite element analysis of anisotropic composites
Computers & Structures, 1990,37(6):1087-1096
[本文引用: 1]