MECHNICAL PROPERTIES AND BEHAVIORS OF HIGH ENTROPY ALLOYS 1)
Li Jianguo, Huang Ruirui, Zhang Qian, Li Xiaoyan2)Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China通讯作者: 2)李晓雁, 长聘副教授, 主要从事新型微纳米材料的设计、制备以及力学性能及行为研究.
收稿日期:2020-01-9接受日期:2020-02-24网络出版日期:2020-03-18
| 基金资助: |
Received:2020-01-9Accepted:2020-02-24Online:2020-03-18
作者简介 About authors
摘要
高熵合金是近年来提出的一种新的合金设计理念,打破了一般合金中以1种或2种元素为主,辅以极少量其他元素来改善合金性能的传统思想,由多种元素以等原子或近似等原子比混合后形成具有独特原子结构特征的单一固溶体合金.高熵合金的多主元特性使其在变形过程中表现出多重机制(包括位错机制、形变孪生、相变等)的协同,因而高熵合金已经展示了优异的力学性能,如高强、高硬、高塑性、抗高温软化、抗辐照、耐磨等,被认为是最具有应用潜力的新型高性能金属结构材料,已经成为国际固体力学和材料科学领域研究的热点.本文首先介绍了高熵合金独特的结构特征, 即具有短程有序结构和严重的晶格畸变;随后对近年来针对不同类型高熵合金(包括具有面心立方相、体心立方相、密排六方相、多相以及亚稳态高熵合金)力学性能、变形行为方面的研究成果,特别是强韧化机制以及相关的原子尺度模拟, 进行了较为系统的综述;最后强调了高熵合金未来研究中所面临的一些主要问题和挑战,并对其研究进行了展望.
关键词：
Abstract
High-entropy alloys (HEAs) are a class of new metallic materials that have revolutionized alloy design over the past ten years. Unlike conventional alloys with one and rarely two base elements, HEAs contain multiple principal elements (at least four principal elements) with equal or nearly equal atomic concertation to promote the formation of simple solid solution phases. Due to the presence of multiple principal elements, multiple deformation mechanisms (including dislocation activities, deformation twinning, and phase transformation) activate during deformation of HEAS. Therefore, HEAs usually exhibited many excellent mechanical properties, such as ultrahigh hardness, high tensile strength, good ductility, high thermal softening resistance, remarkable irradiation resistance, and good wear resistance. HEAs are thought to be the most promising structure materials and have attracted tremendous attention over worldwide in the fields of solid mechanics and material sciences. In this review paper, we first briefly introduce the unique and complicated microstructural features of HEAs, i.e. HEAs have both chemically short-range orderings and severe lattice distortion. Then, we review the recent experimental studies on mechanical properties, behaviors and deformation mechanisms of HEAs with face-centered cubic, body-centered cubic, hexagonal close-packed, dual or meta-stable phases. We also mainly emphasize some effective strengthening and toughening strategies, including solid solution, grain refinement, second phase or precipitation. We further summarize some advanced atomistic simulations/modelling on microstructures, mechanical properties and deformation of various HEAs. Finally, we address a list of open problems and challenges for the future studies about design, fabrication and mechanics of HEAs, and provide some important mechanistic insights into design and fabrication of HEAs with excellent mechanical properties and performances.
Keywords：
PDF (85411KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李建国, 黄瑞瑞, 张倩, 李晓雁. 高熵合金的力学性能及变形行为研究进展 1). 力学学报[J], 2020, 52(2): 333-359 DOI:10.6052/0459-1879-20-009
Li Jianguo, Huang Ruirui, Zhang Qian, Li Xiaoyan.
引言
一直以来, 金属材料在人类文明的进程中起着决定性的作用.随着经济发展和科技的进步, 对材料的综合性能要求越来越高.传统工艺中通过在1种或2种主元中添加少量其他元素来提高合金性能已渐趋发展的瓶颈,少有突破性的进展来满足日益严苛的实际需求.高熵合金这种全新合金设计理念的出现正当其时.高熵合金是由多种主要元素以相等或近等原子比混合而成, 每种主元含量相当,因此并不存在类似于传统合金中的"基体元素", 即没有溶剂与溶质原子的区别.传统合金的设计受限于基体元素的约束, 如图1(a)左上图三元相图蓝色(三角中深色)部分所示,研究范围仅限于几个角落区域,而当$n$种元素以等原子比混合时可能获取的合金种类可达$N=2^{n}-n-1$种,从而使得研究范围逐渐向相图中心区域扩展[1].由此可见, 多主元混合制备合金的策略首先极大地丰富了合金的种类,为寻求高性能金属材料提供了更大的研究空间.图1
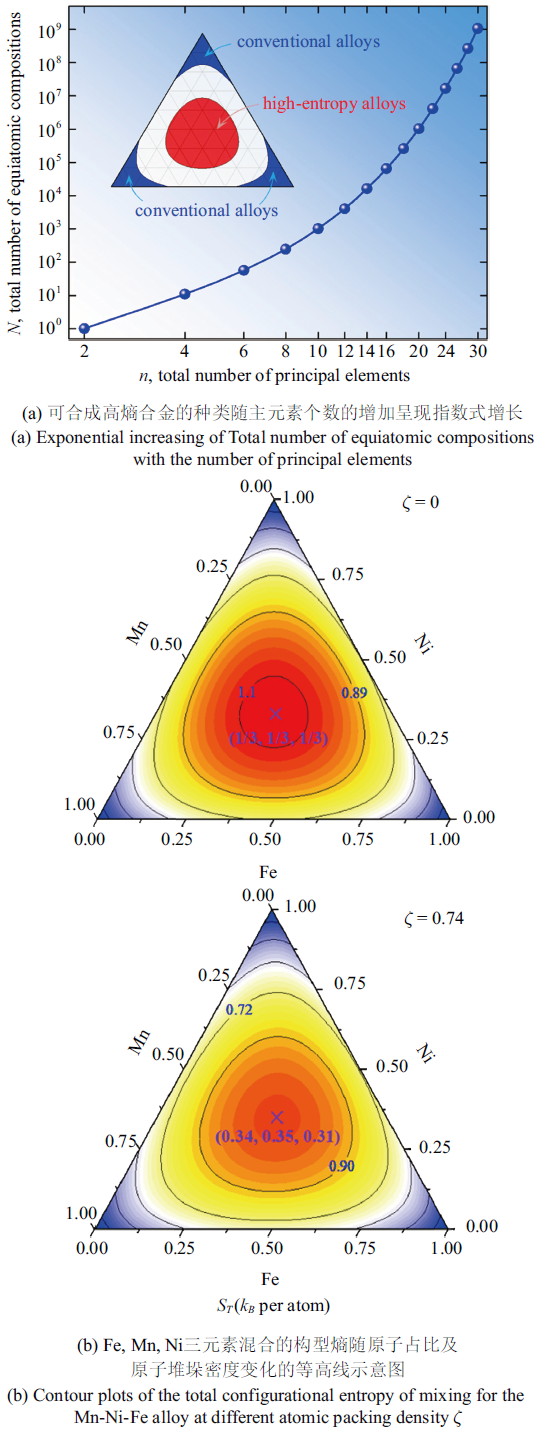新窗口打开|下载原图ZIP|生成PPT图1高熵合金设计的热力学基本原理示意图[1]
Fig. 1Schematic illustrations for thermodynamics principle of design of HEAs [1]
高熵合金的概念于2004年首次见诸于报道, 又被称为多主元合金. 2004年,台湾新竹清华大学Yeh等[2]和英国Birmingham大学Cantor等[3]各自独立地发表了多主元混合制备高熵合金的研究成果.高熵合金这一名称也源于Yeh团队的研究工作[2].一般认为, 合金中元素增多易导致金属间化合物的出现, 使得合金内部结构变得复杂.而不同相或者金属间化合物的形成取决于系统混合的Gibbs自由能$\Delta G_{\rm mix} =\Delta H_{\rm mix} -T\Delta S_{\rm mix}$, 其中$\Delta H_{\rm mix}$和$\Delta S_{\rm mix}$分别表示合金系统的生成焓及混合熵, $T$为绝对温度. Yeh等[2,4]假设所得合金为理想固溶相,$\Delta H_{\rm mix} =0$, 而金属间化合物内部是完美有序的, $\Delta S_{\rm mix}=0$. 因此,多主元合金中是否形成单一固溶相则取决于$-T\Delta S _{\rm mix}$是否小于$\Delta H_{\rm mix} $. 根据热力学原理,
其中, $R$为气体常数, $x_{i}$为第$i$种元素的摩尔含量, $n$为系统中元素的总数. 对于等原子比高熵合金,仅当理想无序状态(如理想气体状态)时, 有$x_i =1/n$, 从而可得出$\Delta S_{\rm mix} =R\ln n$.因此随着元素种类增加, 混合熵升高到一定程度, 混合熵对体系自由能的贡献大于生成焓时, 则形成单一固溶相. 根据上述热力学理论,Yeh等认为元素种类增多导致的高熵效应有助于形成稳定的固溶相, 故而将其命名为高熵合金[1-2].需要指出的是, 对于固态多元合金而言, 不同晶体结构的对称性导致元素分布的微观态存在明显差异, 因而构型熵也不一致.计算系统Gibbs自由能时, 需根据Burnside引理确定晶体结构对称性对构型熵的影响, 计算方法可见参考文献[5]. 此外,随着研究的进一步深入, 有报道指出[6-8]原子尺寸差异$\delta $、原子堆垛密度$\xi $以及混合焓$\Delta H_{\rm mix}$也是影响总体混合熵的重要因素. 如图1(b)所示, 随着原子堆垛密度$\xi$改变, FeMnNi三元合金中混合熵的最大值及其对应原子占比都会发生改变. 综合考虑以上因素, 并根据热力学准则可以判断是否能够获得单一固溶相组织. 至于所形成相组织的晶格类型, 需根据Hume-Rothery准则做进一步判定.合金组分的价电子浓度(valence electron concentration, VEC)是决定晶格类型的重要因素, 大量实验结果[9-10]证实当VEC $>$ 8时为面心立方结构(face-centered cubic, FCC), 而VEC $>$ 6.87时呈现为体心立方结构(body-centered cubic, BCC). 除上述判断准则外,半经验性的相图计算法(CALPHAD)也可用于稳态相的预测[11-13]. 作为这一方法的补充, ****们也会依据高通量第一性原理计算所得参量建立简单模型用于多主元合金相组织的预测. 例如,根据高通量蒙特卡洛方法计算所得焓矩阵能够定量地预测不同铝含量对Al$_{x}$CoCrFeNi高熵合金中相组分的影响,其预测与实验观察结果比较吻合[14]. 总之, 研究者们总结和提出的大量预测方法能够保证通过成分调控控制高熵合金中相稳定性及筛选组成相,目前已经能够制备出上百种不同晶格类型的单一固溶相合金. 因此,当下研究的重点也已经转向这一新型合金的"结构-性能''关联性以及微观变形机理等方面.众多优异性能的争相报道使得高熵合金成为目前材料学及固体力学领域最受关注的研究热点之一[15-18].例如, 典型FCC高熵合金通常表现出高的断裂强度和良好的塑性,特别是低温条件下强度和塑性同时提高,这主要归因于塑性变形机制由位错主导向孪晶主导的转变[19-21];典型BCC高熵合金除了固有的高强度以外,其高温力学稳定性甚至优于现有镍基高温超合金[22-23];密排六方结构(hexagonal close packed, HCP)高熵合金较少见诸于报道,其中Mg系和Ti系高熵合金则表现出低密度、高强度的力学性能[24-25].此外, 高熵合金还表现出良好的耐腐蚀性、耐磨性、抗辐照和超导性等优异的性能.下文中将逐一着重介绍高熵合金优异的力学性能. 有****指出[26], 由于高熵合金具有诸多优异的力学性能,因此高熵合金未来有可能广泛用做一些重要工业领域中的关键材料, 如高超速飞行器发动机超高温材料、高性能战斗部材料、抗辐照核能用材、轻质装甲防护材料、低温服役用材、航空航天轻质材料等.需要指出的是, 由于多主元合金材料在力学性能方面的优势, 可根据实际应用中的需要对结构件进行适当的拓扑优化, 以发挥这一新型结构材料潜在的可持续性使用价值; 同时, 金属结构材料应用的可持续性还表现在材料回收处理时对杂质元素的包容性,而针对多主元合金热力学方面所开展的广泛研究十分有利于对可持续性合金设计的深入理解[27].
通常认为, 高熵合金优异的力学及理化性能与其多主元特性所造成的独特结构特征息息相关. Yeh基于高熵合金的原子结构特征提出四种效应[15,28]解释这一新型多主元合金在性能及变形机理上的特殊性.这4种效应分别为: (1) "高熵效应"——即合金具有高的构型熵(参见上文的简述),这一效应在简化合金微观组织方面起到主要作用, 极大地提高了单一固溶相的稳定性,抑制了金属间化合物的生成[15]; (2)"迟滞扩散效应''——高熵合金中各种元素原子之间相互作用较强,相比于稀固溶合金其原子扩散率较低, 因此合金中析出相成核后不易生长, 这十分有利于纳米尺寸第二相的形成[15]; (3)"晶格畸变效应"——各种元素之间原子尺寸等方面的差异引起了严重的晶格扭曲畸变,被认为是高熵合金高强度的主要原因, 同时会对位错线的形貌及运动方式产生重要的影响, 下文会详细讨论[15];(4)"鸡尾酒效应"——即多种元素混合后形成的合金会表现出其中任意一种元素纯金属都不具备的性能[15],这也意味着通过调整合金组分及其配比可以有效地控制合金的性能. 由此可见, 在对其优异性能及力学行为进行讨论之前,我们有必要先对这些异于传统单一主元合金的结构特征进行详细的阐述,以此为基础再对其变形机理等作出深入的剖析.
1 高熵合金的原子结构特征
1.1 原子排布的长程化学无序性和短程有序性
对于多主元合金而言, 各主元之间并不存在溶质、溶剂元素的区别, 理想状态下在形成合金时各元素原子可随机占据不同晶格位点. 如图2(a)和图2(b)所示, 典型BCC和FCC结构五元高熵合金晶体单胞中各位点上原子并非唯一确定, 因此长期以来****们普遍认为高熵合金虽然具有长程拓扑有序的晶体结构, 但在化学意义上则表现为长程无序的点阵结构[2,6].然而, 理想随机固溶现象只会发生在高熵效应主导体系自由能降低的情况之下(例如在高温环境中)[29],在实际制备或应用时环境温度并不能达到这一条件, 此时生成焓也成为决定体系自由能的关键因素. 同时,各主元自身的属性(如电负性等)以及原子尺寸、键合能等差异都会导致原子对之间相互作用并不一致,因而在长程化学无序的点阵结构中往往会出现局部的化学短程有序结构(chemicallyshort-range ordering)[30]. Zhang等[31]最早通过X射线衍射、中子散射以及扩展X射线吸收精细结构(extendedx-ray absorption fine structure, EXAFS)技术等实验测试手段确认了CrCoNi合金中短程有序结构的存在, 并指出固溶体中Cr原子更容易与Ni和Co构成原子对. 随后, Ding等[30]采用基于密度泛函理论的MonteCarlo方法模拟了CrCoNi三元合金在变形过程中短程有序结构的演变, 发现随着剪切应变的增加模型中短程有序程度逐渐增加,同时伴随着原子结构的演变整个体系的平均层错能由$-42.9$ mJ/m$^{2}$升高到30 mJ/m$^{2}$, 这将会影响到变形过程中形变孪晶或者变形诱导相变的发生, 表现在宏观行为上则为短程有序结构对材料强塑性的作用. 随着原子尺度模拟技术的进步, Li等[29]构筑了原子间相互作用的多体势函数并建立分子动力学模型模拟了三元合金CrCoNi在不同退火温度下的原子稳态结构.如图2(c) $\sim\!$图2(e)所示, 随着退火温度的降低, 原子组态的有序程度越来越明显, 并且呈现出不同取向上的分区结构, 图中红色虚线标注出了各区域之间的边界. 短程有序结构形成对结构层错能造成的变化不仅会影响到形变孪晶、相变的形核,而且也会影响相变区域的生长[30]. 在相变成核以后, 由于变形过程中需要额外的能量打破有序结构,将会使得孪晶及相变区域的生长也受到限制作用, 同时大量纳米尺度短程有序结构的出现也会显著阻碍位错线的滑移,从而对材料起到一定的强化作用[29]. 因此, 相比于传统合金而言, 多主元混合形成的高熵合金中原子结构特征的确具有很高的复杂性,这也是其在力学性能及行为上呈现出一定特殊性的根本原因. 从原子尺度分析其结构特征, 有助于从根本上认知这一新型合金的基本属性,但这一部分工作也尚处于起步阶段, 尤其是实验方面仍需做出突破, 与模拟研究相结合, 从而更加清晰地表征出高熵合金的原子结构特征.图2
新窗口打开|下载原图ZIP|生成PPT图2高熵合金的微结构特征
Fig. 2Microstructural features of HEAs
1.2 严重的晶格畸变
除上述原子结构非均匀分布的影响外, 高熵合金中多主元组分之间原子尺寸的差异往往会造成晶格点阵的严重畸变.图3(a) $\sim\!$图3(c)分别展示了纯金属完美晶格结构、高熵合金严重畸变的晶格结构以及造成X射线衍射峰强度减弱的现象.Yeh等[32]通过在Cu金属中添加不同种类的元素获取多种多主元合金, 并利用X射线衍射研究分析其金相组成. 他们发现随着元素种类的增加, 在相同衍射条件下衍射峰的强度越来越弱(图3(d)所示), 这主要是因为严重的晶格畸变引起的反射发生几何偏转所致. 类比温度波动对X射线衍射造成的弱化作用, Yeh等[32]在模型中引入一个结构因子, 定量地表征了由晶格畸变造成的衍射峰值下降的现象, 这也提供了一种反映晶格畸变程度的测试方法. 大量结果表明, 高熵合金严重的晶格畸变对材料性能起到了极其重要的作用,尤其是高强度[15]. Ding等[33]将Cantor合金(FeCoCrNiMn)中Mn元素替换为Pd元素,由于Pd原子与其他原子之间存在较大的尺寸及电负性差异, 因此晶格畸变程度增加并存在大量的元素富集区域.高角环形暗场TEM结果所得原子应变分布图显示出明显的非均匀应变分布, 内应力显著增大导致位错移动减缓并易发生交滑移[33],因此FeCoCrNiPd合金的屈服强度相较于Cantor合金提升了近一倍, 且其延展性仍能够得以保持. Osetsky等[34]通过分子动力学方法研究了多主元合金中螺旋位错的滑移方式. 结果表明, 在应力较小的条件下, 多主元合金中位错往往在滑移一段距离后会停止, 只有当应力超过某一值后才会发生类似于传统金属中的连续滑移[34],可见严重晶格畸变引起位错滑移阻力的上升可显著影响其滑移方式. 另外, 值得注意的是, 严重晶格畸变的存在对目前已有的一些传统理论也提出了极大的挑战, 主要问题在于经典的固溶强化、析出强化以及位错强化理论均要考虑Burgers矢量$b$. 但当晶格畸变严重时, 晶格常数并不一致, 此时$b$值很可能不是一个定值, 而是一个分布区间[35]. 因此, 采用传统理论来计算和理解高熵合金的变形机制时, 需要谨慎考察传统理论的适用性.图3
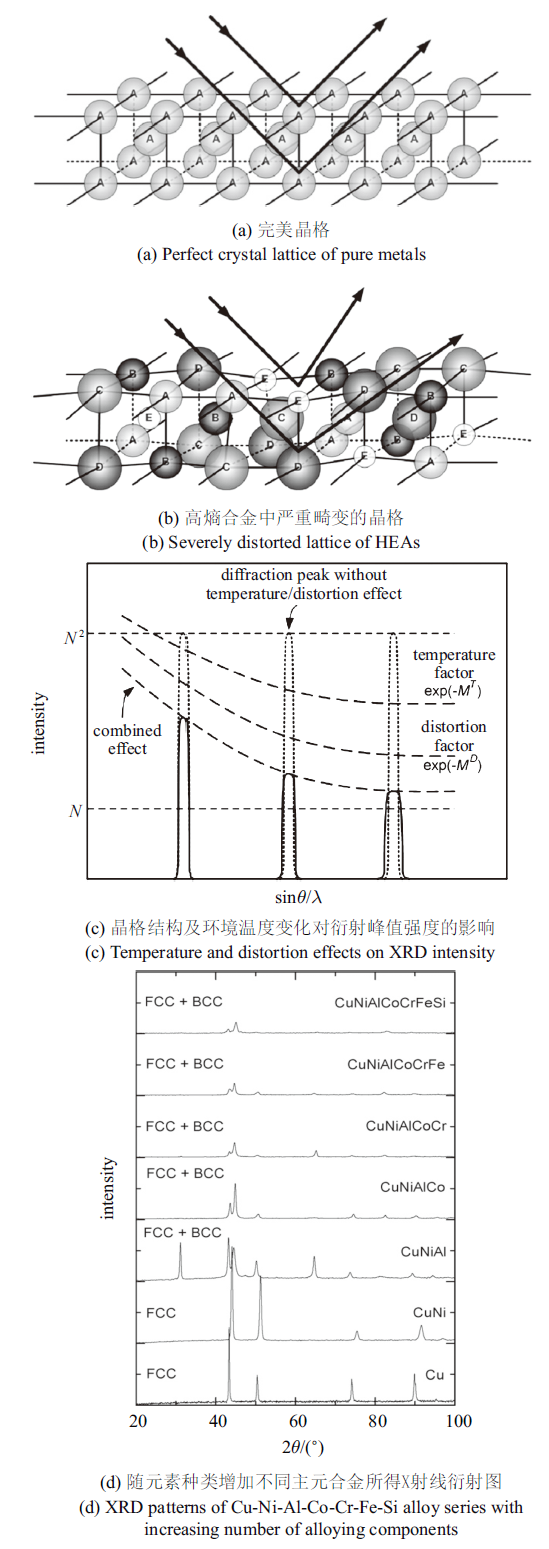新窗口打开|下载原图ZIP|生成PPT图3原子结构示意图显示严重的晶格畸变对X射线Bragg衍射峰值强度的影响[32]
Fig. 3Schematic illustrations of severe lattice distortion effect on Bragg diffraction of X ray[32]
多主元组分决定了高熵合金独特的原子结构特征, 进而会影响到变形过程中不同微观机制的激活, 表现在宏观性能上则为各项优异的力学性能. 因此, 对于新型高熵合金来说, 阐明"组分-结构-性能"三者之间的关系是未来研究和设计新型高性能金属结构材料的关键.上文已对高熵合金特有的微结构特征进行了简要的论述, 接下来, 我们将综述近年来高熵合金力学性能方面所取得的一些重要的研究成果, 并与传统金属材料进行对比, 以突出新型高熵合金在诸多方面的应用前景.
2 高熵合金的力学性能
2.1 硬度和比强度
硬度是一种表征材料力学性能的常用方法, 其中维氏硬度值HV与材料屈服强度$\sigma_{\rm y} $之间存在一定的比例关系: $HV=c\cdot \sigma _{\rm y} $, $c$通常为一常数. 因此, 在一定程度上硬度也能反映材料强度的高低, 而强度对于工程设计和安全评价具有重要的基础意义[36-37].根据高熵合金的组分及制备方法的差异, 其硬度变化范围较大. 例如, 随着CrCoFeNiAl$_{x}$高熵合金中铝含量的增加合金的组成相由FCC逐渐过渡到BCC, 其硬度也由110 HV升高到510 HV[38],添加Cu元素后其硬度可高达655 HV[39]. Zhang等[40]通过激光熔化快速凝固的方法获得FeCoNiCrCuTiMoAlSiB$_{0.5}$高熵合金, 由于大量间隙硼化物和马氏体相的存在, 该合金硬度高达11.3 GPa(约1200 HV). 此外, 在保证高强度的同时, 若能够合理控制材料密度则更为重要, 特别是在航空航天工业、民用运输等领域, 轻量化设计一直以来都是研究的重点和热点, 既要保证结构的安全有效又要降低能量消耗,这也是可持续性结构材料的一大特征[27]. 通常采用比强度的概念(即强度与密度的比值)衡量不同材料的这一属性.Senkov等[41]指出: 在BCC相高熵合金中利用轻质原子替代某一些原子, 在不改变晶格结构的前提下,既能保证强度不发生大的改变又可有效降低材料密度, 例如采用Ti, Al, Mg, Li等元素. 如图4所示, 在FeCoCrNi高熵合金中添加了不同含量的Al和Ti原子, 所得合金密度介于传统钛合金和不锈钢之间, 但高熵合金的强度略高,因此表现出了优于传统材料的比强度[15,42]. 图4中平行分布的虚线代表双对数坐标下比强度等高线, 越靠近左上角则比强度越高,图示含铝、钛元素的高熵合金比强度处于最高水平. 目前, 有关轻质高熵合金的报道中密度最低的材料为Al$_{20}$Li$_{20}$Mg$_{10}$Sc$_{20}$Ti$_{30}$,Youseff等[42]通过机械合金化的方法将五种低密度的元素制备获得HCP单相高熵合金, 密度仅为2.67 g/cm$^{3}$,其强度高达$\sim $2 GPa, 计算可知其比强度为0.74 GPa/(g$\cdot$cm$^{-3}$), 是传统轻质铝合金和钛合金的两到三倍,甚至可以与SiC陶瓷相媲美.图4
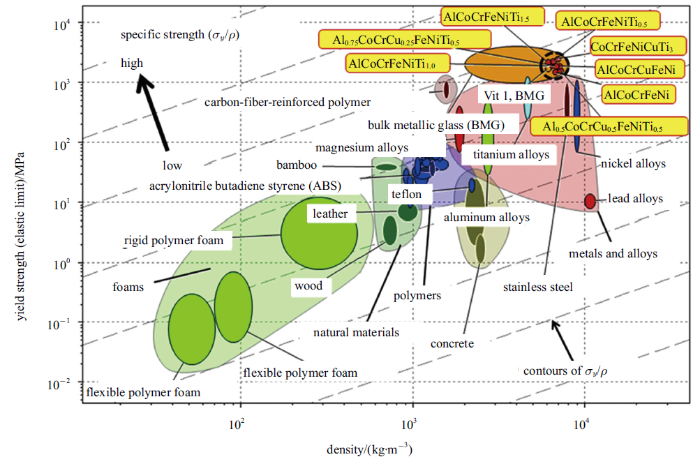新窗口打开|下载原图ZIP|生成PPT图4材料的屈服强度与密度的Ashby图. 与现有的材料相比, 一些高熵合金具有很高的强度和比强度[15]
Fig. 4Yield strength vs. density of various materials, including HEAs and other engineering and biological materials[15]
2.2 良好的延展性和高的断裂韧性
除了高强度以外, 良好的塑性变形能力(即良好的延展性)也是金属结构材料不可或缺的基本性能, 但这两种性能往往不能兼顾. 当前所能制备的高熵合金多为FCC或BCC相, 其中前者表现为延展性好而强度低, 后者则恰恰相反. FeCoCrNiMn作为最早被合成的高熵合金已成为模型材料获得了最为广泛的研究, 其优异的塑性变形能力也引起了****们极大的研究兴趣.图5(a)展示了不同温度下FeCoCrNiMn合金的拉伸应力-应变曲线[19]. 室温环境下, 其屈服强度约为400 MPa, 抗拉强度为760 MPa, 断裂延伸率平均值为56%; 随着温度的降低, 该合金的强度、断裂延伸率以及应变硬化率均出现明显的上升, 拉伸强度超过1.2 GPa并且断裂延伸率超过70%[19]. 大量微观观察[43-45]表明上述现象的发生主要是温度降低导致屈服应力水平升高, 塑性变形机制由位错主导转变为孪晶主导所致,大量孪生变形有利于材料发生均匀塑性变形[46]. 这也与FCC相高熵合金较低的层错能有关, 针对层错能更低的CoCrNi合金的研究表明:其室温下即可形成大量孪晶组织, 因而表现出更加优异的塑性变形能力[47]. 高温条件下, FCC相高熵合金力学性能下降十分明显, 出现显著的应变软化行为, 一定温度下元素易发生定向扩散、富集形成第二相, 导致应力集中并引发断裂失效[21,48].如上所述, 尤其是低温条件下, FCC相高熵合金均表现出高的断裂强度和良好的塑性变形能力, 因而其断裂韧性也成为关注的焦点.Gludovatz等[19,49]在室温和低温下通过测试带有预制裂纹的紧凑拉伸试样(compact-tension samples)研究了FeCoCrNiMn和CoCrNi两种典型FCC相高熵合金的损伤容限能力. 图5(b)所示, 根据J积分计算所得高熵合金的断裂韧性高于绝大多数结构材料. 为了从微观上解释这一现象, Zhang等[50]在室温条件下进行了CoCrNi合金中裂纹扩展的透射电镜原位观察试验. 结果展示了, 在裂纹扩展过程中, 大量纳米孪晶起到了桥连(nano-bridging)的作用. 除了内禀韧化机制(intrinsic mechanism)以外, 这种外禀韧化机制(extrinsicmechanism)也有助于提高FCC相高熵合金的断裂韧性. 相较而言, BCC相高熵合金则具有较高的强度但延展性较差, 例如铝含量较高的(FeCoNiCrMn)$_{89}$Al$_{11}$高熵合金[38], 其屈服强度高达1.2 GPa, 但延伸率不到8%;由多种难熔金属元素混合而成的NbMoTaW高熵合金组成相以BCC相为主, 在晶界附近存在少量偏析相, 室温下压缩应变仅为1.5%,裂纹沿着平行于压缩方向快速扩展导致脆性失效[51]. BCC相高熵合金中塑性变形能力较好的退火态TaNbHfZrTi在室温条件下, 屈服强度超过1 GPa且延伸率大于10%, 特别是单轴压缩加载时应变可超过50%[52]. 这种拉压不对称性在下文讨论典型BCC相高熵合金变形行为时会具体论述. 随着温度上升, BCC相高熵合金的延展性会得到提高, 位错滑移将更容易激活, 甚至有少量孪晶的出现, 一些合金开始由脆性转变为韧性, 但此时强度降低较为明显[53]. 由此可见,与传统金属相类似, 高熵合金中强塑性匹配问题依然是亟需解决的重要问题, 下文中也将介绍针对不同类型高熵合金所提出的一些强韧化策略.图5
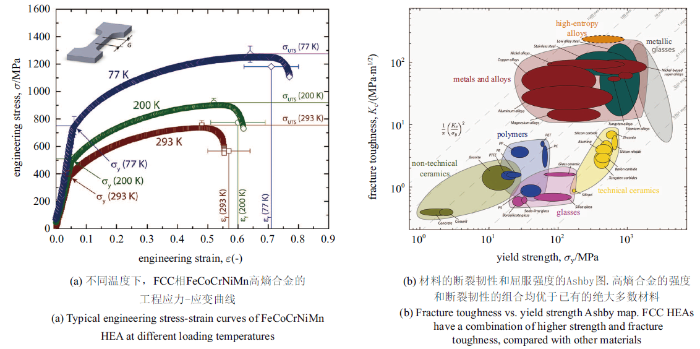新窗口打开|下载原图ZIP|生成PPT图5高熵合金的强度和断裂韧性[19]
Fig. 5Strength and fracture toughness of HEAs[19]
2.3 疲劳性能
高熵合金作为一种极其具有应用前景的金属结构材料, 强韧性决定了其工程应用中的安全性, 而疲劳性能将直接决定实际应用中结构件的使用寿命, 因此研究该新型合金中疲劳裂纹起始、扩展的具体过程及其微观机制也是十分必要的.对于韧性金属材料而言, 决定疲劳裂纹扩展的因素有很多, 诸如加载频率$f$、应力比$R$、环境温度和微观结构等. 但当加载条件确定后,疲劳裂纹扩展速率d$a$/d$N$ ($a$为裂纹长度, $N$为循环次数)主要取决于裂纹尖端应力强度因子的变化$\Delta K$. 从d$a$/d$N$-$\Delta K$曲线上, 可将疲劳裂纹起始后进行扩展直至失效分为3个阶段[54]: (i)初始扩展阶段: 当$\Delta K$大于疲劳裂纹扩展门槛值$\Delta K_{\rm th}$时, 裂纹开始扩展, 此时扩展速率较低但很快达到一定的扩展速率(小于10$^{-9}$ m/cycle), 其中$\Delta K_{\rm th}$越大表明该材料抵抗疲劳裂纹扩展的能力越强; (ii)随后裂纹扩展速率的增长率有所降低, 通常采用Paris公式, 即${\rm d}a/{\rm d}N=c\cdot (\Delta K)^m$, 对这一阶段的演化过程加以描述, 其中$c$和$m$为材料相关的常数; (iii)进入第三阶段后, 裂纹扩展速率d$a$/d$N$已经很高, 很快会发生失稳扩展导致材料发生断裂破坏. 图6(a)所示为Thurston等[55]在不同温度下采用定循环载荷($R=0.1$, $f=25$ HZ)研究FeCoCrNiMn高熵合金中疲劳裂纹扩展行为所得的d$a$/d$N$-$\Delta K$曲线, 图中空心圆圈和方块分别表示293 K和198 K温度下测试的结果. 随着温度降低, FCC相高熵合金通常表现强度和断裂韧性同时提高, 疲劳加载时可以看到$\Delta K_{\rm th}$随温度降低而增加, 由4.8 MPa$\cdot$m$^{1/2}$升高到6.3 MPa$\cdot$m$^{1/2}$, 而且第一阶段裂纹扩展速率下降了近一个量级[55].但是第二阶段低温条件下曲线的斜率有所上升, 即对应的Paris公式中幂指数大小由3升高到了4.5, 这主要是因为低温条件下裂纹扩展主要机制由沿晶界断裂转变为穿晶断裂[55]. 与传统合金钢相比, FCC相高熵合金与孪晶诱导变形的TWIP(Twinning-induced plasticity)钢表现出极为相似的疲劳裂纹扩展行为, 且均明显优于奥氏体不锈钢.图中还给出了由FCC相和BCC相组成的铸态Al$_{0.2}$CrFeNiTi$_{0.2}$和AlCrFeNi$_{0.2}$Cu高熵合金的疲劳裂纹扩展曲线[56],$\Delta K_{\rm th}$值升高到了17 MPa$\cdot$m$^{1/2}$. 相较于均匀细晶组织疲劳失效后平整的断口, 铸态组织断后表面更加粗糙, 裂纹扩展所需能量更多一些, 因此对应的裂纹扩展门槛值则更高. 图6(b)对比了Al$_{0.5}$CrFeCoNiCu高熵合金与其他传统合金和块体非晶材料的疲劳极限[57],如图所示高熵合金在更高的应力水平下表现出更长的疲劳寿命. 但是高熵合金的数据存在一定的分散性, 这可能与该高熵合金中存在大量的氧化铝颗粒以及微裂纹有关, 因此一些****们指出减少这些缺陷的数量能够提高高熵合金的疲劳性能[57],从而进一步确保高熵合金抗疲劳性能的实际应用.图6
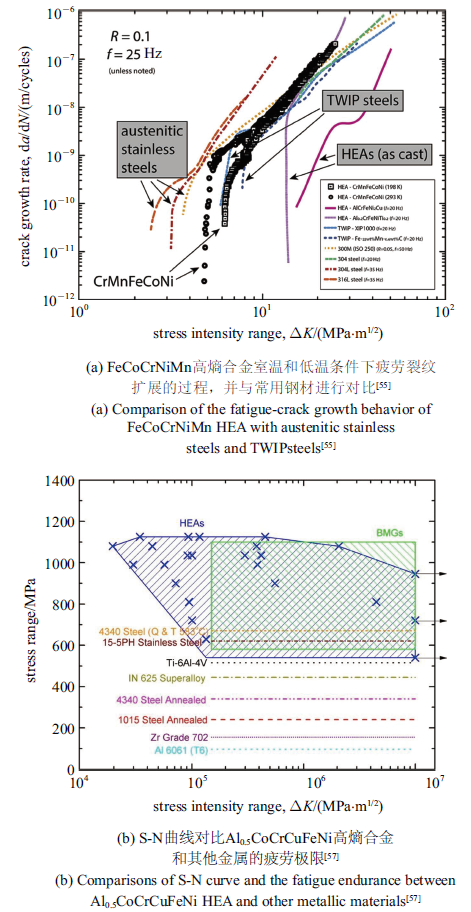新窗口打开|下载原图ZIP|生成PPT图6高熵合金的疲劳性能
Fig. 6Fatigue properties of HEAs
2.4 高温力学性能的稳定性
如前文所述, 高熵效应是多主元合金中易获得单一固溶相的重要原因. 考虑到系统自由能$\Delta G_{\rm mix} $计算时$-T\Delta S_{\rm mix} $中温度的影响, 升高温度十分有利于提高高熵合金中固溶相的稳定性. 同时考虑到高熵合金中多主元之间相互作用引起的迟滞扩散效应, 该新型合金呈现出良好的高温力学性能. 近年来, 大量的实验结果证实了高熵合金的这一性能优势, 使得其在高温结构合金领域有着广阔的应用前景[51,58-60]. 尤其是多种难熔金属元素混合形成的BCC单相高熵合金, 其高温力学性能甚至优于目前被广泛应用于燃气轮机等工业领域的镍基高温超合金. 如图7所示, 两条虚线显示了常用的两个牌号镍基超合金屈服强度随加载温度变化的趋势, 其他实线则表示多种不同组分高熵合金中温度对其力学性能的影响[1]. 低温条件下, 高熵合金与Inconel 718镍基超合金的屈服强度相近, 随着温度升高Inconel 718从700${^\circ}$C开始出现显著的软化, 而NbMoTaW高熵合金发生明显软化时对应的温度则高达1200${^\circ}$C. 在1000${^\circ}$C时, NbCrMo$_{0.5}$Ta$_{0.5}$TiZr的屈服强度依然高于1 GPa, Senkov等[60]将其中的Cr元素用Al元素替代,由于晶粒内形成高密度纳米层状析出相, 室温下其屈服强度高达2 GPa, 800${^\circ}$C时依然能够保持在1.6 GPa, 直到温度上升到1000${^\circ}$C时才会出现明显的强度下降. 但需要注意的是, 以上高熵合金的力学性能均源自于单轴压缩实验,而BCC相高熵合金较低的拉伸延伸率依然是限制其应用的主要因素. 为了在工程应用中对高熵合金优异的高温力学性能加以利用,我们需要进一步综合研究其断裂韧性、疲劳和抵抗蠕变等性能, 系统地分析其各项属性, 以保证实际应用的可靠性.图7
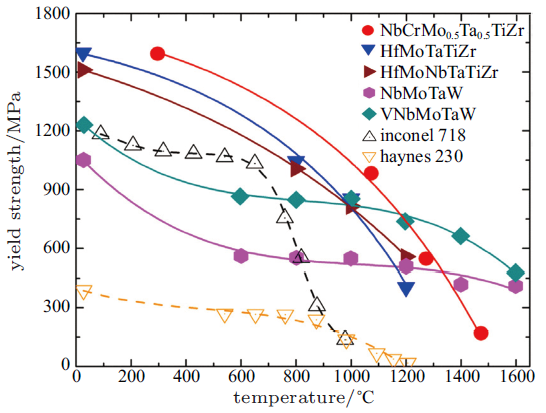新窗口打开|下载原图ZIP|生成PPT图7典型BCC相高熵合金随加载温度改变其屈服强度的变化, 并与现有镍基超合金高温性能进行对比的结果[1]
Fig. 7Variation of yield strength with increasing temperature in typical BCC HEAs and Ni-based superalloys[1]
2.5 蠕变性能
受严重晶格畸变和局部位点结合能不同的影响, 高熵合金通常表现出较高的扩散阻力, 因此相比于传统纯金属或稀合金而言, 高熵合金的蠕变行为也必定有所改变. 根据所施加应力和环境温度的变化, 可将蠕变行为的微观机制分为5种类型[61]: (i)当应力$\sigma $大于理论剪应力时, 原子面的简单滑移将主导塑性流动行为; (ii)当$\sigma /G>10^{-2}$时($G$为材料的剪切模量), 位错滑移会发生;(iii)当$10^{-5}<\sigma /G<10^{-2}$时, 蠕变行为由位错蠕变主导, 包括位错滑移、攀移并伴随有空位扩散; (iv)当$\sigma /G\leqslant 10^{-5}$时, Nabarro等提出一种扩散机制, 空位将沿着晶界扩散, 称之为Nabarro-Herring蠕变, 此时蠕变率反比于平均晶粒尺寸的平方; (v)当环境温度更低时, 晶界扩散成为主导机制, 称之为Coble蠕变, 此时蠕变率反比于平均晶粒尺寸的立方.Kang等[62]在535$\sim$650${^\circ}$C的温度下研究了退火态FeCoCrNiMn高熵合金的蠕变行为, 结果表明: 当应力水平大于40 MPa时, 主导变形机制由位错攀移机制变化为黏性位错滑移机制, 高熵合金中原子尺寸较大的Cr原子与其他原子具有较大尺寸失配, 易发生偏聚,从而对位错滑移产生拖曳作用. 此外, 也可根据蠕变应变率随应力的变化关系$n=\partial \ln\dot{\varepsilon}/\partial \ln\sigma$,推断蠕变行为的主导机制[63]. 通常当$n=1$时, 对应扩散主导的蠕变行为, 即Nabarro-Hering蠕变或Coble蠕变; 当$n=2$时, 对应蠕变机制为晶界滑移; 当$n>3$时, 则为位错蠕变控制. 如图8所示, Lee等[64]研究了纳米晶FeCoCrNiMn高熵合金在球形压头作用下的蠕变行为, 相较于粗晶高熵合金, 纳米晶高熵合金在更高的应力作用下的蠕变应变率与粗晶高熵合金相当. 对比双对数坐标下蠕变应变率$\dot{\varepsilon}$随应力水平$\sigma $变化的曲线斜率可知: 在小晶粒时, 蠕变机制由晶界扩散主导; 而在大晶粒时, 则主要由位错滑移和攀移控制塑性流动. 此外, 图中显示在同样的应力水平下, 纳米晶FeCoCrNiMn高熵合金的蠕变率比纳米晶纯镍的理论值要小3个量级, 这主要归因于高熵合金中特殊晶格结构所引起的迟滞扩散效应[64].图8
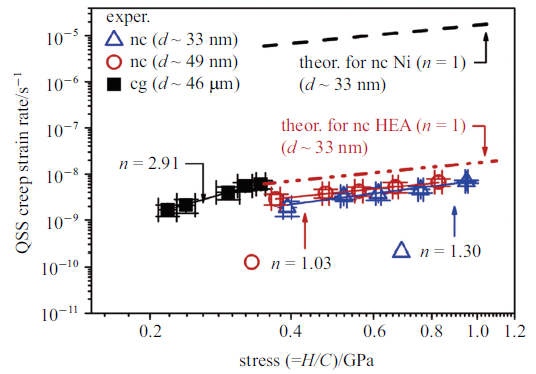新窗口打开|下载原图ZIP|生成PPT图8不同晶粒尺寸FeCoCrNiMn高熵合金蠕变应变率随应力变化, 并与纳米晶纯镍的理论值做对比[64]
Fig. 8Relationship between creep strain rate and stress for FeCoCrNiMn HEAs with different grain sizes[64]
2.6 抗冲击性能
由于具有优异的抗冲击性能, 高强韧合金是冲击防护领域迫切需求的材料.FCC相高熵合金在准静态条件加载时已经表现出了极高的断裂强度和应变硬化能力,特别是在低温环境加载时其强度和延展性均获得显著的提升,这往往归因于塑性变形过程中大量形变孪晶的生成对应变硬化产生的巨大贡献.通常认为低温和高应变率对塑性变形具有类似的影响,因而高熵合金在高应变率下的力学响应也引起了****们极大的研究兴趣.Li等[65]首先系统地研究了Al$_{0.3}$CoCrFeNi高熵合金高应变率压缩力学行为.由于固溶效应、林位错之间相互作用以及孪晶硬化等耦合作用,高熵合金表现出优于传统合金的应变硬化能力及高的应变率敏感性. 随后,Li等[66]采用如图9(a)和图9(b)所示帽形剪切试样,通过Hopkinson压杆在指定区域产生集中的剪切变形,研究了FeCoCrNiMn高熵合金抵抗剪切变形的能力.通过图9(b)中绿色的限制环的厚度控制加载应变的大小. 研究结果表明,FCC相高熵合金优异的应变硬化能力使得剪切应变高达$\varepsilon=7$时才能引起局部热塑性失稳变形(即生成绝热剪切带)[66].为了解决FCC相高熵合金低屈服强度的问题, Ma等[67]在此基础上通过预轧制细晶化和退火处理后获得了高强韧CoCrNi合金,并考察它的高应变率剪切变形能力, 结果如图9(c)和图9(d)所示.类比于具有相似微观结构的传统金属或者合金,CoCrNi高熵合金表现出更加优异的均匀剪切变形能力和高的剪切韧性,尤其是高应变率和低温条件耦合作用时,大量形变孪晶的生成促使硬化能力进一步提升,使该材料表现出更好的抗剪切变形能力.2.7 抗辐照性能
高熵合金复杂而独特的微结构特征有利于各项力学性能的改善.严重的晶格畸变以及组分的复杂性可以有效降低电子、声子和磁振子的平均自由程,并改变缺陷的形成能量、迁移能垒和扩散路径,进而影响到辐射早期缺陷的形成和相互作用以及间隙空位的重组等过程.在传统金属中, 缺陷及元素偏聚的出现往往会影响到材料性能的转变,如辐照脆化现象等[68]. 相较而言,****们认为高熵合金抵抗辐射损伤的能力会远强于传统合金材料[69].Granberg等[69]通过辐照实验和分子动力学模拟,对比研究了Ni、NiFe和NiCoCr合金抵抗辐照损伤的能力,发现多元合金中位错移动的能力大大降低, 导致损伤的数量减少了2$\sim$3倍.Lu等[70]为了更加全面地解释多主元合金抗辐照损伤的微观机制,继续增加合金元素的种类,其研究对象还包括NiCo、NiCoFe、NiCoFeCr和NiCoFeCrMn等合金, 在500${^\circ}$C环境温度下进行不同剂量的离子辐照实验.图10(a)和图10(b)分别给出了一定辐照时长后, 合金内孔洞和位错的分布情况.相比于纯金属或稀合金中分布于表面的较大尺寸孔洞,多主元合金中孔洞数量虽然增多但其尺寸均十分微小, 并且分布在一定的深度范围内.全部孔洞的体积反映了辐照所造成体积肿胀的程度. 根据统计, 3 MeV Ni$^+$离子辐照后纯Ni金属的肿胀率为9%, NiFe合金则降低到0.45%, 而NiCoFe和NiCoFeCrMn的肿胀率仅为0.15%和0.1%[70]. 孔洞是由辐照所致空位的聚集造成的,辐照导致间隙缺陷的聚集(图10(b)中HRTEM所示)也会造成位错环和位错网络的出现. 如图10(b)所示, 大量的位错环或者位错网络由表面一直延伸至一定的深度,分布于孔洞层之上. 因此, 与纯金属或稀合金相比,多主元合金中位错区和孔洞区的分布恰好呈相反的分布,这是因为原子结构的差异使得辐照所致间隙缺陷的迁移方式转变为局部点缺陷的重组,而不是稀合金中由内部直接迁移至表面才消失[70-71].间隙缺陷迁移方式的改变使得辐照损伤的微观特征发生改变, 也大大提升了抵抗辐照的能力[70]. 除了表征孔洞体积以外, Jin等[71]采用一种更加直观的方式表征了不同合金在一定剂量离子辐照后体积肿胀的程度.如图10(c)所示, 采用一定形状的格栅保护使得离子辐照仅发生在特定区域, 可以看到辐照后多主元合金中几乎没有形成台阶, 而纯Ni中则形成很高的台阶. 图10(d)中统计数据更加清晰地展示了不同合金的辐照肿胀程度.图9
新窗口打开|下载原图ZIP|生成PPT图9FCC相CoCrNi合金在高应变率作用下的力学行为[67]
Fig. 9Mechanical behaviors of HEAs under high strain rate[67]
图10
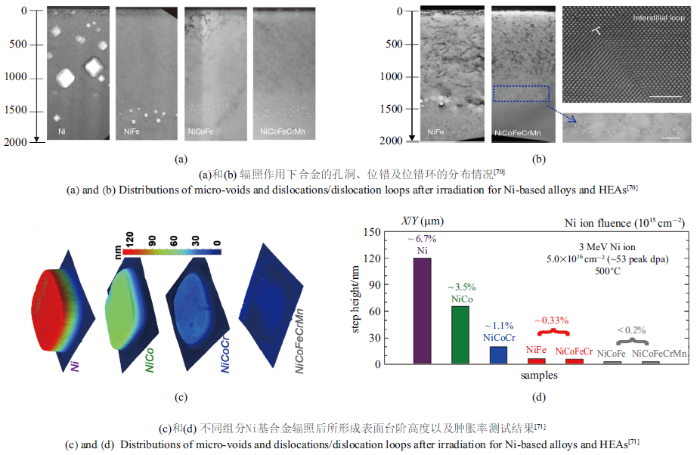新窗口打开|下载原图ZIP|生成PPT图10不同组分Ni基合金及高熵合金在温度为773 K时3 MeV Ni$^+$离子辐射行为.
Fig. 10Behaviors of Ni-based alloys and HEAs under after irradiation with 3 MeV nickle ion at 773 K
2.8 耐磨性
前文提及一些高熵合金具有很高的硬度, 且在高温条件下力学性能更稳定,这使得这些高熵合金有可能进一步成为良好的耐磨材料,因而激发了大量针对不同主元高熵合金耐磨性的研究.Wu等[72]首先研究了不同铝含量Al$_{x}$CoCrCuFeNi高熵合金的黏着磨损行为,他们发现随着高熵合金中铝含量的增大, 组成相由FCC转变为BCC结构,磨损机制也由分层变为氧化磨损, 这主要是由材料硬度的上升所致,同时表面形成氧化膜也有利于耐磨性的进一步提升. 但是, 由于BCC相合金的塑性较差,该类合金材料的可加工性通常比较弱.Chuang等[73]为了能够获得耐磨性较好的FCC相高熵合金,通过调整合金元素比例最终确定了Co$_{1.5}$CrFeNi$_{1.5}$Ti$_{0.5}$合金体系,并系统研究了其耐磨性能. 如图11(a)所示, 与现有的两种耐磨钢相比,该高熵合金抵抗磨损的能力提高近一倍[73].相比而言, 两种耐磨钢室温下的硬度与高熵合金相当甚至还高一些, 但如图11(b)所示, 根据不同温度下各种材料氧化增重实验结果可知高熵合金的抗氧化性更好一些,同时不同温度下硬度测试结果显示高熵合金的高温稳定性更好,因此该型高熵合金的耐磨性更加优异. 此外,Braic等[74]探索将 (TiZrNbHfTa)N和(TiZrNbHfTa)C高熵合金作为Ti合金保护涂层来实现高熵合金薄膜在生物医药领域的应用,以提高植入体的性能及使用寿命. 实验结果展示该合金的硬度可达30 GPa,表面磨损率仅为$0.2\times 10^{-6}$ mm$^{3}$/(N$\cdot$m).图11
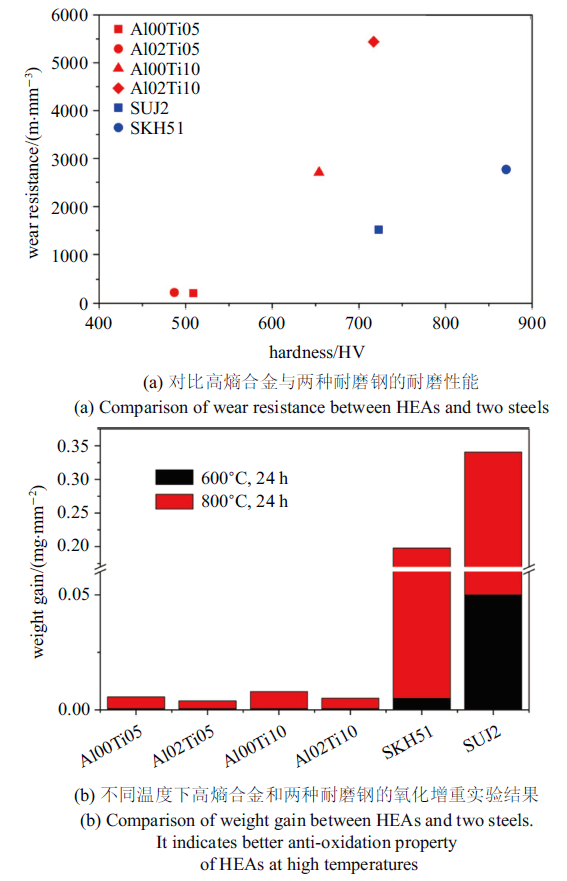新窗口打开|下载原图ZIP|生成PPT图11高熵合金的耐磨性能[73]
Fig. 11Wear resistance of HEAs[73]
3 典型高熵合金的力学行为及变形机理
上一部分内容逐一论述了高熵合金所具有的诸多优异性能,而特定晶格类型的高熵合金往往仅具有某一或某几方面的性能优势.例如FCC相高熵合金具有高的断裂强度和良好的延展性;BCC相则表现出高强度、高温稳定性和耐磨性等等.特殊的微结构特征会对其力学性能有着重要的影响,而具有不同晶格结构的高熵合金所表现出的不同力学行为也取决于变形过程中微结构的演化,即不同材料的塑性变形机理有所差异. 以下将列举几种典型高熵合金的塑性变形行为,并对其微观机理进行详细地阐述.3.1 面心立方相高熵合金的变形行为
FCC单相高熵合金中典型代表就是被广泛研究的Cantor合金(FeCoCrNiMn),其具有优异的塑性变形能力, 尤其是低温条件下同时具有高的强度和良好的延展性,这主要源自于该型合金极强的应变硬化能力, 能够在获得高强度的同时,有效延迟单轴拉伸时局部塑性失稳(即颈缩行为)的发生. 室温下,在塑性变形的初期位错主要在最密排晶面上沿1/2$\langle$110$\rangle$方向进行滑移,随后扩展为1/6$\langle$112$\rangle$方向Shockley偏位错, 并伴随有大量层错,偏位错之间分离的距离对于刃型位错而言约为3$\sim$4 nm, 而螺型位错更可达5$\sim$8 nm,因此位错交滑移较难发生, 这也与实验中观察到大面积平面滑移以及晶界附近位错塞积的现象相符合[43-44,75].原位TEM观察结果表明[50], 偏位错的滑移能力要强于全位错,但快速移动的偏位错也会受到全位错滑移所形成平面滑移带的阻碍作用.在较大应变时, 多个滑移系上偏位错被激活, 这些偏位错在相交滑移面上相互作用促使呈平行六面体结构的体缺陷形成,这也会对平面滑移起到阻碍作用[46]. 当位错密度随变形($\varepsilon _{\rm true}\approx 0.3$)增大到一定程度时,大量胞状位错结构形成, 这意味着位错的产生和湮灭已达到动态平衡,位错之间相互作用只能维持到如此大的变形能力. 在变形的末期, 有少量孪晶的形成,但此时局部变形已经开始, 很快会导致失效[44]. 相比而言,液氮温度下加载时, 初始变形阶段仍表现为位错平面滑移, 但随着低温条件下应力水平的上升, 在较小应变($\varepsilon _{\rm true}\approx0.08$)时孪生变形便被激活, 大量孪晶界的出现有效地阻碍了位错的滑移, 从而大大提升了位错存储能力, 因此合金的硬化能力可维持在一个相对稳定的水平[47], 直到应力水平与应变硬化率大小相当, 根据Considère准则, 此后变形很快会进入局域化, 进而发生颈缩失效. 因此, 研究者们普遍认为变形机制由位错主导转变为孪生主导是延展性提升的主要原因, 这与FCC相高熵合金较低的堆垛层错能有关[76-77], 也取决于孪生激活时所需的临界剪应力的大小[44,47]. 为了进一步更加直观地研究分析低温条件下FCC相高熵合金延展性增加的根本原因, Ding等[78]通过低温条件($-$180$^\circ$C)下原位TEM加载实验实时观察了FCC相高熵合金中微观结构的演化过程. 如图12所示, 除了大量孪晶的出现以外, 他们还观察到了位错交滑移现象(图12(b)所示),以往认为这种变形机制很难在低层错能FCC相高熵合金中发生; 此外, 在位错与晶界相互作用的位置附近, 不同方向滑移系上位错易被激活发射, 同时晶界上偏位错的发射会导致大量形变孪晶的生成(图12(c), 图12(d)所示).正是这一系列微观机制的协同作用, 才导致低温条件下FCC相高熵合金表现出极其优异的塑性变形能力[78].图12
新窗口打开|下载原图ZIP|生成PPT图12低温条件下原位TEM表征面心立方结构高熵合金中多重微观机制的协同作用[78]
Fig. 12In-situ TEM observations showing synergistic actions of multiple deformation mechanisms in FCC HEAs when loaded at cryogenic temperature[78]
3.2 体心立方相高熵合金的变形行为
BCC单相高熵合金则往往表现出极为有限的塑性变形能力,这也是未来限制其应用的关键因素.需要注意的是,一些BCC相高熵合金单轴压缩变形时仍然具有相当的变形能力,室温压缩TaNbHfZrTi高熵合金断裂应变可达约0.4[53].BCC相高熵合金组成元素的熔点都较高,因此在固化过程中形成了大量枝晶结构和不同程度的元素富集现象,例如TaNbHfZrTi高熵合金中枝晶中富含Ta和Nb,枝晶之间的区域则富含其他熔点相对较低的元素,在不含有枝晶的区域则不存在元素富集的现象[79].Dirras等[80]在铸态TaNbHfZrTi高熵合金元素富集程度不同的位置切割拉伸试样后进行测试,发现不同试样的屈服强度和延伸率均存在较大差异,其原因可归结于试样中枝晶元素富集的程度不一样并且铸造缺陷(如孔洞等)也是随机分布的.随后, Senkov等[52]通过对TaNbHfZrTi高熵合金冷轧后退火再结晶处理, 有效改善了其微观结构, 获得平均晶粒尺寸约为22 $\mu$m的均匀等轴晶, 使其延伸率提升至约10%, 断口形貌观察表明断裂模式以晶间断裂为主. 在此基础上,Juan等[81]通过控制退火温度获得晶粒尺寸分别为38 $\mu$m, 81 $\mu$m和128 $\mu$m的合金. 虽然随着晶粒尺寸的增大, 合金的强度有所降低, 但延伸率进一步增大到20%,并且呈现出一定的晶粒尺寸相关性. 由于BCC相高熵合金塑性变形能力很差, 因此当前针对该型高熵合金塑性变形机理方面的研究较为匮乏.仅有的一些微结构演化也是基于压缩变形后微观表征分析得到的. 图13(a) $\sim\!$图13(c)展示了不同压缩应变时BCC相高熵合金中位错组态形貌[82].小应变时, 变形由局部区域内螺型位错的平面滑移主导,缺陷分布呈现出一定的非均匀性, 可分为包含位错环/偶极子的硬区和未变形的软区.大变形时, 随着软区内位错的激活以及交滑移的发生, 这些区域中的微结构变的较为均匀, 但位错间相互作用也使得湮灭率升高,应变硬化率有所下降, 变形进入局部变形阶段. 最近的研究结果[83]表明, 通过控制位错组态的演化可以同时提升BCC相高熵合金的强度和延展性. Lei等[83]在TiZrHfNb高熵合金中掺杂了2at.%的氧原子, 间隙氧原子导致大量有序结构体的形成, 对位错起到了钉扎和增殖的作用, 从而大大改善了其塑性变形能力, 相关的细节将在下文中关于弥散强韧化中做重点介绍. 此外, BCC相高熵合金还表现出优异的高温力学性能. Eleti等[84-85]在不同高温条件下研究了TaNbHfZrTi高熵合金变形过程中微结构的演化, 如图13(d) $\sim\!$图13(f)所示. 应变导致晶界在迁移过程中隆起, 在高温条件下极易导致在晶界处形成图中所示大量的动态再结晶晶粒, 这将引起变形过程中明显的软化现象. 他们同时指出, 变形过程中再结晶区域内晶界滑移和非再结晶区域内位错滑移共同主导其高温环境下塑性变形的发生[84-85].3.3 密排六方相高熵合金的变形行为
目前制备所得密排六方相合金种类还较少,因此针对该型高熵合金的研究也尚未全面展开.已报道的HCP相高熵合金主要以镧系稀土元素为主,例如YGdTbDy系列高熵合金[86],需要注意的是, 这类合金在晶界处往往存在一些元素富集形成的氧化物,且晶粒内也会弥散分布大量的纳米氧化颗粒[87]. Soler等[87]在YGdTbDyHo高熵合金中切出直径为1.25$\sim$10 $\mu$m的微柱后, 沿[$\bar{{1}}$2$\bar{{1}}$2]方向进行压缩加载,随后根据不同滑移系Schmidt因子计算其开动所需临界剪应力. 结果表明,变形以基面滑移系$\langle$a$\rangle$开动为主, 而且除了尺寸效应会影响材料强度以外,随着直径增大试样内部弥散氧化物的增多, 材料强度也会升高. 此外,Rogal等[88]通过等比例混合4种HCP元素后熔炼铸造制备成HfZrTiSc高熵合金,该合金表现出良好的强塑性匹配度, 应变硬化能力很强, TEM结果表明:在HCP固溶相中, 大量局部滑移带内部存在超高密度的位错,可见位错滑移仍是主要的塑性变形机制. 除了调控元素种类以外,近期的研究结果表明相变诱导塑性(transformation-induced plasticity,TRIP)的发生也能使得面心立方相高熵合金转变成密排六方相[89-90].Bu等[91]采用TEM 原位拉伸加载双相(FCC+HCP)高熵合金试样的方式,原位观察了HCP相内微结构的演变过程. 他们发现, 变形过程中,$\langle$a$\rangle$, $\langle$c$\rangle$甚至$\langle$a+c$\rangle$等多种位错形式同时激活,使得HCP相表现出极好的变形能力, 尤其是非基面滑移$\langle$a+c$\rangle$的比例可达31%,这十分有利于位错双交滑移的发生, 如图14所示. 定量分析HCP相晶格常数后,可得$c/a$比值为1.616, 小于理想HCP晶格常数比值1.633,这表明正是晶格结构参数的变化促进了非基面滑移的开动[91].因此, 他们指出可通过调节晶格参数的比值实现HCP相高熵合金的韧化设计[91],这也为今后高性能高熵合金的设计提供了一个新的思路.图13
新窗口打开|下载原图ZIP|生成PPT图13BCC相TiZrHfNbTa高熵合金不同应变时位错组态形貌以及在不同温度下的晶粒结构演化
Fig. 13Dislocation and grain structures of BCC TiZrHfNbTa during deformation at different strains and temperatures
图14
新窗口打开|下载原图ZIP|生成PPT图14HCP相高熵合金中$\langle$c+a$\rangle$位错引起的双交滑移[91]
Fig. 14Double cross slip of $\langle$c+a$\rangle$ dislocations in the HCP HEA[91]
3.4 多相高熵合金的变形行为
如前所述, 类似于传统金属材料, 单相高熵合金依然很难兼有高强度和良好的延展性.为了解决这一难题, Lu等[92]提出将高强度BCC相和高塑性FCC相结合组成多相高熵合金以获得材料综合性能的大幅提升,这种材料也被称为"共晶'' (eutectic)高熵合金. 随后,Gao等[93]详细地分析了AlCoCrFeNi$_{2.1}$共晶高熵合金的微结构,他们认为FCC相和BCC相在变形时的相互协同作用是材料性能提升的主要原因.软的FCC相通过位错平面滑移和层错变形承担了大部分塑性变形, 硬的BCC相则充当强化相. Wani等[94-95]为了进一步提升该型合金的强度,通过细晶化处理将原本呈层状分布的双相组织变为等轴细晶组织,FCC和BCC相呈随机均匀分布, 材料强度提高了一倍以上, 但却损失了部分延展性.可见, 双相组织的空间分布对共晶合金的性能具有较大的影响.Shi等[96]在此基础上通过恰当的热机械处理,既保持了不同相组织的层状分布, 又在层内形成了亚微米尺寸的细晶组织.图15(a)给出了不同退火温度下所得共晶高熵合金的拉伸应力-应变曲线,可以看出在材料强度大幅提升的同时, 延展性也有所增加.图15(b)清晰地展示了不同应变下材料内部微结构的变化. 由于不同相之间强度的差异,材料在微观尺度上呈现出渐进式屈服的过程, FCC相首先发生塑性变形,可观察到大量位错在界面处塞积, 这些位错的形成对软相也起到强化作用;直到应力达到一定水平时BCC相也发生屈服, 但是如图15(c)所示变形仍主要集中在软相FCC区域. 此外, 如图15(b)中所示,层状结构可以有效阻碍微裂纹的扩展, 这表明分层组织会进一步起到韧化的作用.其他共晶高熵合金还包括由FCC相和Fe$_{2}$Nb型Laves相组成的CoFeNi$_{2}$V$_{0.5}$Nb$_{0.75}$以及CoCrFeNiNb$_{x}$高熵合金[97-98],而且熔融状态共晶合金通常具有更好的流动性、良好的可铸造性,使其具有极大的工业应用价值[92].3.5 亚稳态高熵合金的变形行为
在传统合金领域, 亚稳态相组织的设计思想已广泛应用于高锰钢和钛合金等材料,形变诱导相变的发生能够有效提升材料的塑性变形能力.随着高熵合金的设计逐渐演变为非等原子比组分的混合,调节元素比例可以改变合金中相稳定性和堆垛层错能等, 进而影响到高熵合金塑性变形机制的转变. 基于以上想法,Li等[89]调节Fe$_{80-x}$Mn$_{x}$Co$_{10}$Cr$_{10}$中Mn元素的含量$x$,随着$x$值减小, 合金中FCC相的稳定性也越来越低.高熵合金的塑性变形机制由位错滑移主导过渡到孪晶诱导变形进而转变为相变诱导变形.当$x=30$时, 合金中能够稳定存在FCC和HCP双相组织.图16给出了室温下亚稳态双相高熵合金拉伸变形时,随应变增加内部微结构演化的具体过程. 变形引发的马氏体相变(FCC相$\to$ HCP相)成为主要的微观塑性变形机理. SEM电子隧道衬度成像(electron channelcontrast imaging, ECCI)结果表明,局部变形前FCC相内已经存在大量由Shockley偏位错滑移形成的层错组织,层错叠加进而演化为HCP薄层可作为马氏体相变的成核点,随着变形的继续增大则出现大面积的位移型相变. 双相组织中界面的形成和相变的发生均十分有利于增加应变硬化率,这是因为大量面缺陷的形成可有效减小位错滑移的平均自由程,位错在相界面处塞积引起极大的背应力也会阻碍其他位错的滑移,起到促进加工硬化、延缓局部失稳的作用,所以亚稳态高熵合金通常会表现出强度和延展性的同时增加. 类比于FCC金属,Huang等[99]将这一概念推广到了BCC相高熵合金,借助亚稳态设计思想改善BCC相高熵合金较差的塑性变形能力.他们以铸态Ta$_{x}$HfZrTi高熵合金作为研究对象,改变Ta元素比例以获取BCC相和HCP相组成的亚稳态双相组织高熵合金. 拉伸加载时,虽然屈服强度有所降低, 但相变诱导塑性效应极大地提升了高熵合金的变形能力,延伸率由约4%增大到了约30%.图15
新窗口打开|下载原图ZIP|生成PPT图15双相异质层状(dual-phase heterogeneous laminated, DPHL) 高熵合金的变形行为[96]
Fig. 15Deformation behaviors of dual-phase eutectic HEAs[96]
图16
新窗口打开|下载原图ZIP|生成PPT图16室温下随着应变增加亚稳态高熵合金中相变诱发形变的微观结构演化过程[89]
Fig. 16Microstructure evolution in metastable Fe$_{50}$Mn$_{30}$Co$_{10}$Cr$_{10 }$HEA dominated by transformation-induced plasticity at room temperature[89]
4 高熵合金的强韧化
强度和韧性是评判金属结构材料综合性能的两项重要指标, 但是这两者之间往往并不能兼顾.传统金属中提高材料的强度必将以损失其塑性变形能力作为代价,这也是长期以来影响金属材料发展的一个巨大困扰. 直到近年来,针对高熵合金强韧化的研究工作被广泛开展, 由于元素组分及复杂结构等宽域属性,可调控性也大大增强, 众多强韧化策略的提出甚至可以实现强度和韧性的同时提高.例如上文中提及的层状结构双相细晶组织高熵合金(共晶组织强化)[96]以及亚稳态相变高熵合金(TRIP效应强化)[89]均可达到强塑性的良好匹配,下文中将从其他几个方面进一步综述高熵合金强韧化的研究进展.4.1 固溶强化
传统合金中固溶强化是指将金属或非金属原子融入基体材料原子点阵的间隙或者节点上(可称为置换固溶或者间隙固溶),从而引起晶格畸变, 产生局部应力场, 增大位错滑移阻力而达到强化的目的.稀固溶体中位错滑移与溶质原子相互作用会引起强化现象,但高熵合金中所有原子并没有溶剂、溶质之别, 并且本身晶格畸变程度就较为严重,因此早期认为高熵合金中置换固溶引起的强化作用并不明显[38,77,86,99].但Ding等[33]最近的研究结果表明,高熵合金中通过元素调节可实现固溶强化的显著增强.上文论述高熵合金中严重晶格畸变时, 已经提及CrCoFeNiPd高熵合金中,Pd原子引起的尺寸失配导致的严重晶格畸变以及电负性差异引起的元素富集的共同作用,会使得位错滑移阻力增加[33]. 此外,TEM原位加载观察结果表明, 塑性变形过程中大量位错交滑移得以启动,因此CrCoFeNiPd高熵合金不仅强度提升了一倍,同时还能够保持延展性不降低[33].高熵合金中非金属元素的添加则通常以间隙固溶的方式发挥强化作用,包括C, O, N等元素.Wang等[101]在Fe$_{40.4}$Ni$_{11.3}$Mn$_{34.8}$Al$_{7.5}$Cr$_{6}$高熵合金中添加不同含量的C原子,随着C含量的增加合金的层错能显著降低,位错组态由波浪式滑移转变成以平面滑移为主,形成的大量显微滑移带有利于变形的均匀化, 因而表现出较高的强度和延展性.Chen等[102]在BCC相ZrTiHfNb$_{0.5}$Ta$_{0.5}$高熵合金中添加不同含量的O原子,XRD和TEM测试结果表明其微观组织均匀单一, 但随着O含量增加晶格常数发生改变,这说明O原子溶于晶格点阵中. 相关的力学测试也表明O含量的增加不仅能够提高强度,而且能够改善热稳定性.4.2 细晶强化
根据经典的Hall-Petch公式式中, $d$为晶粒尺寸, $k$为材料常数. Hall-Petch公式表明, 随着晶粒尺寸的减小,材料的强度会升高. 这一理论在传统金属中已经得到了大量的验证,晶界对位错滑移的阻碍作用是根本原因. 高熵合金中晶粒细化也是有效的强化手段.Sun等[103]通过大塑性变形后恰当地控制退火温度可将平均晶粒尺寸减小至约500 nm. 图17(a)所示为不同晶粒尺寸Cantor合金的应力-应变曲线. 但需要注意的是,强度提升的同时细晶高熵合金的延展性已经下降至原始粗晶材料的一半以下,这主要是由小晶粒尺寸位错存储能力降低, 加工硬化能力减弱所造成的.他们进一步研究了不同晶粒尺寸Cantor合金力学性能对环境温度的依赖性[104],如图17(b)所示Hall-Petch公式中常数项随着温度降低而增大, 因此,细晶FCC相高熵合金在低温环境下依然能够获得强塑性的良好匹配[105].另外, Yoshida等[106]等在室温下通过对比研究十余种多主元合金力学性能随晶粒尺寸的变化,定量地给出了不同组分中/高熵合金的Hall-Petch关系式,并指明元素之间相互作用对晶体缺陷移动的阻碍作用是多主元合金一种重要的强化机制,这也是组分差异对合金初始摩擦应力$\sigma_{0}$产生显著影响的主要原因.除了通过热机械处理以外, Seol等[107]在FeCoCrNiMn和Fe$_{40}$Mn$_{40}$Cr$_{10}$Co$_{10}$高熵合金中掺杂B元素来控制晶粒的生长以达到细化效果.B元素易在晶界处偏析, 一方面可有效提升界面强度,另外也能够抑制再结晶晶粒的生长粗化, 综合作用起来可以达到有效强化的同时不造成任何延展性的损失.
图17
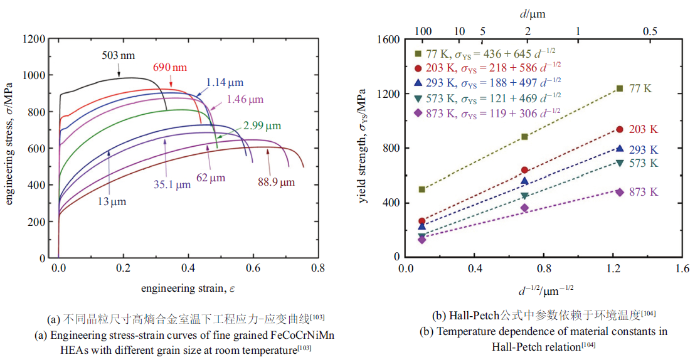新窗口打开|下载原图ZIP|生成PPT图17FCC相高熵合金随晶粒尺寸减小材料强度显著升高
Fig. 17Strengthening of FCC HEA with decreasing of grain size
4.3 第二相强化
利用第二相颗粒阻碍位错的滑移也是传统合金中常用的一种有效强化机制. 近年来,人们将这一思想应用于高熵合金中也取得了众多突出的研究成果.Lei等[83]在BCC相TiZrHfNb高熵合金中掺杂了一定比例的氧原子,不同于传统合金中生成间隙杂质或者脆氧化相而导致材料脆化,高熵合金中化学短程有序效应促使大量有序氧化复合体(ordered oxygencomplex)形成. 相比于TiZrHfNb高熵合金中位错剪切方式以平面滑移为主,有序间隙复合体的生成使得变形过程中位错组态呈现出明显的波浪式,这主要源于弥散分布的有序间隙复合体对位错起到明显的钉扎作用(图18所示),并且能够促进位错交滑移的发生[83]. 因此,含氧高熵合金不仅能够获得强度的显著提升, 同时还表现出很强的加工硬化能力,其拉伸延伸率更高达30%以上. 此外,通过调控高熵合金中元素组分后经恰当的时效处理,可在基体相中引入大量纳米析出相来实现材料的强韧化.He等[108]在FCC相FeCrCoNi合金中添加少量Ti和Al元素后进行热机械处理,成功获得不同种类、大小和空间分布的纳米析出相颗粒.所得(FeCoNiCr)$_{94}$Ti$_{2}$Al$_{4}$高熵合金时效组织中大量弥散着Ni$_{3}$(Ti, Al)型$\gamma'$相, 定量计算表明析出强化与晶界、位错强化等机制共同作用,使得该合金屈服强度超过1 GPa, 同时延伸率仍保持为约17%,但相比于基体材料其延展性的确出现大幅降低.Yang等[109]在最近研究成果中指出,引入韧性多主元金属化合物纳米颗粒能够有效改善GPa级高强合金的强韧性匹配度.他们基于热力学计算提出了一系列析出相强化高熵合金,并系统地分析了其中的(FeCoNi)$_{86}$Al$_{7}$Ti$_{7}$和(FeCoNi)$_{86}$Al$_{8}$Ti$_{6}$.近似球状的析出相颗粒均匀地分散在基体相内, 体积分数可达50%以上,借助第一性原理计算结果确定多主元金属化合物纳米颗粒的组分为(Ni$_{43.3}$Co$_{23.7}$Fe$_{8})_{3}$(Ti$_{14.4}$A$_{l8.6}$Fe$_{2})$,并将其与Ni$_{3}$Al相颗粒高熵合金的压缩性能进行实验对比,其力学性能远胜于脆性的单一相组织颗粒, 可见除了对基体材料变形机制的影响以外,纳米颗粒自身的属性也至关重要. 除此以外, 需要强调的一点是,TEM选区衍射斑点及快速傅里叶转换等结果均表明,多主元纳米颗粒与基体界面上原子排列呈现出高度共格排布状态,点阵失配度仅为0.2%,这也与Liang等[110]利用亚稳态分解促进FCC基体相中低错配度高密度共格析出,实现高熵合金强韧化的设计思想相一致,图19给出了晶粒内部无序的FCC基体相和高度有序的L$_{12}$增强相之间分散的共格界面及其三维分布情况.高度共格的纳米析出相组织对位错的阻碍作用不仅能够起到强化作用,当应力达到一定水平时位错可以切过析出相, 因而不会对塑性变形造成影响.这也是含高密度共格纳米析出相Al$_{0.5}$Cr$_{0.9}$FeNi$_{2.5}$V$_{0.2}$高熵合金在拉伸强度提高至1.9GPa时, 仍能保持一定塑性变形能力的原因.图18
新窗口打开|下载原图ZIP|生成PPT图18BCC相(TiZrHfNb)$_{98}$O$_{2}$高熵合金中间隙氧原子的引入形成大量有序的含氧复合体,能够钉扎可移动位错的滑移,有效改变位错组态[83]
Fig. 18TEM and HRTEM images showing the existence of extensive ordered oxygen complexes in BCC (TiZrHfNb)$_{98}$O$_{2}$ HEA after oxygen doping. These order complexes can act as dislocation pinning to effectively change the dislocation configuration[83]
上述强韧化策略同样也常被应用于传统金属结构材料综合性能的改善,但新型高熵合金则往往表现出更加优异的强韧性匹配度[111-113].这主要是因为高熵合金自身组成的复杂性和多样性易导致微观组织调控时其内部能够形成多层级多尺度的异质结构.Ma和Wu[113]在综合分析现有大量研究成果后从原子尺度到晶粒大小归纳出了5个等级的异构体,包括局部短程有序、密排的空间团簇和复合体、纳米沉淀相、晶内引入的大量缺陷以及多模态晶粒分布等. 在随后的变形过程中,这些微结构的出现不仅能够显著阻碍各种晶格缺陷的移动,并且容易引起非均匀变形的发生, 从而有利于背应力强化和额外硬化的形成,能够促进金属材料强韧性的协同提升[113].
图19
新窗口打开|下载原图ZIP|生成PPT图19Al$_{0.5}$Cr$_{0.9}$FeNi$_{2.5}$V$_{0.2}$高熵合金中的第二相强化[110]
Fig. 19Second phase strengthening in Al$_{0.5}$Cr$_{0.9}$FeNi$_{2.5}$V$_{0.2}$ HEA[110]
5 高熵合金的原子尺度模拟研究
针对高熵合金这一新型金属材料的研究, 不能仅局限于大量实验性研究工作,广泛地开展数值计算及原子尺度模拟工作也是十分必要的,能够帮助我们更加深入地认识和发展新材料.一方面是由于高熵合金自身微结构特征的复杂性,建立相应的原子结构模型能够定量地分析结构特征对材料属性及其性能的影响;另一方面, 这也符合目前新材料设计的趋势, 将实验和数值模拟相结合,以精确的模拟结果指导实验的设计, 打破以往材料设计过程中低效试错法的传统,加速新型高性能结构材料的设计进程, 实现从有目的性设计到实际应用的快速转化.5.1 基于密度泛函理论的第一性原理计算
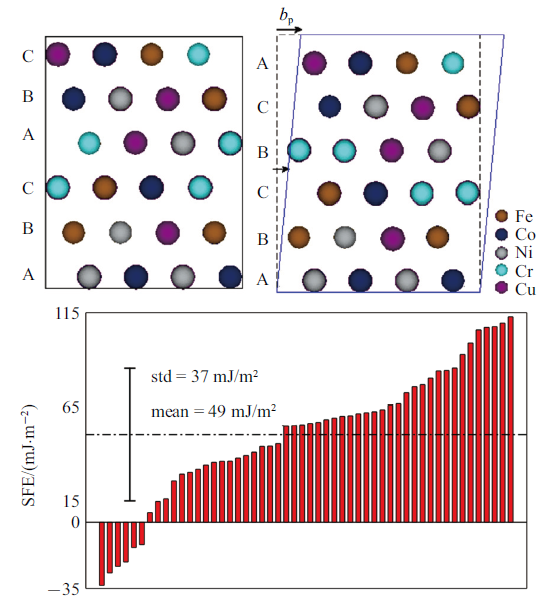
基于密度泛函理论的第一性原理计算是以原子构型做为输入,求解Schrödinger方程来预测材料物理性能(其中包括电子结构、相稳定性、热动力学以及力学性能等)的模拟方法.这一方法被认为是解决多组分合金体系模拟研究的理想方法[114].但当多主元合金的尺寸及组元复杂性增加时计算成本会呈指数式上升,而高熵合金长程化学无序性正是其主要的原子结构特征,因此在计算时需要对局部原子结构进行恰当的统计平均化处理.目前有两种方法用于解决统计抽样的问题: 一种是利用相干势近似(coherentpotential approximation)模拟随机分布的介质;另一种则是重建与真实结构类似的准随机原子结构,两种方法都能取得较为合理的预测结果[115].Liu等[35]在VASP计算过程中选用PAW伪势和Perdew-Wang(1991)进行广义梯度近似处理,研究FeCoNiCrCu高熵合金中原子尺度不均匀性及其堆垛层错能的分布范围. 结果表明,高熵合金中各原子对之间键长满足高斯分布;并且多组计算结果表明层错能并非一个定值而是分布在一个较宽的区间之内,如图20所示. 这也就能在一定程度上解释实验中观察到不同塑性机制的现象.Ding等[30]则是在建立特殊准随机结构(specialquasi-random structure, SQS)以后采用 MonteCarlo方法模拟研究了多主元合金CrCoNi中局部化学有序结构的本质及其形成对材料堆垛层错能的影响,这些微结构的存在会造成材料塑性变形机理的转变, 从而影响到材料的力学性能.Zhang等[115]基于第一性原理计算方法进一步研究了环境温度及局部原子特征(如价电子数、d电子密度等)导致高熵合金中层错能表现为负值的原因,并分析了这一现象对变形过程中孪晶及相变等机制形成的影响. 可见,第一性原理计算能够帮助我们从原子尺度解析结构对材料属性及性能的影响,并且往往都会归结于对变形机理的作用,因而十分有利于我们更加清晰地解读"组分-结构-性能"三者之间的关系.5.2 分子动力学模拟高熵合金的变形行为
第一性原理计算虽然计算精度较高, 但受计算规模和成本的限制,并不适用于大尺度模型的建立.研究材料变形过程中缺陷成核及其演化最直接的方法依然是建立分子动力学原子模型(moleculardynamic simulation, MD), 在更大规模和时间跨度上进行模拟分析.MD模拟的精度及效率很大程度上取决于计算原子能量及力场时所选取的用于描述原子间相互作用的势函数,这也是目前在建立高熵合金MD模型时面临的最大问题[114].高熵合金中元素种类较多,但现有的势函数中仅有少数几种能够用于描述三元合金之间的相互作用.Sharma等[116]最早将三元镶嵌原子方法(embedded atom method, EAM)势函数和Lennard-Jones势函数结合用于研究五元Al$_{0.1}$CrCoFeNi高熵合金中元素非均匀性分布及其对力学性能的影响.Li等[29]将所预测物理属性与实验及密度泛函理论计算所得数据进行了详细对比,发展出一种可用于描述CoCrNi三元合金中原子相互作用的EAM势函数,并用于分析多主元合金中化学短程有序结构对变形过程位错线滑移的作用.如图21所示, 深棕色区域代表Cr-Co成键较多的有序区域,绿色线圈标注的区域为位错线切过短程有序微区后滑移扫过的面积,对应图21(a)中两个时间间隔内红色区域标注的位错扫过的区域,该过程具体地描述了多主元合金中局部化学有序原子微区对可移动位错滑移的有效阻碍作用,因而也可以更加具象地理解这些微结构所起到的强化作用.为了能够模拟更复杂元素组分的高熵合金,Choi等[117]指出MD模拟时至少需要包含多主元合金体系中所有二元相互作用的势函数.根据这一研究思路, 他们提出了第二近邻改进型EAM势形式(second nearest-neighbormodified EAM potential formalism),并将其用于Cantor合金在低温下迟滞扩散效应及形变孪晶形成原因的研究工作.除了构建精确的原子相互作用势以外,Wang等[118]提出了一种介原子分子动力学模拟方法(meta-atom MD method)用于多主元合金的原子尺度模拟.他们认为一种合金的力学性能主要取决于几种材料参数,例如晶格常数、表面能、内禀/外禀层错能、弹性模量,升华能以及孔洞形成能等[118].一旦这一整套材料常数被设定,那么拥有同一参数设置的两个合金体系也会表现出相同的力学性能和变形行为[118].基于这一假设, 介原子之间相互作用仅需用一种原子间势函数来表示,引入一个比例因子后可以调整局部晶格畸变的严重程度[118],根据第一性原理计算结果拟合的整套材料参数可以用于多主元合金力学行为的模拟研究.这一新方法目前已被用于研究复杂合金体系(如TWIP钢)中形变孪生对材料塑性变形行为的影响[117].同时, Wang等[119]在拟合Cantor合金的材料参数后,研究了高熵合金中严重晶格畸变对可移动位错滑移的影响. 此外,还有****提出可以通过机器学习推动多主元势函数的发展; 同时,人工神经网络势函数也被认为有望用于多主元合金的模拟研究工作[114].图20
新窗口打开|下载原图ZIP|生成PPT图20基于密度泛函理论计算所得高熵合金堆垛层错能的分布范围[35]
Fig. 20Initial simulated HEA for calculation based on density functional theory, the generation of one layer fault by forced shift between two neighboring layers during calculation, and the calculated stacking fault energy of FeCoNiCrCu from 52 models[35]
图21
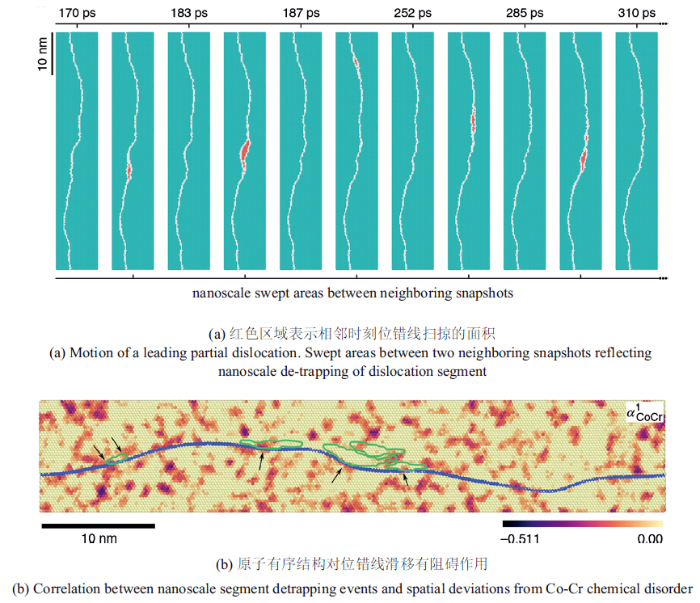新窗口打开|下载原图ZIP|生成PPT图21分子动力学模型模拟CrCoNi合金中受短程有序结构影响位错线滑移过程中形貌演化的过程[29]
Fig. 21MD simulations revealing dislocation line morphology evolution in simple solid solution NiCoCr alloy with short-range-order domains[29]
6 高熵合金研究中挑战及展望
由以上综述可见,高熵合金概念的提出的确为人们研究设计新型高性能金属结构材料指明了新方向,众多优异性能及新机制的发现不断地推动着这一研究领域的快速发展和进步. 同时,有****指出高熵合金已由第一代合金体系中等原子比设计理念,发展为第二代非等原子比亚稳态组织的全新设计思路. 即便如此,目前所研究高熵合金中组成元素仅局限于特定的几类元素,远远少于自然界中可用元素的种类,并且当前研究的多主元合金体系中主元种类多数情况下不超过5种元素. 因此,当前诸多突出研究成果的呈现也只是揭开了高熵合金的冰山一角,这个材料宝库为我们研发设计高性能合金材料提供了广阔的研究空间和无尽的可能及惊喜,我们仍需从不同的角度积极开展大量的研究探索工作.6.1 确定多主元合金相组分的有效准则
大量实验研究表明高熵合金中相组分是影响材料性能的主要因素,在固化过程中固溶相与金属间化合物的形成存在着激烈的竞争.目前用于预测高熵合金中组成相的方法主要包括以下两种:根据组成元素自身属性的差异定义了多种不同的物理变量,例如平均原子尺寸失配度$\delta $、价电子浓度VEC、电负性$\chi$、原子间距失配因子$s_{m}$、平均模量失配因子$K_{m}$等等,通过大量数据的定量对比总结这些变量与高熵合金中所形成相之间的关系,总结出判断准则用于新材料的设计; 另一种方法则是通过热动力学计算相图的方式,即计算体系最小自由能来判断合金中组成相的类别, 但不同于二元或三元体系,由于高熵合金组元结构的复杂性所得热力学计算预测结果往往与实验验证结果相差甚远.前一种方法中, 随着合金体系中元素种类的增多,有效判定组成相所需的物理变量个数也逐渐增加.多个物理变量形成多重准则共同判定并给出一个合金体系能够形成单一或多相固溶组织的概率,这样会更加准确地预测多元合金中组成相的种类,并且该方法可采用机器学习的手段进行物理变量与相组成之间关系的梳理,从而能够用于判定更复杂体系多主元合金的相组分.6.2 高通量方法筛选设计实用新型高熵合金
做为一种非常具有潜在应用价值的新型金属结构材料, 新的高熵合金体系在不断更新,我们亟需一种高通量筛选策略来帮助快速确定适用于不同应用环境的最佳合金材料.众所周知,金属结构材料往往需要同时满足安全性、耐用性以及经济性等多方面的要求,因此综合性能良好的合金材料是必然的选择.然而不同体系的高熵合金往往仅占有某几方面的性能优势, 若基于建立的合金材料库,并遵从一项性能缺失即代表该合金失去实用价值的原则逐层筛选,将有望加速推进新型高性能高熵合金的实际工程应用. 逐层筛选的策略可分步实施,例如, 第一步根据热动力学计算或相组成判定准则确定所需合金体系的微观结构;第二步, 控制合金组分梯度变化, 评价组分变化对材料性能的影响; 第三步,固定材料组分, 控制微观结构改变, 确认最佳合金材料.逐层筛选可大大缩减需要评价材料的种类, 减少工作量, 提升效率.目前仍面临的一个严重问题是缺乏用于结构材料性能评价的高通量实验方法.传统的测试方法过于耗时, 需要提出新方法来加速性能评价的实施.6.3 建立高效的多主元赝势在原子尺度模拟研究多主元合金
此前通过基于密度泛函理论第一性原理计算以及一定规模MD模拟,对多主元高熵合金中原子结构对材料属性及其性能的影响有了初步的认知,但受限于前者模拟计算的规模仅为数百个原子,及经典EAM势函数在高熵合金MD模拟中的可靠性有待进一步验证,并没有开展大规模原子尺度模拟其动态过程, 以揭示微结构与性能关联的微观机制.要突破高熵合金大规模分子动力学模拟的瓶颈,亟需提出兼顾高效与高精度的新赝势构建方法以及跨尺度模拟新方法. 近年来,得益于高通量第一性原理计算及机器学习方法的发展,基于神经网络和支持向量机的赝势已取得部分进展,在保证第一性原理计算精度的同时将计算效率提升了两个量级,但仍与EAM势的计算效率相差甚远. 这一方面的工作仍需进一步推进,希望新赝势的提出有助于大规模MD模型的构筑,从而在原子尺度理清结构与性能之间的关联, 有目的性地指导新合金的设计.7 结束语
从新概念的提出至今, 新型高熵合金的发展历程中存在诸多争议,但同时也是硕果累累. 多主元组分造成原子结构的特殊性,进而激发多重微观机制的共同作用,表现在宏观行为上则为各项优异力学性能的集中体现. 不仅如此,在原子尺度上高熵合金中不同元素掺杂易引起的原子结构改变或者热机械处理导致的元素析出及微结构演化等,均能有效改善材料的综合力学性能,并且多主元特性使得高熵合金表现出极强的可设计性. 可见,高熵合金不仅极大地拓展了新型合金的开发空间,也为突破传统合金性能极限提供了可能. 但是, 我们也必须认识到一点,正是因为该新型合金的复杂性, 我们对它的研究正处于初始阶段,材料和力学领域的****们仍需要从不同的角度着手开展大量的研究工作,既要深化基础研究又要努力推进新型结构材料的应用. 在基础研究方面,除了广泛开展实验研究以外, 需要逐步加强数值计算及模拟研究工作,力求以数值结果有目标性地指导新型材料的设计与研发; 实际应用方面,基于现有高熵合金所具有的优异性能,为特殊环境下工程应用所需先进材料提供有力的支撑.不同方面同步进行以推动这一新型先进结构材料的快速发展.参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 7]
[本文引用: 5]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 10]
[本文引用: 1]
[本文引用: 6]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 6]
[本文引用: 4]
[本文引用: 1]
[本文引用: 4]
[本文引用: 5]
[本文引用: 2]
[本文引用: 4]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 3]
[本文引用: 1]
[本文引用: 2]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
[Master Thesis].
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 4]
[本文引用: 1]
[本文引用: 2]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 4]
[本文引用: 2]
[本文引用: 1]
[本文引用: 4]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 4]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 6]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 5]
[本文引用: 1]
[本文引用: 5]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 4]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
[本文引用: 3]
[本文引用: 3]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 4]
[本文引用: 1]
