刘林^*, 姚仰平^?, 张旭辉^,*,2), 鲁晓兵^*,**, 王淑云^** 中国科学院力学研究所,北京 100190
? 北京航空航天大学交通科学与工程学院,北京 100191
** 中国科学院大学工程科学学院,北京 100049

AN ELASTOPLASTIC CONSTITUTIVE MODEL FOR GAS HYDRATE-BEARING SEDIMENTS ¹⁾

Liu Lin^*, Yao Yangping^?, Zhang Xuhui^,*,2), Lu Xiaobing^*,**, Wang Shuyun^* * Institute of Mechanics, Chinese Academy of Sciences,Beijing 100190,China
? School of Transportation Science and Engineering, Beihang University, Beijing 100191,China
** University of Chinese Academy of Science, School of Engineering Science, Beijing 100049, China

通讯作者: 2)张旭辉,副研究员,主要从事非常规油气开发中的关键力学问题研究.E-mail:zhangxuhui@imech.ac.cn

收稿日期:2019-07-14接受日期:2019-09-2网络出版日期:2020-03-18

基金资助:

1)国家自然科学基金项目.11872365 中国地质调查局项目.DD20190221

Received:2019-07-14Accepted:2019-09-2Online:2020-03-18
作者简介 About authors


摘要
土的密度对其力学特性具有明显影响.水合物以一种固相赋存于沉积物的孔隙中,使得水合物的含量和其赋存形式都会影响含水合物沉积物(GHBS)的密度,因此在研究和描述含水合物沉积物的力学性质时应考虑水合物含量和赋存形式对其密度的影响.本文基于黏土和砂土统一的本构模型(CSUH模型),首先建立水合物体积分数与压硬性参量的关系式来反映水合物对沉积物压缩规律的影响.其次,为了合理考虑水合物含量和赋存形式对沉积物密度的影响,建立了可以描述有效初始孔隙的计算式,并将其引入到状态参量中来描述水合物对沉积物剪胀性和峰值强度的影响.最后,结合CSUH模型中水滴形屈服面,建立了一个含水合物沉积物的弹塑性本构模型.通过与室内试验结果比较,验证了该模型不仅能够合理地描述不同赋存形式、不同水合物含量下含水合物沉积物的应力应变关系,而且在描述具有相同赋存形式含水合物沉积物的力学特性时,不同的水合物含量只需采用一组参数.
关键词： 含水合物沉积物;应力应变关系;赋存形式;水合物含量

Abstract
The density is one of the most important factors for the mechanical behavior of soil. The content and occurrence modes of hydrates obviously affect the density of gas hydrate-bearing sediments (GHBS) because hydrates exist in the pore of sediment as solid phase. Therefore, it is necessary to consider the effect of the hydrate content and occurrences to describe the mechanical properties of hydrate sediments well. In this paper,based on the unified hardening model for clays and sands (CSUH model), the relation between the volume fraction of hydrate and the compressive hardness parameter is firstly established to reflect the influence of hydrate on the compressibility of sediments. Secondly, in order to consider the influence of hydrate content and occurrence modes on sediment density, we propose a formula to describe the effective initial void ratio, and it is then introduced into the state parameter to describe the influence of hydrate on dilatancy of sediment. Finally, combining the drop-shaped yield surface of the CSUH model, an elastoplastic constitutive model for GHBS is developed. Compared with the laboratory test results, it is verified that the model can reasonably describe the mechanical behaviors of GHBS containing hydrates with different occurrence modes and contents. For the same occurrence mode but different contents, the set of parameters is the same.
Keywords：gas hydrate-bearing sediments;stress-strain relation;occurrence mode;hydrate content


PDF (10509KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
刘林, 姚仰平, 张旭辉, 鲁晓兵, 王淑云. 含水合物沉积物的弹塑性本构模型 ¹⁾. 力学学报[J], 2020, 52(2): 556-566 DOI:10.6052/0459-1879-19-184
Liu Lin, Yao Yangping, Zhang Xuhui, Lu Xiaobing, Wang Shuyun. AN ELASTOPLASTIC CONSTITUTIVE MODEL FOR GAS HYDRATE-BEARING SEDIMENTS ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(2): 556-566 DOI:10.6052/0459-1879-19-184

引言

自然界中水合物大都分布于深海和永久冻土区,其力学特性相当复杂.为了能高效开采水合物,减少甚至杜绝工程事故,在进行开采前应对含水合物沉积物的力学特性进行充分了解,并建立合理的理论模型进行模拟.因此,国内外****对含水合物沉积物力学性质及本构模型的研究非常重视^[1-3].

现阶段,一些****已经从不同的角度出发提出了许多含水合物沉积物的本构模型,包括弹性模型^[4-7]和弹塑性模型^[8-14].以上模型主要基于考虑水合物的胶结作用或含水合物沉积物的结构性衰减等方面来进行建模.然而,水合物作为一种固相,其含量和赋存形式明显影响含水合物沉积物的密度.土的密度和围压又是影响其力学性质的关键因素,因此在建立含水合物沉积物的本构模型时,应首先着重考虑水合物含量和赋存形式对含水合物沉积物密度的影响.此外,除了其密度和围压,不含水合物的沉积物的力学性质对含水合物沉积物的力学特性也具有重要的影响,因此在建立含水合物沉积物的本构模型时,选取合理的沉积物本构模型作为基础模型至关重要.

近几年,姚仰平等^[15-18]基于临界状态土力学,通过从等向压缩特性、临界状态特性以及剪胀特性等三方面对黏土和砂土的异同性进行了分析,并将这些异同性均用相应的统一表达式进行描述,建立了黏土和砂土统一的本构模型,即CSUH模型. 该模型相较于修正剑桥模型只增加了3个参数,且均有明确的物理意义.对于砂土,该模型能够合理地描述密砂的剪胀及应变软化,松砂的剪缩及应变硬化,特别是松砂的静态液化现象.对于黏土,模型增加的3个参数均为零, CSUH模型可以完全退回到统一硬化UH模型^[19-21]来描述超固结黏土的剪胀及应变软化,且可以进一步退回到修正剑桥模型来描述正常固结黏土的力学特性.鉴于此,本文首先基于CSUH模型中正常压缩线的表达式,建立了水合物含量指标与压硬性参数的关系式来反映水合物对沉积物压缩特性的影响.其次,建立了不同水合物赋存形式、不同水合物含量下的有效初始孔隙比计算式,并将该有效初始孔隙比引入到状态参量中,通过特征状态应力比来反应水合物对沉积物剪胀性的影响,通过潜在强度应力比来反映水合物对沉积物抗剪强度的影响.最后,结合CSUH模型中水滴形屈服面,建立了一个可以描述水合物含量不同、赋存形式不同的含水合物沉积物弹塑性本构模型,该模型不考虑温度作用下的相变特性.

1 含水合物沉积物的力学特性

1.1 等向压缩特性

Tan^[22] 对 Hydrate ridge的含水合物沉积物进行了一系列的一维压缩试验,试验结果如图1 所示.从试验结果中可以总结得到含水合物沉积物压缩线的两个基本特征：

(1) 在 $e$-lg$p$空间内,当应力较小时压缩线较平缓,随着应力的逐渐增大,压缩线的斜率也逐渐增大.当应力增大到一定程度,压缩线的斜率近似不变.这种变化规律与粒状土压缩线的变化规律相似.之所以粒状土压缩线具有这种变化规律,是因为当应力较小时,颗粒几乎不会发生破碎,土体变形主要由颗粒重新排列引起.随着应力的增大,颗粒破碎逐渐增多,当达到其相应的破碎应力时,土体由颗粒重新排列为主转变为颗粒破碎为主^[23-27].本文将沉积物中水合物看作为另一种固体粒状物质,沉积物是水合物颗粒与土颗粒的混合物.所以可以推断粒状土的受力机理同样适用于没有胶结作用的含水合物沉积物,即水合物和土颗粒的破碎造成含水合物沉积物的压缩线具有这种变化规律.对于具有胶结作用的含水合物沉积物,胶结作用使得沉积物具有一定的结构性,而随着压力的增大,结构性发生破坏,同样形成了类似的压缩线.

(2) 对不同初始孔隙比的含水合物沉积物进行压缩,在围压较大时,压缩线会出现两种情况,一种是压缩线与压缩线会逐渐重合,如图1 中蓝线所示,另一种是压缩线与压缩线会逐渐平行,如图1 中红线和蓝线所示.

图1

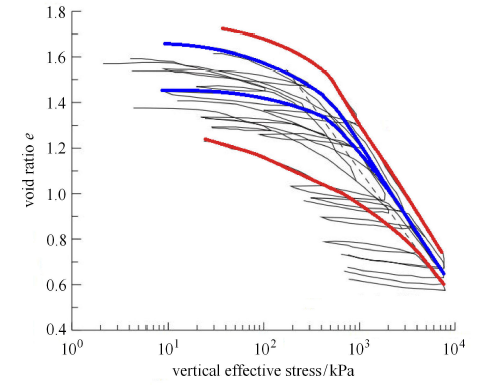新窗口打开|下载原图ZIP|生成PPT
图1含水合物沉积物的一维压缩试验线^[22]

Fig. 1One-dimensional compression line of GHBS^[22]



基于以上一维压缩特性,假设不含水合物沉积物的状态称为初始状态,在不含水合物的沉积物孔隙中填充了相应的固体颗粒被称为加密状态,如图2 所示. 加密状态中,状态A是指在不含水合物的沉积物的孔隙中填充了较小的沉积物颗粒. 状态B是指在不含水合物的沉积物中填充了与状态A 相同体积的水合物.状态C 是指含有与状态A 和B相同体积的水合物,但是水合物对土颗粒具有胶结作用. 由于3种状态(A, B 和C)填充的体积相等,因此图中加密状态的孔隙比也相同.

图2

新窗口打开|下载原图ZIP|生成PPT
图2含水合物沉积物的细观示意图

Fig. 2Microscopic sketch of GHBS



如果分别从初始状态和加密状态出发进行等向压缩,得到的等向压缩线ICL示意图如图3 所示. 图中ICL$_{0}$ 表示不含填充物质的沉积物的等向压缩线,ICL$_{\rm A}$, ICL$_{\rm B}$和ICL$_{\rm C}$ 分别指填充砂或水合物后的等向压缩线. 由于状态A和初始状态的固相相同,所以即使初始孔隙比不同,随着压力的增大,等向压缩线也会趋于重合,如图3 中ICL$_{0}$ 和ICL$_{\rm A}$.然而,水合物力学性质与冰的相近,说明与砂土颗粒相比,水合物更容易破碎,即水合物的破碎应力偏小,因此初始密度相同的情况下,水合物与砂土混合体的破碎应力比纯砂的破碎应力小,所以含水合物沉积物的破碎应力($p_{\rm sB}$) 小于纯砂的破碎应力($p_{\rm sA})$,如图3中蓝实线和黑实线所示.如果水合物具有胶结作用,则使得沉积物会具有一定的结构性,此时其破碎应力会大于无胶结作用的破碎应力,即$p_{\rm sB} < p_{\rm sC}$,而$p_{\rm sC}$ 与$p_{\rm sA}$的大小关系取决于胶结作用的强弱.

图3

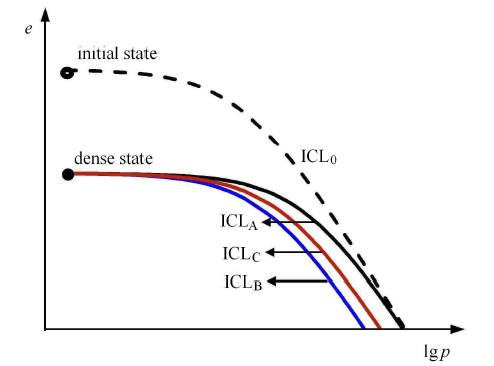新窗口打开|下载原图ZIP|生成PPT
图3沉积物的等向压缩线示意图

Fig. 3Schematic diagram of isotropic compression lines of GHBS

1.2 含水合物沉积物的剪切特性

Masui 等^[28]分别采用两种不同的制样方法对含水合物的沉积物进行了常规三轴排水试验,得出两种水合物饱和度几乎相同的试样,其抗剪强度不同主要是因为试样的密度不同.因此与粒状土类似,含水合物沉积物的密度对其力学特性的影响不容忽视.另外,Soga 等^[29] 通过分析该试验结果,还得出了以下几点结论：

(1)随着水合物含量的增大,含水合物沉积物的内摩擦角和泊松比均没有明显变化.

(2)含水合物沉积物的刚度 (弹性模量)会随着水合物饱和度的增大而增大.

(3)胶结模式下水合物对沉积物力学特性的影响比填充模式下明显,尤其是水合物饱和度较小时.

(4)随着饱和度的增大,含水合物沉积物会表现出应变软化现象和剪胀特性.

2 本构模型的建立

2.1 正常压缩线NCL

等向压缩线是土体在没有剪应力作用下的应力应变关系曲线,其受初始密度或超固结度的影响.然而,不论是黏土还是粒状土均存在一条特殊的等向压缩线,这条线在剑桥模型中为正常固结土的等向压缩线,称为正常压缩线NCL.水合物沉积物作为水合物与土体的混合物,假设其也存在一条特殊的等向压缩线.在众多土的本构模型中,NCL常被选取作为参考线,因此合理地描述NCL是建立含水合物沉积物本构模型的核心之一.

在CSUH 模型(黏土和砂土统一的UH 模型) ^[15]中,利用了破碎应力的概念,提出了砂土NCL 表达式,其形式简单,所用参数物理意义明确. 因此本文利用CSUH 模型中砂土的NCL表达式来描述含水合物沉积物的NCL,表达式为

(1)$ e = Z - \lambda \ln \left( {\dfrac{p + p_{\rm s} }{1 + p_{\rm s} }} \right)$
式中, $\lambda $ 为NCL在$e - ln p$空间内渐近线的斜率,如图4 所示;$Z$ 为NCL 上$p =1$ kPa时 对应的孔隙比; $p_{\rm s} $ 为NCL 在$e - \ln p$空间内曲率最小时所对应的应力,即NCL 上的破碎应力.从图4中可以看出,当$p < p_{\rm s} $ 时,NCL 非常平缓,当$p= p_{\rm s} $ 时,NCL 开始变陡,当$p > p_{\rm s} $ 时,NCL逐渐趋向于渐近线.

图4

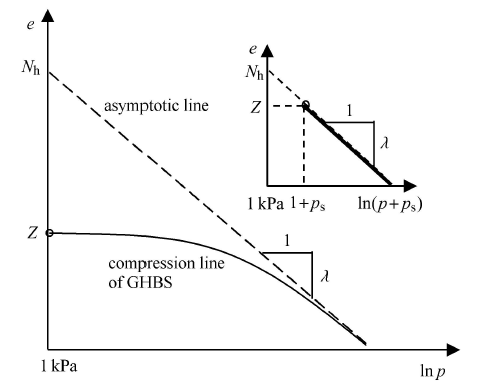新窗口打开|下载原图ZIP|生成PPT
图4水合物沉积物的正常压缩线示意图

Fig. 4Normal compression line of GHBS



压缩线的渐近线可以表示为

(2) $e = N_{\rm h} - \lambda \ln \left( {\dfrac{p}{1}} \right)$
式中,$N_{\rm h} $ 为渐近线上$p = 1$ kPa 时所对应的孔隙比.通过渐近线与NCL 在$p$ 较大时重合的关系,可以得出$p_{\rm s} $的表达式为

(3) $p_{\rm s} = \exp \left( {\dfrac{N_{\rm h} - Z}{\lambda }} \right) - 1$
通过式(3) 可知,当参数$Z$ 与$\lambda $ 不变时$p_{\rm s} $与$N_{\rm h}$ 具有一一对应关系. 1.1节已经指出$p_{\rm s} $受水合物含量的影响,由于没有完整的试验数据可以反映其影响规律,本文假设$N_{\rm h}$ 与水合物体积分数$\theta $ 满足简单的线性插值关系

(4)$ N_{\rm h} = N_0 \left( {1 - \theta } \right) + N_1 \theta $
式中,$N_{0}$为不含水合物沉积物的等向压缩线渐近线的纵轴截距,$N_{1}$是纯水合物颗粒的等向压缩线渐近线的纵轴截距, $\theta $为水合物体积分数,计算式为

(5) $\theta = \dfrac{v_{\rm h} }{v_{\rm h} + v_{\rm s} } = \dfrac{S_{\rm h} e_0 }{1 + e_0 S_{\rm h} }$
式中,$v_{\rm h} $ 为水合物的体积含量,$v_{\rm s} $为土颗粒的体积含量,$S_{\rm h} $ 为含水合物饱和度,$e_0 $为不含水合物的沉积物孔隙比. 从式(4) 中可以看出,当$\theta =0$时,沉积 物不含水合物,$N_{\rm h}=N_{0}$,当$\theta =1$时,$N_{\rm h}=N_{1}$. 因此即使初始孔隙比不同,只要水合物体积分数$\theta $ 相等,等向压缩线最终也会逐渐重合.

2.2 屈服函数

粒状材料易发生破碎,尤其是在剪应力作用下.颗粒破碎的作用使得粒状材料在应力比越大时屈服越快,因此许多研究者认为粒状材料的屈服面并非椭圆形. 姚仰平等^{[15- 18]}在椭圆屈服面的基础上,通过考虑粒状土的临界状态特性,提出水滴形屈服面,屈服函数为

(6)$ f = \dfrac{\left( {1 + \chi } \right)q^2}{M^2p^2 - \chi q^2} + 1 - \dfrac{p_x }{p} = 0$
式中,$M$ 为临界状态应力比. $p_{ x}$ 为屈服面与$p$轴相交所对应的平均正应力,如图5所示. $\chi $被称为临界状态参数,反应了材料破碎的难易程度.当材料易被剪碎时,达到临界状态时产生的变形较大,对应正常压缩线与临界状态线(CSL)之间的距离较大,此时屈服面在 应力比较大时就更加扁平,如图5 所示.

图5

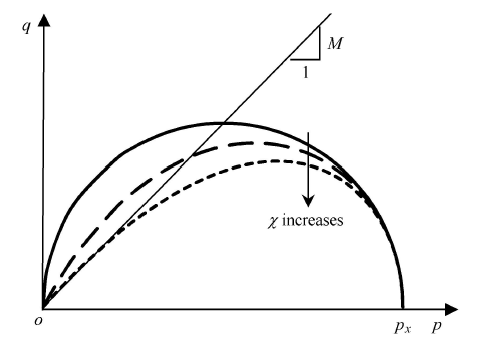新窗口打开|下载原图ZIP|生成PPT
图5水滴形屈服面

Fig. 5Drop-shaped yield surfaces



通过正常固结土的等向压缩应力应变关系可以得出式(6)中的$p_x $ 的表达式为

(7)$ p_x = \left( {p_{x0} + p_{\rm s} } \right)\exp \left( {\dfrac{\varepsilon _{\rm v}^{\rm p} }{c_{\rm p} }} \right) - p_{\rm s}$
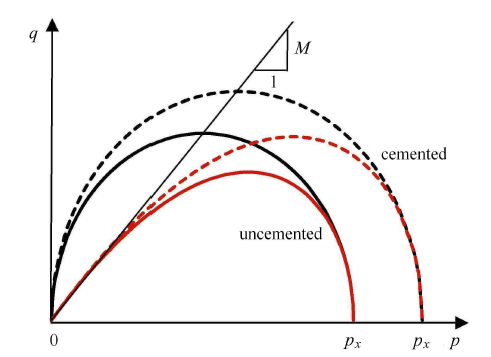
式中,$p_{x0} $ 为屈服面与$p$ 轴的初始交点所对应平均正应力.$c_{\rm p} = \left( {\lambda -\kappa } \right) / \left( {1 + e_{{\rm h}0} } \right) $. 由于水合物含量不同,赋存 形式不同,$p_{\rm s} $ 不同,则$p_x$ 不同,造成屈服面大小不同,见图6 所示.

图6

新窗口打开|下载原图ZIP|生成PPT
图6有胶结作用和无胶结作用下含水合物沉积物的屈服面

Fig. 6Yield surfaces of GHBS with and without cementation



将式(7) 代入 式(6),并用姚仰平等^[19]提出的硬化参数$H$ 直接代替塑性体积应变可得到

(8)$f = \ln \left[ {\left( {1 + \dfrac{\left( {1 + \chi } \right)q^2}{M^2p^2 - \chi q^2}} \right)p + p_{\rm s} } \right] -\\ \qquad \ln \left( {p_{x0} + p_{\rm s} } \right) - \dfrac{H}{c_{\rm p} } = 0$
式中,$H$ 为硬化参数,其增量可表示为

(9)$ d H = \dfrac{M_{\rm f}^4 - \eta ^4}{M_{\rm c}^4 - \eta ^4}d \varepsilon _{\rm v}^{\rm p}$
式中,$M_{\rm f} $ 为含水合物沉积物的潜在破坏强度,可表示为

(10)$ M_{\rm f} = 6\left[ {\sqrt {\dfrac{12\left( {3 - M} \right)}{M^2}\exp \left( { - \dfrac{\xi }{\lambda - \kappa }} \right) + 1} + 1} \right]^{ - 1}$
$M_{\rm c}$ 为含水合物沉积物的特征状态应力比,当$\eta = M_{\rm c} $时达到含水合物沉积物的特征状态(由剪缩转换到剪胀时所对应的点).因此$M_{\rm c} $越小,在剪切过程中越快达到特征状态,具体演化规律见文献^[18].$M_{\rm c} $ 的表达式为

(11)$ M_{\rm c} = M \cdot \exp \left( { - m \cdot \xi } \right)$
式中,$m$ 为特征状态参数,控制着特征状态应力比的演化速度. $\xi $ 为状态参数,详细介绍见下文.

2.3 状态参数

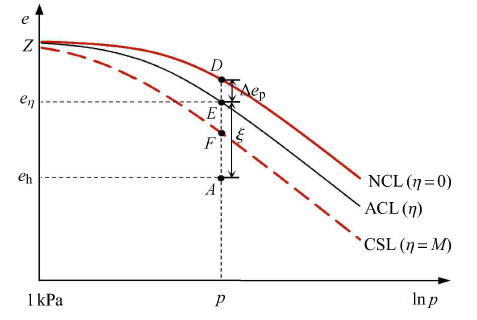
粒状材料的密度对其力学性质有很大的影响,而在本构模型中引入表示当前状态的指标,能够合理地描述粒状材料剪胀剪缩特性.因此,国内外****先后提出了许多这类指标,其中最经典的是Been等^[30] 提出的状态参数$\psi $.该状态参数被定义为当前孔隙比与临界状态线上当前应力所对应的孔隙比之差,其形式简单,应用方便.然而,状态参数$\psi $以临界状态线为参考线,因此应用它不能合理地描述材料的等向压缩和一维压缩力学特性^[31].为了能够合理地描述含水合物沉积物的等向压缩、一维压缩以及剪切特性,本文采用状态参数$\xi$,其表达式为

(12)$ \xi = e_\eta - e_{\rm h}$
式中,$e_\eta $为含水合物沉积物的等应力比线上当前应力所对应的孔隙比,如图7中点$E$ 所对应的孔隙比;$e_{\rm h} $为含水合物沉积物的当前孔隙比,如图7 中点$A$ 所对应的孔隙比.

图7

新窗口打开|下载原图ZIP|生成PPT
图7状态参数的示意图

Fig. 7Schematic diagram of state parameter $\xi $



从图7 中可以看出,点$E$ 的孔隙比可以由点$D$的孔隙比减去$DE$ 之间的竖向距离得到. 其中点$D$ 位于NCL上,所 以点$D$ 的状态代表正常压缩状态,可以根据式(1) 得到.而$DE$ 的竖向距离是指试样从点$D$ (应力比$\eta = 0$)出发进行等$p$ 剪切到点$E$ (应力比$\eta $)所形成的孔隙比变化. 根据屈服函数,可以得出$\Delta e_{\rm p} $的计算式为

(13)$ \Delta e_{\rm p} = \left( {\lambda - \kappa } \right)\ln \left[ {\dfrac{\left( {\dfrac{M^2 + \eta ^2}{M^2 - \chi \eta ^2}} \right)p + p_{\rm s} }{p + p_{\rm s} }} \right]$
结合式(1) 与式(13) 可以求得$e_\eta $ 的计算式为

(14)$ e_\eta = Z - \lambda \ln \left( {\dfrac{p + p_{\rm s} }{1 + p_{\rm s} }} \right) - \left( {\lambda - \kappa } \right)\ln \left[ {\dfrac{\left( {\dfrac{M^2 + \eta ^2}{M^2 - \chi \eta ^2}} \right)p + p_{\rm s} }{p + p_{\rm s} }} \right]$
$e_{\rm h} $ 的 计算式为

(15)$ e_{\rm h} = e_{\rm h0} + \int d e{\rm h}$
式中,$e_{\rm h0} $ 是指含水合物沉积物的初始孔隙比.

土体的密度对其力学特性具有较大的影响,以砂土为例,松砂具有应变硬化和体积剪缩特性,而密砂具有应变软化和体积剪胀特性^[32]. 含水合物沉积物实际是由沉积物颗粒、水合物晶体及孔隙水组成的混合物. 许多文献表明纯水合物具有明显的抗压和抗剪强度,因此可以将水合物看作为土体中另一种固相. 根据土孔隙比的定义,对于非悬浮形式的含水合物沉积物,其孔隙比应该随着水合物这一固相含量的增大而减小.

研究表明,水合物在沉积物孔隙中的赋存模式不同,主要分为胶结模式和填充模式(包含悬浮模式和持力模式). 对于胶结模式,水合物不仅有胶结作用,而且水合物粘结在土颗粒上,起到了骨架作用,因此随着水合物饱和度的增大,沉积物的密度会逐渐增大. 如果水合物仅仅是填充在沉积物孔隙中,没有粘结在土颗粒上,随着水合物饱和度的增大,水合物的赋存模式会由悬浮模式逐渐转变为持力模式. 悬浮模式下水合物不充当骨架作用,因此水合物加入对沉积物的密度没有影响. 持力模式下水合物和土颗粒共同充当了骨架作用,因此水合物的加入会使原来沉积物的密度增大. 针对以上胶结模式和填充模 式两种情况,本文基于颜容涛等^[7] 提出的有效饱和度概念,给出了一个统一的有效饱和度${S}'_{\rm h}$ 的计算式

(16)$ {S}'_{h} = S_{h}\left\{1-exp\left[-\left(\dfrac{S_h}{S_{hc}}\right)^3\right]\right\}$
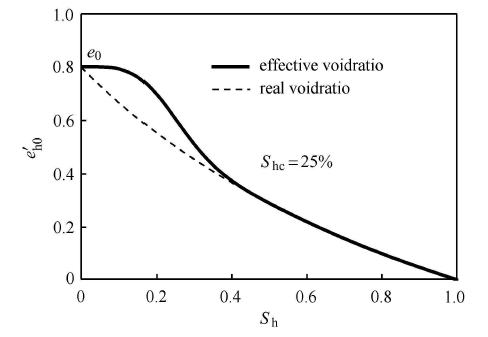
式中,$S_{\rm h} $ 是水合物的真实饱和度;$S_{\rm hc} $是水合物的临界饱和度,其与颜容涛等^[10] 提出的临界饱和度意义相同,确定方法也相同. 当赋存模式为胶结模式,$S_{\rm hc} =0$,此时${S}'_{\rm h} = S_{\rm h} $. 当赋存模式为填充模式时,$S_{\rm hc} $ 一般取25%$\sim $40%.该式是一个连续函数,且是两种赋存形式统一的表达式.

根据饱和度和孔隙比的定义,可以求得含水合物沉积物的初始有效孔隙比

(17)$ e_{\rm h 0} = \dfrac{e_0 \left( {1 - {S}'_{\rm h} } \right)}{1 + e_0 {S}'_{\rm h} }$
式中,$e_0 $ 为不含水合物沉积物的初始孔隙比(图8 ).

图8

新窗口打开|下载原图ZIP|生成PPT
图8有效孔隙比/真实孔隙比与饱和度的关系

Fig. 8Relations between effective/real void ratio and saturation



$d e_{\rm h}$ 可以根据体积应变增量$d \varepsilon _{\rm v} $ 进行计算

(18)$ d e_{\rm h} = \left( {1 + e_{\rm h0} } \right)d \varepsilon_{\rm v}$
通过式(11)、式(12)、式(14)$\sim $式(18)可以看出,水合物含量不同,在相同应力下有效孔隙比不同,从而使得状态参数$\xi$ 不同,而状态参数$\xi $ 进一步影响特征状态应力比$M_{\rm c} $来反映不同饱和度下含水合物沉积物剪胀性的不同.

2.4 塑性势函数

塑性势面决定了塑性应变增量的方向,本文采用CSUH 模型的塑性势函数

(19)$ g = \ln \dfrac{p}{p_y } + \ln \left( {1 + \dfrac{q^2}{M_{\rm c}^{2} p^2}} \right) = 0$
式中,$p_y $ 为塑性势面与$p$ 轴的交点.通过塑性势面可以得到剪胀方程为

(20)$ \dfrac{d \varepsilon _{\rm v}^{\rm p} }{d \varepsilon _{\rm d}^{\rm p} } = \dfrac{M_{\rm c}^2 - \eta ^2}{2\eta }$
式中,$d \varepsilon _{\rm v}^{\rm p} $ 为塑性体积应变增量;$d \varepsilon _{\rm d}^{\rm p} $ 为塑性剪应变增量.

2.5 应力应变关系

2.5.1 弹性应变增量

根据Hooke 定律可求得弹性应变增量为

(21)$ d \varepsilon _{\rm v}^{\rm e} = \dfrac{3\left( {1 - 2\nu } \right)}{E}d p $
(22)$ d \varepsilon _{\rm s}^{\rm e} = \dfrac{2\left( {1 + \nu } \right)}{3E}d q $
式中, $\upsilon $ 为泊松比. $E$为含水合物沉积物的弹性模量,可表示为

(23)$ E = \dfrac{3\left( {1 - 2\nu } \right)\left( {1 + e_{\rm h 0} } \right)}{\kappa }\left( {p + p_{\rm s} } \right) $
在1.2节中已经指出含水合物沉积物的弹性模量会随着水合物含量的增大而增大,因此$\kappa$ 会逐渐减小,表达式为

(24)$ \kappa = \kappa _0 \cdot \exp \left[ { - a \cdot \left( {S_{\rm h} } \right)^b} \right]$
式中,$\kappa _0 $ 是不含水合物的沉积物的回弹系数;$a$ 和$b$分别是材料参数.

2.5.2 塑性应变增量

塑性流动方向与塑性势面正交,因此塑性体积应变可以表示为

(25)$ d \varepsilon _{ij}^{\rm p} = \varLambda \dfrac{\partial g}{\partial \sigma _{ij} } $
式中,$\varLambda $ 是塑性因子,表达式为

(26)$ \varLambda = c_p \dfrac{{ M}_{\rm c}^4 - \eta ^4}{{ M}_{\rm f}^4 - \eta ^4}\dfrac{\dfrac{\partial f}{\partial p}d p + \dfrac{\partial f}{\partial q}d q}{\dfrac{\partial g}{\partial p}}$
式中

(27)$\left.\!\!\begin{array}{l} \dfrac{\partial f}{\partial p} = \dfrac{{ M}^4 - \left( {1 + 3\chi } \right){ M}^2\eta ^2 - \chi \eta ^4}{p\left( {{ M}^2 - \chi \eta ^2} \right)\left[ {{ M}^2 + \eta ^2 + \left( {{ M}^2 - \chi \eta ^2} \right){p_{\rm s} }/ p} \right]} \\ \dfrac{\partial f}{\partial q} = \dfrac{2{ M}^2\left( {1 + \chi } \right)\eta }{p\left( {{ M}^2 - \chi \eta ^2} \right)\left[ {{ M}^2 + \eta ^2 + \left( {{ M}^2 - \chi \eta ^2} \right){p_{\rm s} } / p} \right]} \end{array}\!\! \right\}$
(28)$\left. \!\!\begin{array}{l} \dfrac{\partial g}{\partial p} = \dfrac{{ M}_{\rm c}^2 - \eta ^2}{p\left( {{ M}_{\rm c}^2 + \eta ^2} \right)} \\ \dfrac{\partial g}{\partial q} = \dfrac{2\eta }{p\left( {{ M}_{\rm c}^2 + \eta ^2} \right)} \end{array}\!\! \right\}$
2.5.3 弹塑性应力应变关系

在$p$-$q$ 平面内的应力应变关系表示如下

(29)$ \left\{ \!\!\begin{array}{c} {d p} \\ {d q} \end{array}\!\! \right\} = \left[\!\!\begin{array}{cc} {K A_1 } & {3KG A_2 } \\ {3KG A_3 } & {3G A_4 } \end{array} \!\! \right]\left\{ \!\!\begin{array}{c} {d \varepsilon _{\rm v} }\\ {d \varepsilon _d } \end{array} \!\! \right\}$
式中,$K$ 和$G$分别是弹性体积模量和弹性剪切模量,与弹性模量的关系为

(30)$\left. \!\! \begin{array}{l} K = \dfrac{E}{3\left( {1 - 2\nu } \right)} \\ G = \dfrac{E}{2\left( {1 + \nu } \right)} \end{array} \!\! \right\}$
(31)$\left. \!\! \begin{array}{l} A_1 = \dfrac{B_1 + B_2 }{B_1 + B_2 + Kc_{\rm p} \left( {{\rm M}_{\rm c}^{4} - \eta ^4} \right)B_3 } \\ A_2 = \dfrac{ - 2c_{\rm p} {\rm M}^2\eta \left( {1 + \chi } \right)\left( {{\rm M}_{\rm c}^{4} - \eta ^4} \right)}{B_1 + B_2 + Kc_{\rm p} \left( {{\rm M}_{\rm c}^{4} - \eta ^4} \right)B_3 } \\ A_3 = \dfrac{ - 2c_{\rm p} \eta \left( {{\rm M}_{\rm c}^{2} + \eta ^2} \right)B_3 }{B_1 + B_2 + Kc_{\rm p} \left( {{\rm M}_{\rm c}^{4} - \eta ^4} \right)B_3 } \\ A_4 = \dfrac{B_1 + Kc_{\rm p} \left( {{\rm M}_{\rm c}^{4} - \eta ^4} \right)B_3 }{B_1 + B_2 + Kc_{\rm p} \left( {{\rm M}_{\rm c}^{4} - \eta ^4} \right)B_3 } \end{array} \!\! \right\}$
式中

(32)$ \left. \!\!\begin{array}{l} B_1 = p\left( { { M}_{\rm f}^{4} - \eta ^4} \right)\left( {{ M}^2 - \chi \eta ^2} \right)\left[ {{\rm M}^2 + \eta ^2 + }\right. \\ \qquad \left. { \left( {{ M}^2 - \chi \eta ^2} \right){p_{\rm s} } / p} \right] \\ B_2 = 12Gc_{\rm p} { M}^2\eta ^2\left( {1 + \chi } \right)\left( {{ M}_{\rm c}^{2} + \eta ^2} \right) \\ B_3 = { M}^4 - \left( {1 + 3\chi } \right){\rm M}^2\eta ^2 - \chi \eta ^4 \end{array} \!\!\right\}$

3 模型验证

3.1 验证1

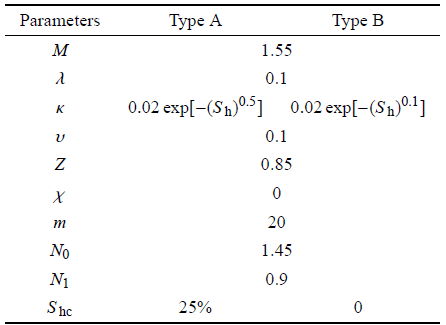
Masui等^[28]采用两种不同的制样方法分别对含水合物沉积物进行了三轴排水试验,两组试验分别称为TypeA 和Type B. 其中Type A 中主砂的初始孔隙比为0.8,Type B中主砂的初始孔隙比为0.59.现采用本文所提出的模型对相应的试验结果进行计算,计算所采用参数见表1.由于Type A试样中水合物主要是以填充模式为主,胶结作用很小,而Type B试样中胶结作用明显,因此两种模式下个别参数会不同.例如Type A中$S_{\rm hc}$ 取为25%,说明饱和度小于25%时,水合物赋存形式主要以悬浮为主. 而Type B中具有较明显的胶结作用,即在饱和度较小时水合物就会起到一定的力学作用,因此其$S_{\rm hc}$ 取为0.

Table 1
表1
表1含水合物沉积物的模型参数
Table 1Model parameters of GHBS

新窗口打开|下载CSV

图9中分别展示了Type A 和Type B 在围压为1 MPa下的三轴排水剪切试验结果和模型计算结果.从图中可以看出,随着饱和度的增大,两种模式下的相同点是含水合物沉积物的抗剪强度均逐渐增大,都会发生应变软化现象,且残余强度都几乎不受水合物的影响. 两种模式下的不同点是在饱和度较低时,Type A的抗剪强度小于Type B,甚至Type A 在$S_{\rm h}$ 为26.4%时的抗剪强度小于Type B 在$S_{\rm h}$ 为0%时的抗剪强度,充分说明了密度对含水合物沉积物力学特性影响的重要性.模型的计算结果(图中实线)表明,该模型能够基本反映含水合物沉积物的以上力学特性.

图9

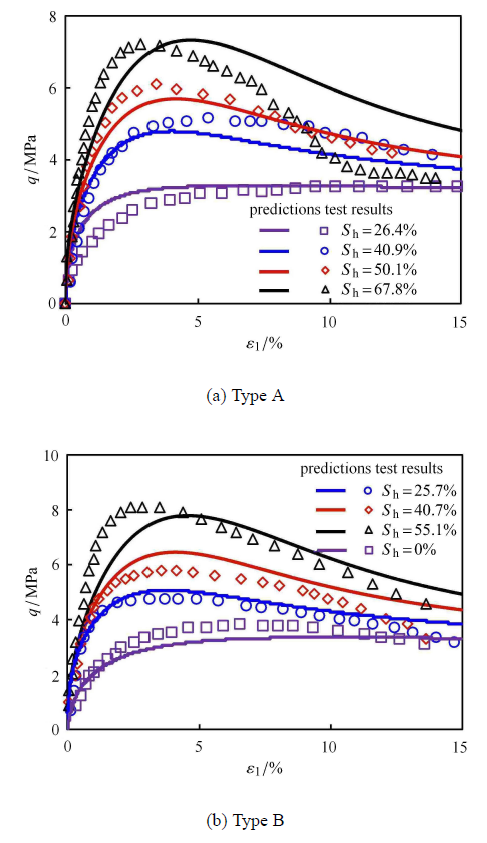新窗口打开|下载原图ZIP|生成PPT
图9应力应变关系^[28]及模型预测

Fig. 9Stress-strain relations^[28] and predictions



图10展示了Type B试样在不同围压下的三轴排水剪切试验结果和模型计算结果. 3种围压下含水合物饱和度$S_{\rm h}$ 几乎相同.图中显示随着围压的增大,含水合物沉积物的抗剪强度逐渐增大,并且在围压较小时发生应变软化更加明显.图中实线说明了本文所提的模型能够反映围压对含水合物沉积物抗剪强度的影响.

图 10

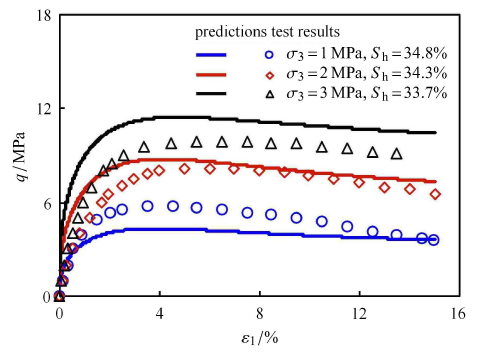新窗口打开|下载原图ZIP|生成PPT
图 10不同围压下Type B 的应力应变关系^[28]及模型预测

Fig. 10Stress-strain relations^[28] of Type B at different confining pressures and predictions



图11展示了相同含水合物饱和度下Type A 和Type B的应力应变关系. 从图中可以看出,Type B 的抗剪强度比Type A的抗剪强度大. Masui等指出造成两种模式下抗剪强度不同的主要原因是试样密度的不同,而不是水合物含量的不同. 再次说明密度对含水合物沉积物的影响至关重要.由于该模型合理考虑了密度的影响,因此能够合理地描述含水合物沉积物的力学特性.

3.2 验证2

Zhang等^[33]采用气饱和试验方法对不同水合物饱和度的含水合物沉积物在不同围压下进行了常规三轴排水试验,试验结果如图12 所示.现采用该实验结果来验证本文所提模型的合理性,模型采用参数见表2,其中主砂试样的初始孔隙比为0.67.

图12是不同水合物饱和度和不同围压下的含水合物沉积砂实验结果和模型预测结果.图中显示,在饱和度较低时应变软化现象发 生在围压较小的情况.随着饱和度的增大,初始刚度明显增大,在高围压下也会逐渐发生应变软化现象.通过模型预测与实验结果的比较可以看出,当饱和度$S_{\rm h}$低于52% 时,模型预测结果与实验结果吻合较好. 当饱和度$S_{\rm h}$ 等于52%时,水合物胶结作用明显,并且在加载过程中胶结状态会发生变化.由于该模型没有考虑水合物胶结状态的变化,使得模型预测结果与实验结果有一定的误差.因此当饱和度较大($S_{\rm h}>50%$) 时,该模型预测结果不是很理想,特别是在围压较小时.

图 11

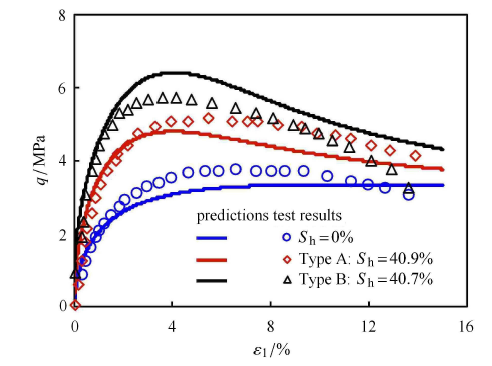新窗口打开|下载原图ZIP|生成PPT
图 11相同饱和度下Type A 和Type B的应力应变关系^[28]及模型预测

Fig. 11Stress-strain relations^[28] of Type A and Type B with same saturations and predictions



Table 2
表2
表2含水合物沉积物的模型参数
Table 2Model parameters of GHBS

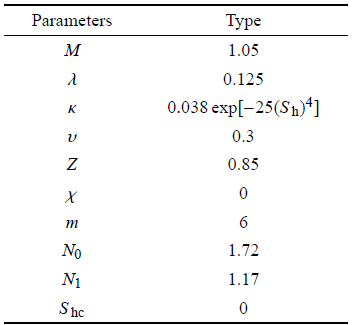新窗口打开|下载CSV

图12

新窗口打开|下载原图ZIP|生成PPT
图12不同围压下含水合物沉积物的应力应变关系^[33] 及模型预测

Fig. 12Stress-strain relations^[33] of GHBS at different confining pressures and predictions



综上,该模型能够合理地描述赋存形式不同、水合物含量不同的含水合物沉积物力学特性.特别注意的是,对于水合物含量不同的含水合物沉积物,本文模型视为同一种沉积物,因此采用一组参数即可描述其不同条件下的应力应变关系.

4 结论

(1) 土密度对土的力学特性影响较大. 本文通过将含水合物沉积物与纯土进行类比分析,指出当水合物悬浮于沉积物孔隙中时,水合物没有起到固相的作用.当水合物以持力或胶结模式赋存于沉积物孔隙中时,即水合物具有骨架或胶结作用,此时水合物具有抗压和抗剪作用,因此均应将水合物视作固相来计算水合物沉积物的密度.所以,在不同赋存模式下,水合物的含量对含水合物沉积物的有效密度具有不同的影响,进而影响含水合物沉积物的力学特性.

(2) 考虑了水合物的固相作用和胶结作用,基 于CSUH模型,引入了水合物的体积分数建立了不同水合物含量下水合物沉积物正常压缩线表达式.

(3) 基于含水合物沉积物有效密度在本构模型中的重要性,提出了含水合物沉积物的初始有效孔隙比计算式,该计算式是一个连续函数,且适用于水合物不同的赋存条件.

(4) 基于CSUH 模型,结合所提正常压缩线表达式,引入了初始有效孔隙比到状态参数,建立了含水合物沉积物的弹塑性本构模型.

(5) 所提本构模型不仅只需采用一组参数就能够描述不同饱和度下含水合物沉积物的力学特性,而且能够合理地描述不同赋存形式的水合物沉积物力学特性.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 石要红, 张旭辉, 鲁晓兵 等. 南海水合物黏土沉积物力学特性试验模拟研究
力学学报, 2015,47(3):521-528
[本文引用: 1]

( Shi Yaohong, Zhang Xuhui, Lu Xiaobing , et al. Experimental study on the static mechanical properties of hydrate-bearing silty-clay in the South China Sea
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(3):521-528 (in Chinese))
[本文引用: 1]

[2] 刘乐乐, 张旭辉, 刘昌玲 等. 含水合物沉积物力学性质三轴剪切试验与损伤统计分析
力学学报, 2016,48(3):720-729


( Liu Lele, Zhang Xuhui, Liu Changling , et al. Triaxial shear tests and statistical analyses of damage for methane hydrate-bearing sediments
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(3):720-729 (in Chinese))


[3] 张旭辉, 鲁晓兵 . 一种新的海洋浅层水合物开采法——机械-热联合法
力学学报, 2016,48(5):1238-1246
[本文引用: 1]

( Zhang Xuhui, Lu Xiaobing . A new exploitation method for gas hydrate in shallow stratum: mechanical-thermal method
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(5):1238-1246 (in Chinese))
[本文引用: 1]

[4] Yu F, Song YC, Liu WG , et al. Analyses of stress strain behavior and constitutive model of artificial methane hydrate
Journal of Petroleum Science and Engineering, 2011,77(2):183-188
[本文引用: 1]

[5] Miyazaki K, Masui A, Sakamoto Y , et al. Triaxial compressive properties of artificial methane-hydrate bearing sediment
Journal of Geophysical Research, 2011,116(B6): doi: 10.1029/2010JB008049


[6] 吴二林, 魏厚振, 颜荣涛 等. 考虑损伤的含天然气水合物沉积物本构模型
岩石力学与工程学报, 2012,31(S1):3045-3050


( Wu Erling, Wei Houzhen, Yan Rongtao , et al. Constitutive model for gas hydrate-bearing sediments considering damage
Chinese Journal of Rock Mechanics and Engineering, 2012,31(S1):3045-3050 (in Chinese))


[7] 颜荣涛, 梁维云, 韦昌富 等. 考虑赋存模式影响的含水合物沉积物的本构模型研究
岩土力学, 2017,38(1):10-18 (in Chinese))
[本文引用: 2]

( Yan Rongtao, Liang Weiyun, Wei Changfu , et al. A constitutive model for gas hydrate-bearing sediments considering hydrate occurring habits
Rock and Soil Mechanics, 2017,38(1):10-18 (in Chinese))
[本文引用: 2]

[8] Kimoto S, Oka F, Masaya F . A chemo-thermo-mechanically coupled numerical simulation of the subsurface ground deformations due to methane hydrates dissociation
Computers and Geotechnics, 2007,34(7):216-228
[本文引用: 1]

[9] Klar A, Uchida S, Soga K , et al. Explicitly coupled thermal flow mechanical formulation for gas-hydrate sediments
SPE Journal, 2013,18(2):196-206


[10] Uchida U, Soga K, Yamamoto K . Critical state soil constitutive model for methane hydrate soil
Journal of Geophysical Research, 2012,117:B03209
[本文引用: 1]

[11] 蒋明镜, 刘俊, 周卫 等. 一个深海能源土弹塑性本构模型
岩土力学, 2018,39(4):1153-1158


( Jiang Mingjing, Liu Jun, Zhou Wei , et al. An elasto-plastic constitutive model for methane hydrate bearing sediments
Rock and Mechanics, 2018,39(4):1153-1158 (in Chinese))


[12] 杨期君, 赵春风 . 含气水合物沉积物弹塑性损伤本构模型探讨
岩土力学, 2014,35(4):991-997


( Yang Qijun, Zhao Chunfeng . A constitutive model coupling elastoplasticity and damage for methane hydrate-bearing sediments
Rock and Soil Mechanics, 2014,35(4):991-997 (in Chinese))


[13] 袁庆盟, 孔亮, 刘锐明 等. 考虑深海能源土结构性的统一硬化模型
科学技术与工程, 2018,18(32):64-70


( Yuan Qingmeng, Kong Liang, Liu Ruiming , et al. Unified hardening model for gas hydrate bearing sediments considering structure
Science Technology and Engineering, 2018,18(32):64-70 (in Chinese))


[14] 邹远晶, 韦昌富, 陈合龙 等. 基于扰动状态概念的含水合物土弹塑性模型
岩土力学, 2019,40(7):1-9
[本文引用: 1]

( Zou Yuanjing, Wei Changfu, Chen Helong , et al. Elastic-plastic model for gas-hydrate soils based on disturbed state concept
Rock and Mechanics, 2019,40(7):1-9 (in Chinese))
[本文引用: 1]

[15] 姚仰平, 刘林, 罗汀 . 砂土的UH模型
岩土工程学报, 2016,38(12):2147-2153
[本文引用: 3]

( Yao Yangping, Liu Lin, Luo Ting . UH model for sands
Chinese Journal of Geotechnical Engineering, 2016,38(12):2147-2153 (in Chinese))
[本文引用: 3]

[16] Yao YP, Liu L, Luo T . A constitutive model for granular soils
Science China Technological Sciences, 2018,61(10):1546-1555


[17] 罗汀, 刘林, 姚仰平 . 考虑颗粒破碎的砂土临界状态特性描述
岩土工程学报, 2017,39(4):592-600


( Luo Ting, Liu Lin, Yao Yangping . Description of critical state for sands considering particle crushing
Chinese Journal of Geotechnical Engineering, 2017,39(4):592-600 (in Chinese))


[18] Yao YP, Liu L, Luo T , et al. Unified hardening (UH) model for clays and sands
Computers and Geotechnics, 2019,110:326-343
[本文引用: 3]

[19] Yao YP, Hou W, Zhou AN . UH model: Three-dimensional unified hardening model for overconsolidated clays
Géotechnique, 2009,59(5):451-469
[本文引用: 2]

[20] Yao YP, Gao ZW, Zhao JD , et al. Modified UH model: constitutive modeling of overconsolidated clays based on a parabolic hvorslev envelope
J Geotech Geoenviron Eng, 2012,138(7):860-868


[21] 姚仰平 . UH 模型系列研究
岩土工程学报, 2015,37(2):193-217
[本文引用: 1]

( Yao Yangping . Advanced UH models for soils
Chinese Journal of Geotechnical Engineering, 2015,37(2):193-217 (in Chinese))
[本文引用: 1]

[22] Tan BB . Geotechnical characteristic of sediments from Hydrate Ridge, Cascadia continental margin. [Master Thesis]
Massachusetts Institute of Technology, 2004
[本文引用: 3]

[23] Roberts JE, Souza JM . The compressibility of sand
Proc, Am. Soc for Testing Mat, 1958,58:1269-1277
[本文引用: 1]

[24] Hendron A . The behavior of sand in one-dimensional compression. [PhD Thesis]
Urbana: University of Illinois, 1963


[25] Hagerty MM, Hite DR, Ullrich CR , et al. One-dimensional high-pressure compression of granular media.
J Geotech Engrg, ASCE, 1993,119(1):1-18


[26] Yamamuro JA, Bopp PA, Lade PV . One-dimensional compression of sands at high pressures.
J Geotech Engrg, ASCE, 1996,122(2):147-154


[27] Yu FW . Experimental study on particle breakage under high pressure. [PhD Thesis]
Tokyo: University of Tokyo, 2014
[本文引用: 1]

[28] Masui A, Haneda H, Ogata Y , et al. The effect of saturation degree of methane hydrate on the shear strength of synthetic methane hydrate sediments
// Proceedings of the 5 th Int. Conf. on Gas Hydrates, June 13-16, 2005, Trondheim, Norway
[本文引用: 8]

[29] Soga K, Lee S, Ng M , et al. Characterization and engineering properties of methane hydrate soils. Characterization and Engineering Properties of Natural Soils
London: Taylor and Francis, 2006: 2591-2642
[本文引用: 1]

[30] Been K, Jefferies MG . A state parameter for sands
Géotechnique, 1985,35(2):99-112
[本文引用: 1]

[31] 刘林 . 粘土和粒状土统一的UH模型. [博士论文]
北京:北京航空航天大学, 2018
[本文引用: 1]

( Liu Lin . UH model for clays and granular soils. [PhD Thesis]
Beijing: Beihang University, 2018 (in Chinese))
[本文引用: 1]

[32] 李广信 . 高等土力学. 北京: 清华大学出版社, 2004: 41-42
[本文引用: 1]

( Li Guangxin . Advanced Soil Mechanics. Beijing: Tsinghua University Press, 2004: 41-42(in Chinese))
[本文引用: 1]

[33] Zhang XH, Lin J, Lu XB , et al. A hypoplastic model for gas hydrate-bearing sandy sediments
Int J Numer Anal Methods Geomech, 2018,42:931-942
[本文引用: 3]