,2)武汉大学土木建筑工程学院工程力学系,武汉 430072A GENERAL METHOD TO INTRODUCE PRE-CRACK IN BULK METALLIC GLASSES FOR PLANE STRAIN FRACTURE TOUGHNESS TEST 1)
Xie Yiling, Liu Ze,2)Department of Engineering Mechanics,School of Civil Engineering,Wuhan University,Wuhan 430072,China通讯作者: 2)刘泽,教授,主要研究方向：先进微制造力学. E-mail:ze.liu@whu.edu.cn
收稿日期:2019-12-30接受日期:2020-03-5网络出版日期:2020-03-18
| 基金资助: |
Received:2019-12-30Accepted:2020-03-5Online:2020-03-18
作者简介 About authors
摘要
介绍了一种简单、低成本且可靠的方法在非晶合金中预制理想裂纹并应用于小试样平面应变断裂韧性的测试.近年来,非晶合金由于高弹性、高强度、耐磨及软磁性等优异性能 展示了广泛的应用前景.断裂韧性作为材料工程应用的一个重要指标,也引起了非晶合金领域的广泛关注. 然而,由于非晶合金的亚稳态结构以及最大可铸造尺寸的限制,目前关于非晶合金断裂韧性的测试还存在较大的挑战.一方面,铸造工艺造成的非晶合金热历史的差异、内部微孔洞和杂质等缺陷以及裂纹预制方式等都会显著影响其断裂韧性测试的可靠性;另一方面,非晶合金可铸造尺寸的限制使得目前绝大多数报导的断裂韧性值都是非平面应变的断裂韧性,导致即使是对于同种非晶合金,所报导的断裂韧性值也存在较大偏差.本文利用非晶合金在过冷液相温度下具有可热塑性成型的特性,对预制有缺口的非晶合金试样进行局部压缩成型,使得预制的缺口裂纹重新闭合形成类似疲劳裂纹的理想裂纹面.基于该方法对Zr基非晶合金进行断裂韧性测试,实验结果表明,随着试样厚度的增加,测试值迅速降低并趋向于一个定值.需要指出的是,通过设计实验使得试样在理想裂纹面区域形成局部凹陷,使得趋于定值的试样厚度远小于平面应变断裂韧性测试标准中的试样厚度要求.
关键词：
Abstract
We report a simple, low-cost but robust method to introduce pre-crack in bulk metallic glasses (BMGS) for plane strain fracture toughness test. In recent years, bulk metallic glasses have shown potential and promising engineering application due to their excellent properties such as high elasticity, high strength, wear resistance and soft magnetism. As an important material parameter for engineering application, fracture toughness has also attracted great attention in the BMG community. However, there is still challenge on the fracture toughness test of BMGs because of the metastable nature and limited maximum castable size of BMGs. On the one hand, the casting induced thermal history difference and the defects such as internal micropores and impurity inclusions in BMGs, and the way of crack prefabrication will significantly affect the reliability of the fracture toughness test. On the other hand, limited by the sample size, most of the measured fracture toughness of BMGs are not the plane strain fracture toughness, resulting in the reported values showing large deviation, even for the same amorphous alloy. In this work, pre-notched BMG samples were thermoplastically compressed at the notched region to form ideal crack by creep flow. As an example, the fracture toughness of Zr-based amorphous alloy is tested by this method. The experimental results show that as the sample thickness increasing, the measured toughness decreases quickly and tends to a constant value. It should be pointed out that in the experiments, the local thermoplastic compression is designed to obtain a neck shaped pre-crack, which makes the minimum thickness of the specimen being far less than the required thickness by the plane strain fracture toughness testing standard.
Keywords：
PDF (19766KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
谢怡玲, 刘泽. 非晶合金理想裂纹预制方法及其在小试样$K_{\rm Ic}$测试中的应用 1). 力学学报[J], 2020, 52(2): 392-399 DOI:10.6052/0459-1879-19-377
Xie Yiling, Liu Ze.
引言
非晶合金,又称金属玻璃 [1-2],是通过快速冷却凝固得到的非晶态金属材料.1960年,美国加州理工的Duwez教授[3]首次报道了通过急冷法制备的Au-Si非晶合金,这一方法带动了非晶合金制备的快速发展.在20世纪90年代末,非晶合金制备取得重大进展——在宏观尺寸上成功制备出块状、棒状的非晶合金[4-5].非晶合金铸造尺寸的突破,引起了学术界和工业界 的广泛关注[6-9].研究发现,源于微观尺度的长程无序、短程有序的亚稳态原子结构[10],非晶合金具有比相应晶态金属更高的弹性极限、更大的强度和硬度以及抗腐蚀耐磨损等特性[11].但也正因为缺乏晶体中的位错形核与运动等塑性变形机制,块体非晶合金在室温下表现为高度局域的剪切带变形[12-14].目前,关于非晶合金的弹性与强度理论已经取得了重要进展.然而,断裂韧性作为非晶合金应用的另一个关键力学性能指标,其测量与理解却还存在较大的挑战[15 - 18].首先,仅极少数非晶合金能够同时满足高玻璃形成能力和高断裂韧性的要求,从而获得可靠的断裂韧性值[15]. 对多数非晶合金,即使它们具有足够大的可铸造尺寸用于断裂韧性实验,其脆性也使得传统的预制疲劳裂纹方法失效[19 -21].其次,研究发现非晶合金铸造过程中的冷速差异[22]、残余应力[23]、组分涨落(包括杂质缺陷)[24,25]、试样 几何[20,26]、预制缺口裂纹的质量[27]等均会显著影响断裂韧性测量值,这也是造成文献中即使对于同种非晶合金所报导的断裂韧性值也非常分散的主要原因,典型的如Zr$_{41.2}$Ti$_{13.8}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$非晶合金,其预制疲劳裂纹测试值为16-68 MPa$\cdot$m$^{1/2}${[19, 26, 28-36].
最近的研究发现,通过硅电子微加工技术制备硅模具,然后加热非晶合金至其过冷液相区,利用外载荷作用下非晶合金的黏性流动复制硅模具可以制得高品质的预制缺口试样 [20, 29, 37].其利用了光刻工艺可获得极高加工精度(可小至1 $\mu$m[38]),而过冷液相温度以及高压可有效消除热历史差异以及组分涨落,因此上述方法可以有效减弱甚至消除冷速差异、残余应力、组分涨落以及预制缺口裂纹质量等因素对断裂韧性测量的影响[29,39-42].然而,由于硅是一种典型的脆性材料,对于热塑性成型能力较差的非晶合金,复制模具过程容易造成硅模具的破碎.此外,硅电子微加工技术显著增加了试验的成本,并且受限于光刻工艺,所制备的试样厚度一般小于300 $\mu $m.同时,该方法不能直接获得理想的裂纹.
本文基于非晶合金的可热塑性成型特性,先用金刚石线锯或金刚石刀片在铸态非晶合金中切出所需形状的试样,同时在试样中预制缺口裂纹.然后在大气环境下、过冷液相温度区间对预制有缺口的非晶合金试样进行压缩成型,使得预制的缺口裂纹闭合形成类似疲劳裂纹的理想裂纹面.为了在薄试样中创造局部的平面应变状态,设计模具使得热塑性成型闭合缺口裂纹的过程中在裂纹面附近形成局部的凹陷.最后,以锆基非晶合金为例,通过上述方法对预制有理想裂纹的断裂试样进行原位准静态单轴拉伸,实现了较薄试样的平面应变断裂韧性的测量.
1 实验材料与方法
1.1 实验材料
本文的实验材料采用了LM-1 (Zr$_{41.2}$Ti$_{13.8}$ Cu$_{12.5}$ Ni$_{10}$ Be$_{22.5}$ (at.%)) [43-46]和LM-1b(Zr$_{44}$ Ti$_{11}$ Cu$_{10}$ Ni$_{10}$\linebreak Be$_{25}$(at.%))$^{[20, 47-49]两种,通过DSC测得上述两种\linebreak BMG的玻璃转化温度分别为$T_{\rm g}$ =349${^\circ}$C,350${^\circ}$C;初始晶化温度分别为$T_{x} = 426{^\circ}$C,471${^\circ}$C(表1).Table 1
表1
表1材料参数表 [45]
Table 1
 |
新窗口打开|下载CSV
1.2 实验方法
本文在5.0 $\times $ 10$^{-5}$ s$^{-1}$的应变率控制下,对LM-1块体非晶合金进行准静态单轴拉伸.研究了试样厚度、缺口半径对LM-1断裂 韧性$K_{Q}$值的影响.样品预制缺口采用0.25 mm直径的金刚石线以0.2 mm/min的速度进行切割(沈阳科晶自动化设备有限公司,STX-202A型金刚石线切割机).热塑性成型闭合缺口裂纹的试验在设计有可加热并控温的平板夹具的万能试验机上完成.平板夹具采用电阻式加热,平板的温度通过与之相连的热电偶及反馈控制电路进行控制,温控精度优于1$^\circ$C.制备理想裂纹的原理如图1所示：当试验机平板夹具的温度到达预设的420 $^\circ$C并稳定后,把预制缺口的LM-1试样与模具叠放在上下平板夹具之间(图1(a)),待试样达到设定温度后,对其施加平均压强为150 MPa的载荷,加载时间控制在5 min以内以避免晶化.加载结束后取出样品快速置于水中冷却(水温为室温).为了在热塑性成型闭合缺口裂纹的过程中在裂纹面附近形成平面应变状态,模具形状设计成" T ''形,使得热塑性成型后的试样 表面形成局部的凹陷(图1(b)).通过上述方法制备的典型缺口试样及缺口裂纹闭合后的试样的光学显微镜照片如图1(c)和图1(d)所示(Keyence,VHX-5000). 图示非晶合金试样在成型后厚度方向的变形约为50 %.图1(e)为所制备的典型断裂试样在加载测试后的XRD表征,图中仅出现一个弥散的馒头峰,表明该试样在经历前述热塑性成型后仍处于非晶态.图1
新窗口打开|下载原图ZIP|生成PPT图1(a)和(b)制备理想裂纹的原理图;(c)通过金刚石绳锯预制缺口后的典型试样;(d)热塑性成型使得缺口裂纹闭合后的典型试样;(e)热塑成型制备的一个理想裂纹试样在断裂后的XRD表征
Fig. 1(a) and (b) Schematics of the experimental procedures; (c) Typical notched sample; (d) Typical pre-cracked sample based on the procedures in (a) and (b); (e) XRD characterization of a typical pre-cracked sample after fracture test
为了表征热压闭合后的裂纹,先对试样表面进行精细抛光(上海光学仪器厂,YMPZ-2),然后利用光学显 微镜(Keyence,VHX-5000)和场发射扫描电子显微镜(SEM, Zeiss, Sigma 500)对磨抛后的试样进行表征.典型的结果如图2所示,缺口已经合拢成为一条"线"(图2(a)),局部放大闭合后的裂纹尖端区域如图2(b)所示.显然,通过上述方法可以制备出含理想裂纹的试样.
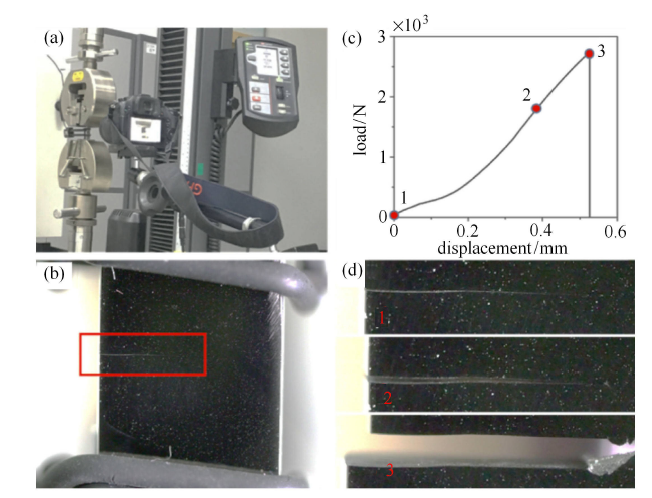
最后,对预制有理想裂纹的试样在电子万能材料试验机(Instron,instron5969)上进行断裂韧性测试,试验以5.0$\times $10$^{ - 5}$ s$^{-1}$的恒应变率加载直至拉断,试样拉伸过程通过相机实时录像(图3(a)).图3(b)为一个典型缺口试样装载后的照片,图3(c)为其对应的位移-载荷曲线,其中位移通过试样上的引伸计测得(图3(b)).图3(d)为拉伸过程中,对应3个时刻(图3(c)中的点1,2,3)的缺口变化.
图2
新窗口打开|下载原图ZIP|生成PPT图2利用光学显微镜和扫描电子显微镜对通过热塑性成型制备的含理想裂纹试样进行表征. (a) 理想裂纹的光学显 微镜图;(b) 对理想裂纹尖区域进行局部放大的扫描电子显微镜图
Fig. 2Characterization of a typical sample after pre-cracking by thermoplastic compression. (a) Optical microscope imaging of the pre-crack; (b) Zoom-in the crack tip region by a SEM
图3
新窗口打开|下载原图ZIP|生成PPT图3(a) 断裂韧性测试装置图;(b) 预制有理想裂纹的试样;(c) 上述试样的位移-载荷曲线;(d) 上述试样拉伸过程中在对应状态下 裂纹的变化
Fig. 3(a) Experimental set-up for fracture toughness test. (b) Typical sample with an ideal crack. (c) Corresponding displacement-force curve. (d) Evolution of the crack in (b)
2 实验结果
2.1 缺口裂尖曲率半径的影响
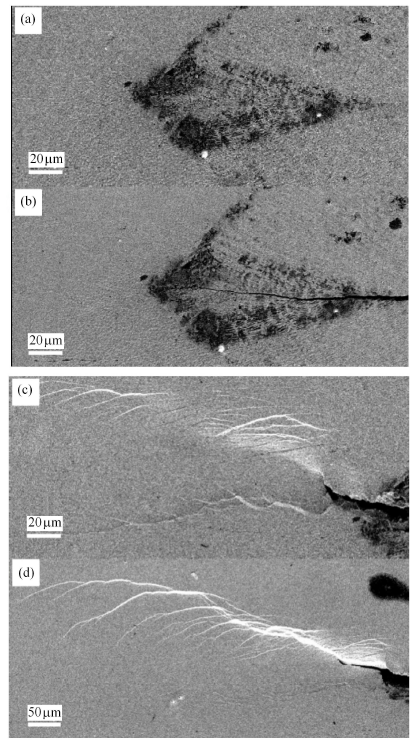
典型缺口裂纹试样与含理想裂纹试样在断裂前后的光学显微镜照片如图4所示.显然,缺口裂纹由于裂尖曲率半径较大,在拉 伸过程中,尖端形成分布的剪切带(图4(b)).而通过热塑性成型使得缺口闭合后的试样,其尖端剪切带更加密集,且剪切带区域的宽度远小于前者(图4(d)).由于非晶合金的塑性变形功集中在剪切带内,因此,具有较大缺口半径的试样在断裂前形成的剪切带更多,其测得的断裂韧性值也就越高.图4(c)中样品的断面形貌如图5所示,图中箭头指向为裂纹扩展方向. 其中,图5(a)为试样断面在显微镜下的全貌图;图5(b) $\sim$ 图5(e)为试样断面的SEM表征;图5(b)为裂纹尖端分界面附近的形貌图;图5(c)为热压闭合区域的原切口表面;图5(d)为裂尖附近裂纹萌生区的断面形貌;图5(e)为裂纹扩展区的断面形貌.从图5(c)可以看出,热压闭合区域没有发生键合(没有非晶合金典型的vein-pattern断面形貌图5(d)和图5(e)),这主要是非晶合金在高温下形成的表面氧化层阻碍了金属键的形成.裂纹萌生区断面相对光滑且呈脉络的油脂分离状,而裂纹扩展区的断面形貌为尺度1$\sim $2 $\mu$m的韧窝结构,反映出裂纹从萌生到扩展过程中主剪切带尖端应力强度的变化.
图 4
新窗口打开|下载原图ZIP|生成PPT图 4缺口尖端曲率半径对剪切带分布的影响. (a)$\sim$(b)曲率半径为130 $\mu$m、厚度为3.4 mm的断裂试样在断裂前后的裂尖区域表征;(c)$\sim$(d)典型含理想裂纹、厚度为2.7 mm的试样在断裂前后的裂尖区域表征
Fig. 4Effect of notch radius on the distribution of shear bands after fracture. (a)$\sim$(b) Typical sample with notch radius of 130 $\mu$m and sample thickness of 3.4 mm. (c)$\sim$(d) Typical pre-crack sample by thermoplastic compression, the thickness of the sample is 2.7 mm
图5
新窗口打开|下载原图ZIP|生成PPT图5典型含理想裂纹试样的断裂面形貌
Fig. 5Characterization of the pre-crack sample in
2.2 SEM下原位断裂试验
文献中报导的LM-1的平面应变断裂韧性值较小(16$\sim $68 MPa$\cdot $m$^{1 / 2}$)[26, 28,30-34, 50],因此其理想裂纹试样在拉伸过程中剪切带区域较小(图4(d)),在光学显微镜下不容易进行观测.为了更好地了解含理想裂纹试样在断裂过程中剪切带的演化规律,下面选择在SEM中进行原位断裂测试.受限于拉伸台的量程(450 N,Mechanical Technology Inc,SEM tester100). 选择了热塑性成型性能更优的LM-1b材料,首先通过复制硅模具[20,38]预制了" V "形缺口试样,然后利用图1(a)和图1(b)工艺制得含理想裂纹试样(图6(a)).尽管缺口已经完全闭合,但仍然能看到"V''形痕迹(黑色区域形状).对所制备的含理想裂纹试样在SEM中进行原位拉伸实验,剪切带演化与裂纹扩展如图6(b) $\sim$ 图6(d)所示.图6
新窗口打开|下载原图ZIP|生成PPT图6典型含理想裂纹试样的SEM原位断裂试验
Fig. 6In-situ tension of a LM-1b sample contains an ideal crack in SEM
2.3 实验数据分析及讨论
对于单边缺口拉伸试样(SENT),其应力强度因子$K$计算公式如下[21, 51-53]式中,$\sigma$为远端均匀应力,$a$为试样裂纹长度,$W$为试样宽度, $f\left( {\dfrac{a}{W}}\right)$为形状修正因子,其计算公式\linebreak 如下[53]
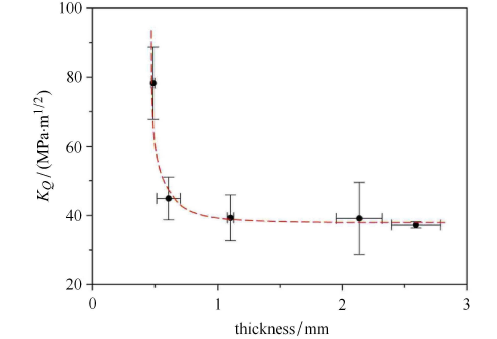
基于上述公式,并根据LM-1含裂纹试样的实验测试数据(表2),可计算获得其断裂韧性值.对于厚度为2.7 mm和3.4 mm的缺口 试样(缺口曲率半径为130 $\mu $m),测得断裂韧性值分别为$\overline {K_Q } = 93.6,91.8 {\rm MPa}\cdot {\rm m}^{\tfrac 12}$.而对于通过热塑性成型制得的含理想裂纹试样,所测得的断裂韧性值明显低于缺口试样,且随厚度增加迅速降低(图7),表明裂尖由平面应力状态逐渐转变为平面应变状态. 需要指出的是,当试样厚度大于约0.6 mm后,断裂韧性即趋向于一个定值$K_Q \approx 38.4 {\rm MPa}\cdot {\rm m}^{\tfrac 12}$ (图7). 根据ASTC E399规定,$K_{\rm Ic}$必须是在平面应变状态下的测试值,试样在尺寸上需满足
对于LM-1,$\sigma _y = 1.755$ GPa. 平面应变断裂韧性要求试样厚度$B \geqslant 2.5\left( {{K_{\rm Ic}}/{\sigma _y }} \right)^2 = 1.3$ mm. 而在本文的实验中(图7),当试样厚度大于$\sim 0.6$ mm后(不到ASTC E399要求的1.3 mm的一半),$K_{\rm Q}$值就已经与$K_{\rm Ic}$值接近,表明通过" T ''形模具制备含理想裂纹的同时可以在裂纹面附近(凹陷区)形成平面应变状态,从而使得平面应变断裂韧性测试对试样厚度的要求显著降低.
Table 2
表2
表2LM-1含裂纹试样的几何参数表
Table 2
 |
新窗口打开|下载CSV
图7
新窗口打开|下载原图ZIP|生成PPT图7通过热塑性成型制备的含理想裂纹试样的断裂韧性测试值对试样厚度的依赖关系
Fig. 7Dependence of the fracture toughness of pre-crack sample on the sample's thickness
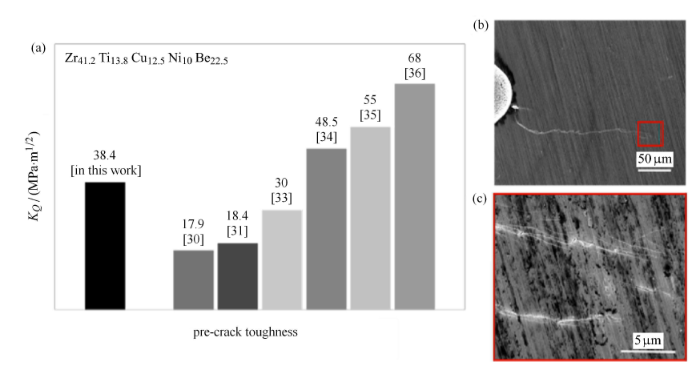
此外,根据文献[26, 28, 30-32, 34, 50]报导,基于预制疲劳裂纹的LM-1的断裂韧性测试值比较离散,大致范围在16$\sim $68 MPa$\cdot $m$^{1/2}$.图8(a)为基于本文实验测得的LM-1断裂韧性值与文献中报导的LM-1的断裂韧性的对比.通过对比可以发现,通过本文预制裂纹方式测得的断裂韧性测试值与文献中的值虽然在同一个水平,但是本文的预制裂纹方式更具有普适性,不再受限于高玻璃形成能力且高韧的非晶合金.尤其需要指出的是,实验发现疲劳裂纹预制过程容易在裂纹前端分叉出剪切带(图8(b)和图8(c)),这些分叉剪切带在主剪切带 形成之前也会发生扩展,从而造成附加的塑性功,使得测试结果偏离理想裂纹测试值.
图8
新窗口打开|下载原图ZIP|生成PPT图8(a)不同研究组测得的LM-1含理想裂纹试样的断裂韧性值;(b)和(c)对缺口裂纹预制疲劳裂纹过程所形成的分叉剪切带损伤
Fig. 8(a) Comparison of the measured pre-crack toughness in LM-1 with other groups. (b) and (c) Fatigue cracking process induces branched shear bands
3 结论
断裂韧性是材料的一个重要力学性能指标. 本文报导了一种通过热塑性成型快速、低成本且可靠的预制理想裂纹 的方法.该方法有效解决了非晶合金疲劳裂纹试样在制备上的困难.同时,通过设计"T"形模具在热塑性成型制备理想裂纹的同时,获得了裂纹面附近(凹陷区)的平面应变状态,使得对薄试样进行平面应变断裂韧性测试成为可能.最后,以LM-1非晶合金为例,展示了通过上述方法实现薄试样非晶合金平面应变断裂韧性测试的有效性.参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 4]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 4]
[本文引用: 1]
[本文引用: 3]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
