海洋天然气水合物降压开采地层井壁力学稳定性分析 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

袁益龙^*^,^?, 许天福^*^,^?, 辛欣^*^,^?, 夏盈莉^*^,^?, 李冰^,^?^,^**^,²⁾

* 吉林大学地下水资源与环境教育部重点实验室, 长春 130021

? 吉林大学新能源与环境学院, 长春 130021

** 吉林大学建设工程学院, 长春 130026

MECHANICAL STABILITY ANALYSIS OF STRATA AND WELLBORE ASSOCIATED WITH GAS PRODUCTION FROM OCEANIC HYDRATE-BEARING SEDIMENTS BY DEPRESSURIZATION ¹⁾

Yuan Yilong^*^,^?, Xu Tianfu^*^,^?, Xin Xin^*^,^?, Xia Yingli^*^,^?, Li Bing^,^?^,^**^,²⁾

* Key Laboratory of Groundwater Resources and Environment, Ministry of Education, Jilin University, Changchun 130021, China

? College of New Energy and Environment, Jilin University, Changchun 130021, China

** College of Construction Engineering, Jilin University, Changchun 130026, China

通讯作者: 2)李冰, 讲师, 主要研究方向: 天然气水合物钻采技术. E-mail:bing@jlu.edu.cn

收稿日期:2019-07-6接受日期:2019-09-10网络出版日期:2020-03-18

基金资助:

1)国家重点研发计划.2017YFC0307304
吉林大学博士研究生交叉学科科研资助计划.10183201841

Received:2019-07-6Accepted:2019-09-10Online:2020-03-18
作者简介 About authors

摘要
降压开采天然气水合物使其分解会导致储层孔隙度、渗透率、孔隙压力和岩层骨架有效应力发生改变, 同时降低沉积物的胶结程度, 使地层的抗剪强度和承载能力降低, 从而引起井壁失稳、海底滑坡、海底面沉降等工程问题. 为此, 在地下多相非等温数值模拟软件TOUGH+Hydrate框架内, 基于扩展的三维Biot固结理论, 考虑水合物分解相变、传热(T)、流动(H)、岩土体变形(M)等过程及其相互耦合作用, 建立了新的水合物开采传热-流动-力学(THM)耦合数学模型, 并开发有限元程序对其进行数值求解. 以中国南海神狐海域GMGS1航次SH2站位水合物储层条件为研究对象, 构建了垂直井降压开采THM耦合地层井壁稳定性分析模型, 预测了水合物开采过程中储层温-压-力场和水合物分解区的演化规律, 揭示了地层优势出砂区域和海底面沉降趋势. 结果表明: 储层降压导致地层有效应力增大, 进而引起井周地层发生沉降, 且地层的沉降主要发生在降压开采前期, 最大沉降位置位于井壁周围, 向储层内部延伸地层沉降量快速减小; 水合物分解导致井周地层力学强度降低, 加剧了储层的沉降; 井筒降压造成射孔段井壁应力集中最为明显, 从而造成井壁破坏的潜在风险, 这些区域正是水合物开采出砂防治的关键区域.
关键词： 天然气水合物;降压开采;传热-流动-力学耦合;地层沉降;井壁稳定

Abstract
Gas production from hydrate-bearing sediment by depressurization will result in the changes of its porosity, permeability, pore pressure, effective stress and cementing strength, which will reduce the shear strength and carrying capacity of the hydrate-bearing sediments. As a consequence, the possible geohazards could trigger, such as wellbore instability, submarine landslide, and seafloor subsidence. Given this, based on the extended 3D Biot consolidation theory, the coupled thermo-hydro- mechanical (THM) model was built in the framework of TOUGH+Hydrate. The new THM model considers the coupling processes, including hydrate dissociation and formation, heat conduction, convection, and mechanical behavior of hydrate-bearing sediments. Taking the geologic data obtained from the Shenhu area SH2 site of South China Sea as an example, the THM coupling model for analyzing the mechanical stability of strata and wellbore using vertical well by depressurization was constructed. The evolution rules of reservoir temperature, pore pressure, stress, and hydrate dissociation zone during depressurization were predicted. In addition, the dominant sand producing region and seabed subsidence trend were revealed. The results show that the drawdown of reservoir pressure controls the increase in effective stress and strata subsidence around the production well. The subsidence mainly occurs in the early stage of depressurization, and the maximum subsidence is located around the production interval. The dissociation of hydrate results in significant decrease in the mechanical strength of sediments, which aggravates the subsidence. Wellbore depressurization results in the stress concentration in the perforation section significantly, which causes the potential wellbore damage. What's more, the stress concentration region is the key area for the prevention and control of sand production associated with hydrate production.
Keywords：natural gas hydrate;depressurization;coupled thermo-hydro-mechanical processes;seafloor subsidence;wellbore stability

PDF (16269KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
袁益龙, 许天福, 辛欣, 夏盈莉, 李冰. 海洋天然气水合物降压开采地层井壁力学稳定性分析 ¹⁾. 力学学报[J], 2020, 52(2): 544-555 DOI:10.6052/0459-1879-19-178
Yuan Yilong, Xu Tianfu, Xin Xin, Xia Yingli, Li Bing. MECHANICAL STABILITY ANALYSIS OF STRATA AND WELLBORE ASSOCIATED WITH GAS PRODUCTION FROM OCEANIC HYDRATE-BEARING SEDIMENTS BY DEPRESSURIZATION ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(2): 544-555 DOI:10.6052/0459-1879-19-178

引言

海洋天然气水合物(简称水合物)通常形成于深水浅覆盖层的松散沉积物中, 其成岩性差、抗剪强度低. 水合物以固体形态赋存于这些沉积层的孔隙中起到了有效的胶结作用, 改变了地层的结构特性^[1-2]. 降压开采水合物使其分解导致地层强度和承载能力大幅度降低, 进而引起生产井周围地层变形, 甚至引发井壁失稳、海底滑坡、海底面沉降等地质灾害^[3-4]. 由此可见, 水合物降压开采涉及到松散沉积层系统中热对流传导(T)、水动力(H)、力学(M)过程以及三者之间的相互耦合作用. 然而, 以往有关水合物开采的研究主要集中于产能评价, 往往忽略对水合物地层和井壁稳定性的评估^[5-8].

目前国内外有关水合物开采地层井壁稳定的模型研究尚处于起步阶段, 能够同时考虑水合物开采THM耦合过程的数值计算软件不多. Rutqvist等^[3]通过耦合TOUGH+Hydrate和力学分析软件FLAC$^{\rm 3D}$形成水合物开采THM耦合软件, 并成功应用到冻土区^[3]和海洋^[2]水合物开采地层力学稳定性分析. Kimoto等^[9]基于化学-热力学-岩土力学耦合分析, 建立了预测甲烷水合物分解引发的地层沉降模型. Lin等^[10]基于印度国家水合物项目第二航次(NGHP-02)16站位的储层资料, 分析了砂泥互层结构水合物储层降压开采的地层力学稳定性. Qiu等^[11]通过MH21-HYDRES和3DFE地质力学模拟器分析了日本南开海槽水合物藏降压开采过程中井筒完整性及海底面沉降. Jin等^[12]分析了水平井降压开采中国南海神狐海域水合物藏时储层的力学响应, 结果表明开采初期沉降量占总沉降量的一半以上. 李令东等^[13-14]综合考虑热传导、对流、水合物分解、地层力学性质变化等过程及其相互耦合作用, 建立了温度影响天然气水合物地层井壁稳定的数学模型, 通过有限元求解, 分析了钻井液温度对地层水合物分解、地层力学性质变化及井壁稳定的影响规律. 程家望等^[15]基于多孔介质流体动力学和弹性力学理论, 建立了天然气水合物降压开采储层稳定性数学模型, 力学分析包括储层沉降和井壁稳定性两个方面, 但该模型忽略了温度对水合物分解过程的影响. 孙嘉鑫等^[16-17]同样搭建了TOUGH+Hydrate和FLAC$^{\rm 3D}$耦合接口程序, 并对钻采条件下南海水合物井壁及储层响应特性进行模拟分析, 较全面地评价了水合物钻进及降压开采过程中井壁稳定、地层沉降和开采潜能等情况, 并进行了敏感性分析.

从整体上看, 已有的数值软件多以搭接不同模拟器来研究水合物开采过程中的多场耦合问题, 这导致了较低的计算效率. 此外, 大多数值模型并未全面考虑温度和水合物分解对地层力学性质的影响. 因此, 本文结合TOUGH+Hydrate已有的传热-流动(TH)数学模型, 基于扩展后的Biot力学固结理论, 建立能够刻画含水合物沉积层特征的传热-流动-力学(THM)耦合数学模型, 开发了有限元程序对其进行数值求解. 以南海神狐海域SH2站位水合物藏条件为例, 进行水合物藏降压开采的模拟计算, 预测水合物开采过程中储层温度场、压力场、应力场的演化, 分析了地层沉降和井壁稳定性问题.

1 传热-流动-力学耦合数学模型

传热-流动-力学耦合模型的建立存在如下假设: 多相流动过程满足达西定律; 相对于对流传输, 溶解气体和抑制剂等在运移过程中的机械弥散作用可以忽略不计; 对于应力场求解, 假定岩土体饱和、骨架线弹性、变形微小; 降压开采过程中不考虑地层出砂.

1.1 渗流连续性方程

含水合物地层孔隙中通常包含水、气和水合物三相, 水合物分解后变成甲烷气体和水, 通常只考虑气体和水为可流动相. 根据连续性方程和达西定律, 可得到气、水两相耦合的渗流方程为

(1)$ \begin{eqnarray} &&\frac{\partial(\phi\rho_{\beta}S_{\beta})}{\partial t}=\nabla\left[\frac{k_{r\beta}\rho_\beta}{\mu_\beta}k(\nabla P_\beta+\rho_\beta g)\right]+m_\beta+q_\beta, \\&&\qquad\beta= {\rm w,\ g} \end{eqnarray}$

水合物分解/形成过程中固相水合物质量守恒方程为

(2)$ \begin{eqnarray} \frac{\partial(\phi\rho_{\rm h}S_{\rm h})}{\partial t}=-m_{\rm h} \end{eqnarray}$

水合物分解/形成过程保持质量守恒, 因此水合物分解速率和甲烷气体生成速率满足如下关系

(3)$ \begin{eqnarray} m_{\rm h}=\left(\frac{M_{\rm w}N_{\rm h}+M_{\rm g}}{M_{\rm g}}\right)m_{\rm g} \end{eqnarray}$

式(1) $\sim\!$式(3)中, $\phi$为储层孔隙度; $\rho_\beta$为相密度, kg/m$^{3}$; $S_\beta$为相饱和度; $k_{r\beta}$为相对渗透率; $\mu_\beta$为相黏滞度, Pa$\cdot$s; $k$为储层广义达西渗透率矩阵, m$^{2}$;$P_\beta$为流体压力, Pa; $g$为重力加速度, m/s$^{2}$; $m_\beta$为单位体积储层内水合物分解产气/产水速率, kg/(m$^{3}\cdot$s); $q_\beta$为气/水源汇项, kg/(m$^{3}\cdot$s); $M_{\rm w}$和$M_{\rm g}$分别为水和甲烷气的摩尔质量; $N_{\rm h}$为水分子数, 甲烷水合物通常取为6.0; $\beta=$ w, g, h分别指水相、气相和水合物相.

1.2 能量守恒方程

水合物分解是一个吸热反应, 因此热传递过程是影响水合物开采过程的重要因素. 综合考虑热传导、对流、水合物分解和外界热量补给等因素, 忽略动能和辐射传热, 得到含水合物地层能量守恒方程如下

(4)$ \begin{eqnarray} &&\frac{\partial}{\partial t}\left[(1-\phi)\rho_{\rm r}C_{\rm r}T+\sum_{\beta={\rm w,g,h}}\phi S_\beta\rho_\beta U_\beta\right]= \\&&\qquad \nabla\cdot(K_{\theta}\nabla T)+Q_{\theta}+Q_{\rm h}-\nabla\cdot\sum_{\beta={\rm w,g}}\rho_\beta u_\beta h_\beta \end{eqnarray}$

式中, $\rho_{\rm r}$为岩石颗粒密度, kg/m$^{3}$; $C_{\rm r}$为比热容, J/(kg$\cdot$K); $T$为地层温度, ${^\circ}$C;$U_\beta$为相内能, J/kg; $K_\theta$为地层有效热传导系数, W/(m$\cdot$K);$Q_\theta$为能量源汇项, W/m$^{3}$; $Q_{\rm h}$为水合物分解热, W/m$^{3}$; $ u_\beta$为相流速, m/s;$h_\beta$为相热焓, J/kg.

1.3 应力场方程

1.3.1 平衡方程

忽略动量的变化量, 平衡方程用有效应力可表示为

(5)$ \begin{eqnarray} \sigma_{ij,j}-(\alpha \delta_{ij}P_i)+F_i=0 \end{eqnarray}$

式中, $\sigma_{ij}$为地层骨架应力, Pa; $P_i$为地层孔隙流体压力, Pa; $\alpha$为Biot系数, 通常取值1.0;$F_i$为体力载荷, Pa; $\delta_{ij}$为Kronecker函数.

1.3.2 几何方程

几何方程定义了位移量与应变之间的关系, 其张量形式为

(6)$ \begin{eqnarray} \varepsilon_{ij}=(u_{i,j}+u_{j,i})/2 \end{eqnarray}$

式中, $\varepsilon_{ij}$为应变张量, $u$为位移.

1.3.3 本构方程

由于固相水合物是含水合物地层的有效胶结成分, 其分解/形成会明显改变地层的力学性质.为了考虑不断演化的含水合物地层力学性质, 采用弹塑性本构方程刻画应力与应变之间的内在联系,其增量形式如下

(7)$ \begin{eqnarray} {\rm d}\varepsilon_{ij}=D_{ijkl}{\rm d}\varepsilon_{kl} \end{eqnarray}$

式中, ${\rm d}\varepsilon_{ij}$为有效应力增量, $D_{ijkl}$为含水合物地层的弹塑性矩阵, ${\rm d}\varepsilon_{kl}$为应变增量矩阵.

1.4 水合物地层相关辅助方程

1.4.1 水合物分解动力学模型

在动力学平衡控制条件下, 采用Kim等^[18]水合物分解动力学模型

(8)$ \begin{eqnarray} m_{\rm h}=-K_0\exp\left(\frac{\Delta E_{\rm a}}{RT}\right)F_{\rm A}A(f_{\rm eq}-f_{\rm g}) \end{eqnarray}$

式中, $K_0$为水合物分解速率常数, kg/(m$^{2}\cdot $Pa$\cdot$s); $\Delta E_{\rm a}$为水合物反应活化能, J/mol; $R$为气体常数, 8.314 J/(mol$\cdot$K); $F_{\rm A}$为反应面积拟合参数; $A$为反应比表面积, m$^{2}$;$f_{\rm eq}$为当前温度下的平衡逃逸度, Pa; $f_{\rm g}$为当前温度下的气相逃逸度, Pa.

1.4.2 含水合物地层渗透率演化模型

水合物分解/形成过程将明显改变多孔介质的渗流通道, 从而影响地层的渗透性能.本次研究采用毛管束模型刻画固相水合物演化引起的地层渗透率变化

(9)$ \begin{eqnarray} k=k_0\left(\frac{\phi_0-S_{\rm h}-\phi_{\rm c}}{\phi_0-\phi_{\rm c}}\right)^n \end{eqnarray}$

式中, $k_0$为$S_{\rm h}=0$时的地层渗透率, m$^{2}$; $\phi_0$为参考状态地层孔隙度; $\phi_{\rm c}$为残余孔隙度;$n$为地层渗透率衰减指数.

1.4.3 含水合物地层力学特性演化模型

大量三轴试验表明, 含水合物地层的力学强度参数, 如弹性模量、体积模量、剪切模量和内聚力等明显受到水合物饱和度的影响, 但是对地层泊松比和内摩擦角的影响较小. 基于Rutqvist等^[2-3]的研究结果, 将含水合物地层的力学强度参数与水合物饱和度表达为如下线性关系

(10)$ \begin{eqnarray} E=E_0+E_{\rm h}S_{\rm h} \end{eqnarray}$

(11)$ \begin{eqnarray} C=C_0+C_{\rm h}S_{\rm h} \end{eqnarray}$

式(10) $\sim\!$式(11)中, $E$和$C$分别为含水合物沉积层的弹性模量和内聚力, Pa; $S_{\rm h}$为水合物饱和度;$E_0$和$C_0$分别为$S_{\rm h}=0$时地层的弹性模量和内聚力, Pa;$E_{\rm h}$和$C_{\rm h}$分别为水合物扰动弹性模量和扰动内聚力, Pa.

1.5 地层井壁稳定性评价准则

井壁坍塌失稳大多是由于井筒周围地层发生剪切破坏引起, 通过地层应力分析结合适当的剪切破坏准则可对地层和井壁的稳定性进行预测. 剪切破坏一般采用Mohr-Coulomb(MC)准则进行预测

(12)$ \begin{eqnarray} \tau\geqslant \tau_{\rm c}=C+\sigma_{\rm n}{\rm tg}\varphi \end{eqnarray}$

式中, $\tau$为地层内某一平面上的剪应力, 由应力分析求得, Pa; $\tau_{\rm c}$为地层临界破坏剪应力, Pa;$\sigma_{\rm n}$为地层破坏面上的有效正应力, Pa; $\varphi$为地层内摩擦角.

1.6 水合物开采传热-流动-力学过程耦合方法

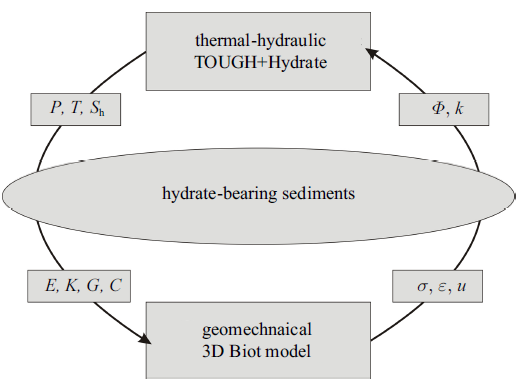
综合以上渗流连续性方程、能量守恒方程、应力场方程、水合物地层相关辅助方程、模型初始条件和边界条件, 便构成了完整的降压开采水合物藏THM耦合分析模型. 传热-流动-力学耦合过程具体分为两步: (1)根据TOUGH+Hydrate计算的地层孔隙压力、温度和水合物饱和度作为已知条件代入到力学模型, 确定含水合物地层力学性质后计算岩体骨架有效应力、应变和位移; (2)完成岩土力学计算后, 根据地层有效应力更新地层孔隙度和渗透率, 并反馈到下一个时间步长的传热和流动计算(图1).

图1

新窗口打开|下载原图ZIP|生成PPT
图1水合物藏开采传热-流动-力学过程耦合方法

Fig. 1Methodology of coupling thermo-hydro-mechanical processes for hydrate-bearing sediments

2 模型建立

2.1 地质条件

2007年中国地质调查局执行GMGS1水合物钻探航次, 分别在神狐海域SH2、SH3和SH7三个钻孔中取得水合物实物样品(图2)^[19-20]. 本次研究以SH2站位地质条件为基础, 分析降压开采水合物藏地层井壁稳定性. SH2站位海底面水深约1235 m, 水合物赋存于海底面以下185 m, 含水合物层厚约40 m. 含水合物地层孔隙度在0.3$\sim$0.48之间变化, 水合物饱和度为25%$\sim $48%, 渗透率为10 mD(1 mD = $1.0\times10^{ - 15}$ m$^{2}$)左右, 地层地温梯度为(45.0$\sim$67.7)${^\circ}$C/km. 水合物储层的上下伏地层岩性与水合物储层一致, 均为弱透水性的泥质粉砂, 因此研究区水合物储层为典型的2类水合物藏^[21].

图2

新窗口打开|下载原图ZIP|生成PPT
图2南海神狐海域GMGS1天然气水合物钻探航次钻孔分布图

Fig. 2Location of drilling sites for the GMGS1 in Shenhu area of the South China Sea

2.2 水合物开采概念模型

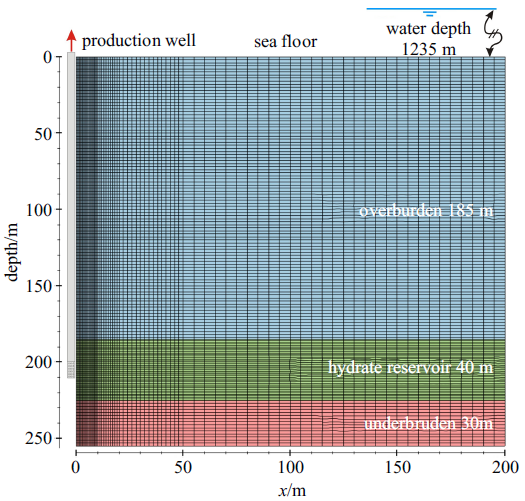
根据SH2站位资料, 将其概化为水平延伸地层, 建立如图3所示的平面应变模型, 模型尺寸为200 m$\times$255 m ($x$, $z$). 垂直方向: 水合物储层厚40 m, 水合物储层之上为185 m厚的透水顶板, 其下为30 m厚的下伏地层, 模型顶面即为海底面; 水平方向模型侧向延伸200 m. 生产井位于$x=0$ m位置处, 半径$r=0.1$ m. 模型顶面为海底面, 设定为定温定压边界; 由于钻探结果表明水合物储层下伏地层未存在隔水泥岩层, 因此模型底面同样设定为透水边界; 模型侧边界设定为零流量边界. 对于力学边界, 将模型的侧面沿法线方向上的位移设为零, 即固定位移边界; 模型底面$z=255$ m的截面, 保持$z$方向上的位移为零; 模型最顶面$z=0$ m的截面为海底面, 模型中设定为自由位移边界, 即降压开采过程中海底面可以发生自由移动; 井壁在模型中设定为刚形体, 井壁和地层之间为刚性接触, 即井壁在模型计算过程中只能承受应力, 但不发生变形.

图3

新窗口打开|下载原图ZIP|生成PPT
图3神狐海域SH2站位水合物降压开采传热-流动-力学耦合概念模型

Fig. 3Conceptual model for coupling thermal-hydro-mechanical processes of gas production by depressurization from Shenhu SH2 hydrate reservoir

已有的数值模拟研究表明水合物开采过程中的关键过程主要发生在生产井附近10$\sim$20 m范围内. 为了准确刻画水合物的分解演化过程, 获取近井地层水合物分解的重要现象, 模型对生产井附近的数值网格进行加密处理(见图3). 水平方向剖分20个0.5 m, 10个1.0 m, 15个2.0 m和30个5.0 m子网格, 共计剖分75列; 垂直方向水合物储层内网格精度均为1.0 m, 边界地层网格精度为2.0 m, 共计剖分148层. 因此, 整个储层模型被离散为$75\times148=11 100$个计算网格.

2.3 模型参数

模型所采用的地层物性参数主要依据现场测试数据, 详见表1. 为便于研究, 水合物储层含水合物饱和度取值0.4, 地层孔隙度依据现场岩性分析数据取值0.38, 渗透率为10 mD. 水合物储层底界初始压力和初始温度分别为14.7 MPa和14.1$^\circ$C, 保证了水合物储层在开采前的稳定存在状态. 含水合物地层的相对渗透率和毛细压力计算分别采用Stone模型和vanGenuchten模型, 这些模型被广泛用于从水合物藏回收甲烷气体的数值模型中^[2,5-6,15].

由于缺乏现场水合物储层力学测试数据, 本次研究含水合物地层力学参数依据Masui等^[22-23]的室内三轴试验结果选取(表2). 水合物藏开采过程中地层的力学强度参数随水合物饱和度的变化而变化^[24-29].

Table 1
表1
表1模型计算所用地层物性参数^{[5-6, 19-20]}
Table 1Parameters of hydrate deposits used for simulation^{[5-6, 19-20]}

新窗口打开|下载CSV

Table 2
表2
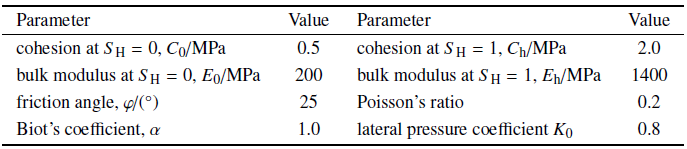
表2含水合物地层力学强度参数
Table 2Mechanical parameters for hydrate-bearing sediments

新窗口打开|下载CSV

2.4 初始条件

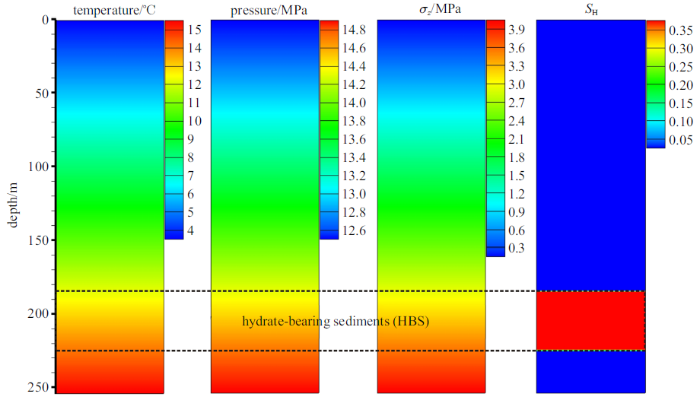
图4显示了模型初始条件, 包括地层温度、孔隙压力、垂向有效应力和水合物分布. 模型垂向上的初始温度场根据海底面的初始温度依地温梯度变化计算得到; 由于研究区地层为未固结沉积层, 初始压力场服从静水压力分布; 模型初始垂向有效应力假设仅仅是由于上覆地层自重引起, 初始有效水平应力依据侧压力系数$K_{0}$计算得到; 水合物储层位于海底面以下185 m至225 m之间, 水合物初始饱和度为0.4.

图4

新窗口打开|下载原图ZIP|生成PPT
图4模型初始温度场、孔隙压力场、垂向有效应力场和水合物储层分布特征

Fig. 4Initial conditions of temperature, pore pressure, effective stress, and hydrate saturation

2.5 生产方案

本次研究利用竖直井进行降压开采条件下的产气能力与沉降规律预测. 由于水合物储层上下为透水地层, 将竖直井射孔段布设于水合物储层中部, 长度为10 m (图3). 生产井射孔段距水合物储层顶底面各15 m, 这样有利于水合物储层的有效降压, 限制边界地层水快速涌入生产井筒. 模型连续开采模拟时间为1年, 井筒降压幅度设定为10 MPa.

3 结果分析

3.1 气水产出动态特征

图5显示了垂直井降压开采2类水合物藏水合物分解甲烷释放速率($Q_{\rm R}$), 生产井产气速率($Q_{\rm P}$),水合物分解($V_{\rm R}$)和生产井($V_{\rm P}$)累积产气体积随时间演化特征. 降压开采初期(前20 d), $Q_{\rm R}$和$Q_{\rm P}$均快速降低, 这主要是由于开采初期生产井和周围储层存在较大的压力梯度, 导致生产井周围大量的水合物发生分解. 随着开采的持续进行, 低压区域逐渐向储层内部发展, 生产井和水合物储层之间的压力梯度逐渐趋于平缓, 从而导致开采后期$Q_{\rm R}$和$Q_{\rm P}$逐渐降低. 连续开采1年后, $V_{\rm R}= 1.36\times 10^{4}$ m$^{3}$, $V_{\rm P} = 1.20\times 10^{4}$ m$^{3}$, 甲烷气体回收效率可达88%, 由此可见降压技术是开采2类水合物藏的有效方法.

图5

新窗口打开|下载原图ZIP|生成PPT
图5水合物分解甲烷释放速率$Q_{\rm R}$、生产井产气速率$Q_{\rm P}$、水合物分解累积产气体积$V_{\rm R}$和生产井累积产气体积$V_{\rm P}$随时间演化特征

Fig. 5Evolution of gas release rate ($Q_{\rm R})$, production rate ($Q_{\rm P})$, and the cumulative volumes of released from hydrate ($V_{\rm R})$ and produced ($V_{\rm P})$ in the production well

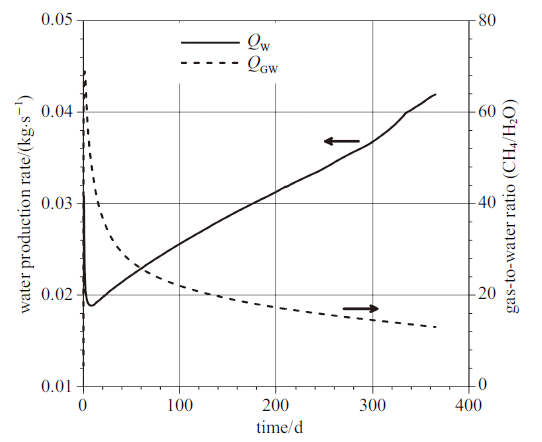
图6显示了生产井产水速率($Q_{\rm W}$)和气水体积比($R_{\rm GW}$)随时间演化特征. 开采初期$Q_{\rm W}$快速降低, 与$Q_{\rm P}$和$Q_{\rm R}$相似, 该阶段产水主要来自于水合物储层. 连续开采大约20 d后, $Q_{\rm W}$随时间逐渐增大. 这主要是由于开采后期水合物储层下部的水合物逐渐分解(图7), 有效渗透率增大, 导致生产井与下伏地层之间的水力连通性增强, 大量自由水从下伏地层涌入生产井造成$Q_{\rm W}$不断增大, 这与苏正等^[5,30]的研究结果一致.

图6

新窗口打开|下载原图ZIP|生成PPT
图6生产井产水速率$Q_{\rm W}$和气水体积比$R_{\rm GW}$随时间演化特征

Fig. 6Evolution of water production rate ($Q_{\rm W})$ and gas to water ratio ($R_{\rm GW})$

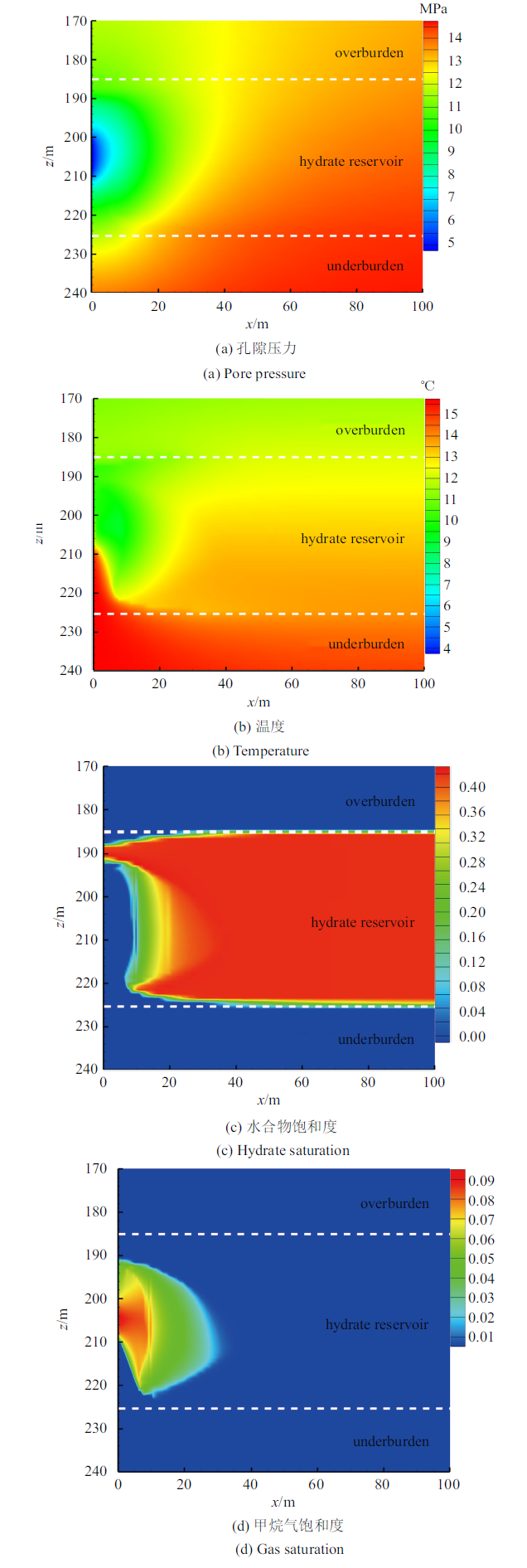
图7显示了模型预测在降压开采1年后, 地层中孔隙水压力、温度、水合物饱和度和甲烷气饱和度的空间分布特征. 从图中可以看出: (1)井筒降压导致井周地层孔隙水压力降低, 并迅速在储层中传播; (2)储层降压打破了水合物的相平衡状态, 根据低压区分布可知射孔段周围水合物优先发生分解, 且连续开采1年后水合物分解前缘已扩展至下伏边界地层; (3)水合物分解吸热导致生产井射孔段周围形成一低温区域, 由于开采后期生产井与下伏地层取得水力连通导致下伏边界层中的相对高温地层水涌入生产井, 并在生产井射孔段以下形成一明显的高温热柱, 这指示出下伏边界层中地层水涌入生产井的流体运移通道; (4)从甲烷气饱和度空间分布图可以看出, 水合物分解区主要集中在生产井周围25 m以内.

图7

新窗口打开|下载原图ZIP|生成PPT
图7降压开采365天后各参数的空间分布特征

Fig. 7Spatial distribution of the parameters after 365 days depressurization

综合分析图5 $\sim\!$图7表明, 开采后期生产井与下伏饱水地层取得水力连通后水合物开采效率随时间快速降低. 这主要是由于(1)大量自由水从下伏地层涌入生产井导致水合物储层降压受到抑制, 水合物分解前缘难以向储层内部扩展; (2)大量回收地层水将过度消耗外部能量. 因此, 今后针对2类水合物藏开采潜力预测研究中应对布井和开采方案进行优化, 以保证较高的水合物开采效率.

3.2 地层沉降特征

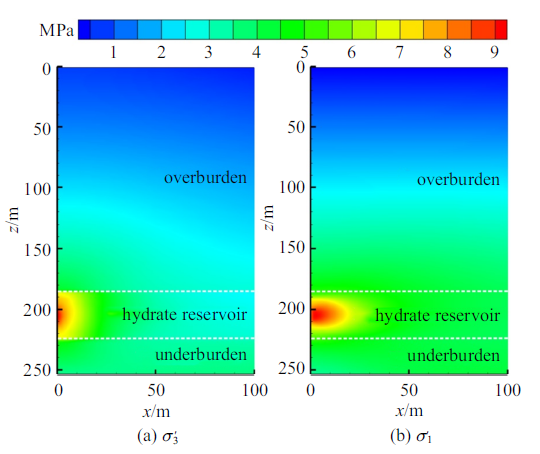
水合物藏降压开采过程中地层有效应力的演化是预测地层破坏和出砂位置的关键. 图8中显示了降压开采1年后地层中(a)最小水平有效主应力和(b)最大有效主应力的空间分布特征. 从图中可以看出, 降压导致生产井射孔段周围地层出现明显应力集中, 因此, 这些区域是井壁破坏和地层出砂的主要位置. 由于下伏透水地层的补给作用, 导致降压难以在水合物储层中传播, 因此有效应力增大区域主要限定在生产井周围地层中.

图8

新窗口打开|下载原图ZIP|生成PPT
图8降压开采365天后地层有效主应力空间分布特征

Fig. 8Spatial distribution of effective stress after 365 days depressurization

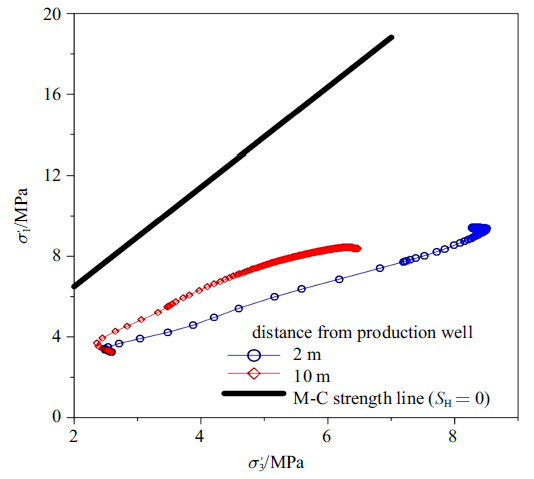
为了进一步定量分析井周地层是否发生屈服破坏, 在应力集中区域选择2个监测点进行有效主应力路径和破坏分析(图9), 监测点坐标($x$, $z$)分别为(2 m, 204.5 m)和(10 m, 204.5 m). 从图中可以看出, 在1年的开采周期内, 生产井周围地层不会发生屈服破坏. 这主要是由于降压引起垂向有效应力和最小水平有效应力同时增大, 并未出现明显的偏应力. 另一方面, 可渗透下伏地层的补给作用限制了井周地层有效应力的增大, 这在一定程度上缓解了地层出现屈服破坏.

地层孔隙压力降低造成骨架有效应力增大, 从而引起地层变形沉降. 图10显示了降压开采过程中水合物储层顶部发生沉降的空间分布特征. 从图中可以看出, 井壁附近地层的沉降量最大, 向储层内部延伸沉降量逐渐减小. 这主要是由于(1)生产井周围地层降压幅度较大, 且出现明显的应力集中现象(图8); (2)生产井周围水合物发生完全分解(图7), 降低了地层的力学强度, 从而加剧了井周地层的沉降. 随着降压开采的持续进行, 地层沉降逐渐增加. 连续开采50 d时, 最大沉降量为0.13 m. 然而, 连续开采1年后, 最大沉降量增大到0.19 m, 相对50 d时的沉降量仅增大了0.06 m. 由此可以看出垂直井降压开采水合物, 地层沉降主要发生在开采初期. 因此, 开采前期可以采用逐步降压的方式缓解快速的地层沉降阶段, 这样可以有效避免快速沉降引起井筒套管破裂的风险.

图9

新窗口打开|下载原图ZIP|生成PPT
图9水合物储层中不同监测点位置有效主应力路径

Fig. 9Effective principal stress paths at different monitoring points in hydrate reservoir

图10

新窗口打开|下载原图ZIP|生成PPT
图10水合物储层顶部空间沉降特征

Fig. 10Spatial distribution of the vertical displacement at the top of hydrate reservoir

3.3 井壁稳定性分析

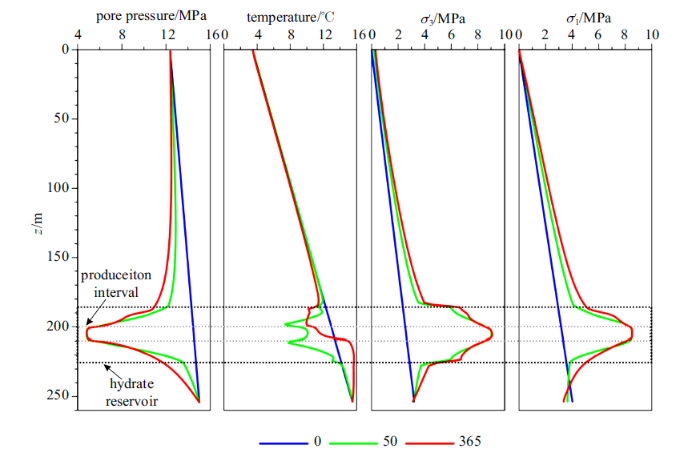
井壁坍塌失稳是制约水合物藏钻井和开采过程顺利实施的关键问题, 一般可通过井周应力状态分析结合适当的剪切破坏准则进行预测. 图11显示了沿生产井壁孔隙压力、温度、水平有效主应力和最大有效主应力在不同时间的分布特征. 从图中可以看出, 井筒降压导致射孔段附近压力快速降低, 降压幅度受井筒内流体压力控制, 随后低压逐渐沿井壁向上下扩展. 水合物分解吸热效应和低温流体流向生产井的共同作用导致射孔段井壁温度明显降低, 最大降温幅度可达6${^\circ}$C, 但是开采后期由于下伏地层的相对高温流体涌入导致射孔段井壁温度升高. 在孔隙压力和温度的共同作用下, 射孔段井壁有效应力出现明显集中. 连续降压开采1年后, 射孔段井壁水平有效主应力最大为9.1 MPa, 相比于初始有效应力增加了6.6 MPa;垂直有效主应力最大为8.5 MPa, 相比于初始有效应力增大了5.2 MPa. 有效应力在水平方向的增加量大于垂直方向, 这主要是由于水平方向受到限制, 而垂直方向地层可以发生自由移动.

图11

新窗口打开|下载原图ZIP|生成PPT
图11沿生产井方向井壁孔隙压力、温度、水平有效主应力和垂向有效主应力分布

Fig. 11The distribution of pore pressure, temperature, horizontally effective stress, and vertically effective stress along the production well

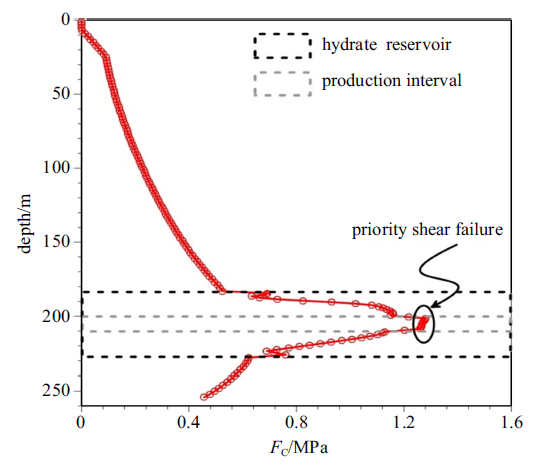
井壁有效应力增大可能诱发井壁发生坍塌破坏, 按照之前提到的破坏分析方法, 计算得到开采1年后的井壁破坏风险分析值, 其沿井筒分布特征如图12所示. 从图中可以看出, 随着开采的持续进行井壁发生剪切破坏的风险逐渐增加, 且在射孔层段井壁破坏风险最大^[31]. 由于射孔段井壁应力集中最为明显, 导致射孔段井壁最易发生剪切破坏(图12). 这表明射孔段是储层出砂和坍塌破坏的高危区域, 一旦射孔段发生坍塌破坏将导致大量的地层骨架介质涌入生产井筒, 造成井筒失效. 为了有效避免生产井壁坍塌, 射孔段井筒套管应具备足够高的力学强度以支撑降压引起的应力集中, 同时防止井周地层发生破坏.

图12

新窗口打开|下载原图ZIP|生成PPT
图12沿生产井方向井壁发生剪切破坏风险

Fig. 12The distribution of possibility of shear failure along the production well

4 结论

本文基于扩展的Biot固结理论, 考虑水合物分解相变、传热、流动、岩土体变形等过程及其相互耦合作用, 建立了天然气水合物开采地层稳定性分析模型. 以神狐海域GMGS1航次SH2站位水合物储层条件为研究对象, 进行了水合物藏降压开采地层井壁稳定性的模拟分析, 得出以下结论:

(1)水合物储层下伏地层透水是限制2类水合物藏降压开采效率的主要因素, 今后的研究中应对布井和开采方案进行优化, 以保证此类水合物储层较高的水合物开采效率.

(2)井筒降压导致地层有效应力增大, 从而引起地层发生沉降, 且地层的沉降主要发生在降压开采前期, 最大沉降位置位于井壁周围, 向储层内部延伸地层沉降量快速减小. 建议降压开采前期利用逐步降压以缓解该阶段出现的快速地层沉降, 这样可以有效避免快速沉降引起井筒套管破裂的风险.

(3)水合物分解导致井周地层力学强度降低, 加剧了水合物储层的沉降. 由于井筒降压造成射孔段井壁应力集中最为明显, 导致射孔段井壁最易发生剪切破坏, 因此, 这些区域是水合物开采出砂防治的主要区域.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

宁伏龙, 张可霓, 吴能友等. 钻井液侵入海洋含水合物地层的一维数值模拟研究
地球物理学报, 2013,56(1):204-218

[本文引用: 1]

( Ning

Fulong

, Zhang

Keni

, Wu

Nengyou

, et al. Invasion of water-based drilling mud into oceanic gas-hydrate-bearing sediment: One-dimensional numerical simulations
Chinese Journal of Geophysics, 2013,56(1):204-218 (in Chinese))

[本文引用: 1]

[2]

Rutqvist

, Moridis

, Grover

, et al. Coupled multiphase fluid flow and wellbore stability analysis associated with gas production from oceanic hydrate-bearing sediments
Journal of Petroleum Science & Engineering, 2012, 92-93(4):65-81

[本文引用: 4]

[3]

Rutqvist

, Moridis

, Grover

, et al. Geomechanical response of permafrost-associated hydrate deposits to depressurization-induced gas production
Journal of Petroleum Science & Engineering, 2009,67(1):1-12

[本文引用: 4]

[4]

Sun

, Zhang

, Ning

, et al. Production potential and stability of hydrate-bearing sediments at the site GMGS3-W19 in the South China Sea: A preliminary feasibility study
Marine & Petroleum Geology, 2017,86:447-473

[本文引用: 1]

[5]

苏正, 吴能友, 张可霓 . 南海北部陆坡神狐天然气水合物开发潜力
海洋地质前沿, 2011(6):16-23

[本文引用: 5]

( Su

Zheng

, Wu

Nengyou

, Zhang

Keni

. Numerical simulation on production potential of hydrate deposits by thermal stimulation
Journal of Tropical Oceanography, 2011(6):16-23 (in Chinese))

[本文引用: 5]

[6]

金光荣, 许天福, 刘肖等. 天然气水合物降压热激法模拟开采方案优化研究
中南大学学报(自然科学版), 2015(4):1534-1543

[本文引用: 3]

( Jin

Guangrong

, Xu

Tianfu

, Liu

Xiao

, et al. Optimization of gas production from hydrate deposit using joint depressurization and thermal stimulation
Journal of Central South University (Science and Technology, 2015(4):1534-1543 (in Chinese))

[本文引用: 3]

[7]

Chen

, Feng

, Kogawa

, et al. Construction and simulation of reservoir scale layered model for production and utilization of methane hydrate: The case of Nankai Trough Japan
Energy, 2018,143:128-140

[8]

Yuan

, Xu

, Xin

, et al. Multiphase flow behavior of layered methane hydrate reservoir induced by gas production
Geofluids, 2017,2017:1-15

[本文引用: 1]

[9]

Kimoto

, Oka

, Fushita

. A Chemo-Thermo-Mechanically coupled analysis of ground deformation induced by methane hydrate dissociation
International Journal of Mechanical Sciences, 2010,52(2):365-376

[本文引用: 1]

[10]

Lin

, Uchida

, Myshakin

, et al. Assessing the geomechanical stability of interbedded hydrate-bearing sediments under gas production by depressurization at NGHP-02 Site 16
Marine and Petroleum Geology, 2019 (in Press)

[本文引用: 1]

[11]

Qiu

, Yamamoto

, Birchwood

, et al. Well-integrity evaluation for methane-hydrate production in the deepwater Nankai Trough
SPE Drilling & Completion, 2015,30(1):52-67

[本文引用: 1]

[12]

Jin

, Lei

, Xu

, et al. Simulated geomechanical responses to marine methane hydrate recovery using horizontal wells in the Shenhu area, South China Sea
Marine and Petroleum Geology, 2018,92:424-436

[本文引用: 1]

[13]

李令东, 程远方, 梅伟等. 温度影响天然气水合物地层井壁稳定的有限元模拟
天然气工业, 2012,32(8):74-78

[本文引用: 1]

( Li

Lingdong

, Cheng

Yuanfang

, Mei

Wei

, et al. Finite element simulation of temperature impact on wellbore stability of gas-hydrate-bearing sediments
Natural Gas Industry, 2012,32(8):74-78 (in Chinese))

[本文引用: 1]

[14]

李令东, 程远方, 周建良等. 深水钻井天然气水合物地层井壁稳定流固耦合数值模拟
中国海上油气, 2012,24(5):40-45

[本文引用: 1]

( Li

Lingdong

, Cheng

Yuanfang

, Zhou

Jianliang

, et al. Fluid-solid coupling numerical simulation on wellbore stability in gas-hydrate-bearing sediments during deep water drilling
China Offshore Oil and Gas, 2012,24(5):40-45 (in Chinese))

[本文引用: 1]

[15]

程家望, 苏正, 吴能友 . 天然气水合物降压开采储层稳定性模型分析
新能源进展, 2016,4(1):33-41

[本文引用: 2]

( Cheng

Jiawang

, Su

Zheng

, Wu

Nengyou

. A geomechanical stability model analysis of hydrate reservoir for gas hydrate production by depressurization
Advances in New and Renewable Energy, 2016,4(1):33-41 (in Chinese))

[本文引用: 2]

[16]

Sun

, Zhang

, Ning

, et al. Production potential and stability of hydrate-bearing sediments at the site GMGS3-W19 in the South China Sea: A preliminary feasibility study
Marine & Petroleum Geology, 2017,86:447-473

[本文引用: 1]

[17]

Sun

, Ning

, Lei

, et al. Wellbore stability analysis during drilling through marine gas hydrate-bearing sediments in Shenhu area: A case study
Journal of Petroleum Science and Engineering, 2018,170:345-367

[本文引用: 1]

[18]

Kim

, Bishnoi

, Heideman

, et al. Kinetics of methane hydrate decomposition
Chemical Engineering Science, 1987,42(7):1645-1653

[本文引用: 1]

[19]

吴能友, 张海啟, 杨胜雄等. 南海神狐海域天然气水合物成藏系统初探
天然气工业, 2007,27(9):1-6

[本文引用: 3]

( Wu

Nengyou

, Zhang

Haiqi

, Yang

Shengxiong

, et al. Preliminary discussion on natural gas hydrate (NGH) reservoir system of Shenhu area, North Slope of South China Sea
Natural Gas Industry, 2007,27(9):1-6 (in Chinese))

[本文引用: 3]

[20]

刘昌岭, 孟庆国, 李承峰等. 南海北部陆坡天然气水合物及其赋存沉积物特征
地学前缘, 2017,24(4):41-50

[本文引用: 3]

( Liu

Changling

, Meng

Qingguo

, Li

Chengfeng

, et al. Characterization of natural gas hydrate and its deposits recovered from the northern slope of the South China Sea
Earth Science Frontiers, 2017,24(4):41-50 (in Chinese))

[本文引用: 3]

[21]

Moridis

, Reagan

. Estimating the upper limit of gas production from Class 2 hydrate accumulations in the permafrost: 1. Concepts, system description, and the production base case
Journal of Petroleum Science & Engineering, 2011,76(3-4):194-204

[本文引用: 1]

[22]

Masui

, Haneda

, Ogata

, et al. The effect of saturation degree of methane hydrate on the shear strength of synthetic methane hydrate sediments//
Proceedings of the 6th International Conference on Gas Hydrates, Trondheim, Norway, 2005

[本文引用: 1]

[23]

Masui

, Miyazaki

, Haneda

, et al. 2008. Mechanical characteristics of natural and artificial gas hydrate bearing sediments//
Proceedings of the 6th International Conference on Gas Hydrates, Vancouver, British Columbia,Canada, 2008

[本文引用: 1]

[24]

石要红, 张旭辉, 鲁晓兵等. 南海水合物黏土沉积物力学特性试验模拟研究
力学学报, 2015,47(3):521-528

[本文引用: 1]

( Shi

Yaohong

, Zhang

Xuhui

, Lu

Xiaobing

, et al. Experimental study on the static mechanical properties of hydrate-bearing silty-clay in the South China Sea
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(3):521-528 (in Chinese))

[本文引用: 1]

[25]

吴二林, 魏厚振, 颜荣涛等. 考虑损伤的含天然气水合物沉积物本构模型
岩石力学与工程学报, 2012,31(a01):3045-3050

( Wu

Erlin

, Wei

Houzhen

, Yan

Rongtao

, et al. Constitutive model for gas hydrate-bearing sediments considering damage
Chinese Journal of Rock Mechanics and Engineering, 2012,31(a01):3045-3050 (in Chinese))

[26]

刘乐乐, 张旭辉, 刘昌玲等. 含水合物沉积物力学性质三轴剪切试验与损伤统计分析
力学学报, 2016,48(3):720-729

( Liu

Lele

, Zhang

Xuhui

, Liu

Changling

, et al. Triaxial shear tests and statistical analyses of damage for methane hydrate-bearing sediments
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(3):720-729 (in Chinese))

[27]

Hyodo

, Li

, Yoneda

, et al. Effects of dissociation on the shear strength and deformation behavior of methane hydrate-bearing sediments
Marine and Petroleum Geology, 2014,51:52-62

[28]

Yoneda

, Masui

, Konno

, et al. Mechanical behavior of hydrate-bearing pressure-core sediments visualized under triaxial compression
Marine and Petroleum Geology, 2015,66:451-459

[29]

Yoneda

, Masui

, Konno

, et al. Pressure-core-based reservoir characterization for geomechanics: Insights from gas hydrate drilling during 2012e2013 at the eastern Nankai Trough
Marine and Petroleum Geology, 2017,86:1-16

[本文引用: 1]

[30]

胡立堂, 张可霓, 高童 . 南海神狐海域天然气水合物注热降压开采数值模拟研究
现代地质, 2011,25(4):675-681

[本文引用: 1]

( Hu

Litang

, Zhang

Keni

, Gao

Tong

. Numerical studies of gas production from gas hydrate zone using heat injection and depressurization in Shenhu area, the South China Sea
Geoscience, 2011,25(4):675-681 (in Chinese))

[本文引用: 1]

[31]

雷宏武, 金光荣, 石岩等. 地下热-水动力-力学耦合过程数值模拟: 以CO$_{2}$地质储存为例
岩土力学, 2014,35(8):2415-2425

[本文引用: 1]

( Lei

Hongwu

, Jin

Guangrong

, Shi

Yan

, et al. Numerical simulation of subsurface coupled thermo-hydro-mechanical (THM) processes: Application to CO$_{2}$ geological sequestration
Rock and Soil Mechanics, 2014,35(8):2415-2425 (in Chinese))

[本文引用: 1]