张德春, 李鹏
, 2) , 梁森, 杨翊仁西南交通大学力学与工程学院, 成都 610031
A THEORETICAL AND EXPERIMENTAL STUDY ON THE STATIC AERO-ELASTIC INSTABILITY OF AN INVERTED CANTILEVERED PLATE IN A CONFINED SUBSONIC FLOW 1) Zhang Dechun, Li Peng
, 2) , Liang Sen, Yang YirenSchool of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China
通讯作者: 2)李鹏, 副教授, 主要研究方向: 非线性气动弹性振动及应用. E-mail:
meiyongyuandeze@163.com .
收稿日期: 2019-09-9
接受日期: 2020-02-28
网络出版日期: 2020-03-18
基金资助: 1)国家自然科学基金 .11302183 国家自然科学基金 .11772273 四川省科技科基础研究项目 .2015JY083
Received: 2019-09-9
Accepted: 2020-02-28
Online: 2020-03-18
作者简介 About authors
摘要 板壳结构在航空航天、高速列车、能量采集等诸多工程领域已经得到了广泛应用. 将悬臂壁板倒置于轴向气流中并在壁板周围流场中设置刚性壁面可有效地调控壁板的失稳速度, 是俘能器优化设计的重要措施之一. 但针对刚性壁面作用下亚音速气流中倒置悬臂壁板的失稳机制仍需要开展深入研究. 本文以受限亚音速气流中倒置的二维悬臂壁板为对象, 以理论分析及风洞实验为手段, 研究了单侧刚性壁面效应对倒置悬臂壁板静态失稳特性的影响规律. 在理论分析中, 首先应用镜像函数法来处理壁面约束条件, 基于算子理论研究获得了以Possio积分方程为表征的壁板气动力, 壁面效应实际表征为一包含移位Tricomi算子的复合算子; 然后将壁板失稳方程的求解问题转化为定区间上的函数逼近问题; 最后, 依据Wererstrass定理并利用最小二乘法求解该最优函数, 以获得系统的失稳临界参数. 在试验研究中依据压杆稳定原理设计了壁板静态失稳的测试方法并完成了风洞实验. 理论分析结果表明, 壁板会发生发散(静气动弹性)失稳, 临界动压随壁板与壁面间距的增加而增大并最终趋于稳定(无壁面情况); 通过理论与风洞实验结果的对比分析, 验证了本文气动力及理论分析的适用性及准确性. 针对倒置悬臂壁板结构的气动弹性失稳问题, 本文提出的方法不涉及系统方程的离散及特征值求解问题, 而是将其转化为了定区间上的函数逼近问题进行求解, 这为弹性结构静气动弹性失稳问题的研究提供了一个可行的新思路.
关键词： 倒置悬臂壁板 ;
Possio积分方程 ;
静气动弹性失稳 ;
最小二乘法 ;
风洞实验 Abstract The plate and shell structures have been widely used in many engineering areas such as aerospace, high-speed trains and energy harvesting. An inverted cantilever plate in an axial airflow confined by a rigid wall has the adjustable critical airflow velocity and is one of the most important ways for the optimization of energy harvesters. However, the mechanism of instability of inverted cantilever plates in rigid wall effect still needs further studies. This paper aims at the static aero-elastic instability of an inverted cantilevered plate in a confined subsonic flow, and such problem is studied by both the theoretical and the experiment analysis. In theory, first the effect of rigid wall is modelled by using the mirror image function and the fluid force on the plate is presented as a Possio integral equation within the frame work of differential operators, and the wall effect is featured by a composite operator involving the shifted Tricomi operator; then the solution of the instability equation is changed into the problem of approximation of function at a given interval; and finally the optimal solution is obtained by using the least square method with the help of the Wererstrass theorem. In experimental analysis, a test method for the static instability of the plate developed from the theory of column is applied for the wind tunnel test. The theoretical results show that the plate experiences the static aero-elastic instability; the critical dynamic pressure increases with the the increasing spacing between the wall and the plate but finally becomes steady (the case without rigid wall). A comparison of the present theoretical results with other existing theory and the experiment shows that the present theory is reliable and accurate. In this paper, the instability problem, which is not solved with the discretization of partial differential equation and by the eigenvalue analysis, has been transformed into the problem of approximation of function, and this can serve as another new thinking way to the problem of static aero-elastic instability of plates.
Keywords： inverted cantilevered plate ;
Possio integral equation ;
static aero-elastic instability ;
least square method ;
wind tunnel experiment PDF (7383KB) 元数据 多维度评价 相关文章 导出 EndNote |
Ris |
Bibtex 收藏本文 本文引用格式 张德春, 李鹏, 梁森, 杨翊仁. 受限亚音速气流中倒置悬臂壁板静气弹稳定性的理论及实验研究
1) .
力学学报 [J], 2020, 52(2): 431-441 DOI:
10.6052/0459-1879-19-255 Zhang Dechun, Li Peng, Liang Sen, Yang Yiren.
A THEORETICAL AND EXPERIMENTAL STUDY ON THE STATIC AERO-ELASTIC INSTABILITY OF AN INVERTED CANTILEVERED PLATE IN A CONFINED SUBSONIC FLOW 1) .
Chinese Journal of Theoretical and Applied Mechanics [J], 2020, 52(2): 431-441 DOI:
10.6052/0459-1879-19-255 引言 壁板是常见的结构形式, 其广泛地应用在诸多工程领域. 壁板结构在气流中的失稳问题是得到广泛关注的一个研究重点. 航空航天中的超音速壁板气动弹性问题已有了丰富的研究
[1 -4 ] . 最近针对亚音速壁板气动弹性问题的研究也随着高速列车的发展越来越受到重视
[5 -7 ] , 研究成果也越来越丰富. 针对壁板失稳问题, 相关的理论及实验研究主要是基于线性模型, 以预测失稳临界参数为目标 , 考察不同结构形式(如初始构型
[6 -7 ] , 边界条件
[8 -9 ] , 质量比及长宽比
[10 -16 ] 等)及不同流体力建模理论(如准定常点源
[5 -6 ,8 ] 及点涡理论
[7 ,12 ,17 ] , 非定常频域Theodorsen理论
[13 ] 及时域Peters有限入流模型
[7 ] , 数值涡格法
[14 -15 ] 及NS-结构方程耦合求解法
[16 ] 等)对分析结果的影响. 虽然线性建模方式简单且缺少对非线性因素的描述, 但对深入了解这类动力系统失稳问题的本质有着不可替代的优势
[1 ] . 已有的研究结果表明
[5 ,7 -9 ,13 -16 ] , 壁板的失稳形式(发散或颤振失稳)与流体速度及壁板边界约束形式密切相关. 两端固定的壁板(简支及固支)在超音速气流中会呈现颤振失稳而在亚音速气流中却仅会出现发散失稳. 然而当悬臂壁板置于亚/超音速流体中时却会分别经历颤振/发散失稳.
亚音速气流中的悬臂壁板相较于两端固定的壁板而言, 一般具有较低的失稳流速, 这使得其被广泛应用于俘能器的设计中
[18 -23 ] . 如何优化壁板的结构形式
[19 -20 ] 或设计流动特征
[21 ] 使得其具有较低的失稳速度、较强的运动幅度及较多的平衡状态是这类能量采集器的研究重点
[18 -21 ] . 已有研究表明, 一方面在壁板周围流场中设计某些流动约束, 如前置圆柱体
[21 ] 、设置壁面限制
[22 ] 等, 都会有效地降低壁板系统的失稳速度. 事实上, 将悬臂壁板倒置于气流中可获得一种简单却具有优良动力学特征的结构形式, 这是由于倒置悬臂壁板在结构
[24 ] 及气动力非线性
[25 ] 的作用下存在多稳态之间的跳跃迁移现象. 从目前的文献调研结果来看, 针对倒置悬臂壁板气动弹性问题的研究还比较有限. 已有的研究主要是通过数值模拟及风洞实验手段对结构失稳后的多稳态非线性特征进行定量分析
[24 -26 ] . 然而若要对多稳态特征进行更灵活的设计则需要对其出现的诱因, 即静态失稳问题, 从理论及实验方面进行有针对性的研究. 相关的研究主要是将未受限气流中的壁板视为升力线(面), 采用已有的气动力理论
[26 ] 进行建模分析, 然而已有气动力理论均只适用于非受限气流, 鲜有理论上考察壁面约束限制作用的研究报道.
事实上, 受限流体中壁板失稳问题也广泛地存在于实际工程中, 如核反应堆中的层叠板、隧道内的列车蒙皮及地效飞行器等. 目前相关的研究主要是采用理论方法(积分变换法及镜像函数法
[27 ] 等)、数值计算(面元法
[9 ] 等)对受限流体中悬臂壁板的颤振稳定性进行分析. 迄今为止, 还未见针对亚音速气流中倒置悬臂壁板这一结构形式开展的相关理论及实验研究, 本文旨在对这一问题进行研究以期更进一步丰富壁板气动弹性失稳问题的研究.
已有的研究表明, 当壁板长宽比小于1时, 可将其近似视为二维问题
[10 ,22 ] . 本文针对这一类受限亚音速气流中的二维倒置悬臂壁板的静态失稳问题进行理论及风洞实验研究, 以期了解刚性壁面效应对这类壁板结构静态失稳特性的影响规律. 首先, 采用镜像函数法描述壁面效应, 基于算子理论对壁板气动力进行研究; 其次, 将壁板失稳方程转化为定区间内的函数逼近问题并进行求解; 最后, 依据压杆稳定原理设计壁板静态失稳的测试方法, 完成风洞实验, 对理论及实验结果进行对比分析.
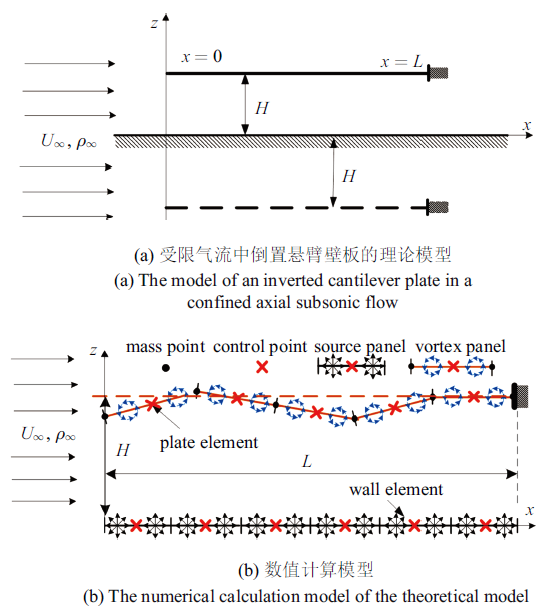
1 力学模型及数学方程 本文考虑如
图1 (a)所示的轴向受限亚音速气流中倒置的二维悬臂壁板模型, 壁板长度为$L$, 左端自由而右端受到固支约束. 气流沿板的轴向$x$方向流动并在壁板的一侧受到刚性壁面的限制, 刚性壁面与壁板平行且两者相距$H$. 本文旨在分析该壁板模型在气流中的失稳特性, 因此仅考虑壁板线性梁式弯曲运动微分方程
图1 新窗口打开 |
下载原图ZIP |
生成PPT 图1 Fig. 1 (1) $ \begin{eqnarray}\label{1} {\rho _s}h\frac{{{\partial ^2}w}}{{\partial {t^2}}} + D\frac{{{\partial ^4}w}}{{\partial {x^4}}} +\Delta p=0 \end{eqnarray}$ 及如下的边界条件
(2) $ \begin{eqnarray}\label{2} {\left. {\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right|_{x = 0}} = {\left. {\frac{{{\partial ^3}w}}{{\partial {x^3}}}} \right|_{x = 0}} = {\left. w \right|_{x = L}} = {\left. {\frac{{\partial w}}{{\partial x}}} \right|_{x = L}} = 0 \end{eqnarray}$ 其中, $w$, $\rho_s$, $h$分别为壁板的横向变形, 密度及厚度, $D = E{h^3}/12\left( {1 - {\nu ^2}} \right)$ 为壁板的抗弯刚度, $\nu$为壁板的泊松比, $\Delta p= {p_{{H^ + }}} - {p_{{H^ - }}}$为壁板上下表面扰动压力差(向下为正).
考虑理想欧拉流体, 通过引入等熵条件、小扰动假设和小扰动速度势可得壁板上下表面压力的近似线化表达式
[28 ] (3) $ \begin{eqnarray}\label{3} {p_{{H^ \pm }}} = {\left. { - {\rho _\infty }\left( {\frac{{\partial \varphi }}{{\partial t}} + U_\infty\frac{{\partial \varphi }}{{\partial x}}} \right)} \right|_{z = {H^ \pm }}} \end{eqnarray}$ 式中, $\rho _\infty$ 为气流密度, $\varphi$ 为扰动速度势函数, 其满足如下的线化速度势方程
(4) $ \begin{eqnarray}\label{4} \frac{{{\partial ^2}\varphi }}{{\partial {t^2}}} + 2{M_\infty }{a_\infty }\frac{{{\partial ^2}\varphi }}{{\partial x\partial t}} = a_\infty ^2{\beta ^2}\frac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + a_\infty ^2\frac{{{\partial ^2}\varphi }}{{\partial {z^2}}} \end{eqnarray}$ 其中${\beta ^2} = {1 - M_\infty ^2}$, 马赫数 $M_\infty$定义为气流来流速度$U_\infty$与 声速${a_\infty }$之比(${M_\infty } = {U_\infty}/{a_\infty }$). 势方程(4)需满足如下的边界条件
(5a) $ \begin{align} {\left. {\frac{{\partial \varphi }}{{\partial z}}} \right|_{z = 0}} = 0 \end{align} $ (5b) $ \begin{align} {\left. {\frac{{\partial \varphi }}{{\partial z}}} \right|_{z = H}} = v\left(z=H \right) = w_a,\ x \in \left[ {0,L} \right] \end{align} $ (5c) $ \begin{align} \Delta p=0,\ \ x \notin \left[ {0,L} \right] \end{align} $ (5d) $ \begin{align} \mathop {\lim }\limits_{x \to {L^ - }} \Delta p = 0 \end{align} $ 式(5a)为刚性壁面约束条件; 式(5b)为气固相容条件, 其中
$\begin{eqnarray*} {w_a} = \frac{{\partial w}}{{\partial t}} + U_\infty\frac{{\partial w}}{{\partial x}} \end{eqnarray*}$
定义为壁板表面的法洗速度; 式(5c)和式(5d)分别为流动的连续及Kutta-Joukowski条件. 方程(4)的定解还需要给定远场扰动量的条件和流场的初始条件
(6a) $\begin{align} &\mathop {\lim }\limits_{\left| x \right| \to \infty ,z \to \infty } u,\ \ v = 0 \end{align}$ (6b) $\begin{align} {\left. {\frac{{\partial \varphi }}{{\partial t}}} \right|_{t = 0}} = \varphi \left( {x,z,0} \right) = 0 \end{align}$ 2 Possio积分方程及其求解 注意到方程(4)为关于时间及空间的偏微分方程, 直接求解有很大困难. 将其左右两边关于时间作用${\cal L}$(Laplace)变换, 并
利用初始条件(6b), 可得
(7) $ \begin{eqnarray}\label{7} {\lambda ^2}\hat \varphi + 2{M_\infty }{a_\infty }\lambda \frac{{\partial \hat \varphi }}{{\partial x}} = a_\infty ^2{\beta ^2}\frac{{{\partial ^2}\hat \varphi }}{{\partial {x^2}}} + a_\infty ^2\frac{{{\partial ^2}\hat \varphi }}{{\partial {z^2}}} \end{eqnarray}$ 其中, $\hat \varphi = \int_0^{ + \infty } {\varphi {{\rm e}^{ - \lambda t}}{\rm d}t} $.
考虑到$\hat \varphi$在空间的变化, 故在式(7)两边关于$x$作用${\cal F}$(Fourier)变换, 得
(8) $ {\lambda ^2}\hat{\hat{\varphi}} + 2{M_\infty }{a_\infty }{\rm i}\omega \lambda \hat{\hat{\varphi}} = - {\omega ^2}a_\infty ^2{\beta ^2}\hat{\hat{\varphi}} + a_\infty ^2\frac{\partial ^2\hat{\hat{\varphi}}}{{\partial {z^2}}} $ 其中, $\hat {\hat \varphi} = \int_{ - \infty }^{ + \infty } {\hat \varphi {{\rm e}^{ - {\rm i}\omega x}}{\rm d}x}$.
整理式(8)并将其写为
(9) $ \begin{eqnarray}\label{9} \frac{{\partial ^2}\hat{\hat \varphi}}{{\partial {z^2}}} = \left[ {M_\infty ^2{{\left( {k + {\rm i}\omega } \right)}^2} + {\omega ^2}} \right]\hat{\hat \varphi} \triangleq A\left( {\omega ,k} \right)\hat{\hat \varphi} \end{eqnarray}$ 其中$k = \lambda /{U_\infty }$ 定义为系统的减缩频率.
对本文研究的亚音速流体而言, $A$具有正实部. 考虑边界条件(6a), 方程(9)的解可以写作
(10) $ \begin{eqnarray}\label{e3.4} {\hat {\hat \varphi}_1} \left( {k,\omega ,z} \right) = \left\{ {\begin{array}{*{20}{l}} {{\hat {\hat \varphi}}^+{{\rm e}^{ - \sqrt A \left( {z - H} \right)}},\ \ z > H}\\ {{\hat {\hat \varphi}}^-{{\rm e}^{+\sqrt A \left( {z - H} \right)}},\ \ z < H} \end{array}} \right. \end{eqnarray}$ 其中, ${\hat {\hat \varphi}}^\pm={\hat {\hat \varphi}}\left( z=H^\pm\right)$. 为满足壁面约束条件(5a), 如
图1 (a)所示, 在$z=-H$处布置壁板的镜像, 其产生的势函数为
(11) $ \begin{eqnarray}\label{e3.5} {{\hat {\hat \varphi}_2}}\left( {k,\omega ,z} \right) = \left\{ {\begin{array}{*{20}{l}} {{\hat {\hat \varphi}}^-{{\rm e}^{ - \sqrt A \left( {z + H} \right)}},\ \ z > - H}\\ {{\hat {\hat \varphi}}^+{{\rm e}^{+\sqrt A \left( {z + H} \right)}},\ \ z < - H} \end{array}} \right. \end{eqnarray}$ 系统势函数$\hat {\hat \varphi}$可由叠加原理获得
(12) $ \begin{eqnarray}\label{e3.5a} \hat {\hat \varphi}={\hat {\hat \varphi} }_1+ {\hat {\hat \varphi} _2} \end{eqnarray}$ 由式(5b)及式(12)可得壁板表面气流的横向速度
(13) $ \begin{eqnarray}\label{e3.7} \left. {\begin{array}{*{20}{l}} {{{\hat {\hat v}}^ + } = - \sqrt A \left( \hat{\hat{\varphi}}^ + + \hat{\hat{\varphi}}^ - {{\rm e}^{ - 2\sqrt A H}} \right)}\\ {{{\hat {\hat v}}^ - } = + \sqrt A \left( \hat{\hat{\varphi}}^ - - \hat{\hat{\varphi}}^ - {{\rm e}^{ - 2\sqrt A H}} \right)} \end{array}} \right\} \end{eqnarray}$ 其中, ${\hat {\hat v}}^\pm={\hat {\hat v}}\left( z=H^\pm\right)$, 且由流场速度的连续条件可知$\hat {\hat v}^+=\hat {\hat v}^-=\hat {\hat v}$.
由式(5b)及式(13)可得壁板上下表面势函数之差
(14) $ \begin{eqnarray}\label{14} \begin{aligned} \Delta {\hat {\hat \varphi}} \equiv \hat {\hat \varphi}^+ - \hat {\hat \varphi}^- = - \frac{{ 2\hat {\hat v}}}{{\sqrt A \left( {1 - {{\rm e}^{ - 2\sqrt A H}}} \right)}} \end{aligned} \end{eqnarray}$ 进一步考虑式(3)后可得
(15) $ \begin{eqnarray}\label{15} \Delta {\hat {\hat p}} = {\rho _\infty U_\infty}{\frac{{2\hat {\hat v}\left( {k + {\rm i}\omega } \right)}}{{\sqrt A \left( {1 - {{\rm e}^{ - 2\sqrt A H}}} \right)}}} \end{eqnarray}$ 虽然式(15)给出了任意运动时壁板表面上的压力, 但其求解仍很困难. 对于本文研究的壁板静态失稳问题, 可令$k=0$并由式(15)解得
(16) $ \begin{eqnarray}\label{16} \hat {\hat v}(H) = \frac{1}{{{\rho _\infty}U_\infty}}\left[ {\frac{{\beta \left| \omega \right|\left( {1 - {{\rm e}^{ - c\left| \omega \right|}}} \right)}}{{2{\rm i}\omega }}\Delta \hat {\hat p}} \right] \end{eqnarray}$ 其中, $c=2H\beta$. 注意到函数$f(t)$的${\cal H}$(Hilbert)变换的${\cal F}$变换
\begin{eqnarray*} {\cal F}\left[ {{\cal H}\left[ {f(t)} \right]} \right] = \frac{{\left| \omega \right|}}{{{\rm i}\omega }}{\cal F}\left[ {f\left( t \right)} \right] \end{eqnarray*}
的形式后, 相应定义如下变换
[29 ] (17) $ \begin{eqnarray}\label{17} {{\cal Q}\left[ {f(t)} \right]} = \frac{1}{{\pi c}}\int_{ - \infty }^{ + \infty } {\frac{{f\left( t \right)}}{{1 + {{\left( {\dfrac{{t - \tau }}{c}} \right)}^2}}}{\rm d}\tau } \end{eqnarray}$ 在式(16)两边首先作用${\cal L}$和${\cal F}$的逆变换, 然后考虑式(5b), 式(5c), 应用投影运算${\cal P}_R $向$[0,L]$投影可得如下的积分方程
(18) $ \begin{eqnarray}\label{18} {w_a} = \frac{{\beta {{\cal P}_R}{\cal H}\left( {\cal{I - Q}} \right)\Delta p}}{{2{\rho _\infty }{U_\infty }}} \end{eqnarray}$ 由式(5d), 有${\cal P}_R \Delta p=\Delta p$, 考虑算子${\cal QH}$满足交换律(简要证明见附录), 则式(18)变为
(19) $ \begin{eqnarray}\label{19} {w_a} = \frac{{\beta \left( {{{\cal P}_R}{\cal H}{{\cal P}_R} - {{\cal P}_R}{\cal QH}{{\cal P}_R}} \right)\Delta p}}{{2{\rho _\infty }{U_\infty }}} \end{eqnarray}$ 其中
\begin{eqnarray*} &&{{\cal P}_R}{\cal H}{{\cal P}_R}[f(t)]= \frac{1}{\pi }\int_{ 0 }^{ L } {\frac{{f\left( \tau \right)}}{{t - \tau }}{\rm d}\tau },\ \ t\in [0,L]\\ &&{{\cal P}_R}{\cal QH}{{\cal P}_R}[f(t)]= \frac{1}{{\pi c}}\int_0^L\frac{ {f\left( \tau \right)} {\left( {\dfrac{{\tau - t}}{c}} \right)}}{{1 + {{\left( {\dfrac{{\tau - t}}{c}} \right)}^2}}}{\rm d}\tau ,\ \ t \in [0,L] \end{eqnarray*}
上式即为Possio积分方程
[29 -31 ] .
考虑式(5d)给出的压力条件, 参考薄翼理论中的Söghen解
[28 ] , 引入移位Tricomi算子${\cal T}$
[29 -30 ] (20) $ \begin{eqnarray}\label{20} {\cal T}\left[ {f\left( x \right)} \right] = \frac{1}{\pi }\sqrt {\frac{{L - x}}{x}} \int_0^L {\sqrt {\frac{\tau }{{L - \tau }}} } \frac{{f\left( \tau \right)}}{{\tau - x}}{\rm d}\tau \end{eqnarray}$ 将算子${\cal T}$作用在式(19)的两边, 可得压力和法洗速度之间的关系
[29 ,31 ] (21) $ \begin{eqnarray}\label{21} {2{\rho _\infty}U _\infty}{\cal T}\left[ {{w_a}} \right] = \beta\left( {\cal I}- {\cal P}\right)\Delta p \end{eqnarray}$ 其中, ${\cal I}$为单位算子, 与未受限流体相关; 而壁面效应则表征为一复合算子$\cal{P}$, 定义为
\begin{eqnarray*}\label{e3.16} &&{\cal P}[f(x)]\triangleq{\cal T}{{\cal P}_R}{\cal QH}{{\cal P}_R}[f(x)]= \frac{1}{{{\pi ^2}c}}\sqrt {\frac{{L - x}}{x}}\cdot \\&&\qquad \int_0^L {\sqrt {\dfrac{t}{{L - t}}} }\frac{1}{{t - x}}\int_0^L\dfrac{ {f\left( \tau \right)} {\left( {\dfrac{{\tau - t}}{c}} \right)}}{{1 + {{\left( {\dfrac{{\tau - t}}{c}} \right)}^2}}}{\rm d}\tau {\rm d}t \end{eqnarray*}
由式(21)可得
(22) $ \begin{eqnarray}\label{e3.17} \frac{\Delta p}{D} = 2\alpha {\left( \cal {I - P} \right)^{ - 1}}{\cal T}\left( {{\frac{{\partial w}}{{\partial x}}}} \right) \end{eqnarray}$ 其中, $\alpha = {{{\rho _\infty }U_\infty ^2}}/({{D\beta }})$.
3 失稳方程及其最小二乘解 考虑壁板的发散失稳方程
(23) $ \begin{eqnarray}\label{23} \frac{{{\partial ^4}w}}{{\partial {x^4}}} = - 2\alpha {\left( \cal {I - P} \right)^{ - 1}}{\cal T}\left[ {\frac{{\partial w}}{{\partial x}}} \right] \end{eqnarray}$ 上式为关于$w$的四阶偏微分方程, 将其扩阶写作
(24) $ \begin{eqnarray}\label{24} &&\frac{{\partial {\cal W}}}{{\partial x}} = \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&0 \end{array}} \right]{\cal W} + \left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&\cal G&0&0 \end{array}} \right]{\cal W} \\ &&\qquad \triangleq {\bf B}{\cal W} + {\cal {B}}{\cal W} \end{eqnarray}$ 其中
\begin{eqnarray*} && {\cal W} = {\left[ {w,\frac{{\partial w}}{{\partial x}},\frac{{{\partial ^2}w}}{{\partial {x^2}}},\frac{{{\partial ^3}w}}{{\partial {x^3}}}} \right]^{\rm T}}\\ &&{\cal G}[f(x)]= - 2\alpha {\left( \cal {I - P} \right)^{ - 1}}{\cal T}\left[ f(x)\right] \end{eqnarray*}
采用常数变易法求解(24)可得
(25) $ \begin{eqnarray}\label{25} { {{\cal D}}} \left[ {{\cal W}\left( x \right)} \right] = {{\rm e}^{{\bf B} x}}{\cal W}\left( 0 \right) \end{eqnarray}$ 其中
\begin{eqnarray*} \begin{aligned} &{\cal D} = \left[ {\begin{array}{*{20}{c}} {\cal I}&{ - {{\cal R}_1}}&0&0\\ 0&{{\cal I} - {{\cal R}_2}}&0&0\\ 0&{ - {{\cal R}_3}}&{\cal I}&0\\ 0&{ - {{\cal R}_4}}&0&{\cal I} \end{array}} \right]\\ &{{\cal R}_n}\left[ {f\left( x \right)} \right] = \int_0^x {\frac{{{{\left( {x - s} \right)}^{4 - n}}}}{{\left( {4 - n} \right)!}}{\cal G}\left[ {f\left( s \right)} \right]} {\rm d}s \end{aligned} \end{eqnarray*}
在式(25)两端作用$\cal D$的逆算子可得
(26) $ \begin{eqnarray}\label{e4.5} {\cal W}\left( x \right) = {{\cal D} ^{ - 1}}{{\rm e}^{{B}x}}{\cal W}\left( 0 \right) \end{eqnarray}$ 其中
$\begin{eqnarray*} {\cal D}^{-1} = \left[ {\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c} {\cal I}&{ {{\cal R}_1}({\cal I-R}_2)^{-1}}&0&0\\ 0&({\cal I-R}_2)^{-1}&0&0\\ 0&{ {{\cal R}_3}({\cal I-R}_2)^{-1}}&{\cal I}&0\\ 0&{ {{\cal R}_4}({\cal I-R}_2)^{-1}}&0&{\cal I} \end{array}} \right] \end{eqnarray*}$
将壁板的边界条件(2)代入式(26)后整理得到
(27) $ \begin{eqnarray}\label{27} {E}{\left. {\left( {{{\cal D}^{-1}}{{\rm e}^{{B}x}}} \right)} \right|_{x = L}}{{E}^{\rm T}}{\left[ {\begin{array}{*{20}{c}} w\\ {\dfrac{{\partial w}}{{\partial x}}} \end{array}} \right]_{x = 0}} = \left[ {\begin{array}{*{20}{c}} 0\\0 \end{array}} \right] \end{eqnarray}$ 其中, ${E}=\left[ {\begin{array}{*{20}{c}}{{{{I}}_{2 \times 2}}}&{{{\bf 0}_{2 \times 2}}}\end{array}} \right]$.
式(27)仅有零解对应系统的稳定状态; 当其系数行列式等于零时系统出现非零解, 意味着系统处于失稳状态, 即
(28) $ \begin{eqnarray}\label{28} {\left( { {\cal I} - {{\cal R}_2}} \right)^{ - 1}}{\left[ {y(x)} \right]_{x = L}}= 0 \end{eqnarray}$ 其中,函数$y(x)$满足$y(x)\equiv 1$.
因算子${ {\cal I} - {{\cal R}_2}}$是紧的
[31 ] , 对所求参数$\alpha$, 其逆都是存在的, 那么
(29) $ \begin{eqnarray}\label{29} ({\cal I-R}_2)^{-1}= {\cal I} + \sum\limits_{n = 1}^{\infty } {{{\left( {{{\cal R}_2}} \right)}^n}} \end{eqnarray}$ 由于${\cal R}_2$中含有需要确定的参数$\alpha$, 直接采用式(29)求解并不利于计算. 但注意到
(30) $ \begin{eqnarray}\label{30} {\left( { {\cal I - {R}}_2} \right)^{ - 1}}\left[ {y(L)} \right] = f(x = L) = 0 \end{eqnarray}$ 上式表明方程(30)的解等价于寻找目标函数$f(x)$使
(31) $ \begin{eqnarray}\label{31} \left( {{\cal I - {R}}_2} \right)\left[ {f\left( x \right)} \right] \equiv 1,\ \ f(x=L)= 0 \end{eqnarray}$ 将${\cal R}_2$代入式(31)有
(32) $ \begin{eqnarray}\label{e4.12} f\left( x \right) + \alpha \int_0^x {{{\left( {x - s} \right)}^2}{{\left( {\cal {I - P}} \right)}^{ - 1}}{\cal T}\left[ {f\left( s \right)} \right]}{\rm d}s = 1 \end{eqnarray}$ 因$(\cal {I - P})$为压缩映射
[29 ] , $\left( \cal {I - P} \right)^{ - 1}{\cal T}\left[ {{f(x)}} \right]$可近似展开为
(33) $ \begin{eqnarray}\label{e4.13} {\left( \cal {I - P} \right)^{ - 1}}{\cal T}\left[ {{f(x)}} \right]\simeq\left( {{\cal I} + \sum\limits_{p = 1}^P {{ {\cal P}^p}} } \right){\cal T}\left[ {{f(x)}} \right] \end{eqnarray}$ 假设所求函数$f(x)$在$ \left[ {0,L} \right]$区间内是连续的, 并注意到$f(L)=0$, 由Weierstrass定理可将$f(x)$近似展开为
(34) $ \begin{eqnarray}\label{34} f\left( x \right) \simeq\sum\limits_{n = 1}^{ N } {{a_n}{{\left( {L - x} \right)}^n}} \end{eqnarray}$ 考虑式(32)在$[0,L]$区间内任意$M,(M\gg N)$个离散点上均成立. 那么求解方程式(32)等价于求解如下的矛盾方程组
(35) $ \begin{eqnarray}\label{e4.14} {{{\tilde{A}}}_{M \times N}}{{a}_{N \times 1}} = {{\bf{1}}_{M \times 1}} \end{eqnarray}$ 其中
$ \begin{eqnarray*} &&{{\tilde A}_{ji}} = \left( {L - x_j} \right)^i+ \alpha \int_0^{x_j} \left( {x_j - s} \right)^2\left( {{\cal I} + \sum\limits_{p = 1}^P {{ {\cal P}^p}} } \right)\cdot \\&&\qquad{\cal T}\left[ \left( L - x_j \right)^i \right]{\rm d}s \end{eqnarray*} $
采用最小二乘方法可获得方程组(35)的最优解为
(36) $ \begin{eqnarray}\label{36} {{{a}}_{N \times 1}} = \left({{{\tilde{A}}}^{\rm T}{{\tilde{A}}}}\right)^{-1}{{\tilde{A}}}^{\rm T}\cdot {{\bf{1}}_{M \times 1}} \end{eqnarray}$ 为寻找临界参数$\alpha_{\rm c}$, 定义关于$\alpha$ 的误差函数
(37) $ \begin{eqnarray}\label{37} {\cal E}(\alpha) = \sum\limits_{m = 1}^M {\frac{{\left| {1 - {{{{\tilde{A}}}}_{M \times N}}{{{a}}_{N \times 1}}}(m) \right|}}{M}} \end{eqnarray}$ 改变$\alpha$使得误差$|{\cal E}|\leqslant 1.0{\rm e}^{-4}$可得临界参数$\alpha_{\rm c}$及其对应的临界气流速度.
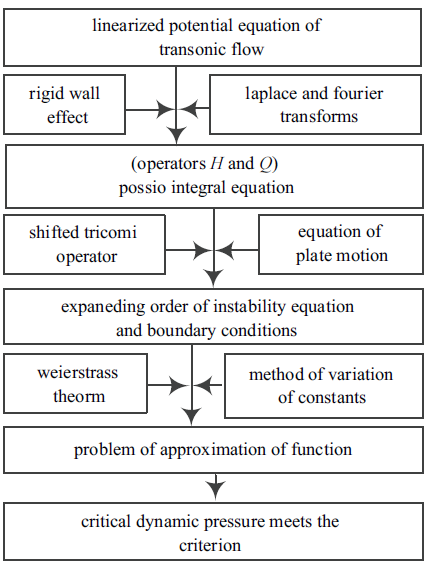
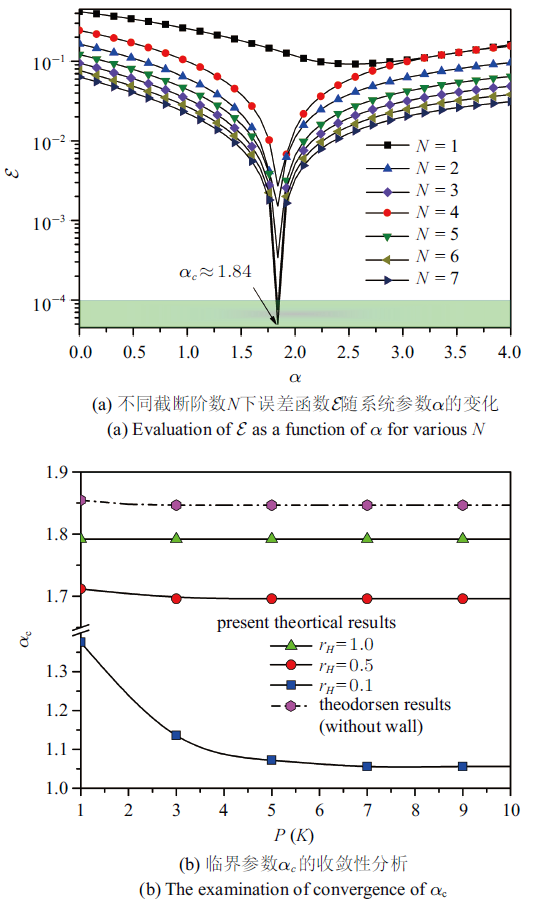
4 理论结果及对比验证 在下面计算中选取无量纲参数$\xi = x/L,{r_H} =H/L$. 为避免间隙$H$过小而导致较强的粘性作用, 本文仅考虑$r_H>0.05$的情况. 基于
图2 给出分析及计算流程进行算例分析. 首先考察${r_H} \to \infty$, 即无壁面的情况. 此时, $\left\| {\cal P}\right\|\to 0,{\left( \cal {I - P} \right)^{ - 1}}\to {\cal I}$.
图3 (a)给出了此工况下, $M=200$时, 误差函数${\cal E}$随截断阶数$N$的变化关系. 由该图可知随着$N$的增加误差会最终会在$\alpha_{\rm c}=1.84$处满足设置的条件(进入绿色阴影区域), 此参数即为系统的临界参数. 下面考察式(33)和式(34)中截断参数$P$和$N$对本文解收敛性的影响.
图3 (b)给出了不同${r_H}$时截断阶数$P$对结果收敛性的影响. 由
图3 可知, 选择$P=N=7,M=200$可以保证本文计算结果的收敛性.
图4 给出了不同$r_H$对应的临界参数$\alpha_{\rm c}$. 与预期一致, $\alpha_{\rm c}$随$r_H$的增大而增大并最终稳定在$\alpha_{\rm c}\simeq1.84$.
图2 新窗口打开 |
下载原图ZIP |
生成PPT 图2本文理论分析和计算的流程 Fig. 2The flowchart of the present theoretical analysis 图3 新窗口打开 |
下载原图ZIP |
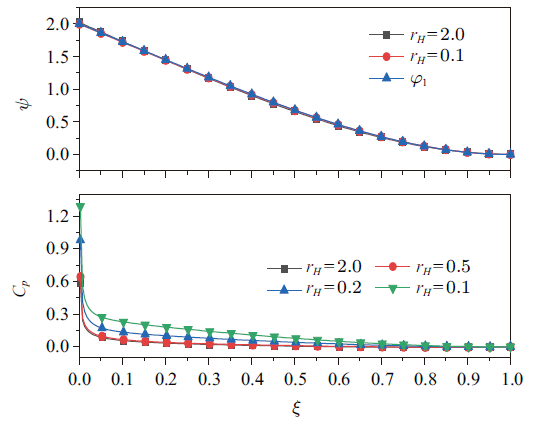
生成PPT 图3 Fig. 3 图5 给出了不同$r_H$下壁板的失稳模态$\psi(\xi)$. 从图可知, 尽管不同$r_H$下的临界动压不同, 但失稳模式都以倒置悬臂梁一阶模态$\varphi_1$为主导. 考察失稳模态下壁板表面气动压力的分布, 定义压强系数
图4 新窗口打开 |
下载原图ZIP |
生成PPT 图4本文理论解与其他理论及数值结果的对比分析 Fig. 4Comparison of the present theoretical results with other existing theory and the numerical method 图5 新窗口打开 |
下载原图ZIP |
生成PPT 图5系统的失稳模态(上)及压强系数(下) Fig. 5The instability model (top) and the pressure coefficient (bottom) of the plate (38) $ \begin{eqnarray}\label{38} {C_{\rm p}}\left( \xi \right) = - \frac{4}{\beta }\left( {{\cal I} + \sum\limits_{p = 1}^P {{{{\cal P}}^p}} } \right){\cal T}\left[ {\frac{{\partial \psi}}{{\partial \xi}}} \right] \end{eqnarray}$ 图5 给出了不同$r_H$对应的压力系数(由于前缘压差为无穷大, 图中已做截断处理). 由图可知, 壁板前缘附近为正压区而尾缘附近为负压区; 随$r_H$的减小正压区扩大且压力值增加, 而负压区缩小且压力值减小. 壁板上合力增大且力矩中心前移, 对应的临界失稳 动压也就越低.
为验证本文的理论结果, 考虑无壁面情况, 此时满足Kutta-Joukowski条件的壁板的压强解 (Theodorsen解
[28 ] )为
(39) $ \begin{eqnarray}\label{39} \Delta p(x)= \frac{{2{\rho _\infty }U_\infty ^2}}{{\pi L}}\frac{{f\left( \theta \right) - f\left( 0 \right)}}{{\sin \theta }} \end{eqnarray}$ 其中
$\begin{eqnarray*} &&f\left( \theta \right) = \int_0^\pi {\frac{{\partial w}}{{\partial \zeta }}\frac{{{{\sin }^2}\varphi }}{{\cos \varphi - \cos \theta }}{\rm d}\varphi }\\ && x = \frac{L}{2}\left( {1 + \cos \theta } \right),\ \zeta = \frac{L}{2}\left( {1 + \cos \varphi } \right) \end{eqnarray*}$
取倒置悬臂梁模态函数$\varphi_k,(k=1,2,...,K)$, 应用伽辽金方法求解方程(1), 通过特征值分析获得系统临界参数. 如
图3 (b)中虚线所示, 选取前三阶模态便可得收敛结果$\alpha_{\rm c}\simeq1.8464$. 本文理论结果与经典Theodorsen解得到的结果吻合很好.
为了进一步考察本文理论方法对$r_H$的适用性, 采用如
图1 (b)所示的离散面元模型进行数值求解. 壁板上的面元分布由线性分布的连续涡来表示以计算满足边界条件的流体势函数, 在质量点处采用有限差分方法求解壁板结构运动方程, 详细的离散和计算过程请参见文献
[12 ] . 本文采用该离散模型计算获得了不同$r_H$时的临界参数, 结果如
图4 所示. 由图可知本文理论与数值结果的变化趋势一致且吻合较好(两者相对误差保持在5%之内, 图中绿色区域内). 上述对比结果均表明了本文气动力理论及失稳分析方法的有效性.
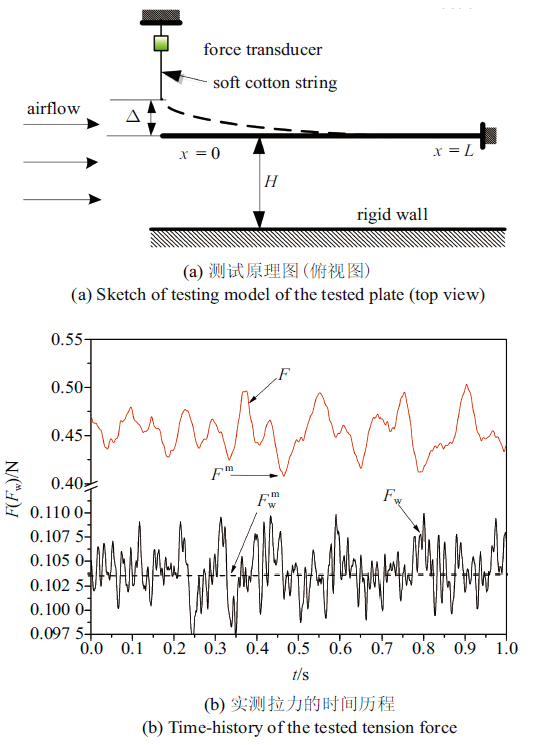
5 风洞实验验证 采用风洞实验研究壁板失稳的临界速度并验证本文理论的正确性. 实验中使用直径1.2 m的开口式风洞, 其具有5 $\sim$ 40 m/s的风速调节范围和低于0.3%的湍流度. 实验中壁板模型采用长宽比为2/3 (20 cm $\times$ 30 cm)的镀锌铁板($\rho_{\rm p}=7.85$ g/cm$^3$, $E_{\rm p}=210$ GPa). 如
图6 所示, 壁板竖直安装, 并用两块厚钢板将其夹持固定在刚性支架上以保证固支约束并进行实验, 夹持段壁板的长度约为3 cm; 壁板一侧竖直放置厚木板以模拟壁面对气流的约束限制. 靠近壁板固定端的根部位置贴有应变片, 实验开始前采用敲击法测试了壁板在无风状态下的自振频率(7.9 Hz), 并与理论结果(8.2 Hz)进行了对比, 检验了固支约束实现及测试设备的可靠性. 实验中缓慢增加风速至目标风速, 稳定至少一分钟后进行数据采集, 以保证实验数据的可靠性.
静态失稳不能像颤振这类动态失稳一样可以依据信号等幅周期变化的特征而直接判定. 本文借鉴材料力学压杆失稳原理设计了一种等效拉力测试方法, 测试原理如
图7 (a)所示. 理论上给定壁板初始变形量为失稳模态的任意小倍数, 当气流速度小于临界值时, 壁板需要外部作用(实验中依靠张紧的细绳提供拉力)才能维持该状态; 而当流速达到临界值时, 则可不依靠任何外部作用. 因此可由是否需要细绳提供拉力而维持给定的初始变形来等效判定系统是否达到了临界状态. 本文的理论分析表明壁板将呈现一阶悬臂梁模态失稳模式, 而该模态形式的初始壁板静变形在实验中却不易精确给出. 依据文献
[26 ] 给出的悬臂梁一阶模态与其端部受集中载荷产生的静变形形态相类似这一结论, 本文实验采用在壁板自由端施加集中力(张紧细绳使其具有一定预拉力)而实现壁板的初始变形.
图6 新窗口打开 |
下载原图ZIP |
生成PPT 图6风洞中模型安装图和不同风速下细绳的状态图 Fig. 6Pictures of the setup of the model in the wind tunnel, and of the string states with different flow velocities 如
图6 及
图7 (a)所示, 悬臂板紧靠前缘正中心位置连接有细棉绳, 细绳的另一端连接在拉力传感器上(量程5 N, 灵敏度0.01 N). 调整细绳的长度可使壁板前缘产生不同的初始挠度$\Delta$, 其在传感器上表现为不同的预拉力值. 当流速小于临界值时, 细绳会处于张紧状态并为壁板提供拉力而维持其初始变形, 如
图6 (a)所示; 而当流速接近于临界值时, 细绳则会处于松弛状态, 如
图6 (b)所示. 注意到细绳仅受气流作用也会导致拉力($F_{\rm w}$)的存在, 传感器的实测拉力($F$)则包含($F_{\rm w}$)及壁板对绳子的拉力($F_{\rm p}$).
图 7 (b)给出了风速12 m/s时时间1 s内两种拉力的实测值. 测试拉力$F_{\rm w}$时, 将细绳保持自然状态, 两端分别固定在刚性支架及夹持端并单独置于风洞中进行测试. 从
图7 (b)可知, 虽然两种拉力均表现出明显的波动性, 但$F_{\rm w}$的变化幅值较小($\pm 0.005$ N之内). 若考虑两种拉力之间的弱关联性则可由下式
图7 新窗口打开 |
下载原图ZIP |
生成PPT 图7 Fig. 7 (40) $ \begin{eqnarray}\label{e6.1} F^{\rm m}\triangleq \min(F)\leqslant {\rm mean}(F_{\rm w})\triangleq F_{\rm w}^{\rm m} \end{eqnarray}$ 作为临界状态的近似判定条件.
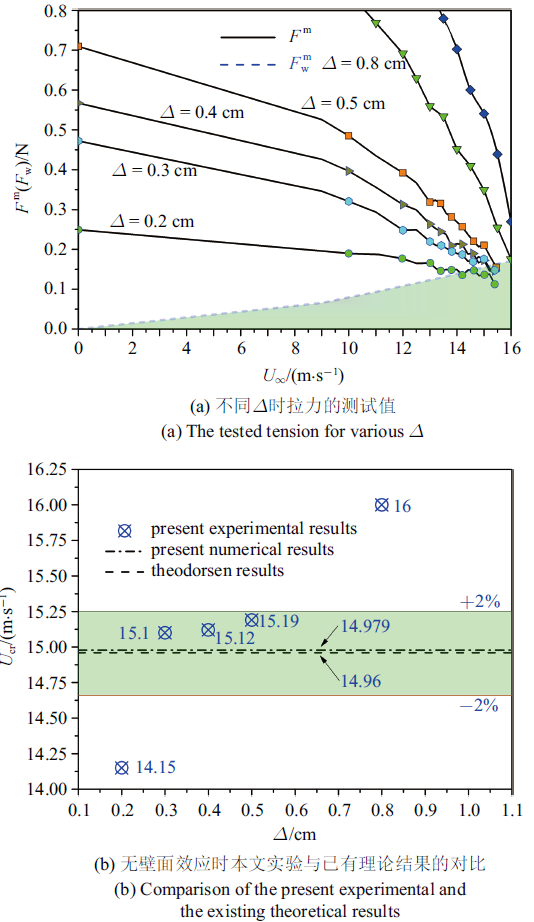
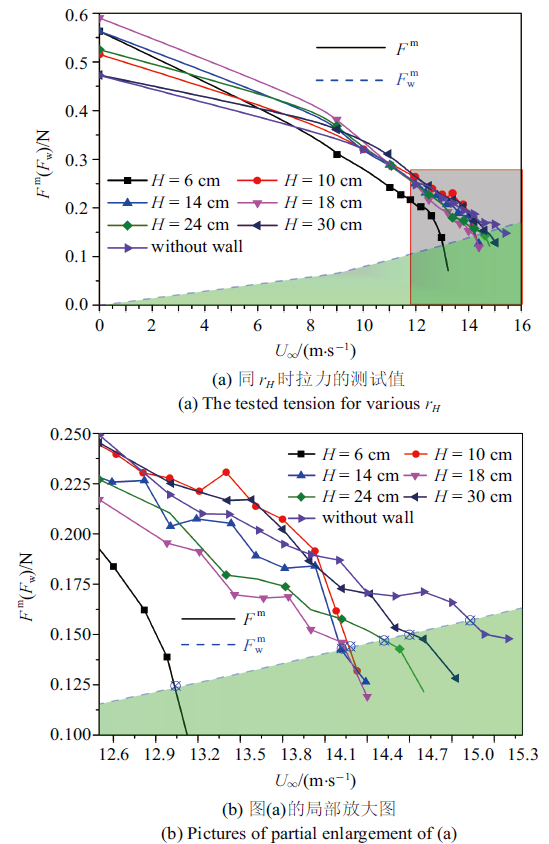
理论上, 对于任意的自由端部挠度$\varDelta$, 实验中均应测试得到相同的临界风速. 然而实验中发现, 较小的值会因较差的抗干扰性而导致测量精度不易满足, 而较大的$\varDelta$则会导致壁板产生几何大变形非线性
[26 ] . 因此, 实验中首先以无壁面的情形进行多组重复测试, 通过对比已有理论及计算结果来确定最佳的$\varDelta$给定范围.
图8 (a)给出了不同$\varDelta$值下$F$及$F_{\rm w}$在不同风速下的测试值. 依据式(40)可判定当拉力$F^{\rm m}$曲线处于
图8 (a)的绿色阴影区域时, 系统处于失稳状态. 依据
图8 (a)得到临界速度$U_{\rm {cr}}$与$\varDelta$之间的变化关系如
图8 (b)所示. 通过与理论值(39)及数值结果(
图4 )对比可知, 当$\varDelta$在0.3 $\sim $ 0.5 cm之间取值时, 实验结果与理论及数值结果吻合较好(实验值与理论值(39)相差2%之内, 图中绿色区域内), 因此本文实验选取该区间的值作为拉出挠度值完成了不同$r_H$下的实验, 结果如
图9 所示.
图9 (a)中无风时细绳中的初始拉力并不完全相等, 这是由于为了保证数据的多样性而在0.3 $\sim $ 0.5 cm内给定不同的$\varDelta$值而导致的.
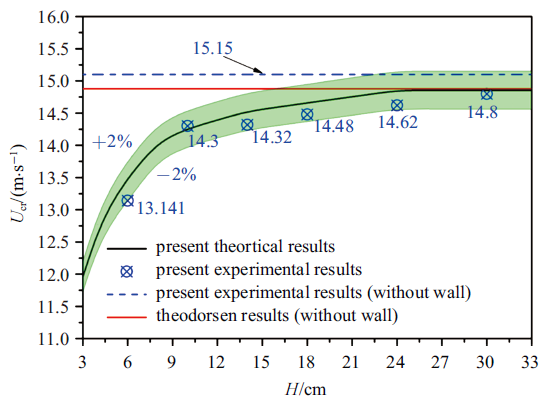
图10 给出了本文理论与试验结果的对比, 由图可知两者吻合很好, 各风速下的实验结果与理论结果之间的相对误差均保持在2%之内(绿色区域内), 这充分表明了本文的理论计算及风洞试验的有效性和准确性.
图8 新窗口打开 |
下载原图ZIP |
生成PPT 图8 Fig. 8 图9 新窗口打开 |
下载原图ZIP |
生成PPT 图9 Fig. 9 图10 新窗口打开 |
下载原图ZIP |
生成PPT 图10本文理论结果与试验结果及已有理论结果的对比 Fig. 10Comparison of the present theoretical results with the experiment and the other existing theory 6 结语 本文考虑壁面效应对亚音速气流中倒置悬臂壁板的静态失稳问题进行了理论及实验研究. 文中采用镜像函数法描述壁面约束条件, 基于算子理论对壁板上的气动力进行了理论分析, 获得了以Possio积分方程为表征的气动力表达式, 壁面效应则表征为一包含$\cal{T}$, $\cal{Q}$及$\cal{H}$算子的复合算子; 壁板的失稳方程转化为了定区间上的函数逼近问题, 并利用Wererstrass定理及最小二乘方法得到了最优逼近函数确定临界动压, 无需进行特征值计算; 给出了壁面效应对失稳的定量影响并对壁面影响失稳的原理进行了探讨; 设计了静态失稳测试方法, 其相比于动态实验对风洞品质要求更低且鲁棒性较高; 风洞实验分析结果与本文理论结果吻合较好, 验证了本文理论方法的正确性.
本文中以Possio积分方程表征的气动力物理含义清晰, 依据微分算子理论将失稳问题转化为了定区间上的函数逼近问题, 为该类问题的求解提供了新的思路. 值得指出的是, 本文方法在壁板颤振问题中的推广及应用正是下一步计划开展的工作.
附录:算子${\cal QH}$的交换性 由本文算子的定义可知
(A1) $ \begin{eqnarray} \left. {\begin{array}{*{20}{l}} {H\left[ {Q\left[ {f(x)} \right]} \right] = \dfrac{1}{{{\pi ^2}c}}\int_{ - \infty }^\infty {f\left( \tau \right){g_1}\left( {x,\tau } \right)} {\rm d}\tau }\\ {Q\left[ {H\left[ {f(x)} \right]} \right] = \dfrac{1}{{{\pi ^2}c}}\int_{ - \infty }^\infty {f\left( \tau \right){g_2}\left( {x,\tau } \right)} {\rm d}\tau } \end{array}} \right\} \end{eqnarray} $ 其中
(A2) $ \begin{eqnarray} \left. {\begin{array}{*{20}{l}} {g_1}\left( {x,\tau } \right) = \int_{ - \infty }^{ + \infty } {\dfrac{1}{{x - t}}\dfrac{1}{{1 + {{\left( {\dfrac{{t - \tau }}{c}} \right)}^2}}}{\rm d}t}\\ {g_2}\left( {x,\tau } \right) =\int_{ - \infty }^{ + \infty } {\dfrac{1}{{t - \tau }}\dfrac{1}{{1 + {{\left( {\dfrac{{x - t}}{c}} \right)}^2}}}{\rm d}t} \end{array}} \right\} \end{eqnarray} $ 分别令$t = \tau + p$及$t=x+q$, 则上式变作
(A3) $ \begin{eqnarray} \left. {\begin{array}{*{20}{l}} {g_1}\left( {x,\tau } \right) = \int_{ - \infty }^{ + \infty } {\dfrac{1}{{\left( {x - \tau } \right) - p}}\dfrac{1}{{1 + {{\left( {\dfrac{p}{c}} \right)}^2}}}{\rm d}p}\\ {g_2}\left( {x,\tau } \right) = \int_{ - \infty }^{ + \infty } {\dfrac{1}{{\left( {x - \tau } \right) + q}}\dfrac{1}{{1 + {{\left( {\dfrac{q}{c}} \right)}^2}}}{\rm d}q} \end{array}} \right\} \end{eqnarray} $ 上式中的积分为瑕积分, 注意到$c>0$, 利用围道积分进行计算后可得
(A4) $ \begin{eqnarray} {g_1}\left( {x,\tau } \right) = {g_2}\left( {x,\tau } \right) = \dfrac{{\pi c\left( {x - \tau } \right)}}{{{{\left( {x - \tau } \right)}^2} + {c^2}}} \end{eqnarray} $ 即得
(A5) $ \begin{eqnarray} {\cal H}\left[ {{\cal Q}\left[ {f(x)} \right]} \right] = {\cal Q}\left[ {{\cal H}\left[ {f(x)} \right]} \right] \end{eqnarray} $ [1] Dowell EH Aeroelasticity of Plates and Shells. Leyden: Noordhoff International Publishing, 1975 [本文引用: 2] [2] 杨智春 , 夏巍 . 壁板颤振的分析模型、数值求解方法和研究进展力学进展 , 2010 ,40(1 ):81 -98 ( Yang Zhichun Xia Wei Advances in Mechancis , 2010 ,40(1 ):81 -98 (in Chinese)) [3] 张蕊丽 , 杨智春 . 曲壁板在超音速气流中的分岔特性力学学报 , 2010 ,42(5 ):863 -869 ( Zhang Ruili Yang Zhichun Chinese Journal of Theoretical and Applied Mechanics , 2010 ,42(5 ):863 -869 (in Chinese)) [4] 刘艮 , 张伟 . 亚音速气流中复合材料悬臂板的非线性振动响应研究力学学报 , 2019 ,51(3 ):912 -921 [本文引用: 1] ( Liu Gen Zhang Wei Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51(3 ):912 -921 (in Chinese)) [本文引用: 1] [5] 李鹏 , 杨翊仁 , 鲁丽 . 外激励作用下亚音速二维壁板分岔及响应研究力学学报 , 2011 ,43(4 ):746 -754 [本文引用: 3] ( Li Peng Yang Yiren Lu Li Chinese Journal of Theoretical and Applied Mechanics , 2011 ,43(4 ):746 -754 (in Chinese)) [本文引用: 3] [6] Li P Zhang DC Li ZW et al . Bifurcations and post-critical behaviors of a nonlinear curved plate in subsonic airflowArchive of Applied Mechanics , 2019 ,89(2 ):343 -362 [本文引用: 2] [7] Li P Li ZW Liu S et al . Non-linear limit cycle flutter of a plate with Hertzian contact in axial flowJournal of Fluids and Structures , 2018 ,81:131 -160 [本文引用: 5] [8] Kornecki A Dowell EH O'brien J Journal of Sound and Vibration , 1976 ,47(2 ):163 -178 [本文引用: 2] [9] Burke MA Lucey AD Howell RM et al . Stability of a flexible insert in one wall of an inviscid channel flowJournal of Fluids and Structures , 2014 ,48:435 -450 [本文引用: 3] [10] Eloy C Souilliez C Schouveiler L Journal of Fluids and Structures , 2007 ,23(6 ):904 -919 [本文引用: 2] [11] Alben S Physics of Fluids , 2008 ,20(10 ):104 -106 [12] Howell RM Lucey AD Journal of Fluids and Structures , 2015 ,59:370 -393 [本文引用: 2] [13] Huang L Zhang C Journal of Fluids and Structures , 2013 ,38:273 -289 [本文引用: 2] [14] De Marqui Jr C Tan D Erturk A Journal of Fluids and Structures , 2018 ,82:492 -504 [本文引用: 1] [15] Colera M Perez-Saborid M Journal of Sound and Vibration , 2018 ,423:442 -458 [本文引用: 1] [16] Huang H Wei H Lu XY Journal of Fluid Mechanics , 2018 ,837:461 -476 [本文引用: 3] [17] Watanabe Y Suzuki S Sugihara M et al . An experimental study of paper flutterJournal of Fluids and Structures , 2002 ,16(4 ):529 -542 [本文引用: 1] [18] Orrego S Shoele K Ruas A et al . Harvesting ambient wind energy with an inverted piezoelectric flagApplied Energy , 2017 ,194:212 -222 [本文引用: 2] [19] Maruai NM Mat Ali. MS Ismail MH et al . Downstream flat plate as the flow-induced vibration enhancer for energy harvestingJournal of Vibration and Control , 2018 ,24(16 ):3555 -3568 [本文引用: 1] [20] Zhou Z Qin W Zhu P et al . Scavenging wind energy by a Y-shaped bi-stable energy harvester with curved wingsEnergy , 2018 ,153:400 -412 [本文引用: 1] [21] Rasani MR Ariffin AK Bashir M et al . Effect of location in a cylinder wake on dynamics of a flexible energy harvesting plateJournal of Advanced Research in Fluid Mechanics and Thermal Sciences , 2019 ,55(2 ):189 -198 [本文引用: 3] [22] Cisonni J Lucey AD Elliott NS et al . The stability of a flexible cantilever in viscous channel flowJournal of Sound and Vibration , 2017 ,396:186 -202 [本文引用: 2] [23] 曹东兴 , 马鸿博 , 张伟 . 附磁压电悬臂梁流致振俘能特性分析力学学报 , 2019 ,51(4 ):1148 -1155 [本文引用: 1] ( Cao Dongxing Ma Hongbo Zhang Wei Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51(4 ):1148 -1155 (in Chinese)) [本文引用: 1] [24] Fan B Huertas-Cerdeira C Cosse J et al . Effect of morphology on the large-amplitude flapping dynamics of an inverted flag in a uniform flowJournal of Fluid Mechanics , 2019 ,874:526 -547 [本文引用: 2] [25] Tavallaeinejad M Paidoussis MP Legrand M Journal of Fluids and Structures , 2018 ,83:413 -428 [本文引用: 1] [26] Sader JE Cossé J Kim D et al . Large-amplitude flapping of an inverted flag in a uniform steady flow-a vortex-induced vibrationJournal of Fluid Mechanics , 2016 ,793:524 -555 [本文引用: 4] [27] Guo CQ Paidoussis MP Journal of Applied Mechanics , 2000 ,67(1 ):171 -176 [本文引用: 1] [28] Bisplinghoff RL Ashley H Halfman RL Aeroelasticty . Cambridge, Mass. : Addison-Wesley Publishing Co., Inc., 1975 [本文引用: 3] [29] Serry MA Sharjah:American University of Sharjah , 2017 [本文引用: 5] [30] Tricomi FG Courier Corporation , 1957 [本文引用: 1] [31] Serry M Tuffaha A Journal of Applied Mathematical Modelling , 2018 ,63:644 -659 [本文引用: 3] 
,2), 梁森, 杨翊仁西南交通大学力学与工程学院, 成都 610031
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
