李聪^,*,?,2), 牛忠荣^,*,3), 胡宗军^*, 胡斌^**合肥工业大学土木与水利工程学院力学系,合肥 230009
^?安徽建筑大学土木工程学院,合肥 230601

ANALYSIS OF 3-D NOTCHED/CRACKED STRUCTURES BY USING EXTENDED BOUNDARY ELEMENT METHOD ¹⁾

Li Cong^,*,?,2), Niu Zhongrong^,*,3), Hu Zongjun^*, Hu Bin^**School of Civil Engineering,Hefei University of Technology,Hefei 230009,China
^?School of Civil Engineering, Anhui Jianzhu University,Hefei 230601,China

通讯作者: 2)李聪,博士,从事固体力学研究. E-mail：478617661@qq.com;3)牛忠荣,教授,从事固体力学研究. E-mail：niu-zr@hfut.edu.cn

收稿日期:2020-04-19接受日期:2020-04-19网络出版日期:2020-09-18

基金资助:

1)国家自然科学基金资助项目.11272111 国家自然科学基金资助项目.11772114

Received:2020-04-19Accepted:2020-04-19Online:2020-09-18
作者简介 About authors


摘要
在线弹性理论中,三维 V 形切口/裂纹结构尖端区域存在多重应力奇异性,常规数值方法不易求解. 本文提出和建立了三维扩展边界元法 (XBEM),用于分析三维线弹性 V 形切口/裂纹结构完整的位移和应力场. 先将三维线弹性 V 形切口/裂纹结构分为尖端小扇形柱和挖去小扇形柱后的外围结构. 尖端小扇形柱内的位移函数采用自尖端径向距离 $r$ 的渐近级数展开式表达,其中尖端区域的应力奇异指数、位移和应力特征角函数通过插值矩阵法获得. 而级数展开式各项的幅值系数作为基本未知量. 挖去扇形域后的外围结构采用常规边界元法分析. 两者方程联立求解可获得三维 V 形切口/裂纹结构完整的位移和应力场,包括切口/裂纹尖端区域精细的应力场. 扩展边界元法具有半解析法特征,适用于一般三维 V 形切口/裂纹结构完整位移场和应力场的分析,其解可精细描述从尖端区域到整体结构区域的完整应力场. 作者研制了三维扩展边界元法程序,文中给出了两个算例,通过计算结果分析,表明了扩展边界元法求解三维 V 形切口/裂纹结构完整应力场的准确性和有效性.
关键词： 三维切口/裂纹;应力场;扩展边界元法;渐近展开式

Abstract
According to the theory of linear elasticity, the conventional numerical methods are difficult to calculate the singular stress fields of three dimensional V-notched/cracked structures because of the stress singularity in the V-notch/crack tip region. In this paper, the extended boundary element method (XBEM) is first proposed to calculate the whole displacement and stress fields of three dimensional V-notch/crack structures. Firstly, the three dimensional V-notched/cracked structure is divided into two parts, which are a small sectoral column around the notch/crack tip and the outer region without the tip sectorial column. The displacement and stress components in the small sector column are expressed as the asymptotic series expansions with respect to the radial coordinate from the tip. The stress singular orders and the associated displacement and stress eigen-functions in the tip region are determined by the interpolating matrix method. The amplitude coefficients in the asymptotic series expansions are taken as the basic unknowns. Secondly, the boundary element method is used to analyze the three dimensional V-notched/cracked structure removed the small sector column. Hence, the whole displacement and stress fields of both the tip region and outer region are obtained by combining the boundary element analysis and the asymptotic series expansions of the displacement and stress fields in the notch/crack tip region, where the XBEM has the characteristics of the semi-analytic approach. The XBEM is suitable for the displacement and stress analysis of the three dimensional V-notched/cracked structures, and its solution can accurately describe the displacement and stress fields from the notch/crack tip to the whole region of the V-notched/cracked structures. Finally, two typical examples are given to demonstrate the effectiveness and accuracy of the extended boundary element method.
Keywords：three dimensional V-notch/crack;stress field;extended boundary element method;asymptotic series expansion


PDF (13036KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李聪, 牛忠荣, 胡宗军, 胡斌. 三维切口/裂纹结构的扩展边界元法分析 ¹⁾. 力学学报[J], 2020, 52(5): 1394-1408 DOI:10.6052/0459-1879-20-129
Li Cong, Niu Zhongrong, Hu Zongjun, Hu Bin. ANALYSIS OF 3-D NOTCHED/CRACKED STRUCTURES BY USING EXTENDED BOUNDARY ELEMENT METHOD ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1394-1408 DOI:10.6052/0459-1879-20-129

引言

在土木、机械和航空等工程结构中经常出现三维 V 形切口/裂纹问题,如地下室方形洞室角区、重力坝踵坝趾区等. 由于几何形状或材料组成的突变会造成三维 V 形切口/裂纹尖端的强应力集中,严重时会导致受力构件甚至结构的整体破坏. 因而,准确计算三维 V 形切口/裂纹结构的应力场具有重要的理论意义和工程实用意义.

目前国内外****对于三维 V 形切口/裂纹结构的研究大多局限于裂尖场的奇异项、应力强度因子、裂纹扩展路径等. Chue 和 Liu^[1]给出了正交各向异性切口应力奇异阶的一般解,并指出解的奇异性取决于切口角度、边界条件及材料特性. Ungamornrat^[2]用弱奇异对称 Galerkin 边界元法 (SGBEM) 分析了三维多相材料线弹性裂纹结构的应力奇异性. Sator 和 Becker^[3]采用复变函数法获得了各向同性多材料接头端部应力奇异性指数的解析解. 胡宗军等^[4]建立了三维位势问题高阶边界单元几乎强奇异和几乎超奇异积分的半解析算法,其数值结果表明该方法可高效计算边界元法中几乎奇异面积分. Wu 等^[5]基于离散的快速傅里叶变换 (FFT) 理论,推导出线弹性各向异性双材料结构的界面应力场的半解析解.

此外,对应力强度因子和裂纹扩展的研究也比较深入. 文龙飞等^[6]基于改进型扩展有限元法,研究了动载荷作用下扩展裂纹尖端应力强度因子的求解方法. Xu 等^[7]在变长径比和双材料参数下,采用体力法计算了三维矩形界面裂纹的应力强度因子. 王振和余天堂^[8]采用自适应多尺度扩展有限元法计算了三维 I 型裂纹和 I-II 复合型裂纹的应力强度因子. 贾旭等^[9]采用裂纹弹性应力场的有限元解计算了三维裂纹的应力强度因子,其结果符合三维裂纹体裂纹尖端实际的应力应变状态. Fakovr 和 Ghoreishi^[10]研究了机械支柱、转速、裂纹取向等因素对旋转盘中应力强度因子的影响. Huang 等^[11]采用有限块法 (FBM) 计算了静载荷和瞬态动态载荷下的应力强度因子和$t$应力. 贾旭等^[12]提出了三维矩形平板内承受复杂非线性载荷下,仅含有3个系数的通用权函数,并采用 FEM 计算了三维含穿透裂纹的矩形板的 3 组参考应力强度因子. Magnus^[13]采用 FEM 分析了三维各向异性低渗透岩石在水压作用下的应力场. Dhanesh 等^[14]采用迭代分析技术 MMEKM 分析了三维弹性复合材料层合板在均匀轴向拉伸、弯曲、扭转和热载荷下的应力场,结果显示了自由边应力场的 MMEKM 解在项数和迭代次数方面具有良好的收敛特性. Stasyuk^[15]基于改进的边界积分方程法,分析了三维弹性无限体和有限弹性体中两个相互作用的圆盘形裂纹附近三维应力强度因子,并给出了裂纹沿法向均匀加载下的应 力场.

Karsten 和 Gunther^[16]采用对偶边界元法模拟了复杂三维线弹性裂纹的裂纹扩展路径,其结果和实验结果吻合较好. Li 和 Guo^[17]采用三维 FEM 研究了有限厚度板在单轴拉应力作用下的 V 形切口尖端弹性应力场,研究结果表明了板厚、切口角度对应力集中系数有明显的影响等. Park 和 Nikishkov^[18]提出了 SGBEM-FEM 交替方法,该方法可有效分析三维平面和非平面裂纹及其扩展. Lan 等^[19]采用三维 FEM 模拟了铝合金板在混合型加载下的裂纹扩展过程,并研究了裂纹尖端有限元尺寸和裂纹扩展增量尺寸对模拟预测结果的影响. Dias 等^[20]采用有限元方法模拟了准脆性材料的三维裂纹扩展问题,该方法可高效模拟位移不连续扩展的性能. Ding 和 Wang^[21]采用三维边界层 (小范围屈服) 公式对三维小应变进行了弹塑性模拟,模拟结果表明了尖端区域非奇异 T 应力对塑性区的尺寸和形状有显著的影响,且应力的大小、方向也受到 T 应力的影响. Wang 等^[22]通过建立三维复合材料的 2 种几何结构模型：微观结构模型和多单元模型,分析了三维碳/环氧复合材料在 $-100^\circ$C 至 $-140^\circ$C 不同温度场下的热膨胀行为和界面热应力.

研究三维线弹性 V 形切口/裂纹的文献很多,但大多局限在研究第 1 阶应力奇性指数及其在此基础上模拟裂纹扩展路径,而关于三维切口/裂纹结构完整位移和应力场的分析缺乏有效方法. 本文基于二维 V 形切口/裂纹结构的全域弹性应力场^[23-24]的求解思想,联合尖端扇形柱的渐近分析和外围结构的边界元法分析求解三维 V 形切口/裂纹结构完整的位移和应力场,称之为扩展边界元法 (XBEM). XBEM 计及了离尖端径向距离 $r$ 的渐近级数展开式中若干项的特征指数和特征函数. 文中将通过算例定量展现 XBEM 求解三维 V 形切口/裂纹结构完整应力场的准确性和适用性.

1 线弹性三维 V 形切口/裂纹尖端附近应力奇异性分析

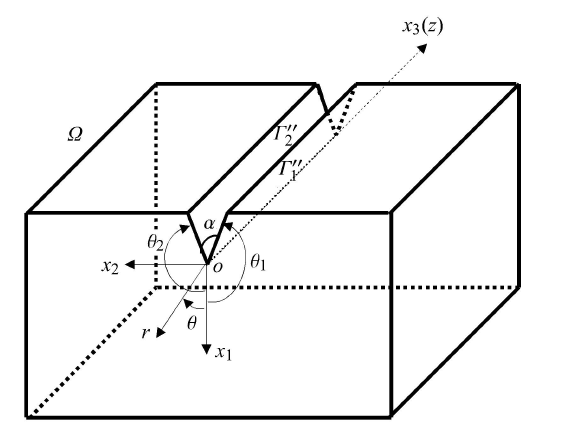
考虑三维柱状 V 形切口结构,如图 1 所示,其柱形切口张 角为 $\alpha =2 \pi - \theta_{1}-\theta_{2}$. 当 $\alpha =0^\circ $ 时,图 1 所示结构为三维裂纹结构. 将三维 V 形切口结构分为一个半径 $r=\rho $ 的扇形柱体 (图 2(b)) 和外围结构 (图 2(a)) 两部分. 外围结构新形成的边界为 ${\varGamma }'_\rho $,在切口尖端处同时定义笛卡尔坐标系 ${ox}_{1}x_{2}x_{3}$ 和柱坐标系 $or \theta z$ (坐标原点 $o$ 在切口尖端). 扇形柱体是应力奇异性区域,外围结构是无应力奇异性的普通弹性区域. 对于一个三维 V 形切口结构,图 2(b) 所示切口尖端附近应力奇异性区域的位移场可表达成关于径向 $r$ 的渐近级数展开式^[25-26]

图 1

新窗口打开|下载原图ZIP|生成PPT
图 1三维V形切口结构

Fig. 1A 3-D V-notched structure

图 2

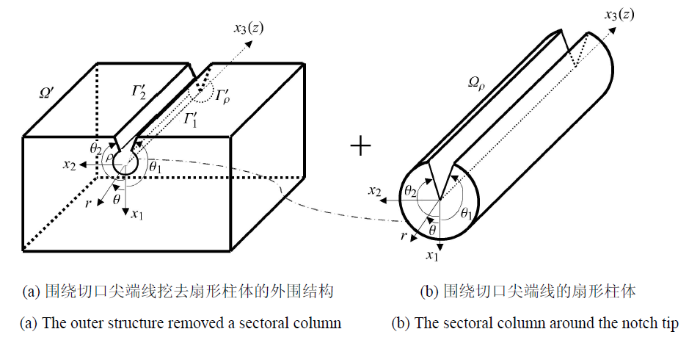
新窗口打开|下载原图ZIP|生成PPT
图 2三维V形切口结构挖去小扇形柱体

Fig. 2A sectoral column is separated from the 3-D V-notched structure



(1) $ \left. \begin{array}{ll} u_r (r,\theta ,z) = \sum_{k = 1}^N {A_k r^{\lambda _k + 1}} \tilde {u}_{rk} (\theta ,z,\lambda _k ) \\ u_\theta (r,\theta ,z) = \sum_{k = 1}^N {A_k r^{\lambda _k + 1}} \tilde {u}_{\theta k} (\theta ,z,\lambda _k ) \\ u_z (r,\theta ,z) = \sum_{k = 1}^N {A_k r^{\lambda _k + 1}} \tilde {u}_{zk} (\theta ,z,\lambda _k ) \end{array} \right \} $
式中,$A_{k}$ 为位移幅值系数,$\lambda _{k}$ 为切口尖端的位移特征指数,$N$ 表示截 取的级数项数,$\tilde {u}_{rk} (\theta ,z,\lambda _k ) $,$\tilde {u}_{\theta k} (\theta ,z,\lambda _k ) $,$\tilde {u}_{zk} (\theta ,z,\lambda _k )$ 为位移特征角函数. 由于图 2(b) 结构形状沿 $z$ 方向是相同的,并不涉及外载荷,因此分析切口尖端扇形柱区域 的奇异性时,式 (1) 中的特征角函数 $\tilde {u}_{rk} (\theta ,z,\lambda _k ) $,$\tilde {u}_{\theta k} (\theta ,z,\lambda _k ) $,$\tilde {u}_{zk} (\theta ,z,\lambda _k )$ 与 $z$ 无关,于是式 (1) 可简化写成

(2) $ \left. \begin{array}{ll} u_r (r,\theta ,z) = \sum_{k = 1}^N {A_k r^{\lambda _k + 1}} \tilde {u}_{rk} (\theta ,\lambda _k ) \\ u_\theta (r,\theta ,z) = \sum_{k = 1}^N {A_k r^{\lambda _k + 1}} \tilde {u}_{\theta k} (\theta ,\lambda _k ) \\ u_z (r,\theta ,z) = \sum_{k = 1}^N {A_k r^{\lambda _k + 1}} \tilde {u}_{zk} (\theta ,\lambda _k ) \end{array} \!\! \right \} $
考虑各向同性均质材料,将式 (2) 代入三维弹性力学几何方程和本构方程,可用位移场函数表示应力场函数 (为简明起见,以下 $\tilde {u}_{rk} (\theta , \lambda _k ) $,$\tilde {u}_{\theta k} (\theta , \lambda _k ) $,$\tilde {u}_{zk} (\theta , \lambda _k )$ 分别简写为 $\tilde {u}_r $,$\tilde {u}_\theta$,$\tilde {u}_z$)

(3) $ \left.\begin{array}{l} \sigma _{rr} (r,\theta ,z) = 2G\sum_{k = 1}^N \dfrac{\nu }{1 - 2\nu }\Big \{ \big [A_k (\lambda _k + 1)r^{\lambda _k }\tilde {u}_r + \\ \qquad A_k r^{\lambda _k }{\tilde {u}}'_\theta + A_k r^{\lambda _k }\tilde {u}_r \big ] + A_k (\lambda _k + 1)r^{\lambda _k }\tilde {u}_r \Big \} \\ \sigma _{\theta \theta } (r,\theta ,z) = 2G\sum_{k = 1}^N \dfrac{\nu }{1 - 2\nu } \Big \{ \big [A_k (\lambda _k + 1)r^{\lambda _k }\tilde {u}_r + \\ \qquad A_k r^{\lambda _k }{\tilde {u}}'_\theta + A_k r^{\lambda _k }\tilde {u}_r \big ] + A_k r^{\lambda _k }{\tilde {u}}'_\theta + A_k r^{\lambda _k }\tilde {u}_r \Big \} \\ \sigma _{zz} (r,\theta ,z) = 2G\sum_{k = 1}^N \dfrac{\nu }{1 - 2\nu }\big [A_k (\lambda _k + 1)r^{\lambda _k }\tilde {u}_r + \\ \qquad A_k r^{\lambda _k }{\tilde {u}}'_\theta + A_k r^{\lambda _k }\tilde {u}_r \big ] \\ \sigma _{\theta z} (r,\theta ,z) = G\sum_{k = 1}^N A_k r^{\lambda _k }{\tilde {u}}'_z \\ \sigma _{rz} (r,\theta ,z) = G\sum_{k = 1}^N A_k (\lambda _k + 1)r^{\lambda _k }\tilde {u}_z \\ \sigma _{r\theta } (r,\theta ,z) = G\sum_{k = 1}^N A_k r^{\lambda _k }[(\lambda _k + 1)\tilde {u}_\theta + {\tilde {u}}'_r - \tilde {u}_\theta ] \end{array} \right \} $
式中,$( \cdots )' = d( \cdots )/ d \theta $,余下同. $G =E /[2(1+ v)]$,$E$ 为材料杨氏模量,$v$ 是泊松比.

注意到式 (1) 的位移特征指数 $\lambda _k $ 和位移特征角函数仅取决于切口的材料性质和楔形边界条件,不依赖载荷,因此应力特征分析不用考虑体力. 取式 (2) 中的典型项 $A_k r^{\lambda _k + 1}\tilde {u}_r (\theta ,\lambda _k )$,$A_k r^{\lambda _k + 1}\tilde {u}_\theta (\theta ,\lambda _k ) $,$A_k r^{\lambda _k + 1}\tilde {u}_z (\theta ,\lambda _k )$代入到忽略体力项的三维弹性力学平衡方程

(4) $ \left.\begin{array}{l} \dfrac{\partial \sigma _{rr} }{\partial r}\dfrac{1}{r}\dfrac{\partial \sigma _{r\theta } }{\partial \theta } + \dfrac{\partial \sigma _{rz} }{\partial z} + \dfrac{1}{r}(\sigma _{rr} - \sigma _{\theta \theta } ) = 0 \\ \dfrac{\partial \sigma _{r\theta } }{\partial r}\dfrac{1}{r}\dfrac{\partial \sigma _{\theta \theta } }{\partial \theta } + \dfrac{\partial \sigma _{\theta z} }{\partial z} + \dfrac{2}{r}\sigma _{r\theta } = 0 \\ \dfrac{\partial \sigma _{rz} }{\partial r}\dfrac{1}{r}\dfrac{\partial \sigma _{\theta z} }{\partial \theta } + \dfrac{\partial \sigma _{zz} }{\partial z} + \dfrac{1}{r}\sigma _{rz} = 0 \end{array} \!\!\right\} $
通过一系列推导,可得关于切口尖端扇形柱区域应力奇异性特征值问题的常微分方程组 (为方便起见,$\tilde {g}_r (\theta ,\lambda ) $,$\tilde {g}_\theta (\theta ,\lambda ) $,$\tilde {g}_z (\theta ,\lambda )$ 分别简写为 $\tilde {g}_r$,$\tilde {g}_\theta$,$\tilde {g}_z$)

(5) $ \left.\begin{array}{l} G{\tilde {u}}"_r - (X + 3G){\tilde {u}}'_\theta - (X + 2G)\tilde {u}_r + \\ \qquad (\lambda _k + 1)(X + G){\tilde {u}}'_\theta + (\lambda _k + 1)(X + 2G)\tilde {g}_r = 0 \\ (X + 2G)\tilde{u}"_\theta + (X + 3G)\tilde {u}'_r - G\tilde {u}_\theta + \\ \qquad (\lambda _k + 1)(X + G){\tilde {u}}'_r + (\lambda _k + 1)G\tilde {g}_\theta = 0 \\ G\tilde {u}"_z + G(\lambda _k + 1)\tilde {g}_z = 0\\ (\lambda _k + 1)\tilde {u}_r = \tilde {g}_r \\ (\lambda _k + 1)\tilde {u}_\theta = \tilde {g}_\theta \\ (\lambda _k + 1)\tilde {u}_z = \tilde {g}_z \end{array} , \theta \in [\theta _1 ,\theta _2 ] \right\} $
式中,$( \cdots )"$ 表示对坐标 $\theta$ 的二阶导数,余类同. $X = E \nu /[(1+ \nu )(1-2 \nu )]=2 G \nu /(1-2 \nu )$.

假定切口两楔边自由,则其上面力为零,边界条件可由式 (6) 表示

(6) $ \left.\begin{array}{l} \sigma _{\theta \theta } (\theta _1 ) = \sigma _{r\theta } (\theta _1 ) = \sigma _{\theta z} (\theta _1 ) = 0 \\ \sigma _{\theta \theta } (\theta _2 ) = \sigma _{r\theta } (\theta _2 ) = \sigma _{\theta z} (\theta _2 ) = 0 \end{array} \right \} $
因此,三维 V 形切口尖端扇形柱附近的位移特征指数 $\lambda _k $ 的计算变成了求解常微分方程组 (5) 和相应的边界条件 (6) 的特征值问题. 采用插值矩阵法^[27-28]求解式 (5) 和式 (6),可得切口尖端扇形柱附近的位移特征指数 $\lambda _k$、相应的位移特征角函数 $\tilde {u}_r$, $\tilde {u}_\theta $, $\tilde {u}_z $ 及其导函数.

一般情况下,$\lambda _{k}, A_{k}, \tilde {u}_r, \tilde {u}_\theta, \tilde {u}_z $ 是复数, 则图 2(a) 中外围结构挖去扇形柱的新边界 ${\varGamma }'_\rho $ 上位 移 $u_{m}$ 和面力 $t_{m } (m =1, 2, 3)$ 在直角坐标系 ${ox}_{1}x_{2}x_{3}$ 下的表达式

(7) $ \left\{ \!\! \begin{array}{c} u_1 \\ u_2 \\ u_3 \end{array} \!\! \right\} = \sum_{k = 1}^N r^{\lambda _{k {\rm R}} + 1} \zeta \left \{ A_{k {\rm R}} \left [ \left\{ \!\! \begin{array}{l} \tilde {u}_{rk{\rm R}} (\theta )\cos \theta - \tilde {u}_{\theta k{\rm R}} (\theta )\sin \theta \\ {\tilde {u}_{rk{\rm R}} (\theta )\sin \theta + \tilde {u}_{\theta k{\rm R}} (\theta )\cos \theta } \\ \tilde {u}_{zk{\rm R}} (\theta ) \end{array} \!\! \right\} \cos (\lambda _{k{\rm I}} \ln r) - \left\{ \!\!\begin{array}{l} \tilde {u}_{rk{\rm I}} (\theta )\cos \theta - \tilde {u}_{\theta k{\rm I}} (\theta )\sin \theta \\ \tilde {u}_{rk{\rm I}} (\theta )\sin \theta + \tilde {u}_{\theta k{\rm I}} (\theta )\cos \theta \\ \tilde {u}_{zk{\rm I}} (\theta ) \end{array} \!\! \right\}\sin (\lambda _{k{\rm I}} \ln r) \right ] \right.- \\ \qquad \left. A_{k{\rm I}} \left [\left\{ \!\! \begin{array}{l} {\tilde {u}_{rk{\rm R}} (\theta )\cos \theta - \tilde {u}_{\theta k{\rm R}} (\theta )\sin \theta } \\ \tilde {u}_{rk{\rm R}} (\theta )\sin \theta + \tilde {u}_{\theta k{\rm R}} (\theta )\cos \theta \\ \tilde {u}_{zk{\rm R}} (\theta ) \end{array} \!\! \right\}\sin (\lambda _{k{\rm I}} \ln r) + \left\{ \!\! \begin{array}{l} \tilde {u}_{rk{\rm I}} (\theta )\cos \theta - \tilde {u}_{\theta k{\rm I}} (\theta )\sin \theta \\ \tilde {u}_{rk{\rm I}} (\theta )\sin \theta + \tilde {u}_{\theta k{\rm I}} (\theta )\cos \theta \\ \tilde {u}_{zk{\rm I}} (\theta ) \end{array} \!\! \right\}\cos (\lambda _{k{\rm I}} \ln r) \right ] \right \} $
(8) $ \left\{\!\! \begin{array}{c} {t_1 } \\ t_2 \\ t_3 \end{array}\!\! \right\} = \sum_{k = 1}^N r^{\lambda _{k{\rm R}} }\zeta \left\{ - A_{k{\rm R}} \left [\left\{ \!\! \begin{array}{l} \tilde {\sigma }_{rrk{\rm R}} (\theta )\cos \theta - \tilde {\sigma }_{r\theta k{\rm R}} (\theta )\sin \theta \\ \tilde {\sigma }_{rrk{\rm R}} (\theta )\sin \theta + \tilde {\sigma }_{r\theta k{\rm R}} (\theta )\cos \theta \\ \tilde {\sigma }_{zrk{\rm R}} (\theta ) \end{array} \!\! \right\}\cos (\lambda _{k{\rm I}} \ln r) - \left\{ \!\! \begin{array}{l} {\tilde {\sigma }_{rrk{\rm I}} (\theta )\cos \theta - \tilde {\sigma }_{r\theta k{\rm I}} (\theta )\sin \theta } \\ {\tilde {\sigma }_{rrk{\rm I}} (\theta )\sin \theta + \tilde {\sigma }_{r\theta k{\rm I}} (\theta )\cos \theta } \\ \tilde {\sigma }_{zrk{\rm I}} (\theta ) \end{array} \!\! \right\}\sin (\lambda _{k{\rm I}} \ln r) \right ] +\right. \\ \qquad A_{k{\rm I}} \left. \left [\left\{ \!\!\begin{array}{l} {\tilde {\sigma }_{rrk{\rm R}} (\theta )\cos \theta - \tilde {\sigma }_{r\theta k{\rm R}} (\theta )\sin \theta } \\ \tilde {\sigma }_{rrk{\rm R}} (\theta )\sin \theta + \tilde {\sigma }_{r\theta k{\rm R}} (\theta )\cos \theta \\ \tilde {\sigma }_{zrk{\rm R}} (\theta ) \end{array} \!\! \right\}\sin (\lambda _{k{\rm I}} \ln r) + \left\{ \!\! \begin{array}{l} {\tilde {\sigma }_{rrk{\rm I}} (\theta )\cos \theta - \tilde {\sigma }_{r\theta k{\rm I}} (\theta )\sin \theta } \\ \tilde {\sigma }_{rrk{\rm I}} (\theta )\sin \theta + \tilde {\sigma }_{r\theta k{\rm I}} (\theta )\cos \theta \\ \tilde {\sigma }_{zrk{\rm I}} (\theta ) \end{array} \!\! \right\}\cos (\lambda _{k{\rm I}} \ln r) \right ] \right \} $
式中,下标 R 表示复数的实部,下标 I 表示复数的虚部. 若 $\lambda _{k}$ 是实根,则其相应虚部项为零,系数 $\zeta= 1$;如果 $\lambda _{k}$ 是共轭复根,则相应虚部项不为零,系数 $\zeta = 2$,因需计及复数共轭项对位移场和应力场的 贡献.

注意：式 (7) 和式 (8) 中位移幅值系数 $A_{k{\rm R}}$ 和 $A_{k{\rm I}} (k=1, 2, \cdots, N)$ 待求. 基于切口尖端应 力奇异性的特征分析结果式 (7) 和式 (8),下面建立求解三维切口结构位移和应力渐近场表达式中幅值 系数 $A_{k{\rm R}}$ 和 $A_{k{\rm I}}$ 的扩展边界元法.

2 分析三维V形切口/裂纹结构完整应力场的扩展边界元法

在图 1 切口结构中挖去尖端扇形柱后剩余的外围结构区域 ${\varOmega }'$ 无应力奇异性,见图 2(a). 其边界位移 $u_{m}(x)$ 和面力分量 $t_{m}(x)$ 可由如下常规边界积分方程描述

(9) $ {\pmb C}_{lm} ({\pmb y}){\pmb u}_m ({\pmb y}) = \int_{\varGamma } {\pmb U}_{lm}^\ast ({\pmb x},{\pmb y}){\pmb t}_m ({\pmb x}) d \varGamma - \\ \qquad - \int_{\varGamma } {\pmb T}_{lm}^\ast ({\pmb x},{\pmb y}){\pmb u}_m ({\pmb x}) d \varGamma + \int_{\varOmega } {\pmb U}_{lm}^\ast {\pmb b}_m d \varOmega $
式中,$- \int_{ \varGamma } ( \cdots ) d \varGamma $ 称为 Cauchy 主值积分; $\varGamma = \partial {\varOmega }'$; ${\pmb C}_{lm}({\pmb y})$ 称为边界节点$y$处形状系数;$l$,$m=1$,2,3; ${\pmb b}_m$ 为体力分量;${\pmb y}$ 是源点;${\pmb x}$ 是场点;积分核函数 ${\pmb U}_{lm}^\ast ({\pmb x},{\pmb y})$,${\pmb T}_{lm}^\ast ({\pmb x},{\pmb y})$ 是基本解,可见于边界元法教科书.

外围结构 ${\varOmega }'$ 内任意点的位移和应力可分别由位移和应力边界积分方程表达

(10) $ {\pmb u}_m ({\pmb y}) = \int_{ \varGamma } {\pmb U}_{lm}^\ast ({\pmb x},{\pmb y}){\pmb t}_m ({\pmb x}) d \varGamma - \\ \qquad \int_{ \varGamma } {\pmb T}_{lm}^\ast ({\pmb x},{\pmb y}) {\pmb u}_m ({\pmb x}) d \varGamma + \\ \qquad \int_{ \varOmega } {\pmb U}_{lm}^\ast ({\pmb x},{\pmb y}){\pmb b}_m d \varOmega , \ \ {\pmb y} \ {\rm in} \ {\varOmega }' $
(11) $ {\pmb \sigma }_{lkm} ({\pmb y}) = \int_{ \Gamma }{\pmb W}_{lkm}^\ast ({\pmb x},{\pmb y}){\pmb t}_m ({\pmb x}) d \varGamma - \\ \qquad \int_{ \varGamma } {\pmb S}_{lkm}^\ast ({\pmb x},{\pmb y}) {\pmb u}_m ({\pmb x}) d \varGamma + \\ \qquad \int_{ \varOmega } {\pmb W}_{lkm}^\ast ({\pmb x},{\pmb y}) {\pmb b}_m d \varOmega , \ \ {\pmb y} \ {\rm in } \ {\varOmega }' $
式中,积分核函数 $W_{lkm}^\ast ({\pmb x}, {\pmb y})$ 和 ${\pmb S}_{lkm}^\ast ({\pmb x}, {\pmb y}) (k=1,2,3)$ 是 ${\pmb U}_{lm}^\ast ({\pmb x},{\pmb y})$,${\pmb T}_{lm}^\ast ({\pmb x},{\pmb y})$ 的线性组合.

将式 (7) 和式 (8) 表示的弧面 ${\varGamma }'_\rho $ 上的位移和面力分量表达式,装配进外围结构 (图 2(a)) 的常规边界积分方程 (9) 中,联立求解代数方程组可获得外围结构 (图 2(a)) 未知的边界位移和应力及式 (1) 中未知的位移幅值系数 $A_{k{\rm R}}$ 和 $A_{k{\rm I}}$. 然后将求得的边界位移和面力代入式 (10) 和式 (11),可得切口外围结构任一内点的位移和应力. 最后将求得的位移 幅值系数 $A_{k{\rm I}}$ 和 $A_{k{\rm R}}$ 代入式 (1) 和式 (3) 可得图 2(b) 切口尖端扇形柱一定 范围内的位移和应力场. 这即为扩展边界元法 (XBEM),可获得三维切口结构完整的位移场和应力场.

3 三维 V 形切口/裂纹问题算例

3.1 含 V 形切口的长方形柱体

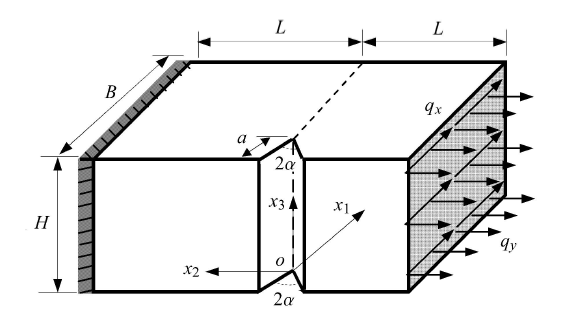
含 V 形切口的长方形柱体,见图 3. 结构尺寸 $L =15$ mm,$H =5$ mm,$B =10$ mm,弹性模量 $E =200$ GPa,泊松 比 $\nu =0.3$. 沿长方形柱体正表面对称线上有一个等深度的 V 形切口,切口深度 $a =2.5$ mm,切口 张角 $2\alpha = 60^ \circ$. 长方形柱体结构左侧面 $(x _{2 } = L)$ 固定,右侧面 ($x_{2 } = - L)$ 施加 均匀的外部拉力 $q_{x} =0$ MPa,$q_{y}=30$ MPa.

图 3

新窗口打开|下载原图ZIP|生成PPT
图 3三维V形切口结构

Fig. 3A 3-D V-notched structure



首先从三维V形切口结构 (如图 3 所示) 中挖取一个 $\rho =0.5$ mm 的扇形柱体 (如图 4(b) 所示),采用插值矩阵法对扇形柱体进行特征分析,获得三维V形切口尖端扇形柱区域的前若干阶位移特征指数 $\lambda_{k}$ 和其相对应的位移特征角函数 $\tilde {u}_r$, $\tilde {u}_\theta$, $\tilde {u}_z $,如表 1 和图 5 和图 6 所示.

图 4

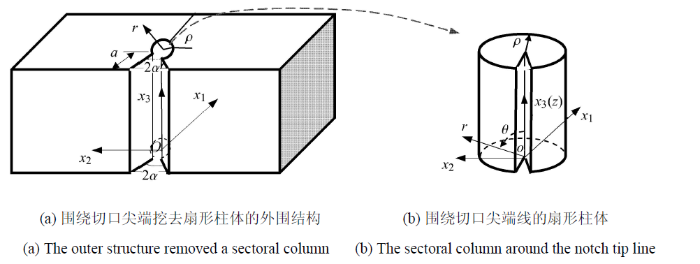
新窗口打开|下载原图ZIP|生成PPT
图 4三维V形切口挖去小扇形柱体

Fig. 4A sectoral column is separated from the 3-D V-notched structure



Table 1
表1
表1三维 V 型切口 $2\alpha =60^\circ$ 尖端的位移特征指数 $\lambda_{k}$
Table 1The displacement indexes $\lambda_{k}$ of the 3-D V-notched structure with $2\alpha =60^\circ$

新窗口打开|下载CSV

图 5

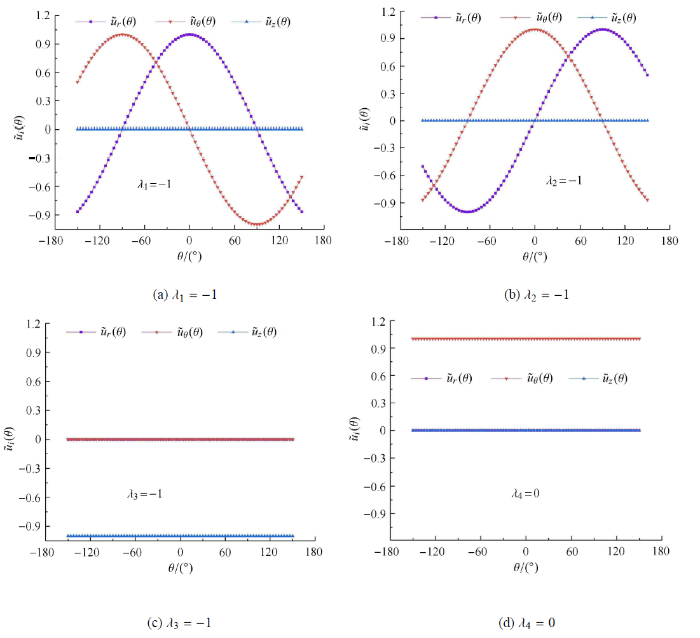
新窗口打开|下载原图ZIP|生成PPT
图 5三维 V 形切口 $2\alpha =60^\circ$ 对应的位移特征角函数

Fig. 5The displacement eigenvectors for the 3-D V-notched structure when $2\alpha =60^\circ$

图 6

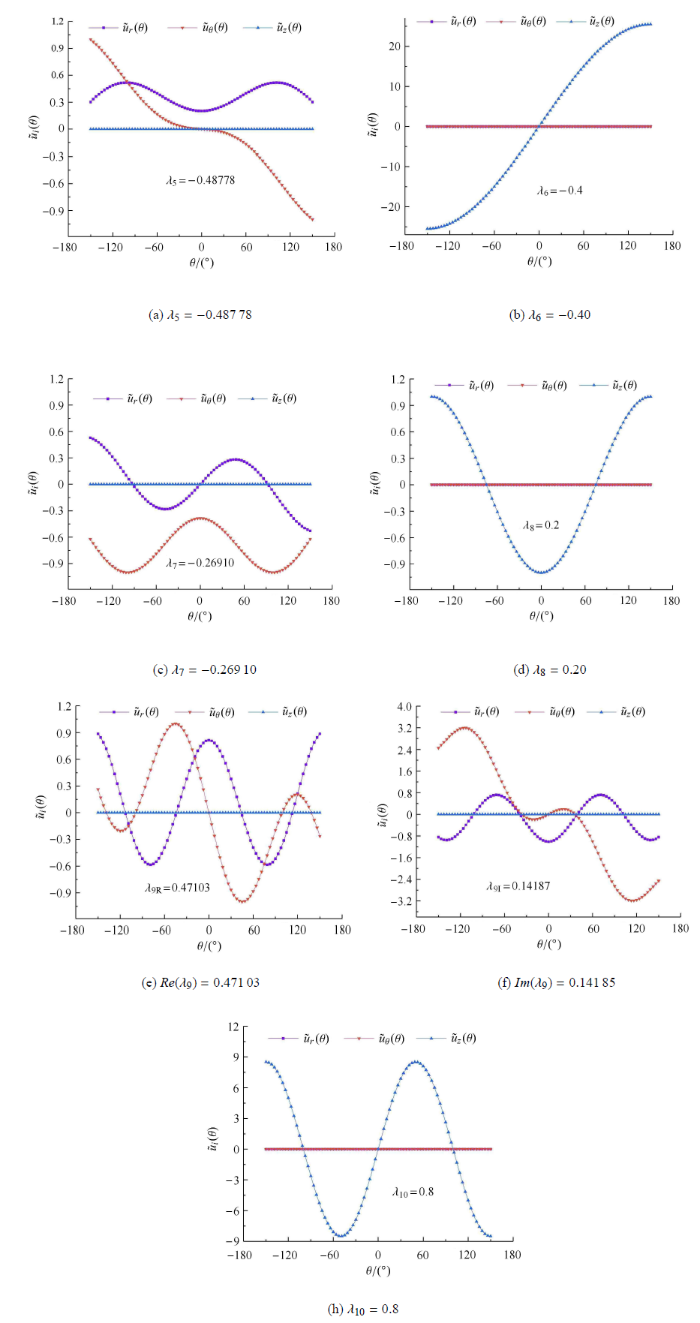
新窗口打开|下载原图ZIP|生成PPT
图 6三维 V 形切口 $2\alpha =60^\circ$ 对应的位移特征角函数

Fig. 6The displacement eigenvectors for the 3-D V-notched structure when $2\alpha =60^\circ$



表 1 中 $\lambda_{k}$ 前 4 项是刚体位移项,相应的特征角函数见图 5. 图 5(a) $\sim $ 图 5(c) 呈现的是平面问题的 3 个刚体位移项,图 5(d) 呈现的是反平面问题的刚体位移项. 这些刚体位移项对应力场的计算没有影响,但对于位移场的计算不可省略.

注意到图 6(b)、图 6(d)、图 6(h) 中 $\tilde {u}_r $ 和 $\tilde {u}_\theta $ 均为 0,故 $\lambda_{6}$, $\lambda_{8}$ 和 $\lambda_{10}$ 为反平面 V 形切口对应的位移特征指数. 图 6(a)、图 6(c)、图 6(e)、图 6(f) 中 $\tilde {u}_z $ 均为 0,故 $\lambda _{5}$, $\lambda _{7}$ 和 $\lambda _{9}$ 为平面 V 形切口对应的位移特征指数;其中, $\lambda_{5}$ 和 $\lambda_{9}$ 为平面内对称位移特征指数, $\lambda_{7}$ 为平面内反对称位移特征指数.

扩展边界元法 (XBEM) 对三维 V 形切口结构进行计算时,初始选取渐近级数展开式 (1) 中截取级数项数 $N =7$ (4 个刚体位移项,1 个平面内对称项,1 个平面内反对称项和 1 个反平面项)作为渐近级数展开式 (1) 的基准项数. 随后在 $N=7$ 的基础上增大 $N$,讨论 $N$ 的取值对三维 V 形切口结构完整位移和应力场精度的影响.

XBEM 分析三维 V 形切口结构的实施过程：首先,采用插值矩阵法求解常微分方程组 (5) 获得切口尖端的位移特征指数 $\lambda_{k}$ 及其相对应的特征角函数,然后对外围结构采用边界元法进行分析,边界采用 8 节点四边形单元,单元数 424,节点数 1274. 联立求解两组方程组 获得了位移幅值系数 $A_{k{\rm R}}$, $A_{k{\rm I}}$ 以及外围结构边界未知的位移和面力. 在 XBEM 执行中,不可避免遇到有些源点到边界单元距离很小的情形—三维 BEM 中几乎奇异积分的难题,本文采用半解析法 ^{[4, 30]}高效解决了这一难题. 最后,将求得的边界位移和面力代入式 (10) 和式 (11) 得外围结构任意内点的位移和应力. 对于扇形柱体区域的位移和应力场,采用渐近级数展开式 (1) 和式 (3) 计算,外围区域 (图 4(a)) 内点的位移和应力场采用内点积分方程 (10) 和式 (11) 计算,其临近扇形柱附近的外围区域内点的位移和应力场也可采用渐近级数展开式 (1) 和式 (3) 计算.

表 2 和表 3 以及图 7 分别给出了切口尖端扇形柱一定范围内应力和位移的 XBEM 计算结果,其中,XBEM-ASY 表示采用渐近级数展开式 (1) 和式 (3) 计算的结果 (扇形柱及其临近区域),XBEM-BEM 表示采用积分方程式 (10) 和式 (11) 计算的结果 (外围区域),FEM 表示采用有限元分析软件计算的结果. 表 2 和表 3 中 XBEM-BEM 计算值和图 7(a) 曲线显示：当截取级数项数 $N >7$ 时,$N$ 的增加对于外围结构区域的 XBEM-BEM 计算结果影响很小. 说明选取了足够的 $N$ 之后,XBEM 的计算精度对 $N$ 的取值不敏感,稳定性很好,这对于 XBEM 求解三维 V 形切口结构的完整应力场非常便利.

Table 2
表2
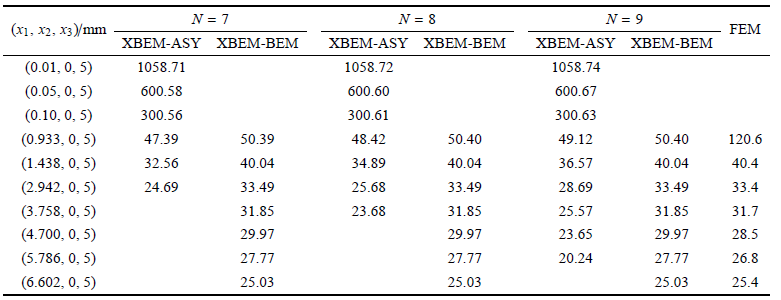
表2XBEM和FEM 计算沿 $x_{2} =0$ mm, $x_{3} =5$ mm 附近内点的应力分量 $\sigma_{x2}$ (MPa)
Table 2Variation of stress component $\sigma_{x2}$ (MPa) along $x_{2} =0$ mm, $x_{3} =5$ mm

新窗口打开|下载CSV

Table 3
表3
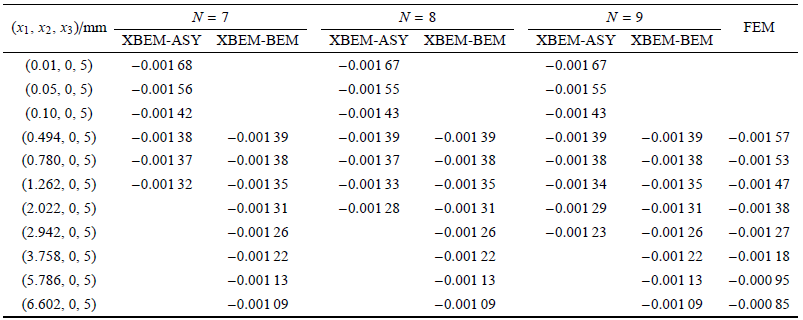
表3XBEM和FEM 计算沿 $x_{2}=0$ mm, $x_{3} =5$ mm 附近内点的位移分量 $u_{x2}$ (mm)
Table 3Variation of displacement component $u_{x2}$ (mm) along $x_{2}=0$ mm, $x_{3} =5$ mm

新窗口打开|下载CSV

图 7

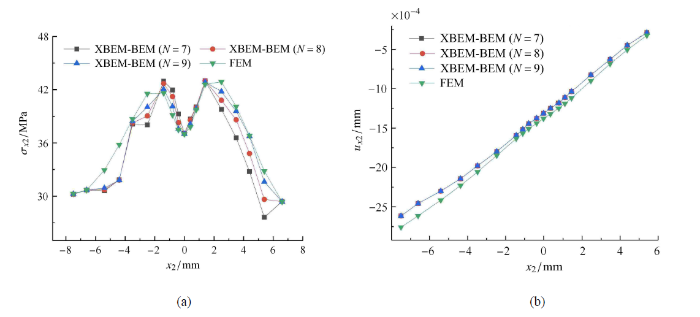
新窗口打开|下载原图ZIP|生成PPT
图 7XBEM-BEM 和 FEM 计算 3-D V 形切口沿 $x_{1} =2$ mm, $x_{3} =5$ mm 线段的 $\sigma_{x2 }$ 和 $u_{x2 }$ 值

Fig. 7$\sigma_{x2 }$ and $u_{x2 }$ along $x_{1} =2$ mm, $x_{3} =5$ mm calculated by XBEM-BEM and FEM



表 2 显示,对外围区域点 (1.438 mm, 0 mm, 5 mm) 处,当 $N =7$ 时,XBEM-ASY 计算的应力值 ($\sigma_{x2}=32.56$ MPa) 和 XBEM-BEM 计算相同点的应力 值 ($\sigma_{x2}=40.04$ MPa) 的相对差为 $-18.7$%. 当 $N =8$ 时,XBEM-ASY 计算的应力值 ($\sigma_{x2}=34.89$ MPa) 和 XBEM-BEM 计算相同点的应力值 ($\sigma_{x2}=40.04$ MPa) 的相对差为 $-12.9$%. 当 $N =9$ 时,XBEM-ASY 计算的应力值 ($\sigma_{x2}=36.57$ MPa) 和 XBEM-BEM 计算相同点的应力值 ($\sigma_{x2}=40.04$ MPa) 的相对差为 $-8.7$%. 说明相对XBEM-BEM计算值而言,XBEM-ASY 计算同一点的相对差随 $N$ 的增大逐渐减小,即 XBEM-ASY 计算切口尖端应力场的有效范围随 $N$ 的增大逐渐增大.

通常情况,外围结构的位移和应力由 XBEM-BEM 解胜任,无需采用 XBEM-ASY 计算,这里关于两者计算值的比较,意在说明 XBEM-ASY 解的有效范围可为扇形柱半径的选取提供参考. 例如,若 XBEM-ASY 计算的切口 尖端应力场在 $r < 1.0$ mm 的范围内是足够准确的,说明 XBEM 使用时,尖端扇形区域半径 $\rho $ 的选取范围较为宽松, $\rho <1.0$ mm 之间均可行. 表 3 中切口结构位移解显示了同样的 规律.

此外,本文还采用有限元法 (FEM) 对图 3 结构进行计算. 这里 FEM 采用 20 节点六边形单元,划分单元数 111 000. 表 2 显示,当 $x_{2} =0$ mm,$x_{3} =5$ mm,$x_{1} >1.262$ mm 的远场区域,FEM 的结果和 XBEM-BEM 的结果吻合较好;而当 $x_{2} =0$ mm,$x_{3} =5$ mm,$x_{1} <1.262$ mm 时 ( 切口尖端近场区域 ),FEM 计算的应力场与 XBEM-BEM 的结果有较大的差异. 对于三维 V 形切口尖端的强应力集中,尽管 FEM 在尖端使用了细密的网格划分,其采用的单元数为 XBEM 单元数的 261 倍,极大地增加了计算量和计算机内存需求,但仍无法准确描述其尖端近场区域的应力场. 随着距尖端距离的增大,应力集中的现象逐渐减弱,FEM 的计算结果方为可信.

3.2 含裂纹的长方形柱体单向受拉和受剪

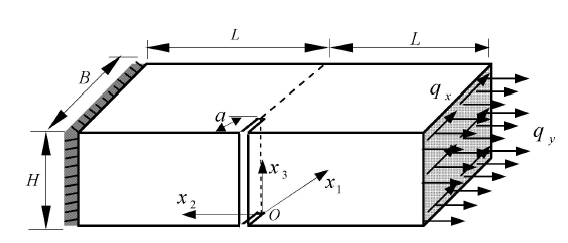
含裂纹的各向同性均质材料长方形柱体,结构尺寸 $L =10.0$ mm,$H =3$ mm,$B =4$ mm,弹性 模量 $E =200$ GPa,泊松比 $\nu =0.3$. 沿长方形柱体正表面对称线上有一个等深度的裂纹,裂纹深度 $a =0.8$ mm,边界条件为长方形柱体结构左侧面固定,右侧面施加均布载荷 $q_{x} =10$ MPa,$q_{y} =10$ MPa,为复合型裂纹,如图 8 所示.

图 8

新窗口打开|下载原图ZIP|生成PPT
图 8三维裂纹结构

Fig. 8A 3-D cracked structure



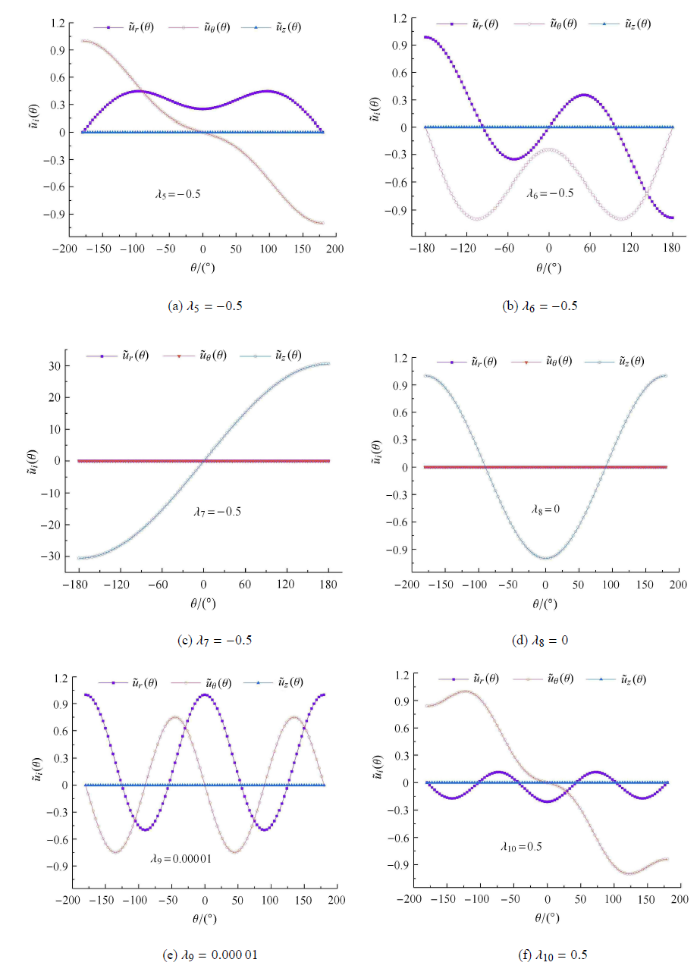
首先从图 8 三维复合型裂纹结构中挖取一个 $\rho =0.2$ mm 的扇形柱体 (如图 9(b) 所示),采用插值 矩阵法对扇形柱体进行特征分析,获得裂纹 尖端扇形柱区域的前若干阶位移特征指数 $\lambda_{1}, \lambda_{2}$, $\lambda_{3}, \cdots, \lambda_{10} $ 分别为 $-1, -1, -1, 0, -0.5, -0.5, -0.5,$ $0, 0.000 01, 0.5$. 其相对应的位移特征角函数 $\tilde {u}_r$, $\tilde {u}_\theta$, $\tilde {u}_z$ 如图 10 所示.

图 9

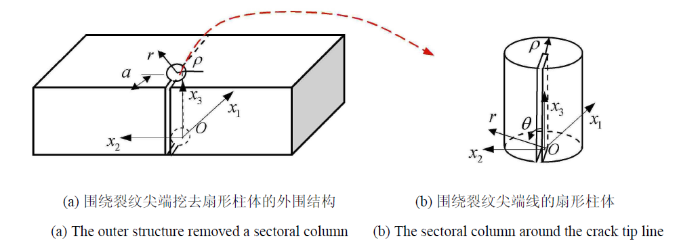
新窗口打开|下载原图ZIP|生成PPT
图 9三维裂纹挖去小扇形柱体

Fig. 9Asectoral column is separated from the 3-D cracked structure

图 10

新窗口打开|下载原图ZIP|生成PPT
图 10三维裂纹对应的位移特征角函数

Fig. 10The displacement eigenvectors for the 3-D cracked structure



$\lambda_{1} \sim \lambda_4$ 前 4 项是刚体位移项,$\lambda_{5} \sim \lambda_{10}$ 为主导的各阶位移特征 指数,其对应的位移特征角函数见图 10. 注意到图 10(b)、图 10(d)、图 10(h) 为反平面裂纹对应的位移特征角 函数;图 10(a)、图 10(c)、图 10(e)、图 10(f) 为平面裂纹对应的位移特征角 函数.

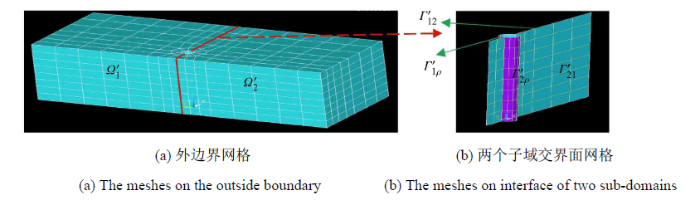
为避免由于裂纹的两条边重合所引起方程的不适定性,本文采用子域法将图 8 所示三维复合型裂纹结构分为两个子域 ${\varOmega }'_1 $ 和 ${\varOmega }'_2 $,如图 11(a) 所示. ${\varGamma }'_{1\rho } $ 和 ${\varGamma }'_{2\rho } $ 分别对应子域 ${\varOmega }'_1 $ 和 ${\Omega }'_2 $ 的扇形柱内边界,${\varGamma }'_{12}({\varGamma }'_{21} )$ 为子域 ${\varOmega }'_1 $和${\varOmega }'_2 $ 的粘结边,如图 11(b) 所示.

图 11

新窗口打开|下载原图ZIP|生成PPT
图 11三维裂纹结构边界元网格

Fig. 11The BE meshes of 3-D cracked structure



采用 XBEM 对其完整应力场进行分析. 采用 8 节点四边形单元离散边界,对子域 ${\varOmega }'_1$,外边界布置 578 个节点,共有 1734 个未知量;扇形柱边界 ${\varGamma }'_{1\rho } $ 布置 489 个节点,每个节点的面力和位移均未知,共 2934 个未知量;交界面 ${\varGamma }'_{12} $ 上布置 147 个节点,每个节点的面力和位移均未知,共 882 个未知量,因此子域 ${\varOmega }'_1 $ 未知量的总数为 5550 个. 类似的,对于子域 ${\varOmega }'_2$,外边界、扇形柱边界 ${\varGamma }'_{2\rho } $ 和交界面 ${\varGamma }'_{21}$ 分别布置 578, 489, 147 个节点,共 5550 个未知量. 由于 ${\varGamma }'_{12}$ 和 ${\varGamma }'_{21}$ 为子域 ${\varOmega }'_1 $ 和 ${\varOmega }'_2 $ 的粘结边,其对应节点的位移分量相等、面力分量相反 (互为作用力和反作用力的关系),因此 ${\varGamma }'_{12} $ 和 ${\varGamma }'_{21}$ 两条边界上的未知量只有 882 个. 子域 ${\varOmega }'_1 $ 和 ${\varOmega }'_2 $ 未知量的总数为 10 218 个.

注意到 ${\varGamma }'_{1\rho } $ 上有 489 个节点共 2934 个未知量,但只能 列取 1467 个方程. 为此,利用式 (8) 给出的面力表达式,在 ${\varGamma }'_{1\rho } $ 上 489 个节点处建立面力与幅值系数 $A_{k{\rm R}}$, $A_{k{\rm I}}$ 的关系式,每个节点可建立 3 个方程,共 1467 个方程. 由于幅值系数 $A_{k{\rm R}}$, $A_{k{\rm I}}$ 是未知的,因此建立 1467 个方程的同时也引入了 $2 N$ 个未知量. 于是在 ${\varGamma }'_{1\rho }$ 上 489 个节点中需选取 $2N/3$个节点建立 $2 N$ 个位移与幅值系数 $A_{k{\rm R}}$, $A_{k{\rm I}}$ 的关系式,此时 ${\varGamma }'_{1\rho } $ 上的未知量数与建立的方程数相等. ${\varGamma }'_{2\rho } $ 亦做同样的处理. 综上,子域 ${\varOmega }'_1 $ 和 ${\varOmega }'_2 $ 共有 $10 218+2N$ 个未知量,建立的方程总数为 $10 218+2N$ 个,方程组有唯一解. 求解方程组可得子域 ${\varOmega }'_1 $ 和 ${\varOmega }'_2 $ 边界的位移、面力和幅值系数 $A_{k{\rm R}}$,$A_{k{\rm I}}$,然后将求得的位移、面力代入边界积 分方程 (10) 和 (11) 可得子域 ${\varOmega }'_1 $ 和 ${\varOmega }'_2 $ 内任一内点的位移和应力,最后将求得的位移幅值系数 $A_{k{\rm R}}$ 和 $A_{k{\rm I}}$ 代入 式 (1) 和式 (3) 可得图 2(b) 切口尖端扇形柱一定范围内的位移和应力场,至此,三维复合型裂纹结构的位移和应力场已完整获得,如表 4 和表 5 和图 12 所示. 表 4;和表;5 以及图 12;中 XBEM-BEM,XBEM-ASY,FEM 的含义如算例 3.1 所述.

Table 4
表4
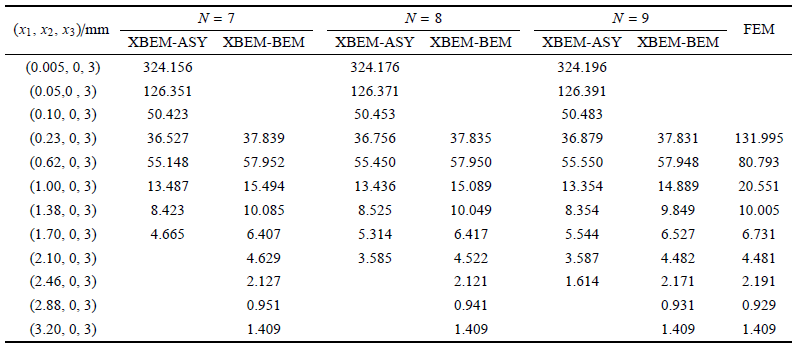
表4XBEM和FEM 计算沿 $x_{2} =0$ mm, $x_{3} =3$ mm 附近内点的应力分量 $\sigma_{x1}$ (MPa)
Table 4Variation of $\sigma_{x1}$ (MPa) along $x_{2} =0$ mm, $x_{3} =3$ mm calculated by XBEM and FEM

新窗口打开|下载CSV

Table 5
表5
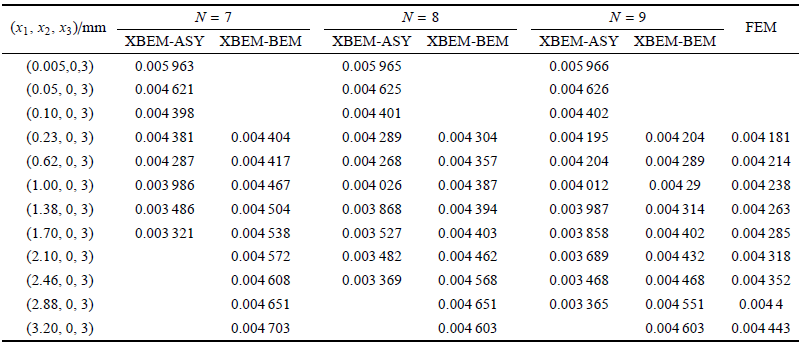
表5XBEM和FEM 计算沿 $x_{2} =0$ mm, $x_{3} =3$ mm 附近内点的位移分量 $u_{x1}$ (mm)
Table 5Variation of $u_{x1}$ (mm) along $x_{2} =0$ mm, $x_{3} =3$ mm calculated by XBEM and FEM

新窗口打开|下载CSV

图 12

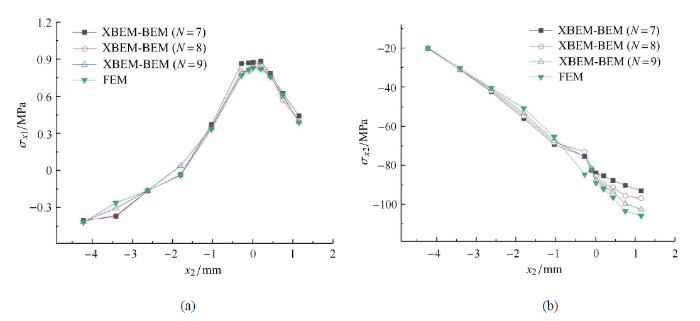
新窗口打开|下载原图ZIP|生成PPT
图 12XBEM-BEM 和 FEM计算沿 $x_{1} =2.88$ mm, $x_{3} =3$ mm 附近内点的应力分量

Fig. 12The stress component along $x_{1} =2.88$ mm, $x_{3} =3$ mm calculated by XBEM-BEM and FEM



表 4 和表 5 以及图 12 结果显示：选取不同的截取级数项数 $N$,XBEM-BEM 计算相同点的应力和位移值基本相等,说明 XBEM 计算三维复合型裂纹结构应力场和位移场的数值稳定,XBEM 的计算精度对截取级数项数 $N$ 的选取不敏感,便于 XBEM 的 应用.

表 4 还显示,在外围区域点 (1.70 mm, 0 mm, 3 mm) 处,当 $N=7$ 时,XBEM-ASY 计算的应力值($\sigma_{x1}=4.665$ MPa) 和 XBEM-BEM 计算相 同点的应力值 ($\sigma_{x1}=6.407$ MPa) 的相对差为 $-27.2$%. 当 $N =8$ 时,XBEM-ASY 计算的应力值 ($\sigma_{x1}=5.314$ MPa) 和 XBEM-BEM 计算相同点的应力值 ($\sigma_{x1} =6.417$ MPa) 的相对差为 $-17.2$%. 当 $N =9$ 时,XBEM-ASY 计 算的应力值 ($\sigma_{x1}$ = $5.544$ MPa) 和 XBEM-BEM 计算% 相同点的应 力值 ( $\sigma_{x1}$ = $6.527$ MPa ) 的相对差为 $-15.1$%. 说明相对 XBEM-BEM 计算值而言,XBEM- ASY 计算同一点应力的相对误差随 $N$ 的增大逐渐减小,即 XBEM-ASY 计算 裂纹尖端应力场的有 效范围随 $N$ 的增大逐渐增大. 同理分析表 5 可得,XBEM-ASY 计算裂纹尖端位移场的有效范围随 $N$ 的增大逐渐增大.

通常情况,外围结构的位移和应力由 XBEM-BEM 解胜任,无需用 XBEM-ASY 计算. 这里关于两者计算值比较,意在说明 XBEM-ASY 解的有效范围内,均可作为扇形柱半径的选择范围. 例如,若 XBEM-ASY 计算的裂纹尖端应力场在 $r < 0.2$ mm 的范围内是足够准确的,说明XBEM使用时,尖端扇形区域半径 $\rho $ 的选取范围较为宽松, $\rho < 0.2$ mm 之间均可行.

表 5 显示,当 $x_{2} = 0$ mm,$x_{3} = 3$ mm, $x_{1}>$ 1.38 mm 的远场区域,FEM 的结果和 XBEM-BEM 的应力结果吻合较好,而当 $x_{2}=0$ mm,$x_{3}=5$ mm,$x_{1} \leqslant 1.38$ mm 时,FEM计算的应力场 (裂纹尖端近场区域) 与 XBEM-BEM 的结果有较大的差异. 对于三维裂纹尖端的强应力集中,尽管 FEM 在尖端使用了细密单元,结构采用 20 节点六边形单元,划分单元数 141 000,XBEM 使用单元数 808,FEM 采用的单元数为 XBEM 的 163 倍,这极大地增加了计算量和计算机内存需求,但仍无法准确描述其尖端近场区域的应力场. 随着距尖端距离的增大,应力集中的现象逐渐减弱,FEM的计算结果变得可信. 而本文方法可采用较少的单元数来准确获取三维裂纹结构完整的应力场,进一步表明了 XBEM 处理 V 形切口应力集中问题的优越性.

4 结论

本文建立了三维线弹性 V 形切口/裂纹结构完整应力场分析的扩展边界元法,并对三维 V 形切口/裂纹结构在典型载荷工况下进行了计算,结论 如下.

(1) 将三维柱状 V 形切口/裂纹结构分离为尖端扇形柱区域和外围结构区域,扩展边界元法发挥了切口尖端扇形柱区域渐近分析和外围结构边界元法分析特长. XBEM 类似于半解析方法,在切口尖端扇形柱区域位移和应力由渐近级数展开式表达,远端区域的力学场由边界元法分析. 文中算例结果显示了 XBEM 可准确获取三维 V 形切口/裂纹结构完整的位移和应力场,有利用于判定三维裂纹结构的起裂扩展.

(2) 尖端扇形柱区域的渐近级数展开式选取的截取级数项数$N$越大,则渐近级数展开式计算尖端应力和位移场的有效范围越大,说明尖端扇形柱半径的选取范围越大.

(3) 按照线弹性理论分析,三维 V 形切口/裂纹尖端附近的应力值随 $r \to 0$ 趋近无限大,尖端区域发生了塑性变形. 后续将研究考虑三维 V 形切口/裂纹结构尖端附近塑性变形的扩展边界元法分析.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Chue CH, Liu CI. A general solution on stress singularities in an an-isotropic wedge
International Journal of Solids & Structures, 2001,38(1):6889-6906
[本文引用: 1]

[2] Ungamornrat J. Analysis of 3D cracks in an isotropic multi-material domain with weakly singular SGBEM
Engineering Analysis with Boundary Elements, 2006,30(10):834-846
DOIURL [本文引用: 1]

Abstract

A weakly singular, symmetric Galerkin boundary element method (SGBEM) is established for analysis of cracks in a three-dimensional, linearly elastic domain consisting of subdomains which are made from different materials. The integral equations governing each subdomain are obtained by employing a pair of weakly singular, weak-form displacement and traction integral equations. A system of governing equations for the entire domain is subsequently obtained in a symmetric form by properly combining the integral equations for each subdomain along with the use of the continuity of displacements and tractions on the subdomain interface. The technique developed possesses several important features: (1) it is applicable for modeling cracks with arbitrary geometry and under general loading; (2) the governing integral equations contain only weakly singular kernels (of O(1/r)) such that their validity requires only the continuity of the displacement boundary data; (3) the formulation is symmetric and gives rise to a system of linear equations with a symmetric coefficient matrix; and (4) the formulation allows the treatment of a multi-material domain where a material constituting each subdomain can be generally anisotropic. In the numerical implementation, standard C^o elements are employed everywhere except along the boundary of the crack surface where special crack-tip elements are utilized to model the asymptotic behavior in the vicinity of the crack front. The use of this crack-tip element allows, additionally, the mixed-mode stress intensity factors to be determined directly and accurately in terms of extra degrees of freedom introduced at nodes along the crack front. Several example problems are presented to demonstrate the accuracy and capability of the technique; numerical results indicate that highly accurate stress intensity factors can be obtained with use of relatively coarse meshes.

[3] Sator C, Becher W. Closed-form solutions for stress singularities at plane bi-and tri-material junctions
Archive of Applied Mechanics, 2012,82(5):643-654
DOIURL [本文引用: 1]
Stress singularities at two-dimensional bi- and trimaterial junctions, consisting of dissimilar, homogeneous, isotropic and linear-elastic wedges under a plane strain state, are considered. The stresses formed at the vertex of this composite situation are analyzed by the complex variable method, based on an appropriate choice of the Kolosov potentials that are applicable in the vicinity of the vertex. In doing so, the identification of the singularity exponent is performed. On the basis of a couple of bi- and trimaterial configurations, it is demonstrated how to derive some closed-form analytical solutions for the orders of the stress singularities from the characteristic equation.

[4] 胡宗军, 牛忠荣, 程长征. 三维边界元法高阶单元几乎奇异积分半解析算法
力学学报, 2014,46(3):417-427
DOIURL [本文引用: 2]
分析了三维边界元法高阶曲面单元几何特征，定义接近度来表征源点与积分单元的接近程度.利用源点在积分单元上的垂足点建立局部极坐标系，构造与几乎奇异积分核函数具有相同奇异性的近似函数.从奇异积分核函数中扣除其近似函数，分离出积分核中主导的奇异函数部分，将奇异积分分解为规则核函数和奇异核函数两项积分.规则核函数积分应用常规Gauss数值积分计算，奇异核函数积分在局部极坐标系ρθ下分离积分变量ρ和θ，对ρ积分建立解析计算列式，对θ积分应用常规Gauss数值积分计算，从而对三维位势问题高阶边界单元几乎强奇异和几乎超奇异积分建立一种新的半解析算法.给出了若干温度场算例，采用边界元法高阶单元几乎奇异积分半解析法计算了近边界内点位势和位势梯度，并与线性单元正则化算法计算结果对比，结果证明提出的半解析法计算几乎奇异面积分和薄壁结构更加高效.
( Hu Zongjun, Niu Zhongrong, Cheng Changzheng. A new semi-analytic algorithm of nearly singular integrals in high order boundary element analysis of 3D potential
Chinese Journal of Theoretical and Applied Mechanics, 2014,46(3):417-427 (in Chinese))
DOIURL [本文引用: 2]
分析了三维边界元法高阶曲面单元几何特征，定义接近度来表征源点与积分单元的接近程度.利用源点在积分单元上的垂足点建立局部极坐标系，构造与几乎奇异积分核函数具有相同奇异性的近似函数.从奇异积分核函数中扣除其近似函数，分离出积分核中主导的奇异函数部分，将奇异积分分解为规则核函数和奇异核函数两项积分.规则核函数积分应用常规Gauss数值积分计算，奇异核函数积分在局部极坐标系ρθ下分离积分变量ρ和θ，对ρ积分建立解析计算列式，对θ积分应用常规Gauss数值积分计算，从而对三维位势问题高阶边界单元几乎强奇异和几乎超奇异积分建立一种新的半解析算法.给出了若干温度场算例，采用边界元法高阶单元几乎奇异积分半解析法计算了近边界内点位势和位势梯度，并与线性单元正则化算法计算结果对比，结果证明提出的半解析法计算几乎奇异面积分和薄壁结构更加高效.

[5] Wu W, Lv C, Zhang JH. Interface traction stress of 3D dislocation loop in an isotropic bio-material
Journal of the Mechanics and Physics of Solids, 2016,87(1):7-37
DOIURL [本文引用: 1]

[6] 文龙飞, 王理想, 田荣. 动载下裂纹应力强度因子计算的改进型扩展有限元法
力学学报, 2018,50(3):599-610
[本文引用: 1]

( Wen Longfei, Wang Lixiang, Tian Rong. Accurate computation on dynamic SIFS using improved XFEM
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):599-610 (in Chinese))
[本文引用: 1]

[7] Xu CH, Qin TY, Noda NA. Numerical solutions of singular integral equations for planar rectangular interfacial crack in three dimensional bio-materials
Applied Mathematics and Mechanics, 2007,28(6):751-757
[本文引用: 1]

[8] 王振, 余天堂. 模拟三维裂纹问题的自适应多尺度扩展有限元法
工程力学, 2016,33(1):32-38
[本文引用: 1]

( Wang Zhen, Yu Tiantang. Adaptive multi scale extended finite element method for modeling three-dimensional crack problems
Engineering Mechanics, 2016,33(1):32-38 (in Chinese))
[本文引用: 1]

[9] 贾旭, 胡绪腾, 宋迎东. 基于三维裂纹尖端应力场的应力强度因子计算方法
航空动力学报, 2016,31(6):1417-1426
[本文引用: 1]

( Jia Xu, Hu Xuteng, Song Yingdong. Calculation method of stress intensity factor based on the three-dimensional stress field at the crack tip
Journal of Aerospace Power, 2016,31(6):1417-1426 (in Chinese))
[本文引用: 1]

[10] Fakoor M, Ghoreishi SMN. Comprehensive investigation of stress intensity factors in rotating disks containing three-dimensional semi-elliptical cracks
Applied Mathematics and Mechanics, 2017,38(1):1565-1578
[本文引用: 1]

[11] Huang T, Zheng JL, Lv ST, et al. Failure criterion of an asphalt mixture under three-dimensional stress state
Construction and Building Materials, 2018,170(1):708-715
DOIURL [本文引用: 1]

[12] 贾旭, 胡绪腾, 宋迎东. 复杂载荷应力强度因子的计算方法
航空动力学报, 2018,33(6):1464-1474
[本文引用: 1]

( Jia Xu, Hu Xuteng, Song Yingdong. Calculation method of stress intensity factors of eccentric through cracks subjected to complex loading
Journal of Aerospace Power, 2018,33(6):1464-1474 (in Chinese))
[本文引用: 1]

[13] Magnus WG. A 3D model of hydraulic fracturing and micro-seismicity in anisotropic stress fields
Aeromechanics and Geophysics for Geo-Energy and Geo-Resources, 2018,5(1):17-35
[本文引用: 1]

[14] Dhanesh N, Kapuria S, Achary GGS. Accurate prediction of three-dimensional free edge stress field in composite laminates using mixed-field multitier extended Kantorovich method
Acta Mechanica, 2016,228(8):1-25
[本文引用: 1]

[15] Stasyuk B. Interacting cracks 3D analysis using boundary integral equation method
Aims Materials Science, 2016,3(4):1796-1810
[本文引用: 1]

[16] Karsten K, Günther K. The advanced simulation of fatigue crack growth in complex 3D structures
Archive of Applied Mechanics, 2006,76(11-12):699-709
[本文引用: 1]

[17] Li Z, Guo W. Three-dimensional elastic stress fields ahead of blunt V-notches in finite thickness plates
International Journal of Fracture, 2001,107(1):53-71
[本文引用: 1]

[18] Park JH, Nikishkov GP. Growth simulation for 3D surface and through thickness cracks using SGBEM-FEM alternating method
Journal of Mechanical Science & Technology, 2011,25(9):2335-2344
[本文引用: 1]

[19] Lan W, Deng X, Sutton MA. Three-dimensional finite element simulations of mixed-mode stable tearing crack growth experiments
Engineering Fracture Mechanics, 2007,74(16):2498-2517
[本文引用: 1]

[20] Dias IF, Oliver J, Lloberas VO. Strain-injection and crack-path field techniques for 3D crack-propagation modeling in quasi-brittle materials
International Journal of Fracture, 2018,212(1):67-87
[本文引用: 1]

[21] Ding P, Wang X. Three-dimensional mixed-mode (I and II) crack-front fields in ductile thin plates effects of T--stress
Fatigue & Fracture of Engineering Materials & Structures, 2017,40(1):349-363
[本文引用: 1]

[22] Wang H, Cao M, Siddique A, et al. Numerical analysis of thermal expansion behaviors and interfacial thermal stress of 3D braided composite materials
Computational Materials Science, 2017,138(1):77-91
[本文引用: 1]

[23] 李聪, 牛忠荣, 胡宗军 等. 求解双材料裂纹结构全域应力场的扩展边界元分法
应用数学与力学, 2019,40(8):909-920
[本文引用: 1]

( Li Cong, Niu Zhongrong, Hu Zongjun, et al. Computation of total stress fields for cracked Bi-Material structure with the extended boundary element method
Applied Mathematics and Mechanics, 2019,40(8):909-920 (in Chinese))
[本文引用: 1]

[24] Li C, Niu ZR, Hu ZJ, et al. Effectiveness of the stress solutions in notch/crack tip regions by using extended boundary element method
Engineering Analysis with Boundary Elements, 2019,108(1):1-13
[本文引用: 1]

[25] Yosibash Z, Szabó BA. A note on numerically computed eigen-functions and generalized stress intensity factors associated with singular points
Engineering Fracture Mechanics, 1996,54:593-595
[本文引用: 1]

[26] Williams ML. Stress singularities resulting from various boundary conditions in angular corners of plates in tension
Journal of Applied Mechanics, 1952,19:526-528
[本文引用: 1]

[27] Niu ZR, Ge DL, Cheng CZ, et al. Evaluation of the stress singularities of plane V-notches in bonded dissimilar materials
Applied Mathematical Modeling, 2009,33(1):1776-1792
[本文引用: 1]

[28] 程长征, 葛仁余, 牛忠荣 等. 三维切口应力奇性指数计算
固体力学学报, 2012,33(6):623-629
[本文引用: 1]

( Cheng Changzheng, Ge Renyu, Niu Zhongrong, et al. Evaluation of the stress singularity order for three-dimensional V-notch
Chinese Journal of Solid Mechanics, 2012,33(6):623-629 (in Chinese))
[本文引用: 1]

[29] 钱俊, 龙驭球. 三维切口尖端应力应变场
应用力学与数学, 1994,15(3):199-208


( Qian Jun, Long Yuqiu. The expression of stress and strain at the tip of three dimensional notch
Applied Mathematics and Mechanics, 1994,15(3):199-208 (in Chinese))


[30] 牛忠荣, 王秀喜, 周焕林. 三维边界元法中几乎奇异积分的正则化算法
力学学报, 2004,36(1):49-56
[本文引用: 1]

( Niu Zhongrong, Wang Xiuxi, Zhou Huanlin. A regularization algorithm for the nearly singular integrals in 3-D BEM
Chinese Journal of Theoretical and Applied Mechanics, 2004,36(1):49-56 (in Chinese))
[本文引用: 1]