刘峰^,*,2), 岳宝增^,*,3), 马伯乐^*, 申云峰^?*北京理工大学宇航学院, 北京100081
^?郑州工业应用技术学院信息工程学院, 郑州451199

EQUIVALENT DYNAMICS MODELING AND ANALYSIS OF LIQUID-FILLED SPACECRAFT WITH FUEL CONSUMPTION ¹⁾

Liu Feng^,*,2), Yue Baozeng^,*,3), Ma Bole^*, Shen Yunfeng^?*School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
^?School of Information Engineering, Zhengzhou University of Industry Technology, Zhengzhou 451199, China

通讯作者: 2)刘峰, 博士研究生. 主要研究方向: 液体晃动等效力学模型研究及航天器刚-液-柔-控耦合动力学等. E-mail:fengyel@foxmail.com3)岳宝增, 教授. 主要研究方向: 非线性动力学与控制, 液体非线性晃动动力学及复杂航天器动力学与控制等. E-mail:bzyue@sohu.com

收稿日期:2020-02-2接受日期:2020-02-2网络出版日期:2020-09-18

基金资助:

1)国家自然科学基金资助项目.11472041 国家自然科学基金资助项目.11772049 国家自然科学基金资助项目.11532002

Received:2020-02-2Accepted:2020-02-2Online:2020-09-18
作者简介 About authors


摘要
在轨航天器贮腔内的液体可能表现出多种不同的运动模式, 主要包括液体相对于贮腔的整体性刚体运动、自由液面横向晃动、液体起旋后逐步发生明显的旋转晃动及液体自旋运动; 复合三自由度刚体摆晃动模型能够较为全面地描述这些液体运动模式, 同时为研究起旋阶段的液体晃动动力学问题提供了有效手段. 本文对非线性液体晃动刚体摆复合模型作进一步发展, 考虑模型等效参数随贮腔充液比的变化, 提出了变参数的刚体摆复合模型, 该模型适用于研究燃料消耗下非线性晃动类充液航天器大范围运动耦合动力学问题. 采用刚体摆复合模型对球形贮腔内的液体晃动进行等效后, 基于混合坐标意义下的拉格朗日方程推导了一类充液航天器轨道-姿态-晃动全耦合的动力学方程组, 并展开了充液航天器大角度三轴稳定姿态机动和零冲量轨道机动仿真以及航天器耦合动力学响应特性分析. 研究表明: 液体相对于贮腔的运动会造成航天器主刚体位置发生偏移, 当航天器在执行零冲量机动时, 燃料消耗会造成航天器的轨道平动速度无法收敛到零; 贮腔偏心布放时, 航天器在执行轨道机动过程中贮腔内液体易发生剧烈而且形式复杂的晃动行为, 进而可能造成航天器刚体运动的不稳定.
关键词： 液体非线性晃动;刚体摆复合模型;燃料消耗;变质量充液航天器;耦合动力学

Abstract
The liquid in the tank of in-orbit spacecraft may experiences different types of motion, mainly including the overall rigid motion of liquid respect to the tank, the lateral sloshing of the liquid free surface, and the liquid rotation starting which will maybe eventually graduate into the rotary sloshing of the liquid free surface and/or the spinning motion of liquid, etc. The composite 3DOF-rigid-pendulum sloshing model is able to describe all of these main motion types of liquid, and it has been validated to be effective for the analysis of the liquid sloshing dynamics during the rotation-starting period. In this paper, the composite rigid-pendulum model is developed to investigate the large motion coupling dynamics of a variable-mass liquid-filled spacecraft with nonlinear liquid slosh and fuel consumption, by taking account of the variation of equivalent model parameters over liquid-fill ratio. Based on the Lagrangian equations, the orbital-attitude-slosh coupling dynamics model of a liquid-filled spacecraft is equivalently established by using the composite rigid-pendulum model to replace the liquid in a spherical tank. Then, simulations of a three-axis stabilized large angle attitude maneuver and a zero-impulse orbital maneuver of spacecraft are given for the coupling dynamics response analysis of the liquid-filled spacecraft system. Simulation results show that the liquid motion with respect to the tank will cause the position offset of spacecraft, and the orbital velocity of spacecraft will not converge to zero when the spacecraft executes zero-impulse maneuvers with fuel consumption; and that the liquid is likely to experience violent and complicated sloshing motion, which may cause the instability in the rigid-body motion of spacecraft, during the orbital maneuvering when the tank is eccentrically installed in the rigid hub.
Keywords：nonlinear liquid slosh;composite rigid-pendulum model;fuel consumption;variable-mass liquid-filled spacecraft;coupling dynamics


PDF (1310KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
刘峰, 岳宝增, 马伯乐, 申云峰. 燃料消耗下充液航天器等效动力学建模与分析 ¹⁾. 力学学报[J], 2020, 52(5): 1454-1464 DOI:10.6052/0459-1879-20-027
Liu Feng, Yue Baozeng, Ma Bole, Shen Yunfeng. EQUIVALENT DYNAMICS MODELING AND ANALYSIS OF LIQUID-FILLED SPACECRAFT WITH FUEL CONSUMPTION ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1454-1464 DOI:10.6052/0459-1879-20-027

引言

在轨运行的充液航天器, 通常处于较低重力(低重力或微重力)环境, 当它执行轨道或姿态机动、交会对接及软着陆等任务时, 贮腔内的液体可能表现出以下几种不同的主要运动模式的叠加运动: (1)横向晃动, 即液体自由液面交替抬升、下沉而引起的不流动的波动行为^[1], 这种晃动模式具有依赖于贮腔形状、尺寸和加速度环境等因素的固有频率和固有模态, 且第一阶横向晃动主模态呈现为反对称形式;(2)旋转晃动, 当贮腔受到的激励频率接近于最低阶液体晃动固有频率时, 将引起横向晃动失稳, 此时横向晃动的节线发生旋转而出现旋转式流动的波^[2]; (3)液体自旋, 即液体发生的绕其对称轴的类似于刚体的自旋运动. 此外, 当航天器受到的有效重力的方向不断变化或者航天器进行大角度姿态机动时, 液体相对于贮腔晃动的平衡位置将时刻变化, 即贮腔内的液体会发生相对于贮腔的整体性刚体运动.

虽然已有不少关于充液航天器动力学与控制方面的研究^[3-26], 但是还有很多新的问题需要进一步研究和解决, 比如: (1)大范围机动下充液航天器发生轨道-姿态-晃动与控制系统之间的动力学耦合问题, 已有的研究大多致力于研究充液航天器小角度姿态机动下的动力学建模与控制, 而忽略轨道运动的影响, 也未考虑大角度姿态运动下航天器系统惯量特性和液体晃动特性变化等因素; (2)在轨微重力(或低重力)环境下充液航天器机动时, 贮腔内液体可能发生复杂的非线性晃动行为, 有相当研究考虑了液体大幅晃动问题, 但是对于液体旋转晃动以及液体起旋时的航天器刚-液或刚-液-控耦合动力学问题鲜有研究; (3)多贮腔布局下, 不同贮腔内液体的物理特性不同, 以及不同贮腔尺寸和充液比等差异导致晃动固有特性差异时, 多贮腔液体组合晃动对航天器系统运动的影响尤为复杂; (4)燃料消耗引起液体晃动特性改变时液体晃动对航天器系统动力学的复杂影响有待进一步研究.

本工作在已完成工作^[27]的基础上, 考虑液体燃料消耗引起液体晃动固有特性变化, 进一步提出变参数的刚体摆复合模型, 模拟航天器球形贮腔内的液体晃动动力学行为, 要研究燃料消耗情形下液体发生非线性晃动时充液航天器的耦合动力学问题. 具体地, 本工作将基于变参数的刚体摆复合模型, 采用混合坐标意义下的拉格朗日方程对一类变质量充液航天器展开等效动力学建模; 随后, 考虑该充液航天器执行大范围机动, 以大角度三轴稳定姿态机动和零冲量大范围轨道机动为例, 展开变质量充液航天器大范围机动仿真和耦合动力学特性分析, 为航天工程实践提供一定的理论指导和参考.

1 考虑燃料消耗的刚体摆复合模型

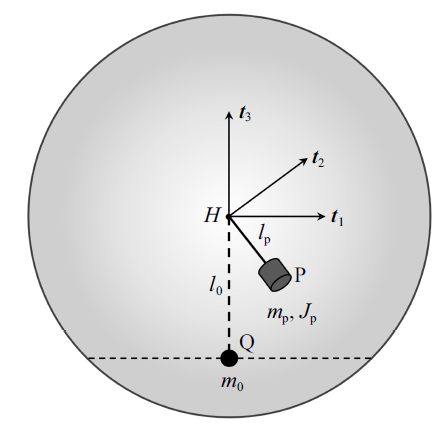
作者前期的工作^[27]针对常/低重力环境下部分充液球形贮腔内液体非线性晃动(包括大幅横向晃动、旋转晃动以及液体自旋运动等) 而提出了一种三自由度刚体摆复合模型. 如图1所示, 该复合模型包含如下两部分: 一是悬挂点H位于贮腔形心的刚体摆P, 它等效的是参与晃动的那部分液体, 其集中质量参数$m_{\rm p} $等于参与晃动的液体质量, 摆长参数$l_{\rm p} $确定的是参与晃动的液体的质心位置, 它也是表征液体晃动固有频率的参数, 而刚体摆关于其轴向的转动惯量$J_{\rm p}$等效的是参与液体旋转(液体发生的旋转晃动和自旋运动统称为液体旋转)的那部分液体所具有的转动惯量; 二是集中质量点Q, 它等效的是未晃动的那部分液体, 其集中质量参数$m_0$等于未晃动液体的质量, 其相对于贮腔形心的距离参数$l_0$确定的是未晃动液体的质心位置.

图 1

新窗口打开|下载原图ZIP|生成PPT
图 1液体晃动刚体摆复合模型及其等效参数

Fig. 1The rigid-pendulum composite model for liquid slosh and its equivalent parameters



传统的弹簧-质量模型和单摆模型只考虑了液体的低阶横向晃动, 球摆模型能够在研究最低阶横向晃动的同时对液体的旋转晃动加以描述; 而作者前期工作^[27]中提出三自由度刚体摆复合模型不仅能够在保证力系等效性的前提下具有尽可能少的模型参数, 而且能较为全面地描述航天器内液体可能表现出的相对于贮腔的多种不同运动模式的叠加运动. 具体地, 三自由度刚体摆复合模型的运动与贮腔内实际液体的运动之间具有以下几点相似性: 一是模型中的集中质量Q (代表未晃动质量)和刚体摆P的集中质量(代表晃动质量)随着静力平衡位置变化(称为动平衡位置, 可能是由于航天器发生大范围姿态运动或者等效重力加速度环境改变等因素引起的)而发生的相对于贮腔的任意转动, 以此可描述贮腔内的液体发生相对于贮腔的整体性刚体运动; 二是刚体摆P在动平衡位置附近的有限幅度(可以是小幅的, 也可以是大幅的)的往复摆动则类似于贮腔内液体自由液面的横向晃动; 三是当刚体摆P作锥形运动时, 所描述的即是液体的旋转晃动; 最后是刚体摆P以$J_{\rm p}$为转动惯量绕其摆轴方向的自旋运动描述了液体的刚体自旋. 后续对该复合模型的发展作进一步研究, 使其适用于研究液体燃料消耗过程中的液体晃动动力学问题.

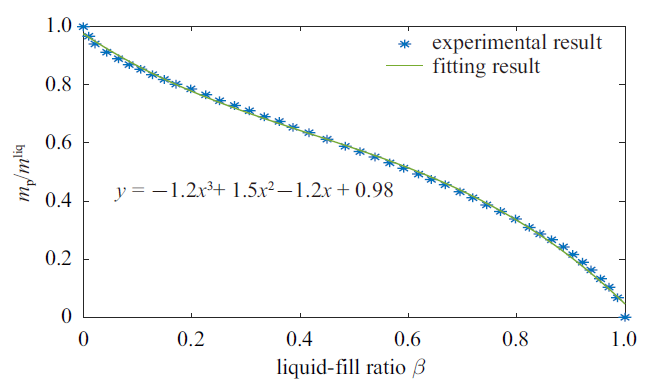
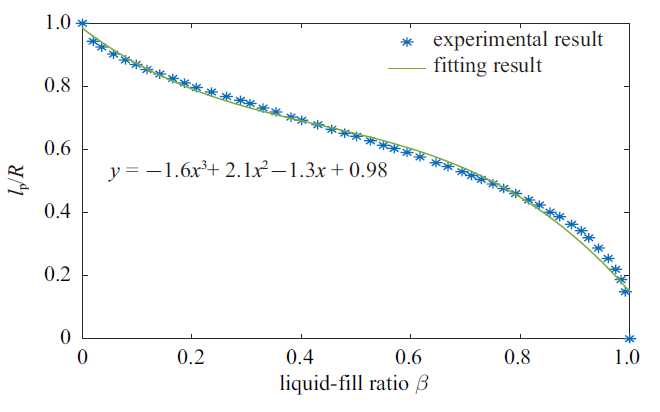
首先, 液体燃料消耗将直接导致贮腔充液比$\beta $减小(此时$\beta $为时变量), 进而导致参与晃动和未晃动两部分液体的质量、转动惯量及其质心位置发生变化, 而这将体现在刚体摆复合模型中的等效参数具有时变性上. 文献^[2]中总结了常规重力或低重力环境下球形贮腔内液体晃动等效摆的质量参数及摆长参数随充液比$\beta $的变化规律. 本文通过提取文献^[2]中的实验结果并将其进行拟合, 如图2和图3所示, 得到刚体摆复合模型中刚体摆的集中质量参数$m_{\rm p}$和摆长参数$l_{\rm p}$随充液比$\beta$变化的近似关系, 具体的表达式分别为

(1) $ \begin{eqnarray} \label{eq1} &&m_{\rm p} =\frac{4}{3}\pi R^3\rho \beta \left( {-1.2\beta ^3+1.5\beta ^2-1.2\beta +0.98} \right) \end{eqnarray}$
(2) $ \begin{eqnarray} \label{eq2} l_{\rm p} =R\left( {-1.6\beta ^3+2.1\beta ^2-1.3\beta +0.98} \right) \end{eqnarray}$

图 2

新窗口打开|下载原图ZIP|生成PPT
图 2刚体摆的集中质量参数随充液比的经验关系

Fig. 2Empirical relationship between the lumped mass of the rigid-pendulum and the liquid-fill ratio

图 3

新窗口打开|下载原图ZIP|生成PPT
图 3刚体摆的摆长参数随充液比的经验关系

Fig. 3Empirical relationship between the length of the rigid-pendulum and the liquid-fill ratio



式中, $R$是球形贮腔的半径, $\rho $是贮腔内液体的密度.

然后, 依据文献^[27]中指出的针对该刚体摆复合模型的参数配置原则, 可得到集中质量点Q的质量参数$m_0 $的具体表达式

(3) $ \begin{eqnarray} \label{eq3} m_0 =\frac{4}{3}\pi R^3\rho \beta \left( {1.2\beta ^3-1.5\beta^2+1.2\beta +0.02} \right) \end{eqnarray}$
以及集中质量点Q相对于贮腔形心的距离参数$l_0 $满足如下关系式

(4) $ \begin{eqnarray} \label{eq4} m_0 l_0 +m_{\rm p} l_{\rm p} =m^{\rm liq}l_{\rm c}^{\rm liq} \end{eqnarray}$
式中, $m^{\rm liq}$是贮腔内所有液体的质量, $l_{\rm c}^{\rm liq}$代表液体不晃动时所有液体的质心相对于贮腔形心的距离.

最后, 需要确定关于刚体摆轴向的转动惯量等效参数$J_{\rm p} $. 考虑到实际情况下参与液体旋转的液体所具有的转动惯量是一个极难确定的物理量, 尤其在液体起旋阶段, 参与液体旋转的那部分液体所具有的转动惯量有着比较复杂的随时间变化规律^[27]. 这里为了简化问题, 假设将液体固化后(可将液体视为一个刚体)液体所具有的关于其对称轴的转动惯量$J_{\rm solid}$等于刚体摆的转动惯量等效参数$J_{\rm p} $, 即$J_{\rm p}=J_{\rm solid}$.

2 充液航天器刚-液耦合动力学模型

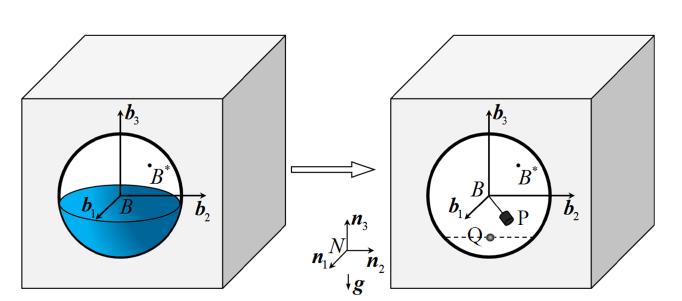
采用混合坐标意义下的拉格朗日方程^[28-29]来建立如图4所示充液航天器的耦合动力模型, 其贮腔内的液体燃料采用刚体摆复合模型进行等效, 同时考虑液体燃料消耗的影响. 图4中, $N:\left\{ {{ n}_1 ,{ n}_2 ,{ n}_3 }\right\}$是牛顿惯性参考系, ${ g}$是航天器系统受到的有效重力加速度, 方向始终与$-{ n}_3 $同向; $B^\ast $是航天器主刚体(指除去液体的部分)的质心; $B:\left\{ {{ b}_1 ,{ b}_2 ,{ b}_3 } \right\}$是原点位于贮腔形心且与航天器主刚体固连的本体坐标系, 并假定$B:\left\{ {{ b}_1 ,{ b}_2 ,{ b}_3 }\right\}$与航天器主刚体的惯性主轴坐标系(其原点位于主刚体质心)对齐(即两个直角坐标系的对应坐标轴同向).

图 4

新窗口打开|下载原图ZIP|生成PPT
图 4带部分充液球形贮腔航天器及其等效物理模型示意图

Fig. 4Illustration of a spacecraft with a partially liquid-filled spherical tank



需要特别指出的是由于液体燃料消耗的影响, 刚体摆复合模型的所有等效参数是时变的, 即整个充液航天器本质上是一类极为复杂的变参数系统. 为简化后续推导, 可作以下简化假设: 认为所有模型参数的变化率(即时间导数)相比于系统的运动为慢变量, 假设燃料消耗过程中, 模型参数都是准静态变化的. 因此, 本文中建立的变质量充液航天器耦合动力学模型适用于燃料消耗速率比较低的情形.

2.1 系统运动描述

2.1.1 航天器主体的姿态运动

航天器在惯性参考系下的姿态运动通过本体坐标系$B$相对于惯性参考系$N$的转动来描述, 转动角速度矢量可以表示为

(5) $ \begin{eqnarray} \label{eq5} {}^N{ \omega }^B=\omega _1 { b}_1 +\omega _2 { b}_2 +\omega _3 { b}_3 \end{eqnarray}$
采用欧拉四元数${ \varepsilon }=\left[ {\varepsilon _0 ,\varepsilon _1 ,\varepsilon _2 ,\varepsilon _3 }\right]^{\rm T}$来描述航天器的当前姿态^[7-9], 则姿态运动的发展方程为

(6) $ \begin{eqnarray} \label{eq6} {\dot{{ \varepsilon }}}=\frac{1}{2} S^{\rm T}\left( { \varepsilon } \right)\left[ {\omega _1 ,\omega _2 ,\omega _3 } \right]^{\rm T} \end{eqnarray}$
式中, $ S\left( { \varepsilon } \right)=\left[ {-{ \varepsilon }_v ,\varepsilon _0 { E}_3 -{\tilde{{ \varepsilon }}}_v } \right]$, ${ \varepsilon }_v =\left[ {\varepsilon _1 ,\varepsilon _2 ,\varepsilon _3 } \right]^{\rm T}$, ${ E}_3 $是三阶单位矩阵, ${\tilde{{ \varepsilon}}}_v $是$\mbox{3}\times \mbox{1}$维矢量${ \varepsilon }_v $所对应的反对称对偶矩阵.

此外, 航天器的姿态矩阵(即惯性参考系$N$到本体坐标系$B$的坐标转换矩阵)在欧拉四元数下的表达式为

(7) $ \begin{eqnarray} \label{eq7} {}^N{ C}^B=\left( {2\varepsilon _0 ^2-1} \right){ E}_3 +2{ \varepsilon }_v { \varepsilon }_v ^{\rm T}-2\varepsilon _0 {\tilde{{ \varepsilon }}}_v \end{eqnarray}$
2.1.2 航天器主体的轨道运动}

航天器在惯性参考系下的平动运动(即轨道运动)通过本体坐标系原点$B$相对于惯性参考系$N$的位置和速度来描述, 相应的位置矢量和速度矢量可分别表示为

(8) $ \begin{eqnarray} \label{eq8} &&{ p}^{NB}=x_B { n}_1 +y_B { n}_2 +z_B { n}_3 \end{eqnarray} $
(9) $ \begin{eqnarray} \label{eq9} { }^N{ v}^B=v_1 { b}_1 +v_2 { b}_2 +v_3 { b}_3 \end{eqnarray}$
由矢量叠加原理, 航天器主刚体质心$B^\ast $相对于惯性参考系的位置矢量为

(10) $ \begin{eqnarray} \label{eq10} { p}^{NB^\ast }={ p}^{NB}+{ p}^{BB^\ast } \end{eqnarray}$
式中, ${ p}^{BB^\ast }$是由航天器整体布局决定的常矢量, 设${ p}^{BB^\ast }=X{ b}_1 +Y{ b}_2 +Z{ b}_3 $. 于是, 航天器主刚体质心$B^\ast $相对于惯性参考系的速度为

(11) $ \begin{eqnarray} \label{eq11} &&{ }^N{ v}^{B^\ast }={ }^N{ v}^B+{ }^N{ \omega }^B\times { p}^{BB^\ast } = \\&&\qquad \left( {v_1 -Y\omega _3 +Z\omega _2 } \right){ b}_1 +\left( {v_2 -Z\omega _1 +X\omega _3 } \right){ b}_2 + \\&&\qquad\left( {v_3 -X\omega _2 +Y\omega _1 } \right){ b}_3 \end{eqnarray}$
2.1.3 等效液体晃动刚体摆复合模型的运动

刚体摆复合模型中等效未晃动液体的集中质量点$Q$, 它相对于惯性参考系$N$的位置矢量为

(12) $ \begin{eqnarray} \label{eq12} { p}^{N\rm Q}={ p}^{NB}+{ p}^{B\rm Q} \end{eqnarray}$
式中, ${ p}^{B\rm Q}$始终指向重力加速度方向, 于是有${ p}^{B\rm Q}=-l_0 { n}_3 $.

对式(12)两端同时求惯性参考系下对时间的微分, 可得到集中质量点Q相对于惯性参考系$N$的速度为

(13) $ \begin{eqnarray} \label{eq13} { }^N{ v}^{\rm Q}=\frac{{}^N{\rm d}}{{\rm d}t}{ p}^{N\rm Q}={ }^N{ v}^B \end{eqnarray}$
另外, 刚体摆复合模型中等效晃动液体的刚体摆P的集中质量, 它相对于惯性参考系$N$的位置矢量为

(14) $ \begin{eqnarray} \label{eq14} { p}^{N\rm P}={ p}^{NB}+{ p}^{B\rm P} \end{eqnarray}$
沿用文献^[27]中采用3个欧拉角$\varphi $, $\theta $和$\psi $来描述刚体摆相对于贮腔运动的方法, 于是有

(15) $ \begin{eqnarray} \label{eq15} { p}^{B\rm P}=-l_{\rm p} \left( {a_1 { b}_1 +a_2 { b}_2 +a_3 { b}_3 }\right) \end{eqnarray}$
式中, $a_1 =\cos \psi \sin \theta +\sin \psi \sin \varphi \cos \theta $, $a_2=\sin \psi \sin \theta -\cos \psi \sin \varphi \cos \theta $, $a_3 =\cos \varphi \cos \theta $.

对式(14)两端同时求惯性参考系下对时间的微分, 可得到刚体摆P的集中质量相对于惯性参考系$N$的速度, 为

(16) $ \begin{eqnarray} &&{ }^N{ v}^{\rm P}=\frac{{ }^N{\rm d}}{{\rm d}t}{ p}^{N\rm P}={ }^N{ v}^B+\frac{{ }^N{\rm d}}{{\rm d}t}{ p}^{B\rm P} = \\&&\qquad{ }^N{ v}^B-{ p}^{B\rm P}\times { }^N{ \omega }^B+\frac{{ }^B{\rm d}}{{\rm d}t}{ p}^{B\rm P} \end{eqnarray}$

2.2 系统动能

充液航天器系统的总动能包括以下3类运动所具有的动能: 航天器主刚体平动(即航天器轨道运动)和转动(即航天器姿态运动)具有的动能、 代表未晃动液体的集中质量点Q所具有的动能以及代表晃动液体的刚体摆P所具有的动能. 设航天器主刚体的质量为$m_{{\rm hub}}$, 主刚体关于其惯量主轴坐标系的惯性张量为${ I}_{{\rm hub}} $, 则该航天器系统总动能的定义式为

(17) $ \begin{eqnarray} &&T=\frac{1}{2}m_{{\rm hub}} { }^N{ v}^{B^\ast }\cdot { }^N{ v}^{B^\ast }+\frac{1}{2}\left( {{ I}_{{\rm hub}} \cdot { }^N{ \omega }^B} \right)\cdot { }^N{ \omega }^B + \\&&\qquad\frac{1}{2}m_0 { }^N{ v}^{\rm Q}\cdot { }^N{ v}^{\rm Q}+\frac{1}{2}m_{\rm p} { }^N{ v}^{\rm P}\cdot { }^N{ v}^{\rm P} + \\&&\qquad\frac{1}{2}J_{\rm p} \left( {\dot{{\psi }}+\omega _1 a_1 +\omega _2 a_2 +\omega _3 a_3 } \right) \end{eqnarray}$
将式(5)、式(9)、式(11)、式(13)和式(16)代入式(17)中, 即可推导出航天器系统总动能的具体表达式. 为方便后续推导, 将得到的系统总动能表达式改写成矩阵表示的形式; 并规定所有参与运算的矢量和二阶张量的坐标分量均统一在本体坐标系下给出. 于是, 可将系统总动能最终表示成如下的矩阵计算式

(18) $ \begin{eqnarray} &&T=\frac{1}{2}m{ v}^{\rm T}{ v}+\frac{1}{2}{ \omega }^{\rm T}{ I\omega }+\frac{1}{2}{\dot{{ \rho }}}^{\rm T}{ M}_{p} {\dot{{ \rho }}} + \\&&\qquad{ v}^{\rm T}{ C}_{\rm TR} { \omega }+{ v}^{\rm T}{ C}_{\rm TS} {\dot{{ \rho }}}+{ \omega }^{\rm T}{ C}_{\rm RS} {\dot{{ \rho }}} \end{eqnarray}$
式中, ${ v}=\left[ {v_1 ,v_2 ,v_3 } \right]^{\rm T}$; ${ \omega }=\left[ {\omega _1 ,\omega _2 ,\omega _3 } \right]^{\rm T}$; ${\dot{{ \rho }}}=\left[ {\dot{{\varphi }},\dot{{\theta }},\dot{{\psi }}} \right]^{\rm T}$; $m=m_{{\rm hub}} +m_0 +m_{\rm p} $, 是航天器系统的总质量; ${ I}$是整个航天器系统关于本体坐标系的惯性张量, 具体表示为

$$\begin{eqnarray*} &&{ I}={ I}_{{\rm hub}} +m_{{\rm hub}} \left[ {{ }^B{\tilde{{ p}}}^{BB^\ast }} \right]\left[ {{ }^B{\tilde{{ p}}}^{BB^\ast }} \right]^{\rm T} +\\&&\qquad m_{\rm p} \left[ {{ }^B{\tilde{{ p}}}^{B\rm P}} \right]\left[ {{ }^B{\tilde{{ p}}}^{B\rm P}} \right]^{\rm T}+J_{\rm p} { a a}^{\rm T} \end{eqnarray*}$$

其中, $\left[ {{ }^B{\tilde{{ p}}}^{BB^\ast }} \right]$和$\left[ {{ }^B{\tilde{{ p}}}^{B\rm P}} \right]$分别是位置矢量${ p}^{BB^\ast}$和${ p}^{B\rm P}$在本体坐标系$B$下表示的$3\times 1$维坐标矩阵所对应的反对称对偶矩阵, ${ a}=\left[ {a_1 ,a_2 ,a_3 } \right]^{\rm T}$; ${ M}_{\rm p} $代表刚体摆运动的广义质量矩阵, 具体表示为

$$\begin{eqnarray*} { M}_{\rm p} =m_{\rm p} l_{\rm p} ^2{ B B}^{\rm T}+J_{\rm p} \left[ {{\begin{array}{c@{\quad }c@{\quad }c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array} }} \right] \end{eqnarray*}$$

其中, ${ B}$是一个$3\times 3$维坐标变换矩阵; ${ C}_{\rm TR} =m_{{\rm hub}} \left[ {{ }^B{\tilde{{ p}}}^{BB^\ast }}\right]^{\rm T}+m_{\rm p} \left[ {{ }^B{\tilde{{ p}}}^{B\rm P}} \right]^{\rm T}$, 是航天器平动(即轨道运动)与转动(即姿态运动)之间的耦合系数矩阵; ${ C}_{\rm TS} =-m_{\rm p} l_{\rm p} { B}^{\rm T}$, 是航天器平动与刚体摆运动(代表液体晃动)之间的耦合系数矩阵; ${ C}_{\rm RS} =-m_{\rm p} l_{\rm p} \left[ {{ }^B{\tilde{{ p}}}^{B\rm P}} \right]{ B}^{\rm T}+\left[ {{\bf 0}_{3\times 1} ,{\bf 0}_{3\times 1} ,J_{\rm p} { a}} \right]$, 是航天器转动与刚体摆运动之间的耦合系数矩阵.

2.3 系统势能

充液航天器系统的势能为整个航天器在重力场中所具有的重力势能, 其表达式如下

(19) $ \begin{eqnarray} \label{eq19} V=-m_{{\rm hub}} { p}^{NB^\ast }\cdot { g}-m_0 { p}^{N\rm Q}\cdot { g}-m_{\rm p} { p}^{N\rm P}\cdot { g} \end{eqnarray}$
将式(10)、式(12)和式(14)代入式(19), 可以得到如下矩阵形式的系统势能表达式

(20) $ \begin{eqnarray} &&V=mgz_B -m_0 gl_0 +m_{{\rm hub}} g\left( {{ }^B{ p}^{BB^\ast }} \right)^{\rm T}{ c}_3 + \\&&\qquad m_{\rm p} g\left( {{ }^B{ p}^{B\rm P}} \right)^{\rm T}{ c}_3 \end{eqnarray}$
式中, ${ c}_3 $是姿态矩阵${ }^N{ C}^B$的第三列元素组成的列向量, 即

$$\begin{eqnarray*} { c}_3 =\left[ {{ }^N{ C}^B\left( {1,3} \right),{ }^N{ C}^B\left({2,3} \right),{ }^N{ C}^B\left( {3,3} \right)} \right]^{\rm T} \end{eqnarray*}$$

2.4 耦合系统的拉格朗日方程

充液航天器系统的拉格朗日函数有如下表述

(21) $ \begin{eqnarray} \label{eq21} {\cal L}(z_B ,{ v},{ \varepsilon },{ \omega },{ \rho },{\dot{{ \rho }}})=T-V \end{eqnarray}$
式中, $z_B $, ${ \varepsilon }$和${ \rho }$均属于广义坐标, ${\dot{{ \rho }}}$是广义速度; 而${ v}$和${ \omega}$是在本体坐标系(非惯性系)下给出的速度和角速度的坐标分量矩阵, 都不是真实坐标的导数, 因此称它们为拟速度^[30].

求解航天器轨道运动的拉格朗日方程为

(22) $ \begin{eqnarray} \label{eq22} \frac{{\rm d}}{{\rm d}t}\left\{ {\frac{\partial {\cal L}}{\partial { v}}} \right\}+\left[ {{\tilde{{ \omega }}}} \right]\frac{\partial {\cal L}}{\partial { v}}-\frac{\partial {\cal L}}{\partial z_B }{ c}_3 ={ F}_{{\rm nc}} \end{eqnarray}$
式中, ${ F}_{{\rm nc}}$是航天器系统受到的非保守力(如推力、外界干扰力等)在本体坐标系下表示的坐标矩阵, 其作用点位于本体坐标系原点$B$. 当不计入航天器主刚体质量时, 由牛顿第二定律, ${ F}_{{\rm nc}} $即表示液体对航天器主刚体的等效作用反力.

求解航天器姿态运动的拉格朗日方程为

(23) $ \begin{eqnarray} \label{eq23} \frac{{\rm d}}{{\rm d}t}\left\{ {\frac{\partial {\cal L}}{\partial { \omega }}} \right\}+\left[ {{\tilde{{ \omega }}}} \right]\frac{\partial {\cal L}}{\partial { \omega }}+\left[ {{\tilde{{ v}}}} \right]\frac{\partial {\cal L}}{\partial { v}}={ T}_{{\rm nc}} +{ T}_g \end{eqnarray}$
式中, ${ T}_{{\rm nc}}$是航天器系统受到的关于本体坐标系原点$B$的非保守力矩(如控制力矩、外界干扰力矩等)在本体坐标系下表示的坐标矩阵; ${ T}_g $是航天器系统受到的重力梯度力矩(一类保守力矩, 当航天器处于空间微重力环境下, 航天器机动过程中重力梯度力矩相比于控制力矩通常很小, 此时可以忽略重力梯度力矩的影响)在本体坐标系下表示的坐标矩阵. 当不计入航天器主刚体的惯量时, 由力矩平衡关系, ${ T}_{{\rm nc}}$即表示液体对航天器主刚体的等效作用反力矩.

求解贮腔内液体晃动等效刚体摆运动的拉格朗日方程为

(24) $ \begin{eqnarray} \label{eq24} \frac{{\rm d}}{{\rm d}t}\left\{ {\frac{\partial {\cal L}}{\partial {\dot{{ \rho }}}}} \right\}-\frac{\partial {\cal L}}{\partial { \rho}}={ T}_d \end{eqnarray}$
式中, ${ T}_d$是为了等效液体晃动时产生的黏性耗散而作用于刚体摆悬挂点的阻尼力矩, 这里采用如下线性的阻尼力矩模型

$$\begin{eqnarray*} { T}_d =-{ C}_p {\dot{{ \rho }}}=-\left[ {\beta _\varphi \dot{{\varphi }},\beta _\theta \dot{{\theta }},\beta _\psi \dot{{\psi }}} \right]^{\rm T}. \end{eqnarray*}$$

2.5 充液航天器动力学方程组

将式(18)和式(20)代入式(21)后, 再分别代入式(22)~式(24), 可得到充液航天器轨道-姿态-晃动全耦合系统的动力学方程

(25a)$ \begin{eqnarray} && m{\dot{{ v}}}+{ C}_{\rm TR} {\dot{{ \omega }}}+{ C}_{\rm TS} { \ddot{{\rho }}}=-\left[ {{\tilde{{ \omega }}}} \right]\left( {m{ v}+{ C}_{\rm TR} { \omega }+{ C}_{\rm TS} {\dot{{ \rho }}}} \right) - \\&&\qquad mg{ c}_3 -{\dot{{ C}}}_{\rm TR} { \omega }-{\dot{{ C}}}_{\rm TS} {\dot{{ \rho }}}+{ F}_{{\rm nc}}\end{eqnarray} $

(25b)$ \begin{eqnarray} && { I\dot{{\omega }}}+{ C}_{\rm TR} ^{\rm T}{\dot{{ v}}}+{ C}_{\rm RS} { \ddot{{\rho }}}=-\left[ {{\tilde{{ \omega }}}} \right]\left( {{ I\omega }+{ C}_{\rm TR} ^{\rm T}{ v}+{ C}_{\rm RS} {\dot{{ \rho }}}}\right) - \\&&\qquad\left[ {{\tilde{{ v}}}} \right]\left( {m{ v}+{ C}_{\rm TR} { \omega }+{ C}_{\rm TS} {\dot{{ \rho }}}} \right)-{\dot{{ I}}\omega }-{\dot{{ C}}}_{\rm TR} ^{\rm T}{ v}-{\dot{{ C}}}_{\rm RS} {\dot{{ \rho }}} + \\&&\qquad{ T}_{{\rm nc}}+{ T}_g\end{eqnarray} $

(25c)$ \begin{eqnarray} && { M}_{p} { \ddot{{\rho }}}+{ C}_{\rm TS} ^{\rm T}{\dot{{ v}}}+{ C}_{\rm RS} ^{\rm T}{\dot{{ \omega }}}=-{ C}_p {\dot{{ \rho }}}-m_{\rm p} g\frac{\partial \left( {{ }^B{ p}^{B\rm P}}\right)^{\rm T}}{\partial { \rho }}{ c}_3 + \\&&\qquad \frac{1}{2}{ \omega }^{\rm T}\frac{\partial { I}}{\partial { \rho }}{ \omega }+{ v}^{\rm T}\frac{\partial { C}_{\rm TR} }{\partial { \rho }}{ \omega }-\frac{1}{2}{\dot{{ \rho }}}^{\rm T}\frac{\partial { M}_{p} }{\partial { \rho }}{\dot{{ \rho }}} \end{eqnarray} $

3 仿真计算与分析

对充液航天器大角度姿态机动和姿态受控稳定下的轨道驱动分别进行相应的MATLAB仿真. 假定: 航天器主刚体的质量为$m_{{\rm hub}} =20$ kg, 主刚体关于其惯性主轴坐标系的惯性张量为${ I}_{{\rm hub}} ={\rm diag}\left\{ {4,6,5} \right\}$ kg$\cdot$m$^2$; 贮腔半径为$R=0.25$ m, 贮腔布放位置参数为${ }^B{ p}^{BB^\ast }=\left[ {\mbox{0.2},-0.3,-0.5} \right]^{\rm T}$ m; 贮腔内液体为燃烧剂甲基肼, 质量密度为$\rho =874.4$ kg$\cdot$m$^{-3}$; 刚体摆的等效阻尼参数取为$\beta _\varphi =\beta _\theta =0.05$, $\beta _\psi =0$; 当地重力加速度大小为$g=1.0$ m$\cdot$s$^{-2}$.

燃料消耗过程中, 假设贮腔充液比$\beta$随时间的变化规律满足如下连续可导的分段函数式

$$\begin{eqnarray*} \beta =\left\{ {\begin{array}{ll} \beta _1, & t=0 \\ \beta _{\rm 1} +\dfrac{\beta _{\rm 2} -\beta _{\rm 1} }{T_0 }t-\dfrac{\beta _{\rm 2} -\beta _{\rm 1} }{2\pi }\sin \left( {\dfrac{2\pi }{T_0 }t} \right), & 0<t<T_0 \\ \beta _{\rm 2} , & t\geqslant T_0 \\ \end{array}} \right. \end{eqnarray*}$$

式中, $\beta _{\rm 1} $和$\beta _{\rm 2} $分别是燃料消耗前后的充液比, 这里取$\beta _{\rm 1} =0.6$, $\beta _{\rm 2} =0.4$; $T_0$是燃料消耗时长, 用来表示燃料消耗速度快慢的物理量.

3.1 大角度三轴稳定姿态机动

采用常用的比例微分控制(PD控制)对该航天器进行三轴稳定姿态机动. 具体地, 假定初始时刻航天器处于静止状态, 即${ \omega }\left( {t=0} \right)=0$; 航天器初始姿态的欧拉四元数为

$$\begin{eqnarray*} \varepsilon _{0} \left( {t=0} \right)=1,\ \ \varepsilon _v \left({t=0} \right)=0 \end{eqnarray*}$$

采用如下的PD控制策略使航天器机动到目标状态

(26) $ \begin{eqnarray} \label{eq26} { \tau }=-{ K}_p \left( {{ \varepsilon }_v -{ \varepsilon }_v^{\rm tar} } \right)-{ K}_d \left( {{ \omega }-{ \omega }^{\rm tar}} \right) \end{eqnarray}$
式中, ${ \varepsilon }_v^{\rm tar} $和${ \omega }^{\rm tar}$是目标状态下航天器姿态的欧拉四元数的矢量部分和航天器角速度的坐标分量矩阵, 这里取${ \varepsilon }_v^{\rm tar} =\left[ {-0.221,0.074,0.442} \right]^{\rm T}$, ${ \omega }^{\rm tar}=0$; ${ K}_{\rm p}$和${ K}_d $是控制反馈增益矩阵, 设计为

$$\begin{eqnarray*} { K}_{\rm p} =k_{\rm p} { I}_{{\rm hub}} , \ \ { K}_d =k_d { I}_{{\rm hub}} \end{eqnarray*}$$

此处$k_{\rm p} =0.05$, $k_d =0.3$.

同时, 航天器姿态控制系统输出的控制力矩还需要对航天器受到的重力梯度力矩进行补偿. 于是, 姿态控制系统输出的控制力矩为

(27) $ \begin{eqnarray} \label{eq27} { T}_{{\rm nc}} ={ \tau }-{ T}_g \end{eqnarray}$
另一方面, 为克服重力, 航天器还需要提供持续的推力, 于是有

(28) $ \begin{eqnarray} { F}_{{\rm nc}} =mg{ c}_3 \end{eqnarray} $
此外, 假设初始时刻液体存在微小的残余横向晃动, 对应地, MATLAB仿真计算中取刚体摆运动的初始条件为$\varphi \left( {t=0} \right)=2\pi /180$ rad (其他状态变量均为零初始条件). 本算例中, 假设燃料消耗时长为$T_0 =20$ s.

图5~图9给出了航天器进行大角度姿态机动时, 贮腔内液体燃料在初始20 s内从充液比$\beta _{\rm 1} =0.6$消耗到充液比$\beta _{\rm 2} =0.4$的情形下, 主刚体和等效液体晃动刚体摆的运动响应结果.

图 5

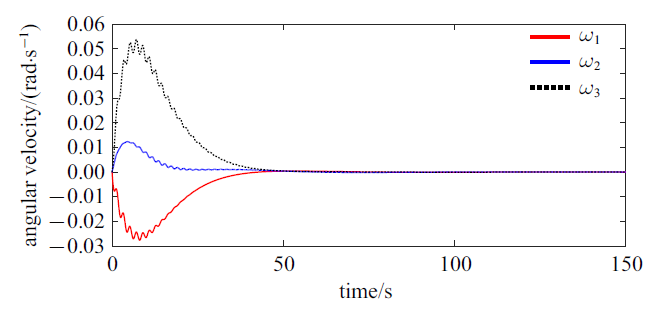
新窗口打开|下载原图ZIP|生成PPT
图 5航天器姿态运动的角速度响应

Fig. 5Angular velocity response of the spacecraft

图 6

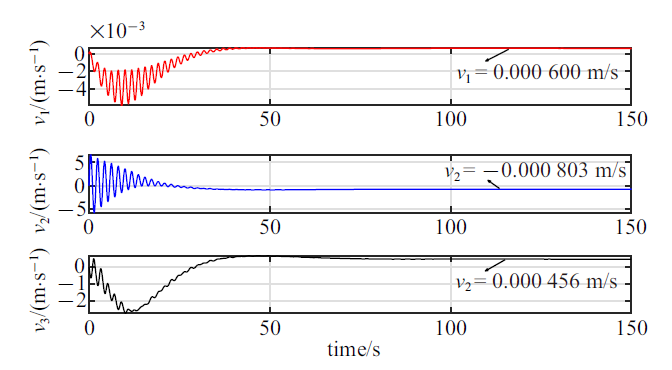
新窗口打开|下载原图ZIP|生成PPT
图 6航天器轨道运动的速度响应

Fig. 6Orbital velocity response of the spacecraft

图 7

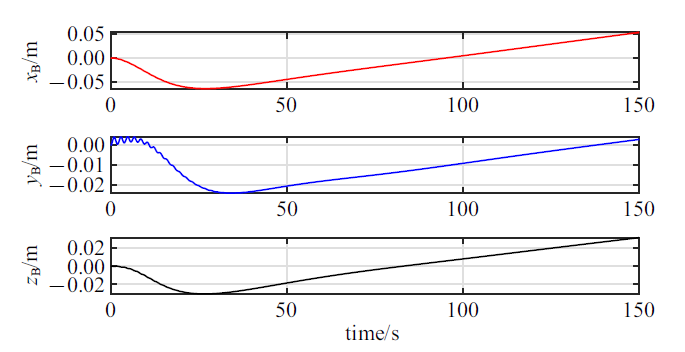
新窗口打开|下载原图ZIP|生成PPT
图 7航天器主刚体在惯性参考系中的位置

Fig. 7Position of the spacecraft hub in the inertial reference frame

图 8

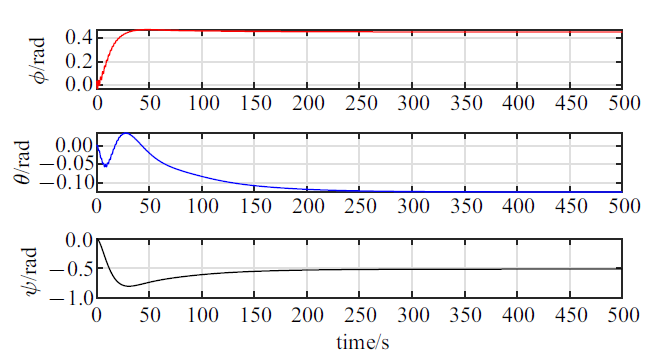
新窗口打开|下载原图ZIP|生成PPT
图 8等效液体晃动刚体摆的运动响应

Fig. 8Motion response of the rigid-pendulum for liquid slosh

图 9

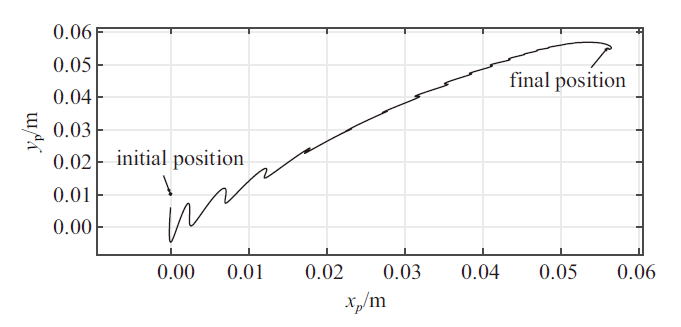
新窗口打开|下载原图ZIP|生成PPT
图 9刚体摆的集中质量的运动轨迹在$B-{ b}_1 { b}_2 $平面内的投影

Fig. 9Trajectory of the lumped mass of the rigid-pendulum on $B-{ b}_1 { b}_2 $ plane



图5给出了航天器进行大角度三轴稳定姿态机动时的角速度响应, 结果显示贮腔内液体晃动对航天器3个方向的姿态运动均产生了局部振荡形式的扰动影响. 另一方面, 图6显示了液体相对于贮腔的运动(包括液体整体性的刚体运动和液体晃动)也会引起航天器主刚体产生微小的平动速度, 但是由于燃料消耗的影响, 导致机动过程中航天器轨道运动的最终速度不会收敛到零(这并不违背航天器系统动量守恒), 即航天器主刚体在惯性参考系中的位置偏移会不断地增大(图7). 这特别提示了燃料消耗下充液航天器在执行交会对接等空间定点任务时, 应当考虑液体晃动的影响.

此外, 图8给出了本工况下描述等效液体晃动刚体摆运动的三个欧拉角的时程响应. 将图8的计算结果的数据进行转化, 可以得到刚体摆的集中质量(它代表的是晃动部分液体的质心)在贮腔坐标系中的运动轨迹, 图9是该轨迹在$B-{ b}_1 { b}_2 $平面内的投影($x_{\rm p} $和$y_{\rm p} $表示刚体摆的集中质量在$B-{ b}_1 { b}_2 $平面内的投影点的坐标), 结果表明此工况下晃动部分液体的运动形式表现为相对于贮腔的整体性的大范围刚体运动和横向晃动的叠加.

3.2 零冲量轨道机动

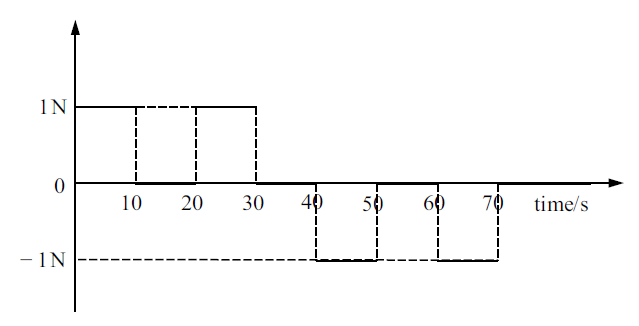
进一步研究变质量充液航天器姿态受控稳定时在零冲量轨道驱动力作用下的动力学响应.

假设航天器在受到方向始终沿惯性参考系${ n}_1 $轴向, 大小(正值表示沿${ n}_1 $轴正方向, 负值表示沿${ n}_1$轴负方向)如图10所示的零冲量阶跃式驱动力的作用进行轨道机动.

图 10

新窗口打开|下载原图ZIP|生成PPT
图 10零冲量阶跃式驱动力

Fig. 10A step type propulsive force with zero impulse



此外, 为了保证航天器在进行轨道机动时的姿态能够保持基本稳定, 采用3.1节中的PD控制(式(26))来实现航天器的姿态稳定, 并取$k_p =0.5$, $k_d =3$. 这里, 航天器的初始姿态和目标姿态所对应的四元数相同, 假设为${ \varepsilon }_v \left( {t=0} \right)={ \varepsilon }_v^{\rm tar} =0$, 且航天器的初始角速度和目标角速度均为零. 本算例中, 假设燃料消耗时长为$T_0=70$ s.

图11~图16给出了贮腔偏心布放(贮腔形心偏离航天器主刚体质心)时, 航天器在进行零冲量轨道机动过程中并保持燃料持续消耗70 s的情况下, 主刚体和等效液体晃动刚体摆的运动响应结果; 图17给出机动过程中为维持航天器姿态稳定所施加的PD控制力矩.

图 11

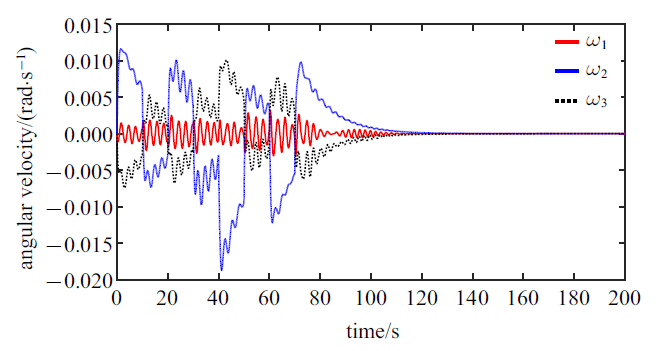
新窗口打开|下载原图ZIP|生成PPT
图 11航天器姿态运动的角速度响应

Fig. 11Angular velocity response of the spacecraft

图 12

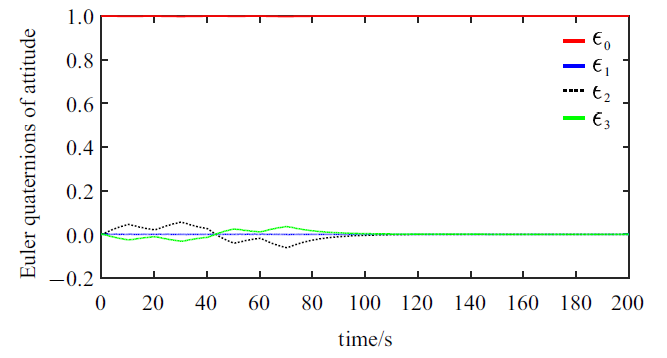
新窗口打开|下载原图ZIP|生成PPT
图 12航天器姿态的欧拉四元数响应

Fig. 12Euler quaternions response of the spacecraft attitude

图 13

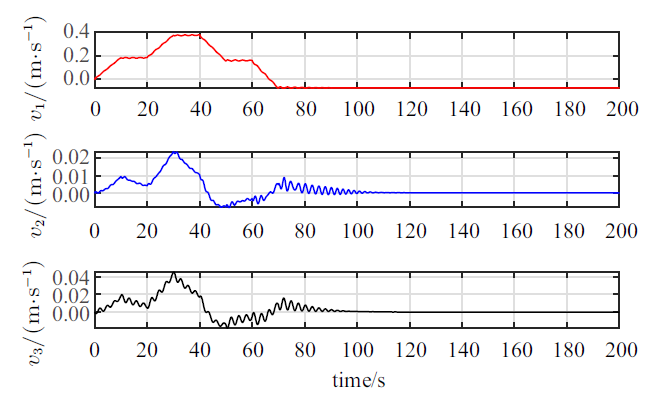
新窗口打开|下载原图ZIP|生成PPT
图 13航天器轨道运动的速度响应

Fig. 13Orbital velocity response of the spacecraft

图 14

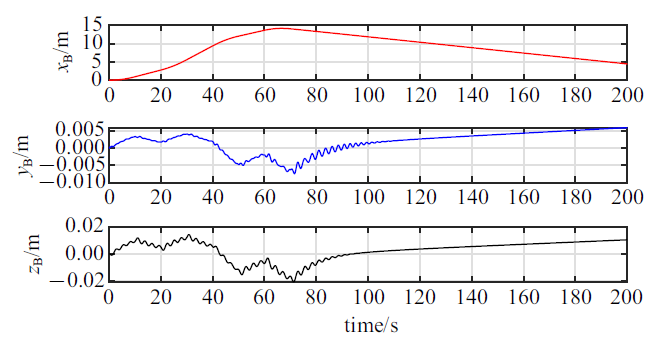
新窗口打开|下载原图ZIP|生成PPT
图 14航天器主刚体在惯性参考系中的位置

Fig. 14Position of the spacecraft hub in the inertial reference frame

图 15

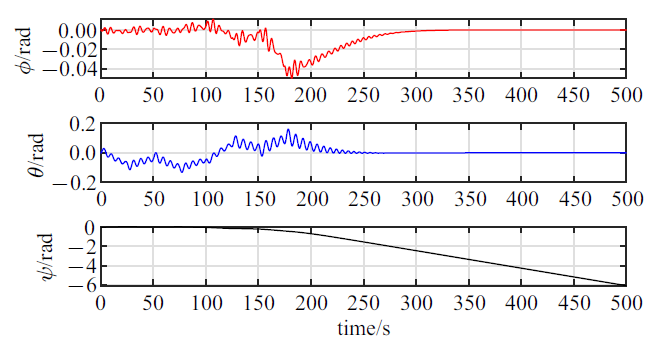
新窗口打开|下载原图ZIP|生成PPT
图 15等效液体晃动刚体摆的运动响应

Fig. 15Motion response of the rigid-pendulum for liquid slosh

图 16

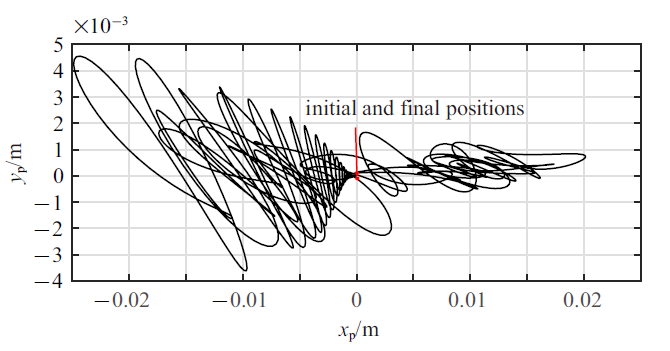
新窗口打开|下载原图ZIP|生成PPT
图 16刚体摆的集中质量的运动轨迹在$B-{ b}_1 { b}_2 $平面内的投影

Fig. 16Trajectory of the lumped mass of the rigid-pendulum on $B-{ b}_1 { b}_2 $ plane

图 17

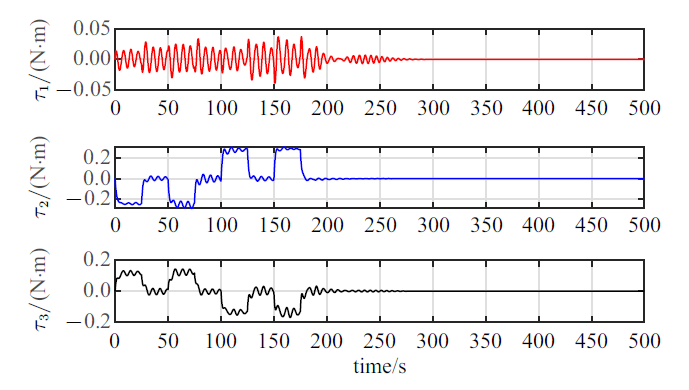新窗口打开|下载原图ZIP|生成PPT
图 17姿态稳定PD控制力矩

Fig. 17PD control torque for attitude stabilization of the spacecraft



仿真结果显示: 航天器在轨道机动过程中, 一方面, 航天器在如图17所示的控制力矩的作用下, 航天器的姿态运动虽然受到了液体晃动的扰动影响(图11), 但是航天器的整体姿态基本上能够维持稳定(图12); 另一方面, 航天器在图10给出的零冲量阶跃式驱动力的作用下, 液体晃动不仅会对航天器轨道平动造成明显扰动影响(图13和图14), 而且由于燃料消耗的影响, 会造成该充液航天器在进行零冲量轨道机动时, 最终的轨道平动速度无法收敛到零, 尤其是在驱动方向(惯性参考系${ n}_1 $轴方向)上航天器将最终获得一个较大的速度(图13), 因此, 在零冲量轨道驱动力作用下, 由于燃料消耗的影响, 虽然航天器沿惯性参考系${ n}_1 $轴方向作了大范围平移, 但是航天器此时仍无法保持静止状态, 此后航天器将不断地偏离预期的机动位置(图14), 导致机动任务失败. 特别值得注意的是, 在以上工况下, 贮腔内液体将发生极为复杂的非平面运动(图15和图16), 贮腔内液体会经历逐步起旋并发生明显的旋转晃动(图16), 此过程中也伴随着液体横向晃动, 但由于液体阻尼耗散等因素, 液体的横向晃动最终会衰减并消失, 贮腔内液体运动最终表现为恒定角速率的刚体自旋运动(图15).

4 结论

本文采用变参数的刚体摆复合等效力学模型模拟燃料消耗下球形贮腔内的液体非线性晃动, 并基于混合坐标下的拉格朗日方程, 建立了变质量充液航天器轨道-姿态-晃动全耦合的动力学模型. 通过编制相应的MATLAB仿真计算程序, 对本文所建立的动力学模型进行求解, 研究了该变质量充液航天器在执行大角度三轴稳定姿态机动以及姿态受控稳定下的零冲量轨道机动过程中的动力学响应. 得到了对航天工程实践有一定指导意义的两点主要结论.

(1)液体相对于贮腔的运动会造成航天器主刚体位置发生偏移, 当航天器在执行零冲量机动时, 燃料消耗会造成航天器的轨道平动速度无法收敛到零, 因此, 在充液航天器执行交会对接等空间定点任务时, 应当充分考虑液体晃动的影响.

(2)贮腔偏心布放时, 航天器在执行轨道机动过程中贮腔内液体易发生剧烈而且形式复杂的晃动行为, 进而可能造成航天器刚体运动的不稳定.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Ibrahim RA. Liquid Sloshing Dynamics: Theory and Applications. Cambridge: Cambridge University Press, 2005
[本文引用: 1]

[2] Dodge FT. The new “dynamic behavior of liquids in moving containers”
San Antonio, TX: Southwest Research Inst, 2000
[本文引用: 3]

[3] 王照林, 刘延柱. 充液系统动力学. 北京: 科学出版社, 2002
[本文引用: 1]

( Wang Zhaolin, Liu Yanzhu. Dynamics of Liquid-Filled System. Beijing: Science Press, 2002 (in Chinese))
[本文引用: 1]

[4] 王照林, 全斌, 邓重平 等. 复杂结构充液航天器晃动动力学与姿态稳定性
宇航学报, 1991(2):1-8


( Wang Zhaolin, Quan Bin, Deng Zhongping, et al. On the sloshing dynamics and attitude stability of liquid-filled spacecraft with complex structures
Journal of Astronautics, 1991(2):1-8 (in Chinese))


[5] 苟兴宇, 王本利, 马兴瑞 等. 航天工程中的贮箱类液固耦合动力学建模及耦合机理研究
强度与环境, 1998(1):9-16


( Gou Xingyu, Wang Benli, Ma Xingrui, et al. Dynamic modelling of liquid-solid coupling system with container in spacecraft engineering and investigation of its coupling mechanism
Structure & Environment Engineering, 1998(1):9-16 (in Chinese))


[6] 岳宝增. 液体大幅晃动动力学. 北京: 科学出版社, 2011


( Yue Baozeng. Large Amplitude Liquid Sloshing Dynamics. Beijing: Science Press, 2011 (in Chinese))


[7] 刘峰, 岳宝增, 唐勇. 多充液贮腔航天器耦合动力学与姿态控制
宇航学报, 2020,41(1):19-26
[本文引用: 1]

( Liu Feng, Yue Baozeng, Tang Yong. Dynamics modeling and attitude control of spacecraft with multiple propellant tanks
Journal of Astronautics, 2020,41(1):19-26 (in Chinese))
[本文引用: 1]

[8] Liu F, Yue BZ, Banerjee AK, et al. Large motion dynamics of in-orbit flexible spacecraft with large amplitude propellant slosh
Journal of Guidance, Control, and Dynamics, 2020,43(3):438-450


[9] Liu F, Yue BZ, Zhao LY. Attitude dynamics and control of spacecraft with a partially filled liquid tank and flexible panels
Acta Astronautica, 2018,143:327-336
[本文引用: 1]

[10] Sances DJ, Gibson JM, Neumann SS, et al. Modeling of free-surface fuel slosh in microgravity for off-axis spacecraft propellant tanks
AIAA Modeling and Simulation Technologies Conference, Chicago, Illinois, 2009


[11] 唐勇. 三维液体大幅晃动数值仿真及航天器刚液柔耦合动力学研究. [博士论文]
北京: 北京理工大学, 2019


( Tang Yong. Studies on numerical simulation of three-dimensional large-amplitude liquid slosh and rigid-liquid-flexible coupling dynamics of spacecraft. [PhD Thesis]
Beijing: Beijing Institute of Technology, 2019 (in Chinese))


[12] Theureau D, Busset B, Bavestrello H, et al. Integration of low g sloshing models with spacecraft attitude control simulators
// AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 2013


[13] Ibrahim RA, Singh B. Assessment of ground vehicle tankers interacting with liquid sloshing dynamics
International Journal of Heavy Vehicle Systems, 2018,25(1):23-112


[14] Yue BZ, Wu WJ, Yan YL. Modeling and coupling dynamics of the spacecraft with multiple propellant tanks
AIAA Journal, 2016,54(11):3608-3618


[15] Peterson LD. The nonlinear coupled dynamics of fluids and spacecraft in low gravity. [PhD Thesis]
Cambridge: Massachusetts Institute of Technology, 1987
URLPMID

[16] Miao N, Li JF, Wang TS. Large-amplitude sloshing analysis and equivalent mechanical modeling in spherical tanks of spacecraft
Journal of Spacecraft and Rockets, 2016,53(3):1-7


[17] 苗楠, 刘战合, 王晓璐 等. 轴对称贮箱内液体大幅晃动的复合等效力学模型
中国科学: 物理学力学天文学, 2020,50(7):074501


( Miao Nan, Liu Zhanhe, Wang Xiaolu, et al. Composite equivalent mechanical models for large-amplitude liquid sloshing in axisymmetrical tanks
Sci Sin-Phys Mech Astron, 2020 50(7):074501 (in Chinese))


[18] 于强, 王天舒. 航天器贮箱内液体大幅晃动动力学分析
中国科学: 物理学力学天文学, 2019,49(2):024514


( Yu Qiang, Wang Tianshu. Dynamic analysis of large-scale amplitude liquid sloshing in the spacecraft
Sci Sin-Phys Mech Astron, 2019,49(2):024514 (in Chinese))


[19] Fonseca IMD, Bainum PM. CSI due to sloshing motion on LEO LSS
// 1st IAA Conference on Dynamics and Control of Space Systems, Porto, Portugal, 2012


[20] Allard C, Ramos MD, Schaub H. Spacecraft dynamics integrating hinged solar panels and lumped-mass fuel slosh model
// AIAA/AAS Astrodynamics Specialist Conference, Long Beach Marriott, Long Beach, USA, 2016


[21] Kang JY, John E. Stability criteria of slosh motion with periodicity in a spinning spacecraft
Journal of Guidance, Control, and Dynamics, 2005,28(3):562-567


[22] Zhou ZC, Huang H. Constraint surface model for large amplitude sloshing of the spacecraft with multiple tanks
Acta Astronautica, 2015,111:222-229


[23] 邓明乐. 液体大幅晃动等效力学模型及航天器刚-液-柔-控耦合动力学研究. [博士论文]
北京: 北京理工大学, 2017


( Deng Mingle. Studies on the equivalent mechanical model of large amplitude liquid slosh and rigid-liquid-flex-control coupling dynamics of spacecraft. [PhD Thesis]
Beijing: Beijing Institute of Technology, 2017 (in Chinese))


[24] Vreeburg JPB. Dynamics and control of a spacecraft with a moving pulsating ball in a spherical cavity
Acta Astronautica, 1997,40(2-8):257-274


[25] Thomas SS, Kang JY, Victoria LC. Analytical control law for spacecraft reorientation via lyapunov theory
AIAA Guidance, Navigation and Control Conference, Toronto, Canada, 2010


[26] 岳宝增, 于嘉瑞, 吴文军. 多储液腔航天器刚液耦合动力学与复合控制
力学学报, 2017,49(2):390-396
[本文引用: 1]

( Yue Baozeng, Yu Jiarui, Wu Wenjun. Rigid and liquid coupling dynamics and hybrid control of spacecraft with multiple propellant tanks
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(2):390-396 (in Chinese))
[本文引用: 1]

[27] Liu F, Yue BZ, Tang Y, et al. 3DOF-rigid-pendulum analogy for nonlinear liquid slosh in spherical propellant tanks
Journal of Sound and Vibration, 2019,460:114907
[本文引用: 6]

[28] Meirovitch L. Hybrid state equations of motion for flexible bodies in terms of quasi-coordinates
Journal of Guidance, Control, and Dynamics, 1991,14(5):1008-1013
[本文引用: 1]

[29] Meirovitch L. Methods of Analytical Dynamics
New York: McGraw-Hill, 1970
[本文引用: 1]

[30] 屠善澄. 卫星姿态动力学与控制. 北京: 宇航出版社, 2001
[本文引用: 1]

( Tu Shancheng. Attitude Dynamics and Control of Satellites. Beijing: Aerospace Press, 2001 (in Chinese))
[本文引用: 1]