 ,*,2), 朱晴*, 王美达*, 金瑶兰?, 王思民?, 孔祥东**
,*,2), 朱晴*, 王美达*, 金瑶兰?, 王思民?, 孔祥东**PIV MEASUREMENT OF CLOSE IMPINGING JET ON FLAT PLATE 1)
Hu Jianjun ,*,2), Zhu Qing*, Wang Meid*, Jin Yaolan?, Wang Simin?, Kong Xiangdong**
,*,2), Zhu Qing*, Wang Meid*, Jin Yaolan?, Wang Simin?, Kong Xiangdong**通讯作者: 2)胡建军, 副教授, 主要研究方向: 流动测量与流动显示技术. E-mail:kewei729@163.com
收稿日期:2020-05-1接受日期:2020-05-1网络出版日期:2020-09-18
| 基金资助: |
Received:2020-05-1Accepted:2020-05-1Online:2020-09-18
作者简介 About authors

摘要
运用时间分辨粒子成像测速系统(time-resolved particle image velocimetry, TR-PIV)对近距离下射流冲击平板时的流场进行了直接测量, 通过对两个正交的平面流场开展测量, 揭示了冲击距离和雷诺数对射流间隙内三维流动特征及涡系结构演化规律的影响. 结果表明: 射流间隙存在三种典型的涡系结构, 分别为双涡环模式、单涡环模式和卷吸模式, 但在大流量湍流状态下, 射流可能会冲破涡环, 形成随机的高速出流, 各流动模式的出现主要与射流流态及壁面约束作用有关. 运用涡量分析对三种典型涡系结构的能量传递和损失特性进行了比较. 结果表明: 近距离冲击时, 射流的能量通过涡环模式向外传递. 在双涡环模式下, 两个涡环的旋向相反, 端面的约束作用使得两个涡环都被严格约束在射流棒端面之内, 且一次涡环强度显著大于二次涡环强度. 最后, 运用本征正交分解方法对射流间隙内的流动模态及其能量分布进行了分析. 单涡和双涡模式前十阶模态分析结果表明: 能量脉动在较低阶时即以配对的模式出现, 这表明一次涡环与二次涡环均具有良好的对称性, 同时在双涡模式中, 一次涡环是占主导作用的大尺度流动结构. 卷吸模式的前三阶模态分析表明: 射流的能量集中在射流上游, 能量随紊动扩散急剧衰减.
关键词:
Abstract
The time-resolved particle image velocimetry (TR-PIV) method was used to measure the flow field of a jet impinging on a flat plate in two orthogonal plane at very close distance. The effects of impinging distance and Reynolds number on the flow characteristics and the vortex topology in the clearance were analyzed. The results show that there are three kinds of typical vortex structure in the clearance, namely, double vortex ring mode, single vortex ring mode and complete entrainment mode. However, under the condition of turbulent state with large flow rate, the jet may break through the vortex ring and form random high-speed outflow. The occurrence of each flow pattern is mainly related to the strength of wall constraints. The energy transportation and flow loss of three typical flow patterns are investigated by vorticity analysis. The results show that the energy of the jet is transmitted outward through the vortex-ring mode at close impingement. In the double vortex ring mode, the two vortex rings have opposite rotational direction. Due to the constraint of the end face, both vortex rings are strictly constrained within the end face of the jet nozzle. The strength of the primary vortex ring is significantly greater than that of the secondary vortex ring. Finally, the proper orthogonal decomposition (POD) method is used to analyze the flow mode and energy distribution of the impinging jet. The first ten modal analysis of single and double vortex mode show that the energy fluctuation occurs in a paired pattern at a lower order, which indicates that both the primary and secondary vortex rings have good symmetry. Meanwhile, in the double vortex ring mode, the primary vortex ring is the dominant large-scale flow structure. The first three modes of the complete entrainment mode show that the energy of the jet is concentrated in the upstream of the jet and decreases sharply with the turbulent diffusion.
Keywords:
PDF (15552KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
胡建军, 朱晴, 王美达, 金瑶兰, 王思民, 孔祥东. 近距离下射流冲击平板PIV实验研究 1). 力学学报[J], 2020, 52(5): 1350-1361 DOI:10.6052/0459-1879-20-142
Hu Jianjun, Zhu Qing, Wang Meid, Jin Yaolan, Wang Simin, Kong Xiangdong.
引言
近距离射流以其高强度的冲击效应, 广泛被应用于破岩采矿、切割、清洗、气流组织、医疗、射流零件开发等领域[1-3]. 由于射流结构的变化以及射流与周围流体流动状态的差异, 射流的混合和扩散带来了许多值得研究的课题[4-6].近年来, 随着计算硬件的进步和计算方法的发展, 研究人员较普遍地采用数值模拟的方法来研究冲击射流的流动特性[7]. 王雄等[8]通过运用雷诺应力模型(RANS)对圆形射流模拟发现, 时均速度分布结果与实验值符合较好, 但是雷诺应力的模拟结果和实验有较大的误差. 有****运用大涡模拟(LES)方法对冲击射流的涡结构进行了研究, 揭示了涡旋强度时间和空间动力学特性[9-10]. Wilke等[11-12]对雷诺数对射流的影响进行了直接数值模拟(DNS), 分析了它们的统计特性. 王鹏[13]运用DDES方法对横流射流进行了模拟, 通过与实验结果对比大涡拟序结构, 验证了DDES方法应用到射流类复杂流动研究中的可行性.
数值模拟虽然可以得到丰富的流场信息, 但一些模拟的结果仍然缺乏直接的实验支持, 得到的结论无法得到有效验证. 因此, 采用实验手段研究冲击射流的流动特性仍是不可或缺的.
在实验方面, 吴迪等[14]采用压敏涂料(PSP)技术对被冲击平面的压力分布进行了测量. Law等[15]利用激光诱导荧光分析(LIF)方法研究了射流和横流混合过程的时均湍流特性. 丁涛等[16]通过LIF实验发现, 射流在发展过程中, 射流边界处的涡会反复出现产生、配对以及合并等复杂现象. LIF方法空间分辨率高, 灵敏度高, 但需要一定的光谱基础. Darisse[17]采用激光多普勒测速(LDV)技术研究了高雷诺数湍流圆射流的远场涡系特征.
近年来, 粒子图像测速(PIV)技术在流场测量中得到了广泛应用. 与LIF和LDV技术相比, 该技术同样具有非接触测量的属性. 其优势是能实现高精度的瞬态全场测量, 但根据其测量原理, 其局限就是所谓的全场只能是平面全场[18-20]. Fairweather等[21]的PIV测量表明, 冲击射流外存在一个大的低速循环区域, 该区域将壁面射流外围的物质带回其初始区域. 徐惊雷等[22]应用PIV技术, 展示了射流涡的形成、发展和破裂等瞬态流场. Roux等[23]通过PIV测量, 对比收缩管和长管射流的剪切层涡环. 陈建刚等[24]应用PIV技术对淹没射流湍流流场进行了测量, 发现了水平涡和垂直涡的形成和消失特性. Mishra等[25]利用PIV技术研究了壁面作用下倾斜射流的扰动涡. Greco等[26]通过PIV实验研究了射流在不同冲击距离下对流场的影响, 并分析了涡环的特性. 上述结果表明, PIV技术能够较好地捕捉瞬时湍流流场信息.
已有研究表明冲击射流在冲击间隙内会有涡环产生的现象, 但尚未解释射流在近距离冲击时, 间隙内微小的流动结构与射流结构参数变化的关系. 为了探讨强壁面约束下高速冲击射流所产生的涡结构, 本文采用TR-PIV技术对近距离冲击射流的流场结构进行了实验测量, 获得了近距离冲击射流涡系的直观图像及其随工况的演化规律, 有助于加深对冲击射流本质的理解. 同时, 本文研究还可为射流元件, 如射流管伺服阀的性能分析及设计优化提供理论基础. 此外, 本文实验模型的边界条件简单, 其测量结果还可作为某些数值算法的验证数据.
1 实验装置
实验模型——圆柱形水池中淹没射流冲击平板实验模型, 其原型是基于射流原理开发的在工业和航天领域有着重要应用的射流管式电液伺服阀. 实验模型是通过对该伺服阀前置级适当简化并通过相似原理放大得到.1.1 实验模型的确定
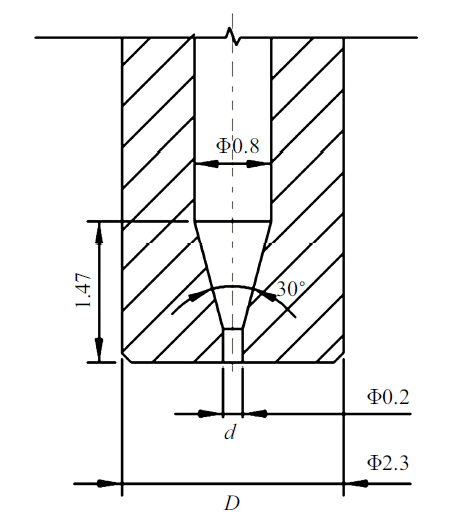
本部分基于相似原理, 从射流管电液伺服阀前置级内冲击射流情形中抽象出本实验的测量模型. 介绍了相似计算过程和实验条件的确定, 并给出了实验装置并确定了实验装置的参数.在原型射流管电液伺服阀中, 工作介质为15号航空液压油, 工作压力高达21 MPa, 喷嘴出口速度可达200 m/s, 射流间隙大小仅为亚毫米级, 喷嘴原型尺寸如图1所示. 现有的流动显示技术无法直接测量阀内高压、高速、小尺度的冲击射流流场, 因此, 需要根据雷诺相似理论对原型进行放大. 此外, 示踪粒子在油介质中的扩散性能较差, 易发生团聚现象, 因此工作介质选择水代替油. 本研究主要聚焦射流间隙内的流动特性和涡结构, 因此对实际射流阀的前置级其他部分的结构进行了适当简化.
图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1原型喷嘴示意图
Fig.1Prototype nozzle
为了保证实验模型与原型的流场特性相同, 根据相似原理确定了实验模型的几何参数和工作参数. 由于实验模型中没有自由表面, 因此不需要考虑表面张力的影响, 重力和可压缩性对流动的影响也可以忽略, 因此不考虑韦伯相似度、弗劳德相似度和马赫相似度. 在实验模型中, 黏性力、压力和惯性力起主导作用. 因此, 在满足几何相似的条件下, 实验模型动力学相似判定准则为雷诺数, 可以表示为
其中, 工作介质的密度为$\rho$; $l$为特征长度, 本文指的喷嘴直径; $v$是流体速度; $\mu$是工作介质的动力黏性系数; 下标p和m分别表示原型和实验模型.
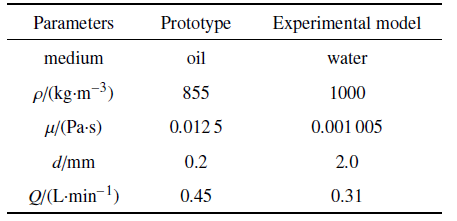
根据原模型真实的工作条件, 基于雷诺相似建立了10倍放大的简化模型. 圆柱池内径150 mm, 高度60 mm, 计算结果如表1所示.
Table 1
表1
表1雷诺相似计算
Table 1
 |
新窗口打开|下载CSV
实验所用的射流管使用7020硬铝材料加工而成, 射流管与喷嘴采用螺纹连接. 射流管长度为110 mm, 外径为23 mm. 喷嘴内径为2 mm, 经过30$^\circ$锥角后变为8 mm, 喷嘴总长度为50 mm. 由于PIV激光片光在射流管金属端面会产生强烈的反射, 形成背景白噪声, 因此, 喷嘴的端面进行了黑化处理. 为了降低加工表面粗糙度对测量结果的影响, 射流管外表面表面粗糙度等级为Ra 3.2, 内表面表面粗糙度等级为Ra 1.6.
根据原型射流管阀前置级几何特征, 实验模型简化为圆柱形水池. 考虑到PIV系统对光路的要求, 所选取的材料应表面光滑无划痕, 透光性好. 因此定制了内径150 mm、高70 mm、壁厚5 mm的石英玻璃圆筒.
为同时满足PIV系统的测量要求和模型连接时的强度要求, 设计并加工了规格为 250 mm $\times$ 250 mm $\times$ 5 mm (长 $\times$ 宽 $\times$ 厚)的有机玻璃板作为圆柱水池的底板. 顶板为7020硬铝材料, 尺寸为250 mm $\times$ 250 mm $\times$ 30 mm, 并在一侧开直径8 mm的螺纹孔, 用于连接排水管. 顶板中心开直径23 mm的通孔, 用于插入射流棒, 冲孔内铣槽, 内置密封圈, 以防止漏水. 底板、顶板均铣出内径150 mm、深度5 mm的槽, 放置密封圈用于密封. 顶板和底板使用螺栓和螺杆夹紧安装, 组装后的实验装置如图2所示.
图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2实验模型
Fig.2Experimental model
1.2 测量工况及测量平面
由于原型射流管伺服阀的冲击距离很小, 冲击过程往往发生在射流的起始段. 因此, 本实验在射流起始段内改变冲击距离, 探讨冲击距离对间隙内涡系结构的影响.本文关注的近距离冲击射流其定义为冲击距离介于1倍喷嘴直径到起始段结束的冲击射流. 其中, 射流核心区长度的半经验公式为
其中$a$是湍流系数, 本实验中取$a=0.066$; $r_0$是射流孔的半径.
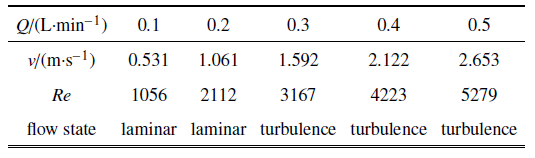
经计算, 射流核心段长度$S_{\rm n}$约为10.2 mm. 因此, 本实验设计的冲击距离分别为2 mm, 3 mm, 4 mm, 5 mm, 7 mm和10 mm. 无量纲距离$H/d$分别为1, 1.5, 2, 2.5, 3.5, 5. 为了探索流量对冲击射流流场涡结构的影响, 测量了5种流量(0.1 L/min到0.5 L/min)下的间隙流场, 其中, 相似计算得到的实验模型流量应为0.31 L/min. 实验中的流动工况如表2所示.
Table 2
表2
表2流量对应的流速与流态
Table 2
 |
新窗口打开|下载CSV
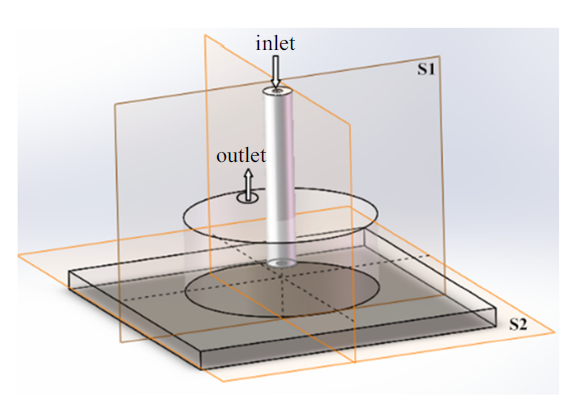
根据PIV技术的测量特点, 本文通过测量两个正交平面的流场, 以此全面反映射流流场的三维特征. 两个正交测量平面如图3所示, 定义S1为对称面, S2为水平近壁面. 当测量S1平面时, 片光从圆柱水池的底面平面垂直入射, 对光路几乎没有影响; 而摄像机观测时, 则从圆柱弧面的法向, 正面观测圆柱中心的射流间隙及其附近流场, 此时圆柱弧面影响下的畸变最小.
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3被测平面示意图
Fig.3Diagram of measurement surface
考虑到PIV技术的另一个局限是光在壁面的反射/散射会形成一条亮线, 继而掩盖粒子的反射, 不能有效测得近壁面的流场信息. 因此, 当测量S2平面时, 本实验激光发生器所产生的片光最窄厚度(光腰处)约为1 mm, 通过调节激光头可以使光腰照亮射流管底面及其附近区域, 使这个区域满足流场测量的需求. 最终, 测量平面S2距离底板的距离约为1.5 mm.
1.3 PIV流场测量系统
图4为搭建的近距离冲击射流流场测量实验台. 该系统主要由进水管道、出水管道、冲击射流实验模型、微型潜水泵(HAONUO-15m)、柱形流量计(LZB-6WB)、Dantec PIV流场测量系统等组成.图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4PIV流场测量试验台
Fig.4PIV flowfield measurement system
循环泵的扬程为15 m, 用于输送实验工质, 为射流提供动力, 克服循环系统的阻力. 柱形转子流量计用于测量并控制流量, 量程为0.06 L/min至0.6 L/min.
本文的PIV是系统是由Dantec公司提供的高频2D-PIV系统, 配有图丽微距镜头(Tokina AT-X M100 F2.8 PRO D0), CCD照相机(DANTEC SpeedSense Lab310, 像素1280 $\times$ 800), 信号同步器, Dynamic Studio 5.1软件和Nd: YLF激光系统(Vite-Hi-20 k, 单个光路最小能量20 mJ, 输出激光波长为527 nm)组成, 最大触发频率为2929 Hz. 激光片光由Beamtec生产的固态激光器产生, 脉冲光由Q-switch触发方式获得. 激光脉冲宽度小于250 ns. 脉冲间隔时间可达微秒级, 具体数值可根据实验条件进行调整. 激光最窄光腰厚度约为1 mm. Dynamic Studio V2.3软件系统用于标定、控制整个数据采集过程和设置采集参数, 并对原始粒子图像进行前后处理. 根据厂家标定数据, 2D-PIV系统的测量误差约为1%.
在本实验中, 每个工况下的有效拍照数约为350张, 每张照片的像素为1280 $\times $ 800, 拍照频率在1500 Hz至2900 Hz间, 对应的瞬态流动时间为0.1 s至0.2 s. 喷嘴出口的速度在0.5 m/s到2.7 m/s之间, 为了保证良好的跟随性和扩散均匀性[27], 选择平均直径5 $\mu$m的聚酰胺作为示踪粒子(PSP-5). 实验结果后处理时, 查询窗口像素设定为32 $\times$ 32, 重叠率25%. 每个查询窗口中有效的示踪粒子约5$\sim $8个, 每个粒子约占4个像素. 连续两个曝光时间间隔内, 示踪粒子最大位移约为查询区域的1/3$\sim $1/2.
根据二维PIV测量对模型、相机和激光片光位置关系的要求, 综合调整激光头、CCD相机的位置和实验模型的方向, 实现对被测截面的测量. 图5为测量不同平面时的光路布置. 图5(a)为S1面被测量时的光路布置, 激光从实验模型底部打入将流域照亮, CCD相机从侧面捕捉流动图像. 测量S2平面时, 只需要将实验模型旋转90$^\circ$, 仍然使用相同的光路布置. 图5(b)为S2面被测量时的光路布置, 激光从实验模型侧面打入将流域照亮, CCD相机从底部捕捉流动图像.
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5不同被测平面的光路布置
Fig.5Optical arrangement for different measuring surface
测量区域确定后, 需要对PIV系统标定, 以建立相机图像与实际物理区域的映射关系. 由于本实验是2D-PIV测量, 所以使用刻度尺进行标定. 考虑到圆柱形水池的放大作用, 将尺子放在注满水的待测水池中, 以模拟真实的测量条件进行标定.
2 流场分析
2.1 冲击距离的影响
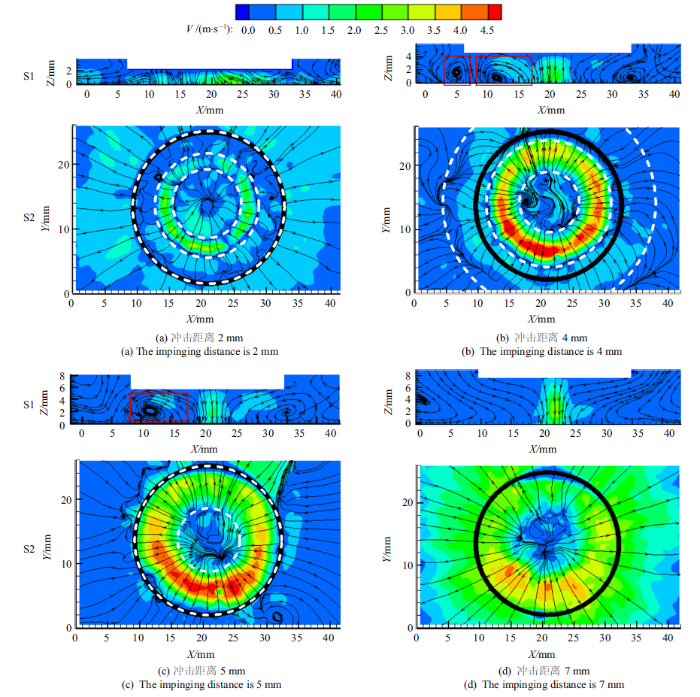
该部分取喷嘴流量为0.3 L/min, 着重分析冲击距离改变对射流间隙内流动涡系的影响. 图6为S1, S2测量平面的PIV流场测量结果. 其中, 黑色粗线示意射流棒端面边界; 白色虚线示意不同涡系的交界线或者流动分离线(separation line, SL).图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图60.3 L/min流量下不同距离速度场
Fig.6Velocity field when the flow rate is 0.3 L/min
如图6(a)所示, 当$H/d=1$时, 即绝对冲击距离为2 mm时, 由S2图中心流线形成的圆形边界可见, 射流还未发生明显扩散. 由于冲击间隙过小, S1测量面的有效测量域内不足以捕捉到完整的涡环, 但在S2测量面上可见一次涡环和二次涡环为两个同心圆环, 两个涡环对转, 即旋向相反. 二次涡环的边界基本与射流棒端面轮廓重合, 说明端面的约束作用使两个涡环都被严格约束在射流棒端面之内. 一次涡环的平均速度略大于二次涡环, 其原因是一次涡环的能量直接来自射流本身, 二次涡环的能量来自一次涡环的诱导, 涡环的形成与射流棒端壁的约束作用也有重大关联. 射流的诱导作用, 加之射流棒端面与下壁面的约束, 使流体在射流间隙中形成内旋且速度较大的一次涡环, 一次涡环强度较大, 继续诱导外围流体, 不足以卷入一次涡环的流体撞壁后分离, 产生了与一次涡环旋转方向相反的外旋二次涡环.
随着冲击距离的增大($H/d=2$), 即绝对冲击距离为4 mm时, 如图6(b), S1面中靠近内侧的方框线1为一次涡环, 靠近外侧的红色框线2为二次涡环. 在此冲击距离下S1和S2面中两个涡环都非常显著. 与图6(a)比较可知, 冲击距离增大后, 一次涡环尺度也在变大, 表现在一次涡外径几乎扩展到射流棒端面边界, 而二次涡环的大部分已经被挤出断面之外. 同时, 一次涡速度显著大于二次涡环, 相比于较小冲击距离, 这种速度差别更为显著. 形成这一现象的原因在于, 随着冲击距离进一步增大, 涡在射流间隙中有更充分的空间发展, 壁面约束作用减弱, 因摩擦造成的流体动能的耗散变小, 更大量的流体被卷吸, 导致了一次涡环的膨胀, 而一次涡环消耗了更多来自射流的动能, 加之二次涡环几乎被排挤至射流棒断面之外, 缺乏壁面的约束作用, 导致二次涡环的强度大幅减弱.
图6(c)为$H/d=2.5$时(绝对冲击距离5 mm)间隙内的速度分布, S1面中方框线内为一次涡环. 由S1面和S2面对照观察可知, 冲击距离继续增大后, 导致一次涡进一步膨胀, 其边界已经扩展至射流棒外端面, 即将间隙内的空间全部占据, 二次涡环被完全排挤到间隙之外, 同时在缺乏端面约束的情形下, 导致二次涡环不能形成. 随着冲击距离继续增大至$H/d=3.5$, 即绝对冲击距离为7 mm, 如图6(d)所示. 由S1和S2面测量结果对照观察可知, 虽然卷吸作用仍然存在, 但更大的冲击距离使一次涡失去了上下壁面的强力约束, 导致一次涡环也无法形成. 当冲击射流达到底板表面后, 速度滞止为零, 会在该处导致一个高压区. 在压力梯度、壁面黏性和外部腔室流体剪切力的共同作用下, 流体的运动方向将会发生改变, 形成贴壁流动的特征.
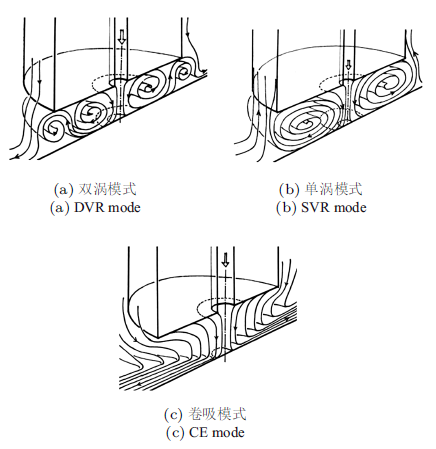
图7将相同流量下, 冲击距离发生变化时衍生的3种流动模式进行了刻画, 以反映冲击距离对近距离下冲击射流间隙内流动拓扑结构的影响. 在小冲击距离下, 间隙内流动主要是射流+对转双涡模式(double vortex ring mode, DVR mode), 如图7(a)所示, 但一次涡强度显著强于二次涡的强度; 当冲击距离增大时, 间隙内流动转变为射流+单涡模式(single vortex ring mode, SVR mode), 如图7(b)所示, 一次涡的膨胀将二次涡挤出射流间隙, 在缺乏壁面有效约束的情况下, 二次涡无法生成; 当冲击距离继续增大时, 间隙内流动转变为射流+卷吸流动模式(complete entrainment mode, CE mode), 如图7(c)所示, 一次涡环尺度继续增大直至超出射流棒端面边界, 最终一次涡破裂, 不能闭合, 流动模式转变为间隙上部从外部吸入流体, 下部流体向外发散射出.
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7间隙涡的三维拓扑结构
Fig.7Topology of vortex system in the clearance
2.2 雷诺数的影响
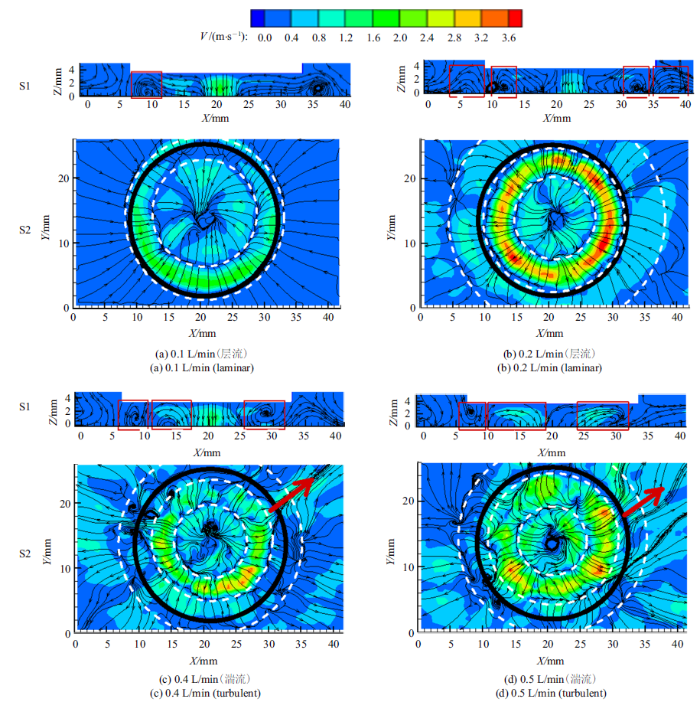
本文主要关注近距离冲击射流流场分布规律, 因此本部分以冲击距离3 mm ($H/d=1.5$)为例, 对不同喷嘴流量对射流间隙内流动涡系的影响进行讨论, 测量结果如图8所示. 通过计算其流动雷诺数可知, 流量范围涵盖了间隙内流体从层流($\leqslant 0.2$ L/min)到湍流($\geqslant 0.3$ L/min)的转变.图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8冲击距离3 mm ($H/d=1.5$)下速度场
Fig.8Velocity field when the impinging distance is 3 mm ($H/d=1.5$)
如图8(a)所示, 当流量为0.1 L/min ($Re=1056$)时, S1和S2面均可说明, 一次涡环边界基本与射流棒端面轮廓重合, 说明端面的约束作用使一次涡环被约束在射流棒端面之内. 当层流冲击距离逐渐增大时($H/d=1.5$), 射流所含的能量减小, 传递给一次涡环的能量不足以诱导二次涡环产生, 因此, 间隙内流动为单涡环模式. 当流量为0.2 L/min ($Re=2112$)时 (图8(b)), 由S1和S2面可见, 一次涡环直径接近端面直径, 说明一次涡环全部在射流棒端面以内. 二次涡环只有小部分处在间隙内, 大部分处于端面之外. 随着流量变大, 传递给一次涡环的能量增大, 因此可以诱导二次涡环产生, 间隙内流动为双涡环模式. 流量越大, 允许二次涡产生的距离的范围越大. 流量0.1 L/min, $H=3$ mm时, 二次涡消失; 流量0.2 L/min, $H=4$ mm时, 二次涡消失; 流量0.3 L/min, $H=5$ mm时, 二次涡才消失. 这是由于射流动能增大, 射流可以在更大距离时将能量传递至一次涡环及诱导二次涡环.
随着流量增大到0.4 L/min ($Re=4223$)时(图8(c)), 在S1和S2平面中, 均可见一次涡环直径小于射流棒端面边界. S2面测量结果表明, 虽然湍流中的二次涡环存在, 但较高的能量使流体从某个方向喷射流出, 因此二次涡环不完整. 当流量增大到0.5 L/min ($Re=5279$)时(图8(d)), 从S2平面可见, 随流量的增大一次涡环直径略增大, 但仍小于端面直径, 此时二次涡环存在且更不完整. 高速流出区的相邻位置由于速度方向交错产生了水平方向的旋涡. 其原因为, 在较高的冲击雷诺数下, 滞止区内冲击射流的动量交换增大, 高压区对壁面流动的影响加剧, 导致冲击射流形成的壁面流动紊乱度增大. 此时仅依靠涡环间的介质交换不能满足空间内的质量守恒, 因此借助水平方向上的旋涡完成质量交换. 高速流出的位置是随机的.
3 涡量分析
前文的分析表明, 射流间隙内的流动模式主要有3种: 双涡、单涡和完全卷吸3种模式. 为了比较不同涡系结构的能量传递和损失, 本节对这3种不同的流动模式进行涡量分析.根据湍流理论, 湍流除了存在强烈的速度脉动之外, 还存在涡旋运动, 是由大小不同的瞬时涡组成, 大涡传递能量, 小涡则通过剪切、摩擦耗散能量, 涡运动剧烈的地方也是能量传递和耗散剧烈的地方[28-29]. 湍流中涡的强弱以涡量表示, 涡量定义为瞬时速度矢量场的旋度, 其值的大小表征了涡旋转运动的强度, 二维平面上某点的涡量表达式为
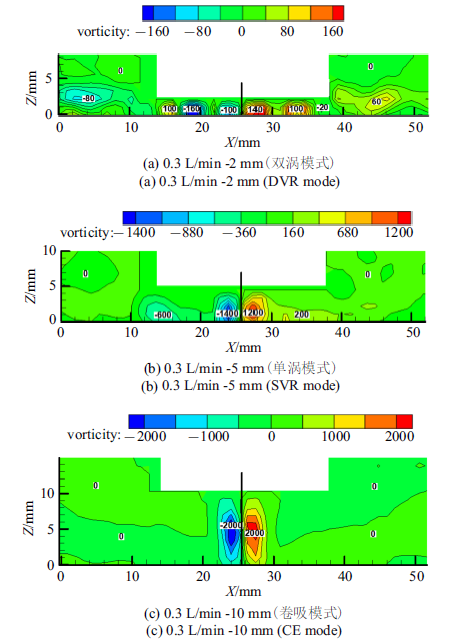
图9为包含350个瞬态涡量的平均涡量场图, 展示了流量为0.3 L/min时, 3种流动模式的涡量分布情况, 其中1与1$^*$为一次涡, 2与2$^*$为二次涡. 从射流的涡量时均分布可知, 在射流轴线上, 涡量的绝对值近似为0, 可以说明在射流在中线上是没有旋度的. 对于射流本身来说, 自射流轴线至射流两侧边界, 涡量的绝对值先增大后减小, 涡量值沿射流轴线近似对称分布. 射流与周围流体间存在较大的速度梯度, 正是这种横向速度梯度的存在才使得湍流涡旋转而产生较高的涡量, 因此射流与流体之间的剪切、掺混剧烈, 能量传递与耗散也较剧烈.
图9
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图9S1面涡量等值线图
Fig.9Vorticity contour of S1
图9(a)中为双涡环模式的涡量等值线图. 以轴线右侧为例, 一次涡涡量最大值约为100 s$^{-1}$, 二次涡涡量最大值约为$-$20 s$^{-1}$, 涡量值的正负说明一次涡环与二次涡环的旋向相反, 即为对转旋涡, 从数值上看, 一次涡涡量显著大于二次涡, 再次证明一次涡环的强度大于二次涡环强度. 图9(b)为单涡环模式的涡量等值线图, 射流本身的涡量最大值为1400 s$^{-1}$, 远大于图9(a)中的140 s$^{-1}$, 可见较大的冲击距离使射流得到发展. 此时一次涡环的涡量最大值约为600 s$^{-1}$, 相比于图双涡模式中一次涡的涡量值明显增加, 说明当射流具有更高能量时, 向一次涡传递的能量增加, 可以验证形成一次涡所需的能量是由射流传递的. 图9(c)中为卷吸模式的涡量等值线图. 射流本身的涡量最大值为2000 s$^{-1}$, 可见随着冲击距离的增大, 射流的发展更充分, 因此含有更多能量. 涡量的最大值约在射流中部, 在射流流至下壁面的过程中, 涡量逐渐减小最终接近零, 说明射流的能量主要集中在起始段.
对相同流量不同冲击距离时所产生的3种主要的流动模式的涡量分析表明, 在近距离射流中, 射流主体的湍流涡运动强度最大, 是能量耗散最剧烈的位置. 能量由射流主体传递至一次涡, 再由一次涡传递至二次涡, 最终在二次涡全部耗散. 但随着冲击距离的增大, 射流边界与周围流体剪切、掺混的程度增加, 当射流达到下壁面时能量耗散更剧烈, 由射流主体传递至一次涡的能量减少, 不足以生成二次涡.
4 POD分析
本征正交分解(POD)方法是一种高效的降阶方法, 可以通过重建低阶模态的速度场来确定测量域中的主要流场结构, 或通过重建高阶模态的速度场来分析微小的流场结构[30].本节以0.3 L/min工况为例, 对不同冲击距离下的实验结果进行POD分析. 对速度场进行POD分解获得的模态表征流场中各种尺度的空间结构. 计算得出, 以上冲击距离时, 前25阶模态分别具有95.16%, 91.27%, 84.39%, 84.36%, 88.47%和86.16%的能量, 可以表征流场中的主要空间结构. 由图10可以看出, 随着模态的增加, 能量衰减速度非常快, 意味着第一模态将与大规模流动结构相关. 选取前10阶模态进行深入分析, 来揭示占主导作用的大尺度结构的空间形态.
图10
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图10不同距离前25阶模态的能量分数曲线
Fig.10Energy fraction curves of the first 25 modes at different distances
表3为0.3 L/min工况下前10阶模态的能量分布, 表示各模态对整个射流场脉动能量的贡献率, 第一模态的能量比例高于其他模态. 由模态的能量分布可知, 同阶模态的能量分数和冲击距离间没有线性关系. 整体来看, 能量大多在较高阶模态时开始成对出现, 即某两阶模态能量分数大小基本相等, 例如在4 mm工况时, 5, 6阶模态能量分别为3.92%和3.60%. 由表3可知, 在相同流量下, 随着冲击距离的增大, 能量在更高阶开始配对.
Table 3
表3
表30.3 L/min不同距离前10阶模态的能量分数
Table 3
 |
新窗口打开|下载CSV
以2 mm工况为例, 由表3可知, 1, 2阶模态能量占比分别为24.76%和23.17%, 6, 7阶模态能量占比分别为4.63%和4.46%, 可见1, 2阶模态和6, 7阶模态产生能量配对的现象.
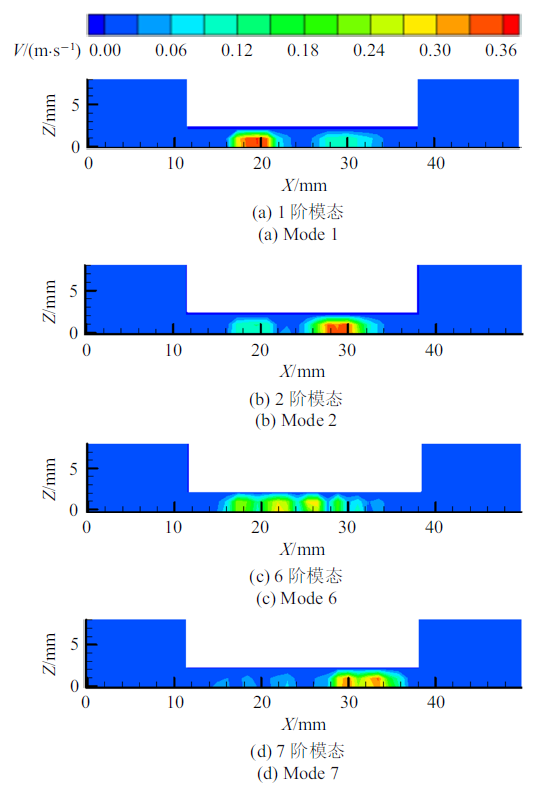
图11展示了1, 2, 6, 7模态的脉动速度分布. 如图11(a)和图11(b)所示, 在1, 2阶配对的模态中, 速度波动较大的位置沿射流中心对称分布, 与一次涡环出现的位置相同, 能量配对说明位置对称的涡对湍动能的贡献程度接近一致, 说明此时一次涡环具有较好的对称性. 图11(c)和图11(d)展示了6, 7阶配对的模态的脉动速度分布. 图11(c)出现了三个较明显的速度波动较大位置, 分别标记为0, 1, 2, 其中0位置对应射流主体, 位置1应为一次涡, 位置2为二次涡. 图11(d)与图11(c)类似, 位置1$^*$应为一次涡, 位置2$^*$应为二次涡, 能量配对说明此时二次涡环也具有较好的对称性. 在该工况下, 一次涡能量脉动在1阶模态时出现, 能量占比为24.76%, 二次涡能量脉动在6阶模态时出现, 能量占比为4.63%, 说明在整个流场中, 一次涡是占主导作用的大尺度结构, 二次涡是次要的结构, 能量占比也说明一次涡环的强度显著大于二次涡环的强度.
图11
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图110.3 L/min-2 mm (双涡模式)的POD模态
Fig.11POD modes of 0.3 L/min-2 mm (DVR mode)
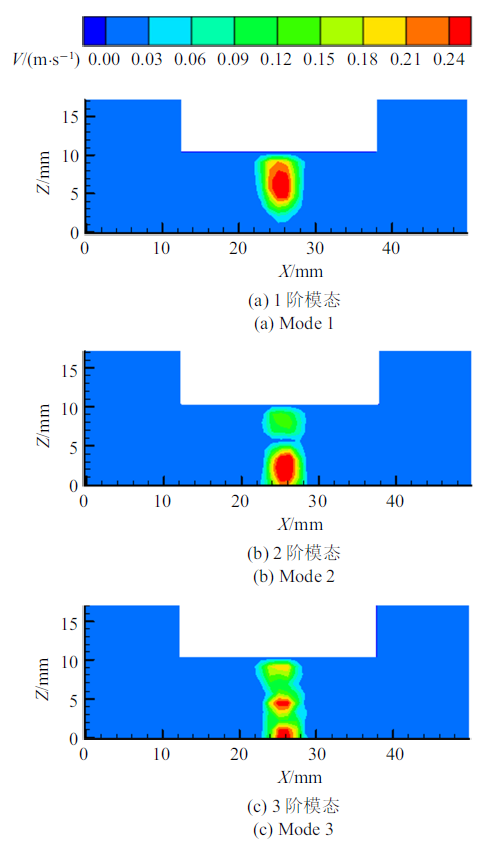
以10 mm工况为例, 前3阶模态, 其能量比例分别为29.99%, 17.24%和7.72%, 可见能量在前3阶快速衰减. 对射流的脉动速度分布进行说明, 见图12.
图12
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图120.3 L/min-10 mm (卷吸模式)POD特征模态
Fig.12POD mode of 0.3 L/min-10 mm (CE mode)
图12(a)中, 射流的脉动速度峰值出现在射流的中上段, 图12(b)中射流的速度波动上下分离, 峰值出现在射流的下段, 图12(c)中射流的速度波动在垂直方向逐渐分布均匀, 峰值不再集中. 说明射流的能量主要集中在上游, 能量随紊动扩散急剧衰减,
因此只有在较小的距离下, 射流才有足够的能量向一次涡传递, 揭示了大距离冲击下不能产生涡环的原因之一.
5 结论
本文运用PIV手段对圆柱形水池中射流近距离冲击平板的流场进行了直接测量, 考察了冲击距离和流量对间隙内涡系结构演化规律的影响. 通过流场、涡量及POD分析, 探究了射流间隙内的3种流动模式及其能量分布, 得到的主要结论如下:(1) 冲击距离和流量均会影响近距离射流冲击平板时的流场结构. 在近距离冲击射流中, 射流间隙内主要会形成3种流动形式, 分别为双涡环模式、单涡环模式和卷吸模式.
(2) 随着冲击距离的增加, 一、二次涡环的尺度增加, 同时逐渐远离射流中心, 实验结果表明失去端面约束是导致一次涡环和二次涡环依次消失的主要原因.
(3) 当$Re=1056$, $H/d=1$时为双涡模式, $H/d=1.5$时为单涡模式, $H/d\geqslant 2$时为卷吸模式; 当$Re=2112$, $H/d\leqslant 1.5$时为双涡模式, $H/d=2$时为单涡模式, $H/d\geqslant 2.5$时为卷吸模式; 当$Re=3167$, $H/d\leqslant 2$时为双涡模式, $H/d=2.5$时为单涡模式, $H/d\geqslant 3.5$时为卷吸模式; 当$Re=4223$和$Re=5279$, $H/d=1.5$和$H/d=2$时为双涡模式, $H/d=1$或$H/d\geqslant 2.5$时为卷吸模式. 其中, 在$H/d<3$的湍流工况中, 射流会冲破涡环, 以随机的方向高速出流.
(4) 涡量分析结果表明, 一次涡和二次涡旋转方向相反, 且一次涡强度显著大于二次涡强度. 能量由射流主体向一次涡环、二次涡环依次传递, 最终在二次涡全部耗散.
(5) POD模态产生能量配对的现象, 说明涡环具有对称性, 双涡模式前10阶模态表明, 一次涡是占主导作用的大尺度结构. 卷吸模式前3阶模态表明, 射流的能量主要集中在上游, 能量随紊动扩散急剧衰减.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]

Abstract
The instantaneous flow characteristics of circular orifice synthetic jet was experimentally studied by a phase-locked Particle Image Velocimetry (PIV) system. The instantaneous flowfields, including the forming, developing and breaking down of the vortex for the jet were clearly shown by the PIV experimental results. As the basis of the study of the instantaneous flow, 36 images were taken and phase-averaged for each condition. The PIV experiment was mainly focused on the time evolution of the vortex pairs formed in the push cycle, the saddle point existing in the suck cycle, the variation of the centerline velocity in the whole cycle and the cross-stream velocity profiles and their self-similarity. Finally, the orifice depth was changed from 1.5 mm to 2 mm and 3.5 mm in order to study the effect of different orifice depths on the flow structure, which shows that at all stream wise sections, the peak of the mass flux and momentum flux increases as the orifice depth increases. Furthermore, the nondimensional distance of the mass flux from the exit is the maximum, while the nondimensional distance of the centerline velocity peak from the exit is the minimum, and nondimensional distance of the momentum flux from the exit section is between them.[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
