 ,*,2), 王新萌*, 汪越胜*,??
,*,2), 王新萌*, 汪越胜*,??TUNABLE CONTROL AND FUNCTIONAL SWITCH OF TRANSMITTED ACOUSTIC WAVES BY AN ARCH-SHAPED METASURFACE1)
Chen Ali ,*,2), Wang Xinmeng*, Wang Yuesheng*,??
,*,2), Wang Xinmeng*, Wang Yuesheng*,??通讯作者: 2) 陈阿丽, 教授, 主要研究方向: 可调声波/弹性波超表面设计及机理, 纳米层状有序结构波动力学, 声子晶体中波的局部化. E-mail:alchen@bjtu.edu.cn
收稿日期:2020-12-30网络出版日期:2021-03-18
| 基金资助: |
Received:2020-12-30Online:2021-03-18
作者简介 About authors

摘要
基于“螺丝-螺母”的工作原理, 设计了可调的透射型三通道螺旋单元,通过调节螺丝的旋拧深度来改变声通道的长度, 从而实现对透射声波相位的调节.利用有限元方法计算了单元的透射波相位差和透射系数随频率和旋拧深度的变化规律.在平面广义Snell定律基础上推导了适用于圆弧形曲面的广义Snell定律.设计了圆弧形超表面, 包括弧状和圆环状两种, 实现了对透射声波波前的可调控制.根据所要实现的声学功能和给定的工作频率,利用单元的透射波相位差随旋拧深度的变化规律和圆弧形表面的广义Snell定律,确定超表面上所需的相位分布梯度及每个单元的旋拧深度,并同时考虑透射系数随旋拧深度的变化规律来对单胞旋拧深度进行适当的调整,以保证超表面具有较高的透射率.利用圆弧形超表面实现了宽频范围内声波的定向折射、波束分离和声束聚焦等声学功能的转换;利用圆环形超表面则实现了三向分波、波场螺旋化及源位置虚拟移动等声学功能的转换.同时针对上述功能进行了全波场的有限元数值模拟和相应的声学实验,实验结果与有限元模拟结果吻合良好, 验证了所设计超表面对声波波前调控的有效性.研究结果将为不规则非平面可调声学器件的设计提供理论指导.
关键词:
Abstract
A tunable transmitted three-tunnel helix unit cell is designed based on the working principle of the “screw-nut”. The length of the acoustic tunnel is changed by the screw-in depth of the screw, and then the phase of the transmitted waves can be tuned accordingly. The variations of the phase shift and transmittance of the unit cell with the screw-in depth and frequency are calculated by the finite element method. The generalized Snell's law of an flat surface is extended to an arc-shaped surface in this paper. The arch-shaped and toroidal metasurfaces are designed to regulate the wavefront of the transmitted acoustic wave. According to the presupposed acoustic function and the working frequency, the phase gradient of the metasurface and the screw-in depth of every unit can be determined by the generalized Snell's law of the arc-shaped surface and the variation of the phase shift of the unit cell with the screw-in depth. And the screw-in depth will be modified according to the variation of the transmittance of the unit cell in order to obtain the high transmission. The functional switch between the directional refraction, beam splitting and beam focusing for the arch-shaped metasurface is realized in a broadband frequency region. And the functional switch between the three-way splitting of wave beam, spiral wave generation and virtual movement of the source position is also realized for the toroidal metasurface. The full-field numerical simulations are performed by using the finite element method. And the experimental measurements are also carried out for both arch-shaped and toroidal metasurfaces. The experimental results have a good agreement with the numerical ones, which shows that the metasurfaces we designed are effective for the wavefront modulation of the transmitted acoustic waves. The study in this paper is relevant to the development of tunable irregular non-planar conformal acoustic devices.
Keywords:
PDF (22512KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
陈阿丽, 王新萌, 汪越胜. 圆弧形超表面对透射声波的可调控制与功能转换1). 力学学报[J], 2021, 53(3): 789-801 DOI:10.6052/0459-1879-20-456
Chen Ali, Wang Xinmeng, Wang Yuesheng.
引言
超构材料(包括声子晶体、超材料、超表面等)能够展现出许多超常的物理或力学特性,具有广阔的应用前景, 因而受到众多****的关注[1-5]. 其中,超表面是指具有亚波长子结构的二维超构材料,超表面的概念首先在光学领域提出并实现了对光波或电磁波的波前调控[6],随后扩展到声学领域[7-11]. 声学超表面使人们可以自如地操控声波,实现异常折反射、聚焦、波束自弯曲、幻象、隐身以及全息等声学功能.根据操控的对象不同, 声学超表面可分为反射型和透射型两种.超表面功能的实现主要依赖于其亚波长子结构, 即超表面单元. 根据单元形式的不同,声学超表面主要可分为空间折叠型(coiling-up space)、赫姆霍兹共振型(Helmholtzcoupling resonance)以及薄膜型(membrane) 3种类型.空间折叠型超表面通过改变声波在卷曲通道内的传播路径长度来实现相位的积累从而得到不同的相位偏移.Li等[7]设计了空间折叠型声学超表面,模拟了异常反射、声波聚焦以及波型转换等多种声学功能.****们也通过实验验证了此类超表面的有效性[12-16].赫姆霍兹共振型通常是由几个共振腔和一个声学通道所组成[17-20],利用共振原理来实现对相位的调控, 此类结构的透射率通常很高.通过此类结构也可以实现低频完美吸收[21-23]或宽频高效吸收[24].薄膜超表面的超薄特性使其在紧凑型的声学仪器上有着潜在的应用.Zhu等[25]利用时空调制的薄膜系统实现了声波的非互易传输;Ma等[26]通过在薄膜中心位置处附加质量块,设计了阻抗匹配的薄膜杂化共振型深亚波长声学超表面, 实现了完美的吸声特性.利用上述各种超表面已经实现了丰富的声学功能,但是目前的研究还存在一定的局限性, 比如超表面一旦成型不能更改,这使得超表面工作频率固定, 功能单一. 为此, 近来****们提出了可调超表面的概念,主要通过结构单元堆砌组合[27-35]、多场耦合[36-40]和单元自身可重构等[41-56]来实现超表面的可调性.单元堆砌组合方式可调超表面是通过有限个具有不同相位的单元进行积木式的排列进而实现可调特性.Xie等[27-28]利用两个具有相同透射率但是相位相差$\pi $的单元堆砌组合设计了声学编码超表面,实现了波束分裂、可调聚焦和非对称传输的功能;Zuo等[31-32]利用单元堆砌组合的方法构造了非对称编码声学超表面,实现了可切换的声学图像投射及声波的完美负反射.单元堆砌组合方式虽然可以在单元层面上通过结构重组实现对超表面的整体重构,但单元本身并不具有可调性, 故调节方式不够灵活.通过引入电场或磁场等外部激励则可实现单元的可调性,但通常集成系统比较复杂且制作成本较为昂贵.由自身结构可调节的单元设计而成的超表面, 则可成功解决上述问题.Chen等[41]在赫姆霍兹共振腔的基础上利用局部组件平移机制设计了可重构单元,实现了声波的定向折射、聚焦和源错觉等功能;Zhai等[42]通过改变单元旋转角度设计了声学超表面结构来调控反射声波的方向并实现了高$Q$值的谱分离;Wang等[43]同样利用旋转机制设计了环形的可调共振单元,实现了透射声波的聚焦功能;Song等[44]通过调节栅格结构中水的深度实现了单元的可重构并设计了多频率、三通道的声波回射器;Li等[47]通过改变梯度圆形孔洞中水的体积实现了单元的可重构特性,并对反射声波进行了三维调控, 实现了空间的定向反射和聚焦等功能.近来还基于螺丝-螺母工作原理设计了可调的螺旋单元,通过调节单元旋进深度来改变相位分布,宽频范围内实现了透射声波[48-49]和反射声波[50]的定向传输、聚焦、自弯曲等功能以及反射声波的全息成像[51]和声涡旋[52]等功能.
上面提到的研究大多涉及的是平直型超表面, 很少涉及可调的曲面超表面.曲面超表面可用来实现声波的地毯隐身和幻象等功能.Song等[53]基于液体填充机制的简单格栅结构制作了可调谐的二维弧形地毯式隐身斗篷;Zhou等[54]设计了弯曲弧形声学超表面结构, 通过自由旋转内部转子的角度,实现了可调谐的宽频地毯隐身效果; Li等[55]利用均匀波纹孔泵水调控反射单元,实现了可调谐的三维任意弯曲超表面上声波的地面幻象;Fan等[56]利用可调螺旋单元设计了弧形可重构的声学超表面,并利用全波模拟和实验测量展示了其宽频可调的地毯隐身和地面幻象功能.本文将基于可调的透射型螺旋单元, 设计圆弧形可调声学超表面,包括圆弧和圆环两种形式. 通过有限元模拟和实验,实现宽频范围内声波的定向折射、波束分离、声束聚焦、波场螺旋化及源位置虚拟移动等声学功能的转换,以期为圆弧形或不规则可调非平面声学器件的设计提供理论指导.
1 透射单元的可调性设计及机理
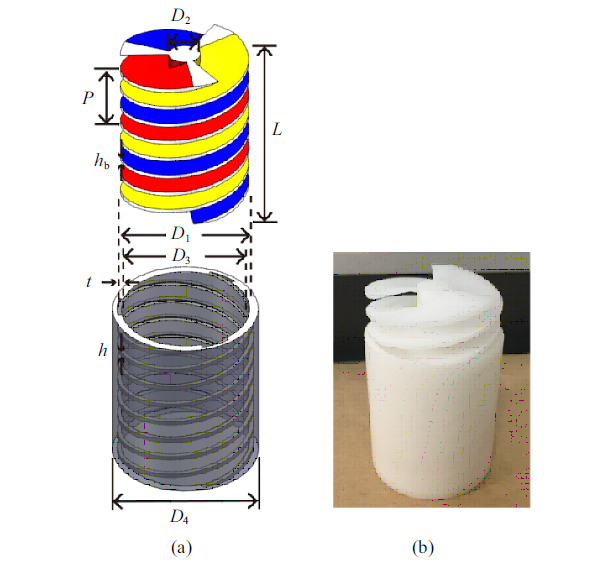
如图1(a)所示, 本文设计的可调单元由三螺旋通道的“螺丝-螺母”结构组成,其中“螺母”是具有内螺纹的圆筒结构, 如图1(a)中灰色部分所示;三螺旋的“螺丝”即螺旋结构是由3个围绕中心圆柱旋转的叶片构成的,图1(a)中红、黄、蓝3种颜色分别代表3个不同的矩形叶片.通过调节“螺丝”的旋拧深度可改变声通道的长度, 从而获得不同的透射波相位.图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1(a)三通道螺旋单元几何结构示意图; (b) 3D打印的三通道螺旋单元
Fig. 1(a) Schematic of the triple channel helical unit; (b) 3D-printed model
单元几何尺寸包括: 单元高度(即超表面厚度)$L$、圆筒内径$D_{3}$、圆筒外径$D_{4}$、“螺母”内螺纹槽的深度$t$、螺纹槽的宽度$h$、螺旋叶片的厚度$h_{b}=h$、螺旋体直径$D_{1}$、中心圆柱直径$D_{2}$和螺距$P$.与直接在超表面孔洞内壁加工螺纹[48-49]相比,这样的设计使旋拧操作变得简单, 可以提高旋拧的精度,并使单元具有更强的可调性和适应性.若螺旋体的几何参数如叶片厚度$h_{b}$、螺距$P$等发生改变,只需改变单元圆筒的相应参数, 而加工的超表面依旧适用. 图1(b)是由光敏树脂材料3D打印制成的三通道螺旋单元模型. 如无特殊说明,本文中选取的螺旋单元的几何尺寸参数分别为: $L=40$ mm, $D_{3}=30$ mm,$D_{4}=34$ mm, $t=1$ mm, $h=1$ mm, $h_{b}=1$ mm, $D_{1}=32$ mm, $D_{2}=8$ mm,$P=15$ mm.
超表面能否很好地实现特定的设计功能, 取决于单元能否提供$2\pi $范围内的相位改变, 对于透射型超表面在满足相位改变的同时还需要保证较高的透射效率.因此本小节将对单元的相位调节能力以及透射率进行有限元模拟计算.
图2(a)是利用SolidWorks构建的并导入到有限元软件ComsolMultiphysics中的声学通道模型. Comsol Multiphysics中选取压力声学模块,在左端部分区域$a$施加背景压力场作为激励, 计算时统一设定压力大小为1 Pa;激励产生的声波通过圆柱形声通道$b$和螺旋声通道$c$后到达圆柱形声通道$d$ (透射区域),在区域$d$中的某信号拾取点可以观察相位与透射系数的变化. 需要注意的是,此点的选择应与螺旋声通道$c$的出口保持一定的距离, 从而避免边界效应带来的影响,计算中选择轴线上距离$c$段出口处为60 mm的点$A$作为信号拾取点; $a$,$b$和$d$部分的长度分别为20 mm, 100 mm和80 mm.
图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2Comsol Multiphysics中螺旋单元构成的声学通道模型图(a)及网格划分图(b)
Fig. 2Acoustic channel formed by the helical unit-cell (a) and its mesh (b) establised in Comsol Multiphysics
边界条件设置如图2(b)所示. 光敏树脂材料相对于空气声波可以认为是刚性材料,故单元螺旋声通道$c$部分的边界可视为刚性边界, 即不考虑流固耦合的作用, 在ComsolMultiphysics中设置声学硬边界条件[57]
其中$\rho =1.21$ kg/m$^{3}$是空气的密度, $n$是边界的法线.根据文献[50], $b$和$d$两部分圆柱形波导的边界也可设置为声学硬边界条件;同时为了消除反射波的影响, 最右侧边界和最左侧边界设置为平面波辐射条件.图2(b)中也给出了有限元网格划分示意图, 包含约10万个自由划分的四面体单元,经验证满足收敛性要求.
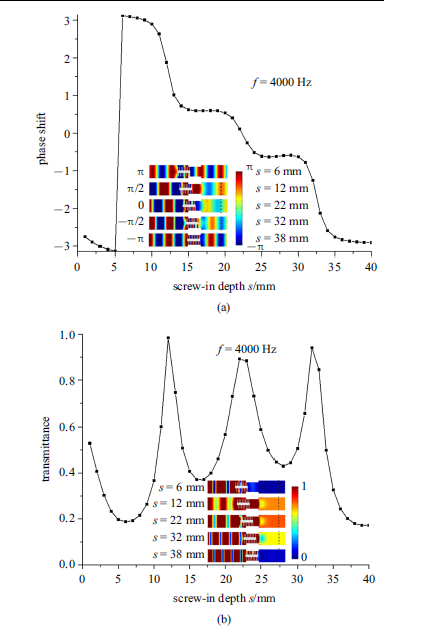
首先以频率4000 Hz为例来检验一下设计的单元是否有效. 图3给出了该频率下旋拧深度与相位的变化关系图3(a)以及旋拧深度与透射率的关系图3(b).图3内的插图分别为旋拧深度$s = 6$, 12, 22, 32和38 mm时$A$点的相位分布和透射场.由图3可以看出, 仅需通过调节单元的旋拧深度, 就可以在该频率下实现$2\pi $范围的相位调控, 透射率也随着旋拧深度的变化而改变.这说明本工作设计的螺旋单元对于透射声波的相位调节是有效的,并在某些旋拧深度具有较高的透射率.
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3工作频率$f=4000$ Hz时, 单元的相位(a)和透射率(b)随旋拧深度的变化图
Fig. 3Phase shift (a) and the transmittance (b) for the unit cells with different screw-in depths at $f = 4000$Hz
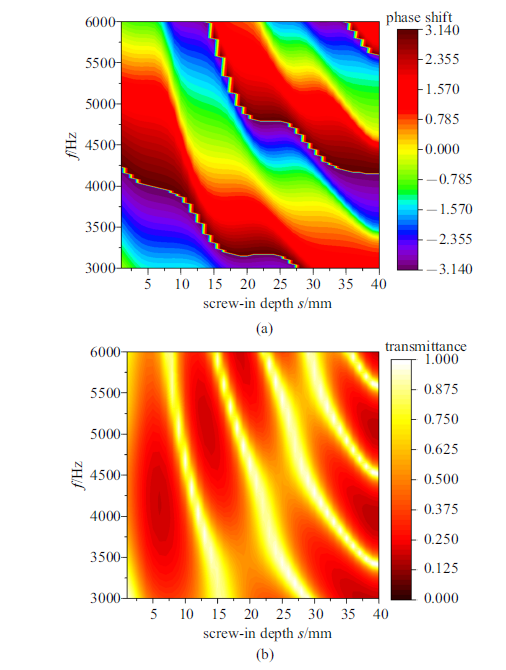
图4(a)和图4(b)分别给出了相位差和透射率随频率与旋拧深度的变化规律,即“频率-旋拧深度-相位差”云图和“频率-旋拧深度-透射率”云图.工作频率范围为3000$\sim$6000 Hz, 对应的波长变化范围为57$\sim$114 mm. 可以看出,单元旋拧深度的调节可以在这一较宽的频率范围内使相位产生2$\pi $范围的改变, 并且可以出现较高的透射率.
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4螺旋单元相位差(a)和透射率(b)随工作频率和旋拧深度的变化云图
Fig. 4Nephograms of the phase shift (a) and transmittance (b) for the unit cell varying with the screw-in depth and frequency
2 圆弧形声学超表面的设计
所设计的圆弧形超表面包括弧形和圆环形两种,结构示意图和用光敏树脂3D打印而成的模型如图5所示. 在圆弧或圆环上设计圆形孔洞,孔洞的直径与三通道螺旋单元的圆筒外径$D_{4} $相等, 然后将单元整体置入孔洞中,这样就形成了螺旋形的声通道. 通道长度沿超表面呈梯度分布,通过调节每个螺旋结构的旋拧深度, 可以改变分布梯度, 进而实现不同的声学功能.实验和数值仿真中取超表面外半径$R=245$ mm、内半径$r=205$ mm、厚40 mm, 每10$^\circ$分布一个单元; 弧形超表面的圆心角为120$^\circ$, 一共有13个单元;圆环形超表面一共有36个单元.图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5弧形和圆环形声学超表面结构示意图及3D打印试件
Fig. 5Schematic diagram and the 3D printed models of the arc-shaped and toroidal acoustic metasurface
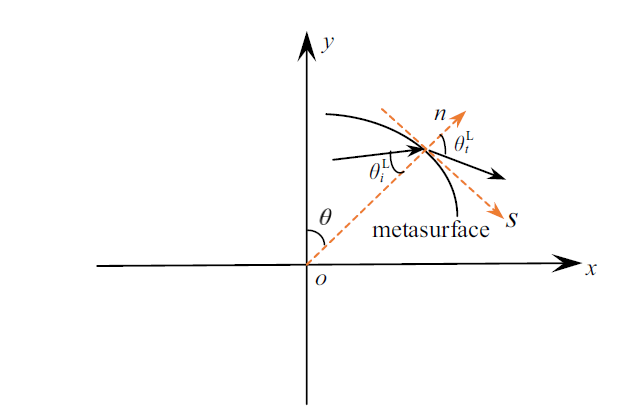
设计的圆弧形超表面两侧均为空气介质, 如图6所示, 在局部坐标系($s$-$n)$中广义Snell定理可以简化为[56]
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6曲面可调超表面的广义Snell 定律示意图
Fig. 6Schematic diagram of the generalized Snell's law of the curved metasurface
其中$\varphi (s)$是超表面提供的相位分布函数, $\theta_{t}^{L} $为折射角, $\lambda ={{c_{0} }/f}$为声波波长, $c_{0} =342$ m/s为空气中的声速. 对于圆弧形超表面, ${d}s=R{d}\theta $, 其中$R$为圆弧的半径, $\theta $为圆弧半径与竖直方向$y$轴的夹角. 式(2)可写为
当超表面实现设定的功能时, 入射角$\theta_{i}^{L} $和折射角$\theta_{t}^{L}$均可以表示为$\theta $的函数, 式(3)两边同时关于$\theta $积分, 即可得到所需的相位分布函数
将柱面波声源置于圆弧超表面中心$O$处, 故对于每个单元来说入射角$\theta_{i}^{L} =0$, 式(4)可以简化为
后续根据单元的分布, 只需要将式(5)离散化即可确定每一个单元所需要的相位, 依据相位差云图就可以确定出每个单元所需要旋拧的深度,最后应结合透射率云图进行适当的选择以获得较高的透射率.
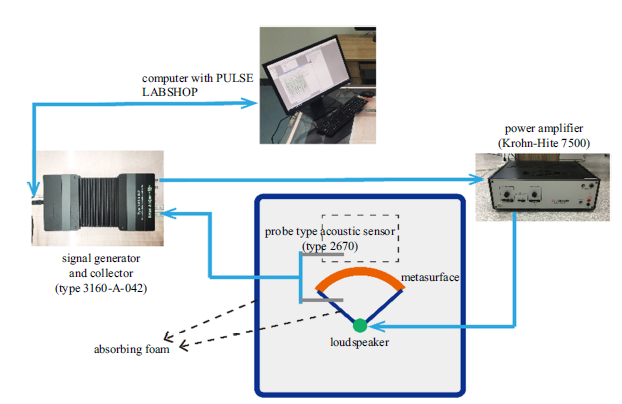
为了验证超表面的有效性, 本文在利用有限元进行全场计算模拟的同时还利用Bruel&Kjaer公司的声学测试设备进行了相应的声学实验.图7为实验流程图, 实验平台如图8(a)和图8(d)所示. 将超表面试件放在两块1.5 m$\times$1.5 m的透明有机玻璃板之间,两块有机玻璃板相互平行形成了一个波导结构. 平台四周以及沿弧形超表面半径处的位置放置总厚度为100 mm的尖劈状吸声棉(图7中深蓝色区域, 其中尖劈部分厚度为80 mm)来抑制声波的反射. 声信号由信号发生/接收器 (Type3160-A-042) 产生, 经功率放大器(Krohn-Hite 7500)放大, 最后由包在盒子中的声源喇叭(图8(c))发出. 声波经过超表面后被超表面调控,通过探针式声学传感器(Type 2670)对透射声场进行逐点扫描测量. 若无特别说明, 实验中的逐点测量间隔为1 cm. 探针传感器与信号发生/接收器相连, 最后由操作计算机和配套的软件(Computer with PULSE LABSHOP)对采集到的声压信号进行分析即可得到测量区域中各点的相位和幅值信息.
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7实验流程图
Fig. 7Flow chart of the experiment for the acoustic metasurface
图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8实验平台(a)和(d), 探针式声学传感器(b)和声源喇叭(c)
Fig. 8Photograph of experimental platform for the acoustic metasurface(a) and (d), the enlarged part is the probe type acoustic sensor (b) and theloudspeaker (c)
3 超表面多功能转换
设计的超表面对声波的调节非常灵活, 如工作频率或设定功能发生改变,不需重新制作超表面整体结构, 只需通过调整单元的旋进深度即可实现不同工作频率和不同功能之间的转换.针对弧形超表面, 实现了声波的定向折射、波束聚焦和波束分离功能之间的转换.在弧形超表面的研究基础之上, 利用圆环形超表面实现了三向分波、波场螺旋化和源位置虚拟移动等声学功能转换.并利用全场数值模拟和实验测试验证了这些功能.3.1 弧形超表面
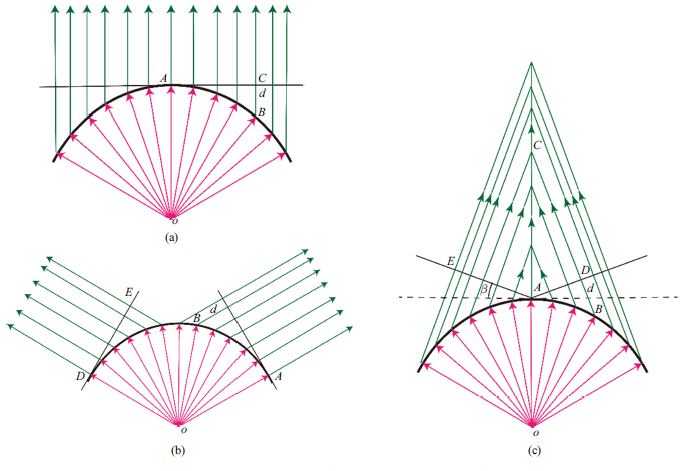
超表面的相位分布可以通过式(5)积分来确定, 也可以依据要实现的具体声学功能给出更简便直接的计算方式.弧形超表面实现声波定向折射、波束分离和波束聚焦功能的原理如图9所示, 图9中红色线条代表从线源$O$发出的柱面波波线,声波透过弧形超表面(黑色弧形粗线条)后将改变传播方向, 按绿色线条方向射出. 根据同一波阵面上相位相等, 可得图9
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图9定向折射(a)、波束分离(b)和波束聚焦(c)原理示意图
Fig. 9Schematic diagram of the directional refraction (a), beam splitting (b) and beam focusing (c)
其中$d$为任一单元相对于初始单元的声波传播路程差, $\varphi_{0}$为初始单元处的相位. 对于定向折射功能取$\varphi_{0} =0$,对波束分离和声束聚焦功能取$\varphi_{0} =1.50$. 之后只要依据不同的功能确定出声波传播路程差$d$即可确定超表面的相位分布.
对于弧形超表面, 考虑定向折射功能波形的特点和几何因素, 选择$A$处的单元为初始单元, 则对任意位置处的某单元$B$, 由图9(a)可得$d=R-R\cos \theta $.
波束分离功能可以使声波能量分流, 对于设计新型的分流器、分波器等具有重要的意义. 假设两束声波的分离角度为$\gamma $, 由图9(b)可以求出, 对应单元$B$有$d=R-R\cos(\gamma /2-\theta )$. 后面设计的两束声波分离角度$\gamma =120^{\circ}$, 正好是超表面的中心角.
弧形超表面还可以实现声束聚焦功能, 如产生贝塞尔声束[9]. 贝塞尔声束在传播过程中具有波束能量不易发散和抗干扰性强等特点.并且在比较长的直线区域内, 都可以保持这些特性, 因此具有极大的应用前景. 与分波原理不同, 如图9(c)所示, 为了达到波束聚焦的效果,透过超表面的两束波需以相同的偏转角度(设为$\beta )$向中心线$OC$偏转. 由图9(c)可以求出, 对应单元$B$有
$\begin{eqnarray*} d=\frac{R}{\sin \beta }\lt[\sin \theta -\sin (\theta +\beta )+\frac{1}{2}\sin 2\beta] \end{eqnarray*}$
偏转角度$\beta $不同则聚焦的位置及聚焦形成的波束长度也不同, 后续计算中设定$\beta =20^{\circ }$.
依据所要实现的不同声学功能, 将上述路程差$d$代入式(6)即可计算出每个单元所需的相位,从而可得到每个单元的旋拧深度. 然后利用Solidworks进行声学通道的建模并将模型导入有限元软件ComsolMultiphysics中进行数值模拟. 图10为包含有限元网格的扇形声场模型,包含约400万个自由划分的四面体单元. 为了保证数值计算的精度和结果的收敛,包含螺旋结构的灰色区域网格较密集, 厚度方向划分为10层;同时为了兼顾总体计算量, 蓝色的声波区域网格较稀疏, 厚度方向为4层.另外需要注意疏密网格之间的缓慢过渡. 选取压力声学模块,在过中心并沿超表面厚度方向的位置处设置体积流量为1 m$^{2}$/s的线源作为激励,线源长度与超表面的厚度相等; 边界条件与单元模拟计算时类似:在四周为无反射边界; 声学通道上下边界在实验中与两块玻璃板相接触,故此上下边界设置为声学硬边界.
图10
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图10包含有限元网格的弧形超表面的扇形声场模型
Fig. 10Schematic diagram of the fanshaped acoustic field with meshes of the arch-shaped metasurface
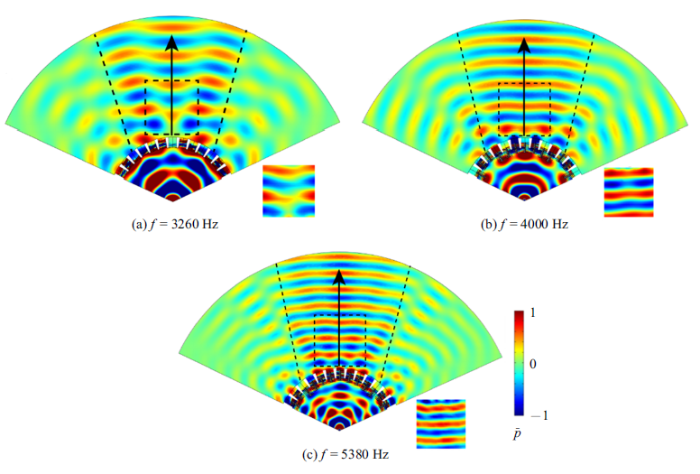
图11(a)$\sim \!$图11(c)分别给出了频率为3260 Hz, 4000 Hz和5380 Hz时,利用有限元模拟和实验测试得到的归一化声压场$\bar{{p}}={p/{p_{0} }}$的分布,其中$p_{0}$为声源处的声压值, 图11中黑色箭头为透射波的传播方向.实验逐点测量的(虚线方框)区域大小为20 cm$\times$20 cm.对比有限元软件的计算结果和实验结果可以看出, 不同频率的声波在经过超表面后,的确沿着设计的方向传播, 实现了定向折射的功能, 同时也将柱面波转化成了平面波.实验很好地验证了理论计算和有限元模拟的结果, 证实了设计的弧形超表面是有效的.同时也可以看到模拟图中两条虚线所划定的范围内定向效果良好, 两侧的效果较差,这可能是两侧波线角度改变过大造成的.
图11
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图11不同工作频率下超表面定向折射功能的有限元模拟和实验结果
Fig. 11Results of the finite element simulations and experiments for the directional propagation function under different working frequencies
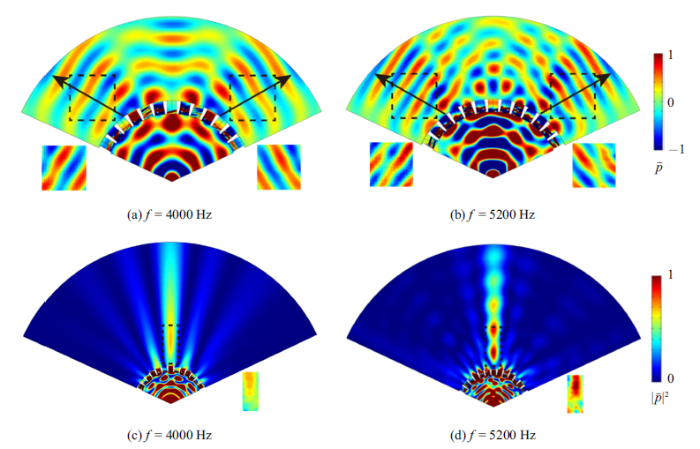
图12给出了不同工作频率下超表面实现波束分离功能(图12(a)和图12(b))和声束聚焦功能(图12(c)和图12(d))的有限元模拟和实验测量结果,其中对于声束聚焦功能给出的是无量纲声场能量$\left| {\bar{{p}}} \right|^{2}=\left| {{p/{p_{0} }}} \right|^{2}$的分布.根据不同功能的需要, 逐点测量的区域大小分别为14 cm$\times$14 cm和10 cm$\times$24 cm,如图12中虚线框所示. 可以看出设计的超表面很好地实现了上述两种功能. 但对于波束分离功能来说, 透射场中部区域因为两列波的叠加而有泄漏,这是由高阶寄生散射[58]引起的, 需要对超表面进行进一步的优化设计, 但这对可调超表面来说非常困难.
图12
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图12不同工作频率下超表面波束分离 (a), (b)和波束聚焦 (c), (d)功能的有限元模拟和实验结果
Fig. 12Results of the finite element simulations and experiments, for the beam splitting (a), (b) and beam focusing (c), (d) functions under different working frequencies
3.2 圆环形超表面
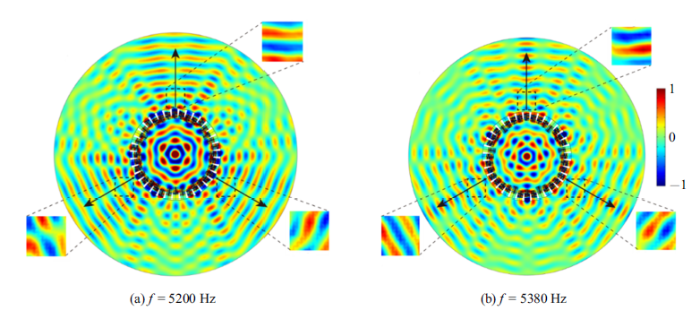
在弧形超表面定向折射功能的基础上,将定向折射的相位分布经旋转对称操作便可利用圆环形超表面实现三向分波的功能.图13(a)和图13(b)分别给出了工作频率为5200 Hz和5380 Hz时,圆环形超表面三向分波功能的有限元模拟和实验结果. 逐点测量的区域如虚线框所示,大小为10 cm$\times$10 cm.图13中给出了归一化声压场$\bar{{p}}={p/{p_{0} }}$的分布,由结果可以看出, 超表面调控声波按照设计的3个方向传播.但从有限元模拟结果也可以看出, 两个方向之间过渡的区域效果较差,这依旧是由高阶寄生散射引起的, 之后的研究中还需进一步对此进行优化.图13
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图13工作频率$f =5200$ Hz (a) and 5380 Hz (b)时, 超表面三向分波功能的有限元模拟和实验结果
Fig. 13Results of the finite element simulations and experiments for the three-way splitting function in case of $f = 5200$ Hz (a) and 5380 Hz (b)
利用圆环形超表面可以使一个简单的声源在远场区域被观察者探测到时,变成另一个任意复杂的声源, 即利用超表面实现源错觉功能.源错觉功能在建筑声学、生物医学工程、军事等领域有着潜在的应用前景.与平直形或圆弧形超表面的反常折射相似,圆环型超表面可以通过控制沿表面的相位分布来实现不同柱面波之间的转换,从而产生新奇的源错觉效果.这里主要介绍波场螺旋化和源位置虚拟移动这两种源错觉效果.
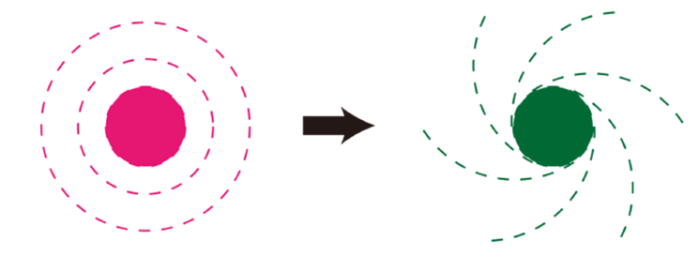
螺旋波场的产生仍然是基于广义Snell定理, 如图14所示.设计好的超表面能够将轨道角动量引入到具有完美轴对称几何形状的声学系统中,这里超表面相位分布与角度具有如下关系[41,59]
图14
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图14螺旋波产生示意图
Fig. 14Schematic diagram of spiral wave generation
其中$L$为额外的角动量, $\theta $为方位角, $\varphi_{0} $为初始相位, 计算中取$L=6$, $\varphi_{0} =-0.2$. 值得注意的是,螺旋波的分支数等于附加角动量$L$, 波经历相变$2\pi L$完成一周的循环.
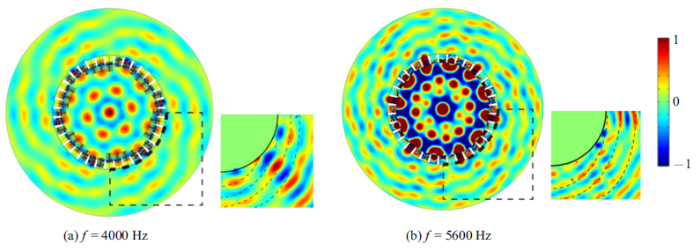
图15给出了声频率为4000 Hz和5600 Hz时, 圆环形超表面产生螺旋波场的有限元模拟和实验结果,实验逐点测量的区域如虚线框所示, 大小为40 cm$\times$40 cm.可以看出实验结果与模拟结果相吻合, 均显示柱面波被转换成均匀分布的6支螺旋波,所有分支都集中在起始线源, 验证了所设计声学超表面产生螺旋波场的源错觉功能.
图15
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图15声频率为4000 Hz和5600 Hz时, 波场螺旋化功能($L=6$)的有限元模拟和实验结果
Fig. 15Results of finite element simulations and experiments for the function of spiral wave generation ($L=6$) in case of $f = 4000$ Hz (a) and 5600 Hz (b)
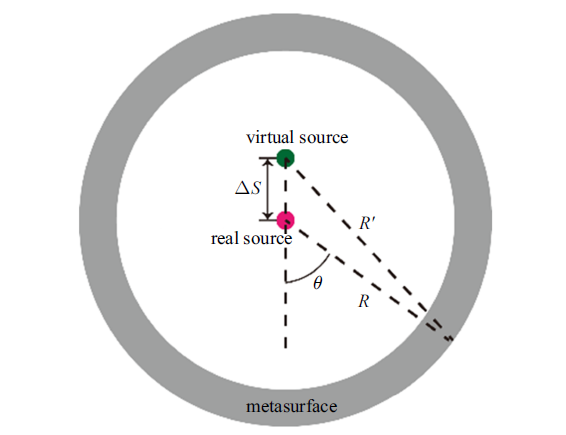
源位置虚拟移动的原理如图16所示, 红色圆点代表真实声源, 绿色圆点代表虚拟声源,即声波经过超表面后, 外部观察者探测到的声波是从虚拟源发出的.也就是说超表面隐藏了真实声源的位置, 并在距离真实声源$\Delta S$处生成了一个虚拟的声源, 因此实现了源位置的虚拟移动功能.
图16
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图16源位置虚拟移动原理示意图
Fig. 16Schematic diagram of virtual movement the source position
通过调节超表面单元的旋拧深度, 可以在一定范围内自由调节虚拟源的位置,从而产生所需的源位移错觉效果. 这里我们设计虚拟的源位于真实源上侧$\Delta S$处, 即真实源从原点(0, 0)处转移到了虚拟的(0, $\Delta S$)处,则超表面离散单元所需相位可由下述公式给出[41,59]
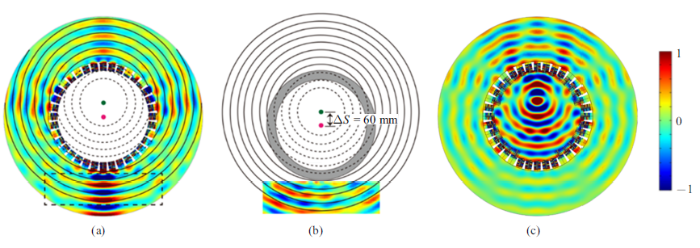
其中${R}'\!=\!\sqrt {(R\cos \theta +\Delta S)^{2}+(R\sin \theta )^{2}} $, 计算中取$\varphi_{0}\!=\!0$.首先以$\Delta S=60$ mm为例, 即源移动距离约为超表面半径的24.5%,来验证源位置虚拟移动的效果. 频率$f=5200$ Hz时有限元模拟和实验测量结果分别如图17(a)和图17(b)所示,实验中逐点测量的区域(虚线框)大小为53 cm$\times$14 cm.由图17(b)中的波面引导线可以看出, 位于原点处的线源发出的波经过超表面后,在超表面外侧观察时, 波似乎是从设计的虚拟声源处发出的.可见本文所设计的声学超表面可以实现声源虚拟移动的功能. 最后,保持工作频率和各单元的旋拧深度不变, 将声源放置在虚拟声源所在的位置(0,60 mm)处, 其声场分布结果如图17(c)所示. 从超表面的外部声场可以直观地看到,此时声波可以看成是从超表面圆心处发出的. 上述两种现象是两种相反的情况,均可证明本文的圆环形超表面可以实现源位置虚拟移动的功能.
图17
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图17工作频率$f=5200$ Hz时, 源位置虚拟移动功能($\Delta S=60$ mm)的有限元模拟(a)和实验(b)结果; 图(c)为声源位置在(0,60 mm)处的声场分布
Fig. 17Results of FEM simulation (a) and experiment (b) for the function of virtual movement of the source position ($\Delta S=60$ mm) in case of $f= 5200$ Hz; (c) is the acoustic field with the source located at (0, 60 mm)
4 结论
基于螺丝-螺母工作原理设计了可调的三通道螺旋单元,验证了单元对透射声波相位和幅值的可调节性. 推导了圆弧形表面的广义Snell定律,设计了圆弧形超表面, 实现了声波定向折射、波束分离、波束聚焦的功能转换;设计了圆环形超表面实现了三向分波功能以及波场螺旋化和源位置虚拟移动等源错觉功能之间的转换.同时对上述功能进行了相应的实验测量, 数值模拟结果和实验结果吻合,验证了所设计超表面的有效性. 另外, 环形超表面表现出来的源错觉功能,可以自由地操纵一个简单声源的辐射模式,使它在超表面外侧看起来像另一个任意复杂的声源或者造成源位置改变的假象等等.这些源错觉功能可以很好地保护或隐藏源的信息,在先进信号调制和军事作战方面均有潜在的应用价值.最后需要指出本文设计的超表面在某些情况下部分区域会出现透射率较低的情况(如图17(c)中的下半部分),这与黏性引起的损耗或文献[24]中提到的多单元耦合时的能量损耗机理不同,是由Fabry-Pérot共振效应所造成的.该效应会导致本文设计的单元对应某些频率和旋拧深度值会出现透射率较低的情况[48],因此当设计超表面时, 在保证相位差满足要求的条件下,应结合透射系数变化云图选择透射率较高的旋拧深度. 但在某些复杂的情况下,所需的相位差和高透射率不能同时满足, 而首先要满足所需的相位差分布,所以此时可能无法保证超表面每个单元都具有较高的透射率.该问题的解决也许需要借助优化方法来实现, 这将是一个具有挑战性的课题,值得后续进行深入研究.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
DOIURL

目前对于声学超材料的传输特性分析和优化大多是基于确定的数值和确定的模型,然而在实际工程和结构设计中存在大量材料自身特性和几何物理参数的不确定性.如果忽略这些不确定变量对声学超材料传输特性分析和优化过程的影响,得到的结果可能不正确.针对这一现状,拟将切比雪夫区间模型引入多层穿孔板超材料,提出多层穿孔板超材料声学透射率的区间切比雪夫展开——蒙特卡洛模拟法(interval Chebyshev expansionMonte Carlo simulation method,ICE-MCSM).该方法采用截断切比雪夫多项式近似拟合多层穿孔板超材料的声学透射率响应曲线,构造声学透射率响应曲线的切比雪夫代理模型;然后采用蒙特卡洛模拟法(Monte Carlosimulation method,MCSM)随机生成一定数量的不确定区间变量的样本数据点,并将生成的不确定区间变量样本数据点代入切比雪夫代理模型,预测单个不确定区间变量和多个不确定区间变量条件下的多层穿孔板超材料声学透射率区间的上界和下界.数值分析结果表明,ICE-MCSM预测的声学透射率变化区间的上界和下界与直接蒙特卡洛法(direct Monte Carlo simulation method,DMCSM)预测的声学透射率上界和下界的结果非常接近.与DMCSM相比,ICE-MCSM具有更高的计算效率.因此,ICE-MCSM可有效且高效地分析不确定区间变量条件下多层穿孔板超材料声学透射率传输特性,具有良好的工程应用前景.
[本文引用: 1]
URLPMID [本文引用: 1]
DOIURLPMID [本文引用: 2]

The introduction of metasurfaces has renewed the Snell's law and opened up new degrees of freedom to tailor the optical wavefront at will. Here, we theoretically demonstrate that the generalized Snell's law can be achieved for reflected acoustic waves based on ultrathin planar acoustic metasurfaces. The metasurfaces are constructed with eight units of a solid structure to provide discrete phase shifts covering the full 2pi span with steps of pi/4 by coiling up the space. By careful selection of the phase profiles in the transverse direction of the metasurfaces, some fascinating wavefront engineering phenomena are demonstrated, such as anomalous reflections, conversion of propagating waves into surface waves, planar aberration-free lens and nondiffracting Bessel beam generated by planar acoustic axicon. Our results could open up a new avenue for acoustic wavefront engineering and manipulations.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
URLPMID
[本文引用: 1]
[本文引用: 1]
DOIURLPMID

We designed a gradient acoustic metasurface to manipulate acoustic wavefront freely. The broad bandwidth and high efficiency transmission are achieved by the acoustic metasurface which is constructed with a series of unit cells to provide desired discrete acoustic velocity distribution. Each unit cell is composed of a decorated metal plate with four periodically arrayed Helmholtz resonators (HRs) and a single slit. The design employs a gradient velocity to redirect refracted wave and the impedance matching between the metasurface and the background medium can be realized by adjusting the slit width of unit cell. The theoretical and numerical results show that some excellent wavefront manipulations are demonstrated by anomalous refraction, non-diffracting Bessel beam, sub-wavelength flat focusing, and effective tunable acoustic negative refraction. Our designed structure may offer potential applications for the imaging system, beam steering and acoustic lens.
DOIURLPMID

This letter analytically and numerically examines sound transmission through a metasurface of hybrid resonances in the presence of thermoviscous dissipation. The metasurface unit of a subwavelength thickness consists of a slit and series of sided resonators embedded in air. Both wall friction and thermoviscous diffusivity in the unit are taken into account. The results reveal that the dissipation has a weak influence on phases even when there is a large loss. The dissipation reduces the transmission by 28% when the thermoviscous boundary layer thickness is only around 2.3% of the slit width. Optimal designs for minimal dissipation are addressed.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
DOIURLPMID [本文引用: 1]

An impedance-matched surface has the property that an incident wave generates no reflection. Here we demonstrate that by using a simple construction, an acoustically reflecting surface can acquire hybrid resonances and becomes impedance-matched to airborne sound at tunable frequencies, such that no reflection is generated. Each resonant cell of the metasurface is deep-subwavelength in all its spatial dimensions, with its thickness less than the peak absorption wavelength by two orders of magnitude. As there can be no transmission, the impedance-matched acoustic wave is hence either completely absorbed at one or multiple frequencies, or converted into other form(s) of energy, such as an electrical current. A high acoustic-electrical energy conversion efficiency of 23% is achieved.
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
URLPMID
DOIURLPMID

A reverberating environment is a common complex medium for airborne sound, with familiar examples such as music halls and lecture theaters. The complexity of reverberating sound fields has hindered their meaningful control. Here, by combining acoustic metasurface and adaptive wavefield shaping, we demonstrate the versatile control of reverberating sound fields in a room. This is achieved through the design and the realization of a binary phase-modulating spatial sound modulator that is based on an actively reconfigurable acoustic metasurface. We demonstrate useful functionalities including the creation of quiet zones and hotspots in a typical reverberating environment.
URLPMID
[本文引用: 1]
[本文引用: 4]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
URLPMID [本文引用: 1]
[本文引用: 3]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
URLPMID [本文引用: 2]
