司震, 钱霙婧
, 2) , 杨晓东, 张伟北京工业大学材料与制造学部, 机械结构非线性振动与强度北京市重点实验室, 北京 100124
HOVERING ORBITS DESIGN FOR PERTURBED ASTEROIDS WITH PARAMETRIC EXCITATION RESONANCE 1) Si Zhen, Qian Yingjing
, 2) , Yang Xiaodong, Zhang WeiBeijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, Faculty of Materials and Manufacturing, Beijing University of Technology, Beijing 100124, China
通讯作者: 2) 钱霙婧, 副教授, 主要研究方向: 探测器轨道动力学、非线性动力学. E-mail:
candiceqyj@163.com 收稿日期: 2020-04-30
接受日期: 2020-07-9
网络出版日期: 2020-11-18
基金资助: 1) 国家自然科学基金面上项目 .11772009
Received: 2020-04-30
Accepted: 2020-07-9
Online: 2020-11-18
作者简介 About authors
摘要 本文将太阳引力摄动视为受摄不规则小行星系统的组成部分,借鉴非线性振动理论中参数激励共振的概念,创新性地设计了不规则小行星平衡点附近稳定的悬停观测轨道.为了同时考虑不规则小行星引力和太阳引力, 本文采用受摄粒杆模型描述系统.通过对未扰系统平衡点以及固有频率的分析, 给出系统存在参激共振轨道的条件.再以第二类参激主共振和1:3内共振为例,采用多尺度方法求得参数激励共振轨道的稳态解, 并对稳态解的稳定性进行判断.通过受摄小行星系统的幅频响应曲线以及力频响应曲线分析了系统的非线性特性以及参数激励效应.此外, 对内共振引起的长短周期能量转移现象进行了分析.本文的研究成果可以拓展现有小行星系统周期轨道族设计方法.
关键词： 小行星 ;
粒杆模型 ;
悬停轨道 ;
参数激励共振 ;
非线性动力学 Abstract In this paper, the solar gravitational perturbation is considered as a part of the asteroid system instead of treating it as perturbation. Based on the concept of parametric excitation resonance in nonlinear vibration theory, a novel stable parametric resonance orbit near the equilibrium point is designed. In order to consider the gravitational field of an irregular asteroid and the gravitational force of the Sun, the perturbed particle-linkage model is adopted. By analyzing the equilibrium points and the natural frequencies of the unperturbed system, the preconditions that the parametric resonance periodic orbit can exist are given. Taking the second principal resonance and 1:3 internal resonance as examples, the steady-state solutions of parametric resonance orbit are obtained by using multi-scale method. The stability of the steady-state solution is determined. The nonlinear dynamic behaviors of the system are analyzed by the amplitude-frequency response curve. In addition, parametric excitation effect caused by solar gravitational perturbation and the energy transfer phenomenon between long and short periodic motions are analyzed. The proposed method of this paper can expand the existing periodic orbit families near asteroids.
Keywords： asteroid ;
particle-linkage model ;
hovering orbit ;
parametric excitation resonance ;
nonlinear dynamic PDF (5286KB) 元数据 多维度评价 相关文章 导出 EndNote |
Ris |
Bibtex 收藏本文 本文引用格式 司震, 钱霙婧, 杨晓东, 张伟. 基于参激共振的受摄小行星悬停轨道设计方法
1) .
力学学报 [J], 2020, 52(6): 1774-1788 DOI:
10.6052/0459-1879-20-141 Si Zhen, Qian Yingjing, Yang Xiaodong, Zhang Wei.
HOVERING ORBITS DESIGN FOR PERTURBED ASTEROIDS WITH PARAMETRIC EXCITATION RESONANCE 1) .
Chinese Journal of Theoretical and Applied Mechanics [J], 2020, 52(6): 1774-1788 DOI:
10.6052/0459-1879-20-141 引言 小行星形成于太阳系早期, 在几十亿年的演化进程中, 完整保留了太阳系早期物质等原始信息, 不仅有助于人类探究太阳系起源及生命起源等谜题, 也便于人类采取有效的应对措施来防御、减缓或消除碰撞威胁
[1 ] . 如今,各国正逐步开展小行星的探测采样任务, JASA的隼鸟号(Hayabusa)探测器于2005年登陆小行星25143 Itokawa, 成为人类第一个小行星采样返回任务
[2 ] . 自此以后, JASA的隼鸟II号(Hayabusa II)探测器、NASA的OSIRIS-Rex探测器相继对小行星162173 Ryugu、101955 Bennu开展探测采样任务
[3 -4 ] .
目前, 小行星的探测采样任务主要采用悬停探测轨道, 但由于探测器所处的动力学环境的差异性, 针对小行星探测任务类型或任务的不同阶段, 需要对各阶段的动力学进行分析进而设计相应的悬停轨道
[5 -6 ] . 隼鸟号探测器在小行星Itokawa附近执行任务的大部分时间里都采用惯性系悬停方式, 即探测器跟随小行星进行公转运动, 在小行星轨道系中进行位置保持. 而在小行星表面附近进行采样时, 则采取本体系悬停操作, 即相对于小行星表面某位置点进行位置保持, 以便于在采样返回任务中进行下降和上升机动
[7 -9 ] .
太阳系中已知小行星自身的引力场普遍呈现十分复杂的不规则特性, 其附近探测器的运行轨道受不规则引力场影响
[10 -11 ] . Scheeres最早提出了考虑不规则引力场影响下本体系悬停轨道的受控运动
[12 ] . Sawai考虑小行星引力场不规则特性, 应用球谐、椭球谐模型、多面体模型等研究了均匀自旋和非均匀自旋小行星附近探测器的本体系悬停轨道
[13 -14 ] . Broschart在不考虑第三体引力及外界干扰情况下, 对探测器施加控制推力来抵消小行星引力及惯性力, 研究了本体系悬停和惯性系悬停的稳定区域
[9 , 15 ] . Zhang等
[16 ] 参照限制性三体问题, 考虑了小行星不规则引力对探测器轨道运动的影响,研究了翻滚小行星附近的惯性系悬停控制问题.Zeng等
[17 ] 从非理想太阳帆模型的角度,分析了小行星不规则引力分布对悬停轨道的影响.
由于小行星普遍呈现质量小、引力场弱的特点,研究表明对于在小行星附近悬停运动的航天器而言,太阳辐射光压以及太阳引力摄动不可忽略
[18 -21 ] . 在光压摄动方面,Morrow等
[22 ] 利用太阳光压辐射设计并分析了小行星附近的太阳帆悬停轨道.Williams等
[23 ] 在Morrow等的基础上, 根据小行星的球形简化模型,研究了太阳光压辐射影响下惯性系和本体系悬停探测轨道设计问题.Giancotti和Funase
[24 ] 对太阳帆在特洛伊小行星附近的人工平衡点以及附近轨迹进行了可行性研究.Feng等
[25 ] 研究了非球面项$C_{20}$和太阳辐射压力对小行星附近航天器轨道的影响.Xin等
[26 -27 ] 以椭球体小行星模型, 考虑太阳光压影响,研究了小行星悬停轨道及其稳定性. 在太阳引力摄动方面,刘莹莹等
[28 ] 研究了非球形摄动、太阳光压摄动以及太阳引力摄动对绕飞小行星航天器轨道的影响.倪彦硕等
[29 ] 研究了考虑太阳引力摄动的小行星附近轨道动力学,结果表明太阳引力对平衡点附近航天器运动的影响较大
[29 ] .
由于太阳的周期运动, 光压摄动与引力摄动在系统动力学方程中均呈现为周期性激励
[30 -33 ] .根据文献分析可知, 光压摄动呈现外激励的形式, 即在系统动力学中表现为非齐次项.然而, 引力摄动则呈现参数激励的形式, 即在系统动力学中表现为周期性刚度项系数.通常, 发生外激励共振时, 外激频率需要接近系统的固有频率; 而发生参激共振时,参数激励频率需要接近系统的两倍固有频率或与两倍固有频率相关的加减组合关系.由非线性振动理论可知, 两种形式的共振并不能同时发生
[34 -35 ] . 因此,本文着重研究小行星不规则引力场与太阳引力摄动下,系统参数激励共振轨道设计问题, 为小行星平衡点附近的悬停轨道设计提出新思路.
为了考虑不规则小行星引力场和太阳引力, 本文采用受摄粒杆模型, 即将小行星视为由无质量杆连接的质量粒子组成
[36 -39 ] ,并加入引力摄动天体部分. 本文把太阳引力视为受摄小行星系统的组成部分, 而非单纯的摄动源, 采用非线性振动理论中的参激共振概念,推导了小行星平衡点附近稳定的参数共振轨道. 研究了受摄小行星系统的幅频响应曲线、力频响应曲线以及长短周期运动之间的能量转移现象等非线性特性.此外, 由于粒杆模型将小行星视为由无质量杆连接的质量粒子组成, 本文的研究成果可以拓展现有小行星附近周期轨道族.
1 受摄不规则小行星系统建模 本文采用粒杆模型模拟小行星的不规则引力场,即根据小行星形状特点及质量分布特征,将小行星系统等效看作由3个质量粒子($m_{1}$, $m_{2}$和$m_{3})$组成,并假定$m_{3}\geqslant m_{1}=m_{2}$. 3个质量粒子由两个恒定距离的无质量杆连接,在空间上呈等腰三角形构型.小行星系统的质心围绕摄动天体$M_{4}$做圆形轨道运动,且$M_{4}$到小行星的距离远大于小行星内部每个质量粒子之间的距离.假定所有天体都在同一个平面内运动, 且探测器质量忽略不计.
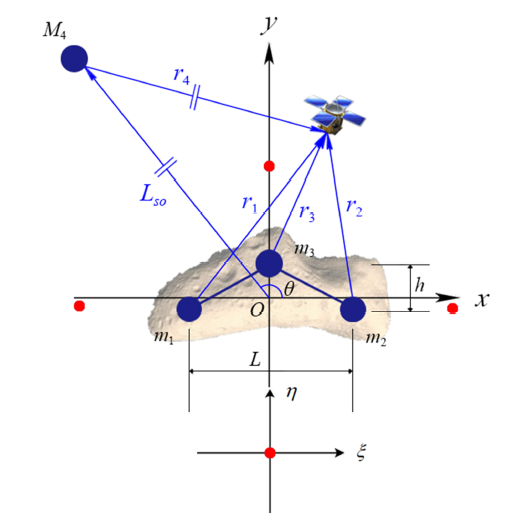
以小行星系统的质心为原点$O$, 建立小行星本体坐标系($O$-$xyz$),受摄粒杆模型示意图如
图1 所示. $Oz$轴沿着小行星的自转角速度$\varOmega $方向,$Ox$轴平行于从粒子$m_{1}$指向粒子$m_{2}$的连线, $Oy$轴由右手坐标系确定.将系统无量纲化, 即设单元长度为粒子$m_{1}$与$m_{2}$之间的距离(表示为$L)$,粒子$m_{3}$与$m_{1}$的距离在$Oy$轴上的投影为$h$,单位质量为$M=m_{1}+m_{2}+m_{3}$. 引入$\mu =m_{1}/M$作为系统的质量参数,则各粒子$m_{1}$, $m_{2}$, $m_{3}$和$M_{4}$的质量可以表示为
(1) $\mu _1 =\mu ,\ \ \mu _2 =\mu ,\ \ \mu _3 =\dfrac{m_3 }{M}=1-2\mu ,\ \ \mu _s =\dfrac{M_4}{M}$ 图1 新窗口打开 |
下载原图ZIP |
生成PPT 图1受摄粒杆模型示意图 Fig. 1Perturbed particle-linkage model 设定长度比$\sigma =h/L$为距离参数. 当粒子$m_{3}$在小行星的质心上方时, $\sigma $数值为正,否则为负. 由于小行星的质心以恒定距离$L_{so}$绕$M_{4}$做圆形轨道运动, 因此摄动天体$M_{4}$的位置可以写为($L_{so}\cos\theta$, $L_{so}\sin\theta$). 其中, $\theta$是$Ox$轴与摄动天体$M_{4}$和小行星质心的连线之间的角度(逆时针测量). 探测器($x$, $y)$在小行星本体坐标系$O$-$xy$中的动力学方程可以表示为
(2) $\left.\begin{array}{l} \ddot{{x}}-2\dot{{y}}=x-k\sum\limits_{i=1}^3 {\dfrac{\mu _i \left( {x-x_i } \right)}{r_i^3 }} -\\ \dfrac{k\mu _s }{r_4^3 }\left( {x-L_{so} \cos \theta } \right)-\dfrac{k\mu _s }{L_{so}^2 }\cos \theta \\ \ddot{{y}}+2\dot{{x}}=y-k\sum\limits_{i=1}^3 {\dfrac{\mu _i \left( {y-y_i } \right)}{r_i^3 }}-\\ \dfrac{k\mu _s }{r_4^3 }\left( {y-L_{so} \sin \theta } \right)-\dfrac{k\mu _s }{L_{so}^2 }\sin \theta \\ \end{array}\right\}$ 其中, $k$是无量纲参数, 代表小行星表面引力和离心力之比
(3) $k=\dfrac{GM}{\varOmega ^2L^3}$ 各质量粒子到探测器的距离$r_{i}$可以展开为
(4) $\left.\begin{array}{l} r_i =\sqrt {\left( {x-x_i } \right)^2+\left( {y-y_i } \right)^2} ,\quad i=1,2,3 \\ r_4 =\sqrt {\left( {x-L_{so} \cos \theta } \right)^2+\left( {y-L_{so} \sin \theta } \right)^2} \\ \end{array}\right\}$ 定义摄动天体的特征参数
(5) $\beta =\dfrac{\mu _s }{L_{so}^3 }$ 由于探测器的运动区域在小行星附近, 因此, 对1/$r_{4}^{3}$进行Taylor展开,运动方程(2)可以进一步简化为
(6) $\left.\begin{array}{l} \ddot{{x}}-2\dot{{y}}=\left( {1+\dfrac{1}{2}k\beta } \right)x-k\sum\limits_{i=1}^3 {\dfrac{\mu _i \left( {x-x_i } \right)}{r_i^3 }} +\\ \dfrac{3}{2}k\beta \left( {x\cos 2\theta +y\sin 2\theta } \right) \\ \ddot{{y}}+2\dot{{x}}=\left( {1+\dfrac{1}{2}k\beta } \right)y-k\sum\limits_{i=1}^3 {\dfrac{\mu _i \left( {y-y_i } \right)}{r_i^3 }} +\\ \dfrac{3}{2}k\beta \left( {x\sin 2\theta -y\cos 2\theta } \right) \\ \end{array}\right\}$ 其中, 以无量纲参数$k=1$为边界, $k>1$时, 引力大于离心力, 小行星处于聚集状态; $k<1$时, 引力小于离心力, 小行星处于离散状态.
观察式(6)可知, 摄动天体$M_{4}$对探测器的引力由两部分组成: 由于平均引力而产生的直接引力部分(以线性刚度项表示为$k\beta x/2$和$k \beta y/2$), 以及因摄动天体位置的周期性变化激励而产生的参数激励部分. 相应地,类似著名的Mathieu方程
[30 ] , 式(6)可被分为两部分: 第一部分, 非扰动系统即小行星系统, 表示为
(7) $\left.\begin{array}{l} \ddot{{x}}-2\dot{{y}}=-\dfrac{\partial V}{\partial x}\\ \ddot{{y}}+2\dot{{x}}=-\dfrac{\partial V}{\partial y} \\ \end{array}\right\}$ 其中, 有效势$V$表示为
(8) $V=-\left( {1+\dfrac{1}{2}k\beta } \right)\dfrac{x^2+y^2}{2}-k\sum\limits_{i=1}^3 {\dfrac{\mu _i }{r_i }}$ 以及第二部分, 参数激励部分, 即式(6)中包含具有非自治正弦函数和余弦函数的项.值得注意的是, 无扰动系统(7)与经典粒杆模型系统并不相同.无扰动系统的有效势函数包含摄动天体的特征参数$\beta $, 而$\beta $最终会影响系统的固有频率.
在本研究中, 摄动小行星系统的平衡点坐标($x_{o}$, $y_{o})$与小行星的质量参数$\mu $, 距离参数$\sigma $, 自旋参数$k$和摄动参数$\beta $均相关. 在给定参数[$\mu $, $\sigma $, $k$, $\beta $]的情况下, 在$xy$平面上生成$V_{x}=\partial V/\partial x$和$V_{y}=\partial V/\partial y$的零值曲线, 从中可以得出交点的初始值. 再通过Newton-Raphson迭代法得到平衡点的精确位置
[40 ] .
当$\beta=0$时, 系统退化为经典的粒杆模型. 根据Yang等
[36 ] 的研究, 可得小行星433 Eros和243 Ida的参数, 按照上述迭代方法求解平衡点, 如
图2 (a)和
图2 (b)所示. 小行星433 Eros和243 Ida都有4个外部平衡点. 当考虑摄动天体的引力即$\beta \ne 0$时, 小行星433 Eros和243 Ida的平衡点的位置将略有改变.
图2 新窗口打开 |
下载原图ZIP |
生成PPT 图2平衡点随参数变化的分布示意图 Fig. 2Distributions of equilibrium points with variations of parameters 为了分析式(6)中的探测器动力学行为, 有必要将坐标系的原点从原有的小行星本体坐标系移动到无扰动系统的平衡点处.相应的, 单位长度调整为平衡点与其最接近的质量粒子($m_{1}$, $m_{2}$或$m_{3})$之间的距离, 表示为$\gamma_{o}$. 这里,选择任意一平衡点$L_{o}$作为原点, 在新的坐标系中, $\xi $-和$\eta $-的方向与小行星本体坐标系的方向平行, 参见
图1 . 需要注意的是, 选择作为新坐标系原点的平衡点应该是稳定的. 对于以$L_{o}-\xi \eta$ (o = 1, 2, 3, $\cdots$)表示的以稳定平衡点$L_{o}$为中心的坐标系和小行星本体坐标系$O$ - $xy$之间的转换关系可以表示为
(9) $\left( {\xi ,\eta } \right)^{T}=\dfrac{1}{\gamma _{o} }\left( {x-x_{o} ,y-y_{o} } \right)^{T}$ 根据式(9), 将各粒子到探测器的距离$r_{i}$ $(i$ = 1, 2, 3)进行Legendre展开到四阶,引入非线性项, 得到非线性系统. 进而可将式(6)表示为
(10) $\left.\begin{array}{l} \ddot{{\xi }}-2\dot{{\eta }}-V_{\xi \xi }^{o} \xi -V_{\xi \eta }^{o} \eta = M_1 \eta ^3+M_2 \xi \eta ^2+\\ M_3 \xi ^2\eta +M_4 \xi ^3 +M_5 \xi ^2+M_6 \xi \eta +M_7 \eta ^2 +\\ \varepsilon ^2\dfrac{3}{2}k\beta \left( {\xi \cos 2\theta +\eta \sin 2\theta } \right)\\ \ddot{{\eta }}+2\dot{{\xi }}-V_{\xi \eta }^{o} \xi -V_{\eta \eta }^{o} \eta = N_1 \eta ^3+N_2 \xi \eta ^2+\\ N_3 \xi ^2\eta +N_4 \xi ^3 +N_5 \xi ^2+N_6 \xi \eta +N_7 \eta ^2 +\\ \varepsilon ^2\dfrac{3}{2}k\beta \left( {\xi \sin 2\theta -\eta \cos 2\theta } \right) \\ \end{array}\right\}$ 其中
(11) $\left.\begin{array}{l} V_{\xi \xi }^{o} =\left( {1+\dfrac{k\beta }{2}} \right)+\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {2E_i^2 -F_i^2 } \right)}{\gamma _{o}^3 D_i^5 }} \\ V_{\eta \eta }^{o} =\left( {1+\dfrac{k\beta }{2}} \right)+\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {2F_i^2 -E_i^2 } \right)}{\gamma _{o}^3 D_i^5 }} \\ V_{\xi \eta }^{o} =\sum\limits_{i=1}^3 {\dfrac{3\mu _i kE_i F_i }{\gamma _{o}^3 D_i^5 }} \\ \end{array}\right\}$ 其中, 有效势函数$V$的第二阶导数由下标$\xi $和$\eta $表示, 上下标中的o表示求导过程取在平衡点处. $E_{i}$, $F_{i}$, $D_{i}$ $(i=1$, 2, 3)定义为新坐标系下平衡点与各质量粒子的位置关系, 其表达式列于附录A中. 由于
图1 中系统模型关于$y$轴对称, 对于平衡点$L_{2}$点和$L_{4}$点, 有$D_{1}=D_{2}$, $E_{1}=-E_{2}$, $E_{3} = 0$, $F_{1}=F_{2}$. $M_{1}$, $M_{2}$, $\cdots$,$M_{7}$, $N_{1}$, $N_{2}$, $\cdots$, $N_{7}$是有效势函数$V$经Legendre展开获得的多项式系数, 其表达式见附录A.$\varepsilon $为小量符号, 用于标记非线性项的量级, 在计算中取值为1.
2 参数激励共振条件分析 根据Nayfeh和Mook
[34 ] 的观点, 参激共振发生有两个重要的前提条件. 首先,参激共振周期轨道设计问题应在稳定平衡点附近进行分析.平衡点的稳定性与其周围轨道的稳定性密切相关,平衡点的稳定性决定了其周围不变流形的稳定性. 其次,参数激励频率与系统固有频率应存在相应二倍关系. 结合这两个前提条件,可以找到发生参数共振的参数区域. 下面依次分析两条件.
条件一: 平衡点稳定性条件. 对于$\xi $ - $\eta $分量, 等式(10)中系统线性部分的特征方程为
(12) $\lambda ^4+B\lambda ^2+C=0$ 其中
(13) $\left.\begin{array}{l} B=4-V_{\xi \xi }^{o} -V_{\eta \eta }^{o} \\ C=V_{\xi \xi }^{o} V_{\eta \eta }^{o} -\left( {V_{\eta \xi }^{o} } \right)^2 \\ \end{array}\right\}$ 如果特征方程(12)具有纯虚部或具有负实部的复数根, 则平衡点将是稳定的. 因此,需满足以下条件
(14) $\left.\begin{array}{l} B>0 \\ C>0 \\ B^2-4C>0 \\ \end{array}\right\}$ 条件二: 参数激励频率与固有频率关系条件. 根据式(12), 得到平衡点$L_{o}$附近的非扰动系统的固有频率为
(15) ${i}\omega _{1,2} =\left( {\dfrac{B\mp \sqrt {B^2-4C} }{2}}\right)^{{1}/{2}}$ 此外, $M_{4}$绕小行星系统质心的圆周运动是二体问题, 且满足开普勒第三定律. 在惯性坐标系中, $M_{4}$的圆周运动频率$\varOmega _{s}$可表示为
(16) $\varOmega _s =\sqrt{{\mu _s}/{L_{so}^3 }} =\sqrt \beta$ 由于$\theta $是
图1 中$x$轴与从质心到$M_{4}$的线之间的夹角, 因此, 在平衡点坐标系中, $\theta $相对于$x$轴旋转的频率为
(17) $\omega _0 =\sqrt {1 / k} -\sqrt \beta$ 这样, 可以将式(10)中的$\theta $改写为$\theta =\omega _{0}t$, 即
(18) $\left.\begin{array}{l} \ddot{{\xi }}-2\dot{{\eta }}-V_{\xi \xi }^{o} \xi -V_{\xi \eta }^{o} \eta = M_1 \eta ^3+M_2 \xi \eta ^2+\\ M_3 \xi ^2\eta +M_4 \xi ^3 +M_5 \xi ^2+M_6 \xi \eta +M_7 \eta ^2 +\\ \varepsilon ^2\dfrac{3}{2}k\beta \left( {\xi \cos \omega t+\eta \sin \omega t} \right) \\ \ddot{{\eta }}+2\dot{{\xi }}-V_{\xi \eta }^{o} \xi -V_{\eta \eta }^{o} \eta = N_1 \eta ^3+N_2 \xi \eta ^2+\\ N_3 \xi ^2\eta +N_4 \xi ^3 +N_5 \xi ^2+N_6 \xi \eta +N_7 \eta ^2 +\\ \varepsilon ^2\dfrac{3}{2}k\beta \left( {\xi \sin \omega t-\eta \cos \omega t} \right) \\ \end{array}\right\}$ 其中, $\omega = 2\omega _{0}$.
通常, 二维系统存在两个固有频率$\omega _{1}$和$\omega _{2}$ (假设$\omega _{2}>\omega _{1})$, 分别对应于长周期和短周期的轨道运动. 因此, 在理论上可能存在第一类和第二类参激的两种主共振类型, 即满足频率关系
(19) $\omega \approx 2\omega _1\ \ {or}\ \ \omega \approx 2\omega _2$ 以及和型参激共振和差型参激共振的两种组合共振, 即满足频率关系
(20) $\omega \approx \omega _1 +\omega _2\ \ {or}\ \ \omega \approx \omega _2 -\omega _1$ 由于平衡点的位置、稳定性以及固有频率均与参数[$\mu $, $\sigma $, $k$, $\beta $]有关,而参数激励频率与$k$, $\beta $参数相关, 因此, 通过条件一和条件二,可获得满足参激共振条件的参数空间.
为了方便观察摄动参数$\beta $对系统的影响, 在仿真中固定参数$\sigma $和$k$, 研究系统参数$\mu $与$\beta $的取值范围.
图3 为$\sigma $ = 0.8, $k$ = 0.9时, 满足条件一和条件二的$\mu $与$\beta $取值范围. 在
图3 中,灰色区域表示满足平衡点稳定条件的取值区域,红线表示满足第二类参激主共振条件的取值区域,蓝线则表示满足和型参激共振条件的取值区域.
图3 新窗口打开 |
下载原图ZIP |
生成PPT 图3满足参激共振条件的参数取值区域$\sigma $ = 0.8, $k$ = 0.9 Fig. 3Parametric resonance region when $\sigma $ = 0.8, $k$ = 0.9 图4 为更多组合取值变化条件下的分析结果,图中红线和蓝线分别为满足第二类参激主共振条件以及和型参激共振条件的共振线.为了观察小行星自旋特性对系统共振区域的影响, 固定参数$\sigma $, 改变参数$k$,得到满足不同参激共振情况的参数取值范围, 如
图4 (a)所示. 由
图4 (a)可知, 当$k$ =0.6时, 系统只能发生第二类参激主共振, 随着参数$k$增大,系统同时出现第二类参激主共振以及和型参激共振.
图4 新窗口打开 |
下载原图ZIP |
生成PPT 图4不同系统参数下满足参激共振条件的参数取值 Fig. 4Parametric resonance regions with different $k$ and $\sigma $ 同样, 为了观察小行星形状对系统共振区域的影响, 固定参数$k$, 改变参数$\sigma $,得到满足不同参激共振情况的参数取值范围, 如
图4 (b). 在
图4 (b)中,随着参数$\sigma $减小, 满足共振条件所对应的系统$\mu $值增大. 因此, 对于不规则形状的小行星,形状越接近细长型, 且处于聚集状态时, 即形状参数$\sigma $越小, 自旋参数$k$越大,系统更容易找到满足参激共振的周期轨道族. 需要说明的是, 在数值模拟的过程中,没有发现满足第一类参激主共振和差型参激共振关系的参数取值区域.
结合
图3 和
图4 的分析可知, 对于摄动小行星系统, 普遍存在第二类参激主共振,在一定条件下, 存在和型参激共振,但是普遍不存在第一类参激主共振和差型参激共振.
此外, 本文分析了系统存在内共振的可能性, 即系统固有频率之间存在关系
(21) $\omega _2 \approx 2\omega _1\ \ {or} \ \ \omega _2 \approx 3\omega _1$ 同样, 以$\sigma =0.8$和$k=0.9$时为例, 结果如
图3 所示. 图中,绿线和黑线分别表示满足1:2和1:3内共振条件的参数范围.
根据分析可知, 系统存在同时发生参激共振以及内共振的可能性. 在此区域内,参数激励共振使得系统在微小引力摄动激励条件下产生较大幅值的响应,即参激共振周期轨道,而内共振则可能使得系统整体的能量在长短周期的轨道运动之间转换,由此产生更为复杂的非线性动力学行为.
3 参数激励共振轨道求解 基于上述分析可知, 受摄小行星系统普遍存在内共振以及第二类参激主共振, 本节以第二类参激主共振和1:3内共振为例, 对参数激励共振轨道进行求解.
为了确定非线性和参数激励对系统振幅和相位的组合影响, 采用多尺度方法, 假定式(18)具有如下形式的解
(22) $\left.\begin{array}{l} \xi =\varepsilon \xi _1 +\varepsilon ^2\xi _2 +\varepsilon ^3\xi _3 \\ \eta =\varepsilon \eta _1 +\varepsilon ^2\eta _2 +\varepsilon ^3\eta _3 \\ \end{array}\right\}$ 其中, 上述解均与快时间尺度$T_{0}=t$以及慢时间尺度$T_{2} = \varepsilon^{2}t$有关.约定算子
(23) $\left.\begin{array}{l} \dfrac{d}{{d}t}=D_0 +\varepsilon ^2D_2 \dfrac{{d}^2}{{d}t^2}=D_0 ^2+2\varepsilon ^2D_0 D_2 \\ \end{array}\right\}$ 把式(22)代入式(18), 比较$\varepsilon $的同次幂, 得到
(24) $\varepsilon ^1:\left\{ {\begin{array}{l} D_0^2 \xi _1 -2D_0 \eta _1 -V_{\xi \xi }^{o} \xi _1 -V_{\xi \eta }^{o} \eta _1 =0 \\ D_0^2 \eta _1 +2D_0 \xi _1 -V_{\xi \eta }^{o} \xi _1 -V_{\eta \eta }^{o} \eta _1 =0 \\ \end{array}} \right.$ (25) $\varepsilon ^2:\left\{ {\begin{array}{l} D_0^2 \xi _2 -2D_0 \eta _2 -V_{\xi \xi }^{o} \xi _2 -V_{\xi \eta }^{o} \eta _2 =\\ M_5 \xi _1^2 +M_6 \xi _1 \eta _1 +M_7 \eta _1^2 \\ D_0^2 \eta _2 +2D_0 \xi _2 -V_{\xi \eta }^{o} \xi _2 -V_{\eta \eta }^{o} \eta _2 =\\ N_5 \xi _1^2 +N_6 \xi _1 \eta _1 +N_7 \eta _1^2 \\ \end{array}} \right.$ (26) $\varepsilon ^3:\left\{ {\begin{array}{l} D_0^2 \xi _3 -2D_0 \eta _3 -V_{\xi \xi }^{o} \xi _3 -V_{\xi \eta }^{o} \eta _3 =\\ -2D_0 D_2 \xi _1 +2D_2 \eta _1 +\\ \dfrac{3}{2}k\beta \cos \omega t\xi _1 +\dfrac{3}{2}k\beta \sin \omega t\eta _1 +\\ M_1 \eta _1^3 +M_2 \xi _1 \eta _1^2 +M_3 \xi _1^2 \eta _1 +\\ M_4 \xi _1^3 +\left( {2M_5 \xi _1 +M_6 \eta _1 } \right)\xi _2 +\\ \left( {M_6 \xi _1 +2M_7 \eta _1 } \right)\eta _2 \\ D_0^2 \eta _3 +2D_0 \xi _3 -V_{\xi \eta }^{o} \xi _3 -V_{\eta \eta }^{o} \eta _3 =\\ -2D_0 D_2 \eta _1 -2D_2 \xi _1 +\\ \dfrac{3}{2}k\beta \sin \omega t\xi _1 -\dfrac{3}{2}k\beta \cos \omega t\eta _1 +\\ N_1 \eta _1^3 +N_2 \xi _1 \eta _1^2 +N_3 \xi _1^2 \eta _1 +\\ N_4 \xi _1^3 +\left( {2N_5 \xi _1 +N_6 \eta _1 } \right)\xi _2 +\\ \left( {N_6 \xi _1 +2N_7 \eta _1 } \right)\eta _2 \\ \end{array}} \right.$ 不难发现, 式(24)为齐次方程. 因此, 式(24)的解可以表示为
(27) $\left.\begin{array}{l} \xi _1 =A_1 {e}^{{i}\omega _1 T_0 }+A_2 {e}^{{i}\omega _2 T_0 }+cc \\ \eta _1 =\varGamma _1 A_1 {e}^{{i}\omega _1 T_0 }+\varGamma _2 A_2 {e}^{{i}\omega _2 T_0 }+cc \\ \end{array}\right\}$ 其中, $A_{1}$和$A_{2}$分别为长短周期轨道振幅,
cc 表示其前面各项的共轭
(28) $\varGamma _r =-\dfrac{\omega _r^2 +V_{\xi \xi }^{o} }{2{i}\omega _r +V_{\xi \eta }^{o} }=\dfrac{2{i}\omega _r -V_{\xi \eta }^{o} }{\omega _r^2 +V_{\eta \eta }^{o}},\ \ r=1,2$ 将式(27)代入式(24), 可以获得式(25)中$\xi _{2}$和$\eta _{2}$的解.考虑参激频率和固有频率间的关系以及1:3的内共振情况, 引入调谐参数$\tau $和$\kappa $,将频率之间的关系表示为
(29) $\left.\begin{array}{l} \omega =2\omega _2 +\varepsilon ^2\tau \\ \omega _2 =3\omega _1 +\varepsilon ^2\kappa \\ \end{array}\right\}$ 由此可得
(30) $\left.\begin{array}{l} \left( {\omega -\omega _2 } \right)T_0 =\omega _2 T_0 +\tau T_2 \\ 3\omega _1 T_0 =\omega _2 T_0 -\kappa T_2 \\ \left( {\omega _2 -2\omega _1 } \right)T_0 =\omega _1 T_0 +\kappa T_2 \\ \end{array}\right\}$ 为了确定式(26)的可解条件, 寻求$\xi _{3}$和$\eta _{3}$的特解, 以此来消除长期项, 可设
(31) $\left.\begin{array}{l} \xi _3 =P_1 {e}^{{i}\omega _1 T_0 }+Q_1 {e}^{{i}\omega _2 T_0 } \\ \eta _3 =P_2 {e}^{{i}\omega _1 T_0 }+Q_2 {e}^{{i}\omega _2 T_0 } \\ \end{array}\right\}$ 然后, 将$\xi _{1}$, $\eta _{1}$和$\xi _{2}$, $\eta _{2}$代入式(26)右端,式(31)代入到式(26)左端, 并使两侧exp(i$\omega _{1}T_{0})$ 和exp(i$\omega _{2}T_{0})$的系数相等, 得到
(32) $\left.\begin{array}{l} \left( {-\omega _1^2 -V_{\xi \xi }^{o} } \right)P_1 +\left( {-2{i}\omega _1 -V_{\xi \eta }^{o} } \right)P_2 =W_1 \\ \left( {2{i}\omega _1 -V_{\xi \eta }^{o} } \right)P_1 +\left( {-\omega _1^2 -V_{\eta \eta }^{o} } \right)P_2 =W_2 \\ \left( {-\omega _2^2 -V_{\xi \xi }^{o} } \right)Q_1 +\left( {-2{i}\omega _2 -V_{\xi \eta }^{o} } \right)Q_2 =S_1 \\ \left( {2{i}\omega _2 -V_{\xi \eta }^{o} } \right)Q_1 +\left( {-\omega _2^2 -V_{\eta \eta }^{o} } \right)Q_2 =S_2 \\ \end{array}\right\}$ 其中
(33) $\left.\begin{array}{l} W_1 =\left( {-2{i}\omega _1 +2\varGamma _1 } \right)D_2 A_1 +W_{11} \\ W_2 =\left( {-2{i}\omega _1 \varGamma _1 -2} \right)D_2 A_1 +W_{22} \\ \end{array}\right\}$ (34) $\left.\begin{array}{l} S_1 =\left( {-2{i}\omega _2 +2\varGamma _2 } \right)D_2 A_2 +S_{11}+ \\ \left( {1-{i}\bar{{\varGamma }}_2 } \right)\dfrac{3k\beta }{4}\bar{{A}}_2 {e}^{{i}\tau T_2 } \\ S_2 =\left( {-2{i}\omega _2 \varGamma _2 -2} \right)D_2 A_2 +S_{22}- \\ \left( {{i}+\bar{{\varGamma }}_2 } \right)\dfrac{3k\beta }{4}\bar{{A}}_2 {e}^{{i}\tau T_2 } \\ \end{array}\right\}$ 且$W_{11}$, $W_{22}$, $S_{11}$, $S_{22}$的表达式列于附录B中, 上标"--"表示相应参数的共轭.
由此, 确定式(27)的可解性条件的问题被简化为确定线性代数方程(32)的系数行列式为零的条件, 考虑式(28)中的关系, 可得
(35) $\left.\begin{array}{l} W_1 +\bar{{\varGamma }}_1 W_2 =0 \\ S_1 +\bar{{\varGamma }}_2 S_2 =0 \\ \end{array}\right\}$ 把式(33)和式(34)代入式(35), 得到
(36) $\left.\begin{array}{l} D_2 A_1 ={i}\dfrac{1}{2}\varLambda_1 \left( G_{11} \bar{{A}}_1^2 A_2 {e}^{{i}\kappa T_2 } +G_{12} A_1 A_2 \bar{{A}}_2 + G_{13} A_1^2 \bar{{A}}_1\right) \\ D_2 A_2 ={i}\dfrac{1}{2}\varLambda_2 \left( G_{20} \bar{{A}}_2 {e}^{{i}\tau T_2 }+G_{21} A_1^3 {e}^{-{i}\kappa T_2 } + G_{22} A_1 \bar{{A}}_1 A_2 +G_{23} A_2^2 \bar{{A}}_2\right) \\ \end{array}\right\}$ 其中
(37) $\varLambda_r =\dfrac{\omega _r^2 +V_{\eta \eta }^{o}}{\omega _r \left( {4-2\omega _r^2 -V_{\xi \xi }^{o} -V_{\eta \eta }^{o} } \right)}$ 式中, $G_{20}$与$G_{r1}$, $G_{r3}$ ($r=1,2$)都是关于系统非线性系数$M_{1}$, $M_{2}$, ${\ldots}$, $M_{7}$, $N_{1}$, $N_{2}$, ${\ldots}$, $N_{7}$的复数, 分离其实虚部为$R_{20}$与$R_{r1}$, $R_{r2}$, $R_{r3}$, $I_{r1}$, $I_{r2}$, $I_{r3}$, ($r=1,2$)表达式列于附录B中, 上标"--"表示相应参数的共轭.
将式(36)中的$A_{1}$和$A_{2}$表示为实数$a_{r}$, $\beta _{r}$的形式
(38) $\left.\begin{array}{l} A_1 \left( {T_2 } \right)=\dfrac{a_1 \left( {T_2 } \right)}{2}{e}^{{i}\beta _1 \left( {T_2 } \right)} \\ A_2 \left( {T_2 } \right)=\dfrac{a_2 \left( {T_2 } \right)}{2}{e}^{{i}\beta _2 \left( {T_2 } \right)} \\ \end{array}\right\}$ 结合欧拉公式, 分离实部和虚部, 并引入新的相位角
(39) $\left.\begin{array}{l} \varphi _1 =\kappa T_2 -3\beta _1 +\beta \\ \varphi _2 =\tau T_2 -2\beta _2 \\ \end{array}\right\}$ 把关系式(39)代入式(36), 得到一次近似解式(27)中振幅和相位应满足的自治微分方程
(40) $\left.\begin{array}{l} 8D_2 a_1 =-R_{11} \varLambda_1 a_1^2 a_2 \sin \varphi _1 -I_{12} \varLambda_1 a_1 a_2^2 -\\ I_{11} \varLambda_1 a_1^2 a_2 \cos \varphi _1 -I_{13} \varLambda_1 a_1^3 \\ 8D_2 a_2 =-4R_{20} \varLambda_2 a_2 \sin \varphi _2 -I_{22} \varLambda_2 a_1^2 a_2 +\\ R_{21} \varLambda_2 a_1^3 \sin \varphi _1 -I_{21} \varLambda_2 a_1^3 \cos \varphi _1 -\\ 4I_{20} \varLambda_2 a_2 \cos \varphi _2 -I_{23} \varLambda_2 a_2^3 \\ \end{array}\right\}$ (41) $\left.\begin{array}{l} 4a_1 D_2 \varphi _2 +8a_1 D_2 \varphi _1 =4a_1 \tau +8a_1 \kappa +\\ 3I_{11} \varLambda_1 a_1^2 a_2 \sin \varphi _1 -3R_{12} \varLambda_1 a_1 a_2^2 -\\ 3R_{11} \varLambda_1 a_1^2 a_2 \cos \varphi _1 -3R_{13} \varLambda_1 a_1^3 \\ 4a_2 D_2 \varphi _2 =4a_2 \tau -R_{22} \varLambda_2 a_1^2 a_2 -R_{23} \varLambda_2 a_2^3 -\\ I_{21} \varLambda_2 a_1^3 \sin \varphi _1 -4R_{20} \varLambda_2 a_2 \cos \varphi _2 -\\ R_{21} \varLambda_2 a_1^3 \cos \varphi _1 +4I_{20} \varLambda_2 a_2 \sin \varphi _2 \\ \end{array}\right\}$ 其中, 方程(40)和(41)明确了系统非线性的影响. 非线性项不仅可以直接影响振幅,还可以通过改变相位间接影响振幅. 由此, 可将系统的一次近似解表示为形式
(42) $\left.\begin{array}{l} \xi _1 =\dfrac{a_1 }{2}{e}^{{i}\left( {\beta _1 +\omega _1 T_0 } \right)}+\dfrac{a_2 }{2}{e}^{{i}\left( {\beta _2 +\omega _2 T_0 } \right)}+cc \\ \eta _1 =\varGamma _1 \dfrac{a_1 }{2}{e}^{{i}\left( {\beta _1 +\omega _1 T_0 } \right)}+\varGamma _2 \dfrac{a_2 }{2}{e}^{{i}\left( {\beta _2 +\omega _2 T_0 } \right)}+cc \\ \end{array}\right\}$ 并根据由式(28)、式(30)和式(39)所给出的相位关系
(43) $\left.\begin{array}{l} \beta _1 +\omega _1 T_0 =\dfrac{1}{6}\left( {\omega t-2\varphi _1 -\varphi _2 } \right) \\ \beta _2 +\omega _2 T_0 =\dfrac{1}{2}\left( {\omega t-\varphi _2 } \right) \\ \end{array}\right\}$ 得到参激共振运动的一次近似解的通解形式
(44) $\left.\begin{array}{l} \xi =a_1 \cos \dfrac{1}{6}\left( {\omega t-2\varphi _1 -\varphi _2 } \right) +\\ a_2 \cos \dfrac{1}{2}\left( {\omega t-\varphi _2 } \right) \\ \eta =\varGamma _1 a_1 \cos \dfrac{1}{6}\left( {\omega t-2\varphi _1 -\varphi _2 } \right) +\\ \varGamma _2 a_2 \cos \dfrac{1}{2}\left( {\omega t-\varphi _2 } \right) \\ \end{array}\right\}$ 其中, $\omega $是参数激励的频率. 需要注意的是, 与式(27)不同, 式(44)并不是系统的线性解, 其包含瞬态和稳态两种运动. 振幅$a_{r}$和相位$\varphi _{r}$ $(r=1,2$)的取值必须严格遵循方程(40)和(41), 而式(27)中系统线性解的振幅可以选择为任意值.
此外, 由式(44)可知, 长周期轨道运动频率为$\omega/6$, 而短周期轨道运动频率为$\omega/2$. 由此可见, 由于系统非线性的影响, 使得短周期轨道的运动频率与参数激励频率之间呈现精确的二倍关系, 与此同时, 长短周期运动之间呈现精确的1:3内共振. 虽然共振响应轨道同时包含长短周期分量,但是由于频率之间的谐振关系依然呈现周期性.
4 参数激励共振轨道特性分析 4.1 系统稳态解及其稳定性判断 由于通解式(44)中包含有周期性的稳态运动, 显然, 考虑到非线性项的影响后,根据式(40)和式(41)可知, 系统可能存在定常振幅${a}'_1 ={a}'_2 =0$和定常相位${\varphi }'_1 ={\varphi }'_2 =0$, 即在摄动天体的影响下,参数激励共振响应的振幅不再是无边界, 而是存在实现稳态周期轨道运动的可能性.该轨道可为小行星探测任务的轨道设计提供参考.
根据式(40)和式(41), 稳态运动的定常解振幅$a_{r0}$和相位$\varphi _{r0}$应满足的代数方程
(45) $0=-R_{11} \varLambda_1 a_{10}^2 a_{20} \sin \varphi _{10}$ (46) $0=4a_{10} \tau +8a_{10} \kappa -3R_{11} \varLambda_1 a_{10}^2 a_{20} \cos \varphi _{10}-\\ 3R_{12} \varLambda_1 a_{10} a_{20}^2 -3R_{13} \varLambda_1 a_{10}^3$ (47) $0=-4R_{20} \varLambda_2 a_{20} \sin \varphi _{20} +R_{21} \varLambda_2 a_{10}^3 \sin \varphi _{10}$ (48) $0=4a_{20} \tau -4R_{20} \varLambda_2 a_{20} \cos \varphi _{20} -R_{23} \varLambda_2 a_{20}^3 -\\ R_{21} \varLambda_2 a_{10}^3 \cos \varphi _{10} -R_{22} \varLambda_2 a_{10}^2 a_{20}$ 其中, $a_{10}$, $a_{20}$, $\varphi _{10}$, $\varphi _{20}$表示$a_{1}$, $a_{2}$, $\varphi _{1}$, $\varphi_{2}$对应的稳态解, 由于模型的对称性, $I_{20}$, $I_{21}$, $I_{22}$, $I_{23}$取值为0.
按照$a_{10}$是否为零, 上述方程组的解可分为平凡解和非平凡解两种情况.当$a_{10}$取平凡解时, 系统退化为只与$\omega _{2}$相关的短周期运动. 本文考虑一般情况,即$a_{10}$取非平凡解情况, $a_{10}\ne $0, $a_{20}\ne $0.由式(45)和式(47)可知
(49) $\left.\begin{array}{l} \sin \varphi _{10} =0\\ \sin \varphi _{20} =0 \\ \end{array}\right\}$ 即系统存在的4种相位组合情形.
给定系统参数, 采用Newton-Raphson法针对不同相位组合情况可求得相应振幅稳态解$a_{10}$, $a_{20}$, 从而得到振幅稳态解与调谐参数$\tau $之间的关系图, 称之为幅频响应曲线. 由式(29)可知, 调谐参数$\tau $可以用于表征参数激励频率的大小, 由此,通过幅频响应曲线可以分析得知不同参数激励频率所对应的系统振幅稳态解.
此外, 为了确保参激共振轨道的稳定性, 需要对其长短周期运动进行分析. 根据式(45)至式(48)可知,长周期运动稳态解的稳定性由式(45)和式(46)的奇点性质判定,短周期运动稳态解的稳定性由式(47)和式(48)的奇点性质判定. 考虑到式(49),参激共振轨道的稳定性可以通过式(46)和式(48)的奇点性质来判断.对式(46)和式(48)的奇点性质进行分析, 得到用于判断长短周期振幅$a_{10}$, $a_{20}$稳定性的Jacobi矩阵为
(50) $A=\left[ {{\begin{array}{*{20}c} {a_{11} } & {a_{12} }\\ {a_{21} } & {a_{22} }\\ \end{array} }} \right]$ 其中
(51) $\left.\begin{array}{l} a_{11} =4\tau +8\kappa -6R_{11} \varLambda_1 a_{10} a_{20} \cos \varphi _{10} -\\ 3R_{12} \varLambda_1 a_{20}^2 -9R_{13} \varLambda_1 a_{10}^2 \\ a_{12} =-3R_{11} \varLambda_1 a_{10}^2 \cos \varphi _{10} -6R_{12} \varLambda_1 a_{10} a_{20} \\ a_{21} =-3R_{21} \varLambda_2 a_{10}^2 \cos \varphi _{10} -2R_{22} \varLambda_2 a_{10} a_{20} \\ a_{22} =4\tau -4R_{20} \varLambda_2 \cos \varphi _{20} -R_{22} \varLambda_2 a_{10}^2 -\\ 3R_{23} \varLambda_2 a_{20}^2 \\ \end{array}\right\}$ 矩阵$A$的特征值可以表示为
(52) $\lambda _{1,2} =\dfrac{1}{2}p\mp \left( {\dfrac{1}{4}p^2-q} \right)^{1 / 2}$ 其中, $p$是$A$的迹, $q$是$A$的行列式
(53) $\left.\begin{array}{l} p=a_{11} +a_{22} \\ q=a_{11} a_{22} -a_{12} a_{21} \\ \end{array}\right\}$ 当$p^{2}-4q>0$时, $\lambda _{1,2}$为互异实特征值. 若$q<0$, 则$\lambda _{1}\lambda _{2}<0$,奇点为鞍点. 若$q>0$, $p<0$, 则$\lambda _{1}\lambda _{2}>$0, 奇点为渐近稳定结点.当$p^{2}-4q<0$时, $\lambda _{1,2}$为共轭复特征值. 若$p<0$, 奇点为渐近稳定焦点.若$p>0$, 奇点为不稳定焦点. 综上所述, 得到奇点渐近稳定的判别条件,即同时满足参激共振轨道长短周期振幅稳定性的条件如下
(54) $\left.\begin{array}{l} p<0 \\ q>0 \\ \end{array}\right\}$ 下面通过数值模拟, 对系统稳态解的性质进一步分析, $\mu =0.001 13$, $\sigma =0.8$, $k=0.9$,$\beta =0.014$为例, 选取稳定的平衡点$L_{4}$, 对4种相位组合情况分别讨论, 绘制幅频响应曲线, 如
图5 和
图6 所示.
图5 新窗口打开 |
下载原图ZIP |
生成PPT 图5幅频响应曲线(情况1、情况3) Fig. 5Frequency-amplitude response curves (Case 1, Case 3) 图6 新窗口打开 |
下载原图ZIP |
生成PPT 图6幅频响应曲线(情况2、情况4) Fig. 6Frequency-amplitude response curves (Case 2, Case 4) 图5 为情况1 ($\varphi _{10}=0$, $\varphi _{20}=0$)和情况3 ($\varphi _{10}=\pi $, $\varphi _{20}=0$)的幅频响应曲线.在
图5 中, 两种情况的曲线重合, 黑线为长周期振幅稳态解$a_{10}$, 蓝线为短周期振幅$a_{20}$. 不难发现, 稳态解$a_{10}$,$a_{20}$均呈现随调谐参数$\tau $的增大而单调递增的趋势, 即一个参数激励频率只对应于一组稳态解. 当调谐参数$\tau =0.000 7$时, 系统存在一组稳态解$a_{10}=0.014 2$, $a_{20}=0.000 3$, 如
图5 中红点所示. 由式(52)和式(54)可得, $a_{10}=0.014 2$, $a_{20}=0.000 3$时, $p=-0.010 6<0$, $q=-0.004 8<0$, $\lambda _{1}=0.004 3$, $\lambda _{2}=-0.074 7$, 该组稳态解是不稳定的. 通过式(54)验证稳态解的稳定性, 发现在幅频响应曲线中, 任何一组稳态解所对应的$q$值均小于0, 稳态解具有不稳定性. 因此, 在设计参激共振周期轨道时, 情况1和情况3将不予以考虑.
图6 为相位组合关系为情况2 ($\varphi _{10}=0$, $\varphi _{20}=\pi$)和情况4 ($\varphi _{10}=\pi $, $\varphi _{20}=\pi$)的幅频响应曲线. 当调谐参数$\tau =0.000 7$, 系统存在一组稳态解$a_{10}=0.013 9$, $a_{20}=0.000 4$, 如
图6 中红点所示. 基于式(52)和式(54)可得, $p=-0.114 1<0$, $q=0.003 1>0$, $p^{2}-4q>0$, $\lambda _{1}=-0.056 7$, $\lambda _{2}=-0.070 0$, 该组稳态解是稳定的. 为了进一步描述调谐参数$\tau $对稳态解的稳定性的影响,将幅频响应曲线分为3个区域, 标记为I, II, III, 对长短周期振幅变化轨迹分别进行标记.
当$\tau $从0增大到0.02时, 长周期振幅$a_{10}$经过$A_{1}$至$A_{4}$点, 轨迹方向由黑色箭头表示; 短周期振幅$a_{20}$经过$B_{1}$至$B_{4}$点, 轨迹方向由蓝色箭头表示, 如
图6 (a)所示. 在$A_{1}$、$B_{1}$点($\tau =0$)到$A_{2}$, $B_{2}$点($\tau=0.010 4$)的区域I内, 系统只存在一组非平凡解, 且通过式(46)和式(48)可分别求出. 基于式(54)可得,$p<0$, $q>0$, 即区域I中的各组稳态解均是稳定的, 如
图6 区域I中的实线所示. 在$A_{2}$, $B_{2}$点到$A_{3}$, $B_{3}$点($\tau =0.012 3$)的区域II中, 长周期振幅$a_{10}$和短周期振幅$a_{20}$分别存在两组非平凡解. 一组非平凡解所对应的$q$值小于0, 为不稳定稳态解, 如
图6 区域II中的虚线所示. 一组非平凡解的$p<0$, $q>0$, 则该组稳态解是稳定的, 如
图6 区域II中的实线所示.但奇点种类有所不同, 当$\tau \in (0.010 4, 0.011 8)$ 时, $p^{2}-4q>0$, $\lambda _{1}$,$\lambda _{2}$为负实数, 呈现"稳定结点"特性, 当$\tau \in (0.011 8, 0.012 3)$时,$p^{2}-4q<0$, $\lambda _{1}$, $\lambda _{2}$为实部为负的复数, 呈现"稳定焦点"特性.特别注意的是, 在$A_{3}$, $B_{3}$点, 两个非平凡解不再以原轨迹变化,出现"跳跃现象", $a_{10}$从$A_{3}$点跳跃到$A_{4}$点, $a_{20}$从$B_{3}$点跳跃到$B_{4}$点. 在区域III内, 即$\tau \in (0.012 3, +\infty)$时, $p<0$, $q<0$, 呈现"鞍点"特征, 该组稳态解是不稳定的, 如
图6 区域III中的虚线所示.
当$\tau $从0.02减小到0时, 长周期振幅$a_{10}$经过$C_{1}$至$C_{4}$点, 轨迹方向由黑色箭头表示; 短周期振幅$a_{20}$经过$D_{1}$至$D_{4}$点, 轨迹方向由蓝色箭头表示, 如
图6 (b)所示. 在$\tau $经过$C_{2}$, $D_{2}$点到达$C_{3}$, $D_{3}$点之前, 系统存在两组非平凡解, 之后可以观察到跳跃到$C_{4}$, $D_{4}$点的现象.与上述$\tau $增大过程类似, 从$C_{4}$, $D_{4}$点之后, 唯一可实现的稳定的非平凡解由式(46)和式(48)给出. 除此之外,系统不存在稳定非平凡解. 因此, 调谐参数的变化方向不同,使得系统稳定非平凡解所对应的调谐参数区域也有所不同.
结合上述长短周期振幅变化的特点, 发现了一个有趣的现象. 在稳定区域I和区域II中, 随着调谐参数$\tau $的增大, 长周期振幅$a_{10}$先增大后减小, 而短周期振幅$a_{20}$不断增大, 直至超过长周期振幅$a_{10}$. 根据式(29)得知, 参数激励$\omega $与系统固有频率$\omega _{2}$之间存在共振关系, 通过参数激励, 能量不断输入系统, 激发系统短周期运动(振幅$a_{20}$相关运动).在区域I的初始阶段, 内共振调谐参数$\kappa <0.005$, 使得在区域I内共振的影响显著, 作用于短周期运动的能量通过内共振不断被转移到长周期运动, 进而出现长周期振幅$a_{10}$为主的稳态运动. 随着调谐参数$\tau $不断增大, 内共振调谐参数$\kappa $也随之增大, 内共振能量转移效应减弱, 从而在区域II内短周期运动的振幅$a_{20}$不断增大直至超过长周期振幅$a_{10}$.
为了进一步描述参数激励能量(引力摄动$\beta $)对系统的影响程度, 以$\mu =0.001 13$, $\sigma =0.8$,$k=0.9$为例, 固定调谐参数$\tau =0.000 7$, 绘制参数激励振幅$1.5k\beta$和参激响应振幅$a_{r0}$的力频关系曲线,如
图7 所示.
图7 新窗口打开 |
下载原图ZIP |
生成PPT 图7力频响应曲线 Fig. 7Amplitude of the excitation-amplitude of response curves 在情况1和情况3中, $\beta \in [0, 0.016 0]$, 稳态解随参激振幅的增大而减小. $p<0$, $q<0$, 稳态解呈现"鞍点"特性, 该组稳态解是不稳定的, 如
图7 (a)中虚线所示. 力频关系分析结果和幅频响应曲线结果一致, 因此, 在设计参激共振周期轨道时,情况1和情况3将不予以考虑.
在情况2和情况4中, 类似于幅频响应曲线, 根据稳态解的个数和稳定性, 可以将力频响应曲线分为3个区域, 如
图7 (b)中虚线所示. 其中,实线表示稳定的稳态解, 虚线表示不稳定的稳态解. 区域边界(红线)为$\beta =0.003 8$ $(1.5k\beta =0.005 1)$和$\beta =0.006 9$ $(1.5k\beta =0.009 3$). 当$\beta \in [0, 0.003 8)$时, 长周期振幅$a_{10}$随参激振幅的增大而减小, 短周期振幅$a_{20}$则呈现不断增大, $p<0$, $q>0$, 该稳态解是稳定的. 当$\beta \in [0.003 8, 0.006 9]$时, 出现两组稳态解, 一组稳态解$p<0$, $q<0$, 是不稳定的; 一组稳态解$p<0$, $q>0$, 是稳定的. 当$\beta \in (0.006 9, 0.016 0]$时,短周期振幅$a_{20}$随参激振幅的增大而减小, 长周期振幅$a_{10}$则呈现先增大后减小的特点, $p<0$, $q>0$,对应的稳态解是不稳定的. 力频关系分析结果和幅频响应曲线结论一致.
4.2 参数激励共振响应轨道 通过上述分析判断, 根据参激共振响应(44)以及所求稳定的稳态解, 最终得到了满足第二主参数共振和1:3内共振条件下稳定的参激周期轨道. 由于在稳定区域I和区域II中, 探测器的动力学行为有所差别. 因此,将用两组数据分别对参激共振轨道进行模拟求解.
以参数$\mu =0.001 13$, $\sigma =0.8$, $k=0.9$, $\beta =0.014$为例, 得到调谐参数$\tau =0.000 7$, $\kappa =0.004 1$,参激周期轨道长短周期的振幅$a_{10}=0.013 9$, $a_{20}=0.000 4$.
图8 (a)中红线和蓝线分别表示长短周期运动振幅随时间的变化情况, 黑线表示长短周期叠加运动振幅随时间变化曲线. 不难发现, 由于非线性效应, 长短周期轨道频率之间呈现精确的1:3内共振比例关系.
图8 新窗口打开 |
下载原图ZIP |
生成PPT 图8当$\sigma =0.8$, $k=0.9$, $\mu =0.001 13$, $\beta=0.014$时参激共振轨道示意图 Fig. 8Stable parametric resonance orbit when $\sigma =0.8$, $k=0.9$, $\mu =0.001 13$, $\beta=0.014$ 图8 (b)中, 蓝线表示摄动天体随时间$t$在$x$方向的运动分量, 黑线表示参数激励响应即探测器周期轨道随时间$t$在$x$方向的运动分量. 由于在该组参数条件下, 内共振引起的能量转移效应显著, 长周期轨道振幅远远大于短周期轨道振幅. 虽然共振响应中同时包含有长短周期的分量, 但是参激周期轨道几乎完全呈现为长周期运动, 如
图8 (c)所示. 此外, 由于非线性因素影响, 摄动天体频率之间精确保持为1:6的关系.
以参数$\mu =0.001$, $\sigma =0.8$, $k=0.9$, $\beta =0.012$为例, 得到调谐参数$\tau =0.000 6$, $\kappa =0.076 7$,以及两组稳态解, (1) $a_{10}=0.023 5$, $a_{20}=0.036 9$, $p<0$, $q>0$,$p^{2}-4q<0$, 稳态解呈稳定特性; (2) $a_{10}=0.013 2$, $a_{20}=0.049 9$, $p<0$,$q<0$, $p^{2}-4q>0$, 稳态解呈现不稳定特性. 取稳定稳态解$a_{10}=0.023 5$,$a_{20}=0.036 9$为参激周期轨道长短周期的振幅, 绘制共振轨道如
图9 所示.
图9 (a)中红线和蓝线分别表示长短周期运动振幅随时间的变化情况,黑线表示长短周期叠加运动振幅随时间变化曲线. 由图可知,该组参数条件下长短周期轨道振幅量级相当, 且由于非线性效应,长短周期轨道频率之间呈现精确的1:3内共振比例关系.
图9 (b)中蓝线和黑线分别表示摄动天体和探测器周期轨道随时间$t$在$x$方向的运动分量.显然共振响应呈现为长短周期叠加运动, 且由于1:3内共振的影响,使得探测器周期轨道振幅呈现亚谐共振状态.此外由于长短周期轨道频率之间的谐振关系, 最终呈现的响应依然呈现周期性,如
图9 (c)所示.
图9 新窗口打开 |
下载原图ZIP |
生成PPT 图9当$\sigma =0.8$, $k=0.9$, $\mu =0.001$, $\beta =0.012$时参激共振轨道示意图 Fig. 9Stable parametric resonance orbit when $\sigma =0.8$, $k=0.9$,$\mu =0.001$, $\beta =0.012$ 通过上述模拟分析, 不难发现, 参激周期轨道与系统参数选取密切相关. 最终参激周期轨道的形状以及周期关系将严格遵循式(44)的表达形式.
值得一提的是: $\mu $, $\sigma $, $k$是与小行星自身特征相关的参数, $\beta $与摄动天体的引力扰动有关. 当参数满足参激共振条件一和条件二时, 系统可得到一个第二类参激主共振轨道或一个和型参激共振轨道. 此外, 参激共振的条件颇为苛刻, 并非所有受摄小行星系统都能满足该条件. 本文所提出的方法为轨道设计中处理引力摄动提供了新的思路.
5 结论 本文将太阳引力视为受摄小行星系统的组成部分,采用非线性振动理论中的参激共振概念,创新性地设计了小行星平衡点附近稳定的参数共振轨道.
(1) 通过引入质量参数$\mu $, 形状参数$\sigma $, 自旋参数$k$以及摄动参数$\beta $,对受摄小行星系统进行建模. 研究发现,系统平衡点位置以及稳定性、平衡点附近运动的固有频率均与4个参数相关.
(2) 通过固定参数$\sigma $和$k$, 定性分析了摄动参数$\beta $对系统的影响. 对于摄动小行星系统而言,普遍存在第二类参激主共振, 在一定条件下, 存在和型参激共振,但是普遍不存在第一类参激主共振和差型参激共振, 且系统普遍存在1:2和1:3内共振.
(3) 以第二类参激主共振和1:3内共振为例, 采用多尺度方法得到参激共振响应的一次近似解,求解了振幅和相位的稳态解并分析其稳定性, 得到由参激共振引起的稳定周期轨道.通过受摄小行星系统的幅频响应曲线和力频响应曲线分析了系统非线性特性.通过分析可知, 由于系统非线性的影响,短周期轨道的运动频率与参数激励频率之间呈现精确的二倍关系, 与此同时,长短周期运动之间呈现精确的1:3内共振. 虽然共振响应轨道同时包含长短周期分量,但是由于频率之间的谐振关系, 使得轨道依然呈现周期性.
此外, 由于粒杆模型将小行星视为由无质量杆连接的质量粒子组成,因此本文提出的参激共振轨道设计方法同样适用于双小行星系统或三小行星系统中参数共振轨道动力学问题.本文的研究成果可以拓展现有小行星附近周期轨道族,为轨道设计中处理引力摄动提供了新的思路.
附录A (A1) $E_i =\dfrac{x_i -x_{o} }{\gamma _{o} },F_i =\dfrac{y_i -y_{o} }{\gamma _{o} }$ (A2) $D_i^2 =E_i^2 +F_i^2$ (A3) $\left.\begin{array}{l} M_1 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {35E_i F_i^3 -15E_i F_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^9 }} \\ M_2 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( 105E_i^2 F_i^2 -15E_i^2 D_i^2 -15F_i^2 D_i^2 +3D_i^4 \right)}{2\gamma _{o}^3 D_i^9 }} \\ M_3 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {105E_i^3 F_i -45E_i F_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^9 }} \\ M_4 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {35E_i^4 -30E_i^2 D_i^2 +3D_i^4 } \right)}{2\gamma _{o}^3 D_i^9 }} \\ \end{array}\right\}$ (A4) $\left.\begin{array}{l} M_5 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {15E_i^3 -9E_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^7 }}\\ M_6 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {15E_i^2 F_i -3F_i D_i^2 } \right)}{\gamma _{o}^3 D_i^7 }} \\ M_7 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {15E_i F_i^2 -3E_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^7 }} \\ \end{array}\right\}$ (A5) $\left.\begin{array}{l} N_1 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {35F_i^4 -30F_i^2 D_i^2 +3D_i^4 } \right)}{2\gamma _{o}^3 D_i^9 }} \\ N_2 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {105E_i F_i^3 -45E_i F_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^9 }} \\ N_3 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( 105E_i^2 F_i^2 -15F_i^2 D_i^2 -15E_i^2 D_i^2 +3D_i^4 \right)}{2\gamma _{o}^3 D_i^9 }} \\ N_4 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {35E_i^3 F_i -15E_i F_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^9 }} \\ \end{array}\right\}$ (A6) $\left.\begin{array}{l} N_5 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {15E_i^2 F_i -3F_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^7 }} \\ N_6 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {15E_i F_i^2 -3E_i D_i^2 } \right)}{\gamma _{o}^3 D_i^7 }} \\ N_7 =\sum\limits_{i=1}^3 {\dfrac{\mu _i k\left( {15F_i^3 -9F_i D_i^2 } \right)}{2\gamma _{o}^3 D_i^7 }} \\ \end{array}\right\}$ 附录B (B1) $\begin{array}{l} W_{11} =\Big(3M_1 \bar{{\varGamma }}_1^2 \varGamma _2 +M_2 \bar{{\varGamma }}_1^2 +2M_2 \bar{{\varGamma }}_1 \varGamma _2 +3M_4 +M_3 \varGamma _2 +\\ 2M_3 \bar{{\varGamma }}_1 \Big){e}^{{i}\kappa T_2 }\bar{{A}}_1^2 A_2 +\Big(6M_1 \varGamma _1 \varGamma _2 \bar{{\varGamma }}_2 +6M_4 +2M_2 \varGamma _1 \bar{{\varGamma }}_2 +\\ 2M_3 \varGamma _2 +2M_3 \varGamma _1 +2M_2 \varGamma _2 \bar{{\varGamma }}_2 +2M_2 \varGamma _1 \varGamma _2 +2M_3 \bar{{\varGamma }}_2 \Big)A_1 A_2 \bar{{A}}_2 +\\ \Big( 3M_1 \varGamma _1^2 \bar{{\varGamma }}_1 +M_2 \varGamma _1^2 +2M_2 \varGamma _1 \bar{{\varGamma }}_1 +M_3 \bar{{\varGamma }}_1 +2M_3 \varGamma _1 +\\ 3M_4\Big)A_1^2 \bar{{A}}_1\end{array}$ (B2) $\begin{array}{l} S_{11} =\Big( M_1 \varGamma _1^3 +M_2 \varGamma _1^2 +M_3 \varGamma _1 +M_4\Big){e}^{-{i}\kappa T_2 }A_1^3 +\Big( 6M_1 \varGamma _1 \bar{{\varGamma }}_1 \varGamma _2 +\\ 6M_4 +2M_2 \varGamma _1 \bar{{\varGamma }}_1 +2M_3 \varGamma _2 +2M_3 \varGamma _1 +2M_2 \bar{{\varGamma }}_1 \varGamma _2 +2M_3 \bar{{\varGamma }}_1 +\\ 2M_2 \varGamma _1 \varGamma _2 \Big)A_1 \bar{{A}}_1 A_2 +\Big( 3M_1 \varGamma _2^2 \bar{{\varGamma }}_2 +M_2 \varGamma _2^2 +2M_2 \varGamma _2 \bar{{\varGamma }}_2 +\\ 2M_3 \varGamma _2 +M_3 \bar{{\varGamma }}_2 +3M_4\Big)A_2^2 \bar{{A}}_2\end{array}$ (B3) $\begin{array}{l} W_{22} =\Big( 3N_1 \bar{{\varGamma }}_1^2 \varGamma _2 +N_2 \bar{{\varGamma }}_1^2 +2N_2 \bar{{\varGamma }}_1 \varGamma _2 +N_3 \varGamma _2 +2N_3 \bar{{\varGamma }}_1 +\\ 3N_4\Big)\bar{{A}}_1^2 A_2 {e}^{{i}\kappa T_2 } +\Big( 6N_1 \varGamma _1 \varGamma _2 \bar{{\varGamma }}_2 +6N_4 +2N_2 \varGamma _1 \bar{{\varGamma }}_2 +2N_3 \varGamma _2 +\\ 2N_3 \varGamma _1 +2N_2 \varGamma _2 \bar{{\varGamma }}_2 +2N_3 \bar{{\varGamma }}_2 +2N_2 \varGamma _1 \varGamma _2 \Big)A_1 A_2 \bar{{A}}_2 +\\ \Big( 3N_1 \varGamma _1^2 \bar{{\varGamma }}_1 +N_2 \varGamma _1^2 +2N_2 \varGamma _1 \bar{{\varGamma }}_1 +N_3 \bar{{\varGamma }}_1 +2N_3 \varGamma _1 +\\ 3N_4\Big)A_1^2 \bar{{A}}_1\end{array}$ (B4) $\begin{array}{l} S_{22} =\Big( N_1 \varGamma _1^3 +N_2 \varGamma _1^2 +N_3 \varGamma _1 +N_4\Big)A_1^3 {e}^{-{i}\kappa T_2 } +\Big( 6N_1 \varGamma _1 \bar{{\varGamma }}_1 \varGamma _2 +6N_4 +\\ 2N_2 \varGamma _1 \bar{{\varGamma }}_1 +2N_3 \varGamma _2 +2N_3 \varGamma _1 +2N_2 \bar{{\varGamma }}_1 \varGamma _2 +2N_3 \bar{{\varGamma }}_1 +\\ 2N_2 \varGamma _1 \varGamma _2\Big)A_1 \bar{{A}}_1 A_2 +\Big( 3N_1 \varGamma _2^2 \bar{{\varGamma }}_2 +N_2 \varGamma _2^2 +2N_2 \varGamma _2 \bar{{\varGamma }}_2 +2N_3 \varGamma _2 +\\ N_3 \bar{{\varGamma }}_2 +3N_4 \Big)A_2^2 \bar{{A}}_2\end{array}$ (B5) $\begin{array}{l} G_{11} =R_{11} +{i}I_{11} =3M_1 \bar{{\varGamma }}_1^2 \varGamma _2 +M_2 \bar{{\varGamma }}_1^2 +2M_2 \bar{{\varGamma }}_1 \varGamma _2 +M_3 \varGamma _2 +\\ 2M_3 \bar{{\varGamma }}_1 +3M_4 +3N_1 \bar{{\varGamma }}_1^3 \varGamma _2 +N_2 \bar{{\varGamma }}_1^3 +2N_2 \bar{{\varGamma }}_1^2 \varGamma _2 + N_3 \bar{{\varGamma }}_1 \varGamma _2 +\\ 2N_3 \bar{{\varGamma }}_1^2 +3N_4 \bar{{\varGamma }}_1\end{array}$ (B6) $\begin{array}{l} G_{12} =R_{12} +{i}I_{12} =6M_1 \varGamma _1 \varGamma _2 \bar{{\varGamma }}_2 +2M_2 \varGamma _1 \varGamma _2 +2M_2 \varGamma _1 \bar{{\varGamma }}_2 +\\ 2M_2 \varGamma _2 \bar{{\varGamma }}_2 +2M_3 \varGamma _1 +2M_3 \varGamma _2 +2M_3 \bar{{\varGamma }}_2 +6M_4 +\\ 6N_1 \varGamma _1 \bar{{\varGamma }}_1 \varGamma _2 \bar{{\varGamma }}_2 + 2N_2 \varGamma _1 \bar{{\varGamma }}_1 \varGamma _2 +2N_2 \varGamma _1 \bar{{\varGamma }}_1 \bar{{\varGamma }}_2 +2N_2 \bar{{\varGamma }}_1 \varGamma _2 \bar{{\varGamma }}_2 +\\ 2N_3 \varGamma _1 \bar{{\varGamma }}_1 +2N_3 \bar{{\varGamma }}_1 \varGamma _2 +2N_3 \bar{{\varGamma }}_1 \bar{{\varGamma }}_2 +6N_4 \bar{{\varGamma }}_1\end{array}$ (B7) $\begin{array}{l} G_{13} =R_{13} +{i}I_{13} =3M_1 \varGamma _1^2 \bar{{\varGamma }}_1 +M_2 \varGamma _1^2 +2M_2 \varGamma _1 \bar{{\varGamma }}_1 +M_3 \bar{{\varGamma }}_1 +\\ 2M_3 \varGamma _1 +3M_4 +3N_1 \varGamma _1^2 \bar{{\varGamma }}_1^2 +N_2 \varGamma _1^2 \bar{{\varGamma }}_1 +2N_2 \varGamma _1 \bar{{\varGamma }}_1^2+ \\ N_3 \bar{{\varGamma }}_1^2 +2N_3 \varGamma _1 \bar{{\varGamma }}_1 +3N_4 \bar{{\varGamma }}_1\end{array}$ (B8) $\begin{array}{l} G_{21} =R_{21} +{i}I_{21} =M_1 \varGamma _1^3 +M_2 \varGamma _1^2 +M_3 \varGamma _1 +M_4 +\\ N_1 \varGamma _1^3 \bar{{\varGamma }}_2 +N_2 \varGamma _1^2 \bar{{\varGamma }}_2 +N_3 \varGamma _1 \bar{{\varGamma }}_2 +N_4 \bar{{\varGamma }}_2\end{array}$ (B9) $\begin{array}{l} G_{22} =R_{22} +{i}I_{22} =6M_1 \varGamma _1 \bar{{\varGamma }}_1 \varGamma _2 +2M_2 \varGamma _1 \varGamma _2 +2M_2 \varGamma _1 \bar{{\varGamma }}_1 + \\ 2M_2 \bar{{\varGamma }}_1 \varGamma _2 +2M_3 \varGamma _1 +2M_3 \varGamma _2 +2M_3 \bar{{\varGamma }}_1 +6M_4 + \\ 6N_1 \varGamma _1 \bar{{\varGamma }}_1 \varGamma _2 \bar{{\varGamma }}_2 +2N_2 \varGamma _1 \varGamma _2 \bar{{\varGamma }}_2 +2N_2 \varGamma _1 \bar{{\varGamma }}_1 \bar{{\varGamma }}_2 +2N_2 \bar{{\varGamma }}_1 \varGamma _2 \bar{{\varGamma }}_2 +\\ 2N_3 \varGamma _1 \bar{{\varGamma }}_2 +2N_3 \varGamma _2 \bar{{\varGamma }}_2 +2N_3 \bar{{\varGamma }}_1 \bar{{\varGamma }}_2 +6N_4 \bar{{\varGamma }}_2\end{array}$ (B10) $\begin{array}{l} G_{23} =R_{23} +{i}I_{23} =3M_1 \varGamma _2^2 \bar{{\varGamma }}_2 +M_2 \varGamma _2^2 +2M_2 \varGamma _2 \bar{{\varGamma }}_2 +2M_3 \varGamma _2 + \\ M_3 \bar{{\varGamma }}_2 +3M_4 +3N_1 \varGamma _2^2 \bar{{\varGamma }}_2^2 +N_2 \varGamma _2^2 \bar{{\varGamma }}_2 +2N_2 \varGamma _2 \bar{{\varGamma }}_2^2+ \\ 2N_3 \varGamma _2 \bar{{\varGamma }}_2 +N_3 \bar{{\varGamma }}_2^2 +3N_4 \bar{{\varGamma }}_2\end{array}$ (B11) $G_{20} =R_{20} +{i}I_{20} =\dfrac{3k\beta \left( {1-\bar{{\varGamma }}_2^2 -2{i}\bar{{\varGamma }}_2 } \right)}{4}$ [1] 柳森 , 党雷宁 , 赵君尧 等 . 小行星撞击地球的超高速问题力学学报 , 2018 ,50(6 ):1311 -1327 [本文引用: 1] ( Liu Sen Dang Leining Zhao Junyao et al . Hypervelocity issues of Earth impact by asteroidsChinese Journal of Theoretical and Applied Mechanics 2018 ,50(6 ):1311 -1327 (in Chinese)) [本文引用: 1] [2] Fujiwara A Kawaguchi J Yeomans DK et al . The rubble-pile asteroid itokawa as observed by HayabusaScience 2006 ,312(5778 ):1330 -1334 DOI URL PMID [本文引用: 1] During the interval from September through early December 2005, the Hayabusa spacecraft was in close proximity to near-Earth asteroid 25143 Itokawa, and a variety of data were taken on its shape, mass, and surface topography as well as its mineralogic and elemental abundances. The asteroid's orthogonal axes are 535, 294, and 209 meters, the mass is 3.51 x 10(10) kilograms, and the estimated bulk density is 1.9 +/- 0.13 grams per cubic centimeter. The correspondence between the smooth areas on the surface (Muses Sea and Sagamihara) and the gravitationally low regions suggests mass movement and an effective resurfacing process by impact jolting. Itokawa is considered to be a rubble-pile body because of its low bulk density, high porosity, boulder-rich appearance, and shape. The existence of very large boulders and pillars suggests an early collisional breakup of a preexisting parent asteroid followed by a re-agglomeration into a rubble-pile object.
[3] Muller T Durech J Ishiguro M et al . Hayabusa-2 Mission Target Asteroid 162173 Ryugu (1999 JU3): Searching for the object's spin-axis orientationAstronomy & Astrophysics 2017 ,599:A103 [本文引用: 1] [4] Lauretta DS Balram-knutson SS Beshore E et al . OSIRIS-REx: Sample Return from Asteroid (101955) BennuSpace Science Reviews 2017 ,212(1-2 ):925 -984 DOI URL [本文引用: 1] [5] 崔平远 , 乔栋 . 小天体附近轨道动力学与控制研究现状与展望力学进展 , 2013 ,43(5 ):526 -539 DOI URL [本文引用: 1] 小天体探测是未来深空探测的重点领域之一, 而小天体附近轨道动力学与控制问题是小天体探测任务迫切需要解决的关键问题. 该问题涉及形状不规则小天体附近的动力学环境建模与小天体附近轨道动力学机理. 本文从不规则形状小天体引力场的建模、小天体附近的自然轨道动力学、小天体附近的受控轨道动力学3 个方面综述了小天体附近轨道动力学与控制的研究现状与发展趋势, 并分析了小天体附近轨道动力学所面临的挑战与难题, 最后对我国未来小天体探测任务可能涉及的轨道动力学与控制问题的发展方向进行了展望.
( Cui Pingyuan Qiao Dong Advances in Mechanics 2013 ,43(5 ):526 -539 (in Chinese)) DOI URL [本文引用: 1] Small celestial body exploration is one of the key areas of deep space exploration in the future. The orbital dynamics and control problem near small celestial bodies is crucial in such explorations, and urgent to be treated. This problem involves the modeling of dynamics environment around an irregularshaped small celestial body, and the orbital dynamics mechanism near the small celestial body. In this paper, we survey the gravitational field modeling of irregular-shaped small celestial body, natural orbital dynamics and control, and controlled orbital dynamics near small celestial body. We introduce state-ofthe-art and trends for the development of orbital dynamics and control near small celestial bodies. The challenges and difficulties encountered are analyzed. Finally, we discuss the prospects for the development direction and key issues of orbital dynamics and control for Chinese future mission for exploring small celestial bodies.
[6] 曾祥远 , 李俊峰 , 刘向东 . 细长小行星探测动力学与控制 . 北京: 清华大学出版社, 2019 [本文引用: 1] ( Zeng Xiangyuan Li Junfeng Liu Xiangdong Dynamics and Control over Elongated Asteroids . Beijing: Tsinghua University Press, 2019 (in Chinese)) [本文引用: 1] [7] Nardi L Palomba E Longobardo A et al . Mapping olivine abundance on asteroid (25143) Itokawa from Hayabusa_NIRS dataIcarus 2019 ,14:321 -349 [本文引用: 1] [8] Scheeres DJ Proceedings of the American Control Conference. Portland, OR: American Control Conference , 2014 : 1584 -1598 . [9] Broschart SB Scheeres DJ Journal of Guidance Control and Dynamics 2005 ,28(2 ):343 -354 [本文引用: 2] [10] 孙加亮 , 田强 , 胡海岩 . 多柔体系统动力学建模与优化研究进展力学学报 , 2019 ,51(6 ):1565 -1586 [本文引用: 1] ( Sun Jialiang Tian Qiang Hu Haiyan Chinese Journal of Theoretical and Applied Mechanics 2019 ,51(6 ):1565 -1586 (in Chinese)) [本文引用: 1] [11] 曹登庆 , 白坤朝 , 丁虎 等 . 大型柔性航天器动力学与振动控制研究进展力学学报 , 2019 ,51(1 ):1 -13 [本文引用: 1] ( Cao Dengqing Bai Kunchao Ding Hu et al . Advances in dynamics and vibration control of large-scale flexible spacecraftChinese Journal of Theoretical and Applied Mechanics 2019 ,51(1 ):1 -13 (in Chinese)) [本文引用: 1] [12] Scheeres DJ 9th Annual Space Flight Mechanics Meeting. Breckenridge, CO: Advances in the Astronautical Sciences , 1999 , 1-2:855 -873 [本文引用: 1] [13] Sawai S Scheeres DJ Broschart SB Journal of Guidance Control and Dynamics 2002 ,25(4 ):786 -795 [本文引用: 1] [14] Sawai S Scheeres DJ Advances in the Astronautical Sciences 2001 ,108:781 -796 [本文引用: 1] [15] Broschart SB Scheeres DJ Journal of Guidance Control and Dynamics 2007 ,30(2 ):601 -610 [本文引用: 1] [16] Zhang P Ma TH Zhao B et al . Robust linear quadratic regulator via sliding mode guidance for spacecraft orbiting a tumbling asteroidMathematical Problems in Engineering 2015 ,2015(Pt.21 ):947843 [本文引用: 1] [17] Zeng XY Gong SP Li JF et al . Solar sail body-fixed hovering over elongated asteroidsJournal of Guidance, Control, and Dynamics 2016 ,39(6 ):1223 -1231 DOI URL [本文引用: 1] [18] Daniel C Alexis P Anne L Celestial Mechanics and Dynamical Astronomy volume 2015 ,123(2 ):223 -238 [本文引用: 1] [19] Zhao CY Zhang MJ Wang HB et al . Two-dimensional phase plane structure and the stability of the orbital motion for space debris in the geosynchronous ringAdvances in Space Research 2013 ,52(4 ):677 -684 DOI URL [20] Hamilton DP Burns JA Icarus 1992 ,96(1 ):43 -64 DOI URL [21] Heiligers J Scheeres DJ Journal of Guidance, Control, and Dynamics 2018 ,41(9 ):1947 -1962 DOI URL [本文引用: 1] [22] Morrow E Scheeres DJ Lubin D Journal of Spacecraft and Rockets 2001 ,38(2 ):279 -286 DOI URL [本文引用: 1] [23] Williams T Abate M Journal of Spacecraft and Rockets 2009 ,46(5 ):967 -975 DOI URL [本文引用: 1] [24] Giancotti M Funase R The 63rd International Astronautical Congress , 2012 [本文引用: 1] [25] Feng JL Hou XY Communications in Nonlinear Science and Numerical Simulation 2019 ,76, 71 -91 DOI URL [本文引用: 1] [26] Xin XS Scheeres DJ Hou XY Celestial Mechanics and Dynamical Astronomy 2016 ,126(4 ):405 -432 DOI URL [本文引用: 1] [27] 辛晓生 . 小行星探测器轨道动力学. [博士论文]南京: 南京大学 , 2017 : 89 -108 [本文引用: 1] ( Xin Xiaosheng Nanjing: Nanjing University , 2017 : 89 -108 (in Chinese)) [本文引用: 1] [28] 刘莹莹 , 刘睿 , 周军 . 摄动力对绕飞小行星航天器轨道的影响飞行力学 , 2008 ,26(3 ):44 -48 [本文引用: 1] ( Liu Yingying Liu Rui Zhou Jun Flight Dynamics 2008 ,26(3 ):44 -48 (in Chinese)) [本文引用: 1] [29] 倪彦硕 , 宝音贺西 , 李俊峰 . 考虑太阳摄动的小行星附近轨道动力学深空探测学报 , 2014 ,1(1 ):67 -74 [本文引用: 2] ( Ni Yanshuo Baoyin Hexi Li Junfeng Journal of Deep Space Exploration 2014 ,1(1 ):67 -74 (in Chinese)) [本文引用: 2] [30] Qian YJ Yang LY Yang XD et al . Parametric stability analysis for planar bicircular restricted four-body problemAstrodynamics 2018 ,2:147 -159 DOI URL [本文引用: 2] [31] Qian YJ Yang XD Wu H et al . Gyroscopic modes decoupling method in parametric instability analysis of gyroscopic systemsActa Mechanica Sinica 2018 ,222(2 ):963 -969 [32] 司震 , 钱霙婧 , 杨晓东 等 . 基于扰动粒杆模型的强不规则小行星的参激稳定分析北京力学会第二十五届学术年会会议论文集 . 2019 : 827 -828 ( Si Zhen Qian Yingjing Yang Xiaodong et al . Parametric stability analysis for irregular-shaped asteroids based on perturbed particle-linkage modelProceedings of the 25th Annual Conference of Beijing Society of Theoretical and Applied mechanics . 2019 : 827 -828 (in Chinese)) [33] Lei Hanlun Circi C Ortore E Monthly Notices of the Royal Astronomical Society 2019 ,485(2 ):2731 -2743 DOI URL [本文引用: 1] [34] Nayfeh AH Mook DT New York: Clarendon , 1979 : 384 -390 [本文引用: 2] [35] 李晓玉 , 岳宝增 . 基于多尺度方法的平动圆柱贮箱航天器刚-液耦合动力学研究力学学报 , 2019 ,51(5 ):1448 -1454 [本文引用: 1] ( Li Xiaoyu Yue Baozeng Chinese Journal of Theoretical and Applied Mechanics 2019 ,51(5 ):1448 -1454 (in Chinese)) [本文引用: 1] [36] Yang HW Li S Xu C Research in Astronomy and Astrophysics 2018 ,18(7 ):84 DOI URL [本文引用: 2] [37] Zeng XY Jiang FH Li JF et al . Study on the connection between the rotating mass dipole and natural elongated bodiesAstrophysics and Space Science 2015 ,356(1 ):29 -42 DOI URL [38] Lan L Yang HW Baoyin HX et al . Retrograde near-circular periodic orbits near equatorial planes of small irregular bodiesAstrophysics & Space Science 2017 ,362(9 ):169 -182 [39] Zeng XY Zhang YL Yu Y et al . The dipole segment model for axisymmetrical elongated asteroidsAstronomical Journal 2018 ,155(2 ):85 -102 DOI URL [本文引用: 1] [40] Lei HL Xu B Communications in Nonlinear Science and Numerical Simulation 2015 ,29(1-3 ):441 -458 DOI URL [本文引用: 1] 
,2), 杨晓东, 张伟北京工业大学材料与制造学部, 机械结构非线性振动与强度北京市重点实验室, 北京 100124
新窗口打开|下载原图ZIP|生成PPT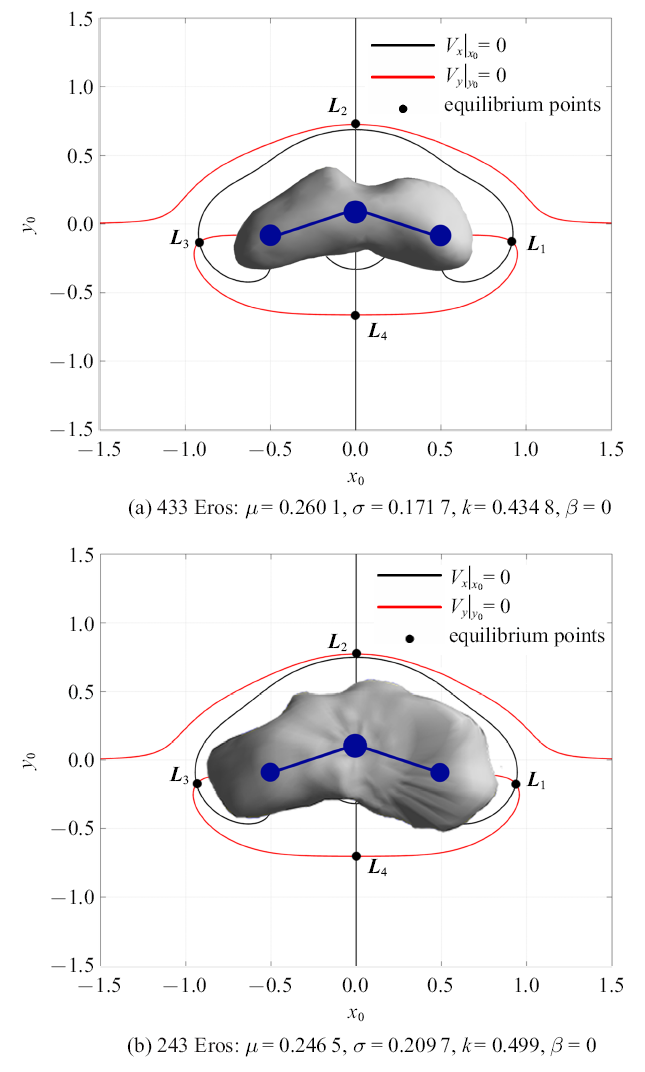
新窗口打开|下载原图ZIP|生成PPT
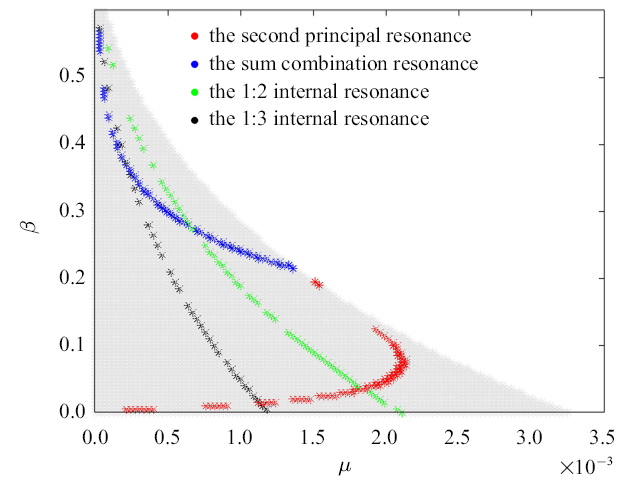新窗口打开|下载原图ZIP|生成PPT
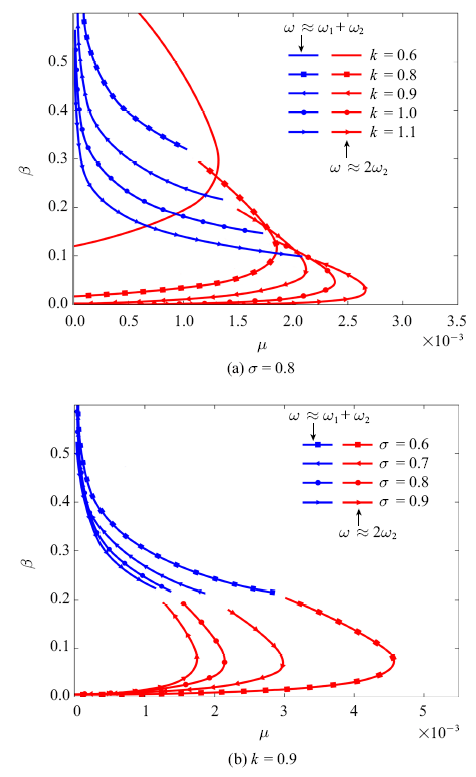新窗口打开|下载原图ZIP|生成PPT
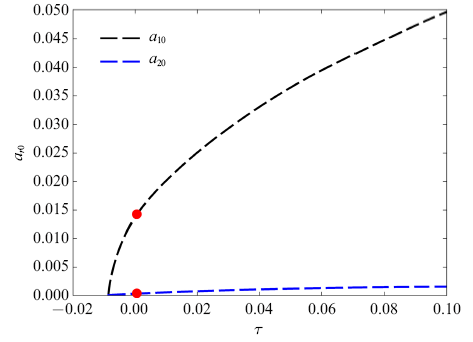新窗口打开|下载原图ZIP|生成PPT
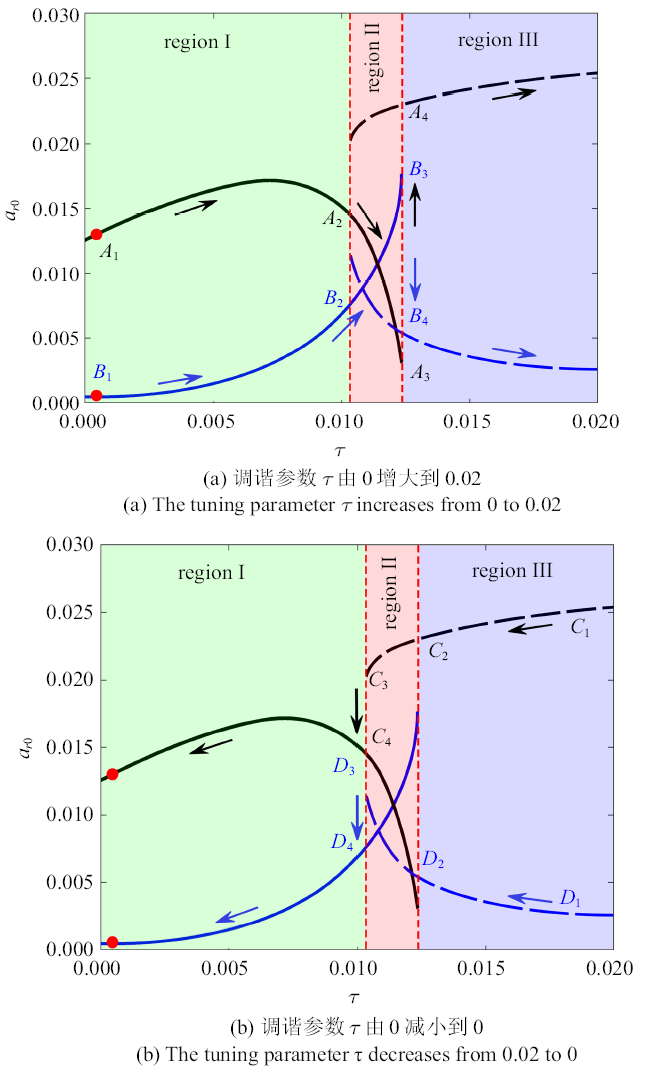新窗口打开|下载原图ZIP|生成PPT
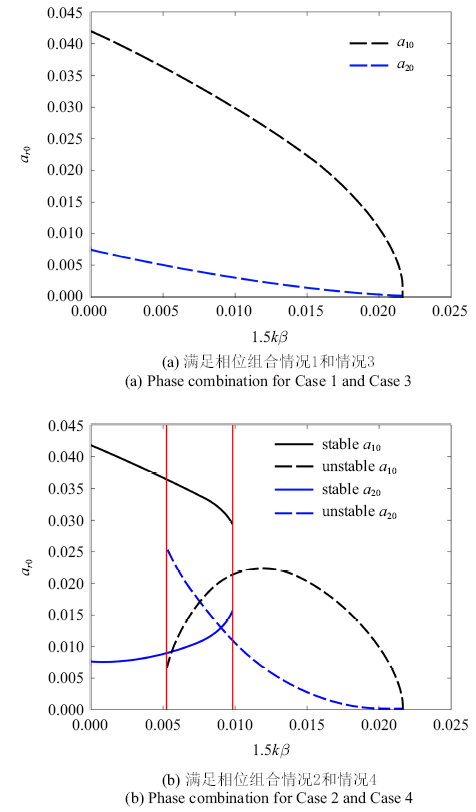新窗口打开|下载原图ZIP|生成PPT
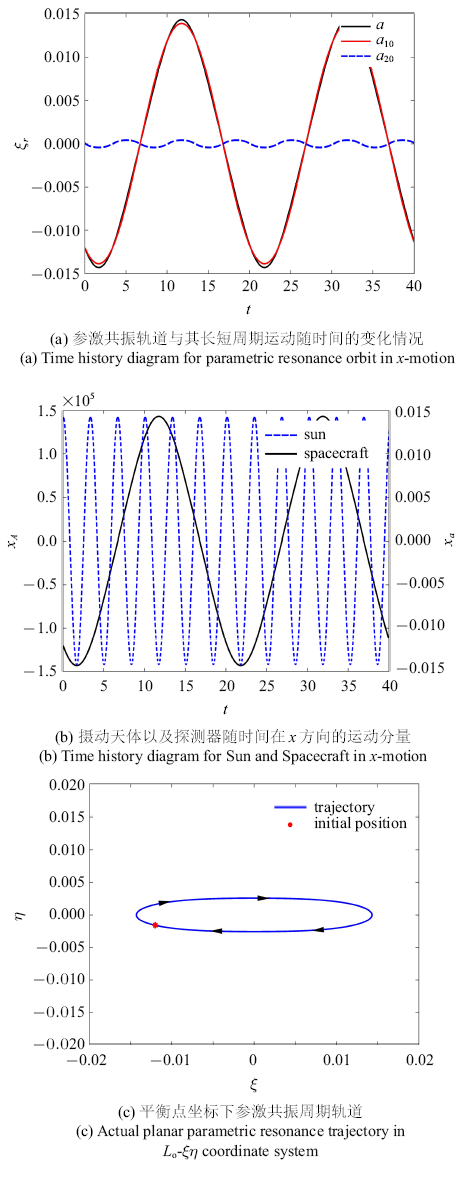新窗口打开|下载原图ZIP|生成PPT
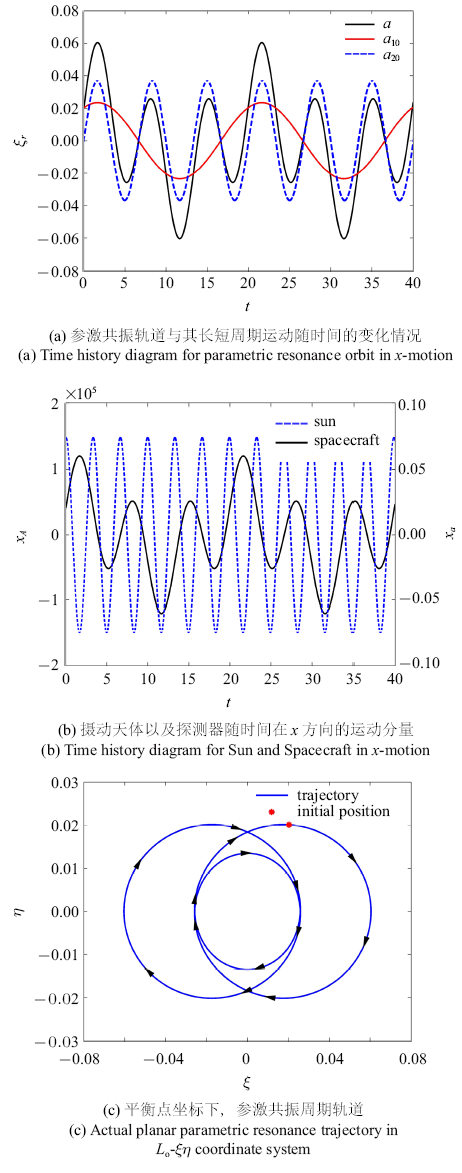新窗口打开|下载原图ZIP|生成PPT
