 ,*,2), 姜文安*,?, 张晓芳*, 韩修静*, 毕勤胜*
,*,2), 姜文安*,?, 张晓芳*, 韩修静*, 毕勤胜*COMPLICATED BURSTING BEHAVIORS AS WELL AS THE MECHANISM OF A THREE DIMENSIONAL NONLINEAR SYSTEM 1)
Ma Xindong ,*,2), Jiang Wenan*,?, Zhang Xiaofang*, Han Xiujing*, Bi Qinsheng*
,*,2), Jiang Wenan*,?, Zhang Xiaofang*, Han Xiujing*, Bi Qinsheng*通讯作者: 2) 马新东, 讲师, 主要研究方向: 非线性动力学. E-mail:1000004942@mail.ujs.edu.cn
收稿日期:2020-06-29接受日期:2020-09-1网络出版日期:2020-11-18
| 基金资助: |
Received:2020-06-29Accepted:2020-09-1Online:2020-11-18
作者简介 About authors

摘要
由多时间尺度耦合效应引起的簇发振荡行为是非线性动力学研究的重要课题之一.本文针对一类参数激励下的三维非线性电机系统(该系统可以描述两种自激同极发电机系统的动力学行为,两种系统在数学上等效),研究了当参数激励频率远小于系统自然频率时的各种复杂簇发振荡行为及其产生机理.通过快慢分析方法, 将参数激励作为慢变参数,得到了非自治系统对应的广义自治系统及快子系统和慢变量,并给出了快子系统的稳定性和分岔条件以及系统关于典型参数的单参数分岔图.借助转换相图与分岔图的叠加, 分析了对称式delayed subHopf/fold cycle簇发振荡的产生机理及其动力学转迁, 即delayed subHopf/fold cycle簇发振荡、焦点/焦点型对称式叉形分岔滞后簇发振荡和焦点/焦点型叉形分岔滞后簇发振荡.研究结果表明, 系统会出现两种不同的分岔滞后形式, 一种是亚临界Hopf分岔滞后,另一种是叉形分岔滞后,而且控制参数显著影响平衡点的稳定性和分岔滞后区间的宽度.同时初始点的选取则会影响系统动力学行为的对称性.本文的研究进一步加深了对由分岔滞后引起的簇发振荡的认识和理解.
关键词:
Abstract
Bursting oscillation behavior induced by multiple time-scale coupling effect is one of the important topics in nonlinear dynamics research. In this paper, complicated bursting oscillation behaviors as well as their generation mechanism of a three-dimensional nonlinear dynamo system with slowly changing parametric excitation are revealed when the excitation frequency is much smaller than the natural frequency. The system can be used to describe the dynamic behaviors of two kinds of self-exciting homopolar dynamo systems, which are mathematically equivalent. By treating the parametric excitation as a slow-varying parameter, the generalized autonomous system corresponding to the nonautonomous system as well as the fast subsystem and the slow variable are got based on the fast-slow analysis method. Then, the stabilities and bifurcations of the fast subsystem are investigated theoretically, and the correctness of the theoretical analysis is verified by a one-parameter bifurcation diagram related to a typical parameter. With the help of the overlapping of the transformed phase diagram and bifurcation diagram, the mechanism of the symmetric delayed subHopf/fold cycle bursting oscillation as well as its dynamic transitions, i.e. delayed subHopf/fold cycle bursting oscillation, symmetric delayed pitchfork bursting oscillation of focus/focus type and delayed pitchfork bursting oscillation of focus/focus type are analyzed. The result shows that, two different forms of bifurcation delay phenomenon will appear under different parameter conditions, one is the subcritical Hopf bifurcation delay, and the other one is the pitchfork bifurcation delay. In addition, our research indicates that the stabilities of the equilibrium points and the width of the pitchfork bifurcation delay interval are both influenced by the control parameter. Meanwhile, we also find that the symmetry of the dynamic behaviors is affected by the choice of the initial values. The study of this paper further deepens the understanding and the comprehending of the different bursting patterns induced by bifurcation delay phenomenon.
Keywords:
PDF (4697KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
马新东, 姜文安, 张晓芳, 韩修静, 毕勤胜. 一类三维非线性系统的复杂簇发振荡行为及其机理1). 力学学报[J], 2020, 52(6): 1789-1799 DOI:10.6052/0459-1879-20-231
Ma Xindong, Jiang Wenan, Zhang Xiaofang, Han Xiujing, Bi Qinsheng.
引言
多尺度效应广泛存在于自然界的各种实际系统中,如不同神经细胞的簇放电行为[1-3]、飞机的高速旋转与慢速平动的耦合[4]、化学系统中的同质液相催化反应[5]和周期激励扰动下齿轮振荡器的快慢行为[6]等.多尺度的耦合往往使系统表现出大幅振动和小幅振动的组合[7],这种现象被称为簇发振荡[8-10].大幅振动通常对应着系统在大振幅极限环内的运动,小幅振动对应着系统在平衡点或小振幅极限环内的运动.连接大幅振动和小幅振动的可以是分岔[11-12],也可以是其他形式的动力学行为, 如脉冲式爆炸(PSE)[13-14]和吸引子的快速逃逸(speed escape of attractor)[15]等.一般说来, 多尺度效应可以分成三类: 第一种是时域上的, 即系统各状态变量之间存在变化速率上的显著差异,数学方程中出现小参数扰动($0<\varepsilon \ll1$); 第二种是频域上的,即系统中存在不同量级的频率耦合,数学方程中出现与系统自然频率有着量级差异的周期激励频率($0<\omega _{周期}\ll \omega _{自然})$;第三种是时域和频域的耦合, 由于快慢分析方法的限制,这类系统的研究存在较大的困难, 目前只有较少的文献[16,17,18].但这几篇文献也仅仅研究了激励频率远大于小参数的情况. 对于前两类多尺度效应,人们进行了深入研究, 取得了丰富的成果. 如在时域多尺度方面,古华光[19]利用实验和理论相结合的方法,揭示了外激、参激和噪声等不同调控机制下神经元的多种簇放电模式及其转迁规律;樊登贵等[20]从基于基底神经节-丘脑皮层电路的帕金森神经元网络出发,给出了电荷平衡双相脉冲-深部脑刺激的最优控制, 并进行了生理实验验证;包伯成等[21]提出了一种具有快慢结构的三维Morris-Lecar神经元模型,通过分岔图、时间序列等分析了混沌簇发和周期簇发等的机理;Desroches等[22]研究了由尖峰加周期分岔引起的簇发振荡现象,在这种动力学行为中鸭式解起到了核心作用.
在频域多尺度方面, 郑健康等[23]研究了参数激励下一类三维混沌电路系统由叉形分岔滞后诱发的不同簇发行为及其机理;韩青爽等[24]利用分岔图、时间历程图等分析了周期激励下水轮机调速系统高温气动薄膜的簇发特性;Zhou等[25]分析了两个参数激励下最小化学反应系统的簇发,给出了4种基于跨临界分岔滞后的新型簇发形式;Makouo和Woafo[26]在数值方面分析了两种激励下van derPol振荡器的周期和混沌簇发现象, 并进行了实验验证;Kovacic和Lenci[27]研究了低角激励频率下纯非线性振子的簇发,这种振动模式是由绕慢流形的快速振荡组成.
自激系统是自然界中广泛存在一类动力系统, 它的振荡由系统自身的运动维持,如薄壁可缩软管的自激振荡现象[28],轮轨摩擦自激振荡引起的钢轨波磨现象[29],热声发动机的起振[30]和激波串的自激振荡[31]等.如果自激系统某些参数发生周期变化且周期变化频率远小于系统固有频率时,系统会出现簇发振荡等丰富的动力学行为.如Zdzislaw[32]研究了圆盘式单极发电机通过一个小振幅正弦电压发生器向直流电动机供电时的簇发振荡、混沌振荡等的产生条件.Shaw等[33]对辉光放电等离子体自激装置中的"fold/foldcycle"型混沌簇发和混沌尖峰振荡等进行了实验研究.Wang和Ma[34]给出了噪声影响下简化光学参量振荡器的簇发振荡产生机理.时培明等[35]分析了一类含准周期参激刚度和摩擦阻尼的非线性扭振系统的周期簇发现象及其动力学转迁.尽管对于自激系统不同形式的簇发及其机理研究已经得到了丰富的成果,但由于多尺度效应的复杂性, 使得这类系统的动力学特性仍需要进一步研究.本文针对一类自激单圆盘单机发电机三维非线性动力系统[36-37],研究了系统在参数激励作用下的不同簇发行为, 如图1所示.该三维非线性系统可以描述两种自激同极发电机系统的动力学行为,这两种发动机系统在数学上是等效的, 都含有法拉第圆盘和线圈,不同的是一个含电容器, 另一个含与线圈串联的电机. 系统的数学模型如下
其中, $x$表示系统的重标电流, $y$表示圆盘的角转动速度, $z$表示电容器的电荷或电机的角速度. $\alpha $表示力偶, $\kappa $表示机械摩擦,$\beta ^{-1}$表示测量电枢的转动惯量或电容, $\rho$表示电动机的机械摩擦或漏泄电阻. 这里将参数$\beta $用函数$\beta _0 +\beta _1\cos \omega t$调制, 其中激励频率$\omega $满足$0<\omega \ll1$. 这样$\omega$与系统固有频率$\omega _0 $之间出现了量级差异,系统(1)成为一个典型的两时间尺度自激系统, 其中方程(1)是快子系统,方程$\dot{{\beta }}=-\omega \beta _1 \sin \omega t$是慢子系统.该系统动力学行为的研究可以作为类似非线性低维系统研究的基础,可以用于描述地球物理流体动力学中某些有趣的现象.诸如地球液态金属核中自激磁流体动力发电机作用产生的主要地磁场和地球大气-海洋系统的"厄尔尼诺-南方涛动"等,它们的动力学行为会表现出类似于非线性弛豫振荡(或簇发振荡)的特性,这是由大气和海洋之间复杂的尺度效应相互作用的结果.
图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1参数$\beta _0 =1$, $\beta _1 =0.8$, $\alpha =2$, $\kappa =1$, $\omega =0.01$时的不同簇发行为
Fig. 1Different patterns of bursting oscillations for $\beta _0 =1$, $\beta _1 =0.8$, $\alpha =2$, $\kappa =1$ and $\omega=0.01$
本文以三维非线性电机系统(1)为例, 围绕多时间尺度簇发振荡问题,旨在揭示亚临界Hopf分岔滞后和叉形分岔滞后行为诱发的多种簇发振荡现象机理,以及典型参数对簇发动力学的影响. 本文的组织结构如下: 在第1节中,研究了快子系统的稳定性和分岔, 给出了Hopf分岔、叉形分岔等典型分岔的产生机制.利用$(\beta ,x)$平面内的相图与分岔图的叠加, 第2节分析了对称式亚临界Hopf分岔滞后簇发产生机理. 第3节给出了对称式亚临界Hopf分岔滞后簇发随参数$\rho $变化的动力学转迁, 得到了亚临界Hopf分岔滞后簇发、焦点/焦点型对称式叉形分岔滞后簇发和焦点/焦点型叉形分岔滞后簇发3种不同簇发模式.最后, 第4节总结全文.
1 系统的稳定性与分岔
对于方程(1), 在任意参数条件下都会存在平衡点$E_0 (0,\alpha /\kappa ,0)$. 在$E_0 $处将系统线性化, 可以得到Jacobian矩阵$E_0 $的稳定性由对应的特征方程$F(\lambda )=a_0 \lambda ^3+a_1 \lambda ^2+a_2 \lambda +a_3 $决定, 其中$a_0 =1$, $a_1 =\kappa +\rho +1-\alpha /\kappa $, $a_2 =\kappa \rho +(\kappa +\rho )(1-\alpha /\kappa )+\beta $, $a_3 =\kappa \rho (1-\alpha /\kappa )+\beta \kappa $. 当参数满足$a_0 a_3 -a_1 a_2 >0$且$a_1 >0$, $a_3 >0$时, $E_0 $是稳定的. 当$a_1 a_2 -a_0 a_3 =0$时, 特征方程出现一对纯虚根, 此时系统出现Hopf分岔, 产生振荡频率为$\varOmega _1^0 =\kappa \rho +(\kappa +\rho )(1-\alpha /\kappa )+\beta $的极限环.
当参数满足$(\alpha \rho -\beta \kappa -\rho \kappa )/\alpha \rho ^3>0$时, 系统出现另外两个平衡点$E_{1,2} (x_{1,2} =\pm \sqrt {(\alpha \rho -\beta\kappa -\rho \kappa )/\alpha \rho } ,\beta /\rho +1,z_{1,2} =\pm \sqrt {(\alpha \rho -\beta \kappa -\rho \kappa )/\alpha \rho ^3} )$. 在$E_{1,2} $处对系统进行线性化, 可以得到Jacobian矩阵
对应的特征方程为$F(\lambda ')=a_0' \lambda ^3+a_1' \lambda ^2+a_2'\lambda +a_3' $, 其中$a_0' =1$, $a_1' =1+\kappa +\rho $, $a_2' =\kappa \rho +\kappa +2\rho +2\alpha x_{1,2}^2 $, $a_3' =2\kappa \rho +2\alpha \rho x_{1,2}^2 $. 同理, 当$a_1' a_2' -a_0' a_3' >0$且$a_1' >0$, $a_3' >0$时, $E_{1,2}$是稳定的. 当稳定性条件受到破坏时, 可能会出现形式多样的分岔.
为了更清晰地说明系统的分岔行为, 固定参数$\rho =0.9$,其他参数取值与图1相同, 对应的系统稳定性和分岔特性如图2所示.从中可以得到如下结论: 平衡点$E_0 $总是不稳定的; 当$\beta >\beta _{LPC}=0.807 1$时, 此时的稳定吸引子为极限环LC1; 当$\beta$随时间慢变穿越叉形分岔点PB, 出现另外两个平衡点$E_{1,2} $,并且在区间$0.823 3=\beta _{subH} <\beta <\beta _{PB} =0.9$内, $E_{1,2}$都是不稳定的; $E_{1,2} $的稳定性可以通过亚临界Hopf分岔subH1和subH2改变,同时产生两个不稳定的极限环LC2和LC3,通过matcont[38]数值模拟可知LC2和LC3的振荡幅值会逐渐增大. 当$\beta$变化到达极限环的fold分岔点LPC和同宿分岔点Homo$(\beta _{LPC}=\beta _{Homo} =0.807 1)$时, LC2和LC3与LC1和不稳定平衡点$E_0 $碰撞消失. 然后,在LPC的左侧只有两个稳定的平衡点$E_{1,2} $.
图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2$\rho =0.9$的单参数分岔图
Fig. 2One-parameter bifurcation diagram for $\rho =0.9$
2 对称式delayed subHopf/fold cycle簇发
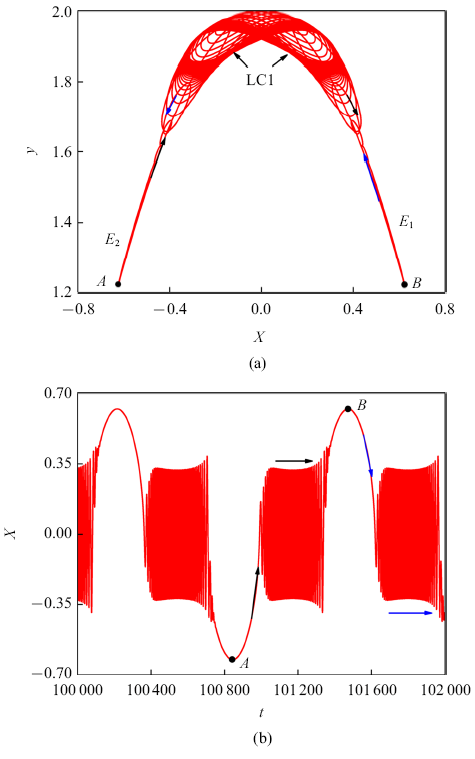
上节以$\rho =0.9$为例研究了系统的稳定性和分岔条件, 基于此,这部分揭示$\rho =0.9$时的动力学行为机理, 其他参数的取值与图1相同.图3给出了$\rho =0.9$的系统相图和时间序列, 可以发现,这种快慢动力学行为显然与稳定极限环和稳定平衡点有关, 这与图2的分析相符.图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3$\rho =0.9$的相图和时间序列图
Fig. 3Phase diagram and time series for $\rho =0.9$
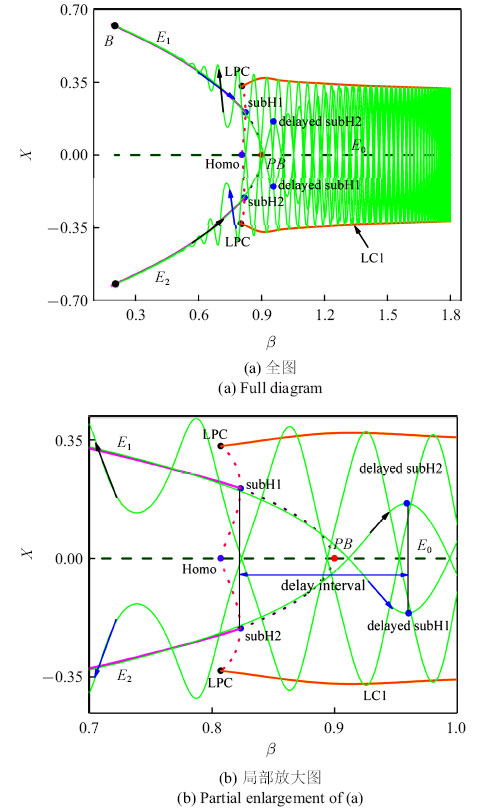
这种快慢动力学行为的产生机制可以通过叠加$(\beta,x)$平面上的相图和分岔图[39]得到, 见图4. 假设轨迹从$\beta$的最大值1.8处开始运动, 此时的稳定吸引子为极限环LC1,LC1的向量场使轨迹在LC1的最大振幅和最小振幅之间大幅运动. 随着$\beta$减小到$\beta _{PB} $, 叉形分岔使系统出现另外两个不稳定的平衡点$E_{1,2} $.当$\beta $穿越$\beta _{subH1} $和$\beta _{subH2} $后, $E_{1,2}$通过亚临界Hopf分岔稳定, 同时产生两个不稳定的极限环. 同时可以看到, 在subH1和subH2附近极限环LC1的振荡幅值变大,然后LC1与两个不稳定极限环在极限环的fold分岔LPC处碰撞消失, 与此同时,两个不稳定的环也与不稳定平衡点$E_0 $曲线碰撞, 出现同宿分岔Homo. 最后,在LPC和Homo的左侧只剩下稳定的平衡点$E_{1,2} $, 轨迹经过短暂的振幅逐渐减小的高频振动后进入平缓的平衡点运动, 直至$\beta$减小到其最小值0.2.
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4$\rho =0.9$时$(\beta ,x)$平面上的相图与分岔图的叠加
Fig. 4The superposition of the phase diagram in $(\beta ,x)$ plane and bifurcation diagram for $\rho =0.9$
当$\beta $从0.2逐渐增大过程中, $E_{1,2} $在subH1和subH2处失稳,但小幅平衡点运动仍未消失, 轨迹会继续沿着不稳定的$E_{1,2} $运动一段时间,表现为参数穿越亚临界Hopf分岔的慢通过效应, 或者亚临界Hopf分岔滞后.经过一段滞后区间(见图4(b), 滞后区间宽度约为0.14),轨迹进入稳定极限环LC1中大幅振荡, 直至$\beta $增大到其最大值1.8,一个周期过程结束.
在这种快慢行为中, 大幅运动开始于亚临界Hopf分岔滞后, 结束于极限环的fold分岔,而且在一个周期内存在两个对称的大幅运动,因此这种簇发模式可以称为对称式delayed subHopf/fold cycle簇发.
3 簇发的动力学转迁
上节给出了$\rho =0.9$时的对称式亚临界Hopf分岔滞后簇发的产生机理, 下面研究这种簇发行为随参数$\rho $变化的动力学转迁,其他参数的取值仍与图1相同.3.1 两参数分岔图
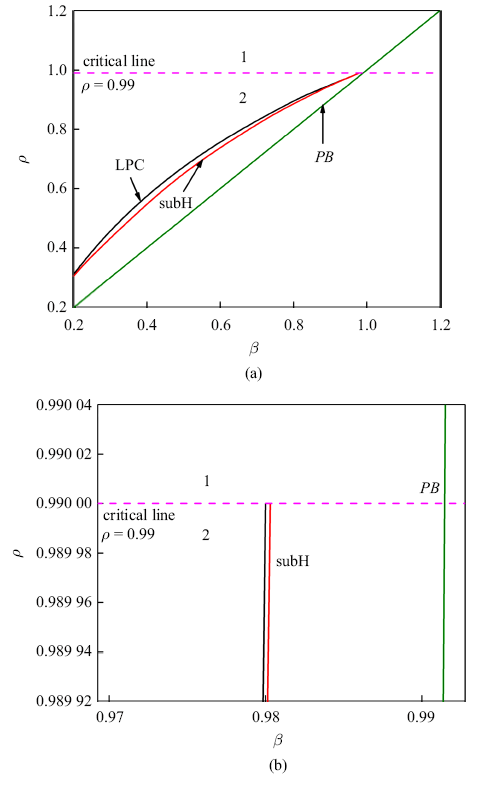
图5给出了系统关于参数$\beta $和$\kappa $的两参数分岔集, 从中可以发现$\beta$从最小值$-4$到最大值4存在两种穿越形式: 一种是区域1,即这个过程只穿越了叉形分岔曲线PB; 另一种是区域2, 这个过程穿越了极限环的fold分岔曲线LPC、亚临界Hopf分岔曲线subH和叉形分岔曲线PB.穿越形式的不同, 会使系统出现不同的动力学行为.图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5系统关于$\beta $和$\rho $两参数分岔图
Fig. 5Two-parameter diagram related to $\beta $ and $\rho $
对称式亚临界Hopf分岔滞后簇发是区域2中当LPC曲线与subH距离较远时的典型行为, $\rho$的取值不会定性改变系统的动力学特性, 因此可以取定参数$\rho=0.9$进行研究.
3.2 Delayed subHopf/fold cycle簇发
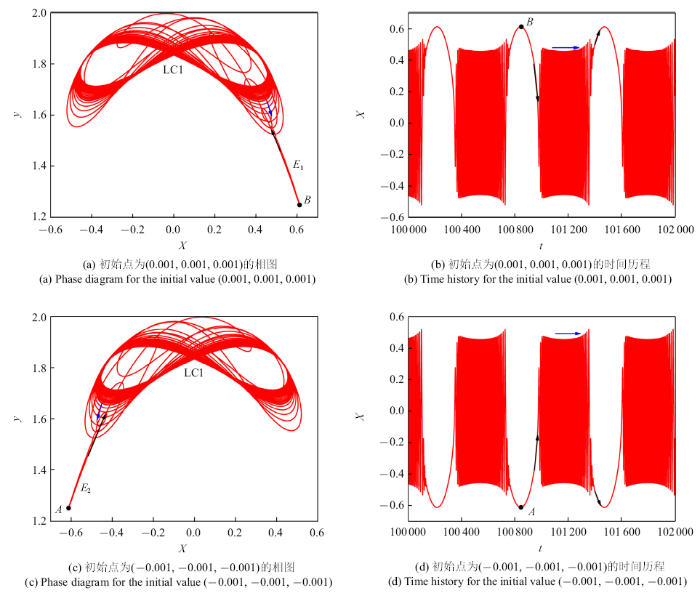
当图5区域2中的LPC曲线与subH距离较远时, 如$\rho =0.8$, 由于LPC分岔点和subH分岔点距离很远, 系统的动力学行为受初始点的影响很大.图6给出了当初始点分别为$(0.001,0.001,0.001)$和$(-0.001,-0.001,-0.001)$时的相图和时间历程, 可以发现这两部分关于$x=0$是对称的.图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6$\rho =0.8$的相图和时间历程图
Fig. 6Phase diagram and time history for $\rho =0.8$
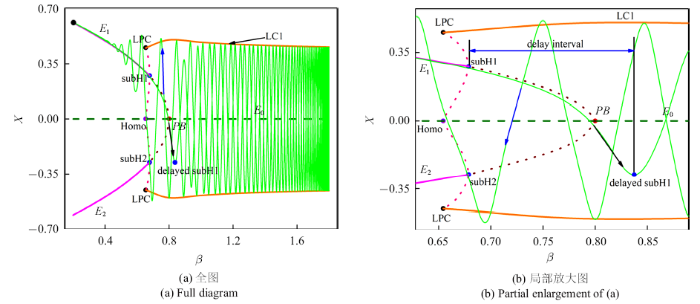
这种簇发行为的产生机制如图7所示. 当轨迹从$\beta $的最大值1.8处开始运动时, 此处的稳定吸引子为LC1, 轨迹在LC1中做大振幅振荡. 当$\beta$穿越叉形分岔PB后, 产生不稳定平衡点$E_1$. $E_1$的稳定性通过亚临界Hopf分岔subH1改变, 同时产生一个不稳定极限环. 当$\beta$到达极限环的fold分岔LPC时, 稳定极限环LC1与不稳定极限环碰撞消失. 然后轨迹沿着稳定平衡点$E_1 $曲线运动, 直至$\beta$的最小值0.2. 在$\beta$增大过程中, $E_1 $ 通过亚临界Hopf分岔失稳, 轨迹继续沿着不稳定$E_1$运动一段时间, 表现出分岔滞后效应(此时滞后区间宽度约为0.16), 随后进入稳定极限环LC1中运动.
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7$\rho =0.8$时$(\beta ,x)$平面上的相图与分岔图的叠加
Fig. 7The superposition of the phase diagram in $(\beta ,x)$ plane and bifurcation diagram for $\rho =0.8$
由图可见, 大幅运动开始于亚临界Hopf分岔滞后, 结束于极限环的fold分岔, 因此这种快慢行为可以称为delayed subHopf/fold cycle簇发.
3.3 焦点/焦点型对称式叉形分岔滞后簇发
当参数$\rho $增大进入区域1时, 可以看到此时$\beta$双向变化只会穿越叉形分岔PB, 表现为系统动力学在不同平衡点之间的转迁. 因此,平衡点的类型会决定系统动力学的特性. 如当$\rho =1.2$时, $E_0$是稳定的焦点(当$\beta =1.52$时, 特征方程的特征根为$\lambda _1=-1$, $\lambda _{2,3} =-0.1\pm 0.557{i})$, $E_{1,2} $也是稳定的焦点(当$\beta =0.906$时, 特征方程的根为$\lambda _1=-1.08$, $\lambda _{2,3} =-0.18\pm 0.714{i})$. 此时, 系统的动力学行为只与焦点有关, 对应的相图和时间序列如图8所示.图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8$\rho =1.2$的相图和时间序列
Fig. 8Phase diagram and time series for $\rho =1.2$
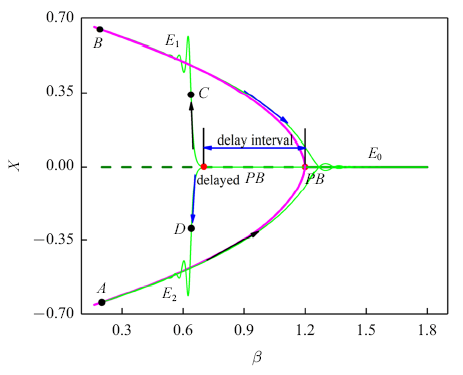
图9给出了$\rho =1.2$时的快慢动力学分析. 当$\beta $从1.8逐渐减小时, 轨迹会沿着稳定平衡点$E_0 $的平衡曲线做近似直线运动. 随着$\beta$穿越叉形分岔PB, 系统出现了另外两个稳定平衡点$E_{1,2} $. 但在图9中可以看到, 由于叉形分岔滞后的原因, 轨迹沿着不稳定的$E_0$又运动很长一段时间才转到$E_{1,2} $中运动, 直到$\beta $到达其最小值0.2. 然后$\beta $又开始逐渐增大, 轨迹从沿着$E_{1,2}$平衡曲线运动经过叉形分岔转入到$E_0 $的平衡曲线运动, 直至完成一个周期运动.
图9
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图9$\rho =1.2$的快慢动力学分析
Fig. 9Fast-slow analysis for $\rho =1.2$
这种快慢动力学行为是轨迹从一个稳定焦点进入另一个稳定焦点的运动, 而且存在上下两个对称结构, 同时又可以看到明显的叉形分岔滞后特性(此时的滞后区间宽度约为0.5), 因此这种簇发行为可称为焦点/焦点型对称式叉形分岔滞后簇发.
3.4 焦点/焦点型叉形分岔滞后簇发
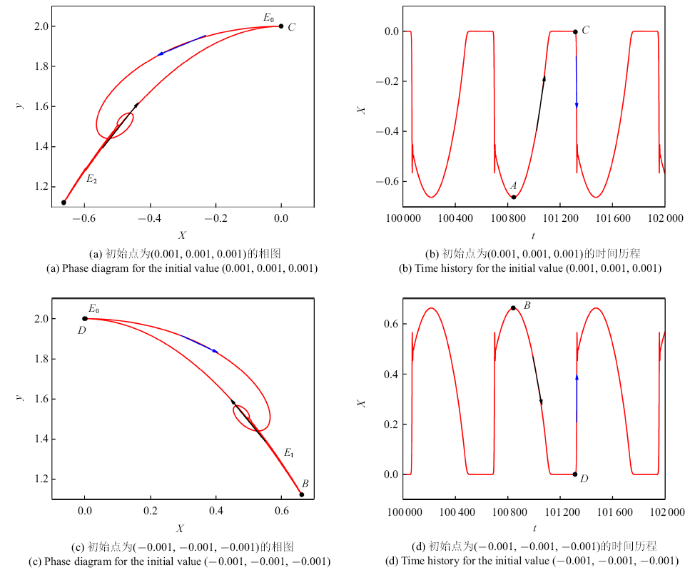
随着$\rho $的增大, 对称结构发生破却, 初始取值决定了系统轨迹离开$E_0$平衡曲线后的走向. 图10给出了当$\rho =1.65$时,初值分别为$(0.001,0.001,0.001)$和$(-0.001, -0.001, -0.001)$的相图和时间历程图.图10
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图10$\rho =1.65$的相图和时间序列
Fig. 10Phase diagrams and time series for $\rho =1.65$
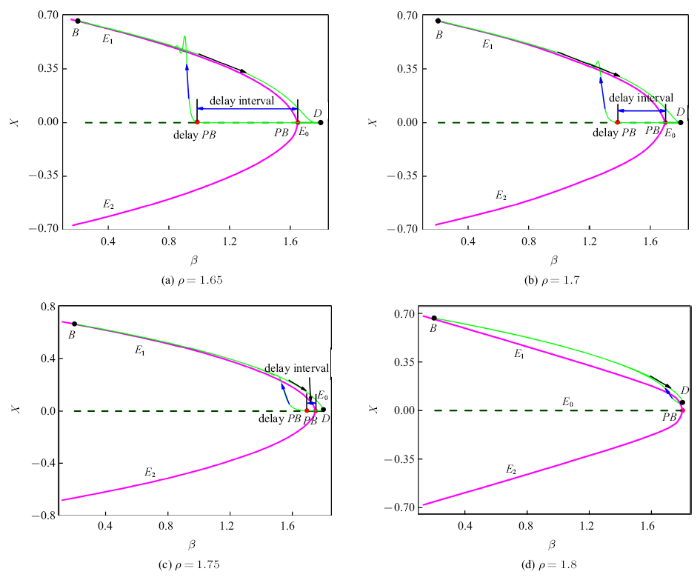
从图11(a)可以看到系统轨迹从$E_0 $的平衡曲线进入$E_1 $的平衡曲线时,出现了一个很大的滞后区间. 并且随着$\rho $的增大,这种叉形滞后区间的宽度越来越小(图11(a)的滞后区间约为0.66,图11(b)的滞后区间约为0.32, 图11(c)的滞后区间约为0.06, 图11(d)的滞后区间为0).这种动力学仍是从焦点到焦点的簇发行为, 并且没有存在对称结构,因此该簇发称为焦点/焦点型叉形分岔滞后簇发.
图11
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图11$(\beta ,x)$平面上的相图与分岔图的叠加
Fig. 11Overlapping of the phase diagram in $(\beta ,x)$ plane and bifurcation diagram
4 结论
参数激励下的两时间尺度非线性系统可以产生非常复杂的簇发行为. 在给定的参数条件下, 对快子系统进行分岔分析, 发现系统会出现叉形分岔、亚临界Hopf分岔、极限环的fold分岔和同宿分岔, 此时系统对应的簇发形式为对称式亚临界Hopf分岔滞后簇发.在这种簇发行为中, 发现了明显的亚临界Hopf分岔滞后现象. 然后, 借助两参数分岔图, 研究了对称式subHopf/fold cycle簇发随参数$\rho$变化的动力学转迁, 得到了delayed subHopf/fold cycle簇发、焦点/焦点型对称式叉形分岔滞后簇发和焦点/焦点型叉形分岔滞后簇发,这些簇发的产生与$\rho $和初始点的选取有关. 同时, 随着$\rho $的增大, 亚临界Hopf分岔滞后区间宽度逐渐减小, 叉形分岔滞后区间宽度先增大后减小.参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]

Chlorite dismutases (Clds) are heme b-containing oxidoreductases that convert chlorite to chloride and dioxygen. In this work, the thermodynamics of the one-electron reduction of the ferric high-spin forms and of the six-coodinate low-spin cyanide adducts of the enzymes from Nitrobacter winogradskyi (NwCld) and Candidatus "nitrospira defluvii" (NdCld) were determined through spectroelectrochemical experiments These proteins belong to two phylogenetically separated lineages that differ subunit (21.5 and 26 kDa, respectively) and, oligomeric dimeric and pentameric, respectively) structure but exhibit similar chlorite degradation activity. The E-o' values for free and Cyanide-bound proteins :were, determined to be -119. and, -397 mV for NwCld and -113 and -404 mV for NdCld, respectively (pH 7.0, 25 degrees C). Variable-temperature,spectroelectrochemical experiments revealed that the oxidized state of both proteins is enthalpically stabilized. Molecular dynamics simulations suggest that changes in the protein structure are negligible, whereas solvent reorganization is mainly responsible for the increase in entropy during the redox reaction. Obtained data are discussed with respect to the known structures of the two Clds and the proposed, reaction mechanism.
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]

Absent exogenous ROS input, and under conditions that retard hydrogen donor autoxidation, PO reactions can manifest low frequency bursting whereby pulses of ROS are produced at clinically significant intervals.]]>
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]

In this paper, we elucidate the extremely complicated bifurcation structure of a weakly driven relaxation oscillator by focusing on chaos, and notably, on complex mixed-mode oscillations (MMOs) generated in a simple dynamical model. Our model uses the Bonhoeffer-van der Pol (BVP) oscillator subjected to a weak periodic perturbation near a subcritical Andronov-Hopf bifurcation (AHB). The mechanisms underlying the chaotic dynamics can be explained using an approximate one-dimensional map. The MMOs that appear in this forced dynamical model may be more sophisticated than those appearing in three-variable slow-fast autonomous dynamics because the approximate one-dimensional mapping of the dynamics used herein is a circle map, whereas the one-dimensional first-return map that is derived from the three-variable slow-fast autonomous dynamics is usually a unimodal map. In this study, we generate novel bifurcations such as an MMO-incrementing bifurcation (MMOIB) and intermittently chaotic MMOs. MMOIBs trigger an MMO sequence that, upon varying a parameter, is followed by another type of MMO sequence. By constructing a two-parameter bifurcation diagram, we confirmed that MMOIBs occur successively. According to our numerical results, MMOIBs are often observed between two neighboring MMOs. Numerically, MMOIBs may occur as many times as desired. We also derive the universal constant of the associated successive MMOIBs. The existence of the universal constant suggests that MMOIBs could occur infinitely many times. Furthermore, intermittently chaotic MMOs appear in this dynamical circuit. The intermittently chaotic MMOs relate to a type of intermittent chaos that resembles MMOs at first glance, but includes rare bursts over a long time interval. Complex intermittently chaotic MMOs of various types are observed, and we clarify that the intermittently chaotic MMOs are generated by crisis-induced intermittency. (C) 2012 Elsevier B.V.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURLPMID [本文引用: 1]

This article concerns the phenomenon of Mixed-Mode Bursting Oscillations (MMBOs). These are solutions of fast-slow systems of ordinary differential equations that exhibit both small-amplitude oscillations (SAOs) and bursts consisting of one or multiple large-amplitude oscillations (LAOs). The name MMBO is given in analogy to Mixed-Mode Oscillations, which consist of alternating SAOs and LAOs, without the LAOs being organized into burst events. In this article, we show how MMBOs are created naturally in systems that have a spike-adding bifurcation or spike-adding mechanism, and in which the dynamics of one (or more) of the slow variables causes the system to pass slowly through that bifurcation. Canards are central to the dynamics of MMBOs, and their role in shaping the MMBOs is two-fold: saddle-type canards are involved in the spike-adding mechanism of the underlying burster and permit one to understand the number of LAOs in each burst event, and folded-node canards arise due to the slow passage effect and control the number of SAOs. The analysis is carried out for a prototypical fourth-order system of this type, which consists of the third-order Hindmarsh-Rose system, known to have the spike-adding mechanism, and in which one of the key bifurcation parameters also varies slowly. We also include a discussion of the MMBO phenomenon for the Morris-Lecar-Terman system. Finally, we discuss the role of the MMBOs to a biological modeling of secreting neurons.
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]

热声发动机的起振过程是一个产生并维持自激振荡的过程, 研究热声自激振荡机理有助于进一步了解热声效应的实质. 根据热声网络理论, 建立了驻波热声发动机的整机网络. 将热声网络比拟成电网络, 利用厄米特式计算了输入热声网络的视在功流, 功流平衡对应自激, 在角频率虚部为零的情况下计算了热声发动机的阈值温度和运行频率. 结果表明, 计算值与实验值符合得较好, 充气压力与阈值温度和运行频率的耦合关系大致相同. 所得结论有助于进一步探究热声效应机理以及热声发动机系统的优化设计.
DOIURL [本文引用: 1]

The onset process of a thermoacoustic prime mover is a process generating and maintaining self-excited oscillation. It is helpful to have a better understanding of thermoacoustic effect by investigating the mechanism of thermoacoustic self-excited oscillation. The network model of a representative standing-wave thermoacoustic prime mover is established on the basis of thermoacoustic network theory. Comparing thermoacoustic network to electric network, the apparent power flux which inputs the thermoacoustic network is calculated by using the Hermitian form. In the network, the apparent power flux balance means establishing the self-excited oscillation. Based on the above, the threshold temperature and operation frequency of a thermoacoustic prime mover are calculated on condition that the imaginary part of angular frequency is equal to zero. The calculation results are in good agreement with the experimental results. For the coupling relationship of the main pressure with the threshold temperature and operation frequency, the calculation results are roughly close to the experimental results. The obtained results are helpful for the further studying of the thermoacoustic effect and the optimal designing of a thermoacoustic system.
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
URL [本文引用: 1]

考虑旋转机械中两种频率不同的周期参数激励同时存在对其传动系统的影响,基于拉格朗日方程,建立一类含准周期参激刚度和摩擦阻尼的非线性扭振系统的动力学方程。运用多尺度法对该扭振系统进行求解,得到系统在1/2亚谐波主参数共振下的幅频特性方程和分岔响应方程。在此基础上,研究了当两种周期参激的频率相差较大时非线性扭振系统的周期簇发现象,分析了快变参激和慢变参激对扭振系统的周期簇发的影响。通过数值仿真,给出了产生周期簇发的参数取值区域。在该区域内系统发生静息态与激发态的相互转迁,当快变激励的幅值减小时,激发态区域扩大,簇发的时间延长,通过调节慢变参激幅值会改变系统簇发的类型和轨迹]]>
URL [本文引用: 1]

Considering the effects caused by the coexist of two different periodic parametric excitation in rotary machinery driving system, the dynamical equation of nonlinear torsional vibration system is established based on Lagrange equation. The model contains quasi-periodic parametrically excited stiffness and friction damping. The amplitude-frequency characteristic equation and bifurcation response equation are obtained by solving the torsional vibration system using multi-scale method. On this basis, the periodic bursting of the nonlinear torsional vibration system is studied when the two periodic parametrical excitations have large difference gap. The influence of fast-varying parametrical excitation and slow-varying parametrical excitation on the periodic bursting of the torsional vibration system is analyzed. The parameter regions of periodic bursting are given by numerical simulation. The mutual transition between the quiescent state and the spiking state of the system occurs in this region, when the amplitude of the fastly varying excitation reduces, the area of spiking state extends, the time of bursting prolongs. The bursting type and trajectory of the system can be changed from regulating amplitude of slow-varying parametric excitation.]]>
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]

2 root 3/9, while if gamma
