,*,2), 杨瑞鑫*,?, 聂少军*,?, 姜宗林*,?DEEP-LEARNING-BASED INTELLIGENT FORCE MEASUREMENT SYSTEM USING IN A SHOCK TUNNEL 1)
Wang Yunpeng,*,2), Yang Ruixin*,?, Nie Shaojun*,?, Jiang Zonglin*,?通讯作者: 2)汪运鹏, 副研究员, 主要研究方向: 激波风洞测力试验与风洞天平技术. E-mail:wangyunpeng@imech.ac.cn
收稿日期:2020-06-6接受日期:2020-06-6网络出版日期:2020-09-18
| 基金资助: |
Received:2020-06-6Accepted:2020-06-6Online:2020-09-18
作者简介 About authors
摘要
高焓条件气动力测量试验对高超声速飞行器气动外形设计和优化起决定性作用. 通常采用脉冲风洞(如激波风洞)产生高温、高压驱动气体以模拟高超声速高焓试验气流. 在脉冲风洞对高超飞行器模型进行测力试验时, 测力天平输出信号结果无法摆脱惯性载荷的干扰影响, 其导致的测力模型低频振动问题基本无法通过滤波彻底解决, 尤其对试验时间只有几毫秒的情况, 六分量测力天平的结构设计研究受到了极大挑战. 因此, 对实现短试验时间条件高性能测力的深入研究发现, 天平动态校准凸显重要性和必要性. 本研究提出一种新的基于人工智能深度学习技术的单矢量动态自校准方法和智能测力系统概念, 并应用于目前激波风洞测力试验中. 该动校方法的最主要特点之一是对整体测力系统的校准, 而非仅仅针对天平, 并且保证校准的测力系统即为风洞试验对象, 确保校准与应用的一致性. 在测试评估中, 测试样本和风洞试验验证均得到了较为理想的效果, 大幅度低频振动干扰基本被消除, 脉冲风洞测力的精度和可靠性得到了大幅提高.
关键词：
Abstract
Aerodynamic force measurement in high-enthalpy flow is very important for the design and optimization of hypersonic vehicles. Currently, impulse facilities are used for generating high-temperature and high-pressure driving gas to simulate the high-enthalpy flow with hypersonic flight-conditions, such as a shock tunnel. However, when force tests are conducted in an impulse facility, the inertial force has a large influence on the measuring results, which creates low-frequency vibrations of the test model and its motion cannot be addressed through digital filtering. In the case of a few milliseconds of test time, the structural design of the six-component balance is greatly challenged. Therefore, dynamic calibration becomes very important for improving the precision and accuracy of force measurement during short-duration. A new method, deep-learning-based single-vector dynamic self-calibration of the force measurement system, and intelligent force measurement system are proposed for obtaining high-accurate aerodynamic force in impulse facilities. One of the main features of this dynamic calibration method is the calibration of the overall force measurement system, not just the balance. Applying this method, the calibrated force measurement system is the wind tunnel test object, which ensures the consistency of calibration and application. In the evaluation, the test verification has achieved relatively ideal results, the large-scale low-frequency vibration interference has been basically eliminated, and the accuracy and reliability of the force measurement in impulse facility have been greatly improved.
Keywords：
PDF (5705KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
汪运鹏, 杨瑞鑫, 聂少军, 姜宗林. 基于深度学习技术的激波风洞智能测力系统研究 1). 力学学报[J], 2020, 52(5): 1304-1313 DOI:10.6052/0459-1879-20-190
Wang Yunpeng, Yang Ruixin, Nie Shaojun, Jiang Zonglin.
引言
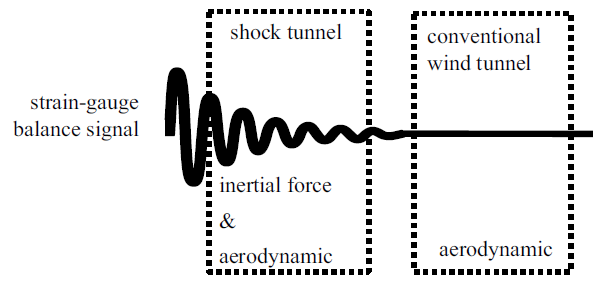
目前应用激波风洞进行测力试验仍存在诸多未解决的关键技术问题[1-3], 常规测力方法的工程应用遇到技术瓶颈. 由于流场瞬时建立, 试验时间短, 在进行气动力试验时, 模型-天平-支撑系统受到激励, 产生瞬态冲击载荷,模型、测力元件、支撑系统及风洞部件被激发产生振动, 测力元件输出产生干扰[4]. 惯性干扰力与真实气动力混杂在一起(见图1), 甚至完全覆盖气动力, 大大降低试验精准度, 导致天平信号出现无法使用的情况, 给激波风洞测力带来了很大困难, 使得试验模型的尺度、质量也受到极大的限制[5]. 国外一些测力和天平专家针对这些难题, 发展了特种天平技术, 如加速度计天平[6-8]、应力波天平[9-11]、自由飞测力技术[12-16]、补偿型天平[17]和 脉冲型应变天平[18-21]等. 但是, 均因为成本高、技术不成熟且精准度低而未能在工程实际应用, 仍处于初步研究阶段.图1
新窗口打开|下载原图ZIP|生成PPT图1激波风洞与传统低速风洞测力试验中天平有效输出信号
Fig.1Signal processing of strain gauge balance in shock tunnel and conventional wind tunnel
近些年, 工程部门越来越关注高超声速飞行器的尺度效应和高温效应, 对飞行器气动力特性的试验指标也要求越来越苛刻, 这就要求脉冲型风洞要大力提高其测力试验的精准度. 这除了对脉冲风洞设备提出更高的要求, 对测力传感器及其附加设备(支撑系统, 数据采集等)也提出了更高要求. 所以, 发展精准度更高、使用更稳定可靠的测力系统(force measurement system, FMS)变得更加迫切, 探求激波风洞中对测力结果影响的关键因素也变得更为重要.
激波风洞气动力测量试验中最主要的测量仪器是风洞天平. 其中, 风洞天平的静态校准技术研究已经发展得非常成熟, 但是动态特性和动态校准方面的研究非常少, 原因是传统风洞试验中动态试验涉及面并不宽. 关于天平动态特性的研究多侧重于天平固有频率特性的研究, 惯性力补偿以及支撑系统阻尼特性对测量精度的影响,实际上惯性力补偿不能完全去除应变天平动态测量误差. 常规测力试验对天平动态特性的要求也逐渐提高, 要求天平不仅具有良好的静态特性,还需有很好的动态性能,跟随速度快、响应时间短,从而能够快速准确跟随动态载荷的变化, 实现对风洞试验中动态过程的连续测量. 在目前的天平的动态特性研究中, 也鲜有涉及脉冲型风洞瞬态或动态测力问题及动态校准应用, 尤其是在激波风洞测力天平动态校准方面的技术研究和工程应用.
因此, 本文提出一种新的基于深度学习技术的单矢量动态自校准方法并应用于脉冲风洞(尤其是高焓激波风洞) FMS中, 力求实现短试验时间风洞FMS的智能化并对惯性振动干扰的测力结果进行智能模型处理, 得到理想气动载荷. 该技术将使得精度高、成本低、发展成熟的应变计天平的设计难度大大降低, 同时提高激波风洞测力试验精度. 从某种角度看, 激波风洞测力技术的进一步发展和完善也对高温真实气体效应的研究提供了更可靠数据, 对我国高超声速飞行器高焓气动特性研究则提供关键技术支撑.
1 基于深度学习技术的单矢量动态自校准方法
针对脉冲型 FMS, 本文提出基于深度学习的单矢量动态自校准技术(deep-learning-based single-vector dynamic self-calibration, SVDC), 引入人工智能(artificial intelligence, AI)技术对FMS结构进行深度学习建模, 采用卷积神经网络 (convolutional neural networks, CNN) 训练模型. 研究目标是通过对动态测力信号进行人工智能建模, 从而实现对结构振动的高精度识别, 使风洞天平输出"纯"气动载荷信息—-不带有惯性振动的干扰或者干扰基本可以忽略掉, 即天平输出的仅为高超声速飞行器测力模型的"定常"或准定常气动力信号.本研究针对脉冲型FMS进行高精度动态校准, 实施对象是整体FMS, 并非对单一测力天平的动态校准. 动校之前需对FMS传感器部分(风洞天平)采用天平校准系统进行高精准度的静态校准. 基于深度学习技术的SVDC方法是采用CNN对动态载荷样本进行建模和训练, 其动态阶跃载荷的加载则采用瞬态卸载的办法, 即剪断钢丝卸载的方式. 载荷的大小可通过静态校准的高精度风洞天平传感器实时读取(即"自校准"概念), 并且可以同时读取多分量载荷信息, 因此任意方向的单载荷加/卸载可实现多分量阶跃载荷的加/卸载(即"单矢量"概念). 基于SVDC技术进行动态校准后的FMS, 我们称之为智能测力系统(intelligent force measurement system, iFMS).
1.1 单矢量动态自校准概念
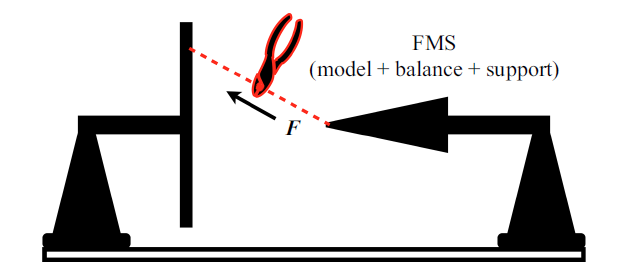
首先提出基于应变天平的"单矢量"加载方法, 即针对风洞中实际吹风试验的FMS, 在模型迎风面任意位置通过一根钢丝悬挂至十字加载支撑架上的任一悬挂点, 实现施加一个矢量载荷并剪断实现卸载. 目前的单矢量加载方法, 其载荷大小、方向、作用点均不受一定约束, 而传统动态校准悬挂砝码的方法中, 施加载荷方向受到一定限制. 此外, 如果天平为多分量(三分量或六分量), 则可实现多分量加载和卸载, 其载荷数值由FMS中的高精度天平实时输出, 即实现"自校准". 该方法可不必采用固定方向悬挂砝码, 并且各分量载荷的分解是严格按照天平静态校准时的坐标系进行的. 图2为单矢量加载阶跃载荷并实现自校准的示意图.图2
新窗口打开|下载原图ZIP|生成PPT图2单矢量动态自校准加载阶跃载荷示意图
Fig.2Loading of SVDC system
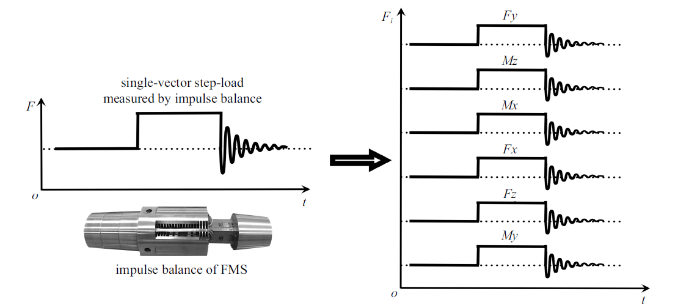
新的SVDC方法不采用传统的悬挂砝码瞬间卸载的方式施加阶跃载荷, 而是采用拉线(一般采用直径小于0.5 mm细钢丝)施加单矢量拉力并通过剪断拉线卸载实现阶跃载荷的方式, 其载荷大小利用高精度静态校准的风洞天平直接读取, 该单矢量拉力通过风洞天平直接输出分解为多分量力, 其合力为单矢量拉力, 施加的单矢量力$ F$, 由风洞天平按照静态校准时的体轴坐标系各个坐标轴方向, 自动分解为多个分量力, 力的大小由风洞天平实时测量输出, 且多个分量力的合力为所述单矢量力$ F$. 图3展示了单矢量加载后天平输出多分量的效果. 因此, 单矢量力的加载即可实现多分量阶跃载荷同时"定量"精确加载, 更接近实际风洞吹风试验时的气动力加载方式, 且精准度更高. 动态校准精准度取决于风洞天平静态校准精准度, 而传统悬挂砝码方法受到拉力方向和砝码精度影响较大, 其带有载荷的拉线方向一般较难做到精确重合所选的坐标系, 并且传统动态校准加载阶跃载荷一般只能对单个方向悬挂砝码载荷进行加载和卸载.
图3
新窗口打开|下载原图ZIP|生成PPT图3SVDC概念: 单次任意方向加载实现多分量阶跃载荷加载和卸载, 载荷数值由天平直接读取
Fig.3SVDC concept: single-vector load generates multi-component step-loads measured by the balance of FMS
此外, SVDC具有便捷性, 装置设备简单易用. 进行动态校准时, FMS可位于风洞试验舱内部, 也可整体置于风洞试验舱外部完成校准过程, 保证了校准后的iFMS即为风洞试验采用FMS. 一般的传统动态校准仅对风洞天平(FMS的一部分, 或FMS的相似结构)进行动态加载、卸载, 而实际在风洞吹风试验的FMS为测力模型、风洞天平和支撑结构, 传统动态校准方法的对象与试验对象在组成结构上有较大差别, 甚至完全不同. 众所周知, 某一结构的振动特性(模态频率)与其质量和结构直接相关, 因此尽管对风洞天平(或FMS相似结构)进行了高精度的动态校准, 但在风洞试验中改变FMS结构, 将产生一定测量误差, 甚至对结果无法评估. 本研究中, 动态校准的整套系统连接安装模式与风洞试验时完全一致.
1.2 基于深度学习技术的动态特征建模
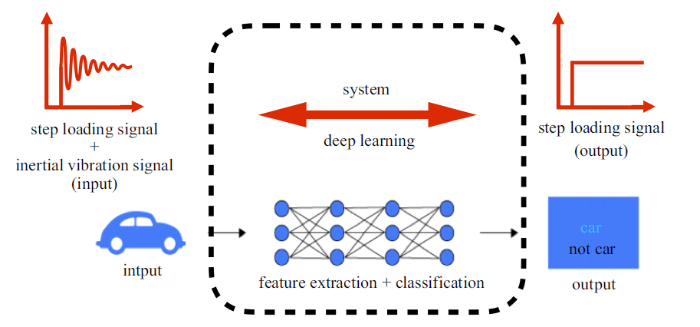
1.2.1 动态校准引入深度学习技术本研究中, 采集提取的动态特征信号后处理未采用系统辨识的方法, 而是引入人工智能深度学习技术, 采用目前相对成熟的CNN对动态信号样本进行模型训练, 其基本的思想见图4. 深度学习是机器学习中一种基于对数据进行表征学习的方法, 观测值可使用多种方式来表示. 含多隐层的多层感知器就是一种深度学习结构, 通过组合低层特征形成更加抽象的高层表示属性, 以发现数据的分布式特征表示[20]. CNN是深度学习的进一步发展, 传统的深度学习由于假设的函数空间过于自由, 对输入的样本不做任何假设, 因此对网络的参数空间不做约束, 结果就是要达到一个较为理想的网络模型精度, 需要训练的网络过大, 需要训练的时间过长, 在实际问题的处理上显得有效性太低. CNN的基本思想就是多层地提取特征, 而在每一层的提取中, 假设了特征是有局部性的, 此时一个卷积核处理了这个特征提取中的全部数据, 大大减小了参数空间的量级[22].
图4
新窗口打开|下载原图ZIP|生成PPT图4基于SVDC技术的iFMS动态载荷的深度学习训练
Fig.4Deep learning training of iFMS based on SVDC
深度学习及CNN技术已在多个领域进行了应用和探索, 相关技术方法及其开源软件较为容易获取和应用, 在此不做展开赘述[22-25]. 基本的想法是将带有惯性振动干扰的动态信号作为输入样本, 理想阶跃载荷作为输出样本(训练目标), 训练出可以较为完整描述该FMS动态振动特征的人工智能模型, 并应用于同一FMS风洞试验数据的处理(可以理解为对于输出振动信号的动态补偿, 其补偿依据是充分"掌握"了FMS结构动态特征的人工智能模型).
1.2.2 CNN网络架构
动态校准数据样本训练中CNN网络采用单块结构, 其中包含多个不同尺寸、不同通道数的卷积核, 所选取的尺寸在多次实验中进行了对比验证. 其中, 每一个块中包含多层卷积层, 其尺寸不断加大(即通道数增多), 用于从细微局部到区域更广的局部中提取振动特征信息, 最后还原回原来输入数据的通道数, 完成天平数据多个维度之间的信息融合.
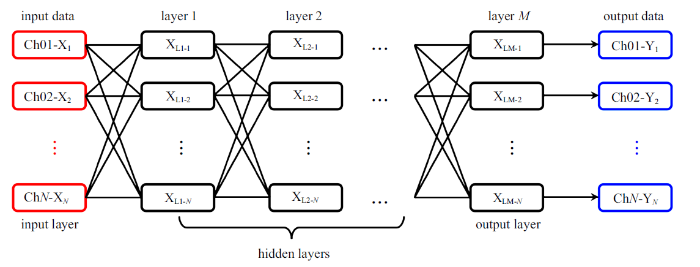
本文深度学习训练模型所采用的CNN结构见图6. 左侧输入数据为样本提取测试试验中iFMS的天平输出得到的阶跃载荷采集信号(带有惯性振动干扰). 其中, $N$为风洞天平分量数, 本研究中采用了三分量风洞天平, 即$N=3$; 右侧输出数据为理想阶跃载荷信号, 通道数须与输入载荷一致; 中间为隐含层, 本文采用三层, 且$L1-N$和$L2-N$均取64, 即将原来的3通道数据信号扩展至64通道信号; $L3-N$取3, 即最终将64通道信号变换成3通道信号并输出, 从而实现与输入数据通道数一致. 本研究初步仅采用简单的一维CNN进行建模.
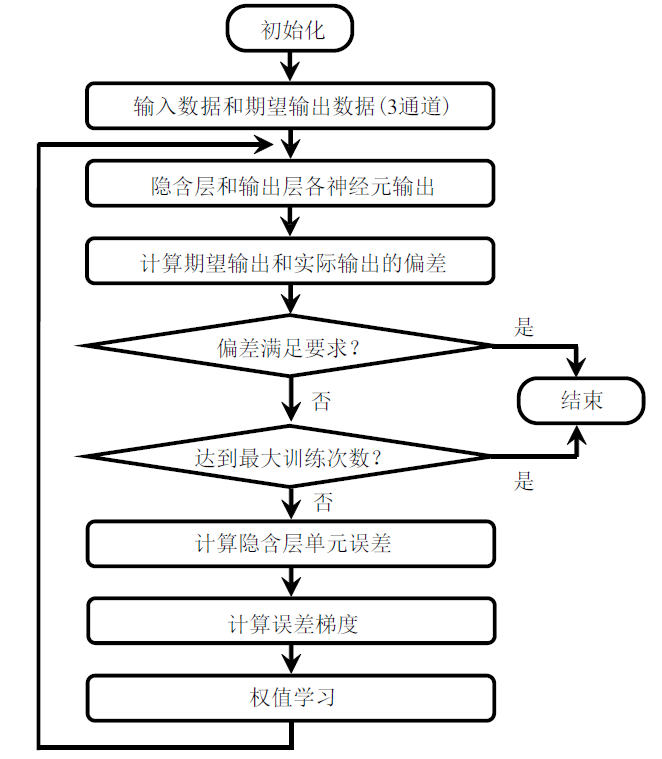
基于上述CNN网络结构, 利用训练样本数据对动态模型进行训练, 训练的过程是逐步提取振动特征的过程. 深度学习模型训练的流程见图5. 当训练中计算的偏差满足设置要求时, 即可结束整个建模训练过程, 输出模型文件.
图5
新窗口打开|下载原图ZIP|生成PPT图5卷积神经网络结构示意图
Fig.5CNN structure
图6
新窗口打开|下载原图ZIP|生成PPT图6深度学习卷积神经网络模型训练流程图
Fig.6Flow chart of CNN training
通过对结果的对比分析, 采用目前简单CNN网络得到的深度学习模型, 对天平动态响应干扰特征的提取是较为充分的. 通道数的结果对比显示, 只要在多个通道中进行了充分的融合, 动态校准结果的精确度会根据融合程度较快饱和, 校准结果是可靠的.
2 基于SVDC测力系统的智能化
2.1 iFMS动校装置与样本数据提取
用于智能模型训练和验证的样本数据的提取方法非常重要, 它决定了用于训练的阶跃载荷样本数据的质量, 从而会直接影响训练的过程和结果. 为验证方法可行性搭建了阶跃载荷加/卸载、动态载荷信号采集简易装置, 详见图7. iFMS由半锥角10$^\circ$、长750 mm尖锥标准测力模型、三分量应变天平、弯刀支撑系统三部分组成, 其与风洞测力试验为同一系统, 详见图7(a). 在FMS对面采用一个"十"字支架结构, 以悬挂和固定由尖锥处施加拉力的细钢丝, 见图7(b); 图7(c)为iFMS系统中的测力传感器——脉冲型应变天平, 该天平为iFMS在动态校准中的关键部件, 用于对施加载荷的实时测量.图7
新窗口打开|下载原图ZIP|生成PPT图7阶跃载荷加载和训练样本采集装置
Fig.7Device for step loading and training
为提取CNN样本训练所需样本, 实现多分量阶跃载荷加载与采集, 本研究基于LabVIEW软件二次开发并编制了动态载荷样本数据采集与处理软件, 可实现多分量动态信号的高精度采集. 阶跃载荷加载装置被设置在尖锥测力模型的前端, 通过悬挂钢丝进行加载, 剪断钢丝进行卸载, 进而实现一组阶跃载荷的施加过程. 整个动态数据提取过程大致分为4个步骤进行, 第一步是利用数采系统对测力天平零载输出作为基准数据进行记录; 第二步, 钢丝的一端与测力模型悬挂点连接, 另一端固定到加载装置, 此时施加载荷为作用在测力模型上、方向为拉线方向的一个单矢量$ F$, 且由三分量天平实时输出为轴向力、法向力和俯仰力矩信号, 即实现多分量载荷加载; 第三步, 在"十" 字加载装置一端剪断钢丝, 此时天平输出的信号为三分量阶跃载荷, 并被数采系统实时记录; 最后一步为数据预处理, 即将带有惯性振动的卸载过程信号作为输入样本, 定常载荷信号与零载荷信号截取、叠加处理后作为输出样本(目标样本数据). 同时, 由于数据量纲和取值范围差异, 样本数据采用归一化处理, 使其数值在$-1\sim1$之间变化, 验证结果或智能模型使用时, 再将处理后的测力信号数据反归一化处理.
2.2 动态建模结果与验证分析
本研究采用120组动态载荷信号样本进行了基于时域特征的深度学习模型训练, 以实现对同一iFMS的单矢量动态自校准, 用于脉冲型风洞测力试验数据的处理, 解决冲击惯性振动干扰问题. 在校准测试中将120组数据划为训练集和验证集两部分, 使用100组训练集(training set)数据训练模型和学习参数, 20组验证集(validation set)数据用来进行验证测试.2.2.1 测试验证结果
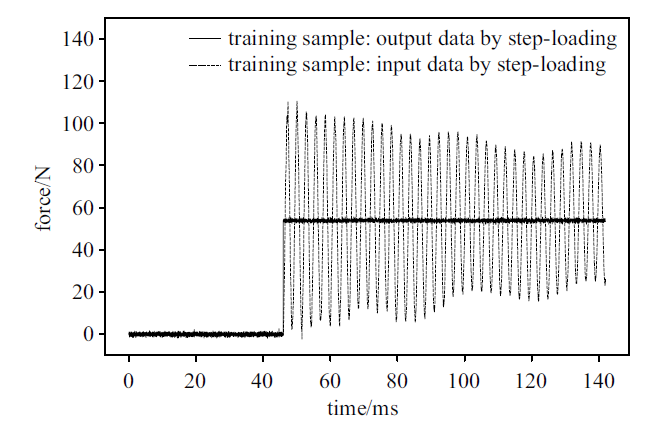
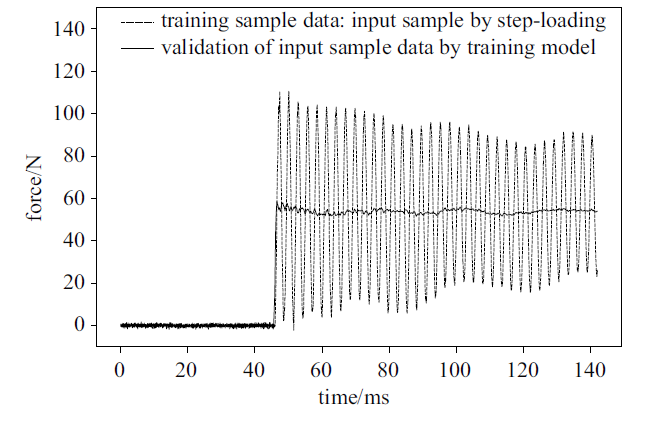
图8将CNN模型训练所用的输入和输出样本信号做了对比, CNN模型训练的目的就是要将带有惯性振动干扰信号消除掉. 基于篇幅限制, 略去训练过程描述. 图9展示了样本振动信号的处理结果, 可以看出其效果已经非常理想, 其样本数据曲线中的惯性振动基本被滤掉, 从某种程度上还原了阶跃载荷的"本真面目".
图8
新窗口打开|下载原图ZIP|生成PPT图8理想阶跃载荷信号(输出样本)和卸载信号(输入样本)
Fig.8Ideal step loading (output data) and unloading (input data)
图9
新窗口打开|下载原图ZIP|生成PPT图9输入样本与经过CNN模型处理信号的对比验证(轴向力)
Fig.9Input sample data and validation by CNN training model (axial force)
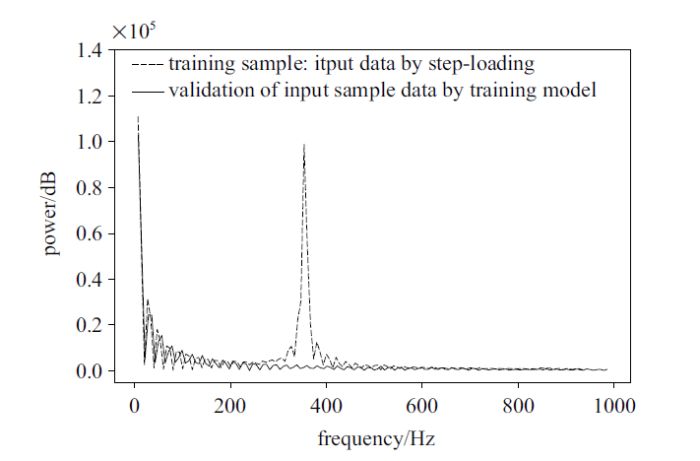
从某个角度看, SVDC方法实施的过程可看作是带有惯性振动干扰信号的"智能滤波"过程, 从以下的频谱对比可以更加清楚的认识这个过程. 从图10对振动样本信号和其经过CNN模型处理后的信号, 进行了快速傅里叶变换(fast Fourier transform, FFT)处理, 可以非常明显的看出, 载荷卸载后的衰减振荡信号中的主要频率均被完全滤除掉了.
图10
新窗口打开|下载原图ZIP|生成PPT图10输入样本与其经过处理后信号的FFT结果对比(轴向力)
Fig.10Data processing and comparison by Fast Fourier Transform (axial force)
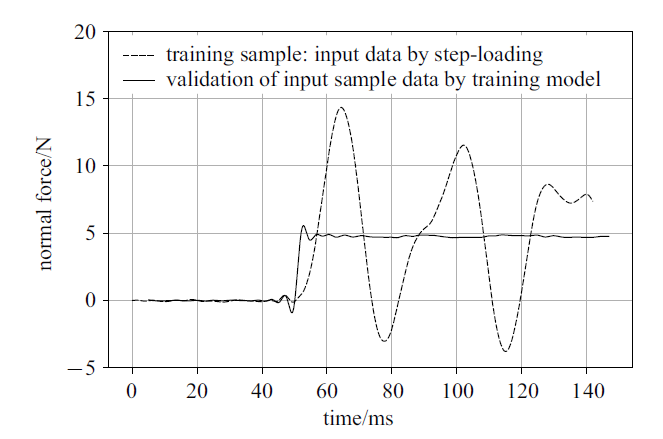
对于其他分量的结果验证, 图11和图12分别给出法向力和俯仰力矩的样本验证结果. 由目前初步结果, 效果比较理想, 但目前深度学习训练和样本采集方法仍需要近一步改进和完善, 诸如某些分量输出较小而产生的噪声干扰占比较大等问题, 相信随着SVDC技术近一步深入研究完善, 会得到非常理想的结果.
图11
新窗口打开|下载原图ZIP|生成PPT图11输入样本信号与经过处理信号的对比(法向力)
Fig.11Input sample data and validation by CNN training model (normal force)
图12
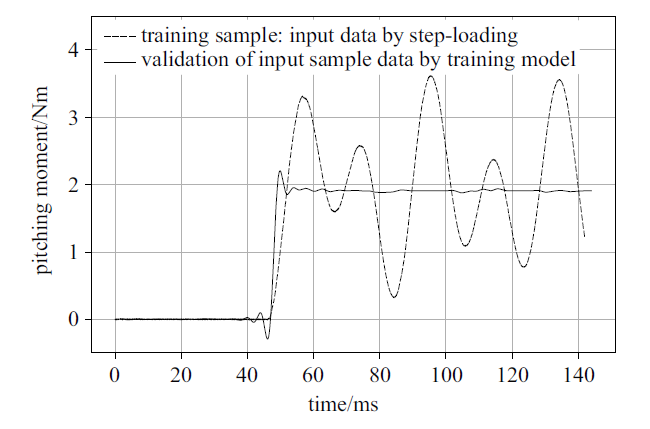新窗口打开|下载原图ZIP|生成PPT图12输入样本信号经过处理信号的对比(俯仰力矩)
Fig.12Input sample data and validation by CNN training model (pitching moment signal)
2.2.2 误差分析
对深度学习模型效果的分析需要对训练模型在训练集和测试集上的表现进行量化, 分别采用训练误差(training error) 和测试误差(test error), 后者也经常称为泛化误差(generalization error). 因此, 理想的模型就是在最小化训练误差的同时, 使泛化误差最小化. 本文采用均方误差指标(mean squared error, MSE)来评估训练误差和测试误差, 即评估深度学习模型的数据处理能力. MSE反映的是模型每一次输出结果与模型输出期望之间的误差, 即模型的稳定性. MSE是逐点误差平方的平均值, 定义如下
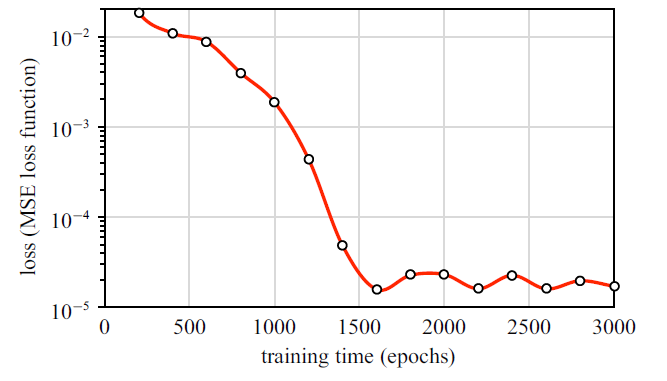
式中, $R_{\rm s}$是评估值, $R_{\rm a}$是真实值, $n$为数据点数. 训练中, 将所得曲线数据与目标曲线逐点作差作为误差. 训练中根据每轮(epochs)计算后输出的$loss$值来判断训练误差是否达到要求. 图13给出了模型训练中的时序变化. 经过1000轮的迭代周期后, 值为$1.88\times10^{-3}$. 此时, CNN卷积层开始识别到动态校准的核心特征, 但对带有高阶误差的细节特征未能充分识别; 经过1500轮计算后, $loss$值降到$3.0\times10^{-5}$以下, 可以认为此时的训练误差足够低, 即对iFMS的结构振动特征达到了较为精确的识别, 从而完成了有效的动态校准过程, 可以实现iFMS数据的智能化处理.
图13
新窗口打开|下载原图ZIP|生成PPT图13训练中Loss随时间的变化
Fig.13Training loss with time (epochs)
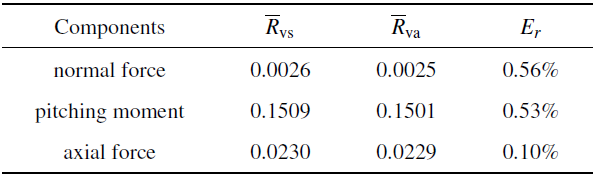
动态模型建立后需采用样本数据进行验证. 首先将验证样本$\overline{R}_{\rm vs}$通过模型处理得到评估数据$\overline{R}_{\rm va}$, 然后截取其中 约40 ms数据(每通道2500点)进行平均计算得到数据均值$\overline{R}_{\rm vs}$, $\overline{R}_{\rm va}$, 通过式(2)直接得到相对误差$E_r$
从表1数据可以看出, 训练模型对振动干扰信号的处理非常理想. 法向力(相对最小输出)数据处理的相对误差可达到5‰ 左右, 轴向力可达1‰. 这个性能指标与天平静态校准的数据趋势一致, 即轴向力的精准度也同样高于法向力和俯仰力矩. 因此, 可以认为单矢量动态校准的精度基本取决于iFMS中应变天平的静态校准性能.
Table 1
表1
表1三分量(通道)载荷验证数据误差(mV)
Table 1
 |
新窗口打开|下载CSV
3 iFMS在激波风洞测力试验中的应用
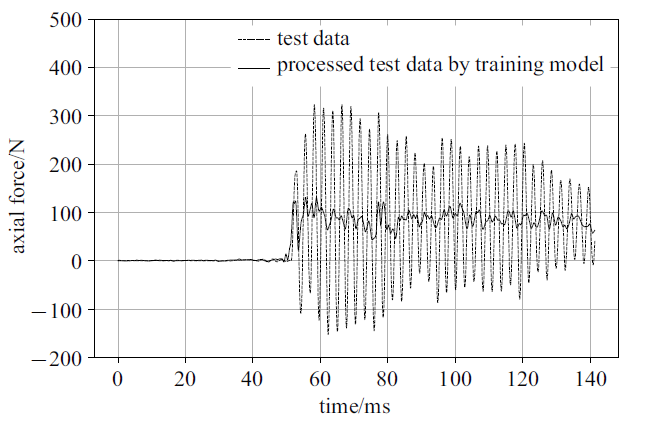
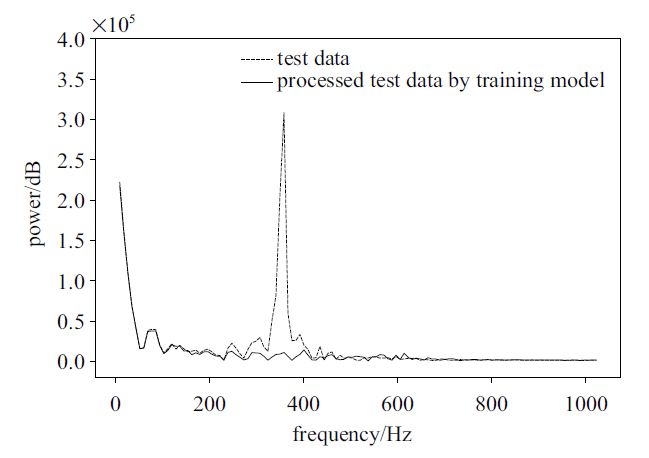
2012年中科院力学所建成JF-12复现飞行条件激波风洞并进行了大量的高超声速飞行器气动力测量试验, 得到了大量高精度的可靠测力数据. JF--12激波风洞的运行特点为可复现25 $\sim $ 50 km高空马赫数5 $\sim $ 9的飞行, 喷管出口直径为1.5 m或2.5 m, 试验气体为纯净空气并且有效试验时间超过了100 ms[26-29].本文对JF-12激波风洞750 mm尖锥标模测力试验的天平输出信号, 通过CNN训练模型进行了再处理. 从图14中轴向力对比结果可以看出智能模型非常理想的"滤除"了大幅度的惯性振动干扰, "还原"了具有阶跃载荷特征的轴向气动力信号. 对模型智能处理前后两个信号进行FFT处理(见图15)后, 更为明显地看出频率为380 Hz左右的振动干扰基本被滤掉, 该频率与动态校准中阶跃载荷施加后的系统结构振动频率完全一致. 因此, iFMS智能处理后的测力信号基本可以认为是尖锥模型在激波风洞流场中所受到的真实气动力.
图14
新窗口打开|下载原图ZIP|生成PPT图14风洞测力信号与经过智能处理后信号的对比(轴向力)
Fig.14Test data and its processing by CNN training model (axial force)
图15
新窗口打开|下载原图ZIP|生成PPT图15风洞测力信号与经过处理后信号的FFT结果对比(轴向力)
Fig.15Test data processing and comparison by fast Fourier transform (axial force)
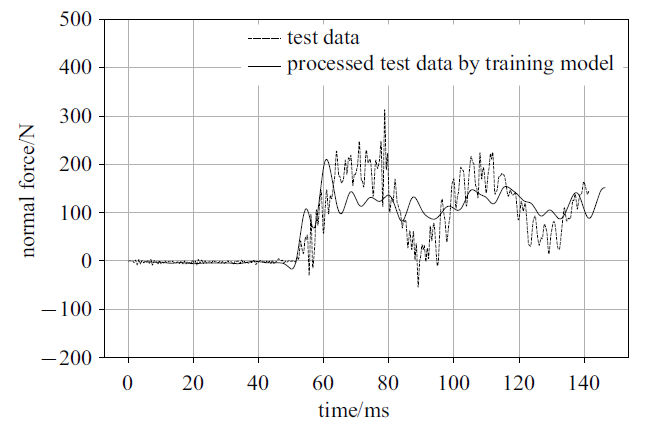
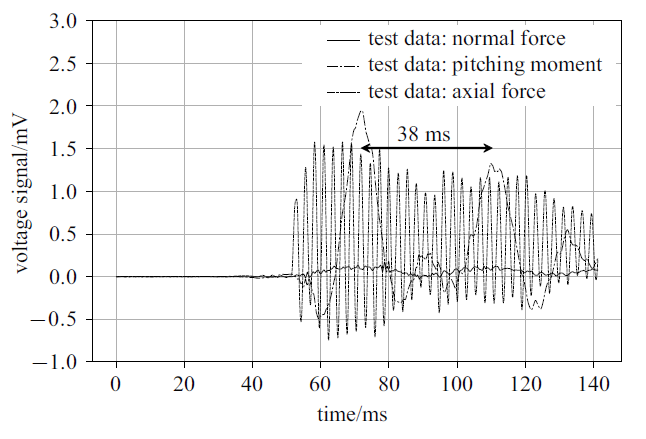
图16和17给出了三分量天平其他两个分量载荷(法向力和俯仰力矩)的CNN模型智能处理前后信号对比. 显然处理的结果消除了大幅度的振动信号干扰. 表2给出了智能动态校准模型处理前后的数据偏差, 图中的数据选取了时间坐标约70 $\sim$ 110 ms区间数据进行平均处理. 图18给出了3个分量信号的大致数据处理范围(约38 ms), 在这个范围内法向载荷(法向力和俯仰力矩)信号为一个整周期. 对轴向力信号则再通过微小区间范围调整, 实现整数周期处理.
图16
新窗口打开|下载原图ZIP|生成PPT图16风洞测力信号与其经过智能处理后信号对比(法向力)
Fig.16Test data and its processing by training model (normal force)
图17
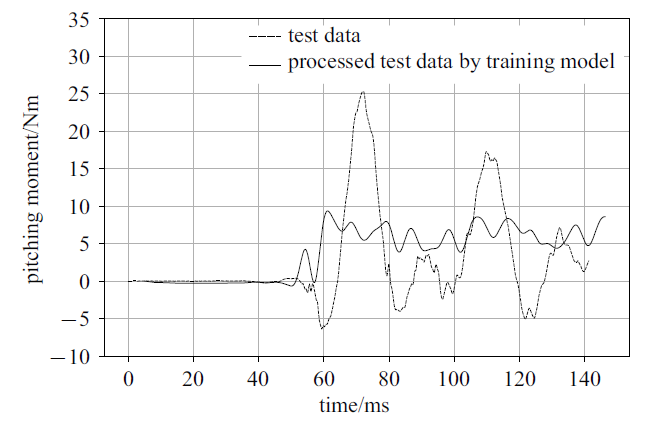
新窗口打开|下载原图ZIP|生成PPT图17风洞测力信号与其经过智能处理后信号对比(俯仰力矩)
Fig.17Test data and its processing by CNN training model (pitching moment)
Table 2
表2
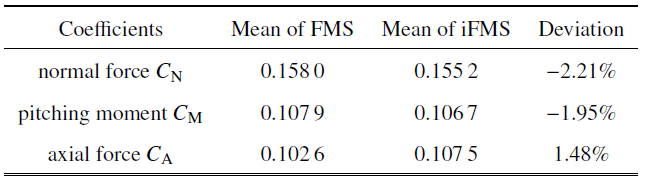
表2三分量载荷系数风洞数据结果
Table 2
 |
新窗口打开|下载CSV
图18
新窗口打开|下载原图ZIP|生成PPT图18三分量测力信号与平均处理区间的确定
Fig.18Comparison and Range of average-processing for three-component test data
此外, 风洞测力试验中天平输出的原始信号数据已经做过误差分析, 其测力试验数据精度均优于于2%[21]. 从表中数据可以看出直接通过选取整数周期信号进行平均处理的结果(FMS均值)与处理后的结果(iFMS均值)有1% $\sim$ 2%左右的偏差. 这种偏差主要原因之一可以认为是大幅度的FMS结构振动所引起的惯性干扰.
此外, 处理后的数据也可以明显看到远大于噪声信号的振动信号. 其主要原因除了风洞来流本身的噪声和不均匀性以外, 天平载荷信号较小的电压输出或载荷本身就相对偏小则可能导致处理数据误差占比较高. 图18三分量载荷信号的比较也发现: 载荷幅值差异较大, 法向力输出相对较小, 信号噪声也占比增大, 一定程度上影响了动态建模和数据处理, 产生一定误差.
4 结论
发展脉冲高焓风洞测力技术、切实提高测量精度是促进我国高超飞行器研制发展中亟待解决的最关键问题之一. 针对脉冲风洞极端测试条件, 传统风洞天平结构设计及其静态校准技术已经出现发展瓶颈问题. 本研究对高超声速脉冲风洞测力技术开展了深入研究和探索. 为实现短试验时间(毫秒量级)高性能气动力测量, 从性能影响因素的根源出发, 动态校准研究凸显其重要性和必要性, 也是高性能FMS中亟需重点关注和开展研究的最关键技术之一. 本文提出一种基于深度学习的单矢量动态自校准技术SVDC和基于该动态校准技术的智能测力系统概念iFMS. SVDC摆脱了传统砝码加载阶跃载荷的束缚, 实现风洞内即可对同一FMS开展高精度动态校准. 其中, 引入AI技术, 对FMS结构振动特征进行深度学习动态建模, 实现对FMS结构振动特性的高精度识别, 实现风洞天平输出不带有惯性振动干扰(或干扰基本可忽略)的"纯"气动力, 进而实现iFMS技术. 通过采集样本和风洞试验的综合验证, iFMS智能数据处理技术得到了较为理想的效果.高焓条件瞬态测力技术的智能化发展将有助于对高超飞行器在"复现"飞行条件下的高温效应问题开展更深入研究, 揭示流动物理规律. 同时也将为我国高超声速飞行器研发提供更可靠试验数据, 具有现实意义和工程实践意义.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
In order to overcome the interference of the model mounting system with the external aerodynamics of the body during shock tunnel testing, a new free floating internally mountable balance system that ensures unrestrained model motion during testing has been designed, fabricated and tested. Minimal friction ball bearings are used for ensuring the free floating condition of the model during tunnel testing. The drag force acting on a blunt leading edge flat plate at hypersonic Mach number has been measured using the new balance system. Finite element modelling (FEM) and CFD are exhaustively used in the design as well as for calibrating the new balance system. The experimentally measured drag force on the blunt leading edge flat plate at stagnation enthalpy of 0.7 MJ/kg and nominal Mach number of 5.75 matches well with FEM results. The concept can also be extended for measuring all the three fundamental aerodynamic forces in short duration test facilities like free piston driven shock tunnels.
DOIURL
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
//
[本文引用: 1]
//
//
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
//
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL
地面试验是先进高超声速飞行器研制的主要手段之一,获得满足高超声速气动实验研究的长时间高焓气流是发展激波风洞技术的关键难题之一.依据反向爆轰驱动方法,针对满足超燃试验有效时间的要求,讨论了爆轰驱动激波风洞运行缝合条件匹配、喷管起动激波干扰控制和激波管末端激波边界层相互作用等因素对激波风洞试验时间的制约及其相应的解决方法.应用这些延长试验时间的激波风洞创新技术,成功研制了基于反向爆轰驱动方法的超大型激波风洞,试验时间长达100ms,并有复现高超声速飞行条件的流动模拟能力.
DOIURL
地面试验是先进高超声速飞行器研制的主要手段之一,获得满足高超声速气动实验研究的长时间高焓气流是发展激波风洞技术的关键难题之一.依据反向爆轰驱动方法,针对满足超燃试验有效时间的要求,讨论了爆轰驱动激波风洞运行缝合条件匹配、喷管起动激波干扰控制和激波管末端激波边界层相互作用等因素对激波风洞试验时间的制约及其相应的解决方法.应用这些延长试验时间的激波风洞创新技术,成功研制了基于反向爆轰驱动方法的超大型激波风洞,试验时间长达100ms,并有复现高超声速飞行条件的流动模拟能力.
[本文引用: 1]
[本文引用: 1]
