引言

近年来, 人工神经网络(artificial?neural?networks, ANN), 尤其是深度神经网络(deep?neural?networks, DNN)因其在处理和预测高维复杂系统方面的优异能力而被广泛应用于自然语言处理^[1]、计算机视觉^[2]与图像处理^[3]等领域. 此外, 深度神经网络凭借其在GPU等异构硬件架构上的高并行效率, 已经成为当前科学计算领域的一个热点研究方向, 甚至为偏微分方程的实时求解提供了可行的实现途径^[4]. 目前国内外****已经提出了多种基于深度神经网络的数值方法, 如Ray和Hesthaven^[5]提出了基于深度神经网络的守恒定律辅助求解方法; Chan和Wang等^[6-7]采用深度神经网络解决了多尺度问题.

根据万能逼近定理^[8-9], 要使深度神经网络可以有效地逼近待拟合算子, 该算子必须是分段连续的. 然而偏微分方程, 尤其是非线性偏微分方程的解通常正则性较低, 深度神经网络对解的直接逼近往往会有精度不足的问题, 且在外推预测时还可能受到可解释性方面的质疑. 因此, 目前已发表的研究主要集中在解的回归分析和半解析方法上. 例如, Owhadi^[10]首先提出了物理信息神经网络, 基于训练过程实现变分问题的优化, 是一种具有代表性的半解析方法. Raissi等^[11-12]在机器学习法的基础上采用高斯过程拟合线性算子, 并进一步将该方法推广到非线性算子的回归. 此外, 在复杂偏微分方程的辅助计算方面, 深度神经网络也有诸多应用, 例如, 谢晨月等^[13]提出了基于深度神经网络的湍流大涡模拟方法.

在传统数值模拟中, 大型线性方程组通常采用Gauss-Seidel等直接求解法或基于Krylov子空间的BiCG和ICPCG等迭代方法^[14-16]求解. 这些方法虽保证了数值精度, 但也在内存消耗与计算时间方面带来了巨大的挑战, 成为目前大规模数值模拟领域的关键瓶颈之一^[17]. 因此, 通过深度神经网络加速求解线性方程组被认为是一种很有前景的研究思路^[18-28]. 例如, Wang等^[18-19]将简单结构的神经网络直接应用于求解线性方程组, 并在后续研究中继续完善了这一方法^[20-23]; 多****^[24-27]也实现了将循环神经网络应用于线性矩阵方程系统的求解中.

但是, 在上述研究中, 深度神经网络模型的精度成为了其在实际数值计算中的瓶颈^[28-29]. 例如, Xiao等^[30]提出了一种基于卷积神经网络的泊松方程求解器, 并将其算法应用于水和烟的实际流体模拟中. 该算法相对经典算法具有显著的加速效果, 在可视化效果上仿真结果也与经典方法较为接近. 但是, 该方法的数值相对误差大约在0.01的量级, 难以应用于精度要求更高的数值仿真中.

深度神经网络模型无法实现更高的预测精度通常有两方面的原因: (1)训练过程停滞于局部最优或梯度消失等问题; (2)模型深度(层数)不足等问题导致的模型参数过少^[29]. 因此, 为了提升深度神经网络求解的精度, 通常需要增加网络模型的深度与参数数量. 但随着层数的加深, 网络退化问题成为了一个新的挑战. 因此, He等^[31]首先提出了残差网络(Res-Net)结构: Res-Net将层间短接结构引入了深度神经网络网络中, 实现了一个天然的恒等映射, 以保证误差信息可以在深度神经网络中各隐藏层间的传播. 目前, Res-Net已经被大量的实际应用证明了其解决网络退化与梯度消失问题时的有效性^[32-35]. 在数值计算领域, Qin等^[36]将Res-Net引入了非线性的自恰系统的模拟中.

虽然万能逼近定理^[8-9]在理论上证明了当神经元数量充分大时, 深度神经网络模型可以实现任意精度直接预测线性方程组的解. 但实际上, 受制于深度神经网络模型的泛化能力等因素, 对于一般的线性方程组, 通过单次深度神经网络模型预测而直接获得足够精确(误差量级小于离散误差)的解往往是不切实际的. 受传统迭代算法的启发, 本文提出一种迭代校正方法来提升深度神经网络模型预测解的精度, 且该方法不需要过大的深度神经网络模型. 该方法通过计算每一次深度神经网络预测解的残差, 将残差作为右端项输入深度神经网络模型计算校正量, 如此循环直至达到收敛准则, 由此以校正迭代的方式逐步减少数值的误差.

深度神经网络模型中, 输入变量通常为向量或向量组, 因此, 为兼顾线性方程组的向量化表示与算法的适用范围, 本文所提出的基于深度神经网络的求解算法主要针对多对角矩阵. 在数值计算中, 多对角矩阵被广泛应用于有限差分法与谱方法中, 此外, 多对角矩阵具有天然的向量化表示方法, 可直接作为深度神经网络模型的输入层.

本工作将采用基于Res-Net的深度神经网络模型与校正迭代方法, 开发一种兼具高计算效率与高数值精度的线性方程组求解算法. 此外, 本文将研究该算法与有限差分法的结合, 以实现偏微分方程数值的加速求解, 并验证该求解算法的计算效率与数值精度, 以期为偏微分方程数值计算提供新型的高效求解方法.

1.
求解算法

1.1
神经网络求解方法

考虑到多对角线性系统${boldsymbol{Ax}} = {boldsymbol{b}}$, 其左侧矩阵${boldsymbol{A}}$可以式(1)的形式分解

$${boldsymbol{A}} = sumlimits_{i = 0, pm 1, pm 2, cdots } {{ m{di}}{{ m{g}}_i}({a_{i,1}},{a_{i,2}}, cdots,{a_{i,(n - i)}})} $$

(1)

其中, ${
m{di}}{{
m{g}}_i}({a_{i,1}},{a_{i,2}}, cdots,{a_{i,(n - i)}})$表示将向量$({a_{i,1}},{a_{i,2}}, cdots, $$ {a_{i,(n - i)}})$的元素排列在第$i$条对角线上, 其他位置均为0的矩阵, 特别地, ${
m{di}}{{
m{g}}_0}( cdot )$表示主对角线; 当$i > 0$时, ${
m{di}}{{
m{g}}_i}( cdot )$表示主对角线上方的对角线, 当$i < 0$时, ${
m{di}}{{
m{g}}_i}( cdot )$表示主对角线下方的对角线. 该表示方法即将任意一个线性系统用数个向量进行表示, 这一表示方法对于多对角矩阵与类多对角矩阵有天然的兼容性. 实际上, 本文提出的算法可适用于多种具有类似结构的矩阵, 如五对角矩阵等, 在本文中, 由于三对角矩阵具有更广泛的应用场景, 且为了简化表述, 故选用了三对角矩阵作为示例以说明.

因为任意的三对角矩阵可以转变成主对角线处的所有元素均为1的三对角矩阵, 所以任意三对角线性方程组均可用3个向量来表示: 左对角线向量${boldsymbol{l}}$, 右对角线向量r与右侧向量${boldsymbol{b}}$, 而这3个向量构成的向量组即可直接作为神经网络模型的输入层.

实际上, 本文提出的方法可以看作是对算子$S({boldsymbol{A}},{boldsymbol{b}}) = {{boldsymbol{A}}^{ - 1}}{boldsymbol{b}}$的回归, 相应地, 选择均方误差作为网络的损失函数${L} (hat x;x)$, 以实现深度神经网络模型对算子S的拟合

$${L} (hat x;x) = frac{1}{{M} }sumlimits_{{i} = 1}^{M} {{{left( {hat {boldsymbol{x}}({{boldsymbol{l}}_i},{{boldsymbol{r}}_i},{{boldsymbol{b}}_i}) - {y_i}} ight)}^2}} $$

(2)

其中$M$为训练集的大小.

本文中, 采用的训练集由服从高斯分布的随机向量构成, 即训练集输入为$left{ ({a_1},{a_2}, cdots,{a_D}):{a_j}sim N(0,
ho ),
ight. $$ left.j leqslant D
ight}$, 其中, $
ho $为训练集的标准差, $D$为待求解方程组的维数, 均为生成训练集时需给定的参数.

1.2
残差网络

Res-Net通过在隐藏层之间建立“短路”连接(称作残差块, 如图1所示), 从而使得网络可以直接近似恒等算子, 即将原本的待拟合算子转换为对输入与输出层间的残差的拟合^[36-38].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
残差网络结构示意图



Figure
1.
Schematic of the Res-Net



下载:
全尺寸图片
幻灯片


在图1中, 传入隐藏层的输入向量在完成激活函数(本文选用ReLU激活函数)的计算后, 会再与输入向量自身相加而得到残差块的输出值. 由此可见, 残差块结构使网络可以直接近似恒等算子, 即将原本的待拟合算子转换为对输入与输出层间的残差的拟合^[36-38]. 目前, Res-Net已经被证明是一种可靠的避免网络退化问题的手段, 且被广泛应用于多种成熟的深度神经网络应用中^[32-35].

除残差块外, 还引入到另一个覆盖整个网络的短连接, 以进一步逼近线性系统的解, 即讲深度神经网络模型的输出替换为$({boldsymbol{I}} - {{boldsymbol{A}}^{ - 1}}){boldsymbol{b}}$. 这一变换将使输出向量的均值为0, 相当于通过正则化的方法优化了采用ReLU激活函数的深度神经网络模型的训练效果.

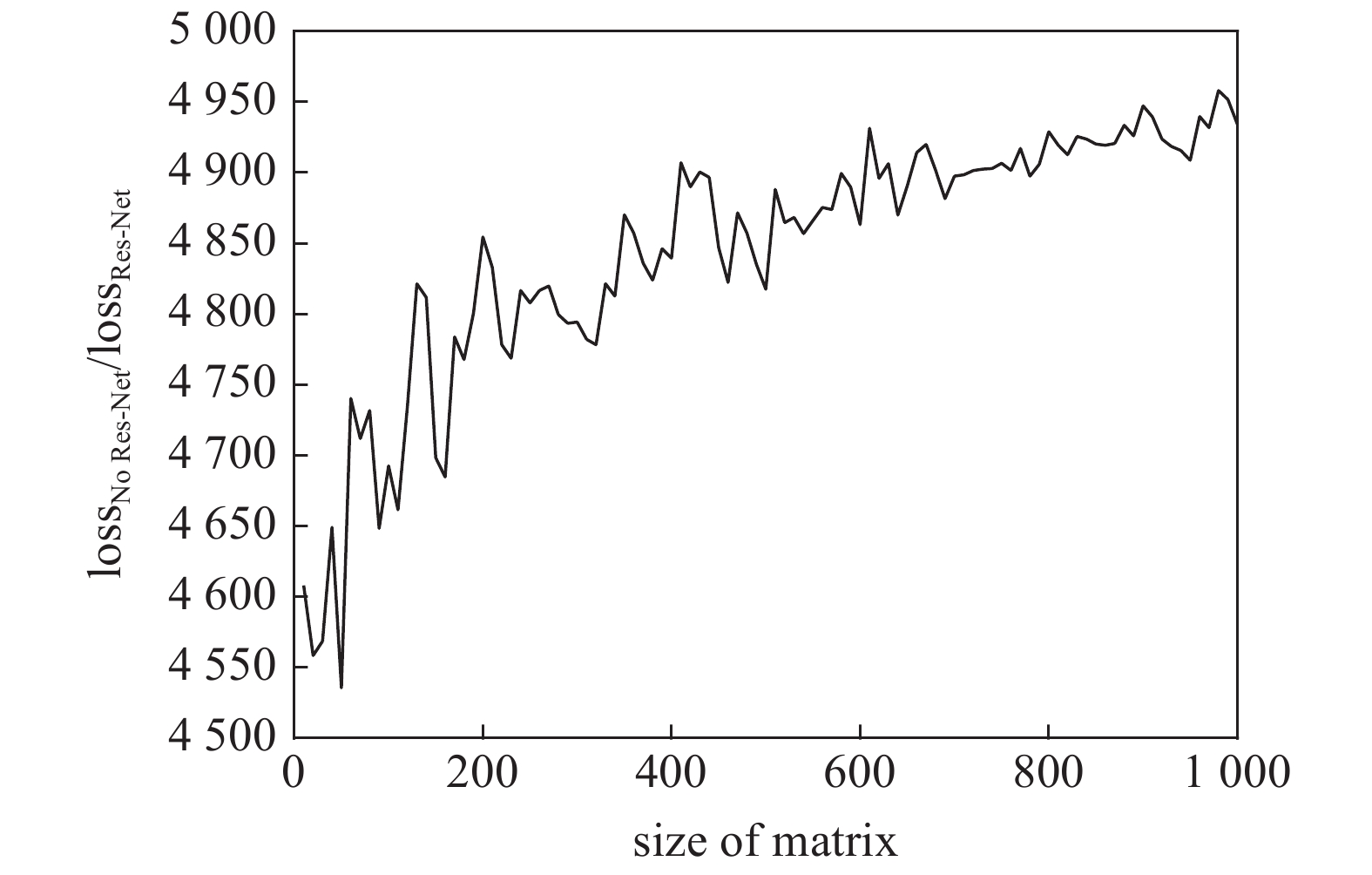
为了评估通过Res-Net的实际优化效果, 测试了一个数值实验进行比较, 图2展示了无Res-Net时深度神经网络模型训练损失函数与有Res-Net模型的损失函数的比值.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
求解不同大小线性方程时Res-Net与非Res-Net的损失函数对比



Figure
2.
Comparison of the loss function for different sizes of the linear equations with Res-Net and no Res-Net



下载:
全尺寸图片
幻灯片


从图2中可以看出, 采用Res-Net后, 对于任意大小的方程组(深度神经网络模型), 模型的损失函数可降低至不采用Res-Net时模型损失函数的1/5000左右, 这说明Res-Net可以显著提升训练后的模型预测精度.

1.3
迭代校正方法

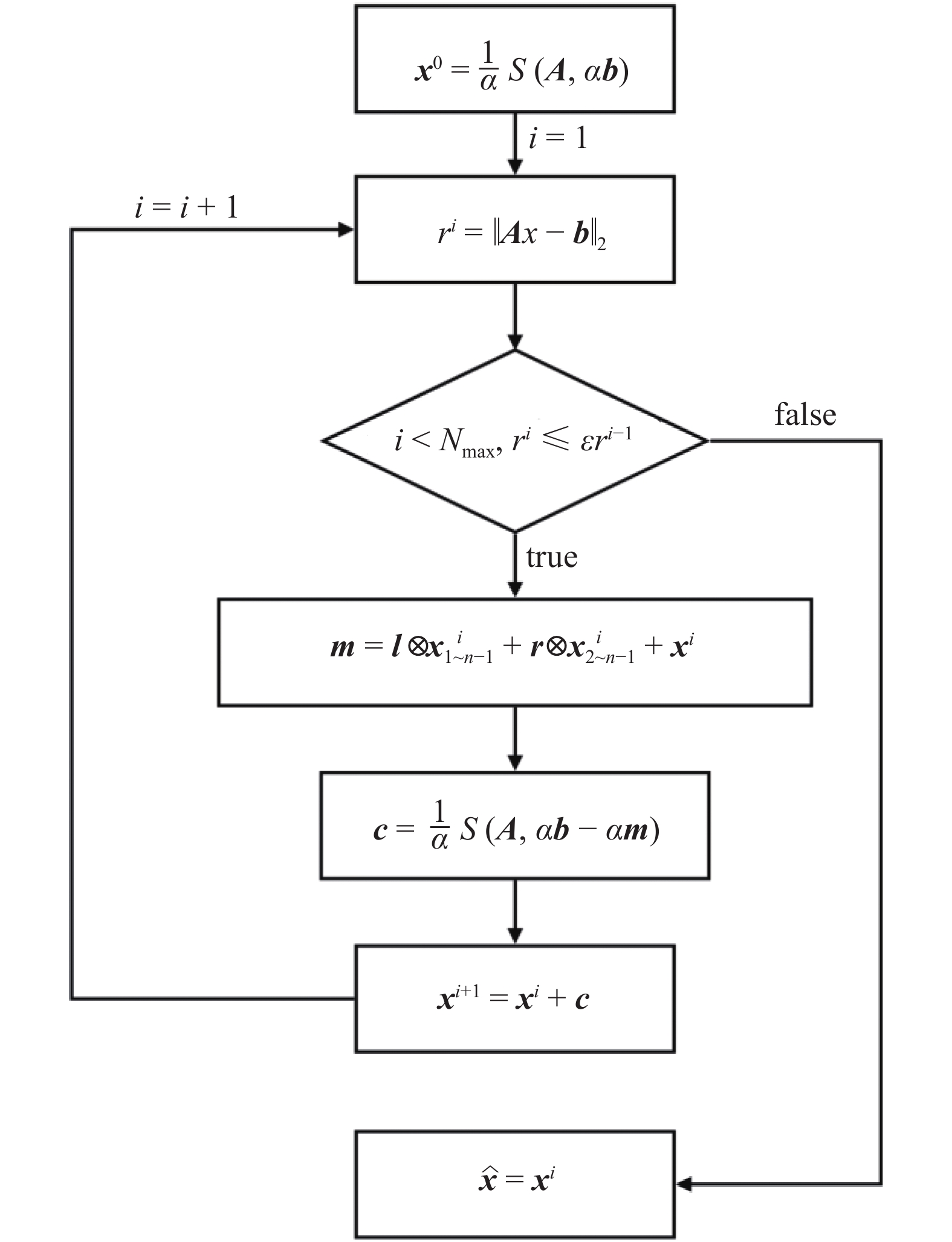
记深度神经网络模型的预测解为$S({boldsymbol{A}},{boldsymbol{b}})$, 则迭代算法如图3所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
迭代算法示意图



Figure
3.
Schematic of the iteration algorithm



下载:
全尺寸图片
幻灯片


在图3中, 参数$varepsilon $为迭代收敛条件; 运算符$ otimes $表示两个向量的对应元素相乘. 每次迭代中的向量$m$表示当前迭代步中${boldsymbol{A}}{{boldsymbol{r}}^i}$的值. 在$m$的计算中, 三对角矩阵和向量的乘积可以拆分成3个向量内积运算的求和, 使计算复杂度和内存使用量最小.

深度神经网络模型拟合的目标算子$S'({boldsymbol{A}},{boldsymbol{b}}) = $$ {{boldsymbol{A}}^{ - 1}}{boldsymbol{b}}$对于常数$k$应具备性质$S'({boldsymbol{A}},k{boldsymbol{b}}) = kS'({boldsymbol{A}},{boldsymbol{b}})$, 受此启发, 本文引入的迭代算法额外引入了一个放大因子(图3中的$alpha $)用于进一步提升求解的精度.

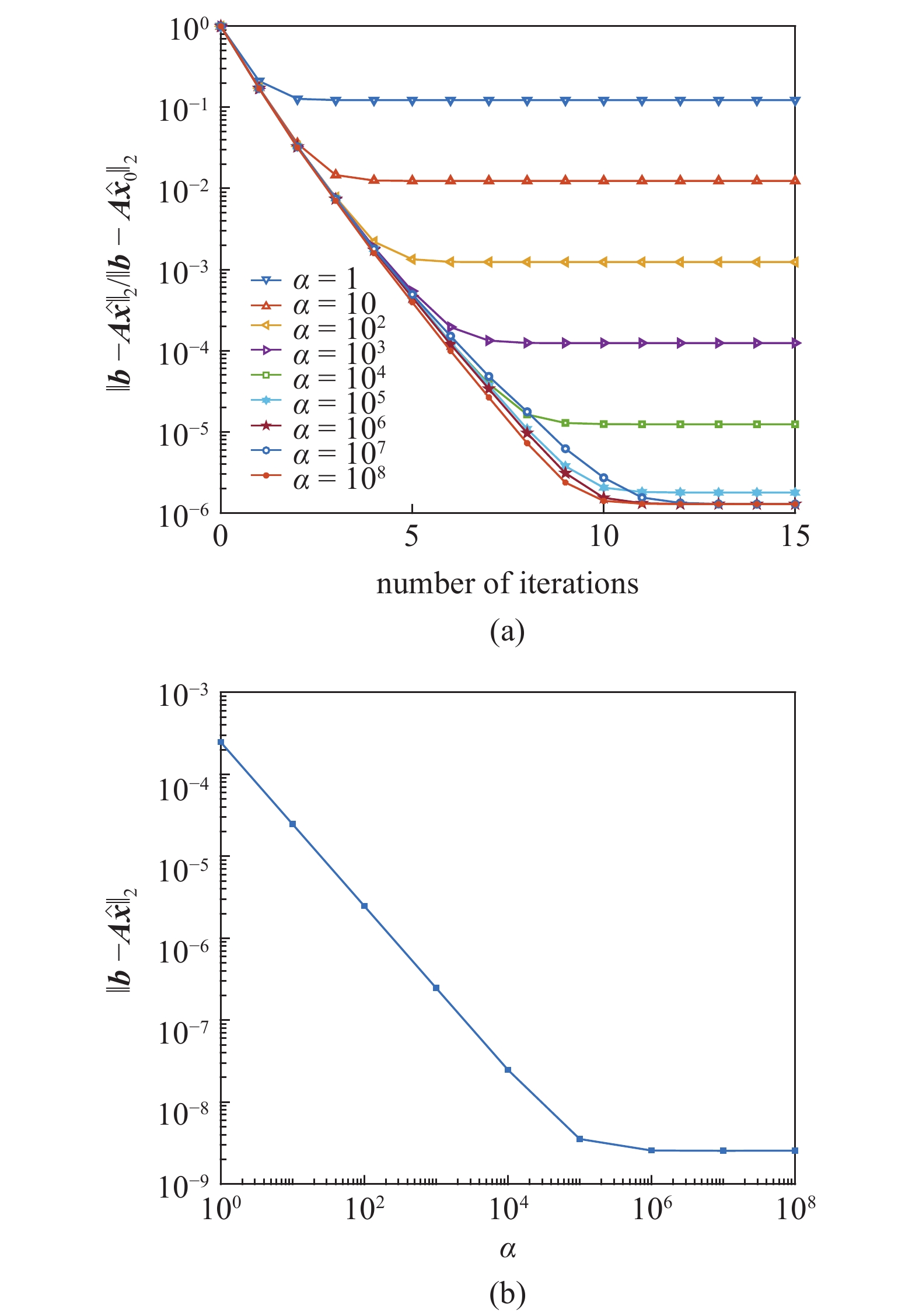
为了论证该迭代算法可以有效地提升深度神经网络的求解精度, 图4展示了对于给定方程组在设置不同的放大因子时迭代过程中残差的变化情况以及对不同的放大因子, 迭代最终收敛时的残差大小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
(a)不同放大因子时残差随迭代的变化情况与(b)放大因子对收敛时残差的影响



Figure
4.
(a) Variation of residuals with iterations for different amplification factors and (b) effect of amplification factors on convergence residuals



下载:
全尺寸图片
幻灯片


由图4可见, 迭代算法可以有效地降低求解的误差, 对给定的线性方程组, 残差可被缩小至迭代初始时的${10^{ - 5}}$倍. 此外, 求解精度随放大因子$alpha $增大而提高, 但是存在一个确定的阈值, 当超过该值时, 增大放大因子不会使精度进一步提升.

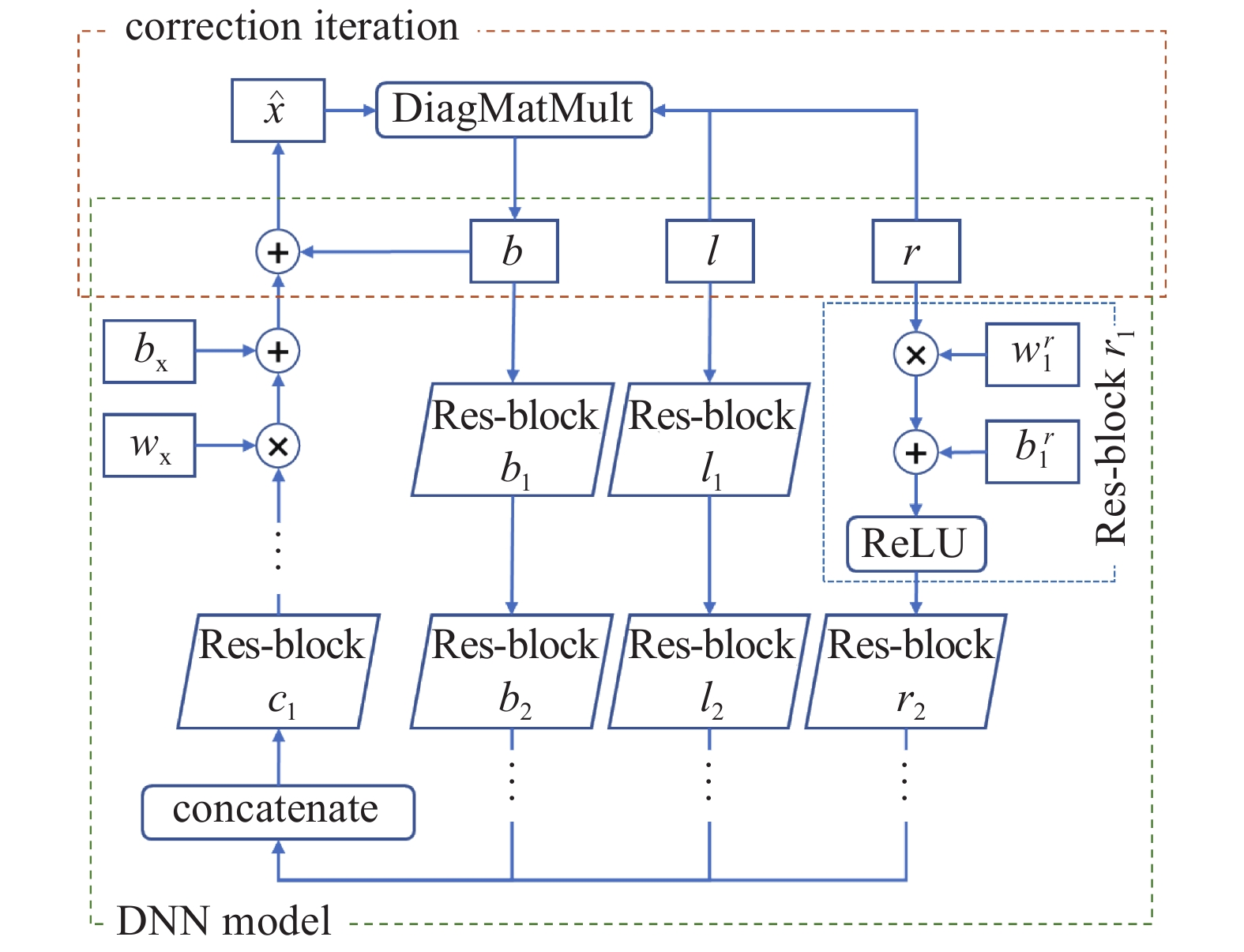
综上所述, 本文提出的求解器的体系结构可以由图5来演示, 它包括带Res-Net的深度神经网络和修正迭代.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
算法求解器架构示意图



Figure
5.
The schematic of the linear solver



下载:
全尺寸图片
幻灯片


在图5中, DiagMatMult子程序表示图3中提到的多对角矩阵与向量的乘积, Concatenate子程序表示对输入向量进行拼接均, 带上下标的$b$与$w$分别为神经元的偏置与权重.

图5的下半部分为包含了Res-Net的深度神经网络模型, 上半部分为校正迭代过程: 在每个迭代步中, 先由深度神经网络模型得到预测解$hat {boldsymbol{x}}$, 再计算$hat {boldsymbol{x}}$的残差, 再作为新的右端向量传入深度神经网络进行下一轮的校正迭代(如图3所示).

由算法架构可见, 该算法除表示线性系统的向量组(即深度神经网络的输入向量)外, 不需要引入额外的矩阵结构, 可完全依托向量化计算实现, 相对传统方法可显著减少空间消耗. 此外, 该方法可同时求解多个具有相同结构的线性方程组, 这对于基于交替方向隐式等方法的数值方法具有显著的效率优势.

2.
数值实验和验证

2.1
求解效率测试

为了验证本文所提出的基于深度神经网络的求解算法在效率方面的优势以及数值计算中的应用前景, 采用本文提出的求解算法和传统方法(LU分解法等)分别对线性方程组进行求解以测试其求解效率.

本文使用Google^[39]的TensorFlow 2.0平台来开发本工作中的所有计算程序. 图6展示了本文新算法与NumPy与SciPy中线性求解器之间的计算效率比较. NumPy默认调用LAPACK库中内置的LU分解求解线性方程组; SciPy基于BLAS和LAPACK的标准线性代数算法. NumPy与SciPy两者均能在多核平台上实现最大CPU核数(本例为28核)的并行求解, 而TensorFlow平台天然支持GPU的加速. 图中测试采用的平台是Intel Xeon-W3175X CPU(28核, 3.1 GHz)和Nvidia RTX2080Ti GPU. 在测试中, 不同求解器求解精度均为${10^{ - 9}}$, 分别测试了多种具有代表性的迭代法, 测试的矩阵大小范围为$20 times $$ 20sim 4000 times 4000$之间, 每次测试均求解5000个重新随机生成的矩阵, 其高斯分布参数与训练集一致, 并计算其平均求解时间, 结果如图6所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
求解不同大小线性方程各种算法的求解时间



Figure
6.
Solving times of DNN and conventional algorithms for different size of linear equations



下载:
全尺寸图片
幻灯片


图6中, LU算法由于虽然在小矩阵的求解中效率比其他方法高, 但是由于其计算复杂度较高, 随着矩阵大小的增加其相对效率也逐渐变低. 而本文所提出的基于深度神经网络的算法随着矩阵大小增加, 求解时间增长速度明显较慢, 其求解时间对矩阵大小的敏感度明显低于BiCG和GMRES等传统方法. 由此, 该算法计算复杂度较经典算法低, 因此在大规模线性系统中更具有优势.

2.2
线性偏微分方程算例

本节将以二维热传导方程为例, 将本文所提出的基于深度神经网络的求解方法结合交替方向隐式方法实现对实际偏微分方程进行数值求解. 交替方向隐式法在基于有限差分法的数值算法中得到了广泛的应用, 它可以将多对角矩阵转换为三对角矩阵, 这与上面介绍的网络具有良好相容性.

考虑在矩形区域$varOmega = left{ {left( {x,y}
ight)|0 < x < 1,0 < y < 1}
ight}$ 的混合边界条件下的二维热传导方程

$$left. begin{array}{l} ;{partial _t}u - beta ;left( {partial _{xx}^2u + partial _{yy}^2u} ight); = 0;;;;left( {x,y} ight) in varOmega {left. {dfrac{{partial u}}{{partial n}}} ight|_{y = 1,y = 0}} = 0 {left. u ight|_{x = 1}} = 0,;;;;;;;;{left. u ight|_{x = 0}} = 1 end{array} ight}$$

(3)

其中, 常系数$;beta $取值为0.1. 本文所采用的交替方向隐式格式如式(4)所示, 其空间精度为2阶, 时间精度为1阶

$$left. begin{array}{l} u_{i,j}^{n + frac{1}{2}} - dfrac{1}{{tau _x^ + Delta {x^2}}}u_{i + 1,j}^{n + frac{1}{2}} - dfrac{1}{{tau _x^ + Delta {x^2}}}u_{i - 1,j}^{n + frac{1}{2}} = quaddfrac{{tau _y^ - }}{{tau _x^ + }}u_{i,j}^n;; + dfrac{1}{{tau _x^ + Delta {y^2}}}left( {u_{i,j + 1}^n + u_{i,j - 1}^n} ight) u_{i,j}^{n + 1} - dfrac{1}{{tau _y^ + Delta {y^2}}}u_{i,j + 1}^{n + 1} - dfrac{1}{{tau _y^ + Delta {y^2}}}u_{i,j - 1}^{n + 1} = quaddfrac{{tau _x^ - }}{{tau _y^ + }}u_{i,j}^{n + frac{1}{2}} + dfrac{1}{{tau _y^ + Delta {x^2}}}left( {u_{i,j + 1}^{n + frac{1}{2}} + u_{i,j - 1}^{n + frac{1}{2}}} ight) end{array} ight}$$

(4)

其中, $tau _x^ pm = 2left( {Delta {t^{ - 1}}{beta ^{ - 1}} pm Delta {x^{ - 2}}}
ight),tau _y^ pm = 2left( {Delta {t^{ - 1}}{beta ^{ - 1}} pm Delta {y^{ - 2}}}
ight)$.

在该方法中, 每个时间步长被分割成两个半步长, 如式(4)所示, 一个三对角线性方程可以代表每个半步, 因此, 本文所提出的求解方法可以直接求解该三对角线性方程.

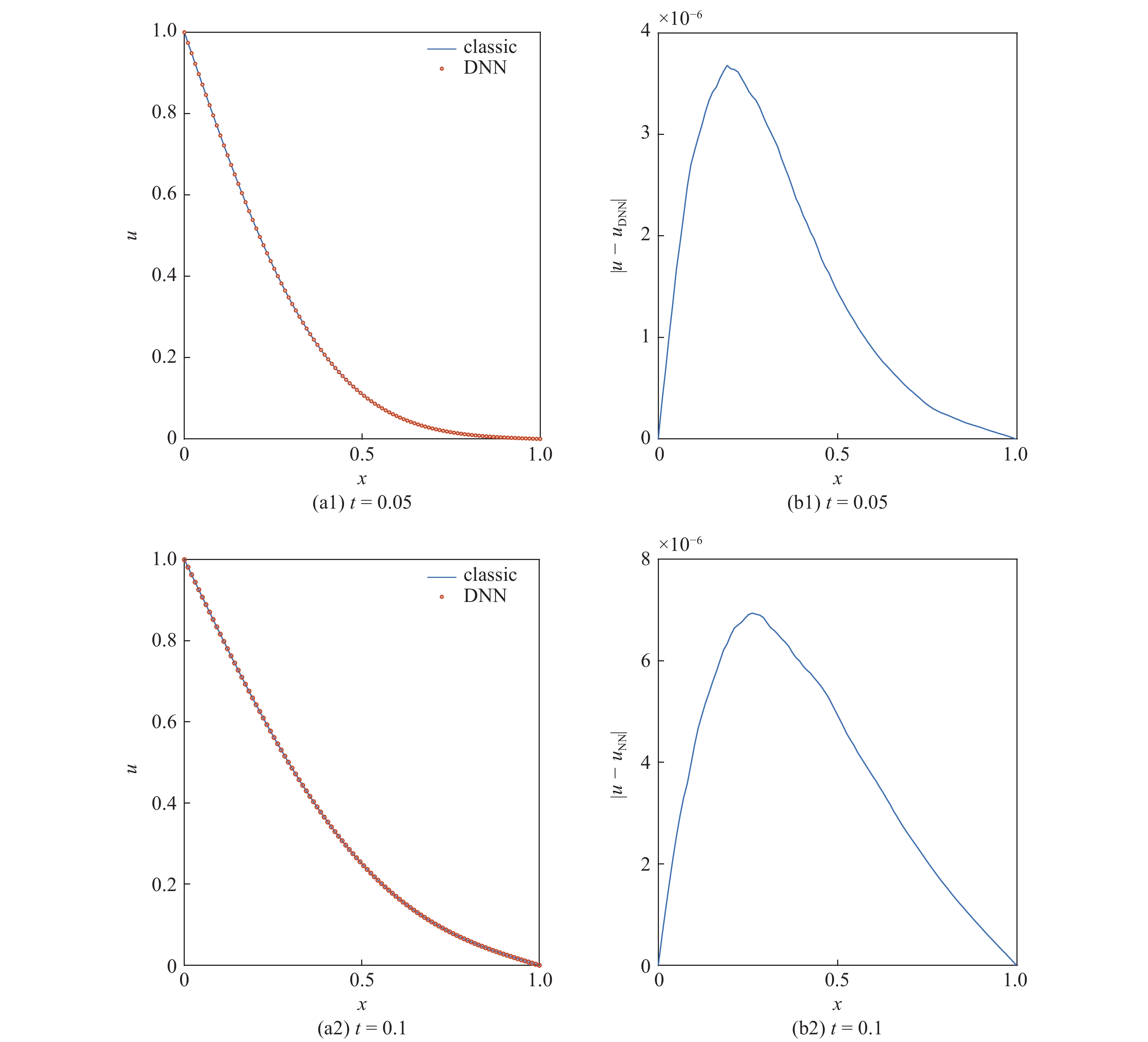
选取时间步长为0.001, 两个方向上的空间步长均为0.01, 方程(3)的求解结果如图7所示. 图7分别展示了在第50, 第100与第200时间步时中心截面($y = 0.5$)处经典方法(LU算法)和本文提出的算法的计算结果(图7(a))及其差值分布(图7(b)).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-7-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7-1" />



7
(a)二维热传导方程的数值求解结果与(b)相对经典方法的求解误差



7.
(a) Numerical solution of the 2D heat conduction equation and (b) the error distribution



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
(a)二维热传导方程的数值求解结果与(b)相对经典方法的求解误差 (续)



Figure
7.
(a) Numerical solution of the 2D heat conduction equation and (b) the error distribution (continued)



下载:
全尺寸图片
幻灯片


图7中, 随计算时间逐渐推进, 由本文提出的基于深度神经网络的求解算法所得结果在整个计算区域内的误差均保持在${10^{ - 5}}$量级, 可以证明其量级不高于与式(4)中格式的截断误差. 由此, 证明了本文所提出的算法对于二维线性方程的求解具有较高的数值精度.

2.3
非线性偏微分方程方程算例

Burgers方程是非线性声学、气体动力学、流体力学等各种应用场景中的基本偏微分方程之一^[40], 最早由Bateman^[41]提出, 在该算例中, 本文将利用所提出算法对一维Burgers方程进行数值求解.

考虑如式(5)所示的非线性Burgers方程

$$left. begin{array}{l} {partial _t}u - u{partial _x}u - beta {partial _{xx}}u = 0,;;;;;;;x in left[ {0,1} ight] u{|_{x = 0}} = 0 u{|_{x = 1}} = 0 u{|_{t = 0}} = sin ;({text{π}} x) end{array} ight}$$

(5)

其中, $beta $为扩散系数, 本算例中, 取$;beta = 0.025$.

该问题存在如式(6)所示的解析解.

$$u(x,t) = frac{{2{text{π}} beta displaystylesumlimits_{m = 1}^infty {m{A_m}{{ m{e}}^{ - beta {m^2}{{text{π}} ^2}t}}sin( m{text{π}} x)} }}{{displaystylesumlimits_{m = 1}^infty {{A_m}{{ m{e}}^{ - beta {m^2}{{text{π}} ^2}t}}cos( m{text{π}} x)} }}$$

(6)

其中, ${A_m}$为积分常数, 且${A_m} = 2displaystyleint_0^1 {{{
m{e}}^{ - frac{1}{{2{text{π}} beta }}cos ({text{π}} x)}}cos( m{text{π}} x)} {
m{ d}}x$.

选择如式(7)所示的二阶精度的差分格式

$$begin{split}& left[ {1 - alpha left( {u_{i + 1}^n - u_{i - 1}^n} ight) + 2hat beta } ight]u_i^{n + 1} + left( {alpha u_i^n - hat beta } ight)u_{i - 1}^{n + 1} - &qquadleft( {alpha u_i^n + hat beta } ight)u_{i + 1}^{n + 1} = u_i^n + hat beta left( {u_{i + 1}^n - 2u_i^n + u_{i - 1}^n} ight) end{split} $$

(7)

其中, 常数$alpha = Delta t/(4Delta x)$, $hat beta = beta Delta t/(2Delta {x^2})$. 本算例中, 时间步长$Delta t = 0.001$, 空间步长$Delta x = 0.01$.

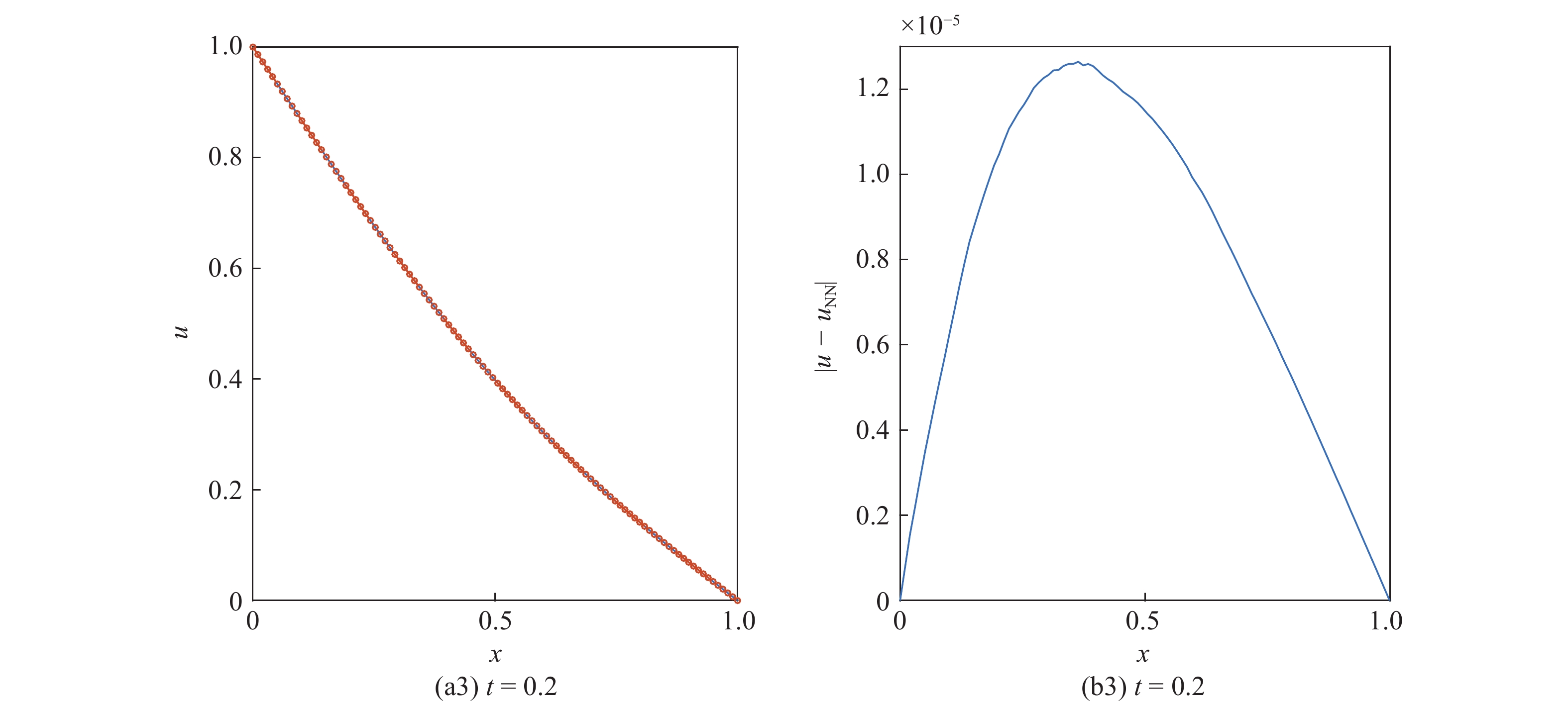
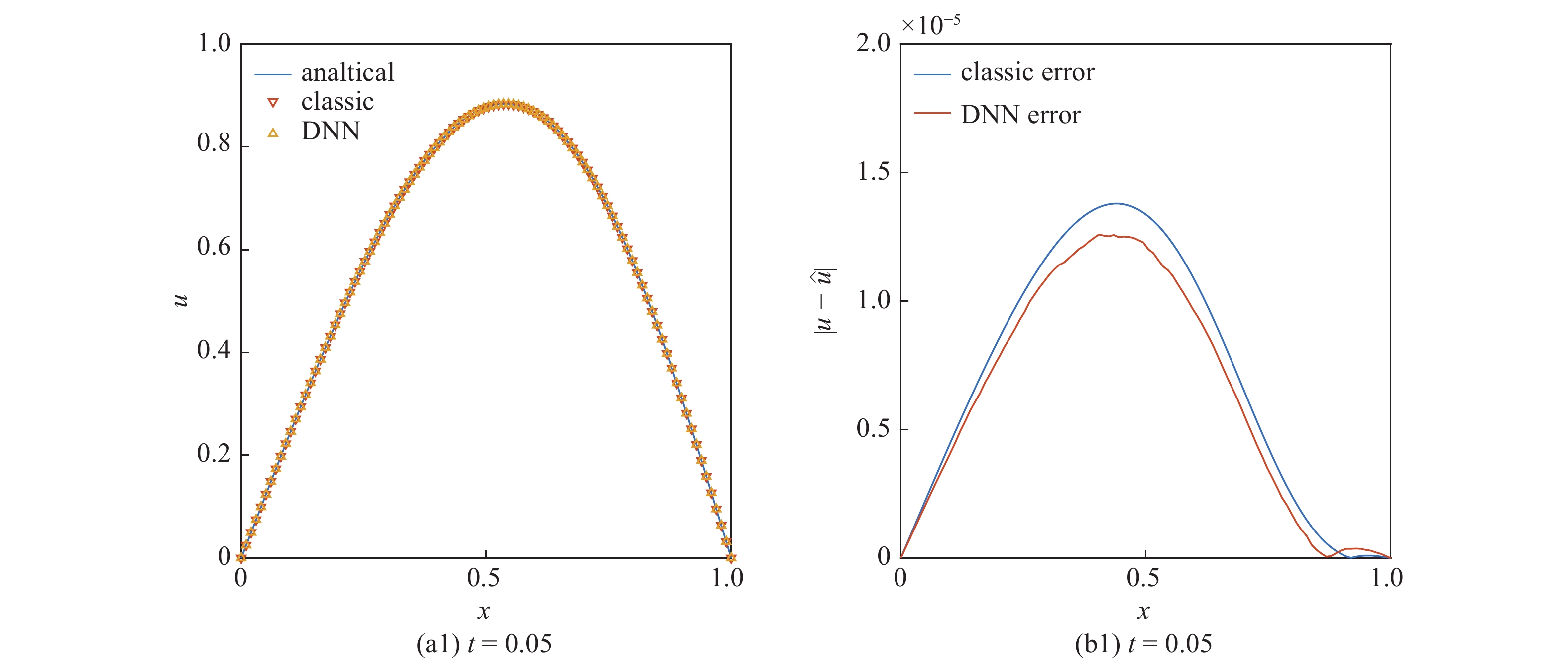
与2.2中算例类似, 图8(a)分别展示了第50、第100、第200时间步时的计算结果. 特别地, 图8(b)中给出了经典线性求解器与本文提出的方法相对解析解的误差对比.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-8-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8-1" />



8
不同时刻下(a)一维Burges方程的数值求解结果与(b)求解误差



8.
Numerical solution of (a) the 1D Burgers equation and (b) the error distribution



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-040-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
不同时刻下(a)一维Burges方程的数值求解结果与(b)求解误差 (续)



Figure
8.
Numerical solution of (a) the 1D Burgers equation and (b) the error distribution (continued)



下载:
全尺寸图片
幻灯片


由图8可见, 随计算时间推进, 由本文提出的求解算法所得结果在整个计算区域内的误差均保持在${10^{ - 5}}$量级, 与2.2节中的线性方程组算例保持一致, 由此说明本算法可适应多种具有类似结构的差分方程组求解.

此外, 由图8(b)中结果可见, 本文所提出的算法求解精度与经典求解方法的精度几乎一致, 均为${10^{ - 5}}$量级, 即不会引入高于截断误差量级的计算误差. 与之相对地, 其他大多数基于神经网络的求解器的误差大小范围在${10^{ - 1}}$到${10^{ - 3}}$之间^{[28, 42]}. 因此, 作为一种基于深度神经网络的求解方法, 本文所提出的求解算法在显著提升计算效率的情况下, 仍保证了高计算精度.

3.
结语

本文结合深度神经网络与Res-Net架构, 引入了修正迭代过程, 提出了一种针对多对角线性系统的新型求解算法, 并将其应用于实际的偏微分方程的有限差分法求解中.

(1)基于深度神经网络, 本文提出的新算法在GPU等混合平台上具有较高的计算效率和原生硬件兼容性. 与经典的求解方法相比, 本文的算法可同时求解多个线性方程组而无需引入额外的数据处理过程, 因此具有更高的求解效率.

(2)通过在算法中加入了Res-Net架构, 本文的算法避免了深层网络的退化问题, 从而提高了新算法的精度. 在此基础上, 本文引入了修正迭代与放大因子, 进一步降低误差, 使深度神经网络求解误差量级低于一般差分格式的离散误差.

(3)相对传统方法, 本文的深度神经网络求解线性方程组的另一优势在于, 该方法可以同时求解多个独立的方程组, 省略了矩阵构建与循环过程, 可显著提升交替方向隐式等方法的求解效率.

(4)由于多对角线性方程组广泛存在于多种差分方法中, 本文的方法可以被应用于多种偏微分方程的求解中, 本文给出了一维非线性方程与二维线性方程的算例, 论证了该方法应用的广泛性.