引言

随着科学技术的不断发展, 机器人的应用范围越来越广泛, 应用场景也越来越多样化. 为了进行灾后搜救、管道清理、未知区域探索等任务, 机器人需要能在有限的工作空间和不规则的地形下移动并完成任务. 于是, 许多****以蚯蚓等蠕虫为仿生对象, 设计了一系列仿蠕虫机器人^[1-8]. 受到蚯蚓的运动来源于体节的轴向变形的启发, 在此类仿蠕虫机器人的设计中, 仿蠕虫机器人通过不同的驱动方式驱动环向和纵向弹性元件使体节单元发生轴向伸缩变形, 从而实现仿蠕虫机器人的运动^[1]. Fang等^[2]使用折纸球结构作为仿蠕虫机器人的体节单元, 通过电机驱动绳索控制体节单元的伸缩变形, 在管道中实现了仿蠕虫机器人的后退蠕动波运动; Luo等^[3]提出了一种剪刀结构单元的仿蠕虫机器人, 该剪刀结构单元可以通过伺服电机控制体节单元的伸缩变形模拟蠕虫环肌与纵肌的变形, 从而实现移动的功能; Pfeil 等^[4]提出了一种介电弹性体驱动的软体仿蠕虫机器人, 其体节单元由内部的保持结构和外部的介电弹性体构成, 通过切换介电弹性体一端电极的电压使体节单元发生伸缩变形. 由于弹簧的拉压变形与蠕虫体节单元的伸缩变形相似, 也有一些****将蠕虫机器人描述为多单元的振动驱动系统^[5], 并针对振动驱动系统的驱动方式^[6]、外部摩擦^[7]和运动形式^[8-9]进行了分析. 然而, 这些仿蠕虫机器人仅通过轴向伸缩变形实现了移动的功能, 并不具备起竖的功能, 因此在管道勘测、地形侦察、精密加工等应用中无法完成特定操作. 为了使仿蠕虫机器人具有执行特定操作的能力, 希望设计一种仿生起竖结构, 使仿蠕虫机器人具有尺蠖、蛇等生物的起竖功能.

与蚯蚓等蠕虫通过体节的伸缩变形来进行移动不同, 起竖这种运动形式需要通过弯曲变形来实现. 根据不同应用场景的需求, 结合材料、结构设计、驱动和控制方法, ****们提出了许多能够产生弯曲变形的仿生结构. 为了代替人类在太空执行任务, ****们针对柔性机械臂提出了相应的控制方法使其产生需求的弯曲变形^[10-12], 从而执行航天器维修、在线装配等任务; 以章鱼手臂为灵感可以实现对不同形状物体的稳定抓取^[13-15]; 为了帮助中风患者恢复抓取的功能, ****们设计了协助手指产生弯曲变形的上肢外骨骼^[16-18]; Zareei等^[19]以实现快速展开机构为目的, 将弹簧的两端分别连接在不同杆的中心位置, 通过在关节处施加几何的位置限制, 得到了一种具有双稳态性质的弯曲关节, 并基于这种弯曲关节提出了一种在初始激励下能发生弯曲变形的串联结构^[19]. 然而, 该研究在对串联结构进行分析时, 假定了弯曲变形发生在水平平面内, 没有考虑在重力作用下竖直平面内的弯曲变形, 也没有对该结构不同构型的触发条件进行分析. 此外, 大部分以弯曲变形为目标的结构只能产生C形的构型, 无法实现更加复杂的构型.

在自然界中, 可观察到蛇、尺蠖等具有起竖能力的生物能根据不同的情况触发不同的稳定构型, 当其在移动或者休息时, 身体紧贴地面, 处于直线稳定构型, 当其在侦察、攻击、防御、捕食时, 身体处于特定的起竖稳定构型. 仿起竖功能的结构设计能够进一步拓展仿蠕虫机器人在不同场景中的应用及其功能. 具有多稳态特征的非线性柔性结构能够实现起竖功能的仿生设计. ****们利用不同的方法, 设计了不同类型的多稳态结构以实现需求的仿生物变形功能^[20-21]. 捕蝇草具有张开状态和闭合状态两种不同的稳定状态, 当昆虫等生物触及其表面时, 捕蝇草便会快速地从张开状态切换至闭合状态以捕获猎物^[22-23]. ****们受其启发, 设计了一系列仿捕蝇草多稳态结构, 并利用电磁驱动^[24-25]、形状记忆合金^[26]、气动^[27]等驱动方法完成状态的切换; Li等^[28]基于捕蝇草细胞组织的分布式加压和内嵌式多稳态这两个特点, 提出了一种仿捕蝇草的射流折纸结构, 该结构能够通过调控压强实现结构在单稳态、双稳态和多稳态之间的切换. Lachenal等^[29]利用两个预应力法兰构造了一种多稳态复合扭转结构, 该结构能在外界力矩下从直线构型转换为扭转构型; Zirbel等^[30]提出了一种有限厚度的折纸结构模型, 可以应用于可展开太阳能电池板. 基于尺蠖、蛇等生物具有的多稳态特征, 我们希望设计一种具有非线性多稳态性质的仿生柔性关节以实现一种起竖功能的机器人.

本文设计了一种仿生柔性关节, 在此基础上构建了多节仿生起竖结构以实现仿蠕虫机器人的起竖功能. 研究给出了仿生起竖结构在直线构型和需求的起竖构型下稳定的结构参数设计准则和使仿生起竖结构能够起竖至需求构型的触发条件准则, 并通过不同稳态的吸引盆得到了满足触发条件准则的初始激励形式. 本研究提出的仿生起竖结构考虑了竖直平面内的重力作用, 因此需要提出整体结构的设计准则. 此外, 本文中的仿生起竖结构除了要实现C形的构型以外, 还希望能够实现更多样的起竖构型, 这种构型的复杂性也对研究工作形成了挑战. 最后, 采用数值方法求解动力学方程来研究起竖构型的触发条件, 对后续协同控制的研究具有指导意义. 本文提出的仿生起竖结构能够进一步拓展仿蠕虫机器人的功能, 为仿蠕虫机器人在航空航天与精密加工等领域的应用提供了理论依据, 也是对仿生设计理论的进一步完善.

1.
仿生起竖结构设计准则

1.1
仿生起竖结构势能

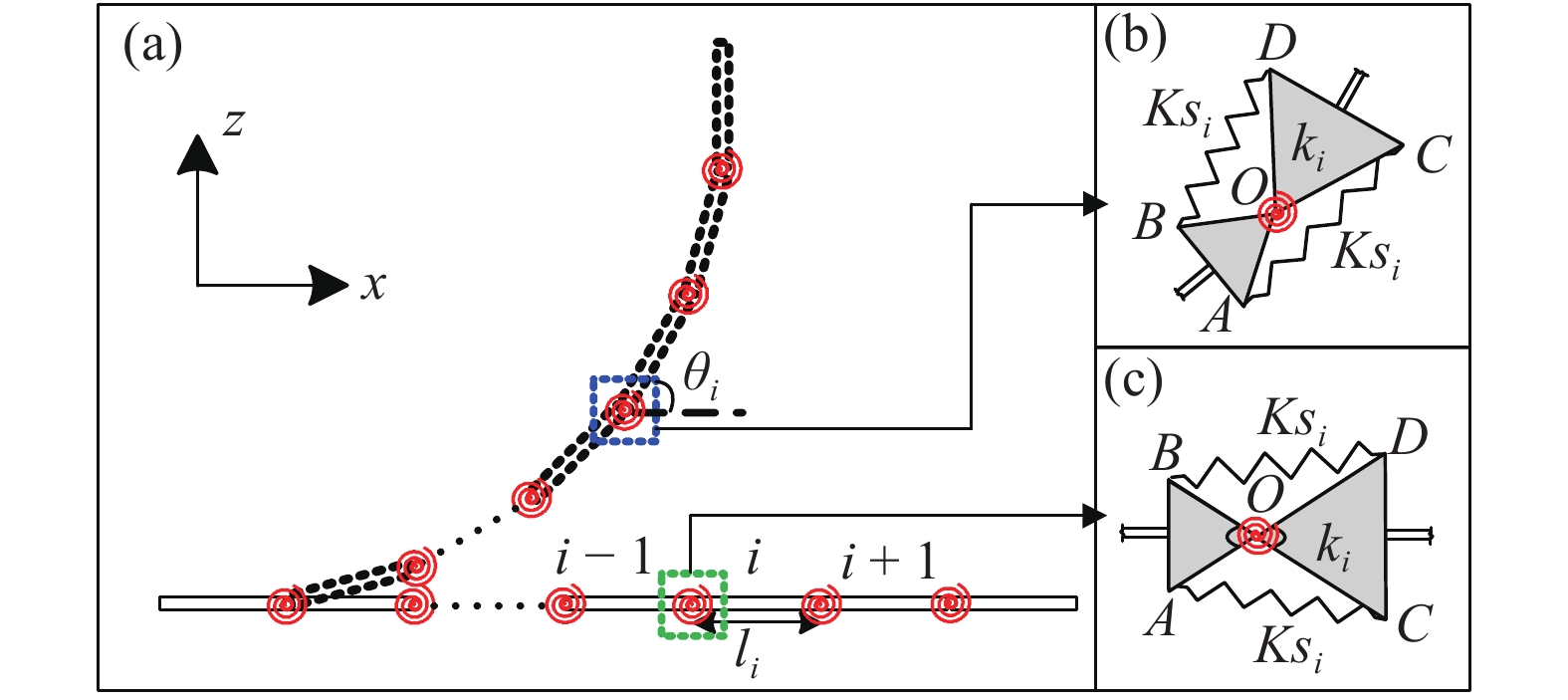
由于蚯蚓等蠕虫类生物能够在管道、泥地等不平整、受限的环境中移动, 仿蠕虫机器人得到了****们的关注, 越来越多的仿蠕虫机器人被提出, 这些仿蠕虫机器人通过不同的方式模仿蚯蚓等蠕虫体节的伸缩变形来实现移动的功能. 然而, 由于蚯蚓这种生物并不具备起竖的能力, 这些仿蠕虫机器人都没有被赋予起竖功能. 具有起竖功能的仿蠕虫机器人能够通过起竖进行侦察、操作等任务, 因此可以进一步应用于管道勘测、复杂地形侦察、精密加工等实际场景, 从而扩展仿蠕虫机器人的应用范围. 在自然界中, 蛇、尺蠖等生物能够将身体的前部直立起来, 通过起竖这种运动形式来进行攻击、防御、侦察、捕食等任务, 这为我们赋予仿蠕虫机器人起竖的功能提供了灵感. 于是, 受到这些生物的启发, 本文设计了一种能够实现生物起竖功能的仿生起竖结构, 其力学模型如图1(a)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
仿生起竖结构模型图: (a) 仿生起竖结构; (b) 仿生柔性关节(变形后); (c) 仿生柔性关节(变形前)



Figure
1.
(a) Bio-inspired erecting structure; (b) bio-inspired flexible joint (after deformation); (c) bio-inspired flexible joint (before deformation)



下载:
全尺寸图片
幻灯片


本文提出的仿生起竖结构如图1所示, 仿生起竖结构由多个连杆和仿生柔性关节串联组成, 其中刚性连杆用来模拟生物的体节和骨骼, 而仿生柔性关节中的弹性元件用来模拟体节单元连接处的弹性肌肉及软组织. 仿生起竖结构每根连杆的长度为${l_i}$, 质量为${m_i}$, 转动惯量为${I_i}$, 连杆与x轴的夹角为${theta _i}$. 图1(b)和图1(c)分别是变形后和变形前的仿生柔性关节示意图, 仿生柔性关节由刚度为${k_i}$、预压角度为${phi _i}$的预压扭转弹簧和一对刚度为$K{s_i}$的拉伸弹簧构成, 并假设拉伸弹簧的原长为0. 变形前后仿生柔性关节的几何尺寸与偏转角如图2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
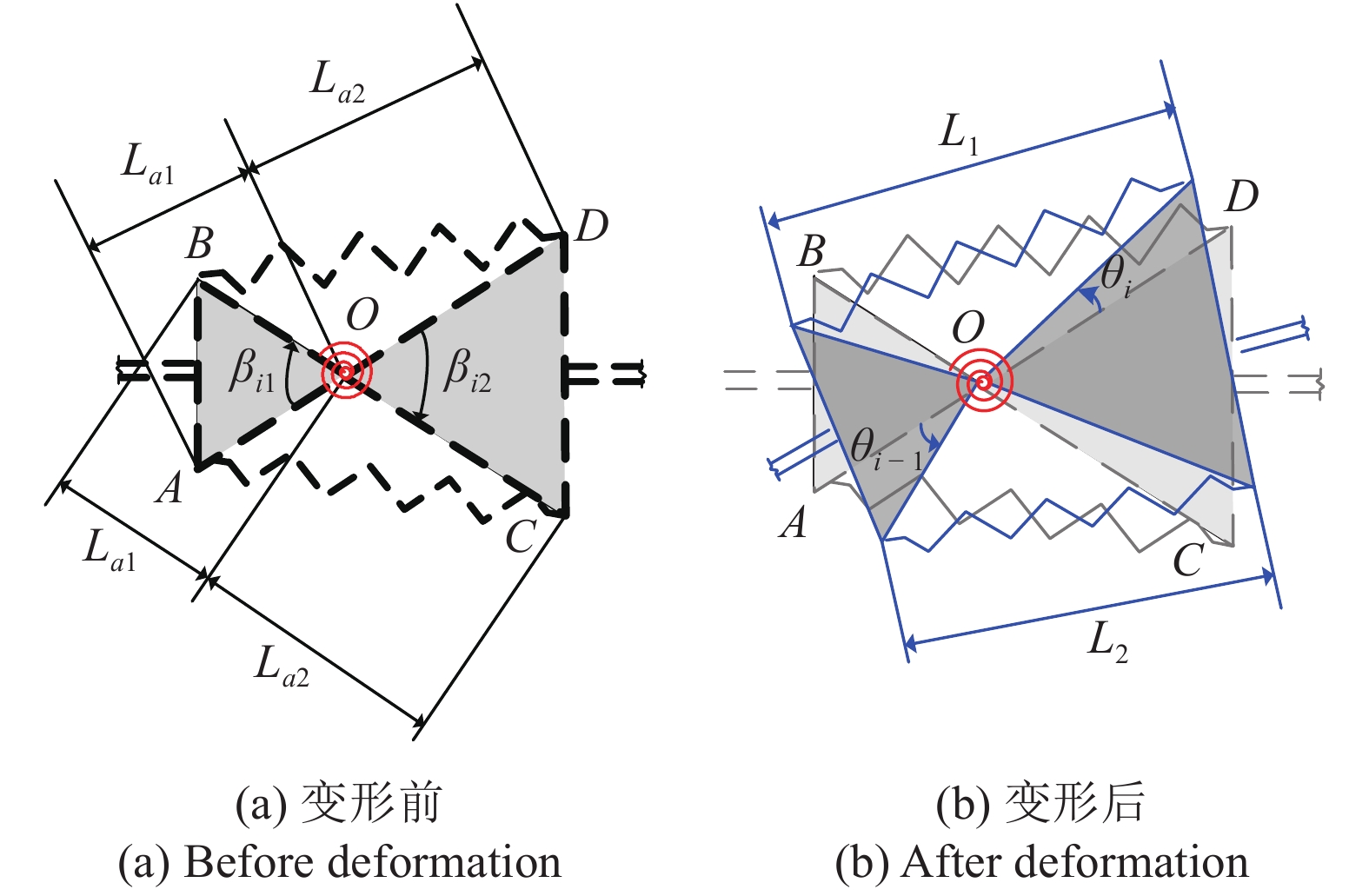
仿生柔性关节的几何尺寸和偏转角



Figure
2.
Geometric parameters and deformation of the bio-inspired flexible joint



下载:
全尺寸图片
幻灯片


在图2所示的仿生柔性关节中, O点为仿生柔性关节的转轴, A, B, C, D为两侧拉伸弹簧的安装位置, 图2中黑色虚线部分代表未变形的仿生柔性关节, 蓝色实线部分代表变形后的柔性关节. 在本文中, 将拉伸弹簧的安装位置与转轴连线的长度定义为安装半径, 分别记作${L_{a1}}{text{和}}{L_{a2}}$, 将一对拉伸弹簧同一端安装位置与转轴连线的夹角定义为安装角度, 分别记作$;{beta _{i1}},{beta _{i2}}$. 将两个安装角度的算术平均值定义为平均安装角度, 记作$;{bar beta _i}$, $;{bar beta _i} = dfrac{{{beta _{i1}} + {beta _{i2}}}}{2}$. 柔性关节变形后, 其连接前后连杆部分转过的角度分别为${theta _i}$和${theta _{i - 1}}$, 两根拉伸弹簧的长度分别为${L_1}$和${L_2}$. 从仿生角度而言, 柔性关节中的扭转弹簧对应于软组织, 拉伸弹簧对应于肌肉. 从力学角度而言, 柔性关节中的扭转弹簧刚度${k_i}$和预压角度${phi _i}$决定了正刚度, 拉伸弹簧刚度$K{s_i}$和平均安装角度$;{bar beta _i}$决定了非线性刚度, 这些结构参数对仿生起竖结构的多稳态特性起关键作用. 因此, ${k_i},{phi _i},K{s_i},{bar beta _i}$为待设计的结构参数.

由于仿生起竖结构的平衡点位置及稳定性都与结构势能密切相关, 为了设计仿生起竖结构的稳定平衡状态位置, 需要得到多节仿生起竖结构的总体势能表达式.单个柔性关节的势能由拉伸弹簧和扭转弹簧的弹性势能构成, 将第i个柔性关节的势能记作$V{q_i}$, 其表达式为

$$V{q_i} = frac{1}{2}{k_i}{({theta _i} - {theta _{i - 1}} - {phi _i})^2} + frac{1}{2}K{s_i}{L_1}^2 + frac{1}{2}K{s_i}{L_2}^2$$

(1)

其中, 第一项为扭转弹簧的弹性势能, 由于扭转弹簧存在预压角, 其变形为${theta _i} - {theta _{i - 1}} - {phi _i}$. 后两项为两侧拉伸弹簧的弹性势能, 由于柔性关节两侧的拉伸弹簧的原长为0, 其变形即为弹簧的长度${L_1},{L_2}$. 在式(1)中, ${L_1},{L_2},{beta _{i1}},{beta _{i2}},{L_{a1}},{L_{a2}}$满足几何关系

$$left. {begin{array}{*{20}{l}}{{L_1}^2 = {L_{a1}}^2 + {L_{a2}}^2 + 2{L_{a1}}{L_{a2}}cos ({{bar beta }_i} + {theta _i} - {theta _{i - 1}})}{{L_2}^2 = {L_{a1}}^2 + {L_{a2}}^2 + 2{L_{a1}}{L_{a2}}cos ({{bar beta }_i} - {theta _i} + {theta _{i - 1}})}end{array}} ight} $$

(2)

将式(2)代入式(1), 得到第i个柔性关节的弹性势能表达式为

$$begin{split}V{q_i} = &frac{1}{2}{k_i}{{({theta _i} - {theta _{i - 1}} - {phi _i})}^2} + K{s_i}({L_{a1}}^2 + {L_{a2}}^2) + &{2K{s_i}{L_{a1}}{L_{a2}}cos left(frac{{{beta _{i1}} + {beta _{i2}}}}{2} ight)cos ({theta _i} - {theta _{i - 1}})}end{split} $$

(3)

基于柔性关节的弹性势能表达式(3)可以得到多节仿生起竖结构的势能表达式. 由于提出的仿生起竖结构由一系列连杆和柔性关节构成, 其总体势能由柔性关节的弹性势能和连杆的重力势能组成, 因此多节仿生起竖结构的总势能表达式为

$$begin{split}V = &sumlimits_{i = 2}^n {V{q_i}} + {V_{ m{G}}} = &{sumlimits_{i = 2}^n {left[2K{s_i}{L_{a1}}{L_{a2}}cos (frac{{{beta _{i1}} + {beta _{i2}}}}{2})cos left({theta _i} - {theta _{i - 1}} ight) + ight.} }&{left.K{s_i}({L_{a1}}^2 + {L_{a2}}^2) + frac{1}{2}{k_i}{{left({theta _i} - {theta _{i - 1}} - {phi _i} ight)}^2} ight] + }&{sumlimits_{i = 1}^n {left[{m_i}gsumlimits_{j = 1}^{i - 1} {({l_j}sin {theta _j}) + {m_i}g{d_i}sin {theta _i}} ight]} }end{split} $$

(4)

其中, $V$代表多节仿生起竖结构的总势能, ${V_{
m{G}}}$代表多节仿生起竖结构的重力势能, ${d_i} = dfrac{{{l_i}}}{2}$.

为了研究结构参数${k_i},K{s_i}$对仿生起竖结构稳定平衡点个数和位置的影响, 对单节起竖的仿生起竖结构的势能曲线进行分析, 单节起竖的仿生起竖结构在不同结构参数${k_1},K{s_1}$下的势能?角位移图如图3所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
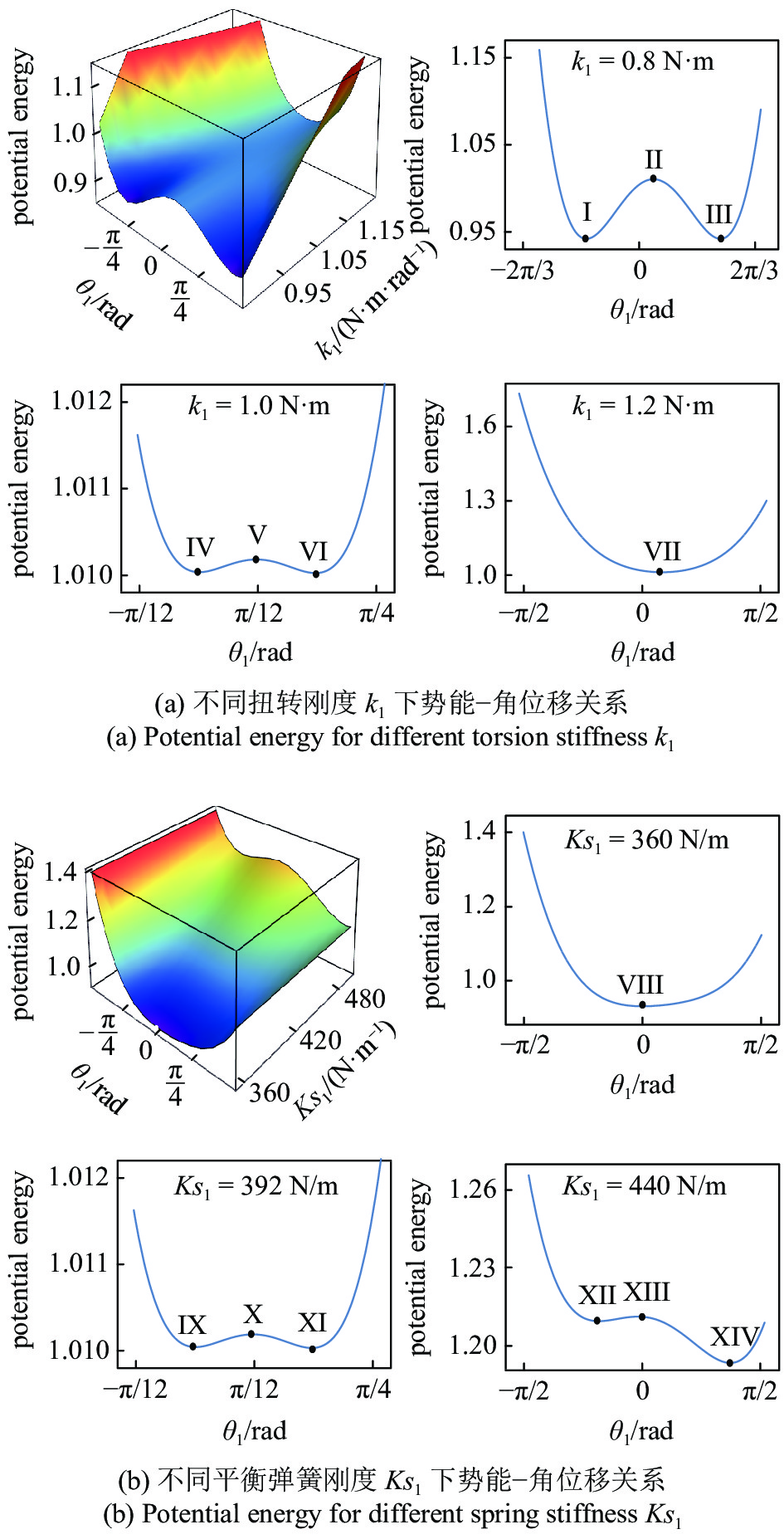
不同结构参数下仿生起竖结构的势能?角位移关系



Figure
3.
Potential energy for different structural parameters



下载:
全尺寸图片
幻灯片


图3(a)是不同扭转刚度${k_1}$下单节仿生起竖结构的势能?角位移图; 图3(b)是不同平衡弹簧刚度$K{s_1}$下单节仿生起竖结构的势能?角位移图. 由图3可知, 仿生起竖结构的平衡点个数、稳定性、位置与结构参数${k_1},K{s_1}$有关. 如图3(a)所示, 由于扭转刚度${k_1}$决定了关节处的正刚度, 因此随着扭转刚度${k_1}$的增大, 单节起竖的仿生起竖结构的平衡点的个数由3个逐渐变为1个, 且中间的平衡点逐渐从不稳定的平衡点变为稳定的平衡点. 当${k_1} = 0.8;{
m{N}} cdot {
m{m/rad}}$时, 单节仿生起竖结构具有3个平衡点I, II, III, 其对应的位置分别为${theta _1} = - 0.91$ rad, 0.24 rad, 1.40 rad. 其中, 平衡点I, III为稳定平衡点, 平衡点II为不稳定平衡点. 当扭转刚度增加到${k_1} = 1;{
m{N}} cdot {
m{m/rad}}$时, 单节仿生起竖结构仍具有3个平衡点IV, V, VI, 平衡点的稳定性与${k_1} = 0.8;{
m{N}} cdot {
m{m/rad}}$时的情况类似, 但3个平衡点的位置变为了${theta _1} = 0$ rad, 0.24 rad, 0.4 rad, 说明不同的扭转刚度${k_1}$下单节仿生起竖结构具有不同的平衡点位置. 当扭转刚度增大到${k_1} = 1.2;{
m{N}} cdot {
m{m/rad}}$时, 单节仿生起竖结构只有一个稳定平衡点VII, 平衡点的个数由3个减少为1个. 如图3(b)所示, 由于平衡弹簧刚度$K{s_1}$决定了关节处的负刚度, 因此随着$K{s_1}$的增大, 单节仿生起竖结构的平衡点的个数逐渐由1个变为3个, 且中间的平衡点逐渐从稳定的平衡点变为不稳定的平衡点. 当$K{s_1} = 360;{
m{N/m}}$时, 单节仿生起竖结构只有一个稳定平衡点VIII. 当平衡弹簧刚度$K{s_1}$由360 N/m增大至392 N/m时, 单节仿生起竖结构的平衡点数量由1个增加至3个, 记为平衡点IX, X, XI, 其位置分别为${theta _1} = 0$ rad, 0.24 rad, 0.49 rad. 当$K{s_1}$增大至440 N/m时, 单节仿生起竖结构的平衡点个数与$K{s_1} = $392 N/m相同, 但平衡点的位置变为了${theta _1} = $?0.48 rad, 0 rad, 1.15 rad. 由于仿生起竖结构的稳定平衡点位置、个数与结构参数密切相关, 为了实现直线构型与起竖构型的稳定平衡, 需要提出相应的结构参数设计准则.

1.2
仿生起竖结构动力学模型

为了构建仿生起竖结构达到特定需求构型的结构参数设计准则及触发条件, 需要建立仿生起竖结构的动力学模型, 并求解仿生起竖结构在初始激励下的动力学响应. 利用拉格朗日方程建立仿生起竖结构的动力学模型

$$frac{{ m{d}}}{{{ m{d}}t}}left(frac{{partial L}}{{partial {dot{theta }}}} ight) - frac{{partial L}}{{partial {{theta }}}} = {{{Q}}_i},;;;{ m{ }}i = 1,2,cdots, n$$

(5)

其中, ${theta _i}$是连杆绝对转角, ${dot theta _i}$是连杆的角速度, L为系统的拉格朗日函数, ${Q_i}$是作用在第i个广义坐标上的广义力, n为连杆的数目.

如图1所示, 仿生起竖结构每一节连杆的长度为${l_i}$, 质量为${m_i}$, 转动惯量为${I_i}$, 连杆与x轴的夹角为${theta _i}$, 质心坐标为$({x_i},{{textit{z}}_i})$. 由几何关系, 可以得到

$$left. {begin{array}{*{20}{l}}{{x_i} = {d_i}cos {theta _i} + displaystylesumlimits_{j = 1}^{i - 1} {{l_j}cos {theta _j}} }{{{textit{z}}_i} = {d_i}sin {theta _i} + displaystylesumlimits_{j = 1}^{i - 1} {{l_j}sin {theta _j}} }end{array}} ight} $$

(6)

将上两式两端对时间求导, 可以得到

$$left. {begin{array}{*{20}{l}}{{{dot x}_i} = - {d_i}{{dot theta }_i}sin {theta _i} - displaystylesumlimits_{j = 1}^{i - 1} {{l_j}{{dot theta }_j}sin {theta _j}} }{{{dot {textit{z}}}_i} = {d_i}{{dot theta }_i}cos {theta _i} + displaystylesumlimits_{j = 1}^{i - 1} {{l_j}{{dot theta }_j}cos {theta _j}} }end{array}} ight} $$

(7)

因此, 仿生起竖结构的动能写为

$$T = sumlimits_{i = 1}^n {left[frac{1}{2}{I_i}{{dot theta }_i}^2 + frac{1}{2}{m_i}left({{dot x}_i}^2 + {{dot {textit{z}}}_i}^2 ight) ight]} $$

(8)

由式(4)和式(8), 可以得到拉格朗日函数的表达式为

$$begin{split}L =& T - V = sumlimits_{i = 1}^n {left[ {frac{1}{2}{I_i}{{dot theta }_i}^2 + frac{1}{2}{m_i}({x_i}^2 + {{textit{z}}_i}^2)} ight]} - &Biggl{{20} {sumlimits_{i = 1}^n {left[ {{m_i}gsumlimits_{j = 1}^{i - 1} {({l_j}sin {theta _j}) + {m_i}g{d_i}sin {theta _i}} } ight]} + } &sumlimits_{i = 2}^n Biggl[{18}{frac{1}{2}{k_i}{{({theta _i} - {theta _{i - 1}} - {phi _i})}^2} + K{s_i}({L_{a1}}^2 + {L_{a2}}^2) + } &{ {2K{s_i}{L_{a1}}{L_{a2}}cos left( {frac{{{beta _{i1}} + {beta _{i2}}}}{2}} ight)cos ({theta _i} - {theta _{i - 1}})} Biggl]{18}} Biggl}{20}end{split} $$

(9)

系统的广义力Q包含关节处阻尼的阻尼力, 假设阻尼所产生的广义力形式为

$${Q_i} = left{ {begin{array}{*{20}{l}}{ - {c_2}({{dot theta }_1} - {{dot theta }_2}) - {c_1}{{dot theta }_1},i = 1}{ - {c_i}({{dot theta }_i} - {{dot theta }_{i - 1}}) - {c_{i + 1}}({{dot theta }_i} - {{dot theta }_{i + 1}}),2 leqslant i leqslant n - 1}{ - {c_n}({{dot theta }_n} - {{dot theta }_{n - 1}}),i = n}end{array}} ight.$$

(10)

将式(6)和式(7)代入式(9), 可以得到由广义坐标${theta _1},{theta _2},cdots,{theta _n}$表示的拉格朗日函数. 将由广义坐标表示的拉格朗日函数和广义力代入拉格朗日方程, 可以得到仿生起竖结构的动力学方程为

$${{{boldsymbol{M}}}}({{{boldsymbol{theta }}}}){{ddot{boldsymbol{ theta }}}} + {{{boldsymbol{C}}}}({{{boldsymbol{theta }}}},{dot{ {boldsymbol{theta }}}}) + {{{boldsymbol{D}}dot {boldsymbol{theta}} }} + {{{boldsymbol{K}}{boldsymbol{theta}} }} + {{{boldsymbol{G}}}}({{{boldsymbol{theta}} }}) + {{{boldsymbol{N}}}}({{{boldsymbol{theta}} }}) = {boldsymbol{0}}$$

(11)

其中, M矩阵为质量阵, C矩阵为科氏阵, D矩阵为阻尼阵, K矩阵为刚度阵, G矩阵为重力项, N矩阵为非线性刚度项, 各矩阵的具体形式见附录.

本文通过求解不同初始条件下仿生起竖结构的动力学模型式(11)得到仿生起竖结构的动力学响应, 以研究实现仿生起竖结构特定需求构型的结构参数设计准则及不同构型的触发条件.

1.3
仿生起竖结构设计准则

基于仿蠕虫机器人在管道勘测、地形侦察、精密加工等应用中实现特定操作的需求, 本文提出的仿生起竖结构需要满足以下要求:

(1)在地面约束下保持直线构型的稳定平衡;

(2)实现需求的起竖构型并保持起竖构型的稳定平衡;

(3)能够通过触发条件来实现起竖构型.

由图3可知, 仿生起竖结构的平衡点及其稳定性与结构参数的选取有关. 在本文中, 连杆的质量${m_i}$, 长度${l_i}$, 转动惯量${I_i}$以及柔性关节的安装半径${L_{a1}},{L_{a2}}$为固定的结构参数, 柔性关节扭转弹簧的刚度${k_i}$, 预压角度${phi _i}$, 平衡弹簧的刚度$K{s_i}$, 平均安装角度$;{bar beta _i}$为待设计的结构参数. 为了实现要求(1)和(2), 基于仿生起竖结构总体势能表达式和多元函数极值原理提出仿生起竖结构的结构参数设计准则. 首先, 要求仿生起竖结构的直线构型在地面的约束下稳定平衡, 即每个关节处扭转弹簧产生的力矩应小于重力产生的力矩. 于是, 结构参数需要满足的条件为${r_{textit{z}}}$, 即

$${r_{textit{z}}} = left{ ({k_i},{phi _i},{overline beta _i},K{s_i})|{left. {frac{{partial V}}{{partial {theta _i}}}} ight|_{{theta _1} = {theta _2} = cdots = {theta _n} = 0}} > 0,i = 1,2,cdots,n ight}$$

(12)

其次, 要求仿生起竖结构能够起竖到需求构型, 并在需求起竖构型处保持稳定平衡, 即结构总势能在起竖构型处取到极小值. 于是, 基于多元函数极值原理, 结构参数需要满足的条件为${r_{w1}}$和${r_{w2}}$, 分别为

$$left. begin{array}{l}{r_{w1}} = left{ {({k_i},{varphi _i},{{bar beta }_i},K{s_i})|dfrac{{partial V}}{{partial {theta _i}}}{|_{{theta _1} = {{bar theta }_1},{theta _2} = {{bar theta }_2}, cdots ,{theta _n} = {{bar theta }_n}}} = 0,i = 1,2, cdots ,n} ight}{r_{w2}} = left{ {({k_i},{varphi _i},{{bar beta }_i},K{s_i})|H({{bar theta }_1},{{bar theta }_2}, cdots ,{{bar theta }_n});,{ m{positive}};{ m{definite}}} ight}end{array} !!!! ight}$$

(13)

其中, ${bar theta _i}$为起竖构型下对应的每一节次与x轴正方向的夹角, ${r_{w1}}$保证仿生起竖结构在需求起竖构型处是一个平衡点, ${r_{w2}}$使仿生起竖结构能够在需求起竖构型处稳定. 在准则${r_{w2}}$中, H矩阵的定义为

$$begin{split}&{boldsymbol{H}}({theta _1},{theta _2}, cdots ,{theta _n}) = &qquadleft( {begin{array}{*{20}{c}}{dfrac{{{partial ^2}V}}{{partial {theta _1}^2}}}&{dfrac{{{partial ^2}V}}{{partial {theta _1}partial {theta _2}}}}& cdots &{dfrac{{{partial ^2}V}}{{partial {theta _1}partial {theta _n}}}}{dfrac{{{partial ^2}V}}{{partial {theta _2}partial {theta _1}}}}&{dfrac{{{partial ^2}V}}{{partial {theta _2}^2}}}& cdots &{dfrac{{{partial ^2}V}}{{partial {theta _2}partial {theta _n}}}} vdots & vdots & ddots & vdots {dfrac{{{partial ^2}V}}{{partial {theta _n}partial {theta _1}}}}&{dfrac{{{partial ^2}V}}{{partial {theta _n}partial {theta _2}}}}& cdots &{dfrac{{{partial ^2}V}}{{partial {theta _n}^2}}}end{array}} ight)end{split}$$

(14)

综上, 为了满足要求(1)和(2), 仿生起竖结构设计参数的设计准则为

$${r_1} = {r_{textit{z}}} cap {r_{w1}} cap {r_{w2}}$$

(15)

最后, 由于所设计的仿生起竖结构具有多稳态性质, 在不同的初始激励下仿生起竖结构最终可能达到的不同的构型. 为了满足要求(3), 需要得到能够实现仿生起竖结构起竖构型的触发条件. 在本文中, 对各关节受到的初始位移激励和速度激励做出以下假设:

(1) 各关节受到的初始位移激励和速度激励的比例一定, 即

$${theta _i}(0) = {eta _i}{theta _k}(0),{dot theta _i}(0) = {eta _i}{dot theta _k}(0),{ m{ }}{eta _i} geqslant 0,i = 1,2,cdots,n$$

(16)

其中, k为起竖构型中绝对转角最大的关节的序号, 且$k in mathbb{N},1 leqslant k leqslant n$, ${eta _i}$是第i个关节初始激励的比例系数.

(2) 相邻关节受到的初始位移激励和速度激励不相等, 即

$${eta _{i + 1}} ne {eta _i},;;;i = 1,2,cdots ,n - 1$$

(17)

为了描述不同关节的比例系数, 基于以上两个假设定义如下的比例系数单调性变量

$$ {varDelta }_{i}=frac{{eta }_{i}-{eta }_{i-1}}{left|{eta }_{i}-{eta }_{i-1} ight|},;;i=1,2,mathrm{cdots},n$$

(18)

由比例系数单调性变量的定义可知, 比例系数单调性变量的取值只可能为$ pm 1$. 在本文中, 定义${eta _0} = 0$, 则有${varDelta _1} = 1$恒成立. ${varDelta _1} = 1$表示在第i个关节处驱动上侧的弹簧, ${varDelta _1} = - 1$表示在第i个关节处驱动下侧的弹簧. 本文将对起竖构型触发条件的研究简化为对初始激励比例系数单调性的研究, 即研究不同关节的比例系数在什么样的单调性下使仿生起竖结构实现起竖构型的概率最大. 基于上述的单调性变量, 提出各关节初始激励的比例系数单调性变量需要满足的准则为${r_2}$, 写为

$${r_2} = { ({varDelta _1},cdots,{varDelta _n})|max { P({theta _1} to {bar theta _1},{theta _2} to {bar theta _2},cdots,{theta _n} to {bar theta _n})} }$$

(19)

其中, $P({theta _1} to {bar theta _1},{theta _2} to {bar theta _2},cdots,{theta _n} to {bar theta _n})$表示触发起竖构型的概率, 该准则表示在所有关节比例系数的单调性情况中选取触发起竖构型概率最大的情况. 本文利用仿生起竖结构不同稳态的吸引盆, 阐明不同关节比例系数单调性情况下触发起竖构型的概率. 对于不同的初始条件${theta _k}(0),{dot theta _k}(0)$, 利用数值方法求解仿生起竖结构的动力学方程, 得到不同初始条件下仿生起竖结构的动力学响应. 通过对仿生起竖结构的稳态响应的判断和分类, 可以得到不同稳态的吸引盆以及触发不同构型的概率, 进而得到仿生起竖结构起竖构型的触发条件.

2.
不同需求下仿生起竖结构的实现及其触发条件

根据第1节提出的仿生起竖结构参数设计准则, 针对不同起竖节数的设计需求, 设计了相应节数的仿生起竖结构来验证设计准则的有效性, 并通过不同稳态的吸引盆研究仿生起竖结构的构型触发条件, 为利用主动控制保持仿蠕虫机器人在移动中的需求构型奠定理论基础.

2.1
单节起竖的仿生起竖结构

首先以单节起竖的仿生起竖结构为例, 即仿生机器人只有最右端的一节进行起竖, 对仿生起竖结构参数设计准则的作用进行展示. 取结构参数为${m_1} = 0.05;{
m{kg}},{l_1} = 0.1;{
m{m}},{L_{a1}} = {L_{a2}} = 0.05;{
m{m}}$, 由式(15)可以得到单节起竖的仿生起竖结构设计参数的设计准则为

$$left. {begin{array}{*{20}{l}}{0.245 - {k_1}{phi _1} > 0}{ - {k_1}{phi _1} + 0.245{ m{cos}}{{bar theta }_1} + {k_1}{{bar theta }_1} - 2times{{10}^{ - 4}}K{s_1}{ m{cos}}{{bar beta }_1}{ m{sin}}{{bar theta }_1} = 0}{{k_1} - 0.245{ m{sin}}{{bar theta }_1} - 2times{{10}^{ - 4}}K{s_1}{ m{cos}}{{bar beta }_1}{ m{cos}}{{bar theta }_1} > 0}end{array}} ight}$$

(20)

在单节起竖的仿生起竖结构中, 取起竖构型的目标位置为${bar theta _1} = dfrac{{text{π}} }{2}$. 式(20)中第1个式子对应于式(15)中的第一条准则${r_{textit{z}}}$, 保证了在地面约束下, 仿生起竖结构的直线构型(${theta _1} = 0$)是一个稳定的平衡状态; 式(20)中第2个式子和第3个式子对应于式(15)中的第2条准则${r_{w1}}$和第3条准则${r_{w2}}$, 分别保证了仿生起竖结构的起竖构型处(${theta _1} = {bar theta _1}$)是一个平衡点以及该平衡点稳定.

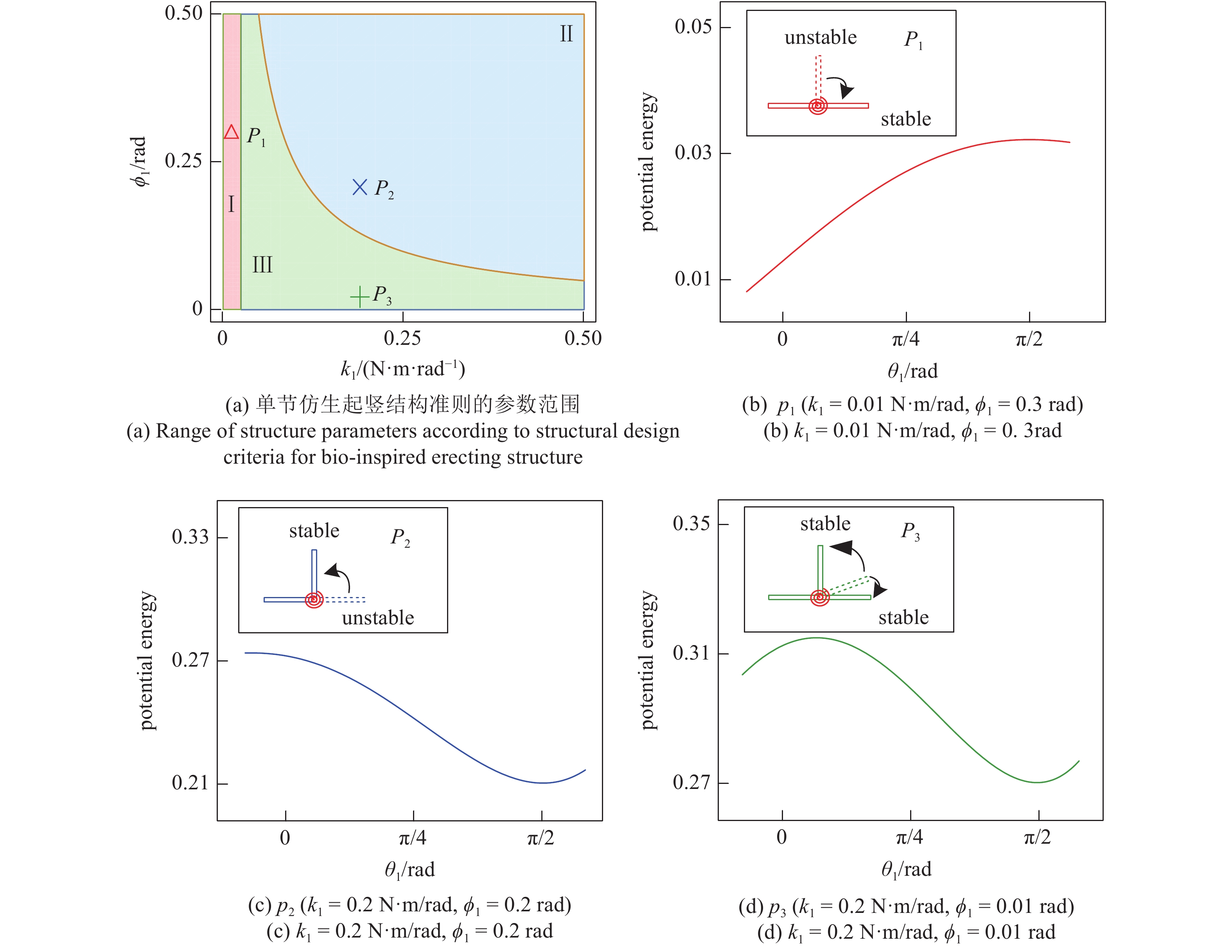
为了验证式(20)中两条不等式条件${r_{textit{z}}},{r_{w2}}$的必要性, 对结构参数在仅满足${r_{textit{z}}}$、仅满足${r_{w2}}$和同时满足${r_{textit{z}}},r{_{w2}}$这3种情况下的势能?角位移曲线进行分析. 通过${r_{w1}}$, 可以建立${k_1}$与$K{s_1},{bar beta _1}$的关系, 代入${r_{textit{z}}},{r_{w2}}$中, 可以得到${k_1} - {phi _1}$平面上某一起竖角度${bar theta _1}$下满足两个不等式的的区域. 图4(a)展示了${bar theta _1} = dfrac{{text{π}} }{2}$时${k_1} - {phi _1}$平面上仅满足${r_{textit{z}}}$、仅满足${r_{w2}}$和同时满足${r_{textit{z}}},{r_{w2}}$的区域. 图4(a)中的区域Ⅰ对应于满足${r_{textit{z}}}$而不满足${r_{w2}}$的情况, 在该区域中选取一个点, 记作${P_1}$, 其对应参数的势能?角位移曲线和构型稳定性示意图如图4(b)所示. 由图4(b)所示的势能?角位移曲线可以注意到, ${theta _1} = 0$处势能曲线切线斜率为正且${theta _1} = dfrac{{text{π}} }{2}$处势能取到极大值, 说明仿生起竖结构能够在地面约束下保持直线构型的稳定, 但仿生起竖结构的起竖构型不稳定. 图4(a)中的区域Ⅱ对应于满足${r_{w2}}$而不满足${r_{textit{z}}}$的情况, 在该区域中选取一个点, 记作${P_2}$, 其对应参数的势能?角位移曲线和构型稳定性示意图如图4(c)所示. 由图4(c)中的势能?角位移曲线可以注意到, ${theta _1} = 0$处势能曲线切线斜率为负且${theta _1} = dfrac{{
m{{text{π}} }}}{2}$处势能取到极小值, 说明仿生起竖结构的起竖构型稳定, 但仿生起竖结构的直线构型在地面约束下不能保持稳定. 图4(a)中的区域Ⅲ对应于${r_{textit{z}}},{r_{w2}}$同时满足的情况, 在该区域中选取一个点, 记作${P_3}$, 其对应参数的势能?角位移曲线和构型稳定性示意图如图4(d)所示. 由图4(d)中的势能?角位移曲线可以注意到, ${theta _1} = 0$处势能曲线切线斜率为正且${theta _1} = dfrac{{
m{{text{π}}}} }{2}$处势能取到极小值, 说明仿生起竖结构的直线构型和起竖构型都能保持稳定. 因此, 只有当${r_{textit{z}}},{r_{w2}}$同时满足的情况下, 即结构参数在区域Ⅲ内时, 仿生起竖结构才能同时在直线构型和起竖构型下稳定平衡.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
势能?角位移曲线和构型稳定性示意图



Figure
4.
Potential energy and corresponding configuration stability schematic diagram



下载:
全尺寸图片
幻灯片

2.2
两节起竖的仿生起竖结构

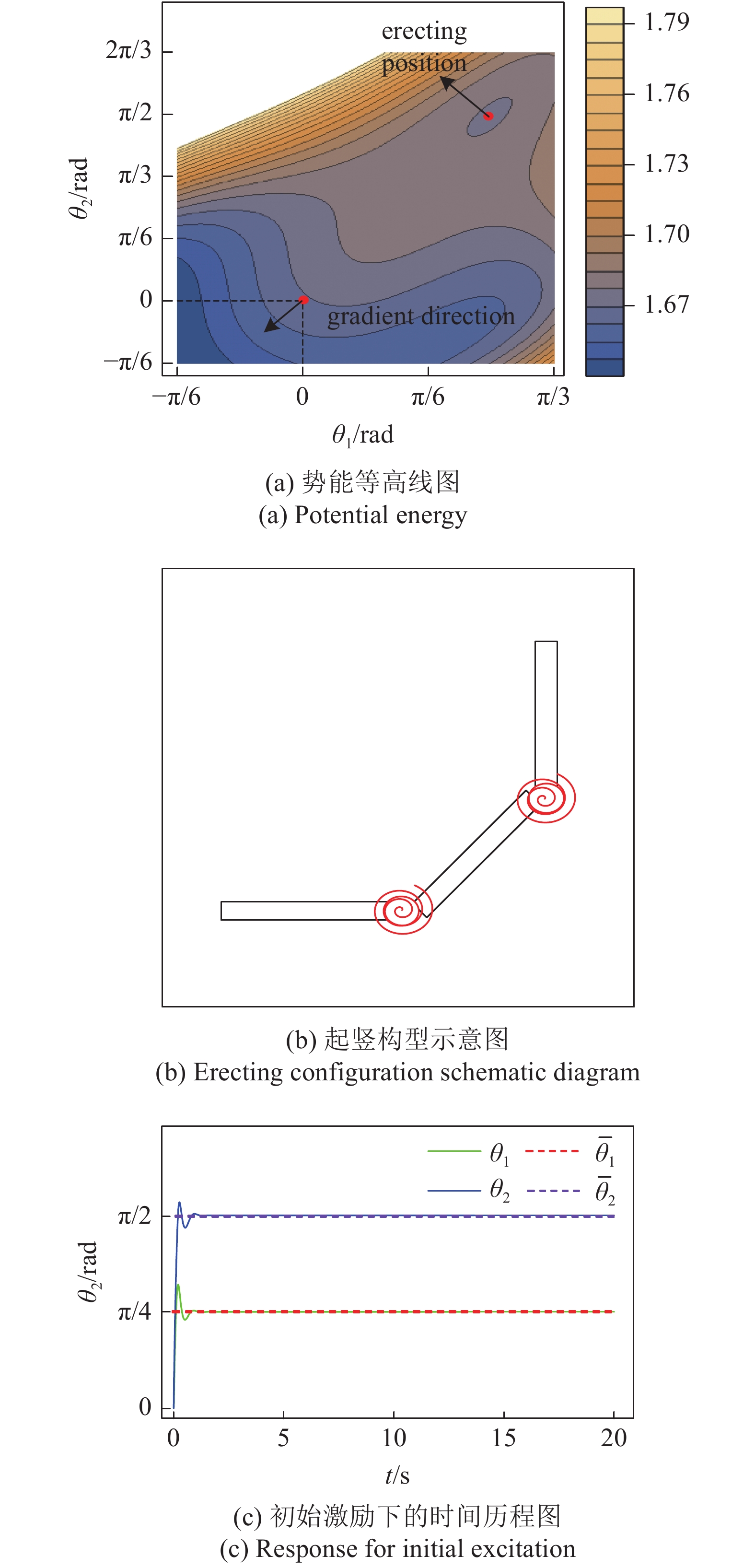
以两节起竖的仿生起竖结构为例, 即仿生机器人只有最右端的两节进行起竖, 验证结构参数设计准则的有效性. 仿生起竖结构需求的起竖构型设为${bar theta _1} = dfrac{{
m{{text{π}}}} }{4},{bar theta _2} = dfrac{{
m{{text{π}}}} }{2}$. 针对具有两节起竖功能的仿生起竖结构, 取结构参数${m_1} = {m_2} = 0.05$ kg, ${l_1} = {l_2} = 0.1$ m, ${L_{a1}} = {L_{a2}} = 0.05$ m, ${c_1} = {c_2} = 0.01$ N·s/m. 根据结构参数设计准则式(15), 两节起竖的仿生起竖结构的设计参数的取值为${k_1} = 1$ N·m/rad, ${k_2} = 0.5$ N·m/rad, ${phi _1} = 0.01$ rad, ${phi _2} = 0.05$ rad, ${bar beta _1} = 0.98$ rad, ${bar beta _2} = 1.29$ rad, $K{s_1} = K{s_2} = 400$ N/m. 在这组结构参数和设计参数下, 两节仿生起竖结构的势能等高线图和起竖构型示意图分别如图5(a)和图5(b)所示. 在图5(a)中, ${theta _1} = {theta _2} = 0$处的梯度方向处于${theta _1}$负半轴与${theta _2}$负半轴之间. 于是, 由于地面的约束, 仿生起竖结构能在${theta _1} = {theta _2} = 0$位置处稳定平衡. 此外, 在图5(a)中, 起竖构型${theta _1} = dfrac{{
m{{text{π}}}} }{4},{theta _2} = dfrac{{
m{{text{π}}}} }{2}$处为势能极小值点, 因此, 仿生起竖结构能在设计的起竖构型位置处稳定平衡. 图5(c)是仿生起竖结构在初始激励下的时间历程曲线, 由图可知仿生起竖结构能在初始激励下从直线构型变成起竖构型, 并能在起竖构型位置处稳定平衡.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
两节仿生起竖结构



Figure
5.
Two-segment bio-inspired erecting structure



下载:
全尺寸图片
幻灯片

2.3
三节起竖的仿生起竖结构

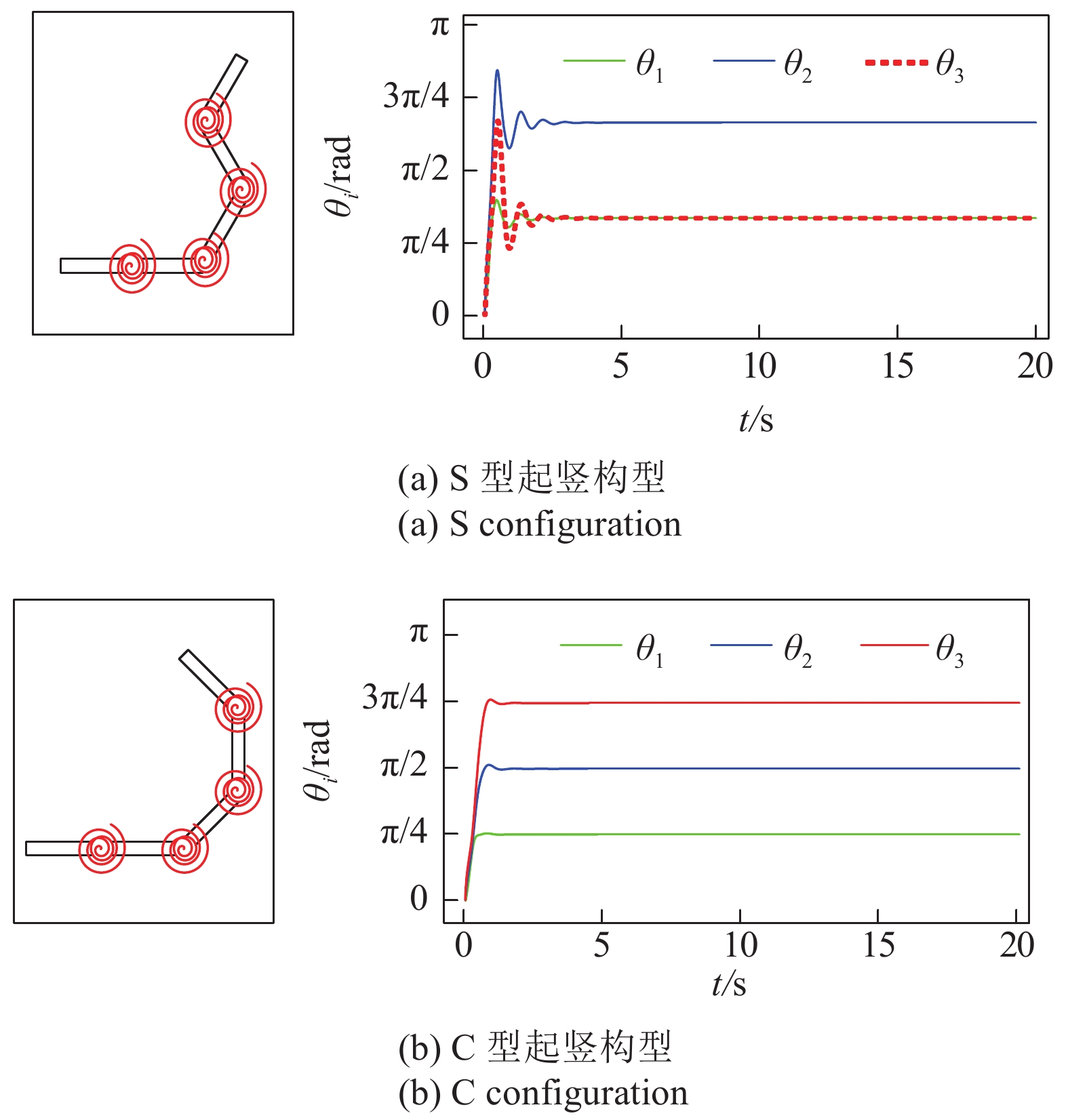
为了说明本文提出的仿生起竖结构不仅能够实现C形构型, 也能够实现C形构型以外的其他构型, 设计了两种不同起竖构型的三节起竖的仿生起竖结构, 即仿生机器人只有最右端的三节进行起竖. 仿生起竖结构的起竖构型分别设为${bar theta _1} = dfrac{{
m{{text{π}}}} }{3}$,${bar theta _2} = dfrac{{2{
m{{text{π}}}} }}{3}$, ${bar theta _3} = $$ dfrac{{
m{{text{π}}}} }{3}$及${bar theta _1} = dfrac{{
m{{text{π}}}} }{4}$,${bar theta _2} = dfrac{{
m{{text{π}}}} }{2}$,${bar theta _3} = dfrac{{3{
m{{text{π}}}} }}{4}$, 其构型示意图如图6(a)和图6(b)所示. 本文将满足${bar theta _1} < {bar theta _2} < cdots < {bar theta _n}$的起竖构型称为C形构型, 并将满足${bar theta _1} < {bar theta _2} < cdots < {bar theta _k}$且${bar theta _k} > {bar theta _{k + 1}} > cdots > {bar theta _n}$的起竖构型称为S形构型. 三节仿生起竖结构的结构参数为${m_1} = {m_2} = {m_3} = 0.05;{
m{kg}}$, ${l_1} = $$ {l_2} = {l_3} = 0.1$m, ${L_{a1}} = {L_{a2}} = $ 0.05 m, ${c_1} = {c_2} = {c_3} = 0.01$ N·s/m. 根据结构参数设计准则式(15), 两种起竖构型的仿生起竖结构对应的设计参数取值分别见表1和表2. 图6(a)和图6(b)中的右图分别是起竖构型为S形和C形的三节仿生起竖结构在受到初始激励后的时间历程图, 由图6(a)和图6(b)可知, 所设计的仿生起竖结构能够在受到初始激励后达到所需求的起竖构型并在起竖构型处稳定. 同时, 由图6可以得知, 本文提出的仿生起竖结构除了可以实现C形的起竖构型, 还可以实现C形构型以外的起竖构型, 这说明本文提出的仿生起竖结构进一步拓展了弯曲变形结构可实现的构型.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
不同起竖构型的三节仿生起竖结构的起竖构型示意图及其动力学验证



Figure
6.
Erecting configuration schematic diagram and dynamics verification of different three-segment bio-inspired erecting structure



下载:
全尺寸图片
幻灯片





表
1
S形构型设计参数



Table
1.
Design parameters values of three-segment bio-inspired erecting structure with S configuration



table_type2 ">

i	ki/(N·m·rad?1)	Ksi/(N·m?1)	${phi _i}$/rad	$;{bar beta _i}$/rad
1	2	600	0.050	0.673
2	0.5	400	0.194	1.336
3	0.5	400	0.048	1.256

下载:
导出CSV
|显示表格






表
2
C形构型设计参数



Table
2.
Design parameters values of three-segment bio-inspired erecting structure with C configuration



table_type2 ">

i	ki/(N·m·rad?1)	Ksi/(N·m?1)	${phi _i}$/rad	$;{bar beta _i}$/rad
1	4	1000	0.050	0.552
2	0.5	400	0.194	1.372
3	0.5	400	0.048	1.320

下载:
导出CSV
|显示表格



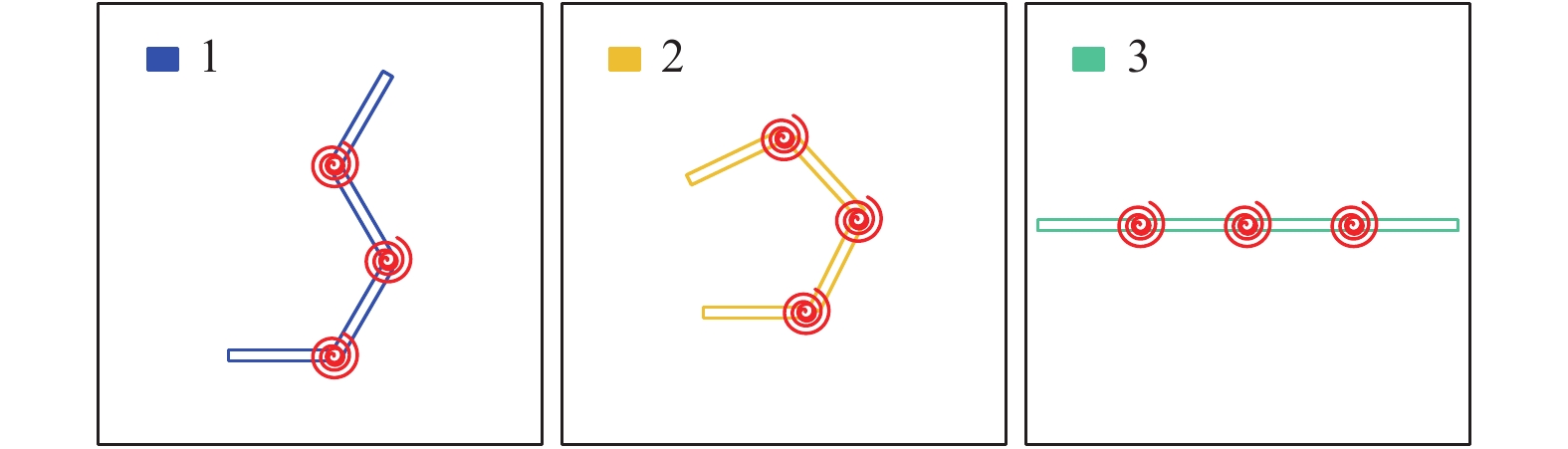
在表1的设计参数下, 仿生起竖结构一共有3个稳定构型, 其稳定构型示意图如图7所示. 在图7中, 蓝色构型表示${theta _1} = dfrac{{
m{{text{π}}}} }{3},{theta _2} = dfrac{{2{
m{{text{π}}}} }}{3},{theta _3} = dfrac{{text{π}} }{3}$的S形构型, 黄色构型表示${theta _1} = 0.35{
m{{text{π}}}},{theta _2} = 0.74{
m{{text{π}}}},{theta _3} = 1.14{
m{{text{π}}}} $的C形构型, 鲜绿色构型表示${theta _1} = 0,{theta _2} = 0,{theta _3} = 0$的直线构型. 接下来, 通过仿生起竖结构不同稳态的吸引盆来研究初始激励对仿生起竖结构最终达到构型的影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
表1参数下仿生起竖结构稳定构型示意图



Figure
7.
Stable configuration of three-segment bio-inspired erecting structure with parameters in Table 1



下载:
全尺寸图片
幻灯片


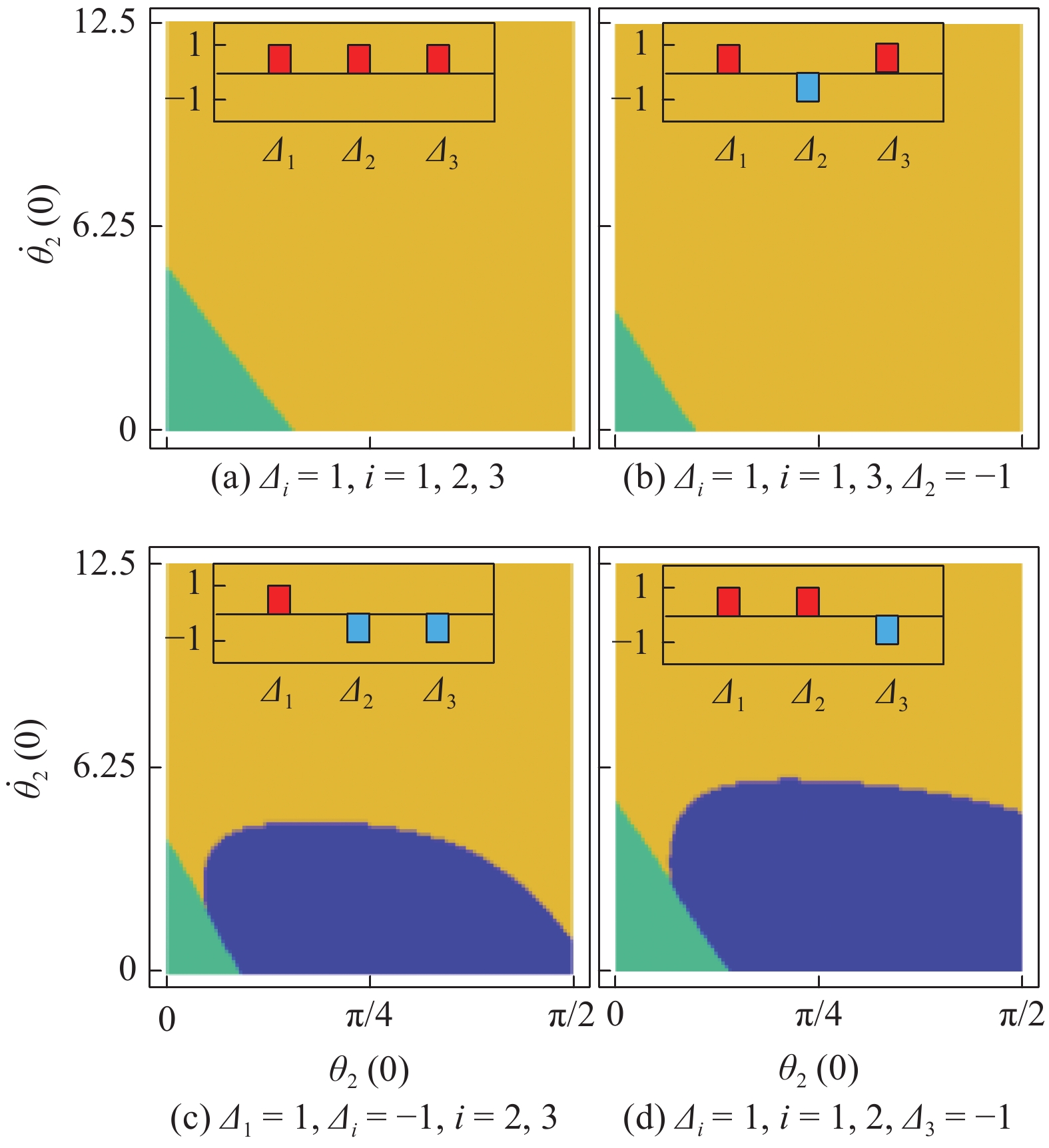
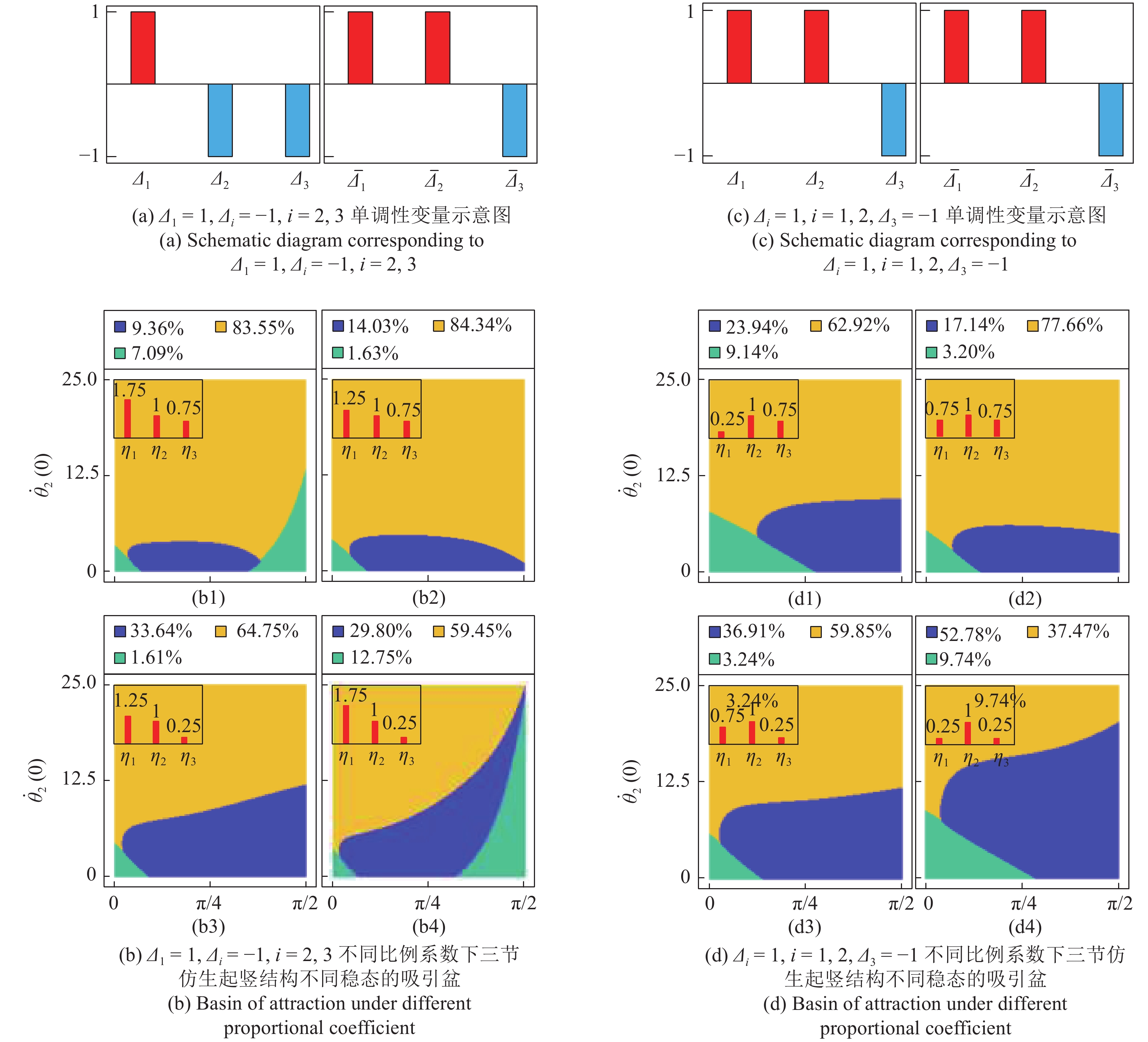
对于三节起竖的仿生起竖结构, 其比例系数单调性变量的取值一共有4种情况, 在图8中分别给出了4种不同情况下仿生起竖结构不同稳态的吸引盆, 并在吸引盆的左上方用柱状图标出了比例系数单调性变量的取值. 其中, 蓝色部分对应于图7中的S形稳定构型, 黄色部分对应于图7中的C形稳定构型, 鲜绿色部分对应于图7中的直线稳定构型. 由图8可以得知, 不同比例系数单调性的情况下, 仿生起竖结构触发S形构型的概率有显著的差异. 在图8(a)和图8(b)所示的吸引盆中没有蓝色的部分, 说明在这两种情况下无法触发仿生起竖结构的S形构型. 在图8(c)和图8(d)中, 吸引盆出现了较大的蓝色区域, 说明图8(c)和图8(d)这两种情况比图8(a)和图8(b)中这两种情况更容易触发仿生起竖结构需求的S形构型, 针对图8(c)和图8(d)对应的两种情况进行进一步讨论, 以确定满足准则${r_2}$的比例系数单调性变量的取值.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
不同单调性变量情况下三节仿生起竖结构不同稳态的吸引盆



Figure
8.
Basin of attraction corresponding to different conditions



下载:
全尺寸图片
幻灯片


为了将初始激励的比例系数单调性与需求的起竖构型联系起来, 定义如下的起竖构型单调性变量

$${bar varDelta _i} = frac{{{{bar theta }_i} - {{bar theta }_{i - 1}}}}{{left| {{{bar theta }_i} - {{bar theta }_{i - 1}}} ight|}},i = 1,2,cdots,n$$

(21)

在式(21)中, 当${bar theta _0} = 0$, 则有${bar varDelta _1} = 1$恒成立. 此外, 在这里不考虑${bar theta _i} = {bar theta _{i - 1}}$的情况. 与比例系数单调性变量一样, 起竖构型单调性变量只能取$ pm 1$. ${bar varDelta _i} = 1$表示起竖构型在第i个关节处逆时针转动, ${bar varDelta _i} = - 1$表示起竖构型在第i个关节处顺时针转动. 图9(a)和图9(c)分别为${varDelta _1} = 1, {varDelta _i} = - 1, i = 2, 3$和${varDelta _i} = 1, i = 1, 2, $$ {varDelta _3} = - 1$两种情况下比例系数单调性变量与起竖构型单调性变量的示意图, 图9(b)为${varDelta _1} = 1,{varDelta _i} = - 1, i = 2, 3$不同比例系数下三节仿生起竖结构不同稳态的吸引盆, 图9(d)为${varDelta _i} = 1, i = 1, 2, {varDelta _3} = - 1$不同比例系数下三节仿生起竖结构不同稳态的吸引盆. 在图9(b)及图9(d)的左上角用柱状图表示该图对应的比例系数, 并在图像上方标出了不同构型在该比例系数下的触发概率. 在图9中, 图9(b1)与图9(d1)、图9(b2)与图9(d2)、图9(b3)与图9(d3)以及图9(b4)与图9(d4)都有相同的$left| {{eta _2} - {eta _1}}
ight|$和$left| {{eta _3} - {eta _2}}
ight|$, 仅是比例系数单调性不同. 通过对这4组吸引盆的对比, 可以得知, ${varDelta _i} = 1, i = 1,2, {varDelta _3} = - 1$情况下触发$;{bar varDelta _i} = 1, i = 1,2, $$ {bar varDelta _3} = $?1起竖构型的概率要大于${varDelta _1} = 1,{varDelta _i} = - 1, i = 2,3$情况下触发该起竖构型的概率. 因此, 当${varDelta _i} = {bar varDelta _i}$时, 触发需求起竖构型的概率最大, 即${varDelta _i} = {bar varDelta _i}$为满足触发条件准则的比例系数单调性变量.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
三节仿生起竖结构比例系数单调性变量与起竖构型单调性变量示意图及不同比例系数情况下不同稳态的吸引盆



Figure
9.
Schematic diagram of excitation variable and configuration variable and basin of attraction under different excitation variable situation for three-segment bio-inspired erecting structure



下载:
全尺寸图片
幻灯片

2.4
多节起竖的仿生起竖结构

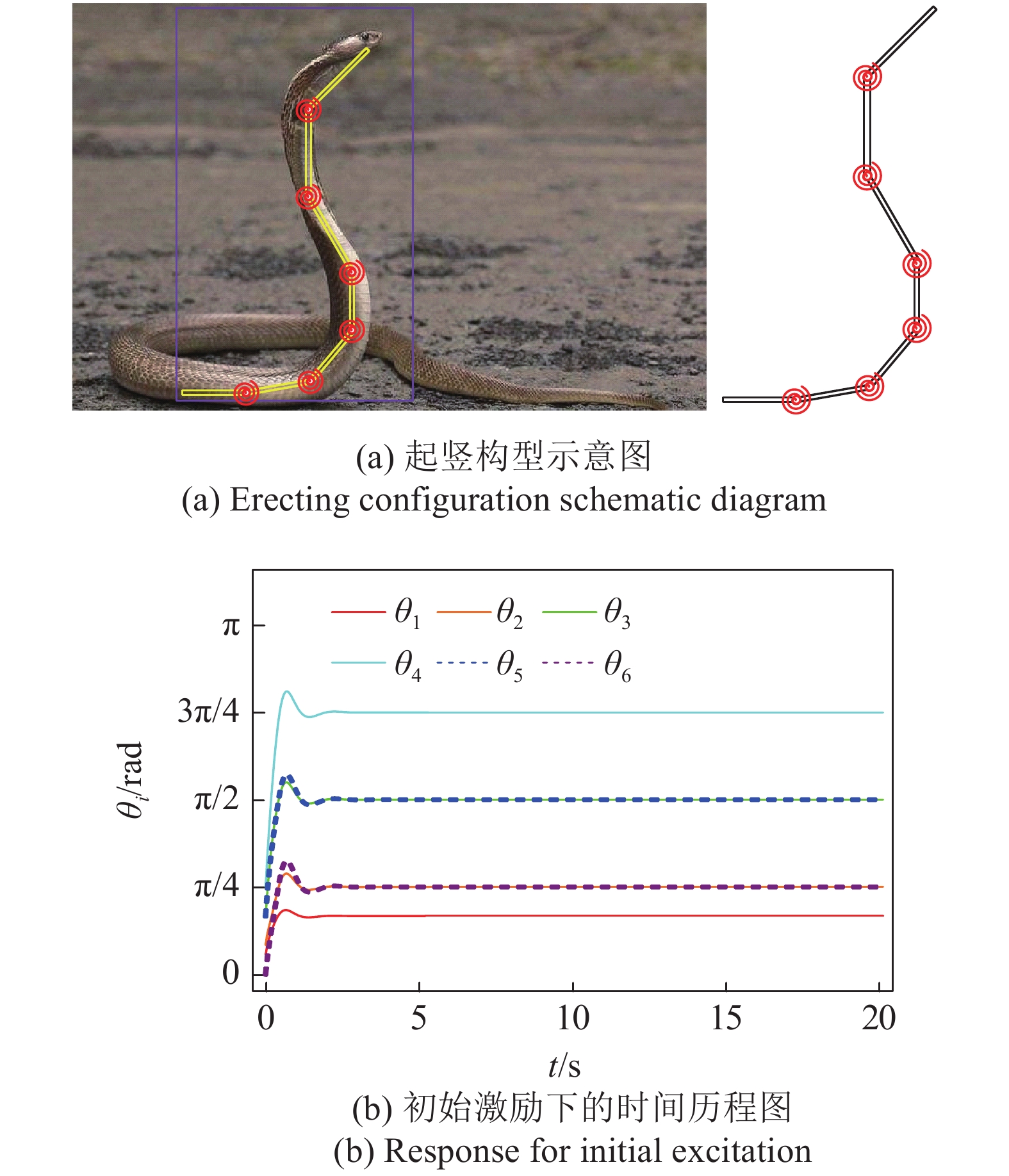
为了说明本文提出的仿生起竖结构能够实现需求的仿生构型, 设计了多节起竖的仿生起竖结构, 多节仿生起竖结构的起竖节数和起竖构型由图10(a)中蛇起竖的构型而来. 多节仿生起竖结构只有最右端的六节进行起竖, 起竖构型为${bar theta _1} = dfrac{{
m{{text{π}}}} }{6}$,${bar theta _2} = dfrac{{
m{{text{π}}}} }{4}$, ${bar theta _3} = $$ dfrac{{
m{{text{π}}}} }{2},{bar theta _4} = dfrac{{3{
m{{text{π}}}} }}{4},{bar theta _5} = dfrac{{
m{{text{π}}}} }{2},{bar theta _6} = dfrac{{
m{{text{π}}}} }{4}$. 仿生起竖结构的结构参数为${m_1} = {m_2} = cdots = {m_6} = 0.005;{
m{kg}}$, ${l_1} = {l_2} = cdots = {l_6}$= 0.1 m,${L_{a1}} = {L_{a2}} = 0.05$ m, ${c_1} = {c_2} = cdots = {c_6} = 0.075$ N·s/m, 其设计参数如表3所示. 图10(b)为多节仿生起竖结构在受到初始激励后的时间历程图, 多节仿生起竖结构受到初始激励后的起竖过程及对应的时间历程的动力学模拟结果在附加材料中. 由图10(b)可以得知, 多节仿生起竖结构能够在受到初始激励后达到设计的起竖构型并在起竖构型处稳定, 说明了本文提出的仿生起竖结构实现了需求的仿生构型.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
多节仿生起竖结构



Figure
10.
Multi-segment bio-inspired erecting structure



下载:
全尺寸图片
幻灯片





表
3
多节仿生起竖结构的设计参数



Table
3.
Design parameters values of multi-segment bio-inspired erecting structure



table_type2 ">

i	ki/(N·m·rad?1)	Ksi/(N·m?1)	${phi _i}$/rad	${bar beta _i}$/rad
1	2	600	0.033	0.829
2	1.5	400	0.031	0.814
3	1	400	0.029	1.012
4	0.5	400	0.033	1.307
5	0.5	400	0.147	1.285
6	0.5	400	0.037	1.289

下载:
导出CSV
|显示表格



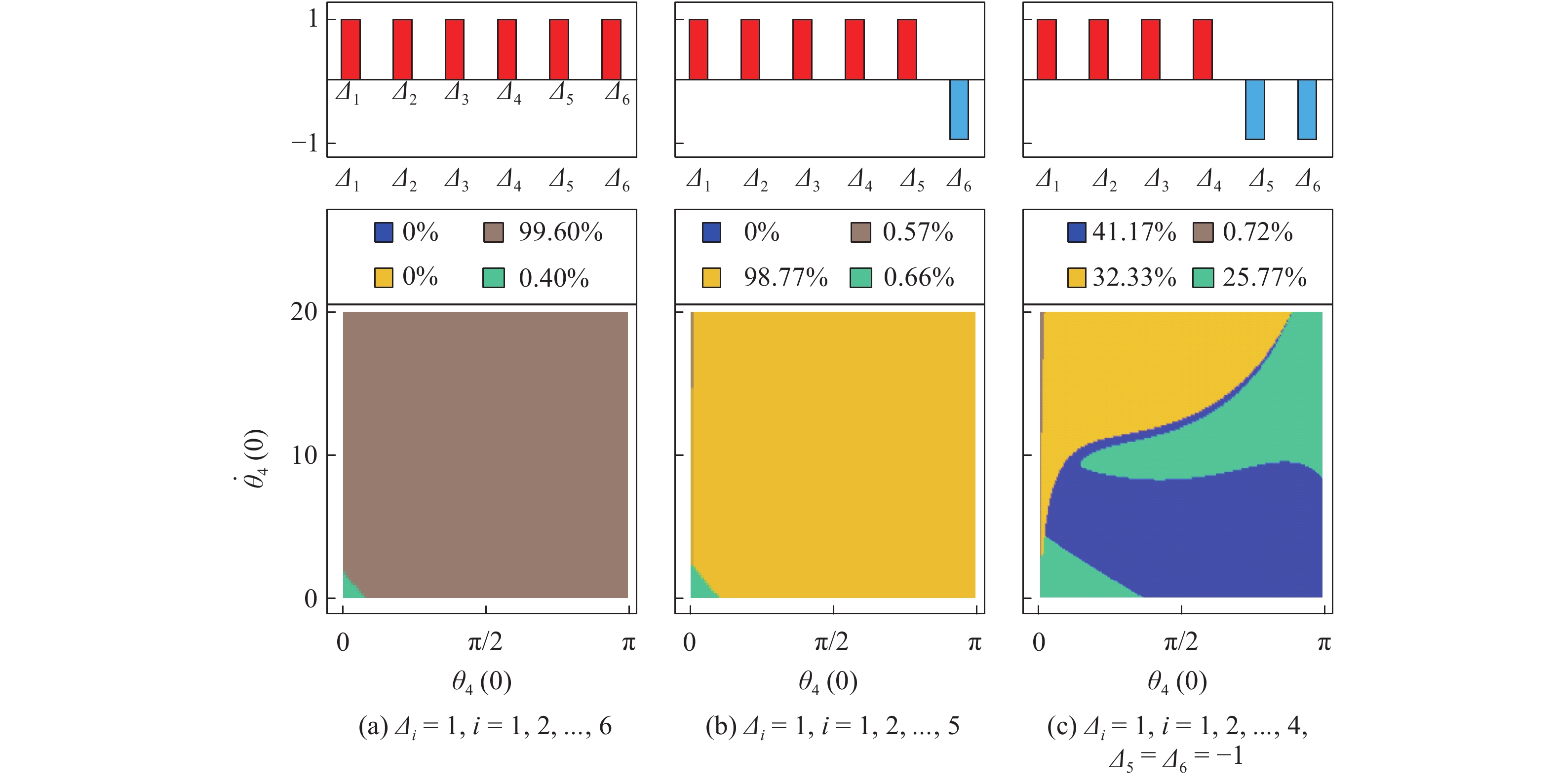
多节仿生起竖结构有多个不同的稳定构型, 通过求解不同初始激励下多节仿生起竖结构的动力学模型, 可以得到仿生起竖结构不同稳态的吸引盆中出现的稳定构型, 其示意图如图11所示. 根据三节起竖的仿生起竖结构中对仿生起竖结构需求构型触发条件的讨论, 可得到了3种不同比例系数单调性下多节仿生起竖结构不同稳态的吸引盆及不同构型出现的概率, 如图12所示. 在吸引盆图像的上方, 我们用柱状图标出了对应的单调性变量的取值. 在多节仿生起竖结构不同稳态的吸引盆中, 蓝色部分表示所设计的S形起竖构型, 棕色部分表示C形构型, 橙色部分表示斜S构型, 绿色部分表示受地面约束的直线构型. 图12(a)为${varDelta _i} = 1,i = $1,2,···,6时多节仿生起竖结构不同稳态的吸引盆. 由图12(a)可以得知, 在${varDelta _i} = 1,i = $1,2,···,6的情况下, 最容易触发${bar varDelta _i} = 1,i = $1,2,···,6的C形构型. 图12(b)为${varDelta _i} = 1,i = $1,2,···,5,${varDelta _6} = - 1$时多节仿生起竖结构不同稳态的吸引盆. 由图12(b)可以得知, 在${varDelta _i} = 1,i = $1,2,···,5,${varDelta _6} = - 1$的情况下, 最容易触发 ${bar varDelta _i} = 1,i = $1,2,···,5,${bar varDelta _6} = - 1$的斜S形构型. 图12(c)为${varDelta _i} = 1,i = $1,2,···,4,${varDelta _5} = {varDelta _6} = - 1$时多节仿生起竖结构不同稳态的吸引盆. 由图12(b)可以得知, 在${varDelta _i} = 1,i = $1,2,···,4,${varDelta _5} = {varDelta _6} = - 1$时的情况下, 最容易触发 ${bar varDelta _i} = 1,i = $1,2,···,4,${bar varDelta _5} = {bar varDelta _6} = - 1$时的S形构型. 通过对图12的分析, 验证了在三节仿生起竖结构中得到的关于触发条件准则的结论, 即${varDelta _i} = {bar varDelta _i}$为满足触发条件准则的比例系数单调性变量.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-11.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11" />



图
11
多节仿生起竖结构稳定构型示意图



Figure
11.
Stable configurations of multi-layer bio-inspired erecting structure



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-176-12.jpg'"
class="figure_img
figure_type2 ccc " id="Figure12" />



图
12
不同比例系数单调性下多节仿生起竖结构不同稳态的吸引盆



Figure
12.
Basin of attractions corresponding to different conditions



下载:
全尺寸图片
幻灯片

3.
结论

本文提出了一种具有多稳态性质的仿生柔性关节以实现仿蠕虫移动机器人的起竖功能, 并针对不同起竖节次和起竖构型的需求, 设计了相应节次的仿生起竖结构. 本文的主要结论如下:

(1) 本文提出的结构参数设计准则能够实现仿蠕虫机器人在直线和起竖两种构型下的稳定平衡. 准则${r_{textit{z}}}$保证了仿生起竖结构直线构型的稳定平衡, 准则${r_{w1}}$使得仿生起竖结构在起竖构型位置处是一个平衡点, 准则${r_{w2}}$确保仿生起竖结构在起竖构型位置处稳定.

(2) 本文定义了初始激励与起竖构型的比例系数单调性变量来研究初始激励与起竖构型的关系, 并建立了触发条件准则来描述触发需求起竖构型的初始激励形式.

(3) 基于不同起竖节次的需求, 设计了相应节数的仿生起竖结构. 结果说明, 本文提出的仿生起竖结构能够在重力作用下实现需求的起竖构型. 在三节和多节仿生起竖结构中, 利用不同稳态下的吸引盆得到了满足触发条件准则的初始激励形式.

本文提出的仿生起竖结构对拓展仿蠕虫机器人的应用场景、丰富仿蠕虫机器人的功能性有指导意义. 同时, 对仿生起竖结构的构型触发条件的研究为我们利用主动控制调控仿生起竖结构的不同构型提供了依据, 也对后续通过主动控制保持需求的构型有参考价值.