引言
声子晶体是一种新型人工周期性复合材料, 具有独特的禁带特性, 即声波或弹性波在声子晶体中传播时, 由于受到周期性结构中波的散射或局部共振的作用, 在某些频段范围即带隙内无法传播[1-4]. 该特性使得声子晶体在工程减振降噪领域具有巨大的应用潜力. 声子晶体的拓扑结构和组分材料的属性决定了其带隙特性. 因此, 根据特定的减振降噪需求设计具有目标带隙的声子晶体具有重要的理论研究意义与工程应用价值.
现有声子晶体设计方法大多是通过对结构几何参数与材料参数的分析, 调整匹配特定的频散特性, 但这样设计出来的声子晶体结构往往带隙位置与宽度达不到最佳需求, 并且需经过反复的调控才能满足实际的减振降噪需求. 按照特定频率设计声子晶体结构是典型的具有挑战性的逆向设计问题. 拓扑优化作为一种代表性的逆向设计方法, 已经被广泛用于结构设计、材料组合设计和多物理场下的器件设计等. Sigmund等[5]最早对二维声子晶体的拓扑优化进行了研究; Gazonas等[6]利用有限元法对二维声子晶体进行了拓扑优化; Zhong等[7]基于平面波展开法对二维固?固体系声子晶体进行了拓扑优化的研究; Hussein等[8-9]对一维、二维声子晶体的拓扑优化进行了研究; Bilal和Hussein[10]讨论了多孔声子晶体中带隙的最宽化问题; Dong等[11-14]针对各种类型的二维声子晶体(含孔隙、不含孔隙、非对称等)的单目标、多目标拓扑优化进行了一系列的研究; Liu等[15-16]提出了二维固?固体系声子晶体的系统拓扑优化; Xu等[17]对三相声子晶体进行了优化设计, 得到了多目标问题的Pareto最优解集. 然而, 以上关于声子晶体的拓扑优化方法主要是基于遗传算法, 需要大量的计算资源和时间, 而且所需时间随着参数数量的增加呈指数增长. 近年来, 人工神经网络和深度学习的发展为声子晶体的逆向设计提供了新的思路. Liu[18]于2019年将有监督学习型神经网络和无监督学习型神经网络模型用于一维声子晶体填充率、剪切模量比和质量密度比的设计. Li等[19]于2020年利用自编码器和多层感知机模型建立了二维声子晶体图像特征、结构拓扑特征、带隙特性的内在联系, 得到了具有预期带隙的声子晶体. 同年, Kollmann等[20]将ResUNet卷积神经网络模型用于超材料的优化设计. Luo等[21]将强化学习方法用于层状声子晶体的逆向设计中.
以上研究说明将机器学习用于声子晶体的逆向设计是可行的且具有巨大潜力, 与此同时, 也可以看出此方面的研究尚处于起步阶段, 相关研究大多是针对由指定的两种材料组成的声子晶体开展的, 其样本分布存在一定的局限性, 尚需进一步探索.
本文以一维层状声子晶体为例, 提出了一种基于Softmax逻辑回归和多任务学习的人工神经网络的声子晶体逆向设计方法. 与以往研究方法不同的是, 本文将机器学习中的两个重要内容“多任务学习和逻辑回归”用于人工神经网络, 将声子晶体逆向设计问题转化为对单元胞元拓扑结构多组分材料的分类问题, 突破了以往研究方法中因材料种类有限和材料分布单一带来的样本分布集中的局限性. 在本文提出的逆向设计方法中, 多任务学习实现了多分层结构各区域材料的分布问题, Softmax逻辑回归则实现了各区域材料种类的选择问题. 本文的主要内容为: 首先, 随机生成大量拓扑结构样本, 进而采用有限元方法得到每个样本的带隙, 然后, 通过神经网络建立带隙和拓扑结构之间的映射关系, 最后利用训练好的神经网络设计具有目标带隙特性的声子晶体.
1.
样本数据生成
不同材料组合及其不同几何排布方式将产生不同拓扑构型的声子晶体, 对应不同的能带结构. 通过计算机程序自动生成大量的单位胞元拓扑构型, 并计算出其相应的能带结构, 对各拓扑构型和其对应能带结构的特征进行提取, 为神经网络的构建提供大量训练样本和测试样本.
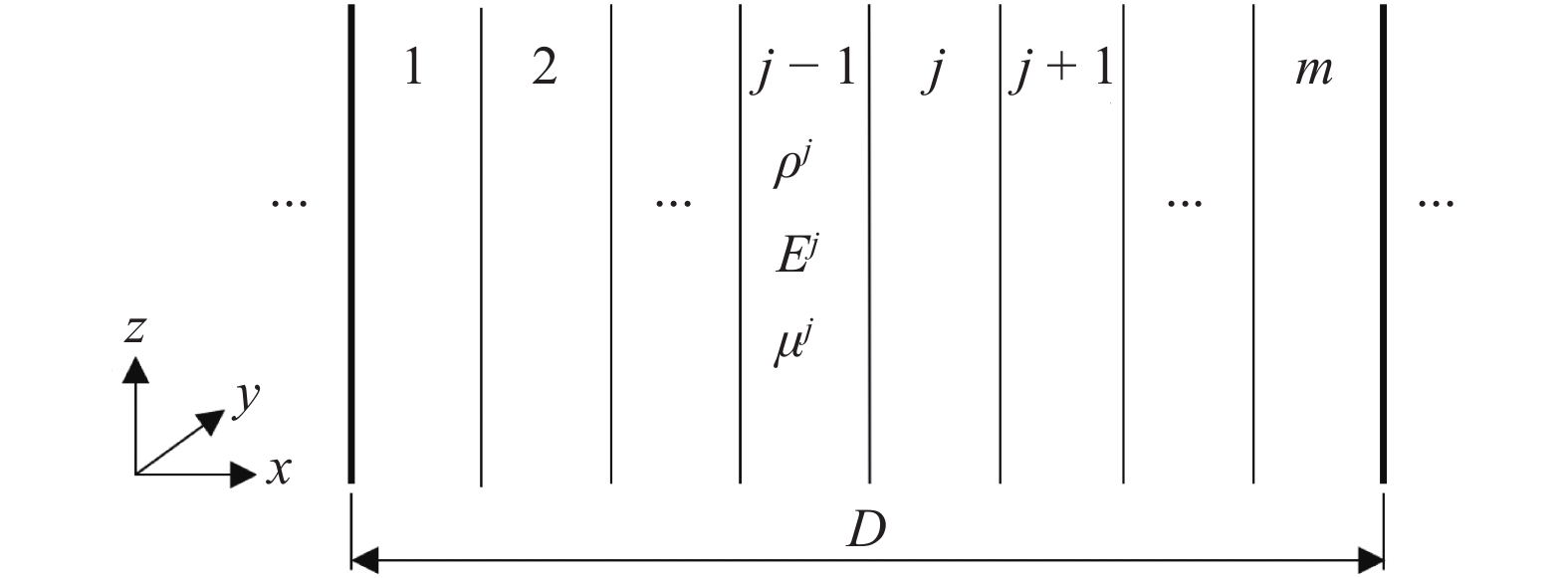
为不失一般性, 考虑一维层状声子晶体单元胞元拓扑构型如图1所示. 其沿
ho ^j}$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-142-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
一维声子晶体单元胞元结构示意图
Figure
1.
Unit-cell structure of the 1D phononic crystal
下载: 全尺寸图片
幻灯片
在采用有限元方法得到声子晶体的能带结构后, 需要进行能带特征的提取以作为神经网络训练的样本数据. 具体步骤如下所述. 首先, 根据能带结构确定禁带(带隙)和通带频率范围; 进而将整个能带频率范围等分为若干个小频率区间, 判断每个小区间是否落在禁带或通带中, 并分别用数字0或1来标识其禁带和通带属性. 这样, 能带特征可通过由0和1组成的一维数组表示出来.
2.
人工神经网络的建立
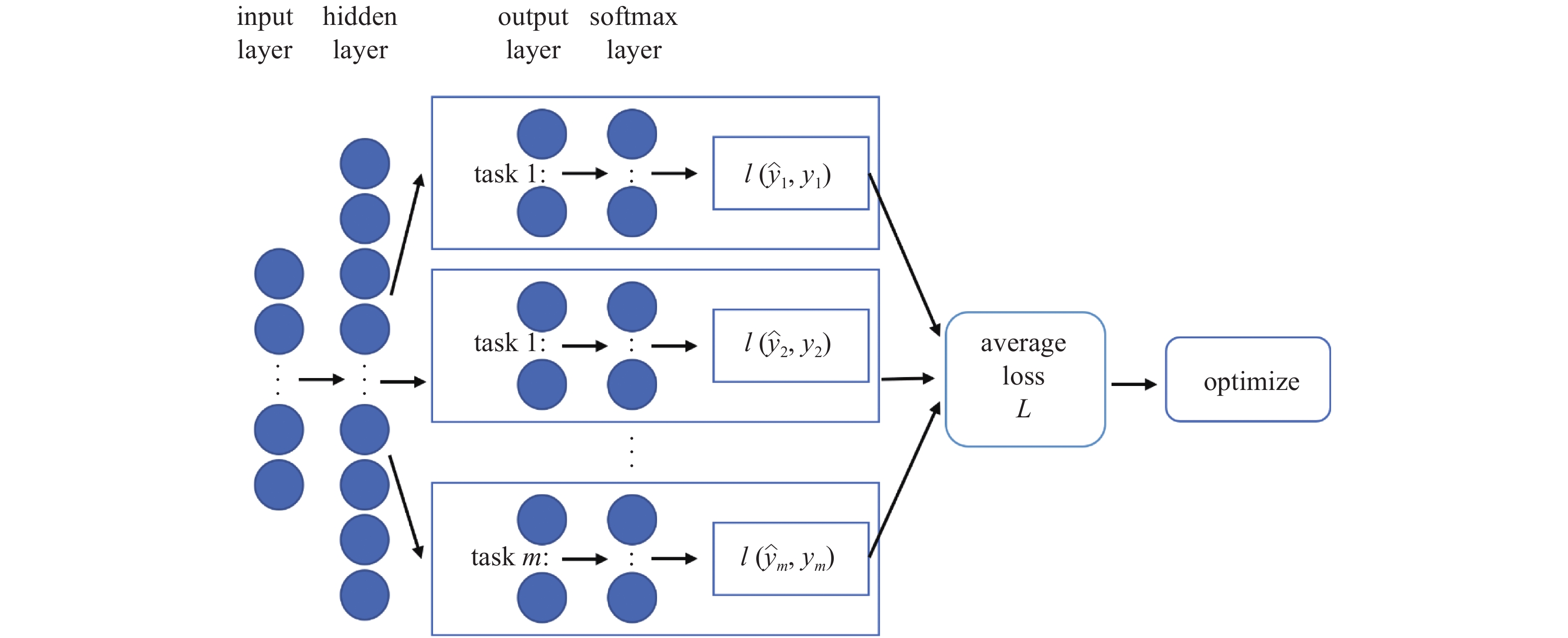
本文采用Softmax逻辑回归和多任务学习的人工神经网络[22-25]来构建一维声子晶体的带隙分布和单元胞元拓扑结构之间的映射关系. 神经网络的模型如图2所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-142-2.jpg'" class="figure_img
figure_type2 ccc " id="Figure2" />
图
2
人工神经网络模型
Figure
2.
Artificial neural network model
下载: 全尺寸图片
幻灯片
神经网络包含输入层、隐藏层、输出层和Softmax层, 相邻层之间的每个神经元相互连接构成完整的神经网络模型. 每个样本的输入数据将作为输入层数据进行前向传播. 在这个过程中, 网络的每一层都会将上一层的输出数据作为本层的输入数据进行相应的数值计算并将结果作为本层的输出数据传递给下一层.
当数据经过隐藏层时, 每个隐藏层按照下式完成计算并进行输出
$${textit{z}}_o^q = sumlimits_{p = 1}^{{r^{q - 1}}} {left( {w_p^qa_p^{q - 1} + {b^q}} ight)} $$  | (1) |
$$a_o^q = Rleft( {{textit{z}}_o^q} ight)qquadqquad$$  | (2) |
即在第q?1层的输出到达第q层的神经元之前, 网络会按照式(1)对第q?1层的输出进行线性变换. 其中,
数据经过隐藏层后进入m个并行的输出层, 第m个输出层输出单位胞元结构第m层材料的参数值. 输出层无需添加激活函数, 只需通过式(1)对上一层的输出进行线性变化并将本层的输出传递给最后的Softmax层.
Softmax层的输出通过以下公式计算得出
$$hat y_m^q = frac{1}{{displaystylesumlimits_{p = 1}^{{r^{q - 1}}} {exp left( {hat y_p^{q - 1}} ight)} }}left[ {begin{array}{*{20}{c}} {exp left( {hat y_1^{q - 1}} ight)} {exp left( {hat y_2^{q - 1}} ight)} vdots {exp left( {hat y_{{r^{q - 1}}}^{q - 1}} ight)} end{array}} ight]$$  | (3) |
其中,
然后通过如下公式的交叉熵函数计算
$$lleft( {{{hat y}_m},{y_m}} ight) = - sumlimits_{p = 1}^r {left[ {{y_p}lg {{hat y}_p} + left( {1 - {y_p}} ight)lg left( {1 - {{hat y}_p}} ight)} ight]} $$  | (4) |
最后将m个任务的损失求均值作为总损失L并使用误差反向传播算法[26]对其进行优化, 直到网络的精度满足要求.
3.
人工神经网络的训练和测试
神经网络模型建立好后, 使用训练集的数据来训练模型, 然后用测试集评估模型的泛化性. 网络模型的训练效果可用总损失L和训练精度Tracc进行评估; 测试效果可用测试精度Teacc进行评估. Tracc和Teacc可由下式进行计算
$$left. begin{array}{l}T{r_{{ m{acc}}}},T{e_{{ m{acc}}}} = dfrac{1}{{{M_{{ m{Tr}}}},{M_{{ m{Te}}}}}}dfrac{1}{m}displaystylesumlimits_{alpha = 1}^{{M_{{ m{Tr}}}},{M_{{ m{Te}}}}} {displaystylesumlimits_{beta = 1}^m {left[ {Eqleft( {{{hat y}_{alpha beta }},{y_{alpha beta }}} ight)} ight]} } Eqleft( {{{hat y}_{alpha beta }},{y_{alpha beta }}} ight) = { m{1}},;;;;;;;{{hat y}_{alpha beta }} = {y_{alpha beta }}Eqleft( {{{hat y}_{alpha beta }},{y_{alpha beta }}} ight) = 0,;;;;;;{{hat y}_{alpha beta }} ne {y_{alpha beta }}end{array} ight} $$  | (5) |
其中, MTr和MTe分别为参与训练和测试的样本数,
4.
算例
已有研究表明, 船用齿轮传动系统中齿轮副的振动会通过轴承座将激励传递至减速箱, 致使减速箱对外界产生辐射噪声, 而辐射噪声对船舶内各舱室的舒适性有着严重的影响, 因此, 选择合适的降噪方法是减少船舶减速箱噪声污染的关键[27]. 目前国内外船舶领域针对减速箱采用的降噪方法主要有: 减速箱的结构改进、阻尼材料敷设、基座导纳安装形式优化以及主动控制等[28]. 相对于主动控制减振, 被动控制减振具有结构简单、造价低、易于维护并且无需外部能量支持等优点[29-31]. 由于声子晶体在噪声与振动的被动控制方面有着巨大的潜力, 因此, 声子晶体为减速箱等机械结构的减振降噪提供了一个全新的途径.
船用单级人字齿轮减速箱的前两阶固有频率分别为208.99 Hz和386.74 Hz[27]. 为此, 通过设计预期带隙包含此固有频率的声子晶体可有效减小减速箱对外界产生辐射噪声. 基于此应用背景, 本文进行目标带隙为200 ~ 400 Hz的一维声子晶体逆向设计. 所选材料为钨(W)、丁腈橡胶(NBR)和硅橡胶(Sil)组成的一维三相声子晶体, 晶格常数D = 0.01 m, 材料的名称、编号、密度
ho $
表
1
材料参数
Table
1.
Material parameters
table_type1 ">
| Name | No. | ρ/(kg·m?3) | E/GPa | μ/GPa |
| W | 0 | 19100 | 354.1 | 131.1 |
| NBR | 1 | 1300 | 0.012 | 4.3×10?3 |
| Sil | 2 | 1300 | 1.175×10?4 | 4×10?5 |
下载: 导出CSV
|显示表格
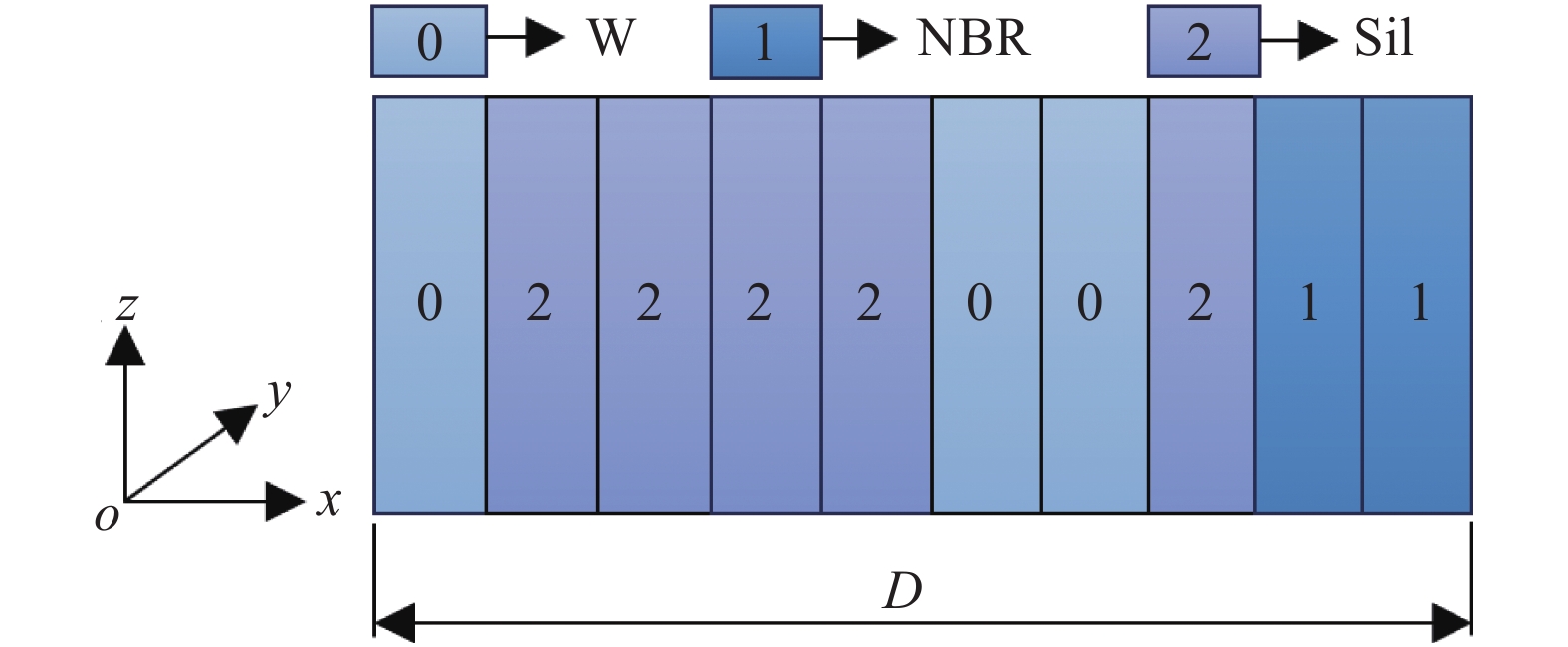
单元胞元结构层数的选取应避免层数过少而导致单元胞元结构及带隙多样性不足的问题, 同时, 也应避免层数过多导致训练难度加大的问题. 为此, 本例中将单元胞元结构等分为10层, 每一层由以上材料中的一种构成, 分别用数字0, 1和2表示, 如一维数组0222200211表示的声子晶体的单元胞元结构如图3所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-142-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
单元胞元结构示例
Figure
3.
Example for a unit-cell structure
下载: 全尺寸图片
幻灯片
将3种材料随机填充在10层中, 可获得310个单元胞元拓扑结构. 因为声子晶体具有周期平移对称性[32], 而具有相同周期平移对称性的声子晶体的带隙分布是相同的, 即会出现不同拓扑构型标签对应着相同的带隙输入情况, 这将会对神经网络的训练过程产生阻碍. 因此, 需要对结构进行筛选以保证神经网络的收敛性. 从筛选后的单位胞元结构中随机取出10000个作为拓扑结构样本, 其中, 9000个作为训练样本, 1000个作为测试样本. 通过MATLAB和COMSOL Multiphysics软件的联合并行仿真得到所有样本的能带结构. 将研究的频率范围设定为0 ~ 2000 Hz以使得目标带隙和每个样本的第一禁带被完整覆盖, 并以单位频率对其进行划分, 对各样本的单位频率小区间落在禁带范围或通带范围进行判断, 分别用数字0和1进行标识, 并存储在一维数组中作为带隙样本. 如图4表示了0 ~ 20 Hz频段内禁带落在6 ~ 12 Hz, 其余为通带的带隙分布.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-142-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
以数组表示带隙
Figure
4.
Band-gaps represented by an array of numbers
下载: 全尺寸图片
幻灯片
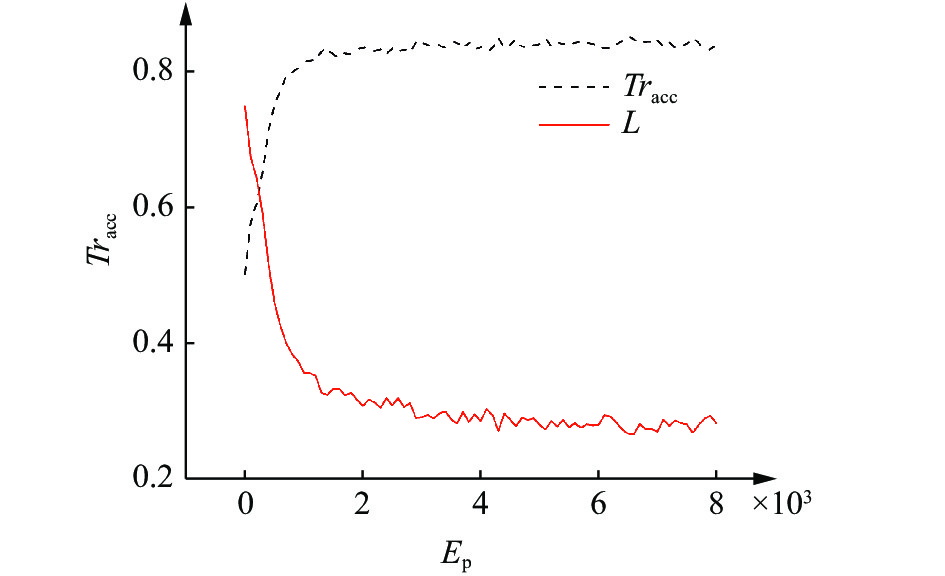
按照图2模型构建神经网络. 其中, 构建神经元数分别为2000, 2000和1000个的3个隐藏层; 为防止过拟合, 在每个隐藏层加入了Dropout[33]操作, 其工作原理是在网络训练过程中随机将该层20%的神经元暂时从网络中丢弃, 减少了中间特征的数量, 从而减少冗余, 增加了每层各个特征之间的正交性; 另外, 为了克服梯度消失问题并加快训练速度, 选择Relu函数[34]作为隐藏层激活函数. 构建10个并行的输出层, 每一个输出层包含3个神经元; 为了提升网络的学习效率, 使用Adam优化算法[35]更新参数并优化总损失L. 训练过程中总损失L和训练精度Tracc随训练次数Ep的变化曲线如图5所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-142-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
L和Tracc随迭代次数Ep的变化曲线
Figure
5.
Variations of the L and Tracc curves with the Ep
下载: 全尺寸图片
幻灯片
由图5可以看出, L随Ep的增加而逐渐减小, 最终稳定在0.27附近; Tracc随Ep的增加而逐渐增大, 最终稳定在85%附近. 采用测试集对网络进行测试, 测试精度Teacc可达到80%, 可用其开展预期带隙的一维声子晶体逆向设计. 下面利用该网络进行声子晶体设计.
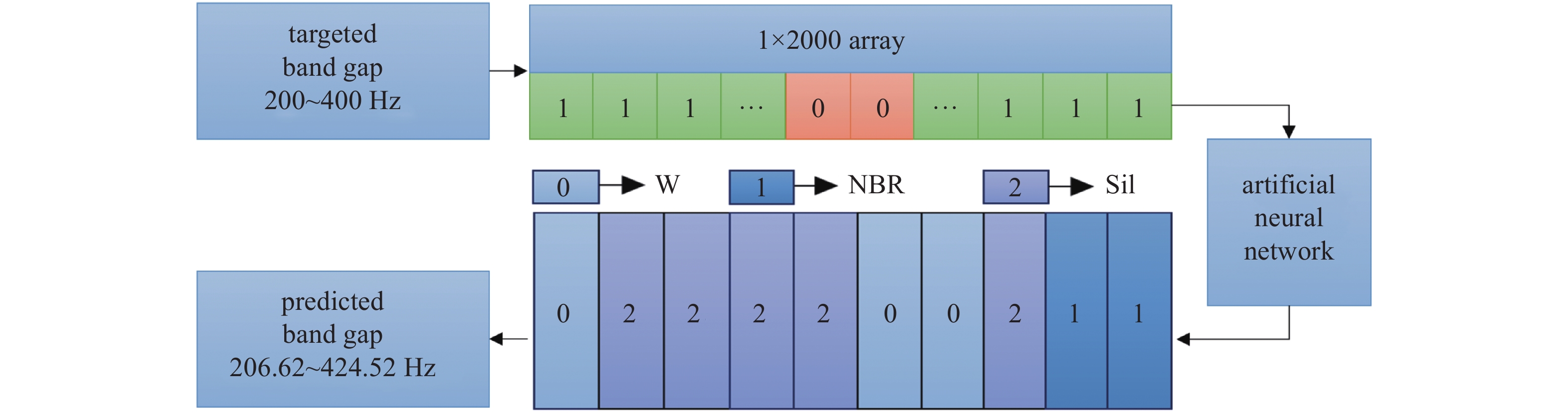
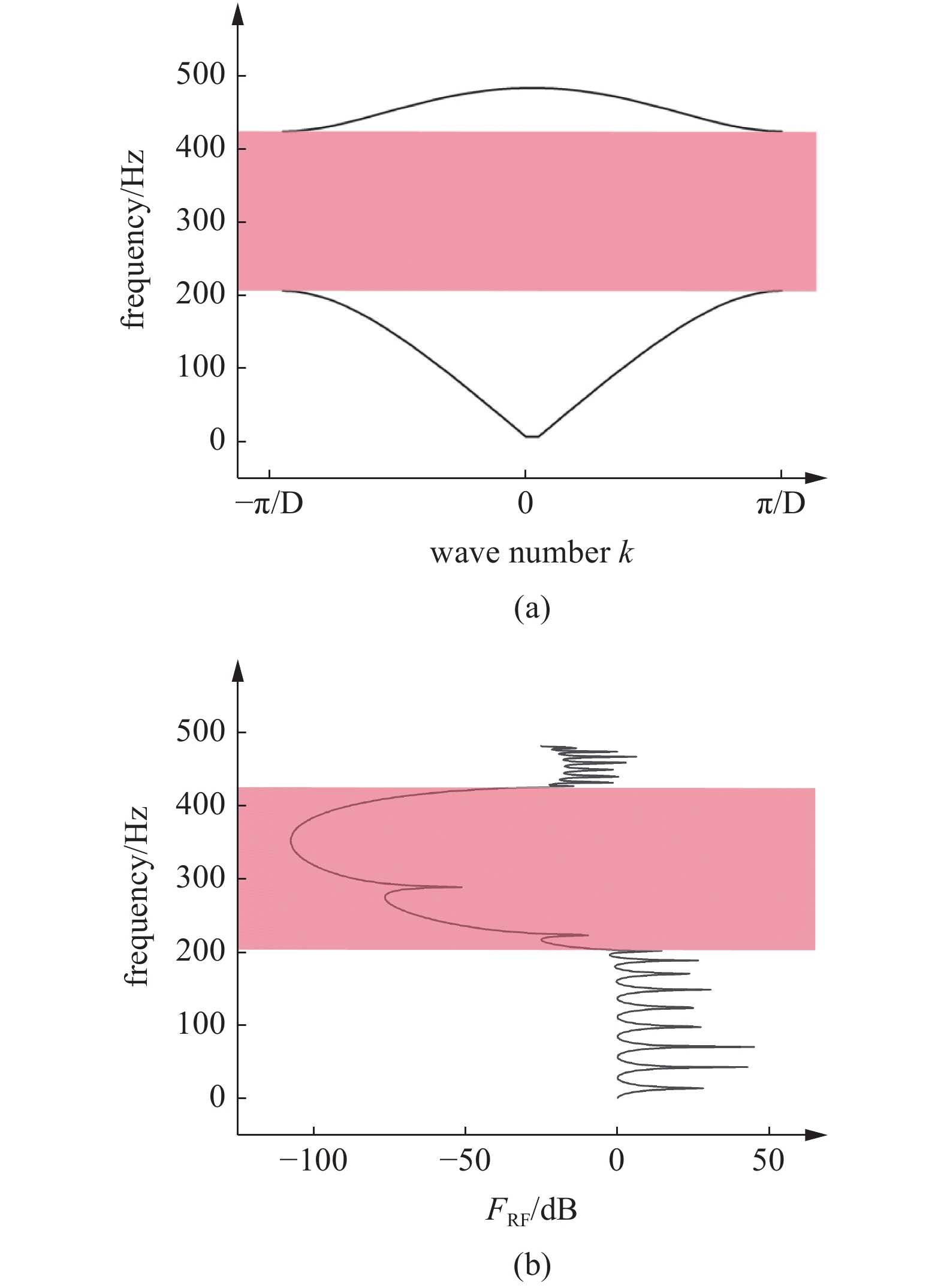
设计过程如图6所示. 首先将目标带隙分布用1 × 2000的一维数组表示; 然后将其输入训练好的神经网络, 网络输出1 × 10的拓扑结构数组, 由此可得到相应的一维声子晶体结构. 该结构的实际能带结构和频率响应如图7所示, 其中, 频响函数是由10个周期单元胞元组成的声子晶体结构按照公式
m{RF}} = 20lg left( {{a_2}/{a_1}}
ight)$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-142-6.jpg'" class="figure_img
figure_type2 ccc " id="Figure6" />
图
6
预测具有目标带隙声子晶体单位胞元的过程
Figure
6.
Prediction process of the unit-cell of the phononic crystal with a target band-gap
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-142-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
(a)能带结构和(b)频率响应
Figure
7.
(a) Band structure and (b) frequency response curve
下载: 全尺寸图片
幻灯片
5.
结论
本文提出了一种基于Softmax逻辑回归和多任务学习的人工神经网络的声子晶体逆向设计方法, 将声子晶体逆向设计问题转化为对单元胞元拓扑结构各组分材料的多分类问题. 该方法以目标带隙为神经网络的输入, 网络将直接输出对应的声子晶体单元胞元拓扑结构. 其中, 神经网络的构建需要对大量的样本进行训练, 这些训练样本通过有限元仿真创建, 虽然需要一定的计算资源和时间, 但该过程可以并行且一次性完成, 较传统设计方法更高效. 同时, 该设计方法可突破传统设计方法强烈依赖于解析理论和参数分析的缺陷, 为声子晶体的逆向设计提供了新颖的途径.
最后需要强调的是, 本文的重点是利用神经网络开展一维声子晶体的逆向设计, 即根据目标带隙设计出满足带隙要求的声子晶体拓扑结构及其材料组成. 目标带隙的确定取决于实际问题的需要, 可以是低频带隙, 也可以是高频带隙. 如果目标带隙为低频带隙, 采用局域共振机理十分奏效, 此时需要引进较薄较柔的层状元素, 因而可能导致整体结构的刚度与强度乃至稳定性下降. 此类问题是一个典型的多目标优化问题, 在实际设计相应声子晶体结构时既要满足低频带隙的要求, 又要兼顾结构的刚度与强度及其稳定性.
