引言

经过初始加载?卸载后的类橡胶材料再一次加载后, 初始卸载应力以下部分会将发生显著的应力软化现象, 该现象也被称为Mullins效应. 随着加载?卸载循环的进行, 应力软化现象逐渐变得显著, 并趋于一个稳定的状态, 而应力?应变曲线也逐渐变化并发展到一个稳定的状态^[1-3]. 天然橡胶和填充橡胶都有可能发生Mullins效应, 而填充物的种类和比重则会影响应力软化的程度.

过去几十年来, 为了从微观尺度解释Mullins效应, 研究人员们进行了大量的理论研究. Bueche^[4-5]认为当材料发生变形后, 填充颗粒之间附着的部分橡胶链发生了断裂和松弛, 使得填充颗粒间的距离发生仿射变形, 从宏观上表现为应力软化现象; Lee和Williams^[6]通过结构重组以及化学键永久性断裂来说明Mullins效应的产生原因; Mullins^[3]列举了两种情况. 对于天然橡胶, 橡胶长链分子之间在剪切过程中的解链和定向导致了应力软化. 对于填充橡胶, 应力软化的发生则是因为填充颗粒之间以及填充颗粒和橡胶分子之间的相互作用被断开而导致. 填充颗粒的存在使得应力软化效应被进一步增强; 以上观点基本都认为应力软化是因为橡胶分子和填充颗粒之间的相互作用而产生, 而Harwood等^[7]提出了不同的见解, 他们认为橡胶微结构中的网络节点位移导致了分子网状结构的重组, 从而产生了应力软化效应. 除此之外, 还有其他的微结构理论^[8-10]对Mullins效应的产生做了理论解释.

在前面微结构理论的基础上, 科研工作者们先构造微观尺度下的本构关系, 再通过一系列平均方法, 建立宏观尺度下的本构模型. Blanchard和Parkinson^[11]提出了一个半经验公式去描述填充硫化橡胶初始加载后的“应力?伸长比”关系, 其中引入了二个微结构相关的参数, 分别表示网状结构数量和分子链受限延伸率. 通过分析应力软化的特征, 他们给出了网状结构数量变化的公式, 并最终得到匹配实验数据的“应力?应变”结果; Govindjee和Simo^[8]在Bueche^[4-5]理论研究的基础上进一步发展, 通过对统计代表样本体积(SRSV)进行宏观平均, 最终得到一个三维的本构模型; Marckmann等^[9]发展了Arruda和Boyce^[12]的八链理论, 将该模型中的两个参数进行改进, 使他们依赖于分子链伸长比的极限值, 得到了能模拟应力软化效应的新模型.

另一部分****不考虑橡胶分子的内部微观结构, 从宏观现象出发构建唯象的本构模型. Mullins和Tobin^[13]将橡胶内部区域分为两大类, 分别是“硬区”和“软区”, 材料的变形主要是在“软区”产生, 而“硬区”对变形几乎没有贡献. 加载过程中“硬区”部分逐渐转为“软区”, 卸载后重新加载, 当加载应力达到初始卸载应力以后, “转化”过程才会继续. 此外, 为了模拟填充橡胶的应力?应变关系, Mullins和Tobin^[14]又引入了应变放大因子; 文献[15-17]在前面研究的基础上进一步优化和完善; Simo^[18]另辟蹊径, 在基于变形梯度的弹性势中加入了一个表征损伤的量, 用来解释类橡胶材料应力软化过程中出现的分子链破坏, 微结构损伤. 在此基础上, 根据引入量演化方程的不同, 提出了各种不同的结果^[19-22]; Ogden和Roxburgh^[23]在伪弹性模型的基础上只引入了一个变量去表示理想化的应力软化效应.

Mullins效应通常伴随着不可恢复变形的产生^[3](随着时间的流逝会慢慢变小, 在退火后静置足够长时间基本消失), 其大小和橡胶中的填充物含量百分比以及加载应力大小均有关系^[24-25]. 通过大量实验证明, 应力软化会使得材料性质变成各向异性, 先前伸长过的方向上应力软化会更加明显^[1-3,26]. 各向异性特征也会直接导致材料发生不可恢复变形. 为了模拟Mullins效应产生的不可恢复变形和各向异性特征, Dorfmann和Ogden^[27]在伪弹性理论^[23]的基础上额外引入了一个表征残余应变的量, 可以模拟单轴拉伸?压缩循环加载下产生的应力软化和不可恢复变形. 他们的模型可以证明材料循环加载下发生了各向异性, 但是无法通过模型进行量化模拟; G?ktepe和Miehe^[10]将分子内部网络结构分解成CC (crosslink-to-crosslink)结构和PP (particle-to-particle)结构. Mullins效应引起的结构损伤和各向异性主要发生在PP结构中, 且会自然而然地使得模型产生不可恢复变形; Diani等^[26]根据Marckmann等^[9]的方法, 定义了不同方向上的耗散, 然后将其引入到Pawelski^[28]的本构法则中, 构建了新的本构模型. 他们的方法可以预测应力软化、残余变形以及各向异性特征; 谈炳东等^[29-30]根据纤维增强复合材料连续介质力学理论, 提出了各向异性超弹性本构模型, 并能很好地预测0° ~ 45°各向异性力学性能.

关于Mullins效应产生不可恢复变形和各向异性特征的最新研究成果主要是在经典的模型上进行改进^[31-34]. 以上提到的模型尽管可以模拟Mullins效应引起的不可恢复变形和各向异性特征, 但是都存在着不足. 微结构模型的参数往往需要迭代求解, 计算量大; 唯象模型则需要引入没有物理意义的隐式参数. 近几年来, Xiao等^[35-36]和Wang等^[37]用显式的方法提出了类橡胶材料的多轴弹性势, 可以精确匹配4个基准实验, 同时预测非等双轴拉伸的变形趋势. 王晓明等^[38]在此基础上引入了耗散量, 并通过分析应力?应变关系, 给出耗散表达, 最终使得模型可以模拟理想的Mullins效应滞回圈. 通过进一步改造形函数的表达, 该方法还能模拟类橡胶材料过载破坏的情况^[39]. 在弹性势中加入温度的项, 可以模拟形状记忆聚合物的热力学行为^[40].

本文以前面的研究为基础, 在形函数中新引入表征不可恢复变形大小和各向异性特征的两个变量, 以上两个量均依赖于依赖耗散大小. 其中, 不可恢复变形量随着耗散的增大而增大, 直到趋于稳定; 各向异性特征量在应力软化之前不起任何作用(材料各向同性), 一旦在某一方向发生Mullins效应, 其值将发生变化, 在任意其他方向加载?卸载后的应力?应变关系将和初始加载方向上的应力?应变关系发生明显的偏离(引入各向异性), 在达到相同的变形情况下, 应力值小于初始方向的应力值. 当加载方向和初始加载方向呈90°时, 这样的差异最为明显.

1.
考虑耗散的多轴可压缩弹性势

类橡胶材料本构模型的建立, 通常需要提出合适的弹性势. 本章通过以下4个步骤构造弹性势: 首先, 通过对数应变张量和耗散标量构造弹性势; 其次, 通过对数应变偏量构造3个不变量, 并将它们引入弹性势, 使其多轴可压缩且能匹配多个变形模式; 再次, 将3种变形模式下考虑耗散的单轴形函数积分得到各自的单轴弹性势; 最后, 通过Hermite插值方法, 利用3个不变量和单轴弹性势, 构造考虑耗散的多轴可压缩弹性势.

1.1
基于对数应变的耗散弹性势

理想的超弹性模型没有能量的耗散, 而Mullins效应的存在表明材料在加载?卸载过程中出现了能量的损耗. 为了使模型具备模拟应力软化的功能, 需要引入一个标量$kappa $来表示耗散. 此外, 相比于其他模式的应变张量, 基于对数应变${boldsymbol{h}}$的弹性势$W$推导得到应力?应变关系的过程更加简单和直接^[41]

$${boldsymbol{tau }} = J{boldsymbol{sigma }} = frac{{partial W}}{{partial {boldsymbol{h}}}}$$

(1)

式中, $W, J, {boldsymbol{tau }}, {boldsymbol{sigma }}$分别表示弹性势、体积比、基尔霍夫应力以及柯西应力.

对数应变与变形梯度的关系为

$${boldsymbol{h}} = frac{1}{2}ln ({boldsymbol{F}} cdot {{boldsymbol{F}}^{ m{T}}}) = frac{1}{2}sumlimits_{i = 1}^3 {(ln lambda _i^2)} {{boldsymbol{n}}_i} otimes {{boldsymbol{n}}_i}$$

(2)

其中${boldsymbol{B}} = {boldsymbol{F}} cdot {{boldsymbol{F}}^{
m{T}}}$, 也称为左柯西?格林张量. 方程(2)中, ${lambda _i},{{boldsymbol{n}}_i}$, i = 1,2,3, 是材料伸长比(特征值)和特征向量. 方程(1)中的弹性势$W$是对数应变张量和耗散标量的函数

$$ W=W({boldsymbol{h}}, kappa )$$

(3)

1.2
基于对数应变偏量的不变量

基于对数应变张量的3个基本不变量表达为

$${i_s} = operatorname{tr} {{boldsymbol{h}}^s} = sumlimits_{i = {{1}}}^{{3}} {{{(ln {lambda _i})}^s}} $$

(4)

其中s = 1, 2, 3. 对数应变偏量的表达为

$${boldsymbol{tilde h}} = {boldsymbol{h}} - frac{1}{3}(operatorname{tr} {boldsymbol{h}}){boldsymbol{I}}$$

(5)

根据方程(5), 当trh = 0时, i₁ = 0, 表示变形前后体积变化忽略不计(材料不可压缩), 使得${boldsymbol{h}} = {{tilde {boldsymbol{h}}}}$. 本文考虑可压缩情况, 所以对数应变偏量和对数应变可以不相等.

类似于方程(4)的表达, 基于对数应变偏量的3个基本不变量为

$${j_s} = operatorname{tr} {{tilde{boldsymbol{h}}}^s}$$

(6)

其中s = 1, 2, 3. 新的3个基本不变量和初始的3个基本不变量之间存在着以下关系

$$left. {begin{array}{*{20}{c}} {{j_1} = 0{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} } {{j_2} = {i_2} - i_1^2{kern 1pt} { m{/3}}{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} } {{j_3} = {i_3} - {i_1}{i_2} + { m{2}}i_1^3{ m{/9}}{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} } end{array}} ight}$$

(7)

从以上3个基本不变量出发构造3个新的不变量. 第1个不变量称为压缩不变量, 用${gamma _{
m{1}}}$表示, 能控制材料是否可压缩的条件. 当材料不可压缩, 其值为0, 当材料可压缩, 其值不为0; 第2个称为桥联不变量, 用${gamma _{
m{2}}}$表示, 能实现模型的多轴扩展. 在单轴情况下会自动退化到相应的对数应变; 第3个不变量称为匹配不变量, 用${gamma _{
m{3}}}$表示, 能将3种不同变形模式(单轴拉伸和压缩、等双轴拉伸和压缩、以及平面应变)整合到一个统一的模型当中. 通过分析我们可以得到满足条件的3个不变量表达为

$$left. {begin{array}{*{20}{l}} {{gamma _{ m{1}}} = {i_1} = ln J } { {gamma _2} = sqrt {{ m{2}}{j_2}{ m{/3}}} } {{gamma _3} = sqrt 6 {j_3}{ m{Biggr/}}sqrt {j_2^3} } end{array}} ight}$$

(8)

1.3
带有耗散的单轴弹性势

理想情况下加载?卸载循环作用下的应力?应变曲线都是重合的, 引入了耗散也就意味着每一次循环都会发生能量损耗, 应力?应变曲线随着循环的进行而逐渐变化, 因此其形函数的给定必须考虑耗散.

单轴拉伸压缩变形模式下, 假设受力方向应力为${tau _{
m{u}}}$, 对数应变为$h$, 耗散用$kappa $表示, 则应力?应变形函数可以表示为

$$ {tau }_{ m{u}}={f}_{ m{u}}(h, kappa )$$

(9)

对方程(9)积分, 就可以得到单轴拉伸情况下的弹性势

$$ {w}_{ m{u}}(h, kappa )={displaystyle underset{0}{overset{h}{int }}{tau }_{ m{u}} { m{d}}h=}{displaystyle underset{0}{overset{h}{int }}{f}_{ m{u}}(h, kappa ){ m{d}}h}$$

(10)

等双轴拉伸的应力?应变关系可以通过单轴实验的关系推导出来(参考文献[35]中的Theorem A), 再通过积分可以得到其弹性势.

平面应变是对一个长条形橡胶块(z方向比x和y方向尺寸大很多), 在z方向进行固定, x方向和y方向, 一端拉伸, 另一端自由. 假设加载方向应力为${tau _{
m{P}}}$, 对数应变为$h$, 固定方向应力为${tau _{{
m{pf}}}}$, 我们给定其两个方向的应力?应变关系为

$$ left. {begin{array}{*{20}{l}}{{tau _{ m{p}}} = g(h,kappa )}{{tau _{ m{pf}}} = {g_{ m{f}}}(h,kappa )}end{array}} ight}$$

(11)

在该变形模式下, 只有在载荷方向做功, 因此我们得到应变能弹性势为

$$ {w}_{ m{p}}(h, kappa )={displaystyle underset{0}{overset{h}{int }}{tau }_{ m{p}}{ m{d}}h}={displaystyle underset{0}{overset{h}{int }}g(h, kappa ){ m{d}}h}$$

(12)

1.4
统一弹性势

方程(3)给定的弹性势依赖于对数应变张量和耗散, 其中前者可以通过1.2节中给定的3个不变量来替换, 即

$$ W=W({gamma }_{1},{gamma }_{2},{gamma }_{3}, kappa )$$

(13)

将方程(13)代入到方程(1), 得到

$${boldsymbol{tau }} = frac{{partial W}}{{partial {gamma _1}}}{boldsymbol{I}} + frac{2}{3}frac{{partial W}}{{partial {gamma _2}}}gamma _2^{ - 1}{tilde{boldsymbol{h}}} + frac{{partial W}}{{partial {gamma _3}}}{mathop {boldsymbol{h}} limits^ smallsmile}$$

(14)

其中

$${mathop {boldsymbol{h}} limits^ smallsmile} = 4gamma _2^{ - 3}{{tilde{boldsymbol{h}}}^2} - 2gamma _2^{ - 2}{gamma _3}{tilde{boldsymbol{h}}} - 2gamma _2^{ - 1}{boldsymbol{I}}$$

(15)

式中${tilde{boldsymbol{h}}}$是对数应变偏量, ${boldsymbol{I}}$是单位二阶张量. 张量${boldsymbol{I}},{tilde{boldsymbol{h}}},{mathop {boldsymbol{h}} limits^ smallsmile}$之间相互正交

$$left. {begin{array}{*{20}{c}} {begin{array}{*{20}{c}} {{boldsymbol{I}}:{tilde{boldsymbol{h}}} = {bf{0}}} {{boldsymbol{I}}:{mathop {boldsymbol{h}} limits^ smallsmile} = {bf{0}}} end{array}} {{tilde{boldsymbol{h}}}:{mathop {boldsymbol{h}} limits^ smallsmile} = {bf{0}}} end{array}} ight}$$

(16)

可以作为对数应变张量的3个基.

接下来利用Hermite插值方法, 我们可以得到多轴可压缩弹性势为

$$W = frac{{1 - 2upsilon }}{3}{w_{ m{u}}}left( {frac{{{gamma _1}}}{{1 - 2upsilon }},kappa } ight) + frac{{1 + upsilon }}{6}left[{{{Z}}^ + }{(1 + {gamma _3})^2} + {{{Z}}^{ m{ - }}}{(1 - {gamma _3})^2} ight]$$

(17)

其中Z ⁺和Z ^?表达为

$$left. {begin{array}{*{20}{c}}{{{{Z}}^ + } = (2 - {gamma _3}){w_{ m{u}}}left( {dfrac{{1.5{gamma _2}}}{{1 + upsilon }},kappa } ight) + ({gamma _3} - 1){Y_ + }}{{{{Z}}^{ m{ - }}} = (2 + {gamma _3}){w_{ m{u}}}left( { - dfrac{{1.5{gamma _2}}}{{1 + upsilon }},kappa } ight) + ({gamma _3} + 1){Y_ - }}end{array}} ight}$$

(18)

${Y_ + },{Y_ - }$分别等于${left. {dfrac{{partial W}}{{partial {gamma _3}}}}
ight|_{{gamma _{
m{3}}}{
m{ = 1}}}}$和${left. {dfrac{{partial W}}{{partial {gamma _3}}}}
ight|_{{gamma _{
m{3}}}{
m{ = - 1}}}}$, 形式为

$$ left. {begin{array}{*{20}{l}}{begin{array}{*{20}{l}}{{Y_ + } = dfrac{5}{2}{w_{ m{u}}}left( {dfrac{{1.5{gamma _2}}}{{1 + upsilon }},kappa } ight) - dfrac{1}{2}{w_{ m{u}}}left( { - dfrac{{1.5{gamma _2}}}{{1 + upsilon }},kappa } ight) - }{;;;;2{w_{ m{p}}}left( {dfrac{{3sqrt 3 {gamma _2}}}{{4(1 + upsilon )}},kappa } ight) - dfrac{{sqrt 3 {gamma _2}}}{{4(1 + upsilon )}}left[ {gleft( {dfrac{{3sqrt 3 {gamma _2}}}{{4(1 + upsilon )}},kappa } ight) - } ight.}{left. {;;;;2{g_{ m{f}}}left( {dfrac{{3sqrt 3 {gamma _2}}}{{4(1 + upsilon )}},kappa } ight)} ight]}end{array}}{begin{array}{*{20}{l}}{{Y_{ m{ - }}} = dfrac{{ m{1}}}{2}{w_{ m{u}}}left( {dfrac{{1.5{gamma _2}}}{{1 + upsilon }},kappa } ight) - dfrac{{ m{5}}}{2}{w_{ m{u}}}left( { - dfrac{{1.5{gamma _2}}}{{1 + upsilon }},kappa } ight) + }{;;;;2{w_{ m{p}}}left( {dfrac{{3sqrt 3 {gamma _2}}}{{4(1 + upsilon )}},kappa } ight) - dfrac{{sqrt 3 {gamma _2}}}{{4(1 + upsilon )}}left[ {gleft( {dfrac{{3sqrt 3 {gamma _2}}}{{4(1 + upsilon )}},kappa } ight) - } ight.}{left. {;;;;2{g_{ m{f}}}left( {dfrac{{3sqrt 3 {gamma _2}}}{{4(1 + upsilon )}},kappa } ight)} ight]}end{array}}end{array}} ight}$$

(19)

式中$upsilon $表示泊松比, 等于侧向应变${h_{
m{l}}}$比上受力方向应变$h$的相反数

$$upsilon { m{ = - }}frac{{{h_{ m{l}}}}}{h}$$

(20)

当材料变形前后体积不变, ${h_l}{
m{ = - 0}}{
m{.5}};h$, 从式(20)可以得到泊松比$upsilon $=0.5.

从式(17)出发, 可以得到单轴实验下的应力应变关系为方程(9), 平面应变下的应力?应变关系为方程(11), 而等双轴下的应力?应变关系^[38]为

$${tau _{ m{e}}} = - frac{1}{{2upsilon }}fleft( { - frac{1}{upsilon }h,kappa } ight)$$

(21)

2.
新的形函数

本节首先通过应变?应力图中面积所代表的能量关系推导出耗散$kappa $的显式表达; 其次, 随着耗散的增加, 分析不可恢复变形大小的演变规律以及各向异性引入对应力?应变关系的影响, 分别通过${h_P}(kappa )$和$ varphi (kappa )$来表示不可恢复变形大小以及各向异性对应力?应变关系的影响程度; 最后, 利用耗散$kappa $, 不可恢复变形大小${h_P}(kappa )$, 以及各向异性影响项$ varphi (kappa )$, 结合球坐标, 构造新的形函数表达形式.

2.1
耗散表达

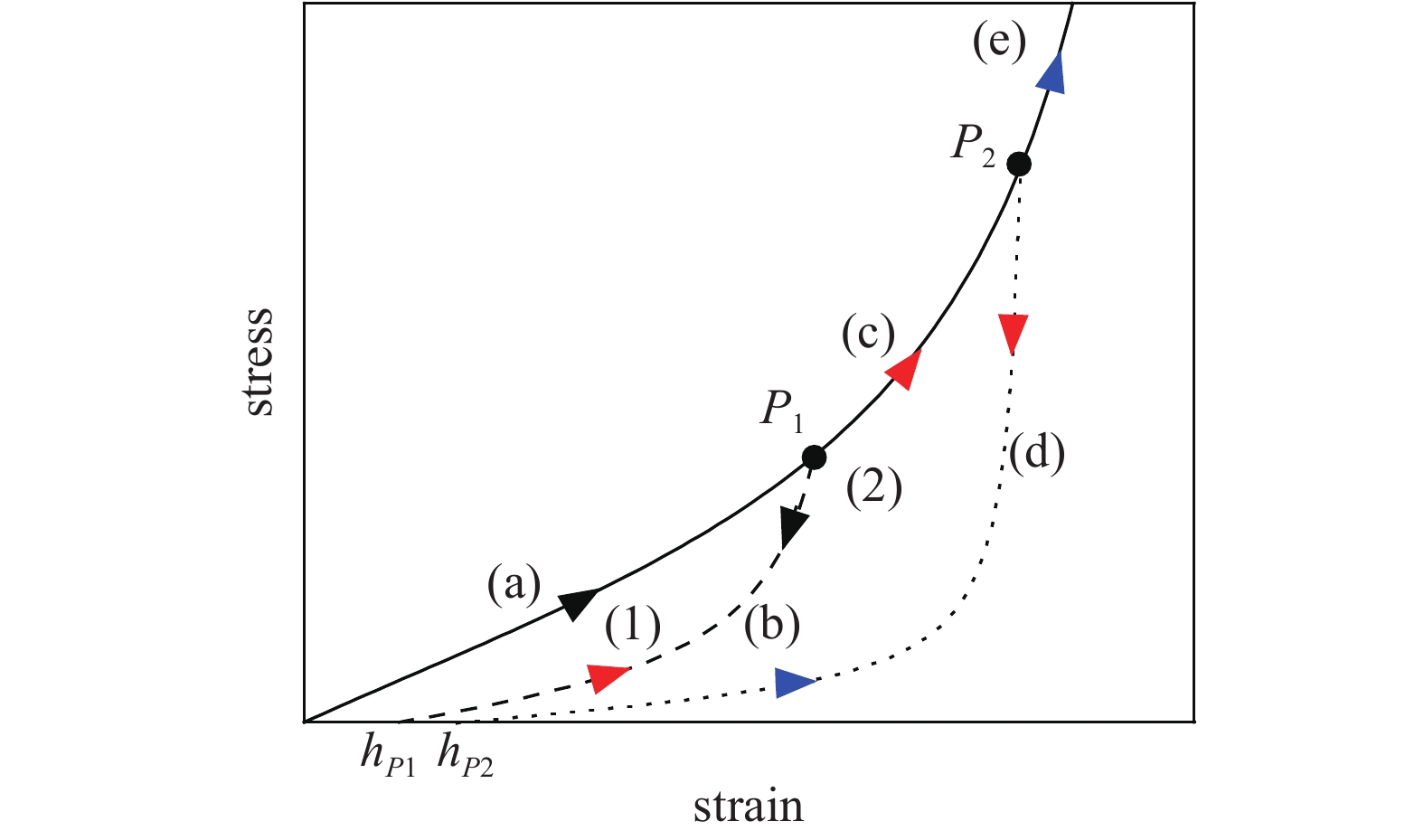
如图1所示, 橡胶材料在初始加载下, 应力?应变沿着(a)前进, 在达到P₁点后开始卸载, 卸载路径沿着(b)运行, 最后产生不可恢复变形h_P1, 完成一个循环, 产生的能量耗散可以用图1中(1)的面积来表示; 再次加载后, 初始卸载应力点以下的部分发生明显的应力软化, 而之后这样的软化就不是很明显^[1-3]. 因此, 第2次加载路径应该是从(b)变成(c), 到达P₂点后再次卸载, 卸载路径沿着(d)走(此时软化现象更加严重, 卸载曲线和初始加载曲线之间的偏离更加严重), 最后产生不可恢复变形h_P2, 产生的能量耗散可以用图中(2)的面积来表示; 第3次循环的路径可以通过类似的规律推导.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-060-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
Mullins效应产生不可恢复变形示意图



Figure
1.
Schematic of Mullins effects with permanent set



下载:
全尺寸图片
幻灯片


通过大量应力软化的实验数据分析, 循环加载?卸载作用下能量耗散的变化规律有以下3点: (1)随着循环加载?卸载的进行, 能量耗散逐渐累积; (2)从单个加载?卸载循环来看, 能量耗散最小的情况是加载和卸载路径重合(不产生应力软化), $kappa {
m{ = 0}}$; (3)从单个加载?卸载循环来看, 能量损耗最大的情况是卸载曲线极度弯曲(应力软化最大化), $kappa = {kappa _{
m{m}}}$. 其中

$${kappa _{ m{m}}} = intlimits_0^{{h_{ m{m}}}} {bar f} (h){ m{d}}h$$

(22)

式中, $bar f(h)$表示单个循环中加载阶段的应力?应变曲线, ${h_{
m{m}}}$表示卸载点应变.

滞回圈面积大小无法超过${kappa _{
m{m}}}$, 因此

$${ m{0}} leqslant kappa { m{/}}{kappa _{ m{m}}} leqslant { m{1}}$$

(23)

耗散随着卸载应力${tau _{
m{m}}}$的变化规律可以通过双曲正切函数得到

$$kappa = frac{{{kappa _{ m{m}}}}}{2}Big{tanh [{alpha _1}({tau _{ m{m}}} - {tau _{ m{r}}})]{ m{ + 1}}Big}$$

(24)

式中, ${tau _{
m{r}}}$和${alpha _1}$是可调参数. 当${tau _{
m{m}}} = {tau _{
m{r}}}$时, $kappa = dfrac{{{kappa _m}}}{2}$; 参数$alpha $表示$kappa $随着${tau _{
m{m}}}$变化的速度.

2.2
不可恢复变形和各向异性

耗散的引入会产生不可恢复变形以及各向异性特征. 本节讨论不可恢复变形以及各向异性特征随着耗散累积的变化规律, 分别通过${h_P}(kappa )$和$ phi (kappa )$来表征不可恢复变形大小和各向异性对应力?应变关系的影响程度.

2.2.1
不可恢复变形

在保持最大应变的情况下, 不可恢复变形的变化规律如下^[27]: (1)不可恢复变形量随着循环的进行会逐渐变大; (2)第一个循环前后产生的变形最大, 后面依次减少; (3)在循环次数足够多的情况下, 不可恢复变形不再变化, 达到一个稳定值. 假设有n次循环, h_Pi表示每一次产生的不可恢复变形, i = 1, 2, ···, n. 则有

$${h_{{{Pn}}}} > {h_{{{P}}(n - 1)}} > cdots > {h_{{{P2}}}} > {h_{{{P1}}}}qquadqquad;;;;;;;;;;;;;;;;;;$$

(25)

$${h_{{{P1}}}} > ({h_{{{P2}}}} - {h_{{{P1}}}}) > ({h_{{{P3}}}} - {h_{{{P2}}}}) > cdots > ({h_{{{Pn}}}} - {h_{{{P(n - 1)}}}})$$

(26)

$$mathop {lim }limits_{{{n}} to infty } {h_{{{Pn}}}} = {h_{{{P(n - 1)}}}} = {h_{{P}}}qquadqquad;;;;;;;;;;;;;;;;;;;;;;;qquad$$

(27)

耗散的引入导致了不可恢复变形的产生. 因此, 假设

$${h_{{P}}} = {h_{{P}}}(kappa ) = {{{p}}_1}tan({{{p}}_2}kappa )$$

(28)

${h_{{P}}}$随着耗散的增大而增大, 直到趋于一个稳定的数值. ${p_1}$和${p_2}$是可调参数.

2.2.2
各向异性

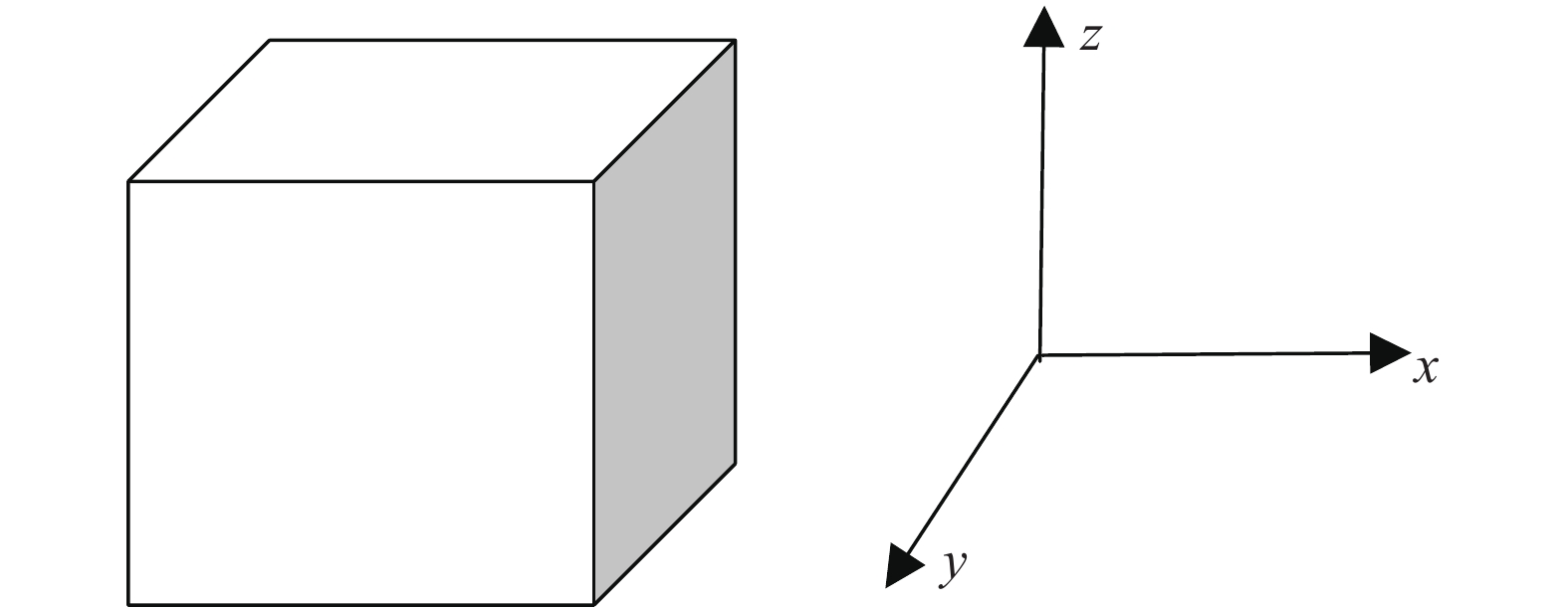
如图2所示, 假设六面体橡胶块初始情况下为各向同性. 从任意方向加载, 其性质都是一样的. 一旦在某一方向(比如x轴方向)加载然后卸载, Mullins效应的产生将导致材料引入了各向异性特征, 此时, 再沿着初始方向(x轴方向)加载?卸载的应力?应变关系将和沿着其他方向(比如y轴或者z轴)的发生明显的差异.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-060-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
六面体橡胶块三维受力示意图



Figure
2.
Schematic of hexahedral rubber block with three-dimensional force



下载:
全尺寸图片
幻灯片


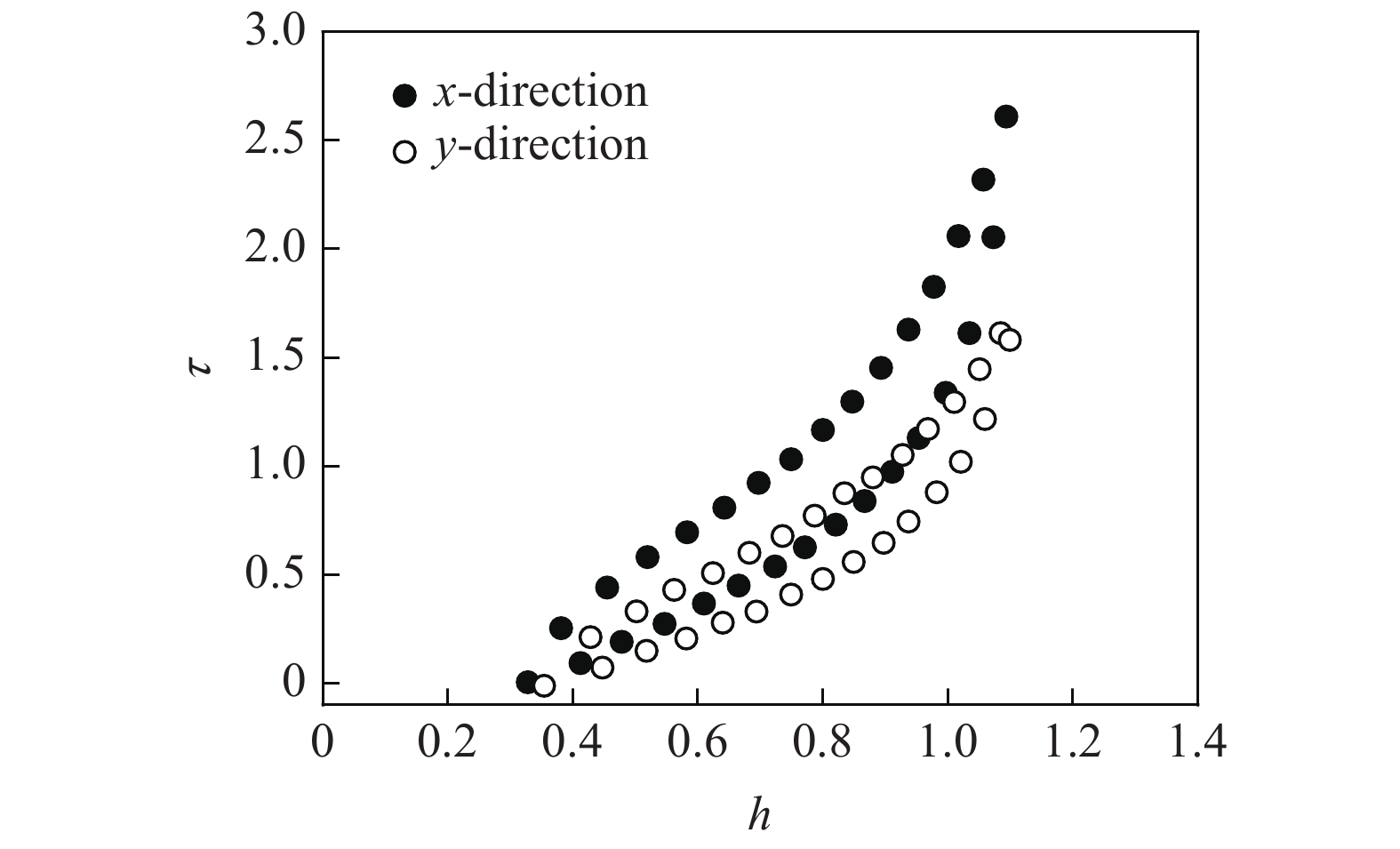
为了证明并量化Mullins效应引入的各向异性性质. Diani等^[26]做了相关实验. 首先, 将A和B两块相同的橡胶六面体同时在x轴方向进行同样的拉伸加载, 然后卸载. 此时两块试样均发生了Mullins效应且都产生了相同的不可恢复变形. 接下来, 对A进行x轴方向的拉伸加载和卸载, 对B进行y轴方向(垂直于初始方向)的拉伸加载和卸载. 将两块试样的第2个循环的应力?应变曲线(Mullins效应已经饱和)进行比较, 结果如图3所示, 其中, 应变类型采用对数应变. 从图3可以得到二个结论: (1) A和B两块试样的应力?应变曲线不重合且有明显的差异, 说明Mullins效应确实引入了各向异性特征; (2) A的曲线明显高于B曲线(同样应变情况下, A的应力更大), 说明B的应力软化更加严重. 假设在x轴上的应力?应变形函数为$f(h,kappa )$, 那么与其垂直方向加载?卸载的形函数为$tilde f(h,kappa ) = varphi (kappa )f(h,kappa )$, 其中$varphi (kappa )$表征了各向异性程度, 其满足以下条件

$$left. {begin{array}{*{20}{c}} {mathop {{ m{lim}}}limits_{kappa to 0} varphi (kappa ){ m{ = 1}}} {mathop {{ m{lim}}}limits_{kappa to infty } varphi (kappa ){ m{ = 0}}} end{array}} ight}$$

(29)

式(29)表示如果没有发生耗散($ kappa =0$), 那么垂直方向的应力?应变关系和初始方向一致, 材料没有发生各向异性特征; 如果耗散很大, 那么材料发生极度的各向异性, 垂直方向几乎没有抵抗变形的能力. 基于以上条件, 可以假设$ varphi (kappa )$的形式为

$$varphi (kappa ){ m{ = - }}frac{1}{2}{ m{tanh[}}{alpha _2}(kappa - {kappa _{ m{r}}}){ m{] + }}frac{1}{2}$$

(30)

式中, ${alpha _2}$和${kappa _{
m{r}}}$是可调参数. 在初始方向和垂直方向中间的形函数, 其各向异性特征项的值理论上介于0 ~ 1之间.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-060-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
Diani等^[26]证明引入各向异性的实验数据



Figure
3.
An experimental evidence of induced anisotropy by Diani et al.^[26]



下载:
全尺寸图片
幻灯片

2.3
统一形函数构造

首先给出各向同性的形函数形式; 然后利用球坐标转换和2.2.2节中给定的各向异性项$ varphi (kappa )$进行扩展, 得到能模拟各向异性特征的形函数; 最后, 在单轴情况下, 利用有理插值的方法给定带有不可恢复变形${h_P}(kappa )$的形函数表达. 将结果代入到前面的各向异性形函数, 从而构造统一的形函数形式.

2.3.1
各向同性的形函数

形函数分为加载曲线和卸载曲线, 如图1所示. 初始加载曲线沿着路径(a)前进, P₁点卸载以后发生应力软化(耗散的产生). 重新加载直到上一次卸载应力之前的部分将沿着上一次卸载曲线路径(b)行走. 一旦应力超过P₁点应力, 应力软化降低, 应力?应变曲线沿着(c)前进. 再次在P₂点卸载后重新加载, 将沿着从(d)到(e)的方向前进; 卸载曲线的变化和耗散紧密相关, 耗散越大, 软化越严重, 和同一滞回圈内的加载曲线偏离就越大. 满足以上条件的形函数构造形式如下

$$begin{split} widehat{f}(h,kappa )=&frac{1}{4}(1+chi )(1+pi )overline{f}(h)+ &[(1+chi )(1-{pi})+2(1-chi )]tilde{f}(h,kappa )end{split}$$

(31)

其中

$$left. {begin{array}{*{20}{l}} {tilde f(h,0) = bar f(h)} {pi = tanh [{alpha _3}(tau - {tau _{ m{m}}})]} {chi = dot h/left| {dot h} ight|} end{array}} ight}$$

(32)

式中${tau _{
m{m}}}$表示上一次卸载应力, ${alpha _3}$是可调参数, $dot h$表示应变率. 参数$chi $和$pi$具有如下性质

$$chi = left{ {begin{array}{*{20}{c}} {{ m{1}},{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} { m{loading}}} {{ m{ - 1}},{kern 1pt} {kern 1pt} {kern 1pt} { m{unloading}}} end{array}} ight.$$

(33)

$$pi = left{ {begin{array}{*{20}{c}} {{ m{1}},{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} tau > {tau _{ m{m}}}} {{ m{ - 1}},{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} tau < {tau _{ m{m}}}} end{array}} ight.$$

(34)

下面分析加载曲线和卸载曲线. 初次加载时, 将$kappa = 0$, $chi = 1$, $pi = 1$代入到方程(31), 得到加载曲线方程为

$$hat f(h,kappa ) = bar f(h)$$

(35)

有了加载历史以后, $chi = 1$不变, $kappa {
m{ > }}0$, 加载曲线方程变为

$$hat f(h,kappa ) = left{ {begin{array}{*{20}{c}} {tilde f(h,kappa ),{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} tau < {tau _{ m{m}}}} {bar f(h),{kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} {kern 1pt} tau > {tau _{ m{m}}}} end{array}} ight.$$

(36)

然后分析卸载曲线, 此时$chi {
m{ = - }}1$, $kappa {
m{ > }}0$, 得到曲线方程为

$$hat f(h,kappa ) = tilde f(h,kappa ){kern 1pt} $$

(37)

2.3.2
各向异性的形函数

方程(31)得到的各向同性形函数还需要进一步改进, 使其能够产生各向异性性质. 改进形式为

$$f(h,kappa ) = hat f(h,kappa ){kern 1pt} ({cos ^{ m{2}}}phi { m{ + }}{kern 1pt} varphi (kappa ){kern 1pt} { m{si}}{{ m{n}}^{ m{2}}}phi { m{si}}{{ m{n}}^{ m{2}}}theta { m{ + }}{kern 1pt} varphi '(kappa ){ m{si}}{{ m{n}}^{ m{2}}}phi { m{co}}{{ m{s}}^{ m{2}}}theta )$$

(38)

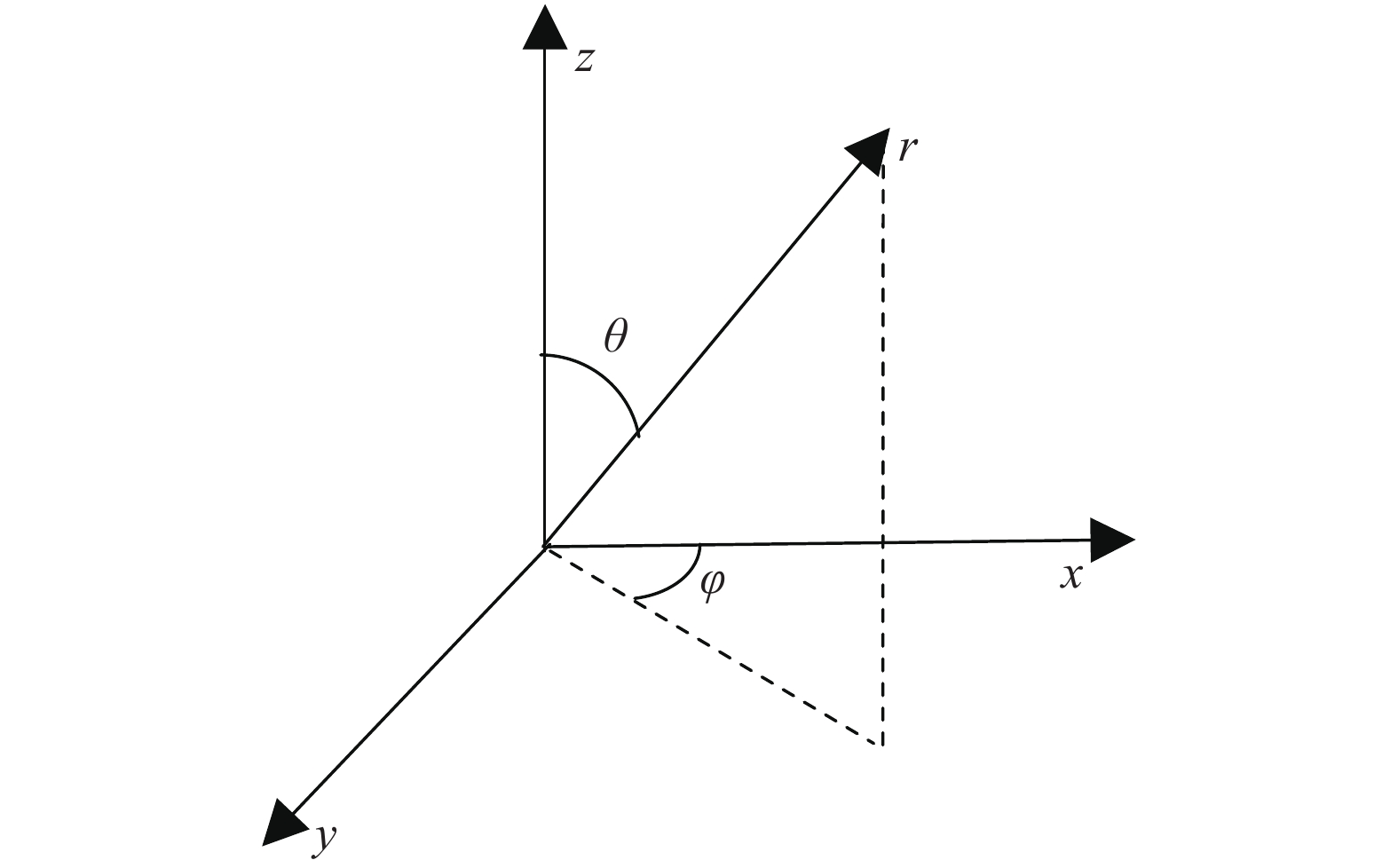
如图4所示, r表示受力方向, $phi $表示受力方向在x轴和y轴组成的平面投影和x轴的夹角, $theta $表示受力方向和z轴的夹角. 假设初始受力方向为x轴, $varphi (kappa )$表示与其垂直的y轴方向各向异性程度, 而$varphi '(kappa )$表示与其垂直的z轴方向各向异性程度, 他们均可用方程(30)的形式给出.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-060-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
任意方向受力的球坐标示意图



Figure
4.
Schematic of loading in arbitrary direction by Spherical coordinate system



下载:
全尺寸图片
幻灯片


在初始x轴方向加载?卸载的基础上, 如果继续在同样的方向进行加载, 那么r方向和x轴重合, 此时$phi = {{
m{0}}^ circ }$, $theta {
m{ = 9}}{{
m{0}}^ circ }$, 得到

$$f(h,kappa ) = hat f(h,kappa )$$

(39)

如果再次加载方向为y轴, 则$phi {
m{ = 9}}{{
m{0}}^ circ }$, $theta {
m{ = 9}}{{
m{0}}^ circ }$, 得到

$$f(h,kappa ) = hat f(h,kappa ){kern 1pt} varphi (kappa )$$

(40)

如果再次加载方向为z轴, 则$phi {
m{ = 9}}{{
m{0}}^ circ }$, $theta = {{
m{0}}^ circ }$, 得到

$$f(h,kappa ) = hat f(h,kappa )varphi '(kappa )$$

(41)

2.3.3
两个基准实验下的单轴形函数

本节需要给出方程(31)中函数$bar f(kappa )$和$tilde f(h{
m{,}}kappa )$具体形式, 然后代入到方程(38), 得到统一的形函数表达. $bar f(kappa )$和$tilde f(h{
m{,}}kappa )$表示的是单轴情况下基准实验形函数, 可以通过有理插值的方法给出. 对于单轴拉伸?压缩变形模式下的形函数给定为

$$bar f(h) = {bar f_{ m{u}}}(h) = {E_0}hleft[ {dfrac{{{alpha _0}}}{{left( {1 - dfrac{h}{{{h_{{ m{10}}}}}}} ight)left( {1 + dfrac{h}{{{h_{{ m{20}}}}}}} ight)}} + 1 - {alpha _0}} ight]$$

(42)

$$begin{split} tilde f(h,kappa ) =& {tilde f_{ m{u}}}(h,kappa ) = E(kappa )(h - {h_{ m{P}}}(kappa ))&left{ {dfrac{{alpha (kappa )}}{{left[ {1 - dfrac{{h - {h_{ m{P}}}(kappa )}}{{{h_{ m{1}}}(kappa )}}} ight]left[ {1 + dfrac{{h - {h_{ m{P}}}(kappa )}}{{{h_{ m{2}}}(kappa )}}} ight]}} + 1 - alpha (kappa )} ight}end{split}$$

(43)

关于以上两个函数具备的性质在前面的研究工作^[38]中已经阐明. 其中方程(43)中的$E(kappa )$, ${h_1}(kappa )$, ${h_2}(kappa )$和$alpha (kappa )$是依赖耗散的函数, 当耗散$kappa {
m{ = 0}}$, 他们的初始值即为方程(42)中的${E_0}$, ${h_{10}}$, ${h_{20}}$和${alpha _0}$. 和前面研究不一样的地方在于本文的方程中加入了依赖耗散的不可恢复变形${h_{{P}}}(kappa )$; 等双轴实验的形函数结合方程(21)和(38)得到平面应变情况下的形函数形式, 其加载方向为

$$left. begin{array}{l}f(h) = bar g(h) = dfrac{2}{3}{E_0}hleft( {dfrac{{{alpha _{{ m{q0}}}}}}{{ {1 - dfrac{{{h^2}}}{{h_{{ m{q0}}}^2}}} }} + 1 - {alpha _{{ m{q0}}}}} ight)tilde f(h,kappa ) = tilde g(h,kappa ) = dfrac{2}{3}E(kappa )[h - {h_P}(kappa )]cdot qquadleft{ {dfrac{{{alpha _{ m{q}}}(kappa )}}{{ {1 - dfrac{{{{[h - {h_P}(kappa )]}^2}}}{{h_{ m{q}}^2(kappa )}}} }} + 1 - {alpha _{ m{q}}}(kappa )} ight}end{array} ight}$$

(44)

固定方向为

$$left. {begin{array}{*{20}{c}}{bar f(h) = {{bar g}_{ m{f}}}(h) = dfrac{{ m{1}}}{3}{E_0}hleft( {dfrac{{{alpha _{{ m{qf0}}}}}}{{ {1 - dfrac{{{h^2}}}{{h_{{ m{q}}0}^2}}} }} + 1 - {alpha _{{ m{qf0}}}}} ight)}tilde f(h,kappa ) = {{tilde g}_{ m{f}}}(h,kappa ) = dfrac{{ m{1}}}{3}E(kappa )[h - {h_P}(kappa )]cdot qquadleft{ {dfrac{{{alpha _{{ m{qf}}}}(kappa )}}{{{1 - dfrac{{{{[h - {h_P}(kappa )]}^2}}}{{h_{ m{q}}^2(kappa )}}} }} + 1 - {alpha _{{ m{qf}}}}(kappa )} ight}end{array}} ight}$$

(45)

式中${h_{
m{q}}}(kappa )$, ${alpha _{
m{q}}}(kappa )$和${alpha _{
m{qf}}}(kappa )$是依赖耗散$kappa $的函数, 他们的初始值分别为${h_{{
m{q0}}}}$, ${alpha _{{
m{q0}}}}$和${alpha _{{
m{qf0}}}}$.

3.
数值模拟

第2节构造的形函数代入到第1节的本构方程中, 能够自动得到对应变形模式的应力?应变关系. 3个基准实验和Mullins效应产生的理想滞回圈数据都能精确匹配^[38]. 本文重新优化了形函数, 加入了考虑不可恢复变形和各向异性的项, 本章给出模型结果和经典实验数据的对比.

3.1
不可恢复变形实验模拟

单轴情况下对数应变$h = ln lambda $, 代入到方程(42)和(43), 再结合方程(31)和(38), 即可得到单轴拉伸?压缩情况下的应力?应变形函数.

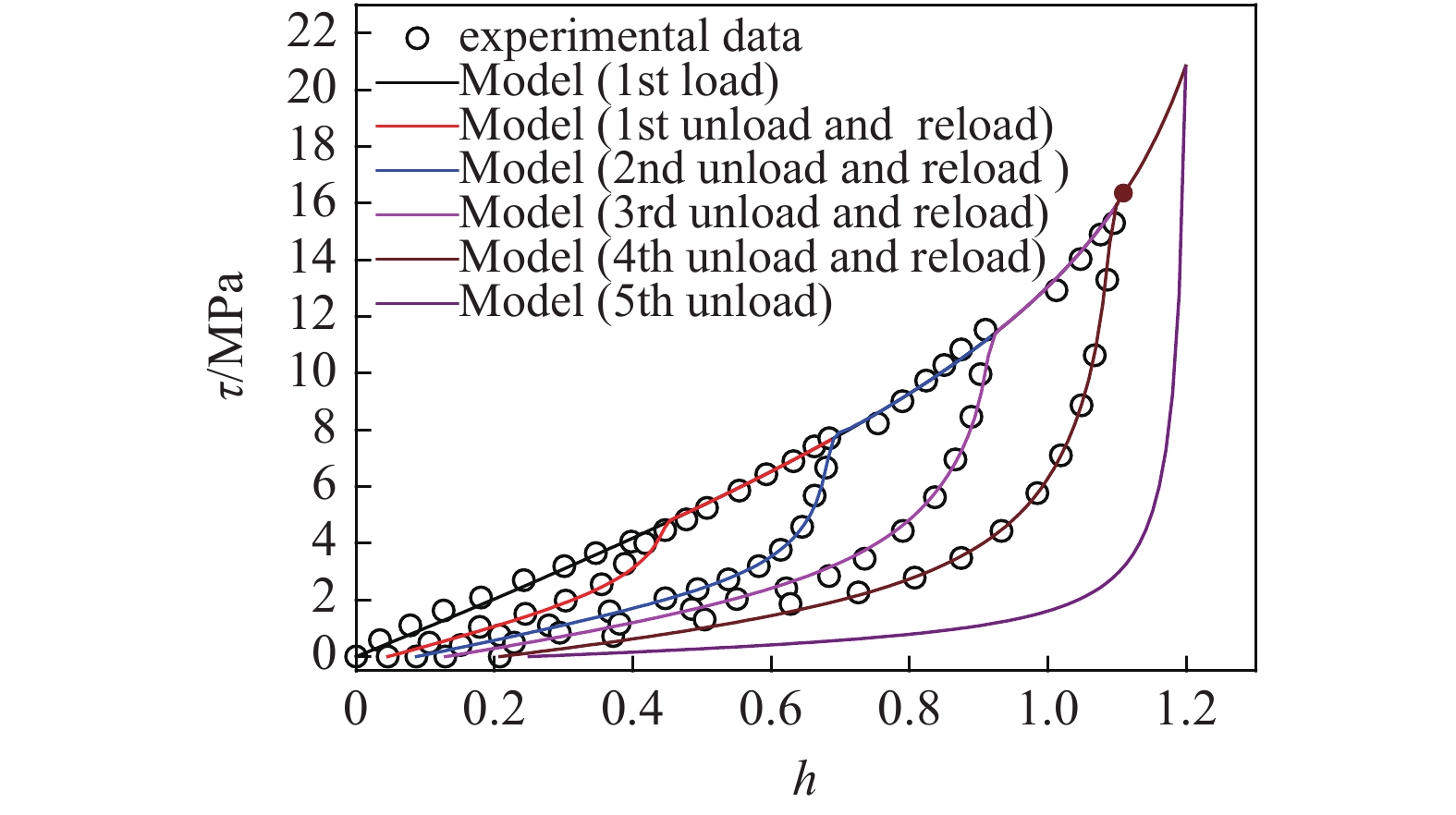
Diani等^[26]做了单轴拉伸加载?卸载循环实验. 分别保持伸长比$lambda $为1.5, 2, 2.5和3不变, 进行10次加载?卸载, 产生了相应的4个稳定的不可恢复变形.

为了得到模型结果, 给出方程(43)中的$E(kappa )$ (MPa), ${h_1}(kappa )$, ${h_2}(kappa )$和$alpha (kappa )$的具体表达为

$$begin{split} E(kappa ) = { m{9}}exp ({ m{ - 0}}{ m{.5}}kappa ) + 1 qquadqquadqquadqquadqquadqquadqquadqquadqquadqquad[-10pt] end{split}$$

(46)

$$begin{split} {h_1}(kappa ) =& {{ m{exp}}( - 8kappa ) + 0.25 + 0.45{tanh [0.5(kappa - 1.6)]{ m{ + }}1}}cdot {kern 1pt} &[ - 0.06tanh (10kappa - 35) + 0.9] [-10pt]end{split} ;;;;;$$

(47)

$$begin{split} {h_2}(kappa ){ m{ = 10}}qquadqquadqquadqquadqquadqquadqquadqquadqquadquad[-10pt]end{split}$$

(48)

$$alpha (kappa ) = { m{0}}{ m{.1 + 0}}{ m{.06}}exp ( - 10kappa ) + 0.13{{ m{tanh}}[1.8(kappa - 2.6)] + 1}$$

(49)

通过方程(46) ~ 式(49)得到, 当$kappa {
m{ = 0}}$时初始值(方程(42)中的参数)分别为${E_0}{
m{ = 10;MPa}}$, ${h_{10}}{
m{ = 1}}{
m{.4}}$, ${h_{20}}{
m{ = }} $$ 10$和${alpha _0}{
m{ = 0}}{
m{.16}}$.

方程(28)中, 取${p_1} = 0.25$, ${p_2} = 0.27$. 方程(24)中控制耗散变化规律的两个参数${tau _{
m{r}}}$和${alpha _1}$分别给定为10.15 MPa和0.056. 实验中的4次卸载应力分别为4.49 MPa, 7.68 MPa, 11.23 MPa和15.98 MPa. 再根据方程(42)确定${kappa _{
m{m}}}$的大小分别为1.01, 2.51, 4.68和7.05, 由此可以确定耗散功大小. 将耗散代入到方程(46) ~ 式(49)确定每一次循环参数值, 方程(32)中的${alpha _3} = 100$. 最后根据方程(31)计算每一次循环的加载曲线和卸载曲线. 与实验结果的对比如图5所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-060-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
模型结果和实验结果^[26]对比图. 横坐标表示对数应变, 纵坐标表示基尔霍夫应力



Figure
5.
Comparison between model result and the experimental data^[26]. “x” axis represents the Hencky strain, and “y” axis represents the Kirchhoff stress



下载:
全尺寸图片
幻灯片


实线表示模型模拟的结果, 其中黑线表示第1次加载路径, 红色表示第1次卸载然后再次加载的路径, 蓝色表示第2次卸载然后再次加载的路径, 洋红色表示第3次卸载然后再次加载的路径, 褐色表示第4次卸载然后再次加载的路径, 紫色表示第5次卸载然后再次加载的路径. 空心圆点表示实验数据. 从图中可以看出模型可以精确模拟和匹配前四次加载?卸载的实验数据, 而对于第5次卸载(假设卸载应力为21.08 MPa, 塑性功为9.17)的曲线, 能够进行合理的预测.

3.2
引入各向异性实验模拟

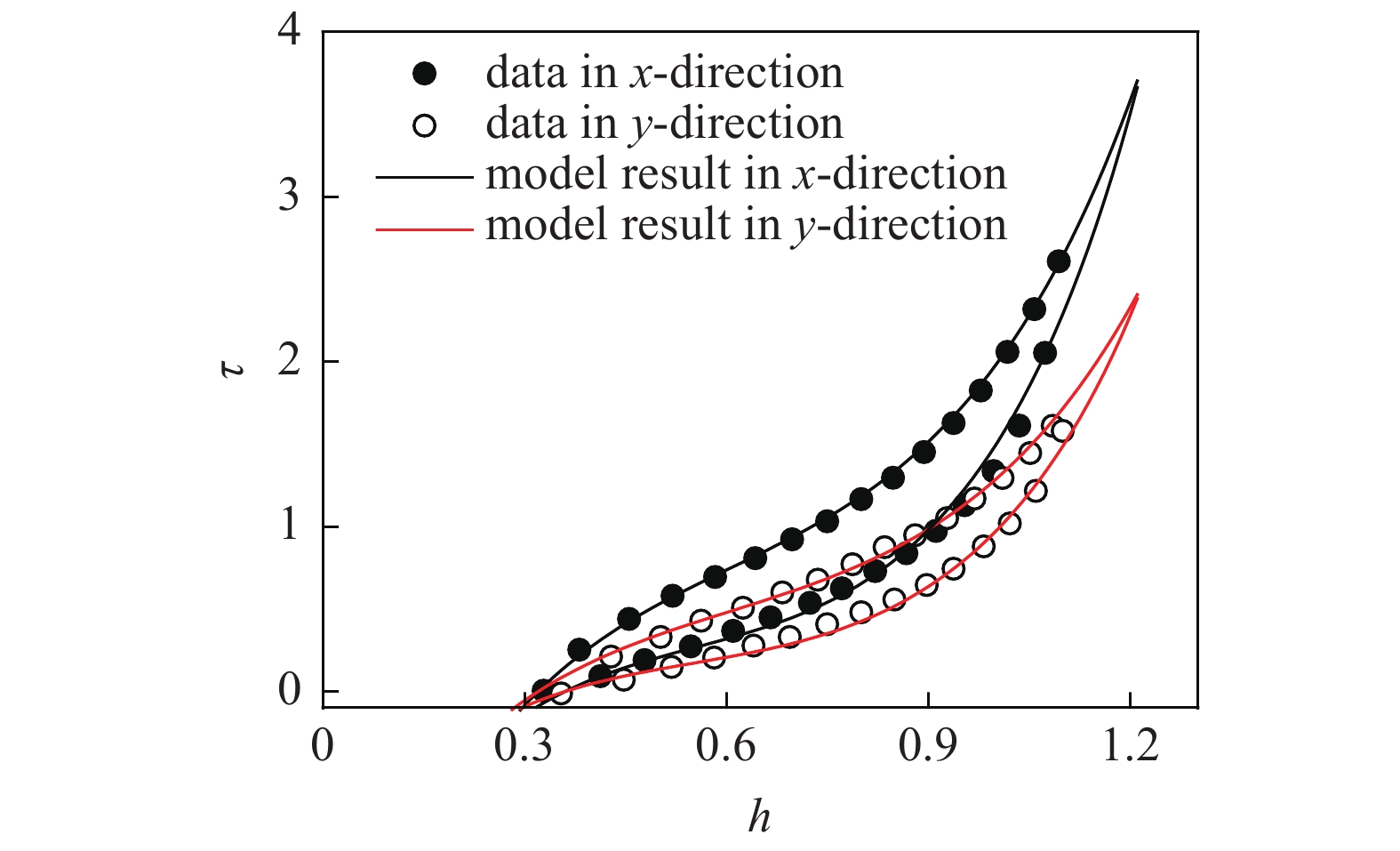
为了证明Mullins效应会引入各向异性特征, Diani等^[26]做了相关实验, 结果如图3所示. 假设方程(38)中的$varphi left( kappa
ight)$和$varphi 'left( kappa
ight)$的形式一致, 都通过方程(30)来确定, 其中参数${alpha _2} = 0.{
m{52}}$, ${kappa _{
m{r}}}{
m{ = 3}}{
m{.11}}$. 初次加载到$lambda {
m{ = 2}}$, 对数应变为$ln lambda {
m{ = 0}}{
m{.6931}}$, 通过前面的方法可得耗散为2.51. 代入到方程(30)得到$varphi left( kappa
ight) = 0.{
m{6}}5$, $varphi 'left( kappa
ight) = 0.{
m{6}}5$. 假设初始加载方向为x轴, 后面再次加载分别在x轴和y轴, 通过方程(38)可以得到模型结果, 和实验结果的对比如图6所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-060-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
Diani等^[26]的实验数据和模型结果对比



Figure
6.
Comparison between experimental data of Diani et al.^[26] and model result



下载:
全尺寸图片
幻灯片


黑色圆点和空心圆点分别表示x方向和y方向的实验数据, 黑色实线和红色实线分别表示x方向和y方向的模型结果. 从图6可以看出, 模型结果和实验结果可以精确匹配.

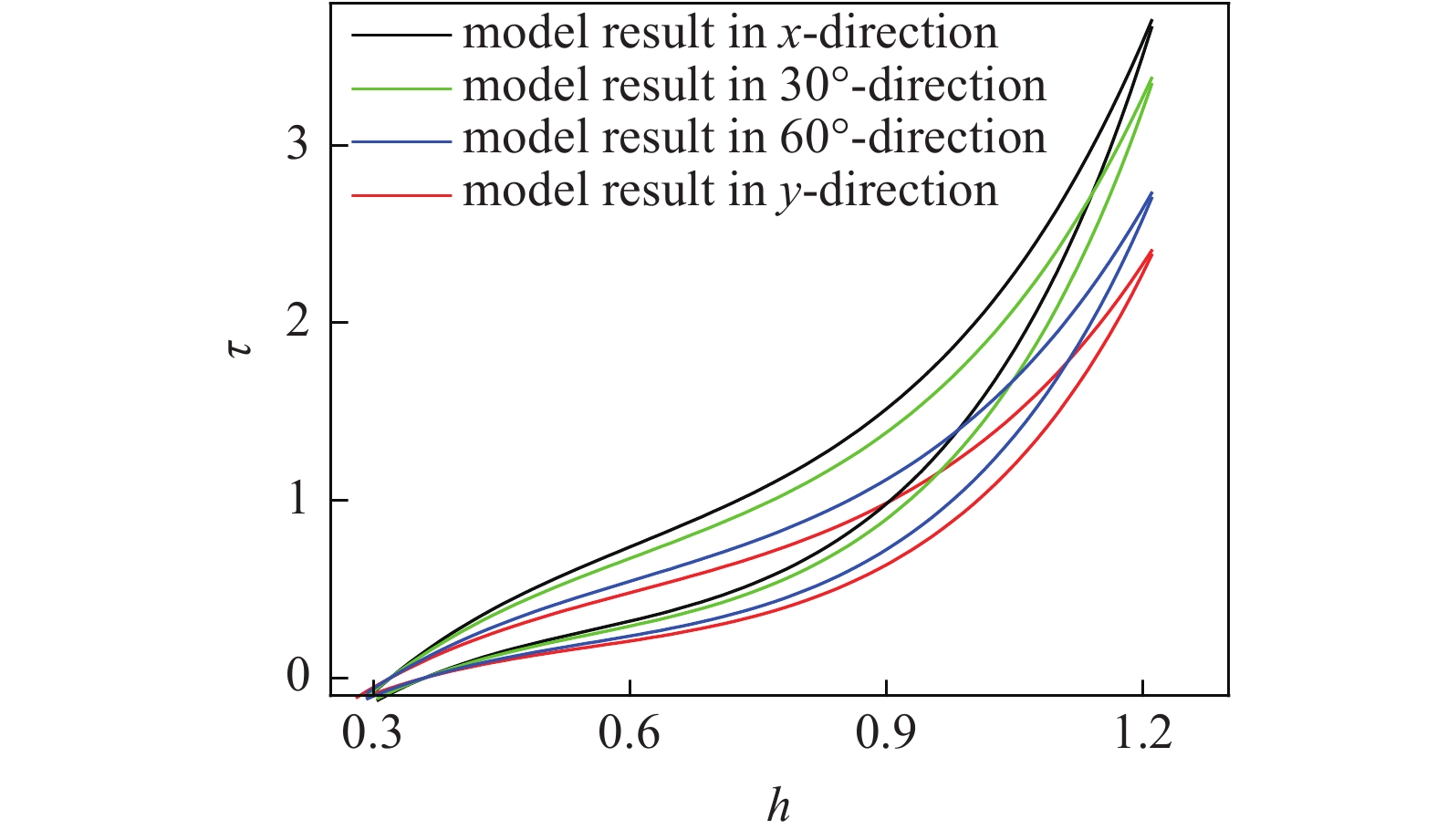
除了匹配实验结果, 模型还能预测其他方向受力的应力?应变滞回圈关系. 在$varphi left( kappa
ight)$和$varphi 'left( kappa
ight)$形式一致的前提下, 方程(38)转化为

$$f(h,kappa ) = hat f(h,kappa ){kern 1pt} [{cos ^{ m{2}}}phi { m{ + }}{kern 1pt} varphi (kappa ){kern 1pt} { m{si}}{{ m{n}}^{ m{2}}}phi ]$$

(51)

在$ phi ={0}^{circ }, {30}^{circ }, {60}^{circ }$和${90}^{circ } $的情况下, 结果对比如图7所示. 其中$ phi ={0}^{circ }$和${90}^{circ } $分别表示x方向和y方向, 图6结果证明这两个方向受力得到的模型结果和实验数据可以精确匹配. 而$ phi ={30}^{circ }$和${60}^{circ } $方向上的应力?应变关系可以通过模型进行合理的预测.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-060-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
不同方向上模型结果对比



Figure
7.
Comparison of model results in different directions



下载:
全尺寸图片
幻灯片

4.
结论

本文在前面研究^[38]的基础上, 改进了形函数的构造形式, 其中加入了依赖耗散的不可恢复变形项和控制各向异性的项. 通过图5 ~ 图7的结果, 模型结果不仅可以精确匹配实验数据, 同时可以对结果做合理的预测. 从而证明新的模型可以模拟Mullins效应产生的不可恢复变形以及由此引入各向异性特征.

本文创新点在于以下3点: (1)改进了加载?卸载形函数的统一模式(方程(31)), 引入了新的量${text{π}} $, 实现了加载曲线从应力显著软化($tau < {tau _{
m{m}}}$)到不显著软化($tau > {tau _{
m{m}}}$)的平滑过度; (2)形函数中引入了不可恢复变形部分${h_{
m{P}}}$, 并给出其具体形式, 且符合2.2节给出的3个条件, 最后能精确匹配和预测实验结果(图5); (3)通过球坐标构建了任意方向受力的形函数改进形式(方程(38)), 并在其中加入了控制各向异性的项$varphi left( kappa
ight)$和$varphi 'left( kappa
ight)$及其具体表达(方程(30)). 引入的各向异性满足2.2.2节中提出的条件且能精确匹配和预测实验结果(图6).