,2), 陈少华,3)A NEW METHOD FOR PREDICTING THE INTERFACIAL MECHANICAL PROPERTY IN PARTICLE-REINFORCED COMPOSITES1)
Guo Xiaolong, Yao Yin,2), Chen Shaohua,3)通讯作者: 2)姚寅, 助理教授, 主要研究方向: 微纳米力学、复合材料力学. E-mail:yaoyin@bit.edu.cn;3)陈少华, 教授, 主要研究方向: 微纳米力学、复合材料力学、仿生结构材料力学、表界面力学. E-mail:shchen@bit.edu.cn
收稿日期:2021-02-22接受日期:2021-03-22网络出版日期:2021-05-19
| 基金资助: |
Received:2021-02-22Accepted:2021-03-22Online:2021-05-19
作者简介 About authors
摘要
界面在颗粒增强复合材料中起到传递载荷的关键作用, 界面性能对复合材料整体力学行为产生重要影响. 然而由于复合材料内部结构较为复杂, 颗粒与基体间的界面强度和界面断裂韧性难以确定, 尤其是法向与切向界面强度的分别预测缺乏有效方法. 本文以氧化锆颗粒增强聚二甲基硅氧烷(PDMS)复合材料为研究对象, 提出一种预测颗粒增强复合材料界面力学性能的新方法. 首先, 实验获得纯PDMS基体材料及单颗粒填充PDMS试样的单轴拉伸应力$\!-\!$应变曲线, 标定出PDMS基体材料的单轴拉伸超弹性本构关系; 其次, 建立与单颗粒填充试样一致的有限元模型, 选择特定的黏结区模型描述界面力学行为, 通过样品不同阶段拉伸力学响应的实验与数值结果对比, 分别给出颗粒与基体界面的法向强度、切向强度及界面断裂韧性; 进一步应用标定的界面力学参数, 开展不同尺寸及不同数目颗粒填充试样的实验与数值结果比较, 验证界面性能预测结果的合理性. 本文提出的界面力学性能预测方法简便、易操作、精度高, 对定量预测颗粒增强复合材料的力学性能具有一定帮助, 亦对定量预测纤维增强复合材料的界面性能具有一定参考意义.
关键词：
Abstract
Interfaces play a key role in the load transfer of particle reinforced composites, and the interface properties have an important impact on the overall mechanical behavior of composites. However, due to the complex internal structure of composites, it is difficult to determine the interfacial strength and fracture toughness, especially for the respective prediction of normal and tangential interfacial strength. In this paper, a new method is proposed to predict the interfacial mechanical properties of particle-reinforced composites based on zirconia particle (ZrO) reinforced polydimethylsiloxane (PDMS) composite materials. Firstly, the uniaxial tensile stress-strain curves of pure PDMS matrix material and single particle filled PDMS sample are obtained, and the uniaxial tensile constitutive relationship of the PDMS matrix material is achieved. Secondly, the finite element model (FEM) consistent with single particle filled sample is established, and a specific cohesive zone model is chosen to describe the mechanical behavior of interface. Comparison of the experimental and numerical results of tensile mechanical response of samples at different stages can yield the normal strength, tangential strength and fracture toughness of the interface, respectively. The achieved interfacial mechanical parameters are further adopted in FEM calculations of samples filled with different sizes and numbers of particles. The rationality of the proposed method of predicting interfacial properties is verified by comparing the corresponding experimental and numerical results. Such a method is simple, easy to operate and has high accuracy, which should be helpful to quantitatively predict the mechanical property of particle reinforced composites, and also has certain reference significance to quantitatively predict the interfacial properties of fiber reinforced composites.
Keywords：
PDF (13948KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
郭晓龙, 姚寅, 陈少华. 一种预测颗粒增强复合材料界面力学性能的新方法1). 力学学报, 2021, 53(5): 1334-1344 DOI:10.6052/0459-1879-21-076
Guo Xiaolong, Yao Yin, Chen Shaohua.
引言
颗粒增强复合材料作为一种典型的复合材料体系, 具有制备工艺简单、可加工性强、近似各向同性等优点, 在航空航天、汽车制造、电子封装、运动器械、医疗器材等领域已经获得了广泛应用[1-2]. 在该类复合材料的制备过程中, 颗粒和基体通过一定物理或化学作用相互连接, 形成所谓的复合材料内部界面. 当复合材料承受载荷作用时, 颗粒和基体之间的载荷传递通过界面得以实现, 界面脱黏亦是导致复合材料损伤的主要微观机制之一[3-6]. 因此, 界面力学性能, 如界面刚度、界面强度、界面断裂韧性等是影响颗粒增强复合材料整体力学行为的重要因素. 大量的研究综合运用界面弹簧模型、界面失效强度准则和能量准则、界面内聚力模型等方法, 将界面力学性能引入颗粒增强复合材料理论和数值模型中, 从而能够更准确地预测复合材料整体力学性能, 揭示界面力学特性对复合材料力学性能的影响机制[7-12].然而, 在定量预测复合材料力学性能的过程中, 基体和增强颗粒的材料性能比较容易获得, 但界面性能仍是颇具挑战性的问题. 已有大量的实验工作测量颗粒增强复合材料的整体力学行为[4,13-18], 或观察界面区域形貌及破坏现象[5,19-23], 但并未给出复合材料的界面性能参数. 由于颗粒增强复合材料内部大量颗粒随机分布, 复合材料的承载变形涉及基体损伤、界面脱黏、颗粒断裂等多种微观机制的耦合作用, 很难从宏观力学行为的实验结果中直接提取出颗粒与基体间的界面力学性能参数[5-6,13-14,18]. 现有理论和数值模型中所采用的界面刚度、界面强度、界面断裂韧性等参量大多基于经验给出[8-11,24], 或者只是定性分析复合材料力学性能, 无法精确定量研究颗粒增强复合材料的力学性能. 界面性能的测量问题已经引起了很多科研者的关注. 王健等[25]应用三氧化二铝(Al$_{2}$O$_{3})$薄片代替Al$_{2}$O$_{3}$颗粒, 通过特殊的剪切试验夹具将压缩载荷转换成Al$_{2}$O$_{3}$薄片与钢基体间界面的剪切载荷, 从而测量界面的剪切强度. Chen等[26]利用黏合剂将镍颗粒和不锈钢基体分别黏贴在拉伸试验机的上下端头, 通过测量颗粒脱出后在基体中残留的孔洞面积, 推算出界面的法向黏附强度. Dariusz等[27]则运用一种电刻蚀的方法制备出含Al$_{2}$O$_{3}$颗粒的铜基复合材料``微线''试样, 然后通过精密的微拉伸测试得到颗粒和基体间的法向界面强度. 此外, 一些****采用实验观测与数值仿真相结合的方法, 确定复合材料界面力学性能, Qu等[8]、Tsui等[28]、Meng等[29]分别建立了碳化硅(SiC)颗粒增强铝基复合材料的单颗粒和双颗粒的代表体元(RVE)有限元模型, 假设界面强度各向同性, 通过复合材料宏观拉伸力学行为的数值结果与实验结果对比得到界面强度. 然而, 以上研究界面力学性能的工作仍存在各自的不足: (1)测量获得的界面法向或剪切强度, 实际为等效的界面耦合强度, 与界面形状及界面受力状态密切相关; (2)有限元常用的代表性体元模型, 已经采用了均匀化假设, 与实验用颗粒增强复合材料试样具有一定差距; (3)实验中, 复合材料内部的界面破坏相对随机, 无法辨别法向或切向的脱黏行为, 及其与复合材料整体力学行为的对应关系; (4)数值计算和实验结果对比中, 普遍假设界面法向强度与切向强度相等[8,28-29], 这一假设与真实界面力学特性并不符合[1,30]; (5)已有工作给出的界面强度预测结果, 未进一步给出系统的验证. 因此, 合理设计测量实验及与实验一致的数值仿真模型, 合理区分界面的法向与切向强度, 定量给出界面性能参数及系统的结果验证等问题, 仍是复合材料界面性能研究的关键问题.
本文以氧化锆颗粒(ZrO$_{2})$增强聚二甲基硅氧烷(PDMS)基复合材料为研究对象, 提出一种预测颗粒增强复合材料界面力学性能的新方法. 首先开展单个颗粒填充PDMS复合材料试样的拉伸力学实验, 测量其单轴拉伸力学性能, 并应用高速摄像方法, 获取颗粒与基体界面脱黏的图像. 然后建立与实验试样一致的单颗粒复合材料有限元模型, 选择具有代表性的黏结区模型描述界面本构, 通过复合材料不同阶段的实验测量结果与数值结果对比, 分别确定界面的法向强度、切向强度及界面断裂韧性. 为了进一步验证结果的合理性及准确性, 通过改变颗粒数目、颗粒尺寸等参数, 设计系列实验试样, 开展实验与有限元结果的比较. 本文可为定量研究实际工程用颗粒增强复合材料力学性能提供简便可行的理论支持, 本文的方法亦可进一步推广到纤维增强复合材料中界面性能的定量测量.
1 单颗粒填充PDMS基复合材料的拉伸实验
首先实验制备单个ZrO$_{2}$球形颗粒填充的PDMS基复合材料试样, 开展单轴拉伸实验, 观察颗粒与基体界面的损伤破坏行为. 该试样结构简单, 便于建立与实验试样一致的数值模型, 亦可以清晰分析和对比实验与数值中颗粒与基体界面的脱黏行为.实验使用的复合材料基体, 由北京莱博源科技有限公司的PDMS(型号为SYLGARD184)与相应固化剂以质量比为10:1制成; 填充颗粒选用湖州雄盛研磨有限公司的实心陶瓷颗粒, 主要成分为ZrO$_{2}$, 直径为2 mm. 将PDMS 基体和固化剂混合均匀后倒入聚四氟乙烯模具(产自深圳骏康塑胶五金加工厂)中, 模具中心放入单个ZrO$_{2}$颗粒, 在80 ${^\circ}$C环境下固化2 h. 制备的试样具有长度20 mm的标距, 宽度和厚度均为5 mm, 如图1(a)和图1(b)所示.
图1
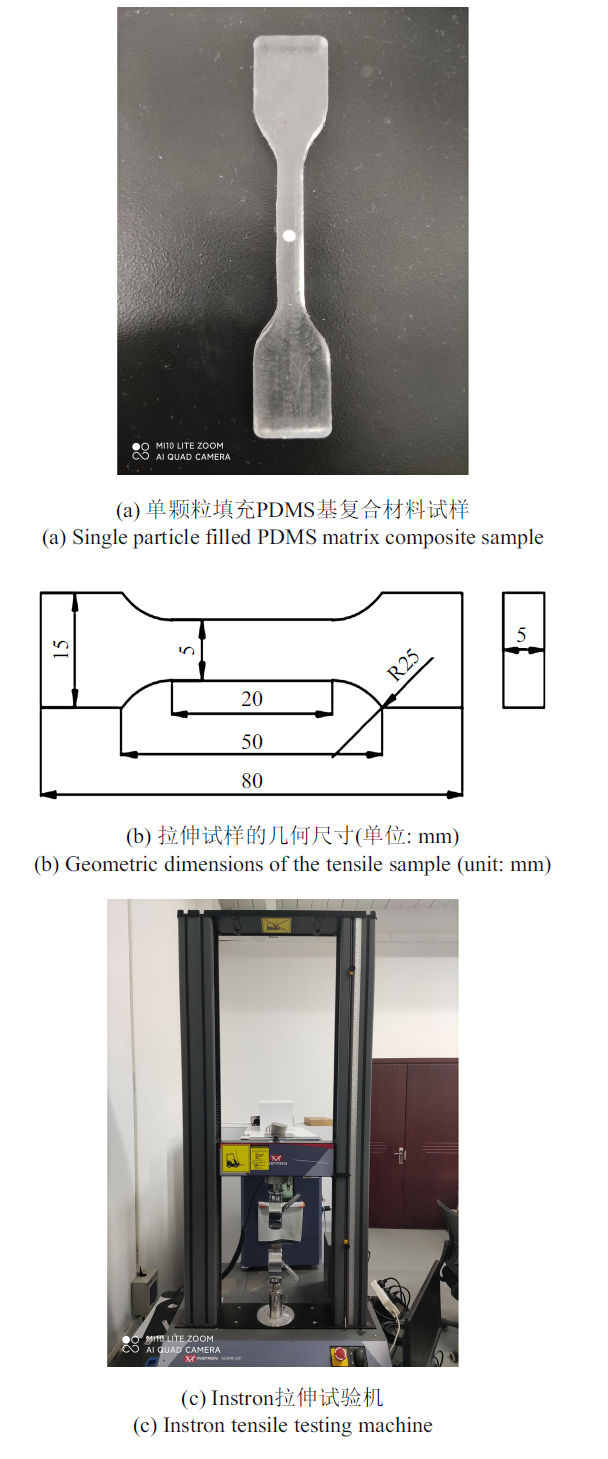新窗口打开|下载原图ZIP|生成PPT图1单颗粒填充PDMS基复合材料的拉伸实验
Fig.1Tensile test of single particle filled PDMS matrix composite
分别在室温下对纯PDMS基体和单颗粒填充复合材料试样进行准静态单向拉伸实验, 拉伸实验仪器为美国Instron公司出产的Instron拉伸试验机(如图1(c)所示), 采用位移加载的方式, 控制加载速率为5 mm/min. 纯基体和单颗粒填充复合材料试样分别测量5次, 最终取平均值. 纯基体及单颗粒填充复合材料的拉伸应力$\!-\!$应变曲线如图2所示.
图2
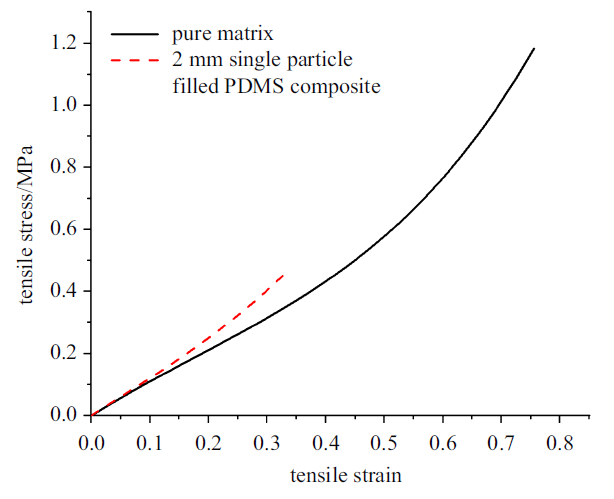新窗口打开|下载原图ZIP|生成PPT图2纯基体和单颗粒增强复合材料的拉伸应力$\!-\!$应变曲线
Fig.2Tensile stress-strain curves of pure matrix and single particle reinforced composites
由图2可以看出, 单颗粒填充PDMS复合材料的弹性模量略高于纯PDMS基体, 与细观力学理论预测一致. 然而, 单颗粒填充PDMS复合材料的极限拉伸强度和断裂应变均小于纯基体的强度和断裂应变, 清晰地揭示了颗粒与基体弱界面对复合材料宏观力学性能的影响. 通过高速摄像机同时观测了复合材料界面及整个试样的破坏过程, 如图3(a)$\sim\!$图3(d) 所示.
图3
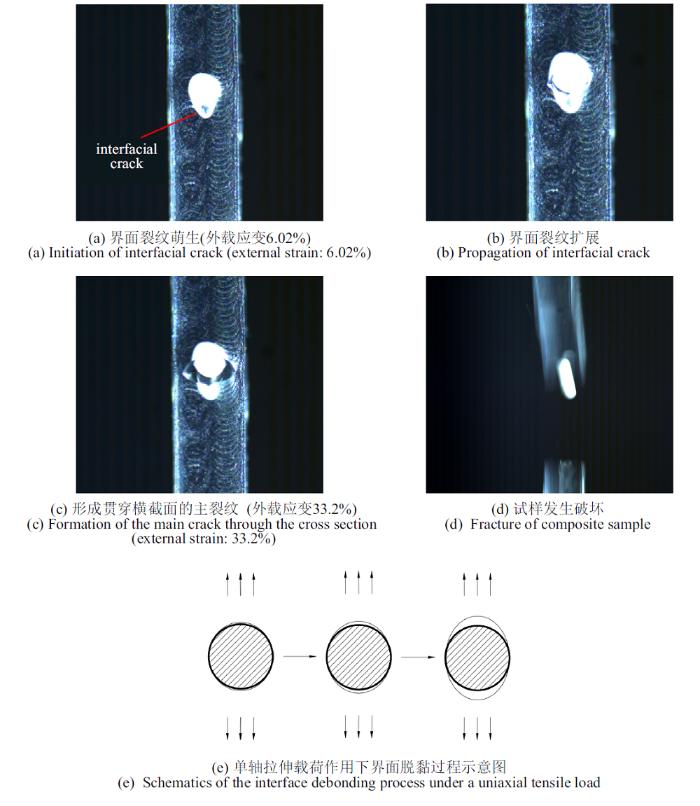新窗口打开|下载原图ZIP|生成PPT图3单颗粒填充复合材料界面及试样的破坏
Fig.3Fracture of the interface and the single particle filled composite sample
图3(a)显示: 当外加拉伸应变达到6.02%时, 单颗粒填充PDMS基复合材料中的界面下端部首先发生脱黏; 界面裂纹初始扩展速度较慢, 当外加应变达到断裂应变(33.2%)时, 裂纹迅速扩展为贯穿裂纹, 试样发生破坏, 并发生颗粒脱落. 所有实验过程表明:氧化锆颗粒与PDMS基体形成了弱界面, 在单轴拉伸载荷下, 氧化锆颗粒的上下极点处, 由于受到法向应力的作用, 界面法向强度决定着界面的起始脱黏; 随后界面破坏呈现法向脱黏及切向滑移的耦合行为, 此时界面法向强度和切向强度同时影响界面裂纹扩展, 最终界面完全脱黏, 且由于颗粒所处位置基体截面面积最小, 试样在此处发生破坏. 在该样品中, 氧化锆颗粒与PDMS基体的界面降低了材料整体的承载能力, 界面脱黏的示意图如图3(e)所示[3,31]; 在拉伸过程中, 相比于界面脱黏, 基体的变形损伤对整体力学行为的影响可以忽略[12,32].
2 界面性能参数的预测
2.1 有限元模型
根据上文实验试样的结构特征和边界条件, 采用商用软件ABAQUS 2018建立了单颗粒填充PDMS复合材料的三维有限元模型, 模型尺寸与实验样品一致, 为20 mm$\times$5 mm$\times$5 mm, 如图4(a)所示. 球形ZrO$_{2}$颗粒位于模型中心, 直径为2 mm, 在$x_{1}$方向(长度方向)施加拉伸位移载荷, $x_{1}=0$处为固定端, 垂直于$x_{2}$和$x_{3}$轴的平面均为自由边界. ZrO$_{2}$颗粒采用小变形线弹性本构, 弹性模量$E=190$ GPa, 泊松比$v=0.3$; PDMS基体的应变能密度函数$W_{\rm m}$采用Yeoh本构图4
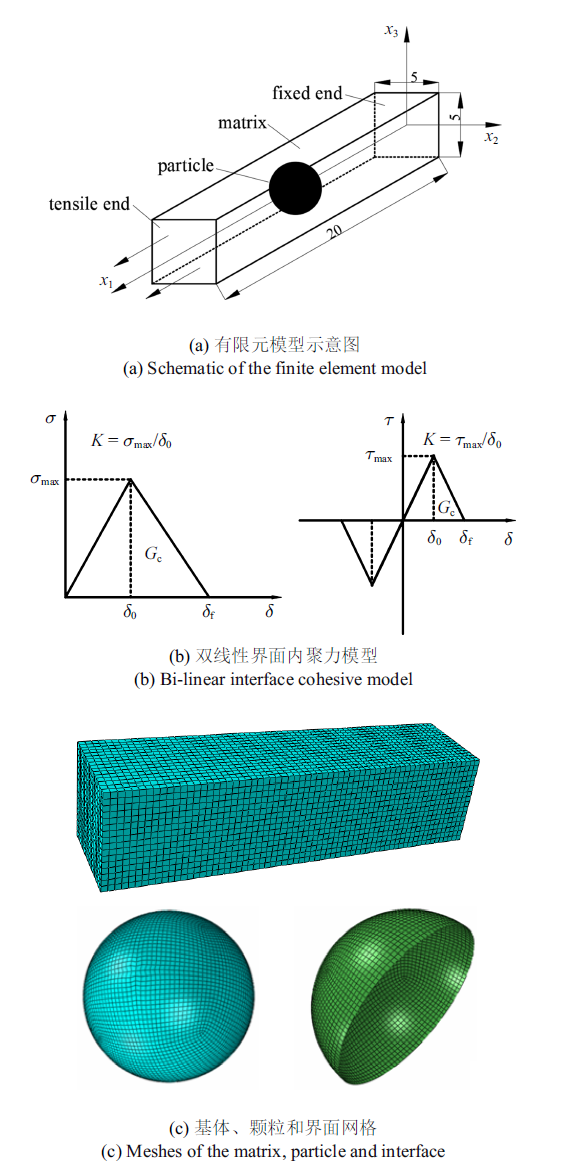新窗口打开|下载原图ZIP|生成PPT图4单颗粒填充PDMS基复合材料的有限元模型
Fig.4Finite element model of single particle filled PDMS matrix composites
式中$C_{01}$, $ C_{02}$, $ C_{03}$为待定系数, 由纯基体的单轴拉伸实验数据拟合确定, $C_{01}=199$ kPa, $C_{02}=72$ kPa, $C_{03}=25$ kPa; $I_{\rm m1}$为PDMS基体右Cauchy-Green变形张量的第一不变量, $\lambda_{\rm m1}$, $\lambda_{\rm m2}$, $\lambda_{\rm m3}$ 分别为沿$x_{1}$, $x_{2}$, $x_{3}$方向的主伸长比.
颗粒与基体间的界面由内聚力单元表征, 选取具有代表性的双线性内聚力本构关系描述界面力学行为(此处仅选择了特定的内聚力本构形式, 并非一般性假设界面内聚力满足双线性本构关系). 如图4(b)所示, $K$为内聚力随位移增大单调增大阶段对应的斜率, 即界面刚度, $\sigma _{\max}$和$\tau_{\max}$分别为法向和切向界面强度, $G_{\rm c}$为界面断裂韧性, $\delta $和$\delta_{\rm f}$为内聚力单元发生软化和破坏时对应的临界位移, 则$K=\sigma_{\max}$/$\delta $或$\tau_{\max}$/$\delta $. 颗粒和基体选用C3D8RH单元, 界面选用COH3D8单元, 基体、颗粒和界面的网格划分如图4(c)所示.
颗粒与基体间的三维界面损伤准则(内聚力单元进入软化阶段)为
式中$\sigma $和$\sigma_{\max}$分别为界面法向应力和界面法向强度, $\tau _{1}$, $\tau_{2}$和$\tau_{1\max}$, $\tau _{2\max}$分别表示与界面平行且相互正交的两个切向方向的界面应力和界面强度. 可合理假设界面切向强度满足各向同性条件, 即$\tau_{1\max}=\tau _{2\max}=\tau_{\max}$. 因此, 下文研究中将主要针对界面法向强度$\sigma_{\max}$、界面切向强度$\tau _{\max}$和界面断裂韧性$G_{\rm c}$三类界面力学性能参数进行预测.
2.2 界面性能参数预测
在已有通过实验和数值结果对比的方法确定界面力学性能的研究中[8,28-29], 普遍采用一定体积分数颗粒增强的复合材料试样, 一方面实验样品中界面破坏行为受内部复杂应力的影响, 且界面位置具有较大随机性, 难以区分界面的法向脱黏和切向脱黏; 另一方面有限元模型多采用代表性体元模型, 有限元模型的均匀化假设与实验样品本身亦存在一定差异. 本文的单颗粒填充复合材料试样, 结构简单且能够清楚地观察到界面失效过程. 当拉伸应变为6.02%时, 颗粒极点处界面首先发生法向脱黏. 因此, 通过实验与数值结果的精确对比, 可以首先确定界面的法向强度.应用从起始加载到界面起始脱黏的应力$\!-\!$应变有限元计算曲线, 与实验曲线进行对比, 该阶段界面切向强度的影响非常微弱, 可以令$\tau_{1\max}$和$\tau _{2\max}$远大于界面切向应力, 计算中取$\tau_{1\max}=\tau _{2\max}=1.0 \times 10^{10}$ MPa. 有限元与实验结果比较得到界面参数$K=0.9$ MPa/mm, $\sigma_{\max}=50$ kPa, $G_{\rm c}=1$ kPa$\cdot$mm. 此阶段的有限元与实验结果对比如图5(a)所示, 有限元计算得到界面起始脱黏的外载应变为6.15%, 与实验中界面极点处萌生裂纹时的外载应变值6.02%非常接近. 随着外加应变载荷继续增大, 界面破坏逐渐由界面法向强度主导转变为法向与切向强度同时主导, 界面破坏表现为法向脱开与切向滑移混合的方式, 此时如果仅考虑界面法向强度的作用, 数值结果将逐渐大于实验结果.
图5
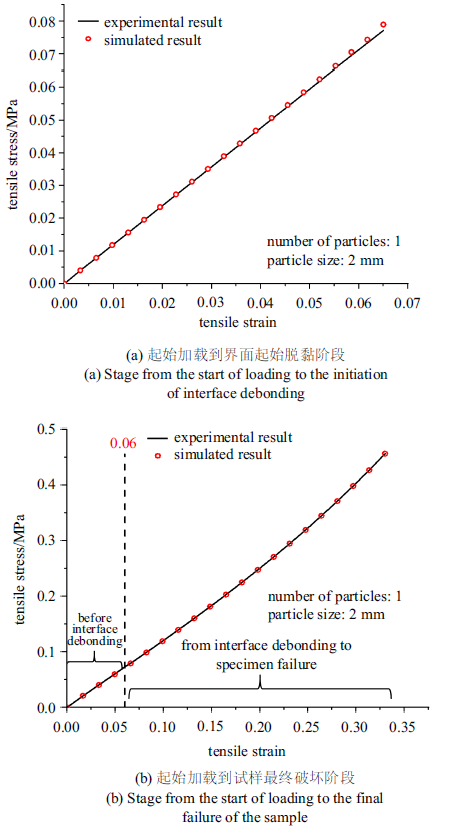新窗口打开|下载原图ZIP|生成PPT图5单颗粒填充PDMS基复合材料的实验和数值结果比较
Fig.5Comparison between experimental and numerical results of single particle filled PDMS matrix composites
有限元计算试样在界面起始脱黏后的拉伸应 力$\!-\!$应变曲线, 与实验结果进行对比, 界面法向强度、界面断裂韧性和界面刚度采用图5(a)所得结果, 进一步确定界面切向强度为$\tau_{\max}=20$ kPa, 如图5(b)所示. 最终, 通过单颗粒填充PDMS基复合材料的实验与有限元结果比较, 得到ZrO$_{2}$颗粒与PDMS基体形成界面的界面力学性能参数为界面刚度$K=0.9$ MPa/mm, 法向强度$\sigma_{\max}=50$ kPa, 切向强度$\tau _{\max}=20$ kPa及界面断裂韧性$G_{\rm c}=1$ kPa$\cdot$mm.
3 界面性能参数预测结果的验证
3.1 填充不同尺寸单颗粒的结果对比
本文采用的颗粒尺寸为mm量级, 该尺度的颗粒与基体形成的界面, 界面力学性能不存在尺寸效应, 因此, 可以合理地改变单颗粒的尺寸, 验证上述预测界面性能参数的准确性.与上述样品的制备方法一致, 分别采用直径为1 mm, 1.5 mm, 3 mm的ZrO$_{2}$单颗粒和PDMS基制备实验试样, 样品整体几何尺寸与图1(b)一致, ZrO$_{2}$单颗粒亦位于样品的中心位置, 如图6(a)所示. 分别针对3种试样开展了与上述加载条件一致的单向拉伸实验, 所测样品的力学性能与2 mm单颗粒试样的力学性能进行对比, 如表1所示. 可以发现复合材料的弹性模量随颗粒尺寸增大的变化并不明显, 但极限强度和断裂应变随颗粒尺寸的增大而减小, 主要由于颗粒尺寸增大导致复合材料中弱界面面积增大, 且颗粒所在位置处的基体承载截面面积减小的缘故.
图6
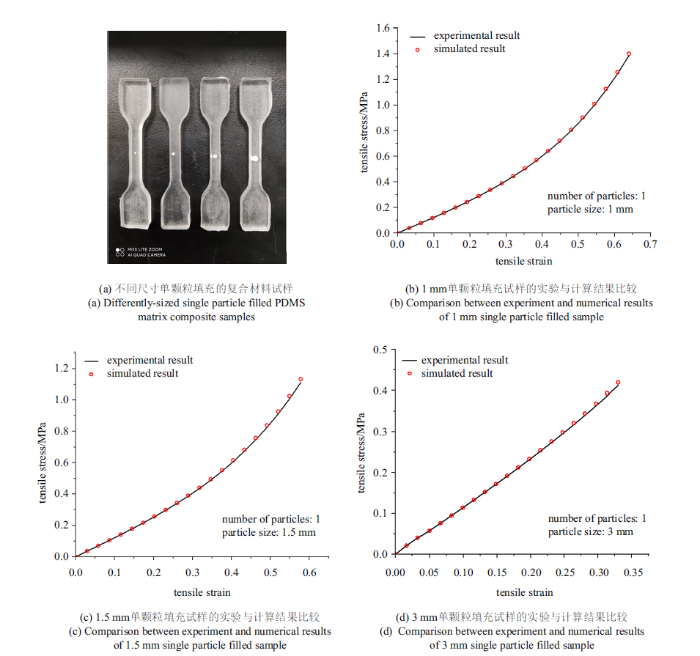新窗口打开|下载原图ZIP|生成PPT图6不同尺寸单颗粒填充复合材料的拉伸应力$\!-\!$应变曲线
Fig.6Tensile stress-strain curves of differently-sized single particle filled composites
Table 1
表1
表1不同尺寸单颗粒填充PDMS基复合材料试样及纯基体的力学性能参数
Table 1
 |
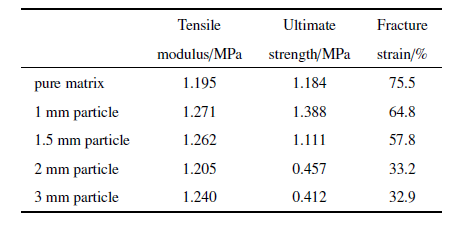新窗口打开|下载CSV
与上文有限元方法一致, 分别建立1 mm, 1.5 mm, 3 mm单颗粒填充的PDMS基复合材料有限元模型, 仍采用双线性内聚力本构描述界面力学行为. 有限元计算中, 界面力学参数直接采用上文确定的值, 即$K=0.9$ MPa/mm, $\sigma _{\max}=50$ kPa, $\tau _{\max}=20$ kPa和$G_{\rm c}=1$ kPa$\cdot$mm. 针对3种不同尺寸ZrO$_{2}$单颗粒填充的复合材料的拉伸应力$\!-\!$应变关系, 其实验结果及有限元计算结果在图6(b)和图6(d)中分别给出. 可以发现, 即使单颗粒复合材料整体应力$\!-\!$应变曲线由于颗粒尺寸的影响, 表现出不一致的函数关系, 实验结果与有限元计算结果仍非常一致.
3.2 填充不同数目颗粒的结果对比
进一步改变填充颗粒的数目, 进行了界面力学性能预测结果的验证. 颗粒尺寸仍为2 mm, 分别采用单个、两个和3个颗粒进行填充, 如图7(a)所示. 颗粒间距为5 mm, 试样整体几何尺寸及加载条件均与上文一致. 不同数目颗粒填充PDMS基复合材料的力学性能在表2中给出. 可以发现, 随着颗粒数目的增加, 复合材料的弹性模量变化并不明显, 主要由于颗粒体积分数远小于基体体积分数, 但复合材料的极限强度和断裂应变均明显减小, 主要由于颗粒数目的增加使得弱界面面积增大.图7
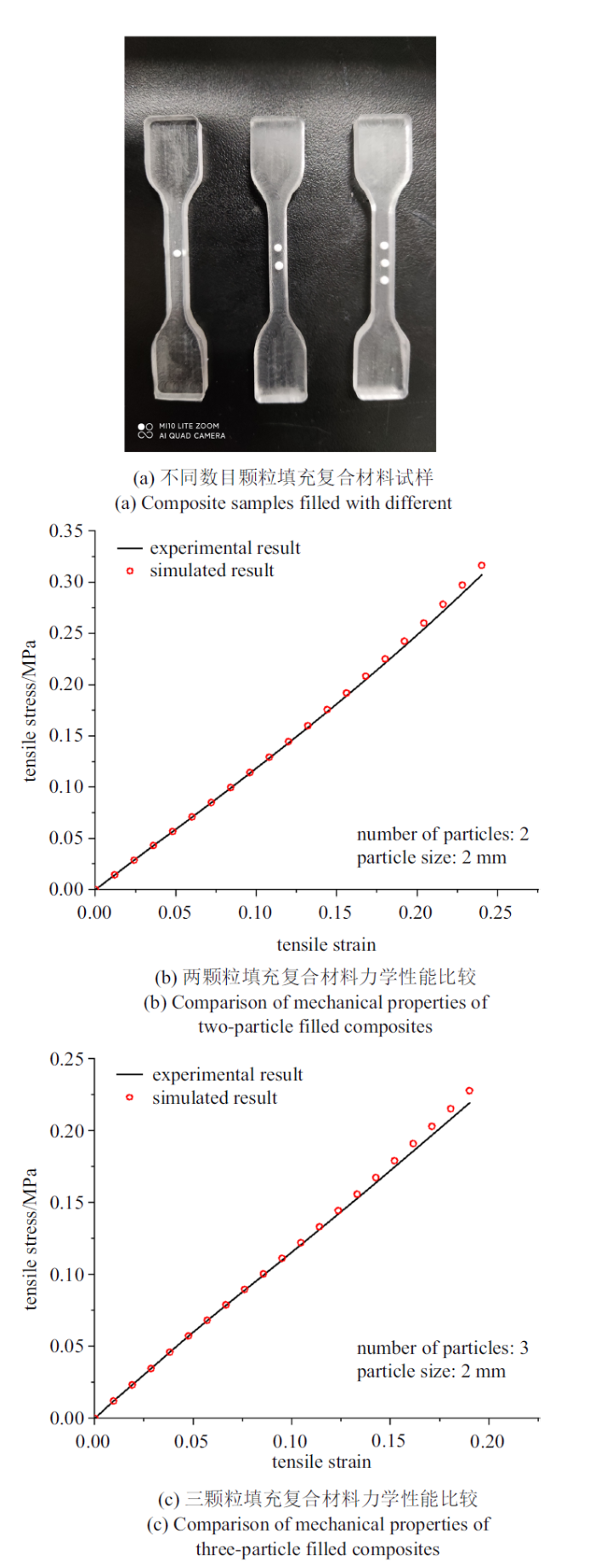新窗口打开|下载原图ZIP|生成PPT图7不同数目颗粒填充复合材料实验结果与数值结果对比
Fig.7Comparison between experimental and numerical results of composites filled with different numbers of particles
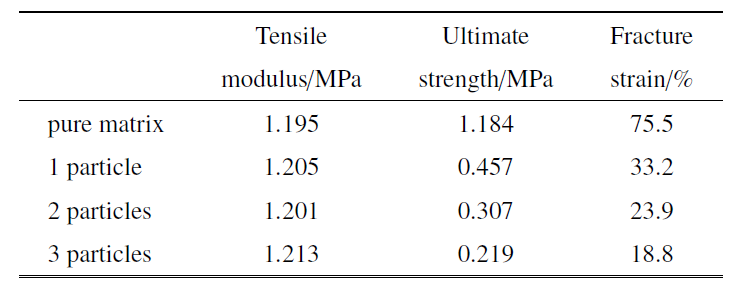
Table 2
表2
表2不同数目颗粒填充复合材料的力学性能参数(颗粒直径2 mm)
Table 2
 |
新窗口打开|下载CSV
进一步建立两颗粒及三颗粒填充的PDMS基复合材料有限元模型, 其基体、颗粒及界面参数与上文完全一致, 开展有限元计算并与相应的实验结果进行对比, 如图7(b)和图7(c)所示. 数值结果与实验结果均符合, 进一步验证了本文界面性能参数预测方法的可行性及准确性. 当外加应变较大时, 实验结果略小于数值结果, 主要由于颗粒数目的增加将产生更多应力集中区域, 导致基体损伤增加, 而有限元模型中基体的损伤只包含了纯基体单轴拉伸时的部分. 这也进一步说明, 利用真实复合材料开展实验结果与代表性体元的有限元计算结果比较, 从而预测界面性能的方法将造成更大的预测误差.
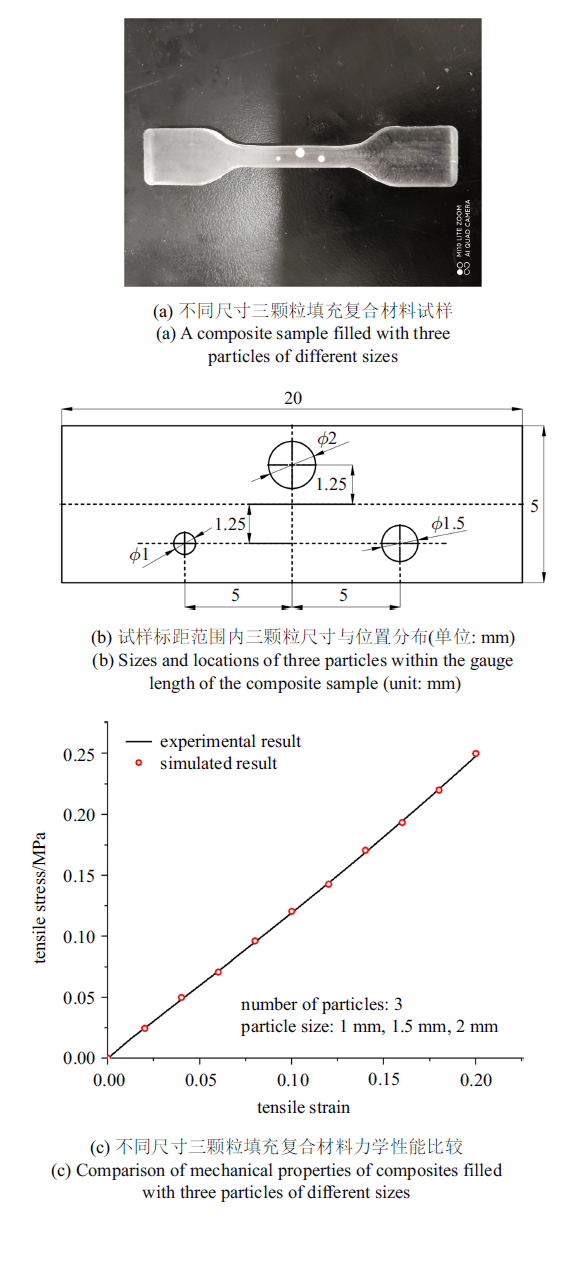
图7中的多颗粒填充试样, 颗粒尺寸均相同, 且沿同一直线等间距排布. 为进一步验证界面力学性能预测结果, 考虑更为复杂的颗粒分布情况. 如图8(a)和图8(b)所示, 在试样标距范围内采用1 mm, 1.5 mm和2 mm的颗粒进行填充, 三颗粒排布不在一条直线上, 试样整体几何尺寸及加载条件仍与单颗粒填充试样相同. 建立与上述试样结构一致的三颗粒填充PDMS基复合材料有限元模型, 基体、颗粒材料性能参数及界面性能参数与上文完全一致, 开展有限元计算并与相应的实验结果进行对比, 如图8(c)所示. 数值结果与实验结果符合较好, 从而说明本文界面性能参数仍然适用于颗粒分布较复杂的情况.
图8
新窗口打开|下载原图ZIP|生成PPT图8不同尺寸三颗粒填充复合材料实验结果与数值结果对比
Fig.8Comparison between experimental and numerical results of composites filled with three particles of different sizes
4 讨论
由分析可以看出, 该确定界面性能参数的方法具有一定的优点, 亦具有一定的适用范围: (1)本文的方法简单易用, 但更适用于颗粒与基体形成的弱界面情况, 对于强界面情况, 复合材料的基体损伤不容忽略. 然而, 对于颗粒与基体形成强界面的复合材料, 复合材料力学性能预测, 一般情况下假设界面完美, 不需要定量确定界面性能参数; (2)本文方法主要针对颗粒与基体的界面性能预测, 而界面性能与颗粒尺寸及颗粒体积分数没有关系, 只有当颗粒尺寸达到纳米量级, 界面性能才会受到颗粒尺寸的影响, 即纳米颗粒填充复合材料力学行为的界面效应问题[33-34]; (3)微米颗粒增强复合材料的力学性能往往表现出尺寸效应现象, 主要指颗粒体积分数一定的情况下, 随着颗粒尺寸的减小, 颗粒与颗粒之间的基体应变非均匀性增强, 应变梯度造成的影响不容忽略[35-36]. 但即使针对微米颗粒增强的复合材料, 其自身界面性能与颗粒尺寸无关; 本文预测大颗粒与基体的界面性能, 同样适用于微米颗粒与基体形成的界面; (4)随着颗粒数目的增多, 基体内的应变非均匀性增强, 基体自身的变形损伤则变得更为复杂[5-6,10,12]. 而本文应用了单轴拉伸时基体的应力$\!-\!$应变关系拟合得到的基体材料参数, 包含了纯基体的变形损伤部分, 虽然与单颗粒填充复合材料中基体的损伤不完全一致, 但从两颗粒、三颗粒及不同尺寸单颗粒填充复合材料的实验结果及有限元结果的比较, 可以合理推断纯基体的变形损伤及数目不多颗粒填充复合材料中基体的损伤并不明显, 对材料整体力学性能的影响亦不明显, 可能也是因为界面较弱的原因; (5)本文主要应用了单颗粒填充复合材料作为界面性能参数定量确定的研究对象, 该方法应该同样适用于测量纤维与基体间的界面性能; (6)本文选择了双线性黏结区本构描述了界面本构, 对于其他的黏结区本构模型同样适用, 例如矩形黏结区模型、梯形黏结区模型、L-J势黏结区模型等等, 且已有研究表明: 使用不同黏结区模型描述界面, 界面强度和界面断裂韧性的参数值基本保持一致[37-38].5 结论
本文提出一种定量预测颗粒增强复合材料界面力学性能的新方法. 针对含ZrO$_{2}$单颗粒填充PDMS基复合材料试样开展了单轴拉伸实验和有限元模拟, 通过界面不同阶段的力学响应确定界面的法向强度、界面切向强度和界面断裂韧性. 为了验证标定方法的可行性及界面参数确定的正确性, 进一步开展了不同尺寸单颗粒及不同数目颗粒填充PDMS基复合材料的实验及有限元对比, 证明了本文提出方法的合理性, 并讨论了该方法的适用性. 该预测复合材料内部界面性能参数的方法, 简便、易操作且精度高, 对进一步定量预测和分析复合材料的整体力学性能具有一定的帮助.参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
DOIURL [本文引用: 1]
DOIURL [本文引用: 3]
DOIURL [本文引用: 3]
DOIURL [本文引用: 1]
DOIURL [本文引用: 4]
DOIURL
DOIURL [本文引用: 1]
DOI [本文引用: 1]
In this article, we developed a three-dimensional multi-particle finite element model to explore the effects of particle size, morphology and interfacial strength on the elastic-plastic behavior of particle-reinforced composites under uniaxial tension. We adopted strain-gradient plasticity to evaluate the size-dependent strengthening effect on matrix. Randomly distribution of spherical or cubic particles was realized in a cubic representative cell and interface damage was described by the cohesive zone model. Numerical analysis quantified the effects of microstructural features on interface damage, load transfer and strengthening effect in matrix: the flow strength of composites increases with decreasing particle size, which is attributed to the increased size-dependent strengthening in matrix, considering that the load bearing capacity of particles is decreased simultaneously. Weaker interface results in earlier and faster development of interface damage, and as the interface damage grows to the order of 0.1, load bearing capacity of particles drops from its peak value.
DOIURL [本文引用: 3]
DOIURL [本文引用: 2]
DOIURL [本文引用: 1]
DOIURL
[本文引用: 2]
[本文引用: 2]
DOIURL [本文引用: 1]
DOIURL
DOIURL
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 3]
DOIURL [本文引用: 3]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
