脆性岩石蠕变裂纹成核宏细观力学机理研究1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

李晓照^,^*^,^†^,^**^,²⁾, 贾亚星^*, 张骐烁^*, 戚承志^*^,^†^,^**

^*北京建筑大学土木与交通工程学院, 北京 100044

^†北京未来城市设计高精尖创新中心, 北京 100044

^**城市交通基础设施建设北京国际科技合作基地, 北京 100044

A STUDY ON MICRO-MACRO MECHANISMS OF CRACK NUCLEATION DURING CREEP IN BRITTLE ROCKS¹⁾

Li Xiaozhao^,^*^,^†^,^**^,²⁾, Jia Yaxing^*, Zhang Qishuo^*, Qi Chengzhi^*^,^†^,^**

^*School of Civil and Transportation Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China

^†Beijing Advanced Innovation Center for Future Urban Design, Beijing 100044, China

^**Beijing International Scientific and Technological Cooperation Base of Construction of Urban Traffic Infrastructure, Beijing 100044, China

通讯作者: 2)李晓照, 副教授, 主要研究方向: 岩石力学与工程方面的研究工作. E-mail:lixiaozhao@bucea.edu.cn

收稿日期:2020-11-27接受日期:2021-03-16网络出版日期:2021-04-08

基金资助:

1)国家自然科学基金.51708016
北京市教委科研计划.KM202110016014
北京建筑大学金字塔人才培养工程.JDYC20200307

Received:2020-11-27Accepted:2021-03-16Online:2021-04-08
作者简介 About authors

摘要
脆性岩石内部细观裂纹扩展、贯通及成核影响下的脆性蠕变行为, 对深部地下工程围岩微震及岩爆事件评价有着重要意义. 然而, 目前能够解释裂纹成核损伤突变影响下, 脆性岩石完整蠕变宏细观力学机理模型的研究很少. 本文基于脆性岩石亚临界裂纹扩展模型、裂纹-应变-声发射事件相关的损伤模型及裂纹成核损伤时间演化路径函数, 提出了一种脆性岩石裂纹成核损伤突变影响下的蠕变宏细观力学模型. 裂纹成核损伤时间演化路径函数通过岩石内部裂纹成核损伤突变大小$\Delta D_{CN}$及相邻裂纹成核损伤时间差$\Delta t$进行定义, 该函数可以结合岩石声发射监测试验数据定义的岩石损伤数据确定. 通过与试验结果对比分析验证模型的合理性. 并讨论了裂纹成核损伤大小、相邻裂纹成核损伤时间间隔、及裂纹成核数量对脆性岩蠕变裂纹长度、裂纹速率、轴向应变及应变率的影响. 该结果对于更加合理、经济、高效的深部地下工程施工及设计提供了一定的理论支持.
关键词： 岩石力学;脆性蠕变;裂纹成核;损伤突变;微震

Abstract
The creep behaviours influenced by the growth, coalescence and nucleation of microcracks in brittle rocks have an essential meaning for evaluating the microseismicity and rock bursts of the surrounding rocks in deep underground engineering. However, the micro-macro mechanisms of the damage catastrophe from the crack nucleation effect on the total creep behaviour of brittle rocks are rarely studied. In this study, based on the subcritical crack growth model, the damage model relating to the crack, strain and acoustic emission events, and the function of the damage path influenced by crack nucleation, a micro-macro model is proposed to explain the effect of crack nucleation on creep of brittle rocks. The function of the damage path influenced by crack nucleation is defined by the parameters of the size of damage catastrophe (i.e., $\Delta D_{CN}$) and the time difference (i.e., $\Delta t$) between the adjacent crack nucleations. The damage and time parameters in this proposed function of the damage path can be determined by the use of the experimental data of acoustic missions. The rationality of this proposed micro-macro model is verified by comparing the experimental results. The effects of the damage catastrophe size from crack nucleation, the happened time of crack nucleation, and the number of crack nucleation on the crack length, crack velocity, axial strain, and axial strain rate are discussed during creep of brittle rocks. The suggested model provides a certain theoretical help for the more reasonable, economical, and efficient construction of deep underground engineering.
Keywords：rock mechanics;brittle creep;microcrack nucleation;damage catastrophe;microseismicity

PDF (1275KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
李晓照, 贾亚星, 张骐烁, 戚承志. 脆性岩石蠕变裂纹成核宏细观力学机理研究¹⁾. 力学学报[J], 2021, 53(4): 1059-1069 DOI:10.6052/0459-1879-20-400
Li Xiaozhao, Jia Yaxing, Zhang Qishuo, Qi Chengzhi. A STUDY ON MICRO-MACRO MECHANISMS OF CRACK NUCLEATION DURING CREEP IN BRITTLE ROCKS¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(4): 1059-1069 DOI:10.6052/0459-1879-20-400

引言

随着我国经济不断发展, 深部地下工程建设需求与日俱增. 深部高地应力环境导致了地下工程围岩具有很强的时间效应, 脆性岩石又是深部地下工程围岩的主要组成, 进而导致深部地下工程围岩表现为明显的脆性蠕变特性, 其对深部地下工程围岩微震及岩爆灾害的评价有着重要的实际意义.

众多****通过蠕变试验研究了脆性岩石的蠕变应变演化曲线, 并分析了不同恒定轴向加载应力、分级轴向加载应力、分级围压卸载等对岩石蠕变应变演化曲线影响^[1-2]. 也有****研究了不同含水率、渗透压及温度对脆性岩石蠕变特性影响^[3-6]. 在以上试验的基础上, 有****通过弹性、黏性及塑性模块进行不同的串并联组合, 提出了岩石蠕变演化模型, 并结合试验对比分析校验模型参数, 进而将模型应用于数值模拟软件中, 分析预测深部地下工程围岩稳定性^[7-8]. 然而, 裂纹变化行为严重影响固体材料变形力学性能^[9-11], 以上研究均是从宏观角度研究了岩石的减速、稳态及加速蠕变应变随时间演化曲线, 无法准确地分析岩石内部局部裂纹扩展、贯通及成核现象对岩石蠕变应变演化曲线的影响.

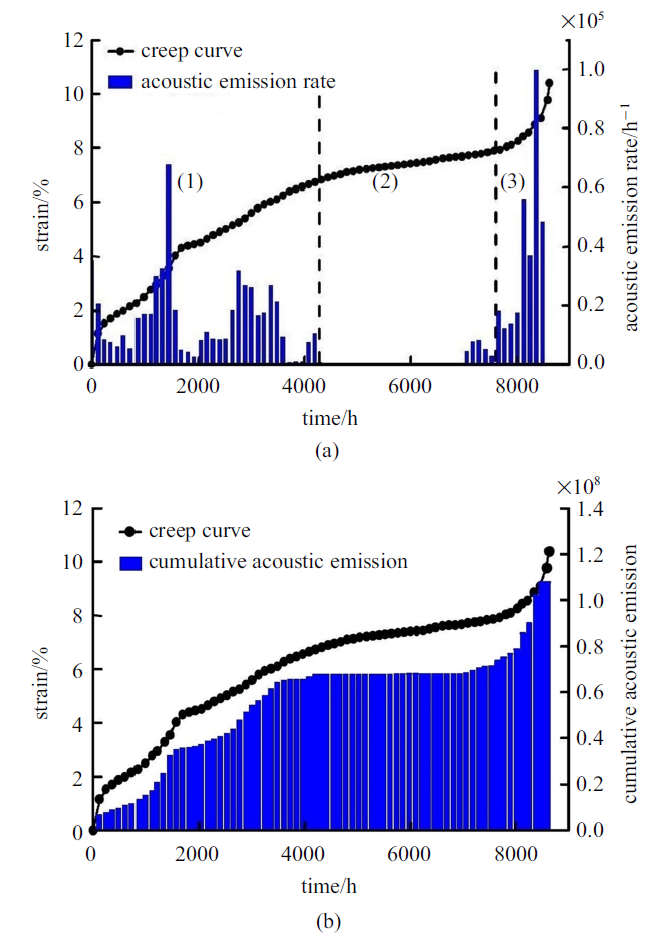
有****通过声发射监测技术, 对脆性岩石蠕变演化过程中, 岩石内部裂纹扩展情况进行了更加精确的分析^[12-13], 图1(a)中, 随着时间演化, 岩石蠕变过程中声发射率是不断变化的, 每一次较大的声发射率的突增, 都对应着一次明显的应变加速增大到减速增大的转化过度, 然而, 在较小的声发射率变化时, 应变值则没有明显的改变; 图1(b)中, 累计声发射率可以更加明显地观测到累计声发射率演化趋势与应变演化趋势相似, 每一次应变加速增大, 对应着累计声发射率的加速的增大, 即岩石的应变率与声发射率成正比例关系, 此外裂纹速率、应变率及声发射率三者之间存在相互正比例对应关系, 本文的理论研究与结果讨论中将给出详细说明. 因此通过上述结果可以看到, 脆性岩石蠕变过程中, 其蠕变演化曲线并不只是经历一次减速、稳态及加速蠕变演化过程, 而是中间可能存在多次应变率突变的情况. 该现象与脆性岩石内部微震事件的发生有着密切关系, 每一次蠕变应变的加速增大, 也就是声发射率的突增现象, 会导致一次微震现象, 多次微震事件的发生, 最终会导致岩石的整体断裂破坏, 甚至会产生严重的岩爆事件^[14-15].

图1

新窗口打开|下载原图ZIP|生成PPT
图1岩石蠕变过程中(a)声发射信号率及(b)累计声发射事件率时间演化关系^[12]

Fig.1Evolutions of (a) rate of acoustic emission and (b) the number accumulated acoustic emission during creep of rocks^[12]

在恒定荷载蠕变演化过程中, 导致这种较大的声发射率及应变率的突增与应变值的加速增大到减速增大的过度变化的原因, 是由于脆性岩石内部局部微裂纹成核损伤突变所导致, 蠕变过程中较小的声发射率出现只是岩石内部裂纹扩展现象导致, 此时并没有局部裂纹成核现象出现^[16]. 此外, 基于岩石细观裂纹扩展模型并结合裂纹亚临界裂纹扩展法则, 脆性岩石压缩蠕变宏细观力学模型被研究^[17]. 然而, 目前能够解释脆性岩石蠕变过程中, 细观裂纹成核损伤突变对岩石宏观变形影响的宏细观力学模型很少, 因此本文将基于固体断裂损伤力学模型, 并结合岩石声发射蠕变监测试验结果, 研究分析细观裂纹成核损伤突变影响下的岩石蠕变演化机理, 进而为深部地下工程脆性蠕变过程中微震、岩爆事件的预测评价提供一定的理论支持.

1 理论模型

本文基于时间依赖的亚临界裂纹扩展力学模型, 引入裂纹成核损伤突变演化路径函数, 并结合裂纹扩展、应变及生发射事件相关的损伤模型, 提出了一种可以解释脆性岩石裂纹成核损伤突变, 对长期承受恒定应力状态(轴向应力$\sigma_{1}$, 围压$\sigma _{3}=\sigma_{2})$下的蠕变应变演化曲线影响的宏细观力学模型(图2).

图2

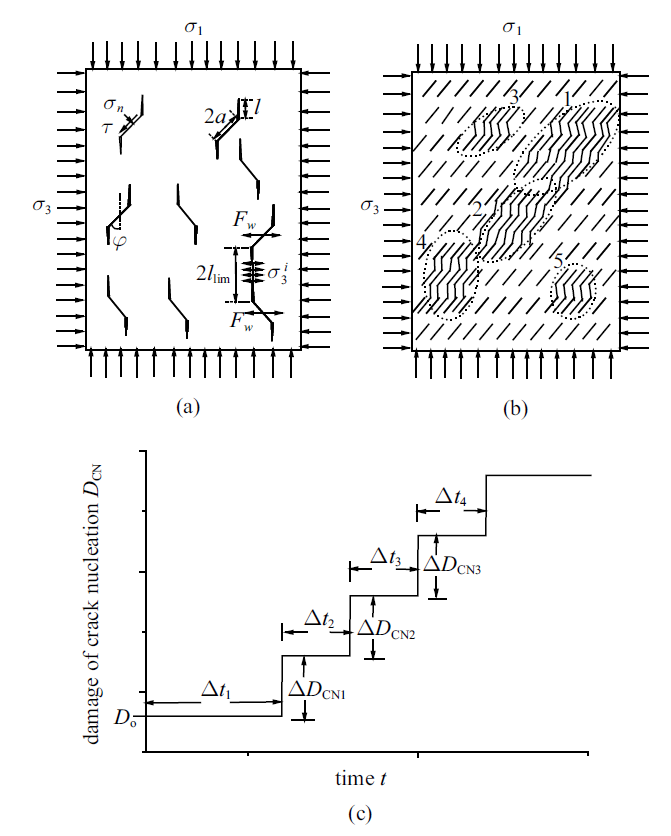
新窗口打开|下载原图ZIP|生成PPT
图2(a)岩石裂纹扩展模型; (b)局部裂纹成核模型; (c)裂纹成核损伤随时间演化曲线

Fig.2(a) Rock model of crack growth; (b) nucleation model of localized cracks; (c) variation of damage from crack nucleation over time

其中图2(b)给出了脆性岩石压缩蠕变过程中, 内部可能形成的5个局部细观裂纹成核现象, 数字1 $\sim$ 5描述了裂纹成核顺序, 每一个局部细观裂纹成核都会导致岩石的损伤出现一个突变情况, 每一个损伤突变导致了岩石蠕变应变的突然加速增大, 文献[16]详细阐述了裂纹成核损伤突变影响下的应力-应变本构机理. 图2(c)给出了一种岩石内部裂纹成核可能导致的损伤突变演化路径, 对于真实岩石内部, 由于细观裂纹随机分布特性, 岩石内部每一个裂纹成核导致的损伤突变大小各不相同, 而且相邻两次裂纹成核损伤突变之间的时间间隔也是随机的, 因此, 图2(c)通过$\Delta D_{CN1}$, $\Delta D_{CN2}$, $\Delta D_{CN3}$ $\cdots$ 来描述裂纹成核损伤突变值, $\Delta t_{1}$描述第一次裂纹成核的时间, $\Delta t_{2}$, $\Delta t_{3}$, $\Delta t_{4}$ $\cdots$ 来描述相邻裂纹成核的间隔时间.

图1(a)中, 压缩应力作用下, 脆性岩石内部随着初始裂纹(其尺寸为$a$, 角度为$\varphi)$沿着裂纹面滑动, 导致其两端新生成翼型裂纹不断扩展(其长度为$l)$, 此翼型裂纹为张开型裂纹, 其应力强度因子为^[17-18]

(1)$\begin{eqnarray} K_{I} \left( l \right)=\sqrt {\pi a} \left[ {\sigma_{3} c_{3} +\left( {\sigma_{3} A_{2} -\sigma_{1} A_{1} } \right)\left( {c_{1} +c_{2} } \right)} \right] \end{eqnarray} $

式中

(2)$c_{1} =\pi^{-2}\left( {{l/a}+\beta } \right)^{-{3/2}} $

(3)$c_{2} =\frac{2\left( {\pi \alpha } \right)^{-2}\sqrt {{l/a}} }{D_{o} ^{-{2/3}}-\left[ {1+{l/{\left( {\alpha a} \right)}}} \right]^{2}} $

(4)$c_{3} =2{{\sqrt {{l/a}} }/\pi } $

(5)$A_{1} =\pi \sqrt {{\beta /3}} \left( {\sqrt {1+\mu^{2}} -\mu } \right) $

(6)$A_{2} =A_{1} {{\left( {\sqrt {1+\mu^{2}} +\mu } \right)}\Bigg/{\left( {\sqrt {1+\mu^{2}} -\mu } \right)}} $

其中, $\beta $为常数, $\mu $为初始裂纹摩擦系数. 模型中$F_{w}$为作用于初始裂纹面的楔力, 其作用可以平衡岩石翼型扩展裂纹之间内应力$\sigma_{3}^{i}$, $l_{lim}$为翼型裂纹扩展极限长度, 其物理意义是两个相邻翼型裂纹尖端相互贯通时的长度(图2(a)), $l_{lim}=\alpha a(D_{o}^{-1/3}-1)$^[19], 式中参数$\alpha =\cos\varphi $, 岩石初始损伤$D_{o}=4\pi N_{V}(\alpha a)^{3}/3$, $N_{V}$为岩石单位体积的微裂纹数量. 模型计算中定义压应力为负, 结果分析图中压应力取正. 图1(a)模型所有初始裂纹尺寸或角度均假设为恒定值, 可理解为真实岩石内部随机分布裂纹尺寸或角度的平均值, 即通过一种平均化方法定性研究细观裂纹影响下的岩石力学性能. 众多****通过试验定性地研究了预制微小裂纹尺寸及角度对岩石力学特性影响^[20-25], 但是微小预制裂纹尺度要远大于与本文模型中提出细观裂纹尺度, 无法解释细观裂纹影响下的完整自然岩石力学特性. 然而细观尺度裂纹对岩石力学特性影响很难试验研究, 随机裂纹尺寸及角度影响的岩石理论方程又很难建立, 所以本文通过平均化假设的方法近似地研究细观裂纹对岩石力学特性影响.

基于式(1)翼型裂纹尖端应力强度因子, 脆性岩石的应力与裂纹扩展关系可表示为^[17,19]

(7)$\begin{eqnarray} \sigma_{1} (l)=\frac{\sigma_{3} \left[ {c_{3} +A_{2} (c_{1} +c_{2} )} \right]-K_{IC} /\sqrt {\pi a} }{A_{1} (c_{1} +c_{2} )} \end{eqnarray} $

式(7)描述了裂纹扩展硬化与裂纹扩展软化曲线结果, 其对应着岩石应变硬化与应变软化的应力-应变曲线, 存在一个裂纹启裂应力值$\sigma_{1ci}$ (即$l=0$时对应的轴向应力), 和一个峰值强度值$\sigma_{1peak}$, 这两个值为岩石蠕变应变演化结果计算的恒定轴向应力$\sigma _{1}$值选取提供了依据(即$\sigma_{1ci}<\sigma _{1}<\sigma_{1peak})$.

张开型亚临界裂纹扩展速率与强度因子的关系式可表示为${d}l/{d}t=v(K_{I}/K_{IC})^{n}$^[26], 引入式(1)应力强度因子表达式, 图1(a)中脆性岩石内部亚临界裂纹扩展速率可表示为^[17]

(8)$\begin{eqnarray} {{{d}l}/{{d}t}}=v(\pi a)^{{n/2}}\left[ {\frac{\sigma_{3} c_{3} +\left( {A_{2} \sigma_{3} -A_{1} \sigma_{1} } \right)\left( {c_{1} +c_{2} }\right)}{K_{IC} }} \right]^{n} \end{eqnarray} $

式中, $v$为特征裂纹速度, $n$为应力侵蚀指数. 根据式(8)解微分方程, 可以求解出恒定应力状态下裂纹长度随时间演化结果$l(t)$, 其中微分方程中给定应力状态的初始裂纹长度$l_{o}$可通过式(7)计算得到.

轴向应变相关的岩石损伤可定义为^[27]

(9)$\begin{eqnarray} D=1-\exp \left[ {-\varepsilon_{o}^{-1}\left( {\varepsilon _{1}-2\gamma E^{-1}\left| {\sigma_{3} } \right|} \right)} \right]^{m} \end{eqnarray} $

式中, $D$为损伤因子, $m$和$\varepsilon_{o}$为材料常数, $\varepsilon_{1}$为轴向应变, $\gamma $为泊松比, $E$为弹性模量, $|\cdot|$ 为取绝对值.

裂纹相关的损伤可定义为^[18]

(10)$\begin{eqnarray} D=\frac{4\pi }{3}N_{V} \left( {l+\alpha a} \right)^{3} \end{eqnarray} $

联立式(9)与式(10), 轴向应变与裂纹长度关系可表示为

(11)$\begin{eqnarray} \varepsilon_{1} =2E^{-1}\gamma \left| {\sigma_{3} } \right|+\varepsilon_{o} \left\{ {-\ln \left[ {1-D_{o} \left( {\frac{l}{\alpha a}+1} \right)^{3}} \right]} \right\}^{{1}/{m}} \end{eqnarray} $

将翼型裂纹极限长度$l_{lim}$代入式(11), 可以计算得到一个极限轴向应变$\varepsilon_{1f}$, 该值为岩石失效应变提供一定参考.

将式(8)计算得到的恒定应力作用下, 亚临界裂纹长度随时间演化结果$l(t)$代入式(11), 也就是用$l(t)$替换$l$, 可以得到岩石的恒定荷载蠕变应变随时间演化表达式

(12)$\begin{eqnarray} \varepsilon_{1} =2E^{-1}\gamma \left| {\sigma_{3} } \right|+\varepsilon_{o} \left\{ {-\ln \left[ {1-D_{o} \left( {\frac{l\left( t \right)}{\alpha a}+1} \right)^{3}} \right]} \right\}^{{1}/{m}} \end{eqnarray} $

式(12)很好地描述了岩石的蠕变应变演化曲线, 然而, 仍然无法描述脆性岩石内部裂纹成核损伤突变对蠕变应变时间演化曲线影响. 本文为了能够通过理论模型描述裂纹成核损伤突变对蠕变演化曲线影响, 引入了图2(c)中裂纹成核损伤蠕变演化路径, 将该损伤函数引入式(12)则可以很好解释裂纹成核损伤突变影响. 然而, 如何将裂纹成核损伤突变演化路径函数引入式(12)是一个关键问题. 具体解决方法如下: 通过式(12)可以看到, 岩石蠕变应变时间演化结果与岩石初始损伤$D_{o}$相关, 针对一个岩石试样来说, 其初始损伤是恒定不变的, 然而, 为了描述裂纹成核损伤突变影响, 将图2(c)提出的裂纹成核损伤蠕变时间演化路径函数$D_{CN}(t)$替换式(12)中的初始损伤$D_{o}$, 即每一次裂纹成核引起的岩石损伤突变值可以通过初始损伤突变近似地描述. 则脆性岩石裂纹成核损伤突变影响下的蠕变时间演化表达式为

(13)$\begin{eqnarray} &&\varepsilon_{1} \left( t \right)=2E^{-1}\gamma \left| {\sigma_{3} } \right|+\varepsilon_{o} \left\{ {-\ln \left[ {1-D_{CN} \left( t \right)\left( {\frac{l\left( t \right)}{\alpha a}+1} \right)^{3}} \right]} \right\}^{1/m} \end{eqnarray} $

此外值得注意的是式(13)中裂纹长度时间演化参数$l(t)$中同时也隐含着裂纹成核损伤突变演化函数$D_{CN}(t)$. 具体用$D_{CN}(t)$替换$D_{o}$的原因: 已知初始损伤$D_{o}=4\pi N_{V}(\alpha a)^{3}/3$, 假设初始裂纹尺寸$a$及角度$\varphi $保持不变, 则在上述理论计算中每一次裂纹成核引起的损伤突变$\Delta D_{CN}$, 导致了裂纹数量的$N_{V}$的突然增大, 这也近似地实现了裂纹成核损伤突变结果. 实际岩石内部裂纹成核损伤突变, 不仅仅是裂纹数量的增多, 裂纹尺寸、方向及位置也可能在不断变化, 由于本文模型局限性, 无法真实模拟这些裂纹变化特征, 所以只能通过改变裂纹数量近似等效的方法实现裂纹成核现象, 为脆性岩石细观裂纹成核与宏观力学特性关系的理解提供一定参考.

此外, 式(10)给出了图2(a)脆性岩石细观裂纹模型的损伤表达式, 拆分变换式(10), 岩石损伤方程也可以表示为

(14)$\begin{eqnarray} D=D_{o} \left[ {\left( {\frac{l}{\alpha a}} \right)^{3}+3\left( {\frac{l}{\alpha a}} \right)^{2}+\frac{3l}{\alpha a}+1} \right] \end{eqnarray} $

在式(14)中, 岩石裂纹损伤演化与初始损伤$D_{o}$密切相关, 因此, 通过控制初始损伤方法近似地实现裂纹成核损伤突变的方法是可行的. 具体理论结果是否合理详见下文结果分析.

此外, 基于声发射监测数据, 岩石损伤为^[28]

(15)$\begin{eqnarray} D=\left( {1-{{\sigma_{r} }/{\sigma_{P} }}} \right){{C_{d}}/{C_{0} }} \end{eqnarray} $

式中, $C_{d}$为岩石某一阶段的累计声发射数, $C_{0}$为岩石压缩破坏全过程中累计声发射数, $\sigma_{r}$为残余强度, $\sigma_{P}$为峰值强度. 式(15)可以很好地呈现蠕变试验过程中, 岩石内部局部微裂纹成核损伤突变现象(见图1). 因此, 可以通过岩石内部裂纹扩展诱发的声发射信号数据更加准确地判断岩石内部裂纹成核损伤突变演化路径函数$D_{CN}(t)$, 进而为通过式(13)更加真实地计算模拟岩石内部裂纹成核规律影响下的岩石蠕变演化曲线结果提供重要依据.

2 模型结果分析

2.1 型合理性验证

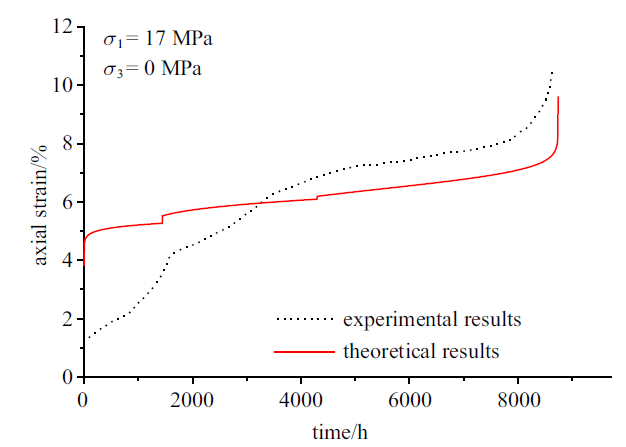
依据盐岩力学性能^[12], 模型参数选取如下: 初始损伤$D_{o}=0.06$, 初始裂纹摩擦系数、尺寸及角度分别为$\mu =0.6$, $a=2.9$ mm, $\varphi =45^\circ$. 材料常数$m=2$, $\varepsilon_{o}=0.1$, $\beta =0.32$, 断裂韧度$K_{IC}=0.32$ MPa$\cdot$m$^{1/2}$, 弹性模量$E=20$ GPa, 泊松比$\gamma =0.3$, 特征裂纹速率$v=0.16$ m/s, 应力侵蚀指数$n=57$, $\Delta t_{1}=1440$ h, $\Delta t_{2}=4296$ h, $\Delta D_{CN1}=0.005$, $\Delta D_{CN2}=0.001 7$. 具体参数选取方法可参考文献[17, 19].

图3中给出了考虑裂纹成核损伤突变影响下的理论蠕变应变演化曲线, 并通过与试验结果^[12] (即图1试验曲线)对比验证模型合理性. 岩石蠕变过程中分别在$t_{1}=1440$ h, $t_{2}=4296$ h时, 经历两次由加速蠕变到减速蠕变的转化, 其分别对应两次局部裂纹成核损伤突变, 在模型中该两次成核损伤分别赋值$\Delta D_{CN1}=0.005$, $\Delta D_{CN1}=0.001 7$, 此外, 岩石在最后产生加速蠕变变形, 导致了岩石的最终破坏.

图3

新窗口打开|下载原图ZIP|生成PPT
图3裂纹成核损伤突变下的理论与试验^[12]蠕变演化曲线

Fig.3Theoretical and experimental^[12] creep curves influenced by damage catastrophe from crack nucleation

此外, 为进一步验证模型合理性, 图4(a)给出了锦屏大理岩试样蠕变演化过程中, 归一化裂纹损伤演化理论结果与数值试验结果^[29]对比分析曲线. 由于本文模型局限性, 理论与试验结果数值上存在一定差异, 因此采用了归一化结果进行对比分析. 模型参数如下: $\Delta D_{CN1}=\Delta D_{CN2}=\cdots \Delta D_{CN9}=0.000 5$, $\Delta t_{1}=$ $\Delta t_{2}=\cdots \Delta t_{9}=2.0 \times 10^{5}$ s. 数值试验结果存在多次裂纹成核损伤突增现象, 只是数值试验更好地呈现了裂纹成核损伤时间、大小及数量的随机特性, 理论结果假设每一次裂纹成核损伤大小及时间间隔一定, 不能很好地呈现随机性, 但是理论与数值试验变化趋势具有一定相似性.

图4

新窗口打开|下载原图ZIP|生成PPT
图4岩石蠕变裂纹成核(a)归一化损伤, (b)应变演化理论与试验^[29-30] 对比曲线

Fig.4Comparison between theoretical and experimental^[29-30] results of the evolution curves in (a) the normalized damage and (b) strain influenced by crack nucleation during creep

图4(b)给出了地壳孕震阶段的地壳应变演化曲线^[30]与本文理论结果的归一化应变演化对比曲线. 由于本文采用实验室尺度岩石模型, 数值上难以与地壳尺度岩石达到一致, 因此采用了归一化对比分析. 模型参数如下: $K_{IC}=1.61$ MPa$\cdot$m$^{1/2}$, $n =57$, $v=0.16$ m/s, $m=1$, $\varepsilon_{o}=1/68$, $\beta=0.276$, $\varphi=32^{\circ}$, $a=3.1$ mm, $\mu=0.51$, $D_{o}=0.048$, $\sigma_{1}=$ $100$ MPa, $\sigma_{3}=4$ MPa, $\gamma=0.2$, $\Delta t_{1}=4.8 \times 10^{5}$ s, $\Delta t=3.6 \times 10^{5}$ s, $\Delta t_{3}=6.2 \times 10^{5}$ s, $\Delta t_{4}=\Delta t_{5}=\Delta t_{8}=1.4 \times 10^{6}$ s, $\Delta t_{6}=\Delta t_{7}=0.6 \times 10^{5}$ s, $\Delta D_{CN1}=\Delta D_{CN3}=\Delta D_{CN5}=\Delta D_{CN6}=\Delta D_{CN7}=5.0 \times 10^{-4}$, $\Delta D_{CN2}=1.0 \times 10^{-3}$, $\Delta D_{CN4}=1.0 \times 10^{-3}$, $\Delta D_{CN8}=2.5 \times 10^{-3}$. 地壳孕震阶段, 变形监测区域的地应力可以近似理解为处于一个恒定应力状态, 此时地壳变形可以近似理解为一个蠕变演化过程, 由于地壳局部裂隙贯通成核损伤突变, 导致了应变的突变, 进而导致局部地震. 成核损伤大小决定了应变增量大小, 进而也影响地震震级. 虽然数值上存在差异, 但是演化趋势相似, 一定程度上解释了裂纹成核损伤突变机理, 为孕震阶段应变演化评价提供了一定参考.

以上理论结果与试验结果变化趋势相似, 然而在数值上存在一定差异, 原因可能是: (1)本文理论模型分别假设岩石内部初始裂纹尺寸及角度均为相同的值, 通过一种平均化方法近似地理论分析了随机分布裂纹岩石力学性能; (2)模型中其他参数选取时存在一定误差.

此外, 不可能为了模拟蠕变结果, 每一个理论模拟都要配合开展声发射试验, 来确定裂纹成核突变发生时间、裂纹成核损伤突变大小, 及裂纹成核数量, 再反过来应用于理论模型中, 实现模拟结果. 对于相同类型的岩石, 可通过监测不同受力状态的大量岩石试样蠕变声发射信号数据规律, 近似地汇总统计出此类岩石不同应力状态下的裂纹成核时间、成核损伤大小及成核数量变化规律, 进而应用于本文模型中, 为预测真实岩石蠕变裂纹成核现象提供一定支持. 本文理论模型还很难模拟真实岩石随机分布裂纹成核时间、成核损伤大小及成核数量的随机特性, 裂纹成核导致的损伤突变大小、裂纹成核发生时间以及裂纹成核数量影响下的脆性岩石蠕变演化, 定性地研究了脆性岩石细观裂纹蠕变成核机理. 下面将对这些因素影响下的蠕变应变演化规律进行详细讨论分析.

2.2 裂纹成核损伤变量对蠕变演化影响

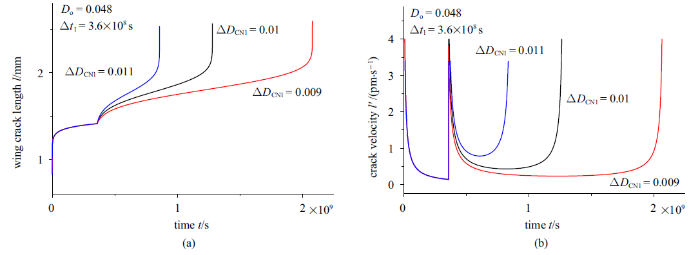
为了便于模型参数对比分析, 下面讨论中模型参数选取如下: $D_{o}=0.048$, $\mu =0.51$, $a=3.1$ mm, $\varphi =45^\circ$, $m=1$, $\varepsilon_{o}=1/68$, $\beta = 0.32$, $K_{IC}=1.61$ MPa$\cdot$m$^{1/2}$, $E=30$ GPa, $v=0.16$ m/s, $n=57$, $\gamma =0.2$, $\sigma_{1}=90$ MPa, $\sigma _{3}=2$ MPa.

图5给出了当岩石整个蠕变演化过程中, 只有一个裂纹成核损伤突变$\Delta D_{CN1}$情况下, 裂纹成核损伤大小对蠕变过程中翼型裂纹扩展长度及裂纹速率随时间演化曲线的影响结果. 对于不同的裂纹成核损伤下, 当发生裂纹成核损伤前, 裂纹长度或裂纹速率随时间演化曲线是一致的; 当裂纹成核损伤发生时, 随着裂纹成核损伤突变值增大, 在给定的时间点, 裂纹长度或裂纹速率均增大, 裂纹扩展至岩石最终失效长度时的时间越短.

图5

新窗口打开|下载原图ZIP|生成PPT
图5中单个裂纹成核损伤大小对蠕变(a)裂纹长度及(b)裂纹速率演化曲线影响

Fig.5Effect of the size of individual crack nucleation damage on creep evolutions of (a) crack length and (b) crack velocity

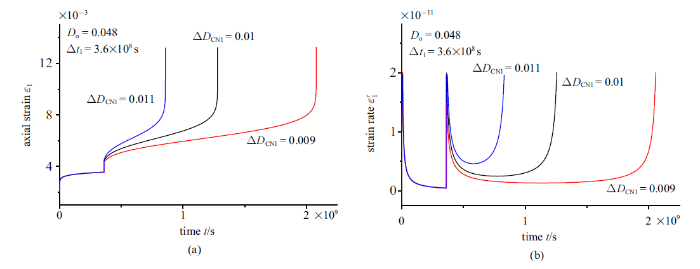
图6给出了岩石蠕变演化过程中, 裂纹成核损伤大小对宏观轴向应变及应变率时间演化曲线的影响结果. 该变化趋势与上述裂纹长度及裂纹速率演化趋势相似. 在裂纹成核损伤突变发生后, 在给定的时间, 随着裂纹成核损伤的增大, 岩石的轴向应变及应变率均增大. 随着裂纹成核损伤突变的增大, 岩石最终蠕变失效时间越短, 图7中也清楚的给出了岩石最终蠕变失效时间随裂纹成核损伤的变化趋势.

图6

新窗口打开|下载原图ZIP|生成PPT
图6单个裂纹成核损伤大小对蠕变(a)轴向应变及(b)应变率演化曲线影响

Fig.6Effect of the size of individual crack nucleation damage on evolutions of (a) axial strain and (b) strain rate during creep

图7

新窗口打开|下载原图ZIP|生成PPT
图7单个裂纹成核损伤大小对岩石蠕变失效时间影响

Fig.7Effect of the size of individual crack nucleation damage on creep failure time of rocks

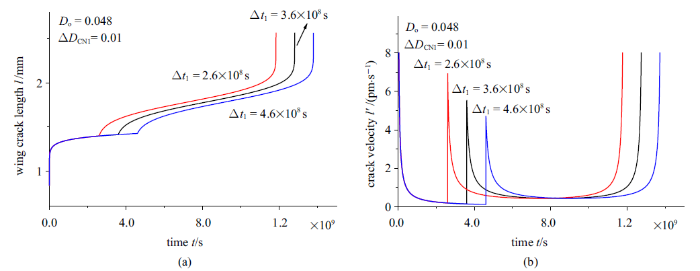
图8中给出了脆性岩石蠕变演化过程中, 当只发生一次裂纹成核损伤突变时, 裂纹成核损伤突变所发生的时间节点$\Delta t_{1}$对岩石蠕变裂纹扩展长度及裂纹速率的影响. 在裂纹成核损伤突变发生后, 随着裂纹成核损伤时间点的增大, 裂纹扩展至最终失效长度的时间越长, 即裂纹成核越晚, 岩石直至最终失效的时间越长, 图10中也进一步给出了证明, 岩石蠕变失效时间随裂纹成核时间成线性增大.

图8

新窗口打开|下载原图ZIP|生成PPT
图8单个裂纹成核损伤发生的时间对蠕变(a)裂纹长度及(b)裂纹速率演化曲线影响

Fig.8Effect of the happened time at individual crack nucleation damage on the evolutions of (a) crack length and (b) crack velocity during creep

图9给出了裂纹成核损伤时间节点对岩石蠕变轴向应变与应变率的影响结果. 轴向应变及应变率演化趋势与裂纹长度变化趋势相似.

图9

新窗口打开|下载原图ZIP|生成PPT
图9单个裂纹成核损伤发生时间对蠕变(a)轴向应变及(b)应变率演化曲线影响

Fig.9Effect of the happened time at individual crack nucleation damage on the evolutions of (a) axial strain and (b) strain rate during creep

以上讨论中, 均是给出了一次裂纹成核损伤突变影响下, 裂纹成核损伤大小及发生时间对岩石蠕变演化的影响. 然而, 对于真实岩石中, 在整个长期蠕变演化过程中, 由于岩石内部裂纹随机分布特性, 导致岩石的非均匀力学性能, 因此岩石内部可能会随机出现多次裂纹成核损伤突变现象. 因此, 下面将对多次裂纹成核损伤发生情况下的岩石蠕变裂纹及应变演化结果进行讨论.

图10

新窗口打开|下载原图ZIP|生成PPT
图10单个裂纹成核损伤发生时间对岩石蠕变失效时间影响

Fig.10Effect of the happened time of individual crack nucleation damage on creep failure time of rocks

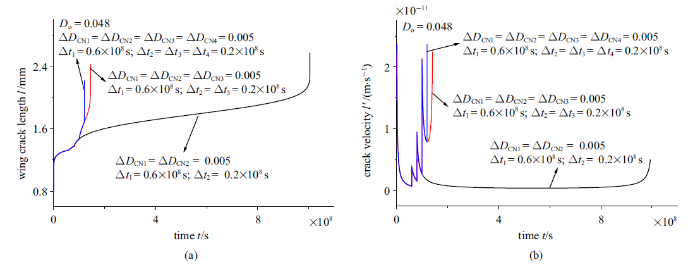
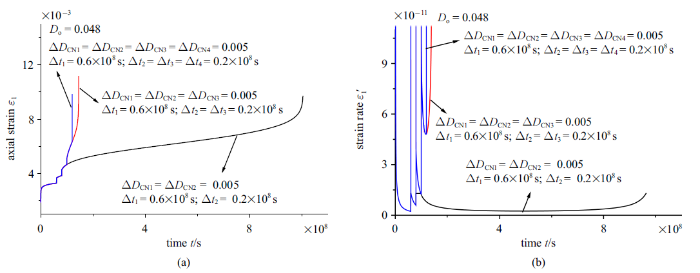
图11(a)分别给出了发生2, 3, 4次裂纹成核损伤突变影响下的裂纹长度随时间演化曲线, 每一次成核损伤值$\Delta D_{CN1}$, $\Delta D_{CN2}$, $\Delta D_{CN3}$, $\Delta D_{CN4}$均为0.005, 第一次裂纹成核$\Delta t$为$0.6\times 10^{8}$ s, 其他裂纹成核损伤之间时间间隔$\Delta t_{2}$, $\Delta t_{3}$, $\Delta t_{4}$均为$0.2\times10^{8}$ s. 图11(b)、图12(a)及图12(b)分别给出了图11(a)相对应的裂纹速率、轴向应变及应变率演化曲线. 当每一次裂纹成核损伤突变值及相邻裂纹成核损伤时间差一定时, 随着裂纹成核数量的增大, 岩石蠕变失效时间减小, 图13也总结归纳出了岩石蠕变失效时间随裂纹成核数量变化规律.

图11

新窗口打开|下载原图ZIP|生成PPT
图11裂纹成核数量对蠕变(a)裂纹长度及(b)裂纹速率演化曲线影响

Fig.11Effect of the number of crack nucleation on the evolutions of (a) crack length and (b) crack velocity during creep

图12

新窗口打开|下载原图ZIP|生成PPT
图12裂纹成核数量对蠕变(a)轴向应变(b)应变率演化曲线影响

Fig.12Effect of the number of crack nucleation on the evolutions of (a) axial strain and (b) strain rate during creep

图13

新窗口打开|下载原图ZIP|生成PPT
图13裂纹成核数量对岩石蠕变失效时间影响

Fig.13Effect of the number of crack nucleation on creep failure time of rocks

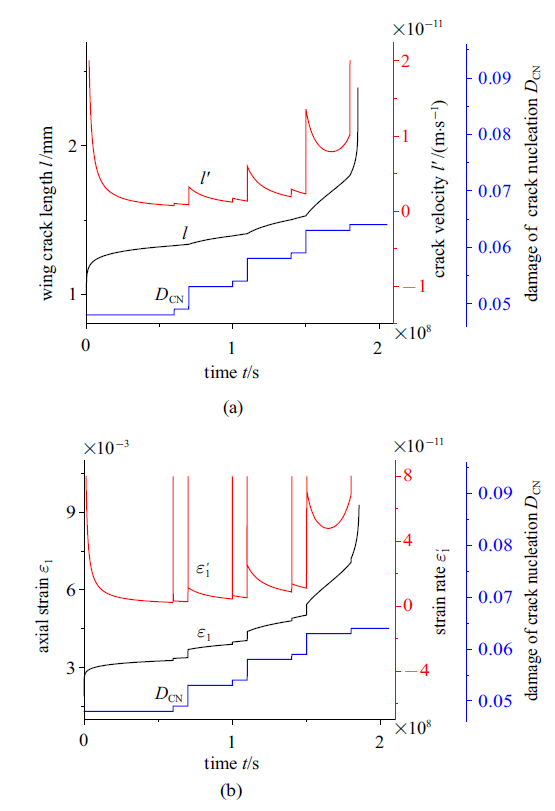
上述关于多次裂纹成核损伤对蠕变演化影响讨论中, 裂纹成核损伤大小及裂纹成核发生时间点均是被假设为定值, 图14给出了岩石蠕变演化过程中, 多次裂纹成核现象出现时, 相邻裂纹成核损伤大小及相邻裂纹成核时间间隔不同的情况下, 岩石内部裂纹长度、裂纹速率、轴向应变及应变随时间演化趋势. 此时, 岩石蠕变过程中, 裂纹长度、裂纹速率、轴向应变及应变率突变性更加接近呈现一种随机特性. 对于深部地下含有随机分布裂纹的自然岩石, 若要更加精确预测岩石非均匀性影响下的蠕变力学性能, 可以通过图1与式(15)中提到的声发射监测数据, 分析不同岩石裂纹扩展导致的声发射率及累计声发射变化值, 预测裂纹成核损伤大小, 并结合本文提出的理论模型方法. 该模型的提出为深部地下工程围岩长期稳定性及短期施工阶段微震及岩爆灾害评价预测提供了重要理论支持.

图14

新窗口打开|下载原图ZIP|生成PPT
图14多变量裂纹成核损伤对蠕变(a)裂纹长度及裂纹速率(b)轴向应变及应变率演化曲线影响

Fig.14Effect of the multiple variables of crack nucleation damage on the evolutions of (a) crack length and crack velocity, (b) axial strain and strain rate during creep

3 结论

基于固体断裂损伤力学理论, 推出了脆性岩石裂纹成核损伤突变影响下的蠕变演化机理模型. 并分析讨论了裂纹成核损伤大小、时间及数量对脆性岩石蠕变裂纹及应变演化特性影响. 具体结论如下:

(1)岩石蠕变过程中, 在同一时间发生一次裂纹成核损伤突变时, 随着裂纹成核损伤大小的增大, 岩石裂纹长度、裂纹速率、轴向应变及应变率均增大, 岩石最终蠕变失效时间减小.

(2)岩石蠕变过程中, 发生一次裂纹成核损伤突变时, 裂纹成核损伤突变发生的时间越早, 岩石最终发生失效的时间越短, 而且岩石蠕变失效时间与裂纹成核时间成线性递增关系.

(3)在岩石蠕变过程中, 发生多次裂纹成核现象时, 当岩石裂纹成核损伤大小及相邻裂纹成核时间间隔相同的情况下, 随着裂纹成核数量的增大, 岩石蠕变失效时间减小; 当岩石裂纹成核损伤大小及裂纹成核时间间隔不同且随机时, 岩石蠕变变形演化更加接近含随机分布裂纹的真实岩石非均匀性导致的蠕变演化规律, 其也为深部地下工程微震及岩爆事件预测评价提供一定参考.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

范庆忠, 高延法. 分级加载条件下岩石流变特性的试验研究
岩土工程学报, 2005,27(11):38-41

[本文引用: 1]

(Fan

Qingzhong

, Gao

Yanfa

. Experimental study on creep properties of rocks under stepwise loading
Chinese Journal of Geotechnical Engineering, 2005,27(11):38-41 (in Chinese))

[本文引用: 1]

[2]

邓华锋, 周美玲, 李建林等. 砂质泥岩三轴卸荷流变力学特性试验研究
岩土力学, 2016,37(2):315-322

[本文引用: 1]

(Deng

Huafeng

, Zhou

Meiling

, Li

Jianlin

, et al. Experimental research on unloading triaxial rheological mechanical properties of sandy mudstone
Rock and Soil Mechanics, 2016,37(2):315-322 (in Chinese))

[本文引用: 1]

[3]

佘成学, 崔旋. 高孔隙水压力对岩石蠕变特性的影响
岩石力学与工程学报, 2010,29(8):1603-1609

[本文引用: 1]

(She

Chengxue

, Cui

Xuan

. Influence of high pore water pressure on creep properties of rock
Chinese Journal of Rock Mechanics and Engineering, 2010,29(8):1603-1609 (in Chinese))

[本文引用: 1]

[4]

江宗斌, 姜谙男, 李宏等. 加卸载条件下石英岩蠕变-渗流耦合规律试验研究
岩土工程学报, 2017,39(10):1832-1841

(Jiang

Zongbin

, Jiang

Annan

, Li

Hong

, et al. Creep-seepage coupling laws of quartzite under cyclic loading-unloading conditions
Chinese Journal of Geotechnical Engineering, 2017,39(10):1832-1841 (in Chinese))

[5]

张强勇, 张龙云, 向文等. 考虑温度效应的片麻状花岗岩三轴蠕变试验研究
岩土力学, 2017,38(9):2507-2514

(Zhang

Qiangyong

, Zhang

Longyun

, Xiang

Wen

, et al. Triaxial creep test of gneissic granite considering thermal effect
Rock and Soil Mechanics, 2017,38(9):2507-2514 (in Chinese))

[6]

陈亮, 刘建锋, 王春萍等. 不同温度及应力状态下北山花岗岩蠕变特征研究
岩石力学与工程学报, 2015,34(6):1228-1235

[本文引用: 1]

(Chen

Liang

, Liu

Jianfeng

, Wang

Chunping

, et al. Creeping behavior of beishan granite under different temperatures and stress conditions
Chinese Journal of Rock Mechanics and Engineering, 2015,34(6):1228-1235 (in Chinese))

[本文引用: 1]

[7]

张明, 毕忠伟, 杨强等. 锦屏一级水电站大理岩蠕变试验与流变模型选择
岩石力学与工程学报, 2010,29(8):1530-1537

[本文引用: 1]

(Zhang

Ming

, Bi

Zhongwei

, Yang

Qiang

, et al. Creep test and rheological model selection of marble of Jinping I hydropower station
Chinese Journal of Rock Mechanics and Engineering, 2010,29(8):1530-1537 (in Chinese))

[本文引用: 1]

[8]

吴斐, 谢和平, 刘建锋等. 分数阶黏弹塑性蠕变模型试验研究
岩石力学与工程学报, 2014,33(5):964-970

[本文引用: 1]

(Wu

Fei

, Xie

Heping

, Liu

Jianfeng

, et al. Experimental study of fractional viscoelastic- plastic creep model
Chinese Journal of Rock Mechanics and Engineering, 2014,33(5):964-970 (in Chinese))

[本文引用: 1]

[9]

卢广达, 陈建兵. 基于一类非局部宏$-$微观损伤模型的裂纹模拟
力学学报, 2020,52(3):749-762

[本文引用: 1]

(Lu

Guangda

, Chen

Jianbing

. Cracking simulation based on a nonlocal macro-meso-scale damage model
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(3):749-762 (in Chinese))

[本文引用: 1]

[10]

吴建营. 固体结构损伤破坏统一相场理论、算法和应用
力学学报, 2021,53(2):301-329

(Wu

Jianying

. On the theoretical and numerical aspects of the unified phase-field theory for damage and failure in solids and structures
Chinese Journal of Theoretical and Applied Mechanics, 2021,53(2):301-329 (in Chinese))

[11]

王勃, 张阳博, 左宏等. 压应力对压剪裂纹扩展的影响研究
力学学报, 2019,51(3):845-851

[本文引用: 1]

(Wang

, Zhang

Yangbo

, Zuo

Hong

, et al. Study on the influence of compressive stress on the compression shear crack propagation
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):845-851 (in Chinese))

[本文引用: 1]

[12]

刘迪, 周宏伟, 赵阳等. 基于声发射特征的盐岩蠕变本构模型研究
岩土力学, 2017,38(7), 1951-1958

[本文引用: 7]

(Liu

, Zhou

Hongwei

, Zhao

Yang

, et al. Study of creep constitutive model of rock salt based on acoustic emission characteristics
Rock and Soil Mechanics, 2017,38(7), 1951-1958 (in Chinese))

[本文引用: 7]

[13]

徐子杰, 齐庆新, 李宏艳等. 不同应力水平下大理石蠕变损伤声发射特性
煤炭学报, 2014,39(S1):70-74

[本文引用: 1]

(Xu

Zijie

, Qi

Qingxin

, Li

Hongyan

, et al. Marble creep damage and acoustic emission characteristics under different stress levels
Journal of China Coal Society, 2014,39(S1):70-74 (in Chinese))

[本文引用: 1]

[14]

于群, 唐春安, 李连崇等. 基于微震监测的锦屏二级水电站深埋隧洞岩爆孕育过程分析
岩土工程学报, 2014,36(12):2315-2322

[本文引用: 1]

(Yu

Qun

, Tang

ChunAn

, Li

Lianchong

, et al. Nucleation process of rockbursts based on microseismic monitoring of deep-buried tunnels for Jinping II Hydropower Station
Chinese Journal of Geotechnical Engineering, 2014,36(12):2315-2322 (in Chinese))

[本文引用: 1]

[15]

陈炳瑞, 冯夏庭, 明华军等. 深埋隧洞岩爆孕育规律与机制: 时滞型岩爆
岩石力学与工程学报, 2012,31(3):561-569

[本文引用: 1]

(Chen

Bingrui

, Feng

Xiating

, Ming

Huajun

, et al. Evolution law and mechanism of rockbursts in deep tunnels: Immediate rockburst
Chinese Journal of Rock Mechanics and Engineering, 2012,31(3):561-569 (in Chinese))

[本文引用: 1]

[16]

李晓照, 戚承志, 邵珠山. 脆性岩石局部细观裂纹成核损伤突变机理研究
中国科学: 技术科学, 2020. doi: 10.1360/SST-2020-0185

[本文引用: 2]

(Li

Xiaozhao

, Qi

Chengzhi

, Shao

Zhushan

. Research on mechanisms of the damage catastrophe from localized microcrack nucleation in brittle rocks

Scientia Sinica Technologica

2020. doi: 10.1360/SST-2020-0185 (in Chinese))

[本文引用: 2]

[17]

李晓照, 邵珠山. 脆性岩石渐进及蠕变失效特性宏细观力学模型研究
岩土工程学报, 2016,38(8):1391-1398

[本文引用: 5]

(Li

Xiaozhao

, Shao

Zhushan

. Macro-micro mechanical model for progressive and creep failure of brittle rock
Chinese Journal of Geotechnical Engineering, 2016,38(8):1391-1398 (in Chinese))

[本文引用: 5]

[18]

Ashby

, Sammis

. The damage mechanics of brittle solids in compression
Pure Applied Geophysics, 1990,133(3):489-521

[本文引用: 2]

[19]

李晓照, 戚承志, 邵珠山等. 基于细观力学脆性岩石剪切特性演化模型研究
岩土力学, 2019,40(4):1358-1367

[本文引用: 3]

(Li

Xiaozhao

, Qi

Chengzhi

, Shao

Zhushan

, et al. Micromechanics-based model study of shear properties of brittle rocks
Rock and Soil Mechanics, 2019,40(4):1358-1367 (in Chinese))

[本文引用: 3]

[20]

赵延林, 万文, 王卫军等. 类岩石材料有序多裂纹体单轴压缩破断试验与翼形断裂数值模拟
岩土工程学报, 2013,35(11):2097-2109

[本文引用: 1]

(Zhao

Yanlin

, Wan

Wen

, Wang

Weijun

, et al. Fracture experiments on ordered multi-crack body in rock-like materials under uniaxial compression and numerical simulation of wing cracks
Chinese Journal of Geotechnical Engineering, 2013,35(11):2097-2109 (in Chinese))

[本文引用: 1]

[21]

Lee

, Jeon

. An experimental and numerical study of fracture coalescence in pre-cracked specimens under uniaxial compression
International Journal of Solids and Structures, 2011,48:979-999

[22]

Zhou

, Zhu

, Ju

, et al. Volumetric fracturing behavior of 3D printed artificial rocks containing single and double 3D internal flaws under static uniaxial compression
Engineering Fracture Mechanics, 2019,205:190-204

[23]

Liu

, Ju

, Fu

, et al. Visualization of full-field stress evolution during 3D penetrated crack propagation through 3D printing and frozen stress techniques
Engineering Fracture Mechanics, 2020,236:107222

[24]

Feng

, Xu

, Dai

. Effects of dynamic strain rate on the energy dissipation and fragment characteristics of cross-fissured rocks
International Journal of Rock Mechanics and Mining Sciences, 2021 138:104600

[25]

Cao

, Cao

, Lin

, et al. Failure characteristics of jointed rock-like material containing multi-joints under a compressive-shear test: Experimental and numerical analyses
Archives of Civil and Mechanical Engineering, 2018,18(3):784-798

[本文引用: 1]

[26]

Atkinson

. Subcritical crack growth in geological materials
Journal of Geophysical Research, 1984,89(B6):4077-4114

[本文引用: 1]

[27]

陈忠辉, 傅宇方, 唐春安. 岩石破裂声发射过程的围压效应
岩石力学与工程学报, 1997,16(1):65-70

[本文引用: 1]

(Chen

Zhonghui

, Fu

Yufang

, Tang Chun'an. Confining pressure effect on acoustic emissions during rock failure
Chinese Journal of Rock Mechanics and Engineering, 1997,16(1):65-70 (in Chinese))

[本文引用: 1]

[28]

杨永杰, 王德超, 郭明福等. 基于三轴压缩声发射试验的岩石损伤特征研究
岩石力学与工程学报, 2014,33(1):98-104

[本文引用: 1]

(Yang

Yongjie

, Wang

Dechao

, Guo

Mingfu

, et al. Study of rock damage characteristics based on acoustic emission tests under triaxial compression
Chinese Journal of Rock Mechanics and Engineering, 2014,33(1):98-104 (in Chinese))

[本文引用: 1]

[29]

孙金山, 陈明, 姜清辉等. 锦屏大理岩蠕变损伤演化细观力学特征的数值模拟研究
岩土力学, 2013,34(12):3601-3608

[本文引用: 3]

(Sun

Jinshan

, Chen

Ming

, Jiang

Qinghui

, et al. Numerical simulation of mesomechanical characteristics of creep demage evolution for Jingping marble
Rock and Soil Mechanics, 2013,34(12):3601-3608 (in Chinese))

[本文引用: 3]

[30]

秦四清, 徐锡伟, 胡平等. 孕震断层的多锁固段脆性破裂机制与地震预测新方法的探索
地球物理学报, 2010,53(4):1001-1014

[本文引用: 3]

(Qin

Siqing

, Xu

Xiwei

, Hu

Ping

, et al. Brittle failure mechanism of multiple locked patches in a seismogenic fault system and exploration on a new way for earthquake prediction
Chinese Journal of Geophysics, 2010,53(4):1001-1014 (in Chinese))

[本文引用: 3]