倪宝玉^,2), 曾令东, 熊航, 吴其远哈尔滨工程大学船舶工程学院,哈尔滨 150001

REVIEW ON THE INTERACTION BETWEEN SEA ICE AND WAVES/CURRENTS¹⁾

Ni Baoyu^,2), Zeng Lingdong, Xiong Hang, Wu QiyuanCollege of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China

通讯作者: 2) 倪宝玉,教授,主要研究方向：冰水船耦合动力学. E-mail:nibaoyu@hrbeu.edu.cn

收稿日期:2020-11-22网络出版日期:2021-03-18

基金资助:

1) 国家重点研发计划.2017YFE0111400 国家自然科学基金.51979051 国家自然科学基金.51979056 国家自然科学基金.51639004 黑龙江省自然科学基金.A2018003

Received:2020-11-22Online:2021-03-18
作者简介 About authors


摘要
随着全球气候变暖,北极活动频次的逐渐增加,海冰与波流的耦合作用成为了国内外的热点研究问题. 海冰的存在会改变波浪的传播特性和色散关系,也会改变海流运动的边界条件,使得海流在冰面下边界处可能产生漩涡脱落等现象;而海冰在波浪、海流等动力作用下,也会不断发生生消、断裂、重叠和堆积等动力学行为.海冰与波流耦合动力学中存在几大难点问题：一是海冰模型的构建,需要针对海冰类型和性质的不同,考虑不同区域的海冰分布情况建立合适的海冰模型.二是冰水之间的耦合问题,海冰边界影响着冰水之间的动量和能量交换,对于冰盖、浮冰等不同类型海冰,需分别处理边界问题;冰水耦合引起的海冰破坏,其破坏模式也是多样的.三是波流联合场的构建,目前尚无较好的方法构建波流联合场,导致海冰与波流联合场作用的相关研究仍极其匮乏.因此,本文针对海冰与波流相互作用问题,回顾和讨论国内外对海冰与波浪、海冰与海流及海冰与波流相互作用的研究现状和技术难点,展望了未来可以进一步深入研究的问题,提出了初步的思路以供参考.
关键词： 海冰;波浪;海流;耦合作用;海冰模型

Abstract
With global warming and the increasing frequency of Arctic activities, the interaction between sea ice and waves/currents has become an attractive research issue at home and abroad. The existence of sea ice changes the propagation characteristics and dispersion relationships of waves, and also changes the boundary conditions of ocean currents, inducing vortex shedding at the lower surface of the sea ice. The sea ices generate and extinct, fracture, overlap and accumulate under the effects of waves and currents. There are several difficulties in studying the interaction between sea ice and waves/currents. The first is the construction of sea ice model appropriately, which needs to consider the differences of the types and properties of sea ice in different cold regions. The distributions of sea ice also should be taken into account in the sea ice model. The second is the coupling problem between sea ice and water. The boundary of sea ice affects the exchange of momentum and energy between sea ice and water. The boundary conditions of sea ice should be dealt with appropriately in terms of ice sheet and ice floes. There are many fracture modes of sea ice, but the sea ice may have complex fracture modes with coexistence of many different fracture modes under the action of sea ice and water coupling. The third is the construction of wave-current joint field. At present, there is no efficient method to construct the wave-current joint field, which leads to lack of relevant research on interaction for sea ice and wave-current joint field to understand the physic problem. Therefore, this paper reviews and discusses the research status and technical difficulties of interactions between sea ice and wave, current and wave-current fields. The problems that can be further studied in the future are predicted and the preliminary ideas are put forward for reference.
Keywords：sea ice;wave;ocean current;coupling;sea ice model


PDF (12864KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
倪宝玉, 曾令东, 熊航, 吴其远. 海冰与波流耦合动力学的研究进展¹⁾. 力学学报[J], 2021, 53(3): 641-654 DOI:10.6052/0459-1879-20-394
Ni Baoyu, Zeng Lingdong, Xiong Hang, Wu Qiyuan. REVIEW ON THE INTERACTION BETWEEN SEA ICE AND WAVES/CURRENTS¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(3): 641-654 DOI:10.6052/0459-1879-20-394

引言

极地地区蕴藏着丰富的自然资源,是未来重要的能源和资源基地,同时也存在巨大的航运潜力,是潜在的国际航运路线. 近年来,随着极地海冰的缩减,北极航道和极地资源开发都变得日渐现实,海洋油气资源开采区域开始向极地地区延伸?^[1],利用北极航线进行商业活动的频次也正在逐年提升?^[2],结构物在冰区的相关研究也受到了极大的关注?^[3].

与敞水环境条件不同,低温多冰的极区环境复杂多变,不同存在形式的冰形态以及冰与波流的相互作用对极区结构物冰载荷和性能有着重要的影响?^[4-5]. 当船舶航行于冰区时,浮冰在 波流的作用下会发生漂移堆积,可能会对船舶预定的航行路线造成阻碍,甚至直接导致船舶发生冰困事故. 因此,了解海冰与波流的耦合作用对于冰区船舶设计以及船舶在极地航行都有着重要的意义.

在自然界中,波流与海冰的相互作用是极地波流演化和海冰生消/运动的主要动力原因之一. 波流与海冰的相互作用可以从波流和海冰两个角度看,从波流特性角度看,海冰的存在改变了波浪的传播特性和色散关系,导致波幅和能量的逐渐衰减;海冰的存在改变了海流运动的边界条件,使得海流在冰面下边界处可能产生漩涡脱落等现象. 从海冰特性角度看,波浪在冰水交界处的动量反射所产生的推力和海流作用下所产生的拖曳力是海冰运动的主要作用力,海冰在波浪、海流等动力作用下,不断发生生消、断裂、重叠和堆积等动力学行为. 尤其近年来海冰面积和厚度的减小,极区波浪密度已经显著增强,使得波流与海冰相互作用越来越引起科研人员的关注.

关于海冰与波流耦合作用研究,冰场模型的构建是其中的一大难点.由于海冰与开阔水域交界区域的波浪作用比较强烈,海冰会被 破碎成一块块的浮冰.因此,从空间上看,根据海冰地理位置的不同,会发生波流与单块浮冰的相互作用,波流与浮冰群的相互作用,波流与大冰盖的相互作用,这就需要针对不同的区域建立不同海冰模型.其次,海冰自身内部结构形式存在卤水通道、裂纹等多种不连续孔隙,其宏观力学行为又会随着内部结构形式的改变而发生变化.最后,海冰在波流作用下还可能发生断裂的力学行为,由于海冰材料的特殊性,其断裂的条件会随着外载荷的作用速率和作用方式发生变化.

波、流是两种不同的外载荷,针对波浪与冰的相互作用研究,新西兰的Squire教授?^[6-9]对这方面进行了较全面的综述.Zhao等?^[10]对波浪与冰相互作用的模拟进行了综述,介绍了海冰类型、波浪海冰相互作用模型、波浪衰减机理、计算波反射和透射的方法和海冰破坏对海冰形态影响几个方面内容,并讨论了模型试验、现场测量和数值模型3种手段在促进波浪与冰相互作用模型中的作用.Shen?^[11]进一步指出了波浪与冰相互作用模型包括基于理论的模型、基于测量数据的模型以及理论和数据结合形成的模型3类,对不同的波浪与海冰作用模型的基本概念以及如何校准和验证这些模型等问题进行了介绍和讨论.在此基础上,本文就海冰与波流耦合动力学的研究从3个方面进行综述,分别为海冰与波浪的相互作用研究、海冰与海流的相互作用研究以及海冰与波流联合场的相互作用研究,以期为相关的研究者提供参考.

1 海冰与波浪相互作用研究

海冰与波浪相互作用研究逻辑关系如图1所示.首先从研究历程看,连续介质模型的出现是研究不可破碎海冰与波浪相互作用的基础,在认识不可破碎海冰与波浪相互作用基础上,需要进一步考虑海冰可破碎的特点.为此将分别从海冰波浪相互作用的连续介质模型、不可破碎海冰与波浪的相互作用、可破碎海冰与波浪的相互作用研究3个方面进行综述. 其次,针对不可破碎海冰与波浪的相互作用,根据海冰尺寸与波长的相互关系,本文进一步分为冰盖(尺寸远大于波长)和浮冰(尺寸小于波长或与波长相同量级)两种类型,分别讨论二者与波浪的相互作用.最后,针对冰盖与波浪的相互作用,本文又根据冰盖物理表现的不同,进一步划分成了4种类型：(1) 连续冰盖;(2)裂缝冰盖;(3) 带水道冰盖;(4) 固结航道冰盖.而针对浮冰与波浪的相互作用,根据浮冰数量不同,又进一步划分为：有限块浮冰和浮冰群.

图1

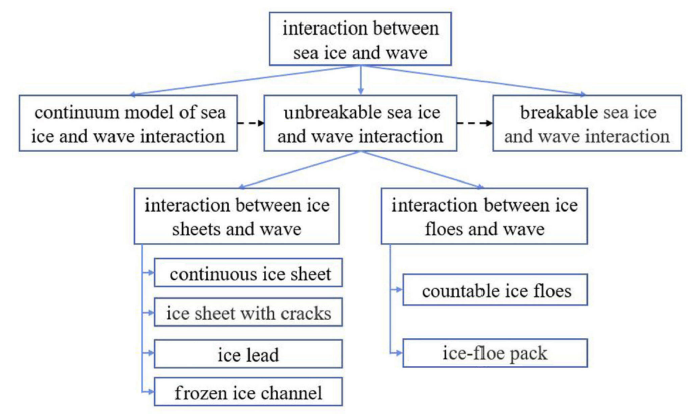新窗口打开|下载原图ZIP|生成PPT
图1海冰与波浪相互作用研究逻辑关系图

Fig. 1Logical diagram of sea ice and wave interaction

1.1 海冰波浪相互作用的连续介质模型

海冰内部结构形式存在卤水通道、裂纹等多种不连续孔隙,海冰的外部形态以及空间分布也是随机的,从而使得很难建立稳定可靠的海冰模型,这对波流与海冰相互作用的研究带来了极大的挑战.

从发展历程来看,目前国内外模拟波浪与海冰的相互作用可以被划分为5个阶段,每个阶段都有对应的代表性海冰模型被提出.最早且最简单的一种模型是由Peters?^[12]和Weitz和Keller?^[13]提出的质量点模型,其将海冰假设为一系列相互独立的质量点所组成,质量点与下方的流体之间存在力的作用,但质量点与质量点之间并没有力的作用.质量点模型比较适用于冰盖形成初期的莲叶冰阶段.第2阶段代表性模型是弹性薄板模型?^[14],也是目前理论分析中应用较广的一种模型,但是这种模型较为理想,无法准确反映波浪在海冰中传播的衰减效应,为此,有****在弹性板模型的基础上引入了冰的应变松弛效应,形成了另一种在解析分析中应用较广的黏弹性薄板模型?^[15].第3阶段发展中,****提出了黏性层模型?^[16-17],此模型将海冰假设为一层黏性流体,以模拟波流经过海冰时的能量衰减效果,黏性层模型比较适用于尺度远小于波长的碎冰形成的油脂冰,但是这种模型又无法模拟出海冰的板结构特性.第4阶段中,Wang和Shen?^[18]发展了一种黏弹性层模型,在黏性层模型中考虑了弹性力的影响,不仅可以用于模拟波浪与海冰的相互作用,还可以用于冰缘区的模拟.在此基础上,Zhao等?^[19]分析了此黏弹性层模型冰在波浪作用下的波模态特点.Zhao和Shen?^[20]更进一步发展该模型,提出包含黏弹性冰层、有旋黏性的湍流边界层以及无黏水层的3层模型来模拟冰盖.除此之外,Zhao和Zhang?^[21]还考虑了由冰面上方风流层,黏弹性冰层以及无黏水层构成的3层系统,结果表明,该模型与现场和实验室内开敞水域的观测数据基本吻合.对真实冰区应用这种黏弹性模型时,需要根据实际海冰区域特点确定有效黏性系数和有效剪切模量.Cheng等?^[22]利用多目标遗传算法以及在秋季的北冰洋西部以饼状冰为主的边缘冰区收集的实验数据,标定了黏弹性模型的有效黏性系数和有效剪切模量,并对标定后的模型进行了验证,模拟结果与饼状冰为主的冰区中的实测波参数吻合良好.除了使用现场测量试验数据以外,还可以利用冰水槽试验?^[23]和理论依据?^[23-24]确定模型冰的有效特征参数.

近5年来,有****开始关注海冰的孔隙特性,开始致力于研究海冰的多孔隙模型.本文将此阶段称为第5阶段,这一阶段 代表性的工作有Meylan等?^[25]和Zheng等?^[26]提出的一种多孔弹性板模型,他们假设自由表面上的海冰为一块多孔结构的弹性板,通过一个假设的渗透系数来控制此多孔弹性板的孔隙参数,渗透系数基于达西定律得到.另一代表性工作是Chen等?^[27]提出的二维多孔弹性介质海冰模型.此模型将海冰假设为黏弹性材料,流体假设为可压缩的理想流体,基于海冰和流体之间的应力应变关系以及毕奥方程建立了一个各向同性的多孔黏弹性模型模拟海冰,模型的孔隙率由自由表面海冰的覆盖率决定,根据不同冰区的海冰分布情况就可以确定相应的海冰模型. 由于实际海冰分布情况是随机且变化的,且海冰本身也是一个具有空间形状特点的多孔结构.因此,对于波浪与海冰的相互作用模型而言,目前的多孔隙海冰模型较之以往的模型能更好地体现真实的海冰状态,但是目前多孔弹性板中孔隙参数的选取并没有实际的物理意义,孔隙大小以及渗透率的确定也没有明确的依据.

1.2 不可破碎海冰与波浪的相互作用

1.2.1 冰盖与波浪的相互作用

(1) 连续冰盖

波浪从敞水向一块被冰盖大范围覆盖的区域,由于大冰盖延伸的长度达到了数十或数百千米,因此可以将此冰盖视为一块半无限大的冰盖,冰盖的另一侧是一片敞水域.这样的场景经常发生在极区的边缘区域,这也是海洋结构物在极地经常活动的区域.对于这样一个问题,波浪在遇到冰盖后的幅值变化,波浪反射和透射的能量变化是****们重点关注的一个问题.

关于此问题的研究,在现有海冰与波浪相互作用模型基础上,针对不同的情况,可以采用不同的模型假设模拟冰面.基于实用和 研究方便的角度考虑,目前主要是采用弹性板假设进行研究.Balmforth和Craster?^[28]基于弹性厚板理论,采用Wiener-Hopf方法和傅里叶变换对波浪与冰相互作用问题进行了研究,但通过无量纲化分析的结果表明1.1节中第2阶段的弹性薄板模型已经能较好地描述此问题.因此,此类大多数研究工作都采用弹性薄板方程描述冰层运动.

由于波浪从敞水域入射到冰盖区域,如图2所示.根据波浪入射的方向可以分为垂直入射和斜入射,波浪垂直入射时可以将此问题简化为二维问题.Fox和Squire?^[29]利用特征函数展开法将冰面和水面下方的速度势分别展开,然后借助共轭梯度法建立冰水分界面的连续条件和冰面边界条件,发现了波浪反射和透射系数的变化规律,随着波浪周期的增加,波浪能量的反射系数趋于1.Fox和Squire?^[30]又进一步研究了波浪斜入射时的传播特性,发现从敞水域向冰层覆盖流域传播的波浪频率增加到某一临界角度后,波浪也会全部被反射到敞水域.Tkacheva?^[31-32]基于Wiener-Hopf方法分别研究了波浪垂直入射和斜入射时的情况,分析了海底深度和冰刚度对冰面变形的影响,发现冰面变形受水深变化影响较小,而受冰面刚度和水波入射角影响较大,当入射角度大于临界角度时,远离冰面边界处的冰面不会发生变形.Sahoo等?^[33]针对波浪垂直入射冰盖内的二维情况,利用傅里叶分析提出了一个新的正交内积应用在特征函数展开法,分析了冰盖边界位置处满足不同边界条件(自由端、简支端、固定端)时的冰面响应.发现固定边界条件反射的波能量最大,透射的波能量最小;而自由边界条件下冰盖的变形最大.Linton和Chung?^[34]采用留数微分技术(RCT)分别考虑了波浪从敞水域入射和冰覆盖区入射两种情况,发现这两种情况下反射系数的模相等,而透射系数间存在一个倍数关系.

图2

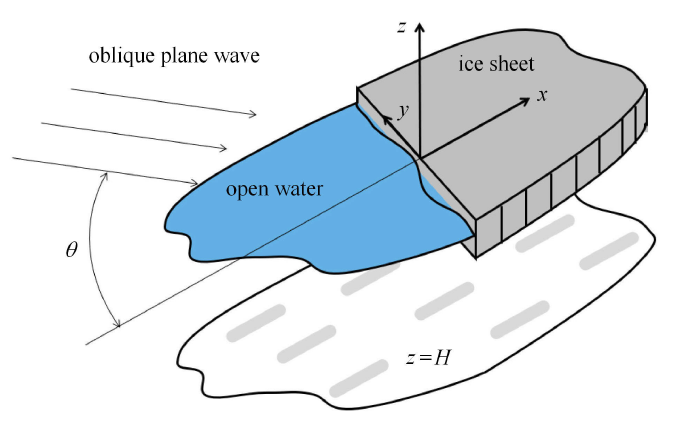新窗口打开|下载原图ZIP|生成PPT
图2波浪与半无限大冰面的相互作用?^[30]

Fig. 2Interaction of waves and semi-infinite ice?^[30]



实际上极地的冰盖并不是一块连续均匀的冰盖,冰盖之间可能会有厚度的变化,基于此,Zhao和Shen?^[35]采用一种双模态近似方法,针对两块不同厚度黏弹性冰组成的冰盖,分析了波浪在此种黏弹性冰盖中传播的二维问题,研究了波浪的透射和反射情况.发现此冰盖的黏度较大时,波浪传播的模态不会产生切换现象(mode switching phenomenon).Zhao和Shen?^[36]采用变分法研究了同样的问题. 发现此变分法比双模态近似法?^[35]更为准确.

除此之外,冰盖中间可能会存在某种缺陷,如裂缝或是冰间水道,这都会影响波浪在冰区的传播特性以及冰盖的水动力响应.

(2) 裂缝冰盖

透射到冰盖下方传播的波浪,当波浪引起冰盖内部产生的弯曲应力超过冰盖的承载极限后,会引起冰盖发生破坏形成一条裂缝,此时裂缝附近的波流场也会发生明显的改变.Barrett和Squire?^[37]研究了完整冰盖上存在一条无限长裂缝的情况,数值结果表明短波遇到裂缝后大部分的波浪能量会被反射回去;当波浪以某些频率传播时,波浪经过裂缝时发生零反射.Evans和Porter?^[38]研究了同样的问题,发现了对称的边缘波(edgewaves)的存在,且边缘波会沿着裂缝传播,并在垂直于裂缝的方向上衰减.Porter和Evans?^[39-40]研究了波浪经过多个平行且周期排布的无限长裂缝和有限长裂缝的冰盖.近几年,Li等?^[41]先研究了无限大冰盖上存在的圆形裂缝对波浪传播的影响,随后,Li等?^[42]又研究了任意形状裂缝对波浪传播的影响,分析了裂缝形状和排布方向对波浪传播的响应,发现沿着波浪传播方向的直裂缝对整体流动没有太大的影响.

关于带裂缝冰面与波浪相互作用研究,经历了从平行裂缝到任意形状裂缝,针对波浪经过不同裂缝的能量变化有了较为完善的研究,但是裂缝两侧的海冰在波浪作用下会如何发生分离形成水道的过程还没有展开,也即冰面裂缝形成水道的变化过程尚未认清.

(3) 带水道冰盖

产生裂缝的冰盖在受到波浪的持续作用下,裂缝两侧的冰盖可能会逐渐分开而形成一条狭窄的敞水航道,此敞水航道的宽度被两侧的两块无限大冰盖所限制,形成了极地常见的冰间水道,如图3所示.Marchenko?^[43]基于浅水假设分析了航道两侧冰盖用弹性薄板和刚体模拟时的情况,得到了波浪在破冰航道内传播的色散关系.对于波浪垂直破冰航道传播时,此时可以简化为二维问题,Chung和Linton?^[44]利用留数微分技术求解了此问题,发现存在无限个入射波频率点使得波浪从航道的一侧传到另一侧时不会有任何的能量损失,即波浪透射系数为1.Shi等?^[45]基于宽空间(widespace)近似,分析了波浪经过多个破冰航道时的相互作用,发现当航道数目增加时,反射系数和透射系数随着波浪频率的增大振动得更为剧烈.最为一般的情况就是波浪斜入射进入破冰航道,Williams和Squire?^[46]考虑了波浪传播到3个具有不同厚度的弹性薄板的更一般情况,板与板之间没有间隙,且板的边缘不受弯曲应力和剪力的作用,位于中间的薄板的厚度可以减小到零,此时就可以直接处理破冰在破冰航道内传播的问题.Porter?^[47]研究了无限水深假设下的情况,证实了冰盖边缘波的存在,即冰盖只能在边缘附近振动,无法传播到冰面内部较远的位置.

图3

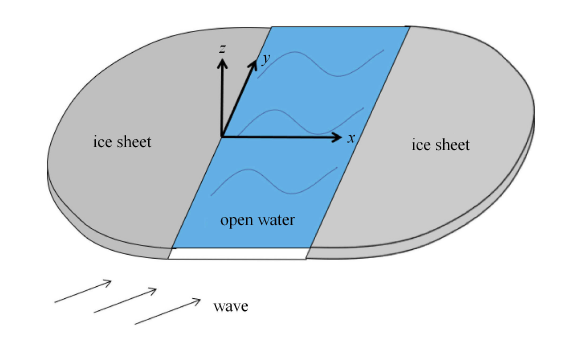新窗口打开|下载原图ZIP|生成PPT
图3波浪与冰间航道相互作用

Fig. 3Interaction between waves and ice channels



由于冰面黏性的影响,波浪无法传播到冰面内部较远的位置,因此,波浪经过冰间水道的能量变化是****们比较关心的方向之一,而边缘波的强度决定了冰间水道是否能够被进一步扩宽,边缘波的特点也受到了关注?^[47].

(4) 固结航道冰盖

固壁面对波浪与海冰耦合作用的影响是极其重要的,因为海冰与固壁面间边界条件的存在会影响波浪传播的色散关系,进而改变波浪的传播特性,同时,冰盖的响应特点也会发生改变.因此,有部分****针对波浪与冻结固壁航道的相互作用进行了相关研究,如图4所示,这种数学模型对应的真实物理情况包括冬季冻结的内河航道以及冰水池等.Korobkin等?^[48]研究了波浪在冻结固壁航道中的传播特性,此时流体在航道壁面处需满足壁面不可穿透条件,而海冰与航道壁面冻结在一起,也需要满足固定边界条件.他们发现波浪在此冻结固壁航道内传播时波的色散关系发生了变化,不同于波浪与无限大弹性冰板相互作用时只存在一个色散关系的情况,此时存在无限多个色散关系;其次,当入射波为短波时,冰盖最大应力在航道中间处取得,也就是冰盖的中间,但是当入射波波长较长时,冰盖的最大应力在航道壁面处取得,这也表明,此时冰盖在发生破坏前会先与壁面发生分离,从而冰盖的边界条件从固壁条件转化为自由边界条件的情况.对于这一种情况,Batyaev和Khabakhpasheva?^[49]进行了相关研究,他们发现短波在固壁航道内传播时,冰盖产生横向裂缝的情况是主要的,而当长波在航道内传播时,冰盖的最大应力在离航道壁面的一定距离处取得,且会产生沿着航道方向的纵向裂缝,此时波浪与冰盖相互作用问题的边界条件又发生了变化.Ren等?^[50]则研究了冰面与冻结固壁航道壁面间不同边界条件组合的影响. 发现对于冰面与航道壁面为自由边界或是固壁边界情况,航道内冰面的最大主应力通常出现在壁面附近.但对于冰面与航道壁面为简支边界时,最大主应力通常出现在与航道壁面相距一定距离的位置.

图4

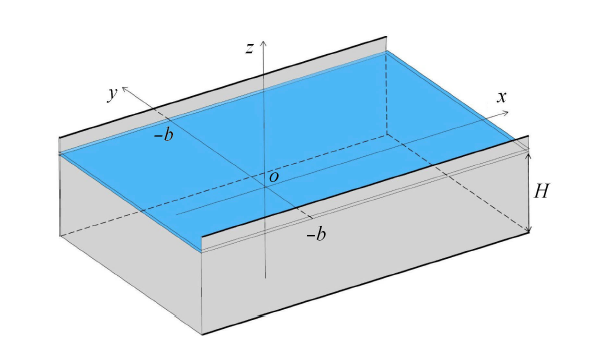新窗口打开|下载原图ZIP|生成PPT
图4波浪与固壁冰航道相互作用?^[48]

Fig. 4Interaction between waves and frozen channels?^[48]



此外,Ren等?^[50]还考虑了波浪在冻结固壁航道内存在一条裂缝时传播的情况,对裂缝在航道内不同位置时的影响进行了分析. 裂缝在波浪的作用下可以进一步形成一条狭窄的敞水航道,此时波浪的传播会发生极大的变化?^[51]. 对于航道内没有冰盖的情况,航道中传播的波是重力波;当航道完全被冰盖覆盖时,传播的波是弯曲重力波,且波数较小时以重力波为主,波数较大时以弯曲波为主;而对于冰盖不完全覆盖的航道,由于敞水表面的存在,短波在航道中的形式将会发生变化,这也导致波浪传播相速度的变化比航道完全被冰面覆盖的情况更加复杂,存在多个极值点,即多个临界速度?^[51]. 这一情况目前人们的理解仍不完全,值得进一步深入研究.

1.2.2 浮冰与波浪的相互作用

实际海洋环境中,海冰并不会一直是无限大尺寸,尤其在冰缘区附近,海冰大部分以有限尺寸漂浮在自由表面上.

(1) 有限块浮冰

关于有限块浮冰与波浪的相互作用研究,Meylan和Squire?^[52]基于Fox和Squire?^[30]建立的半无限大冰面与波浪相互作用模型,得到了水波经过单块浮冰后的反射波和透射波的近似解.Meylan和Squire?^[53]研究 了波浪与单块浮冰在有限水深和无限水深情况下的作用,并进一步将此研究扩展到了波浪与两块浮冰相互作用.随着波浪与海冰相互作用研究的进一步深入,有研究开始关注海冰形状特点对波浪场的影响.Meylan和Squire?^[54]采用特征函数展开匹配法与格林函数法研究了圆形浮冰与波浪的相互作用.圆形浮冰形状给理论分析带来了许多便利,但是不能较好地反映实际情况中海 冰的随机形态.随后,Meylan?^[55]研究了4种几何形状(平行四边形、三角形、梯形、正方形)的海冰在波浪作用下的耦合作用,在计算散射波能量的变化规律时发现散射波受浮冰弯曲刚度的影响最为明显,且存在一个临界刚度值,在该临界刚度值以下,浮冰散射的波浪能量与浮冰几何形状关系不明显,但是当浮冰弯曲刚度超过此临界值时,平均散射能量与浮冰几何形状关系密切.Wang和Meylan?^[56]基于耦合的边界元和有限元方法发展了一种高阶的数值算法研究波浪与任意形状弹性浮冰的相互作用,与Meylan?^[55]的结果符合较好.Bennetts和Williams?^[57]也研究了漂浮在水面上任意形状的浮冰与波浪的相互作用,此外,他们还考虑一种相反的情况,无限大冰盖中间有一片有限宽度的自由水面,即冰间湖. 他们发现,浮冰或冰间湖的尺寸加剧了某些方向上的波反射和透射,随着波数的增加,散射响应 单调增大,对于适中的波长显示出宽波谷,并且此特征随浮冰或冰间湖的形状而显着变化. Porter?^[58]研究了矩形形状的单块海冰对波浪的散射效果,在此基础上又分析了海冰周期阵列排列时对波浪的散射效果,他展示了两个案例来表明水和冰盖之间存在复杂的相互作用,该相互作用使阵列中的冰盖发生明显的弯曲.

Bai等?^[59]采用基于线性辐射方法的势流水动力软件HydroSTAR和基于黏流的CFD求解器OpenFOAM软件对浮冰块在波浪作用下的响应进行了数值模拟,结果表明,相对波长影响浮冰块的垂向和纵向运动,幅值响应算子受浮冰厚度的影响.倪宝玉等?^[60]基于FLUENT软件,对波浪对单块浮冰的相互作用,发现在二维平面进行波中的二阶漂移力的作用下,浮冰会发生接近匀速的纵向漂移运动,同时呈现运动周期与波浪周期相近的纵荡、垂荡和纵摇运动,且垂荡最大时刻对应纵摇角最小时刻.同时浮冰的运动响应和波浪力呈现相位相反的关系,此外,还对比了波浪与两块、三块浮冰相互作用的差异,发现浮冰数的增加将会导致浮冰的漂移速度降低,如图5所示,浮冰的垂荡和纵摇幅值均降低.在多浮冰情况下,当浮冰尺寸相同时,前面的浮冰比后面的浮冰漂移速度大,相邻两块浮冰间的距离在不断减小.此外,倪宝玉等?^[61]还研究了浮冰在Stokes波作用下的响应,发现二阶Stokes漂移速度可以很好地预报浮冰的纵向漂移速度,相对漂移速度与波数和波幅的乘积呈现二次方关系.

图5

新窗口打开|下载原图ZIP|生成PPT
图5单块、两块和多块浮冰作用下中心浮冰的纵向平移运动?^[60]

Fig. 5Longitudinal translational movement of the center ice under the action for single, two or multiple ice floes?^[60]



Meylan等?^[62]通过试验模型验证了理论模型中浮冰的弯曲运动,尽管在试验中观察到了浮冰的上浪现象,但是试验得到的浮冰运动响应与基于弹性薄板假设海冰模型得到的结果吻合较好,这也表明将浮冰假设为弹性薄板进行研究是可行的.郭春雨等?^[63]以非冻结模型冰为对象,研究了不可变形的刚体海冰受波浪作用下的纵向运动,发现海冰的厚度、波长及波陡都会在一定程度上影响海冰的纵向运动;斯托克斯漂移理论与试验测量值随波陡的变化规律是一致的.Dharma等?^[64]通过实验研究了波浪与黏弹性板的相互作用,发现实验结果与Wang和Shen?^[18]的数值预测结果符合较好,实验中的黏弹性冰板分别采用聚二甲硅氧烷和聚丙烯两种材料模拟.

波浪与有限块浮冰的耦合运动是研究波浪与浮冰群运动的基础,目前针对波浪与有限块浮冰作用的研究是基于浮冰不可二次破碎假设的基础上进行的,即假设浮冰足够小. 但是从敞水到冰区中心,浮冰的平均尺寸是逐渐增大的,当浮冰尺寸大到与波浪波长的量纲相近时,浮冰也会发生弯曲运动而破碎.因此浮冰与波浪作用下的二次破碎研究对于发展波浪与海冰相互作用问题将有较大促进作用.

(2) 浮冰群

波浪对海冰的影响主要发生在冰缘区,即海冰与开阔水域的交界处,也是冰面最容易发生破坏的区域. 这导致冰缘区海冰的排布方式和尺寸大小变得不规则,形成了不规则浮冰群.浮冰群内存在着密集的浮冰,此时每一块浮冰都可以自由地向四周运动,浮冰不仅会受到波浪作用而发生弯曲,浮冰与浮冰之间也会由于波浪力的作用发生碰撞.更为重要的是,由于大量不同尺寸的浮冰分布在冰缘区,波浪经过此区域时还会向各个方向散射并发生能量耗散.关于波浪与浮冰群相互作用问题的建立和求解是极具挑战性的.

Masson和LeBlond?^[65]基于多重散射理论和圆形的刚体浮冰假设,提出了第一个关于浮冰群的波浪散射模型.Meylan和Masson?^[66]在Masson和LeBlond?^[65]研究的基础上,提出了一个采用线性波尔茨曼方程来模拟浮冰群波浪的散射,他们介绍了如何从单个浮冰的散射中找到线性波尔茨曼方程中的散射核的细节.但是这些模型都无法预测三维波场经过浮冰群后的变化. Bennetts和Squire?^[67-68],Peter和Meylan?^[69]将浮冰群视为由大量弹性的圆形浮冰规则排列组成的三维空间,从而研究了波浪经过此特定冰缘区后的能量变化,如图6所示.Bennetts等?^[70]则考虑了不同形状浮冰排列组成的浮冰群,研究了由于海冰散射引起的能量衰减,发现浮冰群内浮冰的形状对整体波浪能量衰减几乎没有影响,但是海冰的尺寸和海冰之间的间距对波浪能量衰减的影响较为明显.Montiel等?^[71]提出了波浪经过冰缘区时的能量衰减和定向传播模型,这是在Montiel等?^[72]研究二维的关于声波在相同圆形障碍物的大型有限阵列中传播问题扩展而来.Montiel等?^[71]提出的模型中包含了一个基于观测研究得到的海冰分布规律,用于构建浮冰群的海冰模型;此外,他们将入射波强迫建模为具有指定方向能量分布的随机海洋状态,集合平均后用于计算通过浮冰群波能量衰减和定向传播规律.最近,Meylan和Bennetts?^[73]在时域上研究了浮冰群的三维散射波.

图6

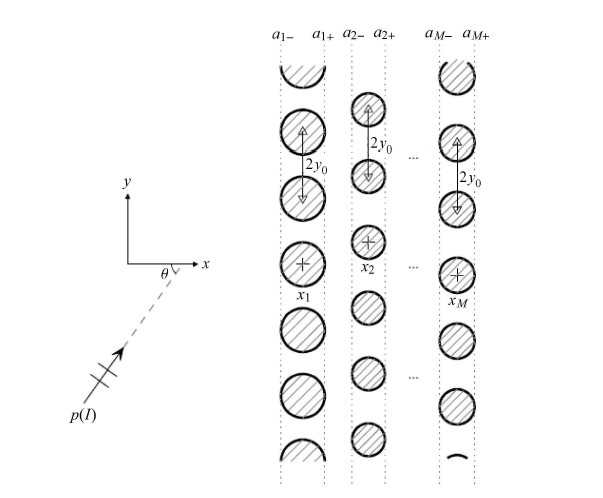新窗口打开|下载原图ZIP|生成PPT
图6浮冰群内浮冰布置示意图?^[67]

Fig. 6Schematic showing the arrangement of ice floes in the marginal ice zone?^[67]



Bennetts和Williams?^[74]通过试验研究了40个和80个圆盘模型冰阵列在波浪水池中与波浪的相互作用,如图7所示.试验研究发现随着波浪周期的增大,波浪透射能量单调增大;80个圆盘阵列比40个圆盘阵列要透射要少的能量,但波能的传递不是密集度的简单函数,无法得到透射波和密集度之间的关系是由于圆盘之间碰撞引起的额外的能量衰减,尤其是密集度较高的阵列.

图7

新窗口打开|下载原图ZIP|生成PPT
图7圆盘模型冰排布?^[74]

Fig. 7Disk modelled ice arrays?^[74]



目前关于浮冰群冰场理论模型的建立还是尚无较好的处理办法. 大部分现有方法主要通过假设碎冰形状为规则的圆形或四边形进行阵列而形成浮冰群,且研究方法是基于波浪与单块浮冰相互作用发展过来,显然浮冰规则阵列形成的冰缘区用来预测波浪与浮冰区相互作用的研究还存在很大缺陷. 为了弥补此缺陷,Zhao和Shen?^[75]针对浮冰在空间上的随机分布,提出了一种漫射近似方法(diffusion approximation, DA),模拟了波浪在随机分布的浮冰中的散射. 在相同的入射波和冰况下,漫射近似法的模拟结果与由波尔茨曼方程计算的结果一致. 后续的研究可以继续尝试通过引入海冰随机性分布函数来建立冰缘区浮冰群模型,从而考虑海冰形状的随机性.

1.3 可破碎海冰与波浪的相互作用

当波浪作用下海冰内部的应力超过其自身能承受的极限时,海冰就会在波浪的作用下发生破碎,海冰破碎的条件与海冰自身的强度有关?^[76].关于海冰在波浪作用下的破坏的研究,Dumont等?^[77]提出了一种模拟冰盖在波浪作用下的破碎模型,此模型从波散射模型中演变而来,被用来估算冰缘区的范围和冰盖破坏可形成的最大浮冰尺寸.此外,这个模型还考虑了冰破坏与波能量传输之间的耦合,发现冰厚和入射波能量是影响碎冰区形成范围最重要的两个因素,而海冰性质的影响是次要的.不足的是,Dumont等?^[77]建立的模型是一维的,海冰破坏的判断标准还是基于海冰的应变/应力是否超过极限应变/应力,并且对碎冰区形成范围的估算较为保守.Williams等?^[78-80]在Dumont等?^[77]的模型基础上进行了改进,将基于单色波波幅的浮冰破坏准则改进为基于波浪统计的破坏准则;此外,还考虑经过冰区后发生能量变化的谱密度函数,并由此定义了波浪能量耗散项.改进的模型可以模拟由于冰盖存在引起的波浪能量耗散,以及波浪运动引起的冰盖破坏,但是此模型的能量衰减率还是基于弹性薄板散射模型计算的.为了更好地描述冰缘区海冰的分布状态,Zhang等?^[81]将浮冰厚度分布理论考虑到浮冰尺寸分布理论中,且只定义了一个控制参数,探讨了在不同参数下,浮冰尺寸分布理论在力学上的浮冰尺寸重新分布行为,以及不同冰盖破碎情况下产生的浮冰尺寸分布,但是没有量化控制参数与浮冰分布尺寸、浮冰厚度分布以及波浪之间的关系.

对于采用模型试验的方法研究波浪作用下的冰的破坏问题,王永学等?^[82]发现了漂浮冰排的长度大于入射波波长时,冰排极易发生脆性断裂,且随着冰排长度与入射波波长比值的增大,使冰排发生断裂的入射波波高成指数函数规律减小.2015年,德国汉堡水池(HSVA)?^[83]在冰水池中采用造波机进行了波浪与平整冰的相互作用试验,如图8所示,完整地观测到了平整冰在波浪作用下的不断破碎过程,碎冰尺寸随着波浪入射冰盖区的距离增大而逐渐增大.

图8

新窗口打开|下载原图ZIP|生成PPT
图8汉堡水池波浪与冰相互作用试验?^[83]

Fig. 8Wave and ice interaction test in Hamburg Pool?^[83]



采用模型试验的手段来研究海冰在波浪作用下的破坏是一个较好的方法,但是成本较高,目前兴起的一种CFD-DEM耦合算法?^[84]对于模拟海冰在波浪作用下具有很好的优势,采用DEM模拟冰面可以很方便地设置冰面的断裂条件,同时模拟出冰面的破坏,而CFD对于流场的模拟也已经较为成熟,因此CFD-DEM耦合方法对于研究海冰在波浪作用下的破坏具有较大发展潜力,从而更全面地研究海冰在波浪作用下的破坏过程、破坏模式以及海冰破坏之后进一步的力学行为.

2 海冰与海流相互作用研究

在海冰和海流相互作用过程中,一方面,海冰在海流的拖曳力作用下会发生生消、断裂、重叠和堆积等动力学行为,其拖曳力包括由于冰侧或冰脊压力梯度产生的形拖曳力和由于水流在冰底面的黏性作用产生的摩拖曳力?^[85];另一方面,海冰的存在改变了海流运动的边界条件,使得海流在冰面下边界处可能产生漩涡脱落等现象,流场状态发生改变. 海流与海冰耦合作用的研究方法主要有数值模拟和实验室物理模拟试验两种,本节从这两种方法的角度阐述海冰与海流的作用研究进展.

2.1 数值方法

关于海冰在海流作用下的漂移和堆积,在数值研究中最常用的方法是在海冰的动力学方程中,直接增加由于海流引起的拖曳力模型,从而可以构建冰场在海流场作用下的变形、漂移和堆积.Hibler?^[86]构建了黏塑性海冰动力学本构模型并被广泛应用于极区以及其边缘区、渤海等副极区的大中尺度海冰动力学模拟.此后,为更好地进行不同条件下的海冰动力学数值模拟,Hunke和Dukowicz?^[87]构建了海冰的黏弹塑性模型,分析了冰场在风流场作用下的变形.季顺迎等?^[88]综合考虑了海冰在小应变和小应变率条件下的黏弹性力学行为,对大应变条件下的塑性流变性质采用Mohr-Coulomb塑性屈服准则并考虑海冰静水压力的影响,建立了一个适用性更强的黏弹-塑性海冰动力学本构模型,并采用光滑质点流体动力学(SPH)方法进行了渤海辽东湾海冰在风流场下辐合和辐散过程的数值模拟,数值模拟结果与现场观测结果吻合良好.基于此黏弹-塑性海冰动力学本构模型,为模拟不同冰类型和时空尺度下的海冰动力学,可通过适当调整模型中的黏性系数、弹性模量、黏结力等部分参数来实现. 李海等?^[89]进一步构建了海冰动力学的混合拉格朗日-欧拉(HLE)数值方法,联合采用SPH方法和有限差分法(FDM)模拟海冰在风流场下的漂移和堆积,提高了数值模拟中的计算精度与计算效率.季顺迎等?^[90]又进一步提出了海冰动力过程中改进的离散元模型(MDEM),并以此模拟渤海湾海冰在风流场作用下的漂移和堆积.但该方法对海冰演化过程尚未考虑热力因素的影响.上述方法可以较好地模拟海冰的运动,但是模拟过程中均没有考虑海冰的存在对于海流的影响,属于数值模拟中的单向耦合方法.

考虑海冰对海流的影响,孙惠?^[91]釆用二维湍流模型分别对水流作用下光滑、粗糙冰底浮冰模型周围流场进行了数值模拟,探究了两种浮冰模型下受影响流场区域的动力特性变化规律以及相应的拖曳力变化情况,但是文中在粗糙浮冰模型中只考虑了规则底纹的两种倾角,没探求拖曳力的大小与粗糙底纹的准确的定量甚至定性关系.卢鹏等?^[85]基于计算流体动力学软件FLUENT针对不同工况下浮冰所受流拖曳力及冰下流场和尾流场水动力特性进行二维数值模拟,结果表明浮冰拖曳力与流速的平方存在良好的线性关系;冰下受影响流场区域以及冰后尾流场的流速衰减区域都随着冰的入水深度增大而增大,在浮冰下前端和冰后尾流场存在涡流.吴岩?^[92]借助FLUENT软件模拟冰脊周围的流场,初步探索了入水深度、水流流速以及冰脊模型的底角这3个因素对流场分布特征的影响,得到了冰脊拖曳系数具体的参数化关系式,但仍然需要其他形状冰脊的计算结果完善该结论.

2.2 模型试验

模型试验是根据流动相似理论,在实验室内模拟各种物理流动,探究冰-流相互作用,可以控制试验条件,重演一些物理现象,还可以通过更细致地观察,发现一些有价值的现象和规律.在模型试验中,由于海流的模拟很难在冰水池内实现,目前的大部分研究均采用非冻结模型冰.王军等?^[93-94]分别在室内水流试验槽和室外天然冷冻水流试验槽内进行流冰的冰塞试验,其中在室内水流试验槽内采用石蜡制作的非冻结模型冰,在室外水流试验槽采用天然真冰.对比分析发现,模型冰与真冰获得的定性规律是一致的,故在研究冰塞的发展机理时,可采用非冻结模型冰.李志军等?^[95-96]在波浪水槽中增加双向造流装置,形成波流水槽,采用自主研发的非冻结可破碎合成模型冰,研究模型冰在海流带动下,与水工结构物桩腿的碰撞.在物理模拟试验中,开展冰下流场测试,可以获取各浮冰尾流场的变化规律,为冰-水拖曳系数参数化方案提供依据.

张强?^[97]利用PIV技术对冰下流场进行了物理模拟实验.主要通过对各浮冰下的流场图像进行整体分析并研究了不同形状浮冰对流场的影响,得到了冰下流场及尾流场影响区域与浮冰尺寸、底纹以及流速的关系.孙惠?^[91]在水槽中用光滑和粗糙底面的两种浮冰模型进行实验并以此为基础开展相应的数值模拟,对比两种结果,探究了影响流场动力学特性的浮冰几何参数并获得孤立冰块形拖曳系数、摩拖曳系数和冰几何参数之间的关系.目前的冰下流场测试探求模型冰对冰下流场区域的影响,旨在完善冰-水拖曳系数参数化,以便更好地描述海冰与海流相互作用的物理过程.

此外,由于海洋运动的真实环境是在海洋边界层内,海冰的融化会导致盐跃层变浅,从而使得冰层下方的流体密度发生了较明显的分层现象. 分层流体与海冰的作用也受到了诸多****的关注.Pite等?^[98]通过模型实验的方法研究了冰龙骨分别在均匀流体和分层流体上受到的拖曳力,发现分层流体上的冰龙骨受到的拖曳力会有一个急剧的增大.McPhee?^[99]根据实际观察结果对漂浮在海面上的海冰受到流体拖曳力模型进行了分析讨论,对比了深密度跃层模型、浅密度跃层模型和罗斯贝近似方法计算的流体对海冰漂移的影响,发现流体密度跃层的深度较浅时,流体的分层对海冰漂移有较大的影响,主要体现在海冰的偏转角度上.

3 海冰与波流相互作用研究

关于波浪与海流联合场与海冰的相互作用研究方面,目前的研究仍十分匮乏. 吴甜宇等?^[100]曾基于线性叠加法,研究海冰与波流联合作用下桥梁的动力响应,在研究中对海冰载荷和波流载荷分别施加,并没有考虑波流和海冰的耦合作用. Dolatshah等?^[101]采用模型试验的方法,探索了在单独波浪和波浪与风场联合作用下海冰的漂移和堆积行为,如图9所示. 试验结果表明,联合场作用下海冰的动力学行为与单一场作用下具有不同的特性,而具体行为特性的本质原因仍需进一步研究. 考虑到风场对海冰的拖曳力与海流对海冰的拖曳力具有很大相似性,波浪与风场联合作用下海冰的运动可为波浪与海流联合作用下海冰的运动提供具有价值的参考. 当然,波浪/海流联合场与海冰作用具有其特殊性,存在大量机理性问题亟待揭示.

图9

新窗口打开|下载原图ZIP|生成PPT
图9风浪联合与碎冰的相互作用?^[101]

Fig. 9Interaction between wind and wave combination and ice floes?^[101]

4 结论与展望

近年来,关于波流与海冰相互作用问题的研究十分丰富,也取得了很大的进步,但就这一问题在以下几方面仍有待于进一步深入研究：

(1) 对于海冰模型的研究,关于考虑海冰孔隙状态的多孔模型还处于萌芽阶段,如何考虑海冰自身结构特点以及空间分布特征的方法缺乏定性的认识,海冰细观特性对海冰模型特点的影响尚未明确. 目前基于弹性板和黏弹性板模型发展而来的多孔弹性板模型?^[25-26]和多孔黏弹性板模型?^[27]是一个新的研究方向,今后进一步研究中可以参照黏弹性冰板模型中黏性系数的确定,来明确海冰的孔隙参数,从而建立基于实际物理意义的多孔弹性板模型.

(2) 相对而言,波浪与有限块浮冰的相互作用比较丰富,但波浪与浮冰群相互作用研究还处于初步发展阶段,许多现象和规律还有待揭示,浮冰群冰场理论模型的建立还是尚无较好的处理办法. 目前主要通过假设碎冰形状为规则的圆形或四边形进行阵列而形成冰缘区,且研究方法是基于波浪与单块浮冰相互作用发展过来,显然浮冰规则阵列形成的冰缘区用来预测波浪与浮冰区相互作用的研究还存在很大缺陷,后续的研究可以尝试通过引入海冰随机性分布函数来建立浮冰群模型,进而考虑海冰形状的随机性. 波流作用下浮冰群之间的碰撞也值得进一步关注?^[102-103].

(3) 关于海冰在波浪作用下破碎问题的研究还较少,仍缺少有效的处理海冰在波浪作用下破碎的数值方法. 考虑到离散元方法在模拟海冰断裂、破碎方面的优势,CFD-DEM耦合方法?^[84]在处理海冰在波浪下的破碎问题具有较大发展潜力. 通过采用DEM对海冰进行建模,在海冰DEM颗粒之间添加粘结键,设置破坏准则,从而在CFD中模拟的海冰破碎. 此外,德国汉堡水池进行的波浪与冰相互作用试验,也给研究波浪与冰相互作用的试验方法提供了开拓工作.

(4) 对于海流与海冰的相互作用,将海流拖曳力直接加到海冰运动方程中是研究海流与海冰相互作用的常用方法,目前也有在海冰运动模型方程中考虑海冰厚度和海冰密集度分布函数来研究海冰的漂移和堆积?^[104],若可以在现有研究海冰运动的海冰厚度分布理论和海冰密集度分布理论中将海流作用函数考虑进去,则对于海冰与海冰相互作用的耦合机制研究会更加完善. 此外,考虑不同厚度、底部形状和密度分布的海冰边界对于海流运动的影响也具有重要意义.

(5) 海冰的破碎、堆积会对海冰的形态产生重要影响,本文主要讨论了冰盖、浮冰、碎冰等简单类型冰与波流的耦合作用. 而在复杂的极地环境载荷作用下,还存在着重叠冰、冰脊、冰山等复杂类型冰,复杂类型冰与波流的耦合作用也需要深入研究.

(6) 实际极地海洋环境中,波浪、海流是共存的,波流联合场与海冰的耦合作用具有很大的科学意义和工程价值. 然而目前关于波流联合场与海冰耦合作用的研究仍极其匮乏,存在大量机理性问题亟待揭示,相关理论研究、数值方法和实验手段均需深入开展.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 卢景美, 邵滋军, 房殿勇, 等. 北极圈油气资源潜力分析
资源与产业, 2010,12(4):29-33
[本文引用: 1]

( Lu Jingmei, Shao Zijun, Fang Dianyong, et al. Analysis of oil-gas resources potential in the arctic circle
Resource & Industries, 2010,12(4):29-33 (in Chinese))
[本文引用: 1]

[2] 寿建敏. 我国极地航运能力建设和高冰级船队发展对策分析
极地研究, 2018,30(4):419-428
[本文引用: 1]

( Shou Jianmin. Analysis on the construction of China's polar shipping capacity and countermeasures for the development of high ice class fleet
Chinese Journal of Polar Research, 2018,30(4):29-33 (in Chinese))
[本文引用: 1]

[3] Ni BY, Han DF, Di SC, et al. On the development of ice-water-structure interaction
Journal of Hydrodynamics, 2020,32(4):629-652
[本文引用: 1]

[4] 刘璐, 尹振宇, 季顺迎. 船舶与海洋平台结构冰载荷的高性能扩展多面体离散元方法
力学学报, 2019,51(6):1720-1739
[本文引用: 1]

( Liu Lu, Yin Zhenyu, Ji Shunying. High-performance dilated polyhedral based DEM for ice loads on ship and offshore platform structures
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(6):1720-1739 (in Chinese))
[本文引用: 1]

[5] 龙雪, 刘社文, 季顺迎. 水位变化对正倒锥体冰载荷影响的离散元分析
力学学报, 2019,51(1):74-84
[本文引用: 1]

( Long Xue, Liu Shewen, Ji Shunying. Influence of water level on ice load on upward-downward conical structure based on DEM analysis
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(1):74-84 (in Chinese))
[本文引用: 1]

[6] Squire VA. Of ocean waves and sea ice
Annual Review of Fluid Mechanics, 2003,27(1):115-168
[本文引用: 1]

[7] Squire VA. Of ocean waves and sea-ice revisited
Cold Regions Science and Technology, 2007,49(2):110-133


[8] Squire VA. Past present and impendent hydroelastic challenges in the polar and subpolar seas
Philosophical Transactions of The Royal Society A, 2011,369:2813-2831


[9] Squire VA. Ocean wave interactions with sea ice: A reappraisal
Annual Review of Fluid Mechanics, 2020,52(1):37-60
[本文引用: 1]

[10] Zhao X, Shen HH, Cheng S. Modeling ocean wave propagation under sea ice covers
Acta Mechanica Sinica, 2015,31(1):1-15
[本文引用: 1]

[11] Shen HH. Modelling ocean waves in ice-covered seas
Applied Ocean Research, 2019,83:30-36
[本文引用: 1]

[12] Peters AS. The effect of a floating mat on water waves
Communications on Pure and Applied Mathematics, 1950,3(4):319-354
[本文引用: 1]

[13] Weitz M, Keller JB. Reflection of water waves from floating ice in water of finite depth
Communications on Pure and Applied Mathematics, 1950,3(3):305-318
[本文引用: 1]

[14] Wadhams P. The Seasonal Ice Zone, the Geophysics of Sea Ice
US: Springer, 1986: 825-991
[本文引用: 1]

[15] Hosking RJ, Sneyd AD, Waugh DW. Viscoelastic response of a floating ice plate to a steadily moving load
Journal of Fluid Mechanics, 2006,196(1):409-430
[本文引用: 1]

[16] Keller JB. Gravity waves on ice covered water
Journal of Geophysical Research: Oceans( 1978-2012), 1998,103(C4):7663-7669
[本文引用: 1]

[17] Carolis DG, Desiderio D. Dispersion and attenuation of gravity waves in ice: A two layer viscous fluid model with experimental data validation
Physics Letters A, 2002,305(6):399-412
[本文引用: 1]

[18] Wang R, Shen HH. Gravity waves propagating into an ice covered ocean: A viscoelastic model
Journal of Geophysical Research}: Oceans (1978-2012), 2010,115:C06024
[本文引用: 2]

[19] Zhao X, Cheng S, Shen HH. Nature of wave modes in a coupled viscoelastic layer over water
Journal of Engineering Mechanics, 2017,143(10):04017114
[本文引用: 1]

[20] Zhao X, Shen HH. Three-layer viscoelastic model with eddy viscosity effect for flexural-gravity wave propagation through ice cover
Ocean Modelling, 2018,131:15-23
[本文引用: 1]

[21] Zhao X, Zhang CP. A theoretical model of the Wind-wave growth over an ice-covered sea
Boundary Layer Meteorology, 2021,178:1-19
[本文引用: 1]

[22] Cheng SK, Rogers WE, Thomson J, et al. Calibrating a viscoelastic sea ice model for wave propagation in the arctic fall marginal ice zone
Journal of Geophysical Research-Oceans, 2017,122(11):8770-8793
[本文引用: 1]

[23] Cheng SK, Tsarau A, Evers KU, et al. Floe size effect on gravity wave propagation through ice covers
Journal of Geophysical Research-Oceans, 2019,124(1):320-334
[本文引用: 2]

[24] 赵欣. 海浪模式中海冰弹性模量计算的理论方法
//第十四届全国环境力学学术会议论文集, 大连, 2018-08-5-7
[本文引用: 1]

( Zhao Xin. A theoretical method for calculating the elastic modulus of sea ice in wave models
//Proceedings of the 14th National Conference on Environmental Mechanics, Dalian, 2018-08-5-7 (in Chinese))
[本文引用: 1]

[25] Meylan MH, Bennetts LG, Peter MA. Water-wave scattering and energy dissipation by a floating porous elastic plate in three dimensions
Wave Motion, 2016:S0165212516300695
[本文引用: 2]

[26] Zheng S, Meylan MH, Fan L, et al. Wave scattering by a floating porous elastic plate of arbitrary shape: A semi-analytical study
Journal of Fluids and Structures, 2019,92:102827
[本文引用: 2]

[27] Chen H, Gilbert RP, Guyenne P. Dispersion and attenuation in a porous viscoelastic model for gravity waves on an ice-covered ocean
European Journal of Mechanics-B/Fluids, 2019,78:88-105
[本文引用: 2]

[28] Balmforth NJ, Craster RV. Ocean waves and ice sheets
Journal of Fluid Mechanics, 1999,395:89-124
[本文引用: 1]

[29] Fox C, Squire VA. Reflection and transmission characteristics at the edge of shore fast sea ice
Journal of Geophysical Research Oceans, 1990,95(C7):11629-11639
[本文引用: 1]

[30] Fox C, Squire VA. On the oblique reflexion and transmission of ocean waves at shore fast sea ice
Philosophical Transactions of the Royal Society A Mathematical Physical & Engineering Sciences, 1994,347:185-218
[本文引用: 4]

[31] Tkacheva LA. Hydroelastic behavior of a floating plate in waves
Journal of Applied Mechanics & Technical Physics, 2001,42(6):991-996
[本文引用: 1]

[32] Tkacheva LA . The diffraction of surface waves by a floating elastic plate at oblique incidence
Journal of Applied Mathematics & Mechanics, 2004,68(3):425-436
[本文引用: 1]

[33] Sahoo T, Yip TL, Chwang AT. Scattering of surface waves by a semi-infinite floating elastic plate
Physics of Fluids, 13(11):3215-3222
[本文引用: 1]

[34] Linton CM, Chung H. Reflection and transmission at the ocean/sea-ice boundary
Wave Motion, 2003,38:43-52
[本文引用: 1]

[35] Zhao X, Shen HH. Ocean wave transmission and reflection between two connecting viscoelastic ice covers: An approximate solution
Ocean Modelling, 2013,71(7):102-113
[本文引用: 2]

[36] Zhao X, Shen HH. Ocean wave transmission and reflection by viscoelastic ice covers
Ocean Modelling, 2015,92:1-10.
[本文引用: 1]

[37] Barrett MD, Squire VA. Ice-coupled wave propagation across an abrupt change in ice rigidity, density, or thickness
Journal of Geophysical Research Oceans, 1996,101(C9):20825-20832
[本文引用: 1]

[38] Evans DV, Porter R. Wave scattering by narrow cracks in ice sheets floating on water of finite depth
Journal of Fluid Mechanics, 2003,484:143-165
[本文引用: 1]

[39] Porter R, Evans DV. Scattering of flexural waves by multiple narrow cracks in ice sheets floating on water
Wave Motion, 2006,43(5):425-443
[本文引用: 1]

[40] Porter R, Evans DV. Diffraction of flexural waves by finite straight cracks in an elastic sheet over water
Journal of Fluids & Structures, 2007,23(2):309-327
[本文引用: 1]

[41] Li ZF, Wu GX, Shi YY. Wave diffraction by a circular crack in an ice sheet floating on water of finite depth
Physics of Fluids, 2018,30(11):117103
[本文引用: 1]

[42] Li ZF, Wu GX, Ren K. Wave diffraction by multiple arbitrary shaped cracks in an infinitely extended ice sheet of finite water depth
Journal of Fluid Mechanics, 2020,893:A14
[本文引用: 1]

[43] Marchenko AV. Resonance interactions of waves in an ice channel
Journal of Applied Mathematics & Mechanics, 1997,61(6):931-940
[本文引用: 1]

[44] Chung H, Linton CM. Reflection and transmission of waves across a gap between two semi-infinite elastic plates on water
The Quarterly Journal of Mechanics and Applied Mathematics, 2005,58(1):1-15
[本文引用: 1]

[45] Shi YY, Li ZF, Wu GX. Wave excited motion of a body floating on water confined between two semi-infinite ice sheets
Physics of Fluids, 2019,31(6):067111
[本文引用: 1]

[46] Williams TD, Squire VA. Scattering of flexural--gravity waves at the boundaries between three floating sheets with applications
Journal of Fluid Mechanics, 2006,569:113-140
[本文引用: 1]

[47] Porter R. Trapping of waves by thin floating ice floes
The Quarterly Journal of Mechanics and Applied Mathematics, 2018,71(4):463-483
[本文引用: 2]

[48] Korobkin AA, Khabakhpasheva TI, Papin AA. Waves propagating along a channel with ice cover
European Journal of Mechanics, 2014,47:166-175
[本文引用: 3]

[49] Khabakhpasheva TI, Batyaev EV. Hydroelastic waves in a channel covered with a free ice sheet
Fluid Dynamics, 2015,50(6):775-788
[本文引用: 1]

[50] Ren K, Wu GX, Li ZF. Hydroelastic waves propagating in an ice-covered channel
Journal of Fluid Mechanics, 2020,886(A18):1-24
[本文引用: 2]

[51] Zeng LD, Korobkin AA, Ni BY, et al. Hydroelastic waves propagating in a shallow fluid contained in a channel covered by two ice sheets of finite width
//25th IAHR International Symposium on Ice, Trondheim, 2020-11-23-25
[本文引用: 2]

[52] Meylan M, Squire VA. Finite-floe wave reflection and transmission coefficients from a semi-infinite model
Journal of Geophysical Research Oceans, 1993,98(C7):12537-12542
[本文引用: 1]

[53] Meylan M, Squire VA. The response of ice floes to ocean waves
Journal of Geophysical Research, 1994,99(C1):891-900
[本文引用: 1]

[54] Meylan MH, Squire VA. Response of a circular ice floe to ocean waves
Journal of Geophysical Research: Oceans, 1996,101(C4):8869
[本文引用: 1]

[55] Meylan MH. Wave response of an ice floe of arbitrary geometry
Journal of Geophysical Research Oceans, 2002,107(C1):3005
[本文引用: 2]

[56] Wand CD, Meylan MH. A higher-order-coupled boundary element and finite element method for the wave forcing of a floating elastic plate
Journal of Fluids and Structures, 2004,19(4):557-572
[本文引用: 1]

[57] Bennetts LG, Williams TD. Wave scattering by ice floes and polynyas of arbitrary shape
J Fluid Mech, 2010,662:5-35
[本文引用: 1]

[58] Porter R. The coupling between ocean waves and rectangular ice sheets
Journal of Fluids and Structures, 2019,84:171-181
[本文引用: 1]

[59] Bai W, Zhang T, Mcgovern DJ. Response of small sea ice floes in regular waves: A comparison of numerical and experimental results
Ocean Engineering, 2017,129:495-506
[本文引用: 1]

[60] 倪宝玉, 刘晨辉, 胡文进, 等. 二维Stokes波与多块浮冰相互作用数值模拟
水动力学研究与进展(A辑), 2019,34(2):141-148
[本文引用: 3]

( Ni Baoyu, Liu Chenhui, Hu Wenjin, et al. Numerical simulation on the interaction between two-dimensional Stokes wave and multiple ice floes
Chinese Journal of Hydrodynamics (A), 2019,34(2):151-148 (in Chinese))
[本文引用: 3]

[61] 倪宝玉, 叶昱图, 胡文进, 等. 浮冰在Stokes波作用下运动响应研究
华中科技大学学报(自然科学版), 2020,48(10):75-80
[本文引用: 1]

( Ni Boayu, Ye Yutu, Hu Wenjin, et al. Study on motion response of ice floe under Stokes wave
Journal of Huazhong University of Science and Technology (Natural Science Edition), 2020,48(10):75-80 (in chinese))
[本文引用: 1]

[62] Meylan MH, Bennetts LG, Cavaliere C, et al. Experimental and theoretical models of wave-induced flexure of a sea ice floe
Physics of Fluids, 2015,27(4):1-7
[本文引用: 1]

[63] 郭春雨, 宋妙妍, 骆婉珍, 等. 海冰在波浪中纵向运动的试验研究
华中科技大学学报(自然科学版), 2017,45(6):85-90
[本文引用: 1]

( Guo Chunyu, Song Miaoyan, Luo Wanzhen, et al. Experimental study on longitudinal motion of sea ice in waves
Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017,45(6):85-90 (in Chinese))
[本文引用: 1]

[64] Sree DK, Law AWK, Shen HH, et al. An experimental study on the interactions between surface waves and floating viscoelastic covers
Wave Motion, 2017,70:195-208
[本文引用: 1]

[65] Masson D, Leblond P H. Spectral evolution of wind-generated surface gravity waves in a dispersed ice field
Journal of Fluid Mechanics, 2006,202:43-81
[本文引用: 2]

[66] Meylan MH, Masson D. A linear Boltzmann equation to model wave scattering in the marginal ice zone
Ocean Modelling, 2006,11(3):417-427
[本文引用: 1]

[67] Bennetts LG, Squire VA. Wave scattering by multiple rows of circular ice floes
Journal of Fluid Mechanics, 2009,639:213-238
[本文引用: 3]

[68] Bennetts LG, Squire VA. Linear wave forcing of an array of axisymmetric ice floes
Ima Journal of Applied Mathematics, 2010,75(1):108-138
[本文引用: 1]

[69] Peter MA, Meylan MH. Water-wave scattering by vast fields of bodies
Siam Journal on Applied Mathematics, 2009,70(5):1567-1586
[本文引用: 1]

[70] Bennetts LG, Peter MA, Squire VA, et al. A three-dimensional model of wave attenuation in the marginal ice zone
Journal of Geophysical Research Oceans, 2010,115:C12043
[本文引用: 1]

[71] Montiel F, Squire VA, Bennetts LG. Attenuation and directional spreading of ocean wave spectra in the marginal ice zone
Journal of Fluid Mechanics, 2016,790:492-522
[本文引用: 2]

[72] Montiel F, Squire VA, Bennetts LG. Evolution of directional wave spectra through finite regular and randomly perturbed arrays of scatterers
SIAM Journal on Applied Mathematics, 2015,75(2):630-651
[本文引用: 1]

[73] Meylan MH, Bennetts LG. Three-dimensional time-domain scattering of waves in the marginal ice zone
Philosophical Transactions of the Royal Society A Mathematical Physical & Engineering Sciences, 2018,376(2129):20170334
[本文引用: 1]

[74] Bennetts L, Williams T. Water wave transmission by an array of floating disks
Proceedings of the Royal Society A Mathematical Physical & Engineeringences, 2015,471(2173):20140698
[本文引用: 3]

[75] Zhao X, Shen HH. A diffusion approximation for wave scatterings by randomly distributed ice floes
Ocean Modeling, 2016,107:21-27
DOIURL [本文引用: 1]

[76] 陈晓东, 崔海鑫, 王安良, 等. 基于巴西盘试验的海冰拉伸强度研究
力学学报, 2020,52(3):625-634
[本文引用: 1]

( Chen Xiaodong, Cui Haixin, Wang Anliang, et al. Experimental study on sea ice tensile strength based on Brazilian tests
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(3):625-634 (in Chinese))
[本文引用: 1]

[77] Dumont D, Kohout A, Bertino L. A wave-based model for the marginal ice zone including a floe breaking parameterization
Journal of Geophysical Research Oceans, 2011,116:C04081
[本文引用: 3]

[78] Williams TD, Bennetts LG, Squire VA, et al. Wave-ice interactions in the marginal ice zone. Part 1: Theoretical foundations
Ocean Modelling, 2013,71:81-91
[本文引用: 1]

[79] Williams TD, Bennetts LG, Squire VA, et al. Wave-ice interactions in the marginal ice zone. Part 2: Numerical implementation and sensitivity studies along 1D transects of the ocean surface
Ocean Modelling, 2013,71:92-101


[80] Williams TD, Rampal P, Bouillon S. Wave-ice interactions in the neXtSIM sea-ice model
The Cryosphere, 2017,11:2117-2135.
[本文引用: 1]

[81] Zhang JL, Schweiger A, Steele M, et al. Sea ice floe size distribution in the marginal ice zone: Theory and numerical experiments
Journal of Geophysical Research: Oceans, 2015,120(5):3484-3498
[本文引用: 1]

[82] 王永学, 李广伟, 李春花, 等. 波浪作用下海冰断裂的试验研究
自然科学进展, 2000,10(6):549-553
[本文引用: 1]

( Wang Yongxue, Li Guangwei, Li Chunhua, et al. Experimental study on sea ice fracture under wave action
Progress in Natural Science, 2000,10(6):549-553 (in Chinese))
[本文引用: 1]

[83] http://www.hsva.de.
URL [本文引用: 3]

[84] Ni BY, Chen ZW, Zhong K, et al. Numerical simulation of a polar ship moving in level ice based on a one-way coupling method
Journal of Marine Science and Engineering, 2020,8(9):692
[本文引用: 2]

[85] 孙惠, 卢鹏, 李志军. 冰下流场动力学特性的数值模拟研究
数学的实践与认识, 2015,45(3):69-77
[本文引用: 2]

( Sun Hui, Lu Peng, Li Zhijun. Numerical simulation on dynamic characteristics of flow field under ice
Journal of Mathematics in Practice and Theory, 2015,45(3):69-77 (in Chinese))
[本文引用: 2]

[86] Hibler WD. A dynamic thermodynamic sea ice mode
Journal of Physical Oceanography, 1979,9(4):815-846
[本文引用: 1]

[87] Hunke EC, Dukowicz JK. An elastic--viscous--plastic model for sea ice dynamics
Journal of Physical Oceanography, 1997,27(9):1849-1867
[本文引用: 1]

[88] 季顺迎, 沈洪道, 王志联, 等. 基于Mohr-Coulomb准则的黏弹-塑性海冰动力学本构模型
海洋学报, 2005(4):19-30
[本文引用: 1]

( Ji Shunying, Shen Hongtao, Wang Zhilian, et al. A viscoelastic-plastic constitutive model with Mohr-Coulomb yielding criterion for sea ice dynamics
Acta Oceanologica Sinica, 2005(4):19-30 (in Chinese))
[本文引用: 1]

[89] 李海, 季顺迎, 沈洪道, 等. 海冰动力学的混合拉格朗日-欧拉数值方法
海洋学报, 2008,30(2):1-11
[本文引用: 1]

( Li Hai, Ji Shunying, Shen Hongtao, et al. A hybrid Lagrangian-Eulerian numerical model for sea ice dynamics
Acta Oceanologica Sinica, 2008,30(2):1-11 (in Chinese))
[本文引用: 1]

[90] 季顺迎, 王安良, 米丽丽, 等. 海冰动力过程的改进离散元模型及在渤海的应用
海洋学报, 2015,37(5):54-67
[本文引用: 1]

( Ji Shunying, Wang Anliang, Mi Lili, et al. Modified discrete element model for sea ice dynamics and its applications in the Bohai Sea
Acta Oceanologica Sinica, 2015,37(5):54-67 (in Chinese))
[本文引用: 1]

[91] 孙惠. 冰底形态对流场特性影响的数值模拟研究
[硕士论文]. 大连: 大连理工大学, 2014
[本文引用: 2]

( Sun Hui. Numerical simulation on the influence of ice bottom morphology on flow field
[Master Thesis]. Dalian: Dalian University of Technology, 2014 (in Chinese))
[本文引用: 2]

[92] 吴岩. 冰脊对冰下流场影响的数值模拟研究
[硕士论文]. 大连: 大连理工大学, 2016
[本文引用: 1]

( Wu Yan. Numerical simulation on the influence of ice ridges on flow field under ice
[Master Thesis]. Dalian: Dalian University of Technology, 2016 (in Chinese))
[本文引用: 1]

[93] 王军. 初始冰塞厚度与水流条件及冰流量关系的试验研究
水利水运工程学报, 1999(4):385-389
[本文引用: 1]

( Wang Jun. A study on the relationship about initial ice jam thickness with its stream conditions and ice discharge
Hydro-Science and Engineering, 1999(4):385-389 (in Chinese))
[本文引用: 1]

[94] 王军. 平衡冰塞厚度与水流条件和冰流量关系的试验研究
兰州大学学报(自然科学版), 2002,38(1):117-121
[本文引用: 1]

( Wang Jun. A study on the relations about balance ice jam thickness with its flow conditions and ice discharge
Journal of Lanzhou University(Natural Sciences) 2002,38(1):117-121 (in Chinese))
[本文引用: 1]

[95] 李志军, 贾青, 董吉武, 等. 冰对水工结构物作用力的物理模拟
中国水论坛, 2010: 217-225
[本文引用: 1]

( Li Zhijun, Jia Qing, Dong Jiwu, et al. Physical simulation of the force of ice on hydraulic structures
China Water Forum, 2010: 217-225 (in Chinese))
[本文引用: 1]

[96] 李志军, 贾青, 王国玉, 等. 流冰对码头排桩撞击力的物理模拟试验研究
工程力学, 2010,27(3):169-173
[本文引用: 1]

( Li Zhijun, Jia Qing, Wang Guoyu, et al. Physical simulation of ice floe impact forces on pile structres of wharfs
Engineering Mechanics, 2010,27(3):169-173 (in Chinese))
[本文引用: 1]

[97] 张强. PIV技术在实验室模拟冰下流场测试中的应用
[博士论文]. 大连: 大连理工大学, 2009
[本文引用: 1]

( Zhang Qiang. Application of PIV on flow field measurement under floe ice in laboratory modeling
[PhD Thesis]. Dalian: Dalian University of Technology, 2009 (in Chinese))
[本文引用: 1]

[98] Pite HD, Topham DR, Van HBJ. Laboratory measurements of the drag force on a family of two-dimensional ice keel models in a two-layer flow
Journal of Physical Oceanography, 1995,25(12):3008-3031
[本文引用: 1]

[99] McPhee MG. Advances in understanding ice ocean stress during and since AIDJEX
Cold Regions Science & Technology, 2012, 76-77-24-36
[本文引用: 1]

[100] 吴甜宇, 邱文亮, 胡哈斯. 海冰与波流联合作用下深水基础桥梁动力反应分析
武汉理工大学学报(交通科学与工程版), 2018,42(6):930-936
[本文引用: 1]

( Wu Tianyu, Qiu Wenliang, Hu Hasi. Dynamic response analysis of deep water foundation bridge under combined action of sea ice and wave current
Journal of Wuhan University of Technology(Transportation Science & Engineering), 2018,42(6):930-936 (in Chinese))
[本文引用: 1]

[101] Dolatshah A, Bennetts LG, Meylan MH, et al. An experimental model of wind-induced rafting of pancake ice floating on waves
// 34th International Workshop on Water Waves and Floating Bodies, 2019, April 7-10, Newcastle, Australia
[本文引用: 3]

[102] Bennetts LG, Yiew LJ, Meylan MH, et al. An experimental model of non-rafting collisions between ice floes caused by monochromatic water waves
// 19th Australasian Fluid Mechanics Conference, 2014, April 8-11, Melbourne, Australia
[本文引用: 1]

[103] Yiew LJ, Bennetts LG, Meylan MH, et al. Wave-induced collisions of thin floating disks
Physics of Fluids, 2018,29(12):127102
[本文引用: 1]

[104] M?rtensson S, Meier HEM, Pemberton P, et al. Ridged sea ice characteristics in the Arctic from a coupled multicategory sea ice model
Journal of Geophysical Research Oceans, 2012, 117:C00D15
[本文引用: 1]