黄建亮^,2), 王腾, 陈树辉中山大学应用力学与工程系, 广州 510275

NONLINEAR DYNAMIC ANALYSIS OF A VAN DER POL-MATHIEU EQUATION WITH EXTERNAL EXCITATION¹⁾

Huang Jianliang^,2), Wang Teng, Chen ShuhuiDepartment of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou 510275, China

通讯作者: 2) 黄建亮, 教授, 主要研究方向: 非线性动力学与控制. E-mail:huangjl@mail.sysu.edu.cn

收稿日期:2020-09-6接受日期:2020-11-2网络出版日期:2021-02-07

基金资助:

1) 国家自然科学基金资助项目.11972381

Received:2020-09-6Accepted:2020-11-2Online:2021-02-07
作者简介 About authors


摘要
本文针对含有自激励, 参数激励和外激励等三种激励联合作用下van der Pol-Mathieu方程的周期响应和准周期运动进行分析, 发现其准周期运动的频谱中含有均匀边频带这一新的特性. 首先, 采用传统的增量谐波平衡法(IHB法)分析了van der Pol-Mathieu方程的周期响应, 得到了其非线性频率响应曲线; 再利用Floquet理论对周期解进行稳定性分析, 得到了两种类型的分岔及它们的位置. 然后, 基于van der Pol-Mathieu方程准周期运动的频谱中边频带相邻频率之间是等距的且含有两个不可约的基频的特性(其中一个基频是已知的, 另一个基频事先是未知的), 推导了相应的两时间尺度IHB法, 精确计算出van der Pol-Mathieu方程的准周期运动的另一个未知基频和所有的频率成份及其对应的幅值, 尤其在临界点附近处的准周期运动响应. 得到的准周期运动结果和利用四阶龙格-库塔(RK)数值法得到的结果高度吻合. 最后, 研究发现了含外激励van der Pol-Mathieu方程在不同激励频率时的一些丰富而有趣的非线性动力学现象.
关键词： van der Pol-Mathieu方程;两时间尺度增量谐波平衡法;分岔;准周期运动;边频带

Abstract
The periodic responses and quasi-periodic motions of a van der Pol-Mathieu equation subjected to three excitations, i.e., self-excited, parametric excitation, and external excitation, are studied in this paper. A new characteristic is observed that the spectra of the quasi-periodic motions contain uniformly spaced sideband frequencies. Firstly, the traditional incremental harmonic balance (IHB) method is used to obtain periodic responses of the van der Pol-Mathieu equation and to trace their nonlinear frequency response curves automaically. Then the Floquet theory is used to analyze stability of the periodic responses and their bifurcations. Based on the characteristic that the spectra of quasi-periodic motions contain two incommensurate basic frequencies, i.e., the excitation frequency and a priori unknown frequency related to uniformly spaced sideband frequencies. Then the IHB method with two time-scales basing on the two basic frequencies is formulated to accurately calculate all frequency components and their corresponding amplitudes even at critical points. All the results obtained from the IHB method with two time-scales are in excellent agreement with those from numerical integration using the fourth-order Runge-Kutta method. Finally, this investigation reveals rich dynamic characteristics of the van der Pol-Mathieu equation in a range of excitation frequencies.
Keywords：van der Pol-Mathieu equation;incremental harmonic balance method with two time-scales;bifurcation;quasi-periodic motion;sideband


PDF (1983KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
黄建亮, 王腾, 陈树辉. 含外激励van der Pol-Mathieu方程的非线性动力学特性分析¹⁾. 力学学报[J], 2021, 53(2): 496-510 DOI:10.6052/0459-1879-20-310
Huang Jianliang, Wang Teng, Chen Shuhui. NONLINEAR DYNAMIC ANALYSIS OF A VAN DER POL-MATHIEU EQUATION WITH EXTERNAL EXCITATION¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(2): 496-510 DOI:10.6052/0459-1879-20-310

引言

在工程中存在着很多可以用自激振动和参数激振联合作用的van der Pol-Mathieu方程来描述的振动, 例如, 含有万向接头的转子系统的横向振动^[1], 卡盘作业过程中的参数激振^[2], 含有自振和参数激振的齿轮装置系统的振动^[3], 尘埃等离子体中的颗粒电荷的动力学行为^[4], 高层建筑结构在风荷载下的振动^[5-6]等, 都是可用van der Pol-Mathieu方程来描述振动的典型例子. van der Pol-Mathieu方程同时含有自激振动和参数激振, 蕴含着丰富的动力学行为, 多年来一直是众多****关注点之一.

Tondl^[7]首先分析了van der Pol-Mathieu方程中自激振动和参数激振的相互作用, 并在共振区域发现了周期响应. Kotera和Yano^[8]用两个频率的和分析了van der Pol-Mathieu方程在参数共振区域的近似一阶和二阶的周期解. 陈予恕和徐鉴^[9]研究了van der Pol-Duffing-Mathieu型系统主参数共振分岔解, 得到该非线性参数激励系统依赖于物理参数变化的振动模式. Szabelski和Warminski^[10]分析了自激振动和参数激励对van der Pol-Mathieu方程的影响, 并且研究了附加外激励在同步区域内动力学行为的影响. Warminski等^[3]对含有自激振动和参数激励的两自由度系统进行分析, 并得到了不同类型的响应, 包含有周期响应, 准周期运动响应和混沌. 彭献和陈自力^[11]引入参数变换, 将强非线性系统转化为弱非线性系统, 利用摄动思想分析得到了van der Pol-Mathieu方程的1/2亚谐共振周期解. Belhaq和Fahsi^[12]和Pandey等^[13]分析了van der Pol-Mathieu-Duffing系统的响应, 得到该类系统可含有1:1锁频, 2:1次谐波锁频和准周期运动响应. 张琪昌等^[14]利用改进的类Padé方法计算了van der Pol-Duffing方程的同异宿轨道. Warminski^[15]研究了含有van der Pol和Rayleigh函数在两个不同自激振动模型下具有时滞状态的自激振动, 参数激振和强迫振动作用下的相互作用. 许多****也对各类含有参数激振的非线性系统进行研究^[16-19], 得到了不同的非线性振动特性和运动分岔.

早期对于van der Pol-Mathieu方程的众多研究主要集中在含有一个基频的周期响应及其稳定性分析. 可以利用不同的摄动方法求得这类方程的近似解析解^[20]. 然而, 对于van der Pol-Mathieu方程来说, 因有自激振动与参数激励振动的相互耦合作用, 使得系统不仅有周期响应, 而且还有准周期运动响应, 甚至产生混沌, 近年来受到众多****的关注. Belhaq和Houssni^[21]为了构造准周期运动的近似解, 提出了双摄动的思想, 其方法包含了两个步骤: 第一步利用广义的平均法将准周期系统变为周期减化系统; 第二步是用多尺度法对周期减化系统构造出近似的准周期运动解. 他们利用双摄动方法得到了同时含有二次和三次非线性项的参数激励和外激励的单自由度系统的准周期解. 该双摄动方法的本质就是对周期减化系统在平衡点附近的周期解进行非线性近似, 该方法可进一步推广到各类非线性系统的准周期运动分析中^[5-6,12,22]. Fan等^[23]也利用了双摄动方法分析了van der Pol-Mathieu方程在有外激励和无外激励两种情况下的周期解和准周期运动近似解的包络线. 然而, 双摄动方法只能得到准周期运动包络线的最大和最小幅值, 无法得到系统准周期运动的具体响应情况, 更无法得到系统准周期运动的各个响应频率. Warminski等^[3]和Warminski^[15]利用多尺度法分别分析了含有自激励和参数激励的两个自由度时滞系统, 并利用数值法得到了两个时滞系统的准周期运动响应和混沌. Veerman和Verhulst^[24]利用平均法分析了van der Pol-Mathieu方程, 并得到了由1阶和1/$\varepsilon$阶基础周期构造而成的准周期运动响应, 其中$\varepsilon$是小量. 上述的各种摄动法只能得到van der Pol-Mathieu方程准周期运动近似解, 有些方法得到的结果只能描述准周期运动的最大和最小振幅, 特别是在邻近分岔点处用摄动法得到的准周期运动解与数值解相差甚大, 据作者所知, 迄今为止尚未有有效的摄动法能精确地计算并得到此类van der Pol-Mathieu方程的精确准周期运动解.

本文针对含有外激励的van der Pol-Mathieu方程进行研究, 主要是发现了单自由度的van der Pol-Mathieu方程准周期运动的频谱含有均匀边频带的新特性。 此新特性与之前研究分析的多自由度非线性系统中内共振引起的准周期运动的频谱特性^[25-27]相类似, 即都含有均匀的边频带, 不同之处在于多自由度非线性系统中的准周期运动是由于不同振动模态之间在内共振条件下相互作用产生的, 而单自由度的van der Pol-Mathieu方程的准周期运动是由于自激振动与参数激振耦合产生的, 仅是van der Pol方程中的自激振动或仅是Mathieu方程中的参数激振并不能产生准周期运动. 根据此准周期运动频谱含有均匀边频带的特性, 它包含了两个基频, 一个是已知激励频率$\omega$; 另一个是事先未知的频率$\omega_{\rm d}$, 即为边频带中相邻两个频率之间的距离, 那么准周期运动中所有的频率成份都可表示为这两个基频的线性组合. 因此, 本文利用传统的增量谐波平衡法(IHB法)分析单自由度含有外激励的van der Pol-Mathieu方程的周期响应, 并推广两时间尺度的IHB法, 其中一个时间尺度是快时间尺度$\tau_1=\omega t$; 另外一个是慢时间尺度$\tau_2=\omega_{\rm d}t(\omega\gg\omega_{\rm d}$), 应用于分析此van der Pol-Mathieu方程的准周期运动响应.

1 含外激励van der Pol-Mathieu方程的周期解及其稳定性

对于含有外激励van der Pol-Mathieu方程, 有3种激励共同作用, 即自激励, 参数激励和外激励, 可描述为下列的微分方程

(1)$\begin{eqnarray} &&\frac{{\rm d}^2x}{{\rm d}t^2}-\left(k_1-k_2x^2\right)\frac{{\rm d}x}{{\rm d}t}+\left(\tilde{\omega}_0^2+k_3\cos{2\omega t}\right)x=\\&&\qquad f\cos\omega t \label{eq1} \end{eqnarray}$
其中, $x$是因变量, $t$是时间, $k_1$, $k_2$和$k_3$是常数, $\tilde{\omega}_0$是线性固有频率, $\omega$是激励频率, $f$是外激励幅度. 方程(1)包含了自激励, 即van der Pol项$-\left(k_1-k_2x^2\right){{\rm d}x}/{{\rm d}t}$; 参数激励, 即Mathieu项$k_3\cos\left({2\omega t}\right)x$和简谐外激励$f\cos\omega t$. 对于此方程, 首先利用传统的IHB法确定其周期解, 然后利用Floquet理论, 并结合精细的Hsu法判断其周期解的稳定性及分岔, 最后得到了Saddle-node和Hopf这两种分岔类型.

1.1 传统的IHB法

对于含外激励的van der Pol-Mathieu方程, 可以利用传统的IHB法来确定其周期解. 引入一个新的时间变量

(2)$\begin{eqnarray} \tau=\omega t \label{eq2} \end{eqnarray}$
方程(1)可变为

(3)$\begin{eqnarray} &&\omega^2x"-\omega\left(k_1-k_2x^2\right)x'+\left(\tilde{\omega}_0^2+k_3\cos2\tau\right)x=\\&&\qquad f\cos\tau \label{eq3} \end{eqnarray}$
其中, $'$表示对时间$\tau$的导数.

传统的IHB法包含两个过程, 增量过程和谐波平衡过程. 增量过程即Newton-Raphson迭代过程, 是对微分方程(3)进行线性化. 设$x_0, \omega_0, f_0$是方程(3)的解, 则其邻近点可表示为

(4)$\begin{eqnarray} x=x_0+\Delta x, \ \ \omega=\omega_0+\Delta\omega, \ \ f=f_0+\Delta f \label{eq4} \end{eqnarray}$
式中, $\Delta x,\Delta\omega, \Delta f$为增量, 将式(4)代入方程(3), 并略去高阶小量后可得到以$\Delta x,\Delta\omega, \Delta f$为未知量的增量方程

(5)$\begin{eqnarray} &&\omega_0^2 \Delta x"-\omega_0\left(k_1-k_2x^2_0\right)\Delta x' +\\&&\qquad\left(\tilde{\omega}_0^2+k_3\cos2\tau+2\omega_0k_2x_0x_0'\right)\Delta x =\\&&\qquad R-\left[2\omega_0x_0"-\left(k_1-k_2x_0^2\right)\right]\Delta\omega+\cos\tau\Delta f \label{eq5} \end{eqnarray}$
其中

(6)$\begin{eqnarray} &&R=f_0\cos\tau -\Big[\omega_0^2x"_0 -\omega_0\left(k_1-k_2x_0^2\right)x'_0 +\\&&\qquad\left(\tilde{\omega}_0^2+k_3\cos2\tau\right)x_0\Big] \label{eq6} \end{eqnarray}$
为不平衡力. 如果$x_0, \omega_0, f_0$是方程(3)的准确解, 那么$R=0$.

传统IHB法的第二个过程是谐波平衡过程(Galerkin过程). 因方程(1)是自激励和参数激励的系统, 包含了奇次非线性项, 所以对于其周期解, 可设

(7)$\begin{eqnarray} &&x_0=\sum_{k=1}^{n_{\rm c}}a_k\cos\left(2k-1\right)\tau+\\&&\qquad \sum_{k=1}^{n_{\rm s}}b_k\sin\left(2k-1\right)\tau=\boldsymbol C _{\rm s}\boldsymbol A \label{eq7} \end{eqnarray}$
(8)$\begin{eqnarray} \Delta x=\sum_{k=1}^{n_{\rm c}}\Delta a_k\cos\left(2k-1\right)\tau+\\ \qquad\sum_{k=1}^{n_{\rm s}}\Delta b_k\sin\left(2k-1\right)\tau =\boldsymbol C_{\rm s}\Delta\boldsymbol A \label{eq8} \end{eqnarray}$
式中

(9)$\begin{eqnarray} \boldsymbol C_{\rm s}= [\cos\tau \ \cos3\tau \ \cdots \ \cos\left(2n_{\rm c}-1\right)\tau \\ \qquad \sin\tau \ \sin3\tau \ \cdots \ \sin \left(2n_{\rm s}-1\right) ] \end{eqnarray}$
(10)$\begin{eqnarray} \boldsymbol A= \begin{bmatrix} a_1 & a_2 & \cdots & a_{n_{\rm c}} & b_1 & b_2 & \cdots & b_{n_{\rm s}} \end{bmatrix} ^{\rm T} \label{eq10} \end{eqnarray}$
(11)$\begin{eqnarray} \Delta \boldsymbol A= \begin{bmatrix}\Delta a_1 & \Delta a_2 & \cdots & \Delta a_{n_{\rm c}} & \Delta b_1 & \Delta b_2 & \cdots & \Delta b_{n_{\rm s}} \end{bmatrix} ^{\rm T} \label{eq11} \end{eqnarray}$
这里, $a_k$和$b_k$是傅里叶系数, $n_{\rm c}$和$n_{\rm s}$分别是cosine和sine谐波项的项数

对式(7)和式(8)进行微分, 得

(12)$\begin{eqnarray} &&x'_0=\boldsymbol C'_{\rm s}\boldsymbol A, \ \ \Delta x'=\boldsymbol C'_{\rm s}\Delta\boldsymbol A \label{eq12} \end{eqnarray}$
(13)$\begin{eqnarray} x"_0=\boldsymbol C"_{\rm s}\boldsymbol A, \ \ \Delta x"=\boldsymbol C"_{\rm s}\Delta\boldsymbol A \label{eq13} \end{eqnarray}$
将式(7), 式(8), 式(12)和式(13)代入方程(5), 并利用Galerkin过程平衡谐波项, 得

(14)$\begin{eqnarray}\label{eq14} &&\int_{0}^{2\pi} \delta \left(\Delta x\right)\Big[\omega_0^2 \Delta x"-\omega_0\left(k_1-k_2x_0^2\right)\Delta x'+\\&&\qquad\left(\tilde{\omega}_0 ^2+k_3\cos2\tau+2\omega_0k_2x_0x'_0\right)\Delta x \Big]{\rm d}\tau =\\&&\qquad \int_{0}^{2\pi}\delta\left(\Delta x\right)\Big\{ R-\left[2\omega_0x"_0-\left(k_1-k_2x_0^2\right)x'_0\right]\Delta\omega +\\&&\qquad \cos\tau\Delta f\Big\}{\rm d}\tau \end{eqnarray}$
积分上式并整理归并为以$\Delta \boldsymbol A, \Delta\omega$和$\Delta f$为未知量的代数方程组

(15)$\begin{eqnarray} \boldsymbol K_A\Delta \boldsymbol A=\bar{\boldsymbol R}-\boldsymbol R_\omega \Delta \omega+\boldsymbol R_f\Delta f \label{eq15} \end{eqnarray}$
其中

(16)$\begin{eqnarray} \boldsymbol K_A=\int_{0}^{2\pi}\boldsymbol C_{\rm s}^{\rm T}\Big[\omega_0^2\boldsymbol C"_{\rm s}-\omega_0\left(k_1-k_2\boldsymbol C_{\rm s}\boldsymbol A\boldsymbol C_{\rm s}\boldsymbol A\right)\boldsymbol C'_{\rm s}+\\ \qquad \left(\tilde{\omega}_0^2+k_3\cos2\tau+2\omega_0k_2\boldsymbol{C}_{\rm s}\boldsymbol{A}\boldsymbol{C}'_{\rm s}\boldsymbol{A}\right)\Big]{\rm d}\tau \label{eq16} \end{eqnarray}$
(17)$\begin{eqnarray} \bar{\boldsymbol{R}}=-\int_{0}^{2\pi}\boldsymbol{C}_{\rm s}^{\rm T}\Big[\omega_0^2\boldsymbol{C}"_{\rm s}-\omega_0\left(k_1-k_2\boldsymbol{C}_{\rm s}\boldsymbol{A}\boldsymbol{C}_{\rm s}\boldsymbol{A}\right)\boldsymbol{C}'_{\rm s}+\\ \qquad\left(\tilde{\omega}_0^2+k_3\cos2\tau\right)\Big]{\rm d}\tau \label{eq17} \end{eqnarray}$
(18)$\boldsymbol{R}_{\omega}=\int_{0}^{2 \pi} \boldsymbol{C}_{\mathrm{s}}^{\mathrm{T}}\left[2 \omega_{0} \boldsymbol{C}_{\mathrm{s}}^{\prime \prime}-\left(k_{1}-k_{2} \boldsymbol{C}_{\mathrm{s}} \boldsymbol{A} \boldsymbol{C}_{\mathrm{s}} \boldsymbol{A}\right) \boldsymbol{C}_{\mathrm{s}}^{\prime}\right] \boldsymbol{A} \mathrm{d} \tau$
(19)$\begin{eqnarray} \boldsymbol{R}_f=\int_{0}^{2\pi}\boldsymbol{C}'_{\rm s}\cos\tau {\rm d}\tau \label{eq19} \end{eqnarray}$
这里, 上标$^{\rm T}$表示为矩阵的转置, $\boldsymbol{K}_A$是 $n\times n$的矩阵, $\bar{\boldsymbol{R}}$和$\boldsymbol{R}_\omega$是 $n\times1$的矩阵, $n=n_{\rm c}+n_{\rm s}$. 本文只考虑在某一固定外激励幅值下的频率响应曲线, 那么$f$取固定值, $\Delta f=0$,于是方程(15)成为

(20)$\begin{eqnarray} \boldsymbol{K}_A\Delta \boldsymbol{A}=\bar{\boldsymbol{R}}-\boldsymbol{R}_\omega \Delta \omega\label{eq20} \end{eqnarray}$
用传统的IHB法求解时, 可事先给定一个初值, 然后利用增量过程和谐波平衡过程追踪出所有的解. 在求解过程中, 可采用振幅增量, 频率增量或弧长增量, 具体可参见Cheung等^[28], 陈树辉^[29]的研究结果.

1.2 周期解的稳定性与分岔

利用传统的IHB法确定含外激励van der Pol-Mathieu方程的周期解后, 需要分析其稳定性. 设$x_0$为已求得的解, 给$x_0$一个小的扰动$\Delta x$

(21)$\begin{eqnarray} x=x_0+\Delta x\label{eq21} \end{eqnarray}$
将式(21)代入方程(1), 略去高阶小量, 并注意$x_0$满足方程(1), 可得

(22)$\begin{eqnarray} && \omega^2\Delta x"-\omega \left(k_1-k_2x_0^2\right)\Delta x' +\\&&\qquad \left(\tilde{\omega}_0^2+k_3\cos2\tau+2k_2x_0x'_0\right)\Delta x=0 \label{eq22} \end{eqnarray}$
方程(22)称为扰动方程, 即从已知的平衡位置扰动而得的方程. 方程(22)的稳定性特征可以用Floquet理论来分析. 将方程(22)重新写为状态方程

(23)$\begin{eqnarray} \boldsymbol{X}'=\boldsymbol{Q}\left(\tau\right)\boldsymbol{X} \label{eq23} \end{eqnarray}$
其中

(24)$\begin{eqnarray} &&\boldsymbol{X}=\begin{bmatrix} \Delta x & \Delta x' \end{bmatrix}^{\rm T} \label{eq24} \\ \end{eqnarray}$
(25)$\begin{eqnarray} &&\boldsymbol{Q}=\begin{bmatrix} 0 & 1 \\ Q_{21}\left(\tau\right) & Q_{22}\left(\tau\right) \end{bmatrix} \label{eq25} \end{eqnarray}$
这里

(26)$\begin{eqnarray} &&Q_{21}\left(\tau\right)=-\frac{1}{\omega^2}\left(\tilde{\omega}_0^2+k_3\cos2\tau+2k_2x_0x'_0\right) \label{eq26} \end{eqnarray}$
(27)$\begin{eqnarray} &&Q_{22}\left(\tau\right)=\frac{1}{\omega}\left(k_1-k_2x_0^2\right) \label{eq27} \end{eqnarray}$
由于$x_0$是$\tau$的周期为$T=2\pi$的函数, 所以$Q_{21}$和$Q_{22}$也是周期为$T=2\pi$的函数.

对于方程(23), 存在着一组基础解系

(28)$\begin{eqnarray} \boldsymbol{y}_k=\begin{bmatrix} y_{1k} & y_{2k} \end{bmatrix},\ \ k=1,2 \label{eq28} \end{eqnarray}$
这一基础解系可用矩阵来表示

(29)$\begin{eqnarray} \boldsymbol{Y}= \begin{bmatrix} y_{11} & y_{12} \\ y_{21} & y_{22} \end{bmatrix} \label{eq29} \end{eqnarray}$
可以看到, $\boldsymbol{Y}$满足矩阵方程

(30)$\begin{eqnarray} \boldsymbol{Y}'=\boldsymbol{Q}\left(\tau\right)\boldsymbol{Y} \label{eq30} \end{eqnarray}$
由于 $\boldsymbol{Q}\left(\tau+T\right)=\boldsymbol{Q}\left(\tau\right)$, $\boldsymbol{Y}\left(\tau+T\right)$也是基础矩阵解, 因此, 它可表示为

(31)$\begin{eqnarray} \boldsymbol{Y}\left(\tau+T\right)=\boldsymbol{PY}\left(\tau\right)\label{eq31} \end{eqnarray}$
式中, $\boldsymbol{P}$为非奇异常数矩阵, 称为转移矩阵. 根据Floquet理论, 方程(23)的稳定性准则与矩阵$\boldsymbol{P}$的特征值$\lambda_i$有关. 如果转移矩阵$\boldsymbol{P}$的所有特征值的模都小于1, 则方程(23)的运动是有界的, 因而此周期解是稳定的; 如果转移矩阵$\boldsymbol{P}$中至少有一个特征值的模大于1, 则方程(23)的运动是无界的, 此周期解也就不稳定.

采用数值方法求解方程(30)的基础解系, 其中有效地计算转移矩阵$P$是稳定性分析的关键. Hsu^[30-31]和Hsu和Cheng^[32]提出一个近似求解转移矩阵$\boldsymbol{P}$的有效方法, 其主要思想是把一个周期等分为若干时间间段, 在每一时间段上进行积分. Friedmann等^[33]给出了该方法的具体推导表达式. Huang等^[34]在此基础上, 结合了精细积分算法^[35], 提出了精细的Hsu法, 有效地减小了计算转移矩阵$\boldsymbol{P}$的舍入误差.

1.3 含外激励van der Pol-Mathieu方程周期解的响应特性

在用传统的IHB求解过程中, 取谐波项项数$n_{\rm c}=n_{\rm s}=3$, 式(7)可写为

(32)$\begin{eqnarray} &&x_0=a_1\cos\tau+a_2\cos 3\tau+a_3\cos 5\tau+b_1\sin\tau+\\&&\qquad b_2\sin 3\tau+ b_3\sin 5\tau =A_1\cos\left(\tau+\varphi_1\right)+\\&&\qquad A_2\cos\left(3\tau+\varphi_2\right)+ A_3\cos\left(5\tau+\varphi_3\right) \label{eq32} \end{eqnarray}$
式中

(33)$\begin{eqnarray} A_i=\sqrt{a_i^2+b_i^2}, \ \ \varphi_i=\arctan\left(-b_i/a_i\right), \ \ i=1,2,3\quad \label{eq33} \end{eqnarray}$
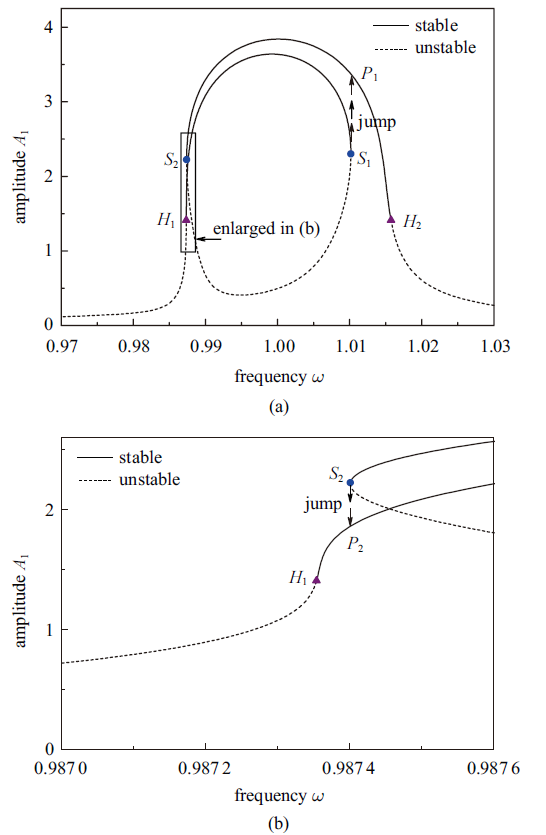
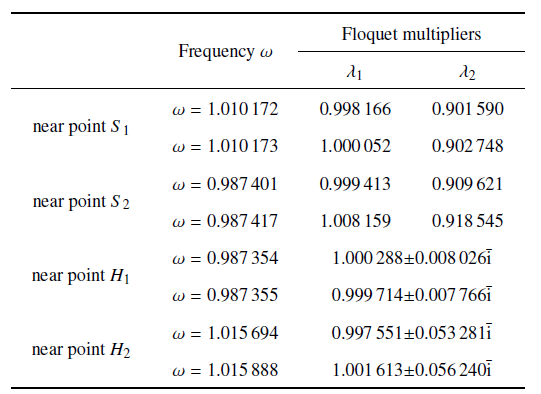
图1所示为当$k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$时van der Pol-Mathieu方程周期响应的频率响应曲线$\omega$-$A_1$, 高阶的谐波项较小而没有在此显示, 图1(b)是图1(a)中标示区域的放大图, 其中实线表示稳定的周期解, 虚线表示不稳定的周期解, 实圆点表示Saddle-node分岔, 实三角形点表示Hopf分岔. 图1中4个临近分岔点的响应点的Floquet乘子如表1所示. 从表1 可以看出, 在复平面上其中的一个Floquet乘子从+1方向穿出单位圆, 导致了Saddle-node分岔($S_1$和$S_2$), 从而出现跳跃现象; 而一对共轭的Floquet乘子穿出单位圆, 导致了Hopf分岔($H_1$和$H_2$), 从而出现了准周期运动.

图1

新窗口打开|下载原图ZIP|生成PPT
图1含外激励van der Pol-Mathieu方程周期响应的频率响应曲线, $\omega$-$A_1$ 其中 $k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$, (b)为(a)中标示区域的放大图

Fig.1Frequency response curve $\omega$-$A_1$ of periodic response of the van der Pol-Mathieu equation with external excitation with $k_1=0.01$, $k_2=0.01$, $k_3=0.05$, and $f=0.01$, (b) is an enlarged view of a zone highlighted in (a)



Table 1
表1
表1频率$\omega$在4个分岔点$S_1$, $S_2$, $H_1$和$H_2$临近点响应的Floquet乘子$\lambda_1$和$\lambda_2$, 其中$\bar{\rm i}=\sqrt{-1}$
Table 1Floquet multipliers $\lambda_1$ and $\lambda_2$ for the frequency $\omega$ near the four bifurcation points $S_1$, $S_2$, $H_1$, and $H_2$, where $\bar{\rm i}=\sqrt{-1}$

新窗口打开|下载CSV

在含有外激励van der Pol-Mathieu方程中, 由于非线性的影响, 周期解的频率响应曲线出现了多值性, 从而出现了一些重要而且有趣的动力学现象, 如图1所示的跳跃现象. 假设外激励幅值$f$不变而频率$\omega$慢慢地变化, 先考察向右扫频的过程, 周期解从分岔点$H_1$出发, 当频率$\omega$逐渐增大时, 振幅$A_1$开始变大, 在$\omega=1.0$附近达到最大值, 过了最大值后振indent 幅$A_1$变小到达分岔点$S_1$, 如果$\omega$继续增大, 则振幅$A_1$突然从点$S_1$跳跃到点$\text{P}_1$(如图1(a)所示), 然后沿曲线逐渐变小, 最后到达点$H_2$. 反之, 考察向左扫频的过程, 周期解从分岔点$H_2$出发, 当频率$\omega$逐渐减小时, 振幅$A_1$开始变大, 在$\omega=1.0$附近也达到最大值, 过了最大值后振幅$A_1$变小到达分岔点$S_2$, 如果$\omega$继续减小, 则振幅$A_1$突然从点$S_2$跳跃到点$\text{P}_2$(如图1(b)所示), 然后沿曲线逐渐变小, 最后到达点$H_1$.

在图1中从点$S_1$到$S_2$的区域, 存在着两个稳定的周期解和一个不稳定的周期解. 图2所示为频率$\omega=1.0$时van der Pol-Mathieu方程含有3个不同解的周期响应, 其中图2(a)和图2(b)是两个稳定周期解的时间历程图, 其中实线表示用Runge-Kutta(RK)数值法求得的解, 圆圈表示用传统的IHB法得到的结果, 可以看出, 两个方法得到的结果非常吻合; 图2(c)所示为3个解的相图, 可以看出3条都是封闭的曲线, 进一步表明系统的响应为周期响应; 图2(d)所示为两个稳定周期解的频谱图, 可以看出$\left|A_1\right|\gg\left|A_2\right|\gg\left|A_3\right|$, 系统的响应主要以第一阶响应为主, 其频率是参数激励频率$2\omega$的一半, 与外激励频率一样, 因此系统的响应为自激振动, 1:2参数激振和外激励的联合作用.

图2

新窗口打开|下载原图ZIP|生成PPT
图2$\omega=1.0$时含外激励van der Pol-Mathieu方程含有3个周期解, 其中 $k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$: (a) 第一个稳定周期解的时间历程图; (b) 第二个稳定周期解的时间历程图; (c) 3个不同周期解的相图; (d) 两个稳定周期解的频谱图

Fig.2Three different periodic solutions of the van der Pol-Mathieu equation with external excitation for $\omega=1.0$ with $k_1=0.01$, $k_2=0.01$, $k_3=0.05$, and $f=0.01$: (a) Time history of the first stable periodic response; (b) time history of the second stable periodic response; (c) phase plane portraits of the three solutions; (d) Fourier spectra of the two stable periodic response

2 含外激励van der Pol-Mathieu方程的准周期运动

对于含外激励van der Pol-Mathieu方程的周期响应, 其频率成份之间是可约的, 例如在本文中, 系统的频率成份为$\omega$, $3\omega$和$5\omega$. 在上节分析得知, 系统的周期解经Hopf分岔后会产生准周期运动. 对准周期运动来说, 其频率成份至少含有两个或以上的不可约频率. 事实上, 本文首次发现了van der Pol-Mathieu方程的准周期运动的新特性, 即其频率成份是由落在$\omega$, $3\omega$和$5\omega$附近的边频带组成, 并且这些边频带里的频率是等相距的, 即为均匀的边频带. 此准周期运动的新特性, 正是由于van der Pol-Mathieu方程中的自激振动和参数激振相互作用产生的. 如若只考察van der Pol方程中的自激振动或只考察Mathieu方程的参数激振, 并不会产生准周期运动. 根据此准周期运动的新特性, 其频谱中含有两个基频, 一个是已知的频率$\omega$, 另一个可把它看作是均匀边频带里相邻频率的距离$\omega_{\rm d}$, 且$\omega_{\rm d}$事先是未知的, 此时准周期运动中所有的频率都可由这两个基频线性组合而成. 根据此特性, 发展了传统的IHB法, 引入两个时间尺度, 使之适用于精确求解含外激励van der Pol-Mathieu方程的准周期运动, 并且可以得到此准周期运动所有的频率成份.

2.1 两时间尺度的IHB法

相较于传统的IHB法, 两时间尺度的IHB法在求解含外激励van der Pol-Mathieu方程的准周期运动过程中有3点改进之处, 具体推导如下.

(1) 第一点改进是引入两个时间变量代替式(2)中针对于周期解的一个时间变量$\tau=\omega t$, 如下

(34)$\begin{eqnarray} \tau_1=\omega t, \ \ \tau_2=\omega_{\rm d}t \label{eq34} \end{eqnarray}$
那么$x\left(t\right)$是$\tau_1$和$\tau_2$的函数, 即$x\left(t\right)=x\left(\omega t, \omega_{\rm d}t\right)=x\left(\tau_1,\tau_2\right)$. 记

(35)$\left. \begin{array} \\ \Theta=\dfrac{\rm d}{{\rm d}t}=\omega\dfrac{\partial}{\partial \tau_1}+\omega_{\rm d}\dfrac{\partial}{\tau_2} \\[3mm]\Theta^2=\dfrac{{\rm d}^2}{{\rm d}^2t}=\omega^2\dfrac{\partial^2}{\partial\tau_1^2}+2\omega\omega_{\rm d}\dfrac{\partial^2}{\partial\tau_1\partial\tau_2}+\omega_{\rm d}^2\dfrac{\partial^2}{\partial\tau_2^2} \label{eq35} \\ \end{array} \right\}$
式中, 引入算子$\Theta$和$\Theta^2$是为了简洁. 将式(35)代入

方程(1)可写为

(36)$\begin{eqnarray} &&\Theta^2x-\left(k_1-k_2x^2\right)\Theta x+\left(\tilde{\omega}_0^2+k_3\cos2\tau_1\right)x=\\&&\qquad f\cos\tau_1 \label{eq36} \end{eqnarray}$
同样, 利用增量过程, 对于第一步的两时间尺度IHB法, 设$x_0, \omega_0, \omega_{\rm d0}, f_0$是方程(36)的解, 则其邻近点可表示为

(37)$\left. \begin{array} \\ x=x_0+\Delta x, \ \ \omega=\omega_0+\Delta\omega\\ \omega_{\rm d}=\omega_{\rm d0}+\Delta\omega_{\rm d}, \ \ f=f_0+\Delta f \end{array} \right\}$
记

(38)$\left. \begin{array} \\ \Theta_0=\omega_0\dfrac{\partial}{\partial \tau_1}+\omega_{\rm d0}\dfrac{\partial}{\tau_2} \\ \Theta_0^2=\omega_0^2\dfrac{\partial^2}{\partial\tau_1^2}+2\omega_0\omega_{\rm d0} \dfrac{\partial^2}{\partial\tau_1\partial\tau_2}+\omega_{\rm d0}^2\dfrac{\partial^2}{\partial\tau_2^2} \label{eq38} \\ \end{array} \right\}$
将式(37)代入方程(36), 并忽略高阶小量, 得到以$\Delta x, \Delta\omega, \Delta\omega_{\rm d}, \Delta f$为未知量的增量方程

(39)$\begin{array}{l}\Theta_{0}^{2} \Delta x-\left(k_{1}-k_{2} x_{0}^{2}\right) \Theta_{0} \Delta x+\left(\tilde{\omega}_{0}^{2}+k_{3} \cos 2 \tau_{1}+\right. \\\left.2 x_{0} \Theta_{0} x_{0}\right) \Delta x=\tilde{R}-\left[2\left(\omega_{0} \frac{\partial^{2} x_{0}}{\partial \tau_{1}^{2}}+\omega_{\mathrm{d} 0} \frac{\partial^{2} x_{0}}{\partial \tau_{1} \partial \tau_{2}}\right)-\right. \\\left.\left(k_{1}-k_{2} x^{2}\right) \frac{\partial x_{0}}{\partial \tau_{1}}\right] \Delta \omega-\left[2\left(\omega_{0} \frac{\partial^{2} x_{0}}{\partial \tau_{1} \partial \tau_{2}}+\omega_{\mathrm{d} 0} \frac{\partial^{2} x_{0}}{\partial \tau_{2}^{2}}\right)-\right. \\\left.\left(k_{1}-k_{2} x^{2}\right) \frac{\partial x_{0}}{\partial \tau_{2}}\right] \Delta \omega_{\mathrm{d}}+\cos \tau \Delta f\end{array}$
其中

(40)$\begin{aligned}\tilde{R}=& f_{0} \cos \tau_{1}-\left[\Theta_{0}^{2} x_{0}-\left(k_{1}-k_{2} x^{2}\right) \Theta_{0} x_{0}+\right.\\&\left.\left(\tilde{\omega}_{0}^{2}+k_{3} \cos 2 \tau_{1}\right) x_{0}\right]\end{aligned}$
(2) 第二点改进是将$x_0$展开为含有两个时间变量$\tau_1$和$\tau_2$的二重傅里叶级数形式

(41)$\begin{eqnarray} &&x_0=\sum_{j_1=1}^{N_m}\sum_{j_2=-N_m}^{N_m}\tilde{a}_{j_1,j_2}\cos\left(j_1\tau_1+j_2\tau_2\right) +\\&&\qquad\sum_{j_1=1}^{N_m}\sum_{j_2=-N_m}^{N_m}\tilde{b}_{j_1,j_2}\sin\left(j_1\tau_1+j_2\tau_2\right) \label{eq41} \end{eqnarray}$
式中, $N_m$是傅里叶级数中保留到最高阶谐波项的项数, $\tilde{a}_{j_1,j_2}$和$\tilde{b}_{j_1,j_2}$是谐波项系数. 在含外激励van der Pol-Mathieu方程的准周期运动中, 发现了其频谱的边频带是集中在频率$\omega$及其奇数倍频上, 即$\omega,3\omega,5\omega,\cdots$, 而且边频带内相邻频率之间的距离是相等的, 也就是说, 所有含外激励van der Pol-Mathieu方程的准周期运动的频率成份可表示为$\omega, \omega\pm\omega_{\rm d}, \omega\pm2\omega_{\rm d}, \cdots, \omega\pm m_1\omega_{\rm d}, 3\omega, 3\omega\pm\omega_{\rm d}, 3\omega\pm2\omega_{\rm d}, \cdots, 3\omega\pm m_2\omega_{\rm d},\cdots, \left(2n_{\rm c}-1\right)\omega, \left(2n_{\rm c}-1\right)\omega\pm\omega_{\rm d}, \left(2n_{\rm c}-1\right)\omega\pm2\omega_{\rm d}, \cdots, \left(2n_{\rm c}-1\right)\omega\pm m_{n_{\rm c}}\omega_{\rm d}$, 其中$2m_1+1, 2m_2+1, \cdots$, $2m_{n_{\rm c}}+1$是对应于$\omega, 3\omega, \cdots$, $\left(2n_{\rm c}-1\right)\omega$边频带中谐波项的项数. 那么式(41)可表示为

(42)$\begin{eqnarray} &&x_0=\underbrace{\sum_{j_2=-m_1}^{m_1}\tilde{a}_{1,j_2}\cos\left(\tau_1+j_2\tau_2\right)}_{2m_1+1}+\\&&\qquad \underbrace{\sum_{j_2=-m_2}^{m_2}\tilde{a}_{3,j_2}\cos\left(3\tau_1+j_2\tau_2\right)}_{2m_2+1} +\cdots+\\&&\qquad\underbrace{\sum_{j_2=-m_{n_{\rm c}}}^{m_{n_{\rm c}}}\tilde{a}_{\left(2n_{\rm c}-1\right),j_2}\cos\left[\left(2n_{\rm c}-1\right)\tau_1+j_2\tau_2\right]}_{2m_{n_{\rm c}}+1} +\\&&\qquad\underbrace{\sum_{j_2=-m_1}^{m_1}\tilde{b}_{1,j_2}\sin\left(\tau_1+j_2\tau_2\right)}_{2m_1+1}+\\&&\qquad \underbrace{\sum_{j_2=-m_2}^{m_2}\tilde{b}_{3,j_2}\sin\left(3\tau_1+j_2\tau_2\right)}_{2m_2+1} +\cdots+\\&&\qquad\underbrace{\sum_{j_2=-m_{n_{\rm s}}}^{m_{n_{\rm s}}}\tilde{b}_{\left(2n_{\rm s}-1\right),j_2}\sin\left[\left(2n_{\rm s}-1\right)\tau_1+j_2\tau_2\right]}_\text{2m_{n_{\rm s}}+1}=\\&&\qquad \tilde{\boldsymbol{C}}_{\rm s}\tilde{\boldsymbol{A}} \end{eqnarray}$
式中

(43)\begin{eqnarray} &&\tilde{\boldsymbol{C}}_{\rm s}=\begin{bmatrix} \tilde{\boldsymbol{C}}_1 & \tilde{\boldsymbol{C}}_2 & \cdots & \tilde{\boldsymbol{C}}_{n_{\rm c}} & \tilde{\boldsymbol{S}}_1 & \tilde{\boldsymbol{S}}_2 & \cdots & \tilde{\boldsymbol{S}}_{n_{\rm s}} \end{bmatrix} \label{eq43} \end{eqnarray}
(44)\begin{eqnarray} &&\tilde{\boldsymbol{A}}=\begin{bmatrix} \tilde{\boldsymbol{A}}_1 & \tilde{\boldsymbol{A}}_2 & \cdots & \tilde{\boldsymbol{A}}_{n_{\rm c}} & \tilde{\boldsymbol{B}}_1 & \tilde{\boldsymbol{B}}_2 & \cdots & \tilde{\boldsymbol{B}}_{n_{\rm s}} \end{bmatrix}^{\rm T} \label{eq44} \end{eqnarray}
其中, $\tilde{\boldsymbol{C}}_k$和$\tilde{\boldsymbol{S}}_k$对应于cosine和sine的谐波项, $\tilde{\boldsymbol{A}}_k$和$\tilde{\boldsymbol{B}}_k$是对应的系数. 同时, 增量$\Delta x$也展开为下面的傅里叶级数形式

(45)$\begin{eqnarray} \Delta x= \tilde{\boldsymbol{C}}_{\rm s}\Delta\tilde{\boldsymbol{A}} \label{eq45} \end{eqnarray}$
式中, $\Delta\tilde{\boldsymbol{A}}=\begin{bmatrix} \Delta\tilde{\boldsymbol{A}}_1 & \Delta\tilde{\boldsymbol{A}}_2 & \cdots & \Delta\tilde{\boldsymbol{A}}_{n_{\rm c}} & \Delta\tilde{\boldsymbol{B}}_1 & \Delta\tilde{\boldsymbol{B}}_2 & \cdots & \Delta\tilde{\boldsymbol{B}}_{n_{\rm s}} \end{bmatrix}^{\rm T}$. 利用Galerkin平均过程去平衡方程(39)中的谐波项得

(46)$\begin{array}{l}\int_{0}^{2 \pi} \int_{0}^{2 \pi} \delta(\Delta x)\left\{\Theta_{0}^{2} \Delta x-\left(k_{1}-k_{2} x_{0}^{2}\right) \Theta_{0} \Delta x+\right. \\\left.\left[\tilde{\omega}_{0}^{2}+k_{3} \cos 2 \tau_{1}+2 x_{0} \Theta_{0} x_{0}\right] \Delta x\right\} \mathrm{d} \tau_{1} \mathrm{~d} \tau_{2}= \\\int_{0}^{2 \pi} \int_{0}^{2 \pi} \delta(\Delta x)\left\{\tilde{R}-\left[2\left(\omega_{0} \frac{\partial^{2} x_{0}}{\partial \tau_{1}^{2}}+\omega_{\mathrm{d} 0} \frac{\partial^{2} x_{0}}{\partial \tau_{1} \partial \tau_{2}}\right)-\right.\right. \\\left.\left(k_{1}-k_{2} x^{2}\right) \frac{\partial x_{0}}{\partial \tau_{1}}\right] \Delta \omega-\left[2\left(\omega_{0} \frac{\partial^{2} x_{0}}{\partial \tau_{1} \partial \tau_{2}}+\omega_{\mathrm{d} 0} \frac{\partial^{2} x_{0}}{\partial \tau_{2}^{2}}\right)-\right. \\\left.\left.\left(k_{1}-k_{2} x^{2}\right) \frac{\partial x_{0}}{\partial \tau_{2}}\right] \Delta \omega_{\mathrm{d}}+\cos \tau \Delta f\right\} \mathrm{d} \tau_{1} \mathrm{~d} \tau_{2}\end{array}$
将式(42)和式(45)中的$x_0$和$\Delta x$代入方程(46)得到以$\Delta \tilde{\boldsymbol{A}}$, $\Delta\omega$和 $\Delta\omega_{\rm d}$为未知量的线性方程组

(47)$\begin{eqnarray} \tilde{\boldsymbol{K}}_A\Delta\tilde{\boldsymbol{A}}=\tilde{\boldsymbol{R}}-\tilde{\boldsymbol{R}}_\omega\Delta\omega-\tilde{\boldsymbol{R}}_{\rm d}\Delta\omega_{\rm d}+\Delta\tilde{\boldsymbol{F}}\label{eq47} \end{eqnarray}$
其中, $\tilde{\boldsymbol{K}}_A$是切线矩阵, $\tilde{\boldsymbol{R}}$是修正矩阵, $\tilde{\boldsymbol{R}}_\omega$和$\tilde{\boldsymbol{R}}_{\rm d}$分别是对应于$\Delta\omega$和$\Delta\omega$变化的不平衡力向量, $\Delta\tilde{\boldsymbol{F}}$是力的增量向量.

(3) 第三点改进是设两个控制变量满足方程(47)的可解性条件以得到准周期运动响应解. 如果考察的是系统的频率响应曲线, 即在某一固定的外激励振幅下的频率变化时的系统响应, 那么$\Delta\tilde{\boldsymbol{F}}=0$, 未知增量$\left(\Delta\tilde{\boldsymbol{A}},\Delta\omega,\Delta\omega_{\rm d}\right)$的个数比方程组(47)的方程数目多了2个; 如果考察的是系统的强迫响应曲线, 即在某一固定的频率下的外激励振幅变化时的系统响应, 那么$\Delta\omega=0$, 未知增量$\left(\Delta\tilde{\boldsymbol{A}},\Delta\tilde{\boldsymbol{F}},\Delta\omega_{\rm d}\right)$的个数也比方程组(47)的方程数目多了2个. 所以在每次增量过程中, 其中两个增量需要预先设定; 另外迭代过程中, 一般可取向量$\tilde{\boldsymbol{R}}$的模小于$1.0\times10^{-10}$作为收敛的条件. 在增量过程中, 可用频率增量、振幅增量, 或弧长增量来得到整个准周期运动的频率或强迫响应曲线图.

2.2 准周期运动的频率响应曲线

在用两时间尺度IHB法求解准周期运动解的过程中, 同样取$n_{\rm c}=n_{\rm s}=3$ (即对于第一个时间变量$\tau_1$, 取$\tau_1$, $3\tau_1$和$5\tau_1$), 那么cosine和sine谐波项项数$\tilde{n}_{\rm c}$和$\tilde{n}_{\rm s}$和所有的谐波项项数$\tilde{n}$分别为$\tilde{n}_{\rm c}=\tilde{n}_{\rm s}=2m_1+2m_2+2m_3+3$, $\tilde{n}=\tilde{n}_{\rm c}+\tilde{n}_{\rm s}=4m_1+4m_2+4m_3+6$, 式(42)可表示为

(48)$\begin{eqnarray} &&x_0=\underbrace{\left\{ \tilde{A}_{1,0}\cos\left(\tau_1+\tilde{\varphi}_{1,0}\right)+\tilde{A}_{1,\pm 1}\cos\left(\tau_1\pm \tau_2+\tilde{\varphi}_{1,\pm 1}\right)+\cdots +\tilde{A}_{1,\pm m_1}\cos\left(\tau_1\pm m_1\tau_{m_1}+\tilde{\varphi}_{1,\pm m_1}\right) \right\}}_{2m_1+1} + \\&&\qquad \underbrace{ \left\{ \tilde{A}_{3,0}\cos\left(3\tau_1+\tilde{\varphi}_{3,0}\right)+\tilde{A}_{3,\pm 1}\cos\left(3\tau_1\pm \tau_2+\tilde{\varphi}_{3,\pm 1}\right)+\cdots +\tilde{A}_{3,\pm m_2}\cos\left(3\tau_1\pm m_2\tau_{m_2}+\tilde{\varphi}_{3,\pm m_2}\right)\right\}}_{2m_2+1}+ \\&&\qquad \underbrace{ \left\{ \tilde{A}_{5,0}\cos\left(5\tau_1+\tilde{\varphi}_{5,0}\right)+\tilde{A}_{5,\pm 1}\cos\left(5\tau_1\pm \tau_2+\tilde{\varphi}_{5,\pm 1}\right)+\cdots +\tilde{A}_{5,\pm m_3}\cos\left(5\tau_1\pm m_3\tau_{m_3}+\tilde{\varphi}_{5,\pm m_3}\right)\right\}}_{2m_3+1}\label{eq48} \end{eqnarray}$
式中

(49)$\begin{eqnarray} &&\tilde{A}_{i,j}=\sqrt{\tilde{a}_{i,j}^2+\tilde{b}_{i,j}^2}, \ \ \tilde{\varphi}_{i,j}=\arctan\left(-\tilde{b}_{i,j}/\tilde{a}_{i,j}\right) \\ &&\qquad i=1,3,5, \ \ j=0,1,2,\cdots, m_1,\ m_2, \ \text{or} \ m_3 \label{eq49} \end{eqnarray}$
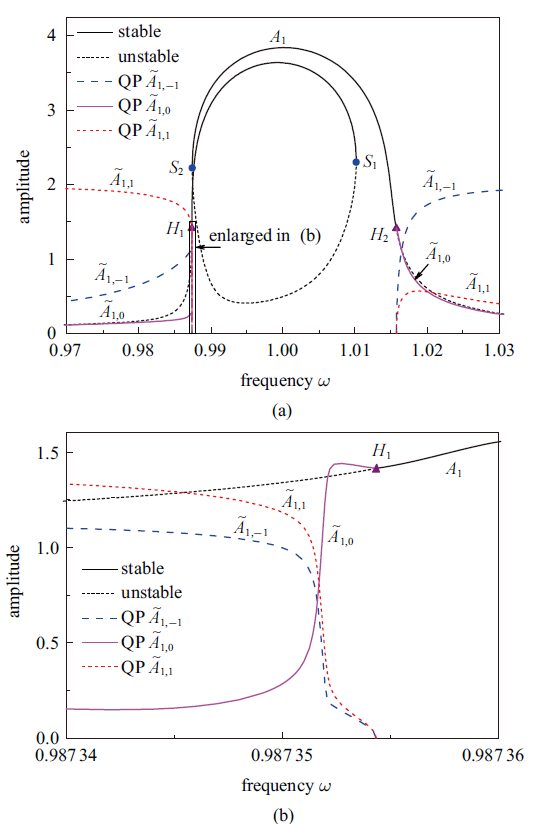
图3所示为当$k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$时含外激励van der Pol-Mathieu方程的周期解频率响应曲线$\omega$-$A_1$和准周期运动解频率响应曲线$\omega$-$\tilde{A}_{1,-1}$, $\omega$-$\tilde{A}_{1,0}$和$\omega$-$\tilde{A}_{1,1}$, 其中振幅$\tilde{A}_{1,-1}$, $\tilde{A}_{1,0}$和$\tilde{A}_{1,1}$分别对应于谐波项$\cos\left(\tau_1-\tau_2+\tilde{\varphi}_{1,-1}\right)$, $\cos\left(\tau_1+\tilde{\varphi}_{1,0}\right)$和$\cos\left(\tau_1+\tau_2+\tilde{\varphi}_{1,1}\right)$的系数, 在这里准周期运动解中的谐波项系数$\tilde{A}_{1,0}$与周期解中的谐波项系数$A_1$都对应于谐波项$\cos\left(\tau_1+\tilde{\varphi}_{1,0}\right)$. 图3(b)为图3(a)中标示区域的放大图.

图3

新窗口打开|下载原图ZIP|生成PPT
图3含外激励van der Pol-Mathieu方程周期响应的频率响应曲线$\omega$ -$A_1$和准周期运动(QP)的频率响应曲线$\omega$ -$\tilde{A}_{1,-1}$, $\omega$ -$\tilde{A}_{1,0}$和$\omega$ -$\tilde{A}_{1,1}$, 其中 $k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$, (b)为(a)中标示区域的放大图

Fig.3Frequency response curves $\omega$ -$A_1$ of periodic response and $\omega$ -$\tilde{A}_{1,-1}$, $\omega$ -$\tilde{A}_{1,0}$, and $\omega$ -$\tilde{A}_{1,1}$ of quasi-periodic (QP) motion of the van der Pol-Mathieu equation with external excitation with $k_1=0.01$, $k_2=0.01$, $k_3=0.05$, and $f=0.01$, (b) is an enlarged view of a zone highlighted in (a)



在图3中, 利用传统的IHB法得到的周期解有两个Hopf分岔点$H_1$和$H_2$, 在Hopf分岔点的两侧分别有稳定的周期解和不稳定的周期解. 而在不稳定周期解区域内, 实际的系统响应是稳态的准周期运动(由两时间尺度的IHB法求得), 此时系统分别有从两个分岔点$H_1$和$H_2$开始的准周期运动频率响应曲线. 先考察左侧的准周期运动频率响应曲线, $\tilde{A}_{1,0}$(相应于周期解中的$A_1$)从点$H_1$出发, 一开始随着频率$\omega$的减小而缓慢地增大, 然后急剧地减小, 从$\omega=0.987 35$开始又随着频率的减小而缓慢地减小(如图3所示); 而$\tilde{A}_{1,-1}$和$\tilde{A}_{1,1}$一开始的振幅为零, 随着频率频率$\omega$的减小而急剧地增大, 从$\omega=0.987 35$开始随着频率减小而缓慢地增大(如图3(b)所示); 从$\omega=0.987 35$开始, $\tilde{A}_{1,1}$随着频率$\omega$的减小而较为平缓地增大, 而$\tilde{A}_{1,-1}$随着频率$\omega$的减小而较为平缓地减小(如图3(a)所示). 再考察右侧的准周期运动频率响应曲线, $\tilde{A}_{1,0}$从点$H_2$出发, 随着频率$\omega$的增大而减小, 在此频率响应曲线上$\tilde{A}_{1,0}$的幅值接近于$A_1$; $\tilde{A}_{1,-1}$一开始的振幅为零, 随着频率$\omega$的增大而增大; $\tilde{A}_{1,1}$一开始的振幅也为零, 先随着频率$\omega$的增大而增大, 从$\omega=1.019$开始随着频率的增大而减小. 从图3还可看出, 准周期运动频率响应曲线在接近于分岔点区域$\tilde{A}_{1,0}$大于$\tilde{A}_{1,-1}$和$\tilde{A}_{1,1}$, 而远离分岔点区域$\tilde{A}_{1,0}$则小于$\tilde{A}_{1,-1}$和$\tilde{A}_{1,1}$.

2.3 不同频率$\omega$点的准周期运动

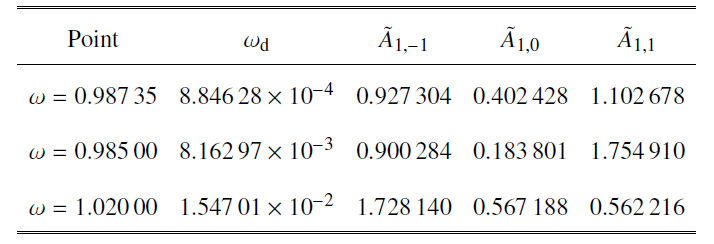
为了考察含外激励van der Pol-Mathieu方程的准周期运动特性, 在图3中选取3个不同频率$\omega$点来分析, 第一个点是$\omega=0.987 35$, 即在左侧曲线上临近于分岔点$H_1$; 第二个点是$\omega=0.985$, 即在左侧比第一个点较远离分岔点$H_1$; 第三个点是$\omega=1.02$, 即在右侧曲线上的一点. 图4至图6所示分别为在图3中上述3个点的时间历程图, 频谱图和庞加莱截面图. 表2所示为利用两时间尺度IHB法求出在图3中3个点$\omega=0.987 35$, 0.985, 1.02处的$\omega_{\rm d}$和$\tilde{A}_{1,-1},\tilde{A}_{1,0},\tilde{A}_{1,1}$. 从表2可以看出, 在系统的准周期运动中, 当频率$\omega$越远离Hopf分岔点时, 均匀边频带的频率间的间距$\omega_{\rm d}$越大.

图4

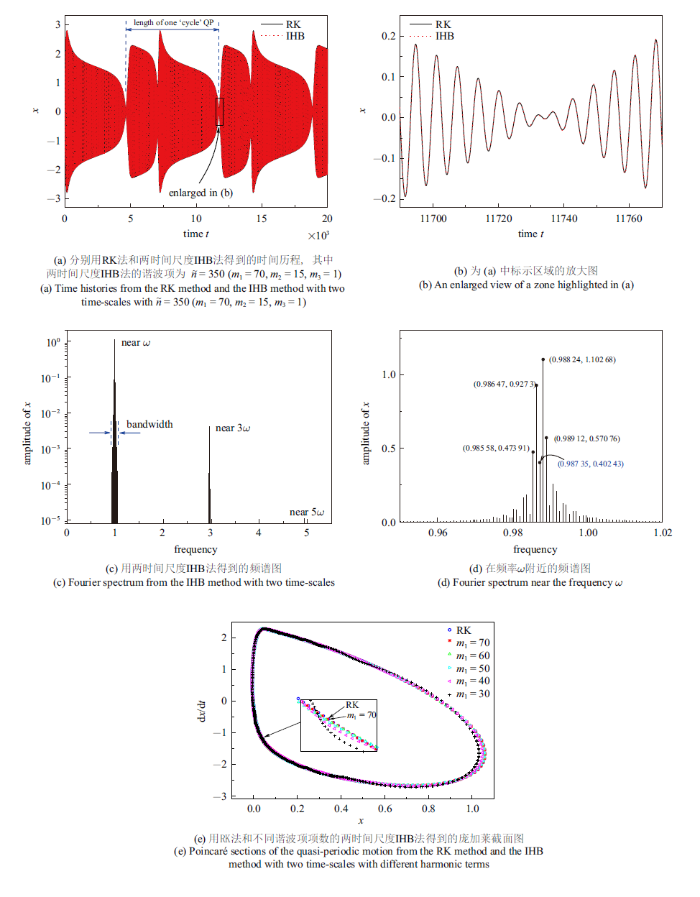
新窗口打开|下载原图ZIP|生成PPT
图4在分岔点$H_1$附近频率$\omega=0.987 35$时含外激励van der Pol-Mathieu方程的准周期运动, 其中 $k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$

Fig.4Quasi-periodic motion of the van der Pol-Mathieu equation with external excitation with $k_1=0.01$, $k_2=0.01$, $k_3=0.05$, and $f=0.01$ at the freqeuncy $\omega=0.987 35$ near the bifurcation point $H_1$

图5

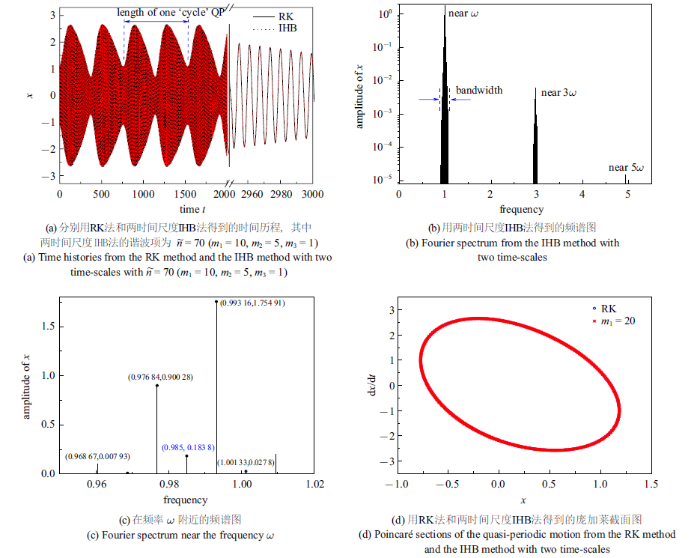
新窗口打开|下载原图ZIP|生成PPT
图5频率$\omega=0.985$时含外激励van der Pol-Mathieu方程的准周期运动, 其中 $k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$

Fig.5Quasi-periodic motion of the van der Pol-Mathieu equation with external excitation with $k_1=0.01$, $k_2=0.01$, $k_3=0.05$, and $f=0.01$ at the parametric excitation freqeuncy $\omega=0.985$

图6

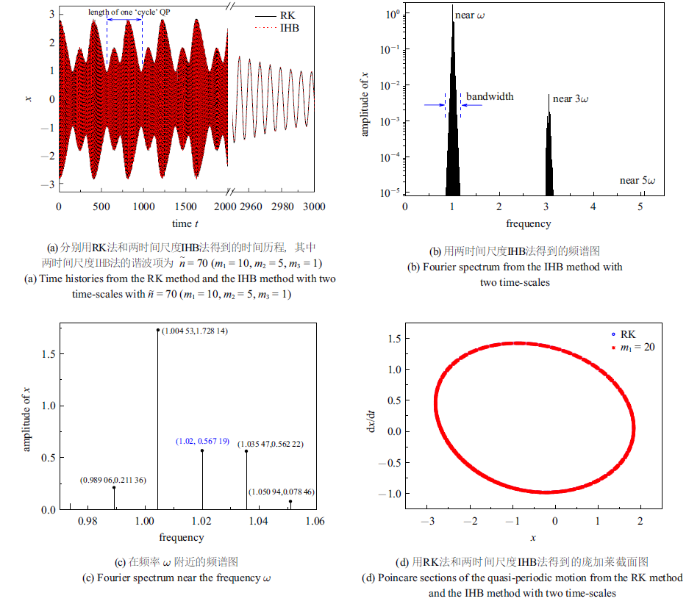
新窗口打开|下载原图ZIP|生成PPT
图6频率$\omega=1.020$时含外激励van der Pol-Mathieu方程的准周期运动, 其中 $k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$

Fig.6Quasi-periodic motion of the van der Pol-Mathieu equation with external excitation with $k_1=0.01$, $k_2=0.01$, $k_3=0.05$, and $f=0.01$ at the freqeuncy $\omega=1.020$}



Table 2
表2
表2利用两时间尺度IHB法求出在图3中三个点$\omega=0.987 35,0.985,1.02$处的$\omega_{\rm d}$和$\tilde{A}_{1,-1},\tilde{A}_{1,0},\tilde{A}_{1,1}$
Table 2A prior unknown $\omega_{\rm d}$ and three amplitudes $\tilde{A}_{1,-1}$, $\tilde{A}_{1,0}$, and $\tilde{A}_{1,1}$ in frequency response curves of the van der Pol-Mathieu equation with external excitation that are calculated by the IHB method with two time-scales at the three points $\omega=0.987 35,0.985,1.02$ in Fig.3

新窗口打开|下载CSV

图4(a)所示为在分岔点$H_1$附近频率$\omega=0.987 35$时分别用四阶的RK数值法和用含有350个谐波项的两时间尺度IHB法计算得到的含外激励van der Pol-Mathieu方程准周期(QP)运动的时间历程图, 其中$k_1=0.01$, $k_2=0.01$, $k_3=0.05$和$f=0.01$. 可以看出, 准周期运动具有`拍'现象, 且有明显的包络线. 图4(b)是图4(a)中标示区域的放大图, 可以看出不管是在振幅较大的区域, 还是在如图4(a)中振幅较小的区域, 两时间尺度IHB法得到的结果与RK法得到的结果完全一致. 图4(c)和图4(d)是频率$\omega=0.987 35$点上的准周期运动的频谱图, 其中图4(d)是在频率$\omega$附近的频谱放大图. 从图4(c)可以看出, 频率成份主要集中在$\omega$, $3\omega$和$5\omega$附近, 且集中在$\omega$的幅值远大于其他幅值; 在图4(d)上标示出在靠近$\omega$的5个频率及其幅值, 可以得到相邻频率间的间距为$\omega_{\rm d}=8.846 28\times10^{-4}$, 最大的幅值在频率为$\omega+\omega_{\rm d}=0.988 24$上.

图4(e)是取不同的谐波项的两时间尺度IHB法和采用RK法得到的频率$\omega=0.987 35$时含外激励van der Pol-Mathieu方程准周期运动的庞加莱截面图. 图中所示为RK法得到的和取不同谐波项的两时间IHB法得到的庞加莱截面图, 可以看出随着$m_1$越大, 其结果是收敛的, 且越接近于RK法的结果; 当取到$m_1=70, m_2=15, m_3=1$时(即谐波总项数$\tilde{n}=350$), 两时间尺度IHB法得到的结果与RK法得到的结果相吻合, 这也说明了含外激励van der Pol-Mathieu方程在频率$\omega=0.987 35$点上的准周期运动至少含有175个频率. 表3所示为用RK法和取不同谐波项项数的两时间尺度IHB法得到在$\omega=0.987 35$处的$A_{\text{max}}$和$A_{\text{min}}$的对比, 其中$A_{\text{max}}$和$A_{\text{min}}$分别是准周期运动包络线幅值的最大值和最小值. 从表3可以看出, 随着谐波项项数的增加, 两时间尺度IHB的结果越接近于RK法的结果, 进一步说明了在某些频率点上, 两时间尺度IHB法需要取足够的谐波项项数, 才能得到精确的结果.

Table 3
表3
表3用RK法和取不同谐波项项数的两时间尺度IHB法得到在$\omega=0.987 35$处的$A_{\text{max}}$和$A_{\text{min}}$的对比, 其中$A_{\text{max}}$和$A_{\text{min}}$分别是准周期运动包络线幅值的最大值和最小值
Table 3Comparison of $A_{\text{max}}$ and $A_{\text{min}}$ from the RK method and the IHB method with two time-scales with different harmonic terms at the point $\omega=0.987 35$, where $A_{\text{max}}$ and $A_{\text{min}}$ are the maximal and minimal value of envelops of the quasi-periodic motions, respectively

新窗口打开|下载CSV

图5和图6分别是在另外两个点$\omega=0.985$和$\omega=1.02$上的准周期运动响应情况, 得到与点$\omega=0.987 35$上相似的准周期运动特征, 其中利用两时间尺度IHB法得到的结果所用到的谐波项项数为$\tilde{n}=70 \left(m_1=10,m_2=5,m_3=1\right)$. 图5(a)和图6(a)的左部分是在$\left[0,2000\right]$紧缩时间尺度上的时间历程图, 具有明显的包络线, 右部分是在$\left[2960,3000\right]$扩张时间尺度上的时间历程图, 从图中可以看出两时间尺度IHB法得到的结果与RK法得到的结果完全一致.

观测在不同频率$\omega$点的准周期运动, 可以得到一些有趣的动力学现象. 比较3个点准周期运动的时间历程图4(a), 图5(a)和图6(a)可以得知, 准周期运动的包络线似乎都有`周期', 且其`周期'长度恰似为$2\pi\omega/\omega_{\rm d}$, 即分别为7012.78, 758.17和414.27, 说明越接近分岔点的准周期运动的包络线的`周期'长度越长; 比较3个点准周期运动的频谱图4(c), 图5(b)和图6(b)可以得知, 越远离分岔点的准周期运动的边频带的带宽越宽且其频率分布越稀疏, 此原因是由于边频带相邻频率间的间距变大; 比较3个点准周期运动的庞加莱截面图4(e), 图5(d)和图6(d)可以得知, 利用两时间尺度IHB法需要不同的谐波项项数以满足计算的精度, 如在频率$\omega=0.987 35$点上需要350个谐波项, 而在其他两个点上只需70个谐波项, 表明了在不同点上的准周期运动含有不同的频率数.

3 结论

本文基于含外激励van der Pol-Mathieu方程的非线性系统, 针对系统在自激励, 参数激励和外激励3种激励共同作用下, 利用传统的IHB法和两时间尺度IHB法分别分析了系统的周期响应和准周期运动响应, 得到的结果与数值RK法得到的结果完全吻合, 并得到以下结论.

(1) 在含外激励van der Pol-Mathieu方程的周期响应中含有两种类型的分岔, Saddle-node分岔和Hopf分岔. Saddle-node分岔会导致跳跃现象, 即系统响应从一个稳态的周期响应跳跃到另一个稳态的周期响应; Hopf分岔会导致准周期运动, 即系统响应从周期响应变化到准周期运动响应. 另外, 在两个周期解的Saddle-node分岔点区域间含有两个稳定的周期解.

(2) 含外激励van der Pol-Mathieu方程中, 由于自激振动和参数激振联合作用下, 会产生准周期运动响应, 并发现其新特性. 在准周期运动的频谱中,频率$\omega, 3\omega, 5\omega$附近含有边频带, 且边频带是均匀的,即边频带中相邻频率的间距$\omega_{\rm d}$是一样的;在准周期运动的时间历程图中,准周期的包络线也有`周期', 其`周期'为$2\pi\omega/\omega_{\rm d}$.

(3) 在不同点上的准周期运动响应有不同的动力学特征. 越靠近Hopf分岔点的准周期运动响应, 其边频带的带宽越小, 且其频率分布越密集, 同时其包络线的`周期'越长. 另外, 在不同点上的准周期运动响应所含的频率数目也不同.

此外, 针对准周期运动响应含有大量的频率成份, 如何有效提高两时间尺度IHB法的计算效率将是进一步的研究工作.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Iwatsubo T, Saigo M. Transverse vibration of a rotor system driven by a cardan joint
Journal of Sound and Vibration, 1984,95(1):9-18
[本文引用: 1]

[2] Doi M, Masuko I, Ito Y. et al. A study on parametric vibration in chuck work
Bulletin of JSME, 1985,28(245):2774-2780
[本文引用: 1]

[3] Warminski J, Litak G, Szabelski K. Synchronisation and chaos in a parametrically and self-excited system with two degrees of freedom
Nonlinear Dynamics, 2000,22(2):125-143
[本文引用: 3]

[4] Momeni M, Kourakis I, Moslehi-Fard M. et al. A van der Pol-Mathieu equation for the dynamics of dust grain charge in dusty plasmas,
Journal of Physics A: Mathematical and Theoreitcal, 2007,40(24):F473-F481
[本文引用: 1]

[5] Belhaq M, Kirrou I, Mokni L. Periodic and quasiperiodic galloping of a wind-excited tower under external excitation
Nonlinear Dynamics, 2013,74(3):849-867
[本文引用: 2]

[6] Kirrou I, Mokni L, Belhaq M. On the quasiperiodic galloping of a wind-excited tower
Journal of Sound and Vibration, 2013,332(18):4059-4066
[本文引用: 2]

[7] Tondl A. On the interaction between self-excited and parametric vibrations. National Research Institute for Machine Design, Monographs and Memoranda No. 25,
Prague 1978
[本文引用: 1]

[8] Kotera T, Yano S. Periodic solutions and the stability in a non-linear parametric excitation system
Bulletin of JSME, 1985,28(241):1473-1480
[本文引用: 1]

[9] 陈予恕, 徐鉴. Van der pol-Duffing-Mathieu型系统主参数共振分岔解的普适分类
中国科学A辑, 1995,25(12):1287-1297
[本文引用: 1]

( Chen Yushu, Xu Jian. Van der Pol type-Duffing-Mathieu system primary parameter resonance bifurcation solution of the general classfication
Science in China A. 1995,25(12):1287-1297 (in Chinese))
[本文引用: 1]

[10] Szabelski K, Warminski J. Self-excited system vibrations with parametric and external excitation
Journal of Sound and Vibration, 1995,187(4):595-607
[本文引用: 1]

[11] 彭献, 陈自力. 一类强非线性系统共振周期解的渐近分析
动力学与控制, 2004,2(1):46-50
[本文引用: 1]

( Peng Xian, Chen Zili. Asymptotic analysis for resonance cycle solution of a type of strongly nonlinear systems
Journal of Dynamics and Control. 2004,2(1):46-50 (in Chinese))
[本文引用: 1]

[12] Belhaq M, Fahsi A. 2:1 and 1:1 frequency-locking in fast excited van der Pol-Mathieu-Duffing oscillator
Nonlinear Dynamics, 2007,53(1-2):139-152
[本文引用: 2]

[13] Pandey M, Rand RH, Zehnder AT. Frequency locking in a forced Mathieu-van der Pol-Duffing system
Nonlinear Dynamics, 2007,54(1-2):3-12
[本文引用: 1]

[14] 张琪昌, 冯晶晶, 王炜. 类Padé逼近方法在二维非线性振动系统的应用
力学学报, 2011,43(5):914-921
[本文引用: 1]

( Zhang Qichang, Feng Jingjing, Wang Wei. The construction of homoclinic and heteroclinic orbit in two-dimentsional nonlinear systems based on the quasi-Padé approximation,
Chinese Journal of Theoretical and Applied Mechanics, 2011,43(5):914-921 (in Chinese))
[本文引用: 1]

[15] Warminski J. Nonlinear dynamics of self-, parametric, and externally excited oscillator with time delay: van der Pol versus Rayleigh models
Nonlinear Dynamics, 2019,99(1):35-56
[本文引用: 2]

[16] 王延庆, 郭星辉, 梁宏琨 等. 凸肩叶片的非线性振动特性与运动分岔
力学学报, 2011,43(4):755-764
[本文引用: 1]

( Wang Yanqing, Guo Xinghui, Liang Hongkun, et al. Nonlinear vibratory characteristics and bifurcations of shrouded blades
Chinese Journal of Theoretical and Applied Mechanics. 2011,43(4):755-764 (in Chinese))
[本文引用: 1]

[17] 张登博, 唐有绮, 陈立群. 非齐次边界条件下轴向运动梁的非线性振动
力学学报, 2019,51(1):218-227


( Zhang Dengbo, Tang Youqi, Chen Liqun. Nonlinear vibration of axially moving beams with nonhomogeneous boundary conditions
Chinese Journal of Theoretical and Applied Mechanics. 2019,51(1):218-227 (in Chinese))


[18] 顾伟, 张博, 丁虎 等. 2:1 内共振条件下变转速预变形叶片的非线性动力学响应
力学学报, 2020,52(4):1131-1142


( Gu Wei, Zhang Bo, Ding Hu, et al. Nonlinear dynamic response of pre-deformation blade with variable rotational speed under 2:1 internal resonance
Chinese Journal of, Theoretical and Applied Mechanics, 2020,52(4):1131-1142 (in Chinese))


[19] 陈娅昵, 孟文静, 钱有华 . 一类 Duffing 型系统的不动点混沌和 Fold/Fold 簇发现象及机理分析
力学学报, 2020,52(5):1475-1484
[本文引用: 1]

( Chen Yani, Meng Wenjing, Qian Youhua. Fixed point chaos and Fold/Fold bursting of a class of Duffing systems and the mechanism analysis
Chinese Journal of Theoretical and Applied Mechanics. 2020,52(5):1475-1484 (in Chinese))
[本文引用: 1]

[20] Nayfeh AH, Mook DT. Nonlinear Oscillations
Wiley, 1995
[本文引用: 1]

[21] Belhaq M, Houssni M. Quasi-periodic oscillations, chaos and suppression of chaos in a nonlinear oscillator driven by parametric and external excitations
Nonlinear Dynamics, 1999,18(1):1-24
[本文引用: 1]

[22] Abouhazim N, Belhaq M, Lakrad F. Three-period quasi-periodic solutions in the self-excited quasi-periodic Mathieu oscillator
Nonlinear Dynamics, 2005,39(4):395-409
[本文引用: 1]

[23] Fan Q, Leung AYT, Lee YY. Periodic and quasi-periodic responses of van der Pol-Mathieu system subject to various excitation
International Journal of Nonlinear Sciences and Numerical Simulation, 2016,17(1):29-40
[本文引用: 1]

[24] Veerman F, Verhulst F. Quasiperiodic phenomena in the van der Pol-Mathieu equation
Journal of Sound and Vibration, 2009,326(1-2):314-320
[本文引用: 1]

[25] Huang JL, Zhu WD. An incremental harmonic balance method with two timescales for quasiperiodic motion of nonlinear systems whose spectrum contains uniformly spaced sideband frequencies
Nonlinear Dynamics, 2017,90(2):1015-1033
[本文引用: 1]

[26] Huang JL, Zhu WD. A new incremental harmonic balance method with two time scales for quasi-periodic motions of an axially moving beam with internal resonance under single-tone external excitation
Journal of Vibration and Acoustics, 2017,139(2):021010


[27] Huang JL, Zhou WJ, Zhu WD. Quasi-periodic motions of high-dimensional nonlinear models of a translating beam with a stationary load subsystem under harmonic boundary excitation
Journal of Sound and Vibration, 2019,462:114870
[本文引用: 1]

[28] Cheung YK, Chen SH, Lau SL. Application of the incremental harmonic balance method to cubic non-linearity systems
Journal of Sound and Vibration, 1990,140(2):273-286
[本文引用: 1]

[29] 陈树辉. 强非线性振动系统的定量分析方法. 北京: 科学出版社, 2007
[本文引用: 1]

( Chen Shuhui. Quantitative Analysis Methods for Strongly Nonlinear Vibration. Beijing: Science Press, 2007 (in Chinese))
[本文引用: 1]

[30] Hsu CS. Impulsive parametric excitation: Theory
Journal of Applied Mechanics, 1972,39(2):551-558
[本文引用: 1]

[31] Hsu CS. On approximating a general linear periodic systems
Journal of Mathematical Analysis and Applications, 1974,45(1):234-251
[本文引用: 1]

[32] Hsu CS, Cheng WH. Applications of the theory of impulsive parametric excitation and new treatments of general parametric excitation problems
Journal of Applied Mechanics, 1973,40(1):78-86
[本文引用: 1]

[33] Friedmann P, Hammond CE, Woo TH. Efficient numerical treatment of periodic systems with application to stability problems
International Journal of Numerical Methods in Engineering, 1977,11(7):1117-1136
[本文引用: 1]

[34] Huang JL, Su RKL, Chen SH. Precise Hsu's method for analyzing the stability of periodic solutions of multi-degrees-of-freedom systems with cubic nonlinearity
Computers and Structures, 2009,87(23-24):1624-1630
[本文引用: 1]

[35] Zhong WX, Williams FW. A precise time step integration method
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 1994,208(6):427-430
[本文引用: 1]