RM不稳定过程中预混火焰界面演化及混合区增长预测1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

汪洋, 董刚^,²⁾南京理工大学瞬态物理重点实验室, 南京 210094

INTERFACE EVOLUTIONS AND GROWTH PREDICTIONS OF MIXING ZONE ON PREMIXED FLAME INTERFACE DURING RM INSTABILITY ¹⁾

Wang Yang, Dong Gang^,²⁾Key Laboratory of Transient Physics, Nanjing University of Science and Technology, Nanjing 210094, China

通讯作者: 2) 董刚, 研究员, 主要研究方向: 可压缩反应流的数值模拟. E-mail:gdong@njust.edu.cn

收稿日期:2020-08-10接受日期:2020-09-25网络出版日期:2020-11-18

基金资助:

1) 国家自然科学基金资助项目.11872213

Received:2020-08-10Accepted:2020-09-25Online:2020-11-18
作者简介 About authors

摘要
预混火焰界面的RM (Richtmyer-Meshkov)不稳定导致的界面混合区增长过程在自然界和工程实践中十分常见,但化学反应对其增长的影响机理仍不明确,反应性界面混合区增长速率的预测也未见报道, 因此,开展RM不稳定过程中火焰界面演化和混合区预测的研究十分必要.本文采用带单步化学反应的Navier-Stokes方程和高精度数值格式,研究了正弦形预混火焰界面在平面入射激波及其反射激波作用下的RM不稳定过程.结果表明, 在入射激波作用后的阶段,除RM不稳定本身导致的界面演化为"钉-帽"和"泡"形结构外,化学反应一方面以预混火焰传播的方式促进了界面中"泡"结构的增长,另一方面通过与涡结构的复杂相互作用促进了"钉-帽"结构的增长.化学反应活性越强, 火焰界面的"泡" 结构和"钉-帽"结构的增长越快.在第一次反射激波作用后的阶段,化学反应以相同的火焰传播方式对"泡"和"钉-帽"结构产生影响, 两者效应相抵,因而导致反射激波作用后的阶段中界面混合区增长不受化学反应活性的影响.根据以上分析,分别针对入射激波和第一次反射激波作用后的火焰界面混合区增长速率提出了相应的预测模型,为探索反应性RM不稳定过程的理论预测方法提供了有益参考.
关键词： RM不稳定;预混火焰界面;混合区增长;数值模拟;预测

Abstract
Growth of mixing zone on premixed flame interface induced by Richtmyer-Meshkov (RM) instability occurs frequently in natural phenomena and in engineering applications. The effect of chemical reaction on the growth mechanism of mixing zone on the interface still remains unknown, and the predictions on growth rate of mixing zone on reactive interface were seldom reported. Therefore, it is necessary to study the interface evolutions and the predictions of mixing zone on the premixed flame interface during the RM instability. The present study adopted the Navier-Stokes equations with a single-step reaction and the computational scheme with high resolutions to numerically research the RM instability of flame interface with sinusoidal pattern, induced by a planar incident shock wave and its reflected shock wave. The results in present study show that during the stage after the passage of incident shock wave, besides the RM instability mechanism which leads to the "spike-cap" and "bubble" structures of the interface, the chemical reaction not only promotes the "bubble" structure growth in the form the premixed flame propagation, but also gives rise to the growth of "spike-cap" structure through the interaction with vortices structure. The more reactive the premixed gases, the rapider the growth for both "spike-cap" and "bubble" structures. The results also show that during the stage after the passage of first reflected shock wave, the chemical reaction has the same effects on the developments of both "spike-cap" and "bubble" structures in the mode of premixed flame propagation. The counteraction between both effects results in the independence of mixing zone growth on the chemical reaction. Based on above analyses, the predicted models for the stages after passages of incident shock wave and reflected shock wave are proposed, respectively, in order to provide a useful method for predictions of mixing zone growth during the reactive RM instability.
Keywords：RM instability;premixed flame interface;mixing zone growth;numerical simulation;prediction

PDF (4793KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
汪洋, 董刚. RM不稳定过程中预混火焰界面演化及混合区增长预测¹⁾. 力学学报[J], 2020, 52(6): 1655-1665 DOI:10.6052/0459-1879-20-278
Wang Yang, Dong Gang. INTERFACE EVOLUTIONS AND GROWTH PREDICTIONS OF MIXING ZONE ON PREMIXED FLAME INTERFACE DURING RM INSTABILITY ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(6): 1655-1665 DOI:10.6052/0459-1879-20-278

引言

Richtmyer-Meshkov(RM)不稳定是指不同密度且互不浸润的介质间所形成的有一定曲率的界面,在脉冲加速(impulsive acceleration)作用下,其两侧介质发生混合并导致其混合区(mixing zone, MZ)增长的行为,其中脉冲加速通常可由激波冲击来实现. RM不稳定的机制来自斜压效应(barocliniceffect), 即, 当激波与密度界面作用时,界面形成的密度梯度与激波形成的压力梯度的方向不一致会导致界面上的涡量沉积,在涡量的诱导下界面上的混合区逐渐增长, 后期这种增长还会逐渐发展为湍流混合.当界面本身具有化学反应活性时(如预混火焰界面),化学反应会进一步增加RM不稳定的复杂性. 作为一种重要而又复杂的力学现象,带化学反应的RM不稳定频繁地出现在自然现象(如宇宙超新星爆炸^[1])和人类生产生活 (如航空发动机超燃混合^[2]、惯性约束聚变^[3]、工业爆炸灾害^[4]等)中.因此, 开展带化学反应的RM不稳定过程的研究,对认识、控制和利用这一现象具有非常重要的现实意义.

对惰性界面条件下的RM不稳定过程,国内外已经开展了大量的理论、实验和数值模拟研究.界面混合区增长的理论预测模型包含了早期的线性模型^[5]以及随后针对激波单次作用下界面RM不稳定非线性发展过程的渐进模型^[6]和势流模型^[7-8]等,基于实验结果的适于激波多次作用下的界面混合区增长模型也得到了进一步研究^[9-11].文献^[12,13]对这些预测模型进行了很好的总结. 此外,有****也采用实验测试的方法针对不同入射激波强度和形状^[14-17]、不同初始界面形态^[18-21]条件下,RM不稳定过程的发展进行了细致的研究. 数值模拟方面, 蒋华等^[22-23]采用高精度数值模拟的方法研究了界面初始形态对混合区早期发展过程的影响,并采用理论模型对混合区的增长进行了预测^[23];Schilling等^[24]采用类似的数值格式模拟了激波及其反射激波作用下的单模形态界面RM不稳定过程;Thornber等^[25]采用三维数值模拟,考察了不同初始波长下的界面混合区的增长行为;Lombardini等^[26]利用三维大涡模拟方法研究了单次激波作用下,激波强度对界面混合区发展后期的影响, 重点考察了后期界面混合发展特性;Tritschler等^[27]采用两种不同的大涡模拟方法研究了激波及其反射波作用下界面混合区的发展,对界面发展后期小尺度湍流混合特性进行了详尽的分析.

尽管激波与惰性界面相互作用的研究得到了广泛深入地开展,但反应性界面在激波诱导下的发展过程的研究却远远不够.由于特定形态的反应性界面在实验控制上比较困难, 因此实验研究几乎未见报道,相关文献仅限于少量的数值模拟研究.Khokhlov等^[28]采用二维带化学反应的Navier-Stokes (NS)方程,数值模拟了单次激波与单模态预混火焰界面的相互作用过程,指出RM不稳定可促进燃烧放热率, 并增加火焰的面积;Kilchyk等^[29]采用带单步化学反应的二维NS方程,研究了单次激波或膨胀波与单模预混火焰界面相互作用的过程,指出激波压缩效应和火焰长度对反应性RM不稳定有显著影响.Massa和Jha^[30]采用推导得到的二维线化扰动方程,研究了单次激波作用下预混火焰界面的RM不稳定过程,指出化学反应诱导的压力梯度所形成的斜压效应可以减少火焰表面的小尺度结构、减弱火焰界面的增长,因而很可能会弱化激波驱动的小尺度混合过程.Dong等采用带单步化学反应的NS方程对激波及其反射激波与预混火焰界面的多次作用的二维^[31-32]和三维^[33]过程开展了系列研究,研究了大尺度流动、化学反应以及小尺度扩散等几个因素对反应性RM不稳定过程的影响,发现化学反应在一定程度上可以削弱大尺度流动带来的界面混合效应,从而证实了文献^[30]的推测. 此外,Attal和Ramaprabhu^[34]还报道了非预混单模火焰界面的RM不稳定过程,考察了反射激波对界面的影响, 其结果亦表明激波的多次作用明显增加了燃烧效率,该工作同时也反映了反应性RM不稳定研究开始向多样性发展.

上述研究表明, 化学反应的存在进一步增加了RM不稳定现象的复杂性.虽然目前已有众多的理论模型可以预测激波诱导下惰性界面的混合区增长过程,但对于反应性界面的混合区在激波诱导下的增长规律目前并不明确, 例如,文献^[31,32,33]主要关注的是RM不稳定过程中流动和化学反应的时间尺度的变化规律及其对RM不稳定的影响,而化学反应作用下混合区增长的定量预测并未得到研究, 也未见其它文献报道. 为此,本文采用高精度数值模拟的方法,研究平面入射激波及其反射激波与正弦形状的预混火焰界面的相互作用过程,重点考察不同化学反应活性条件下界面混合区的发展过程,对化学反应条件下的界面混合区增长速率进行预测,以期为反应性RM不稳定的混合区发展模型的建立提供参考.

1 数值方法

1.1 控制方程及其计算方法

控制方程采用二维带单步化学反应的Navier-Stokes (NS)方程, 表达如下

(1)$\frac{\partial {U}}{\partial t}+\frac{\partial ({F}-{F}_{D} )}{\partial x}+\frac{\partial ({G}-{G}_{D} )}{\partial y}={S}$

其中

(2)${U}=(\rho ,\rho u,\rho v,\rho e,\rho Y)^{T}$

(3)${F}=(\rho u,\rho u^{2}+p,\rho uv,(p+\rho e)u,\rho Yu)^{T}$

(4)${G}=(\rho v,\rho vu,\rho v^{2}+p,(p+\rho e)v,\rho Yv)^{T}$

(5)${F}_{D} =(0,\tau_{xx} ,\tau_{xy} ,q_{x} +u\tau_{xx} +v\tau _{xy} ,D{{\partial (\rho Y)}/{\partial x}})^{T}$

(6)${G}_{D} =(0,\tau_{yx} ,\tau_{yy} ,q_{y} +u\tau_{yx} +v\tau _{yy} ,D{{\partial (\rho Y)}/{\partial y}})^{T}$

(7)${S}=(0,0,0,0,\rho \dot{{\omega }})^{T}$

以上各式中, $t$代表时间, $x$和$y$代表空间坐标长度, $\rho $代表体系的密度,$u$和$v$分别为$x$和$y$方向的速度分量, $Y$代表反应物的质量分数, $p$为体系压力,$e$是单位质量的总能, 表达为

(8)$e={{p(\gamma -1)}/\rho }+0.5(u^{2}+v^{2})+QY$

式(8)中, $\gamma $为绝热指数, $Q$代表单位质量的化学反应放热.$q_{x}$和$q_{y}$分别代表$x$和$y$方向的热流量, 表达为$q_{x}=-k\partial T/\partial x$和$q_{y}=-k\partial T/\partial x$, $T$是温度. $\tau_{ij}$ ($i=x$, $y$; $j=x$, $y)$为黏性应力张量分量, 表达为

(9)$\tau_{ij} =\rho \upsilon \left( {\frac{\partial u_{i} }{\partial x_{j} }+\frac{\partial u_{j} }{\partial x_{i} }-\frac{2}{3}\delta_{ij} \frac{\partial u_{k} }{\partial x_{k} }} \right){\begin{array}{*{20}c} & {(i=x,y;{\begin{array}{*{20}c} \\ \end{array} }j=x,y)} \\ \end{array} }$

其中, $\delta_{ij}$为Kronecker函数. 以上各式中出现的输运系数,如导热系数$k$, 扩散系数$D$和运动学黏度$\upsilon $可统一表达为^[4]

(10)$\frac{k}{\rho c_{p} }=k_{0} \frac{T^{n}}{\rho }, \quad D=D_{0} \frac{T^{n}}{\rho }, \quad \upsilon =\upsilon_{0} \frac{T^{n}}{\rho }$

本文计算使用的预混气体参照了文献^[35]中采用的C$_{2}$H$_{4}+$3O$_{2}+$4N$_{2}$气体,同时假定该预混气的Lewis数、Prandtl数和Schemidt数均为1,则式(10)中的$k_{0}$, $D_{0}$和$\upsilon_{0}$为相同的常数, 根据文献^[4],这些输运系数取值为$k_{0}=D_{0}=\upsilon_{0}=3.2\times 10^{-7}$ kg/(s$\cdot $m$\cdot $K$^{0.7})$, $n$取值为0.7.这些取值能够保证输运系数随温度的变化关系很好地符合实际C$_{2}$H$_{4}+$3O$_{2}+$4N$_{2}$气体的这种变化.

本文采用了基于Arrhenius形式的单步化学反应描述燃烧现象,因此式(7)中的反应速率$\dot{{\omega }}$可以表达为

(11)$\dot{{\omega }}=\rho Y\beta \exp ({{-E_{a} }/{RT}})$

式中$\beta $代表指前因子, $E_{a}$为活化能, $R$代表通用气体常数.

对控制方程(1)采用了分裂算法进行求解, 其中对流通量的空间导数项$\partial F/\partial x$和$\partial G/\partial y$采用的是LF (Lax-Friedrichs)格式结合9阶WENO (weighted essentially non-oscillatory)模板的方法求解^[36]; 输运通量的空间导数项$\partial F_{D}/\partial x$和$\partial G_{D}/\partial y$采用了10阶中心差分的格式进行求解; 而化学反应源项$S$和解$U$的时间导数项$\partial U/\partial t$则采用了3阶Runge-Kutta方法进行求解.上述控制方程及其计算方法在以前的研究中已经得到了广泛应用^[31-33].

1.2 计算条件与验证

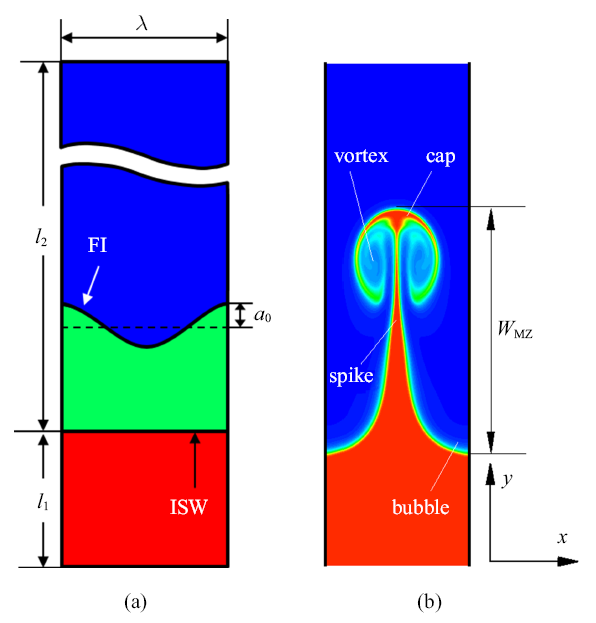
本文模拟的激波与预混火焰界面相互作用的计算构型如图1(a)所示,计算域为二维矩形形状. 初始时刻, 平面入射激波(incident shock wave,ISW)位于计算域距下边界为$l_{1}$的位置并开始向上运动,在运动过程中与波长为$\lambda $,初始振幅为$a_{0}$的正弦形预混火焰界面(flame interface, FI)发生相互作用.令火焰界面的下方为密度较大的未燃预混气(绿色部分),火焰上方为密度较小的等压燃烧条件下的已燃气体(蓝色部分),则激波从大密度侧向小密度侧越过火焰界面后会形成继续上行的激波和向下反射的稀疏波.上行激波行至计算域顶端的刚性壁面后会反射下行,下行激波则再次和火焰界面发生相互作用,作用后的激波会继续反射向顶端壁面方向运动,经过再次反射后又会下行与界面发生作用. 这个过程会一直进行下去,直至反射激波强度逐渐减小至激波不再明显为止.

图1

新窗口打开|下载原图ZIP|生成PPT
图1正弦预混火焰界面的(a)初始形态和(b)典型的发展过程.ISW为入射激波,FI为火焰界面令初始的正弦形火焰界面

Fig. 1(a) Initially sinusoidal pattern and (b) developed pattern of flame interface induced by shock wave. ISW is incident shock wave, FI is flame interface

数学形式如下

(12)$a(x)=a_{0} \sin (\frac{2{\pi}x}{\lambda }+\frac{{\pi}}{2})$

这里$a(x)$代表正弦火焰界面的流向($y$方向)振幅沿$x$方向的变化. 从界面的角度看,在入射激波的作用下, 火焰界面经RM不稳定过程发生变化, 典型的形态如图1(b)所示.可以看到, 二维正弦形界面在激波的单次作用下演变为"钉(spike)-泡(bubble)"结构,其中钉结构比较复杂,它还包含了其上的"帽(cap)"结构和两侧的"涡(vortex)"结构.定义"帽"的顶部到"泡"的底部的流向长度为界面混合区宽度$W_{MZ}$,则该量是评价界面RM不稳定发展过程的重要物理量^[12,24].

本文计算中, 选取计算域流向长度为$l_{1}+l_{2}=0.6$ m,其中$l_{1}=0.1$ m以保证整个计算过程中入射激波与界面作用后形成的下行稀疏波不会走出下边界而影响边界条件;计算域的横向长度为正弦界面波长$\lambda =0.012 8$ m.计算域的左右边界为周期性边界条件, 上边界为绝热刚性无滑移的壁面条件,下边界为零梯度边界条件. 假设本文气体符合量热完全气体的假设,并令初始时刻波前未燃气体(图1(a)中绿色区域)的初始温度和初始压力分别为$T_{0}$和$p_{0}$,则波后未燃气(图1(a)中红色区域)的状态可由激波关系式求出.本文界面初始形态参数、预混气的热力学和动力学参数的取值^[33]均列入表1.

Table 1
表1
表1计算参数^[33]
Table 1Computational parameters^[33]

新窗口打开|下载CSV

此外, 在本文计算中设初始平面入射激波Mach数为$M_{0}$, 则根据一维激波与界面相互作用的数值模拟,可以确定入射激波作用后的界面Atwood数$A=(\rho_{1}-\rho _{2})/(\rho_{1}+\rho_{2})$ (这里$\rho_{1}$和$\rho_{2}$分别代表界面两侧重和轻介质的密度)和界面两侧流向速度差$\Delta V$,以及第一次反射激波作用后的界面Atwood数$A_{1}$和界面两侧的流向速度差$\Delta V_{1}$, 这些与一维流动有关的参数值也列入表1.

为研究不同预混气的化学活性对RM不稳定发展的影响,用不同活化能的数值来表征不同的化学反应活性, 活化能的变化的范围列入表1中,此外, 还计算了化学冻结流条件下的预混火焰界面的发展过程.化学冻结流是一种保留了预混火焰热力学状态但将化学动力学过程进行冻结(设$E_{a}$无穷大,即反应速率为零)的理想状态,考虑的目的是为了通过与反应流计算结果的对比来分析活化能的影响. 在本文计算中,计算了7种不同活化能($E_{a}/RT_{0}=30.0$, 31.2, 31.6, 32.0, 32.5, 38.2,50.0)的反应流以及冻结流($E_{a}/RT_{0}=\infty )$的界面混合区发展过程.但在后面的分析中, 主要是以$E_{a}/RT_{0}=30.0$, 38.2,50.0和冻结流等4种典型条件的结果为主,其中活化能$E_{a}/RT_{0}=38.2$的算例为基准算例, 其活化能取值来自文献^[37].

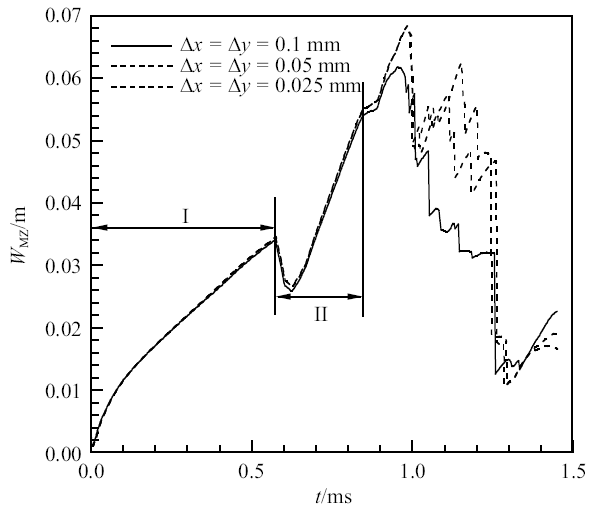
为考察本文计算结果的有效性, 首先针对$E_{a}=38.2RT_{0}$条件下的激波与预混火焰相互作用过程的数值模拟进行了网格无关性验证.本文采用了均匀正交的正方形网格来划分计算区域, 选取了三种不同的网格尺寸($\Delta x=\Delta y=0.1$ mm,0.05 mm和0.025 mm)进行激波与正弦形预混火焰界面相互作用过程的数值模拟.图2给出了3种网格尺寸下计算得到的火焰界面发展过程中混合区宽度($W_{MZ}$, 定义见图1(b))随时间的变化过程.图中时间范围I, II分别为入射激波和第一次反射激波作用后$W_{MZ}$的变化阶段,可以发现阶段II的初期存在一个短暂的$W_{MZ}$下降的过程,这是由于反射激波掠过火焰界面时对界面的压缩所导致的. 图中结果表明,在阶段I和II中, 3种网格尺寸计算的结果均相互吻合较好,但在阶段II之后的后继反射激波与火焰界面的作用过程中, $\Delta x=\Delta y=0.1$ mm尺寸下计算的结果要明显低于$\Delta x=\Delta y=0.05$ mm和0.025 mm两种尺寸下计算的结果, 尽管后两者的计算结果之间也略有差别.阶段II后计算结果的差异不仅体现了计算网格尺寸的影响,实际上也表明火焰界面的失稳向着小尺度结构甚至是湍流混合的方向发展,这超出了本文采用的控制方程和网格尺寸所研究的范围, 因此,本文研究仅考虑阶段I和II的相互作用过程. 根据网格无关性测试的结果,本文采用$\Delta x=\Delta y=0.05$ mm的网格尺寸对所有算例开展数值模拟,每一个算例总网格数均为307.2万个, 为提高计算效率采用了基于MPI的并行策略编制程序开展计算.

图2

新窗口打开|下载原图ZIP|生成PPT
图2不同网格尺寸下计算的混合区宽度随时间的变化

Fig. 2Time histories of width of mixing zone with different grid resolutions

2 结果与讨论

2.1 阶段I的界面演化

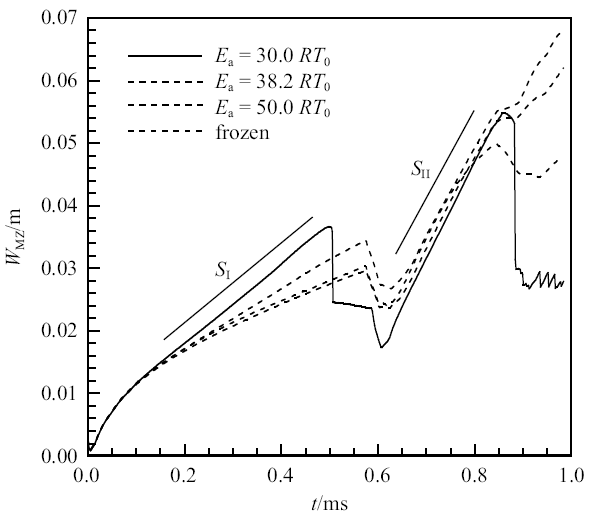
图3首先给出了3个典型活化能($E_{a}=30.0RT_{0}$,38.2$RT_{0}$和50.0$RT_{0})$的反应流以及冻结流下反应区宽度($W_{MZ})$随时间的变化.可以看到, 阶段I中四个算例在经历了短暂的相同的发展过程 ($t<0.1$ ms)之后, 其$W_{MZ}$的增长快慢开始不同,活化能最小($E_{a}=30.0RT_{0})$的算例增长最快,而活化能最大($E_{a}=50.0RT_{0}$)以及冻结流的算例增长最慢.进一步观察可以发现, 阶段I的发展过程中尽管不同化学反应活性下的界面混合区增长快慢不同,但均呈现线性增长的形式, 通过对计算结果的线性拟合可以确定其$W_{MZ}$的增长速率$S_{I}$.

图3

新窗口打开|下载原图ZIP|生成PPT
图3不同化学活性下混合区宽度随时间的变化. $S_{I}$为入射激波作用阶段混合区增长速率, $S_{II}$为反射激波作用阶段混合区增长速率

Fig. 3Time histories of width of mixing zone with different chemical activities. $S_{I}$ is growth rate of mixing zone at incident shock wave stage, $S_{II}$ is growth rate of mixing zone at reflected shock wave stage

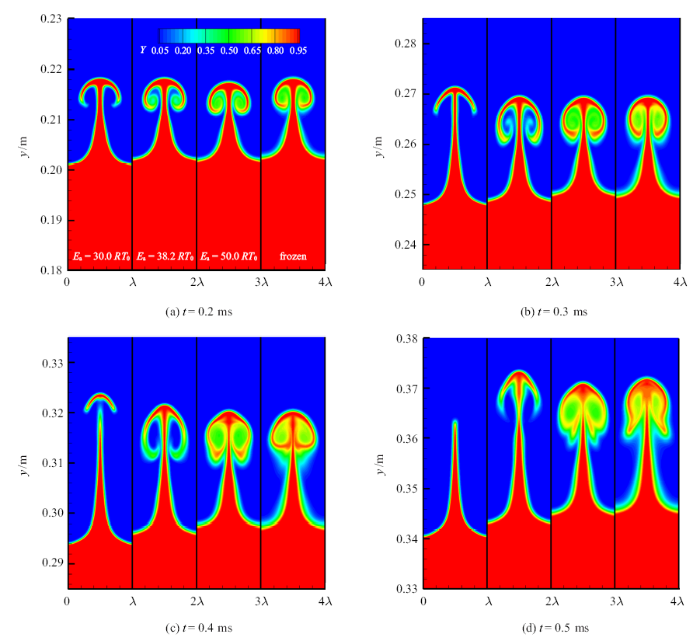
在进一步定量研究$S_{I}$之前, 首先考察了火焰界面在阶段I的演化规律和混合区宽度的增长行为.图4显示了阶段I中4个典型时刻($t=0.2$, 0.3, 0.4和0.5 ms)下,用反应物质量分数($Y)$标记的界面形态的变化,每个时刻下的4个子图从左到右分别代表了活化能为$E_{a}=30.0RT_{0}$,38.2$RT_{0}$和50.0$RT_{0}$的反应流以及冻结流等4种不同反应活性的情况.在$t=0.2$ ms时(图4(a)), 4种条件下的界面结构均呈现出"钉-泡"结构,钉结构的上方和两侧也分别呈现出"帽"结构和涡结构(见图1(b)的说明). 但是,当反应活性强($E_{a}=30.0RT_{0})$时, 涡结构内反应物几乎完全消耗,这说明化学反应的作用首先是发生在涡结构中的,其原因主要是因为RM不稳定过程中形成的涡结构使得界面两侧的未燃气与已燃气进行了充分的掺混,这种强化的传热和传质过程进一步促进了化学反应的进行. 该时刻下的结果还表明,不同反应活性下混合区宽度的变化差异不大. 当$t=0.3$ ms时(图4(b)),可以发现随着反应活性的增强, 涡结构内的混合过程逐渐被化学反应过程所替代,其中, $E_{a}=30.0RT_{0}$条件下的反应流其涡结构不再明显, 界面上方形态主要以"钉-帽"结构为主并明显向上移动, 从而导致其混合区宽度也较其他几种情况更长. 当$t=0.4$ ms时(图4(c)), 除了界面上方的"钉-帽-涡"结构继续发展外, 还可以看到界面下方的泡结构随着反应活性的增强也逐渐向下移动, 活性越强, "泡"结构向下发展越快, 因此导致整个混合区宽度随着活性的增强而逐渐变大, 进而导致图3中阶段I的$W_{MZ}$变化规律. 到$t=0.5$ ms时(图4(d)), 可以看到, 反应活性最强($E_{a}=30.0RT_{0})$的算例, 其"帽"结构已经由化学反应所消耗, 因而只留下钉结构, 这也导致其反应区宽度出现了突然的下降(见图3); 而活性次强($E_{a}=38.2RT_{0})$的算例, 其涡结构不再明显, 但形成的"钉-帽"结构开始使界面混合区明显向上发展, 这与$E_{a}=30.0RT_{0}$的算例在$t=0.3$ ms时的结构类似. 此外, 随着反应活性的增强, 界面下方的泡结构也进一步向下发展.

图4

新窗口打开|下载原图ZIP|生成PPT
图4阶段I中不同时刻的界面形态

Fig. 4Patterns of flame interface at the different instants for stage I

根据以上的界面形态的演化过程, 可以发现,阶段I中混合区宽度随时间的变化是由"钉-帽"结构向上发展以及泡结构向下发展所共同决定的.化学反应活性对这一过程的影响十分显著, 化学反应越强(活化能越小),"钉-帽"向上发展以及"泡"向下发展越显著, 因此使得反应区宽度越大.

2.2 阶段I混合区宽度预测

2.1节首先观察了不同反应活性条件下界面形态及界面混合区宽度随时间的演化规律,发现化学反应对界面上方的"钉-帽"结构以及下方的"泡"结构均有显著影响.为发展定量预测阶段I的混合区增长速率$S_{I}$的模型,图5进一步考察了$t=0.4$ ms时的界面结构及流场特征.图5(a)将四种反应活性条件下界面轮廓(用$Y=0.9$的等值线表示)进行了叠加对比,可以发现, 界面下方"泡"结构下缘随着反应活性的增加不断下移,这种下移符合预混火焰传播的特征: 反应活性越大, 化学反应速率越大,则火焰传播速度也越大. 因此可以得出结论:反应性预混火焰界面混合区宽度的增长其部分原因是由预混火焰传播所贡献的.根据经典的Frank-Kamenetsky层流火焰传播理论^[38],层流预混火焰的传播速度可以表达为

(13)$S_{b} =\left[ {\alpha \cdot \beta \exp(-E_{a} /RT)} \right]^{1/2}$

式中, $S_{b}$为"泡"结构的向下发展速度, 也代表了层流预混火焰的传播速度;$\alpha $为热输运系数, $\alpha =k_{0}T^{n}$, $n=0.7$; $k_{0}$, $\beta $, $E_{a}$和$R$的含义及取值见表1; $T$代表入射波后的已燃区温度, 本文取$T=7.0T_{0}$.

图5

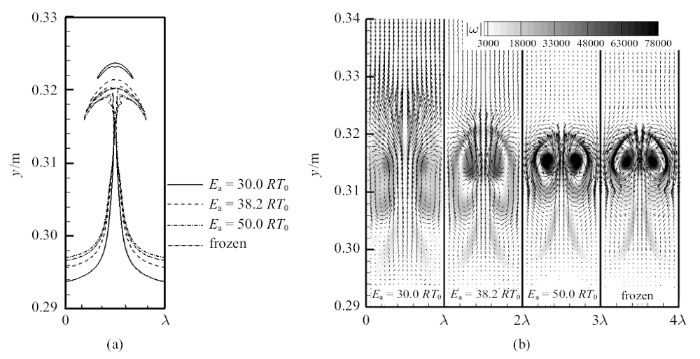
新窗口打开|下载原图ZIP|生成PPT
图5$t=0.4$ ms时不同化学活性条件下(a)反应物质量分数$Y=0.9$的等值线对比,(b)流场涡量幅度和速度矢量分布对比

Fig. 5(a) Comparisons of (a) mass fraction contours with $Y =0.9$ and of (b) vorticity amplitude and velocity vector among cases with different chemical activities at $t=0.4$ ms

此外, 观察界面上方"钉-帽"结构, 可以看出, 反应活性越强,则"帽"结构的上缘越向上移, 但其结构较为复杂, 并不符合预混火焰的传播规律.为此, 图5(b)进一步给出了界面附近的涡量幅值$|\omega|=|-0.5(\partial u/\partial y-\partial v\prime/\partial x)|$以及速度矢量$V=(u, v\prime )$的分布,这里$v\prime =v-v_{p}$, $v_{p}$为入射激波波后流场的平均速度.首先观察涡量幅值分布可以看出, 随着反应活性的增强, 流场的涡量明显减弱,这说明化学反应的加入可以抑制涡量的形成,这与之前研究得到的结论相一致^[30]. 接下来观察速度矢量的分布可以看到,当化学反应较强(如$E_{a}=30.0RT_{0})$时, 钉结构两侧的涡量变弱,漩涡结构不明显, 因此对入射激波波后流动速度抑制不够明显,因此"钉-帽"结构上方的流体流向速度较大. 反之,当化学反应较弱(如$E_{a}=50.0RT_{0})$或化学反应冻结时,由于钉两侧存在较强的互为反向的涡旋,涡旋外侧诱导的向下的运动速度实际上抵消了波后流体向上的运动.

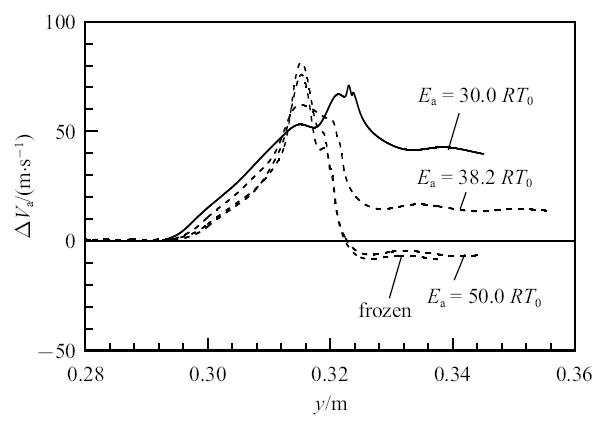
为验证上述分析, 图6给出了计算域中心($x=\lambda/2)$处由于涡的旋转所诱导的界面两侧的速度差$\Delta V_{a}$ (本文称诱导速度)沿流向的分布, 该速度差由界面上、下侧中心处流向速度的差值所确定. 图6的结果表明,虽然在较弱活性($E_{a}=50.0RT_{0})$或冻结流的条件下,较强的漩涡对在其之间($y=0.031 6$ m左右)的流体所诱导的流向速度差较大,但在"钉-帽"结构的上方($y>0.032 5$ m)其速度差迅速变小至反向流动,说明漩涡外侧的向下流动对速度差的减小起着很大作用. 相反,对活性较强的反应流($E_{a}=30.0RT_{0})$, 由于漩涡强度弱,漩涡外侧诱导的反向流动速度较小, 因此涡对之间形成的正向速度差可以一直维持.通过以上分析可知, 界面"钉-帽"结构受化学反应的影响比较复杂,但是较强的反应活性导致了其上方的具有较大的诱导速度差,进而使得"钉-帽"结构向上发展得更快, 由此可将其向上的发展速度表达为

(14)$S_{s} =\Delta V\delta_{1}\exp(-E_{a} /RT)$

式中$\Delta V$代表一维构型下入射激波波后的界面两侧流向速度差, 其值参见表1,$\delta_{1}$为阶段I的经验常数.式(14)等号右端$\exp(-E_{a}/RT)$反映了化学反应活性对界面上缘"钉-帽"结构发展的影响,反应活性越强, 该项越大, 则$S_{s}$越大, 因此符合图5(b)和图6的分析.

图6

新窗口打开|下载原图ZIP|生成PPT
图6$t=0.4$ ms时不同化学活性条件下轴线上流向诱导速度分布

Fig. 6Distributions of streamwise induced velocity at centerline for cases with different chemical activities at $t=0.4$ ms

本文假设所考虑的流场具有层流流动特性, 因此化学反应和湍流的相互作用可以忽略,故综合上述分析, 可以采用线性叠加的方式给出阶段I中火焰界面的混合区宽度增长速率$S_{I}$的表达式

(15)$S_{I} = S_{RM}+ S_{c}$

式中, $S_{RM}$代表RM不稳定导致的混合区宽度增长速率, $S_{c}$代表化学反应导致的混合区宽度增长速率. 前者可以采用传统的各类基于RM不稳定的理论模型进行预测^[12-13], 后者由于层流流动的假设仍可采用如下线性叠加的方法进行求解

(16)$S_{c} = S_{b} + S_{s}$

式中$S_{b}$和$S_{s}$分别由式(13)和式(14)进行求解,其中涉及到的变量仅为活化能$E_{a}$, 表明了化学反应活性的影响,而其余各常量均可由初始条件和一维激波界面作用得到的参数来确定.

注意到式(14)中$\delta_{1}$为经验参数, 为确定该值,本文对图3数值模拟得到的结果进行线性拟合可以得到$S_{I}$,令冻结流的$S_{I}=S_{RM}$ (即冻结流的$W_{MZ}$增长速率不考虑化学反应,仅由RM不稳定所导致), 则由式(15)可以求得数值模拟条件下的不同$E_{a}$的$S_{c}$值.图7给出了采用数值模拟得到的$S_{c}$随$E_{a}$的变化关系, 可以看出,随着活化能的减小, $S_{c}$呈指数增大. 进一步采用式(13)、式(14)和式(16)进行计算,发现当$\delta_{1} =9.3$时, 利用式(16)预测模型得到的$S_{c}$与数值模拟得到的$S_{c}$吻合良好.图7中还给出预测模型中$S_{b}$和$S_{s}$随活化能的变化, 可以发现,随着活化能的减小, 火焰界面上方"钉-帽"结构的增长速度比界面下方"泡"的增长速度要更快.

图7

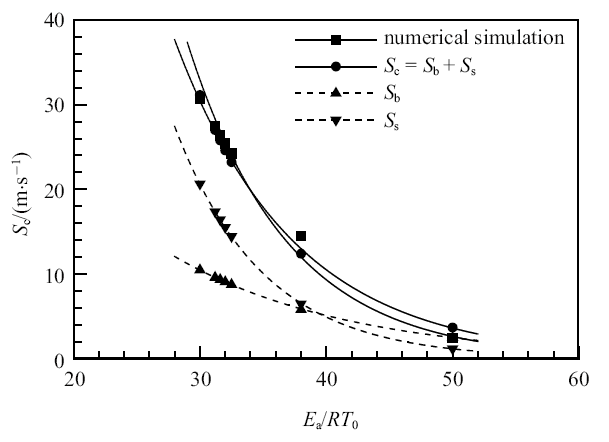新窗口打开|下载原图ZIP|生成PPT
图7数值模拟与理论预测的$S_{c}$的比较

Fig. 7Comparisons of $S_{c}$ between numerical and predicted results

2.3 阶段II界面演化及混合区宽度分析

观察图3中阶段II (即第一次反射激波作用后的火焰界面发展阶段)可以看出,反射激波作用后, 不同化学反应活性的反应流和冻结流条件下,界面混合区宽度的增长速率(用$S_{II}$表示)趋于一致,其增长速率也明显大于阶段I的增长速率. 为了解$W_{MZ}$的增长规律,图8显示了阶段II的两个典型时刻($t=0.7$ ms和0.8 ms)下,不同化学反应活性下界面的发展形态. 图8(a)的结果($t=0.7$ ms)表明,反射激波与火焰界面作用后, 混合区宽度仍然沿流向持续增长, 当反应活性较强时,界面呈现出沿流向的细长结构, 随着反应活性的下降, 界面形状逐渐变得复杂,已燃气和未燃气相互掺混形成的二维混合区变得越来越明显.然而从混合区宽度的变化来看, 不同活性下的混合区宽度变化并不明显, 即,随着反应活性的增强, 界面上方的"钉-帽"结构和下方的"泡结构"均同时下移,表明此时界面上下存在同样的预混火焰传播过程, 两者传播方向相同,因此对界面上、下方发展的影响相互抵消,从而导致混合区宽度对反应活性的依赖不再变得明显.图8(b)的结果($t=0.8$ ms)也显示了类似的规律. 需要注意的是冻结流条件下,界面形态开始失去对称性, 这表明到第一次反射激波后期界面的小尺度流动开始增加,界面逐渐向湍流混合的阶段发展, 因此,本文的研究仅限于第一次反射激波作用后的阶段II.后继的二次及多次激波与火焰界面的相互作用不在本文研究的范畴.

图8

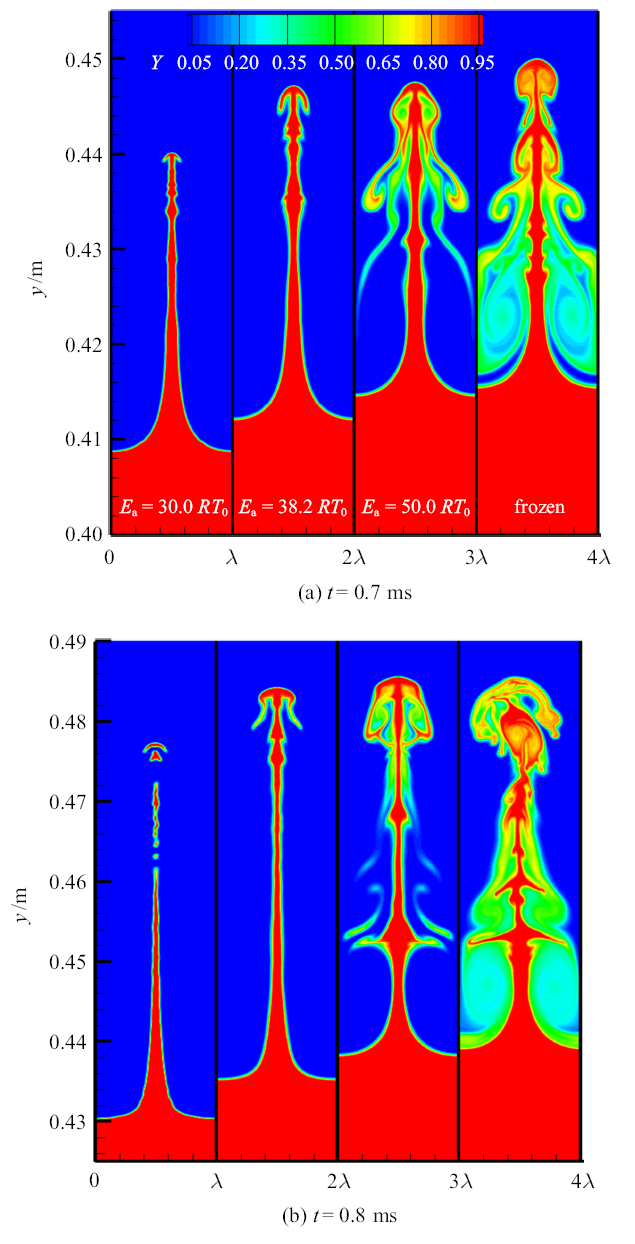新窗口打开|下载原图ZIP|生成PPT
图8阶段II中不同时刻的界面形态

Fig. 8Patterns of flame interface at the different instants for stage II

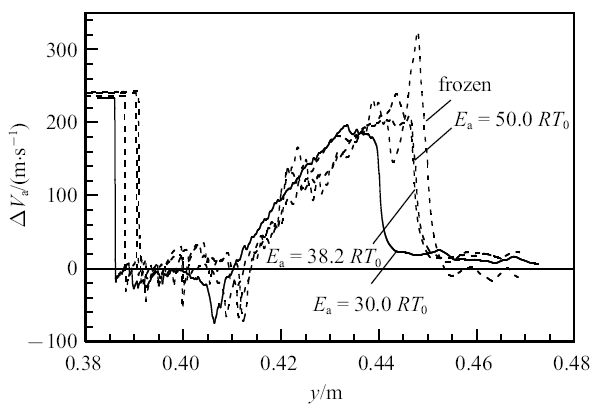
图9进一步给出阶段II中$t=0.7$ ms时, 不同反应活性条件下中心线上流向诱导速度$\Delta V_{a}$沿流向的分布.由结果也可以看出界面下方反射激波作用之后的区域($y=0.39\sim 0.41$ m)和界面上方的区域($y>0.45$ m)诱导速度均趋于零, 这说明入射激波和反射激波对火焰界面附近的涡旋运动的影响相互抵消, 因而界面混合区的发展不再考虑涡旋运动对化学反应的影响,这一点与阶段I中界面混合区的发展有所不同.

图9

新窗口打开|下载原图ZIP|生成PPT
图9$t=0.7$ ms时不同化学活性条件下中心线上流向诱导速度分布

Fig. 9Distributions of streamwise induced velocity at centerline for cases with different chemical activities at $t=0.7$ ms

采用与式(15)相同的形式表达阶段II的混合区增长速率$S_{II}$

(17)$S_{II} =S_{RM,II} +S_{c,II} =S_{RM,II}$

式中变量符号与式(15)相同, 下标II代表阶段II. 根据前面分析,由于涡旋运动不再对火焰界面产生额外影响,界面下方"泡"结构和上方的"钉-帽"结构仅存在相似的火焰向下传播的过程,因此导致两者作用相互抵消, 即$S_{c,II}=0$. 因此,混合区宽度的变化仅由惰性RM不稳定过程所决定,采用反射波后的Mikaelian模型^[8]对其增长速度进行预测, 式(17)可表达为

(18)$S_{II} =S_{RM,II} =\delta_{2} \Delta V_{1} A_{1}$

式中$\delta_{2}$为阶段II的经验常数, $\Delta V_{1}$和$A_{1}$的取值见表1.由7种不同活化能条件下的反应流以及冻结流的数值模拟结果可以拟合得到不同的$S_{II}$值,由此得到的平均值为149.1 m/s, 标准偏差为3.2 m/s,将平均增长速度(149.1 m/s)代入式(17)可以得出$\delta_{2}=0.79$.需要说明的是, 原始的Mikaelian模型^[8]中经验常数$\delta_{2}=0.28$,但进一步的研究也表明^[12], $\delta_{2}$的数值依赖于界面的形态与结构,比如对惰性界面和密度梯度很大的界面, 二维和三维计算采用的$\delta_{2}$分别可取0.55和0.84. 本文$\delta_{2}$取0.79反映了预混火焰界面与原始Mikaelian模型中不存在温差的界面是有所区别的.

3 结论

采用带单步反应的Navier-Stokes方程, 对入射激波及其反射激波与正弦形状的预混火焰界面相互作用过程进行了二维数值模拟,考察了介质反应活性对界面形态演化和混合区增长过程的影响. 得到的主要结论如下:

(1)正弦形预混火焰界面在入射激波作用后沿流向不断拉伸,除常规RM不稳定诱导的界面混合区增长外,与化学反应相关的预混火焰传播对界面下方的"泡"结构的发展起到了促进作用,而化学反应与涡结构的相互作用减弱了涡的强度,促进了界面上方的流体流向运动进而使"钉-帽"结构沿流向不断发展.化学活性越强, 界面的流向增长越快.

(2)沿流向发展的火焰界面在反射激波的作用下, 沿流向继续发展,其中界面下方的"泡"结构和上方"钉-帽"结构均受到火焰向下传播的影响,故化学反应的作用抵消,从而导致反射激波作用后界面的发展基本不依赖于介质的化学反应活性.

(3)根据上述界面演化机理, 一方面提出了入射激波作用阶段,化学反应导致的界面增长速率$S_{c}$的表达式,该表达式仅依赖于介质的反应活化能和初始条件, 具有较好的通用性;另一方面指出仍可以采用Mikaelian的模型预测反射激波作用下火焰界面的混合区增长速率,但模型常数要进行修正.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Poludnenko

, Chambers

, Ahmed

, et al. A unified mechanism for unconfined deflagration-to-detonation transition in terrestrial
Science, 2019, 366(6465), eaau7365

DOI URL PMID [本文引用: 1]

The nature of type Ia supernovae (SNIa)-thermonuclear explosions of white dwarf stars-is an open question in astrophysics. Virtually all existing theoretical models of normal, bright SNIa require the explosion to produce a detonation in order to consume all of stellar material, but the mechanism for the deflagration-to-detonation transition (DDT) remains unclear. We present a unified theory of turbulence-induced DDT that describes the mechanism and conditions for initiating detonation both in unconfined chemical and thermonuclear explosions. The model is validated by using experiments with chemical flames and numerical simulations of thermonuclear flames. We use the developed theory to determine criteria for detonation initiation in the single-degenerate Chandrasekhar-mass SNIa model and show that DDT is almost inevitable at densities of 10(7) to 10(8) grams per cubic centimeter.

[2]

Yang

, Kubota

, Zukoski

. Applications of shock-induced mixing to supersonic combustion
AIAA Journal, 1994,31:854-862

DOI URL [本文引用: 1]

[3]

徐建于, 黄生洪. 圆柱形汇聚激波诱导Richtmyer-Meshkov不稳定的SPH模拟
力学学报, 2019,51(4):998-1011

[本文引用: 1]

( Xu

Jianyu

, Huang

Shenghong

. Numerical simulation of cylindrical converging shock induced Richtmyer-Meshkov instability with SPH
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(4):998-1011 (in Chinese))

[本文引用: 1]

[4]

Oran

, Gamezo

. Origins of the deflagration-to-detonation transition in gas-phase combustion
Combustion and Flame, 2007,148:4-47

DOI URL [本文引用: 3]

[5]

Richtmyer

. Taylor instability in shock acceleration of compressible fluids
Communications on Pure and Applied Mathematics, 1960,13(2):297-319

DOI URL [本文引用: 1]

[6]

Zhang

, Sohn

. Non-linear theory of unstable fluid mixing driven by shock wave
Physics of Fluids, 1997,9:1106-1124

DOI URL [本文引用: 1]

[7]

Sohn

. Simple potential-flow model of Rayleigh-Taylor and Richtmyer-Meshkov instabilities for all density ratios
Physical Review E, 2003,67:026301

DOI URL [本文引用: 1]

[8]

Mikaelian

. Explicit expressions for the single-mode Rayleigh-Taylor and Richtmyer-Meshkov instabilities at arbitrary Atwood numbers
Physical Review E, 2003,67:026319

DOI URL [本文引用: 3]

[9]

Brouillette

, Sturtevant

. Experiments on the Richtmyer-Meshkov instability: small-scale perturbations on a plane interface
Physics of Fluids, 1993,A5(4):916-930

[本文引用: 1]

[10]

Mikaelian

. Turbulent mixing generated by Rayleigh-Taylor and Richtmyer-Meshkov instabilities
Physica D, 1989,36:343-357

DOI URL

[11]

Mikaelian

. Extended model for Richtmyer-Meshkov mix
Physica D, 2011,240:935-942

DOI URL [本文引用: 1]

Mixing between two adjacent fluids has important consequences for inertial fusion capsule implosions and for supernova explosions. Consider an interface with small, random perturbations between two fluids of densities rho(A) and rho(B). When a shock passes through the interface, those perturbations grow and the two fluids begin mixing in a process called Richtmyer-Meshkov (RM) mix, in analogy with Rayleigh-Taylor (RT) mix generated when the system undergoes a constant acceleration. Around the interface a time-dependent mixing width h evolves from the initial value h(0) and grows very large for strong shocks. If the interface sees a second shock, also called a reshock, the mixing is again intensified. In this paper we examine four RM experiments on shock-generated turbulent mix and find them to be in good agreement with our earlier simple model in which the growth rate h of the mixing layer following a shock or reshock is constant and given by 2 alpha A Delta v. Here A is the Atwood number (rho(B) - rho(A))/(rho(B) + rho(A)), Delta v is the jump in velocity induced by the shock or reshock, and alpha is the constant measured in RT experiments: alpha(bubble) approximate to 0.05-0.07, alpha(spike) approximate to (1.8-2.5)alpha(bubble) for A approximate to 0.7-1.0. We then extend the model to t > t* or, equivalently, h > h* when the growth rate begins to decay and exhibit Is t We ascribe this changeover to loss of memory of the direction of the shock or reshock, signaling the transition from highly directional to isotropic turbulence. In the simplest extension of the model, h*/h(0) is independent of Delta v and depends only on A: h*/h(0) approximate to 2.5 - 3.5 for A approximate to 0.7 - 1.0. (C) 2011 Elsevier B.V.

[12]

Ukai

, Balakrishnan

, Menon

. Growth rate predictions of single- and multi-mode Richtmyer-Meshkov instability with reshock
Shock Waves, 2011,21:533-546

DOI URL [本文引用: 4]

The single- and multi-mode Richtmyer-Meshkov instabilities (RMI) with reshock are numerically analyzed in two- and three-dimensional domains. Four different types of air/SF (6) interface shapes are investigated in a shock tube configuration, and the predicted post-reshock growth rates are compared with available empirical models of Mikaelian's (Physica D 36(3):343-347, 1989) and Charakhch'an's (J Appl Mech Tech Phys 41(1):23-31, 2000). The simulation of 3D multi-mode RMI shows good agreement with a past experimental study, but other interface types (2D single-mode, 2D multi-mode and 3D single-mode) result in different growth rates after reshock. Parametric studies are therefore performed to investigate the sensitivities of the post-reshock growth rates to model the empirical parameters. For single-mode RMI configurations, the interface shape is found to be only a weak function of the post-reshock growth rate, as also predicted by previous reshock models. The post-reshock growth rate shows a linear correlation to the velocity jump due to reshock; however, it is only about a half of the prediction of Charakhch'an's model even though the growth before reshock compares well with pre-reshock models. The 3D single-mode post-reshock RMI growth rate is nearly 1.6 times larger than the 2D single-mode RMI. The parametric studies of multi-mode RMI show two distinctly different growth rates depending on the mixing conditions at reshock. If the interface remains sharp at the time of reshock, the post-reshock growth rate is as large as the single-mode cases. However, if the interface is mixed due to non-linear interactions of bubbles and spikes, the growth rates becomes slow and independent of the interface shapes. Overall, this study provides new insights into the flow features of reshocked RMI for different initial perturbation types.

[13]

Zhou

. Rayleigh-Taylor and Richtmyer-Meshkov instability induced flow, turbulence and mixing. I
Physics Reports, 2017, 720-722:1-136

DOI URL [本文引用: 2]

[14]

Vetter

, Sturtevant

. Experiments on the Richtmyer-Meshkov instability of an air/SF$_6$ interface
Shock Waves, 1995,4(5):247-252

DOI URL [本文引用: 1]

[15]

Leinov

, Malamud

, Elbaz

, et al. Experimental and numerical investigation of the Richtmyer-Meshkov instability under re-shock conditions
Journal of Fluid Mechanics, 2009,626:449-475

DOI URL

[16]

Zou

, Liu

, Liao

, et al. Richtmyer-Meshkov instability of a flat interface subjected to a rippled shock wave
Physical Review E, 2017,95:013107

DOI URL PMID

The Richtmyer-Meshkov (RM) instability of a nominally flat interface (N_{2}/SF_{6}) subjected to a rippled shock, as the counterpart of a corrugated interface interacting with a planar shock, is studied experimentally in a vertical shock tube using both schlieren photography and fog visualization diagnostics. The nonplanar incident shock wave is produced by a planar shock diffracting around a rigid cylinder, and the flat interface is created by a membraneless technique. Three different distances eta (the ratio of spacing from cylinder to interface over cylinder diameter) are considered. Schlieren images indicate that the nonplanar incident shock can be divided into three different segments separated by two triple points. Fog visualization pictures show the formation of overall

[17]

刘金宏, 邹立勇, 曹仁义等. 绕射激波和反射激波作用下N$_{2}$/SF$_{6}$界面R-M不稳定性实验研究
力学学报, 2014,46(3):475-479

DOI URL [本文引用: 1]

2/SF6平面界面，以及来自固壁的反射激波再冲击过程的（Richmyer-Meshkov，R-M）不稳定性特征.与平面激波作用不同的是，绕射后的激波会在界面处生成局部扰动.实验结果显示，入射激波作用下界面宽度增长缓慢，而反射激波再冲击后，局部扰动会产生大的“尖钉”和“气泡”结构；以及反射激波与边界层相互作用产生壁面涡，它们会加剧湍流混合区的增长；实验中反射激波过后混合区增长率不十分依赖于波前状态，增长规律同Mikaelian模型较吻合；来自尾部固壁的反射稀疏波会再次加剧湍流混合区的增长.]]>

( Liu

Jinhong

, Zou

Liyong

, Cao

Renyi

, et al. Experimentally study of the Richtmyer-Meshkov instability at N$_{2}$/SF$_{6}$ flat interface by diffracted incident shock waves and reshock
Chinese Journal of Theoretical and Applied Mechanics, 2014,46(3):475-479 (in Chinese))

DOI URL [本文引用: 1]

The developments of Richtmyer-Meshkov instability at gas interface subjected to a diffracted incident shock wave of low Mach number and reshock wave have been experimentally studied using the high-speed schlieren photography. The planar shock wave diffracted over a cylindrical column produces local perturbation at the gas interface. It has been demonstrated that the thickness of the interface grows slowly under the incident shock wave, while spike and bubble are clearly observed upon reshock. Moreover, the interaction between the reshock wave and the boundary layer generates wall vortices, which accelerates the development of turbulence mixing zone (TMZ). The post-reshock growth rate of TMZ is almost independent of pre-reshock conditions and in good agreement with the prediction of Mikaelian model. The reflected rarefaction wave from wall-end also accelerates the development of TMZ.

[18]

Liang

, Zhai

, Ding

, et al. Richtmyer-Meshkov instability on a quasi-single-mode interface
Journal of Fluid Mechanics, 2019,872:729-751

DOI URL [本文引用: 1]

[19]

Guo

, Ding

, Luo

, et al. Evolution of shocked multi-mode interface with sharp corners
Physical Review Fluids, 2018,3:114004

DOI URL

[20]

Luo

, Dong

, Si

, et al. The Richtmyer-Meshkov instability of a 'V' shaped air/SF$_{6}$ interface
Journal of Fluid Mechanics, 2016,802:186-202

DOI URL

[21]

Bai

, Liu

, Wang

, et al. Investigation of the Richtmyer-Meshkov instability with double perturbation interface in nonuniform flows
Physical Review E, 2010,81:056302

DOI URL [本文引用: 1]

[22]

蒋华, 董刚, 陈霄. 小扰动界面形态对RM 不稳定性影响的数值分析
力学学报, 2014,46(4):544-552

DOI URL [本文引用: 1]

采用Navier-Stokes 方程对入射激波及其反射激波连续诱导小振幅扰动界面的Richtmyer-Meshkov 不稳定性增长过程进行了二维数值模拟，分析了单模和随机多模两种不同初始形态的界面上钉结构和泡结构在反射激波作用前后的发展特性. 研究结果发现：单模扰动的初始界面形态对反射激波前、后界面的扰动增长都有影响，反射激波前的界面形态信息可以通过钉和泡结构之间的反转传递到反射激波过后. 扰动界面上钉结构的发展速度控制了界面混合区总体的发展速度，反射激波前界面上发展成具有完整冠部形态的钉，在反射激波后会反转成复杂的泡结构，此泡结构对反射激波后钉的发展不利. 随机多模界面显示了与单模界面类似的发展规律，但随机多模界面上的复杂泡结构分布的不对称性使得其对钉结构增长的拖曳效应相对要弱，这导致了相似扰动波长下多模随机界面的扰动发展相对单模界面扰动发展要快.

( Jiang

Hua

, Dong

Gang

, Chen

Xiao

. Numerical study on the effects of small-amplitude initial perturbations on RM instability
Chinese Journal of Theoretical and Applied Mechanics, 2014,46(4):544-552 (in Chinese))

DOI URL [本文引用: 1]

Two-dimensional simulations of Richtmyer-Meshkov (RM) instability of small-amplitude initial perturbed interface induced by shock waves are performed by using Navier-Stokes equations. The evolution of interface mixing zone, which is considered as a combination of a bubble and a spike before and after the passages of reshock wave, is analyzed under the single-mode and random multi-mode initial perturbed conditions. The results show that the perturbation growth is influenced by the initial patterns of interface before and after the passages of reshock wave. The information of initial perturbed interface pattern can be transmitted to that of the interface after reshock wave by transforming between the bubble and spike. The growth rate of spike on the interface dominates the whole growth rate of the mixing zone. The developed spike with crown shape before the passage of reshock is transformed into the complex bubble structure that drags the development of spike after the passage of reshock wave. The evolution of random multi-mode perturbed interface shows the similar behavior as that of single-mode perturbed interface. However, the asymmetric feature of complex bubble structure on random multi-mode interface weakens the drag effect on the development of spike, and thus gives rise to the faster growth of the random multi-mode interface than that of the single-mode interface, under the conditions of similar initial wave length for both interfaces.

[23]

蒋华, 董刚, 朱跃进等. 界面初始扰动形态影响RM不稳定过程的数值研究
工程力学, 2013,31(11):244-250

[本文引用: 2]

( Jiang

Hua

, Dong

Gang

, Zhu

Yuejin

, et al. Numerical study on influence of initial perturbations on RM instability
Engineering Mechanics, 2013,31(11):244-250 (in Chinese))

[本文引用: 2]

[24]

Schilling

, Latini

, Don

. Physics of reshock and mixing in single-mode Richtmyer-Meshkov instability
Physical Review E, 2007,76:026319

DOI URL [本文引用: 2]

[25]

Thornber

, Drikakis

, Youngs

, et al. Physics of the single-shocked and reshocked Richtmyer-Meshkov instability
Journal of Turbulence, 2012,13(10):1-17

DOI URL [本文引用: 1]

This paper presents a numerical study of a single-shocked turbulent mixing layer using high-order accurate implicit large-eddy simulations (ILES) for low-and high-amplitude (linear and non-linear) perturbations and for a reshocked turbulent layer. It investigates the differences in flow physics between these three cases, examining a recent proposition that single-shocked high-amplitude initial perturbations can be employed to model a reshocked turbulent layer. At early times, the shocked high-amplitude perturbation has high levels of mixing; however, at later times, it grows in an almost identical manner to the low-amplitude case. Despite exploration of several choices of scaling to map the reshocked results to the single-shocked study, a satisfactory agreement could not be reached and mixing parameters remain disparate. The conclusion is that a single-shock interaction with a high-amplitude perturbation is not a good representation of reshock of a turbulent mixing layer.

[26]

Lombardini

, Pullin

, Meiron

. Transition to turbulence in shock-driven mixing: A Mach number study
Journal of Fluid Mechanics, 2012,690:203-226

DOI URL [本文引用: 1]

Large-eddy simulations of single-shock-driven mixing suggest that, for sufficiently high incident Mach numbers, a two-gas mixing layer ultimately evolves to a late-time, fully developed turbulent flow, with Kolmogorov-like inertial subrange following a -5/3 power law. After estimating the kinetic energy injected into the diffuse density layer during the initial shock interface interaction, we propose a semi-empirical characterization of fully developed turbulence in such flows, based on scale separation, as a function of the initial parameter space, as (eta(0)+Delta u/nu) (eta(0)+L-rho)A(+)/root 1-A(+2) greater than or similar to 1.53 x 10(4)/l(2), which corresponds to late-time Taylor-scale Reynolds numbers greater than or similar to 250. In this expression, eta(0+) represents the post-shock perturbation amplitude, Delta u the change in interface velocity induced by the shock refraction, nu the characteristic kinematic viscosity of the mixture, L-rho the inner diffuse thickness of the initial density profile, A(+) the post-shock Atwood ratio, and W(A(+), eta(0)+lambda(0)) approximate to 0.3 for the gas combination and post-shock perturbation amplitude considered. The initially perturbed interface separating air and SF6 (pre-shock Atwood ratio A approximate to 0.67) was impacted in a heavy light configuration by a shock wave of Mach number M-1 = 1.05, 1.25, 1.56, 3.0 or 5.0, for which eta(0+) is fixed at about 25% of the dominant wavelength lambda(0) of an initial, Gaussian perturbation spectrum. Only partial isotropization of the flow (in the sense of turbulent kinetic energy and dissipation) is observed during the late-time evolution of the mixing zone. For all Mach numbers considered, the late-time flow resembles homogeneous decaying turbulence of Batchelor type, with a turbulent kinetic energy decay exponent n approximate to 1.4 and large-scale (k -> 0) energy spectrum similar to k(4), and a molecular mixing fraction parameter, Theta approximate to 0.85. An appropriate time scale characterizing the Taylor-scale Reynolds number decay, as well as the evolution of mixing parameters such as Theta and the effective Atwood ratio A(e), seem to indicate the existence of low- and high-Mach-number regimes.

[27]

Tritschler

, Olson

, Lele

, et al. On the Richtmyer- Meshkov instability evolving from a deterministic multimode planar interface
Journal of Fluid Mechanics, 2014,755:429-462

DOI URL [本文引用: 1]

(xyz) approaches an asymptotic limit of approximate to 0.04, implying that no full recovery of isotropy within the mixing zone is obtained, even after re-shock. Spectra of density, turbulence kinetic energy, scalar dissipation rate and enstrophy are presented and show excellent agreement for the resolved scales. The probability density function of the heavy-gas mass fraction and vorticity reveal that the light-heavy gas composition within the mixing zone is accurately predicted, whereas it is more difficult to capture the long-term behaviour of the vorticity.]]>

[28]

Khokhlov

, Oran

, Chtchelkanova

, et al. Interaction of a shock with a sinusoidally perturbed flame
Combustion and Flame, 1999,117:99-116

DOI URL [本文引用: 1]

[29]

Kilchyk

, Nalim

, Merkle

. Laminar premixed flame fuel consumption rate modulation by shocks and expansion waves
Combustion and Flame, 2011,158:1140-1148

DOI URL [本文引用: 1]

The main contributing effects leading to premixed laminar flame fuel consumption rate changes following variable strength shock or expansion wave passage were studied analytically and numerically. The effects were separated into two groups: gas compression, or one-dimensional effects, and flame front distortion, or two-dimensional effects. The first group was examined analytically using a one-dimensional flame model and solution of shock and expansion wave refraction. Two-dimensional effects were examined numerically using both shock and expansion wave passage through a sinusoidally perturbed propane-air laminar flame. Flame fuel consumption amplification due to the gas compression increased rapidly (from 1.3 to 24 times for Mach 1.1-1.7 shocks), while flame length amplification peaked (similar to 15 times) at a given shock strength (similar to Mach 1.3). Thus gas compression became the dominant effect for stronger shocks. In contrast to the shocks, a slower reaction kinetic produced by the expansion wave passage allowed for a significantly longer period of flame length growth. This resulted in a temporary burning rate increase above initial values. The negative chemical kinetic effect of the weak expansion wave passage was temporarily offset by the flame length increase. The overall reaction rate amplification was up to four times stronger in fast/slow refractions. Also, the observed values of the flame stretch are reported in the paper. (C) 2010 The Combustion Institute. Published by Elsevier Inc.

[30]

Massa

, Jha

. Linear analysis of the Richtmyer-Meshkov instability in shock-flame interactions
Physics of Fluids, 2012,24:056101

DOI URL [本文引用: 3]

[31]

Jiang

, Dong

, Chen

, et al. Numerical simulations of the process of multiple shock-flame interactions
Acta Mechanica Sinica, 2016,32(4):659-669

DOI URL [本文引用: 3]

[32]

Jiang

, Dong

, Chen

, et al. A parameterization of the Richtmyer-Meshkov instability on a premixed flame interface induced by the successive passages of shock waves
Combustion and Flame, 2016,169:229-241

DOI URL [本文引用: 2]

[33]

Chen

, Dong

, Li

. Numerical study of three-dimensional developments of premixed flame induced by multiple shock waves
Acta Mechanica Sinica, 2018,34(6):1035-1047

DOI URL [本文引用: 6]

[34]

Attal

, Ramaprabhu

. Numerical investigation of a single-mode chemically reacting Richtmyer-Meshkov instability
Shock Waves, 2015,25:307-328

DOI URL [本文引用: 1]

[35]

Thomas

, Bambrey

, Brown

. Experimental observations of flame acceleration and transition to detonation following shock-flame interaction
Combustion and Theory Modelling, 2001,5(4):573-594

DOI URL [本文引用: 1]

[36]

Balsara

, Shu

. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy
Journal of Computational Physics, 2000,160:405-452

DOI URL [本文引用: 1]

[37]

Khokhlov

, Austin

, Pintgen

, et al. Numerical study of the detonation wave structure in ethylene-oxygen mixtures
// 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, USA, 2004. 1. 5-8, 792

[本文引用: 1]

[38]

Kuo

. Principles of Combustion, 2nd Edition
Hoboken, New Jersey, John Wiley & Sons, Inc., 2005

[本文引用: 1]