 ,?,2)*
,?,2)* ?
SENSITIVITY ANALYSIS AND OPTIMIZATION ON PARAMETERS OF HIGH SPEEDPANTOGRAPH-CATENARY SYSTEM 1)
Wu Mengzhen*,?, Liu Yang?, Xu Xianghong ,?,2)*
,?,2)* ?
通讯作者: 2)许向红, 副研究员. 主要研究领域: 受电弓力学特性与结构优化、仿生微结构设计及3D打印. E-mail:xxh@lnm.imech.ac.cn
收稿日期:2020-06-16接受日期:2020-08-6网络出版日期:2021-12-31
| 基金资助: |
Received:2020-06-16Accepted:2020-08-6Online:2021-12-31
作者简介 About authors

摘要
随着高速列车运行速度的提升, 弓网关系这一基础力学问题备受关注. 良好的弓网关系是确保列车安全高效运行、稳定可靠受流、降低接触线与受电弓滑板磨耗等的基本前提. 其中, 受电弓和接触网的动力学参数对弓网耦合作用起至关重要的作用. 本文采用弓网接触力随机统计特征作为优化目标函数,进行受电弓动力学参数的敏度分析和优化设计. 首先, 建立了二维弹性链悬挂接触网-三质量块受电弓动力学模型,根据EN50318: 2018标准验证了动力学建模和分析结果的正确性. 然后, 基于高速弓网系统的动力学仿真, 进行了DSA380型高速受电弓三质量块参数的动力学敏度分析, 确定了9个动力学参数的敏感度级别, 弓头等效质量敏度评级最高,下框架等效阻尼次之, 下框架等效质量和上框架等效阻尼第三. 最后, 研究了弓头等效刚度和等效阻尼联合变化对弓网耦合动力学性能的影响,给出了提升弓网耦合性能的弓头双参数优化方案, 建议同时减小弓头等效阻尼和增大弓头等效刚度, 能够实现比单参数优化更好的弓网耦合性能.
关键词:
Abstract
With the improvement in the speed of high-speed trains, thedynamic interaction between pantograph and catenary, a basic mechanicalproblem, has attracted more attention. Good pantograph-catenary relationshipis a basic premise to ensure the security and efficiency of the trainoperation, the stability and reliability of the current collection andreduce the wear of the contact line and pantograph slide. The couplingperformance of the pantograph-catenary system mainly depends on its kineticparameter. In this paper, the stochastic statistical characteristics of thecontact force of the pantograph-catenary system are adopted as theoptimization objective function, and the sensitivity analysis andoptimization design of pantograph dynamic parameters are carried out.Firstly, a dynamic model of 2D stitched catenary and three lumped parameterpantograph is established, and the validation of dynamic analysis of themodel is verified according to British Standard EN50318:2018. Secondly,based on dynamic simulation of the high-speed pantograph-catenary system, adynamic sensitivity analysis on three lumped nine dynamic parameters ofDSA380 high-speed pantograph is carried out, and the sensitivity level ofthe parameters is determined. The sensitivity level of the equivalent massof the pantograph head is the highest, followed by the equivalent damping ofthe lower frame and the equivalent mass of lower frame and the equivalentdamping of the upper frame are the third. Finally, the effect of jointvariation in equivalent stiffness and equivalent damping of the pantographhead on the pantograph-catenary coupling dynamic performance is studied, anda dual-parameter optimization scheme of equivalent stiffness and equivalentdamping of the pantograph head is proposed to improve the current collectionquality pantograph-catenary system. It is suggested to reduce the equivalentdamping of pantograph head and increase the equivalent stiffness ofpantograph head at the same time, and the dual-parameter optimization schemecan achieve a better quality of the pantograph-catenary system than thesingle parameter optimization scheme
Keywords:
PDF (1269KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
吴孟臻, 刘洋, 许向红. 高速弓网系统动力学参数敏度分析及优化 1). 力学学报[J], 2021, 53(1): 75-83 DOI:10.6052/0459-1879-20-207
Wu Mengzhen, Liu Yang, Xu Xianghong.
引言
高速列车速度的大幅提升,给高速受电弓与接触网关系提出了更高的技术要求[1-2]受电弓安装于列车顶部, 在升弓装置作用下与接触网耦合, 为列车运行提供电能. 当列车高速运行时, 受电弓弓头滑板与接触网动态接触, 此时受电弓作用到架空接触网上会产生垂向的弓网接触力[3-4]弓网接触力是弓网间耦合作用的直接反映. 弓网接触力过大, 会加剧弓头滑板、接触线等部件的机械磨损, 降低弓网系统的使用寿命; 接触力过小, 会增大接触电阻, 造成电能浪费, 甚至产生离线和电弧烧损.良好的弓网关系是确保列车稳定可靠受流、降低接触线与受电弓滑板磨耗的基本前提. 在线路实测和仿真分析中, 采用平均接触力$F_{m}$和标准差$\sigma $作为受流质量的主要评价指标[3-6]其中, $F_{m}$表征弓头碳滑板与接触线间作用力水平, 当列车运行速度$v >200$ km/h (AC)时, 需满足$F_{m} < 70 + 0.000 97$ $v^{2}$; $\sigma $表征接触力的振荡程度,需满足$\sigma < 0.3F_{m}$. $F_{m}$越小, 碳滑板与接触线间的机械磨损越轻; $\sigma $越小, 弓网接触力涨落越小, 弓网接触性能越优良. 因此, 良好的弓网关系要求满足$F_{m}$的前提下$\sigma $尽可能小, 这也是弓网耦合动力学参数优化的主要目标. 在进行弓网动力学优化研究时, 采用上述接触力随机统计特征作为优化目标函数, 是相关问题研究的挑战.
弓网耦合性能主要取决于受电弓和接触网的动力学参数. 近年来, 进行受电弓模型参数优化以期提升弓网耦合性能, 成为弓网动力学仿真研究的重要方向之一. 基于DSA250, DSA380和CX等受电弓现有参数, 通过弓网动力学仿真分析, 研究者们提出了三质量块参数的许多优化建议. 对弓头的等效质量和等效阻尼、上框架等效阻尼这3个参数, ****们基本达成共识,认为减小弓头等效质量[7-12], 或增大弓头等效阻尼[9,13]、上框架等效阻尼[9,13], 均可以降低接触力标准差. 然而,关于弓头等效刚度等5个三质量块参数的研究结果差别较大. 为了实现降低接触力标准差, 文献[7-9, 11]认为应增大弓头等效刚度,他们给出的弓头等效刚度的最优值较为分散, 覆盖7860~23 380 N/m;文献[10, 12-14]则认为减小弓头等效刚度. 文献[7, 10, 12]认为减小上框架等效质量, 唐周林[15]认为应保持上框架等效质量不变.文献[10, 12-13]认为应减小上框架等效刚度, 但周宁[16]认为应增大上框架等效刚度. Lee等[7]和Wang等[12]认为减小下框架等效质量, 而Kim等[10]认为应该增大下框架等效质量.文献[7-8, 12]认为需增大下框架等效阻尼, Kim等[10]认为应该保持下框架等效阻尼不变. 此外, 下框架等效刚度的研究较少,Wang等[12]认为应增大下框架等效刚度. 需要注意的是, 同一参数在不同文献中的优化范围大多不同, 例如, 弓头刚度的优化范围众多,取原参数的0.9~1.1倍[7], 0.017~1.65倍[14]、1~3.98倍[11]等; 联合优化的参数个数也不同, 涵盖1个[8,11,13-14]到7个[12]不等. 事实上, 受电弓动力学特性对弓网耦合性能的影响, 与敏度分析时的参数起点和变化范围、多参数联合优化时的参数个数等都密切相关.这也是已有报道的研究结果较为分散甚至完全相反的原因之一.
本文利用有限元法建立了二维弹性链悬挂接触网-三质量块受电弓动力学模型, 依据EN50318规范结果校验了动力学分析结果的正确性. 以实验测得的DSA380型高速受电弓在1600 mm工作高度下的三质量块参数为基础, 根据工程设计可行性确定模型参数的实现范围, 进行了350 km/h时速下受电弓三质量块参数的敏度分析, 确定了在DSA380现有基础上的参数敏感性级别. 研究了当弓头等效刚度与等效阻尼联合变化时, 弓网耦合系统动力学关系的变化, 结果表明弓头双参数优化相比于单参数优化, 能够实现更高的弓网耦合性能.
1 弓网耦合动力学模型
1.1 受电弓动力学方程
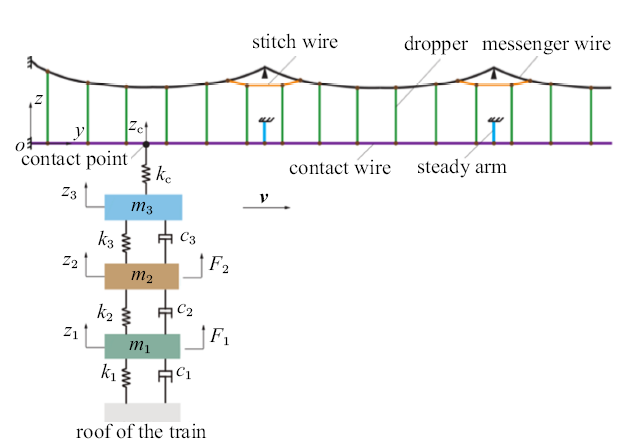
受电弓底座安装于列车顶部, 弓头滑板与接触线接触. 图1所示的三质量块受电弓模型的动力学方程如下[13,17-18]式中, $m_{i}$, $k_{i}$, $c_{i}$和$z_{i}$ ($i$ = 3, 2, 1)分别为弓头、上框架和下框架的等效质量、等效刚度、等效阻尼和垂向位移.
施加在质量块$m_{2}$和$m_{1}$上的抬升力分别为$F_{2}$和$F_{1}$; 接触力为$F_{c}$.
图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1高速弓网系统示意图
Fig.1Illustration of high speed pantograph-catenary system
1.2 接触网动力学方程
忽略接触网拉出值和接触线横向运动, 建立包括接触线、承力索、弹性吊索、吊弦和定位器的二维弹性悬挂接触网模型(图1)[19-21]其中, 接触线、承力索和弹性吊索的长度远大于其截面尺寸, 由弯曲变形引起的弯曲应力远小于预张力引起的拉伸应力, 弯曲应力对50 Hz以下动态接触力的影响很小[22-23], 故接触线、承力索和弹性吊索简化为细长杆模型[20,24-27]吊弦是只能承受拉力的细长绳索, 主要发生轴向伸缩运动, 简化为只具有抗拉刚度的弹簧模型[7,13,28]定位器呈一定角度斜向提拉接触线, 接触线上下振动会引起拉力方向改变, 且接触线承担定位器的部分重力, 可将定位器简化为弹簧-质量点组合模型, 取定位器质量一半与定位线夹质量之和为质量点质量, 弹簧刚度为213 N/m[7,29]在上述模型简化前提下, 可得接触网动力学方程式中, $M_{c}$为接触网的质量矩阵, $C_{c}$为接触网阻尼矩阵, $K_{c}$为接触网刚度矩阵, $z_{c}$为接触网上节点的位移向量, $P$为接触网上节点的外载荷向量.
1.3 弓网耦合关系模型
受电弓与接触网之间通过接触力形成耦合动力学系统, 可用罚函数法模拟弓头滑板与接触线的耦合行为以求解接触力[30]式中, $z_{3}$为弓头垂向位移, $z_{c}$为接触位置接触线上的节点垂向位移; 取接触刚度$k_{c} = 50 000$ N/m[27,31].
2 耦合动力学方程的数值方法及校验
2.1 耦合动力学方程的数值方法
按照几何参数建立接触网初始几何构型. 接触网的高度$H_{C}$方向为$z$向、长度方向为$y$向. 接触线位于$z = 0$的直线上,其左端起点为坐标原点(0, 0); 承力索和弹性吊索位于$z=H_{C}$的直线上.采用有限单元法对结构进行离散. 接触网模型中的接触线、承力索和弹性吊索采用杆单元, 单元长度均为0.2 m. 吊弦采用只承拉的弹簧单元, 每根吊弦只划分一个单元. 定位器采用质量块与弹簧的组合单元. 三质量块模型中的质量点和弹簧分别采用质量单元和弹簧单元. 弓网耦合模型中,采用Conta175和Targe169单元分别覆盖弓头质量点和接触线下表面, 二者形成接触对.接触线、承力索两端施加全约束, 承力索每一跨的节点上施加$z$方向平动约束,在定位器端部施加全约束, 在各质量块上施加只释放$z$方向平动的约束.
对各个部件进行弹性模量、泊松比、结构阻尼、质量、预张力等参数赋值. 利用负驰度法[23,32]计算接触网的初始平衡状态,使得在重力和预张力作用下接触线保持水平. 联立方程(1)~(3)可得接触网和受电弓动力学平衡方程
式中, $M$为整体质量矩阵、$C$为整体阻尼矩阵、$K$为整体刚度矩阵、$z$为节点位移向量、$F$为节点的外载荷向量. 采用Newmark法进行时间积分计算, 引入如下假设
式中, $z_{t}$为$t$时刻节点位移向量、$\Delta t$为时间积分步长、$z_{t+\Delta t}$为$t+\Delta t$时刻节点位移向量、$\alpha $和$\beta $为时间积分参数, 计算时选取$\alpha = 0.5$、$\beta = 0.25$.
联立方程(4)~(6)即可求解弓网耦合动力学方程. 在数值计算中, 最大时间积分步长0.001 67 s, 结果输出时间间隔0.005 s, 接触网跨数 30, 受电弓起始位置为$y = 0$, 运行速度$v = 350$ km/h.
首先, 进行动力学计算、迭代, 确定质量块$m_{2}$和$m_{1}$上的抬升力$F_{2}$和$F_{1}$, 使得接触力均值$F_{m}$达到目标值$70 + 0.000 97v^{2} = 189$ N. 然后, 计算弓网系统的接触力、抬升位移等参数. 在具体仿真计算过程中, 采用ANSYS商用软件实现.
2.2 EN 50318:2018标准算例校验
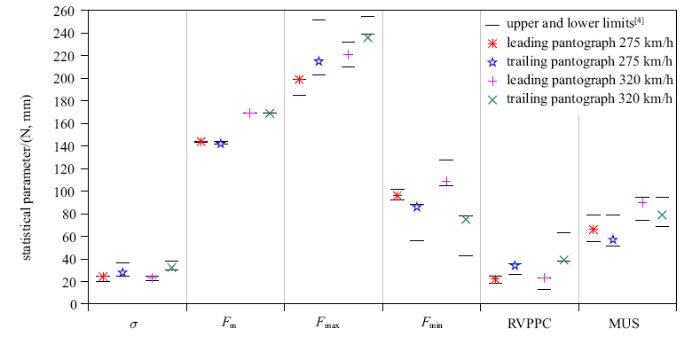
基于二维弹性链悬挂接触网-三质量块受电弓动力学模型, 针对EN 50318:2018给定的接触网-双受电弓参数[4], 进行弓网接触力动力学计算, 统计10~20跨内前、后受电弓与接触网之间的接触力标准差$\sigma $、平均值$F_{m}$、实际最大值$F_{\max}$和实际最小值$ F_{\min}$, 以及接触点垂向位移范围RVPPC和定位器处最大抬升量MUS (图2). 当受电弓运行速度$v = 275$ km/h和320 km/h时, 仿真计算结果均位于EN 50318:2018规定的范围. 因此, 本文建立的二维弹性链悬挂接触网-三质量块受电弓动力学模型计算结果可信.3 弓网耦合参数分析及优化
基于二维弹性链悬挂接触网-三质量块受电弓动力学模型, 计算DSA380型高速受电弓在大西线上运行的动力学行为. 针对DSA380型高速受电弓在图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2EN 50318接触网-双受电弓模型的仿真结果
Fig.2Simulation results of catenary--two pantographs system in EN 50318
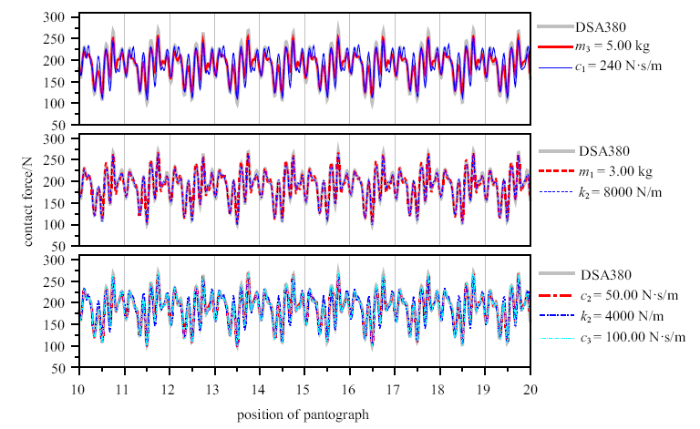
1600 mm工作高度情形, 实测的弓头、上框架和下框架的等效质量分别为7.94 kg, 8.22 kg和5.90 kg, 等效刚度分别为6650 N/m, 13 181 N/m和74.0 N/m, 等效阻尼分别为85.31 N$\cdot$s/m, 11.90 N$\cdot$s/m和67.41 N$\cdot $s/m. 大西线接触网的高度1.8 m、跨距55 m、吊弦间距9.4 m; 接触线、承力索和弹性吊索的杨氏模量分别为120 GPa, 105 GPa和113 GPa, 预张力分别为30 kN, 21 kN和3.5 kN. 取接触网跨数30、受电弓起始位置$y = 0$、运行速度$v = 350$ km/h, 计算得到弓网接触力和接触点垂向位移的时程曲线(图3), 统计10~20跨稳定段内的数据, 得到$F_{m}=189.02$ N, $\sigma = 35.44$ N, $F_{\max}= 269.69$ N和$F_{\min}= 97.96$ N. 下文的仿真计算中, 保持所有受电弓参数情形的静态接触力均为80 N.
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3弓网接触力时程曲线
Fig.3Time history curves of contact force
3.1 三质量块参数的敏度分析
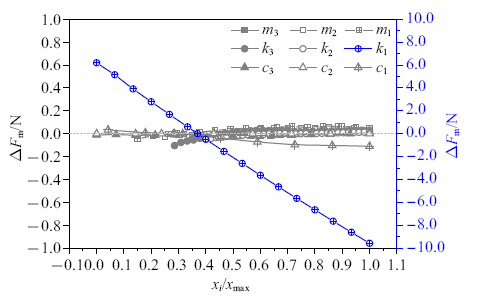
假设9个三质量块参数相互独立, 以控制变量法计算单个归算参数在取值区间内变化时, 弓网接触力的平均值、标准差、最大值和最小值相对于DSA380归算参数时的变化量$\Delta F_{m}$, $\Delta \sigma $, $\Delta F_{\max}$与$\Delta F_{\min}$. 根据工程设计的可行性, 确定$m_{3}$、$m_{2}$和$m_{1}$的取值范围分别为5~11 kg, 5~20 kg和3~20 kg; $k_{3}$, $k_{2}$和$k_{1}$的取值范围分别为4000~14 000 N/m, 8000~20 000 N/m和0~200 N/m; $c_{3}$, $c_{2}$和$c_{1}$的取值范围分别为0~100 N$\cdot$s/m, 0~50 N$\cdot $s/m和10~240 N$\cdot $s/m.图4给出了三质量块参数变化对$\Delta F_{m}$的影响. 将每个归算参数$x_{i}$除以其取值上限$x_{\max}$, 得到无量纲量$x_{i}/x_{\max}$. 其中, 当改变下框架等效刚度$k_{1}$时, 接触力均值$F_{m}$的变化显著, 当$k_{1}$从0 N/m增大到200 N/m时, $\Delta F_{m}=-15.78$ N. 这表明, 如果$k_{1}$发生变化, 则需要调整受电弓的静态接触力, 以使得线路运行的接触力均值达到预期. 当改变其他8个参数时,$F_{m}$几乎不变, 在这8个参数的整个参数变化区间内, $\vert\Delta F_{m}\vert $不高于0.11 N, 即保证静态接触力相等, 可以保证运行过程中的$F_{m}$恒定.
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4三质量块参数对$\Delta F_{m}$的影响
Fig.4$\Delta F_{m}$ versus normalized three lumped mass parameters
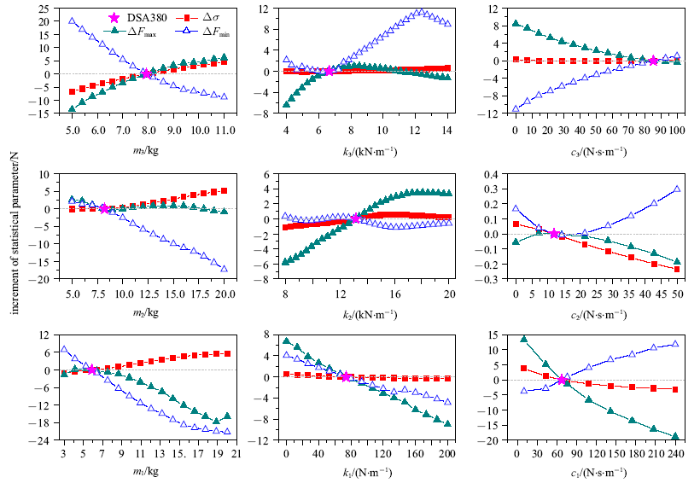
图5给出了三质量块参数变化对$\Delta \sigma $, $\Delta F_{\max}$与$\Delta F_{\min}$的影响. 以DSA380参数为基准, 关注引起 $\Delta \sigma < 0$的参数变化范围; 若$\Delta \sigma \approx 0$, 则考察$\Delta F_{\max }< 0$且$\Delta F_{\min}> 0$的参数区间. 可以看出, 减小弓头或下框架等效质量、或弓头或上框架等效刚度, 或增大3个等效阻尼, 都可以有效提升弓网耦合性能, 即在降低接触力标准差$\sigma $的同时, 降低接触力最大值$F_{\max}$、且增大接触力最小值$F_{\min}$. 然而, 对下框架等效刚度$k_{1}$和上框架等效质量$m_{2}$, 当其改变使得$\Delta \sigma < 0$时, 却会引起$F_{\max}$增大或$F_{\min}$减小, 建议维持不变.
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5三质量块参数对$\Delta \sigma $, $\Delta F_{\max}$与$\Delta F_{\min}$的影响
Fig.5$\Delta \sigma $, $\Delta F_{\max}$ and $\Delta F_{\min}$ versus normalized three lumped mass parameters
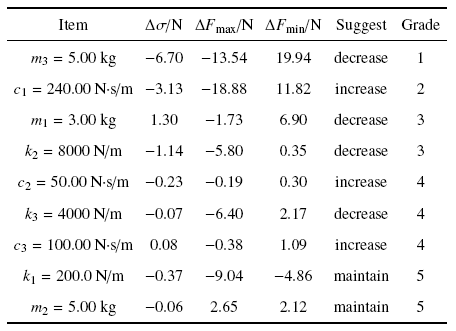
进一步地, 基于敏度分析得到的单参数最优情形的$\Delta \sigma $, $\Delta F_{\max}$和$\Delta F_{\min}$ (图6和表1),给出DSA380型高速受电弓三质量块参数的敏度评级. 其中, $m_{3}$敏度评级为1, 当$m_{3}$减至5.00 kg时, $\Delta \sigma = -6.70$ N, $\Delta F_{\max} = -13.54$ N, $\Delta F_{\min} = 19.94$ N. $c_{1}$敏度评级为2, 当$c_{1}$增至240 N$\cdot$s/m时, $\Delta \sigma $为$m_{3}$情形的1/2, 其$F_{\max}$降低更为显著, $\Delta F_{\max}$ 约为$m_{3}$情形的1.5倍. $m_{1}$, $k_{2}$敏度评级为3, 相应参数变化会使得$\Delta \sigma $下降1.14 N以上, 二者相比, $m_{1}$减小侧重于增大$F_{\min}$, 而$k_{2}$减小倾向于降低$F_{\max}$. $c_{2}$, $k_{3}$, $c_{3}$敏度评级为4, 它们引起的接触力标准差改变量接近于0.$k_{1}$和$m_{2}$敏度评级为5.
因此, 如果只进行DSA380型高速受电弓单参数优化, 建议参数为$m_{3} = 5.00$ kg, $m_{2}= 8.22$ kg, $m_{1}= 3.00$ kg, $k_{3}= 4000$ N/m, $k_{2}= 8000$ N/m, $k_{1}= 74.0$ N/m, $c_{3}= 100.00$ N$\cdot $s/m, $c_{2}= 50.00$ N$\cdot$s/m和$c_{1}= 240.00$ N$\cdot $s/m.
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6单参数变化取最优值时的$\Delta \sigma $, $\Delta F_{\max}$与$\Delta F_{\min}$
Fig.6Optimal values of $\Delta \sigma $, $\Delta F_{\max}$ and $\Delta F_{\min}$ under sigle parameter variation
Table 1
Table 1Sensitivity analysis of three lumped mass parameters
 |
新窗口打开|下载CSV
3.2 弓头等效刚度和等效阻尼耦合作用
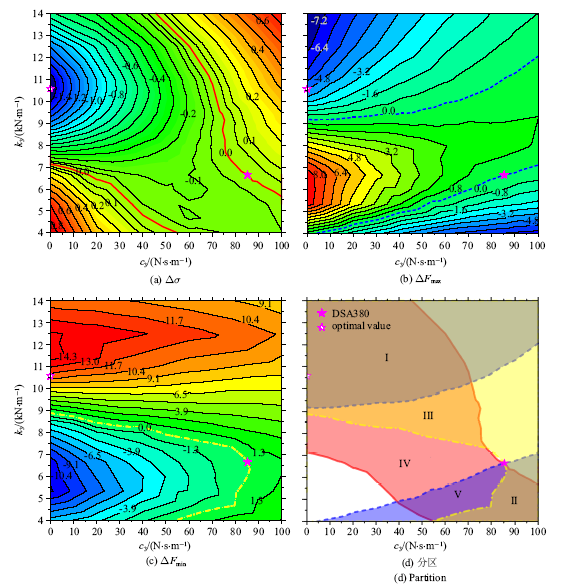
相比于框架归算参数, 改变弓头等效参数从工程设计角度更容易实现. 但3.1节的敏度分析结果表明, 弓头等效刚度和等效阻尼的敏度评级较低,在取值范围内单独改变$k_{3}$或$c_{3}$几乎对接触力标准差没有影响.图7(a)为$k_{3}$和$c_{3}$联合变化情形的$\Delta \sigma $云图. 两条粗实线范围内均有$\Delta \sigma <0$, 比DSA380 (图中符号$\star)$的接触力标准差低. 当$k_{3} = 10 575$ N/m, $c_{3} = 0.00$ N$\cdot $s/m时, $\Delta \sigma $取最小值$-$1.58 N, $\sigma$ 取最优值33.87 N(图中符号☆). 由此可见, 弓头等效刚度和等效阻尼双参数优化结果明显高于单参数变化情形.
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7弓头双参数优化
Fig.7Dual-parameter optimization of pantograph head
此外, $k_{3}$不同时, $\sigma $随$c_{3}$的变化趋势不同. 随着$c_{3}$减小, 当$k_{3}$较低, 4000 N/m $\leqslant$ $k_{3}<7900$ N/m时, $\sigma $先减小再增大; 当$k_{3}$较高, 7900 N/m $\leqslant k_{3 }\leqslant 14 000$ N/m时, $\sigma $单调降低. $c_{3}$不同时, $\sigma $随$k_{3}$的变化趋势不同. 随着$k_{3}$减小, 当$c_{3}$较低, 0 N$\cdot $s/m $\leqslant c_{3 }< 90$ N$\cdot $s/m时, $\sigma $先减小再增大; 当$c_{3}$较高, 90 N$\cdot $s/m $\leqslant k_{3 }\leqslant 100$ N$\cdot $s/m时, $\sigma $单调减小.
综合$\Delta \sigma $、$\Delta F_{\max}$ (图7(b))和$\Delta F_{\min}$ (图7(c))云图, 得到图7(d), 在优化区域弓头双参数变化时的弓网耦合性能分区. 在区域I-V, 均有$\Delta \sigma < 0$. 其中, 在区域I和II同时有$\Delta F_{\max} <0$、且$\Delta F_{\min }> 0$, 为可行的参数优化区, 且I区比II区更优, 双参数最优值位于I区; 然而, 区域III的$\Delta F_{\max}>0$, 区域IV的$\Delta F_{\max} >0$, $\Delta F_{\min }<0$, 区域V的$\Delta F_{\min }<0$, 不建议参数处于这3个区.
4 结论
在保证静态接触力相同的条件下, 下框架等效刚度变化会对接触力均值有显著影响, 弓头等效质量等其他8个参数改变对接触力均值几乎没影响. 因此, 在受电弓设计或使用中, 若下框架等效刚度变化较大, 则需要调整静态接触力经验值, 以使线路运行的接触力均值达到预期.针对DSA380型高速受电弓在1600 mm工作高度下三质量块参数的敏度分析结果表明, 减小弓头或下框架等效质量、或弓头或上框架等效刚度, 或增大3个等效阻尼, 都可以提升受流质量. 其中, 弓头等效质量敏度评级最高, 下框架等效阻尼次之, 下框架等效质量和上框架等效阻尼第三.
弓头等效刚度与等效阻尼双参数联合变化情形, 呈现与单参数变化时不同的参数优化方案, 建议同时减小弓头等效阻尼和增大弓头等效刚度, 使得联合参数位于I区. 此外, 在不同的参数区间, 接触力标准差随弓头等效刚度或弓头等效阻尼的变化规律也会发生变化, 这可能是众多已有研究成果存在差异的原因.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 8]
[本文引用: 2]
[本文引用: 3]
[本文引用: 5]
[本文引用: 3]
[本文引用: 3]
[本文引用: 8]
[本文引用: 6]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
