丁一凡, 魏德安, 陆宋江, 刘金铃, 康国政, 张旭^,2)西南交通大学力学与工程学院应用力学与结构安全四川省重点实验室, 成都 610031

DISCRETE DISLOCATION DYNAMICS SIMULATIONS FOR COMPRESSION OF PARTICLE REINFORCED COMPOSITES¹⁾

Ding Yifan, Wei Dean, Lu Songjiang, Liu Jinling, Kang Guozheng, Zhang Xu^,2)Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China

通讯作者: 2)张旭, 教授, 主要研究方向: 高强高韧材料的多尺度力学. E-mail:xzhang@swjtu.edu.cn

收稿日期:2021-01-17接受日期:2021-04-25网络出版日期:2021-06-18

基金资助:

1)国家自然科学基金资助项目.11672251 国家自然科学基金资助项目.11872321

Received:2021-01-17Accepted:2021-04-25Online:2021-06-18
作者简介 About authors


摘要
颗粒增强铜基复合材料因具有极高的强度和弹性模量, 优异的导电、导热性能和抗磨损能力, 被广泛应用于航天航空、汽车、电子工业等领域. 第二相强化是其主要的强化方式, 其通过合金中弥散的微粒阻碍位错运动, 可有效提高金属材料的力学性能, 提高其服役安全. 针对该问题本文采用三维离散位错动力学(three-dimensional discrete dislocation dynamics, 3D-DDD)方法, 对微尺度颗粒增强铜基复合材料进行了微柱压缩模拟, 分析了位错与第二相颗粒交互作用对材料力学响应的影响, 揭示第二相颗粒强化的微观机理. 本研究将第二相颗粒视为位错不可穿透的球形微粒, 采用位错绕过机制模拟颗粒与位错的交互作用过程. 通过调控滑移面相对于第二相颗粒中心的距离发现: 屈服应力和应变硬化率均随距离的增大而减小. 研究也发现Schmid因子越高的滑移系, 屈服应力越低, 后续应变硬化率越低. 多位错与颗粒交互作用的模拟发现, 同一滑移面中位错间的反应和不同滑移系中位错的交互作用可能是导致屈服应力和应变硬化率降低的关键.
关键词： 离散位错动力学;颗粒强化;取向效应;面心立方金属

Abstract
Particle reinforced copper matrix composites have high strength, elastic modulus, excellent electrical and thermal conductivity and wear resistance, they are widely used in aerospace, rail transit, equipment manufacturing and other fields. In particle reinforced composites, the dislocation movement is prevented by small dispersed particles in the alloy, thus effectively improving the mechanical properties of metallic materials and enhancing their service safety. In this paper, the three-dimensional discrete dislocation dynamics (3D-DDD) method was used to simulate the compression of particles reinforced copper matrix composites micro-pillar. The influence of the dislocation-precipitate interaction on the mechanical response of the material was analyzed to reveal the microscopic mechanism of the precipitation strengthening. In this study, the precipitate was regarded as a spherical particle with an impenetrable surface. The dislocation bypass mechanism was used to simulate the interaction between the precipitates and the dislocations. By changing the relative distance of dislocation slip plane against the center of spherical particle, it is found that when the distance is zero, the yield strength and the subsequent strain hardening rate are the highest. As the slip plane is far away from the center of spherical particle, the yield strength and the strain hardening rate decreases. The study also found that the higher the Schmid factor, the lower the yield strength and the lower strain hardening rate. In the simulation of multiple dislocations, it was found that the reaction of dislocations in same slip planes and the interaction of dislocations in different slip systems may be responsible for the reduction of the yield strength and the strain hardening rate.
Keywords：discrete dislocation dynamics;precipitation strengthening;orientation effect;face-centered cubic metal


PDF (3003KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
丁一凡, 魏德安, 陆宋江, 刘金铃, 康国政, 张旭. 颗粒增强复合材料压缩行为的位错动力学模拟¹⁾. 力学学报, 2021, 53(6): 1622-1633 DOI:10.6052/0459-1879-21-028
Ding Yifan, Wei Dean, Lu Songjiang, Liu Jinling, Kang Guozheng, Zhang Xu. DISCRETE DISLOCATION DYNAMICS SIMULATIONS FOR COMPRESSION OF PARTICLE REINFORCED COMPOSITES¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1622-1633 DOI:10.6052/0459-1879-21-028

引言

金属材料具有优异的综合力学性能和物理性能, 是重要的结构材料, 广泛应用于航空航天、轨道交通、装备制造等领域. 但是面对苛刻的服役条件, 金属的强度和韧性等往往难以满足要求. 强化金属的常见方式有固溶强化、晶界强化、加工硬化、第二相强化等^[1]. 其中第二相强化是通过合金中细小弥散的微粒阻碍位错运动, 进而有效提高金属材料的力学性能, 提高其服役安全. 当运动中的位错遇到第二相颗粒时受到阻碍作用, 或切过, 或绕过, 滑移变形才能继续进行. 这一过程要消耗额外的能量, 需要提高外加应力, 以至于造成强化^[2]. 根据已有研究, 第二相粒子越细小越弥散, 间距越小, 其强化效果越好.

颗粒增强铜基复合材料, 以其极高的强度和弹性模量, 优异的导电、导热性能还有良好的抗电弧侵蚀和抗磨损能力, 在国防、航天航空、汽车、电子工业等领域具有广泛的应用前景^[3-4]. 以电子电气行业为例, 颗粒增强铜基复合材料以优异的电性能被用作电导体和电连接件, 以优异的热性能被用作电子封装材料、半导体引线框等散热部件, 以优异的耐磨性能和导电性被用作电刷、点焊电极^[5-6]. 颗粒增强铜基复合材料的性能主要取决于增强相的类型、尺寸和体积分数. 常见的增强相主要有Al$_{2}$O$_{3}$, SiC, WC, TiB$_{2}$, TiC等. 增强体的选择是在不降低铜合金导电导热性能的前提下, 提高材料的力学性能, 使其满足更多应用场景.

近年来许多****对颗粒增强铜基复合材料开展了研究. Li等^[7-8]通过观察TiC$_{0.5}$颗粒增强AlCu合金的微结构, 分析拉伸和压缩实验, 研究了材料的强化机理. Schubert等^[9]和Ren等^[10]提出了改善金刚石颗粒与基体结合的新方法, 显著提升了材料的结合强度和热物理性能. Celebi等^[11]和Prosviryakov^[12]研究了SiC颗粒的尺寸和含量对铜基复合材料硬度、导电性和密度的影响. Kiani等^[13-14]采用原位实验获取了含单个Au颗粒的Cu纳米微柱的应力-应变行为, 并研究颗粒和微柱尺寸对屈服强度和应变硬化的影响.

颗粒增强复合材料强度的提升与第二相颗粒阻碍位错运动紧密相关. 离散位错动力学(discrete dislocation dynamics, DDD)通过直接考虑大量离散位错段的动态演化来模拟材料的塑性行为, 是研究颗粒增强复合材料强化机理及微结构尺度效应的重要手段^[15-17]. Huang等^[15]研究了镍基高温合金中位错与第二相颗粒的交互作用及其对材料力学性能的影响. Fan等^[18]基于分子动力学模拟获得了纳米尺度下位错-颗粒相互作用规律, 并将其引入离散位错动力学方法研究微观尺度下的颗粒强化效应. Xiang等^[19-20]在离散位错动力学框架中采用水平集方法研究了位错与球形颗粒之间的相互作用, 指出位错攀移和交滑移在沉淀强化中具有重要作用. 在对位错与球形颗粒相互作用更进一步的研究中, Queyreau等^[21]在离散位错动力学程序中实现了Orowan强化机制和林硬化机制的叠加作用; Záleák 等^[22]模拟了高温下位错在颗粒增强材料中的运动过程; Monnet等^[23-24]和Shin等^[25]考虑了位错滑移和交滑移的晶体学特征; Takahashi等^[26-27]考虑了基体与颗粒因弹性模量失配引起的镜像力的影响. 此外, Santos-Güemes等^[28-29]建立了AlCu合金中第二相强化的多尺度模型, 并能与实验结果互相验证.

但是, 以上工作并未对滑移面相对于第二相颗粒中心的距离、滑移系方位等问题进行详细研究. 基于以上考虑, 本文采用三维离散位错动力学(three-dimensional discrete dislocation dynamics, 3D-DDD)方法, 对微尺度面心立方(face-centered cubic, FCC)颗粒增强铜基复合材料中位错与第二相颗粒的交互作用进行模拟, 并分析了滑移面相对于第二相颗粒中心的距离、滑移系取向方位等因素对第二相颗粒强化效果的影响, 揭示第二相强化的微观机理.

1 三维离散位错动力学方法

晶体材料的塑性行为主要是由大量位错的运动演化而引起^[30]. DDD方法基于位错弹性理论, 通过求解弹性体中位错线的运动方程来计算塑性应变^[31-35]. 其基本思路为首先将位错线离散为更小的位错段, 然后计算位错段节点受力, 再通过运动方程计算位错段节点运动速度、时间步积分更新位错的位置. 当位错之间距离很近时, 还要处理位错之间的反应、执行拓扑操作. 最后更新外载条件, 计算位错产生的塑性应变^[36]. 上述过程不断循环, 直到加载完成.

本文模拟使用的是由美国劳伦斯国家实验室开发的能进行应变硬化模拟的大尺度离散位错动力学模拟平台ParaDiS^[37].

1.1 节点力的计算

离散位错动力学模拟首先将位错线离散为具有一定长度的位错段, 每个位错段拥有两个节点. 节点$i$的受力$ F_{i}$由系统中的储能函数$E$对节点位置的负偏导得到^[37]

(1)${ F}_{i} \equiv -\frac{\partial E\left( {\left\{ {{ X}_{j} , { b}_{jk} , { T}^s} \right\}} \right)}{\partial { X}_{i} }$
式中, $ X_{i}$和$ X_{j}$分别为节点$i$和$j$的空间坐标, $ b_{jk}$为位错段$ l_{jk}$的Burgers矢量, $ T^s$为表面施加的载荷. 储能函数$E$是与节点坐标、位错段Burgers矢量和模型表面载荷相关的函数. 通常将系统总储能函数分为与位错芯局部原子畸变($E^c$)和长程弹性变形相关($E^el$)的两部分, 这样就能用连续介质弹性理论进行描述^[37]

(2)$E=E^c+E^el$
相应地, 作用在节点$i$上的力分为${ F}_{i}^c$和${ F}_{i}^el$两部分, 它们分别由位错芯能和弹性能的空间偏导数得到^[37]

(3)${ F}_{i} ={ F}_{i}^c +{ F}_{i}^el$
离散位错网的位错芯总能量可以表示为^[37]

(4)$E^c=\sum_{i=1}^{n-1} {\sum_{j=i+1}^n {\varepsilon ^c} } \left( {{ b}_{ij} , { t}_{ij} } \right)\left\| {{ l}_{ij} } \right\|$
式中, $|| l_{ij}||$为位错段$ l_{ij}$的长度, $ t_{ij}= l_{ij}/|| l_{ij}||$ 是位错段方向, $\varepsilon^c$ ($ b_{ij}, t_{ij})$描述了单位长度位错段的位错芯能量随位错Burgers矢量和位错段方向的变化, 可通过原子模拟得到. 对式(4)求空间偏导数, 可求得与位错芯能量相关的节点力^[37]

(5)${ F}_{i}^c =-\frac{\partial E^c}{\partial { X}_{i} }=\sum_j {{ f }_{ij}^c }$
其中${ f }_{ij}^c $是与节点$i$相连的位错段$ l_{ij}$对节点力的贡献

(6)${ f }_{ij}^c =\varepsilon^c\left( {{ b}_{ij}, { t}_{ij} } \right){ t}_{ij} +\left( {{ I}_{2} -{ t}_{ij} \otimes { t}_{ij} } \right)\cdot \frac{\partial \varepsilon^c\left({{ b}_{ij} , { t}_{ij} } \right)}{\partial { t}_{ij} }$
式中, $ I_{2}$是二阶单位张量, 第一项是使位错段收缩的线张力, 第二项是旋转位错段的方向以降低位错芯能量的力矩.

由于弹性能, 作用在位错节点上的力${ F}_{i}^el $为^[37]

(7)${ F}_{i}^el =\sum_j {{ f }_{ij}^el }$
式中, ${ f }_{ij}^el$是所有与节点$i$相连的节点$j$对节点$i$产生的弹性相互作用力. 将虚功原理应用于节点$i$的运动, 得到${ f }_{ij}^el$的积分表达式^[37-38]

(8)${ f }_{ij}^el \equiv \left\| {{ l}_{ij} } \right\|\int_l^ N (-l){ f }_{ij}^{pk}dl$
式中, $N$为形函数$N(l)={1}/{2}+l$, 其中$-{1}/{2}\leqslant l\leqslant {1}/{2}$, ${ f }_{ij}^{pk} $是位错段$ l_{ij}$受到的Peach-Koehler力, 它由外力产生的应力场 $\sigma_ext$、位错段自身产生的应力场 $\sigma_s$以及模型中其他所有位错段产生的应力场$\sum_{k=1}^{n-1}\sum_{l=k+1}^n { \sigma }_{ij}^{kl} $叠加而成^[37-38]

(9)${ f }_{ij}^{pk} ={\left[ {\left( {{ \sigma }_{ext} +{ \sigma }_{s} +\sum_{k=1}^{n-1} \sum_{l=k+1}^n {{ \sigma }_{ij}^{kl} } } \right)} \cdot { b}_{ij} \right]}\times { t}_{ij}, [k, l]\ne [i, j] or [j, i]$

1.2 运动方程

开展DDD模拟时, 当设置的积分时间步长足够大时, 位错段运动的惯性可以忽略, 运动方程简化为

(10)${ F}_{i} ={B} { v}_{i}$
式中$B$为阻尼系数, 代入之前计算的节点力$ F_{i}$便可计算得到节点运动速度$ v_{i}$. 而后通过时间步的积分得到位错节点下一时刻的位置.

1.3 位错与第二相颗粒交互作用的拓扑处理

根据位错理论, 位错与第二相颗粒的交互作用可分为不同的类别. 根据第二相颗粒的强度可以将其分为可变形第二相颗粒和不可变形第二相颗粒. Kelly和Nicholson^[39]将位错和颗粒之间的两种基本相互作用形式分为"切过机制"和"绕过机制", 它们会带来不同的临界分切应力提高.

对于可变形第二相颗粒, 颗粒对位错的阻碍作用较小, 位错可以直接切过第二相颗粒, 使颗粒被切成上下两部分, 并在切割面上产生台阶, 颗粒与基体间的界面面积增大, 从而使界面能增大, 需要额外做功. 并且, 由于第二相颗粒与基体结构不同, 位错扫过颗粒必然引起局部原子错排, 这也会增大位错运动的阻力, 从而使金属强化.

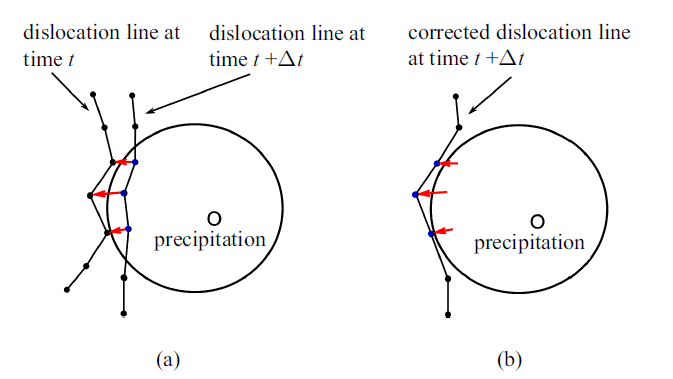
对于不可变形第二相颗粒, 基体与第二相颗粒的界面上存在点阵畸变和应力场, 成为位错运动的障碍. 滑动位错遇到这种障碍变得弯曲, 切应力随之增大, 位错弯曲程度加剧, 并逐渐成为环状. 由于绕过颗粒的位错线方向相反, 它们相遇后将湮灭断开, 形成包围小颗粒的位错环和越过颗粒继续向前滑动的位错. 随着位错不断绕过第二相颗粒, 颗粒周围的位错环数量逐渐增加, 对后来的位错造成更大的阻力, 这一机制也称为Orowan机制^[39-40]. 本研究中将第二相颗粒视为位错不可穿透的球形微粒, 采用位错绕过机制模拟第二相颗粒与位错的交互作用过程. 通常第二相颗粒对位错的作用力包含两部分. 一是镜像应力场, 当第二相和基体弹性模量接近时, 可以忽略^[13-14]. 二是由于基体和第二相晶格不匹配引起的失配应力场, 它通常只在界面附近很小的区域内存在并快速衰减, 并会与第二相界面位错网的应力场相互抵消^[15]. 因此, 离散位错动力学研究中, 许多****采用忽略第二相应力场的简化方式^{[21-22, 24, 41]}. 为简化计算分析, 本文也不考虑第二相引起的应力畸变场, 而仅在拓扑构型上考虑位错与位错不可穿透颗粒的相互作用过程^{[21, 23-24]}. 在DDD程序中, 位错节点在位移积分中未考虑第二相对其阻碍作用, 因此位错节点会进入第二相中, 如图1(a)所示. 在位移积分后, 考虑了对位错节点位移的修正, 将本不该进入第二相的位错节点修正到其上一时间步所在位置, 如图1(b)所示. 这种处理方法的好处在于可以避免(1)第二相颗粒太小导致节点退回到颗粒前表面或后表面的判断困难;(2)位错段中点可能进入第二相颗粒; (3)退回的节点可能不在原来的滑移面上.

图1

新窗口打开|下载原图ZIP|生成PPT
图1离散位错动力学模拟框架中位错与第二相颗粒交互作用过程: (a)位错节点进入第二相颗粒; (b)将进入第二相颗粒的位错节点退回到它上一步所在位置

Fig.1Interactions between the dislocation and the precipitation in the discrete dislocation dynamics simulation framework: (a) Discrete dislocation nodes enter the second phase; (b) pull them back to the previous step

2 计算模型

本文为研究滑移面相对于颗粒中心距离、滑移系方位等因素对位错与第二相颗粒交互作用的影响. 建立边长为512 nm (2000 $b$)的单晶铜模型, 模型中心(坐标原点)处设置一个半径为76.8 nm (300 $b$)的球形第二相颗粒. 模型的$X$, $Y$, $Z$轴分别对应晶向$[1\bar{{1}}0]$, [111], $[\bar{1} \bar{1}2]$. 加载方向沿$Z$轴$[\bar{{1}}\bar{{1}}2]$.

应变率对材料的力学行为有重要影响. 在现有的计算资源条件下, 大规模DDD模拟的应变率通常大于1000 s$^{-1}$.

由于DDD框架特点在于生动反映位错间的相互作用和位错运动过程, 基于位错运动速度和模型几何尺寸的考虑, DDD模拟的时间步在纳秒量级. 位错间交互作用和运动演化计算耗时, DDD模拟材料变形的物理时间受限, 只能通过增大应变率(通常大于1000 s$^{-1}$)来提高模拟效率, 且大多模拟局限于0.5% $\sim$ 2%的小应变范围. 根据Fan等^[42]、郭祥如等^[43]的研究, 应变率在1000 $\sim$ 10 000 s$^{-1}$之间不会对DDD模拟的屈服强度结果产生很大影响. 基于DDD模拟本身的特点, 并参考大多数DDD模拟的加载率设置, 本研究采用恒应变率$\dot{{\varepsilon }}=5000$ s$^{-1}$加载. 模型外界面为自由表面, 当位错到达自由表面时即会逃逸.

在DDD框架中, 本文具体开展下述研究:

(1)探究滑移面相对于第二相颗粒中心距离的影响. 分别在距离第二相颗粒中心0 nm, 12.8 nm, 25.6 nm, 38.4 nm, 51.2 nm, 64 nm, 76.8 nm的7个平行滑移面上布置单个位错源.

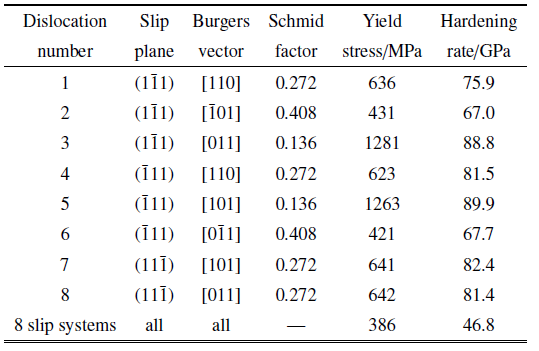
(2)探究第二相颗粒对不同滑移系取向位错的影响. FCC晶体有4个滑移面共12个滑移系, 由于加载轴$[\bar{{1}}\bar{{1}}2]$平行于滑移面$(111)$, 且垂直于滑移方向$[\bar{{1}}10]$, 因此只有8个滑移系的Schmid因子不为0.分别在此8个可动滑移系(表1)中布置单个位错源, 保证第二相颗粒中心在滑移面上. 为避免位错源类型的影响, 设定初始位错源均为纯螺型Frank-Read (F-R)位错源. 位错源距离第二相颗粒中心500$b$.

Table 1
表1
表1计算模型的基本材料参数
Table 1Basic material parameters of the model

新窗口打开|下载CSV

(3)探究多滑移系中位错与第二相颗粒的交互作用, 将(2)中8个滑移系的位错源合到一个模型中进行模拟.

上述研究中位错源类型为两端钉扎的Frank-Read (F-R)型位错源, 位错线方向垂直于位错源中点与第二相颗粒中心的连线, 位错源长度均为256 nm (1000 $b)$. 情形(1)和(2)中, 每个模型初始位错源数量为1, 初始位错密度为$1.91\times 10^{12}$ m$^{-2}$; 情形(3)初始位错密度为$1.54\times 10^{13}$ m$^{-2}$.

在目前的离散位错动力学模拟框架中, 通常忽略材料的各向异性, 采用各向同性处理. FCC结构颗粒增强铜基复合材料微柱压缩模拟的材料参数见表1.

3 结果与讨论

3.1 滑移面相对于第二相颗粒中心距离的影响

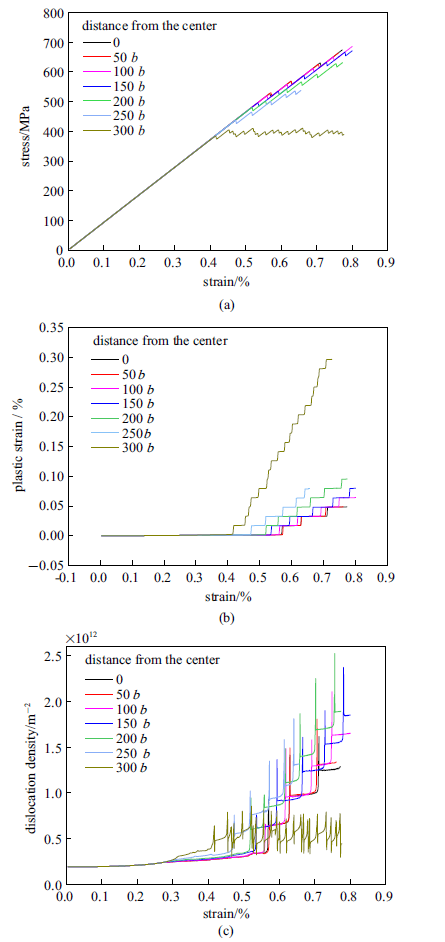
为了分析滑移面相对于第二相颗粒中心距离对材料力学响应的影响, 在距第二相颗粒中心0 $\sim$ 300$b$ (0 $\sim$ 76.8 nm)的多个平行滑移面上布置位错, 分别为间距50$b$(12.8 nm)的7个滑移面. 每种工况模拟得到的应力-应变曲线、塑性应变和位错密度随应变的演化曲线如图2所示, 表2是计算得到的屈服应力和后续阶段的应变硬化率. 其中屈服应力定义为位错源首次开动时的应力, 应变硬化率定义为屈服点后应力-应变($\sigma -\varepsilon )$曲线经线性拟合后的斜率($\varTheta =d\sigma /d\varepsilon$ ).

图2

新窗口打开|下载原图ZIP|生成PPT
图2滑移面相对于第二相颗粒中心不同距离模型的(a)应力-应变曲线; (b)塑性应变-应变曲线; (c)位错密度-应变曲线

Fig.2Results of the cases of different distances from the particle center to the slip plane: (a) Stress-strain curves; (b) plastic strain-strain curves; (c) dislocation density-strain curves



Table 2
表2
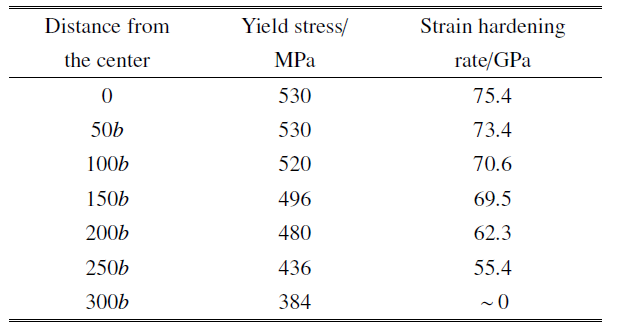
表2不同滑移面模型的屈服应力与应变硬化率
Table 2Yield stress and strain hardening rate of the different relative distance slip planes models

新窗口打开|下载CSV

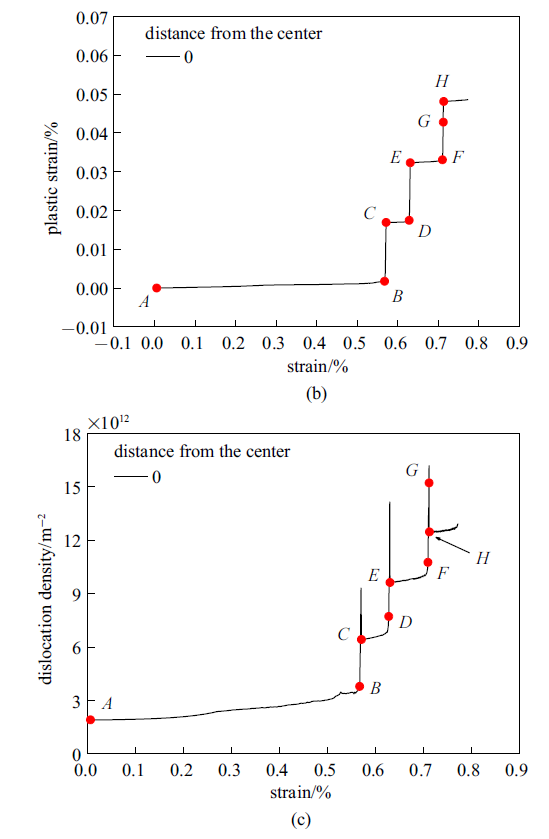
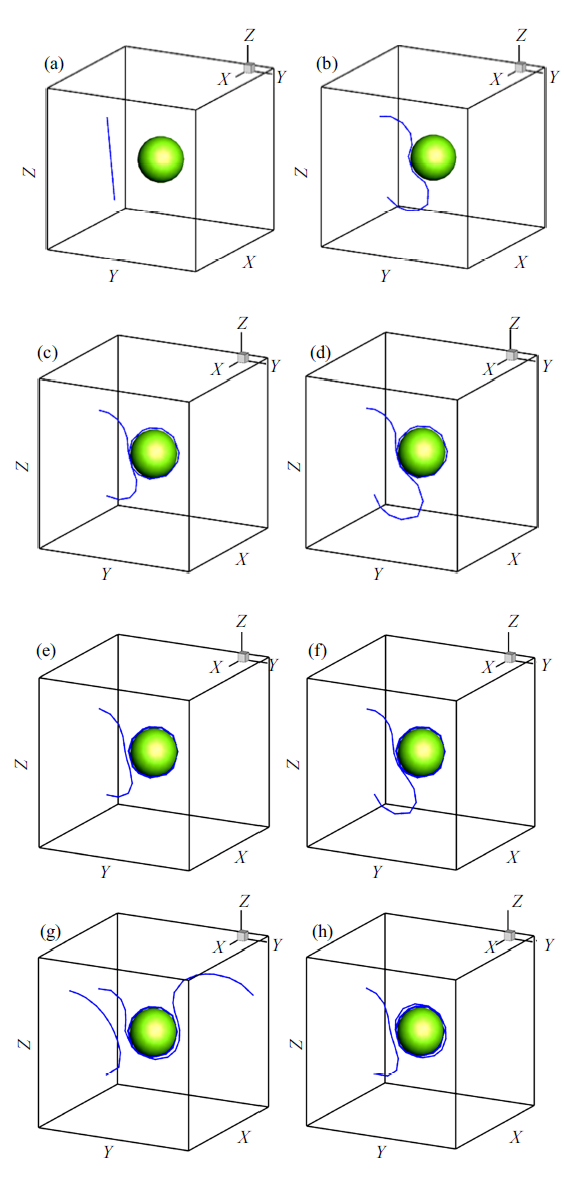
先分析滑移面相对于第二相颗粒中心距离为0的情形, 图3为模拟得到的应力-应变曲线、塑性应变-应变曲线和位错密度演化曲线, 图3中各曲线的$A$ $\sim$ $H$点的位错结构分别对应图4(a) $\sim\!$图4(h). 变形前计算模型的初始位错结构见图4(a), 对应图3中$A$点状态. 在变形到达$B$点之前, F-R位错源逐渐弓出, 在$B$点时位错包裹了部分第二相颗粒, 此过程只发生准弹性变形. 随着应变继续增大至$C$点, F-R位错源继续包裹第二相颗粒, 直到两个符号相反的位错相遇, 产生位错湮灭, 形成包围第二相颗粒的位错环和一段继续滑移的位错. 继续滑移的位错不受阻碍并在表面湮灭, 从而发生从$B$-$C$的应力陡降. 随后, 位错源继续开动对应着应力重新升高($C$-$D$), 直至下一次生成包围第二相颗粒的位错环后、位错继续前行导致应力再次小幅下降($D$-$E$). 位错每一次绕过第二相颗粒时, 应力水平都在不断升高, 这是因为包围第二相颗粒的位错环数量不断增加, 位错环的应力场使得位错源激活所需的临界分应力越来越大, 运动的位错在到达第二相颗粒前受到的阻碍作用更大, 材料产生应变硬化.

图3

新窗口打开|下载原图ZIP|生成PPT
图3位错源滑移面相对于第二相颗粒中心距离为的模拟结果: (a)应力-应变曲线; (b)塑性应变-应变曲线; (c)位错密度-应变曲线. $A$ $\sim$ $H$为特殊状态点

Fig.3Results of the cases of the distance from the particle center to the slip plane is zero: (a) Stress-strain curves; (b) plastic strain-strain curves and (c) dislocation density-strain curves. $A$ $\sim$ $H$ are the points of specific moment

图4

新窗口打开|下载原图ZIP|生成PPT
图4位错源滑移面相对于第二相颗粒中心距离为模型特定时刻的位错结构: (a) $\sim$ (h)分别为图3中各曲线$A$ $\sim$ $H$点对应的位错结构

Fig.4Dislocation structures of particle reinforced copper with dislocation source located at the slip plane with zero distance from the precipitate center. (a) $\sim$ (h) are the dislocation structures corresponding to points $A$ $\sim$ $H$ of each curve in Fig.3



通过对比不同模拟之间的临界应力与应变硬化率(见表2)可以发现, 随着滑移面相对第二相颗粒中心距离从0增大至250$b$, 屈服强度从530 MPa降至436 MPa, 应变硬化率从75.4 GPa降至55.4 GPa. 这是因为, 产生包围第二相颗粒的位错环有效半径越大, 位错源越靠近位错环, 它们之间的相互作用力越大, 使得位错源难以开动, 背应力越大, 反映出应变硬化率增大. 值得注意的是, 当滑移面与第二相颗粒中心相对距离为300$b$时, 滑移面与第二相颗粒相切, 此时位错源开动过程中没有生成位错环, 所以模拟表现出理想塑性.

3.2 滑移面相对于第二相颗粒取向方位的影响

保持单晶模型大小与参数一致, 模拟FCC中12个滑移系的位错源与第二相颗粒的相互作用. 12个滑移系的Schmid因子^[38]如表3所示. 由于Schmid因子为0时滑移系无法开动, 故分别建立8种Schmid因子不为0的滑移系模型, 每个模型中只在当前滑移系设置一个位错源进行模拟, 如图5 $\sim\!$图7所示.

Table 3
表3
表3各个滑移系的屈服应力及应变硬化率
Table 3Yield stress and strain hardening rate of each slip system

新窗口打开|下载CSV

图5

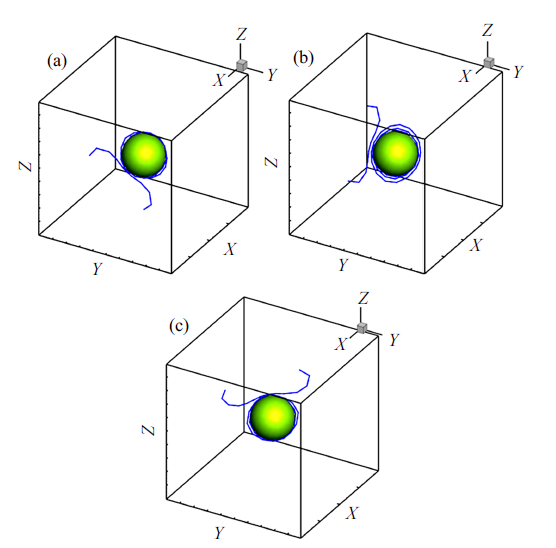
新窗口打开|下载原图ZIP|生成PPT
图5$(1\bar{{1}}1)$面各位错在模拟最终步的结构图: (a)滑移方向[110];(b)滑移方向$[\bar{{1}}01]$; (c)滑移方向[011]

Fig.5Dislocation structure diagram of $(1\bar{{1}}1)$ plane [110] (a); $[\bar{{1}}01]$ (b) and [011] (c) slip system at the final step of the simulation

图6

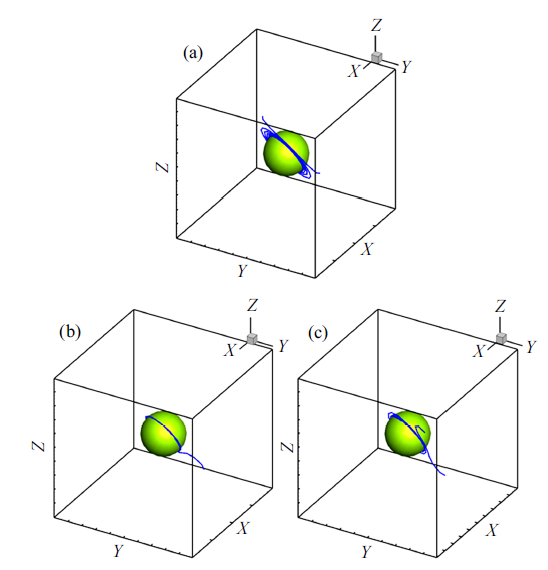
新窗口打开|下载原图ZIP|生成PPT
图6$(1\bar{{1}}\bar{{1}})$面各位错在模拟最终步的结构图: (a)滑移方向[110];(b)滑移方向$[\bar{{1}}0\bar{{1}}]$; (c)滑移方向$[0\bar{{1}}1]$

Fig.6Dislocation structure diagram of $(1\bar{{1}}\bar{{1}})$ plane [110] (a); $[\bar{{1}}0\bar{{1}}]$ (b) and $[0\bar{{1}}1]$ (c) slip system at the final step of the simulation

图7

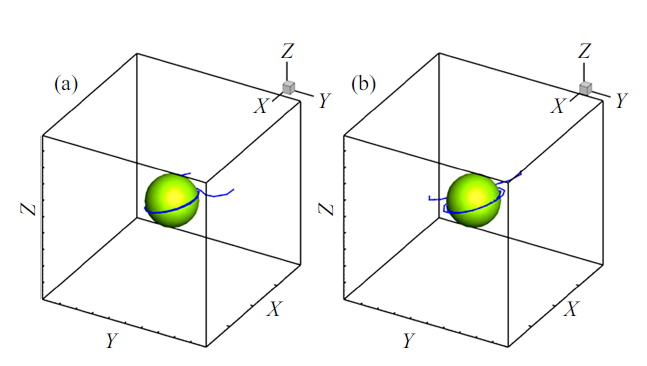新窗口打开|下载原图ZIP|生成PPT
图7$(11\bar{{1}})$面各位错在模拟最终步的结构图: (a)滑移方向$[\bar{{1}}0\bar{{1}}]$; (b)滑移方向$[011]$

Fig.7Dislocation structure diagram of $(11\bar{{1}})$ plane $[\bar{{1}}0\bar{{1}}]$ (a); $[011]$ (b) slip system at the final step of the simulation



图8 $\sim\!$图10各模型的应力-应变曲线、塑性应变-应变曲线和位错密度-应变曲线图, 计算得到的各模型屈服应力及应变硬化率见表3.因为第二相颗粒的存在, 所有模型进入塑性后的应力都会不断增加持续强化. 可以发现Schmid因子最大(0.408)的滑移系($(1\bar{{1}}1)[\bar{{1}}01]$ 和 $(\bar{{1}}11)[0\bar{{1}}1]$), 最早进入塑性阶段, 屈服强度最低(约425 MPa), 并且进入塑性阶段后的应变硬化率最低(约67 GPa), 即位错源越容易开动和增殖, 因此材料更容易发生位错滑移导致塑性变形. 而Schmid因子较小(0.272)的滑移系($(1\bar{{1}}1)$[110] 和$(\bar{{1}}11)$ [110]、$(11\bar{{1}})$ [101] 和 $(11\bar{{1}})$ [011]), 不仅屈服强度增大(约630 MPa), 而且后续的应变硬化率也增大(约80 GPa), 此滑移系上的位错较难开动. Schmid因子最小(0.136)的两个滑移系($(1\bar{{1}}1)$ [011] 和 $(\bar{{1}}11)$ [101]), 位错源在应变达到1.35%左右才开动, 屈服应力很高(约1270 MPa), 应变硬化率最高(约90 GPa), 与模拟结果的弹性模量近似相同, 此滑移系上的位错最难开动, 可以形象地称之为硬滑移系.

图8

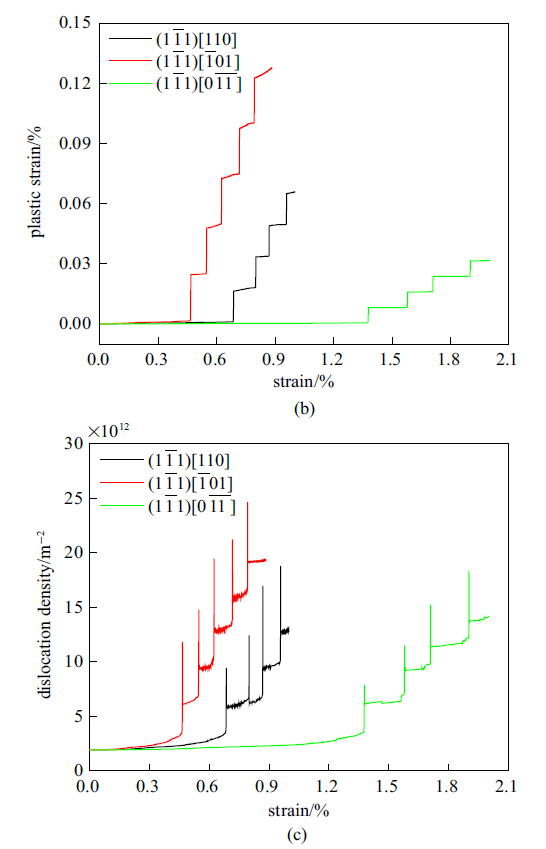新窗口打开|下载原图ZIP|生成PPT
图8$(1\bar{{1}}1)$面位错源的(a)应力-应变曲线, (b)塑性应变-应变曲线, (c)位错密度-应变曲线

Fig.8Results of the dislocation sources on $(1\bar{{1}}1)$ plane (a) stress-strain curves, (b) plastic strain-strain curves and (c) dislocation density-strain curves

图9

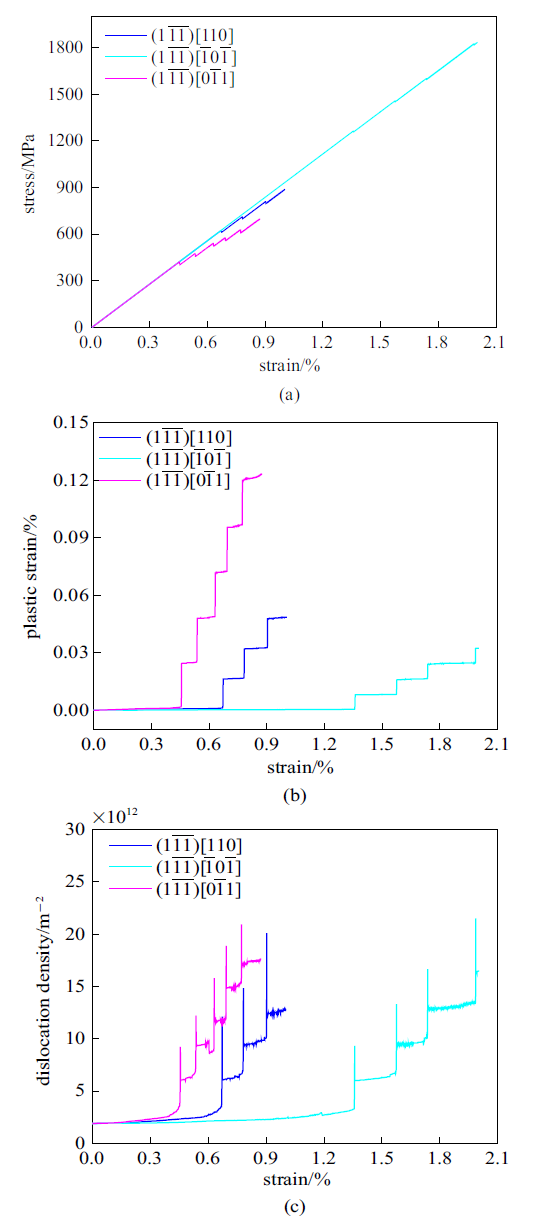新窗口打开|下载原图ZIP|生成PPT
图9$(\bar{{1}}11)$面位错源的(a)应力-应变曲线, (b)塑性应变-应变曲线, (c)位错密度-应变曲线

Fig.9Results of the dislocation sources on $(\bar{{1}}11)$ plane (a) stress-strain curves, (b) plastic strain-strain curves and (c) dislocation density-strain curves

图10

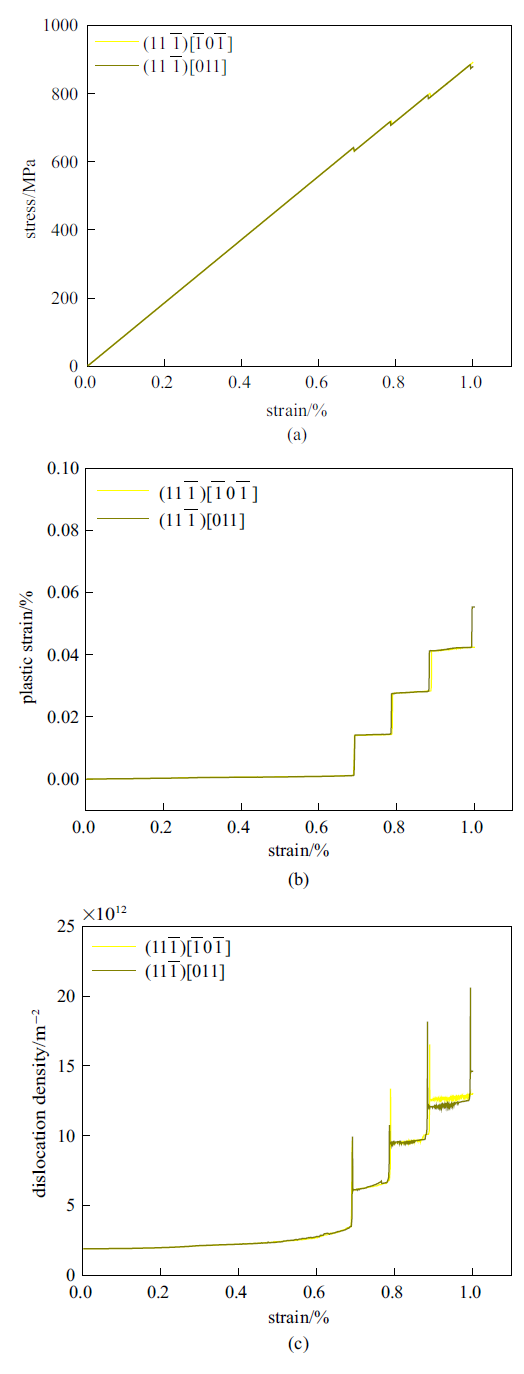新窗口打开|下载原图ZIP|生成PPT
图10$(11\bar{{1}})$面位错源的(a)应力-应变曲线, (b)塑性应变-应变曲线, (c)位错密度-应变曲线

Fig.10Results of the dislocation sources on $(11\bar{{1}})$ plane (a) stress-strain curves, (b) plastic strain-strain curves and (c) dislocation density-strain curves

3.3 滑移系交互作用的影响

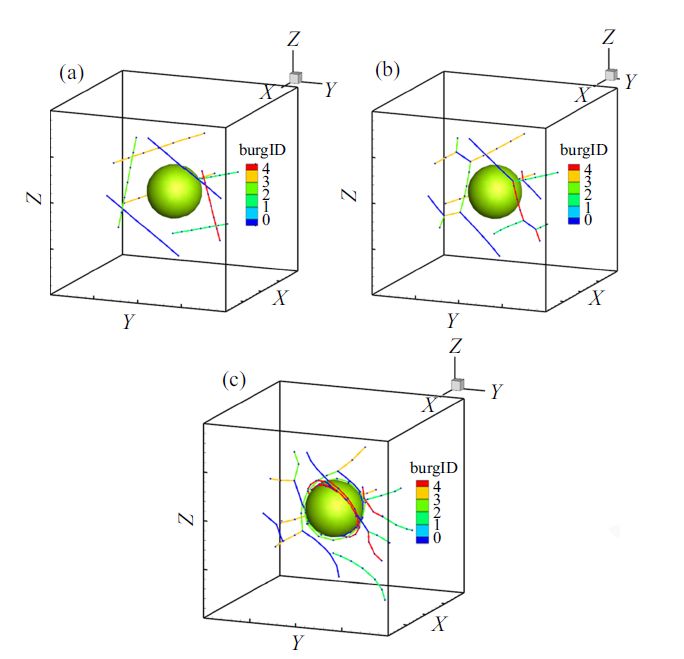
为探究不同滑移系位错交互作用的影响, 将3.2节中8个不同滑移系的位错放入同一模型进行一次模拟, 如图11所示, Burgers矢量不同的位错以不同颜色区分, 各个位错滑移面都交于第二相颗粒中心.

图11

新窗口打开|下载原图ZIP|生成PPT
图11应变为0 (a), 0.005% (b), 和0.7% (c)时8个滑移系均布置位错的微结构演化图

Fig.11Microstructure evolution diagram of 8 slip systems with dislocation arrangement at strains of (a) 0, (b) 0.005%, (c) 0.7%



图12是8滑移系位错合一模型和各滑移系单个位错模型的应力-应变曲线、塑性应变-应变曲线对比图, 计算得到的屈服应力及应变硬化率见表3, 可见, Schmid因子相同的滑移系结果曲线相似, 它们各自的屈服应力和应变硬化率也相近. 曲线有略微差异是因为Schmid因子相同的两个滑移系中位错的初始构型不完全相同, 所以位错受到由自由表面产生的镜像力不同.

图12

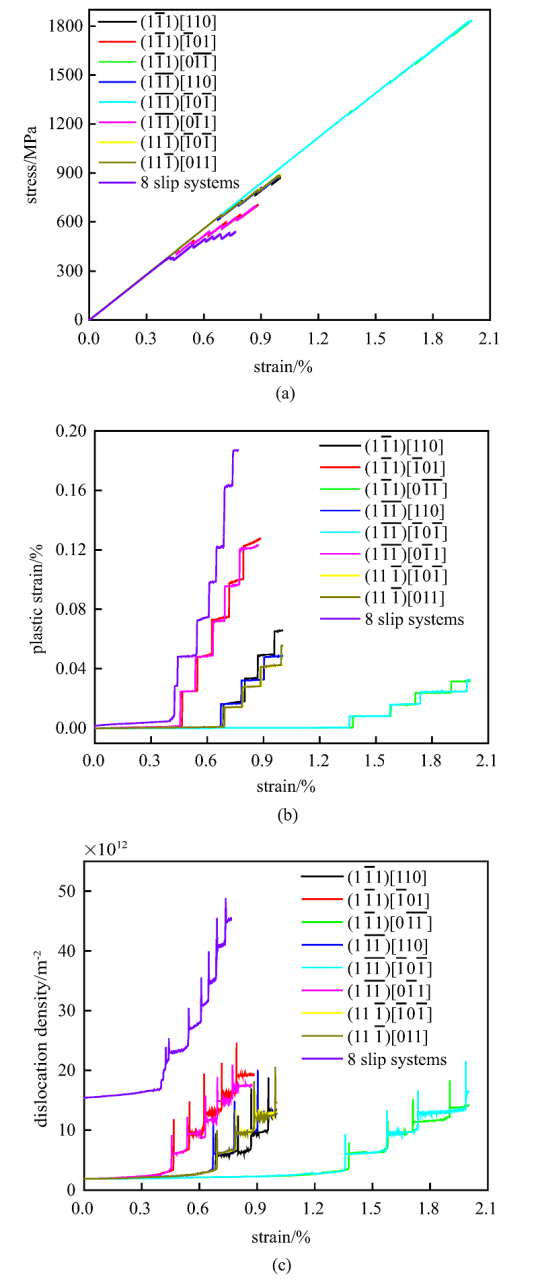新窗口打开|下载原图ZIP|生成PPT
图128位错合一模型及8个单位错模型的(a)应力-应变曲线图, (b)塑性应变-应变曲线, (c)位错密度-应变曲线图

Fig.12Results of the 8 slip systems and each slip system model (a) stress-strain curves, (b) plastic strain-strain curves and (c) dislocation density-strain curves



相比单滑移系模型, 发现8位错合一模型的屈服应力更低(约386 MPa), 且应变硬化率最低(47 GPa), 由模拟开始阶段的位错演化(图11(b))可见, 同一滑移面的位错源之间发生反应生成新的位错结构, 导致材料的屈服应力下降. 且屈服后, 随着应力水平的增加, 多个位错源共同开动, 提供比单个位错源开动更多的塑性变形, 导致硬化率降低. 也就是说, 位错源密度越高, 硬化率越低. 观察位错演化图可知, 8位错合一模型开动的滑移系亦为Schmid因子最大(0.408)的滑移系($(\bar{{1}}11)[0\bar{{1}}1]$和$(1\bar{{1}}1)[\bar{{1}}01]$).

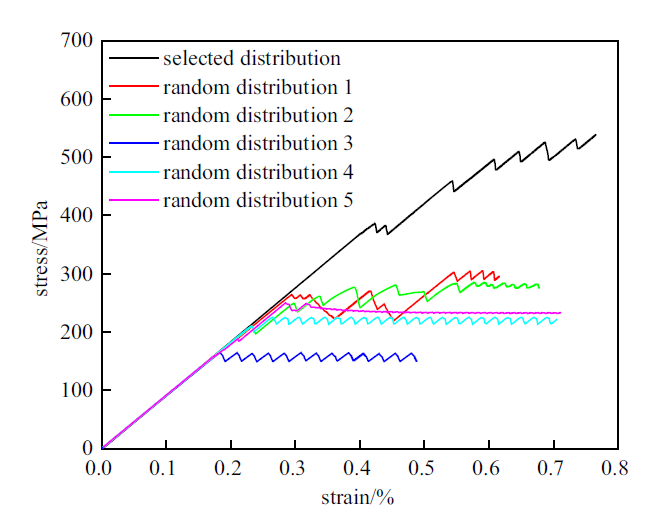
考虑到实际材料中, 位错源的分布是随机的, 为了探究此随机性对研究结果的影响, 将8个滑移系中位错源的位置随机分布进行了5次模拟, 结果如图13所示, 黑色曲线是所有滑移系都过颗粒中心的结果, 彩色曲线是将8个位错源位置随机分布得到的结果, 对比可以发现位错源随机分布的模型在塑性达到一定值后应力总能在一定值附近趋于稳定, 即体现出了理想塑性. 通过观察位错演化图, 发现由于第二相颗粒的大小限制, 不能保证位错源在开动过程中均和第二相颗粒产生相互作用生成位错环. 对于理想塑性情形应力达到平稳后, 继续开动的位错源都是与第二相颗粒不相交的滑移面上的位错源.

图13

新窗口打开|下载原图ZIP|生成PPT
图138位错源滑移面均固定且过第二相颗粒中心与滑移面完全随机时的应力-应变曲线

Fig.13Stress-strain curves of 8 dislocation sources when the slip planes are all fixed across the precipitate center or completely random



本文仅针对位错与单一颗粒的交互作用开展了相关的模拟研究, 而位错与多颗粒的相互作用值得进一步探索. 位错与多颗粒交互作用受到颗粒尺寸, 颗粒间距, 颗粒体积分数等因素的影响, 可调控的微结构参数较多, 机理比较复杂. 通过DDD模拟可深入揭示位错与多颗粒交互作用机理及其对塑性行为的影响. 此外, 本文为简化计算分析, 暂未考虑第二相引起的应力畸变场. 但是, 畸变应力场较大时, 将会对位错的运动产生影响, 如使位错攀移、增加位错交滑移发生的概率等. 在第二相应力场的影响下, 第二相周围也会生成新的复杂位错结构, 从而引发新的位错运动机制. 因此, 在DDD模拟中有必要考虑第二相畸变应力场, 进而更全面地揭示第二相微结构对位错行为的调控和对材料力学行为的影响.

4 结论

(1)单一位错源与第二相颗粒交互作用的模拟可以看出滑移面距离第二相颗粒中心越近, 屈服应力越高, 后续应变硬化率更高. 这是因为相对距离越小, 生成的位错环越大, 位错源越靠近位错环, 它们之间的相互作用力越大, 使得位错源难以开动, 背应力越大, 导致较高的屈服应力和应变硬化率.

(2)根据不同滑移系位错源与第二相颗粒作用的模拟发现, Schmid因子越高的滑移系, 进入塑性阶段的屈服应力越低, 后续应变硬化率越低, Schmid因子相同的滑移系位错运动状态相似.

(3)多位错与第二相颗粒交互作用的模拟发现, 相比于单位错模型, 多位错合一模型的屈服应力和应变硬化率均最低, 同一滑移面中位错源反应生成新的位错结构和不同滑移系位错的交互作用可能是导致屈服应力和应变硬化率降低的关键.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Lu K, Lu L, Suresh S. Strengthening materials by engineering coherent internal boundaries at the nanoscale
Science, 2009, 324(5925): 349-352
DOIURL [本文引用: 1]

[2] 吕昭平, 蒋虽合, 何骏阳 等. 先进金属材料的第二相强化
金属学报, 2016, 52(10): 1183-1198
[本文引用: 1]

(Lü Zhaoping, Jiang Suihe, He Junyang, et al. Second phase strengthening in advanced metal materials
Acta Metallurgica Sinica, 2016, 52(10): 1183-1198 (in Chinese))
[本文引用: 1]

[3] Gao X, Yue HY, Guo EJ, et al. Mechanical properties and thermal conductivity of graphene reinforced copper matrix composites
Powder Technology, 2016, 301: 601-607
DOIURL [本文引用: 1]

[4] Qu XH, Zhang L, Wu M, et al. Review of metal matrix composites with high thermal conductivity for thermal management applications
Progress in Natural Science, 2011, 21(3): 189-197
DOIURL [本文引用: 1]

[5] Li ZD, Lin CG, Cui S. Development of research and application of copper alloys with high strength and high conductivity
Advanced Materials Research, 2014, 1053: 61-68
DOIURL [本文引用: 1]

[41] Shin CS, Fivel MC, Verdier M, et al. Dislocation dynamics simulations of fatigue of precipitation-hardened materials
Materials Science and Engineering, 2005, 400: 166-169
[本文引用: 1]

[42] Fan HD, Wang Q, El-Awady JA, et al. Strain rate dependency of dislocation plasticity
Nature Communications, 2021, 12(1): 1845
DOIURL [本文引用: 1]

[6] Tjong SC. Recent progress in the development and properties of novel metal matrix nanocomposites reinforced with carbon nanotubes and graphene nanosheets
Materials Science & Engineering R-Reports, 2013, 74(10): 281-350
[本文引用: 1]

[7] Li M Q, Zhai H X, Huang Z Y, et al. Microstructure and mechanical properties of TiC0.5 reinforced copper matrix composites
Materials Science and Engineering, 2013, 588(dec. 20): 335-339
[本文引用: 1]

[43] 郭祥如, 孙朝阳, 王春晖 等. 基于三维离散位错动力学的fcc结构单晶压缩应变率效应研究
金属学报, 2018, 54(9): 1322-1332
[本文引用: 1]

(Guo Xiangru, Sun Chaoyang, Wang Chunhui, et al. Investigation of strain rate effect by three-dimensional discrete dislocation dynamics for fcc single crystal during compression process
Acta Metallurgica Sinica, 2018, 54(9): 1322-1332 (in Chinese))
[本文引用: 1]

[8] Li MQ, Zhai HX, Huang ZY, et al. Tensile behavior and strengthening mechanism in ultrafine TiC0.5 particle reinforced Cu-Al matrix composites
Journal of Alloys and Compounds, 2015, 628: 186-194
DOIURL [本文引用: 1]

[9] Schubert T, Ciupiński ?, Zieliński W, et al. Interfacial characterization of Cu/diamond composites prepared by powder metallurgy for heat sink applications
Scripta Mater, 2008, 58(4): 263-266
DOIURL [本文引用: 1]

[10] Ren SB, Shen XY, Guo CY, et al. Effect of coating on the microstructure and thermal conductivities of diamond-Cu composites prepared by powder metallurgy
Composites Science and Technology, 2011, 71(13): 1550-1555
DOIURL [本文引用: 1]

[11] Celebi Efe G, Zeytin S, Bindal C. The effect of SiC particle size on the properties of Cu-SiC composites
Materials and Design, 2012, 36(Apr. ): 633-639
DOIURL [本文引用: 1]

[12] Prosviryakov AS. SiC content effect on the properties of Cu-SiC composites produced by mechanical alloying
Journal of Alloys and Compounds, 2015, 632: 707-710
DOIURL [本文引用: 1]

[13] Kiani MT, Murayama M, Gu XW. Deformation of a nanocube with a single incoherent precipitate: Role of precipitate size and dislocation looping
Philosophical Magazine, 2020, 100(13): 1749-1770
DOIURL [本文引用: 2]

[14] Kiani MT, Wang Y, Bertin N, et al. Strengthening mechanism of a single precipitate in a metallic nanocube
Nano Letter, 2019, 19(1): 255-260
DOIURL [本文引用: 2]

[15] Huang MS, Zhao LG, Tong J. Discrete dislocation dynamics modelling of mechanical deformation of nickel-based single crystal superalloys
International Journal of Plasticity, 2012, 28(1): 141-158
DOIURL [本文引用: 3]

[16] Cui YN. The Investigation of Plastic Behavior by Discrete Dislocation Dynamics for Single Crystal Pillar at Submicron Scale
Singapore: Springer, 2017: 11-12


[17] 黄敏生, 黄嵩, 梁爽 等. 离散位错动力学算法及其在材料塑性行为模拟中的应用
科学通报, 2019, 64(18): 1864-1877
[本文引用: 1]

(Huang Minsheng, Huang Song, Liang Shuang, et al. Discrete dislocation dynamics algorithms and their application in modeling of plastic behaviors of crystalline materials
Chinese Science Bulletin, 2019, 64(18): 1864-1877 (in Chinese))
[本文引用: 1]

[18] Fan HD, Ngan AHW, Gan K, et al. Origin of double-peak precipitation hardening in metallic alloys
International Journal of Plasticity, 2018, 111: 152-167
DOIURL [本文引用: 1]

[19] Xiang Y, Srolovitz DJ, Cheng LT, et al. Level set simulations of dislocation-particle bypass mechanisms
Acta Materialia, 2004, 52(7): 1745-1760
DOIURL [本文引用: 1]

[20] Xiang Y, Srolovitz DJ. Dislocation climb effects on particle bypass mechanisms
Philosophical Magazine, 2006, 86(25-26): 3937-3957
DOIURL [本文引用: 1]

[21] Queyreau S, Monnet G, Devincre B. Orowan strengthening and forest hardening superposition examined by dislocation dynamics simulations
Acta Materialia, 2010, 58(17): 5586-5595
DOIURL [本文引用: 3]

[22] Záleák T, Svoboda J, Dlouhy A. High temperature dislocation processes in precipitation hardened crystals investigated by a 3D discrete dislocation dynamics
International Journal of Plasticity, 2017, 97: 1-23
DOIURL [本文引用: 2]

[23] Monnet G. Investigation of precipitation hardening by dislocation dynamics simulations
Philosophical Magazine, 2006, 86(36): 5927-5941
DOIURL [本文引用: 2]

[24] Monnet G, Naamane S, Devincre B. Orowan strengthening at low temperatures in bcc materials studied by dislocation dynamics simulations
Acta Materialia, 2011, 59(2): 451-461
DOIURL [本文引用: 3]

[25] Shin CS, Fivel MC, Verdier M, et al. Dislocation-impenetrable precipitate interaction: A three-dimensional discrete dislocation dynamics analysis
Philosophical Magazine, 2003, 83(31-34): 3691-3704
DOIURL [本文引用: 1]

[26] Takahashi A, Ghoniem NM. A computational method for dislocation-precipitate interaction
Journal of the Mechanics and Physics of Solids, 2008, 56(4): 1534-1553
DOIURL [本文引用: 1]

[27] Takahashi A, Terada Y. Numerical simulation of dislocation-precipitate interactions using dislocation dynamics combined with voxel-based finite elements
Key Eng. Mat., 2011, 462-463: 395-400
[本文引用: 1]

[28] Santos-Güemes R, Esteban-Manzanares G, Papadimitriou I, et al. Discrete dislocation dynamics simulations of dislocation-$\theta $' precipitate interaction in Al-Cu alloys
J. Mech. Phys. Solids, 2018, 118: 228-244
DOIURL [本文引用: 1]

[29] Santos-Güemes R, Bellón B, Esteban-Manzanares G, et al. Multiscale modelling of precipitation hardening in Al-Cu alloys: Dislocation dynamics simulations and experimental validation
Acta Materialia, 2020, 188: 475-485
DOIURL [本文引用: 1]

[30] Hull D, Bacon DJ. Introduction to Dislocations
5th Ed. Oxford: Butterworth-Heinemann, 2011: 43-62
[本文引用: 1]

[31] Huang MS, Li ZH. Coupled DDD-FEM modeling on the mechanical behavior of microlayered metallic multilayer film at elevated temperature
Journal of the Mechanics and Physics of Solids, 2015, 85(DEC): 74-97
DOIURL [本文引用: 1]

[32] Huang S, Huang MS, Li ZH. Effect of interfacial dislocation networks on the evolution of matrix dislocations in nickel-based superalloy
International Journal of Plasticity, 2018, 110: 1-18
DOIURL

[33] Lu SJ, Zhang B, Li XY, et al. Grain boundary effect on nanoindentation: A multiscale discrete dislocation dynamics model
Journal of the Mechanics and Physics of Solids, 2019, 126(MAY): 117-135
DOIURL

[34] Wei DA, Zaiser M, Feng ZQ, et al. Effects of twin boundary orientation on plasticity of bicrystalline copper micropillars: A discrete dislocation dynamics simulation study
Acta Materialia, 2019, 176: 289-296
DOIURL

[35] Zhang X, Lu SJ, Zhang B, et al. Dislocation-grain boundary interaction-based discrete dislocation dynamics modeling and its application to bicrystals with different misorientations
Acta Materialia, 2021, 202: 88-98
DOIURL [本文引用: 1]

[36] 崔一南, 柳占立, 胡剑桥 等. 位错动力学在极端环境力学中的发展及应用
高压物理学报, 2020, 34(3): 1-18
[本文引用: 1]

(Cui Yinan, Liu Zhanli, Hu Jianqiao, et al. Advances and application of dislocation dynamics in the mechanics of extreme environment
Chinese Jouenal of High Pressure Physics, 2020, 34(3): 1-18 (in Chinese))
[本文引用: 1]

[37] Arsenlis A, Cai W, Tang M, et al. Enabling strain hardening simulations with dislocation dynamics
Model Simul Mater Sc Modelling And Simulation in Materials Science and Engineering, 2006, 15(6): 553-595
[本文引用: 9]

[38] 38熊健, 魏德安, 陆宋江 等. 位错密度梯度结构Cu单晶微柱压缩的三维离散位错动力学模拟
金属学报, 2019, 55(11): 1477-1486
[本文引用: 3]

(Xiong Jian, Wei De'an, Lu Songjiang, et al. A three-dimensional discrete dislocation dynamics simulation on micropillar compression of single crystal copper with dislocation density gradient
Acta Metallurgica Sinica, 2019, 55(11): 1477-1486 (in Chinese))
[本文引用: 3]

[39] Kelly A, Nicholson RS. Strengthening methods in crystals
International Materials Reviews, 1971, 17(1): 147
[本文引用: 2]

[40] Nie JF. Effects of precipitate shape and orientation on dispersion strengthening in magnesium alloys
Scripta Mater, 2003, 48(8): 1009-1015
DOIURL [本文引用: 1]