王怡舒^*, 沈超敏^*, 刘斯宏^,*,2), 陈静涛^†*河海大学 水利水电学院, 南京 210098
^†中国建筑第二工程局有限公司, 上海 200135

SHEAR-INDUCED ANISOTROPY ANALYSIS OF CONTACT NETWORKS INCORPORATING PARTICLE ROLLING RESISTANCE¹⁾

Wang Yishu^*, Shen Chaomin^*, Liu Sihong^,*,2), Chen Jingtao^†*College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China
^†China Construction Second Engineering Bureau Ltd., Shanghai 200135, China

通讯作者: 2)刘斯宏, 教授, 主要研究方向: 土石坝工程、粒状体力学和地基处理等. E-mail:sihongliu@hhu.edu.cn

收稿日期:2021-03-4接受日期:2021-04-21网络出版日期:2021-06-18

基金资助:

1)国家自然科学基金雅砻江联合基金.U1765205 国家自然科学基金.51979091 国家自然科学基金.52009036

Received:2021-03-4Accepted:2021-04-21Online:2021-06-18
作者简介 About authors


摘要
颗粒材料的宏观力学行为与接触网络的组构各向异性密切相关, 根据接触点的滑动与否、转动与否和强弱力情况, 可以将颗粒间的接触系统分为不同的子接触网络. 一般而言, 不同的子接触网络在颗粒体系中的传力机制不同, 对宏观力学响应的贡献也有不同. 采用离散单元法(discrete element method, DEM)模拟了不同抗转动系数$\mu_r$下颗粒材料三轴剪切试验, 分析了剪切过程中不同子接触网络的组构张量的演变规律, 并探究了颗粒抗转动效应对子接触网络各向异性指标演变规律的影响. 研究发现: 剪切过程中转动、非转动接触的组构张量变化不是独立的, 受到颗粒间滑动与否的影响; 非滑动、强接触网络是颗粒间的主要传力结构, 非滑动接触网络的接触法向和法向接触力各向异性均随$\mu_r$的增大而增大, 其对宏观应力的贡献程度随$\mu_r$的增大而减小;强接触网络的接触法向各向异性随$\mu_r$的增大而增大, 但法向接触力各向异性随$\mu_r$的增大无明显变化, 强接触网络对宏观应力的贡献程度在不同$\mu_r$情况下均相同.
关键词： 颗粒材料;转动力矩;组构张量;接触网络;各向异性

Abstract
The macroscopic mechanical behaviour of granular materials is closely related to the fabric anisotropy of the contact networks. The interparticle contact system can be divided into different sub contact networks according to whether the contacts slide or not, rotate or not and the magnitude of interparticle contact forces. It is generally accepted that the mechanism of force transfer of different sub contact networks varies, which would result in the different contribution to the macroscopic mechanical responses. Based on the discrete element method (DEM), a series of conventional triaxial tests for granular materials with different rolling resistance coefficients $\mu_r$ are carried out. The evolutions of the fabric tensor of different sub contact networks during shearing process are analyzed. The influence of rolling resistance coefficients on the evolution of contact normal and normal contact force anisotropy indexes of different sub contact networks is explored. The numerical results demonstrate that the evolutions of fabric tensors of rolling and non-rolling contacts are not independent and are affected by the sliding between particles. The non-sliding and the strong force related contact networks are the main force transfer structures of the granular system. The contact normal and normal contact force anisotropy indexes of the non-sliding contact networks increase with the increase of $\mu_r$, and the contribution of the non-sliding contact networks to the macro stress decreases with the increase of $\mu_r$. For the strong force contact networks, the contact normal anisotropy index increases with the increasing $\mu_r$ while the normal contact force anisotropy index has no obvious change with the increase of $\mu_r$. The contribution of strong contact network to the macro stress is the same under different $\mu_r$.
Keywords：granular materials;rolling resistance;fabric tensor;contact networks;anisotropy


PDF (6528KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
王怡舒, 沈超敏, 刘斯宏, 陈静涛. 考虑颗粒转矩的接触网络诱发各向异性分析¹⁾. 力学学报, 2021, 53(6): 1634-1646 DOI:10.6052/0459-1879-21-090
Wang Yishu, Shen Chaomin, Liu Sihong, Chen Jingtao. SHEAR-INDUCED ANISOTROPY ANALYSIS OF CONTACT NETWORKS INCORPORATING PARTICLE ROLLING RESISTANCE¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(6): 1634-1646 DOI:10.6052/0459-1879-21-090

引言

颗粒材料是由大量相互接触的离散颗粒组成的系统^[1], 其宏观力学行为与内部颗粒间复杂接触密切相关, 而基于连续介质力学的唯象描述主要建立在颗粒材料宏观物理试验的基础上, 不能追踪颗粒间的相互作用. 离散单元法(discrete element method, DEM)^[2]作为研究颗粒材料内部接触结构(组构)特性的一种有效模拟方法, 被广泛用于探究颗粒材料细观与宏观力学特性的联系^[3-6]. 从细观角度出发, 研究颗粒间的传力机制^[7], 并建立宏细观尺度间的联系, 是研究颗粒材料宏细观力学性质的必要方法.

颗粒材料内部力的传递通过颗粒间的接触实现, 在外部载荷的作用下, 当接触点处的切向接触力大于最大静摩擦时, 形成滑动接触; 另一方面, 由于颗粒形状的不规则性, 在颗粒转动过程中会产生抗转动力矩, 当颗粒点的转动力矩大于最大抗转动力矩时, 形成转动接触. 采用滑动摩擦和抗转动力矩是反映颗粒材料的摩擦性和抗转动特性的重要途径, 被广泛应用于颗粒材料的理论模型和数值模拟中^[8-11], 如在DEM模拟时, 为了考虑颗粒的粗糙程度, 颗粒的接触通常设置Mohr-Coulomb摩擦, 为了考虑颗粒形状的影响则在颗粒接触模型中引入抗转动力矩^[12-13].

颗粒间接触也可以根据法向接触力的大小, 采用平均法向接触力的大小作为分界线, 将体系的接触分为大于平均法向接触力的强接触和小于平均法向接触力的弱接触, 相互连接形成的强弱力链网络抵抗外部载荷^[14-15], 该分类方法被很多****采用^{[3, 16-18]}. 目前, 一些****发现滑动接触对颗粒材料的宏观力学行为影响深刻, 如Aloso-Marroquin等^[19]认为滑动接触对颗粒材料的塑性行为非常重要, 可以将全局接触划分为非滑动-滑动接触网络, 以便理解颗粒体系的宏观力学响应. 此外, 研究发现强弱力链扮演的角色也有所差异, Radjai等^[14]指出强接触对宏观力学响应有着决定性的影响, 强接触承担全部偏载荷, 而几乎所有的摩擦耗散发生在弱接触. 与滑动接触形成较鲜明对比的是, 尽管转动接触对真实颗粒的动力学影响显著, 目前针对转动接触力链的类似研究较少.

颗粒材料细观尺度组构各向异性的产生及变化是其宏观尺度各向异性力学特征的本质原因, 组构各向异性分为两类: 原生各向异性和诱发各向异性, 原生各向异性是材料的固有属性, 在岩土材料中典型表现为横观各向同性和沉积面铅直方向的各向异性, 由颗粒本身的性质(裂隙或者孔隙)以及沉积过程造成; 诱发各向异性随着应力状态的改变而发生变化. 各向异性可以通过颗粒接触的组构张量定量表征, Oda^[20]较早提出了组构张量的概念定量统计组构各向异性; 在此基础上, Rothenburg等^[21-22]首先推导了二维颗粒体系的诱发各向异性表达式, 并提出了颗粒材料应力-接触力-组构理论关系; Chantawarangul^[23]推导了三维条件下的应力-接触力-组构关系; Zhao和Guo^[24]初步揭示了颗粒材料中组构各向异性与宏观应变局部化的直接联系. 各向异性与颗粒内部的接触类型密切相关, Sufian等^[25]将颗粒体系中的接触网络分为非滑动-强接触、非滑动-弱接触、滑动-强接触和滑动-弱接触, 发现非滑动-强接触的组构各向异性参数对颗粒材料抗剪能力的贡献最大, 在不同应力路径下偏应力比与非滑动-强接触的组构各向异性参数具有唯一的线性关系. 然而, 目前关于抗转动效应对不同子接触网络的组构各向异性演变规律的影响仍缺乏系统的研究.

本文根据剪切过程中颗粒接触点的滑动与否、转动与否和强弱力情况, 将全局接触网络分为不同的子接触网络. 基于不同抗转动系数下颗粒材料的常规三轴剪切试验数值模拟结果, 分析剪切过程中不同子接触网络的组构张量的演变规律, 并探究抗转动系数对子接触网络的各向异性演变规律及对宏观应力的贡献程度的影响.

1 DEM模拟试验

1.1 颗粒接触模型

颗粒间的相互作用可用接触法向$ n$、枝向量$ b$、法向接触力$ f_n$、切向接触力$ f_t$等矢量进行描述. 接触法向指颗粒接触点处切平面外法线方向, 可用其方向余弦表征; 枝向量是指两接触颗粒几何中心的连线, $ b=(R_{1} + R_{2}) n$, 其中$R_{1}$和$R_{2}$分别为两接触颗粒的半径; 颗粒间的法向和切向接触力分别指两接触颗粒沿接触法向和在接触切平面上的接触力, 如图1(a)所示. 在进行离散元数值模拟时, 考虑颗粒抗转动效应的线性接触模型^[26]包括3个部分: 法向、切向和转动接触模型, 如图1(b)所示.

图1

新窗口打开|下载原图ZIP|生成PPT
图1抗转动-线性接触模型

Fig.1Linear-based rolling resistance contact model



颗粒间的法向接触力和切向接触力分别用下式进行计算

(1)$f_n =k_n u_n$
(2)$\Delta f_s =-k_s \Delta u_s$
式中, $f_n$, $k_n$和$u_n$分别为法向接触力、法向接触刚度和法向重叠量; $\Delta f_s$, $k_s$和$\Delta u_s$分别为切向接触力增量、切向接触刚度和切向相对位移. 颗粒间法向接触刚度$k_n$和切向接触刚度$k_s$可根据下式计算^[26]

(3)$k_n =AE/L$
(4)$k_s =k_n /\kappa^{\ast }$
式中, $E$为颗粒弹性模量, $A$和$L$分别为接触点处的横截面积和长度, $A=\pi r^{2}$, $r =\min(R_{1}, R_{2})$, $L=R_{1}+R_{2}$; $\kappa^{\ast }$为刚度比. 当计算的切向接触力$f_s$大于最大静摩擦$\mu_sf_n$时, 颗粒间发生滑动, 此时的颗粒接触为滑动接触. 滑动接触点的切向接触力$f_s=\mu_sf_n\ (\mu _s$为颗粒间滑动摩擦系数).

转动接触模型^[27-28]主要是通过在颗粒间加入一个抗转动力矩$m_r$, 其定义为

(5)$m_r =k_r \theta_r$
式中, $\theta_r$为颗粒间相对转角; $k_r$为颗粒转动刚度, 与切向接触刚度$k_s$相关, 可按下式计算

(6)$k_r =k_s \bar{{R}}^{2}, \ \ \frac{1}{\bar{{R}}}=\frac{1}{R_{1} }+\frac{1}{R_{2} }$
当颗粒点的转动力矩$m_r$大于最大抗转动力矩$\mu_r \bar{{R}}f_n $时, 颗粒间发生相对转动, 此时的接触为转动接触. 转动接触点的抗转动力矩$m_r =\mu_r \bar{{R}}f_n\ (\mu_r$为颗粒间的抗转动系数).

1.2 数值模拟方案

本文离散单元模拟的材料为粗颗粒材料, 其初始尺寸为0.3 m$\times$0.3 m$\times$0.6 m (长$\times$宽$\times$高), 根据试样尺寸与颗粒的最大粒径比不应小于5的原则^[29], 控制最大颗粒粒径$d_{\max}$为60 mm. 考虑DEM的计算效率, 试样最小粒径$d_{\min}$设定为10 mm. 有关研究表明粗粒料的级配可以用分形分布的函数来描述^[30]

(7)$\frac{M\left( {L<d} \right)}{M_T }=\left( {\frac{d}{d_{\max } }} \right)^{3-D}$
式中, $d$为颗粒的粒径; $d_{\max}$为最大粒径; $M(L <d)$为小于粒径$d$的土体质量; $M_T$为土体总质量; $D$为分形维数. 对于最大粒径在60 mm以内的粗粒料, $D =1.88 \sim 2.63$为级配良好区间^[30], 因此本文数值试样级配的分形维数$D = 1.9$.

在制备试样时, 首先在模型尺寸范围内随机生成粒径服从图2(a)所示分形分布的球体颗粒, 数量为13 584, 然后采用等向压缩的方法固结至目标围压, 在等向压缩的过程中可以通过控制颗粒间滑动摩擦系数$\mu _s$生成不同初始孔隙比的试样. 图2(b)给出了在不同滑动摩擦系数$\mu_s$下等向固结至200 kPa时试样孔隙比$e$的变化规律, 发现孔隙比$e$随着$\mu_s$的增大而增大, 且增大幅度逐渐减小. 在试样从固结状态的不同$\mu_s$值变成$\mu_s=0.3$的稳定状态中, 对于固结过程采用$\mu_s>0.3$的试样其孔隙比会降低, 而对于固结过程采用$\mu_s< 0.3$的试样其孔隙比保持不变. 这种孔隙比降低的现象是由于减小滑动摩擦系数导致了颗粒间容许最大切向接触力$\mu _sf_n$的减小, 造成了更多颗粒接触间的滑移, 突然释放的剪切弹簧中的应变能转化为动能驱动颗粒重排, 最终形成一个新的稳定结构.

图2

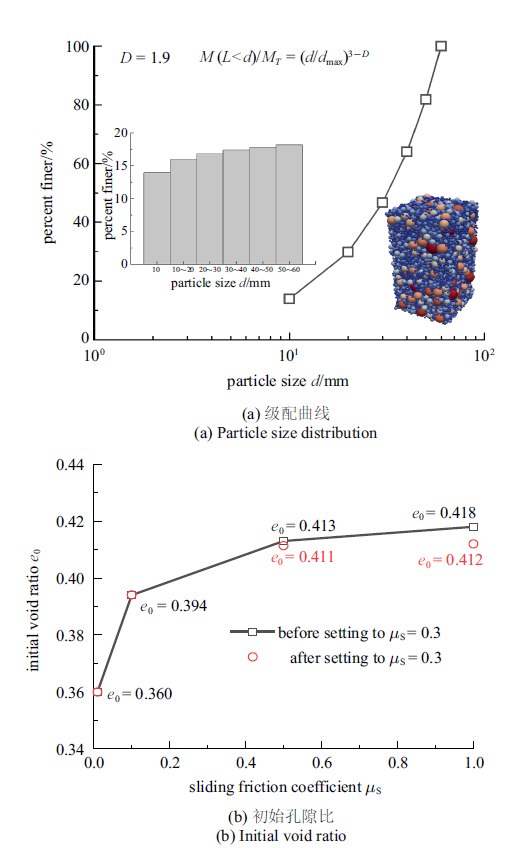新窗口打开|下载原图ZIP|生成PPT
图2DEM数值试样级配与初始孔隙比

Fig.2Particle size distribution and initial void ratio of DEM specimen



本文在等向压缩至预定围压值200 kPa的过程中设定$\mu_s = 1.0$, $\mu _r = 0.0$, 采用周期性边界的伺服机制, 制备得到相对密实度较低、边界效应较小的试样. 本文的主要目的是研究剪切过程中的宏细观力学特性而非重现室内试验过程, 因此在保证宏观力学规律合理的前提下, 通过试算得到模拟中细观参数取值见表1, 其中弹性模量与Guo^[31]和Yan等^[32]的取值在同一数量级, 刚度比取为1.0^[33-34], 在准静态加载情况下局部阻尼系数取为0.0^[35]. 粒间抗转动系数$\mu_r$取为0.0, 0.01, 0.05, 0.1, 0.15, 0.2, 共进行6组数值模拟试验.

Table 1
表1
表1剪切过程DEM计算参数
Table 1Input DEM simulation parameters

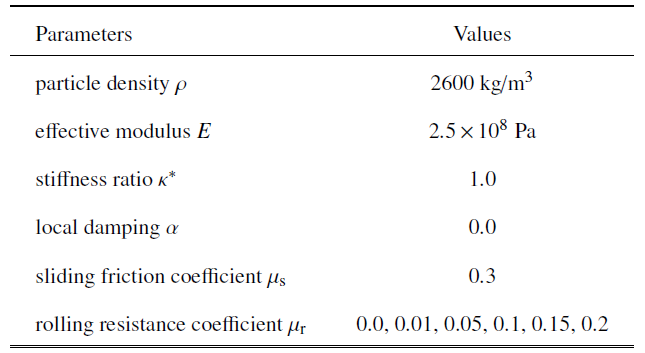新窗口打开|下载CSV

2 颗粒体系的接触网络及表征方法

根据颗粒间的接触特性, 如接触点的滑动与否、转动与否和强弱力情况, 可以定义不同的子接触网络$k$, 其中$k$可以代表非滑动(ns)、滑动(s)或非滑动-非滚动(ns-nr)子接触网络等. 图3为摩擦系数$\mu_s=0.3$, $\mu _r= 0.05$的试样在轴向应变$\varepsilon_1=25.0\%$时颗粒体系的全局接触网络和不同子接触网络的力链图.

图3

新窗口打开|下载原图ZIP|生成PPT
图3颗粒接触网络分类方法

Fig.3Classification of contact networks (CNs)



为了定量表征不同子接触网络$k$的各向异性, 一般用接触法向$ n$和枝向量$ b$的分布特征描述颗粒材料的几何各向异性, 法向接触力$ f_n$和切向接触力$ f_t$的分布特征描述颗粒材料的力学各向异性. Oda^[20]建议采用接触法向来表征全局组构张量$\phi _{ij}$, 定义为

(8)$\phi _{ij} =\frac{1}{N_c }\sum\limits_{\alpha =1}^{N_c } {n_{i}^{\alpha } n_{j}^{\alpha } }$
子接触网络$k$的各向异性参数可以根据接触法向、枝向量、法向接触力和切向接触力的各向异性二阶张量表示

(9)$\phi _{ij}^{k} =\frac{1}{N_c^{k} }\sum\limits_{\alpha =1}^{N_c^{k} } {n_{i}^{\alpha } n_{j}^{\alpha } }$
(10)$b_{ij}^{k} =\frac{1}{N_c^{k} }\sum\limits_{\alpha =1}^{N_c^{k} }{\frac{b^{\alpha }n_{i}^{\alpha } n_{j}^{\alpha } }{1+a_{k\rm l}^{c, k} n_{k}^{\alpha } n_{l}^{\alpha } }}$
(11)$f_{ij}^{n, k} =\frac{1}{N_c^{k} }\sum\limits_{\alpha =1}^{N_c^{k} } {\frac{f_n^{\alpha } n_{i}^{\alpha } n_{j}^{\alpha } }{1+a_{k\rm l}^{c, k} n_{k}^{\alpha } n_{l}^{\alpha } }}$
(12)$f_{ij}^{t, k} =\frac{1}{N_c^{k} }\sum\limits_{\alpha =1}^{N_c^{k} } {\frac{f_t^{\alpha } t_{i}^{\alpha } n_{j}^{\alpha } }{1+a_{k\rm l}^{c, k} n_{k}^{\alpha } n_{l}^{\alpha } }}$
式中, $N_c^{k} $为子接触网络$k$的接触点数, $a_{ij}^{c, k} $为表征子接触网络$k$中接触法向各向异性程度的二阶偏张量, 可由下式得到^[36]

(13)$a_{ij}^{c, k} =\frac{15}{2}\left( {\phi _{ij}^{k} -\frac{\phi _{kk}^{k} }{3}\Delta _{ij} } \right)$
表征子接触网络$k$中枝向量、法向接触力和切向接触力各向异性程度的二阶偏张量$a_{ij}^{b, k} $, $a_{ij}^{n, k} $和$a_{ij}^{t, k} $可分别由下式进行计算

(14)$a_{ij}^{b, k} =\frac{15}{2\bar{{b}}_{0}^{k} }\left( {b_{ij}^{k} -\frac{b_{kk}^{k} }{3}\Delta _{ij} } \right)$
(15)$a_{ij}^{n, k} =\frac{15}{2\bar{{f}}_{0}^{n, k} }\left( {f_{ij}^{n, k} -\frac{f_{kk}^{n, k} }{3}\Delta _{ij} } \right)$
(16)$a_{ij}^{t, k} =\frac{15}{3\bar{{f}}_{0}^{n, k} }\left( {f_{ij}^{t, k} -\frac{f_{kk}^{t, k} }{3}\Delta _{ij} } \right)$
式中, $\bar{{b}}_{0}^{k} =b_{kk}^{k} $为考虑所有方向的平均枝向量, $\bar{{f}}_{0}^{n, k} =f_{kk}^{n, k} $为考虑所有方向的平均法向接触力. 不同的各向异性参数可由对应的二阶张量不变量表示, 分别为

(17)$a_{\ast }^{k} =\sqrt {\frac{3}{2}a_{ij}^{\ast , k} a_{ij}^{\ast , k} }$

3 组构各向异性演变规律

3.1 子接触网络组构张量演变规律

图4给出了摩擦系数$\mu_s=0.3$, $\mu_r= 0.05$的试样在剪切过程中全局组构张量$\phi _{ij}$和滑动、非滑动两种子接触网络的组构张量变化规律, 以及轴向应变$\varepsilon_{1} =25%$时颗粒接触点数按接触角的空间分布玫瑰图. 不同虚线表示全局组构张量$\phi _{ij}$在剪切过程中的变化, 可以发现在$\varepsilon_{1} = 0%$时, 系统的组构$\phi _{11} = \phi _{22} = \phi _{33} = 0.33$, 表明试样此时处于各向同性阶段; 随着轴向应变增大, 大主应力方向组构$\phi _{11}$先增大, 之后随着加载过程稍微减小并最终趋于一个相对稳定的状态; 相应地, 中主应力方向$\phi _{22}$和小主应力方向$\phi _{33}$先减小, 之后稍微增大并保持相对稳定. 对于滑动、非滑动两种子接触网络, 非滑动接触的各向异性明显, 主要沿大主应力方向集中, 滑动接触在残余状态时各向异性较小, 沿小主应力方向有轻微的集中.

图4

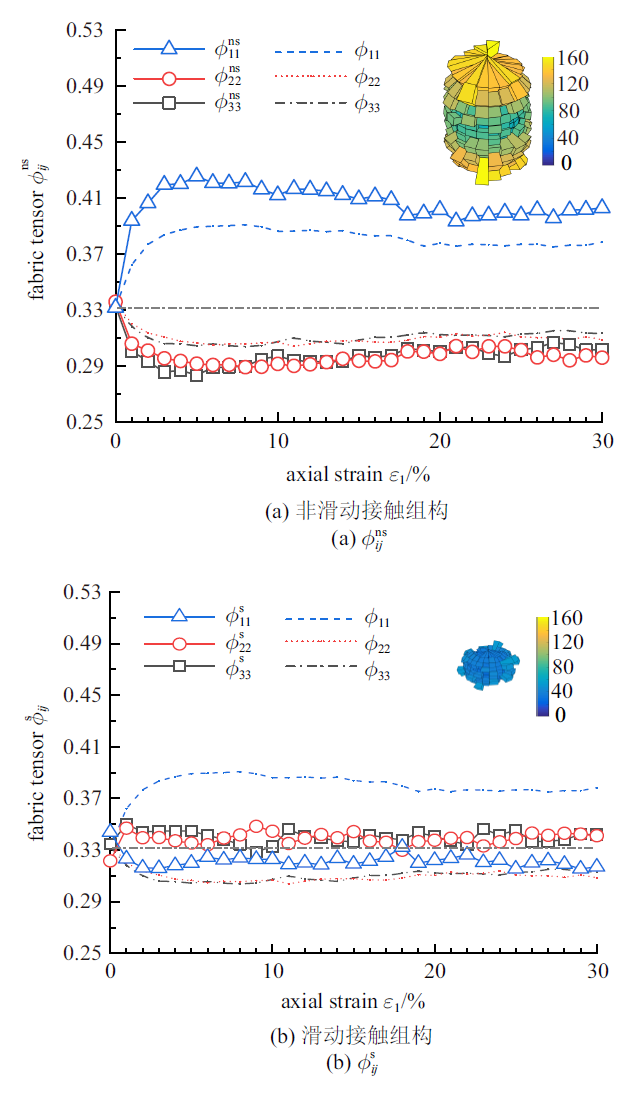新窗口打开|下载原图ZIP|生成PPT
图4滑动、非滑动接触的组构张量演变规律

Fig.4Evolution of fabric tensor of non-sliding and sliding contact networks



考虑到颗粒的抗转动特性, 将接触网络进一步划分为非滑动-非转动、非滑动-转动(ns-r)、滑动-非转动(s-nr)和滑动-转动(s-r) 4种子接触网络, 图5给出了这4种子接触网络的组构张量变化规律, 发现:

图5

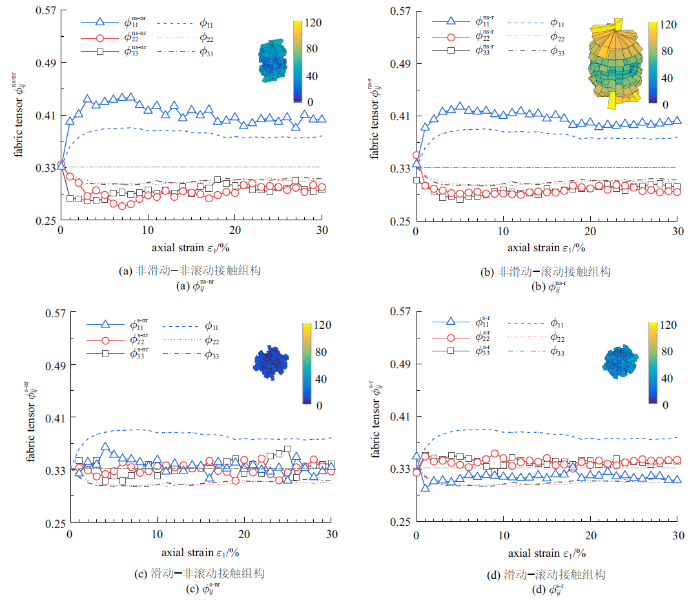新窗口打开|下载原图ZIP|生成PPT
图5非滑动-滑动-非转动-转动接触的组构张量演变规律

Fig.5Evolution of fabric tensor of the nonsliding-sliding-nonrolling-rolling contact neworks



(1) 与非滑动接触相关的组构张量($\phi _{ij}^ns-nr$和$\phi _{ij}^ns-r)$演变规律和$\phi _{ij}$的演变规律类似(图5(a)和图5(b)), 均沿大主应力方向集中, 但$\phi _{11}^ns-nr$和$\phi _{11}^ns-r$的值稍大于$\phi _{11}$, $\phi _{22}^ns-nr$和$\phi _{22}^ns-r$的值稍小于$\phi _{22}$;

(2) 与滑动接触相关组构($\phi _{ij}^s-nr$和$\phi _{ij}^s-r)$与$\phi _{ij}$的演变规律完全不同(图5(c)和图5(d)), $\phi _{ij}^s-r$的值一直在0.33左右波动, 说明滑动-转动接触在加载过程中趋于各向同性的分布;而滑动-非转动接触组构$\phi _{ij}^s-nr$在大主应力方向减小, 在小主应力和中主应力方向增大, 当轴向应变较大时在0.33附近趋于稳定, 但仍呈现一定的各向异性, 说明滑动-非转动接触在剪切过程中沿小主应力方向有一定的集中;

(3) 与转动、非转动接触的相关组构张量的变化不是独立的, 受到颗粒间是否滑动的影响, 剪切过程中系统的应力诱发各向异性主要是由非滑动接触引起的.

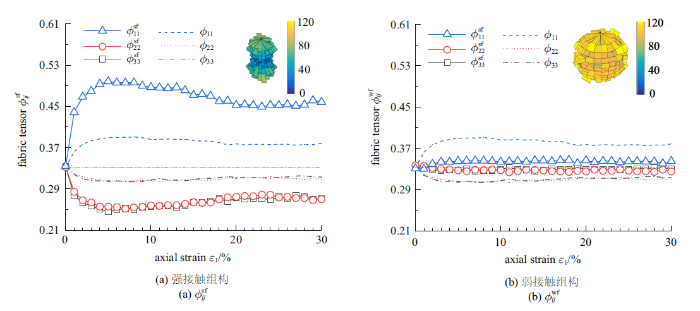
研究发现, 接触网络中的强接触和弱接触对系统的力学作用机制完全不同, 强接触对宏观力学贡献有决定性的影响. 图6给出了剪切过程中强、弱接触网络的组构张量演变规律, 发现强接触sf的数量小于弱接触wf的数量, 强接触sf表现出大于整体的各向异性, 且沿竖向集中, 弱接触wf在残余状态时各向异性不明显, 沿大主应力方向有很小的集中. 该现象与文献[3]的结论一致, 证实了强接触形成柱状结构承担外部载荷, 并由较多的弱接触沿四周支撑.

图6

新窗口打开|下载原图ZIP|生成PPT
图6强、弱接触的组构张量演变规律

Fig.6Evolution of fabric tensor of strong force and weak force contact networks



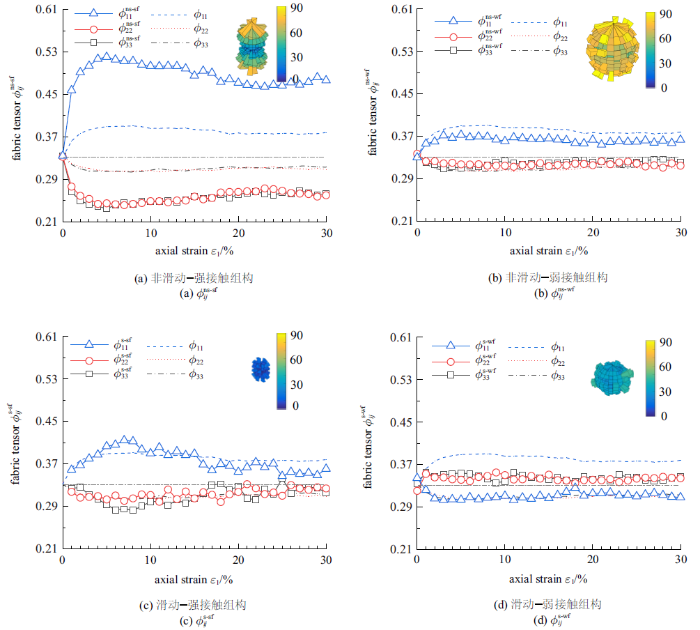
进一步地, 当接触网络划分为非滑动-强接触(ns-sf)、非滑动-弱接触(ns-wf)、滑动-强接触(s-sf)、滑动-弱接触(s-wf)时, 4种子接触网络的组构变化有较大地差异(图7), 发现非滑动-强接触(图7(a))的组构各向异性最明显, 非滑动-弱接触(图7(b))和滑动-强接触(图7(c))的组构与系统组构的大小相差不大, 该3种接触均沿大主应力方向集中, 而滑动-弱接触(图7(d))沿小主应力方向有轻微的集中.

图7

新窗口打开|下载原图ZIP|生成PPT
图7非滑动-滑动-强-弱接触的组构张量演变规律

Fig.7Evolution of fabric tensor of nonsliding-sliding-strong-weak contact networks

3.2 抗转动特性对各向异性参数的影响

基于不同子接触网络的各向异性指标可以用来分析颗粒体系的细观力学机理. 图8分别给出了摩擦系数$\mu_s=0.3$, $\mu_r= 0.05$的试样在剪切过程中不同子接触网络$k$的接触法向各向异性参数$a_c^{k}$和法向接触力各向异性参数$a_n^{k}$的演变规律, 从图8(a)可以看出非滑动、强接触和非滑动-强接触网络的$a_c^{k}$均大于全局接触法向各向异性$a_c$, 其中强接触(特别是非滑动-强接触)是几何各向异性的主要贡献者, 该规律与本文第2节组构张量的演变规律一致. 图8(b)显示全局的接触法向力各向异性$a_n$最大, 这是因为子接触网络仅可以从有限的接触法向力中进行选择, 该结果与文献[25]的模拟结果一致.

图8

新窗口打开|下载原图ZIP|生成PPT
图8剪切过程中子接触网络的各向异性演变规律

Fig.8Evolution of anisotropy indexes of sub-contact networks during shearing



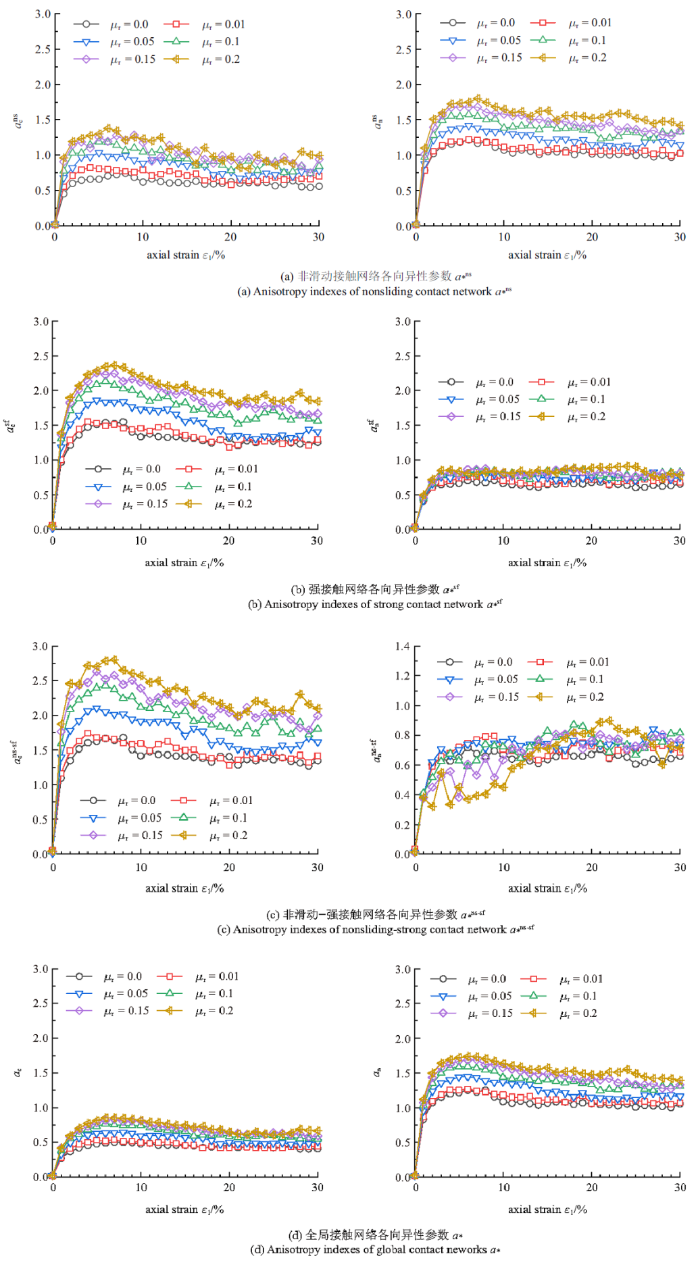
图9选取了对各向异性贡献较大的3个子接触网络(ns, sf, ns-sf)和全局接触网络, 研究抗转动效应对四种接触网络的各向异性参数的影响规律, 发现:

图9

新窗口打开|下载原图ZIP|生成PPT
图9抗转动系数对不同接触网络各向异性指标演变规律的影响

Fig.9Influence of rolling resistance on the evolution of anisotropy indexes of different contact networks



(1) 不同接触网络的接触法向各向异性参数$a_c^{k}$随着抗转动系数$\mu _r$的增大而增大, 说明提高抗转动效应会导致组构各向异性的增大, 表明此时力链需要更少的侧向支撑, 即接触网络的稳定性提高.

(2) 非滑动接触网络和全局网络的法向接触力各向异性$a_n^ns$和$a_n$随抗转动系数$\mu _r$的增大而增大, 且法向接触力各向异性比接触法向各向异性大. 而令人比较意外的发现是, 与强接触相关的子接触网络的法向接触力各向异性$a_n^sf$和$a_n^ns-sf$随抗转动系数$\mu _r$的增大变化不大, 且接触法向各向异性占主导地位, 该规律说明抗转动系数对强接触相关的子接触网络的影响主要体现在接触法向各向异性上, 而对法向接触力各向异性的影响不大.

4 应力-接触力-组构关系

Christonffersen等^[37]提出了基于全局接触网络的颗粒体系应力张量

(18)$\sigma_{ij} =\frac{1}{V}\sum\limits_{\alpha =1}^{N_c } {f_{i}^{\alpha } b_{j}^{\alpha } }$
式中, $V$为颗粒体系总体积; $f_{i}^{c} $为接触点$c$处的法向接触力; $b_{j}^{c}$为接触点$c$处的枝向量; $N_{c}$为颗粒体系的总接触点数. 系统的平均有效应力$p$, 广义剪应力$q$, 不同方向主应变$\varepsilon_{i}$ ($i = 1$, 2, 3)和体应变$\varepsilon_v$分别由下式进行计算

(19)$p=\frac{1}{3}\sigma_{ii}, \ \ q=\sqrt {\frac{3}{2}\sigma_{ij} \sigma_{ij} }$
(20)$\varepsilon_{i} =\ln \frac{l_{i0} }{l_{i} }, \ \ \varepsilon_v =\varepsilon_{1} +\varepsilon_{2} +\varepsilon_{3}$
式中, $l_{i0}$是剪切开始时试样不同方向的初始长度, $l_{i}$是剪切过程中试样不同方向的长度.

图10给出了剪切过程中应力应变变化规律, 可以看出, 应力比出现较为明显的峰值, 并随抗转动系数$\mu_r$的增大而增大, 对体应变的影响也较为明显, 剪胀性增大.

图10

新窗口打开|下载原图ZIP|生成PPT
图10不同抗转动系数下宏观应力-应变关系曲线

Fig.10Curves of macro stress-strain relationship under different rolling friction coefficients



Ouadfel等^[22]与Li等^[38]针对全局接触推导了应力-接触力-组构 (stress-force- fabric, SFF)关系, 当进一步将全局接触分为不同接触网络时, Sufian等^[25]推导了在若干子接触网络中的SFF关系, 全局偏应力比$q/p$*可以表示为子接触体系中不同各向异性参数的函数

(21)$\frac{q}{p}=\frac{2}{5}\sum\limits_{k} {\xi_{k} \left( {a_c^{k} +a_b^{k} +a_n^{k} +\frac{3}{2}a_t^{k} } \right)}$
式中, $a_c^{k} $, $a_b^{k} $, $a_n^{k} $和$a_t^{k} $分别为子接触网络$k$中的接触法向、枝向量、法向接触力和切向接触力的各向异性参数; $\xi_{k} $是权重指标, 代表子接触网络$k$中接触数目和平均法向接触力对宏观应力的贡献程度

(22)$\xi_{k} =\zeta_{k} \gamma_{k} /\left( {\sum\limits_{k} {\zeta_{k} \gamma _{k} } } \right)$
式中, $\zeta_{k} =N^{k}/N$是子接触网络$k$中接触数目$N^{k}$占整个体系接触数$N$的比例, $\gamma_{k} =\bar{{f}}_n^{k} /\bar{{f}}_n $是子接触网络的平均法向接触力与体系平均法向接触力之比.

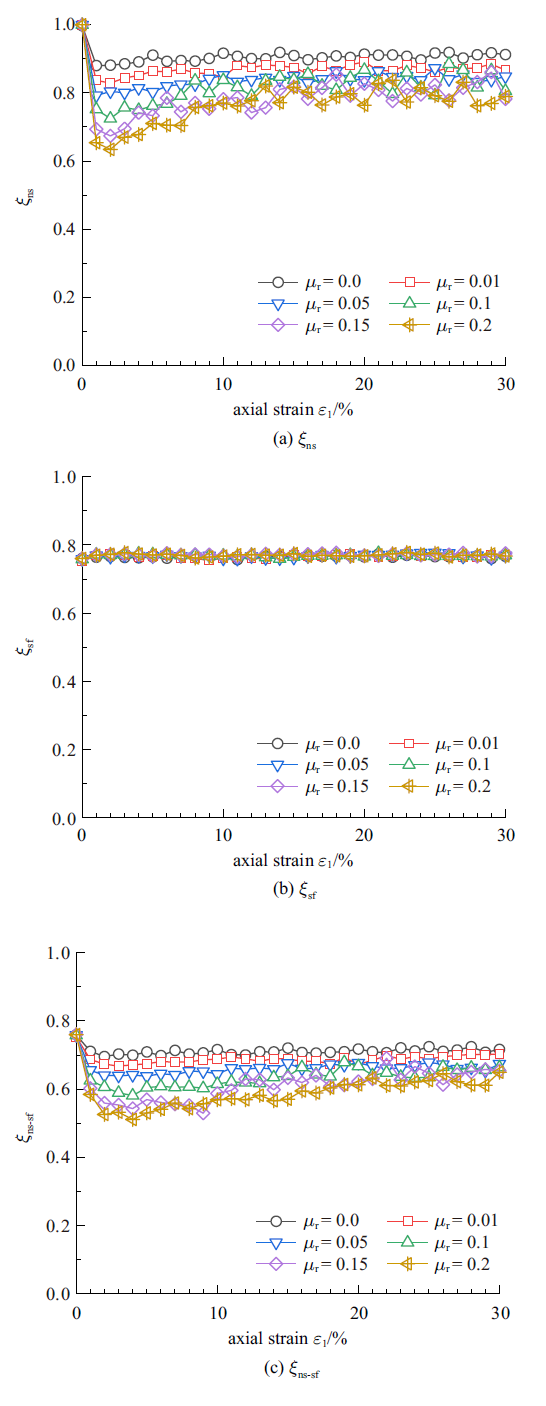
图11给出了抗转动效应对不同子接触网络$\xi_{k}$的影响规律, 发现非滑动和非滑动强接触网络的$\xi_ns$和$\xi _ns-sf$随着抗转动系数$\mu_r$的增大而减小, 说明提高抗转动效应会减小接触数目和平均法向接触力的贡献程度; 而强接触网络的$\xi_sf$不随抗转动系数的改变而改变, 说明强接触网络对宏观应力的贡献程度在不同$\mu_r$情况下均相同.

图11

新窗口打开|下载原图ZIP|生成PPT
图11抗转动系数对$\xi_{k}$的影响规律

Fig.11Influence of rolling resistance on $\xi_{k}$



图12对比了由SFF关系得到的ns-s-sf-wf接触网络应力比$q/p^{\ast }$与由式(19)计算的应力比$q/p$, 可以看出, 对于采用不同抗转动系数的颗粒体系, SFF的理论预测值与实际的应力比非常接近, 从而表明了SFF理论的适用性.

图12

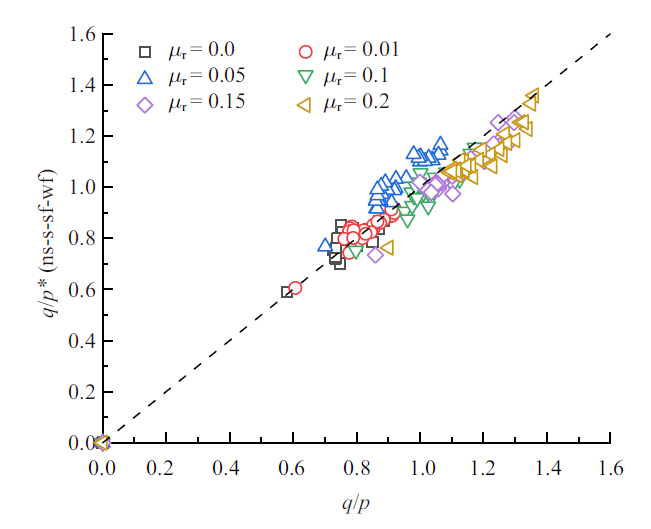新窗口打开|下载原图ZIP|生成PPT
图12SFF理论应力比验证

Fig.12Validation of SFF relationship

5 结论

本文采用离散单元法模拟了不同抗转动系数$\mu_r$情况下颗粒材料三轴剪切试验, 根据接触点的滑动与否、转动与否和强弱力情况, 将颗粒体系分为不同的子接触网络, 分析了剪切过程中不同子接触网络的组构张量的演变规律, 并通过统计不同子接触网络的各向异性参数, 研究了抗转动效应对各向异性演变规律的影响, 主要结论有:

(1) 分析了剪切过程中非滑动-滑动-非转动-转动4种子接触网络的组构张量变化规律, 发现转动、非转动接触的组构变化不是独立的, 受到颗粒间是否滑动的影响, 剪切过程中系统的应力诱发各向异性主要是由非滑动接触引起的.

(2) 剪切过程中非滑动接触的各向异性明显, 主要沿大主应力方向集中, 滑动接触在残余状态时各向异性较小, 沿小主应力方向有轻微的集中; 强接触表现出大于整体的各向异性, 且沿竖向集中, 弱接触在残余状态时各向异性不明显, 沿大主应力方向有很小的集中.

(3) 通过分析抗转动效应对不同子接触网络的各向异性参数影响, 发现提高抗转动效应会导致组构各向异性的增大, 并提高接触网络的稳定性. 非滑动接触网络和全局网络的法向接触力各向异性$a_n^ns$和$a_n$均随抗转动系数$\mu_r$的增大而增大, 且法向接触力各向异性比接触法向各向异性大; 而与强接触相关的子接触网络的法向接触力各向异性$a_n^sf$和$a_n^sf-ns$变化不大, 且接触法向各向异性占主导地位.

(4) 非滑动和非滑动-强接触网络的$\xi_ns$和$\xi _ns-sf$均随着抗转动系数$\mu_r$的增大而减小, 说明提高抗转动效应会减小接触数目和平均法向接触力对宏观应力的贡献程度; 而强接触网络的$\xi_sf$不随抗转动系数的改变而改变, 说明强接触网络对宏观应力的贡献程度在不同$\mu_r$情况下均相同.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 孙其诚, 程晓辉, 季顺迎 等. 岩土类颗粒物质宏-细观力学研究进展
力学进展, 2011, 41(3): 351-371
[本文引用: 1]

(Sun Qicheng, Cheng Xiaohui, Ji Shunying, et al. Advances in the micro-macro mechanics of granular soil materials
Advances in Mechanics, 2011, 41(3): 351-371 (in Chinese))
[本文引用: 1]

[2] Cundall PA, Strack ODL. A discrete numerical model for granular assemblies
Géotechnique, 1979, 29(1): 47-65
DOIURL [本文引用: 1]

[3] Guo N, Zhao J. The signature of shear-induced anisotropy in granular media
Computers and Geotechnics, 2013, 47: 1-15
DOIURL [本文引用: 3]

[4] 钱劲松, 陈康为, 张磊. 粒料固有各向异性的离散元模拟与细观分析
力学学报, 2018, 50(5): 1041-1050
DOI
料在摊铺后形成的颗粒定向排列将导致其力学性质的固有各向异性. 依据粒料的实际不规则形状, 构建了可模拟粒间咬合嵌挤作用的三维离散元复杂形状颗粒; 生成了5 种不同沉积方向的各向异性试件和1种各向同性试件, 对比了各试件在三轴压缩试验中的宏观力学特性差异; 引入组构张量以量化各向异性程度, 利用玫瑰图表达接触法向与接触力的分布特征, 探究了粒料各向异性的细观发展规律. 结果表明: 颗粒长轴愈趋向水平排布, 峰值应力比愈大, 剪缩与剪胀程度愈明显; 相较于各向同性试件, 沉积角$\theta$为$0^\circ$时, 峰值应力比和最大体积压缩应变分别提高了12.6\%和18.8\%, 其原因在于加载过程中颗粒旋转和滑动百分比更小, 内部调整时间更短、更易被剪密; 固有各向异性对颗粒法向接触力分布的影响不大, 但显著影响接触法向分布特征; 剪切过程中, $\theta$为$90^\circ$时的接触法向各向异性系数先快速减小后逐渐增大, 而$\theta$为$0^\circ$到$60^\circ$时则呈现出增大后稍有回落或趋于稳定的趋势, 且$\theta$ 愈小的试件各向异性系数增大愈快.
(Qian Jinsong, Chen Kangwei, Zhang Lei. Simulation and micro-mechanics analysis of inherent anisotropy of granular by distinct element method
Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(5): 1041-1050 (in Chinese))


[5] Zhao S, Evans TM, Zhou X. Shear-induced anisotropy of granular materials with rolling resistance and particle shape effects
International Journal of Solids and Structures, 2018, 150: 268-281
DOIURL

[6] 刘嘉英, 周伟, 马刚 等. 颗粒材料三维应力路径下的接触组构特性
力学学报, 2019, 51(1): 26-35
DOI [本文引用: 1]
颗粒材料的宏观应力变形特征与其微观接触力、组构等紧密相关.一般而言,强接触系统属于颗粒内部体系的传力结构,其对应的组构张量是影响宏观应力性质的重要因素.细观数值方法(如离散单元法)能够反映物理试验的基本规律,并且可以方便地提取宏微观数据来研究颗粒体系的应力变形机制.采用离散单元法(discrete element method,DEM)进行一系列等$p$等$b$应力路径下颗粒材料的真三轴试验,在此基础上研究了三维应力路径下颗粒材料的宏微观力学参数的演化过程、三维组构张量与应力张量多重联系以及强接触体系反映的宏观应力特征.研究表明：颗粒体系偏应力峰值状态和临界状态均存在与加载路径无关的宏微观特征;三维应力路径下组构张量与应力张量存在非共轴性,但其联合不变量演化过程表现出加载路径无关的特征;与弱接触系统的组构张量相比,强接触系统的组构张量更能反映宏观应力张量的特征;强弱接触体系的组构张量对颗粒体系宏观响应的贡献不同,其分界点存在一定取值范围,但采用平均接触力较为简单合理.
(Liu Jiaying, Zhou Wei, Ma Gang, et al. Contact fabric characteristics of granular materials under three dimensional stress paths
Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(1): 26-35 (in Chinese))
[本文引用: 1]

[7] 蒋明镜. 现代土力学研究的新视野-宏微观土力学
岩土工程学报, 2019, 41(2): 195-254
[本文引用: 1]

(Jiang Mingjing. New paradigm for modern soil mechanics: Geomechanics from micro to macro
Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254 (in Chinese))
[本文引用: 1]

[8] 刘一鸣, 杨春和, 霍永胜 等. 考虑转动阻抗的粗粒土离散元模拟
岩土力学, 2013, 34(S1): 486-493
[本文引用: 1]

(Liu Yiming, Yang Chunhe, Huo Yongsheng, et al. Discrete element modeling of behaviors of coarse grained soils considering rolling resistance
Rock and Soil Mechanics, 2013, 34(S1): 486-493 (in Chinese))
[本文引用: 1]

[9] Liu Y, Liu H, Mao H. The influence of rolling resistance on the stress-dilatancy and fabric anisotropy of granular materials
Granular Matter, 2018, 20(1): 1-16
DOIURL

[10] 刘嘉英, 马刚, 周伟 等. 抗转动特性对颗粒材料分散性失稳的影响研究
岩土力学, 2017, 38(5): 1472-1480


(Liu Jiaying, Ma Gang, Zhou Wei, et al. Impact of rotation resistance on diffuse failure of granular materials
Rock and Soil Mechanics, 2017, 38(5): 1472-1480 (in Chinese))


[11] 邹宇雄, 马刚, 李易奥 等. 抗转动对颗粒材料组构特性的影响研究
岩土力学, 2020, 41(8): 2829-2838
[本文引用: 1]

(Zou Yuxiong, Ma Gang, Li Yiao, et al. Impact of rotation resistance on fabric of granular materials
Rock and Soil Mechanics, 2020, 41(8): 2829-2838 (in Chinese))
[本文引用: 1]

[12] Iwashita K, Oda M. Rolling resistance at contacts in simulation of shear band development by DEM
Journal of Engineering Mechanics, 1998, 124(3): 285-292
DOIURL [本文引用: 1]

[13] Jiang M, Shen Z, Wang J. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances
Computers and Geotechnics, 2015, 65: 147-163
DOIURL [本文引用: 1]

[14] Radjai F, Wolf DE, Jean M, et al. Bimodal character of stress transmission in granular packings
Physical Review Letters, 1998, 80(1): 61-64
DOIURL [本文引用: 2]

[15] Estrada N, Taboada A, Radjai F. Shear strength and force transmission in granular media with rolling resistance
Physical Review E, 2008, 78(2): 021301
DOIURL [本文引用: 1]

[16] Tordesillas A. Force chain buckling, unjamming transitions and shear banding in dense granular assemblies
Philosophical Magazine, 2007, 87(32): 4987-5016
DOIURL [本文引用: 1]

[17] Antony SJ, Kruyt NP. Role of interparticle friction and particle-scale elasticity in the shear-strength mechanism of three-dimensional granular media
Physical Review E, 2009, 79(3): 031308
DOIURL

[18] Ben-Nun O, Einav I, Tordesillas A. Force attractor in confined comminution of granular materials
Physical Review Letters, 2010, 104(10): 108001
PMID [本文引用: 1]
We reveal a novel attractor in the space of contact forces that bounds the behavior of granular materials during confined comminution. The attractor is reached asymptotically as the porosity reduces and the grain size distribution attains an ultimate power law scaling. The ultimate distribution of the contact forces follows a clear log-normal distribution, distinctively different from previous observations in uncrushable systems. Supporting evidence comes both from comprehensive discrete element simulations and a theoretical Apollonian model.

[19] Alonso-Marroquin F, Luding S, Herrmann HJ, et al. Role of anisotropy in the elastoplastic response of a polygonal packing
Physical Review E, 2005, 71(5): 051304
DOIURL [本文引用: 1]

[20] Oda M. Fabric tensor for discontinuous geological materials
Soils and Foundations, 1982, 22(4): 96-108.
DOIURL [本文引用: 2]

[21] Rothenburg L, Bathurst RJ. Analytical study of induced anisotropy in idealized granular materials
Géotechnique, 1989, 39(4): 601-614
DOIURL [本文引用: 1]

[22] Ouadfel H, Rothenburg L. Stress-force-fabric' relationship for assemblies of ellipsoids
Mechanics of Materials, 2001, 33(4): 201-221
DOIURL [本文引用: 2]

[23] Chantawarangul K. Numerical simulations of three-dimensional granular assemblies. [PhD Thesis]
University of Waterloo, 1993: 219
[本文引用: 1]

[24] Zhao J, Guo N. The interplay between anisotropy and strain localisation in granular soils: A multiscale insight
Géotechnique, 2015, 65(8): 642-656
DOIURL [本文引用: 1]

[25] Sufian A, Russell AR, Whittle AJ. Anisotropy of contact networks in granular media and its influence on mobilised internal friction
Géotechnique, 2017, 67(12): 1067-1080
[本文引用: 3]

[26] Itasca Consulting Group Inc., Particle Flow Code in Three Dimensions (PFC3D), Version 5.0, Minneapolis, MN. 2015
[本文引用: 2]

[27] Iwashita K, Oda M. Rolling resistance at contacts in simulation of shear band development by DEM
Journal of Engineering Mechanics, 1998, 124(3): 285-292
DOIURL [本文引用: 1]

[28] Ai J, Chen JF, Rotter JM, et al. Assessment of rolling resistance models in discrete element simulations
Powder Technology, 2011, 206(3): 269-282
DOIURL [本文引用: 1]

[29] 土工试验规程SL237-1999. 北京: 中国水利水电出版社, 1999
[本文引用: 1]

(Specification of soil test SL 237-1999. Beijing: China Water Resources and Hydropower Press, 1999 (in Chinese))
[本文引用: 1]

[30] 朱晟, 邓石德, 宁志远 等. 基于分形理论的堆石料级配设计方法
岩土工程学报, 2017, 39(6): 1151-1155
[本文引用: 2]

(Zhu Sheng, Deng Shide, Ning Zhiyuan, et al. Gradation design method for rockfill materials based on fractal theory
Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1151-1155 (in Chinese))
[本文引用: 2]

[31] Guo N. Multiscale characterization of the shear behavior of granular media. [PhD Thesis]
Hong Kong: Hong Kong University of Science and Technology, 2014
[本文引用: 1]

[32] Yan WM, Dong J. Effect of particle grading on the response of an idealized granular assemblage
International Journal of Geomechanics, 2011, 11(4): 276-285
DOIURL [本文引用: 1]

[33] Shen C, Liu S, Wang Y. Microscopic interpretation of one-dimensional compressibility of granular materials
Computers and Geotechnics, 2017, 91(11): 161-168
DOIURL [本文引用: 1]

[34] Minh NH, Cheng YP. A DEM investigation of the effect of particle-size distribution on one-dimensional compression
Géotechnique, 2013, 63(1): 44-53
DOIURL [本文引用: 1]

[35] Hanley K, Huang X, O'Sullivan, et al. Energy dissipation in soil samples during drained triaxial shearing
Géotechnique, 2018, 68(5), 421-433
DOIURL [本文引用: 1]

[36] Kenichi K. Distribution of directional data and fabric tensors
International Journal of Engineering Science, 1984, 22(2): 149-164
DOIURL [本文引用: 1]

[37] Christoffersen J, Mehrabadi MM, Nemat-Nasser S. A micromechanical description of granular material behavior
ASME Journal of Applied Mechanics, 1981, 48, 339-344
DOIURL [本文引用: 1]

[38] Li X, Yu HS. Applicability of stress-force-fabric relationship for non-proportional loading
Computers & Structures, 2011, 89(11-12): 1094-1102
DOIURL [本文引用: 1]