王群, 富庆飞^,2)北京航空航天大学宇航学院, 北京 100190

MOLECULAR DYNAMICS SIMULATION OF SINGLE DROPLET EVAPORATION UNDER ALTERNATING ELECTRIC FIELD¹⁾

Wang Qun, Fu Qingfei^,2)School of Astronautics, Beihang University, Beijing 100190, China

通讯作者: 2)富庆飞, 教授, 主要研究方向: 流体雾化. E-mail:fuqingfei@buaa.edu.cn

收稿日期:2020-12-1接受日期:2021-02-5网络出版日期:2021-05-19

基金资助:

1)国家自然科学基金.11922201 北京航空航天大学高性能计算中心支持项目

Received:2020-12-1Accepted:2021-02-5Online:2021-05-19
作者简介 About authors


摘要
利用分子动力学方法研究了正弦形式的交变电场对三维悬浮水滴在超临界氮气环境下蒸发特性的影响, 主要考虑了电场幅值和频率对液滴蒸发寿命和液滴瞬时蒸发速率的影响. 其中水滴由8000个水分子组成, 环境气体由27000个氮气分子组成. 首先利用分子动力学方法模拟计算了不同状态下水的物性参数以及亚临界条件下匀强电场对液滴蒸发特性的影响, 从而验证了分子模型和蒸发模型的正确性. 接着模拟了在不同幅值和频率的交变电场作用下水滴在氮气环境下的蒸发过程, 结果表明, 相比于无电场或匀强电场, 交变电场能够更显著地促进水滴的蒸发. 在频率一定时, 随着电场幅值的增大, 液滴的蒸发速率不断升高, 蒸发寿命不断下降, 且液滴的瞬时蒸发速率、液滴温度、水分子的排列结构等参数都会产生频率为所加电场二倍的振荡特性, 且电场幅值越大, 振荡幅值也越大. 而在电场幅值一定时, 随着频率的增大, 液滴蒸发寿命和速率并不是单调变化的, 而是在频率$f=5$GHz时, 分别达到一个极大值和极小值, 文中从液滴能量和分子排列结构两个方面解释了产生了这一现象的原因.
关键词： 分子动力学;交变电场;液滴蒸发

Abstract
In this paper, the effect of sinusoidal alternating electric field on evaporation characteristics of three-dimensional suspended water droplet in supercritical nitrogen was studied by molecular dynamics method. And the effects of amplitude and frequency of alternating electric field on evaporation life and instantaneous evaporation rate of single droplet were mainly considered. The evaporation of droplet with 8000 water molecules in the environment of 27 000 nitrogen molecules was simulated and analyzed. Firstly, the physical parameters of water such as thermal conductivity at different temperatures and pressures were simulated using molecular dynamics method, and compared with the theoretical or experimental data. Then, the effect of uniform electric field on single droplet evaporation under subcritical conditions was studied, which was in good agreement with the results in literature, and verified the correctness of the molecular model and evaporation model. Lastly, the evaporation of single water droplet under the action of alternating electric field with different amplitudes and frequencies was simulated. The results showed that compared with the case of no electric field or uniform electric field, the alternating electric field could promote the evaporation of water droplet more significantly. When the electric field frequency was constant, with the increase of the electric field amplitude, the evaporation life of water droplet decreased gradually. Besides, the instantaneous evaporation rate, droplet temperature, and the arrangement structure of water molecules would produce oscillation characteristics with the frequency twice that of the applied electric field at a certain amplitude, and the larger the electric field amplitude, the greater the oscillation amplitude. However, when the electric field amplitude was constant, the evaporation life of droplet did not change monotonically with the increase of frequency, but reached a maximum and a minimum respectively at $f=5$GHz. The reasons for this phenomenon were explained from two aspects of water droplet energy and water molecular arrangement structure.
Keywords：molecule dynamics;alternating electric field;droplet evaporation


PDF (5862KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
王群, 富庆飞. 交变电场作用下单液滴蒸发的分子动力学模拟¹⁾. 力学学报, 2021, 53(5): 1324-1333 DOI:10.6052/0459-1879-20-410
Wang Qun, Fu Qingfei. MOLECULAR DYNAMICS SIMULATION OF SINGLE DROPLET EVAPORATION UNDER ALTERNATING ELECTRIC FIELD¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(5): 1324-1333 DOI:10.6052/0459-1879-20-410

引言

液滴的蒸发是自然界的一种常见现象, 在许多领域中都起着重要的作用^[1-4]. 1976年, 日本****浅川勇吉发现了"浅川效应", 即把水放在高压静电场中, 而电场能够显著促进水蒸发的一种现象^[5]. 因此, 很多****的研究集中在电场对传热传质、流体流动、液滴蒸发等方面的影响上. 外加电场作为流体的驱动力已经被应用在很多技术上, 如静电纺丝^[6]、喷墨打印^[7-8]、喷雾干燥^[9]、静电雾化^[10-11]等.

在电场力作用下, 水分子的排列结构和动力学都会发生改变, 从而影响液滴的蒸发过程^[12]. 到目前为止, 外加电场对液滴蒸发过程的影响一直是研究的热点. Kiyoshi等^[13]、Hashinaga等^[14]和Li等^[15]通过实验发现, 当电场垂直作用于高温壁面上的液滴时, 电场对液滴蒸发有着较强的促进作用, 且交变电场比匀强电场更显著地促进液滴蒸发. Heidarinejad等^[16]对直流电场作用下通道内的水蒸发进行了数值研究. 结果表明, 在电场作用下, 水的蒸发速率增大, 但在高雷诺数下, 电场的作用减弱. 常景彩等^[17]通过数值模拟方法得到了高压静电场下液膜的蒸发速率会升高. Jaiswal等^[18]利用PIV技术观察到在电场作用下的三维悬浮液滴, 其内部的热对流被大大加强了, 从而导致液滴蒸发速率加快. 但Zuo等^[19]利用数值模拟方法发现, 当外部静电场平行于高温壁面时, 会抑制高温壁面上的液滴内部的流动, 从而降低了液滴的蒸发速率, 这与Almohammadi等^[20]通过实验得到的结论定性上保持一致.

分子动力学(molecular dynamics, MD)模拟是基于粒子模型的微观尺度研究方法, 是从微观上分析液滴蒸发行为的有力工具. Wu等^[21]利用分子动力学方法研究了二氟甲烷纳米液滴的蒸发特性, 包括环境温度、液滴尺寸、液滴初始温度等因素的影响. Vaitheeswaran等^[22]、Peng等^[23]采用MD方法研究了电场作用下板之间的水或水模的蒸发行为, 发现在外加电场作用下, 会增强水的蒸发. Okuno等^[24]利用分子动力学方法研究了不同方向的匀强电场对水滴蒸发过程的影响, 结果表明, 电场方向垂直于气液界面时, 电场会促进水滴蒸发; 电场方向平行于气液界面时, 电场会抑制水滴的蒸发^[25]. Hens等^[26]利用分子动力学方法模拟了水平和垂直方向的电场对固体壁面上液滴的扩散和蒸发行为, 结论与文献[24]类似. Wang等^[27]利用MD方法研究了电场对悬浮三维微纳米水滴以及盐溶液液滴蒸发过程特性的影响, 主要探讨了在电场下不同的盐溶液以及盐溶液浓度对蒸发特性的影响.

综上所述, ****研究的焦点主要集中在匀强电场的影响上, 而匀强电场对液滴或水膜蒸发的影响与电场的方向有关. 交变电场的方向总是随时间的变化而不断变化的, 目前交变电场对蒸发影响的研究相对较少. 张立等^[28]通过实验研究了均匀和不均匀电场对液滴蒸发的影响, 结果表明, 当电场强度足够大时, 不均匀电场相比于匀强电场更显著地促进液滴的蒸发. Zhang等^[29]利用MD方法研究了方波电场下水膜和盐溶液膜的蒸发特性, 表明方波电场比匀强电场更能够促进水薄膜的蒸发, 且频率越大, 蒸发越快, 但在交变电场作用下液滴蒸发过程中参数的变化和机理尚未详细讨论. 本文利用分子动力学模拟方法, 研究正弦交变电场对三维悬浮水滴在超临界氮气环境下蒸发过程的影响, 系统地讨论了电场幅值和频率对液滴蒸发特性的影响, 包括液滴的蒸发寿命和速率、瞬时蒸发速率、液滴温度变化等方面. 并从水分子的排列结构、能量变化和所加交变电场的关系等角度解释了交变电场作用下液滴蒸发特性的不同.

1 模型建立及验证

1.1 模型建立

建立了如图1所示的液滴蒸发模型. 其中, 模拟区域为正六面体, 其边长$l=24$ nm, 分为气态和液态两个区域. 其中气态的成分为27 000个氮气分子, 均匀地分布在整个模拟区域内, 位于模拟区域中心位置的球形液滴由8000个水分子组成.

图1

新窗口打开|下载原图ZIP|生成PPT
图1液滴蒸发模型

Fig.1Droplet evaporation model



在模拟过程中, 蒸发模型采用的是周期性边界条件, 即原子从一个边界出去, 会从另一个边界进来, 保证了蒸发过程中原子数的恒定, 同时克服了模拟体系较小的问题.

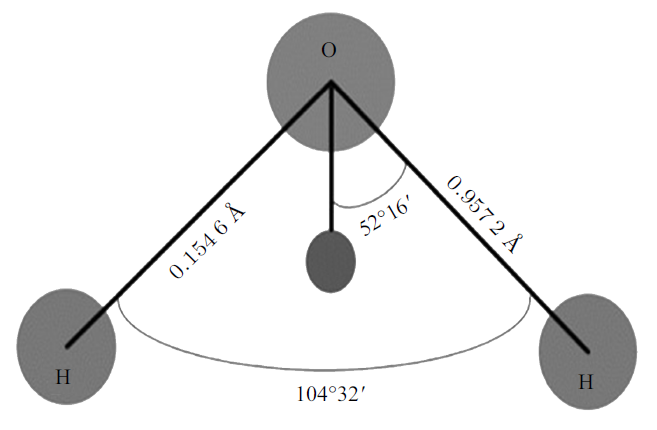
在上述建立的模型中, 水分子选取了刚性四点(TIP4P/2005)水模型^[30], 由3个固定点电荷和一个Lennard-Jones中心组成, 如图2所示. 其中, $m$点为引入的无质量电荷点. 这里采用简单的L-J势能模型描述水分子和氮气分子中原子间的相互作用力, 如式(1)所示

(1)$\begin{eqnarray} E=4\varepsilon \left[ {\left( {\frac{\sigma }{r}} \right)^{12}-\left({\frac{\sigma }{r}} \right)^{6}} \right]+\frac{Cq_{i} q_{j}}{\varepsilon _{\rm r} r}\exp \left( {-\kappa r} \right)(r<r_{\rm c} ) \end{eqnarray}$

图2

新窗口打开|下载原图ZIP|生成PPT
图2TIP4P/2005水模型示意图

Fig.2TIP4P/2005 water model diagram



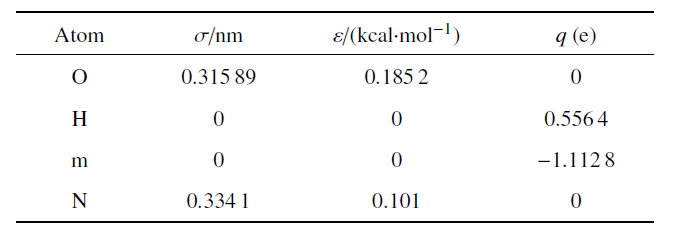
式中, $\varepsilon $为势阱深度; $\sigma $为势能为零的点距原子核心的距离; $r$为原子间的距离, $r_{\rm c}$为截断距离; $\exp \left( {-\kappa r} \right)$ 为阻尼因子; $C$为库伦常数, $C=9$ GN$\cdot$m$^{2}$/c$^{2}$; $\varepsilon_{\rm r}$ 为相对介电常数. 其中, 水分子和氮分子的L-J势能参数设置如表1所示^[30]. 表中1 kcal = 4.18 kJ.

Table 1
表1
表1水和氮气分子的L-J势能参数
Table 1L-J potential energy parameters of water and nitrogen molecules

新窗口打开|下载CSV

对于不同原子间的相互作用的L-J势能参数, 可按以下公式选取

(2)$\begin{eqnarray}\sigma_{ij} =\sqrt {\sigma_{i} \sigma_{j}} ,\ \ \varepsilon_{ij} =\sqrt {\varepsilon_{i} \varepsilon_{j}} \end{eqnarray}$
此外, 水、氮气的成键作用力或键角由谐振函数控制

(3)$E\left( l \right)=K_{\rm l} \left( {l-l_{0}} \right)^{2}$
(4)$E\left( \theta \right)=K_{\theta } \left( {\theta -\theta_{0}} \right)$
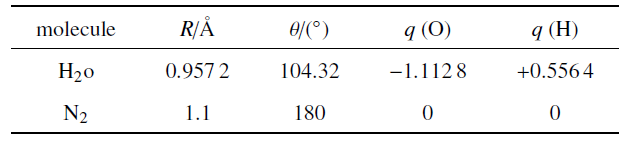
式中, $K_{\rm l}$为拉伸强度, $l$为瞬时键长, $l_{0}$为平衡键长; $K_{\theta}$为旋转强度, $\theta $为瞬时键角, $\theta_{0}$为平衡键角. 表2中给出了水和氮气分子的结构参数.

Table 2
表2
表2水和氮气分子的结构参数
Table 2Structural parameters of water and nitrogen molecules

新窗口打开|下载CSV

1.2 模型验证

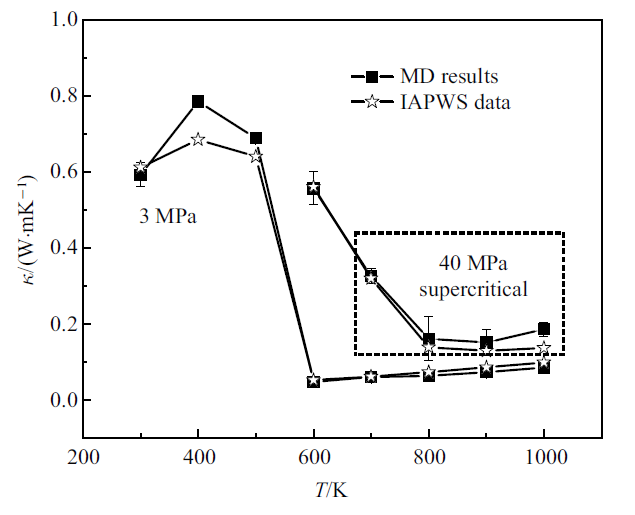
为了验证上述建立的分子模型以及蒸发模型的正确性, 下面分别计算了水的部分物性参数和液滴在亚临界环境下的蒸发特性, 并分别与理论数据或文献中的结果进行对比.

首先模拟计算了水在不同状态下的热导率. 在本文中, 热导率是通过Green-Kubo公式计算求得, 如式(5)和式(6), 表明输运系数等于自关联函数对时间的积分^[31-32], 其中, 热导率是热流$J$的自关联函数的积分^[33]

(5)$\chi =\int_0^\infty {\langle \psi_{x} (\tau )\psi_{x} (0)\rangle {\rm d}\tau }$
(6)$\kappa =\frac{V}{3k_{\rm B} T^{2}}\int_0^\infty {\left\langle {{J}\left( 0 \right)\cdot {J}\left( t \right)} \right\rangle } {\rm d}t$
式中, $V$表示模拟区域体积, $K_{\rm B}$表示玻尔兹曼常数, $T$为模拟体系的温度大小. 利用式(5)和式(6), 得到了不同状态下水的热导率模拟结果, 如图3所示. 可以看出, 无论是在液态、气态或是超临界状态下, 模拟计算得到的热导率和黏性系数结果与IAPWS理论数据均符合良好, 分子模型可以正确反映水的宏观性质, 从而验证了分子模型的正确性, 同时也验证了微观小尺度的模拟可以反映物质的宏观现象规律的结论.

图3

新窗口打开|下载原图ZIP|生成PPT
图3水的热导率模拟结果

Fig.3Simulation results of thermal conductivity of water



接着, 为了验证蒸发模型的正确性, 选取了与文献[27]中一致的参数, 模拟了水滴在亚临界氮气环境下和匀强电场作用下的蒸发过程. 首先使用NVT系综使环境和液滴达到平衡状态, 即使氮气分子均匀地充满整个空间, 液滴在表面张力作用下变成球形, 并使液滴温度保持为298 K. 接着提高环境气体的温度如1000 K, 然后去掉NVT系综并利用NVE系综, 使系统中能量自由交换, 能量从高温的氮气流向低温的水分子^[34-35], 从而使液滴的温度升高, 不断蒸发.

在模拟过程中, 匀强电场的施加是通过对体系中每一个带电的原子施加一个电场力$F=q E$来实现的, 其中$F$的正负表示电场力的方向. 需要注意的是, 电场的施加是在体系达到平衡后, 即在NVE系综下施加.

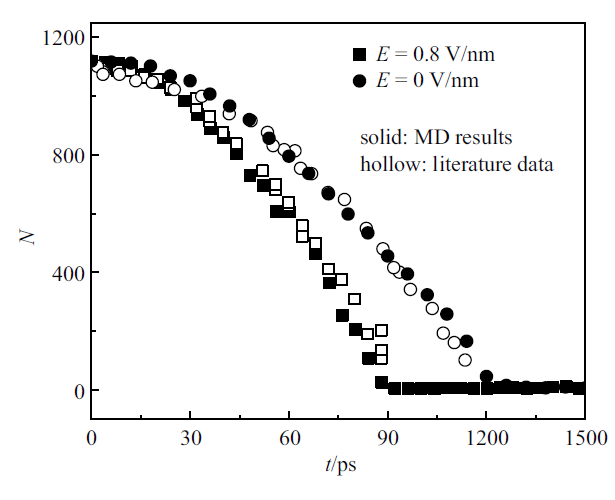
对模拟得到的结果与文献中结果进行对比, 如图4所示. 可以看出, 模拟得到液滴分子数变化曲线与文献中的数据几乎重合, 表明蒸发模型以及蒸发流程是正确的.

图4

新窗口打开|下载原图ZIP|生成PPT
图4液滴内分子数随时间的变化

Fig.4Change of molecular number in droplet with time

2 结果及讨论

2.1 电场幅值的影响

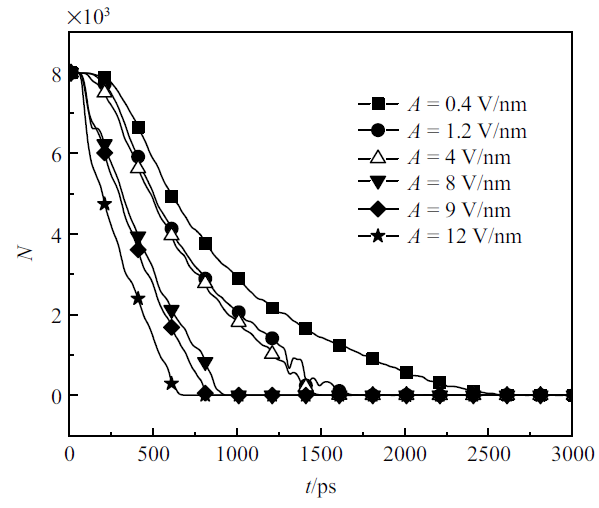
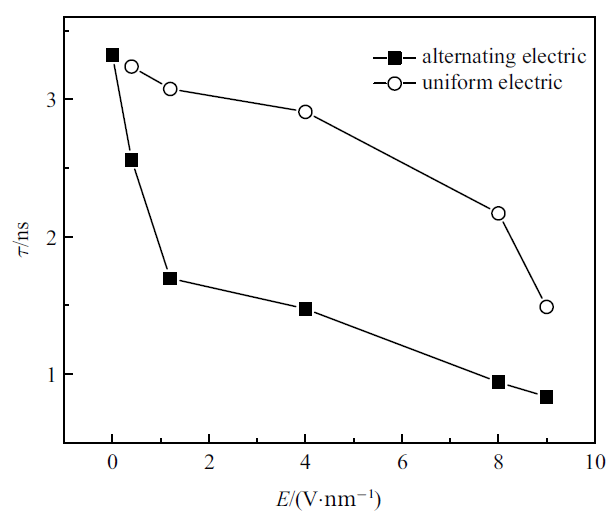
选定电场频率$f=5$ GHz, 分别设置电场幅值$E_{0}=0.4$, 1.2, 4, 8以及12 V/nm, 其电场形式如式(7)所示, 其中电场在$t=80$ ps时刻施加到模拟区域中.

(7)$\begin{eqnarray} E=E_0\sin(\pi/t_0\cdot t) \end{eqnarray}$
接着, 在初始环境温度$T=1000$ K, 初始环境压力$P=26.961$ MPa工况下, 耦合上述电场, 模拟了水滴在氮气环境中的蒸发过程, 得到了不同电场幅值下液滴内的水分子数随时间的变化关系, 如图5所示. 对图5中的数据进行处理, 得到了液滴的蒸发寿命, 并与匀强电场下液滴蒸发的寿命进行对比, 如图6所示. 可以看出, 在交变电场下, 随着电场幅值的增大, 液滴蒸发的寿命是不断下降的, 且相比于匀强电场, 相同幅值的交变电场更能够促进液滴的蒸发, 这与文献[14]中的结果在定性上保持一致.

图5

新窗口打开|下载原图ZIP|生成PPT
图5不同电场幅值下液滴内分子数随时间的变化

Fig.5Change of molecular number in droplet with different electric field amplitudes

图6

新窗口打开|下载原图ZIP|生成PPT
图6交变电场和匀强电场下的液滴蒸发寿命对比

Fig.6Comparison of droplet evaporation lifetime under alternating and uniform electric field



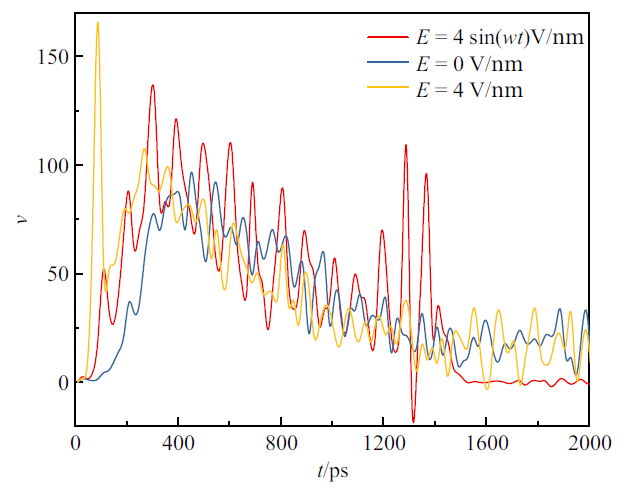
相比于匀强电场, 交变电场的方向和大小总是随时间周期性变化, 这会导致液滴内水分子所受到的电场力也是周期性变化的. 图7给出了液滴的瞬时蒸发速率随时间的变化. 在本文中, 液滴瞬时蒸发速率表示在一个步长的时间内, 液滴内水分子数的变化, 用来表示液滴的瞬时质量蒸发速率.

图7

新窗口打开|下载原图ZIP|生成PPT
图7不同电场形式下液滴的瞬时蒸发速率

Fig.7Instantaneous evaporation rate of droplet under different electric field



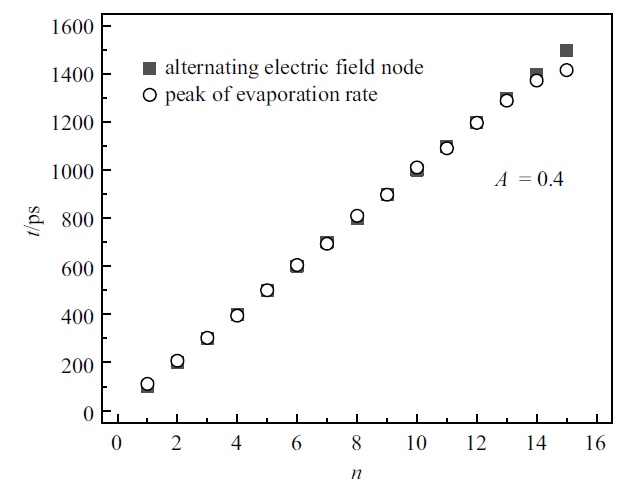
图7中分别给出了无电场、匀强电场以及交变电场作用下的液滴瞬时蒸发速率(电场强度或幅值均为4 V/nm). 可以看出, 当电场为匀强电场或不存在电场时, 瞬时蒸发速率曲线表现出无规则的振荡特性, 主要表现为小振荡幅值的无规则的振荡, 这是由分子动力学本身的热力学涨落和统计误差造成的波动; 而当电场为交变电场时(红色曲线), 曲线振荡变得更加有规律, 主要表现为更显著的振荡幅值以及两个振荡峰值之间的间距几乎保持一致. 为了进一步探究交变电场下液滴瞬时蒸发速率的振荡特性与所加电场的关系, 统计了蒸发速率的峰值对应的时刻, 并与电场的节点时刻进行对比, 如图8所示. 可以看出, 液滴瞬时蒸发速率的振荡峰值总是发生在电场的节点所对应的时刻, 这表明液滴的瞬时蒸发速率的振荡频率是所加电场频率的二倍, 且总是在每一个电场的节点处, 液滴瞬时蒸发速率达到最大.

图8

新窗口打开|下载原图ZIP|生成PPT
图8蒸发速率振荡峰值与交变电场的对应关系

Fig.8Relationship between evaporation rate frequency and electric field frequency



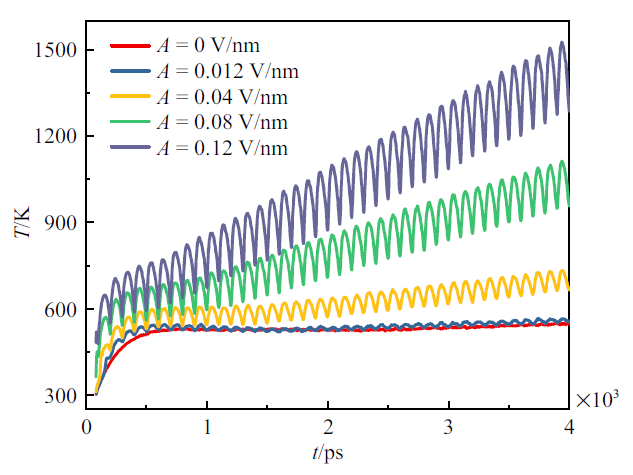
为了解释交变电场对液滴蒸发寿命和瞬时蒸发速率的影响, 下面主要从液滴的能量和水分子的排列结构两个方面进行分析. 不同幅值的交变电场作用下蒸发过程中液滴的温度随时间的变化 如图9所示. 当不存在电场或电场强度较小, $A=0.12$时, 液滴温度的变化曲线几乎重合, 且液滴温度会达到一个稳定温度. 随着电场幅值的继续增大, 液滴温度变化曲线表现出明显的振荡特性, 通过分析, 可以得到其振荡频率仍然是是所加电场频率的二倍, 而可以明显看出振荡幅值随着电场幅值的增大而不断增大. 同时, 液滴温度随时间是不断增大的, 没有表现出与无电场下液滴温度相对稳定类似的性质, 且电场幅值越大, 液滴温度上升地越快, 在同一时刻液滴温度越大. 这就导致了电场幅值越大, 液滴蒸发的寿命越小.

图9

新窗口打开|下载原图ZIP|生成PPT
图9液滴温度随时间的变化

Fig.9Change of droplet temperature with time



接着, 从水分子排列结构方面分析交变电场对液滴蒸发的影响. 水分子间O-H的归一化径向分布函数的定义为: 系统中一个氧原子周围的氢原子的局域密度与系统中氢原子的平均密度之比(不包括与该氧原子组成水分子的氢原子), 可表示为

(8)$\begin{eqnarray} g(r)=\frac{{\rm d}M}{\rho 4\pi r^{2}{\rm d}r} \end{eqnarray}$
式中, ${\rm d}M$为距离一个氧原子$r+{\rm d}r$内的氢原子数, $\rho $为氢原子的平均数密度. 图10给出了不同时刻下体系中水分子间O-H的归一化径向分布函数.

图10

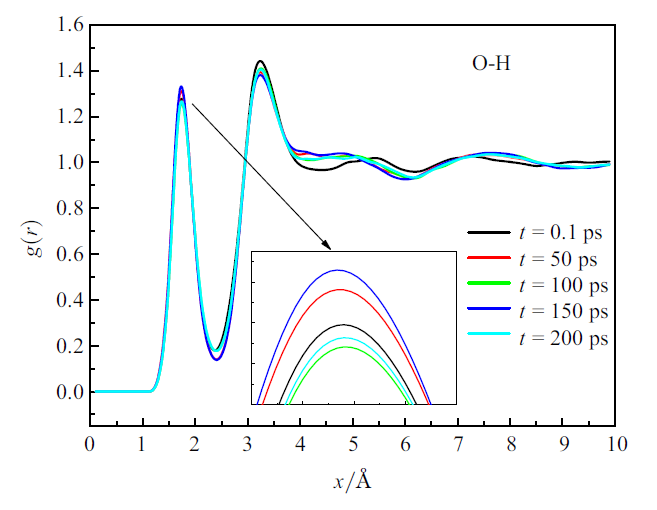
新窗口打开|下载原图ZIP|生成PPT
图10$E=8$ V/nm水分子的O-H归一化径向分布函数

Fig.10O-H normalized radial distribution function of water molecules at $E=8$ V/nm



图10中给出了在电场一个周期内的O-H的归一化径向分布函数变化, 可以看出, 在不同的时刻, 第一峰值的位置几乎不发生变化, 而第一峰值的大小并不是单调变化的, 而是随着时间时而下降时而升高. 有****认为0.18 nm是形成氢键的氧原子和氢原子间最可能的距离^[31], 而径向分布函数中第一峰值的位置为0.173 5 nm, 在一定程度上可认为是形成氢键的最可能的长度. 第一峰值的大小表示一个水分子最可能的归一化氢键密度. 第一峰值位置和大小可以表示一个水分子受到的作用力大小.

为了更清楚地研究水分子排列结构在交变电场下的变化规律, 下面给出了电场幅值$E=8$ V/nm下的第一峰值大小随时间的变化关系, 如图11所示. 可以看出, 第一峰值的大小也会产生与所加正弦电场类似的振荡, 且第一峰值振荡的峰值发生在所加电场对应的结点时刻附近. 这表明体系中水分子间的相互作用力也是周期性变化的, 同时观察图11可以看出, 在施加电场后, 第一峰值的振荡波谷是与电场的节点相对应的, 表明在该时刻水分子间的相互作用力相对最小, 使水分子更容易从液滴内扩散到环境中, 这导致了液滴的瞬时蒸发速率在电场的节点时刻会产生一个峰值.

图11

新窗口打开|下载原图ZIP|生成PPT
图11$E=8$ V/nm下径向分布函数第一峰值随时间的变化

Fig.11Change of the first peak value with time at $E=8$ V/nm

2.2 电场频率的影响

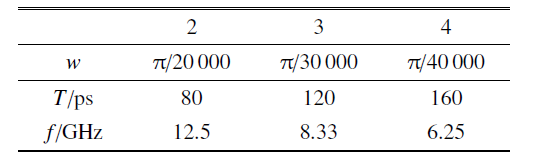
本节中研究了电场频率对液滴蒸发过程的影响. 选定电场幅值$E=4$ V/nm, 通过改变式(7)中的$t_{0}$大小, 来改变电场的频率大小, 表3给出了部分选定的$t_{0}$以及对应的周期和频率大小.

Table 3
表3
表3选择的部分交变电场频率
Table 3Frequency of alternating electric field

新窗口打开|下载CSV

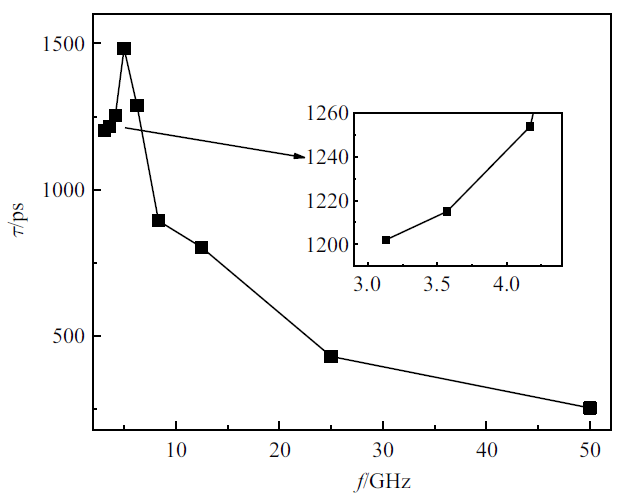
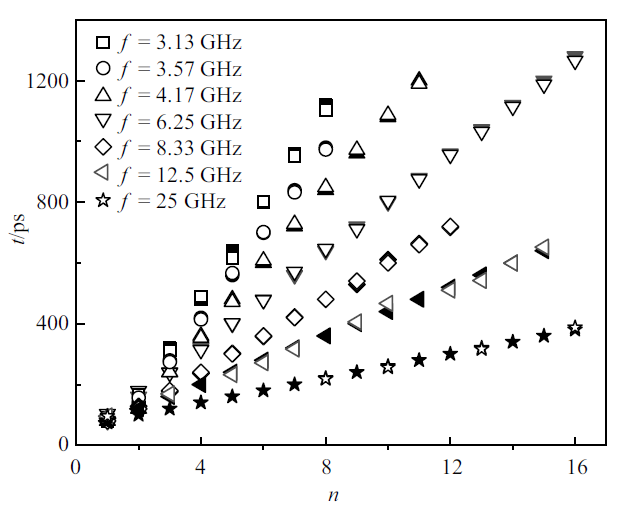
图12给出了不同频率的交变电场作用下, 液滴蒸发寿命的变化规律. 可以看出, 蒸发寿命随着频率的增加并不是单调变化的, 在$f=5$ GHz时, 液滴的蒸发寿命达到一个极大值. 当$f<5$ GHz时, 随着频率的增大, 液滴蒸发寿命不断升高, 但通过对数据进行分析, 可以得出在$f=3.13\sim 5$ GHz内, 液滴蒸发寿命的变化较为不明显, 这与文献中频率对液滴蒸发的影响较小的结论保持一致. 当频率继续增大, $f>5$ GHz时, 液滴蒸发寿命开始逐渐下降, 且随着频率的大幅增大, 液滴的蒸发寿命也会急剧下降, 这与文献[29]中的结论一致. 但作者仅对0.5 GHz, 100 GHz, 200 GHz, 500 GHz的方波对液膜蒸发的影响进行了模拟, 缺少频率较小时的数据.

图12

新窗口打开|下载原图ZIP|生成PPT
图12液滴蒸发寿命和频率的关系

Fig.12Relationship between droplet evaporation life and frequency



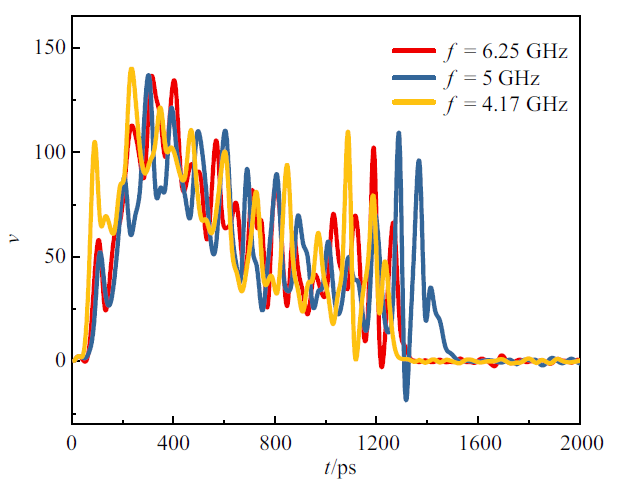
为了进一步研究交变电场对液滴蒸发过程的影响, 图13给出了液滴的瞬时蒸发速率.

图13

新窗口打开|下载原图ZIP|生成PPT
图13$f<6.25$ GHz电场下的液滴瞬时蒸发速率

Fig.13Droplet evaporation rate at $f<6.25$ GHz



可以看出, 在不同频率的电场作用下液滴的瞬时蒸发速率都存在着明显的规律, 如显著的振荡幅值、几乎一致的振荡时间间隔等. 在$f=5$ GHz时, 液滴的瞬时蒸发速率会产生所加电场频率二倍频率的振荡特性, 下面给出了不同频率下液滴的瞬时蒸发速率振荡峰值对应的时刻与电场波节时刻的关系, 如图14所示, 其中空心符号表示液滴瞬时蒸发速率的峰值对应的时刻, 实心符号表示电场节点的时刻. 可以看出, 随着电场频率的增大, 蒸发速率峰值的时刻与电场波节对应的时刻符合得更好, 当电场较小时, 二者存在一些偏差, 而当频率较大时, 蒸发速率峰值出现的频率明显下降, 在某些电场波节时刻, 蒸发速率并不产生峰值, 表示不再满足二倍频率的关系. 这是由于当频率较大时, 所加电场的变化较快, 电场力与粒子本身的热运动相互耗散, 导致液滴瞬时蒸发速率的振荡特性逐渐消失.

图14

新窗口打开|下载原图ZIP|生成PPT
图14不同频率下蒸发速率峰值和电场波节对应关系

Fig.14Relationship between evaporation rate frequency and electric field frequency



为了研究上述液滴蒸发的寿命以及瞬时蒸发速率变化趋势的产生原因, 同样从液滴的能量变化和水分子的排列结构变化两个方面进行分析. 由2.1节中内容可知, 交变电场对水分子结构的影响主要体现在第一壳层水分子的密度, 即径向分布函数的第一峰值大小, 而对第一峰值的位置几乎没有影响.

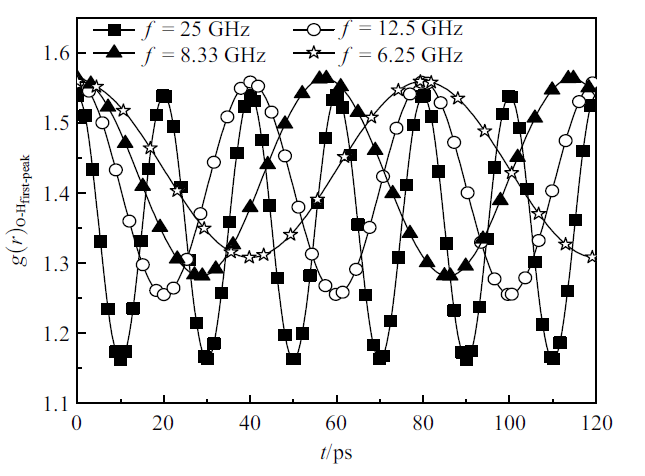
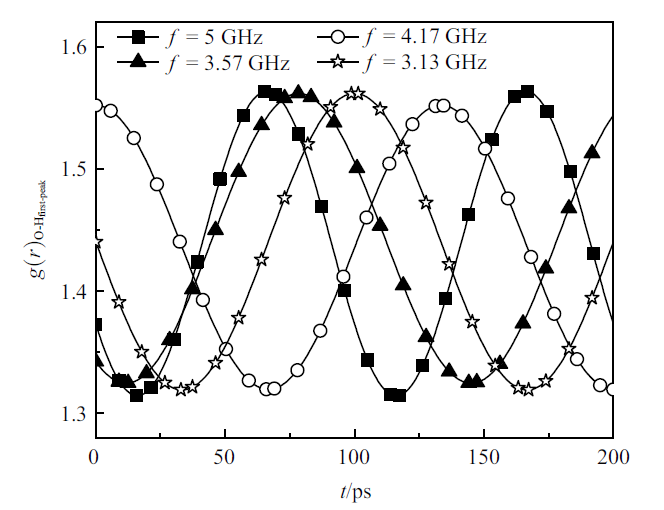
因此, 图15和图16给出了不同频率的电场作用下归一化O-H径向分布函数的第一峰值大小随时间的变化关系. 可以看到, 当$f<5$ GHz时, 第一峰值的振荡峰值和波谷几乎不发生变化, 而频率继续增大时, 峰值同样不发生变化, 而波谷显著下降, 如图 17所示, 表明分子间作用力显著下降, 从而造成了当频率较大时, 液滴的蒸发寿命不断下降.

图15

新窗口打开|下载原图ZIP|生成PPT
图15$f\geqslant 6.25$ GHz下O-H径向分布函数第一峰值大小随时间的变化

Fig.15The first peak value of O-H radial distribution function at $f\geqslant 6.25$ GHz

图16

新窗口打开|下载原图ZIP|生成PPT
图16$f\leqslant 5$ GHz下O-H径向分布函数第一峰值大小随时间的变化

Fig.16The first peak value of O-H radial distribution function at $f\leqslant 5$ GHz

图17

新窗口打开|下载原图ZIP|生成PPT
图17第一峰值振荡的波谷值与频率的关系

Fig.17Relationship between the trough value and the frequency of the first peak oscillation



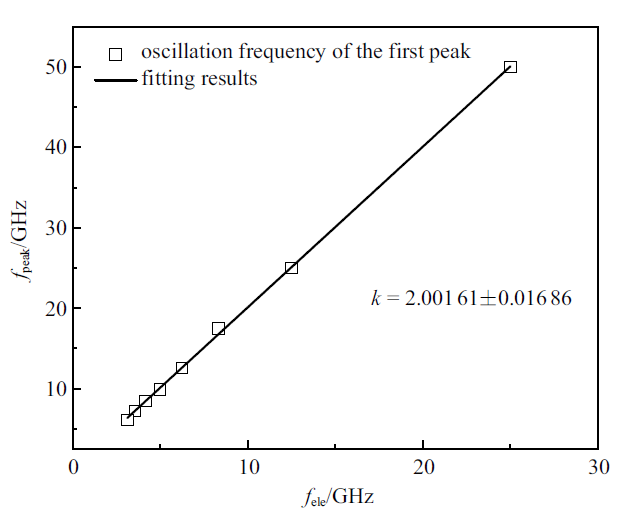
接着对图15和图16中的径向分布函数的第一峰值的振荡频率进行了分析, 如图 18所示. 可以看出, 第一峰值的振荡频率和交变电场的频率有着良好的线性关系, 通过拟合处理可以得到斜率$k=2.001 61$, 表明第一峰值的振荡频率为所加交变电场频率的二倍.

图18

新窗口打开|下载原图ZIP|生成PPT
图18第一峰值振荡频率与所加电场频率的关系

Fig.18Relationship between the oscillation frequency and the frequency of the electric field



上面的结论可以解释在高频电场下($f>6.25$ GHz)液滴蒸发寿命下降的原因, 以及液滴的瞬时蒸发速率产生所加电场频率二倍的振荡特性的原因. 但无法解释在$f=5$ GHz时, 液滴的蒸发寿命产生极值点. 在$f<6.25$ GHz时径向分布函数的第一峰值的振荡幅值几乎保持一致, 对水分子结构的影响也应是一致的, 但考虑到水分子排列结构变化频率的不同, 造成在一个电场周期内的一定时间内, 电场对液滴做的功是不一致的, 这会导致水分子能量变化的不一致, 从而导致液滴蒸发寿命产生差异.

接着, 给出了不同频率的交变电场下液滴的动能随时间的变化, 如图19所示. 可以看到, 液滴的动能同样会产生与所加电场频率的二倍频率的振荡. 当频率较大$f> 6.25$ GHz时, 随着频率的增大, 液滴动能的振荡幅值也在逐渐增大, 同时液滴所达到的稳定的动能也更大, 这也会导致液滴蒸发的加快; 而当频率较小($f<5$ GHz)时, 动能的振荡幅值和液滴最终达到的平均温度几乎保持一致, 且$f=5$ GHz时所达到的稳定动能要稍微小一些, $f=6.25$ GHz所达到的稳定动能要稍微大一些, 此外, 在初始阶段, $f=5$ GHz比$f<5$ GHz以及$f=6.25$ GHz时的动能变化更慢, 且随着频率升高, 动能在初始阶段的变化更慢, 而在$f=6.25$ GHz时, 动能在初始阶段变化又加快, 这些都会导致液滴的蒸发寿命在$f=5$ GHz时达到极大值.

图19

新窗口打开|下载原图ZIP|生成PPT
图19不同频率下液滴的动能随时间的变化

Fig.19Variation of kinetic energy of droplets with time at different frequencies

3 结论

本文利用分子动力学方法研究了交变电场对液滴蒸发过程的影响, 主要考虑了电场幅值和频率对液滴蒸发特性的影响. 主要结论如下:

(1)相比于不加电场或匀强电场的工况, 相同幅值下的交变电场能够更有效地促进液滴的蒸发.

(2)在电场频率恒定的情况下, 随着电场幅值的不断增大, 液滴的蒸发寿命不断下降、蒸发速率不断升高.

(3)在电场幅值不变的工况下, 随着频率的不断增大, 液滴蒸发寿命的变化并不是单调变化的. 当频率较小时, 频率的变化对液滴蒸发过程的影响也相对较小, 且随着频率增大, 液滴蒸发寿命不断增大, 在频率$f=5$GHz处达到极值, 随着频率的继续增大, 液滴蒸发寿命迅速下降.

(4)在交变电场作用下, 液滴内分子的排列结构、液滴温度等参数都会产生所加电场二倍频率的振荡特性. 分子排列结构的周期性振荡和液滴温度或动能的周期性振荡也正是造成上述液滴蒸发寿命变化规律的原因.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Vysokomornaya OV, Voytkov IS, Kuznetsov GV, et al. High temperature evaporation of water emulsion droplets used in thermal fluid treatment
International Journal of Heat and Mass Transfer, 2018,126:1043-1048
DOIURL [本文引用: 1]

[2] El-Dessouky HT, Ettouney HM, Mandani F. Performance of parallel feed multiple effect evaporation system for seawater desalination
Applied Thermal Engineering, 2000,20:1679-1706
DOIURL

[3] 费舒波, 齐运亮, 李雁飞 等. 高温高压下机油液滴蒸发特性的数值模拟
内燃机学报, 2019,37(2):114-122


(Fei Shubo, Qi Yunliang, Li Yanfei, et al. Numerical simulation of oil droplet evaporation characteristics under high temperature and high pressure
Transactions of Csice, 2019,37(2):114-122 (in Chinese))


[4] Hashinaga F, Kharel GP, Shintani R. Effect of ordinary frequency high electric fields on evaporation and drying
Food Science & Technology International Tokyo, 1995,1(2):77-81
[本文引用: 1]

[5] 李贤勇, 李露远, 张龙凡 等. 浅析浅川效应的产生机理
科技创新导报, 2012,26:72-72, 75
[本文引用: 1]

(Li Xianyong, Li Luyuan, Zhang Longfan, et al. Analysis on the mechanism of shoal effect
Science and Technology Innovation Herald, 2012,26:72-72, 75 (in Chinese))
[本文引用: 1]

[6] Liang X, Zhang W, Li M, et al. Electrostatic force-assisted nanoimprint lithography
Nano Letters, 2005,5:527-530
DOIURL [本文引用: 1]

[7] Twardeck TG. Effect of parameter variations on drop placement in an electrostatic ink jet printer
Ibm Journal of Rearch and Development, 2010,21(1):31-36
[本文引用: 1]

[8] Barletta M, Gisario A. Electrostatic spray painting of carbon fibrerein-forced epoxy composites
Process in Organic Coatings, 2009,64(4):339-349
[本文引用: 1]

[9] Wang R, Pan G, Qian S, et al. Influence of nanoparticles on the evaporation behavior of nanofluid droplets: A Dh law and underlying mechanism
Langmuir, 2020,36(4):919-930
DOIURL [本文引用: 1]

[10] Miller JA, Biblarz O, Zajdman A, et al. Electrostatic spray modification in gas turbine combustion
Journal of Propulsion & Power, 1987,3(2):187-192
[本文引用: 1]

[11] 李星. 静电雾化太阳能海水淡化蒸发系统分析. [博士论文]
南昌: 东华理工大学, 2019
[本文引用: 1]

(Li Xing. Analysis of electrostatic atomization solar desalination evaporation system. [PhD Thesis]
Nanchang: East China University of Technology, 2019 (in Chinese))
[本文引用: 1]

[12] 霍元平. 荷电液滴破碎机理及电流体动力学特性研究. [博士论文]
镇江: 江苏大学, 2015
[本文引用: 1]

(Huo Yuanping. Invesyigation on breakup mechanism and electro-hydrodynamics characteristics of charged droplet. [PhD Thesis]
Zhenjiang: Jiangsu University, 2015 (in Chinese))
[本文引用: 1]

[13] Kiyoshi T, Ichiro T, Shigefumi N. Enhancement of evaporation of droplet using EHD effect
Transactions of the Japan Society of Mechanical Engineers Series B, 1991,57(534):297-302
DOIURL [本文引用: 1]

[14] Hashinaga F, Kharel GP, Shintani R. Effect of ordinary frequency high electric fields on evaporation and drying
Food Science & Technology International Tokyo, 1995,1(2):77-81
[本文引用: 2]

[15] Li L, Li F, Eizo T. Effects of high voltage electrostatic field on evaporation of distilled water
Transactions of the Chinese Society of Agricultural Engineering, 2001,17(2):12-15
[本文引用: 1]

[16] Heidarinejad G, Babaei R. Numerical investigation of electrohydro-dynamics (EHD) enhanced water evaporation using large eddy simulation turbulent model
Journal of Electrostat, 2015: 76-87
[本文引用: 1]

[17] 常景彩, 王翔, 王鹏 等. 静电场中极板表面液膜蒸发特性研究
化工学报, 2019,70(3):865-873
[本文引用: 1]

(Chang Jingcai, Wang Xiang, Wang Peng, et al. Evaporation characteristics of water film over collecting electrode in high-voltage electrical field
Journal of Chemical Industry and Engineering, 2019,70(3):865-873 (in Chinese))
[本文引用: 1]

[18] Jaiswal V, Dhar P. Interplay of electro-thermo-solutal advection and internal electrohydrodynamics governed enhanced evaporation of droplets
Proceedings of The Royal Society A Mathematical Physical and Engineering ences, 2019,475(2225):20190046
[本文引用: 1]

[19] Zuo Z, Wang J, Huo Y, et al. Numerical study of droplet evaporation in coupled high-temperature and electrostatic fields
Advances in Mechanical Engineering, 2015,7(3):1-11
[本文引用: 1]

[20] Almohammadi H, Amirfazli A. Sessile drop evaporation under an electric field
Colloids and Surfaces A$:$ Physicochemical and Engineering Aspects, 2018,555:580-585
[本文引用: 1]

[21] Wu X, Yang Z, Duan Y. Molecular dynamics simulation on evaporation of a suspending difluoromethane nanodroplet
International Journal of Heat and Mass Transfer, 2020,158:120024
DOIURL [本文引用: 1]

[22] Vaitheeswaran S, Yin H, Rasaiah JC, Water between plates in the presence of an electric field in an open system
The Journal of Physical Chemistry B, 2005,109:6629-6635
DOIURL [本文引用: 1]

[23] Peng T, Li Q, Liu C. Accelerated aqueous nano-film rupture and evapo ration induced by electric field: A molecular dynamics approach
International Journal of Heat & Mass Transfer, 2016,94:39-48
[本文引用: 1]

[24] Okuno Y, Minagawa M, Matsumoto H, et al. Simulation study on the influence of an electric field on water evaporation
Journal of Molecular Structure Theochem, 2009,904(1):83-90
DOIURL [本文引用: 2]

[25] Wang BB, Zhang HH, Xu ZM, et al. Acceleration of aqueous nano-film evaporation by applying parallel electric field: A molecular dynamics simulation
International Journal of Heat and Mass Transfer, 2019,138:68-74
DOIURL [本文引用: 1]

[26] Hens A, Biswas G, De S. Evaporation of water droplets on pt-surface in presence of external electric field—A molecular dynamics study
Journal of Chemical Physics, 2015,143(9):094702
DOIURL [本文引用: 1]

[27] Wang BB, Wang XD, Duan YY, et al. Molecular dynamics simulation on evaporation of water and aqueous droplets in the presence of electric field
International Journal of Heat and Mass Transfer, 2014,73:533-541
DOIURL [本文引用: 2]

[28] 张立, 杨兰均, 喻梦晗 等. 均匀电场和极不均匀电场对水蒸发的影响
电工技术学报, 2019,34(18):3920-3927
[本文引用: 1]

(Zhang Li, Yang Lanjun, Yu Menghan, et al. The influence of uniform electric field and extremely non-uniform electric field on water evaporation
Transactions of China Electrotechnical Society, 2019,34(18):3920-3927 (in Chinese))
[本文引用: 1]

[29] Zhang HH, Wang BB, Xu ZM, et al. Molecular dynamics simulation on evaporation enhancement of water and aqueous nano-films by the application of alternating electric field
International Journal of Heat and Mass Transfer, 2019,145:118735
DOIURL [本文引用: 2]

[30] Abascal JLF, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005
Journal of Chemical Physics, 2005,123(23):219
[本文引用: 2]

[31] Jaki V, Ogata Y, Pillet CA. The green-kubo formula and the onsager reciprocity relations in quantum statistical mechanics
Communications in Mathematical Physics, 2006,265(3):721-738
DOIURL [本文引用: 2]

[32] Tian CS, Yu H, Zhang C, et al. The first principle calculation of green-kubo formula with the two-time ensemble technique
Communications in Theoretical Physics, 2001,35(4):412-416
DOIURL [本文引用: 1]

[33] 陈利, 张燕平, 高伟. 超临界Cu-水纳米流体热导率分子动力学研究
动力工程学报, 2019,296(8):35-40
[本文引用: 1]

(Chen Li, Zhang Yanping, Gao Wei. Molecular dynamics study on thermal conductivity of supercritical Cu-water nanofluids
Journal of Chinese Society Of Power Engineering, 2019,296(8):35-40 (in Chinese))
[本文引用: 1]

[34] Zhou J, Lu XH, Wang YR, et al. Molecular dynamics simulation for liquid water
Journal of Nanjing Chemical Engineering University, 1998,20(3):1-5
[本文引用: 1]

[35] Deng X, Li Z, Li W. Molecular dynamics simulation of evaporation of R32 on the solid surface
Modern Physics Letters B, 2020,35(7):2150133
DOIURL [本文引用: 1]