,*,2), 刘青泉*, 张静?NUMERICAL STUDY OF COALESCENCE IN ROLL WAVE DEVELOPMENT1)
Chen Xinyi*, Wang Xiaoliang,*,2), Liu Qingquan*, Zhang Jing?通讯作者: 2)王晓亮, 特别副研究员, 主要研究方向: 环境流体力学和颗粒物质力学. E-mail:wangxiaoliang36@bit.edu.cn
收稿日期:2020-12-31接受日期:2021-01-29网络出版日期:2021-05-19
| 基金资助: |
Received:2020-12-31Accepted:2021-01-29Online:2021-05-19
作者简介 About authors
摘要
滚波是一种重力作用下自由液面失稳诱发的水面波动现象, 通常可分为具有相对稳定波形和波速的周期性滚波与波形和波速不断变化的不规则滚波(自然滚波). 不规则滚波的相互作用和发展演化过程十分复杂, 至今对其认识尚不成熟. 本文采用基于雷诺平均Navier-Stokes方程的立面二维数值模型, 对不规则滚波发展过程中的吸收聚合和追赶聚合现象进行了数值模拟研究. 分析了两种聚合模式的演化过程, 给出了滚波聚合过程中完整的波形、波速、速度剖面以及湍流黏性等重要信息. 结果表明滚波的聚合过程是不规则滚波演化和增长的重要机制, 在特定条件下滚波增长由自然增长模式转变为以吸收聚合和追赶聚合为主的增长模式. 滚波聚合过程中, 依次经历后波追赶、爬升、与前波合并、内部流场调制等多个步骤, 最终形成一个具有更大波长和波高的滚波. 本文发现了在3个滚波间距较近的情况下, 会发生二重聚合现象, 即后两个滚波首先聚合, 然后与前波进一步聚合形成一个新的滚波.
关键词：
Abstract
Roll wave is a kind of unstable gravity driven free surface fluctuation in inclined open channel, which could be classified into two types: periodic roll wave with relatively stable waveform and wave speeds, and irregular roll wave with constantly changing waveform and wave speeds (natural roll wave). The development of irregular roll wave is a complicated process, which is studied however far from enough as compared with the regular roll waves. In this study, a numerical model based on the two-dimensional Reynolds averaged Navier-Stokes equation and the renormalization group $k$-$\varepsilon$ turbulence model was adopted. A large number of numerical simulations and statistical analyses were conducted to provide more dynamical and turbulence information about coalescence processes in irregular roll waves. The evolution processes of both absorption and overtake modes of coalescence were systematically studied to obtain the waveform, wave speeds, velocity profile and turbulence viscosity etc. Results imply that coalescence plays an important role on natural roll wave development, where under certain conditions, roll wave growth changes from regular natural growth mode to irregular mode dominated by coalescence, during which a following wave chases, climbs, and merges with the leading wave successively, along with adjustments of internal flow fields, to finally produce a new combined roll wave with larger wave length and wave height. Furthermore, it is found for the first time that when three roll waves were located closely enough, double coalescences would take place. The two tailing roll waves first coalesce to form a new following wave, which then interacts with the leading wave to produce another stronger roll wave propagating downstream.
Keywords：
PDF (1097KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
陈歆怡, 王晓亮, 刘青泉, 张静. 滚波演化中聚合过程的数值模拟研究1). 力学学报, 2021, 53(5): 1457-1470 DOI:10.6052/0459-1879-20-459
Chen Xinyi, Wang Xiaoliang, Liu Qingquan, Zhang Jing.
引言
滚波是一种重力作用下自由液面失稳形成的水面波动现象[1-5], 其形成受流速、水深、底床摩擦、扰动、液体黏性等诸多因素的影响[6-8]. 滚波的出现会引起一些潜在危害, 如波峰处水深明显大于平均水深而产生溢流, 底面切应力显著增大而导致的河床侵蚀等[9-21]. 一般认为, 滚波分为两种, 一种是具有相对稳定波形和波速的周期性滚波, 另一种是波形和波速不断变化的自然滚波(不规则滚波)[22]. 自然滚波中由于波高和波速大小不同, 常常伴随着滚波的聚合现象[22-23].Brock[22]最早通过实验观测发现, 当滚波的波高大小不一时, 传播较快的滚波会追赶传播较慢的滚波, 在其背面爬升, 最终聚合形成一个新的滚波, 并记录了滚波聚合前后几个位置的波高时程曲线. Kranenburg[24]忽略水流黏性和湍流作用, 采用圣维南方程模拟了滚波的聚合过程, 给出了滚波聚合前后的波形图, 并指出尽管以往的理论研究表明存在永久周期性滚波, 然而实验的结果则暗示滚波的周期性充其量是准周期. Huang[23]进一步使用带黏性项的圣维南方程对滚波的聚合现象进行了探讨, 认为滚波的聚合存在吸收聚合与追赶聚合的不同形式, 将小波赶超大波并被大波吞并的现象称为吸收聚合(absorption), 而大波追赶吞并小波的聚合现象被称为追赶聚合(overtake). 按照Huang的定义, Brock实验中展示的三组滚波聚合中[22], 有两次吸收聚合现象和一次追赶聚合现象.
Cao等[15]首先将$k$-$\varepsilon $湍流模型引入圣维南方程, 模拟了滚波的形成和演化过程. 发现即便入口处施加周期性扰动, 在一定的条件下, 也可能会形成非周期性滚波. 他们认为浅水流动具有稳定周期性发展的固有波, 其频谱由流动的水深、速度、坡度和河床粗糙度确定. 当周期足够小的初始扰动向下游传播时, 固有波可以适应这些扰动并与之发生了共振, 最终形成了周期性滚波; 而当初始扰动的周期过大时, 固有波的周期无法容纳下这些扰动, 则会发展为不规则滚波, 最终形成自然滚波.
Cao等[15]和Kranenburg[24]都发现了滚波中一个非常重要的现象, 即便是周期性扰动, 发展过程中也可能会发生聚合现象. 事实上早在Brock的实验中就发现, 滚波波高的增长主要有两种方式, 分别是自然增长和聚合增长. 自然增长往往发生在滚波发展的初期阶段; 聚合增长发生在滚波的后期演化阶段, 不同大小滚波通过聚合而形成新的滚波, 其波高和波长往往比聚合前的单个滚波更大. Brock的实验观测[22]、Kranenburg[24]对滚波聚合现象的分析, 以及Cao等[15]对自然滚波形成过程的研究均表明, 滚波的发展是一个非常复杂的过程, 聚合增长是滚波发展演化的重要形式. 首先, 滚波由初始的小扰动开始增长、加强, 经历自然增长阶段; 当自然增长发展到一定阶段后, 扰动停止增长, 形成一个较为平稳的平台期. 这一阶段往往被称为``周期性滚波''. 然而, 周期性滚波是否可以长期保持, 取决于滚波的频率与浅水流动的固有波频率是否一致. 如果一致, 那么滚波的状态将维持很长时间, 发展为所谓的永久周期性滚波; 如果不一致, 在发展过程中单个滚波可以发展出微小的波速差, 导致滚波以不同的波速传播, 进一步诱发滚波聚合, 并最终形成自然滚波.
以往对滚波的研究主要使用基于垂向平均的浅水波模型[25-33], 不考虑或以比较简单的形式考虑湍流和黏性的影响, 滚波发生和演化过程中的很多物理机理和流动演化特征被隐藏. 为了更好地探讨滚波发展过程中的聚合现象, 本文采用基于雷诺平均Navier-Stokes方程和重整化群湍流模式的立面二维数值模型[34]对滚波的发展演化进行数值模拟, 深入研究滚波演化中的聚合现象, 探讨滚波相互作用过程中的波速、波高、速度剖面和湍流特征. 为统一表述, 本文将规则滚波发展到自然滚波的中间阶段以及自然滚波统称为不规则滚波.
1 数值模型
沿斜槽水流方向建立求解域, 数值模型采用雷诺平均不可压缩Navier-Stokes方程模型, 为更好地模拟包含充分发展湍流和低强度湍流并存的滚波发展和演化过程[34], 采用重整化群湍流模式, 界面捕捉采用TruVOF方法. 模型的建立和验证详见文献[34]. 本文采用入口出口边界条件, 初始小扰动以入口处水深的变化给出, 如图1所示. 入口处水深采用周期扰动, $h=h_{\rm n} +\alpha \sin [(2\pi/T)t]$, 其中$h_{\rm n}$为计算域中的初始水深, $\alpha $为入口扰动的幅值, $T$为入口扰动的周期, $t$为时间. 图1中的$v_{\rm n} $为计算域中的入口速度, $g$为重力加速度, $\theta$为斜坡与水平面的夹角. 该模型成功模拟了多组周期性滚波的发生和演化过程[34].图1
新窗口打开|下载原图ZIP|生成PPT图1求解域及边界条件示意图
Fig.1Schematic diagram of computational domain and boundary conditions
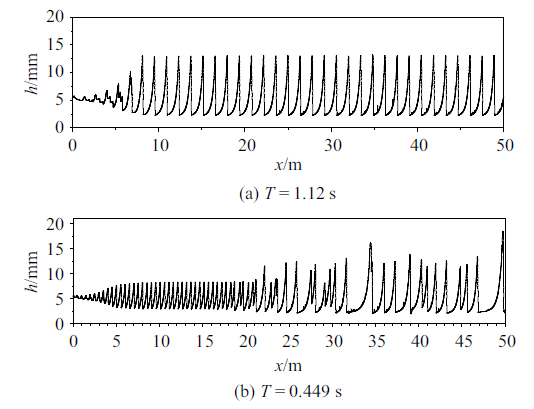
与Cao等[15]和Kranenburg[24]的结论类似, 当扰动周期满足一定条件时, 周期性扰动在传播一定距离后会发展为不规则滚波, 如图2所示. 图2(a)显示了一种发展为周期性滚波的模拟结果, 图2(b)则表明在扰动周期较小时, 扰动首先会稳定增长, 到达平台期. 周期性滚波会稳定传播一段距离, 然后逐渐形成不规则滚波. 与Cao等[15]的结论有所不同, 本文研究发现扰动周期在某一个范围内会形成周期性滚波, 而过小或过大的扰动周期均会诱发不规则滚波. 这里并不试图探讨形成不规则滚波的临界条件, 而是主要分析不规则滚波中的聚合现象.
图2
新窗口打开|下载原图ZIP|生成PPT图2(a) 当扰动周期$T= 1.12$ s时滚波运行至$t= 50$ s时的波形图; (b) 当扰动周期$T= 0.449$ s时滚波运行至$t= 50$ s时的波形图
Fig.2(a) Roll wave form at $t= 50$ s when the perturbation period $T= 1.12$ s; (b) roll wave form at $t = 50$ s when the perturbation period $T = 0.449$ s
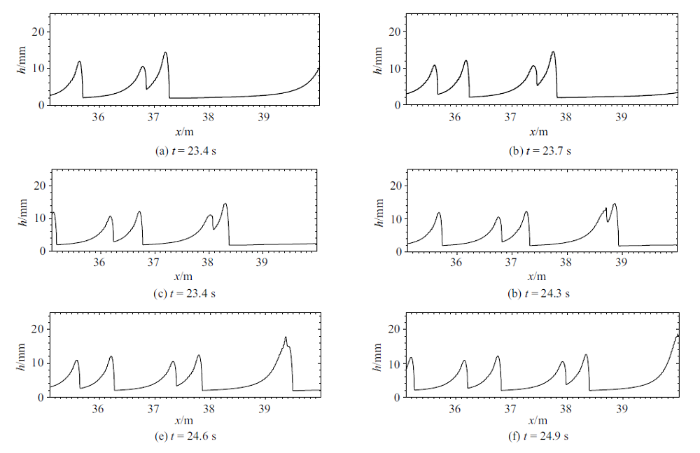
本文模拟了Brock[22]的一组经典滚波实验, 通过定量比较展示本文模型模拟滚波聚合的能力, 计算参数如表1所示. 图3给出了滚波聚合前后的发展演化过程, 给出了后波逐步追赶前波, 最终合并成一个新滚波的过程, 这是一个典型的吸收聚合.
Table 1
表1
表1滚波聚合数值算例基本参数[22]
Table 1
 |
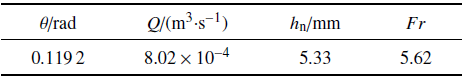新窗口打开|下载CSV
图3
新窗口打开|下载原图ZIP|生成PPT图3吸收聚合滚波波形发展演化
Fig.3Waveform evolution during the absorption process of roll wave
计算得到的滚波波速如表2所示. 滚波聚合大约发生在22.6 s, 完全聚合发生在24.9 s, Brock实验中得到的波速值如表3所示. 数值模拟得到的滚波聚合前后的波速大小与Brock实验结果吻合较好, 由此可见本文模型可较好地模拟不规则滚波的聚合行为.
Table 2
表2
表2滚波波速数值模拟结果
Table 2
 |
新窗口打开|下载CSV
Table 3
表3
表3Brock实验测量滚波聚合前后波速[22]
Table 3
 |
新窗口打开|下载CSV
2 吸收聚合
2.1 波形演化
为研究滚波的吸收聚合现象, 本文计算了大量的算例, 并进行了分析, 表4给出了两组典型的滚波吸收聚合算例的参数.Table 4
表 4
表 4滚波吸收聚合算例基本参数
Table 4
 |
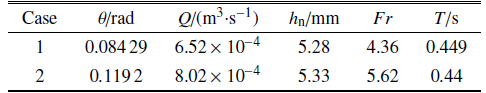新窗口打开|下载CSV
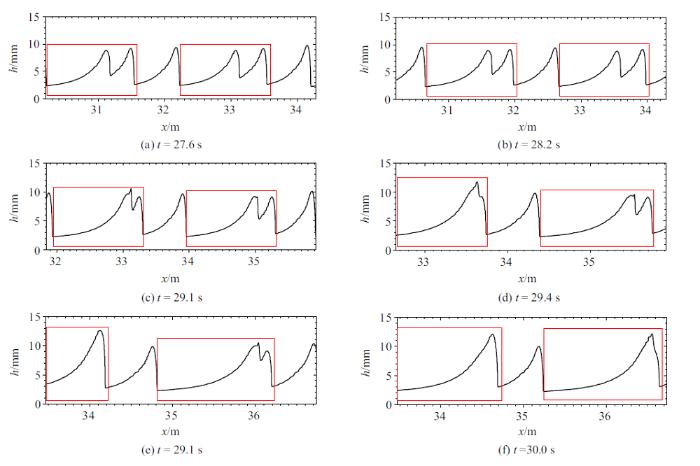
图4给出了组次1的波形演变图, 发生了2次吸收聚合事件, 称为吸收聚合事件A和吸收聚合事件B. 当$t=26.4$ s时, 后波的波高均略小于前方滚波的波高. 在追赶过程中, 后波以略高于前方滚波的波速逐渐拉近与前方滚波的距离, 并经历追赶、爬升、吞并和融合的过程, 最终形成一个波长和波高更大的滚波向下游传播.
图4
新窗口打开|下载原图ZIP|生成PPT图4滚波吸收聚合过程中波形演化图, 左侧框图表征吸收聚合事件A, 右侧框图表征吸收聚合事件B
Fig.4Waveform evolution during the absorption process of roll wave. The left box depicts absorption A, and the right box shows absorption B
滚波聚合前后最大波高的演化如图5所示, 聚合前, 后波的波高小于前波, 在聚合过程中, 后波逐渐爬升, 波高逐渐变大, 而前波的波高在组次1的两个例子中基本保持不变, 在组次2中略微增大, 但是幅度都低于后波, 最终后波与前波合并形成一个新的滚波继续向下游传播.
图5
新窗口打开|下载原图ZIP|生成PPT图5滚波吸收聚合过程中波高演化图
Fig.5Maximum wave height evolution during the absorption process of roll wave
2.2 滚波波速
图6展示了滚波聚合过程中波峰位置的演变, 其斜率表示波速. 滚波聚合过程中, 前后两波几乎保持各自的速度传播, 后波的速度大于前波, 后波逐步赶上前波, 最终合并形成一个新滚波, 并继续向下游传播, 如图6蓝线所示.图6
新窗口打开|下载原图ZIP|生成PPT图6滚波吸收聚合过程中波峰位置演变
Fig.6Evolution of wave crest position during the absorption process of roll wave
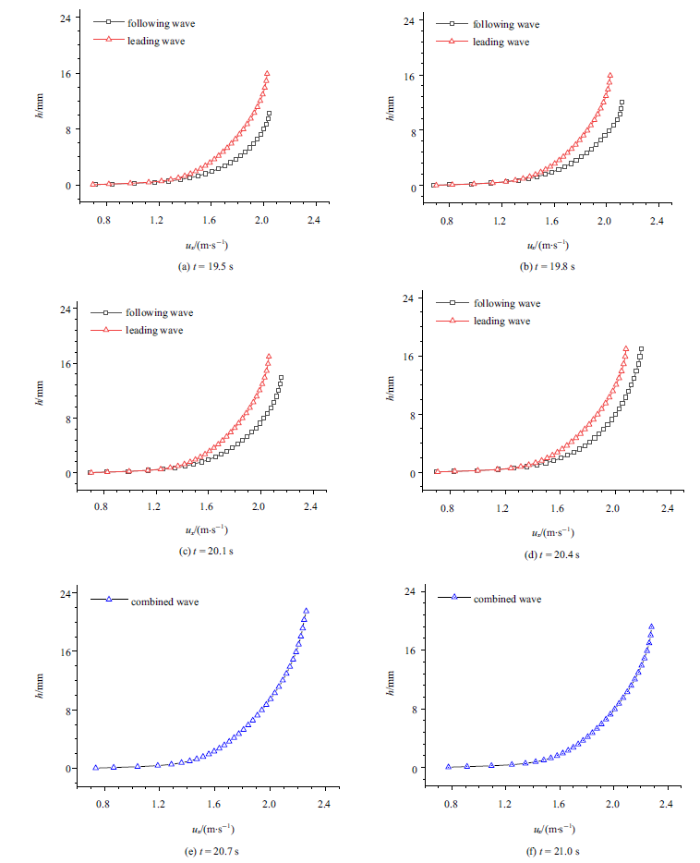
滚波在聚合过程中内部流场结构复杂, 单一的波形图并不能完整表征滚波聚合作用, 本文的立面二维模型可以给出滚波吸收聚合过程中波峰处的速度剖面分布与演变过程. 图7给出了组次2滚波吸收聚合过程中两个波峰处的速度剖面演变过程, 其中黑色点代表前波, 红色点代表后波, 蓝色点为聚合后形成的滚波.
图7
新窗口打开|下载原图ZIP|生成PPT图7组次2滚波聚合过程中滚波峰值处速度剖面随时间的变化
Fig.7Evolution of velocity profile at the roll wave crest along with time during the absorption process of roll wave from case 2
图7表明后波追赶前波过程中速度剖面基本维持不变, 在滚波发生作用时, 后波的波高由于爬升逐步增大, 直至追上前波, 逐步融合形成一个新滚波的速度剖面. 滚波聚合初始时刻速度剖面和单个滚波速度剖面相比有一些差别, 随时间推进会稍作调整演变成单个滚波的速度剖面, 这主要是由于湍流作用稍微落后于波形的演变, 湍流对聚合滚波具有一定的调制所致, 这一点将在第2.3节给出.
2.3 组次2湍流黏性
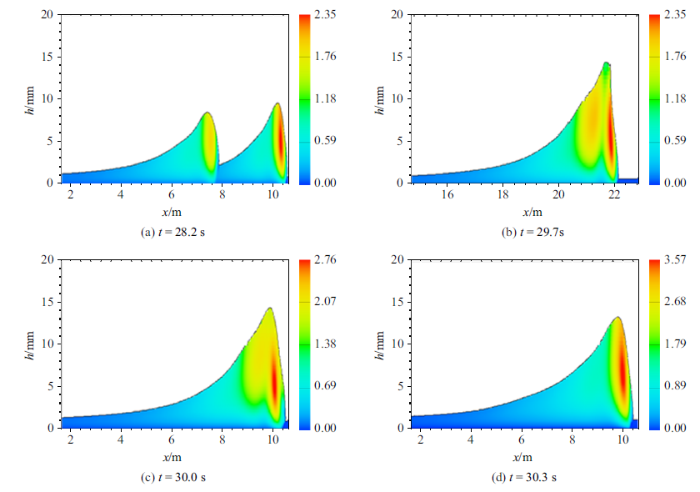
图8给出了组次2滚波吸收聚合过程中湍流黏性的分布和演化过程. 在两个滚波聚合时, 滚波波高到达最大值, 而滚波聚合后湍流黏性分布并没有直接转变为类似单个滚波的湍流黏性分布. 刚聚合形成的滚波中, 有两个湍流黏性高能区, 其形状类似聚合前的湍流黏性分布, 随着时间的推移, 这两个湍流黏性区逐步合并调整变成单个滚波的湍流黏性分布. 表明湍流黏性的演变稍微落后于滚波波形的发展, 对滚波聚合过程起着一定的调制作用, 基于浅水波方程的滚波模型无法表征这个机制.图8
新窗口打开|下载原图ZIP|生成PPT图8组次2滚波吸收聚合过程中湍流黏性分布随时间的演化
Fig.8Evolution of turbulent viscosity distribution with time during the absorption process of roll wave in case 2
3 追赶聚合
3.1 波形演化
表5中给出了3组典型滚波追赶聚合算例的参数.Table 5
表 5
表 5滚波追赶聚合算例基本参数
Table 5
 |
新窗口打开|下载CSV
图9展示了组次3滚波追赶聚合的波高演化. 由图9(a)可以明显看出, 与吸收聚合不同, 追赶聚合中后波的波高大于前波. 与吸收聚合的过程类似, 追赶聚合也会经历后波爬升, 波高逐渐增大的过程, 而在这一过程中前波的形貌则没有明显变化. 在后波和前波聚合后, 最终形成一个波高和波长都更大的新滚波向下游传播.
图9
新窗口打开|下载原图ZIP|生成PPT图9组次3滚波追赶聚合过程中波形演化图
Fig.9Waveform evolution during the overtake process of roll wave in case 3
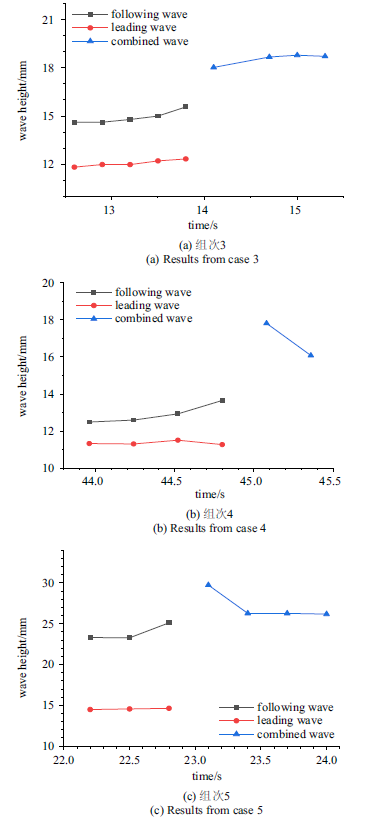
滚波追赶聚合前后最大波高的演化如图10所示, 与吸收聚合不同的是, 追赶聚合前后波的波高大于前波; 在后波爬升过程中, 后波的波高变化较为平缓, 在短时间内最大波高的增大较有限, 不像吸收聚合那样会经历最大波高短时间内的激增. 这是由于追赶聚合中滚波虽然也需要在追赶时爬升前方滚波, 但由于后波本身波高相较于被爬升的滚波就较高, 因此较小的变化对其影响不明显. 在被吞并的过程中, 前波的形貌没有明显的变化, 波高基本维持不变. 与吸收聚合过程相同的是, 最终所形成新滚波的波高和波长相比于聚合前的两个滚波均更大.
图10
新窗口打开|下载原图ZIP|生成PPT图10滚波追赶聚合过程中波高演化图
Fig.10Maximum wave height evolution during the overtake process of roll wave
3.2 滚波波速
图11展示了滚波追赶聚合过程中波峰位置的位置变化. 后波和前波在运动过程中的波速基本维持不变, 由其斜率不同可以看出, 后波的波速略高于前波, 追赶聚合后形成的全新滚波也基本维持等速传播.图11
新窗口打开|下载原图ZIP|生成PPT图11滚波追赶聚合过程中波峰位置演变
Fig.11Evolution of wave crest position during the overtake process of roll wave
表6给出了组次3的滚波波速变化. 结合图11(a)可知, 追赶聚合过程中后波的波速大于前方滚波, 当两波聚合时, 波速达到最大值, 之后趋于下降. 与吸收聚合类似, 内部湍流调制导致波速和波高下降.
Table 6
表 6
表 6组次3中追赶聚合过程中滚波波速变化
Table 6
 |
新窗口打开|下载CSV
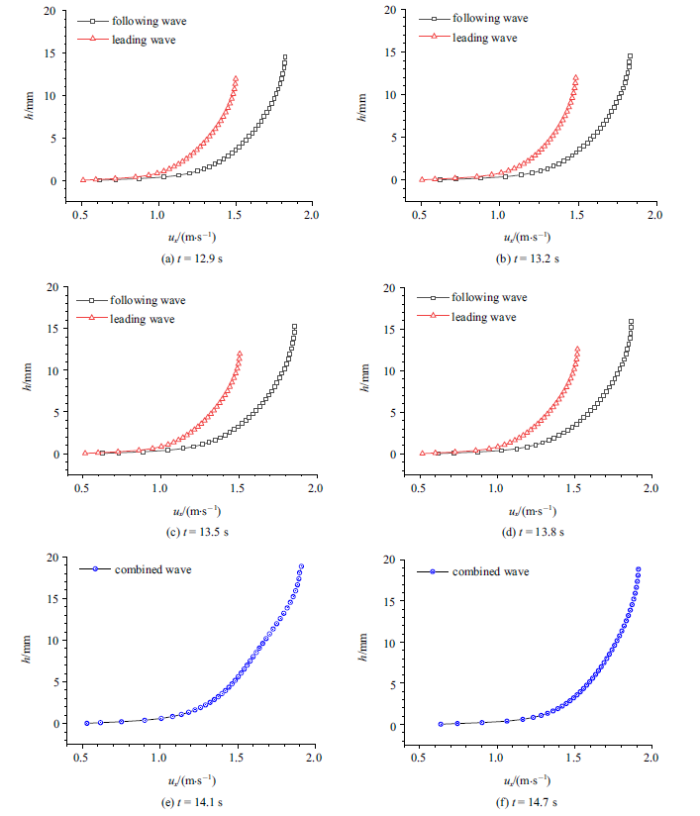
图12给出了组次3追赶聚合过程中滚波和聚合滚波波峰处的速度剖面演变过程, 图12的时间与图10(a)和图11(a)以及表6中的时刻一一对应, 其中黑色点为后波, 红色点为前波, 蓝色点为聚合后形成的滚波. 追赶聚合中, 黑线高度超过红线高度表明后波的波高高于前波, 随着演化进行, 后波逐渐追上前波, 并聚合为一个滚波. 在图12(e)可以观察到滚波聚合后速度剖面有所调整, 出现了微小振荡, 这是由于滚波聚合过程受到了湍流调制作用. 聚合后的滚波波高首先增大到了极大值, 随着振荡松弛, 波高稍有下降, 基于浅水波方程的滚波模型也发下了类似的现象[23].
图12
新窗口打开|下载原图ZIP|生成PPT图12组次3滚波追赶聚合过程中滚波峰值处速度剖面随之间的变化
Fig.12Evolution of velocity profile at the roll wave crest along with time during the overtake process of roll wave from case 3
3.3 组次4湍流黏性
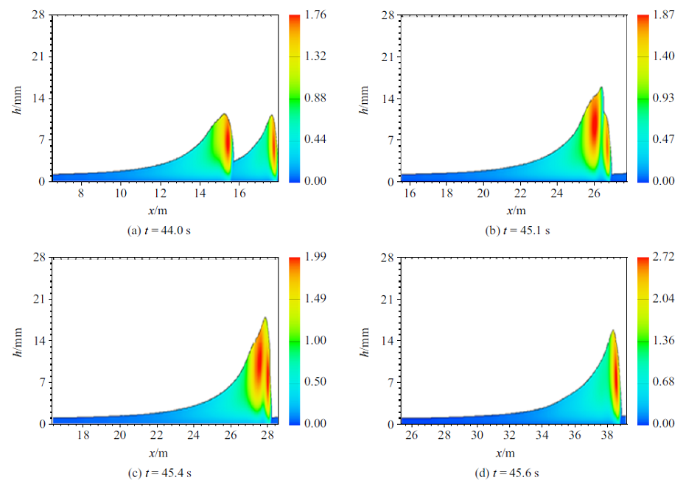
图13给出了组次4追赶聚合过程中湍流黏性的分布和演化. 滚波追赶聚合过程中, 在两个波刚刚发生融合的时刻, 滚波的波高到达最大值, 有两个湍流黏性高能区, 其形状类似聚合前的湍流黏性分布. 随着时间的推移, 来自后波的能量逐渐转移进了前方滚波中, 原先保留的两个湍流黏性高能区逐渐融合成一个高湍流黏性区. 这也说明追赶聚合中湍流作用稍微落后于波高演化, 对追赶聚合形成一定的调制作用.图13
新窗口打开|下载原图ZIP|生成PPT图13组次4滚波追赶聚合过程中湍流黏性分布随时间的演化
Fig.13Evolution of turbulent viscosity distribution with time during the overtake process of roll wave in case 4
3.4 二重追赶聚合
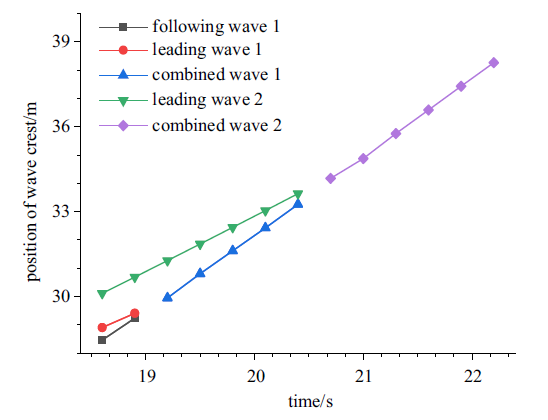
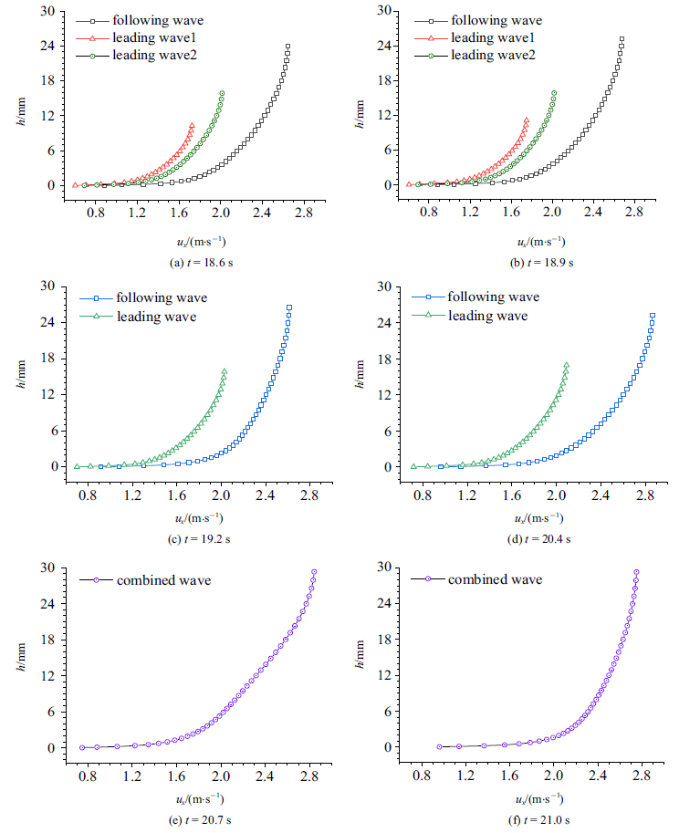
在模拟算例中还发现, 在多个滚波距离接近的情况下, 可能发生多重聚合现象. 图14展示了滚波二重聚合时波峰处空间位置随时间的演化图, 斜率变化表明, 后波的波速大于被吞并的1号滚波(红色)和2号滚波(绿色). 图15给出了二重聚合过程中三个滚波波峰处速度剖面及其演变过程, 后两个波首先聚合形成一个滚波, 然后再度追赶第一个滚波并发生聚合, 最终形成一个滚波向下游传播.图14
新窗口打开|下载原图ZIP|生成PPT图14二重聚合滚波波峰位置
Fig.14Evolution of wave crest positions during double coalescences
图15
新窗口打开|下载原图ZIP|生成PPT图15滚波二重聚合过程中滚波峰值处速度剖面随时间的变化
Fig.15Evolution of velocity profile at the roll wave crest along with time during the double coalescences
4 结论
本文采用基于雷诺平均Navier-Stokes方程和重组化群$k\mbox{-}\varepsilon $湍流模式的立面二维数值模型, 系统研究了不规则滚波发展和演化过程中的聚合现象, 给出了滚波聚合过程中的波速、波形、速度剖面以及湍流黏性分布等关键信息, 结论总结如下.(1) 滚波在特定条件下, 在足够长的空间自然增长后, 会演变成以吸收聚合和追赶聚合为主要增长模式的不规则滚波, 并进一步向自然滚波发展.
(2) 在滚波的吸收聚合和追赶聚合中, 后波经历追赶、爬升、合并以及调制等多个步骤, 最终和前波聚合成一个波长和波高更大的滚波向下游传播. 滚波聚合过程中湍流黏性演化比波形发展稍慢, 湍流作用对吸收聚合和追赶聚合起一定的调制作用.
(3) 本文还首次发现, 在多个滚波位置相互接近的情况下, 将发生多重聚合现象, 后两个滚波首先聚合形成一个后波, 该后波追赶前波并聚合形成一个新的滚波向下游传播.
本文研究, 初步分析了两类典型滚波聚合中的相互作用特征, 这一领域还有许多工作可以开展, 如滚波从规则滚波转变成不规则滚波增长的条件, 湍流在滚波聚合过程中所扮演的作用等.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
DOIURL
DOIURL
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL
DOIURL [本文引用: 5]
[本文引用: 1]
[本文引用: 1]
[本文引用: 10]
[本文引用: 3]
DOIURL [本文引用: 4]
[本文引用: 1]
DOIURL
DOIURL
DOIURL
DOIURL
DOIURL
DOIURL
DOIURL
[本文引用: 1]
[本文引用: 1]
[本文引用: 4]
