李翔宇^,2), 乔栋^,3), 程潏北京理工大学宇航学院, 北京 100081
飞行器动力学与控制教育部重点实验室, 北京 100081
深空探测导航与控制工信部重点实验室, 北京 100081

PROGRESS OF THREE-BODY ORBITAL DYNAMICS STUDY¹⁾

Li Xiangyu^,2), Qiao Dong^,3), Cheng YuSchool of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China
Key Laboratory of Dynamics and Control of Flight Vehicle of Ministry of Education, Beijing 100081, China
Key Laboratory of Autonomous Navigation and Control for Deep Space Exploration of Ministry of Industry and Information Technology, Beijing 100081, China

通讯作者: 3)乔栋, 教授, 主要研究方向: 深空探测轨道动力学与控制. E-mail:qiaodong@bit.edu.cn

第一联系人: 2)李翔宇, 博士后, 主要研究方向: 多体系统轨道设计与优化. E-mail:lixiangy@bit.edu.cn
收稿日期:2020-10-23接受日期:2021-01-13网络出版日期:2021-05-19

基金资助:

1)青年****人才支持计划.Q2016183 国家自然科学基金.12002028 国家自然科学基金.11902027 博士后基金特别资助.2019QT0038

Received:2020-10-23Accepted:2021-01-13Online:2021-05-19
作者简介 About authors


摘要
三体系统轨道动力学问题是航天动力学领域中的经典问题, 具有丰富的理论与工程意义, 并将在人类由近地延伸到深空的航天活动过程中起到至关重要的作用. 本文回顾并总结了三体系统轨道动力学相关研究进展, 并结合未来的深空探测的发展趋势, 展望了三体系统轨道动力学研究中的热点与挑战. 首先阐述了三体问题的研究背景及意义, 简要回顾了三体系统动力学模型的发展历程. 其次, 系统概述了三体系统平衡点附近的局部运动特性, 介绍了平衡点附近周期轨道解析与数值求解方法, 给出了拟周期运动的最新进展. 同时总结了共振轨道、循环轨道、自由返回轨道等三类三体系统全局周期运动的动力学特性与研究进展. 再次, 从不变流形理论和弱稳定边界理论两个方面综述了三体系统中低能量转移与捕获轨道设计的研究进展. 最后, 综述了三体系统轨道动力学在编队飞行、导航星座设计两方面的应用, 并展望了全月面覆盖轨道设计、三体系统下的小推力轨道优化和三体系统的三角平衡点开发利用中值得关注的轨道动力学与控制问题.
关键词： 三体问题;轨道动力学;周期运动;捕获轨道;转移轨道

Abstract
The orbital dynamics in the three-body system is a classical problem in the field of astrodynamics. It has rich theoretical and engineering significance, and have played an important role in the process of space activities extending from near-earth space to deep space. This paper reviews and summarizes the progress of the study of orbital dynamics in the three-body system. Combined with the development trend of deep space exploration in the future, the hotspots and challenges in the research of three-body orbital dynamics are prospected. First, the research background and significance of the three-body problem are surveyed, and the development of the dynamics model of the three-body system is briefly reviewed. Secondly, characteristics of the local motion near the equilibrium point in the three-body problem are systematically summarized. The analytical and numerical methods for periodic orbits are introduced. The latest development of quasi-periodic motion is discussed. Meanwhile, the characteristics and research progress of global periodic motions in the three-body system including resonance orbits, cycler trajectories, and free return orbits are summarized. Next, the research progress of the low-energy transfer and capture trajectory design in the three-body system is analyzed from two aspects of invariant manifold theory and weak stability boundary theory. Finally, the applications of orbital dynamics in the three-body system in formation flight and navigation constellation design are summarized. Several orbital dynamics and control problems in the design of landing trajectories for full lunar-surface coverage, the low thrust orbit optimization of the three-body system, and the utilization of non-linear equilibrium points in the three-body system are addressed for future study.
Keywords：three-body problem;orbital dynamics;periodic motion;capture trajectory;transfer trajectory


PDF (7693KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李翔宇, 乔栋, 程潏. 三体轨道动力学研究进展¹⁾. 力学学报, 2021, 53(5): 1223-1245 DOI:10.6052/0459-1879-20-367
Li Xiangyu, Qiao Dong, Cheng Yu. PROGRESS OF THREE-BODY ORBITAL DYNAMICS STUDY¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(5): 1223-1245 DOI:10.6052/0459-1879-20-367

引言

物理学和经典力学中, 三体问题是指: 已知三质点的初始位置和速度, 根据牛顿运动定律和牛顿万有引力定律求解其后续运动的问题^[1]. 三体问题动力学模型是天体力学中继传统二体模型、受摄二体模型后更为精确的动力学模型, 也是当前航天动力学中广泛采用的动力学模型之一. 研究三体问题具有丰富的理论与工程意义. 理论上, 三体问题研究能推动天体力学的发展, 为探索更为复杂的$N$体问题奠定基础, 进而帮助人类更好地理解自然界天体运动, 丰富天文学理论; 工程上, 三体问题研究有助于建立精确的动力学模型, 为空间探测任务提供有力的理论支撑.

三体问题可分为一般三体问题和限制性三体问题两类. 一般三体问题的研究可以追溯到17世纪80年代. 1687年, Newton在其《自然哲学的数学原理》中首次研究了3个大质量物体在相互扰动的引力作用下的运动问题, 并将其应用于日地月系统. 18世纪40年代, d'Alembert等曾尝试在更普遍的意义上研究此问题, 并首次使用名词"三体问题". Bruns和Poincaré分别于1887年和1889年指出, 由代数表达式与积分式表示的三体问题不存在通解. 1913年, Sundman^[2]证明了三体问题存在一类幂级数解, 但其收敛速度极其缓慢. 此后, 一般三体问题的研究重点由寻求通解转向特解, 并找到了三族周期性特解: Lagrange-Euler族, 即3个天体等间距地在圆轨道上运动; Broucke-Hénon族, 即两个天体在一个区域内运动, 第3个天体在它们外围做环绕运动; "8"字形族, 即3个天体运动在一条"8"字形的轨道上互相追赶. 2013年, Suvakov等^[3]借助计算机模拟发现了新的13族周期性特解, 将三体问题的周期解扩充至16族. 研究表明除了Lagrange-Euler族轨道适用于任意质量比的三体系统外, 其他族周期轨道要求三天体的质量相等.

以上研究针对一般的三体问题, 它与现实航天动力学的情况存在较大的差异. 为了将三体模型应用于航天动力学, 科学家对模型进行了简化与改进, 将三体问题简化成限制性三体问题RTBP, 即认为系统中某一天体的质量相对于另两天体可忽略. 根据两个质量天体的相互运动, 可以将限制性三体问题分为圆型限制性三体问题CRTBP和椭圆限制性三体问题ERTBP^[4]. 此外, 为了研究类似日地月系统这类存在卫星的行星系统, ****们又建立了四体问题模型, 包括双圆模型^[5]和拟双圆模型^[6]等.

基于简化的三体问题模型, 科学家对运动形式进行了深入研究, 并发现了平衡点这一特殊解集. 但受限于数学认知, 简化模型下的全局运动仍然无法完全求解. 随着航天技术的发展, 20世纪60年代开始, 科学家将研究重点转向平衡点附近的运动, 并讨论了平衡点在航天领域的潜在应用. 平衡点附近周期轨道的近似解析解^[7]和数值计算方法^[8]被相继发展并应用于地月系统的轨道设计. 随后, 平衡点附近不同类型的周期运动及其转移轨道成为科学家研究的热点, 基于周期轨道的应用设想也如雨后春笋般出现.

进入21世纪, 随着人们对非线性动力学理论研究的深入, 不变流形理论^[9]被引入三体系统研究中, 并用于三体系统内的低能量转移轨道设计. 随后, 三体系统的研究也由平衡点附近区域的运动进一步拓展至三体系统中质量较小天体附近区域, 提出了弱稳定边界理论^[10]和稳定集理论^[11], 并应用于三体系统下的弹道捕获轨道设计. 弱稳定边界理论与不变流形间的联系也得到了****的关注^[12], 有望建立起三体系统中统一的轨道描述方法.

三体系统动力学的理论研究也推动了航天工程应用的发展, 尤其在月球探测和深空探测领域得到了广泛的应用. 三体系统平衡点可对主天体形成全面的覆盖, 决定了其在深空导航和通信中的巨大应用价值. 就地月系统而言, $L_{2}$点附近Halo轨道上运行的飞行器能够提供对地球和月球背面连续不间断的通信, 因而是月球背面探测中通信卫星的理想飞行轨道; $L_{4}$点和$L_{5}$点的卫星能形成非常大的基线, 是天基VLBI基站的理想部署位置. 1978年, ISEE-3成为首颗进入日地平衡点轨道的人造卫星^[13]. 此后1991年, Belbruno等^[14]创造性地将弱稳定转移方式应用于日本失控卫星Hiten的任务救援中, 在太阳引力摄动下, 经过两次月球借力飞行, 成功实现月球捕获. 2018年, 我国的嫦娥4号中继星也成功进入地月$L_{2}$点Halo轨道中^[15], 成为首个在地月周期轨道长期稳定运行的通讯卫星, 为月球背面探测提供通信中继服务. 截止目前共有15颗探测器到达地月或日地平衡点开展探测, NASA, ESA, JAXA等均有相关任务计划, 平衡点探测任务如表1所示.

Table 1
表1
表1平衡点探测任务概述
Table 1Summary of libration point exploration missions

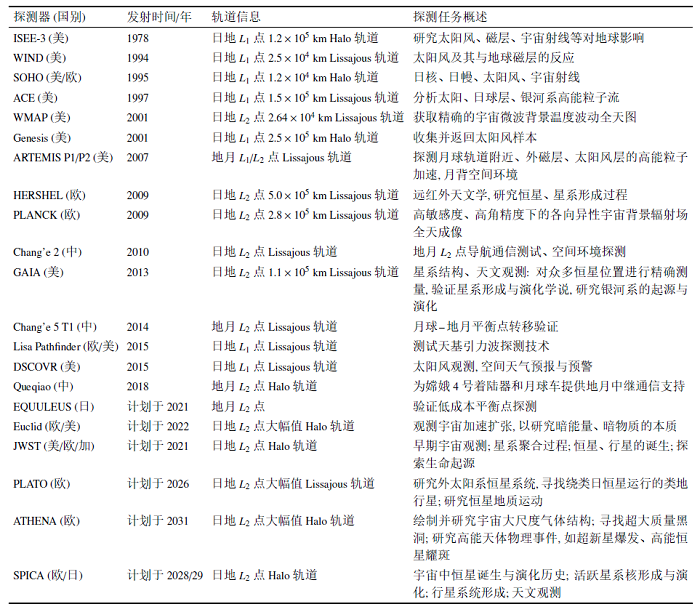新窗口打开|下载CSV

随着各国小行星探测和月球探测计划的稳步推进, 三体系统动力学的应用将更加深入与广泛. 本文以当前和未来的深空探测任务为背景, 对航天动力学中三体问题相关研究进展进行全面的回顾与总结.

1 三体系统的动力学模型

三体系统的动力学建模是研究三体系统内运动的基础, 长期以来, 科学家对三体系统动力学模型开展了深入研究, 根据运动的特性进行了不同程度的简化与假设, 提出了圆型限制性三体模型、椭圆限制性三体问题模型、Hill模型、双圆模型和拟双圆模型等动力学模型.

下面将对各动力学模型的特性与应用范围进行综述.

1.1 圆型限制性三体模型

圆型限制性三体问题CRTBP由于其形式简单且能较好的描述平衡点附近的动力学特性而成为广泛采用的三体系统动力学模型.圆型限制性三体问题中两个主天体 ($P_{1} $和$P_{2}$)绕它们的公共质心做圆周运动, 第三体的质量可忽略, 即不考虑第三体对两个主天体运动的影响. 通过归一化, 质心旋转系下的圆型限制性三体动力学可以表示为

(1)$\begin{eqnarray} \label{eq1} \left. {\begin{array}{l} \ddot{{x}}-2\dot{{y}}=-\dfrac{\left( {1-\mu } \right)\left( {x+\mu } \right)}{r_{1}^{3} }-\dfrac{\mu \left( {x-1+\mu } \right)}{r_{2}^{3} }+x \\[4mm] \ddot{{y}}+2\dot{{x}}=-\dfrac{\left( {1-\mu } \right)y}{r_{1}^{3} }-\dfrac{\mu y}{r_{2}^{3} }+y \\[4mm] \ddot{{z}}=-\dfrac{\left( {1-\mu } \right)z}{r_{1}^{3} }-\dfrac{\mu z}{r_{2}^{3} } \\ \end{array}} \right\} \end{eqnarray}$
其中

$\begin{eqnarray*} r_{1} =\sqrt {\left( {x+\mu } \right)^{2}+y^{2}+z^{2}},\ \ r_{2} =\sqrt {\left( {x+\mu -1} \right)^{2}+y^{2}+z^{2}} \end{eqnarray*}$

质量系数

(2)$\begin{eqnarray} \label{eq2} \mu =\dfrac{m_{2} }{m_{1} +m_{2} },\ \ {m_{2} <m_{1} } \end{eqnarray}$
$m_{1} $和$m_{2} $为两个主天体的质量.

1.1.1 Jacobi常数与零速度曲面

1836年, Jacobi发现圆型限制性三体模型在旋转坐标系下的能量积分为常数, 即Jacobi常数$C$, 也是目前为止CRTBP中唯一存在的积分常数

(3)$\begin{eqnarray} \label{eq3} C=2\varOmega -v^{2} \end{eqnarray}$
其中$v^{2}=\dot{{x}}^{2}+\dot{{y}}^{2}+\dot{{z}}^{2}$, $\varOmega =\left( {x^{2}+y^{2}} \right)/2+({1-\mu })/{r_{1} }+{\mu }/{r_{2} }$.

令方程(3)中的速度$v=0$, 可得曲面方程$2\varOmega \left( {x,y,z}\right)=C$, 即为零速度曲面. 零速度曲面的结构随Jacobi常数$C$的变化而变化, 如图1所示. 通过计算平衡点对应的Jacobi常数, 可以确定探测器在系统内的可能运动区域. 当$C>C_{1} $时, 探测器只能在两个主天体各自附近的空间内运动; $C_{1} >C>C_{2} $时, 探测器可以经$L_{1} $点实现主天体附近空间的转移; $C_{2} >C>C_{3} $时, 探测器可以经$L_{2} $点进入外部空间, 因而通常称日地$L_{2} $点为通往深空的大门; 进一步增大探测器能量$C_{3} >C$时, 探测器可以从$L_{3} $点进入外部空间, 因而Jacobi常数和零速度曲面是表述三体系统内轨道运动的重要指标.

图1

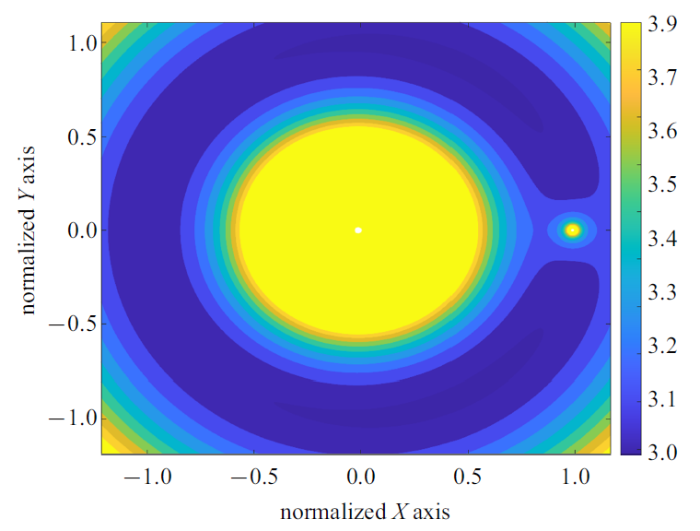新窗口打开|下载原图ZIP|生成PPT
图1三体系统中的零速度曲面

Fig.1Zero-velocity curve in the three-body system



1.1.2 Hill三体模型

为了研究日地月系统中月球的运动, Hill对CRTBP进行了进一步简化, 将旋转坐标的原点由系统质心平移至第二个主天体中心, 同时假设${R/{R_{1}}}\ll 1$, 从而对方程(1)右侧的引力项进行线性化, 从而得到方程

(4)$\begin{eqnarray} \label{eq4} \left.{\begin{array}{l} \ddot{{X}}-2\dot{{Y}}=-\dfrac{\mu }{R^{3}}X+3X \\[1mm] \ddot{{Y}}+2\dot{{X}}=-\dfrac{\mu }{R^{3}}Y \\[1mm] \ddot{{Z}}+Z=-\dfrac{\mu }{R^{3}}Z \\ \end{array}} \right\} \end{eqnarray}$
若忽略探测器在$Z$方向的运动, 方程(4)即为Hill模型, 此后Brown^[16]做了改进, 形成了Hill-Brown理论, 用于描述月球的运动. Hill模型同样可以近似描述质量比较小系统中探测器在第二主天体附近的运动.

1.1.3 圆型限制性三体问题的局限性

圆型限制性三体模型是研究三体问题的基础, 但其存在两个很重要的假设: (1)主天体的运行轨道为圆; (2)系统中不存在其他天体对探测器的运动产生摄动作用. 圆型限制性可以较好地应用于太阳$\!-\!$地球 (日地)三体系统的运动分析, 但在研究地球$\!-\!$月球 (地月)三体系统和太阳$\!-\!$火星 (日火)、太阳$\!-\!$水星 (日水)三体系统时遇到了问题.

对于地月系统内的运动, 太阳引力的影响不可忽略. 太阳引力对地月系统内探测器的影响分为直接和间接影响两方面: 一方面, Farquhar^[17]对太阳引力的影响作了全面评估并得出结论: 太阳引力对探测器的直接影响不可忽略; 另一方面, 太阳引力还会影响地月系统的运动^[18], 从而间接影响探测器的运动. 太阳引力对地月系统运动的影响体现在: (1)月球绕地球的运行轨道不再是理想的圆或椭圆. 月球轨道的实际偏心率在1/15$\sim$1/23之间变化 (周期为31.8 d)^[19]; (2)月球绕地球运行的轨道平面不再是空间中的固定平面, 而是存在着章动 (平均周期为173 d)和进动 (平均周期18.6年)^[20]. 因此, 对地月系统, 圆型限制性三体模型的理论计算与实际结果存在较大误差.

此外, 水星、火星的轨道偏心率分别约为0.205 6, 0.093 4, 日$\!-\!$火和日$\!-\!$水系统内的运动若采用圆型限制性三体模型, 主天体的运动与实际椭圆轨道存在较大差异, 因而相关结果也无法直接应用于轨道设计.

为了进一步提高动力学模型在处理上述问题中的精度, 科学家分别考虑主天体的椭圆运动和太阳引力摄动作用, 建立了椭圆型限制性三体模型与限制性四体模型.

1.2 椭圆限制性三体问题

椭圆型限制性三体模型ERTBP中考虑了两主天体轨道运动的偏心率, 如图2所示^[21], 动力学方程被改写为

(5)$\begin{eqnarray} \label{eq5} \left. {\begin{array}{l} \ddot{{x}}-2\omega \dot{{y}}-\dot{{\omega }}y=\omega^{2}x-\dfrac{\left( {1-\mu } \right)\left( {x+\mu } \right)}{r_{\rm s}^{3} }-\\[2mm]\qquad\dfrac{\mu \left( {x-1+\mu } \right)}{r_{\rm m}^{3} } \\[2mm] \ddot{{y}}+2\omega \dot{{x}}+\dot{{\omega }}x=\omega^{2}y-\dfrac{\left( {1-\mu } \right)y}{r_{\rm s}^{3} }-\dfrac{\mu y}{r_{\rm m}^{3} } \\[2mm] \ddot{{z}}=-\dfrac{\left( {1-\mu } \right)z}{r_{\rm s}^{3} }-\dfrac{\mu z}{r_{\rm m}^{3} } \\ \end{array}} \right\} \end{eqnarray}$

图2

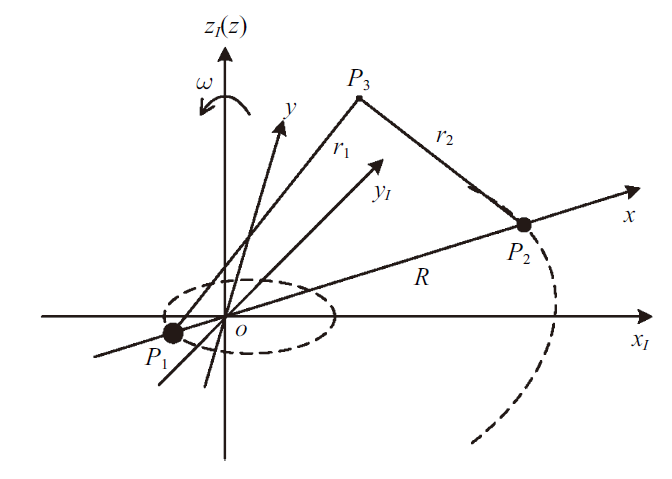新窗口打开|下载原图ZIP|生成PPT
图2椭圆型限制性三体模型^[21]

Fig.2Elliptic restricted three-body problem^[21]



式中, $\omega $为旋转坐标系相对惯性系的瞬时角速度, $\dot{{\omega}}$为瞬时角加速度. 半长轴, $e$为该椭圆运动的偏心率, $\nu $为真近点角. 同时两主天体$P_{1} $和$P_{2} $在旋转坐标系$x$轴上的位置也不再固定不变.

ERTBP为时变系统, 系统中不存在Jacobi积分, 进而不存在CRTBP中的零速度面和平衡点, 仅存在任一瞬时方程(5)左端项为0对应的瞬时平衡点. 针对ERTBP的研究主要集中于周期轨道及其稳定性. 研究发现, 在平面内有一族稳定轨道和六族不稳定轨道^[4]. ERTBP模型被应用于分析探测器在水星附近的运动及稳定性^[22-23]. 2018年10月, ESA和JAXA合作研制的"Bepi-Colombo"水星探测器于圭亚那太空中心发射升空, 该任务基于ERTBP模型开展设计转移与捕获轨道设计^[24].

1.3 四体模型

为了考虑太阳的引力影响, 从20世纪50年代开始, 国内外的****对受摄三体系统进行了大量的研究^[5,20,25]. 针对日$\!-\!$地$\!-\!$月系统提出了双圆四体动力学模型, 即认为地$\!-\!$月系统和日$\!-\!$地$\!-\!$月质心系统为两个独立的圆型限制性三体系统, 在此基础上研究探测器的运动. Nicholson^[18]忽略了月球轨道相对于黄道面的轨道倾角, 讨论了太阳扰动下的地月共线平衡点附近轨道. Lewallen和Tapley^[20]考虑了月球轨道倾角并分析了地月三角平衡点的变化, 但没有考虑月球轨道的进动和偏心率. Gómez等^[26]同样基于双圆四体模型, 分析了三角平衡点的运动稳定性. Castelli^[27]基于惯性系对双圆模型和三体动力学模型下运动的误差进行了对比分析, 并给出了各模型的最佳适用范围. 由于双圆四体动力学模型中两个三体模型相互独立, 实际上并不符合牛顿第二定律, 模型非自洽. 为了满足自洽性, Andréa等^[28]提出了拟双圆四体动力学模型, 如图3所示^[29].

图3

新窗口打开|下载原图ZIP|生成PPT
图3拟双圆四体动力学模型^[29]

Fig.3Quasi-bicircular four-body problem^[29]



对于日$\!-\!$地$\!-\!$月系统, 拟双圆四体模型的哈密顿函数可表示为

(6)$\begin{eqnarray} \label{eq6} && H_{\rm QBCP} =\dfrac{1}{2}\alpha_{1} \left( {p_{x}^{2} +p_{y}^{2} } \right)+\alpha_{2} \left( {xp_{x} +yp_{y} } \right)+\\&&\qquad\alpha_{3} \left( {yp_{x} -xp_{y} } \right)+ \alpha_{4} x+\alpha_{5} y-\\&&\qquad\alpha_{6} \left( {\dfrac{1-\mu }{r_{1} }+\dfrac{\mu }{r_{2} }+\dfrac{m_{\rm s} }{r_{\rm s} }} \right) \end{eqnarray}$
其中$\alpha_{i} $表示成参数方程的形式

$\begin{eqnarray*} \alpha_{k} \left( \theta \right)=\left\{\begin{array}{l@{\quad}l} \alpha_{k0} +\sum\limits_{j\geqslant 1} {\alpha_{kj} \cos \left( {j\theta } \right)}, & k=1,3,4,6,7\\ \sum\limits_{j\geqslant 1} \alpha_{kj} \sin \left( {j\theta } \right), & k=2,5,8 \\ \end{array} \right. \end{eqnarray*}$

式中, $\theta =\omega_{\rm s} t$, $\omega_{\rm s}$为太阳的归一化运动频率, 方程 (6)中系数的具体值可参见文献[29].

拟双圆四体模型保证日$\!-\!$地$\!-\!$月的运动满足三体问题的解. 基于该模型, Andréa^[29]讨论了平衡点的不变流形与低能量转移. 此后Guzman^[30]通过多步打靶法实现拟双圆四体动力学模型下地月平衡点附近的周期轨道/拟周期轨道的设计, 结果与真实星历情况接近, 验证了拟双圆模型在轨道设计中的可行性.

此外, 在研究火星$\!-\!$火卫系统以及双小行星系统内的运动时, 也有****将小天体的形状摄动力加入三体动力学模型中^[31-33], 用来分析不规则小天体系统内的运动, 扩展了三体动力学模型的应用范围.

从以上研究可以看出, 对三体系统的动力学建模经历了由繁到简再到繁的过程, 当前的动力学模型已能够满足多数太阳$\!-\!$行星, 行星$\!-\!$卫星系统内的运动分析, 目前的研究集中在将除天体质心引力外的其他摄动力融入三体系统动力学, 如天体非球型摄动、太阳光压、洛伦兹力等, 从而更精确地描述真实空间环境下三体系统内的运动特征.

2 三体系统平衡点附近的局部运动

三体系统内的运动始终是三体问题研究的重点. 根据运动分布的区域, 三体系统内的运动可分为在三体系统平衡点附近的局部运动、主天体附近的局部运动以及三体系统内的全局运动, 其中主天体附近的局部运动与受摄二体轨道较为相似, 但在三体动力学下将表现出不同的运动形式. 而平衡点及其附近的周期运动由于其独特的动力学特性得到了广泛的关注, 并在一系列的深空探测任务中得到了应用. 本节将着重介绍平衡点附近的局部运动, 首先给出三体系统的平衡点, 然后回顾圆型限制性模型下平衡点附近周期运动的求解及轨道保持方法, 最后给出拟周期轨道与特殊周期轨道的求解.

2.1 三体系统平衡点

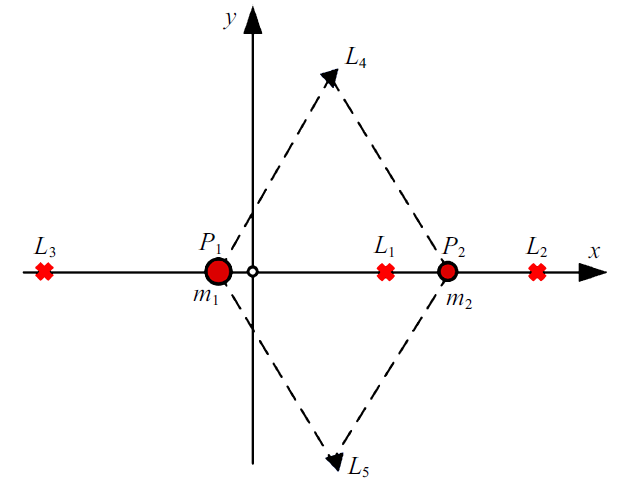
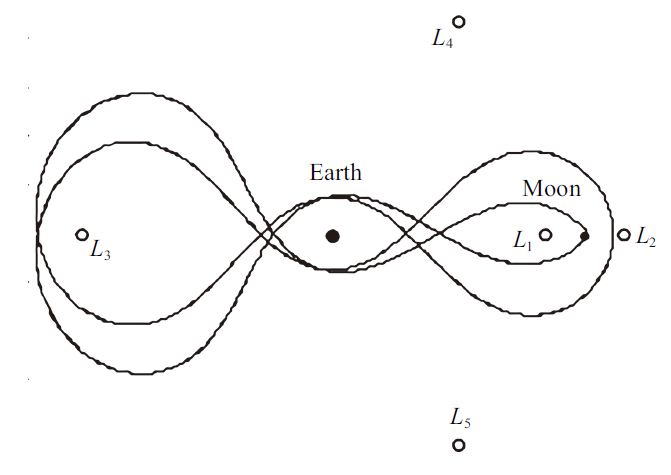
若令方程(1)中$\ddot{{x}}=\ddot{{y}}=\ddot{{z}}=0$, $\dot{{x}}=\dot{{y}}=\dot{{z}}=0$, 对应的解即为三体系统的平衡点, 位于平衡点的质点将与主天体保持相对不变的位置和速度. 圆型限制性三体系统中共存在5个平衡点, 其中包括3个共线平衡点和两个三角平衡点. Euler于1767年发现了的3个共线平衡点$L_{1} $, $L_{2} $和$L_{3} $, 其中$L_{1} $点位于两个主天体之间, $L_{2} $点位于$P_{2} $外侧, 而$L_{3} $点位于$P_{1}$一侧, $L_{1} $和$L_{2} $点距离$P_{2} $较近, 而$L_{3} $距离主天体较远. 此后, Lagrange于1772年求解了三角平衡点$L_{4} $和$L_{5} $, 它们与主天体构成等边三角形. 随着人们在太阳$\!-\!$木星 (日木)系统$L_{4} $和$L_{5}$点附近发现大量的小行星群落 (特洛伊族小天体), 三体动力学模型平衡点的存在得以证实. 图 4给出了三体系统平衡点分布示意图.

图4

新窗口打开|下载原图ZIP|生成PPT
图4三体系统平衡点分布示意图

Fig.4Distributions of five libration points in the three-body system



将方程(1)在平衡点附近线性化, 通过求解对应的特征方程可以判断平衡点的稳定性. 共线平衡点为不稳定平衡点, 施加扰动后将无法继续保持在平衡点位置; 三角平衡点为条件稳定平衡点, 当两主天体质量满足以下条件时, 三角平衡点是稳定的

(7)$\begin{eqnarray} \label{eq7} m_{1} \geqslant 25m_{2} \left( {\dfrac{1+\sqrt {1-{4/{625}}} }{2}} \right) \end{eqnarray}$
探测器位于稳定的三角平衡点, 受到扰动后仍维持在平衡点附近, 不会发生逃逸. 目前太阳系常见的三体系统, 如日地系统、地月系统、日木系统等均满足上述质量约束条件, 因此它们的三角平衡点均是稳定的, 但部分质量接近的双小行星系统具有不稳定的平衡点, 此外研究表明小行星的不规则形状摄动也会影响三角平衡点的稳定性^[32]. 地月系统三角平衡点的卫星能形成非常大的基线, 是天基VLBI基站的理想部署位置.

2.2 平衡点附近的周期与拟周期运动

共线平衡点 ($L_{1} $, $L_{2} $和$L_{3} $)的拓扑类型为"中心$\times$中心$\times$鞍点", 鞍点型的分量使其成为不稳定的平衡点^[34], 而"中心$\times$中心"的分量则形成为四维中心流形, 分别对应着平衡点附近的两族周期轨道: 平面Lyapunov轨道和垂直Lyapunov轨道. 从平面Lyapunov轨道族中还分岔出另一族周期轨道: Halo轨道. 由KAM定理可知^[35], 四维中心流形内存在两个频率不共振的周期运动耦合而成的无数拟周期轨道, 也称为Lissajous轨道. 需要指出的是, Halo轨道对应着两个频率相等的特殊情况. 当频率的比值可以表示成两个整数比时, 拟周期轨道将退化为共振轨道. 圆型限制性三体系统中平衡点附近的周期轨道求解经历了解析近似解和精确数值解两个阶段, 在周期解的基础上, ****又通过延拓和频闪映射得到了拟周期轨道以及特殊的周期运动族.

2.2.1 周期轨道的近似解析解

解析法的基础是摄动理论中求解常微分方程近似周期解的经典方法——LP方法(linstedt-poincare), 构建平衡点运动的扰动方程并将扰动项进行幂级数展开, 消除长期项后得到正余弦形式的扰动运动周期解. 利用LP法, 20世纪70年代, Farquhar等^[36]推导了日地系和地月系点附近的大幅值Halo轨道以及小幅值的Lissajous轨道的线性解析表达式. Richardson^[7]进一步推导了Halo轨道的三阶展开式, 成为求解Halo轨道近似解析解的经典解法. 此后, 尽管也有****求解了Halo轨道和Lissajous轨道的高阶解析表达式^[37], 但计算形式繁琐, 且三阶解析解已可满足数值计算的精度要求. 总体来看, 解析法的形式较复杂, 且由于受到展开式级数的限制, 解析法的精度有限, 无法直接用于周期轨道设计. 随着轨道距离平衡点的距离增大, 解析解的拟合误差也显著增大. 但其可以为数值求解提供较好的初值猜测, 为更大范围相空间内周期轨道的求解奠定了基础.

2.2.2 数值法求解精确周期轨道

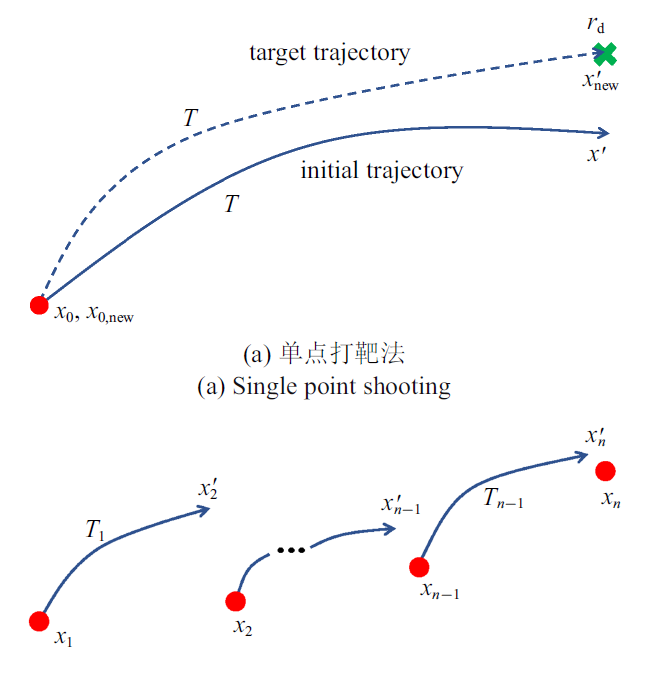
数值法求解周期轨道的本质为微分修正法, 其求解过程可描述为: 将解析法求得的周期轨道作为初值猜测, 迭代修正初始点的状态直至满足周期性条件, 也即轨道在经过一个周期的积分后返回初始点. Howell^[38]为周期轨道的数值法求解做出了突出的贡献, 首次提出了微分修正法求解Halo轨道的思路, 取三阶解析解作为初值, 通过修正初值来获得满足周期性条件的轨道, 该方法也称为单点打靶法, 如图5(a)所示. 此外, 利用CRTBP系统的对称性, 选择初始点从对称轴 (或平面)出发, 可降低问题的维度并缩减积分时间. 然而, 上述方法并不适用于Lissajous轨道, 这是由于Lissajous轨道拟周期的属性使其永远无法返回同一初始点. 针对这一问题, Howell等^[8]提出了用于求解Lissajous轨道的两级微分修正法 (图5(b)): 首先, 利用解析法得到一系列的离散点; 然后, 利用单点打靶法得到一条位置连续的轨道, 此为第一级修正; 最后, 再利用微分修正法抵消中间拼接点的速度误差, 从而得到一条位置与速度都连续的轨道. Folta等^[39]进一步将多点打靶法扩展到了高精度星历模型下, 成功设计了ARTEMIS探测器的轨道, 这也是人类历史上第一颗地月平衡点探测器.

图5

新窗口打开|下载原图ZIP|生成PPT
图5微分修正法的示意图

Fig.5Illustration of the differential correction method



基于微分修正的数值方法只适用于单个周期轨道的求解. 若要获得整个轨道族, 需要求解不同的解析解初值进行修正, 过程繁琐且对于振幅较大的周期轨道失效. 而利用数值延拓技术可以较快地获得轨道族. 延拓法从已知的轨道出发, 选择合适的延拓参数来猜测出新的周期轨道的初值, 然后利用微分修正法得到一条新的周期轨道. 延拓参数一般为表征周期轨道的特征参数, 比如雅可比积分或轨道周期. 针对单参数延拓法容易遇到奇点的情况, Simo^[40]提出了稳定且高效的变步长弧长延拓法, 沿着特征曲线方向进行延拓, 猜测初值的精度较高且延拓速度快. 利用变步长弧长延拓法, 图6给出了几类典型的平衡点轨道族, 包括平面与垂直Lyapunov轨道族、Halo轨道族、以及Lissajous轨道^[41].

图6

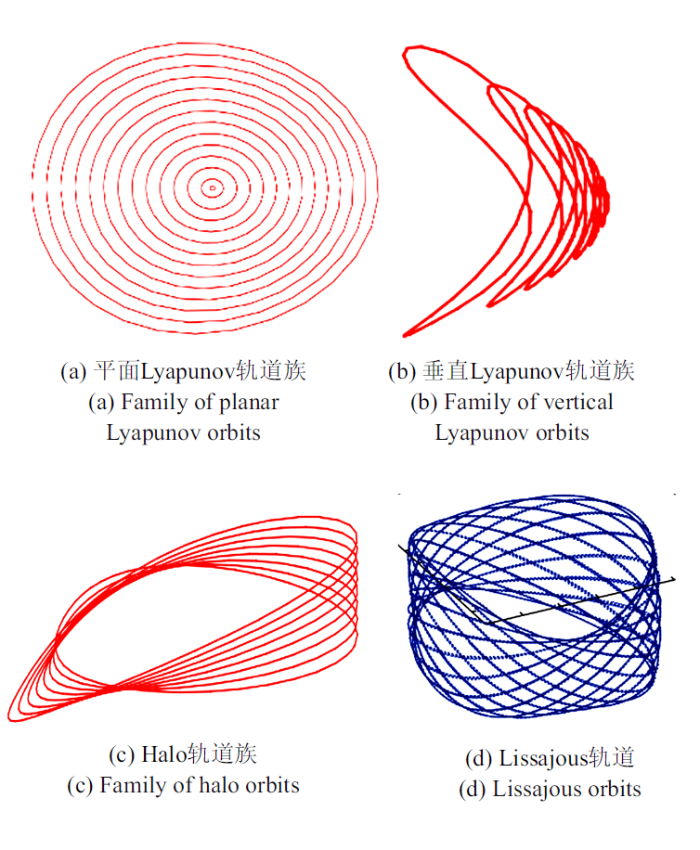新窗口打开|下载原图ZIP|生成PPT
图6几类典型的平衡点轨道示意图

Fig.6Typical orbits about libration points



2.2.3 平衡点周期轨道的保持

由于平衡点轨道具有弱稳定的特性, 受到复杂的自然扰动力的影响, 航天器将会偏离标称轨道, 因此必须定期执行轨道保持机动将其控制在平衡点轨道附近的一定区域内. 1961年 Colombo^[42]首次评估了稳定地月$L_{1}$点附近平衡点轨道所需的能量, 受限于当时对平衡点轨道的认识, 控制目标仅仅是将航天器维持在平衡点附近. 1966年Farquhar^[17]评估了地月$L_{2}$点的中继卫星轨道保持每年所需的能量约为10 m/s. 随着有关于平衡点附近的周期、拟周期轨道理论的完善, 轨道保持理论也得到了充分的发展.

平衡点轨道保持策略的研究可以分为3个阶段. 1974年 Breakwell等^[43]基于最优控制理论, 详细论述了地月$L_{2}$点附近周期轨道跟踪标称轨道的方案, 该方法可看作是靶点法的雏形. Howell和Pernicka^[44-45]基于线性控制思想, 对靶点法进行了改进, 给出了靶点模式的脉冲控制策略, 可作为研究的第一阶段. 在这一阶段的研究通常假设导航数据足够精确、修正脉冲 (或者小推力)可以频繁施加. 在该假设下, 对于一个日地系平衡点探测器 (周期约为6 m), 每一周或两周施加一次微小的脉冲修正, 甚至可以得出轨道保持能量接近于零的结论. Dunham等^[46]则指出: 研究无工程应用价值的轨道保持方案是无意义的.

随着第一次平衡点飞行任务ISEE-3的执行, 来自工程执行方面的约束和导航测量的约束被考虑到轨道保持策略的设计中^[47]. 自此, 平衡点轨道保持策略的研究进入第2个阶段. 脉冲控制方案由于其在工程上易实现、可靠性高、计算效率高而被广泛采用, 其中文献[46]中记载的$X$轴速度控制法被用于日地系统平衡点飞行器SOHO以及ACE的轨道保持中. 该算法根据三体条件下周期轨道穿越$X-Z$平面 (日地连线与地球公转轨道角动量方向确定的平面)时刻, $X$方向速度为零的特征, 对探测器每次穿越$X-Z$平面的$X$轴方向的速度进行限制. 文献[48,49]中的方法都延续了ISEE-3的控制思想, 对日地系统平衡点轨道使用多次的脉冲来建立一种"松"控制的轨道保持策略, 将探测器保持在标称轨道附近.

随着平衡点探测研究的不断深入以及对于地月系统平衡点探测成为热点, 平衡点轨道保持的研究进入第3个阶段, 即星历模型条件下的轨道保持研究阶段. 第2阶段的研究中, 研究的对象通常是日地系统平衡点附近轨道上的探测器, 或者是忽略了太阳引力的地月平衡点探测器. 对应的目标轨道由圆型或者椭圆型限制性三体模型生成, 对于日地系统 (或者忽略第四体引力的地月系统), 模型较为合理, 但对于考虑太阳引力影响的地月系统误差较大. 相应的轨道保持方案将不能胜任地月系统的平衡点任务. 例如, 在星历模型中, $X$轴速度控制法在穿越$X$轴时$X$方向速度为零的假设将不成立.

第3阶段的研究延续了第2阶段中对于工程实用性以及导航测量的考虑, 但仅要求探测器的实际轨迹在标称轨迹的附近运行, 并不要求其严格按照标称轨迹飞行. Pavlak等^[50]在靶点法的基础上提出了基准轨迹靶点法, 轨道保持仅要求探测器能朝向下一目标靶点的位置靠近即可. Folta等^[51]针对ARTEMIS任务, 从工程实际的角度对Floquet法、最优轨迹延续法和全局最优搜索法进行了验证, 并指出最优轨迹延续法是工程上可实施控制的最优方法, 该方法不严格依赖于标称轨道, 但需要进行轨迹优化, 计算量较大.

2.2.4 拟周期轨道的参数化求解方法

由于拟周期轨道不满足周期性条件, 拟周期轨道族的求解比周期轨道族复杂. 拟周期轨道上的点经过一个周期的积分后不会返回同一点, 而是返回与初始点相差固定相位角的另外一点, 使得微分修正法中目标函数构造成为难题. 因此, 除了文献[8]中两级微分修正算法, Lissajous拟周期轨道的求解一直没有实质性的突破. 直至21世纪初, Gómez等^[52]首次提出了Lissajous轨道的参数化求解方法, 利用关于两个不共振频率的Fourier级数来参数化表示Lissajous轨道, 从而可以利用数值延拓法, 通过延拓Fourier级数表达式的系数来求解Lissajous轨道族.

参数化方法的思路可将Lissajous轨道表示为两个频率$\left( {\xi ,\eta }\right)$的函数$\psi \left( {\xi ,\eta } \right)$

(8)$\left.\begin{array}{l}\psi\left(\xi+t \omega_{1}, \eta+t \omega_{2}\right)=\phi_{t}[\psi(\xi, \eta)] \\\forall t \in \mathbb{R}, \quad \forall \xi, \eta \in[0,2 \pi]\end{array}\right\}$
式中, $\omega_{1} $和$\omega_{2} $为两个周期性运动的频率, $\phi_{t} $为CRTBP微分方程的映射流, $\phi_{t} \left[ {\psi \left( {\xi ,\eta } \right)} \right]$则为$\psi \left( {\xi ,\eta } \right)$在映射$\phi_{t} $下经过时间$t$的象.

通过引入频闪映射, 也即时间固定的映射$\phi_{T}$, 可以将Lissajous轨道的求解问题简化为其频闪映射——不变曲线的求解问题. 通过固定两个频率中的任意一个 (如令$\eta =0$), 得到不变曲线$\varphi \left(\xi \right)=\psi \left( {\xi ,0} \right)$, 其满足不变方程

(9)$\begin{eqnarray} \label{eq9} \varphi \left( {\xi +\rho } \right)=\phi_{T} \left[ {\varphi \left( \xi \right)} \right] \end{eqnarray}$
式中, $T=2\pi/\omega_{2} $为由频率$\omega_{2} $确定的返回时间, $\rho =2\pi \omega_{1} /\omega_{2} $为旋转数.

将不变曲线$\varphi \left( \xi \right)$表示成Fourier级数的形式

(10)$\begin{eqnarray} \label{eq10} \varphi \left( \xi \right)=C_{0} +\sum\limits_{k=1}^M {\left[ {{C}_{k} \cos \left( {k\xi } \right)+{S}_{k} \sin \left( {k\xi } \right)} \right]} \end{eqnarray}$
式中, Fourier系数$C_{0} \in \mathbb{R}^{6},{C}_{k} \in \mathbb{R}^{6},{S}_{k} \in \mathbb{R}^{6}$为待求解变量.

经过以上处理, Lissajous轨道的求解问题就转化为其频闪映射下不变曲线的Fourier系数的求解问题. 通过对$\xi $在$\left[ {0,2\pi } \right]$ 之间进行离散, 从而得到由不变方程(9)构成的方程组, 然后利用类牛顿法来迭代求解^[53].

基于频闪映射的参数化方法可以用于数值求解Lissajous轨道并进行延拓, 且具有较强的普适性, 可以很容易扩展到高维 (频率$\geqslant 3$)的拟周期轨道求解, 也可以应用于其他系统中周期轨道的求解. 但是该方法每一次牛顿迭代都需要求解$6\left( {2N_{\rm f} +1} \right)\times \left[{6\left( {2N_{\rm f} +1} \right)-1} \right]$个方程, 运算量相对较大. Kolemen等^[54]基于庞加莱映射进行降维处理, 然后利用参数化方法来求解不变曲线, 但是受限于拟周期轨道的几何形状, 需要谨慎选取庞加莱截面, 以免出现庞加莱截面上的曲线不闭合的情况.

2.2.5 椭圆型限制性三体问题中的周期与拟周期轨道

以上的研究大都是基于CRTBP模型展开的, 然而在实际的三体系统中, 小主天体的轨道通常为绕大主天体的椭圆轨道, 轨道偏心率将对三体系统内航天器的运动产生不可忽略的影响. 如何在更精确的动力学模型下, 比如ERTBP或者星历模型, 高效并快速地求解周期轨道或者拟周期轨道, 成为国内外的热点研究问题. 由于小主天体轨道偏心率的周期性扰动, CRTBP模型下的周期轨道将无法一直满足其周期性条件, 只存在周期为小主天体轨道的周期整数倍的周期轨道, 也即共振轨道, 因此也不再存在连续的周期轨道族. Campagnola等^[55]将CRTBP模型下Halo轨道在ERTBP下对应的周期轨道称为椭圆Halo轨道 (elliptic Halo orbit), 通过以Halo轨道为初值并基于偏心率的数值延拓来求解. Peng等^[56]将ERTBP下的周期轨道命名为多圈Halo轨道 (multi-revolution Halo orbit), 采用了弧长延拓法来求解多圈Halo轨道, 有效解决了基于偏心率单参数延拓出现奇点的问题. Ferrari等^[57]则研究了ERTBP模型下与质量较小的主天体轨道周期呈整数倍的周期轨道, 通过以CRTBP下的共线平衡点$L_{1}$, $L_{2}$和$L_{3}$附近的Halo轨道、Lyapunov轨道和垂直Lyapunov轨道为初值, 沿着偏心率进行延拓求解. 图7给出了ERTBP模型下的多圈周期轨道及其对应于CRTBP模型下的周期轨道^[57].

图7

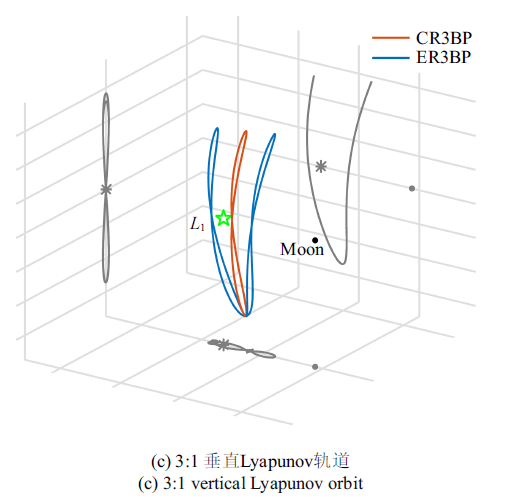新窗口打开|下载原图ZIP|生成PPT
图7ERTBP下的多圈周期轨道

Fig.7Multi-revolutions periodic orbits in the ERTBP



2.2.6 特殊类型的局部周期运动

除了以上介绍的几类常见的平衡点周期轨道, 如水平Lyapunov轨道、垂直Lyapunov轨道、Halo轨道和Lissajous轨道, 通过数值延拓和微分修正, ****们还发现了几类独特的、具有特殊应用前景的三体系统内局部周期运动, 包括近垂直Halo轨道 (near-rectilinear Halo orbit, NRHO)、蝴蝶形轨道(butterfly orbit)^[58]和大幅值逆行轨道 (distant retrograde orbit, DRO)^[59]. 其中, NRHO作为NASA未来月球门户的参考任务轨道, 最近几年得到了一系列深入的研究, 包括以其为出发或到达轨道的转移轨道设计、从NRHO逃逸或者在轨航天器的抛弃轨道设计等等. DRO也在转移轨道设计中得到了关注^[60], 由于其可以延展到地球附近, 并与Lyapunov轨道相切, 可以与后者拼接实现地月空间的转移. Butterfly轨道的形状较为特殊, 同时途径$L_1$点、$L_2$点和质量较小的主天体, 且轨道在空间中有较大的弯折. 几类特殊的平衡点周期轨道如图8所示.

从平衡点轨道研究的发展历程可以看出, 其经历了从解析法到数值法、从单个轨道到整个轨道族、从简单的CRTBP到更复杂的ERTBP或四体模型、从周期轨道到多个频率耦合的拟周期轨道的过程. 随着周期轨道种类与数量的增加, 对三体系统相空间的认知也在加深, 可以从平衡点的小范围邻域扩展到了有界运动的边界. 从已开展的平衡点任务中可以看出, 实际任务实施中受到测控精度、空间复杂摄动干扰和模型不确定性的影响, 理想的周期运动并不存在或无法实现, 拟周期运动更具有实际应用价值. 在未来的研究中, 高精度的动力学模型下的拟周期轨道设计与特性分析将成为研究的难点. 如何提出更高效的算法求解, 并探索拟周期轨道在航天任务中的应用潜能, 已成为亟待解决的问题.

图8

新窗口打开|下载原图ZIP|生成PPT
图8几类特殊的平衡点周期轨道示意图

Fig.8Several types of special periodic orbits around libration points

3 三体系统中的全局周期运动

除平衡点附近轨道外, 三体系统下还存在着全局周期轨道, 由于不存在类似平衡点的解析初值, 只能采用纯数值的方法进行求解. 由于CRTBP问题状态空间的维度为六维, 采用遍历搜索方法所需的计算量时间和存储空间巨大. 因此, ****们多利用CRTBP系统的对称性来研究周期轨道, 通过选择对称轴或者对称面, 可将需要遍历的状态空间减半, 且积分时间也可减半, 从而极大的提高了计算效率. Russell在三体问题全局轨道的遍历求解中做出了重要的贡献, 在文献[61]中对木星$\!-\!$木卫二CRTBP模型下木卫二附近的对称周期轨道进行了遍历求解, 利用微分修正法和网格搜索法得到了大量的周期轨道, 并进行了稳定性分析, 部分轨道的示意图如图9所示^[61].

图9

新窗口打开|下载原图ZIP|生成PPT
图9木星$\!-\!$木卫二系统下的全局周期轨道

Fig.9Global periodic orbits in the Jupiter-Europa system



在三体系统全局周期轨道中, 存在几类特殊的轨道, 包括共振轨道、循环轨道、自由返回轨道等, 他们具有较好的稳定性或途径主天体, 因此在航天任务设计中得到广泛的应用.

3.1 共振轨道

共振轨道(resonance orbit)指轨道周期与主天体的轨道周期呈整数比关系的轨道. 如果定义B与A形成$p$$q$的共振轨道, 那么B绕中心天体飞行$p$圈所需的时间与A绕中心天体飞行$q$圈相同. 靠近主天体的共振轨道通常具有较好的稳定性, 受扰后不会发散或与天体发生碰撞, 是探测任务理想的任务轨道. Escribano和Vaquero^[62-63]从动力学结构方面, 对地月系统共振轨道进行了深入分析, 基于庞加莱截面求解了平面以及空间的共振轨道, 并将共振轨道与不变流形相结合, 提出了低能量转移轨道的设计方法. 地月三体系统下的平面以及空间共振轨道如图10所示^[63]. 此后, Antoniadou等^[64]研究了地外行星系统中共振比为4:3, 3:2, 5:2, 3:1及4:1的平面及空间共振轨道并讨论了轨道稳定性, 发现稳定共振轨道对应的偏心率较大. Anderson等^[65]进一步利用网格搜索方法对木卫系统中共振轨道进行了研究, 利用连续法在稳定共振轨道的计算得到不稳定的共振轨道.

图10

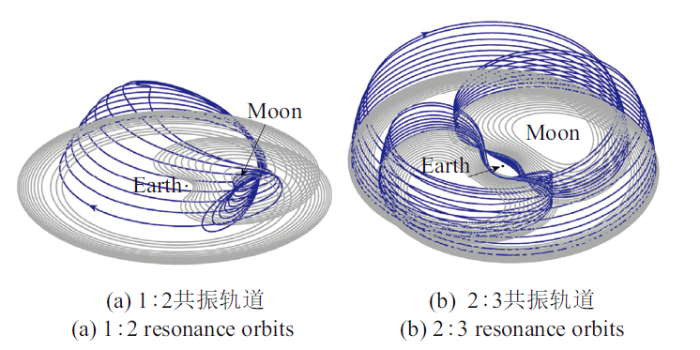新窗口打开|下载原图ZIP|生成PPT
图10地月三体系统下的共振轨道示意图

Fig.10Resonance orbits in the Earth-Moon three-body system

3.2 循环轨道

循环轨道 (cycler trajectory)为连接两颗天体的自然周期轨道, 可以看作是一种特殊的共振轨道. 通过循环轨道可以实现天体之间的连续往返, 然而无法在其中任意一颗天体上逗留, 典型的地月循环轨道如图11所示^[66]. Aldrin^[67]于1985年首次提出了地月循环轨道的概念, 为载人登月、开采月球资源等任务提供了一种经济可行的方案, 该方案通常包括两类飞行器, 第一类转移飞行器利用循环轨道实现地月往返, 另一类运输飞行器则负责在转移飞行器与月球表面之间输送人员和物资. 由于转移飞行器无需被地球或者月球捕获, 并能多次重复使用, 从而能显著的节省入轨燃料. 随着月球探测任务的增加和"地月经济带"等概念的提出, 地月循环轨道有望得到实际的应用. 但目前针对该类轨道的研究较少且模型仅基于圆型限制性三体问题, 考虑月球轨道偏心率和其他摄动因素, 研究地月循环轨道的稳定性, 转移周期和与近地/近月飞行器的交会窗口将更有现实意义.

图11

新窗口打开|下载原图ZIP|生成PPT
图11地月循环轨道

Fig.11Earth-Moon cycler trajectory

3.3 自由返回轨道

自由返回轨道 (free return orbit)则是另外一类特殊的周期轨道, 主要应用于载人任务的备用轨道. 自由返回轨道能保证在近月点变轨时点火失败的情况下, 即使不进行月球捕获机动, 也可经自由返回轨道返回地球附近. 图12为地月自由返回轨道的示意图. 阿波罗13号探测器利用了自由返回轨道, 在发生动力故障后安全返回地球^[68].

图12

新窗口打开|下载原图ZIP|生成PPT
图12地月自由返回轨道

Fig.12Earth-Moon free return orbit



早期的关于地月转移轨道的研究大多是在双二体模型下展开的. 黄文德等^[69]给出了自由返回轨道的设计方法, 并对影响返回轨道的主要参数, 比如飞行时间、近月距、轨道倾角等进行了分析. 彭祺擘等^[70]则将优化算法引入自由返回轨道的设计过程中, 大大加快了轨道的搜索速度. 然而, 以上文献都没有考虑载人登月中固定近月点高度的工程约束. 王丹阳和邓辉^[71]针对该问题, 提出了固定近月点高度的搜索策略, 通过调节其他约束参数来设计更符合工程实际需求的自由返回轨道. 候锡云等^[72]则在限制性三体模型的框架下, 研究了白道面内自由转移轨道的性质, 并分析了近月段与近地段轨道倾角的变化规律.

由于人类对三体系统认知仍不全面, 特别是引力常数对周期运动存在性和稳定性的影响尚不清楚, 因此, 除以上几类周期轨道外, 三体系统中可能仍有大量具有良好性能的全局周期运动未被发现. 相比于平衡点附近的局部运动, 对三体系统内全局周期运动的认识仍是一个漫长的过程, 一方面可以结合机器学习和人工智能^[73], 开发更高效和高精度的轨道搜索算法, 另一方面, 采用先进的数学工具 (如辛几何、李群^[74]等)重新认识三体系统, 探寻其中周期运动的共同特征和特殊描述方式, 可能为三体系统全局周期运动的研究带来新的思路. 同时, 如何将工程约束、复杂的动力学环境与特殊轨道的应用潜能结合起来, 提出快速高效的参考轨道设计方法, 也是未来的研究中需要思考与解决的问题.

4 三体系统中的转移轨道设计

针对文中讨论三体系统中的周期运动, 实现不同周期运动间的转移也是三体系统轨道动力学研究的重点. 根据不同的初始与终端状态, 转移轨道包括主天体至平衡点的转移、同一系统不同平衡点轨道间的转移、不同系统平衡点轨道之间的转移等. 其中主天体至平衡点的转移又包括较大主天体至平衡点的转移 (如地球至地月平衡点转移)和较小主天体至平衡点的转移 (如地球至日地平衡点转移). 从设计思路及其所依赖的动力学模型来讲, 转移轨道又可以分为直接转移、基于不变流形理论的低能量转移、考虑主天体引力影响的弱稳定边界弹道转移等. 下面将分别针对这3种设计思路进行总结.

4.1 直接转移方式

直接转移方式与传统二体模型下的双脉冲转移方式类似, 以地月系统下地球至地月$L_{1}$/$L_{2}$点转移为例, 探测器的第一次为月球转移脉冲, 从地球停泊轨道离轨进入地球转移段; 第2次脉冲为月球附近轨道 (比如Halo轨道)的入轨脉冲. 直接双脉冲转移如图13所示^[75], 目标轨道分别为地月$L_{1} $或者$L_{2}$点附近的Halo轨道. Parker等^[75]对地月系统下的直接转移方式进行详尽的研究与分析, 并指出直接转移所消耗的时间通常较短, 约5 d$\sim$2 m之间. 针对$L_{1} $和$L_{2} $的目标Halo轨道, 月球转移脉冲对应的能量分别为$-2.6\sim-2.0$ km$^{2}$/s$^{2}$和$-2.6\sim -1.0$ km$^{2}$/s$^{2}$; 而第2个Halo入轨脉冲的大小通常为$500\sim600$ m/s之间, 最大与最小值则分别约为950 m/s与430 m/s.

图13

新窗口打开|下载原图ZIP|生成PPT
图13地月$L_{1} $/$L_{2} $ Halo轨道直接转移示意图

Fig.13Direct transfer trajectory to the Earth-Moon $L_{1} $/$L_{2} $ Halo orbit

4.2 基于不变流形的低能量转移轨道设计

随着对平衡点轨道认知的深入, ****们开始将平衡点轨道的不变流形引入到低能量转移轨道的设计中. 20世纪90年代, Gómez等^[76]首次将动力系统理论应用到CRTBP的动力学分析中, 发现Halo轨道的稳定流形能够延展到月球, 并利用这类自然的轨道实现了从地球到地月$L_{1}$点Halo轨道的转移轨道设计. 研究发现基于不变流形的低能量转移轨道所消耗的能量要远小于直接转移方式. 图14给出了典型的地月低能量转移的示意图. 低能量转移轨道沿着Halo轨道的流形方向切入Halo轨道, 因此无需施第2次入轨脉冲.

图14

新窗口打开|下载原图ZIP|生成PPT
图14地月$L_{1} $/$L_{2} $ Halo轨道低能量转移示意图

Fig.14Low-energy transfer trajectory to Earth-Moon $L_{1} $/$L_{2}$ Halo orbits



在此之后, 很多****开始广泛研究不变流形理论在低能量轨道转移中的应用. Barden等^[77]展开了一系列的研究, 包括利用稳定流形实现地球至Halo轨道的转移, 利用不稳定流形实现Halo轨道返回至地球的转移, 不同Halo轨道之间的转移等. Born和Parker^[78-79]则全面研究了地月低能量转移的问题, 考虑了不同的近地出发轨道, 不同的环月目标轨道, 以及不同的转移方式, 并从发射能量$C_{3}$、转移时间、转移总脉冲大小等方面对以上各种情况进行了比较与分析, 并将不同路线下低能量地月转移的各种性能指标总结如图15所示.

图15

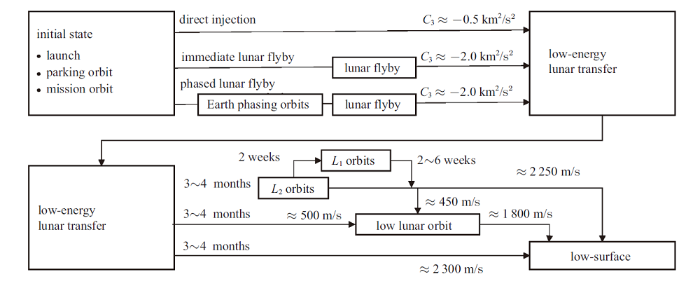新窗口打开|下载原图ZIP|生成PPT
图15不同路线的低能量地月转移概览图

Fig.15Flowchart of different low-energy lunar transfer itineraries



Parker等^[75]在研究中发现, 当Halo轨道的稳定流形经由月球附近时, 转移所需消耗的脉冲更少, 但是转移时间会增长. Gordon^[80]对这一现象进行了深入的研究, 将不变流形与月球近旁飞越相结合, 设计了地球至地月$L_{2}$点Halo轨道的双脉冲转移轨道. 然而以上研究中只考虑了沿着Halo轨道的自然流形进入Halo轨道的情况, 转移时间通常较长. Li等^[81]则提出了基于月球飞越的三脉冲转移方式, 通过增加Halo轨道入轨脉冲这一额外的机动, 可极大缩减在流形上滑行的时间. Zeng等^[82]对文献[81]提出的方法进行了深入的研究, 详细分析了不同的借力高度、飞行角以及Halo轨道入轨点等对转移总脉冲的影响. 图16为考虑月球旁近飞越的低能量转移方式示意图. Cheng等^[83]研究了利用流形实现平衡点轨道向其他轨道 (环月轨道)的转移问题, 考虑了月球自转轴与白道面之间的夹角, 提出了适用于任意倾角、任意高度环月轨道的双脉冲通用转移方案.

图16

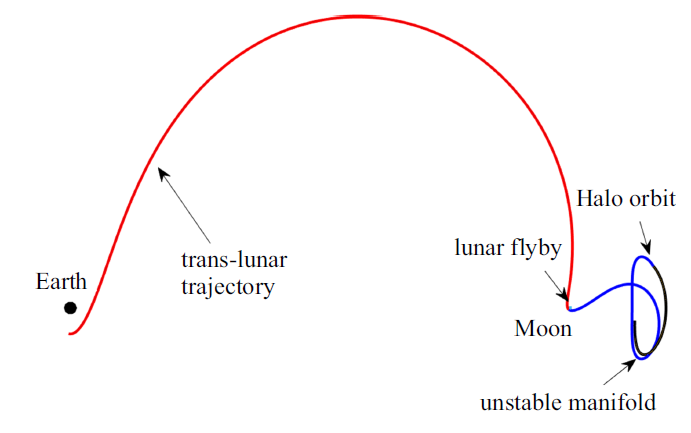新窗口打开|下载原图ZIP|生成PPT
图16基于月球旁近的地月$L_2$点Halo轨道低能量转移示意图

Fig.16Low-energy transfer trajectory to Earth-Moon $L_{2}$ Halo via lunar flyby



另外, ****们还利用不变流形研究了平衡点轨道间的转移, 包括同一平衡点之间的转移 (接)以及不同平衡点之间的转移 (异宿连接). Gómez等^[84]首先考虑能量相等的两个Halo轨道, 发现利用异宿连接可以实现零燃耗转移; 此后, Gómez等^[85]针对能量不相等的情况, 又提出了基于双脉冲转移方法, 也即分别沿着出发Halo轨道的切向和目标Halo轨道稳定流形的方向施加一次机动. Davis等^[86]进一步研究了不同能量的平衡点轨道之间的转移问题, 通过拼接出发Halo轨道的不稳定流形与目标Halo轨道的稳定流形, 设计了双脉冲低能量转移轨道, 并利用主矢量法优化了施加脉冲的位置和大小^[87].同宿连不变流形理论还可以用于两个或多个三体系统之间的转移^[88]. Howell等^[89]研究了出发轨道为月球轨道或者地月$L_{1}$/$L_{2}$ Halo轨道, 目标轨道为日$\!-\!$地/月系统$L_{2}$ Halo轨道的转移轨道设计问题, 并考虑了不变流形以及穿越轨道两种不同的转移思路. Kakoi等^[90]利用地$\!-\!$月系统$L_{1}$/$L_{2}$ Halo轨道的不变流形, 研究了向日$\!-\!$火系统$L_{1}$/$L_{2}$ Halo轨道转移的低能量设计问题. Peng等^[91]则研究了主天体轨道偏心率对低能量转移轨道的影响, 以日地ERTBP和地月ERTBP拼接双椭圆三体问题模型为动力学模型, 研究了从日地平衡点轨道至地月ERTBP模型下的多圈Halo轨道的转移轨道.

除了Halo轨道以外, 近年来受到美国重返月球计划的驱动, NASA提出了以NRHO为参考轨道的月球门户任务. 以NASA与普渡大学的Howell团队为主的****们, 对NRHO在低能量转移轨道中的应用进行了一系列全面的探索, 包括NRHO分别作为出发轨道、中转轨道或目标轨道的转移轨道设计问题^[92-94], 以及航天器从NRHO逃逸或者废弃处理等任务. 未来对低能量转移的研究将会向着实际工程任务发展, 结合探测器的可达性^[95], 如何处理复杂工程约束, 探索更多类型的平衡点轨道在空间探测任务中的应用前景, 必将成为未来研究的趋势.

4.3 三体/四体系统的弱稳定边界理论与低能量捕获轨道设计

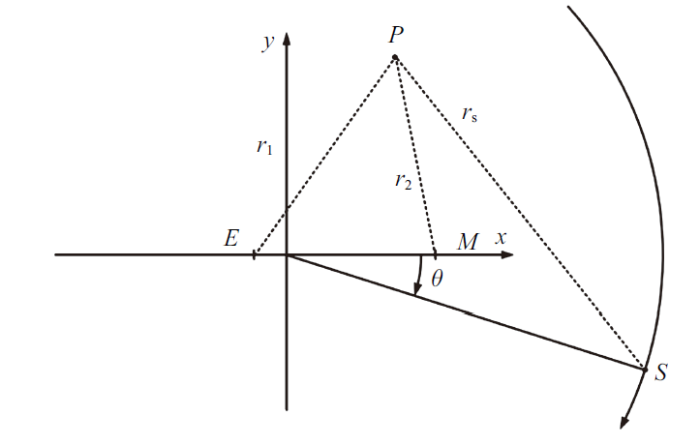
在三体系统中, 除了利用不变流形的低能量转移方式外, 还存在一种利用弱稳定边界理论的低能量转移. Belbruno^[96]在研究地月低能转移轨道时发现, 若转移过程中探测器相对地球的远地点距离远大于月球轨道半径时, 探测器可以利用太阳扰动力实现转移, 到达月球附近无需施加捕获机动即可被月球临时捕获, 形成月球环绕轨道. 该现象反映在月球附近存在一个区域, 区域内的运动经多天体的引力作用可实现自然的逃逸或捕获. Belbruno^[97]将该边界定义为弱稳定边界 (WSB). 此后****们从理论角度对三体系统中较小天体附近的运动稳定性进行了详细的研究, 并发展成为弱稳定边界理论. 利用弱稳定边界理论可以设计低能量的弹道捕获轨道, 相比传统的脉冲捕获形式大大节省了燃料消耗.

4.3.1 弱稳定边界理论的发展

弱稳定边界最初基于限制性三体问题的模型确定, 表示质量较小天体附近二体运动稳定与逃逸的边界. 随后, Belbruno^[97]给出了更准确的数学描述, 如图17所示.

图17

新窗口打开|下载原图ZIP|生成PPT
图17弱稳定边界的定义

Fig.17Definition of the weak stability boundary



弱稳定边界将三体系统中平衡点附近的研究拓展到主星附近, 并利用二体运动的参数对运动进行表述, 进而建立了主天体捕获与逃逸运动的联系. 同时, 尽管弱稳定边界在三体问题模型下定义, 但其运动稳定性分析并不受限于三体动力学. 采用四体模型甚至考虑其他摄动力的动力学模型同样可以得到相应的弱稳定边界^[98], 进而使得弱稳定边界的研究可由三体系统拓展到四体和多体系统中. 基于限制性三体与四体系统模型, 地$\!-\!$月、日$\!-\!$火系统的弱稳定边界结构和运动特性被详细研究^[99-100], 其中日$\!-\!$火系统的弱稳定边界如图18所示.

图18

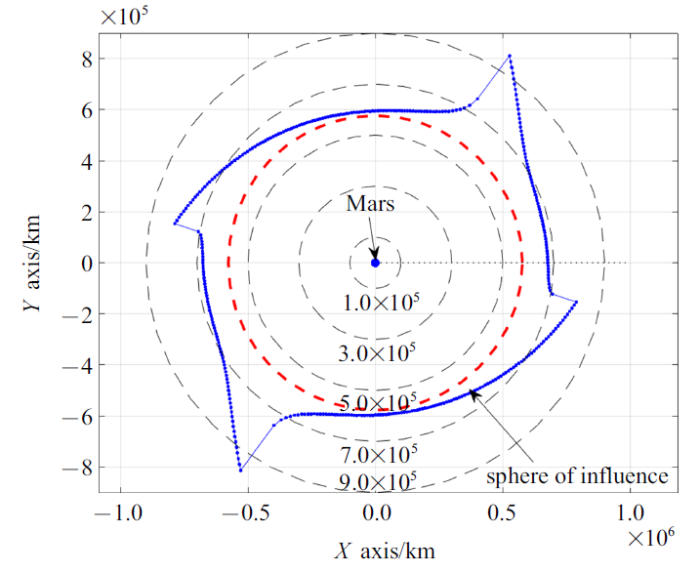新窗口打开|下载原图ZIP|生成PPT
图18日$\!-\!$火系统的弱稳定边界结构

Fig.18Geometry structure of the weak stability boundary of the Sun-Marssystem



此外, Garcia等^[11]发现质量较小主天体附近的稳定区域并非为以天体为中心的闭合区域, 随着探测器在射线上初始半径的增大, 对应的运动稳定区域和不稳定区域交替出现.因而Garcia和Gómez将运动稳定的区域定义为稳定集.稳定集是若干个闭合的区域, 其内部可能不包含主天体, 稳定集可看作弱稳定边界理论的拓展与精细化描述. 此后, Topputo等^[101]改进了稳定集的求解算法并应用于日$\!-\!$木系统附近的稳定区域计算. 利用圆型限制性模型和椭圆型限制性模型, 地$\!-\!$月系统、日$\!-\!$木系统、木星$\!-\!$木卫系统、日$\!-\!$水系统、日$\!-\!$火系统的稳定集结构相继被研究^[102-104]. 逆向稳定集的概念也被提出^[105], 用于描述探测器沿时间逆向积分对应的运动稳定性, 对稳定集结构的研究, 为低能量的捕获轨道设计奠定了重要的基础.

弱稳定边界和稳定集与三体系统内不变流形的联系是弱稳定边界理论研究的另一热点. 文献[99]指出, 利用Jacobi常数$C$ ($L_{1}$)的等势面可以非常粗略的估计弱稳定边界的范围. Fantino等^[105]定义了固定Jacobi常数时的弱稳定边界, 发现相同Jacobi常数下$L_{1}$和$L_{2}$附近周期轨道的稳定流形上速度和位置垂直的点和弱稳定边界基本一致. 通过几何证明和数值仿真, 验证在一定Jacobi常数范围内, 流形上径向速度为零的点就是弱稳定边界上的点^[12], 为统一弱稳定边界理论和不变流形理论做出了重要的贡献.

4.3.2 弱稳定边界理论的应用

弱稳定边界理论的重要应用是设计低能量的捕获轨道. 日本的Hiten卫星是第一个成功应用利用弱稳定边界理论实现月球弹道捕获的任务^[106]. 由于发动机故障, Hiten卫星采用传统的霍曼转移方式无法实现月球捕获, Belbruno利用月球借力增大探测器的远地点, 并利用太阳摄动力使探测器进入月球的弱稳定边界, 实现临时捕获. 计算发现相比霍曼转移可以节省15%的速度增量.

此后针对地$\!-\!$月系统的弹道捕获被深入研究^[107-108]. Sweetser^[109]总结了利用不同方法从地球停泊轨道转移至环月圆极轨所需的速度脉冲, 并发现弹道捕获所需的速度增量最小, 且接近CRTBP模型下理论计算的最小值. 弹道捕获轨道设计的关键是构造恰当的日$\!-\!$地$\!-\!$月构型使得太阳引力可以有效提高轨道的近地点. Koon等^[110]创造性的采用流形拼接的方法构造了地$\!-\!$月系统弹道捕获轨道, 解释了弹道捕获转移轨道的原理, 使得月球弹道捕获轨道可以通过双三体模型研究来进行初步设计, 提高了转移轨道的设计效率.

此外, 针对其他天体系统的弱稳定边界转移与弹道捕获轨道也进行了广泛的研究. Hyeraci等^[103]提出捕获集的概念. Circi等^[111]分析了行星公转轨道的偏心率对捕获集的影响, 发现偏心率越大越有利于生成捕获轨道. 在日$\!-\!$火系统的弹道捕获轨道的研究中, ****们发现由于地$\!-\!$火转移对应的火星交会速度较大, 较难得到弹道捕获的机会. 一种方式是采用小推力轨道与相应的火星弱稳定边界状态匹配^[112]; 另一种策略是将探测器在距离火星较远的星际空间捕获进入弹道轨道, 然后自然的进入火星弱稳定边界, 与霍曼转移结果相对比, Topputo等^[113]发现该方法在近火点高度较高的捕获任务中有优势且增加了火星转移的灵活性. Li等^[21,114]利用逆向稳定集的思想, 将弱稳定边界轨道应用于火星高轨道的捕获中, 作为星际转移轨道和任务轨道间的过渡轨道, 尽管捕获过程中需要施加两次机动, 但相比直接捕获可以明显降低速度增量.

除Hiten卫星外, NASA的GRAIL月球探测器也采用了弹道捕获方式进入月球轨道^[115-116], 如图19所示. Bepi-Colombo水星探测器同样计划借助水星的弱稳定边界逐渐降低探测器的能量^[24], 实现低能量的弹道捕获. 弱稳定边界因其较小的燃料消耗将在未来深空探测中有更广泛的应用前景, 但其主要劣势在于转移时间较长. 深入了解弱稳定边界内的运动机理, 在不显著增大燃料消耗的情况下通过施加人为扰动, 改变弹道捕获轨道的运动轨迹, 缩短转移时间将是一个值得深入研究的动力学问题.

图19

新窗口打开|下载原图ZIP|生成PPT
图19GRAIL地月转移轨道

Fig.19Translunar trajectory for GRAIL

5 三体系统轨道动力学的应用

随着对三体系统轨道动力学研究的深入和对运动特性了解, ****们也将三体系统轨道动力学与航天动力学中其他技术和概念相结合, 将三体系统的运动特性应用于相关问题的研究中. 较有代表性的应用包括三体系统下的编队飞行与导航定位星座设计.

5.1 三体系统中的编队飞行

在空间观测任务中, 为了提高观测分辨率, 需要增大光学设备的基线长度, 但单个探测器尺寸受到运载器尺寸和运载能力的限制存在极限, 无法实现几十米甚至上百米的基线长度, 因此, 编队飞行的概念应运而生. 通过多个探测器组成飞行阵列, 探测器按一定的构型保持相对位置和速度, 从而形成一个虚拟的探测器整体, 通过协同控制共同实现观测任务, 可以大大增加探测器的观测能力. 编队飞行早期主要针对近地轨道, 随着三体系统动力学研究的深入和平衡点附近轨道独特的观测条件, 针对三体系统平衡点附近的编队动力学研究也成为近年来的研究热点之一.

日地平衡点距离地球较远, 受到地球的电磁干扰较少, 因此适合开展对深空天体或太阳的高分辨率观测. 美国国家航空航天局 (NASA)、欧空局 (ESA)先后启动了类地行星探测器(terrestrial planet finder, TPF)计划、Darwin计划、MAXIM (X射线干涉测量)任务等空间观测计划. 中国也提出了觅音计划, 计划在日地平衡点开展干涉测量, 而三体系统中的编队飞行动力学研究是任务开展的基础.

5.1.1 平衡点编队轨道动力学

与近地轨道的编队飞行不同, 平衡点轨道编队飞行所面临的动力学环境更加复杂. 轨道编队在平衡点附近的运动演化是研究的关键问题. 基于圆型限制性三体模型, Héritier等 ^[117]研究了探测器编队的自然演化过程和稳定性, 发现线性化无控自然编队的相对距离将逐渐发散. Héritier和Howell定义了编队误差较小的稳定域. 探测器在稳定域内可以形成松散编队, 相对位置将在一定范围内波动但不会发散. 研究发现, Halo轨道的稳定域为二次曲面. 日地$L_{2}$点大尺度Lissajous轨道下的低自然漂移区域也被研究^[118], 可实现$6.0\times10^5$ km振幅的Lissajous轨道100 d内的误差$<5.0\times10^4$ km. 以上研究给星间相对位置精度要求较低的编队提供了构型设计依据. 此外, 利用平衡点邻域自然存在的中心流形^[119-120], 可以将编队设计在一定幅度的周期或拟周期轨道上, 各探测器间的距离在一定范围内波动, 可以形成松散的卫星编队.

针对平衡点高精度编队的动力学问题, Out^[121]研究了日地$L_{2}$ Halo轨道上100 m量级的双星编队, 分别考虑了圆型和椭圆型限制性三体问题、椭圆限制性四体问题、考虑太阳光压的四体问题下的编队演化情况. 研究发现, 太阳光压是影响最大的扰动因素. 太阳光压受航天器的面质比和表面材质属性和探测器姿态影响, 如探测器相对于太阳光压的法向旋转1$^\circ$, 将引起1 $\mu$m/s$^{2}$的相对加速度变化, 是引力相对加速度的1000倍. 在高精度的星历模型下的TPF任务仿真表明^[122], 高精度平衡点编队对速度增量需求较小, 但对推进器的控制精度要求高, 且轨道维持频繁, 同时也对相对测量精度提出了较高的要求.

5.1.2 编队轨控策略

由于环境摄动力和测控与执行误差的存在, 想要实现高精度的平衡点编队, 编队控制必不可少, 即形成非自然编队. Howell和Marchand等^[123-125]对自然编队和非自然编队做了比较, 并对非自然编队的控制策略给出概述. 目前针对平衡点编队的控制策略主要分为两类, 一类是编队的每颗星分别进行标称轨道的跟踪控制, 另一类是编队主星进行周期轨道保持, 子星只考虑与主星的相对距离控制. 仿真分析表明采用相对控制所需的燃料消耗较省. 基于线性化模型的LQR方法被用于编队保持^[126], 但是由于线性模型为实际模型在平衡点附近的近似, 因此此类基于线性模型设计的控制算法难以到达较高的精度要求. 非线性自适应控制器^[127] 和自抗扰控制^[128] (active disturbance rejection control, ADRC)等非线性编队飞行控制方法被应用于编队控制中, 在理论模型下可以得到较好的位置保持精度, 误差优于0.5 mm. 此外, Infeld等^[129]还将卫星编队问题处理为多智能体、非线性、有约束的最优控制问题, 同时解决了轨道设计和编队控制. 但以上控制方法的研究采用的动力学较简单, 且未考虑测量与控制误差, 实际的编队控制情况仍有待验证.

从以上研究可以看出目前针对三体平衡点编队飞行的动力学与控制研究相比单航天器的研究还较为基础, 三体系统中的相对运动规律仍未探明, 影响相对运动稳定性的关键参数仍不清晰, 同时多星编队的姿轨高精度测量与协同控制也有待解决. 三体系统下的多星编队具有潜在的应用价值和空间探测需求, 相关任务也仍在研究论证中, 解决上述问题将为任务的精确实施奠定基础.

5.2 三体系统中的导航与定位问题

5.2.1 三体系统导航方法研究

截至目前, 所有在轨的平衡点探测器均采用地面测控站测定轨的导航方式来实现. 采用两次轨控之间所有的数据或部分数据进行交叉定轨, 定轨时间段较长, 定轨的精度在千米量级, 外推的精度在10 km量级. 典型的有: (1) ISEE-3使用地基的S波段雷达进行测控, 测量的弧长不固定, 一般由多个5 min左右的短弧段构成; (2) ACE和SOHO都主要使用26 m的美国深空网 (deep space network, DSN)天线数据; (3) MAP, WIND, Genesis以及2010年成功到达地月平衡点的ARTEMIS都使用34 m的DSN天线数据为主, 辅助以34 m和70 m天线数据或者26 m的天线数据; (4) HERSCHEL和PLANCK等欧空局的飞行器则是使用欧空局deep space antenna-2, DSA-2天线数据. 随着平衡点任务的增多, 地面测控站将难以兼顾所有的测定轨任务. 此外, 地基测控导航本身也存在着时延以及精度不够高的缺陷^[130]. 对于需要频繁机动的平衡点飞行器, 研究能够提高导航能力和在轨生存能力的自主导航方式是重要的任务.

尽管国内外的****已经根据不同测量方式提出了几种适用于行星际飞行的自主导航方法, 包括基于太阳和地球方位矢量、基于相对测量信息、天体方位测量与多普勒雷达组合等. 但以上自主定轨在三体系统下的应用还较少. 2005年 Hill等^[131]提出一种称为LiAISON (linked autonomous interplanetary satellite orbit navigation)的导航概念, 仅利用星间伪距测量信息即可进行卫星的绝对导航^[132], 其可行性就建立在平衡点轨道的非对称性和局部唯一性之上. 通过利用交联测距 (crosslink range), Hill等^[133]还提出了平衡点自主导航方法, 实时在轨测量精度可达到10 m量级, 大大提高了三体系统下轨道的定轨精度. 但当前针对三体系统的自主导航研究主要针对平衡点轨道卫星, 且采用的动力学模型较为简单, 当考虑高精度的星历模型和摄动因素后, 探测器的运动将变得复杂, 星间相对测量数据的解算将相应变得复杂, 且可能需要引入其他观测量, 如何在降低系统复杂度的同时利用三体动力学特性提高定轨精度仍需进一步探讨.

5.2.2 三体系统导航星座设计

除了三体系统内自主导航方法的研究, ****们还研究了利用三体系统特性的导航星座设计, 特别是服务于月球探测的中继与导航星座设计. 由于月球公转与自转同步, 月球背面无法与地面直接通信, 在20世纪60年代末Apollo计划期间, Farquhar等^[134]即提出利用地月平衡点$L_{2}$点Halo轨道实现地球和月球背面通信的方案. 此后William等^[135]提出了通过载人进入地月$L_{2}$点轨道, 对月背表面探测器进行遥操作的月球背面探测方案, 并分析了不同平衡点轨道的月球覆盖率, 发现小振幅的北向Halo轨道对月球南极附近着陆点的覆盖性较好. 中国的嫦娥4号中继星是首个在地月$L_{2}$点Halo轨道实现月背中继通信的通讯卫星. 结合工程约束, ****们在日$\!-\!$地$\!-\!$月系统下开展了任务轨道选择^[136-137], 月背通讯覆盖率^[138]等方面的研究, 发现月背通讯覆盖与轨道类型和轨道振幅密切相关, 振幅较小的周期轨道对月面整体的覆盖性较好而较大振幅的任务轨道对月球极地的覆盖较好.

此外, 为实现未来载人登月和月球基地的建设, 需连续无间断和有冗余的地月通讯, 甚至实现类似GPS功能实时定位能力. 相比月球低轨导航星座, 放置在平衡点轨道的导航星座在相同的覆盖性下所需的卫星数量较少, 且导航卫星受月影影响小, 可以长期与地球保持通信. 轨道上的光照时长也比月球低轨要长. Zhang等^[139-141]提出了地月$L_{1}$/$L_{2}$点的双星星座方案, 并分析了导航性能. 而根据伪距方程, 至少需要采用4颗卫星实现对月面的导航定位. Daniele等^[142]提出在$L_{1}$和$L_{2}$点附近的轨道周期约为1年的Lissajous轨道上各放置4颗卫星的星座方案, 且XY平面和$Z$方向上的相角平均分布. Ren等^[143]在此基础上讨论了该星座方案的定位精度因子. 研究发现, 由于Lissajous轨道星座靠近平衡点, 从月面观测的相角接近, 定位精度因子较大, 对应的定位精度较差. Ren等还提出了其他平衡点轨道组成的最小星座构型, 包括Halo构型和水平和垂直Lyapunov构型. 研究同时发现, 在真实星历下, 受太阳扰动的作用Halo轨道和Lissajous轨道变成了不变环面, 理想模型下的全覆盖星座仅能覆盖83.25%的区域, 为保证可见性, 需要在任两个轨道上各添加一颗卫星, 星座的卫星个数为14颗, 但仍小于Walker星座构型 (18颗).

从以上分析可以看出, 当前针对地月三体系统的导航星座研究已较为成熟, 多种星座构形被提出并分析了其观测性能. 同时嫦娥4号中继星任务的成功实施也为中继星座的轨道设计与轨道维持提供了宝贵的经验. 随着月球表面和附近探测活动的增多, 未来地月三体系统下的导航星座必将成为现实. 针对导航星座的研究也应从理论化的方案设计转向考虑更多工程约束的任务分析, 如星座系统的发射规模分析, 星座维护成本评估, 以及冗余备份设计等, 同时真实星历模型下多星的精确部署与构形初始化是保证导航星座性能的关键, 也是三体系统轨道动力学应用研究中值得深入探讨的问题.

6 总结与展望

随着人类航天任务由近地走向深空, 三体系统轨道动力学在任务设计中将扮演越来越重要的角色. 例如, 美国计划在地月$L_{2}$点近垂直Halo轨道上建造"深空之门"空间站, 用于长期低成本的地月往返任务. 我国也计划在日地$L_{2}$点开展空间探测活动. 同时, 随着商业航天的迅速发展, 利用低成本小尺寸的立方星开展太空活动成为未来发展的趋势, 基于微小卫星进行月球和火星探测也已被验证. 低成本深空探测发展趋势给三体系统的轨道动力学提出了新的命题和挑战. 结合未来的月球和深空探测活动, 未来三体系统的轨道动力学方面的研究可在以下3个方向展开.

6.1 地月高效可重复利用的转移与全月面到达轨道设计

未来的月球探测需满足全月面覆盖、高效且可重复利用的要求. 利用三体系统的不变流形可以从平衡点轨道实现弹道着陆, 但自然流形所能覆盖的月球表面区域有限. 地月三体系统存在多种转移方式, 但存在转移时间和燃料消耗间的矛盾. 如何设计着陆轨道, 实现尽可能少的燃料消耗下全球到达?如何实现货物运输与人员往返?如何针对不同的探测任务需求, 快速对地月往返轨道, 特别是地球与平衡点周期轨道间的往返轨道, 进行设计与重规划?这些问题将是未来建立月球基地开展长期月球探测的关键, 是未来三体系统轨道动力学值得系统研究的问题.

6.2 三体系统下的小推力轨道优化问题

小推力相比化学推进具有比冲高, 效率高, 工作时间长的优点, 适合开展长期的深空探测任务. 对于微小卫星, 小推力推进器更具有质量和体积上的优势, 将是未来重要的推进方式. 然而小推力转移轨道优化始终是轨道设计的难点, 经过科学家多年的研究与实践, 基于惯性系下的二体与二体摄动模型的小推力转移优化设计取得较大的研究进展. 但在三体动力学模型下的小推力转移优化研究有限, 优化算法收敛性差、计算效率低. 小推力与三体系统相结合的低能量转移轨道仍处在理论研究阶段, 未得到很好的解决, 也是未来值得深入探讨的问题之一.

6.3 三体系统中$L_4$和$L_5$点附近的运动特性与开发利用

相比三体系统共线平衡点, 三角平衡点的稳定性更好, 所需的轨道保持消耗更省, 具有较大的开发应用潜力. 但三角平衡点附近的动力学特性研究相比共线平衡点较少, 对其附近的运动行为认知有限. 三角平衡点稳定的特性使其无法通过简单的流形拼接实现低能量转移, 也给转移轨道的设计提出了挑战. 在日木、日火和日地的三角平衡点均发现了小天体族群. 对三角平衡点的研究可以解释小行星族群的迁徙与演化, 也为开展小天体探测提供理论支持.

7 结论

三体系统轨道动力学是近代轨道动力学领域研究的重点. 国内外对三体系统的轨道动力学与控制问题已经进行了大量的理论研究和工程应用, 构建了成熟的理论体系, 提出了一系列服务于工程应用的任务轨道设计与控制方法. 但随着月球与深空探测活动的日益频繁、工程约束与任务需求的增加, 对三体系统轨道动力学研究提出了新的要求, 分析三体系统内运动状态和运动特性还面临着诸多基础性的理论难题. 因此, 未来三体系统轨道动力学研究有必要结合工程需求, 对三体系统轨道动力学机理等问题展开更为深入和系统的研究, 为未来深空探测任务奠定理论基础.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Valtonen M, Karttunen H. The Three-Body Problem. Cambridge: Cambridge University Press, 2006
[本文引用: 1]

[2] Sundman KF. Mémoire sur le problème des trois corps
Acta Mathematica, 1913,36(1):105-179
DOIURL [本文引用: 1]

[3] Suvakov M, Dmitrasinovic V. Three classes of newtonian three-body planar periodic orbits
Physical Review Letters, 2013,110(11):114301
DOIURL [本文引用: 1]

[4] Broucke R. Stability of periodic orbits in the elliptic restricted three-body problem
AIAA Journal, 1969,7(6):1003-1009
DOIURL [本文引用: 2]

[5] Huang SS. Very restricted four-body problem
The Astronomical Journal, 1960,65:347
[本文引用: 2]

[6] Andreu MA. The quasi-bicircular problem
[PhD Thesis]. Barcelona: University of Barcelona, 1998
[本文引用: 1]

[7] Richardson DL. Analytic construction of periodic orbits about the collinear points
Celestial Mechanics and Dynamical Astronomy, 1980,22(3):241-253
[本文引用: 2]

[8] Howell KC, Pernicka HJ. Numerical determination of Lissajous trajectories in the restricted three-body problem
Celestial Mechanics, 1987,41(1):107-124
DOIURL [本文引用: 3]

[9] Gómez G, Koon WS, Lo MW, et al. Connecting orbits and invariant manifolds in the spatial restricted three-body problem
Nonlinearity, 2004,17(5):1571-1606
DOIURL [本文引用: 1]

[10] Belbruno E, Carrico J. Calculation of weak stability boundary ballistic lunar transfer trajectories//AIAA/AAS Astrodynamics Specialist Conference
2000-8-14-17, USA CO, Denver, AIAA 2000-4142
[本文引用: 1]

[11] García F, Gómez G. A note on weak stability boundaries
Celestial Mechanics and Dynamical Astronomy, 2007,97(2):87-100
DOIURL [本文引用: 2]

[12] Belbruno E, Gidea M, Topputo F. Weak stability boundary and invariant manifolds
SIAM Journal on Applied Dynamical Systems, 2010,9(3):1061-1089
DOIURL [本文引用: 2]

[13] Richardson DL. Halo orbit formulation for the ISEE-3 mission
Journal of Guidance, Control, and Dynamics, 1980,3(6):543-548
[本文引用: 1]

[14] Belbruno EA, Miller JK. Sun-perturbed Earth-to-moon transfers with ballistic capture
Journal of Guidance, Control, and Dynamics, 1993,16(4):770-775
DOIURL [本文引用: 1]

[15] 吴伟仁, 王琼, 唐玉华 等. "嫦娥4号"月球背面软着陆任务设计
深空探测学报, 2017,4(2):111-117
[本文引用: 1]

(Wu Weiren, Wang Qiong, Tang Yuhua, et al. Design of Chang'e-4 lunar farside soft-landing mission
Journal of Deep Space Exploration, 2017,4(2):111-117 (in Chinese))
[本文引用: 1]

[16] Brown EW. An Introductory Treatise on the Lunar Theory
NY: Dover Publications Inc., 1896
[本文引用: 1]

[17] Farquhar RW. The control and use of libration-point satellites
NASA Technical Report, NASA TR R-346, 1970
[本文引用: 2]

[18] Nicholson FT. Effect of solar perturbation on motion near the collinear earth-moon libration points
AIAA Journal, 1967,5(12):2237-2241
DOIURL [本文引用: 2]

[19] 刘林, 王歆. 月球探测器轨道力学. 北京: 国防工业出版社, 2006
[本文引用: 1]

(Liu Lin, Wang Xin. Beijing: National Defense Industry Press (in Chinese))
[本文引用: 1]

[20] Lewallen JM, Tapley BD. Solar influence on satellite motion near the stable earth-moon libration points
AIAA Journal, 2015,2(4):728-732
DOIURL [本文引用: 3]

[21] Li XY, Qiao D, Macdonald M. Energy-saving capture at Mars via backward-stable orbits
Journal of Guidance, Control, and Dynamics, 2019,42(5):1-10
DOIURL [本文引用: 4]

[22] Makó Z, Szenkovits F, Salamon J, et al. Stable and unstable orbits around Mercury
Celestial Mechanics and Dynamical Astronomy, 2010,108(4):357-370
DOIURL [本文引用: 1]

[23] Ma X, Li JF. Distant quasi-periodic orbits around Mercury
Astrophysics and Space Science, 2013,343(1):83-93
DOIURL [本文引用: 1]

[24] Campagnola S, Lo M. BepiColombo gravitational capture and the elliptic restricted three-body problem
Proceedings in Applied Mathematics and Mechanics, 2008,7(1):1030905-1030906
DOIURL [本文引用: 2]

[25] Schechter HB. Three-dimensional nonlinear stability analysis of the Sun-perturbed Earth-moon equilateral points
AIAA Journal, 2008,6(7):1223-1228
DOIURL [本文引用: 1]

[26] Gómez G, Llibre J, Martínez R, et al. Study on orbits near the triangular libration points in the perturbed restricted three body problem
Final Report Fundacio Empresa i Ciencia, Spain: Barcelona, 1987
[本文引用: 1]

[27] Castelli R. Regions of prevalence in the coupled restricted three-body problems approximation
Communications in Nonlinear Science and Numerical Simulation, 2012,17(2):804-816
DOIURL [本文引用: 1]

[28] Andreu MA, Simó C. Translunar halo orbits in the quasi-bicircular problem//The Dynamics of Small Bodies in the Solar System
Springer, Dordrecht, 1999: 309-314
[本文引用: 1]

[29] Andreu MA. Dynamics in the center manifold around $L_2$ in the quasi-bicircular problem
Celestial Mechanics and Dynamical Astronomy, 2002,84(2):105-133
DOIURL [本文引用: 5]

[30] Guzman JJ. Spacecraft trajectory design in the context of a coherent restricted four-body problem
[PhD Thesis]. Lafayette: Perdue University, 2001
[本文引用: 1]

[31] Shang HB, Wu XY, Cui PY. Periodic orbits in the doubly synchronous binary asteroid systems and their applications in space missions
Astrophysics and Space Science, 2015,355(1):69-87
DOIURL [本文引用: 1]

[32] Li XY, Qiao D, Barucci MA. Analysis of equilibria in the doubly synchronous binary asteroid systems concerned with non-spherical shape
Astrodynamics, 2018,2(2):133-146
DOIURL [本文引用: 1]

[33] Li XY, Qiao D, Li P. Bounded trajectory design and self-adaptive maintenance control near non-synchronized binary systems comprised of small irregular bodies
Acta Astronautica, 2018,152:768-781
DOIURL [本文引用: 1]

[34] Szebehely V. Theory of Orbits: The Restricted Problem of Three Bodies. New York and London: Academic Press, 1967
[本文引用: 1]

[35] Jorba A, Villanueva J. On the persistence of lower dimensional invariant tori under quasiperiodic perturbations
Journal of Nonlinear Science, 1997,7(5):427-473
DOIURL [本文引用: 1]

[36] Farquhar RW, Kamel AA. Quasi-periodic orbits about the translunar libration point
Celestial Mechanics, 1973,7(4):458-473
DOIURL [本文引用: 1]

[37] Gómez G, Marcote M. High-order analytical solutions of Hill's equations
Celestial Mechanics and Dynamical Astronomy, 2006,94(2):197-211
DOIURL [本文引用: 1]

[38] Howell KC. Three-dimensional, periodic, 'halo' orbits
Celestial Mechanics & Dynamical Astronomy, 1984,32(1):53-71
[本文引用: 1]

[39] Folta DC, Woodard M, Howell KC, et al. Applications of multi-body dynamical environments: The ARTEMIS transfer trajectory design
Acta Astronautica, 2012,73:237-249
DOIURL [本文引用: 1]

[40] Simo C. On the analytical and numerical approximation of invariant manifolds
In Modern Methods in Celestial Mechanics, Eds. D. Benest, C. Froeschlé, Editions Frontières, 1990: 285-329
[本文引用: 1]

[41] Alessi EM. The role and usage of libration point orbits in the Earth — Moon system
[PhD Thesis]. Barcelona: University of Barcelona, 2010
[本文引用: 1]

[42] Colombo G. The stabilization of an artificial satellite at the inferior conjunction point of the Earth-Moon system
Journal of the Astronautical Sciences, 1961,6(1):213
[本文引用: 1]

[43] Breakwell JV, Kamel AA, Ratner MJ. Station-keeping for a translunar communication station
Celestial Mechanics, 1974,10(3):357-373
DOIURL [本文引用: 1]

[44] Howell KC, Pernicka HJ. Station-keeping method for libration point trajectories
Journal of Guidance, Control, and Dynamics, 1993,16(1):713-723
[本文引用: 1]

[45] Pernicka HJ. The numerical determination of nominal libration point trajectories and development of a station-keeping strategy
[PhD Thesis]. Lafayette: Purdue University, 1990
[本文引用: 1]

[46] Dunham DW, Roberts CE. Stationkeeping techniques for libration point satellites
Journal of the Astronautical Sciences, 2001,49(1):127-144
DOIURL [本文引用: 2]

[47] Farquhar RW, Muhonen DP, Newman CR, et al. Trajectories and orbital maneuvers for the first libration-point satellite
Journal of Guidance, Control, and Dynamics, 1980,3(6):549-554
[本文引用: 1]

[48] Howell KC, Marchand BG. Control strategies for formation flight in the vicinity of the libration points
Journal of Guidance, Control, and Dynamics, 2005,28(6):1210-1219
DOIURL [本文引用: 1]

[49] Gómez G, Howell KC, Masdemont J, et al. Station-keeping strategies for translunar libration point orbits
Advances in the Astronautical Sciences, 1998,99(2):949-967
[本文引用: 1]

[50] Pavlak TA, Howell KC. Strategy for long-term libration point orbit stationkeeping in the Earth-Moon system//Proceedings of the AAS/AIAA Astrodynamics Specialist Conference
2011-7-31-8-4, Girdwood, Alaska, AAS Paper 11-516
[本文引用: 1]

[51] Folta DC, Woodard M, Cosgrove D. Stationkeeping of the first Earth-Moon libration orbiters: The ARTEMIS mission//Proceedings of the AAS/AIAA Astrodynamics Specialist Conference
2011-07-31—08-04, Girdwood, Alaska, AAS Paper 11-515
[本文引用: 1]

[52] Gómez G, Mondelo JM. The dynamics around the collinear equilibrium points of the RTBP
Physica D Nonlinear Phenomena, 2001,157(4):283-321
DOIURL [本文引用: 1]

[53] Baresi N, Scheeres DJ. Quasi-periodic invariant tori of time-periodic dynamical systems: Applications to small body exploration// Proceedings of the International Astronautical Congress
2016-9-26-30, Mexico, Guadalajara
[本文引用: 1]

[54] Kolemen E, Kasdin NJ, Gurfil P. Multiple Poincaré sections method for finding the quasiperiodic orbits of the restricted three body problem
Celestial Mechanics and Dynamical Astronomy, 2012,112(1):47-74
DOIURL [本文引用: 1]

[55] Campagnola S, Lo MW, Newton P. Subregions of motion and elliptic Halo orbits in the elliptic restricted three-body problem
Advances in the Astronautical Sciences, 2008,130(2):1541-1555
[本文引用: 1]

[56] Peng H, Xu SJ. Stability of two groups of multi-revolution elliptic halo orbits in the elliptic restricted three-body problem
Celestial Mechanics and Dynamical Astronomy, 2015,123:279-303
DOIURL [本文引用: 1]

[57] Ferrari F, Lavagna M. Periodic motion around libration points in the elliptic restricted three-body problem
Nonlinear Dynamics, 2018,93(2):453-462
DOIURL [本文引用: 2]

[58] Whitley R, Davis DC, Burke L, et al. Earth-Moon near rectilinear halo and butterfly orbits for lunar surface exploration//AAS/AIAA Astrodynamics Specialist Conference
2018-8-19-23, USA, UT, Snowbird, AAS 18-406
[本文引用: 1]

[59] Hénon M, Guyot M. Stability of periodic orbits in the restricted problem//In: Giacaglia G.E.O. ed. Periodic Orbits, Stability and Resonances
Dordrecht: Springer, 1970, 349-374
[本文引用: 1]

[60] Capdevila L, Guzzetti D, Howell KC. Various transfer options from Earth into distant retrograde orbits in the vicinity of the Moon
Advances in the Astronautical Sciences, 2014,152(1):3659-3678
[本文引用: 1]

[61] Russell RP. Global search for planar and three-dimensional periodic orbits near Europa
Journal of the Astronautical Sciences, 2006,54(2):199-226
DOIURL [本文引用: 2]

[62] Escribano TV. Spacecraft transfer trajectory design exploiting resonant orbits in multi-body environments
[PhD Thesis]. Lafayette: Purdue University, 2013
[本文引用: 1]

[63] Vaquero M, Howell KC. Design of transfer trajectories between resonant orbits in the Earth-Moon restricted problem
Acta Astronautica, 2014,94(1):302-317
DOIURL [本文引用: 2]

[64] Antoniadou KI, Voyatzis G. Resonant periodic orbits in the exoplanetary systems
Astrophysics and Space Science, 2014,349(2):657-676
DOIURL [本文引用: 1]

[65] Anderson RL, Campagnola S, Lantoine G. Broad search for unstable resonant orbits in the planar circular restricted three-body problem
Celestial Mechanics and Dynamical Astronomy, 2016,124(2):177-199
DOIURL [本文引用: 1]

[66] 张文博, 成跃, 王宁飞. 地月系统循环轨道初步设计与特性分析
航空学报, 2015,36(7):2197-2206
[本文引用: 1]

(Zhang Wenbo, Cheng Yue, Wang Ningfei. Preliminary design and characteristic analysis of cycler orbits in Earth-Moon system
Acta Aeronautica ET Astronautica Sinica, 2015,36(7):2197-2206 (in Chinese))
[本文引用: 1]

[67] Aldrin B. Cyclic trajectory concepts//SAIC presentation to the interplanetary rapid transit study meeting, Jet Propulsion Laboratory
California: 1985,28
[本文引用: 1]

[68] Kauffman J. A successful failure: NASA's crisis communications regarding Apollo 13
Public Relations Review, 2001,27(4):437-448
DOIURL [本文引用: 1]

[69] 黄文德, 郗晓宁, 王威 等. 基于双二体假设的载人登月自由返回轨道特性分析及设计
宇航学报, 2010,31(5):1297-1303
[本文引用: 1]

(Huang Wende, Xi Xiaoning, Wang Wei, et al. Characteristic analysis and design of free return orbit for lunar manned landing based on the double two-body model
Journal of Astronautics, 2010,31(5):1297-1303 (in Chinese))
[本文引用: 1]

[70] 彭祺擘, 沈红新, 李海阳. 载人登月自由返回轨道设计及特性分析
中国科学: 技术科学, 2012,42(3):333-341
[本文引用: 1]

(Peng Qibo, Shen Hongxin, Li Haiyang. Free return orbit design and characteristics analysis for manned lunar mission
Science China Technique Science, 2012,42(3):333-341 (in Chinese))
[本文引用: 1]

[71] 王丹阳, 邓辉. 地月自由返回轨道设计
中国空间科学技术, 2017,37(1):57-65
[本文引用: 1]

(Wang Danyang, Deng Hui. Cislunar free return trajectory design
Chinese Space Science and Technology, 2017,37(1):57-65 (in Chinese))
[本文引用: 1]

[72] 侯锡云, 赵玉晖, 刘林. 月球探测中的无动力返回轨道
天文学报, 2012,53(4):308-318
[本文引用: 1]

(Hou Xiyun, Zhao Yuhui, Liu Lin. Free return trajectories in lunar missions
Acta Astronomica Sinica, 2012,53(4):308-318 (in Chinese))
[本文引用: 1]

[73] 谢晨月, 袁泽龙, 王建春 等. 基于人工神经网络的湍流大涡模拟方法
力学学报, 2021,53(1):1-16
[本文引用: 1]

(Xie Chenyue, Yuan Zelong, Wang Jianchun, et al. Artificial neural network-based subgrid-scale models for large-eddy simulation of turbulence
Chinese Journal of Theoretical and Applied Mechanics, 2021,53(1):1-16 (in Chinese))
[本文引用: 1]

[74] 刘铖, 胡海岩. 基于李群局部标架的多柔体系统动力学建模与计算
力学学报, 2021,53(1):213-233
[本文引用: 1]

(Liu Cheng, Hu Haiyan. Dynamic modeling and computation for flexible multibody systems based on the local frame of Lie group
Chinese Journal of Theoretical and Applied Mechanics, 2021,53(1):213-233 (in Chinese))
[本文引用: 1]

[75] Parker JS, Anderson RL. Low-Energy Lunar Trajectory Design
John Wiley & Sons, Inc., 2013
[本文引用: 3]

[76] Gómez G, Jorba A, Masdemont J, et al. Study of the transfer from the Earth to a halo orbit around the equilibrium point L1
Celestial Mechanics and Dynamical Astronomy, 1993,56(4):541-562
DOIURL [本文引用: 1]

[77] Barden BT, Howell KC, Lo MW. Application of dynamical systems theory to trajectory design for a libration point mission//Astrodynamics Conference
1996-07-29, Reston, Virigina, AIAA-96-3602
[本文引用: 1]

[78] Parker JS. Low-energy ballistic lunar transfers. [PhD Thesis]
Colorado: University of Colorado, 2007
[本文引用: 1]

[79] Parker JS, Born GH. Modeling a low-energy ballistic lunar transfer using dynamical systems theory
Journal of Spacecraft and Rockets, 2008,45(6):1269-1281
DOIURL [本文引用: 1]

[80] Gordon DP. Transfer to Earth-Moon L2 halo orbits using lunar proximity and invariant manifolds
[Master Thesis]. Lafayette: Purdue University, 2008
[本文引用: 1]

[81] Li MT, Zheng JH. Impulsive lunar halo transfers using the stable manifolds and lunar flybys
Acta Astronautica, 2010,66(9-10):1481-1492
DOIURL [本文引用: 2]

[82] Zeng H, Zhang JR. Design of impulsive Earth-Moon halo transfers: lunar proximity and direct options
Astrophysics and Space Science, 2016,361(10):328
DOIURL [本文引用: 1]

[83] Cheng Y, Gómez G, Masdemont JJ, et al. Study of the transfer between libration point orbits and lunar orbits in Earth-Moon system
Celestial Mechanics & Dynamical Astronomy, 2017,128(4):409-433
[本文引用: 1]

[84] Gómez G, Masdemont JJ. Some zero cost transfers between libration point orbits
Advances in the Astronautical Sciences, 2000,105(2):1199-1216
[本文引用: 1]

[85] Gómez G, Jorba A, Simo C. Study of the transfer between halo orbits
Acta Astronautica, 1998,43(9/10):493-520
DOIURL [本文引用: 1]

[86] Davis KE, Anderson RL, Scheeres DJ, et al. The use of invariant manifolds for transfers between unstable periodic orbits of different energies
Celestial Mechanics and Dynamical Astronomy, 2010,107(4):471-485
DOIURL [本文引用: 1]

[87] Davis KE, Anderson RL, Scheeres DJ, et al. Optimal transfers between unstable periodic orbits using invariant manifolds
Celestial Mechanics and Dynamical Astronomy, 2011,109(3):241-264
DOIURL [本文引用: 1]

[88] Koon W, Lo M, Marsden JE, et al. Dynamical Systems, the Three-Body Problem and Space Mission Design
Springer-Verlag, Berlin, 2008.
[本文引用: 1]

[89] Howell KC, Kakoi M. Transfers between the Earth-Moon and Sun-Earth systems using manifolds and transit orbits
Acta Astronautica, 2006,59(1-5):367-380
DOIURL [本文引用: 1]

[90] Kakoi M, Howell KC, Folta D. Access to Mars from Earth-Moon libration point orbits: Manifold and direct options
Acta Astronautica, 2014,102:269-286
DOIURL [本文引用: 1]

[91] Peng H, Xu SJ. Low-energy transfers to a Lunar multi-revolution elliptic halo orbit
Astrophysics and Space Science, 2015,357(1):1-15
DOIURL [本文引用: 1]

[92] Whitley R, Martinez R. Options for staging orbits in cislunar space//2016 IEEE Aerospace Conference
2016-3-5-12, USA, MT, Big Sky, 16121824
[本文引用: 1]

[93] Davis DC, Phillips SM, Howell KC, et al. Stationkeeping and transfer trajectory design for spacecraft in cislunar space
Advances in the Astronautical Sciences, 2018,162:3483-3502


[94] Guzzetti D, Zimovan EM, Howell KC, et al. Stationkeeping analysis for spacecraft in lunar near rectilinear halo orbits
Advances in the Astronautical Sciences, 2017,160:3199-3218
[本文引用: 1]

[95] 杜向南, 杨震. 航天器单脉冲机动可达域求解算法
力学学报, 2020,52(6):1621-1631
[本文引用: 1]

(Du Xiangnan, Yang Zhen. An algorithm for solving spacecraft reachable domain with single-impulse maneuvering
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(6):1621-1631 (in Chinese))
[本文引用: 1]

[96] Belbruno E. Examples of the nonlinear dynamics of ballistic capture and escape in the Earth-Moon system//Astrodynamics Conference
1990-8-20-22, USA, OR, Portland, AIAA-90-2896
[本文引用: 1]

[97] Belbruno E. Capture dynamics and chaotic motions in celestial mechanics: With applications to the construction of low energy transfers//Capture Dynamics and Chaotic Motions in Celestial Mechanics: With Applications to the Construction of Low Energy Transfers. Princeton University Press, 2018
[本文引用: 2]

[98] Hyeraci N, Topputo F. The role of true anomaly in ballistic capture
Celestial Mechanics and Dynamical Astronomy, 2013,116(2):175-193
DOIURL [本文引用: 1]

[99] Romagnoli D, Circi C. Earth-Moon weak stability boundaries in the restricted three and four body problem
Celestial Mechanics and Dynamical Astronomy, 2009,103(1):79-103
DOIURL [本文引用: 2]

[100] Li J, Sun YS. A survey of weak stability boundaries in the Sun-Mars system
Research in Astronomy and Astrophysics, 2015,15(3):376-392
DOIURL [本文引用: 1]

[101] Topputo F, Belbruno E. Computation of weak stability boundaries: Sun-Jupiter system
Celestial Mechanics and Dynamical Astronomy, 2009,105(1-3):3-17
DOIURL [本文引用: 1]

[102] Koon WS, Marsden JE, Ross SD, et al. Constructing a low energy transfer between Jovian moons//Celestial Mechanics//Dedicated to Donald Saari for His 60th Birthday: Proceedings of an International Conference on Celestial Mechanics
1999-12-15—19, USA, Illinois, Evanston, 2002,292:129
[本文引用: 1]

[103] Hyeraci N, Topputo F. Method to design ballistic capture in the elliptic restricted three-body problem
Journal of Guidance, Control, and Dynamics, 2012,33(6):1814-1823
DOIURL [本文引用: 1]

[104] Luo ZF, Topputo F, Bernelli-Zazzera F, et al. Constructing ballistic capture orbits in the real solar system model
Celestial Mechanics and Dynamical Astronomy, 2014,120(4):433-450
DOIURL [本文引用: 1]

[105] Fantino E, Gómez G, Masdemont JJ, et al. A note on libration point orbits, temporary capture and low-energy transfers
Acta Astronautica, 2010,67(9-10):1038-1052
DOIURL [本文引用: 2]

[106] Belbruno EA, Miller J. A ballistic lunar capture trajectory for the Japanese spacecraft hiten
Jet Propulsion Laboratory, IOM, 1990,312:90-94
[本文引用: 1]

[107] Circi C, Teofilatto P. Weak stability boundary trajectories for the deployment of lunar spacecraft constellations
Celestial Mechanics and Dynamical Astronomy, 2006,95(1-4):371-390
DOIURL [本文引用: 1]

[108] Parker JS, Anderson RL, Peterson A. Surveying ballistic transfers to low lunar orbit
Journal of Guidance, Control, and Dynamics, 2013,36(5):1501-1511
DOIURL [本文引用: 1]

[109] Sweetser TH. An estimate of the global minimum DV needed for earth-moon transfer
Advances in the Astronautical Sciences, 1991,75:111-120
[本文引用: 1]

[110] Koon WS, Lo MW, Marsden JE, et al. Low energy transfer to the Moon
Celestial Mechanics and Dynamical Astronomy, 2001,81(1-2):63-73
DOIURL [本文引用: 1]

[111] Circi C, Teofilatto P. Effect of planetary eccentricity on ballistic capture in the solar system
Celestial Mechanics and Dynamical Astronomy, 2005,93(1-4):69-86
DOIURL [本文引用: 1]

[112] Mingotti G, Topputo F, Bernelli-Zazzera F. Earth-Mars transfers with ballistic escape and low-thrust capture
Celestial Mechanics and Dynamical Astronomy, 2011
[本文引用: 1]

[113] Topputo F, Belbruno E. Earth-Mars transfers with ballistic capture
Celestial Mechanics and Dynamical Astronomy, 2014,121(4):329-346
DOIURL [本文引用: 1]

[114] Li XY, Qiao D. Earth-Phobos transfer with ballistic trajectory in the Sun-Mars system//2018 AIAA SPACE and Astronautics Forum and Exposition
2018-9-17-19, USA, FL, Orlando, AIAA 2018-5309
[本文引用: 1]

[115] Roncoli R, Fujii K. Mission design overview for the gravity recovery and interior laboratory (GRAIL) mission//AIAA/AAS Astrodynamics Specialist Conference
2010-08-02—05, Canada, Ontario, Toronto, AIAA 2010-8383
[本文引用: 1]

[116] Hatch S, Chung M, Kangas J. et al. Trans-Lunar cruise trajectory design of GRAIL (Gravity recovery and interior laboratory) mission//AIAA/AAS Astrodynamics Specialist Conference
2010-08-02—05, Canada, Ontario, Toronto, AIAA 2010-8394
[本文引用: 1]

[117] Héritier A, Howell KC. Dynamical evolution of natural formations in libration point orbits in a multi-body regime
Acta Astronautica, 2014,102:332-340
DOIURL [本文引用: 1]

[118] Héritier A, Howell KC. Natural regions near the collinear libration points ideal for space observations with large formations
Journal of the Astronautical Sciences, 2013,60(1):87-108
DOIURL [本文引用: 1]

[119] Howell KC, Millard LD. Control of satellite imaging formations in multi-body regimes
Acta Astronautica, 2009,64(5-6):554-570
DOIURL [本文引用: 1]

[120] Millard LD. Control of satellite imaging arrays in multi-body regimes. [PhD Thesis]
Lafayette: Purdue University, 2008
[本文引用: 1]

[121] Out IA. Formation flying in the Sun-Earth/Moon perturbed restricted three-body problem
[Master's Thesis]. Netherlands: Delft University of Technology Faculty of Aerospace Engineering, 2017
[本文引用: 1]

[122] Gómez G, Lo MW, Masdemont JJ, et al. Simulation of formation flight near L2 for the TPF mission//AAS/AIAA Spaceflight Mechanics Meeting
2001-02-11—15, USA, California, Santa Barbara, AAS 01-305
[本文引用: 1]

[123] Howell KC, Marchand BG. Natural and non-natural spacecraft formations near the L1 and L2 libration points in the Sun-Earth/Moon ephemeris system
Dynamics and Stability of Systems, 2005,20(1):149-173
[本文引用: 1]

[124] Howell KC, Marchand BG. Formations near the libration points: Design strategies using natural and non-natural arcs//Proceedings of GSFC 2nd International Symposium on Formation Flying Missions and Technologies
2004-09-14—16, USA, Washington, D.C., 20060048521


[125] Marchand BG. Spacecraft formation keeping near the libration points of the Sun-Earth/Moon system
[PhD Thesis]. Lafayette: School of Aeronautics and Astronautics, Purdue University, 2004
[本文引用: 1]

[126] 王峰, 陈雪芹, 张世杰 等. 基于改进PEA的日地L2平动点编队飞行高精度位置保持
宇航学报, 2011,32(5):982-990
[本文引用: 1]

(Wang Feng, Chen Xueqin, Zhang Shijie, et al. Improved PEA-Based high accuracy relative position keeping for spacecraft formation flight in Sun-Earth L2 point
Journal of Astronautics, 2011,32(5):982-990 (in Chinese))
[本文引用: 1]

[127] Wong H, Kapila V. Spacecraft formation flying near Sun-Earth L2 lagrange point: trajectory generation and adaptive full-state feedback control//Proceedings of GSFC 2nd International Symposium on Formation Flying Missions and Technologies
2004-9-14-16, USA, Washington, D.C., 20060048533
[本文引用: 1]

[128] 姜春生, 王永, 李恒年 等. 日地平动点编队飞行自抗扰轨道维持控制
空间控制技术与应用, 2017,43(1):49-54, 60
[本文引用: 1]

(Jiang Chunsheng, Wang Yong, Li Hengnian, et al. ADRC-Based orbit maintaining control of spacecraft formation flying around halo orbits about the Sun-Earth libration points
Aerospace Control and Application, 2017,43(1):49-54,60 (in Chinese))
[本文引用: 1]

[129] Infeld SI, Josselyn SB, Murray W, et al. Design and control of libration point spacecraft formations
Journal of Guidance, Control, and Dynamics, 2007,30(4):899-909
DOIURL [本文引用: 1]

[130] 张燕, 荆武兴. 基于日地月方位信息的月球卫星自主导航
宇航学报, 2005,26(4):495-498, 523
[本文引用: 1]

(Zhang Yan, Jing Wuxing. Autonomous navigation for lunar satellite based on the optical information of Sun-Earth-Moon
Journal of Astronautics, 2005,26(4):495-498, 523 (in Chinese))
[本文引用: 1]

[131] Hill K, Lo MW, Born GH. Linked, autonomous, interplanetary satellite orbit navigation (LiAISON) in lunar halo orbits//AAS/AIAA Astrodynamics Specialist Conference
2005-08-07—11, USA, California, Lake Tahoe, AAS 05-400
[本文引用: 1]

[132] Hill K, Born GH. Autonomous interplanetary orbit determination using satellite-to-satellite tracking
Journal of Guidance, Control, and Dynamics, 2012,30(3):679-686
DOIURL [本文引用: 1]

[133] Hill K, Born GH. Autonomous orbit determination from lunar halo orbits using crosslink range
Journal of Spacecraft and Rockets, 2012,45(3):548-553
DOIURL [本文引用: 1]

[134] Farquhar RW, Dunham DW, Guo YP, et al. Utilization of libration points for human exploration in the Sun-Earth-Moon system and beyond
Acta Astronautica, 2004,55(3-9):687-700
DOIURL [本文引用: 1]

[135] William DP, Caley B, Selena H, et al. Trajectory design considerations for human missions to explore the lunar farside from the Earth-Moon lagrange point EM-L2//AIAA Space 2013 Conference and Exposition
2013-09-10—12, USA, CA, San Diego, AIAA 2013-5478
[本文引用: 1]

[136] 孙超, 唐玉华, 李翔宇 等. 地$\!-\!$月$L_2$点中继星月球近旁转移轨道设计
深空探测学报, 2017,4(3):264-269, 275
[本文引用: 1]

(Sun Chao, Tang Yuhua, Li Xiangyu, et al. Design of Earth-Moon $L_2$ halo orbit transfer trajectory for relay satellites using lunar flybys
Journal of Deep Space Exploration, 2017,4(3):264-269, 275 (in Chinese))
[本文引用: 1]

[137] 唐玉华. 地月$L_2$点中继卫星轨道设计与控制问题研究. [博士论文]
北京: 北京理工大学, 2018
[本文引用: 1]

(Tang Yuhua. Study of trajectory design and control of Earth-Moon $L_2$ relay satellite. [PhD Thesis].
Beijing: Beijing Institute of Technology 2018 (in Chinese))
[本文引用: 1]

[138] 刘磊, 曹建峰, 胡松杰 等. 地月$L_2$点周期轨道的月球背面覆盖分析
深空探测学报, 2017,4(4):361-366
[本文引用: 1]

(Liu Lei, Cao Jianfeng, Hu Songjie, et al. Coverage of lunar farside surface of the Earth-Moon $L_2$ periodic orbits
Journal of Deep Space Exploration, 2017,4(4):361-366 (in Chinese))
[本文引用: 1]

[139] Zhang L, Xu B. A Universe Light House - Candidate architectures of the libration point satellite navigation system
Journal of Navigation, 2014,67(5):737-752
DOIURL [本文引用: 1]

[140] Zhang L, Xu B. Navigation performance of the libration point satellite navigation system in cislunar space
Journal of Navigation, 2015,68(2):367-382
DOIURL

[141] Zhang L, Xu B. Simplified constellation architecture for the libration point satellite navigation system
Journal of Navigation, 2016,69(5):1082-1096
DOIURL [本文引用: 1]

[142] Daniele R, Christian C. Lissajous trajectories for lunar global positioning and communication systems
Celestial Mechanics and Dynamical Astronomy, 2010,107(4):409-425
DOIURL [本文引用: 1]

[143] Ren Y, Shan JJ. Libration point orbits for lunar global positioning systems
Advances in Space Research, 2013,51(7):1065-1079
DOIURL [本文引用: 1]