引 言

在冲击载荷作用下, 吸能材料的应用具有重要的工程意义. 传统的减振吸能方法主要有两种: 其一, 利用材料的塑性变形实现能量吸收耗散^[1], 如汽车保险杠和轻型自行车头盔均是基于这一原理进行结构以及超材料设计, 然而破坏性的塑性变形使得材料无法重复利用; 其二, 利用材料的黏弹特性^[2-3], 实现重复性的能量吸收, 如橡胶鞋底和汽油活塞减振器等都是基于材料黏弹性理论实现的能量吸收, 但这种情况下的吸能效果严重依赖于加载和卸载的速度. 工程中理想的减振吸能材料显然需要满足如: 可重复使用、轻质、自主耗能、持续吸能等特点^[4-5]. 近几年, 基于多孔结构轻质高强等优异的力学性能^[6-11], 利用多孔结构的负刚度特性实现自主耗能, 受到国内外学术界的广泛关注^[12-16].

Qiu等^[17]设计出一种“双曲梁”双稳态结构, 这种新型多孔结构不依赖于预应力即可实现双稳态屈曲变形; 模态分析以及有限元模拟结果表明: 该结构的双稳态特征取决于曲梁的截面尺寸以及曲率的大小. Restrepo等^[18]通过设计具有“柔性双稳态机构”的曲梁单胞, 引入解析模型分析了PXCM(phase transforming cellular materials)材料的本构行为, 研究表明PXCM的渐进相变产生了加载?卸载的滞回环现象, 从而实现了能量吸收; PXCM的这种吸能特征不仅可与金属及聚合物蜂窝结构的吸能能力相媲美, 而且其变形是可恢复的. 但由于结构存在多稳态, 每次使用后都将借助外力恢复初稳态才能再次使用, 在使用效能上严重受限. Findeisen等^[19]提出了由双稳态曲梁单元组成的三维晶格结构, 通过半解析以及有限元方法对该三维力学超材料进行稳定性分析, 研究结果表明: 区别于以往依靠材料的破坏性塑性变形以及黏弹性耗能, 该超材料能量耗散主要是将外部冲击载荷的冲击能转化为超材料结构的振动, 令其变形具有可重复、可恢复以及可设计性等特征. Pan等^[20]通过设计三维 PM(pixel mechanical)结构, 利用自我反弹的负刚度特性实现减振耗能.

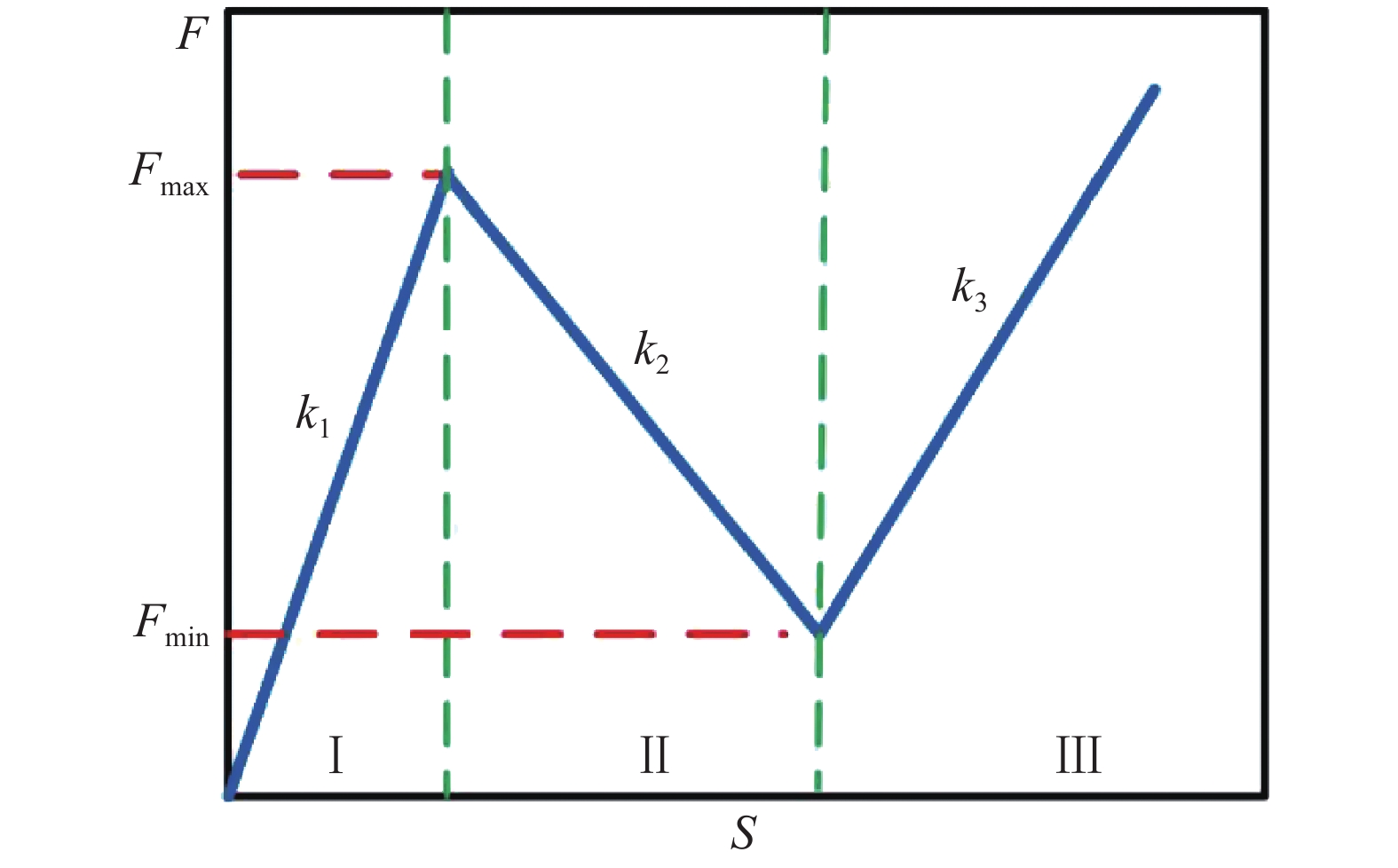
结构产生振动的主要原因是外部冲击载荷的能量(动能)输入, 如要迅速减小冲击载荷引起的结构振动, 可通过增大结构弹性变形(加载?卸载)过程中吸收的能量来实现. 负刚度结构的吸能能力, 主要取决于负刚度单胞临界载荷最大值与最小值的差值 , 如图1所示, 然而对于大多数不具双稳态的负刚度结构, 其负刚度临界载荷最大与最小值间的差值较小, 能量吸收效果不明显, 结构将出现弹性应变能与动能的反复转换, 从而出现持续性的振动. 而具有双稳态特征的负刚度结构虽然具有较强能量吸收效力, 但因其不能自主反弹, 无法实现持续性的吸能, 当被压实后, 结构也将出现持续性的振动. 为了有效地解决这一问题, 本文通过负刚度超材料构型设计, 利用具有多稳态特征的曲梁作为单胞的胞壁, 通过单胞构型控制, 在抑制结构多稳态出现的同时, 提高结构负刚度临界载荷最大值与最小值的差值, 从而实现结构吸能效率的提升, 加快能量的衰减, 减小载荷引起的持续性振动.

本文提出了一种由曲梁单元增加约束(在曲梁中点增加竖向柱、在曲梁两端点增加侧壁、在曲梁底部进行凹槽设计)所构建的新型三维负刚度结构, 并研究了其在冲击载荷作用下的吸能特性. 与已有的单稳态负刚度结构相比, 该新型结构通过增加约束抑制曲梁多稳态的出现, 同时通过弹性范围内曲梁大变形压缩过程中内部单元的自主回弹, 实现了结构吸能效率的提升. 采用数值模拟方法分析了单胞几何参数, 结构周期性对屈曲模态以及吸能效率等力学性能的影响, 同时进行了梯度结构设计, 并解析其在不同冲击载荷下能量的吸收效率, 为工程结构减振耗能提供技术支持.

1.
分析模型

1.1
负刚度结构吸能特性分析

负刚度结构, 也称为负刚度超材料, 通常定义为由具有负刚度行为的单胞组成的结构. 对于传统结构, 其沿外力方向的变形随载荷增大而增大, 而负刚度单胞表现出相反的行为, 即变形随着载荷的减小而增大, 如图1所示, 力?位移曲线在负刚度行为区间存在最大值${F_{max }}$和最小值${F_{min }}$, 若最小值小于0, 结构存在双稳态, 在压缩后将无法反弹至最初形态; 若最小值大于0, 结构不存在双稳态, 在压缩后将能自主恢复到最初形态. 由多个负刚度单胞组成的负刚度结构的加载?卸载力?位移曲线如图2所示, 由图2可知, 加载?卸载滞回曲线存在一个封闭的区间, 该区间面积即为负刚度结构一个加载?卸载周期吸收的能量. 曲线是周期性的, 且其最大值和最小值随串联的负刚度单元个数增加而分别收敛于负刚度单胞的临界载荷最大值与最小值. 在${F_{min }} > 0$的情况下, 负刚度结构之所以能够实现自主回弹, 这是因为串联的负刚度结构在受到压缩载荷时, 由于制造缺陷, 结构会出现某一层先到达负刚度临界值点, 该层单胞结构会继续压缩而其他层单胞回弹, 导致这种回弹的原因为^[18]: 由图1所示, 负刚度单胞的刚度变化呈现出3个阶段, 即${k_1} to {k_2} to {k_3}$. 设负刚度结构单胞串联个数为$n$, 压缩过程中处于3个阶段的单胞个数分别为${n_1},{n_2},{n_3}$. 结构压缩过程中的有效刚度可表示为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
负刚度单胞力(F)?位移(S)曲线示意图



Figure
1.
Sketch of force (F)-displacement (S) relation for a negative stiffness cell



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
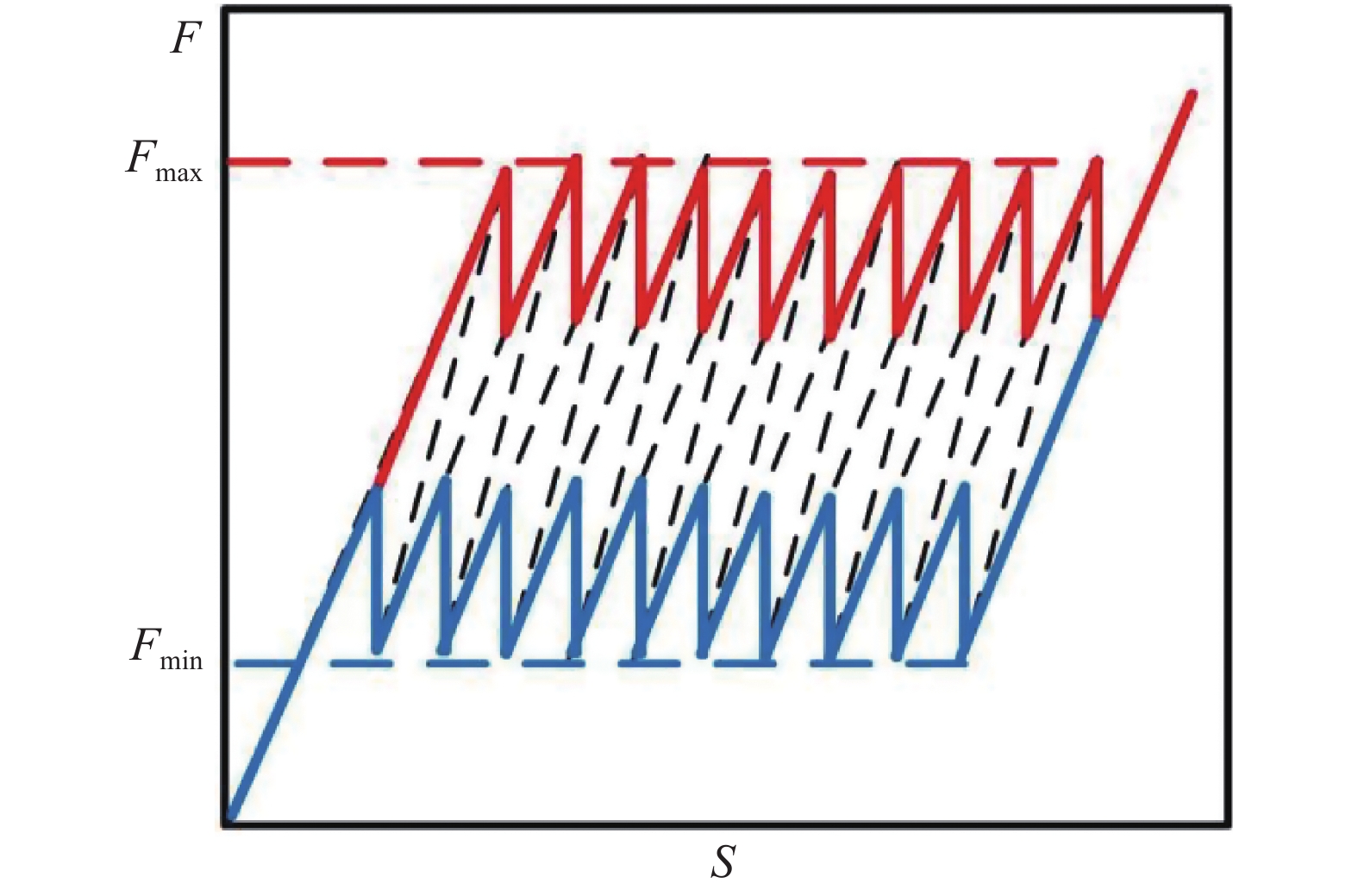
2
负刚度结构力($F$)?位移($S$)曲线示意图^[1]



Figure
2.
Sketch of force ($F$) -displacement ($S$) relation for a negative stiffness structure^[1]



下载:
全尺寸图片
幻灯片

$$k =left( { {frac{{{n_1}}}{{{k_1}}}} + {frac{{{n_2}}}{{{k_2}}}} + {frac{{{n_3}}}{{{k_3}}}} } ight)^{ - 1}$$

(1)

这表明在结构上增加单胞个数会降低结构的有效刚度. 假设结构压缩过程只某一行单胞处于负刚度阶段, 则处于第Ⅰ和Ⅲ阶段结构部分的有效刚度随$n$值增大而减小, 而处于第 Ⅱ 阶段的部分刚度(其只有一行)保持不变为${k_2}$, 当$n$达到或超过某一临界值时, 满足条件

$${ {left( {frac{{{n_1}}}{{{k_1}}}} + {frac{{{n_3}}}{{{k_3}}}} ight)} ^{ - 1}} < {k_2}$$

(2)

结构将表现出回弹行为, 即位移的反转以及驱动转换所需平衡力的减小导致的回弹行为; 同样, 卸载过程中, 结构某一层将先达到负刚度临界载荷值的最小值点, 该层单胞会出现回弹而其他层单胞发生压缩变形. 由于加载?卸载过程中内部单胞的自我调整和回弹振动消耗能量, 使其储存在单元内部的部分弹性应变能在回弹过程中被消耗, 从而实现耗能, 并且克服了双稳态吸能结构借助外力恢复变形才能再次使用的弊端, 这一特性已被用于相关结构吸能设计^[21-22].

1.2
单胞构型设计

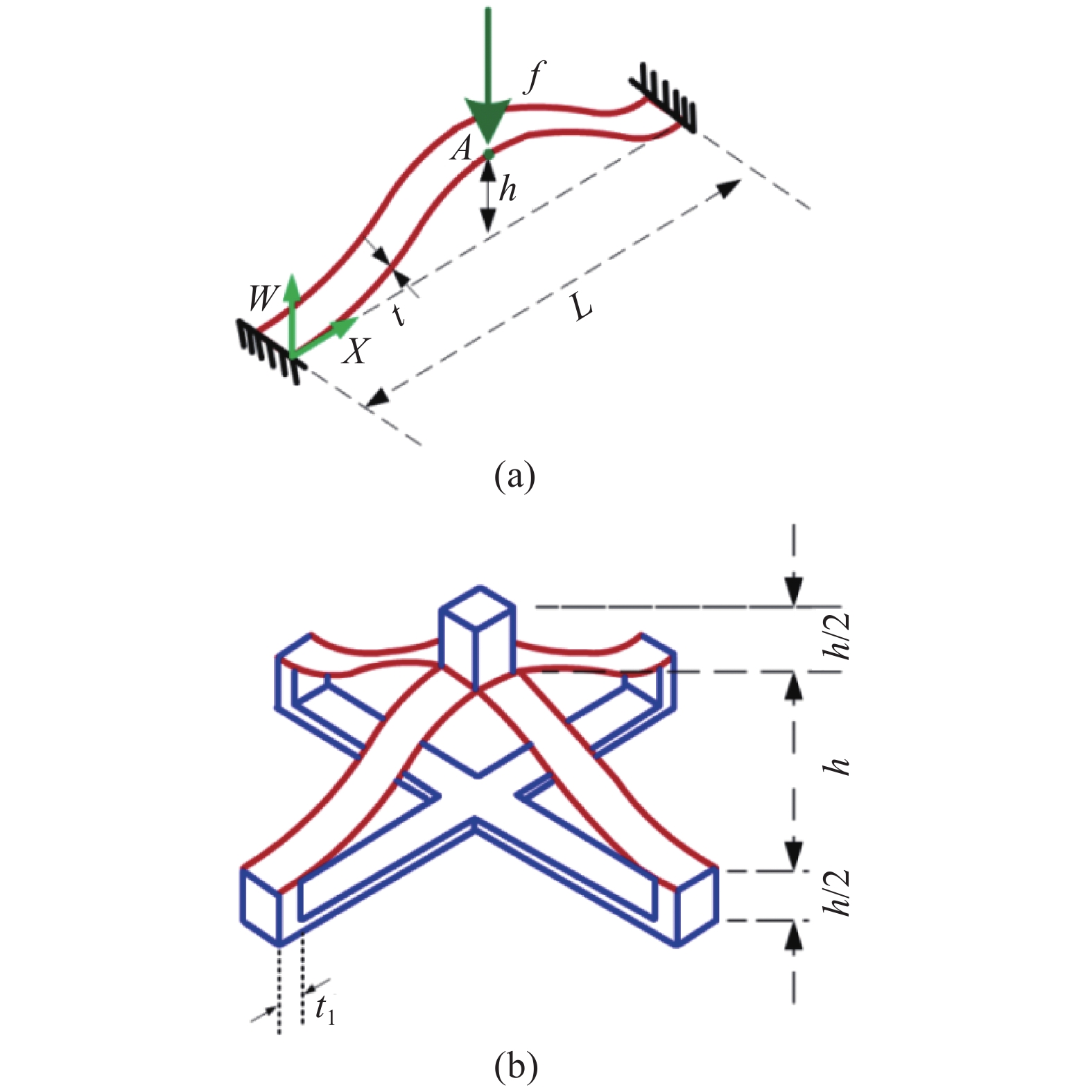
本文以如图3(a)所示曲梁为基本组件, 设计出三维单胞构型如图3(b)所示, 其中曲梁初挠度设为两端固支直梁的第一阶屈曲模态, 即



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
曲梁组件及三维单胞



Figure
3.
Curved beam module and 3D unit cell



下载:
全尺寸图片
幻灯片

$$wleft( x ight) = frac{h}{2}left[ {1 - cos left( {2{ m{{text{π}} }}frac{x}{L}} ight)} ight],x in left[ {0,L} ight]$$

(3)

其中, $h$为曲梁的初始顶点高度, $L$为梁的跨度, $t$为曲梁壁厚度, ${t_1}$为侧壁厚度. 定义$Q = {h/t}$为曲梁的形状因子.

当曲梁两端受固定约束时, 在曲梁跨中顶点处施加外载荷$f$, 采用模态叠加法并忽略高阶模态, 可得到如下封闭解^{[17, 23]}:

若二阶模态未被限制

$${F_1} = frac{{3{{ m{{text{π}} }}^4}{Q^2}}}{2}varDelta left(varDelta - frac{3}{2} + sqrt {frac{1}{4} - frac{4}{{3{Q^2}}}} ight)left(varDelta - frac{3}{2} - sqrt {frac{1}{4} - frac{4}{{3{Q^2}}}} ight)$$

(4)

$${F_2} = 4.18{{ m{{text{π}} }}^4} - 2.18{{ m{{text{π}} }}^4}varDelta qquadqquadqquadqquadqquadqquad;;;;;;;; $$

(5)

若二阶模态受到限制

$${F_1} = frac{{3{{ m{{text{π}} }}^4}{Q^2}}}{2}varDelta left(varDelta - frac{3}{2} + sqrt {frac{1}{4} - frac{4}{{3{Q^2}}}} ight)left(varDelta - frac{3}{2} - sqrt {frac{1}{4} - frac{4}{{3{Q^2}}}} ight)$$

(6)

$${F_3} = 8{{ m{{text{π}} }}^4} - 6{{ m{{text{π}} }}^4}varDelta ;;;;;;;;;;qquadqquadqquadqquadqquadqquadqquad $$

(7)

参数无量纲化

$${F_i} = frac{{{L^3}}}{{EIh}}{f_i};left( {i = 1,2,3} ight), varDelta = frac{d}{h}$$

其中，$E$为材料弹性模量, $I$为截面惯性矩, $d$为曲梁顶点A的位移.

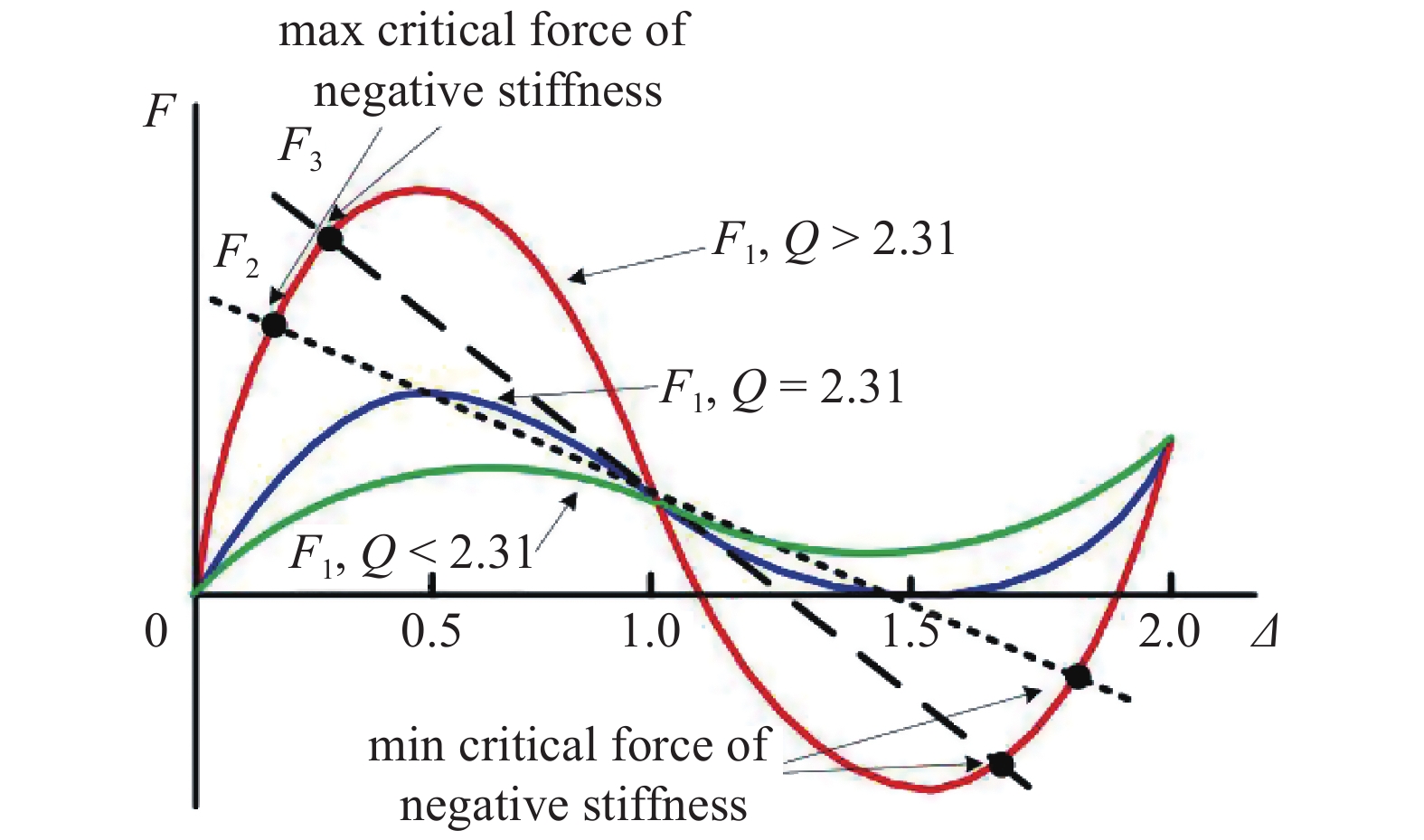
由式(4) ~ 式(7)可得曲梁顶点作用载荷时的力?位移曲线, 如图4所示. 可得: 只具有负刚度而不具多稳态的曲梁$ (Q<2.31)$, 其负刚度临界载荷最值间差值较小; 而具有多稳态的曲梁($Q > 2.31$), 其负刚度临界载荷最大与最小值间的差值较大. 而负刚度结构一个周期内能量吸收值的大小取决于负刚度临界载荷最大值与最小值的差值(见图2), 因此利用构型设计, 使曲梁$Q > 2.31$的同时, 通过在单胞顶点增加高为${h/2}$的竖向柱, 抑制曲梁二阶模态的出现, 从而提高负刚度单胞临界载荷最大值${F_{max }}$(即式(7)对应的${F_3}$). 同时通过在曲梁底部进行凹槽设计, 以抑制曲梁在$Q > 2.31$时多稳态的出现, 从而形成如图3(b)所示的三维负刚度单胞. 该结构将增大负刚度临界载荷最值间的差值, 实现结构的完全自主反弹和减振耗能能力的提升.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
归一化的曲梁力?位移关系的几种解^[17]



Figure
4.
Several solutions of the normalized force-displacement relations of curved beams^[17]



下载:
全尺寸图片
幻灯片

2.
力学性能参数分析

以金属铝($E = 68;{
m{GPa}}$, $
ho = 2300;{
m{kg}}/{{
m{m}}^3}$)为基底材料, 取如图3(b)所示三维单胞的一部分, 用ABAQUS有限元软件分析侧壁厚度${t_1}$对屈曲模态的影响. 由于结构具有大变形, 采用了动力显示分析步, 并且考虑几何非线性, 采用修正的二次四面体单元, 即C3D10M单元, 该非线性积分单元具有10个节点, 分别位于四面体的4个顶点和6条边中点, 每个节点具有3个自由度, 在位移控制下, 能够捕捉到后屈曲以及负刚度单元的跳跃现象, 可以避免剪切和体积自锁, 适用于ABAQUS/explicit分析步下大变形和接触问题的分析. 边界条件设置上, 单胞底部为完全固定, 将单胞顶部耦合到一参考点, 并输出该参考点在加载过程中的力?位移曲线. 选取的分析模型如图5所示, 其中图5(a)侧壁厚度${t_1} = 2t$, 图5(b)侧壁厚度${t_1} = t$. 已知两端固定的曲梁, 在二阶模态受到抑制时, 其在顶点载荷的作用下, 产生的屈曲模态如图6所示. 通过对比可知, 当侧壁厚度取$2t$时, 侧壁相对刚度较大, 单胞压缩过程中产生与固端约束相同的屈曲模态, 且引起较大的负刚度临界载荷最大值, 如图7所示; 同时由于单胞凹槽底部胞壁的限制, 负刚度临界载荷最小值大于0, 从而使多稳态单胞结构能够实现自主反弹. 而对于图5(b), 由于单胞侧向壁厚与曲梁壁厚大小相当, 从而使侧壁相对刚度较小, 不足以限制曲梁的转动, 因此侧向胞壁产生较大转角, 出现了与两端固定的受压曲梁不同的屈曲模态, 且其负刚度临界载荷最大值与固端屈曲模态相较, 有明显减小, 如图7中实线所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
侧壁厚度${t_1}$对曲梁屈曲模态的影响



Figure
5.
Effect of lateral wall thickness ${t_1}$on the buckling mode of curved beam



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
两端固定曲梁在二阶模态受到抑制后的屈曲模态



Figure
6.
Buckling mode of a curved beam fixed at both ends after the second-order buckling mode being suppressed



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
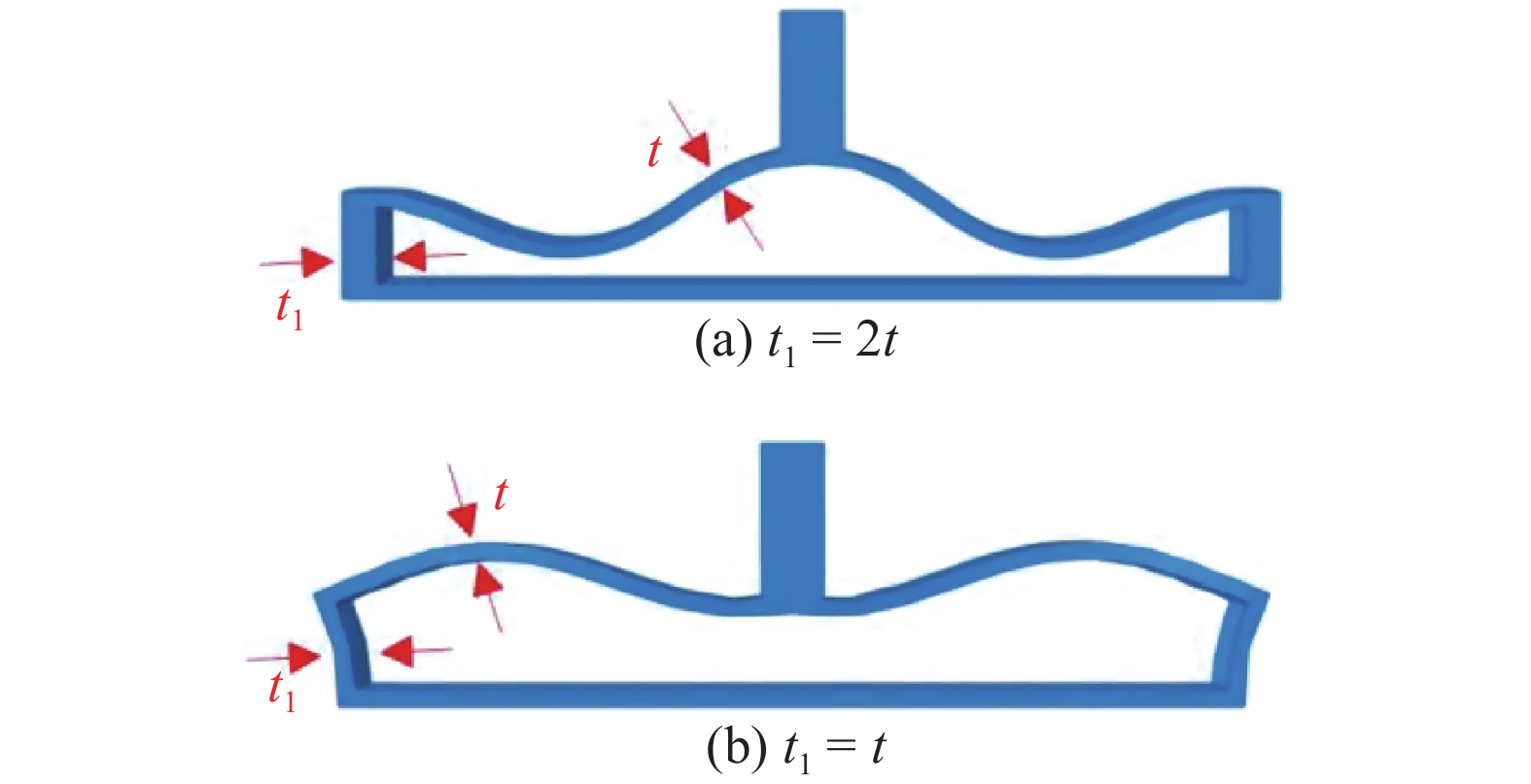
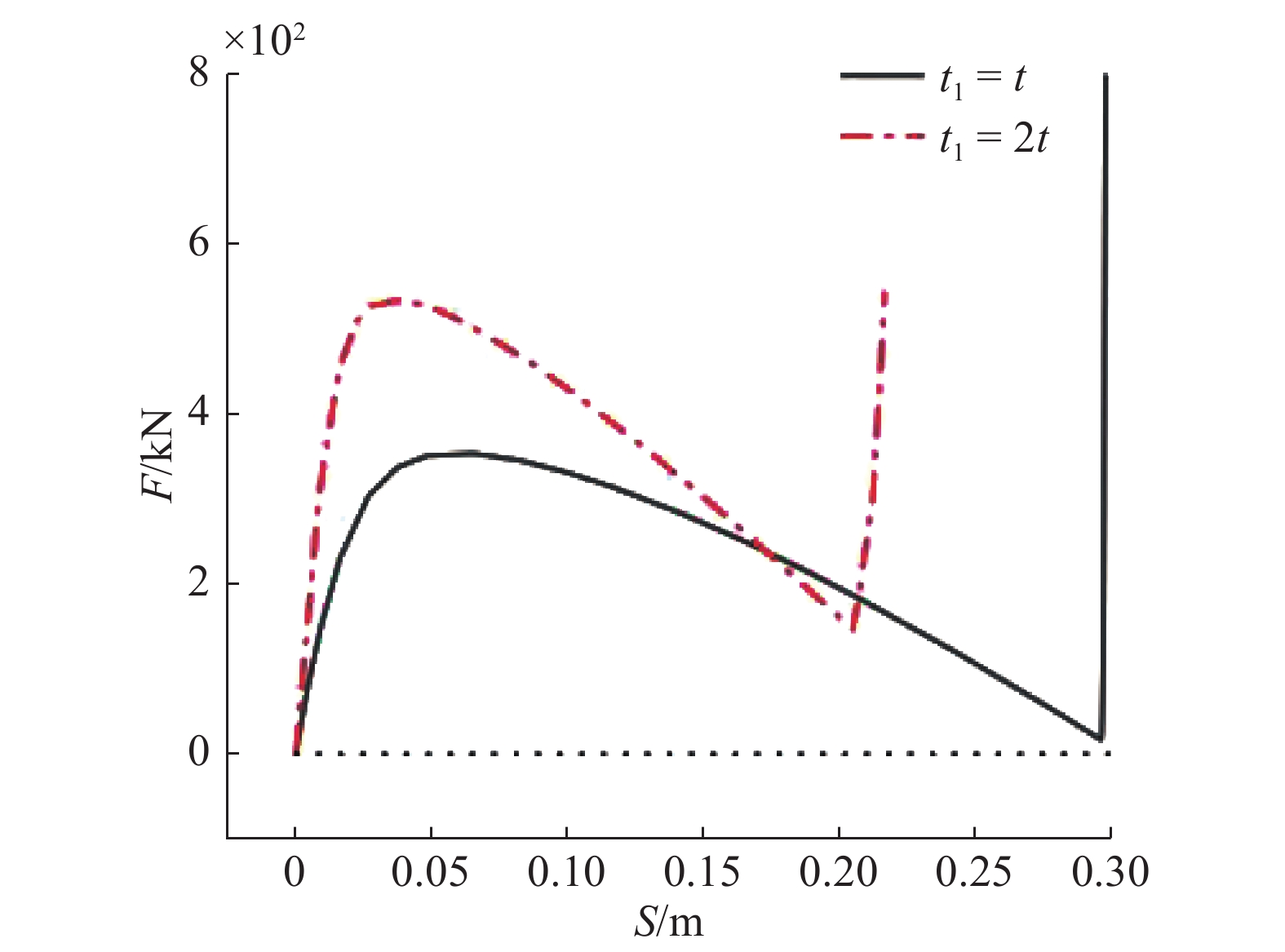
不同侧壁厚度(${t_1}$)下单胞的力($F$)?位移($S$)曲线



Figure
7.
Force ($F$)-displacement ($S$) relation of the unit cell with different lateral wall thicknesses (${t_1}$)



下载:
全尺寸图片
幻灯片


由此可知, 当侧壁厚度相对曲梁壁厚较大时(${t_1} geqslant 2t$), 可将其视为曲梁端点的固端约束, 在高为${h/2}$的竖向柱的作用下, 曲梁的二阶模态受到抑制, 从而产生如图6所示的屈曲模态.

针对相对壁厚(侧壁与曲梁的壁厚比值${{{t_1}}/t}$)的临界值, 进行了理论及有限元分析, 即探讨在何种侧向壁厚条件下, 可以获得如图6所示的屈曲模态. 在曲梁顶点施加外载荷$f$, 侧向胞壁将会受力弯曲, 其中侧向胞壁底端的弯矩大小为

$$M = frac{{EIhF}}{{8{L^2}}}$$

(8)

其中$I = {{b{t^3}}/{12}}$为曲梁胞壁的截面惯性矩.

在该弯矩作用下, 侧向胞壁相对竖直方向转角为

$$theta = - frac{M}{{E{I_1}}}frac{h}{2}$$

(9)

其中${I_1} = {{bt_1^3}/{12}}$为侧向胞壁的截面惯性矩, $b$为侧向胞壁平面外厚度(设为常数).

将式(8)代入式(9), 可得

$$theta = frac{{{Q^2}{{left( {{t/L}} ight)}^2}}}{{16{{left( {{{{t_1}}/t}} ight)}^3}}}F$$

(10)

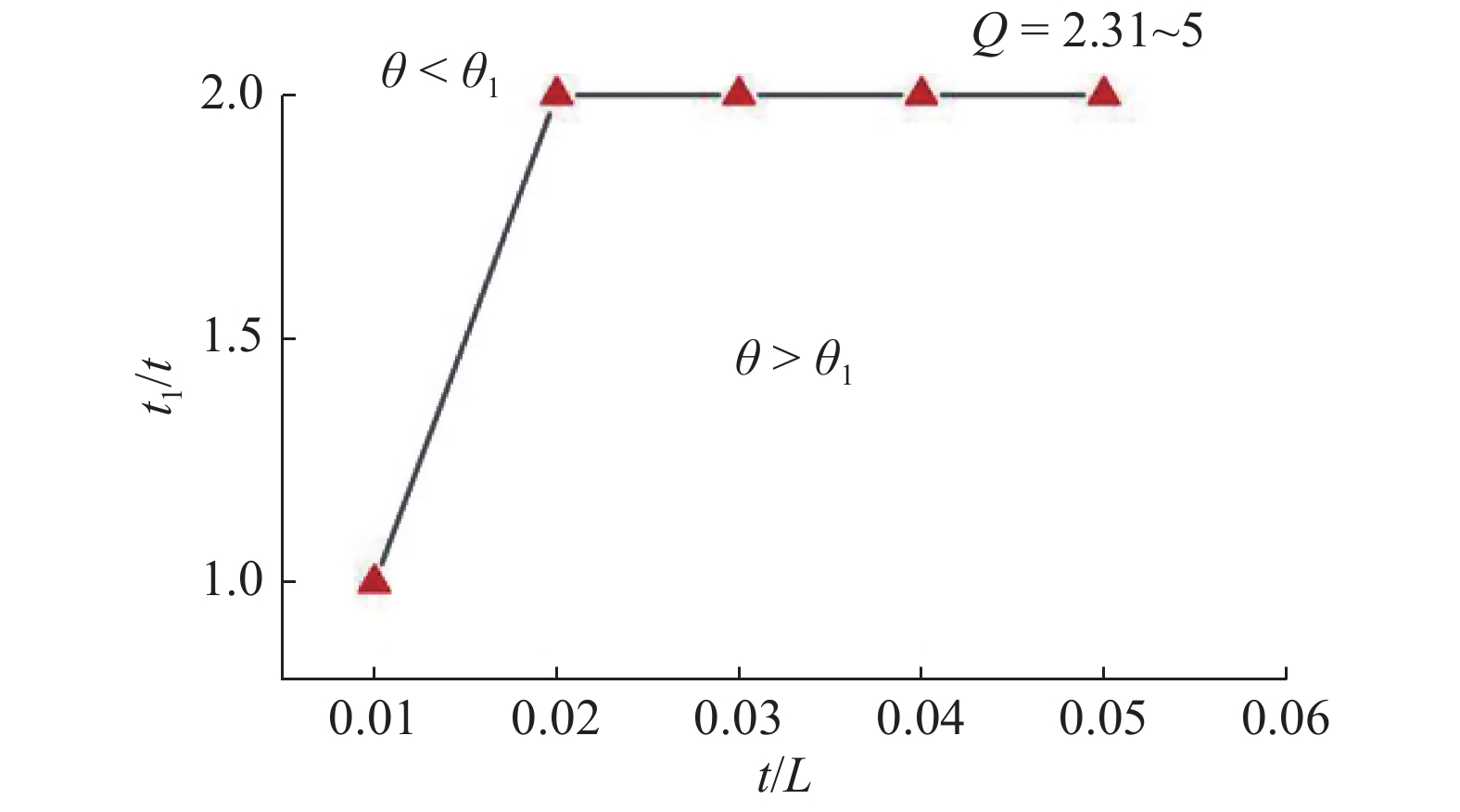
由式(10)可知, 端部受约束的曲梁结构的屈曲模态由除外载$f$之外的结构几何参数 $Q = {h/t},;{t/L},{t_1}/t$ 所决定.

用有限元软件模拟不同 $Q,;{t/L},{{{t_1}}/t}$ 取值下曲梁的屈曲模态, 从而确定侧向胞壁对曲梁端点的约束效果, 如图8所示. 在两种情况下, 结构会呈现出固端屈曲模态:



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
$Q,;{t/L},{{{t_1}}/t}$对结构屈曲模态的影响(${theta _1}$为 ${t_1} = 2t$时侧向胞壁相对竖直方向的转角)



Figure
8.
Effects of $Q,;{t/L},{{{t_1}}/t}$on buckling modes of the new developed structure (${theta _1}$ represents the angle of the lateral wall relative to the vertical direction when ${t_1} = 2t$)



下载:
全尺寸图片
幻灯片


(1)当$ t/L<0.01;{text{且}};{t}_{1}/t>1$时, 即曲梁壁厚 $t$相对曲梁长度 L较小, 而侧向壁厚 ${t_1}$大于曲梁壁厚 $t$时, $theta < {theta _1}$, 其中${theta _1}$为${t_1} = 2t$时侧向胞壁相对竖直方向的转角.

(2)当$ 0.01<t/L<0.05;{text{且}};{t}_{1}/t>2$ 时, 即曲梁壁厚 $t$相对曲梁长度$L$较大, 而同时侧向壁厚 ${t_1}$大于曲梁壁厚 $t$ 的2倍时, $theta < {theta _1}$.

形状因子$Q$的影响, 由图8可知, 当形状因子$2.31 < Q < 5$时, $Q$值的增大对曲梁屈曲变形模态影响很小.

3.
吸能特性分析

3.1
单胞吸能效率分析

随着单胞串联个数的增加, 负刚度结构的耗能比也会逐渐增大. 当串联的单胞数量足够多时, 结构整体的耗能比最后趋于一个稳定的值, 并且在加载?卸载过程中, 结构所受载荷趋近于单胞负刚度临界载荷的最值. 本文通过理论解析, 利用单胞加载?卸载的力?位移响应计算单胞吸收的能量大小, 并比较了不同参数对单胞吸能效率的影响.

单胞单位质量吸收的能量可表示为^[24]

$${W_{ m{m}}} = frac{W}{{ ho V}}qquadqquad;;;;;;;;$$

(11)

$$W = int_0^s {left[ {{f_1}(delta ) - {f_2}(delta )} ight]} { m{d}}delta $$

(12)

$$V = {V_{{ m{wall}}}} + {V_{{ m{beam}}}}qquad;;$$

(13)

$${V_{{ m{wall}}}} = bt(L + 4t + 2Qt);;$$

(14)

$${V_{{ m{beam}}}} = btint_0^L {w(x)} { m{d}}xquad;;$$

(15)

其中, $W$为单胞吸收的能量, $s$为最大位移, $
ho $为基底材料的密度, $V$为单胞的体积, ${f_1}(delta )$与${f_2}(delta )$分别为结构加载?卸载过程中变化的外力值. $V$可以通过将单胞凹槽胞壁体积${V_{{
m{wall}}}}$和曲梁体积${V_{{
m{beam}}}}$相加得到, 曲梁的体积$ {V}_{{
m{beam}}} $的计算方法是将曲梁的长度$displaystyleint_0^L {wleft( x
ight)} {
m{d}}x$, 曲梁平面外厚度$b$及曲梁面内壁厚$t$相乘. 其中通过对曲梁形状的线性函数$wleft( x
ight)$积分得到曲梁的长度.

在加载?卸载过程中, 当单胞个数足够多时: ${f_1}(delta ) - $$ {f_2}(delta ) = {f_{max }} - {f_{min }}$其中${f_{max }},{f_{min }}$由式(6)与式(7)联立求解. 在这种情况下, 计算了不同 $Q,;{t/L}$ 下曲梁单胞吸收的能量大小. 其中曲梁I相应参数为

$${Q^{left( { m{I}} ight)}} = 2.31,t = 0.01;{ m{m}},b = 0.01;{ m{m}},L = 1;{ m{m}}$$

$${V_1} = {V_{{ m{wall}}}} + {V_{{ m{beam}}}} = 0.042;264;{{ m{m}}^3};;;;;;;;;;;;;;$$

$${W_1} = ({f_{max }} - {f_{min }}) times 2hqquadqquadqquad;;;;;;;$$

$$f = frac{{FEIh}}{{{L^3}}},{F_{max }} = 389,{F_{min }} = 0;;;;;;;;;;;;;;;;$$

$${W_{{ m{m}}1}} = frac{{{W_1}}}{{ ho {V_1}}} = 6284;{ m{J}}/{ m{kg}};;;;;;;;;;;;;;;;;;;;;;;;;;;;;;$$

曲梁II (要求${Q^{left( {{
m{II}}}
ight)}} > 2.31$, 此处取${Q^{left( {{
m{II}}}
ight)}} = 5$), 相应参数为

$${Q^{left( {{ m{II}}} ight)}} = 5,t = 0.01;{ m{m}},b = 0.01;{ m{m}},L = 1;{ m{m}}$$

$${V_2} = {V_{{ m{wall}}}} + {V_{{ m{beam}}}} = 0.042;907;{{ m{m}}^3};;;;;;;;;;;$$

$${W_2} = ({f_{max }} - {f_{min }}) times 1.5h;;;;;;;;;;;;;;;;;;;;;;;;;;;;$$

$$f = frac{{FEIh}}{{{L^3}}},{F_{max }} = 711,{F_{min }} = 194;;;;;;;$$

$${W_{{ m{m}}2}} = frac{{{W_2}}}{{ ho {V_2}}} = 19;640;{ m{J}}/{ m{kg}};;;;;;;;;;;;;;;;;;;;;;$$

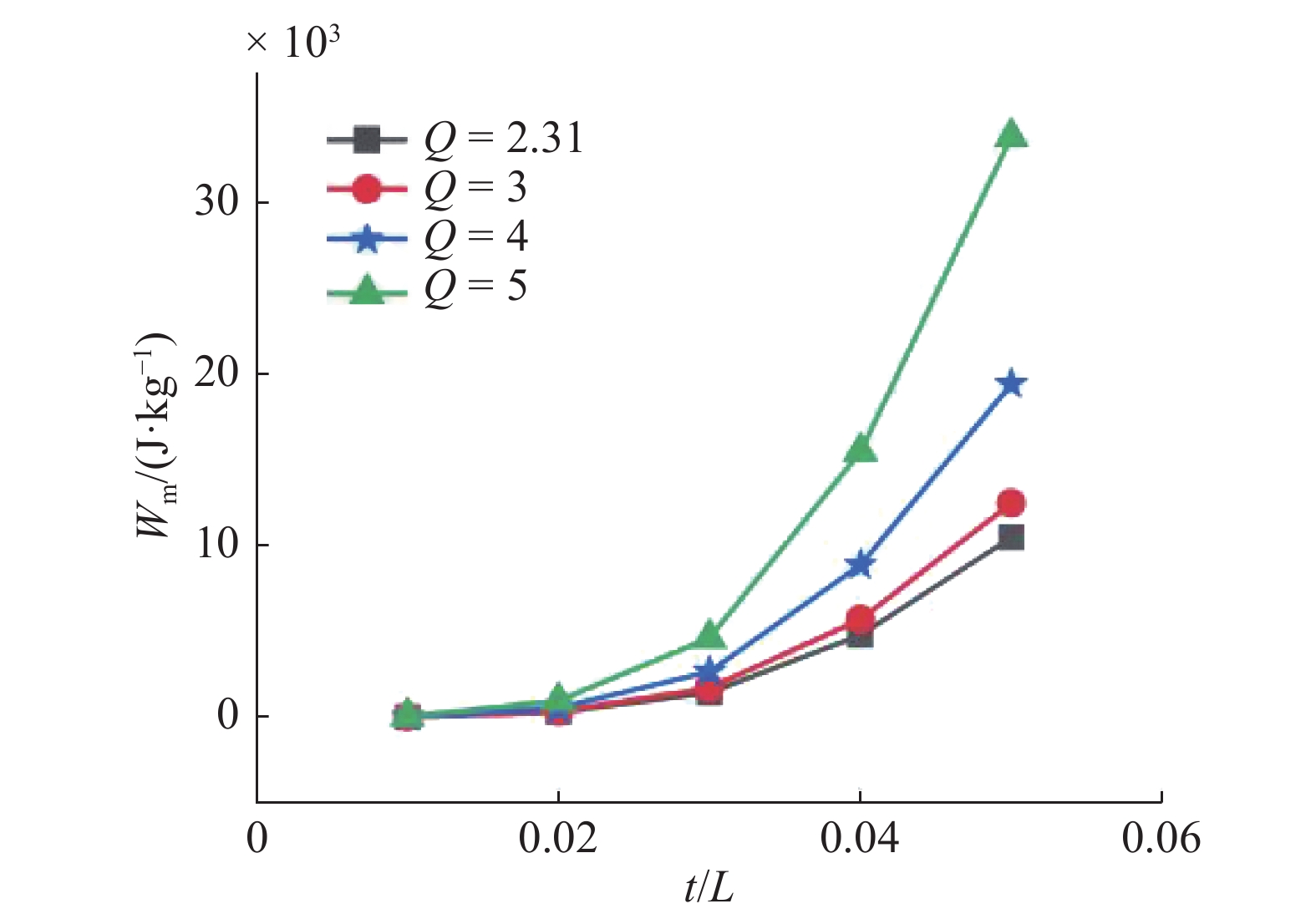
在不同${t/L}$值下, 曲梁I (${Q^{left( {
m{I}}
ight)}} = 2.31$)和曲梁II (${Q^{left( {{
m{II}}}
ight)}} > 2.31$)单位质量的能量吸收大小如图9所示. 结果显示曲梁II的吸能效果比曲梁I有大幅度提高, 且随着曲梁相对壁厚(${t/L}$)的增大, 该负刚度结构吸收能量的能力迅速增强, 这是因为此单胞负刚度临界载荷最大值是壁厚$t$的三次方, 在相同$Q$值下, 不同${t/L}$对单胞吸能大小有显著影响. 定义曲梁I (${Q^{left( {
m{I}}
ight)}} = $$ 2.31$)单位质量能量吸收值$({W_{{
m{m}}1}})$与曲梁II (${Q^{left( {{
m{II}}}
ight)}} > 2.31$)单位质量能量吸收值$({W_{{
m{m}}2}})$的比值为$eta = {{{W_{{
m{m}}1}}}/{{W_{{
m{m}}2}}}}$, 如图10所示. 在相同${t/L}$值下, $eta $值将随着${Q^{left( {{
m{II}}}
ight)}}$值的增大而减小, 但是不同${t/L}$值的变化对$eta $无显著影响, 这是因为在相同${t/L}$值下, Q值对结构质量和体积影响很小, 单胞结构吸能比值大小主要取决于$Q$值对负刚度临界值的影响. 由图9和图10的对比分析可知, 本文所设计的三维曲梁结构(曲梁II )在实现自主反弹的基础上, 吸能效率得到了显著提升.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同$Q$值下, 结构吸收的能量随${t/L}$的变化关系



Figure
9.
Variation of energy absorption${W_m}$ with ${t/L}$under different shape factors $Q$



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
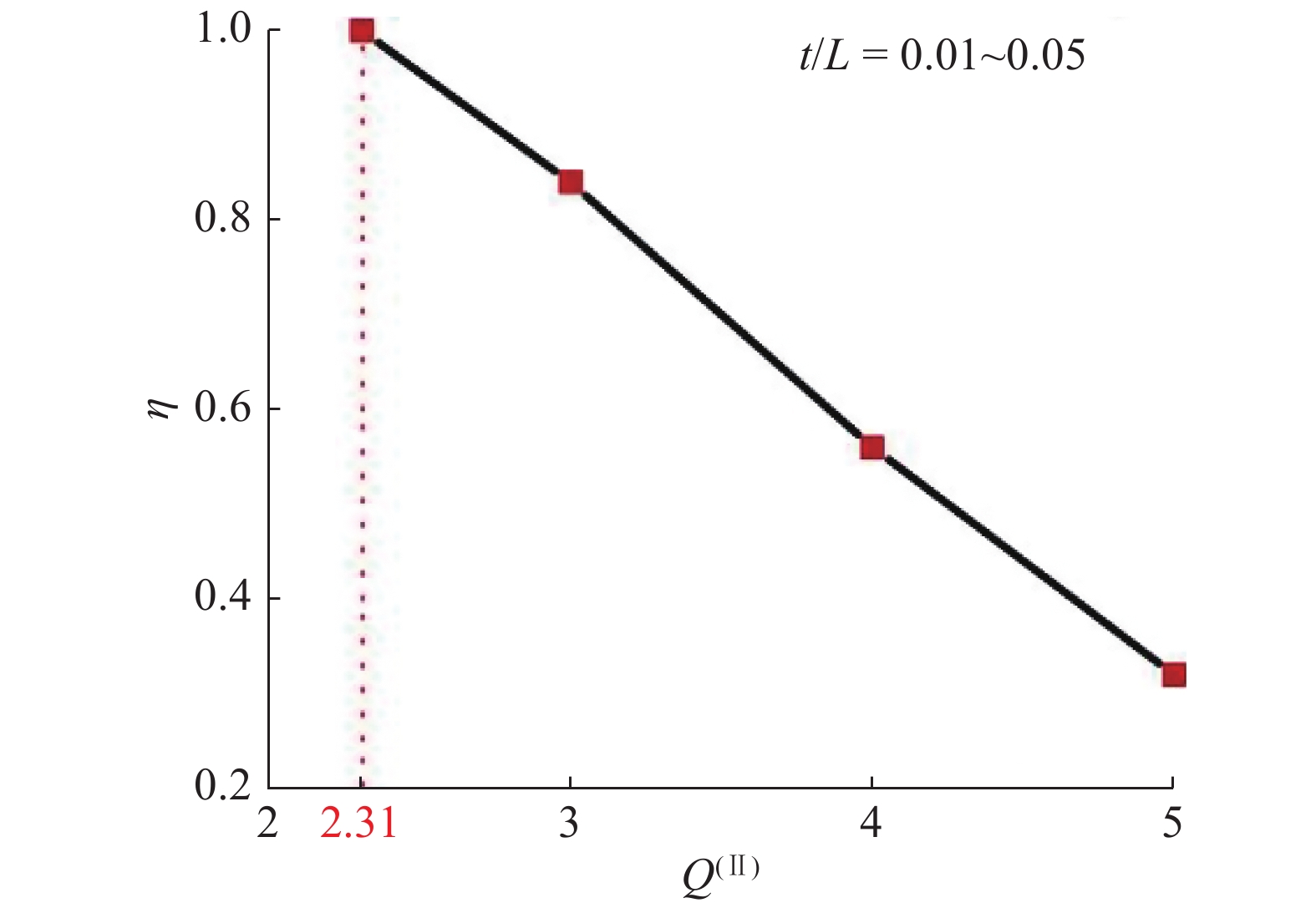
单胞吸能比值$eta $随形状因子${Q^{left( {{
m{II}}}
ight)}}$的变化关系



Figure
10.
Variation of energy absorption efficiency $eta $ with different shape factors ${Q^{left( {{
m{II}}}
ight)}}$



下载:
全尺寸图片
幻灯片

3.2
周期结构吸能效率分析

为进一步验证上述结果的正确性, 采用$Q = 5, $$ ;h = 0.1;{
m{m}},;L = 1;{
m{m}},;t = 0.02;{
m{m}}$的单胞, 并将该单胞按照$ 3times 3 $和$ 6times 6 $的排列方式组成周期结构, 分别用9倍面积和36倍面积的刚性板以$5;{
m{m/s}}$的速度冲击周期结构(见图11). 记录刚性板在冲击前后的速度变化, 如图12所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
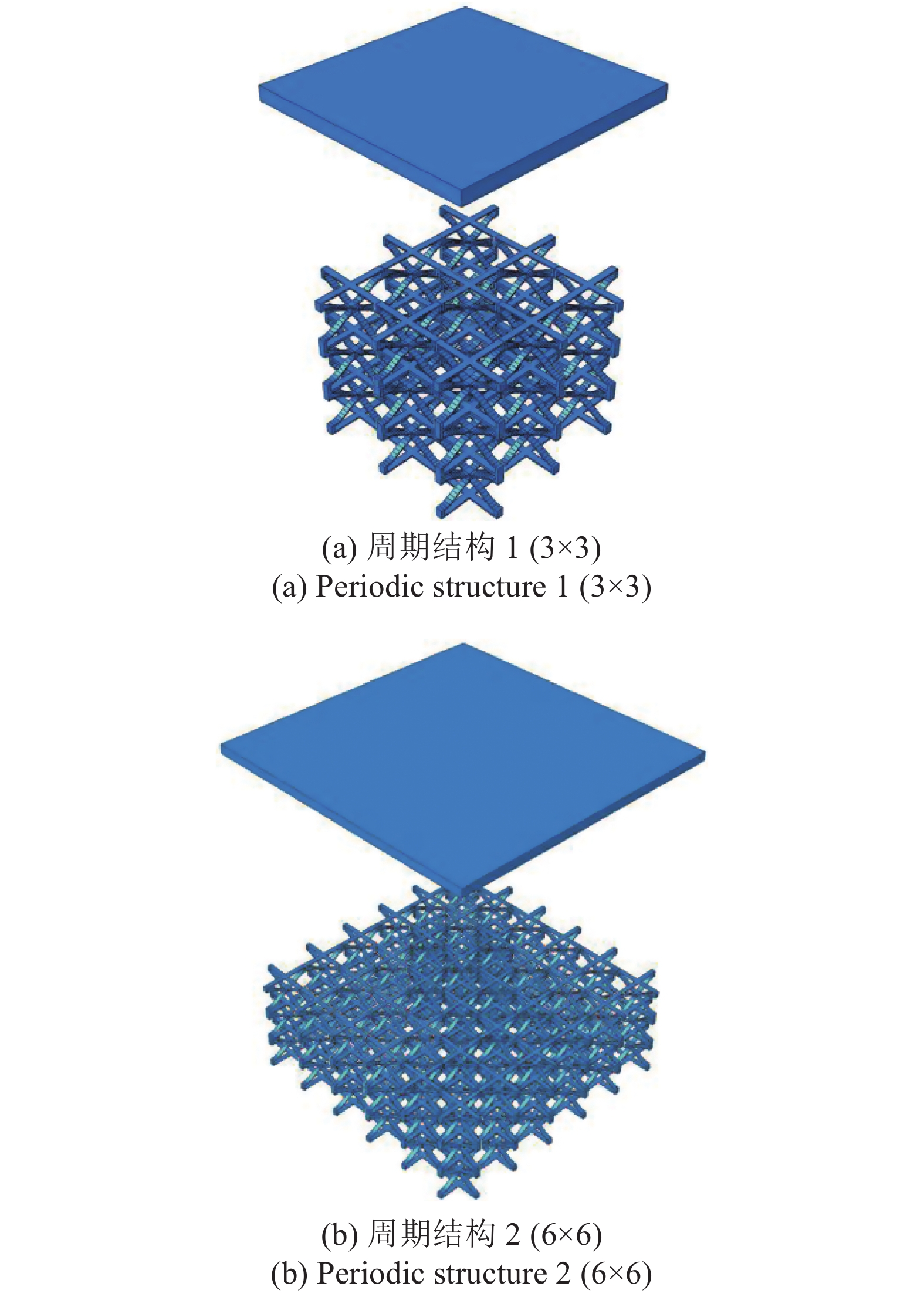
11
周期结构分析模型



Figure
11.
Analytical models for periodic structure



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
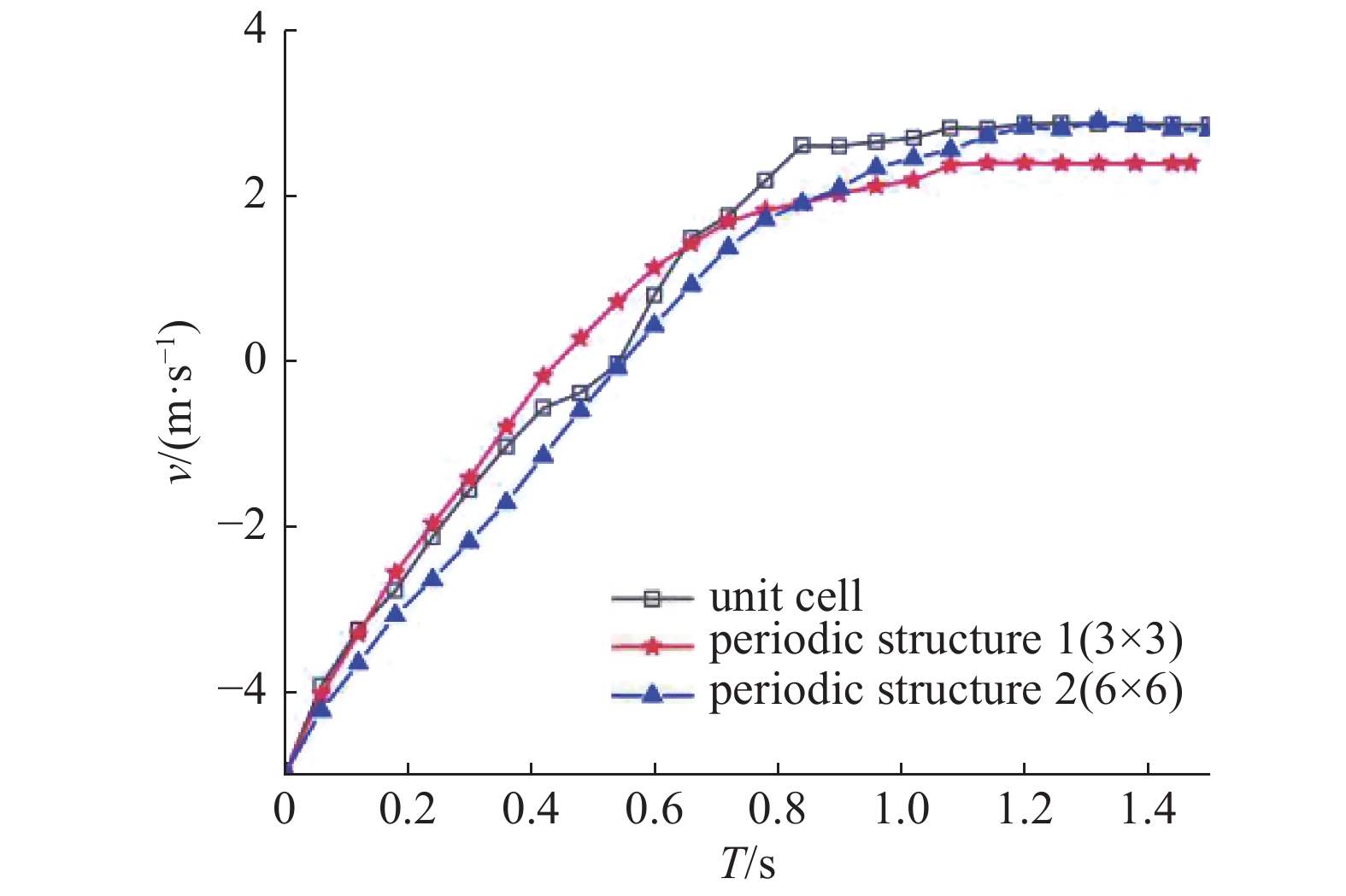
12
单胞和周期结构在相同冲击速度下的力学响应



Figure
12.
Mechanical responses of unit cell and periodic structures under the same impact velocities



下载:
全尺寸图片
幻灯片


结果显示: 在结构变形趋于稳定之后($T > {
m{1;s}}$), 相比于单胞结构, 刚性板冲击周期结构1($ 3times 3 $单胞排列)之后的速度误差最大值为$15% $, 刚性板冲击周期结构2($ 6times 6 $单胞排列)之后的速度误差最大值为$8% $, 这说明针对较大规模的周期结构, 可以选取代表性单胞研究其力学性能.

4.
梯度结构吸能特性分析

4.1
梯度结构设计

具有单一几何尺寸的单胞结构, 其负刚度临界载荷最大值为一确定量值, 因此当冲击载荷未达到该临界载荷值时, 结构将不能进入负刚度阶段(图1中的阶段II), 也即无法实现结构内部单元自主回弹耗能. 因此, 可以对结构进行梯度设计, 以使其在不同冲击载荷作用下, 都能够产生负刚度特性, 从而提高结构在不同载荷环境下的能量损耗, 实现更优的减振耗能^[25].

对于单一几何尺寸的均匀单胞结构, 设其在顶点受到外力$f$作用, 由式(6), 在已知无量纲化外载荷$F$时, 可以得到$f = dfrac{{EIh}}{{{L^3}}}F$, 其中$h = Qt$, $I = {{b{t^3}}/{12}}$, 则

$$f = frac{{QEb{t^4}}}{{12{L^3}}}F$$

(16)

由此可进行梯度结构设计, 令部分曲梁胞壁厚度为${t_2}$, 且${t_2} = {t/alpha }$, 设 $0 < alpha < 2$, 为常系数. 在相同的$Q,E,b$ 值下, 由式(6)可知, F是相同的, 则所设计梯度单胞顶点所加外载荷为

$${f_2} = frac{{QEbt_2^4}}{{12L_{}^3}}F$$

(17)

令$D{F_{{
m{cr}}}} = dfrac{f}{{{f_2}}}$, 则具有不同壁厚单胞结构的负刚度临界载荷值间存在以下关系

$$D{F_{{ m{cr}}}} = frac{f}{{{f_2}}} = {alpha ^4}$$

(18)

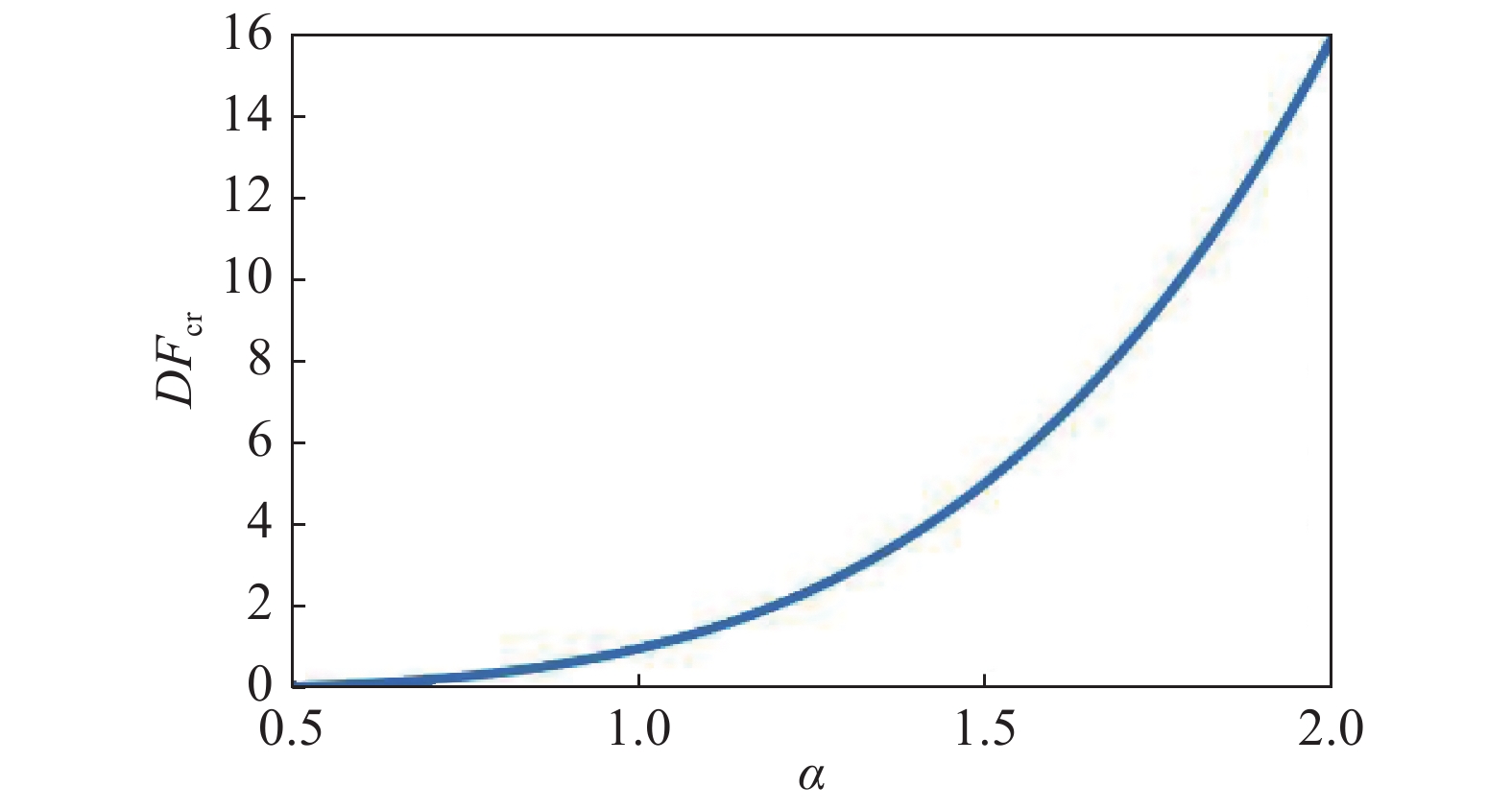
图13表示$D{F_{{
m{cr}}}}$随$alpha $的变化关系, 可知单胞负刚度临界载荷最大值随曲梁壁厚的变化十分明显. 故通过改变单胞结构中曲梁壁厚, 可以得到具有多个负刚度临界载荷最大值的单胞结构, 由此可见, 通过在结构中设计具有不同壁厚的曲梁单胞, 构造梯度结构, 以实现在同一结构中产生多种负刚度临界载荷最大值, 从而提高结构在不同冲击载荷作用下的耗能效率.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
梯度结构负刚度临界载荷比值($D{F_{{
m{cr}}}}$)随曲梁壁厚比值($alpha $)的变化关系



Figure
13.
Variations of negative stiffness critical force ratio ($D{F_{{
m{cr}}}}$) with the curved beam wall thickness ratio ($alpha $) for the gradient structure



下载:
全尺寸图片
幻灯片


由图13可知, 梯度结构存在不同的负刚度临界载荷最大值, 在不同冲击载荷下, 其结构内部单胞都会出现自主回弹, 实现能量的吸收; 而均匀单胞结构的负刚度临界载荷最大值单一, 当外载荷作用小于该值时, 不会出现结构的内部回弹调整, 结构将无法实现对能量的吸收而只存在弹性应变能与动能之间的转换. 因此不同冲击载荷作用下, 梯度结构更具有吸能优势和更好的环境适应性. 此外, 如果可以预设冲击载荷可能的峰值, 则可通过调整单胞结构的相关参数, 如曲梁厚度、侧壁厚度, 顶点高度等, 使负刚度临界载荷最大值小于相应冲击载荷峰值, 从而获得可调控的吸能效果. 此外, 在相同冲击载荷作用下, 通过对梯度结构梯度尺寸进行函数关系设计^[26], 使其吸能效果最优, 亦是一个值得探讨的方向.

4.2
梯度结构吸能效率对比分析

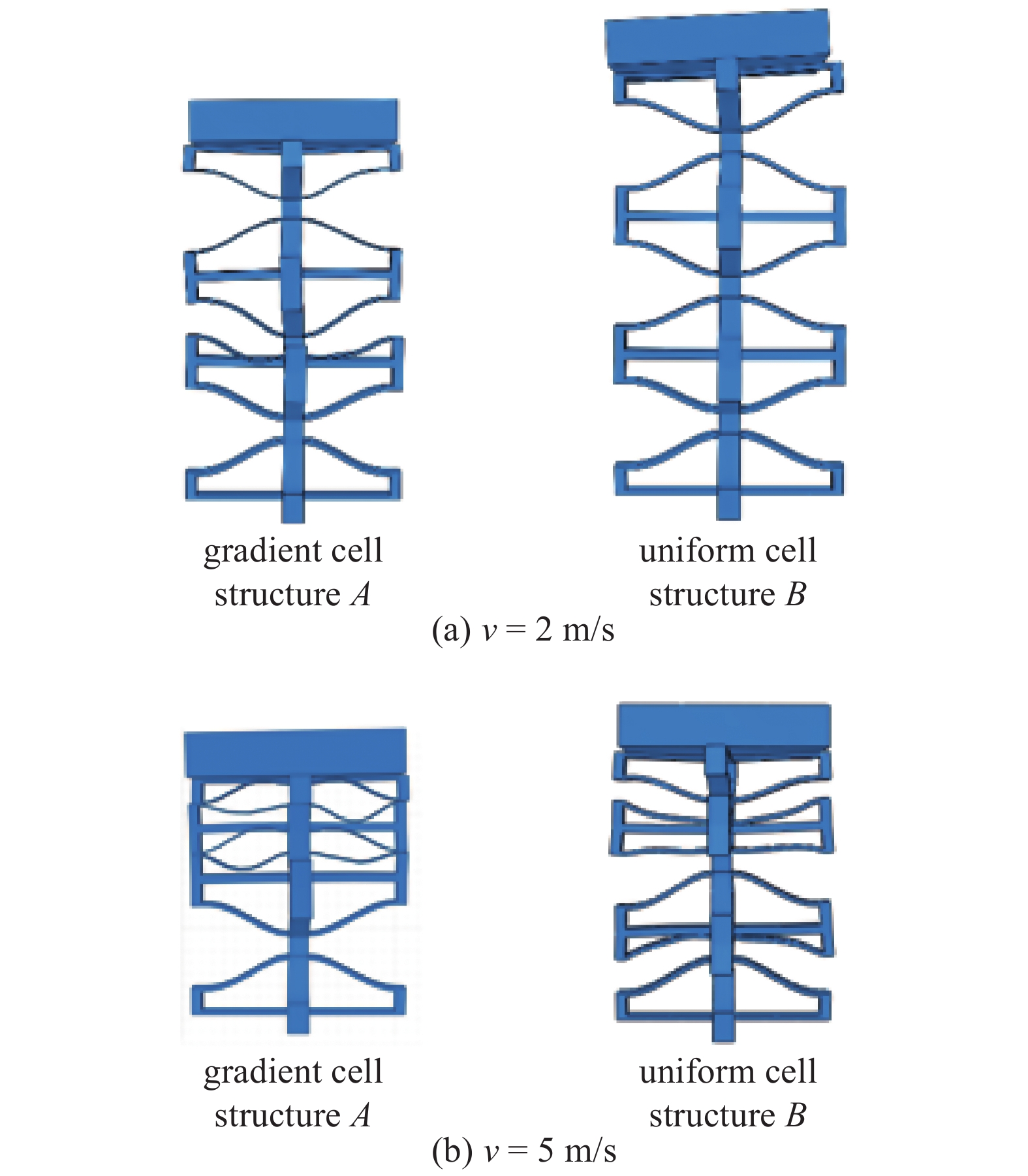
为进一步比较梯度单胞结构与均匀单胞结构的吸能效果, 本文利用ABAQUS软件模拟相同冲击载荷下梯度单胞结构和均匀单胞结构的力学响应, 有限元模型如图14所示, 其中模型底部完全固定, 采用C3D10M实体单元, 刚板施加了预定义速度场分别为$2;{
m{m}}/{
m{s}}$和$5;{
m{m}}/{
m{s}}$, 冲击梯度结构A和均匀结构B, 并将刚性板上表面耦合到一参考点, 输出该点速度, 通过监测冲击载荷反弹后的速度来分析结构吸能的效率. 其中针对梯度结构的梯度布置问题, 主要通过改变曲梁胞壁的厚度 $t$ 来实现梯度设计, 如图14所示, 梯度结构A采用两种不同单胞组成: 在保持$h = 0.1;{
m{m}},;L = 1;{
m{m}}$不变的情况下, 上部4个单胞选取曲梁壁厚${t^{left( 2
ight)}} = 0.01;{
m{m}}$, 下部两个单胞选取曲梁壁厚$;{t^{left( 1
ight)}} = 0.02;{
m{m}}$, 则根据形状因子定义$Q = {h/t}$, 可知${Q^{left( 1
ight)}} = $$ 5$, ${Q^{left( 2
ight)}} = 10$; 均匀单胞结构B: $Q = 5,;h = 0.1;{
m{m}},;L = 1;{
m{m}},;$$t = 0.02;{
m{m}} $.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
两种结构在不同冲击速度下的屈曲模态



Figure
14.
Buckling modes of two structures under different impact velocities



下载:
全尺寸图片
幻灯片


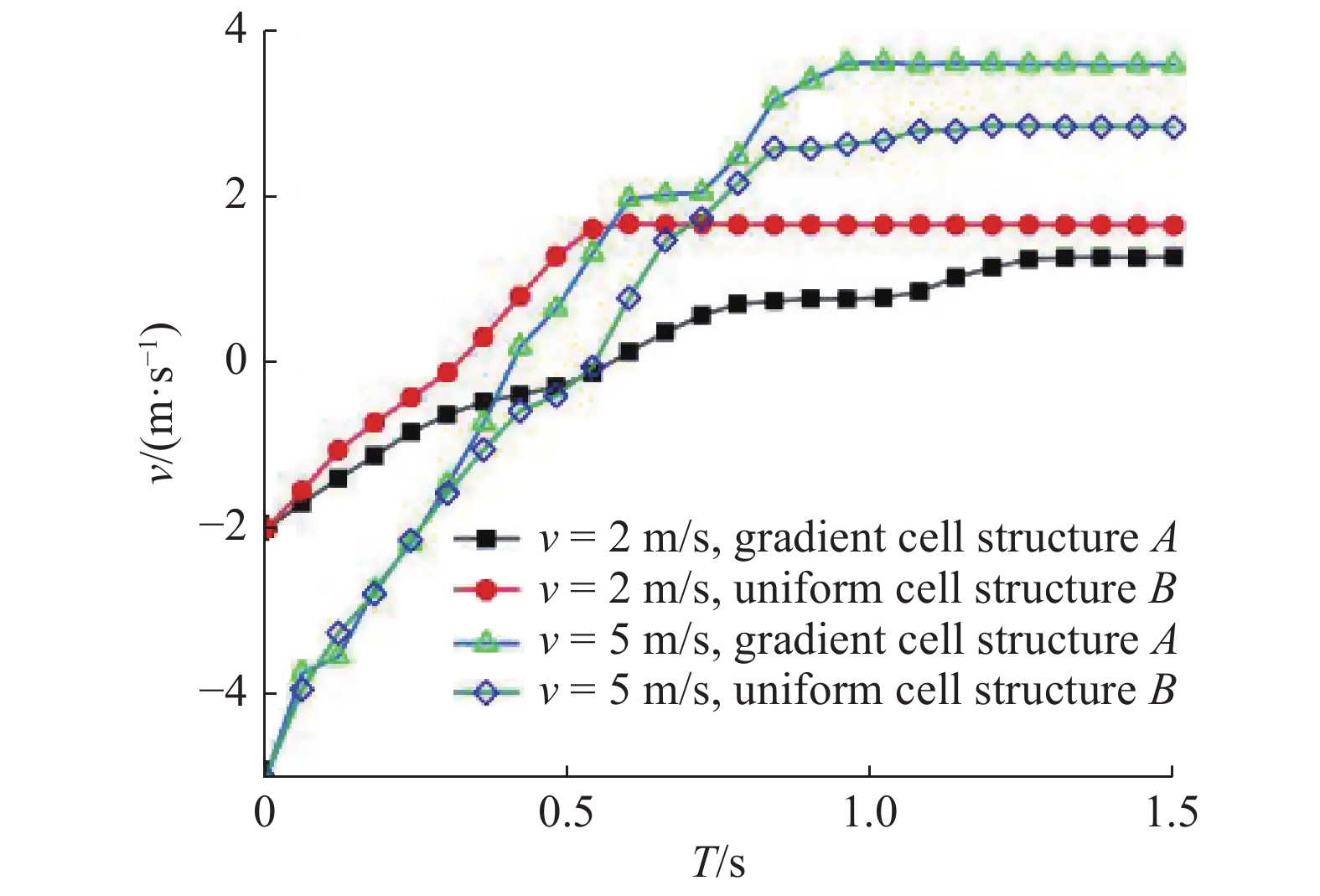
在冲击载荷作用下, 两种结构的力学响应如图15所示, 在相同的冲击速度$v = 2;{
m{m}}/{
m{s}}$下, 冲击梯度单胞结构A的刚板, 在压缩反弹过程中, 其反弹速度小于冲击均匀单胞结构B的刚板; 且在冲击过程中, 梯度单胞结构A部分单胞已进入负刚度阶段, 而均匀单胞结构B所有单胞均仍处于正刚度阶段, 如图14(a)所示, 这是由于均匀单胞结构B只存在单一的负刚度临界值点, 必须在冲击载荷达到单胞负刚度临界载荷最大值时, 结构才会进入负刚度阶段. 如图16所示, 当冲击载荷速度为$2;{
m{m}}/{
m{s}}$时, 均匀结构B中的单胞受到的冲击载荷未能达到其负刚度临界载荷最大值(${F_{max 1}}$), 结构内部将不会出现自我回弹调整; 而梯度单胞结构A存在不同的负刚度临界值点, 在$2;{
m{m}}/{
m{s}}$的冲击载荷速度下, 梯度单胞结构A部分单胞受到的载荷达到了其负刚度临界载荷最大值${F_{max 2}}$, 进入负刚度阶段, 因而结构内部出现了自主回弹调整, 从而提高了冲击载荷作用下的能量吸收效能.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
两种结构在不同冲击速度下的力学响应



Figure
15.
Mechanical responses of two structures under different impact velocities



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
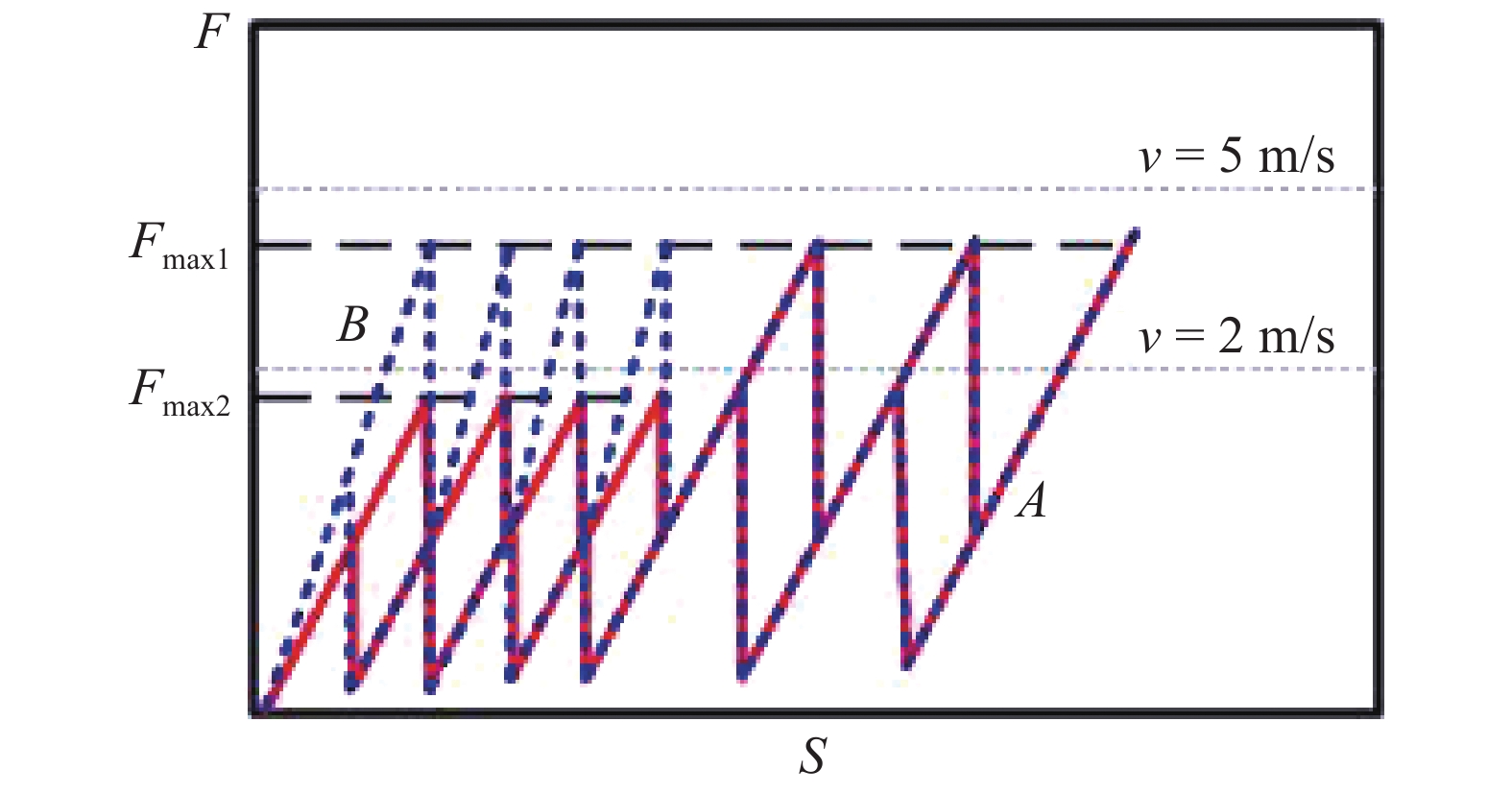
16
梯度单胞结构A与均匀单胞结构B的力?位移曲线



Figure
16.
Force-displacement relations for gradient cell structure A and uniform cell structure B



下载:
全尺寸图片
幻灯片


当冲击载荷速度增大到$5;{
m{m}}/{
m{s}}$时, 如图15所示, 均匀单胞结构B在冲击载荷作用后的反弹速度小于梯度单胞结构A; 究其原因, 虽然两种结构的单胞均进入负刚度屈曲模态阶段, 如图14(b)所示, 但均匀单胞结构B的负刚度临界载荷最大值较大(图16), 其滞回曲线所围成的面积(图16虚线围成的面积)大于梯度结构滞回曲线所围成的面积(图16实线围成的面积), 因此耗能大于梯度结构, 回弹速度更小.

5.
讨论

观察图14, 发现曲梁已与单元上下边界发生接触, 因此需要考虑弹塑性变形以及接触对本部分冲击吸能的影响, 但本文在有限元建模时采用的是弹性模型, 这是因为负刚度结构实现循环(重复)加载的基础即初弯曲梁的弹性变形. 不同基底杆件所能承受的最大应力?应变不同, 采用不同基底杆件时, 结构有可能出现塑性变形, 而本文为了实现完全回弹(不存在残余变形), 在选取基底材料时, 首要保证结构的弹性变形; 此外本文保持低速冲击状态($v leqslant $$ 5;{
m{m/s}}$), 结构会发生大变形, 但塑性变形相比而言较小. 因此这里忽略了弹塑性变形对冲击吸能的影响. 同时针对接触问题, 该负刚度结构在静力加载过程中存在曲梁胞壁与基底杆件相接触的现象, 该接触是结构设计时提前预设的, 其主要目的是通过曲梁胞壁与基底杆件的接触, 阻止曲梁第二稳态(负刚度临界载荷最小值${F_{min }} < 0$)的出现, 以实现负刚度结构的完全自主反弹.

同时, 在冲击载荷作用下, 不同屈曲模态对应不同的单胞微结构构型, Bertoldi^[27]指出,利用结构的不稳定性可以实现多孔结构的功能性设计, 如负泊松比、吸能与弹性波传播控制. 基于结构不稳定性进行能带调控可以实现滤波、导波、降噪等. 本文所设计的三维吸能结构, 在不同的屈曲模态下, 具有不同的微结构构型, 如图14所示, 因此将呈现不同的能带特性, 必然具有与禁带类似的滤波行为, 作者前期针对多孔结构禁带特性, 进行了一系列的研究^[28-29], 因此如何表征隔离特性、以及同时利用禁带与吸能, 将是一项很有意义的研究. 这也是作者后续的主要研究方向.

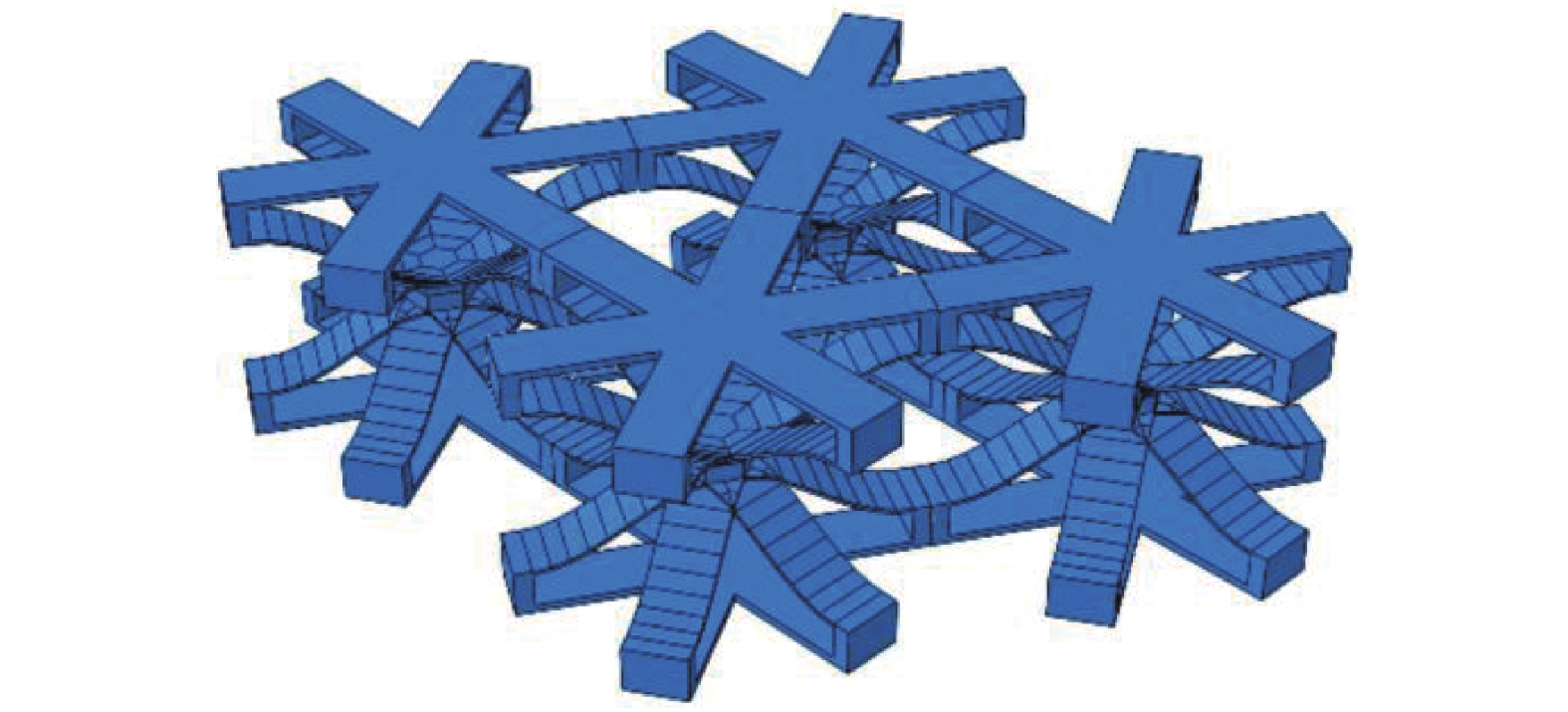
此外, 在不同的载荷环境下, 将上述独立的单胞结构进行重组^[30], 可获得更优的吸能效果. 例如通过增加组成单胞单元组件个数(图17), 可提高结构稳定性, 更好地实现结构内部回弹, 防止结构出现非预设的屈曲模态变形及失稳; 同时, 充分利用了结构空间, 利于实现低体积下的高耗能.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-083-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
重组多单元负刚度结构



Figure
17.
Reassembled multi-element negative stiffness structure



下载:
全尺寸图片
幻灯片

6.
总结

利用结构多稳态特征进行多孔结构多功能设计, 受到了广泛的关注. 然而多稳态结构无法实现自主反弹以及重复形变, 限制了其工程应用. 针对这一问题, 本文通过单胞构型设计抑制其多稳态的出现, 从而提出一种新型三维可回弹负刚度结构, 采用理论解析和数值模拟对该结构的吸能特性进行了系统分析. 分析结果表明: 该新型负刚度结构具有较大的负刚度临界载荷差值, 因此在实现结构完全自主反弹以及重复利用的基础上, 获得了更高的吸能效率. 同时, 为了适应复杂载荷环境, 本文通过调整单胞几何参数实现梯度结构设计, 以获得不同载荷状态下不同的负刚度临界载荷最大值, 从而使得结构在不同载荷环境下, 均能够实现自主反弹, 进而提高吸能效率, 减小结构持续性的振动. 本文的研究有望摆脱对外界冲击条件的依赖, 对工程结构的减振吸能应用具有重要的意义.