引言

颗粒悬浮液广泛存在于自然界及工程应用领域, 其黏性特征对悬浮液的流动行为有着重要的影响^[1-4]. 早在1905年, Einstein^[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响, 给出了悬浮液等效黏度系数计算的一个强有力的理论框架, 并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式, 即$;{mu _{
m{s}}} = {mu _{
m{f}}}(1 + varLambda phi )$, 这里分别$;{mu _{
m{s}}}$, $;{mu _{
m{f}}}$和 $;phi$为悬浮液等效黏性系数、液体本身黏性系数和固体颗粒体积分数, $varLambda = 2.5$即为此时的特性黏度. Einstein的工作引发了大量的后继研究, 很多****对更为复杂情形下的颗粒悬浮液等效黏性系数计算进行了研究, 主要包括了高浓度条件、考虑惯性效应以及非球形颗粒3个方向的拓展. 在高颗粒浓度的研究方面, 典型工作包括: Batchelor和Green^[6]首先考虑了固体颗粒间的相互作用, 将等效黏性系数公式拓展至体积分数的二次项, 在颗粒大小相等情形下有$;{mu _{
m{s}}} = $$ {;mu _{
m{f}}}(1 + 2.5phi {
m{ + }}5.2{phi ^2})$. 其后Batchelor^[7]进一步考虑了流体中布朗运动的影响, 将公式修正为${mu _{
m{s}}} = {mu _{
m{f}}}(1 + 2.5phi + $$ {
m{ 6}}.2{phi ^2})$. 近来, Zhu等^[8]结合前人的研究成果, 提出了一个简单的等效黏性系数关系式, 能够覆盖较宽的颗粒浓度范围. 在考虑惯性效应的研究方面, 典型工作包括: Lin等^[9]首先从理论上给出了一个修正公式, 即$;{mu _{
m{s}}} = {mu _{
m{f}}}[1 + (2.5 + 1.34{{Re} ^{1.5}})phi ]$, 其中${Re}$为雷诺数. Kulkarni和Morris^[10], Yeo和Maxey^[11-12]分别采用介观和宏观尺度的直接数值模拟方法, 研究了有限雷诺数条件下剪切流中颗粒悬浮液的流变特性, 并给出了较高浓度条件下等效黏性系数随雷诺数的变化规律. 在非球形颗粒的研究方面, 典型工作包括: Jeffery^[13]首先考察了低浓度条件下椭球形颗粒悬浮液的等效黏性系数, 并得到了长椭球体和扁球体颗粒悬浮液在不同偏心率情形下对应的特性黏度. Yamamoto和Matsuoka^[14]采用粒子模拟方法研究了低浓度棒状颗粒的等效黏性系数, 获得了刚体棒和柔性棒两种情形下特性黏度随方位角和轨道参数的变化规律. Huang等^[15]采用数值方法研究了低浓度条件下长椭球体和扁球体颗粒悬浮液的等效黏性系数, 结果表明低雷诺数时特性黏度和雷诺数呈线性相关, 而在高雷诺数时呈非线性关系.

值得注意的是, 上述研究涉及的颗粒均为不可渗透性的固体颗粒. 由于多孔介质材料在众多领域中得广泛应用^[16-17], 近年来一些国内外****也开始关注多孔介质颗粒悬浮液的黏性特征, 主要包括理论分析和数值模拟两方面的工作. 理论分析方面的典型工作包括: Natraj和Chen^[18]研究了带电多孔介质颗粒悬浮液中的电黏性效应, 首次给出了特性黏度和达西数的关系式. 其后Ohshima^[19-22]进一步拓展了Natraj和Chen^[18]的工作, 分别研究了较高浓度颗粒悬浮液以及内含实心核的多孔介质颗粒悬浮液的等效黏性特征. 上述工作均采用Darcy-Brinkman模型^[23-24]描述多孔介质区域的流场, 自由流区域采用Stokes方程, 界面上则采用速度连续和应力连续条件^[25]. Prakash和Sekhar^[26]则引入剪切应力跳跃条件, 给出了多孔介质悬浮液特性黏度与达西数、剪切应力跳跃系数的关系. 数值模拟方面的主要工作包括: Xu等^[27]采用介观尺度的格子Boltzmann方法模拟了含多孔介质球的Couette剪切流问题, 并通过直接计算边界剪切应力的方法确定了等效黏性系数和达西数、雷诺数的关系. Huang等^[28]则采用格子Boltzmann方法研究了较高浓度、考虑流体惯性效应以及边界限制因素影响下的多孔介质悬浮液黏性特征, 结果表明在达西数较小时, 流体惯性和边界限制对等效黏性系数有着显著的影响, 而达西数较大时, 流体惯性和边界限制的影响可忽略不计. Liu等^[29]进一步采用研究了低浓度低雷诺数条件下椭圆形颗粒悬浮液的等效黏性特征, 发现特性黏度随达西数增加而单调递减, 并给出了特性黏度一个简单的经验公式. 上述数值方面的工作均是采用介观尺度数值方法求解描述多孔介质流动的广义Navier-Stokes方程^[30-31], 自由流区域和多孔介质区域统一处理, 界面上不做特殊处理, 也就是界面上速度和应力仍保持连续.

综上所述, 已有的多孔介质颗粒悬浮液等效黏性的研究工作均基于Darcy-Brinkman模型或更为复杂的广义Navier-Stokes模型. 根据Nield的分析^[32], 当采用Darcy-Brinkman模型或广义Navier-Stokes模型在处理自由流/多孔介质流耦合问题时, 模型自由度过大, 一是模型本身包含了一个未定参数, 即所谓的有效黏性系数, 同时界面上还需考虑剪切应力的跳跃. 因此, 本工作基于Darcy-Stokes耦合模型及Beavers-Joseph(-Saffman)界面条件^[33-39], 研究了低雷诺数条件下多孔介质球对纯应变流动的流场的影响, 给出了自由流和多孔介质区域的流场解析解, 根据流场解析解计算了由于多孔介质球的存在额外产生的黏性热耗散率, 获得了多孔介质颗粒悬浮液的一个新的等效黏性系数计算公式, 并与基于Darcy-Brinkman模型的结果进行了比较.

1.
问题模型和求解方法

为了获得低浓度多孔介质颗粒悬浮液的等效黏度的解析表达式, 首先考虑多孔介质球对纯应变流动的影响. 如图1所示, 不可压缩流场内包含球心位于坐标轴原点、直径为${
m{2}}a$的各向同性多孔介质球. 多孔介质区域${varOmega _0}$内的流体运动满足Darcy方程, 即



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-144-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
包含多孔介质球形颗粒的流场区域的示意图



Figure
1.
Schematic diagram of the flow field containing a spherical porous particle



下载:
全尺寸图片
幻灯片

$$frac{{partial {u_{{ m{pm}},i}}}}{{partial {x_i}}} = 0quadquadquad$$

(1)

$$ - frac{{{mu _{ m{f}}}}}{K}{u_{{ m{pm}},i}} = frac{{partial {p_{{ m{pm}}}}}}{{partial {x_i}}}$$

(2)

式中${u_{{
m{pm}},i}}$和${p_{{
m{pm}}}}$分别为多孔介质区速度的第i个分量和压强, ${mu _{
m{f}}}$和$K$分别为流体黏性系数和多孔介质渗透率. 自由流区域${varOmega _1}$的流场控制方程为

$$frac{{partial {u_{{ m{f}},i}}}}{{partial {x_i}}} = 0quadquadquadquadquad$$

(3)

$${mu _{ m{f}}}frac{partial }{{partial {x_i}}}left( {frac{{partial {u_{{ m{f}},j}}}}{{partial {x_i}}}} ight) = frac{{partial {p_{ m{f}}}}}{{partial {x_j}}}$$

(4)

其中${u_{{{{
m{f}},i}}}}, {u_{{{{
m{f}},j}}}}$和${p_{{{{
m{f}}}}}}$分别为自由流区速度的第i, j个分量和压强.

自由流–多孔介质界面上 ${A_0}$ 的条件为

$${n_i}({u_{{ m{pm}},i}} - {u_{f,i}}) = 0,qquadqquadqquadqquadqquadquad;;$$

(5)

$$ - {p_{ m{f}}} + {mu _{ m{f}}}{n_i}left(frac{{partial {u_{{ m{f}},i}}}}{{partial {x_j}}} + frac{{partial {u_{{ m{f}},j}}}}{{partial {x_i}}} ight){n_j} = - {p_{{ m{pm}}}}quadquadquadquad;;;$$

(6)

$$begin{split}& ({u_{{ m{f}},i}} - {u_{{ m{pm}},i}}){tau _{{{s}},i}} + dfrac{{sqrt K }}{{{alpha _{{ m{BJ}}}}}}{n_j}left(dfrac{{partial {u_{{ m{f}},i}}}}{{partial {x_j}}} + dfrac{{partial {u_{{ m{f}},j}}}}{{partial {x_i}}} ight){tau _{s,i}} = 0;;&qquadqquadqquadqquadqquadqquad s = 1,2end{split} $$

(7)

或

$$ {u_{{ m{f}},i}}{tau _{{{s}},i}} + frac{{sqrt K }}{{{alpha _{{ m{BJ}}}}}}{n_j}left(dfrac{{partial {u_{{ m{f}},i}}}}{{partial {x_j}}} + dfrac{{partial {u_{{ m{f}},j}}}}{{partial {x_i}}} ight){tau _{s,i}} = 0,;;s = 1,2 $$

(8)

式中${n_i, n_j}$分别为沿界面指向自由流区域单位法向量的第i, j个分量, ${tau _{s,i}}$为沿界面的切平面一个向量正交系的第i个分量. 式(5)和式(6)分别表示界面上质量守恒和法向力的平衡. 式(7)即为Beavers-Joseph界面条件, 其中${alpha _{{
m{BJ}}}}$即所谓的Beavers-Joseph系数. 式(8)为Saffman修改的界面条件, 即文献中提到的Beavers-Joseph-Saffman条件. 两类条件都被用于接下来的计算. 无量纲数${alpha _{
m{BJ}}}$可用于表征自由流?多孔介质界面上速度滑移的程度, ${alpha _{
m{BJ}}}$越大, 两侧速度滑移则越小. ${alpha _{
m{BJ}}}$的值依赖于多孔介质界面附近的几何和结构特征. Beavers和Joseph使用泡沫金属、铝土制作了平均孔隙尺寸在0.033 cm ~ 0.116 cm之间的多孔介质材料, 并通过实验方法确定${alpha _{
m{BJ}}}$的范围为[0.1, 4], 一般的数值研究中采用的${alpha _{
m{BJ}}}$的值也在该范围之内.

考虑未受多孔介质圆球扰动的纯应变流场具有如下线性速度分布

$${u_{0,i}} = {e_{ij}}{x_j}$$

(9)

式中${e_{ij}}$为常对称张量. 根据流场的不可压缩条件, 对角元${e_{ii}}$应满足

$${e_{ii}} = 0$$

(10)

由于流场的对称性, 多孔介质小球将保持静止, 同时流场出现了一个扰动$delta {u_i}$, 这时速度场为

$${u_{{ m{f}},i}} = {u_{0,i}} + delta {u_i}$$

(11)

自由流区域的速度扰动有如下解^[40]

$$delta {u_i} = {e_{ij}}{x_j}f(r) + {e_{jk}}{x_j}{x_k}{x_i}g(r)$$

(12)

式中$r = sqrt {{x^2} + {y^2} + {{textit{z}}^2}}$, 函数$f(r)$和$g(r)$具有如下表达式

$$f(r) = frac{A}{{{r^5}}},;g(r) = frac{B}{{2{r^5}}} - frac{{5A}}{{2{r^7}}}$$

(13)

式中A和B为常数. 自由流区域的压力场的表达式为

$${p_{ m{f}}} = B{mu _{ m{f}}}frac{{{e_{ij}}{x_i}{x_j}}}{{{r^5}}}$$

(14)

圆球内多孔介质区域的速度场和压力场的解为

$${u_{{ m{pm}},i}} = C{e_{ij}}{x_j};;;;;;;;;;$$

(15)

$${p_{{ m{pm}}}} = - frac{C}{2}frac{{{mu _{ m{f}}}}}{K}{e_{ij}}{x_i}{x_j}$$

(16)

式中$C$为常数. 为了确定常数A, B和C的值, 将自由流区域和多孔介质区域速度和压力的解析表达式(11) ~式(16)代入界面条件式(5) ~ 式(8), 可得

$$1 + f(a) + {a^2}g(a) = Cqquad;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;$$

(17)

$$ 2 + 2f(a){ m{ + }}2af'(a) + {a^3}g'(a) + 6{a^2}g(a) - dfrac{B}{{{a^3}}} = dfrac{C}{2}frac{{{a^2}}}{K}$$

(18)

$$ 1 + frac{A}{{{a^5}}} - C - frac{{sqrt K }}{{{alpha _{{ m{BJ}}}}a}}left[2 + 2f(a) + af'(a) + 2g(a){a^2} ight] = 0 quad $$

(19)

或

$$ 1 + frac{A}{{{a^5}}} - frac{{sqrt K }}{{{alpha _{{ m{BJ}}}}a}}left[2 + 2f(a) + af'(a) + 2g(a){a^2} ight] = 0 $$

(20)

这里以推导式(19)或式(20)为例, 给出一些计算细节. 应变率张量的表达式为

$$begin{split}& frac{{partial {u_{{ m{f}},i}}}}{{partial {x_j}}} + frac{{partial {u_{{ m{f}},j}}}}{{partial {x_i}}} = 2{e_{ij}}[1 + f(r)] + &quad frac{{f'(r)}}{r}({e_{ik}}{x_k}{x_j} + {e_{jk}}{x_k}{x_i}) + &quad {e_{kl}}{x_k}{x_l}left[2g(r){delta _{ij}} + 2frac{{g'(r)}}{r}{x_i}{x_j} ight] + &quad g(r)({e_{ik}}{x_j}{x_l} + {e_{il}}{x_k}{x_j} + {e_{jk}}{x_i}{x_l} + {e_{jl}}{x_i}{x_k})end{split} $$

(21)

利用恒等式${n_k}{x_k} = r$和${tau _{s,k}}{x_k} = 0$, 则可得

$$begin{split}& {n_j}left(frac{{partial {u_{f,i}}}}{{partial {x_j}}} + frac{{partial {u_{f,j}}}}{{partial {x_i}}} ight){tau _{s,i}} = &quad {e_{ij}}{x_j}{tau _{s,i}}[2 + 2f(r) + rf'(r) + 2{r^2}g(r)] end{split} $$

(22)

同理可得

$$({u_{{ m{f}},i}} - {u_{{ m{pm}},i}}){tau _{s,i}} = {e_{ij}}{x_j}{tau _{s,i}}[1 + f(r) - C]$$

(23)

将$f(r)$和$g(r)$及其导数的表达式代入式(22)和式(23), 即可得到式(19)或式(20). 式(17) ~ 式(20)简化可得

$$1 - frac{{3A}}{{2{a^5}}} + frac{B}{{2{a^3}}} = Cqquadqquadqquad;;;;;;;;;;$$

(24)

$$2 - frac{{11A}}{{2{a^5}}} - frac{B}{{2{a^3}}} = frac{C}{2}frac{{{a^2}}}{K};;;;qquadqquad;;;;;;$$

(25)

$$1 + dfrac{A}{{{a^5}}} - C - frac{{sqrt K }}{{{alpha _{{ m{BJ}}}}a}}left( - dfrac{{8A}}{{{a^5}}} + dfrac{B}{{{a^3}}} + 2 ight) = 0$$

(26)

或

$$1 + dfrac{A}{{{a^5}}} - dfrac{{sqrt K }}{{{alpha _{{ m{BJ}}}}a}}left( - dfrac{{8A}}{{{a^5}}} + dfrac{B}{{{a^3}}} + 2 ight) = 0$$

(27)

上述三元一次方程组的解为

$$A = dfrac{{16Da + 12Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} - 1}}{{16Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}{a^5}$$

(28)

$$B = dfrac{{20Da - 10dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 20Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} - 5}}{{16Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}{a^3}$$

(29)

$$C = dfrac{{20Da + 30Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}}}}{{16Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}};;;;;;$$

(30)

或

$$A = dfrac{{ - { m{2}}Da + 12Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} - 1}}{{{ m{2}}Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}{a^5};;$$

(31)

$$B = dfrac{{30Da - 10dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 20Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} - 5}}{{2Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}{a^3}$$

(32)

$$C = dfrac{{20Da + 30Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}}}}{{2Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}};;;;;;;;$$

(33)

式中$Da = dfrac{K}{{{a^2}}}$为达西数. 这样便得到整个流场的解.

2.
多孔介质悬浮液等效黏性系数的计算

由上所述, 由于多孔介质球的存在, 流场在线性分布的基础上增加了一个扰动, 从而增加了所考虑的流场边界${A_1}$上的黏性耗散率. 另一方面, 从等效的观点看, 可以认为多孔介质球的存在使得流体的黏性由${mu _{
m{f}}}$等效变为${mu _{
m{s}}}$, 但流场仍保持原来的线性分布, 同时两种情形下边界${A_1}$上的黏性耗散率相等, 即有如下关系式

$$intlimits_{{A_1}} {{n_i}{sigma _{s,ij}}{u_{0,j}}{ m{d}}S} = intlimits_{{A_1}} {{n_i}{sigma _{ij}}{u_{{ m{f}},j}}{ m{d}}S}$$

(34)

式中应力张量${sigma _{s,ij}}$和${sigma _{ij}}$的表达式为

$${sigma _{s,ij}} = 2{mu _s}{e_{ij}}qquadqquadqquadqquad;;$$

(35)

$$begin{split}& {sigma _{ij}} = {sigma _{0,ij}} + delta {sigma _{ij}} = 2{mu _{ m{f}}}{e_{ij}} + delta {sigma _{ij}} =&quad 2{mu _{ m{f}}}{e_{ij}} - {p_{ m{f}}}{delta _{ij}} + 2{mu _{ m{f}}}left(frac{{delta {u_i}}}{{partial {x_j}}} + frac{{delta {u_j}}}{{partial {x_i}}} ight) end{split}$$

(36)

应用高斯散度定理, 流场边界${A_1}$上的积分可化为多孔介质球面${A_0}$上的积分. 根据Batchelor的推导^[40], 式(36)可化为

$$ 2({mu _s} - {mu _{ m{f}}}){e_{ij}}{e_{ij}} = dfrac{{{e_{ik}}}}{{{V_1}}}displaystyleintlimits_{{A_0}} {(delta {sigma _{ij}}{x_k}{n_j} - 2{mu _{ m{f}}}delta {u_i}{n_k}){{{ m{d}}S}}} $$

(37)

式中${V_1}$为整个流场区域的体积. 将流场扰动$delta {u_i}$的解析表达式代入式(39)右端的被积函数, 可得

$$begin{split}& delta {sigma _{ij}}{x_k}{n_j} - 2{mu _{ m{f}}}delta {u_i}{n_k} = {mu _{ m{f}}}{e_{ij}}{n_j}{n_k}left(frac{B}{r} - frac{{10A}}{{{r^3}}} ight) + &quad {mu _{ m{f}}}{e_{jl}}{n_j}{n_l}{n_i}{n_k}left( - frac{{5B}}{{{r^3}}} + frac{{25A}}{{{r^5}}} ight)end{split} $$

(38)

应用如下两个恒等式

$$intlimits_{{A_0}} {{n_j}{n_k}{ m{d}}S = frac{{16}}{3}{text{π}} {delta _{jk}}{a^2}};;qquadqquadqquadqquad$$

(39)

$$ intlimits_{{A_0}} {{n_j}{n_l}{n_i}{n_k}{ m{d}}S} = frac{{16}}{{15}}{text{π}} ({delta _{jl}}{delta _{ik}} + {delta _{ji}}{delta _{lk}} + {delta _{il}}{delta _{jk}}){a^2} $$

(40)

式(39)化为

$$2({mu _s} - {mu _{ m{f}}}) = - {mu _{ m{f}}}frac{{4{text{π}} B{a^3}}}{{3{V_1}}}$$

(41)

很显然$dfrac{{4{text{π}} {a^3}}}{{3{V_1}}}$为多孔介质球在整个流场区域的体积占比, 即体积分数, 记为$phi $. 由式(43)则可得到基于Darcy-Stokes耦合模型的低浓度多孔介质颗粒悬浮液的等效黏性系数${mu _s}$的公式

$${mu _s} = {mu _{ m{f}}}left(1 + {varLambda _D}phi ight)$$

(42)

其中特性黏度${varLambda _D}$为

$${varLambda _D} = dfrac{5}{2}dfrac{{ - 4Da + 2dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} - 4Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}{{16Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}$$

(43)

或

$${varLambda _D} = dfrac{5}{2}dfrac{{ - 6Da + 2dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} - 4Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}{{16Da + 5dfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 38Dadfrac{{sqrt {Da} }}{{{alpha _{ m{BJ}}}}} + 1}}$$

(44)

当$Da to 0$, 即多孔介质颗粒变为常规的实心颗粒, 流体无法穿透壁面, ${varLambda _D} to 2.5$成立, 式(44)退化为经典的Einstein黏度公式. 此外, 可以看到两类界面条件式(7)或式(8)给出的结果非常接近, 差别在$O(Da)$量级. 如无特殊说明, 接下来的结果部分仅采用式(45)进行讨论和分析.

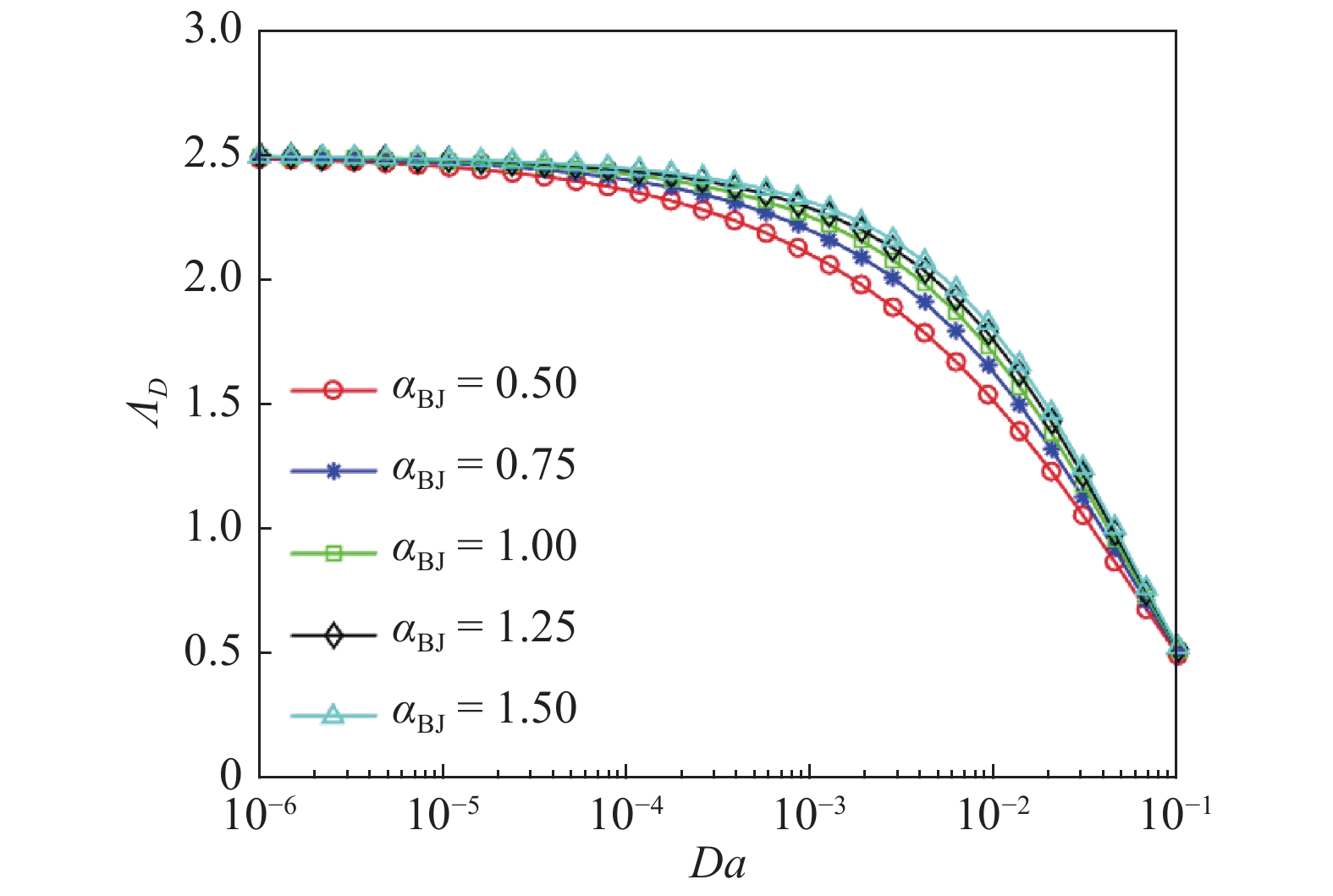
注意到等效黏性系数${mu _s}$和Beavers-Joseph系数${alpha _{
m{BJ}}}$相关, 图2给出了${alpha _{
m{BJ}}}$取不同的值时特性黏度${varLambda _D}$随达西数$Da$的变化. 可以看到${alpha _{
m{BJ}}}$增大时, 特性黏度${varLambda _D}$也随之增大. 此外, ${alpha _{
m{BJ}}}$越大, ${varLambda _D}$增加的幅度也越小, ${alpha _{
m{BJ}}} = 1.25$和${alpha _{
m{BJ}}} = 1.5$时的两条曲线非常接近. 如前所述, ${alpha _{
m{BJ}}}$越大表明自由流?多孔介质界面上速度滑移越小, 即自由流区域的速度有较大的扰动, 从而导致特性黏度${varLambda _D}$增加. 另一方面, $Da$和${varLambda _D}$之间呈现非线性变化. 当${10^{ - 6}} leqslant Da leqslant {10^{ - 4}}$时, 多孔介质颗粒的渗透率很小, 接近于固体实心颗粒, 因而特性黏度${varLambda _D}$接近于2.5. 当${10^{ - 4}} leqslant Da leqslant {10^{ - 1}}$时, 此时多孔介质球内部的流体阻碍明显减弱, 特性黏度${varLambda _D}$快速下降, 因而等效黏性系数更加接近于流体本身的黏性, 这与已有的理论和数值方法给出的结果是一致的.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-144-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
${alpha _{
m{BJ}}} = 0.5,0.75,1,1.25$和$1.5$时特性黏度${varLambda _D}$随达西数$Da$的变化



Figure
2.
Intrinsic viscosity ${varLambda _D}$ versus the Darcy number $Da$ when ${alpha _{
m{BJ}}} = 0.5,0.75,1,1.25$ and $1.5$



下载:
全尺寸图片
幻灯片

3.
与Darcy-Brinkman模型的结果的比较

如前所述, 除了Darcy模型, 一些****也采用Darcy-Brinkman模型对多孔介质悬浮液的等效黏性系数进行了计算. Darcy-Brinkman模型的控制方程为

$${mu _{{ m{eff}}}}frac{partial }{{partial {x_j}}}left(frac{{partial {u_{{ m{pm}},i}}}}{{partial {x_j}}} ight) - frac{{{mu _{ m{f}}}}}{K}{u_{{ m{pm}},i}} = frac{{partial {p_{{ m{pm}}}}}}{{partial {x_i}}}$$

(45)

式中${mu _{{
m{eff}}}}$为有效黏性系数. 自由流区域和多孔介质区域界面上采用如下剪切应力跳跃模型^[26]

$$frac{{partial {u_{{ m{pm}},i}}}}{{partial r}} - frac{{partial {u_{{ m{f}},i}}}}{{partial r}} = frac{zeta }{{sqrt K }}{u_{{ m{pm}},i}}$$

(46)

其中$zeta $为界面应力跳跃系数. 当 ${mu _{{
m{eff}}}} = {mu _{
m{f}}}$时, Prakash和Sekhar^[26]得出了参数$varLambda$如下形式的表达式

$${varLambda _{DB}} = frac{5}{2}frac{{{lambda ^2}left[ {3left( {lambda + 2zeta } ight)left( {sinh lambda - lambda cosh lambda } ight) + lambda left( {3zeta lambda + {lambda ^2} - zeta } ight)sinh lambda } ight]}}{{30left( {lambda + 2zeta } ight)left( {sinh lambda - lambda cosh lambda } ight) + {lambda ^3}left( {{lambda ^2} + 10} ight)left( {sinh lambda - zeta cosh lambda } ight) + 3zeta {lambda ^2}left( {{lambda ^2} + 10} ight)sinh lambda }}$$

(47)

其中无量纲参数$lambda = dfrac{1}{{sqrt {Da} }}$.

将式(43)和式(47)做展开, 即

$${varLambda _{DB}} = 2.5 + 7.5frac{{sqrt {Da} }}{{zeta - 1}} + O(Da)$$

(48)

$${varLambda _D} = 2.5 - 7.5frac{{sqrt {Da} }}{{{alpha _{BJ}}}} + O(Da)$$

(49)

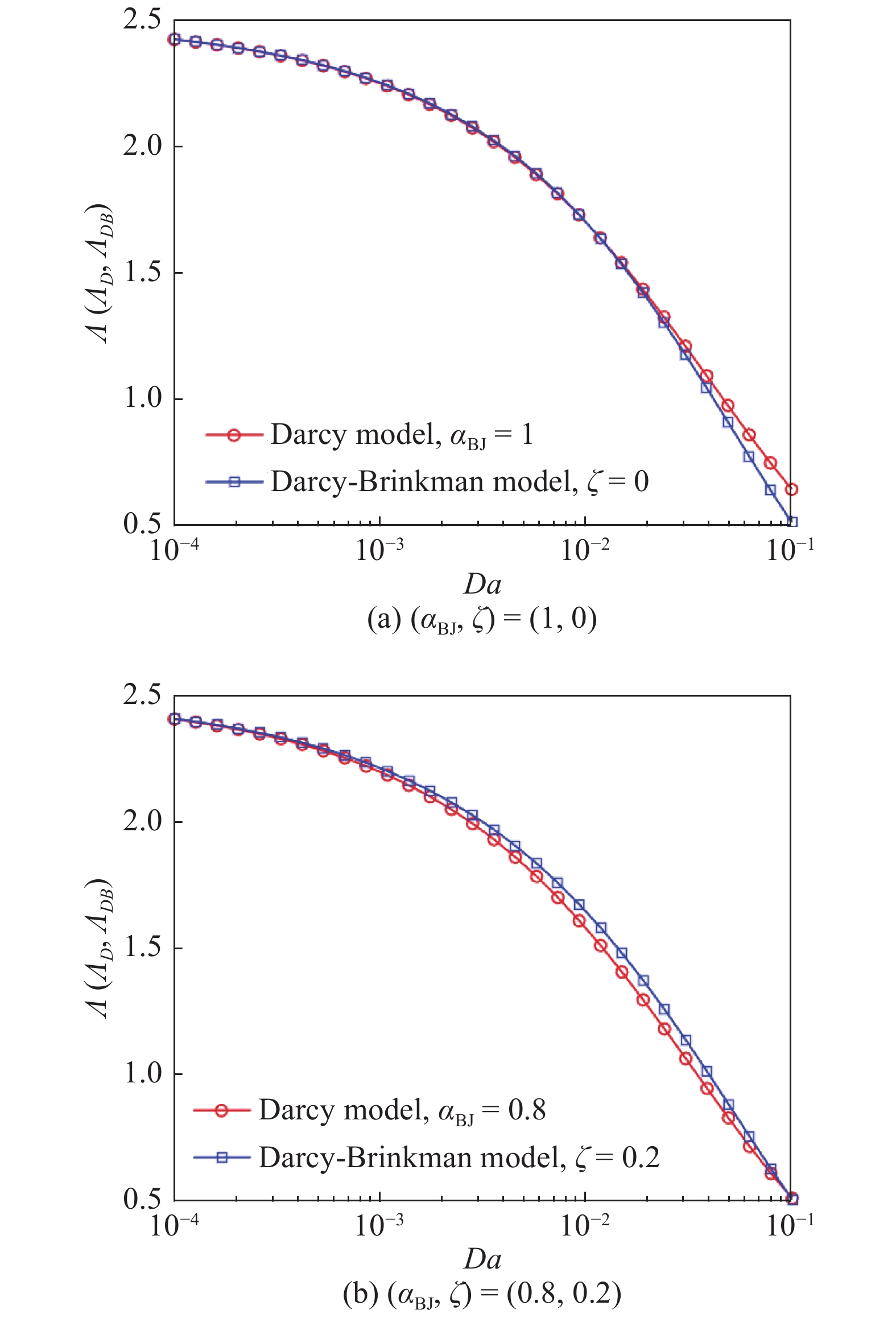
很显然, 如果Beavers-Joseph系数和界面应力跳跃系数满足条件${alpha _{
m{BJ}}} = 1 - zeta $, Darcy模型和Darcy-Brinkman模型在低达西数条件下将给出较为一致的结果. 图3给出了两类模型在${10^{ - 4}} leqslant Da leqslant {10^{ - 1}}$范围内特性黏度$varLambda $的变化,考虑的3组参数$({alpha _{
m{BJ}}},zeta )$如下: $(1,0)$,$(0.8,0.2)$和$(1.2, - 0.2)$. 可以看到达西数较小时, 两类模型的确给出了几乎相同的结果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-144-3-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3-1" />



3
两类模型在${10^{ - 4}} leqslant Da leqslant {10^{ - 1}}$范围内特性黏度$varLambda$的变化



3.
Relationship between the intrinsic viscosity $varLambda$ and the Darcy number based on the Darcy model and Darcy-Brinkman model.



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-144-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
两类模型在${10^{ - 4}} leqslant Da leqslant {10^{ - 1}}$范围内特性黏度$varLambda$的变化(续)



Figure
3.
Relationship between the intrinsic viscosity $varLambda$ and the Darcy number based on the Darcy model and Darcy-Brinkman model (continued)



下载:
全尺寸图片
幻灯片

4.
结论

本文首先研究了线性分布的流场中多孔介质球引起的扰动问题. 在低雷诺数条件下, 自由流区域满足Stokes方程, 而多孔介质球内部的流场采用Darcy模型描述. 多孔介质球表面满足质量守恒律、法向应力平衡条件以及描述速度滑移的Beavers-Joseph条件或Beavers-Joseph-Saffman条件. 通过求解上述Darcy-Stokes耦合模型, 获得了自由流/多孔介质区域速度场和压力场的解析表达式. 其后根据Batchelor提出的定义计算了低浓度多孔介质颗粒悬浮液的等效黏性系数, 得到了其与达西数、Beavers-Joseph系数和颗粒体积分数的定量关系. 分析结果表明等效黏性系数随着Beavers-Joseph系数增加而增加, 在低达西数条件下多孔介质悬浮液特性黏度有如下渐进公式${varLambda _D} = 1 - 3dfrac{{sqrt {Da} }}{{{alpha _{
m{BJ}}}}} + O(Da).$此外, 所得到的等效黏性计算公式与基于Darcy-Brinkman模型的结果进行了比较, 结果显示当Beavers-Joseph系数和界面应力跳跃系数之和为1时, 两类计算公式在低达西数条件下给出几乎一致的结果.