引言

分数阶微积分几乎和整数阶微积分同时存在, 它的导数和积分的阶数可以是任意数^[1]. 由于分数阶微分方程具有独特的能力来描述自然现象的共同特征?异常行为和记忆效应^[2], 因此分数阶微分方程能比整数阶微分方程更准确地描述许多实际问题. 分数阶微分方程理论是数学的一个重要分支, 包括连续分数阶微分方程和离散分数阶差分方程. 在过去的数十年里, 分数阶微分方程理论得到了广泛的普及和应用^[3-8], 但这些连续分数阶微分方程和离散分数阶差分方程是被分开研究的. 1988年Hilger^[9]发现了离散系统和连续系统之间有许多相似之处, 因此提出了一个关于微分方程和差分方程的统一理论?时间尺度. 随后, Bohner等^[10-12]意识到时间尺度微积分弥合了连续和离散系统之间的差距, 这个统一的方法意味着在复杂的新模型中可以考虑更多的变量. 不仅如此, 当时间尺度为${T} = {q^{{mathbb{N}_0}}}$(q>1, $mathbb{N}$为自然整数集)或$ {T} = {q^mathbb{Z}} cup left{ 0
ight} $时, 时间尺度上的微分方程可以表示成在量子理论中有着重要应用的$ q $差分方程^[11]. 因此, 利用不同的时间尺度$ {T} $, 分数阶时间尺度微积分可以同时处理连续、离散和量子分数阶微积分. 例如, 取$ {T} = mathbb{R} $($mathbb{R} $为实数集)时, 分数阶时间尺度微分方程则成为^[1]中经典的分数阶微分方程; 当$ {T} = mathbb{Z} $($ mathbb{Z} $为整数集)时, 其分数阶时间尺度微分方程与文献[6]中步长为1的离散分数阶差分方程是一致的; 若$ {T} = {q^{{mathbb{N}_0}}}left( {q > 1}
ight) $, 其微分方程则成为文献[7]中的离散分数阶$ q $差分方程. 近年来, 分数阶时间尺度微积分已被应用于动力学方程^[13]、最优控制^[14]等领域. 虽然力学系统的分数阶Noether定理和时间尺度Noether定理被广泛研究与应用, 但分数阶时间尺度Noether定理是一个新的研究课题^[15].

众所周知, Noether定理揭示了对称性和守恒量之间的内在关系^[16]. 在群的无限小变换下作用量的不变性(Noether对称性)意味着沿着系统的动力学真实运动轨道上存在一个守恒量(Noether守恒量). 相比牛顿力学和Lagrange力学, 运用Noether对称性可以找到除了能量守恒、动量守恒或动量矩守恒之外更多的且相互独立的守恒量^[17]. 因此, 近些年人们致力于研究力学系统的Noether定理^[18-25]. 而利用时间尺度理论得到的Noether定理, 通过选择不同的尺度可同时表示连续时间变量、离散时间变量甚至分段时间变量的Noether定理.

2004年Bohner^[26]研究了$ Delta $导数的时间尺度变分问题, 建立了时间尺度Lagrange方程. 此后, 有关时间尺度变分原理和时间尺度Lagrange方程的理论不断得到完善^[27-30], 为研究时间尺度Noether定理奠定了基础. 2008年Bartosiewicz和Torres^[31]分别在特殊无限小变换和一般无限小变换的情况下研究了时间尺度的Noether定理. 随后, Bartosiewicz等^[32]给出了$Delta$导数的时间尺度第二类Lagrange方程, 并利用该方程证明了文献[31]中的Noether定理. 之后, 各种力学系统的时间尺度Noether定理被建立, 如最优控制问题^[33]、非保守系统^[34-36]、非完整系统^[37-38]、Hamilton系统^[39-40]、Birkhoff系统^[40-42]、时滞系统^[43-44]等. 然而, 最近Anerot等^[45]指出文献[32]中所推导的时间尺度第二类Lagrange方程是错误的. 因此, 在上述列举的文章中, 利用该方程得到的力学系统的Noether定理其正确性有待商榷. Anerot等^[45]利用一种广义Jost方法来研究$ nabla $导数时间尺度迁移和非迁移系统的Noether定理, 并且用了一些算例来证明他们的结果. 同样, Cresson等^[46]将Jost方法推广到分数阶理论, 建立了分数阶Noether定理, 并给出了一些应用和仿真. 本工作利用分数阶时间尺度Hamilton原理, 推导了Caputo $ Delta $型分数阶时间尺度Lagrange方程, 在一般无限小变换下利用广义Jost方法建立了Caputo $ Delta $型的分数阶时间尺度Noether定理. 文末对分数阶时间尺度Kepler问题和线性振动系统进行模拟, 说明了定理的正确性.

1.
预备知识

设$ {T} $是一时间尺度, $ t in {T} $, 定义前跳算子$ sigma: $$ {T} to {T} $为 $ sigmaleft(t
ight) = infleft{{sin {T}:s>t}
ight} $, 后跳算子$
ho:{T} to {T} $为$
holeft(t
ight) = supleft{{sin{T}:s<t}
ight} $. 其中, 若 $ sup{T}in{T} $, 则$ sigmaleft({sup{T}}
ight) = sup{T} $; 若 $ inf{T}in{T} $, 则$
holeft({inf{T}}
ight) = inf{T} $. 步差函数$ mu:{T}tomathbb{R} $为$ muleft(t
ight) = sigmaleft(t
ight)-t $, $muleft(t
ight)geqslant 0$. 若 $ sup{T}<infty $, 定义$ {{T}^k} = {T}backslashleft({
holeft({sup{T}}
ight)}
ight.,left.{sup{T}}
ight] $; 若 $ {T} = infty $, 则定义$ {{T}^k} = {T} $. 对任意的 $ varepsilon>0 $, 存在 $ t $的一个小领域$U = left({t-delta,t+delta}
ight)cap{T}$, 当 $ sin U $, 都有 $left| {fleft( {sigma left( t
ight)}
ight) - fleft( s
ight) - }
ight.$$left. {{f^Delta }left( t
ight)left( {sigma left( t
ight) - s}
ight)}
ight|leqslant varepsilon left| {sigma left( t
ight) - s}
ight|$, 则称函数$ f $在点$ t $处是$ Delta $可微的, 并称${f^Delta}left(t
ight)$是函数$ f $在点$ t $处的$Delta $导数. 记${T} $上$Delta $可微且其$ Delta $导数右稠连续的函数集合为$C_{{
m{rd}}}^1$. 有关时间尺度的定义和性质可具体参考文献[10, 12, 47], 本节将重点回顾分数阶时间尺度积分和导数的定义.

定义1 设$ {T} $是一时间尺度且$ {{T}^kappa } = {T} $, 定义右连续函数$ {h_alpha}: {T}times {T} to mathbb{R} $, $alphageqslant 0$为^[48]

$$ {h_{alpha+1}}left( {t,s} ight) = int_s^t {{h_alpha}left( {tau ,s} ight)Delta tau }, {kern 4pt} {h_0}left( {t,s} ight) = 1,{kern 4pt} t,s in {T} $$

(1)

定义2 设$ {T} $是一时间尺度, 函数$ f:left[ {a,b}
ight] subset mathbb{R} $, 其中, $alpha geqslant 0$, $ a,b in mathbb{R} $, $ a < b $, 定义左Riemann-Liouville分数阶$ Delta $积分为^[47]

$$ left. begin{array}{l} {}_aI_{Delta ,t}^alpha fleft( t ight) = fleft( t ight),{kern 79pt} { m{if}}{kern 4pt} alpha = 0 {}_aI_{Delta ,t}^alpha fleft( t ight) = displaystyleint_a^t {{h_{alpha - 1}}left( {t,sigma left( tau ight)} ight)fleft( tau ight)Delta tau } ,{kern 4pt} t > a,{kern 8pt} { m{if}}{kern 4pt} alpha > 0 end{array} ight} $$

(2)

右Riemann-Liouville分数阶$ Delta $积分为

$$ left. begin{array}{l} {}_tI_{Delta ,b}^alpha fleft( t ight) = fleft( t ight),{kern 82pt} { m{if}}{kern 4pt} alpha = 0 _tI_{Delta ,b}^alpha fleft( t ight) = displaystyleint_t^b {{h_{alpha - 1}}left( {sigma left( tau ight),t} ight)fleft( tau ight)Delta tau } ,{kern 4pt} t < b,{kern 8pt} { m{if}}{kern 4pt} alpha > 0 end{array} ight} $$

(3)

注1:　若$ {T} = mathbb{R} $, 有${h_{alpha - 1}}left( {t,a}
ight) = dfrac{{{{left( {t - a}
ight)}^{alpha - 1}}}}{{varGamma left( alpha
ight)}}$, 则

$$ {}_aI_t^alpha fleft( t ight) =int_a^t {frac{{left( {t - tau } ight){}^{alpha - 1}}}{{varGamma left( alpha ight)}}fleft( tau ight){ m{d}}tau } ,{kern 4pt} t > a $$

(4)

并且有${h_{alpha - 1}}left( {b,t}
ight) = dfrac{{{{left( {b - t}
ight)}^{alpha - 1}}}}{{varGamma left( alpha
ight)}}$, 则

$$ {}_tI_b^alpha fleft( t ight) = int_t^b {frac{{left( {tau - t} ight){}^{alpha - 1}}}{{varGamma left( alpha ight)}}fleft( tau ight){ m{d}}tau } ,{kern 4pt} t < b $$

(5)

式(4)和式(5)是传统的左、右Riemann-Liouville分数阶积分^[1].

注2:　 若$ {T} = mathbb{Z} $, 可定义

$$ {t^{left( alpha ight)}} = frac{{varGamma left( {t + 1} ight)}}{{varGamma left( {t + 1 - alpha } ight)}},{kern 4pt} t in {T}, {kern 4pt} alpha in mathbb{R} $$

(6)

则有${h_{alpha - 1}}left( {t,s}
ight) = dfrac{{{{left( {t - s}
ight)}^{left( {alpha - 1}
ight)}}}}{{varGamma left( alpha
ight)}}$, $b-1 geqslant t geqslant s geqslant a + 1$, 此时有

$$ begin{split}{}_aI_{Delta ,t}^alpha fleft( t ight) =& int_a^t {{h_{alpha - 1}}left( {t,sigma left( s ight)} ight)fleft( s ight)Delta s} = &int_a^t {frac{{left( {t - sigma left( s ight)} ight){}^{left( {alpha - 1} ight)}}}{{varGamma left( alpha ight)}}fleft( s ight)Delta s} =& frac{1}{{varGamma left( alpha ight)}}sumlimits_{s = a}^{t - 1} {left( {t - s - 1} ight){}^{left( {alpha - 1} ight)}fleft( s ight)} ,{kern 4pt} t geqslant a + 1 end{split} $$

(7)

和

$$ begin{split} {}_tI_{Delta ,b}^alpha fleft( t ight) = & int_t^b {{h_{alpha - 1}}left( {sigma left( s ight),t} ight)fleft( s ight)Delta s} =& int_t^b {frac{{left( {sigma left( s ight) - t} ight){}^{left( {alpha - 1} ight)}}}{{varGamma left( alpha ight)}}fleft( s ight)Delta s} =& frac{1}{{varGamma left( alpha ight)}}sumlimits_{s = t}^{b-1} {left( {s + 1 - t} ight){}^{left( {alpha - 1} ight)}fleft( s ight)} ,{kern 4pt} t leqslant b-1 end{split} $$

(8)

式(7)和式(8)是离散的左、右Riemann-Liouville分数阶积分.

注3:　若$ {T} = {p^{{mathbb{N}_0}}} $, $ p>1 $, 令$ alpha in left[ {0,infty }
ight)backslash {mathbb{N}_0} $, $ a,t in {T} $, $t geqslant a$, $ p $分数阶函数可定义为

$$ left( {t - a} ight)_p^alpha = {t^alpha }mathop prod limits_{n = 0}^infty frac{{1 - dfrac{a}{t}{p^n}}}{{1 - dfrac{a}{t}{p^{alpha + n}}}} = {t^alpha }mathop prod limits_{n = 0}^infty frac{{t - a{p^n}}}{{t - a{p^{alpha + n}}}} $$

(9)

定义$ p $?$ varGamma $函数为 $ {varGamma _p}: mathbb{R}backslash mathbb{Z} to mathbb{R} $, 并且有 $ {varGamma _p}left( {dfrac{1}{2}}
ight) = 1 $, ${varGamma _p}left( alpha
ight)dfrac{{{p^alpha } !-! 1}}{{p!-! 1}} !=! {varGamma _p}left( {alpha !-! 1}
ight)$, $ alpha in mathbb{R} backslash mathbb{Z} $, 那么${h_alpha }left( {t,a}
ight) = {varGamma _p}left( alpha
ight) cdot $$ left( {t -a}
ight)_p^alpha$, 则有

$$ begin{split} {}_aI_{Delta ,t}^alpha fleft( t ight) = & int_a^t {{h_{alpha - 1}}left( {t,sigma left( s ight)} ight)fleft( s ight)Delta s} = & {varGamma _p}left( {alpha - 1} ight)int_a^t {left( {t - ps} ight)_p^{alpha - 1}fleft( s ight)Delta s}, & t,s in {T}, {kern 4pt} t geqslant s geqslant a end{split} $$

(10)

同样地, 有$ {h_alpha }left( {b,t}
ight) = {varGamma _p}left( alpha
ight)left( {b - t}
ight)_p^alpha $, 则有

$$ begin{split}{}_tI_{Delta ,b}^alpha fleft( t ight) = & int_t^b {{h_{alpha - 1}}left( {sigma left( s ight),t} ight)fleft( s ight)Delta s} = & {varGamma _p}left( {alpha - 1} ight)int_t^b {left( {ps - t} ight)_p^{alpha - 1}fleft( s ight)Delta s}& t,s in {T},{kern 4pt} t leqslant s leqslant b end{split} $$

(11)

式(10)和式(11)可分别称为$ p $离散的左、右Riemann-Liouville分数阶积分.

定义3 设$ {T} $是一时间尺度, 函数$ f: {T}to mathbb{R} $, 定义$ {f^{{Delta ^n}}} = D_Delta ^nf $, $ n in {mathbb{N}_0} $, 定义左Riemann-Liouville分数阶$ Delta $导数为^[47]

$$ begin{split} _aD_{Delta ,t}^alpha fleft( t ight) = &D_Delta ^mleft( {{}_aI_{Delta ,t}^{m - alpha }fleft( t ight)} ight) = &D_Delta ^mleft[ {int_a^t {{h_{m - alpha - 1}}left( {t,sigma left( tau ight)} ight)fleft( tau ight)Delta tau } } ight], &t in {T},{kern 4pt} t > a end{split} $$

(12)

右Riemann-Liouville分数阶$ Delta $导数为

$$ begin{split} {}_tD_{Delta ,b}^alpha fleft( t ight) = &- D_Delta ^mleft( {{}_tI_{Delta ,b}^{m - alpha }fleft( t ight)} ight) = & - D_Delta ^mleft[ {int_t^b {{h_{m - alpha - 1}}left( {sigma left( tau ight),t} ight)fleft( tau ight)Delta tau } } ight], & t in {T},{kern 4pt} t <b end{split} $$

(13)

式中$alpha geqslant 0$, $ m = overline {left[ alpha
ight]} + 1 $, $ a,b in {{T}^{{kappa ^m}}} $, $ a<b $.

注4:　若$ alpha < 0 $, 可定义

$$ _aD_{Delta ,t}^alpha fleft( t ight){ = _a}I_{Delta ,t}^{ - alpha }fleft( t ight),{kern 4pt} a,t in {T},{kern 4pt} t > a qquadqquadqquad $$

(14)

$$ _aI_{Delta ,t}^alpha fleft( t ight){ = _a}D_{Delta ,t}^{ - alpha }fleft( t ight),{kern 4pt} a,t in {{T}^{{kappa ^r}}},{kern 4pt} t > a,{kern 4pt} r = overline {left[ { - alpha } ight]} + 1 $$

(15)

注5:　假设$alpha geqslant 0$, $ m = overline {left[ alpha
ight]} + 1 $. 若$ m = 0 $, 则有

$$ _aD_{Delta ,t}^alpha fleft( t ight) = int_a^t {{h_{ - alpha - 1}}left( {t,sigma left( tau ight)} ight)fleft( tau ight)Delta tau },{kern 4pt} t in {T},{kern 4pt} t > a $$

(16)

若$ m = 1 $, 则有

$$ begin{split} {}_aD_{Delta ,t}^alpha fleft( t ight) =& {D_Delta }left[ {int_a^t {{h_{ - alpha }}left( {t,sigma left( tau ight)} ight)fleft( tau ight)Delta tau } } ight] = & int_a^t {h_{ - alpha }^{{Delta _t}}left( {t,sigma left( tau ight)} ight)fleft( tau ight)Delta tau } + {h_{ - alpha }}left( {sigma left( t ight),sigma left( t ight)} ight)fleft( t ight) = & int_a^t {{h_{ - alpha - 1}}left( {t,sigma left( tau ight)} ight)fleft( tau ight)Delta tau } + {h_{ - alpha }}left( {sigma left( t ight),sigma left( t ight)} ight)fleft( t ight) &t in {T},{kern 4pt} t > a [-12pt]end{split} $$

(17)

定义4 设$ {T} $是一时间尺度, $ tin{T} $, $ alphageqslant 0 $, 定义左Caputo分数阶$ Delta $导数为^[47]

$$ begin{split} {}_a^CD_{Delta ,t}^alpha fleft( t ight) = & {}_aI_{Delta ,t}^{1 - alpha }{f^Delta }left( t ight) = int_a^t {{h_{ - alpha }}left( {t,sigma left( tau ight)} ight){f^Delta }left( tau ight)Delta tau } =& { _a}D_{Delta ,t}^alpha left( {fleft( t ight) - sumlimits_{k = 0}^{m - 1} {{h_k}left( {t,a} ight){f^{{Delta ^k}}}left( a ight)} } ight)[-12pt] end{split} $$

(18)

右Caputo分数阶$ Delta $导数为

$$ begin{split} {}_t^CD_{Delta ,b}^alpha fleft( t ight) = & - {}_tI_{Delta ,b}^{1 - alpha }{f^Delta }left( t ight) = - int_t^b {{h_{ - alpha }}left( {sigma left( tau ight),t} ight){f^Delta }left( tau ight)Delta tau } = & { _t}D_{Delta ,b}^alpha left( {fleft( t ight) - sumlimits_{k = 0}^{m - 1} {{h_k}left( {b,t} ight){f^{{Delta ^k}}}left( b ight)} } ight)[-12pt] end{split} $$

(19)

式中若$ alpha notin mathbb{N} $, 则$ m = overline {left[ alpha
ight]} + 1 $; 若$ alpha in mathbb{N} $, 则$ m = overline {left[ alpha
ight]} $.

注6:　若$ alpha in left( {0,1}
ight) $, 即$ m = 1 $, 则有

$$ begin{split} {}_a^CD_{Delta ,t}^alpha fleft( t ight) =& { _a}D_{Delta ,t}^alpha left( {fleft( t ight) - sumlimits_{k = 0}^0 {{h_k}left( {t,a} ight){f^{{Delta ^k}}}left( a ight)} } ight)= & {_a}D_{Delta ,t}^alpha left( {fleft( t ight) - {h_0}left( {t,a} ight)fleft( a ight)} ight) =& {_a}D_{Delta ,t}^alpha left( {fleft( t ight) - fleft( a ight)} ight) end{split} $$

(20)

$$ {}_t^CD_{Delta ,b}^alpha fleft( t ight){ = _t}D_{Delta ,b}^alpha left( {fleft( b ight) - fleft( t ight)} ight)qquadqquadqquad $$

(21)

当$ fleft( a
ight) = 0 $时, 左Caputo分数阶$Delta$导数与左Riemann-Liouville分数阶$ Delta $导数一致; 当$ fleft( b
ight) = 0 $时, 右Caputo分数阶$ Delta $导数就与右Riemann-Liouville分数阶$Delta$导数一致.

同样地, 当$ {T} = mathbb{R} $, 式(18)和式(19)则成为传统的左、右Caputo分数阶导数; 当$ {T} = mathbb{Z} $, 式(18)和式(19)成为离散的左、右Caputo分数阶导数; 当$ {T} = {p^{{mathbb{N}_0}}} $, $ p>1 $, 式(18)和式(19)则成为$ p $离散的左、右Caputo分数阶导数.

引理1 设函数$ f,g:{T} to mathbb{R} $在点$ t in {{T}^k} $是$Delta$可微的, $ a,b in {T} $, 则有^[10]

$$ {left( {fg} ight)^Delta }left( t ight) = {f^Delta }left( t ight)gleft( t ight) + {f^sigma }left( t ight){g^Delta }left( t ight) = fleft( t ight){g^Delta }left( t ight) + {f^Delta }left( t ight){g^sigma }left( t ight) $$

(22)

引理2 令函数$f in {C_{{
m{rd}}}}$, $ f:left[ {a,b}
ight] to {mathbb{R}^n} $, 若对所有的$g in C_{{
m{rd}}}^1$且$ g left( a
ight) = g left( b
ight) = 0 $, 都有 $displaystyleint_a^b {{f^{
m{T}}}} left( t
ight){g^Delta }left( t
ight)Delta t = 0$成立, 那么有$ fleft( t
ight) = c $, 其中$ c in {mathbb{R}^n} $^[26].

引理3 令$ nu : {T}tomathbb{R} $是一个严格递增函数, 则$ bar{{T}} = nu left( {T}
ight) $是一个新的时间尺度. 定义$ bar{{T}} $上的前跳函数为$ bar sigma $, $ bar{{T}} $上的导数为$ barDelta $, 则有$ nu circ sigma = bar sigma circ nu $. 令$ omega :bar{{T}} tomathbb{R} $, 对$ t in {{T} ^k }$, 若$ {nu ^Delta }left( t
ight) $和$ {omega ^{bar Delta }}left( {nu left( t
ight)}
ight) $存在, 则有^[10]

$$ {left( {omega circ nu } ight)^Delta } = left( {{omega ^{bar Delta }} circ nu } ight){nu ^Delta } $$

(23)

若$ omega = {nu ^{ - 1}}:bar {{T}} to {T} $, 则有

$$ frac{1}{{{nu ^Delta }}} = {left( {{nu ^{ - 1}}} ight)^{bar Delta }} circ nu $$

(24)

其中$ {nu ^Delta }neq 0 $. 若$ f: {T}to mathbb{R} $是右连续的, 并且$ nu $的右连续导数可微, 则有

$$ int_a^b {fleft( t ight){nu ^Delta }left( t ight)Delta t} = int_{nu left( a ight)}^{nu left( b ight)} {left( {f circ {nu ^{ - 1}}} ight)left( s ight)bar Delta s} $$

(25)

其中$ a,b in {T} $.

引理4 假设函数$ f,g: {T}to mathbb{R} $, $ a,b in {T} $, 分数阶时间尺度分部积分公式如下^[49]

$$ begin{split}& int_a^b {gleft( t ight)} {{}_a^CD_{Delta ,t}^alpha fleft( t ight)} Delta t = &qquadint_a^b {{f^sigma }left( t ight)}{{}_tD_{Delta ,b}^alpha gleft( t ight)} Delta t + left. {left( {fleft( t ight) {{}_tI_{Delta ,b}^{1 - alpha }gleft( t ight)} } ight)} ight|_a^b end{split} $$

(26)

$$ begin{split} &int_a^b {gleft( t ight)} {{}_t^CD_{Delta ,b}^alpha fleft( t ight)} Delta t =&qquadint_a^b {{f^sigma }left( t ight)} {{}_aD_{Delta ,t}^alpha gleft( t ight)} Delta t - left. {left( {fleft( t ight){{}_aI_{Delta ,t}^{1 - alpha }gleft( t ight)}} ight)} ight|_a^b end{split} $$

(27)

2.
Caputo $ {boldsymbol{Delta}} $型分数阶时间尺度Lagrange方程

假设力学系统的位形是由$ n $个广义坐标$ {q_k}left( {k = 1,2, cdots ,n}
ight) $确定的. 设分数阶时间尺度系统的作用量为

$$ Sleft[ {qleft( cdot ight)} ight] = int_a^b {Lleft( {t,q_k^sigma left( t ight),{}_a^CD_{Delta ,t}^alpha {q_k}left( t ight)} ight)Delta t} $$

(28)

其中$ left[ {a,b}
ight] subsetmathbb{R} $, $ a<b $, $ alpha in (0, 1] $, $ q_k^sigma left( t
ight) = {q_k}left( {sigma left( t
ight)}
ight) $, $ L: $$ left[ {a,b}
ight] times {{mathbb{R}}^n} times {{mathbb{R}}^n} tomathbb{R} $. 可称函数$ Lleft( {t,q_k^sigma left( t
ight),{}_a^CD_{Delta ,t}^alpha {q_k}left( t
ight)}
ight) $为分数阶时间尺度Lagrange函数. 当$ {T} = mathbb{R} $ 且$ alpha = 1 $时, $ L = Lleft( {t,{q_k}left( t
ight),{{dot q}_k}left( t
ight)}
ight) $则为经典Lagrange函数.

Caputo $ Delta $型分数阶时间尺度Hamilton原理为

$$ delta S = 0 $$

(29)

其满足交换关系

$$ delta {}_a^CD_{Delta ,t}^alpha {q_k} = {}_a^CD_{Delta ,t}^alpha delta {q_k}, {kern 4pt} {left( {delta {q_k}} ight)^sigma } = delta q_k^sigma $$

(30)

和边界条件

$$ {left. {delta {q_k}left( t ight)} ight|_{t = a}} = 0, {kern 4pt} delta {left. {{q_k}left( t ight)} ight|_{t = b}} = 0 $$

(31)

对式(28)进行变分运算, 得

$$ delta S = displaystyleint_a^b {left( {frac{{partial L}}{{partial q_k^sigma }}delta q_k^sigma + frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}delta {}_a^CD_{Delta ,t}^alpha {q_k}} ight)Delta t} $$

(32)

根据分数阶时间尺度分部积分公式(26), 再由式(30)和式(32), 可得

$$ begin{split}&displaystyleint_a^b {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}delta {}_a^CD_{Delta ,t}^alpha {q_k}Delta t} = & qquad displaystyleint_a^b {delta q_k^sigma left[ {{}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight)} ight]Delta t} +& qquad left. {left{delta {q_k}left[ {{}_tI_{Delta ,b}^{1 - alpha }left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight)} ight] ight}} ight|_a^b = & qquad displaystyleint_a^b {delta q_k^sigma left[ {{}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight)} ight]Delta t} end{split} $$

(33)

将式(33)代入式(32), 则有

$$ displaystyleint_a^b {left[ {frac{{partial L}}{{partial q_k^sigma }} + {}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight)} ight]delta q_k^sigma Delta t} = 0 $$

(34)

由式(22)和式(31), 方程(34)可写为

$$ begin{split} &displaystyleint_a^b {left[ {frac{{partial L}}{{partial q_k^sigma }} + {}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight)} ight]delta q_k^sigma Delta t} = &qquad displaystyleint_a^b {{{left{ {left{ {left{ {displaystyleint_a^t {left[ {frac{{partial L}}{{partial q_k^sigma }} + {}_theta D_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,theta}^alpha {q_k}}}} ight)} ight]Delta theta } } ight}delta {q_k}} ight}} ight.}^Delta }} - &qquad left. {left{ {displaystyleint_a^t {left[ {frac{{partial L}}{{partial q_k^sigma }} + {}_theta D_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,theta}^alpha {q_k}}}} ight)} ight]Delta theta } } ight}{{left( {delta {q_k}} ight)}^Delta }} ight}Delta t = &qquadleft. {left{ {left{ {displaystyleint_a^t {left[ {frac{{partial L}}{{partial q_k^sigma }} + {}_theta D_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,theta}^alpha {q_k}}}} ight)} ight]Delta theta } } ight}delta {q_k}} ight}} ight|_a^b -&qquad displaystyleint_a^b {left{ {displaystyleint_a^t {left[ {frac{{partial L}}{{partial q_k^sigma }} + {}_theta D_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,theta}^alpha {q_k}}}} ight)} ight]Delta theta} } ight}{{left( {delta {q_k}} ight)}^Delta }Delta t} = &qquad -!displaystyleint_a^b {left{ {displaystyleint_a^t {left[ {frac{{partial L}}{{partial q_k^sigma }} !+! {}_theta D_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,theta}^alpha {q_k}}}} ight)} ight]Delta theta } } ight}{{left( {delta {q_k}} ight)}^Delta }Delta t} !!=!!0 end{split} $$

(35)

根据引理2, 可得

$$ int_a^t {left[ {frac{{partial L}}{{partial q_k^sigma }} + {}_theta D_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,theta}^alpha {q_k}}}} ight)} ight]Delta theta} = { m{const}} . $$

(36)

在式(36)两边对$ t $求$ Delta $导数, 有

$$ frac{{partial L}}{{partial q_k^sigma }} + {}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight) = 0 $$

(37)

方程(37)则是Caputo $ Delta $型分数阶时间尺度运动微分方程, 将它称为分数阶时间尺度Lagrange方程.

注7:　若$ alpha = 1 $, 方程(37)则成为时间尺度Lagrange方程^[31]

$$ frac{{partial L}}{{partial q_k^sigma }} - frac{Delta }{{Delta t}}left( {frac{{partial L}}{{partial q_k^Delta }}} ight) = 0 $$

(38)

注8:　若$ {T} = mathbb{R} $, 方程(37)则成为Caputo型分数阶Lagrange方程

$$ frac{{partial L}}{{partial {q_k}}} + {}_tD_b^alpha left( {frac{{partial L}}{{partial {}_a^CD_t^alpha {q_k}}}} ight) = 0 $$

(39)

注9:　若$ alpha = 1 $, $ {T} = mathbb{R} $, 方程(37)则成为经典的Lagrange方程

$$ frac{{partial L}}{{partial {q_k}}} - frac{{ m{d}} }{{{ m{d}} t}}left( {frac{{partial L}}{{partial {dot{q}_k}}}} ight) = 0 $$

(40)

3.
特殊无限小变换下的分数阶时间尺度Noether定理

引进单参数群的特殊无限小变换

$$ {bar q_k}left( t ight) = {q_k}left( t ight) + varepsilon {xi _k}left( {t,{q_j}} ight) + oleft( varepsilon ight),{kern 4pt} k = 1,2,cdots,n $$

(41)

式中$ {xi_k}left(k = 1,2,cdots,n
ight) $是无限小生成元, $ varepsilon $是无限小参数.

定义5 对任意的$ left[ {{t_a},{t_b}}
ight] subseteq left[ {a,b}
ight] $, $ {t_a},{t_b} in {T} $, 若有

$$ begin{split}&int_{{t_a}}^{{t_b}} {Lleft( {t,q_k^sigma left( t ight),{}_a^CD_{Delta ,t}^alpha {q_k}left( t ight)} ight)Delta t} =&qquadint_{{t_a}}^{{t_b}} {Lleft( {t,bar q_k^sigma left( t ight),{}_a^CD_{Delta ,t}^alpha {{bar q}_k}left( t ight)} ight)Delta t} end{split} $$

(42)

则称Hamilton作用量式(28)在特殊无限小变换式(41)下是不变的.

判据1 若Hamilton作用量式(28)在特殊无限小变换式(41)下是不变的, 则有

$$ xi _k^sigma frac{{partial L}}{{partial q_k^sigma }} + frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}{}_a^CD_{Delta ,t}^alpha {xi _k} = 0 $$

(43)

证明: 由定义5可知, 对任意的子空间$ left[ {{t_a},{t_b}}
ight] subseteq left[ {a,b}
ight] $, 条件式(42)都成立, 所以有

$$ Lleft( {t,q_k^sigma ,{}_a^CD_{Delta ,t}^alpha {q_k}} ight) = Lleft( {t,q_k^sigma + varepsilon xi _k^sigma ,{}_a^CD_{Delta ,t}^alpha left( {{q_k} + varepsilon {xi _k}} ight)} ight) $$

(44)

在式(44)中对$ varepsilon $求导, 再令$ varepsilon = 0 $, 利用分数阶时间尺度Caputo导数的定义和性质, 可得

$$ begin{split} 0 = & xi _k^sigma frac{{partial L}}{{partial q_k^sigma }} + {left. {left{ {frac{Delta }{{Delta varepsilon }}left[ {int_a^t {{h_{ - alpha }}left( {t,sigma left( tau ight)} ight)bar q_k^Delta left( tau ight)Delta tau } } ight]} ight}} ight|_{varepsilon = 0}}cdot& frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}} = xi _k^sigma frac{{partial L}}{{partial q_k^sigma }} + frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}{}_a^CD_{Delta ,t}^alpha {xi _k} end{split} $$

(45)

记符号$ {cal{D}}_Delta ^alpha $表示为

$$ {cal{D}}_Delta ^alpha left[ {f,g} ight] = g cdot {}_a^CD_{Delta ,t}^alpha f - {f^sigma } cdot {}_tD_{Delta ,b}^alpha g $$

(46)

则记

$$ begin{split}&{cal{D}}_Delta ^alpha left[ {{xi _k},frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight] = &qquadfrac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}{}_a^CD_{Delta ,t}^alpha {xi _k}- xi _k^sigma cdot {}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight) end{split} $$

(47)

定理1 若Hamilton作用量(28)在定义5的意义上是不变的, 则存在守恒量

$$ I = int_a^t {{{cal{D}}}_Delta ^alpha left[ {{xi _k},frac{{partial L}}{{partial _a^CD_{Delta ,t}^alpha {q_k}}}} ight]} Delta t = { m{const}}. $$

(48)

证明: 对式(48)中的$ I $求$ Delta $导数, 则有

$$ I^{Delta} = frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}{}_a^CD_{Delta ,t}^alpha {xi _k}- xi _k^sigma cdot {}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight) $$

(49)

由分数阶时间尺度Lagrange方程(37)可知

$$ frac{{partial L}}{{partial q_k^sigma }} = - {}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight) $$

(50)

将式(50)代入式(43), 可得

$$ - xi _k^sigma cdot {}_tD_{Delta ,b}^alpha left( {frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}} ight) + frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}{}_a^CD_{Delta ,t}^alpha {xi _k} = 0 $$

(51)

即$ I^{Delta } = 0 $, 因此可证明式(48)是特殊无限小变换下的Noether守恒量.

注10:　若$ alpha = 1 $, 定理1成为特殊无限小变换下的时间尺度Noether定理^[31]

$$ I = xi_kcdotfrac{{partial L}}{{partial {q_k^Delta }}} = { m{const}} . $$

(52)

4.
一般无限小变换下的分数阶时间尺度Noether定理

本节研究一般无限小变换下的分数阶时间尺度Noether定理. 首先, 引进单参数$ left(Delta , {T}
ight) $可容许投射群^[45]的一般无限小变换

$$ left. begin{array}{l} begin{array}{l} bar t = {T_varepsilon }left( t ight) = t + varepsilon zeta left( {t,{q_j}} ight) + oleft( varepsilon ight) {bar q_k}left( {bar t} ight) = Q_varepsilon ^kleft( {t,{q_j}} ight) = {q_k} left( t ight)+ varepsilon {xi _k}left( {t,{q_j}} ight) + oleft( varepsilon ight) end{array} end{array} ight} $$

(53)

式中$ zeta $, $ {xi_k}left(k = 1,2,cdots,n
ight) $是无限小生成元, $ varepsilon $是无限小参数.

定义6 对任意的$ left[ {{t_a},{t_b}}
ight] subseteq left[ {a,b}
ight] $, $ {t_a},{t_b} in {T} $, 若有

$$ begin{split} &int_{{t_a}}^{{t_b}} {Lleft( {t,q_k^sigma left( t ight),{}_a^CD_{Delta ,t}^alpha {q_k}left( t ight)} ight)Delta t} = &qquadint_{nu left( {{t_a}} ight)}^{nu left( {{t_b}} ight)} {Lleft( {bar t,bar q_k^{bar sigma }left( {bar t} ight),left( {{}_{nu left(a ight)}^CD_{bar Delta ,bar t}^alpha {{bar q}_k}} ight)left( {bar t} ight)} ight)bar Delta bar t} end{split} $$

(54)

则称Hamilton作用量式(28)在一般无限小变换式(53)下是不变的.

判据2 若Hamilton作用量式(28)在一般无限小变换式(53)下是不变的, 则有

$$ begin{split}&frac{{partial L}}{{partial t}}{zeta} + frac{{partial L}}{{partial q_k^sigma }}xi _k^sigma + frac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}left( {{}_a^CD_{Delta ,t}^alpha {xi _k} -alpha cdot{zeta ^Delta } cdot {}_a^CD_{Delta ,t}^alpha {q_k}} ight)+&qquad Lzeta^Delta = 0 [-12pt]end{split} $$

(55)

证明: 由定义4和引理3, 可得

$$ begin{split}&left( {{}_{nu left( a ight)}^CD_{bar Delta ,bar t}^alpha {{bar q}_k}} ight)left( {bar t} ight) = &qquad int_{nu left( a ight)}^{nu left( t ight)} {{h_{ - alpha }}left( {bar t,bar sigma left( {bar theta } ight)} ight)} bar q_k^{bar Delta }left( {bar theta } ight)bar Delta {bar theta } = &qquad int_a^t {{h_{ - alpha }}left( {nu left( t ight),left( {bar sigma circ nu } ight)left( theta ight)} ight) cdot bar q_k^{bar Delta }left( {nu left( theta ight)} ight) cdot {nu ^Delta }left( theta ight)Delta theta } =&qquad int_a^t {{h_{ - alpha }}left( {nu left( t ight),left( {bar sigma circ nu } ight)left( theta ight)} ight) cdot {{left( {{{bar q}_k} circ nu left( theta ight)} ight)}^Delta }Delta theta } =&qquad frac{{{}_a^CD_{Delta ,t}^alpha left( {{{bar q}_k} circ nu } ight)left( t ight)}}{{left( {{nu ^Delta }left( t ight)} ight)}^alpha} end{split} $$

(56)

由定义6可知

$$ begin{split} & displaystyleint_{{t_a}}^{{t_b}} {Lleft( {t,q_k^sigma left( t ight),{}_a^CD_{Delta ,t}^alpha {q_k}left( t ight)} ight)Delta t} = & qquad displaystyleint_{nu left( {{t_a}} ight)}^{nu left( {{t_b}} ight)} {Lleft( {bar t,bar q_k^{bar sigma }left( {bar t} ight),left( {{}_a^CD_{bar Delta ,bar t}^alpha {{bar q}_k}} ight)left( {bar t} ight)} ight)bar Delta bar t} = & qquad displaystyleint_{{t_a}}^{{t_b}} {Lleft( {nu left( t ight),left( {{{bar q}_k} circ bar sigma circ nu } ight)left( t ight),frac{{{}_a^CD_{Delta ,t}^alpha left( {{{bar q}_k} circ nu } ight)left( t ight)}}{{left( {{nu ^Delta }left( t ight)} ight)^alpha}}} ight)cdot {nu ^Delta }left( t ight)Delta t} !!= & qquaddisplaystyleint_{{t_a}}^{{t_b}} {Lleft( {{T_varepsilon },{{left( {Q_varepsilon ^k} ight)}^sigma },frac{{{}_a^CD_{Delta ,t}^alpha Q_varepsilon ^k}}{{left( {T_varepsilon ^Delta } ight)^alpha}}} ight)cdot T_varepsilon ^Delta Delta t}[-12pt] end{split} $$

(57)

由于$ left[ {{t_a},{t_b}}
ight] $是 $ left[ a,b
ight] $的任意子空间, 则方程(57)等价于

$$ Lleft( {t,q_k^sigma left( t ight),{}_a^CD_{Delta ,t}^alpha {q_k}left( t ight)} ight) = Lleft( {{T_varepsilon },{{left( {Q_varepsilon ^k} ight)}^sigma },frac{{{}_a^CD_{Delta ,t}^alpha Q_varepsilon ^k}}{{left( {T_varepsilon ^Delta } ight)^alpha}}} ight)cdot T_varepsilon ^Delta $$

(58)

在式(58)中对$ varepsilon $求导, 再令$ varepsilon = 0 $, 得

$$ begin{split}&0 = frac{{partial L}}{{partial t}}{zeta} + frac{{partial L}}{{partial q_k^sigma }}xi _k^sigma + left( {{}_a^CD_{Delta ,t}^alpha {xi _k} -alpha cdot{zeta ^Delta } cdot {}_a^CD_{Delta ,t}^alpha {q_k}} ight)cdot &qquadfrac{{partial L}}{{partial {}_a^CD_{Delta ,t}^alpha {q_k}}}+ Lzeta^Delta end{split} $$

(59)

注11: 　考虑到

$$ {T_varepsilon } = T_varepsilon ^sigma - mu left( t ight)T_varepsilon ^Delta $$

(60)

不变性的条件(57)可写为

$$ begin{split} & displaystyleint_{{t_a}}^{{t_b}} {Lleft( {t,q_k^sigma left( t ight),{}_a^CD_{Delta ,t}^alpha {q_k}left( t ight)} ight)Delta t} = & qquad displaystyleint_{{t_a}}^{{t_b}} {Lleft( {T_varepsilon ^sigma - mu left( t ight)T_varepsilon ^Delta ,{{left( {Q_varepsilon ^k} ight)}^sigma },frac{{{}_a^CD_{Delta ,t}^alpha Q_varepsilon ^k}}{{left( {T_varepsilon ^Delta } ight)^alpha}}} ight) cdot T_varepsilon ^Delta Delta t} end{split} $$

(61)

接下来, 引进扩展Lagrange函数$boldsymbol{L}: mathbb{R}times left[ {a,b}
ight] times {mathbb{R}^n} times $$ {mathbb{R}^*} times {mathbb{R}^n} tomathbb{R}$被定义为

$$ {boldsymbol{L}}left( {tau ;t,q,w,v} ight) = Lleft( {t - mu left( tau ight)w,q,frac{v}{w^alpha}} ight)w $$

(62)

其作用量用$ {S_{{boldsymbol{L} }}} $表示, 被定义为

$$ begin{split}&{S_{{boldsymbol{L}}}}left( {t,q_k} ight) = &qquad int_{{t_a}}^{{t_b}} {boldsymbol{L}left( {tau ;{t^sigma }left( tau ight),left( {q_k^sigma circ t} ight)left( tau ight),{t^Delta }left( tau ight),{}_{a}^CD_{Delta ,tleft(tau ight)}^alpha {q_k}left( tau ight)} ight)} Delta tau end{split} $$

(63)

设时间尺度束类路径^[45]被定义为

$$ begin{split}{cal{F}} = & left{ {left( {t,q} ight) in C_{{ m{rd}}}^{1,Delta }left( {T} ight) times C_{{ m{rd}}}^{1,Delta }left( {T} ight);} ight. & {tau mapsto left( {tleft( tau ight),left( {q circ t} ight)left( t ight)} ight) = left( {tau ,qleft( tau ight)} ight)} Big} end{split} $$

(64)

当$ { t ^Delta } = 1 $, 则有

$$ begin{split} &{boldsymbol{L}}left( {tau ;{t^sigma }left( tau ight),q_k^sigma left( tau ight),{tau ^Delta },{}_{a}^CD_{Delta ,tau}^alpha {q_k}left( tau ight)} ight) =&qquad Lleft( {tau ,q_k^sigma left( tau ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) end{split} $$

(65)

在$ {cal{F}} $上的不变性条件(57)可写成

$$ {S_{{boldsymbol{L}}}}left( {t,q_k} ight) = int_{{t_a}}^{{t_b}} {boldsymbol{L} left( {tau ;T_varepsilon ^sigma ,{{left( {Q_varepsilon ^k} ight)}^sigma },T_varepsilon ^{bar Delta },{}_a^CD_{bar Delta ,tau }^alpha Q_varepsilon ^k} ight)} bar Delta tau $$

(66)

在方程(66)中对$ varepsilon $求导, 再令$ varepsilon = 0 $, 则有

$$ begin{split}&{partial _t}{boldsymbol{L}}left( * ight) cdot {zeta ^sigma } + {partial _q}{boldsymbol{L} }left( * ight) cdot xi _k^sigma + {partial _w}{boldsymbol{L}}left( * ight) cdot {zeta ^Delta }+&qquad {partial _v}{boldsymbol{L} }left( * ight) cdot {{}_a^CD_{bar Delta ,tau }^alpha {xi_k }} = 0 end{split} $$

(67)

式中$ left( *
ight) buildrel Delta over = left( {tau ;{tau ^sigma },q_k^sigma left( tau
ight),{tau ^{bar Delta }},{}_{a}^CD_{bar Delta ,tau }^alpha {q_k}left( tau
ight)}
ight) $. 由关系式(62), 可得

$$ left. begin{array}{l} {partial _t}{boldsymbol{L} }left( {tau ;{t^sigma },q,w,v} ight) = {partial _t}Lleft( {{t^sigma } - mu left( tau ight)w,q,dfrac{v}{w^alpha}} ight) cdot w {partial _q}{boldsymbol{L}}left( {tau ;{t^sigma },q,w,v} ight) = {partial _q}Lleft( {{t^sigma } - mu left( tau ight)w,q,dfrac{v}{w^alpha}} ight) cdot w {partial _w}{boldsymbol{L} }left( {tau ;{t^sigma },q,w,v} ight)= quad Lleft( {{t^sigma } - mu left( tau ight)w,q,dfrac{v}{w^alpha}} ight) - {partial _v}Lleft( {{t^sigma } - mu left( tau ight)w,q,dfrac{v}{w^alpha}} ight) cdot quad dfrac{alpha cdot v}{w^alpha}- {partial _t}Lleft( {{t^sigma } - mu left( tau ight)w,q,dfrac{v}{w^alpha}} ight) cdot mu left( tau ight) cdot w {partial _v}{boldsymbol{L} }left( {tau ;{t^sigma },q,w,v} ight) = {partial _v}Lleft( {{t^sigma } - mu left( tau ight)w,q,dfrac{v}{w^alpha}} ight)cdot w end{array} ight} $$

(68)

在$ {cal{F}} $上可简化成如下的方程组

$$ left. begin{array}{l} {partial _t}{boldsymbol{L} }left( {tau ;{tau ^sigma },{q_k}left( tau ight),1,{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) = quad {partial _t}Lleft( {tau ,q_k^sigma left( tau ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) {partial _{{q_k}}}{boldsymbol{L} }left( {tau ;{tau ^sigma },{q_k}left( tau ight),1,{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) = quad {partial _{{q_k}}}Lleft( {tau ,q_k^sigma left( tau ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) {partial _w}{boldsymbol{L} }left( {tau ;{tau ^sigma },{q_k}left( tau ight),1,{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) = quad Lleft( {tau ,q_k^sigma left( tau ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight)quad -{partial _v}Lleft( {tau ,q_k^sigma left( tau ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) cdot alpha cdot{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)quad - {partial _t}Lleft( {tau ,q_k^sigma left( tau ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) cdot mu left( tau ight) {partial _v}{boldsymbol{L} }left( {tau ;{tau ^sigma },{q_k}left( tau ight),1,{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) = quad {partial _v}Lleft( {tau ,q_k^sigma left( tau ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau ight)} ight) end{array} ight} $$

(69)

将式(69)代入式(67), 得

$$ begin{split}&{partial _t}Lleft( bullet ight) cdot {zeta ^sigma } + left( {Lleft( bullet ight) -alpha cdot {partial _v}Lleft( bullet ight) cdot {}_a^CD_{Delta ,t}^alpha {q_k} - {partial _t}Lleft( bullet ight) cdot mu left( tau ight)} ight) cdot &qquad{zeta ^Delta }+ {partial _{q_k}}Lleft( bullet ight) cdot xi _k^sigma + {partial _v}Lleft( bullet ight) cdot {{}_a^CD_{Delta ,tau }^alpha {xi_k }} = 0[-12pt] end{split} $$

(70)

式中$ left( bullet
ight) buildrel Delta over = left( {tau ,q_k^sigma left( tau
ight),{}_a^CD_{Delta ,tau }^alpha {q_k}left( tau
ight)}
ight) $. 利用分数阶时间尺度Lagrange方程(37), 很容易得到

$$ begin{split}& {partial _t}Lleft( bullet ight) cdot {zeta ^sigma } + Big( Lleft( bullet ight) - alpha cdot {partial _v}Lleft( bullet ight) cdot {}_a^CD_{Delta ,t}^alpha {q_k} - &qquad {partial _t}Lleft( bullet ight) cdot mu left( tau ight) Big) cdot{zeta ^Delta } + {cal{D}}_Delta ^alpha left[ {{xi _k},{partial _v}L} ight] = 0 end{split} $$

(71)

令

$$ {cal{H}}left( bullet ight) = -Lleft( bullet ight) + alpha cdot {partial _v}Lleft( bullet ight) cdot {}_a^CD_{Delta ,t}^alpha {q_k} + {partial _t}Lleft( bullet ight) cdot mu left( tau ight) $$

(72)

则有

$$ left( {{partial _t}Lleft( bullet ight) +{{cal{H}}^Deltaleft( bullet ight)}} ight) cdot {zeta ^sigma } - {left( { {cal{H}}left( bullet ight) cdot zeta } ight)^Delta } + {cal{D}}_Delta ^alpha left[ {{xi _k},{partial _v}L} ight] = 0 $$

(73)

因此, 可得到如下的Caputo $ Delta $型分数阶时间尺度Noether定理.

定理2 若Hamilton作用量(28)在定义6的意义上是不变的, 则存在守恒量

$$ begin{split} I = & int_a^t {left( {{partial _t}Lleft( bullet ight) + {{cal{H}}^Delta left( bullet ight)}} ight) cdot {zeta ^sigma }Delta tau}-& {cal{H}}left( {t,q_k^sigma left( t ight),{}_{a}^CD_{Delta ,t }^alpha {q_k}left(t ight)} ight) cdot zeta+ {{xi _k}cdot {{}_tI_{Delta ,b}^{1 - alpha }{partial _v}L}}= { m{const}}. end{split} $$

(74)

注12:　若$ alpha = 1 $, 式(73)成为

$$ begin{array}{l} left( {{partial _t}Lleft( star ight) +{{cal{H}}^Delta left( star ight)}} ight) cdot {zeta ^sigma } + {Big(- { {cal{H}}left( star ight) cdot zeta } +{partial _v}Lleft( star ight)cdot{xi _k} Big)^Delta } = 0 end{array} $$

(75)

式中$ left( star
ight) = left( {tau ,q_k^sigma left( tau
ight),{q_k^Delta}left( tau
ight)}
ight) $. 这是文献[45]的式(72). 对其从$ a $到$ t $ 进行积分, 得到时间尺度Noether定理

$$ begin{split}I =& int_a^t {left( {{partial _t}Lleft( star ight) + {{cal{H}}^Delta left( star ight)}} ight) cdot {zeta ^sigma }Delta tau}- & { {cal{H}}left( star ight) cdot zeta } +{partial _v}Lleft( star ight)cdot{xi _k} = { m{const}}.end{split} $$

(76)

注13:　若$ {T} = mathbb{R} $, 式(73)成为

$$ begin{split}&{partial _t}Lleft( {diamond} ight) cdot zeta + {partial _q}Lleft( {diamond} ight) cdot {xi _k} + Lleft( {diamond} ight) cdot dot zeta + &qquad{partial _v}Lleft( {diamond} ight) cdot left( { - alpha cdot dot zeta cdot {}_a^CD_tau^alpha {q_k} + {}_a^CD_tau^alpha {xi _k}} ight) = 0 end{split} $$

(77)

式中$ left( diamond
ight) = left( {tau ,q_k left( tau
ight),{}_a^CD_tau^alpha {q_k}left( tau
ight)}
ight) $. 由于$ dot Lleft( {diamond}
ight) = {partial _t}Lleft( {diamond}
ight) + $$ {partial _q}Lleft( {diamond}
ight) cdot {{dot q}_k} + {partial _v}Lleft( {diamond}
ight) cdot {}_a^CD_t^alpha {{dot q}_k} $, $dfrac{{
m{d}}}{{{
m{d}}t}}Big( {Lleft( {diamond}
ight)zeta } Big) = dot Lleft( {diamond}
ight)zeta + Lleft( {diamond}
ight)dot zeta$. 再根据分数阶Lagrange方程(39), 定理2可退化为Caputo型分数阶Noether定理

$$ begin{split}I =& Lleft( diamondsuit ight) cdot zeta + int_a^t {left[ {_tD_b^alpha Big( {{partial _v}Lleft( diamondsuit ight)} Big) cdot left( {{{dot q}_k}zeta - {xi _k}} ight) - {partial _v}Lleft( diamondsuit ight)} ight.}cdot &left. { left( {zeta cdot _a^CD_{tau}^alpha {{dot q}_k} + alpha cdot dot zeta cdot _a^CD_{tau}^alpha {q_k} - _a^CD_{tau}^alpha {xi _k}} ight)} ight]{ m{d}}tau end{split} $$

(78)

5.
算例

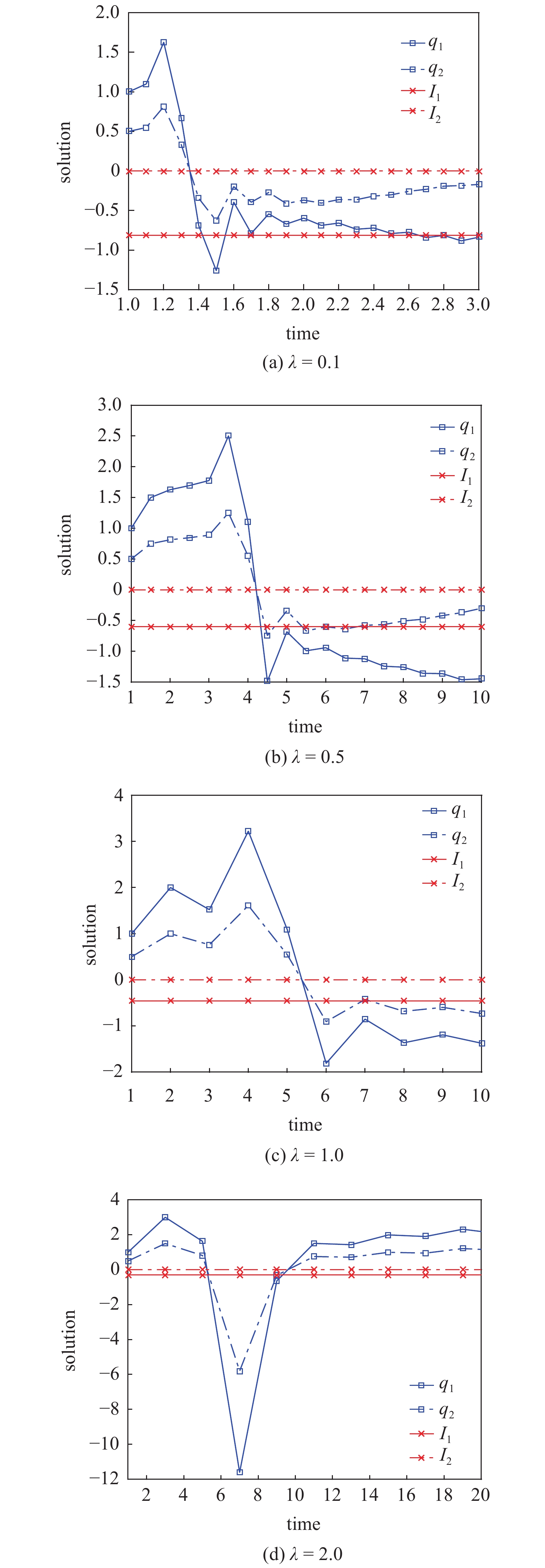
例1 众所周知, Kepler问题是牛顿力学中最早解决的问题之一, Kepler系统也是最早发现的可积系统之一. Kepler问题仍在研究中, 并被广泛应用于各个领域. Eleonski?等^[50]指出分数阶Kepler问题中所有有限运动的轨道也是封闭的. Anerot等^[45] 研究了平面上的时间尺度Kepler问题的Noether定理. 在这里, 我们考虑定义在$ left( {{{mathbb{R}}^2}backslash left{ 0
ight}}
ight) times {{mathbb{R}}^2} $上的Caputo $ Delta $型分数阶时间尺度Lagrange函数

$$ begin{split}&Lleft( {q_1^sigma ,q_2^sigma ,{}_a^CD_{Delta ,t}^alpha {q_1},{}_a^CD_{Delta ,t}^alpha {q_2}} ight) =&qquad frac{1}{2}left[ {{{left( {{}_a^CD_{Delta ,t}^alpha {q_1}} ight)}^2} + {{left( {{}_a^CD_{Delta ,t}^alpha {q_2}} ight)}^2}} ight] + {left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]^{ - frac{1}{2}}} end{split} $$

(79)

其表示Kepler问题中两个质量为1的相互作用粒子的Lagrange函数. 其中, 用分数阶导数$ _a^CD_{Delta ,t}^alpha {q_k}left( t
ight) $代替了存在能量耗散的运动的速度. 当$ {T} = mathbb{R} $且$ alpha = 1 $时, 分数阶时间尺度Lagrange函数式(79)就是传统的Kepler问题. 根据分数阶时间尺度Lagrange方程(37), 可得

$$ left. begin{array}{l} - q_1^sigma {left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]^{ - frac{3}{2}}} + {}_tD_{Delta ,b}^alpha left( {{}_a^CD_{Delta ,t}^alpha {q_1}} ight) = 0 - q_2^sigma {left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]^{ - frac{3}{2}}} + {}_tD_{Delta ,b}^alpha left( {{}_a^CD_{Delta ,t}^alpha {q_2}} ight) = 0 end{array} ight} $$

(80)

考虑到判据2, 可得

$$ begin{split}& - q_1^sigma {left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]^{ - frac{3}{2}}} cdot xi _1^sigma - q_2^sigma {left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]^{ - frac{3}{2}}} cdot xi _2^sigma +&qquad {}_a^CD_{Delta ,t}^alpha {q_1}left( {{}_a^CD_{Delta ,t}^alpha {xi _1} - alpha cdot {zeta ^Delta } cdot {}_a^CD_{Delta ,t}^alpha {q_1}} ight) + &qquad {}_a^CD_{Delta ,t}^alpha {q_2}left( {{}_a^CD_{Delta ,t}^alpha {xi _2} - alpha cdot {zeta ^Delta } cdot {}_a^CD_{Delta ,t}^alpha {q_2}} ight) +&qquad left{ {frac{1}{2}left[ {{{left( {_a^CD_{Delta ,t}^alpha {q_1}} ight)}^2} + {{left( {_a^CD_{Delta ,t}^alpha {q_2}} ight)}^2}} ight] + } ight.&qquadleft. {{{left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]}^{ - frac{1}{2}}}} ight}{zeta ^Delta } = 0[-12pt]end{split} $$

(81)

这样, 我们可以得到两组无限小变换的解

$$ zeta = - 1,{kern 4pt} {xi _1} = {xi _2} = 0 qquad$$

(82)

$$ zeta = 0,{kern 4pt} {xi _1} = - {q_2},{kern 4pt} {xi _2} = {q_1} $$

(83)

由定理2, 可以得到两个守恒量

$$ {I_1} = int_a^t {{{cal{H}}^Delta }} Delta tau - {cal{H}} qquadqquadqquadqquadqquad $$

(84)

$$ {I_2} = - {q_2} cdot {}_tI_{Delta ,b}^alpha left( {{}_a^CD_{Delta ,t}^alpha {q_1}} ight) + {q_1} cdot {}_tI_{Delta ,b}^alpha left( {{}_a^CD_{Delta ,t}^alpha {q_2}} ight) $$

(85)

式中${cal{H}} !!=!! - L !+! alpha !cdot! left( {dfrac{{partial L}}{{partial _a^CD_{Delta ,t}^alpha {q_1}}} !cdot! _a^CD_{Delta ,t}^alpha {q_1} !+! }
ight.left. {dfrac{{partial L}}{{partial _a^CD_{Delta ,t}^alpha {q_2}}} !cdot! _a^CD_{Delta ,t}^alpha {q_2}}
ight) !+$$dfrac{{partial L}}{{partial t}} cdot mu$.

如果初始条件满足$ q_1(1) = 1 $, $ q_2(1) = 0.5 $, $v_1(1) = $$ 1$和$ v_2(1) = 0.5 $, 考虑在时间尺度为$ {T} = lambdamathbb{Z} $上研究运动轨迹$ q_1 $, $ q_2 $和守恒量$ I_1 $, $ I_2 $. 此时$ {h_alpha }left( {t,s}
ight) $则为

$$ {h_alpha }left( {t,s} ight) = frac{{{lambda ^alpha }{{left( {frac{{t - s}}{lambda }} ight)}^{left( alpha ight)}}}}{{varGamma left( {alpha + 1} ight)}} $$

(86)

令$ a = 0 $, 则$t geqslant 1$. 首先, 当$ alpha = 0.5 $时, 分别在$ lambda = 0.1 $, $ lambda = 0.5 $, $ lambda = 1 $和$ lambda = 2 $的情况下模拟$ q_1 $, $ q_2 $, $ I_1 $, $ I_2 $的值, 得到的结果如图1所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-108-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
$alpha=0.5$时$q_1$, $q_2$, $I_1$, $I_2$的值



Figure
1.
Simulation of $q_1$, $q_2$, $I_1$, $I_2$ with $alpha=0.5$



下载:
全尺寸图片
幻灯片


从图1可以看出, 在不同的时间尺度上, 轨迹$ q_1 $和$ q_2 $各不同, $ I_1 $的值也不同, 但是$ I_2equiv 0 $. 这表明在这些初始条件下$ I_2 $是一个平凡守恒量. 但在不同的时间尺度上, $ I_1 $和$ I_2 $始终是常数, 从而验证了定理2的正确性. $ I_1 $和$ I_2 $不仅在不同的时间尺度上是常数, 并且在分数阶导数$ alpha $取不同值的情况下也是常数. 令$ lambda = 0.1 $, 当$ alpha = 1/3 $, $ alpha = 0.5 $, $ alpha = 2/3 $时$ q_1 $, $ q_2 $, $ I_1 $, $ I_2 $在时间段$ left [1,3
ight] $上的值如图2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-108-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
$lambda=0.1$时$q_1$, $q_2$, $I_1$, $I_2$在$left [1,3
ight]$上的值



Figure
2.
Simulation of $q_1$, $q_2$, $I_1$, $I_2$ on $left [1,3
ight]$ with $lambda=0.1$



下载:
全尺寸图片
幻灯片


从图2可以看出, 当在同一时间尺度上而$ alpha $不同时, $ I_1 $和$ I_2 $不仅是常数且其值也没发生变化. 若$ alpha = 1 $, 则Kepler问题的时间尺度Lagrange方程为

$$ left. begin{array}{l} q_1^sigma {left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]^{ - frac{3}{2}}} + q_1^{Delta Delta } = 0 q_2^sigma {left[ {{{left( {q_1^sigma } ight)}^2} + {{left( {q_2^sigma } ight)}^2}} ight]^{ - frac{3}{2}}} + q_2^{Delta Delta } = 0 end{array} ight} $$

(87)

从而守恒量为

$$ {I_1} = int_a^t {{{{cal{H}}}^Delta }} Delta tau - {cal{H}} $$

(88)

$$ {I_2} = - {q_2}cdot{q_1^Delta } + {q_1}cdot{q_2^Delta } $$

(89)

式中$ {cal{H}} = frac{1}{2}left[ {{{left( {q_1^Delta }
ight)}^2} + {{left( {q_2^Delta }
ight)}^2}}
ight] - {left[ {{{left( {q_1^sigma }
ight)}^2} + {{left( {q_2^sigma }
ight)}^2}}
ight]^{ - frac{1}{2}}} $. 所以, 当$ alpha = 1 $并且初始条件不变时, $ q_1 $, $ q_2 $, $ I_1 $, $ I_2 $在时间段为$ left [0,10
ight] $上模拟的结果如图3所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-108-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
$alpha=1$时$q_1$, $q_2$, $I_1$, $I_2$在$left [0,10
ight]$的值



Figure
3.
Simulation of $q_1$, $q_2$, $I_1$, $I_2$ on $left [0,10
ight]$ with $alpha=1$



下载:
全尺寸图片
幻灯片


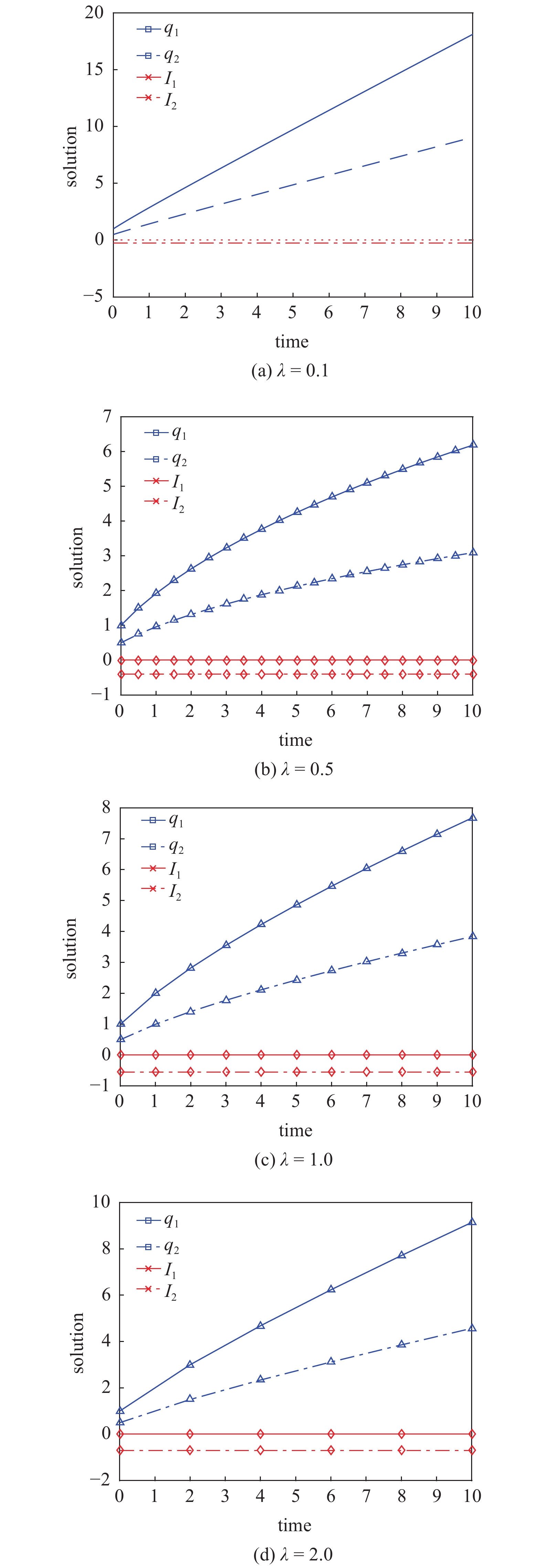
图3证明了当$ alpha = 1 $时, Caputo $ Delta $型分数阶时间尺度Noether定理可以简化为文献[45]中的时间尺度的Noether定理.

例2 由于分数阶导数和积分具有记忆效应, 分数阶微积分为描述阻尼材料和黏弹性材料提供了更切实的模型. 以单自由度线性分数阶振动系统为例, 其Lagrange函数为

$$ L = frac{1}{2}exp left( {gamma t} ight) cdot left[ {{{left( {{}_a^CD_{Delta ,t}^alpha q} ight)}^2} - {{left( {{q^sigma }} ight)}^2}} ight] $$

(90)

在时间尺度$ {T} = left{ {{t_k} = a + kh,k in mathbb{N}}
ight} $上求其Noether守恒量.

由分数阶时间尺度Lagrange方程(37), 得

$$ - exp left( {gamma t} ight) cdot {q^sigma } = - {}_tD_{Delta ,b}^alpha left[ {exp left( {gamma t} ight) cdot {}_a^CD_{Delta ,t}^alpha q} ight] $$

(91)

若${T} = mathbb{R}$, $ alpha = 1 $, 方程(91)则成为经典的阻尼振子

$$ ddot q + gamma dot q + q = 0 $$

(92)

则可称方程(91)为分数阶时间尺度阻尼振子. 由判据2, 有

$$ begin{split}& frac{gamma }{2}exp left( {gamma t} ight) cdot left[ {{{left( {{}_a^CD_{Delta ,t}^alpha q} ight)}^2} - {{left( {{q^sigma }} ight)}^2}} ight] cdot zeta - exp left( {gamma t} ight) cdot {q^sigma } cdot {xi ^sigma } + &qquadexp left( {gamma t} ight) cdot {}_a^CD_{Delta ,t}^alpha qleft( {{}_a^CD_{Delta ,t}^alpha {xi} - alpha cdot {zeta ^Delta } cdot {}_a^CD_{Delta ,t}^alpha q} ight) + &qquadfrac{1}{2}exp left( {gamma t} ight) cdot left[ {{{left( {{}_a^CD_{Delta ,t}^alpha q} ight)}^2} - {{left( {{q^sigma }} ight)}^2}} ight] cdot {zeta ^Delta } = 0 [-12pt]end{split} $$

(93)

方程(93)有解

$$ zeta = 1,{kern 4pt} xi = - frac{gamma }{2}q $$

(94)

由定理2, 得到守恒量

$$ begin{split} I =&int_a^t {frac{{gamma }}{2}exp left( {gamma tau} ight) cdot left[ {{{left( {{}_a^CD_{Delta ,t}^alpha q left(tau ight)} ight)}^2} - {{left( {{q^sigma }left(tau ight)} ight)}^2}} ight]} Delta tau-&{frac{{gamma q}}{2}}cdot{}_tI_{Delta ,b}^{1 - alpha }left[ {exp left( {gamma t} ight) {{}_a^CD_{Delta ,t}^alpha q} } ight] end{split} $$

(95)

令$ a = 0 $, $ gamma = 1 $, $ alpha = 0.5 $, $ h = 1 $, 初始位置为$ {q_0} = 1 $, 初始速度为$ {v_0} = -0.5 $. 当$ t = t_0 $时, $ I_0 = -0.125 $, 并且

$$ begin{split}{I^Delta } = &frac{gamma }{2}exp left( {gamma t} ight) cdot left[ {{{left( {_a^CD_{Delta ,t}^alpha q} ight)}^2} - {{left( {{q^sigma }} ight)}^2}} ight] - exp left( gamma t ight) cdot & {q^sigma } cdot {xi ^sigma } + exp left( gamma t ight) cdot _a^CD_{Delta ,t}^alpha q cdot _a^CD_{Delta ,t}^alpha xi = 0 end{split} $$

(96)

由此可证明式(95)是一守恒量. 若$ alpha = 1 $, 此时, 时间尺度上的Lagrange方程为

$$ - exp left( {gamma t} ight) cdot {q^sigma } = {D_Delta }left[ {exp left( {gamma t} ight) cdot {q^Delta }} ight] $$

(97)

其守恒量为

$$ begin{split} I = & int_a^t {frac{gamma }{2}exp left( {gamma tau } ight) cdot left[ {{{left( {{q^Delta }left( tau ight)} ight)}^2} - {{left( {{q^sigma }left( tau ight)} ight)}^2}} ight]} Delta tau - &frac{{gamma q}}{2} cdot exp left( {gamma t} ight) cdot {q^Delta } end{split} $$

(98)

在上述给出的初始条件下, 当$ h = 1 $和$ h = 0.1 $时, 分别给出了$ q $和$ I $在时间段$ left[0,10
ight] $和$ left[0,3.5
ight] $的模拟结果, 如图4所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-108-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
$alpha=1$时$q$和$I$的值



Figure
4.
Simulation of $q$ and $I$ with $alpha=1$



下载:
全尺寸图片
幻灯片

6.
结论

将分数阶理论和时间尺度理论应用到动力学问题的研究中, 建立的分数阶时间尺度模型更具有广泛的应用性、更切合实际问题. 结合分数阶微积分和时间尺度微积分, 我们研究了Caputo $ Delta $型分数阶时间尺度Noether定理. 若$ alpha = 1 $, 文献[31]在特殊无限小变换下得到的时间尺度Noether定理与我们的定理1一致, 但其一般无限小变换下的Noether定理却不能成为文中的定理2. 利用文献[45]中的广义Jost方法得到了一般无限小变换下的分数阶时间尺度Noether定理, 并通过算例验证了用该方法得到的守恒量是常数, 验证了定理的正确性. 进一步地说明了运用文献[31]中的时间重新参数化技术处理时间尺度Noether定理是存在一些问题的.

分数阶时间尺度Noether定理为求解复杂系统的方程提供了一种新方法, 当然它还需要被进一步地研究和完善. 在今后的工作中, 还可考虑以下几个问题.

(1) 研究如何将该方法进一步拓展到非完整系统和Birkhoff系统或其他复杂动力学系统.

(2) 本工作只研究了Caputo型分数阶导数和$ Delta $型时间尺度导数, 也可研究其他分数阶导数和时间尺度导数以及它们之间的差异.

(3) 在实际问题中, 需要讨论分数阶时间尺度模型中Noether守恒量的物理意义.

(4) 值得注意的是, 由于分数阶导数具有记忆性, 一般算法并不适用于分数阶微积分, 算例仅根据分数阶时间尺度积分和导数的定义进行计算的. 分数阶时间尺度的保结构算法是一个新的、艰巨的领域, 将是我们今后的主要工作.