DVC中内部散斑质量评价及计算体素点的优化选择

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

引言

数字体图像相关方法(digital volume correlation, DVC)是二维数字图像相关方法(two-dimensional digital image correlation, 2D DIC)在三维体图像上的拓展. 通过比较体成像设备获取的被测试样变形前后数字体图像, 该方法可测量物体内部三维全场变形^[1-2]. 由于可以提供被测试样内部(而不仅仅是表面)更为丰富的变形信息, DVC在多孔材料(如骨^[3]、金属泡沫^[4]、木材^[5])、半透明生物材料(如细胞^[6]等)、建筑材料(如混凝土^[7]等)、复杂结构(如3D打印结构^[8]、生物植入物^[9]等)的内部变形场测量、力学行为表征和有限元模拟互证等方面都有着重要应用^[10-12].

DVC的基本原理是从参考体图像中围绕感兴趣的计算点选择一个立方体的图像子体块(subvolume), 通过跟踪该图像子体块在变形后图像中的位置以获得图像子体块中心点的三维位移矢量. 在实际分析计算时, 被测试样体图像需呈现随机的灰度分布(通常称作内部散斑), 该散斑场作为变形信息的载体随试样一起变形. 因此被测试样内部散斑质量和DVC位移测量精度密切相关. 为对散斑图质量进行评价, 在DIC方法研究中已提出多个参数^[13], 这些评价参数可分为局部参数和全局参数^[14-16]. 局部参数主要用于单个图像子区内散斑质量的评价, 如Pan等^[17]通过理论分析和模拟实验证明了DIC图像子区的灰度梯度平方和(sum of square subset intensity gradient, SSSIG)参数与其位移测量结果的随机误差成反比, 因此图像子区SSSIG参数越大, 其内部散斑质量越好; Bomarito等^[18]将SSSIG参数和二次自相关峰高参数结合提出了一种组合式的散斑评价参数, 该参数能够解决原有SSSIG参数不适用于规则散斑图像(如棋盘格图案)的情况. 此外, 如假设散斑质量在整个图像内的分布是均匀的, 则可在散斑质量局部评价参数的基础上提出可评价整幅散斑图质量的全局参数, 如Pan等^[19]在SSSIG局部参数的基础上提出了用于整幅散斑图评价的平均灰度梯度(mean intensity gradient, MIG)全局参数等.

类似地, 在利用DVC测量内部变形时, 由于被测对象、体成像设备类型和参数以及实验条件等的差异^[20], 获取的被测物体内部散斑图像千差万别. 因此, 如何定量评价图像内部散斑的优劣也是DVC中一个重要的基本问题. 将DIC中已有的散斑评价参数直接推广到DVC中是最有效的方法之一. 在DIC中的诸多散斑评价参数中, SSSIG参数是从DIC位移测量精度的理论模型中推导出来, 具有严格的理论基础, 具有普适性. 并且该参数是一种典型的局部评价参数, 能够克服全局参数在遇到材料内部出现空洞等非连续和非均匀分布时失效的问题^[21], 因此更适合于材料内部散斑质量的评价. 然而, 在将SSSIG参数在DVC内部散斑评价中推广应用需要解决以下几个问题: (1) SSSIG参数在DVC中最新的三维反向组合高斯?牛顿亚体素配准算法^[22](3D inverse compositional Gauss-Newton, 3D IC-GN)中应用的可行性问题. SSSIG最初被提出来时是基于DIC经典亚像素配准算法牛顿?拉普森算法^[17], 因具有更优的抗噪性能和更高的计算效率, IC-GN算法已成为DIC/DVC方法中的标准算法, 因此系统地研究SSSIG参数与该算法测量精度的关系是有必要的; (2)由于DVC内部散斑类型的多样性, 这就要求评价指标应具有广泛的适用性, 因此需要研究SSSIG参数在不同类型内部散斑中的适用性; (3)与DIC通过人工制作散斑不同, DVC主要通过被测物体自身内部纹理的灰度对比度来形成散斑场. 由于被测物体内部组成和结构难以改变, 无法通过人工优化DVC测量对象的内部散斑质量, 因此从计算方法层面研究减弱低质量散斑对DVC位移测量精度的影响无疑是有价值的.

基于以上考虑, 本文研究了DVC中体图像的内部散斑质量评价参数及其适用性, 并通过优化选取子体块内的体素点来实现增大子体块尺寸以减小测量误差的同时使计算量没有显著增加. 论文首先从DVC方法的位移测量精度理论分析出发, 系统介绍了SSSIG评价参数的理论基础; 然后, 通过数值模拟平移实验, 检验了该参数在不同类型内部散斑中的有效性; 最后, 为了在算法层面上改善DVC子体块的SSSIG参数, 提出了基于灰度梯度的体素点选择DVC方法, 并通过模拟实验和实际实验验证了该方法的有效性.

1.
DVC位移测量误差的理论分析及模拟实验验证

本节首先对最新的3D IC-GN亚体素配准算法^[22]进行简单介绍, 然后给出基于3D IC-GN算法的DVC位移测量误差的理论公式推导^[23-25]. 该公式显示位移测量误差与SSSIG参数、体图像噪声、亚体素灰度插值算法直接相关. 最后通过模拟数值平移实验验证了SSSIG参数用于不同类型内部散斑质量评价的有效性.

1.1
3D IC-GN算法

DVC方法在具体实现过程中需执行两个步骤: 初值估计和亚体素位移测量. 对任一计算点, 首先需要通过简单的整体素搜索(种子点)或可靠性导向的位移初值传递策略(非种子点)来确定其位移迭代初值. 为进一步提高位移测量精度, 需进行亚体素配准计算^[26-27]. 在众多DVC亚体素配准算法中, 3D IC-GN算法因具有高精度、高效率的优点而获得广泛使用, 该算法利用迭代运算使非线性相关函数由初始估计值逐渐收敛至局部最佳极值(即使参考和变形子体块获得最佳匹配的变形参数矢量)以获得具有亚体素精度的位移计算结果.

3D IC-GN算法计算流程图如图1所示, 该算法通过优化如式(1)所示的零均值归一化最小平方距离相关函数(zero-mean normalized sum-of-square difference, ZNSSD)获得亚体素位移

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />

图
1
3D IC-GN算法计算流程图^[22]

Figure
1.
Flow chart of the 3D IC-GN algorithm^[22]

下载:
全尺寸图片
幻灯片

$$begin{split} &{C_{{
m{ZNSSD}}}}(Delta {boldsymbol{p}}) =&sumlimits_{boldsymbol{xi }} {{{left[ {frac{{fleft( {{boldsymbol{x}} + {boldsymbol{W}}left( {{boldsymbol{xi }};Delta {boldsymbol{p}}}
ight)}
ight) - {f_{
m{m}}}}}{{Delta f}} - frac{{gleft( {{boldsymbol{x}} + {boldsymbol{W}}left( {{boldsymbol{xi }};{boldsymbol{p}}}
ight)}
ight) - {g_{
m{m}}}}}{{Delta g}}}
ight]}^2}} end{split}$$

(1)

式中$f({boldsymbol{x}})$

和$g({boldsymbol{x}})$

分别表示参考和变形子体块中点${boldsymbol{x}} = {(x,y,{textit{z}})^{
m{T}}}$

处的灰度值; ${boldsymbol{xi }} = {(Delta x,Delta y,Delta {textit{z}})^{
m{T}}}$

表示参考子体块中各体素点的局部坐标; ${f_{
m{m}}}$

和${g_{
m{m}}}$

分别表示参考和变形子体块的灰度平均值; $Delta f$

和$Delta g$

分别是参考和变形子体块中所有体素点的灰度标准差; ${boldsymbol{p}} = (u,{u_x}, $

$ {u_y},{u_{textit{z}}},v,{v_x},{v_y},{v_{textit{z}}},w,{w_x},{w_y},{w_{textit{z}}})$

是描述目标子体块的位置和形状变化的变形矢量;$Delta {boldsymbol{p}} = (Delta u,Delta {u_x},Delta {u_y},Delta {u_{textit{z}}},Delta v,Delta {v_x}, $

$ Delta {v_y},Delta {v_{textit{z}}},Delta w,Delta {w_x},$

$Delta {w_y},Delta {w_{textit{z}}})$

表示参考子体块的增量变形矢量; ${boldsymbol{W}}({boldsymbol{xi }};{boldsymbol{p}})$

为目标子体块的翘曲函数; ${boldsymbol{W}}({boldsymbol{xi }};Delta {boldsymbol{p}})$

为参考子体块的增量翘曲函数.

采用高斯牛顿算法对ZNSSD相关函数进行迭代优化, 则变形矢量增量可写为

$$begin{split}&Delta {boldsymbol{p}} = - {{boldsymbol{H}}^{ - 1}} times sumlimits_{boldsymbol{xi}} {Biggl{{18} {{{left( {nabla ffrac{{partial {boldsymbol{W}}}}{{partial {boldsymbol{p}}}}}
ight)}^{
m{T}}} times } } & {left[ {left( {fleft( {{boldsymbol{x}} + {boldsymbol{xi}} }
ight) - {f_{
m{m}}}}
ight) - frac{{Delta f}}{{Delta g}}left( {gleft( {{boldsymbol{x}} + {boldsymbol{W}}!!left( {{boldsymbol{xi}} ;{boldsymbol{p}}}
ight)}
ight) - {g_{
m{m}}}}
ight)}
ight]} Bigggr}{18}end{split}$$

(2)

其中$nabla f$

是参考体图像中各点的灰度梯度, H为Hessian矩阵. 在确定变形矢量增量$Delta {boldsymbol{p}}$

之后, 就可以确定子体块的增量翘曲函数${boldsymbol{W}}!!left( {{boldsymbol{xi }};Delta {boldsymbol{p}}}
ight)$

. 然后将该增量翘曲函数与现有的翘曲函数${boldsymbol{W}}!!left( {{boldsymbol{xi }};{boldsymbol{p}}}
ight)$

反向组合, 以更新目标子体块的翘曲函数. 对于每个参考子体块, 重复进行式(1)的迭代运算, 直至满足预设的收敛条件, 从而获取最终优化的变形矢量${boldsymbol{p'}} = (u',{u'_x}, {u'_y}, $

$ {u'_{textit{z}}},v',{v'_x},{v'_y},{v'_{textit{z}}},w',{w'_x},{w'_y},{w'_{textit{z}}})$

. 此外, 为表征目标子体块中更为复杂的局部变形模式, 也可采用包含二阶变形分量的翘曲函数^[28].

1.2
位移测量误差的理论分析

实际实验中获得的体图像不可避免含有随机噪声^{[3, 28-29]}, 且各体素点的图像噪声相互独立, 设参考体图像和变形体图像实际的灰度值分别为$tilde f({boldsymbol{x}})$

和$tilde g({boldsymbol{x}})$

, 真实的图像灰度值为$f({boldsymbol{x}})$

和$g({boldsymbol{x}})$

, 则

$$left. {begin{array}{*{20}{c}} {tilde f({boldsymbol{x}}) = f({boldsymbol{x}}) + {delta _{
m{f}}}({boldsymbol{x}})} {tilde g({boldsymbol{x}}) = g({boldsymbol{x}}) + {delta _{
m{g}}}({boldsymbol{x}})} end{array}}
ight}$$

(3)

式中${delta _{
m{f}}}({boldsymbol{x}})$

和${delta _{
m{g}}}({boldsymbol{x}})$

分别表示在参考体图像和变形体图像中的图像噪声(假设标准差分别为${sigma _{
m{f}}}({boldsymbol{x}})$

和${sigma _{
m{g}}}({boldsymbol{x}})$

)引起的灰度偏差. 因此, 在实际实验中, 式(2)的实际形式为

$$begin{split} Delta {boldsymbol{p}} =& - {{boldsymbol{tilde H}}^{ - 1}} times sumlimits_{boldsymbol{xi }} Biggl{{18} left( {nabla {boldsymbol{tilde f}}frac{{partial {boldsymbol{W}}}}{{partial {boldsymbol{p}}}}}
ight)_{}^{
m{T}} times Biggl[{15} left( {tilde fleft( {{boldsymbol{x}} + {boldsymbol{xi }}}
ight) - {{bar f}_{
m{m}}}}
ight) -&left.frac{{Delta tilde f}}{{Delta tilde g}}left( {tilde gleft( {{boldsymbol{x}} + {boldsymbol{W}}!!left( {{boldsymbol{xi }};{boldsymbol{p}}}
ight)}
ight) - {{bar g}_{
m{m}}}}
ight)
ight] Bigggr}{18}end{split} $$

(4)

将式(3)代入式(4), 又$dfrac{{Delta tilde f}}{{Delta tilde g}} approx 1$

, 令${{boldsymbol{x}}_1}{
m{ = }}{boldsymbol{x}} + {boldsymbol{xi }}$

, ${{boldsymbol{x}}_2}{
m{ = }} $

$ {boldsymbol{x}} + {boldsymbol{W}}!!left( {{boldsymbol{xi }};{boldsymbol{p}}}
ight)$

, 则式(4)可简化为

$$begin{split} Delta {boldsymbol{p}} approx & - {{boldsymbol{tilde H}}^{ - 1}} times sumlimits_{boldsymbol{xi }} Biggl{{18} left( {nabla {boldsymbol{tilde f}}frac{{partial {boldsymbol{W}}}}{{partial {boldsymbol{p}}}}}
ight)_{}^{
m{T}} times left[ left( {fleft( {{{boldsymbol{x}}_1}}
ight) + {delta _{
m{f}}}left( {{{boldsymbol{x}}_1}}
ight) - {{bar f}_{
m{m}}}}
ight) -
ight.[-2pt]&left.left( {gleft( {{{boldsymbol{x}}_2}}
ight) + {delta _{
m{g}}}left( {{{boldsymbol{x}}_2}}
ight) - {{bar g}_{
m{m}}}}
ight)
ight] Bigggr}{18} [-12pt]end{split} $$

(5)

根据高斯白噪声的统计特性, 变形矢量增量$Delta {boldsymbol{p}}$

的期望和方差为

$$left. {begin{array}{*{20}{l}} {E(Delta {boldsymbol{p}}) approx - {{{boldsymbol{tilde H}}}^{ - 1}} times Eleft[ {displaystylesumlimits_{boldsymbol{xi }} {{{left( {nabla {boldsymbol{tilde f}}dfrac{{partial {boldsymbol{W}}}}{{partial {boldsymbol{p}}}}}
ight)}^{
m{T}}} times hleft( {{{boldsymbol{x}}_1}}
ight)} }
ight]} {Var(Delta {boldsymbol{p}}) = {
m{diag}}({{{boldsymbol{tilde H}}}^{ - 1}})(sigma _{
m{f}}^2 + sigma _{
m{g}}^2)} end{array}}
ight}$$

(6)

式中$hleft( {{{boldsymbol{x}}_1}}
ight){
m{ = }}f({{boldsymbol{x}}_1}) - g({{boldsymbol{x}}_2})$

表示灰度插值偏差.

为了更加直观地展示式(6), 将其应用到沿x方向的平移工况中, 由上节分析可知, 如果u为子体块真实变形量, 当采用3D IC-GN算法迭代1次时, 则位移结果为$u' approx u{
m{ + }}Delta u{
m{ + }}{u_x}Delta u{
m{ + }}{u_y}Delta v + {u_{textit{z}}}Delta w$

$ approx u{
m{ + }}Delta u$

, 此时移u测量误差${u_{
m{e}}} = u' - u approx Delta u$

, 因此由式(6)可知

$$left. {begin{array}{*{20}{l}} {E({u_{
m{e}}}) approx E(Delta u) approx frac{{displaystylesumlimits_{boldsymbol{xi }} {{f_x}left( {{{boldsymbol{x}}_1}}
ight)hleft( {{{boldsymbol{x}}_1}}
ight)} }}{{{{displaystylesumlimits_{boldsymbol{xi }} {{{tilde f}_x}left( {{{boldsymbol{x}}_1}}
ight)} }^2}}}} {Var({u_{
m{e}}}) approx Var(Delta u) approx frac{{sigma _{
m{f}}^2 + sigma _{
m{g}}^2}}{{{{displaystylesumlimits_{boldsymbol{xi }} {{{tilde f}_x}left( {{{boldsymbol{x}}_1}}
ight)} }^2}}}} end{array}}
ight}$$

(7)

其中${tilde f_x}left( {{{boldsymbol{x}}_1}}
ight)$

为体素点${{boldsymbol{x}}_1}$

处在x方向的灰度导数, 可利用常用的梯度算子(如Barron算子^{[22, 30]})进行计算.

由式(7)可知, 当不考虑形函数欠匹配问题时, 在3D IC-GN算法中位移u的系统误差$E(Delta u)$

和随机误差$Var(Delta u)$

均与子体块灰度梯度和${displaystylesumlimits_{{S_{{
m{sub}}}}} {{{tilde f}_x}left( {{{boldsymbol{x}}_1}}
ight)} ^2}$

(即SSSIG参数)大小有关. 但系统误差主要受灰度插值误差$hleft( {{{boldsymbol{x}}_1}}
ight)$

影响, 当采用精度较高的插值算法, 并对图像进行预滤波, 3D IC-GN算法的系统误差可控制在较低水平, 而随机误差$Var({u_{
m{e}}})$

与子体块SSSIG参数呈反相关关系. 也就是说, 在DVC计算中, 某方向的SSSIG参数越大, 其位移测量结果越精确.

1.3
内部散斑质量评价参数的模拟实验验证

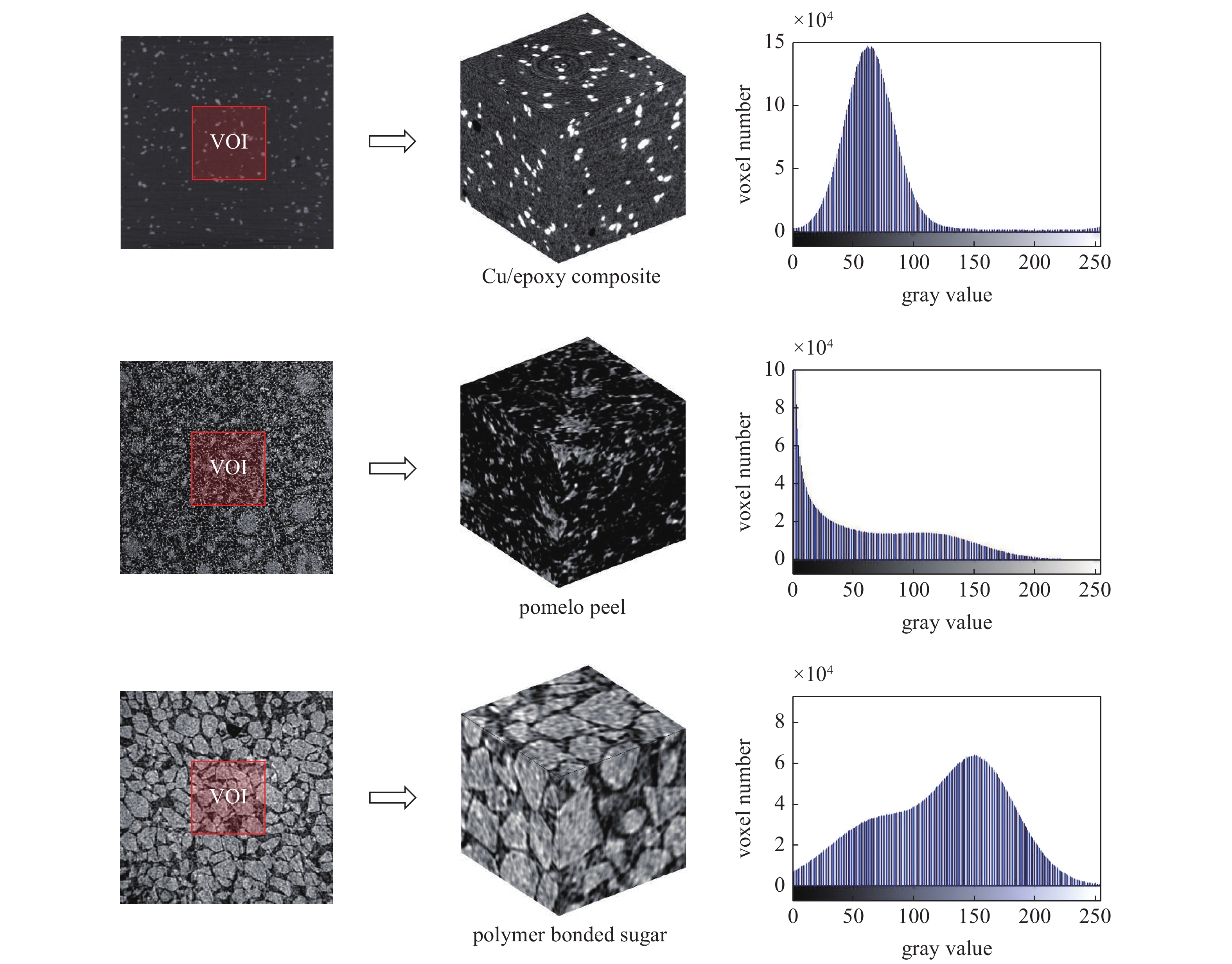
为验证上节推导的理论公式的正确性, 本文对3种不同类型内部散斑进行了数值模拟平移实验. 与实际实验相比, 数值模拟实验不但可以精确控制散斑图的位移和应变信息, 还能够排除由体图像采集系统(如设备自热)、非理想加载条件等非理想实验因素对位移测量的影响^[15], 最大程度地保证了计算结果的可靠性. 验证实验选取的参考体图像是由不同X-ray CT获取的3种具有代表性的材料(铜颗粒填充环氧树脂基复合材料、柚子皮多孔材料和多聚物粘结糖)的体图像, 图2给出了3种材料体图像的切片图、以及选取的感兴趣区域(volume of interest, VOI)及其灰度分布直方图.

在平移实验中, 利用傅里叶变换对3种材料的体图像做精确的位置平移. 具体为: 将原体图像作为参考体图像, 参考体图像沿x方向平移0.2体素而得到平移变形体图像. 为模拟真实情况下的图像噪声, 在参考和变形体图像中分别加入标准差为3灰度值的高斯白噪声. DVC分析中均选取大小为200×200×200体素的体图像中心区域VOI进行研究, 计算采用3D IC-GN亚体素配准算法和一阶形函数, 子体块尺寸为41×41×41体素, 计算步长为10体素.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-2.jpg'"
class="figure_img
figure_type2 ccc " id="Figure2" />

图
2
3种不同类型内部散斑的切片图、VOI及其灰度分布直方图

Figure
2.
Slice figures, VOI and histograms of three speckle patterns

下载:
全尺寸图片
幻灯片

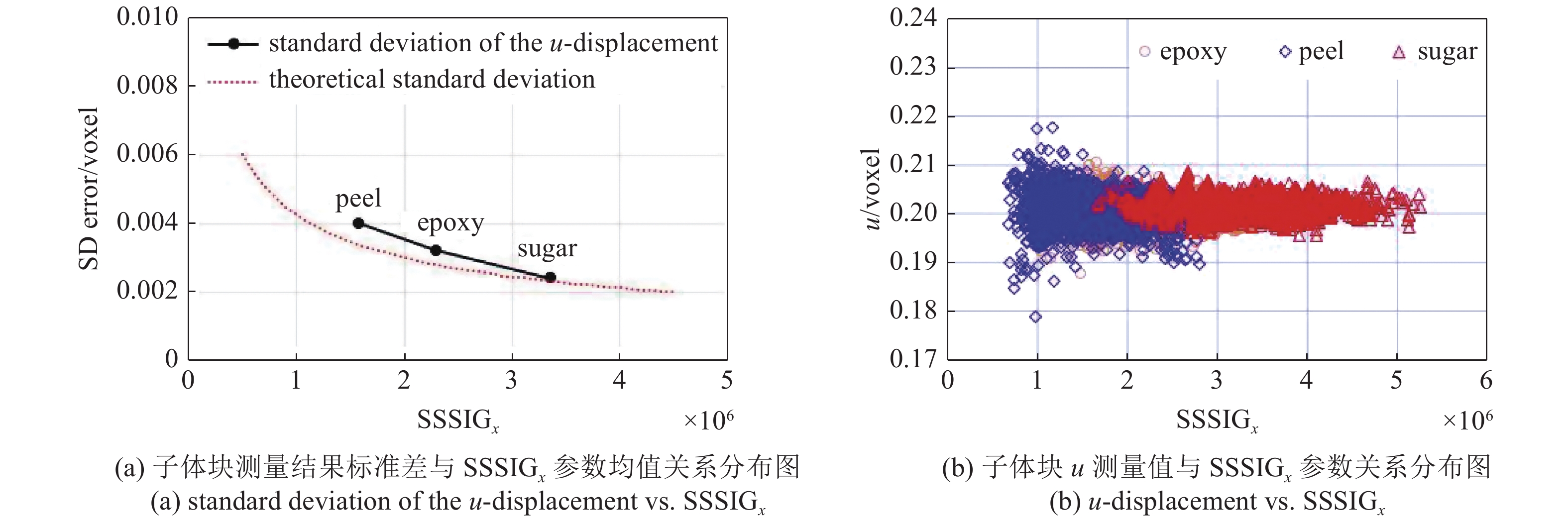
图3(a)给出了3种材料位移u测量结果的标准差(standard deviation (SD) error)与子体块图像x方向SSSIG (简记为SSSIG_x)参数平均值的关系的理论结果和测量结果, 由表可知, 在不同材料中, 位移测量结果的标准差与理论预测值吻合良好; 不同材料间, 散斑图像SSSIG_x参数越大的材料, 位移测量结果标准差也较小, 这和上面的理论公式相一致. 需要说明的是, 由式(7)可知, 均值误差不仅与图像SSSIG有关还与子体块内各体素点灰度插值偏差有关, 而灰度插值偏差在分析中难以统计, 因此本文不再对均值偏差进行重点分析. 但是为了降低位移测量结果的均值误差, 在DVC计算前需要对体图像进行低通预滤波^[31].

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-3.jpg'"
class="figure_img
figure_type2 ccc " id="Figure3" />

图
3
3种不同类型内部散斑测量结果

Figure
3.
Measurement results of three speckle patterns

下载:
全尺寸图片
幻灯片

图3(b)还给出了3种材料中子体块测量值u与其子体块散斑图像参数SSSIG_x之间的关系, 从图3中可以看出: 尽管各材料之间测量结果差别较大, 然而对同一散斑材料中, 测量结果的变化幅度均整体上与散斑图像SSSIG_x参数呈现负相关关系, 即随子体块散斑图像参数SSSIG_x的增大, 其测量结果变化幅度越小; 此外, 由图3可知, 3种材料中, 柚子皮多孔材料的位移标准差最大, 其次是铜颗粒填充环氧树脂基复合材料, 而多聚物粘结糖最小.

以上的研究结果表明, 散斑图像SSSIG_x参数能够反映出材料内部散斑质量, 对同一种材料而言, 其散斑图像SSSIG_x值越大, 则DVC位移测量精度越高.

2.
DVC方法中计算体素点的优化选择

2.1
SSSIG参数的优化

为提高位移测量精度, 在DIC中通常采用增大子区尺寸来优化子区SSSIG参数^{[17, 21]}, 该方法也可以推广到DVC中. 但由于DVC处理的是三维数据, 简单地通过增大子体块尺寸来优化子体块SSSIG参数将大幅度增加计算量, 进而影响计算效率. 通常, 在DVC计算时子体块内所有的体素点均参与相关性计算, 这将耗费大量的计算时间. 另外一方面, 通过式(7)可以看出子体块的SSSIG参数实质上其内部所有体素点灰度梯度平方的总和, 子体块内灰度梯度小的体素点对提高SSSIG值影响较小, 即这些点对子体块计算精度影响较小, 因此可在增大子体块尺寸的同时将子体块内灰度梯度平方偏小的体素点剔除出DVC计算, 以实现在增大子体块SSSIG的同时尽可能的降低计算量. 在实际实验需要对3个方向均进行优化, 因此选择了3个方向的SSSIG参数的均值(简记为SSSIG_mean)作为目标函数, 见式(8).

为了更加直观地展示材料中灰度梯度的分布情况, 图4给出了多孔材料中一子体块内部灰度梯度和的分布情况, 由图可知, 在子体块内部有较大一部分体素点的灰度梯度平方和处于较低的水平, 因此将这些体素点排除出DVC计算将能够有效减轻计算量.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />

图
4
多孔材料灰度梯度分布图

Figure
4.
Intensity gradient distribution of porous materials

下载:
全尺寸图片
幻灯片

$${C_{{
m{3D SSSIG}}}} = sumlimits_{mathbf{xi }} {left[ {{f_x}{{(i,j,k)}^2} + {f_y}{{(i,j,k)}^2} + {f_{textit{z}}}{{(i,j,k)}^2}}
ight]} $$

(8)

2.2
体素点优化选择方法

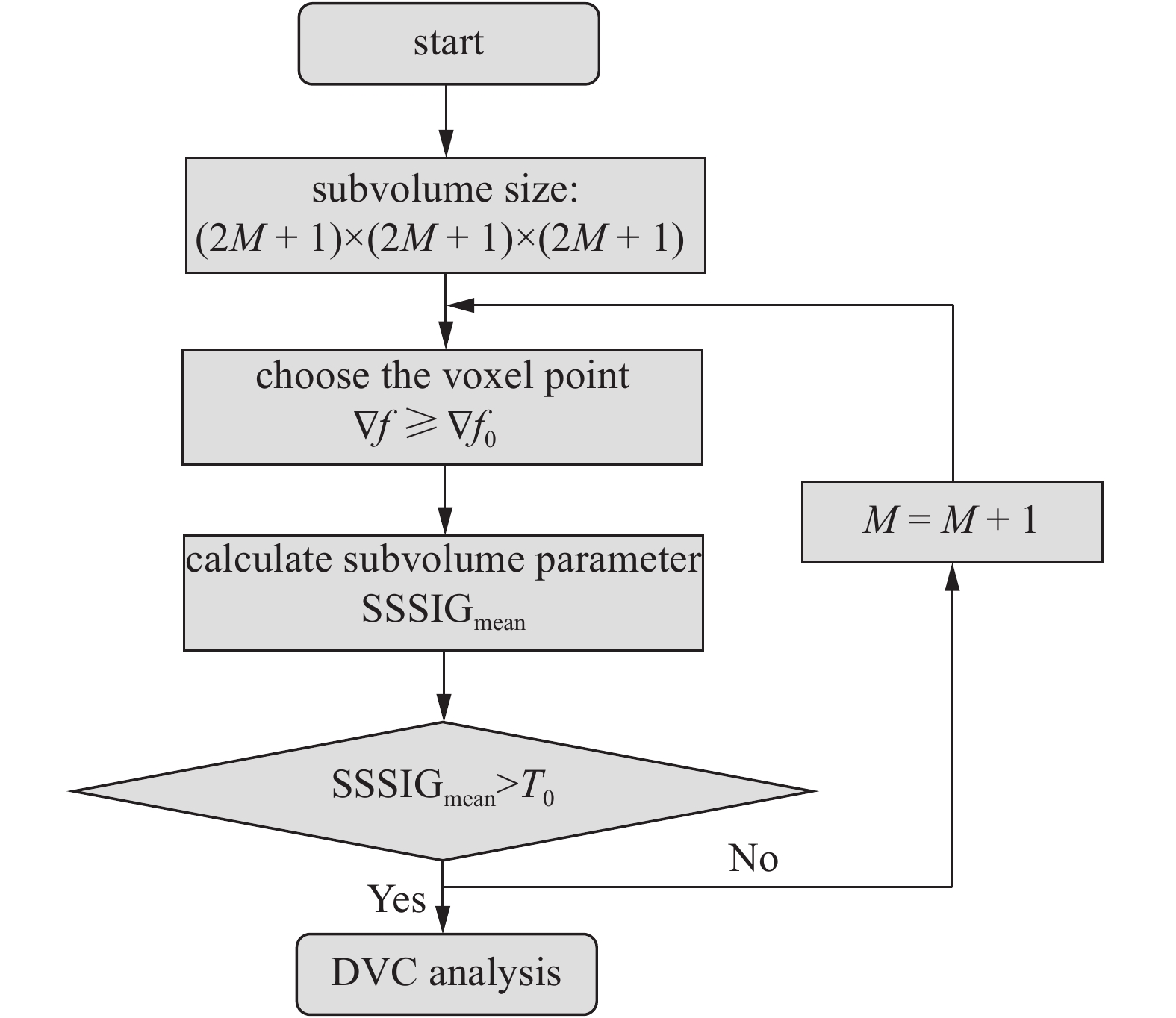
基于上述的SSSIG参数优化思想, 提出了一种基于灰度梯度的计算体素点优化选择方法, 图5给出了该方法在计算一子体块位移时采取的计算流程图. 该方法的具体计算步骤为:

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />

图
5
体素点优化选择方法计算流程图

Figure
5.
Calculation flow chart of voxel selection DVC method

下载:
全尺寸图片
幻灯片

(1) 在每一个子体块开始DVC计算前首先计算其内部所有体素点3个方向的灰度梯度平方的总和$nabla $

f, 只有总和大于所设定灰度梯度阈值$nabla $

f₀的体素点(有效点)才会参与到该子体块SSSIG_mean参数的计算和之后的DVC计算;

(2) 计算该子体块SSSIG_mean参数, 将该子体块SSSIG_mean参数与所设定的SSSIG_mean参数阈值T₀对比, 如果低于该阈值, 则将该子体块半边长M增大1体素;

(3) 重复以上步骤, 直到子体块SSSIG_mean参数大于所设定的阈值T₀, 然后基于选定的体素点, 完成该子体块的DVC计算.

在该方法中, 体素点灰度梯度阈值$nabla $

f₀和SSSIG_mean参数阈值T₀的设定是重点, 在子体块中, 3个方向的灰度梯度平方的总和小于灰度梯度阈值$nabla $

f₀的体素点将被删除, 而只有高于灰度梯度阈值$nabla $

f₀的体素点才会参与到DVC计算. 灰度梯度阈值$nabla $

f₀过小, 将起不到提高测量精度的作用, 灰度梯度阈值$nabla $

f₀过大, 将会使子体块有效体素点大大减小, 进而影响测量结果. 同时, SSSIG_mean参数阈值T₀设置过大, 则使计算量增加, 太小又起不到优化作用, 因此实际应用中要根据不同的情况选择合适的灰度梯度阈值$nabla $

f₀和SSSIG_mean参数阈值T₀.

2.3
模拟实验验证与讨论

为验证体素点优化选择方法的有效性, 将该方法应用于1.3节中模拟平移实验, 通过3种材料原有的$nabla $

f的分布情况确定了其灰度梯度阈值$nabla $

f₀和SSSIG_mean参数阈值T₀, 其中子体块灰度梯度阈值$nabla $

f₀的取法为: 将子体块所有体素点(记为N)按灰度梯度总和$nabla $

f大小递增排列, 选用编号${N_1} = {mathop{
m int}} left( {N/2}
ight)$

体素点对应的灰度梯度总和为阈值$nabla $

f₀, SSSIG_mean参数阈值T₀设为该子体块原有SSSIG_mean的1.5倍.

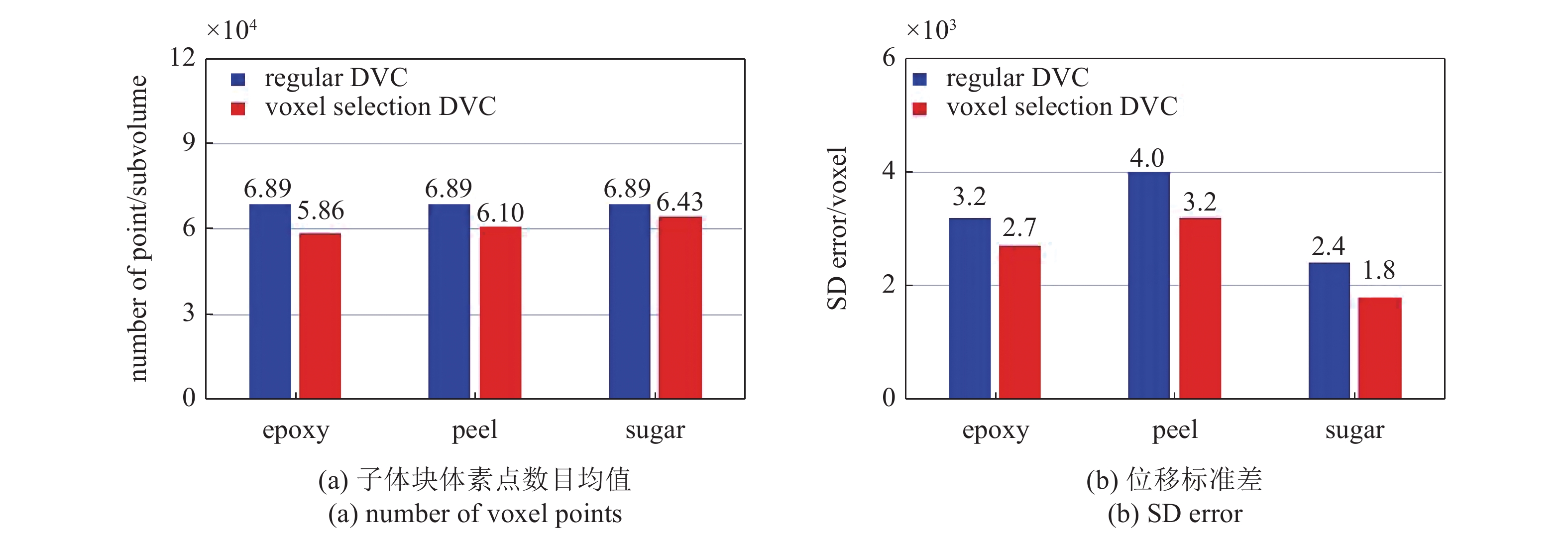
DVC计算中, 子体块尺寸设为41×41×41体素, 计算步长10体素. 图6给出了常规DVC和体素点选择DVC位移测量结果的对比情况.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />

图
6
两种方法测量结果对比

Figure
6.
Comparison of the results of two methods

下载:
全尺寸图片
幻灯片

由图可知, 常规DVC中每个子体块中体素点的数目是一定的, 具体为41×41×41 = 68921个体素点, 而在体素点选择DVC中, 尽管子体块尺寸增加了, 但3种材料子体块中有效体素点的平均数量依次为58619, 61016和64521, 比常规DVC略低, 这说明优化后的DVC方法计算量不仅没有增加, 还存在一定程度的降低. 而在测量误差方面, 优化后3种材料散斑图像的测量标准差分别下降了15.63%, 25.00%和18.75%. 通过以上的分析结果可知, 体素点优化选择方法能够在保证计算精度的前提下有效降低由于子体块尺寸增大所引起的计算量的急剧增加.

2.4
泡沫铜材料重扫描实验

为进一步检验体素点选择DVC方法的有效性, 将该方法应用到泡沫铜材料重扫描实验.

重扫描实验是DVC中一种常用的测量精度评价方法, 在重扫描实验中, 被测试件静止, 且不对其施加任何载荷, 利用体成像设备对试件进行两次连续扫描, 通过DVC分析两次扫描获得的体图像可以获得试件在静止状态下的变形量测量值, 通过此实验可以检验DVC方法的测试精准度. 实验所用试件是孔隙率为97.5%泡沫铜材料, 试件尺寸为11 mm×11 mm×8 mm. 体成像设备选用的是 Skyscan1172 台式 X 射线 CT 系统(Bruker Corporation, 美国), 空间采样率选取为 2000×1336 像素, 体素尺寸设定为 9 μm, 旋转步长为 0.4°. 每次CT扫描持续 45 min, 共获取试件2组灰度体图像.

图7给出了CT实验装置图和试件切片图. 在DVC分析中, 采用 3D IC-GN亚体素配准算法和一阶形函数. 感兴趣计算区域选在图像中心, 大小为300×300×500体素, 子体块尺寸预设为41×41×41体素, 计算步长为20体素, 共有15×15×25=5625个规则分布的计算点. 体素点选择采用了和3.3节一致的灰度梯度阈值$nabla$

f₀和SSSIG_mean参数阈值T₀.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />

图
7
实验设置

Figure
7.
Compression experimental setup

下载:
全尺寸图片
幻灯片

图8对比给了采用常规和体素点选择DVC计算获得的位移场, 由图可以很直观地看出, 采用体素点选择DVC的测量误差要小于常规DVC. 表1还给出了两种方法计算量和位移测量结果的详细对比情况. 由表1可知, 优化后位移u, v, w的标准差分别下降了22.80%, 27.73%和28.55%; 与此同时, 优化前后各位移分量的均值误差变化较小. 由此可见, 在泡沫铜重扫描实验中, 本文提出的体素点选择DVC可有效降低DVC的位移测量误差, 但没有明显增加其计算量.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-8-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8-1" />

8
重扫描实验结果

8.
Rescan results

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-158-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />

图
8
重扫描实验结果 (续)

Figure
8.
Rescan results (continued)

下载:
全尺寸图片
幻灯片

表
1
重扫描实验位移测量结果对比

Table
1.
Comparison of displacement measurement results in rescan experiment

table_type2 ">

Method	Number of points (subvolume)	Mean bias error ±SD error/voxels
Method	Number of points (subvolume)	u	v	w
regular DVC	68921	?0.0519 ± 0.0706	?0.3498 ± 0.0642	?0.5477 ± 0.0718
voxel selection DVC	63514	?0.0526 ± 0.0545	?0.3569 ± 0.0464	?0.5498 ± 0.0513

下载:
导出CSV
|显示表格

3.
结论

提出了适用于DVC 的内部散斑质量评价参数?SSSIG, 并通过模拟平移实验验证了SSSIG参数在3种(铜颗粒填充环氧树脂基复合材料、柚子皮多孔材料和多聚物粘结糖)不同类型内部散斑图像中的有效性. 结果表明, 在DVC中, 子体块散斑图像SSSIG参数越大, 测量误差越小; 更进一步, 为了在增大子体块SSSIG参数的同时尽可能的降低计算量, 提出了一种体素点优化选择方法, 该方法通过将子体块中灰度梯度较小的体素点剔除出DVC计算来实现在增大子体块尺寸的同时而不增加计算量, 从而实现高精度、高效率的DVC分析. 3种不同类型材料散斑图像的模拟平移实验和泡沫铜的重扫描实验均验证了体素点优化选择方法在有效降低DVC方法的测量误差同时提高计算效率.