删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

循环神经网络在智能天平研究中的应用

本站小编 Free考研考试/2022-01-01


引 言


随着航空航天技术的不断发展, 高超声速技术受到各个航空航天大国的广泛关注和深入研究, 其科学问题具有重要的战略意义[1]. 对于高超声速飞行器气动外形布局设计和优化问题, 高精度气动力测量试验起到决定性作用. 激波风洞测力试验可以为高温真实气体效应的研究提供可靠的数据, 同时为我国高超声速飞行器研究提供关键技术支撑.

目前, 激波风洞测力试验仍存在许多未解决的关键技术问题, 这些问题导致激波风洞测力试验成为一个具有挑战性的研究课题[2-4]. 最重要的问题之一是模型测力系统(force measurement system, FMS)受瞬态流场起动冲击引起的结构惯性振动. 在进行测力试验时, 由模型?天平?支撑构成的测力系统受到瞬时冲击而产生结构振动, 这些振动信号在短时间内无法快速衰减, 导致测力系统的输出信号中包含惯性振动产生的干扰信号, 严重影响测力试验的精准度[5].

为了解决短试验时间内激波风洞高精度测力问题, 国内外****开展了许多相关研究, 发展了多种类型的脉冲型风洞天平, 如压电天平、加速度计天平、应力波天平、补偿型天平和脉冲型应变天平等. 在上述天平测力技术中, 采用压电陶瓷的压电天平稳定性相对较差, 电荷泄露导致衰减相对较快, 提高测量精度非常困难[6-7]. 加速度计天平[8-11]和应力波天平[12-15]试验装置成本较高且数据处理方法比较复杂. 补偿型天平只能对信号中的主频分量进行补偿, 无法改善非主频分量, 所以其精度有待进一步提高[16]. 应变天平刚度较低, 不能直接应用于激波风洞这类脉冲型设备中. 脉冲型应变天平在应变天平的基础上进行了改善, 提升了天平的刚度, 能够在较短的有效试验时间内获得多个周期的信号, 但仍无法摆脱系统振动带来的干扰[17-19]. 所以, 为了满足高超声速飞行器高精度测力试验的需求, 发展测量精准度更高、频率响应更快、稳定性更强的新型测力系统很有必要, 是研究激波风洞中影响测力结果的关键因素, 其意义非常重大.

作为激波风洞测力试验中的主要测量仪器, 风洞天平的校准技术是测量试验中确保天平性能的关键技术. 一些****将风洞天平的动态校准定义为在静态校准的基础上, 利用飞行器测力标准模型在风洞中校验天平性能[20]. 由于传统风洞试验中涉及到天平的动态性能研究不多, 所以关于激波风洞测力天平动态校准方面的技术研究和工程应用比较少. 目前, 有****提出基于深度学习技术的单矢量动态自校准(single-vector dynamic self-calibration, SVDC)方法并应用于脉冲型风洞测力系统中, 在其动态天平信号样本训练过程中已经成功将卷积神经网络(convolutional neural network, CNN)模型应用于天平测量结果的智能化处理, 得到了较为理想的气动力载荷结果[21]. 基于深度学习技术的风洞天平动态校准技术比较新颖, 目前处于初步研究阶段.

本文在SVDC方法的基础上, 寻求新的有效训练模型, 探索各个模型间的差异, 进一步提高智能型天平的数据处理性能及其应用的可靠性. 在神经网络模型的选取上, 首先利用循环神经网络(recurrent neural network, RNN)对激波风洞中的测力系统进行人工智能建模, 识别并滤除测力系统中的惯性振动干扰信号, 力求输出较为理想的气动载荷信号. 将RNN模型与CNN模型训练的结果进行对比, 为风洞天平的高精度动态校准方法提供可靠的数据支撑.


1.
RNN在天平动态校准中的应用



1.1
单矢量动态校准技术简介


传统的风洞天平一般采用阶跃响应法进行动态校准, 即通过负阶跃载荷单元加载方法对其施加动态激励进行校准. 该方法只能在固定的加载方向上对天平进行动态标定, 每次标定试验时在该方向通过悬挂砝码的方式加载, 待天平结构稳定后, 瞬间卸载产生阶跃载荷, 从而实现对天平施加负阶跃载荷[22-25]. 这种动态标定的方法存在一定的局限性, 对载荷施加方向有严格要求. 为了满足天平在任意方向实时输出多分量载荷信号, 发展了单矢量动态自校准技术[21]. 该技术中“单矢量”并不是指输出的通道为单一方向载荷信号, 而是指在任意单一方向加载, 该单矢量载荷可以沿着天平体轴系自动分解成可实时输出的多分量载荷.

单矢量动态校准技术采用十字架悬挂钢丝的方法激励整个测力系统, 通过在任意方向悬挂钢丝施加单矢量载荷, 剪断钢丝瞬间卸载产生阶跃载荷. 在钢丝弹性极限和悬挂钢丝十字架的范围内, 这种加载方法对载荷的施加大小、方向和作用点均无特殊限制. 单矢量载荷的加载可以实现多分量阶跃载荷同时精确加载, 更符合实际风洞试验中的气动力加载方式, 且精准度更高. 单矢量动态校准详细的实施步骤参见文献[21].


1.2
基于RNN的动态模型训练



1.2.1
RNN模型的构建

对于许多复杂的机器学习问题来说, 特征提取是一件至关重要且非常困难的事情. 传统的机器学习方法采用人工提取特征, 这种方法不仅需要花费大量的时间和精力, 而且无法很好地提取实体中的特征. 深度学习方法很好的解决了这个问题, 通过堆叠多层非线性映射逼近复杂的函数, 自动地从原始数据中学习层次化的特征表示, 并且利用这些组合特征去解决问题. 深度学习最早应用于图像识别, 现在已经推广到机器学习的各个领域, 如语音识别、音频识别、自然语言处理等[26].

针对天平输出信号中的振动干扰信号, 在采集完大量样本数据后, 采用深度学习技术中的神经网络对其进行监督学习, 可以自动提取到振动干扰信号的基本特征, 将这些基本特征自动组合成复杂特征, 从而完成对天平干扰信号的识别.

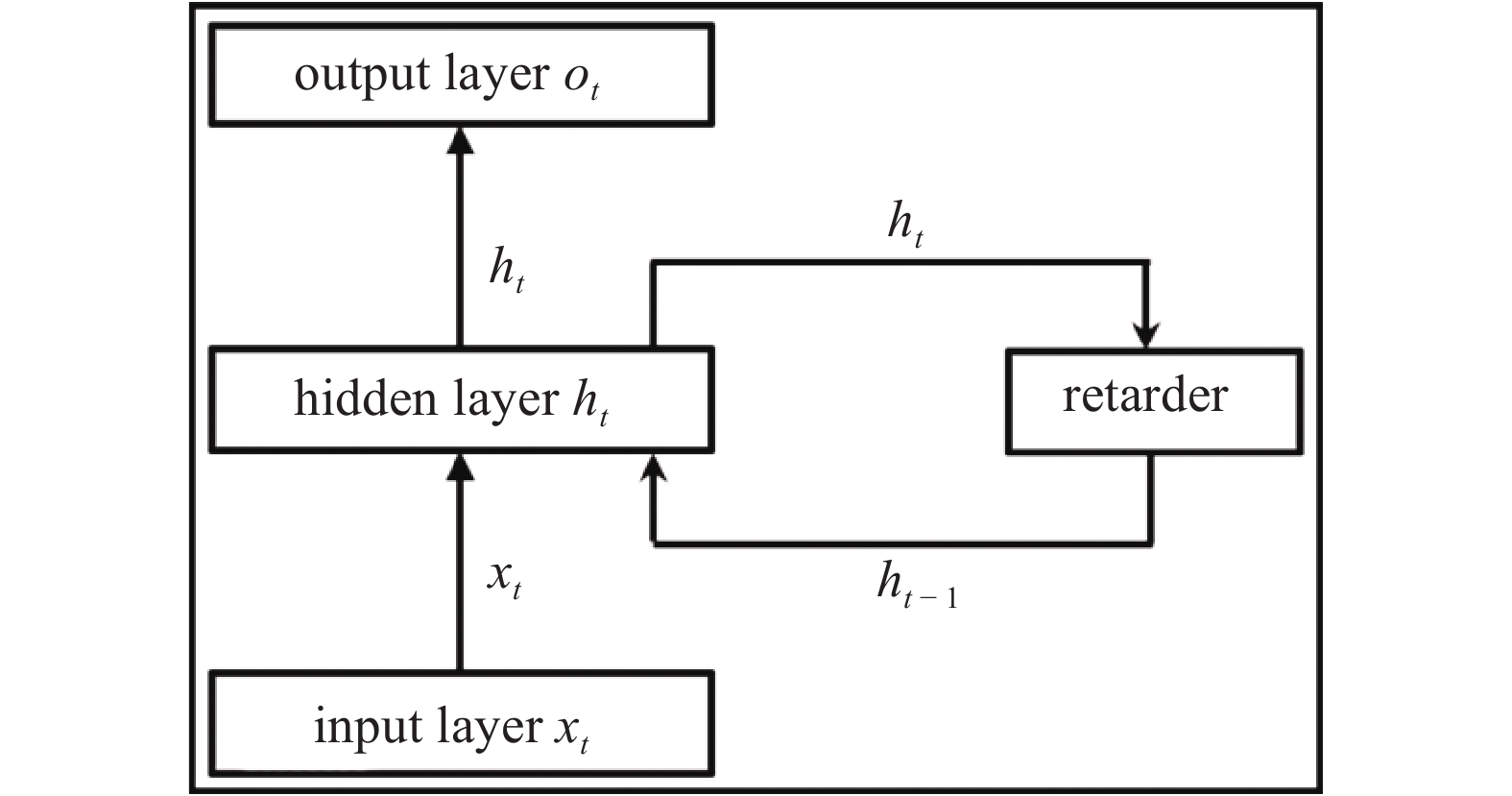
传统的前馈神经网络同层神经元之间没有连接, 无法处理含有时间序列的信息, 因此在许多应用中存在局限性. RNN是深度学习技术中常见的神经网络结构, 其主要解决时序问题, 处理和预测序列数据, 在RNN模型中, 网络具有“记忆”功能, 网络结构每层之间的节点是有连接的, 其中隐藏层(hidden layer)的输入不仅包含输入层(input layer)的输出, 还包含上一时刻隐藏层的输出. 图1展示了RNN的网络结构, 下标$t$和$t - 1$分别表示当前时刻和上一时刻. 从图中可以看出, 对于当前时刻$t$, 隐藏单元${h_t}$共同接受当前输入层数据${x_t}$和前一时刻的隐藏层状态${h_{t - 1}}$来产生输出${o_t}$(output layer). 隐藏层的回路提供了信息传递的通路, 从而实现信息的存储和依赖. RNN由于自身网络结构存在延迟器(retarder)构成回路, 是一种强大的建模序列数据的神经网络, 模型训练通常采用基于时间的反向传播算法(back-propagation through time, BPTT).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
循环神经网络单元结构示意图



Figure
1.
Diagram of RNN unit



下载:
全尺寸图片
幻灯片


由于天平的输出信号本质上是一个时序动态信号, 包括加载前的零值信号和加载后的气动力信号, 根据作用时间可以判断测力系统的受力状态, 而RNN模型擅长解决与时序相关的问题, 故采用RNN模型对天平输出信号进行动态校准训练.

在实际训练过程中, 样本序列过长会导致优化时出现梯度消失和梯度爆炸的问题[27]. 长短时记忆网络(long short-term memory, LSTM)的出现解决了该问题, LSTM在RNN的基础上增加了“门”结构, 并通过一些“门”结构有选择性地影响循环神经网络中每个时刻的状态. 实践证明采用LSTM结构的RNN模型比标准的RNN模型表现更好. 同时, 在标准的RNN模型中, 状态的传输是单向的, 每一层的状态传输都是从前往后单向进行, 然而在实践中, 当前时刻的输出不仅和之前的状态有关, 也和之后的状态有关, 所以需要采用基于LSTM的双向循环神经网络(bidirectional long short-term memory, Bi-LSTM).


1.2.2
样本采集与数据处理

采用RNN训练智能模型前, 需要对拟标定测力系统采集足够的动态信号训练样本. 训练样本信号需要与实际风洞试验中的天平信号具有相同的特征, 需要包含系统振动干扰信号. 基于SVDC技术在风洞外搭建阶跃载荷采集装置, 该装置与激波风洞测力系统相同, 由模型、风洞天平和支撑结构组成, 其中模型采用半锥角为10°、长度为750 mm的标准尖锥测力模型, 天平采用三分量脉冲型应变天平, 三分量依次为法向力Y、俯仰力矩MZ和轴向力X, 支撑采用弯刀支撑结构, 具体结构如图2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
阶跃载荷采集装置[21]



Figure
2.
Step load acquisition device[21]



下载:
全尺寸图片
幻灯片


本文基于已搭建完的阶跃载荷采集装置采集了120组动态载荷信号样本, 用于RNN模型训练. 由于受到阶跃载荷加载装置中钢丝的强度限制, 采集装置的天平输出信号相对于实际风洞试验时的输出信号比较微弱. 为了确保训练样本和风洞试验数据的一致性, 在训练模型时, 统一对天平输出信号进行标准化处理, 将数据按比例缩放, 统一映射到一个小的特定区间内. 数据的标准化便于网络模型的训练, 有利于模型收敛速度和计算精度的提升. 在训练结束后, 为了便于验证计算结果, 再对数据进行逆映射处理.

在标准化处理数据时, 采用线性转化函数将天平的输出信号值映射到[?1, 1]之间, 具体转换函数为







$${x^*} = frac{x}{{max left( {left| x
ight|}
ight)}}$$
(1)

式中$x$是原始数据, $max left( {left| x
ight|}
ight)$是原始数据中绝对值最大的值, ${x^*}$是标准化之后的数据. 逆映射转换函数为







$$x' = max left( {left| x
ight|}
ight){x^*}$$
(2)

式中$x'$是将标准化后的数据逆映射得到的原始数据.

因此, 本文的基本思路就是将带有惯性振动干扰的动态信号作为输入样本, 理想阶跃载荷作为目标输出样本, 通过构建LSTM和Bi-LSTM模型训练样本, 对样本中的干扰信号进行学习, 识别并滤掉干扰信号, 从而输出理想的气动力载荷信号. 然后将训练后的模型应用于激波风洞测力试验中, 得到低惯性干扰或无惯性干扰的气动力信号, 进而确保测力结果的准确性.


2.
RNN动态校准模型的训练结果及分析



2.1
模型训练结果验证


在RNN训练模型应用于激波风洞测力试验之前, 需要对智能模型进行测试, 验证模型的可靠性. 在训练模型前需要先打乱样本顺序, 然后划分为若干批, 每一批包含部分样本, 因为随机打乱后的样本比排序后的样本更接近真实的概率分布. 将采集的120组动态载荷信号样本打乱顺序后用于RNN模型训练, 其中80%的样本作为训练集用来训练模型和学习网络参数, 20%的样本作为验证集进行验证校准测试. 将采集到的阶跃载荷样本作为输入, 其对应的理想阶跃载荷作为目标输出. 选取其中任意一个样本, 将其轴向力通道载荷绘制成图3所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
阶跃载荷信号



Figure
3.
Step load signal



下载:
全尺寸图片
幻灯片


图3中虚线表示采集到的阶跃载荷(输入样本), 实线表示期望输出的理想阶跃载荷(目标样本). 该样本的采样时间为150 ms, 理想阶跃载荷前50 ms内轴向力在0 N附近小幅波动, 在第50 ms时发生阶跃, 边沿触发时间可以忽略不计, 轴向力由0 N突变为4.7 N左右, 在后100 ms内保持4.7 N不变.

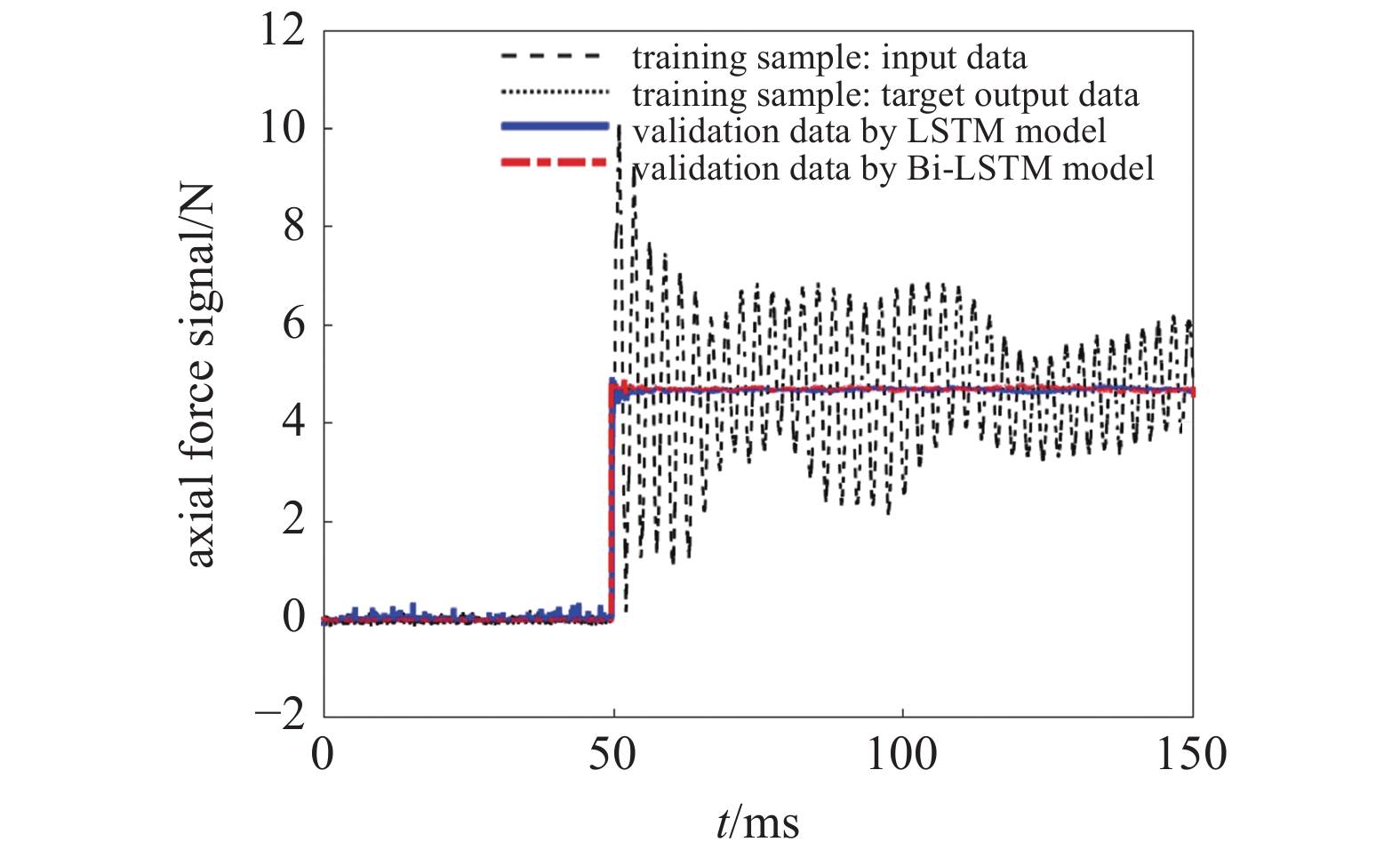
采用LSTM和Bi-LSTM模型训练采集到的动态载荷信号, 将输入的训练样本信号与经过网络训练后的3个通道的信号结果进行对比. 图4展示的是轴向力通道输入信号与经过LSTM和Bi-LSTM模型训练后的信号的对比结果. 图中虚线代表未经网络模型处理的输入信号, 实线和点划线分别表示经过LSTM和Bi-LSTM模型处理后得到的输出信号, 点线表示期望输出的理想阶跃载荷信号.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
轴向力通道输入信号与经过网络模型处理后信号的对比



Figure
4.
Comparison of the input signal and validation data by training model (axial force)



下载:
全尺寸图片
幻灯片


由图4可以看出, 经过网络模型处理后的信号曲线与期望输出的理想阶跃载荷信号曲线基本贴合在一起, 在前50 ms内, LSTM和Bi-LSTM模型的处理结果均比较理想, 将输入样本中的干扰信号基本除掉了. 在第50 ms时, 载荷产生突变. 在后续100 ms内, 处理后的输出信号基本保持为一个固定值, 达到理想阶跃载荷的稳定状态. 所以经过循环神经网络模型训练后的信号基本滤掉了大部分干扰信号, 整体上满足了理想阶跃载荷的要求.

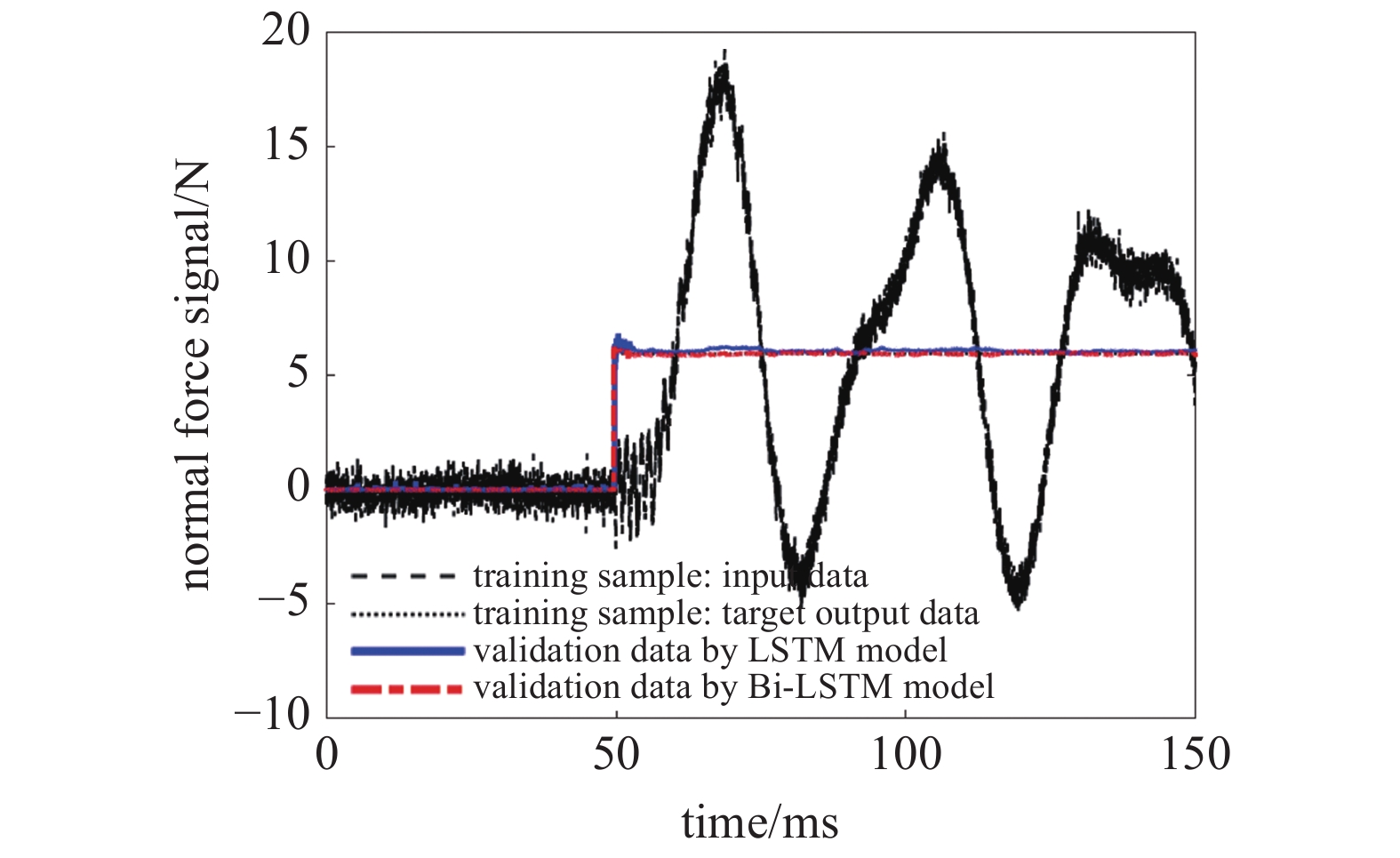
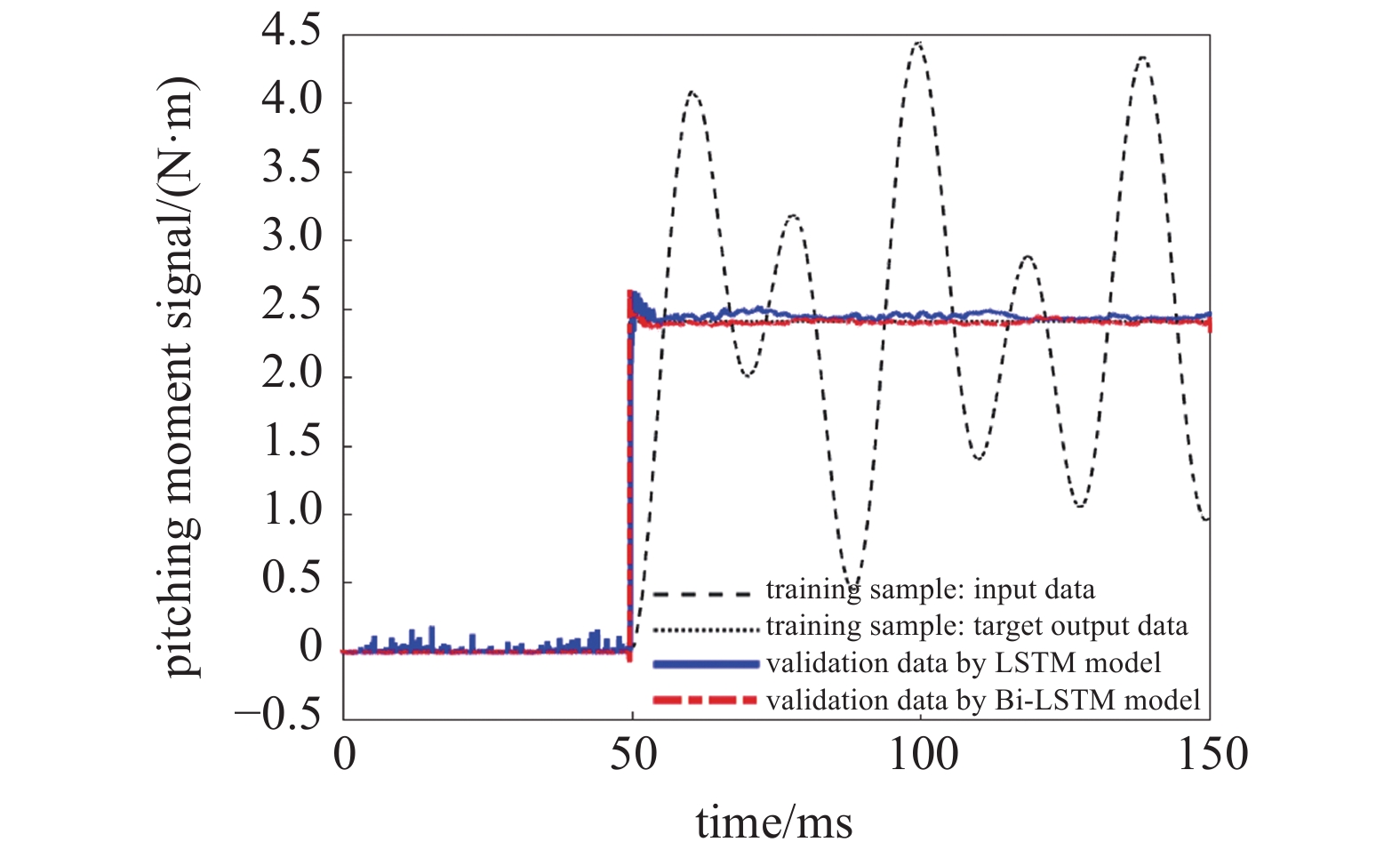
按照同样的方式对天平法向力和俯仰力矩通道的样本进行处理, 将处理后的结果整理成图5和图6所示. 由图5和图6可知, 经过LSTM和Bi-LSTM模型处理过后的信号符合理想阶跃载荷的初始状态和稳定状态, 而且边沿时间足够短.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
法向力通道输入信号与经过网络模型处理后信号的对比



Figure
5.
Comparison of the input signal and validation data by training model (normal force)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
俯仰力矩通道输入信号与经过网络模型处理后信号的对比



Figure
6.
Comparison of the input signal and validation data by training model (pitching moment)



下载:
全尺寸图片
幻灯片


经过LSTM和Bi-LSTM模型训练后的结果比较理想, 滤掉了大部分振动信号, 符合理想阶跃载荷的要求, 达到了预期目标. 但是相比于LSTM模型, Bi-LSTM模型的训练结果更好, 尤其是在初始状态和边沿处, LSTM模型处理的结果仍然存在一些干扰信号, Bi-LSTM模型处理的结果更稳定, 更理想.


2.2
训练结果误差分析


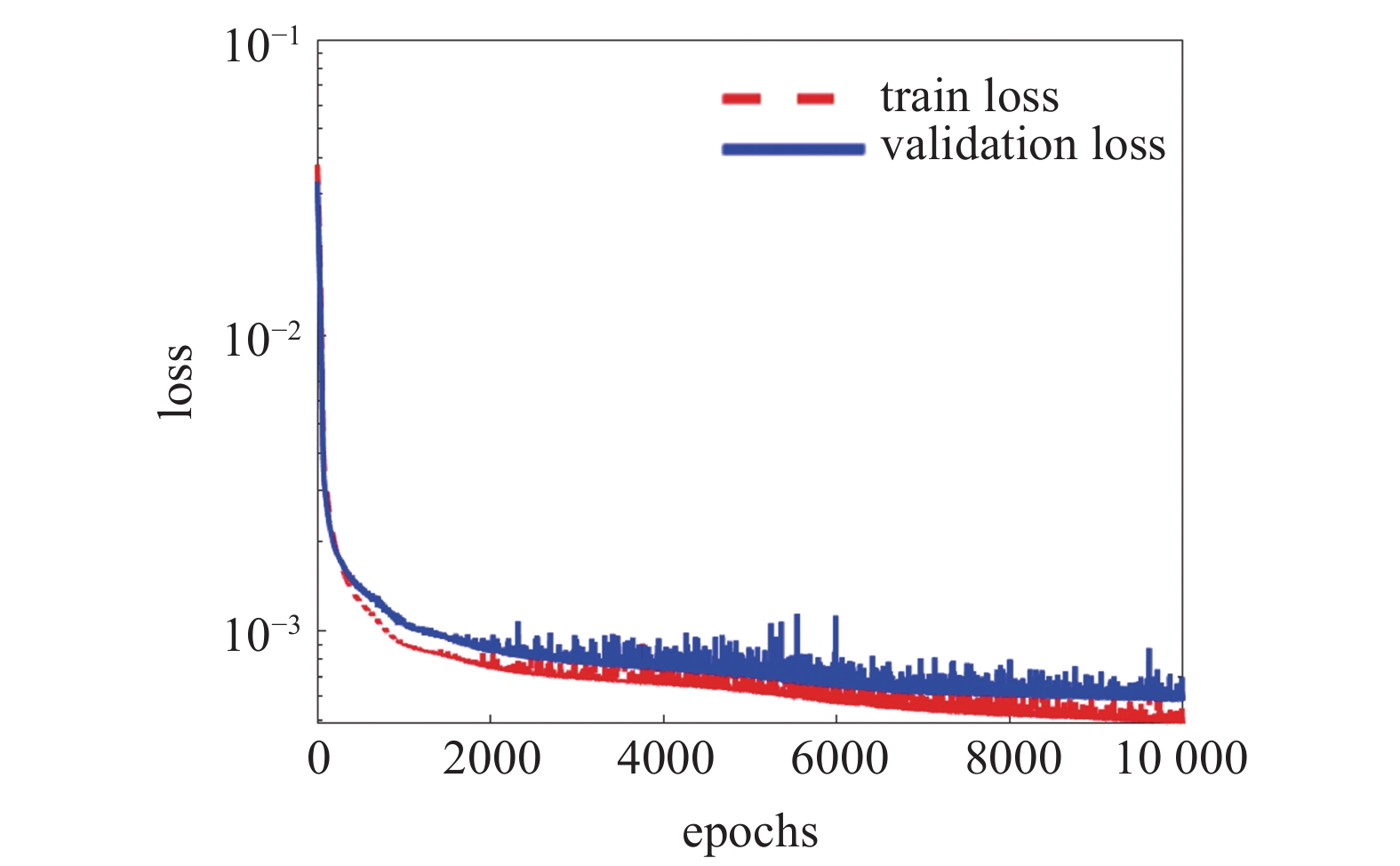
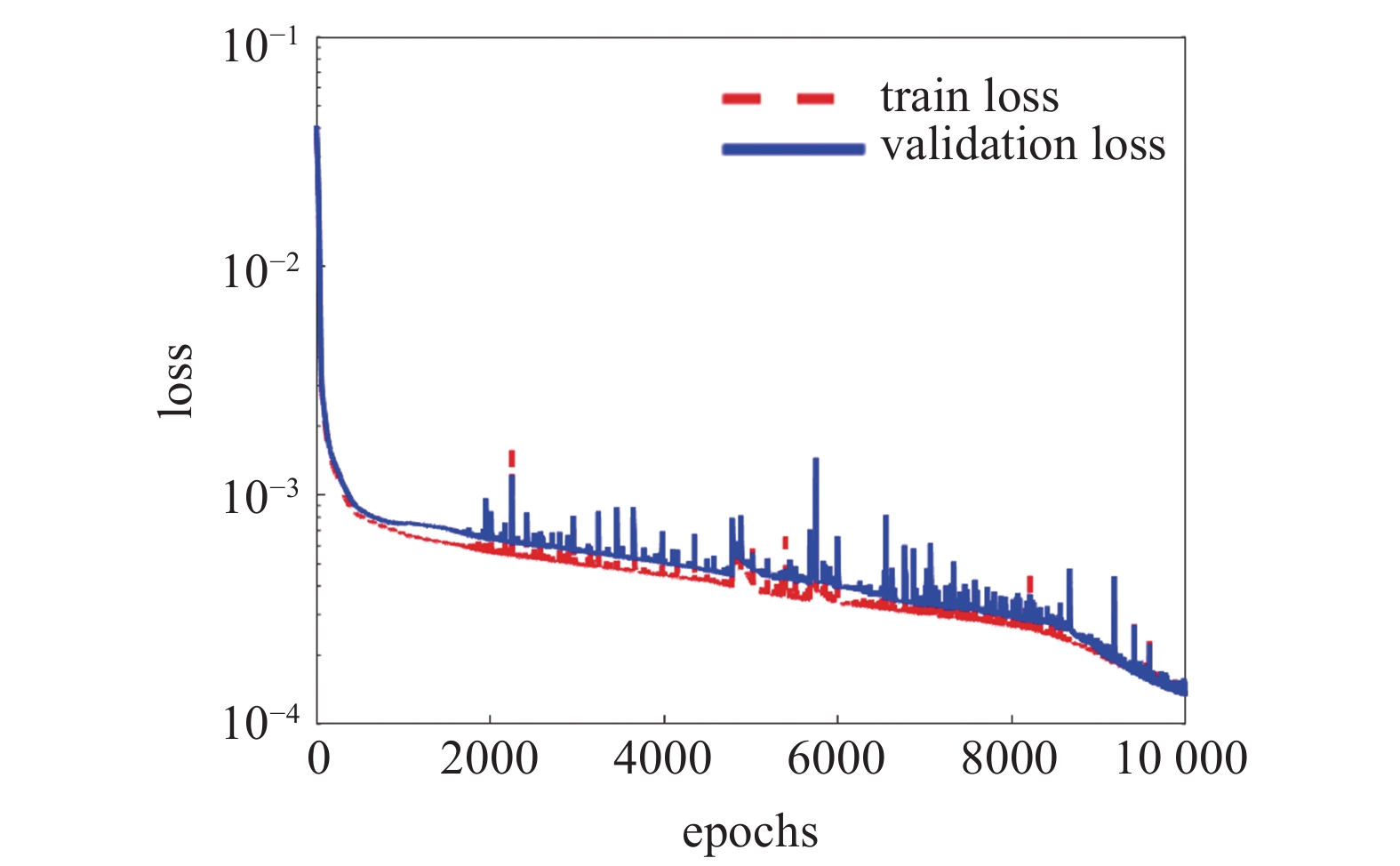
在RNN模型训练过程中, 通过最小化损失函数(loss)使模型达到收敛状态. 本研究采用均方误差指标(mean squared error, MSE)作为损失函数来评估模型的数据处理能力. MSE指的是模型每一次输出结果与模型输出期望之间的误差, MSE的值越小, 说明预测模型试验数据的精确度越高. 将LSTM和Bi-LSTM模型的loss值随训练轮数(epochs)的变化情况绘制成图7和图8所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
LSTM模型loss值随训练轮数的变化



Figure
7.
Loss changes with epochs in LSTM model



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
Bi-LSTM模型loss值随训练轮数的变化



Figure
8.
Loss changes with epochs in Bi-LSTM model



下载:
全尺寸图片
幻灯片


图7和图8中虚线和实线分别代表模型训练过程中的训练误差和验证误差. 模型的初始loss值在10?2量级, 随着训练轮数的增加, 模型的loss值逐渐减小并趋于稳定. 当训练轮数达到10000次时, LSTM模型的验证误差值降到5.8 × 10?4, Bi-LSTM模型的验证误差值降到1.3 × 10?4. 此时认为模型的误差足够小, 已经达到有效动态校准的标准, 从而验证了循环神经网络模型处理数据方法的可行性. 根据模型训练的loss数据, 发现Bi-LSTM模型比LSTM模型训练效果更理想.

同时, 为了评估训练结果的好坏, 可以采用相对误差$delta $对训练结果进行比较验证. 选取阶跃载荷卸载后的数据进行分析, 考虑到与激波风洞试验实际有效时间相对应, 对图4 ~ 图6中经过模型处理后的信号进行处理, 截取时间区间为70 ~ 110 ms内的数据平均化处理得到近似值${bar F^*}$和真实值$bar F$, 其中$bar F_{
m{L}}^*$和$bar F_{
m{B}}^*$分别代表LSTM和Bi-LSTM模型训练得到的近似值, 根据相对误差的定义式(3)计算得到相对误差$delta $, ${delta _{
m{L}}}$和${delta _{
m{B}}}$分别表示LSTM和Bi-LSTM模型训练得到的相对误差, 将计算结果整理成表1所示







$$delta {
m{ = }}frac{{{{bar F}^*} - bar F}}{{bar F}} times 100{text{%}}$$
(3)

表1的数据是LSTM和Bi-LSTM模型经过训练后的输出信号与理想输出信号之间的相对误差值, 两个模型训练的相对误差值均比较小, LSTM和Bi-LSTM模型的相对误差${delta _{
m{L}}} $和${delta _{
m{B}}} $分别在3%和0.3%以内, 与文献[21]中采用CNN模型训练得到结果的相对误差(1%以内)相当, 精准度均比较高, 且轴向力信号的相对误差明显小于其他两个载荷分量的误差. 原因是在采集训练样本过程中, 轴向力的值比较大, 占主导地位, 其他两个分量的值比较小, 受到外界环境噪声的干扰比较大, 所以轴向力的结果相应比较理想. 同时, 根据表1中${delta _{
m{L}}}$和${delta _{
m{B}}}$的数据, 发现在输入样本训练过程中, Bi-LSTM模型的训练效果较LSTM模型的训练效果更精确.




表
1
LSTM和Bi-LSTM模型的相对误差



Table
1.
Relative error of LSTM and Bi-LSTM model



table_type2 ">
Components$bar F$$bar F_{
m{L}}^*$		$bar F_{
m{B}}^*$		${delta _{
m{L}}}$		${delta _{
m{B}}}$
normal force/N5.9436.0815.9472.32%0.07%
pitching moment/(N·m)2.4092.4502.4031.70%?0.25%
axial force/N4.6994.6834.6997?0.34%0.01%





下载:
导出CSV
|显示表格



3.
脉冲风洞瞬态测力试验数据的智能化处理



3.1
RNN模型应用于激波风洞测力系统


经过对LSTM和Bi-LSTM模型训练结果的验证分析, 发现模型对输入样本中惯性振动干扰信号的处理非常理想, 因此尝试将该模型应用于激波风洞试验智能天平的动态校准研究中. 自中国科学院力学研究所成功研制复现高超声速飞行条件激波风洞(简称“JF-12复现风洞”)以来, 在该风洞中完成了大量的高超声速飞行器气动力测量试验, 并获得了大量高精度的可靠测力数据[28]. JF-12复现风洞采用反向爆轰驱动技术[29], 同时集成应用一系列的延长试验时间的创新技术[30-32], 拥有复现25 ~ 50 km飞行高度, 马赫数5 ~ 9的纯净空气气流能力, 有效试验时间超过了100 ms. 本研究利用LSTM和Bi-LSTM模型对在JF-12复现风洞中进行的750 mm标准尖锥模型测力试验中的三分量天平输出信号进行处理, 将轴向力通道的处理结果展示在图9中.

图9中虚线代表风洞试验中天平输出的原始信号, 实线和点划线分别代表经过LSTM和Bi-LSTM模型处理后的输出信号, 可以发现处理后的信号基本滤掉了大部分振动干扰信号, 但是仍然表现出一定的周期性. 在模型训练过程中, 由于输入样本与风洞试验测力信号存在一定的区别, 而且风洞试验中的真实气动力信号并不完全是理想的阶跃载荷信号, 所以处理过后的信号与理想阶跃载荷信号仍存在一定的偏差. 在下一步模型训练中, 可以考虑增加训练样本数目, 同时在采集样本的过程, 适当消除环境噪声的干扰, 最大程度的保证采集样本与风洞试验测力信号的一致性, 从而提升模型处理样本的能力, 获得更高精度的结果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
轴向力通道风洞试验信号与模型处理的信号



Figure
9.
Wind tunnel test signal and model processed signal (axial force)



下载:
全尺寸图片
幻灯片


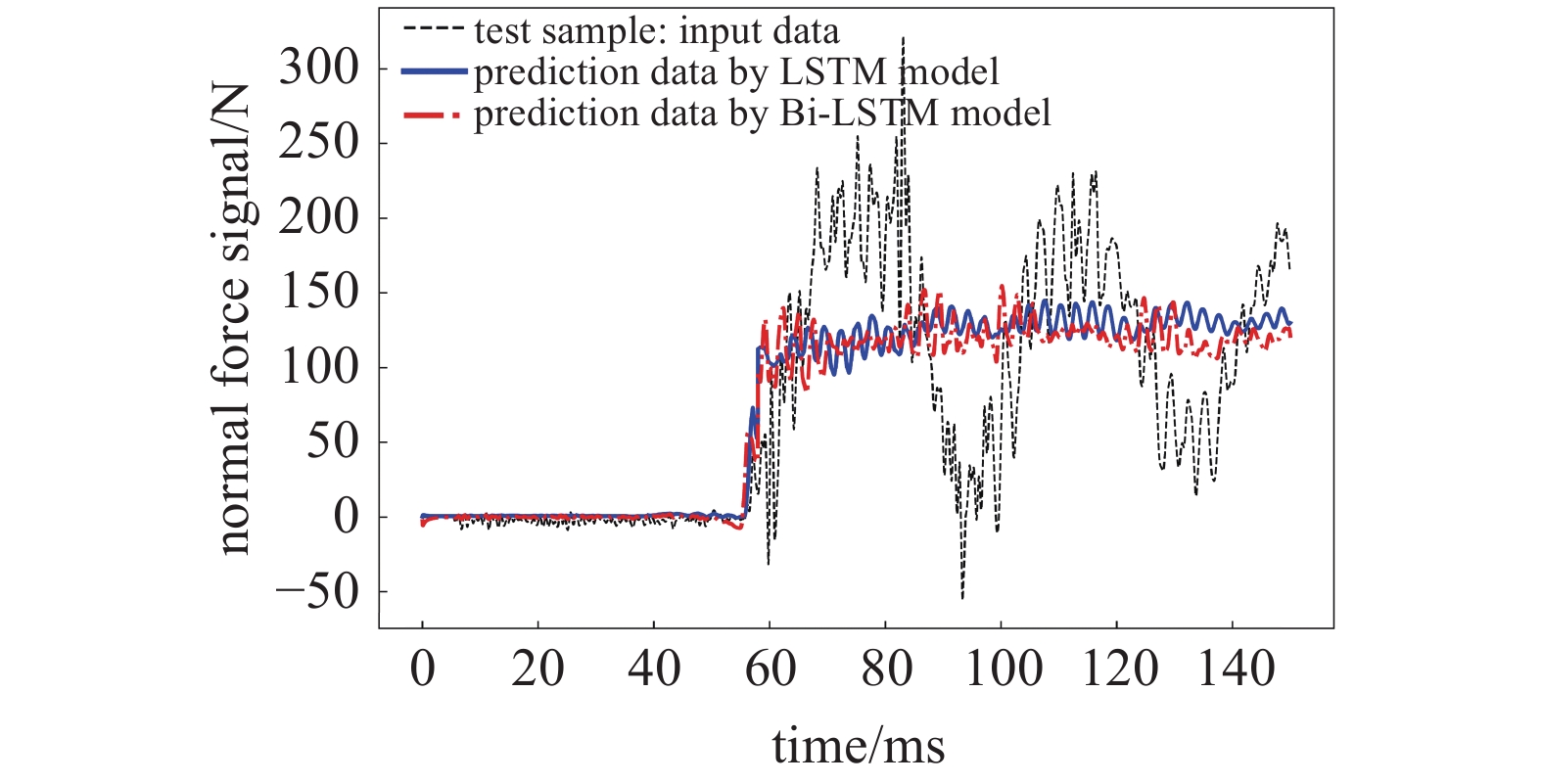
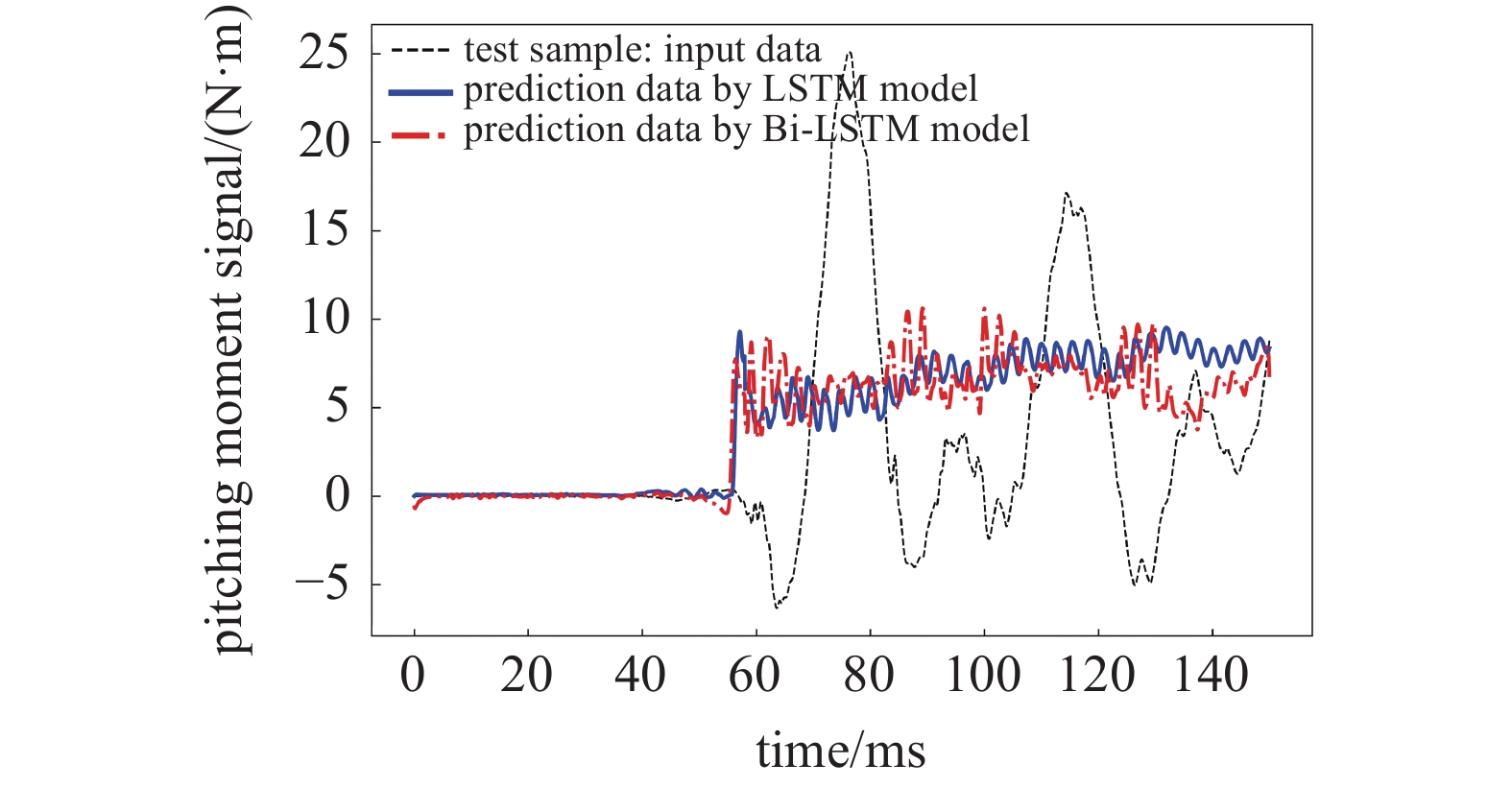
按照同样的方式将法向力通道和俯仰力矩通道的处理结果整理成图10和图11所示. 经过LSTM和Bi-LSTM模型处理后的结果与风洞试验信号存在明显的区别, 基本将风洞试验信号中的振动干扰信号去除掉, 达到了预期目标.


3.2
RNN与CNN训练结果对比


对风洞试验测力信号进行误差分析, 将经过RNN模型处理后的结果与文献[21]中经过CNN模型处理后的结果进行对比, 对图9 ~ 图11中经过模型处理后的信号进行处理, 截取时间为70 ~ 110 ms内的数据进行平均化处理, 将结果整理至表2中, ${delta _{
m{L}}}$和${delta _{
m{B}}}$分别表示风洞试验信号经过LSTM和Bi-LSTM模型训练后得到的相对误差. 对比发现LSTM与CNN模型的误差在4%以内, Bi-LSTM与CNN模型的误差在2%以内, 表明基于RNN和CNN模型的智能校准方法均具有较高的可靠性. 此外, CNN模型常用于图像识别, 处理空间信息, RNN模型通过挖掘数据中的时序信息, 更适合处理解决时序问题, 两种神经网络模型在脉冲风洞瞬态测力试验中均具有应用前景.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
法向力通道风洞试验信号与模型处理的信号



Figure
10.
Wind tunnel test signal and model processed signal (normal force)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-168-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
俯仰力矩通道风洞试验信号与模型处理的信号



Figure
11.
Wind tunnel test signal and model processed signal (pitching moment)



下载:
全尺寸图片
幻灯片





表
2
RNN与CNN模型处理数据的相对误差



Table
2.
The relative errors of RNN and CNN models in processing data



table_type2 ">
CoefficientsCNNLSTMBi-LSTM${delta _{
m{L}}}$		${delta _{
m{B}}}$
normal force0.1550.1600.1573.23%1.27%
pitching moment0.1070.1030.109?3.74%1.87%
axial force0.1080.1110.1062.78%?1.85%





下载:
导出CSV
|显示表格



由于训练样本信号与风洞试验信号存在一定的差别, 真实气动力信号较理想阶跃载荷信号更为复杂, 因此尽管采用LSTM型和Bi-LSTM模型训练的采集样本验证结果十分理想, 但是将模型应用于风洞试验测力信号中仍存在一些偏差. 就目前基于RNN模型的激波风洞智能天平研究结果而言, 该智能动态校准方法在激波风洞测力试验中具有应用价值, 采用该技术方法处理的测力结果的精准度具有较大提升空间.


4.
结 论


为了在激波风洞短试验时间内开展高超声速飞行器模型的精确气动力测量, 本文在单矢量动态自校准技术的基础上, 在动态信号训练过程中采用了RNN对激波风洞测力系统振动特性进行了高效建模, 智能模型有效地去除了动态测力信号中的惯性干扰信号, 输出了“定常”的气动力载荷信号. 对采用RNN模型的动态校准方法进行了误差分析, 并将该方法与基于CNN模型动态校准方法进行了对比, 验证了该方法的可靠性. 将RNN模型动态校准方法应用于激波风洞测力系统中, 基本消除了天平输出信号中的大幅振动干扰信号, 取得了较为理想的效果.

目前, 基于人工智能技术的测力天平智能化研究比较新颖, 相关方法和技术在具有可行性和可靠性基础上有待进一步发展和完善. 本研究进一步验证了该方法的实用性, 证明该方法在激波风洞测力试验中具有应用前景, 其将为我国高超声速飞行器高焓气动特性精确评估提供关键技术支撑.

相关话题/信号 数据 干扰 技术 网络
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 激波/湍流边界层干扰压力脉动特性数值研究
    引言激波与湍流边界层的相互作用问题广泛存在于各类高速飞行器中.已有研究表明[1-2],在强激波作用下,干扰区内压力脉动峰值急剧升高,分离激波的非定常运动导致物面脉动压力低频能量的急剧增强,这将使得飞行器结构出现振动疲劳问题,进而严重影响飞行安全.因此,深入研究激波/湍流边界层干扰区内压力脉动特性对认 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于神经网络的差分方程快速求解方法
    引言近年来,人工神经网络(artificial?neural?networks,ANN),尤其是深度神经网络(deep?neural?networks,DNN)因其在处理和预测高维复杂系统方面的优异能力而被广泛应用于自然语言处理[1]、计算机视觉[2]与图像处理[3]等领域.此外,深度神经网络凭借其 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 数字化光处理立体成型技术中吸附力的影响机制
    引言增材制造是一项具有革命意义的新兴制造技术,被誉为决定未来经济的十二大颠覆技术之一[1],在工业界与学术界有广泛的应用前景,如生物医疗[2-5]、航天航空[6-7]、机器人技术[8-9]、智能传感器[10-11]、结构设计[12-13]以及微流控芯片[14-15]等.数字化光处理(digitall ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工神经网络的声子晶体逆向设计
    引言声子晶体是一种新型人工周期性复合材料,具有独特的禁带特性,即声波或弹性波在声子晶体中传播时,由于受到周期性结构中波的散射或局部共振的作用,在某些频段范围即带隙内无法传播[1-4].该特性使得声子晶体在工程减振降噪领域具有巨大的应用潜力.声子晶体的拓扑结构和组分材料的属性决定了其带隙特性.因此,根 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于LSTM模型的飞行器智能制导技术研究
    引言高升阻比飞行器具有飞行速度快、升阻比高、航程远、机动突防能力强等特点,在军事和民用领域发挥着重要的作用.高升阻比飞行器再入制导技术是通过设计制导律,在动力学方程、过程约束、控制量约束等条件下,使得飞行器在中末交班点满足再入终端约束.因临近空间环境的复杂性和不确定性,飞行器再入制导技术已成为航空航 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于数据驱动的流场控制方程的稀疏识别1)
    江昊,王伯福,卢志明,2)上海大学,力学与工程科学学院,上海市应用数学和力学研究所,上海200072DATA-DRIVENSPARSEIDENTIFICATIONOFGOVERNINGEQUATIONSFORFLUIDDYNAMICS1)JiangHao,WangBofu,LuZhiming,2)S ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于组合神经网络的雷诺平均湍流模型 多次修正方法1)
    张珍*,&,叶舒然*,&,岳杰顺*,&,王一伟,*,&,2),黄晨光*,&,***中国科学院力学研究所流固耦合系统力学重点实验室,北京100190&中国科学院大学工程科学学院,北京100049**中国科学 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑颗粒转矩的接触网络诱发各向异性分析1)
    王怡舒*,沈超敏*,刘斯宏,*,2),陈静涛&*河海大学水利水电学院,南京210098&中国建筑第二工程局有限公司,上海200135SHEAR-INDUCEDANISOTROPYANALYSISOFCONTACTNETWORKSINCORPORATINGPARTICL ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 水下发射水动力的多尺度预测网络研究1)
    岳杰顺*,权晓波?,叶舒然*,王静竹*,王一伟,*,2)*中国科学院力学研究所流固耦合系统力学重点实验室,北京100190?北京宇航系统工程研究所,北京100076AMULTI-SCALENETWORKFORTHEPREDICTIONOFHYDRODYNAMICSINUNDERWATERLAUNCH ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于卷积神经网络的涵洞式直立堤波浪透射预测1)
    赵西增*,徐天宇*,谢玉林*,吕超凡*,姚炎明,*,2),解静?,常江***浙江大学海洋学院,浙江舟山316021?交通运输部天津水运工程科学研究所,天津300456**天津水运工程勘察设计院,天津市水运工程测绘技术重点实验室,天津300456PREDICTIONOFWAVETRANSMISSION ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.