引 言

高升阻比飞行器具有飞行速度快、升阻比高、航程远、机动突防能力强等特点, 在军事和民用领域发挥着重要的作用. 高升阻比飞行器再入制导技术是通过设计制导律, 在动力学方程、过程约束、控制量约束等条件下, 使得飞行器在中末交班点满足再入终端约束. 因临近空间环境的复杂性和不确定性, 飞行器再入制导技术已成为航空航天领域研究的热点之一^[1].

高升阻比飞行器再入制导方法主要分为两种: 基于标称轨迹的制导方法和预测校正制导^[2-3]. 基于标称轨迹的制导方法离线设计标称轨迹, 在飞行过程中跟踪标称轨迹进行制导. 离线设计的标称轨迹可以是阻力加速度?速度剖面、高度?速度剖面等. 由于标称轨迹是离线设计所得, 因而该方法对复杂环境的适应性和鲁棒性方面存在明显的不足. 预测校正制导方法基于当前飞行状态, 对动力学方程进行积分预测飞行器的终端状态, 并基于终端状态与目标点的偏差来校正制导指令, 从而实现对飞行器的精确制导. 相比于基于标称轨迹跟踪的制导方法, 预测校正制导具有更强的自主性和对复杂环境的适应能力.

近年来, 人工智能(artificial intelligence)技术的突破性发展为飞行器再入制导技术的研究提供了新的技术途径, 已成为学术界和工业界的研究热点. 人工智能的核心目标是让机器在复杂、不确定、多变化场景下具备类似于人类的感知、决策和行动等能力. 机器学习(machine learning)技术是支撑人工智能发展的核心技术, 机器学习主要包括监督学习(supervised learning)、无监督学习(unsupervised learning)和强化学习(reinforcement learning). 尤其是以深度学习^[4]和强化学习^[5]为代表的智能技术, 包括经典的深度学习模型如AlexNet^[6], VGG^[7], ResNet^[8], SSD^[9], YOLO v4^[10]等, 以及经典的强化学习算法如DQN^[11], DDPG^[12], PPO^[13], SAC^[14]等, 其具备网络映射能力强、学习速率快、在与环境交互“试错”中学习等能力, 已经广泛应用于目标检测与识别、自然语言处理、文本处理、智能机器人等领域, 其表现出的卓越性能已经超出人类的想象.

基于人工智能的飞行器制导控制技术研究尚处于起步阶段. 程林等^[15]综述了深度学习在飞行器动力学与控制中的应用, 从3个方面总结了深度学习在飞行器动力学与控制中的应用, 包括: 在动力学建模中应用深度学习来提升模型计算效率和建模精度、求解模型反问题; 在最优控制中应用深度学习来提升轨迹规划速度、最优控制实时性和自主性; 在飞行器任务设计中应用深度学习来提升任务优化的计算效率和决策水平. 在制导律设计方面, 文献[16-18]将深度学习技术应用于飞行器制导和在线轨迹优化问题, 基于大量的飞行轨迹训练神经网络模型, 从而实现飞行器实时状态到制导指令的快速映射; 文献[19-24]研究了基于Q-Learning、PPO等强化学习算法的智能制导律, 该方法消除了传统制导律对飞行器附加的一些不必要约束, 通过飞行器与环境的大量交互和试错, 并基于奖励信息来学习制导律, 使得飞行器初步具备了自主决策能力. 在姿态控制方面, 文献[25-26]在传统PID控制的基础上, 进一步利用强化学习技术实现对飞行器六自由度的稳定控制, 并验证了该方法在控制精度和实时性方面的优势. 在飞行器协同制导与轨迹规划方面, 方科等^[27]开展了高升阻比飞行器时间协同再入制导研究, 将协同再入制导结构分为两层, 其中底层提出了基于神经网络的时间可控再入制导律, 以再入飞行时间的可知性与可控性为实现目标; 上层根据不同再入阶段特点设计相应的协调函数, 生成时间协调信息. 周宏宇等^[28]提出了一种改进粒子群优化(PSO)算法的飞行器协同轨迹规划, 并借助强化学习方法构建协同需求与惯性权重间的动态映射网络, 提高在线轨迹规划效率.

本文首先针对预测校正制导算法进行深入地分析, 其存在两方面的不足, 一是由于对预测校正制导的实时性要求很高, 因此在纵向制导中每隔固定的周期(一般为50 s, 20 s等量级)预测飞行器的待飞射程并校正一次倾侧角的幅值, 而在横向制导中, 需要时刻(一般每隔0.1 s)判断横程误差或航向角与视线角的误差是否超出走廊边界. 因而, 对于倾侧角这一控制量来说, 存在两个制导周期, 其幅值的制导周期是其符号制导周期的上百倍, 存在明显的不匹配. 二是, 预测校正制导需分别在纵向和横向制导中对动力学方程进行两次积分, 纵向制导中的积分预测飞行器的待飞射程, 横向制导中的积分确定飞行状态, 进而确定倾侧角的符号, 两次积分过程存在明显的冗余计算, 所需要的制导指令解算时间较长.

针对上述预测校正制导中存在的不足, 本文提出基于长短期记忆网络(long short-term memory, LSTM)^[29]模型的飞行器再入制导, 其核心思想: 一是不再通过对动力学方程进行积分来预测飞行器的待飞射程和基于割线法校正倾侧角的幅值; 二是将预测校正中“纵向制导确定倾侧角的幅值”和“横向制导确定倾侧角的符号反转”两个过程相融合, 即去除“预测”环节、“校正”环节. 利用深度学习在神经网络映射能力和实时性方面的天然优势, 基于飞行器再入段的实时状态信息, 采用LSTM模型实时生成倾侧角, 包括其幅值和符号. 倾侧角的制导将只有一个周期, 从而进一步确保制导系统满足在线制导实时性的要求. 选取LSTM模型的根本原因在于飞行器的倾侧角决策过程是一个典型的序贯决策过程. 这是因为在传统的预测校正制导中每一时刻的倾侧角符号不仅取决于当前时刻的状态, 还与上一时刻的倾侧角符号以及上一时刻航向角误差与走廊的关系有关. 因而, 飞行器倾侧角的确定不仅需要基于当前时刻的状态信息还需要历史时刻的状态信息. 从智能决策的角度来说, 在决策倾侧角时需考虑飞行器在相邻时刻的状态关系, 而LSTM是解决序贯决策问题的经典模型.

本文围绕基于LSTM模型的飞行器再入制导开展研究, 首先在第1章描述了飞行器再入制导问题, 包括再入飞行器运动模型以及再入制导的约束; 第2章研究了预测校正制导, 包括倾侧角幅值的求解、倾侧角幅值的约束以及倾侧角符号的设计; 第3章深入研究基于LSTM模型的再入飞行器制导律设计, 详细描述了模型的架构和设计; 在第4章的仿真中, 给出了LSTM模型的训练、测试、蒙特·卡罗仿真分析和实时性分析.

1.
飞行器再入制导问题

1.1
再入飞行器运动模型

再入飞行器三自由度动力学方程如下

$$left. begin{array}{l}dfrac{{{ m{d}}r}}{{{ m{d}}t}} = Vsin gamma dfrac{{{ m{d}}theta }}{{{ m{d}}t}} = dfrac{{Vcos gamma sin psi }}{{rcos phi }}dfrac{{{ m{d}}phi }}{{{ m{d}}t}} = dfrac{{Vcos gamma cos psi }}{r}dfrac{{{ m{d}}V}}{{{ m{d}}t}} = - dfrac{D}{m} - gsin gamma dfrac{{{ m{d}}gamma }}{{{ m{d}}t}} = dfrac{1}{V}left[ {dfrac{{Lcos sigma }}{m} - left( {g - dfrac{{{V^2}}}{r}} ight)cos gamma } ight]dfrac{{{ m{d}}psi }}{{{ m{d}}t}} = dfrac{1}{V}left( {dfrac{{Lsin sigma }}{{mcos gamma }} + dfrac{{{V^2}}}{r}cos gamma sin psi tan phi } ight)end{array} ight}$$

(1)

其中, $r$为地心距, $theta $和$phi $分别表示飞行器的经纬度, $V$为飞行速度, $gamma $和$psi $分别表示飞行器的航迹角和航向角, $sigma $表示倾侧角, $m$为飞行器的质量, $g$为重力加速度, $L$和$D$分别表示飞行器受到的升力和阻力. 升力$L$和阻力$D$的计算公式为

$$left. begin{gathered} L = {C_{ m{L}}}frac{1}{2} ho {V^2}S D = {C_{ m{D}}}frac{1}{2} ho {V^2}S end{gathered} ight}$$

(2)

式中, $
ho = {
ho _0}{{
m{e}}^{ - beta H}}$为飞行器所在高度的大气密度, $;{
ho _0}$为海平面大气密度, $;beta = {1/{{H_{{
m{MCP}}}}}}$, ${H_{{
m{MCP}}}} = 7.11;{
m{km}}$为基准高度; $S$为特征面积; ${C_{
m{L}}}$和${C_{
m{D}}}$分别为升力系数和阻力系数, 一般为飞行器攻角$alpha $和速度$V$的函数, 具体视不同的飞行器而定. 再入飞行器的状态量${pmb{s}} = $$ {left[ {r,theta ,phi ,V,gamma ,psi }
ight]^{
m{T}}}$, 控制量 ${pmb{u}} = {left[ {alpha ,sigma }
ight]^{
m{T}}}$.

1.2
再入制导约束

为了保证再入飞行器成功地完成飞行任务, 飞行器需满足各种条件约束, 其中核心的约束条件包括再入过程约束、终端约束和倾侧角控制约束.

1.2.1
硬约束

飞行器再入过程中高超声速气流会产生严重的气动热, 尤其是飞行器的驻点区域. 为保证飞行器各个部件正常运行, 再入段制导必须考虑驻点区的热流率约束. 其次, 飞行器机身和机翼结构强度的上限以及气动舵面铰支链的承受能力, 决定了再入飞行过程中的最大允许过载和动压. 热流率约束、过载约束和动压约束是飞行器再入飞行中必须要满足的“硬约束”条件. 其表达式为

$$left. {begin{array}{*{20}{l}}{dot Q{ m{ = }}{k_Q}{ ho ^{0.5}}{V^{3.15}} leqslant {{dot Q}_{max }}}{n = sqrt {{L^2} + {D^2}} /m{g_0} leqslant {n_{max }}}{q = dfrac{1}{2} ho {V^2} leqslant {q_{max }}}end{array}} ight}$$

(3)

式中, $dot Q$表示驻点处热流率, ${k_Q}$为热流率模型系数, 与飞行器头部半径及防热材料有关, ${dot Q_{max }}$表示驻点处最大允许热流率; $n$表示飞行器的过载, ${g_0}$为海平面地球引力加速度, ${n_{max }}$为最大允许过载; $q$表示飞行器的动压, ${q_{max }}$表示最大允许动压.

1.2.2
软约束

相比于上述的“硬约束”, 拟平衡滑翔条件(qusi-equilibrium glide condition, QEGC)是飞行器再入制导的一种“软约束”, 即保证飞行器不再跳出大气层. 拟平衡滑翔条件是令三自由度动力学方程中航迹角$gamma $及其导数$dot gamma $同时为零, 即

$$Lcos sigma approx mleft( {g - frac{{{V^2}}}{r}} ight)$$

(4)

当满足拟平衡滑翔条件时, 飞行器所受重力与升力的合力恰好与其所受的向心力平衡, 此时飞行轨迹高度变化较小, 航迹角保持很小的量.

1.2.3
再入终端约束

再入段的终端约束为中末交班点参数, 再入终端约束一般包括高度、速度、经纬度等约束, 可表示为

$$rleft( {{t_{ m{f}}}} ight) = {r_{ m{f}}},Vleft( {{t_{ m{f}}}} ight) = {V_{ m{f}}},theta left( {{t_{ m{f}}}} ight) = {theta _{ m{f}}},phi left( {{t_{ m{f}}}} ight) = {phi _{ m{f}}}$$

(5)

式中, ${t_{
m{f}}}$表示中末交班时刻, ${r_{
m{f}}},{V_{
m{f}}},{theta _{
m{f}}},{phi _{
m{f}}}$分别为交班时刻的地心距、速度、经度和纬度.

1.2.4
控制量约束

在三自由度飞行器再入制导中, 攻角$alpha $和倾侧角$sigma $为控制量, 由于飞行器内部控制机构的作用, 控制量的变化需要一定的变化时间和变化速度, 不能瞬间变化到指定值. 由于攻角采用标准攻角剖面, 因而控制量的约束主要限制在倾侧角的幅值及其变化率上, 即

$$left| sigma ight| leqslant {sigma _{max }},left| {dot sigma } ight| leqslant {dot sigma _{max }}$$

(6)

式中, ${sigma _{max }}$和${dot sigma _{max }}$表示倾侧角的幅值和变化率的上界.

2.
再入飞行器预测校正制导

在再入飞行器制导中, 控制量包括攻角$alpha $和倾侧角$sigma $. 在纵向制导中, 设计攻角$alpha $和倾侧角的幅值$left| sigma
ight|$, 在侧向制导中, 设计倾侧角$sigma $的符号.

2.1
攻角剖面

攻角$alpha $一般通过预先设定的速度?攻角剖面生成. 在再入初期为满足热流率约束采用大攻角飞行, 在中后段为满足飞行器的射程需求, 采用最大升阻比对应的攻角飞行. 本文采用的攻角剖面为

$$alpha = left{ {begin{array}{*{20}{l}}{{alpha _{max }},}&{{V_1} leqslant V leqslant {V_0}}{dfrac{{{alpha _{max }} - {alpha _{max L/D}}}}{{{V_1} - {V_2}}}(V - {V_1}) + {alpha _{max }},}&{{V_2} leqslant V < {V_1}}{{alpha _{max L/D}},}&{{V_{ m{f}}} leqslant V < {V_2}}end{array}} ight.$$

(7)

式中, ${V_0}$, ${V_{
m{f}}}$分别为初始、末端速度; ${V_1}$, ${V_2}$为可调的速度参数; ${alpha _{max }}$, ${alpha _{max L/D}}$分别为最大攻角和最大升阻比对应的攻角.

2.2
倾侧角幅值求解

倾侧角$sigma $需通过纵向制导和横向制导两个步骤来确定. 在弹道坐标系中, 气动力的投影为

$$pmb R = left[ {begin{array}{*{20}{c}} { - D} {Lcos sigma } {Lsin sigma } end{array}} ight]$$

(8)

由上式可以看出, 在攻角剖面确定的情况下, 再入飞行器的纵向制导只与倾侧角$sigma $的幅值有关, 与其正负号无关, 倾侧角$sigma $的正负号需通过横向制导律来确定, 这也可以从式(1)的三自由度动力学方程中得出相同的结论.

由再入飞行器运动学模型可知, 在一个纵向预测校正周期内, 飞行器以当前的倾侧角$sigma $为控制量, 通过对动力学方程积分, 得到满足终端能量约束的纵平面射程$Sleft( sigma
ight)$, 射程$Sleft( sigma
ight)$关于时间的导数为

$$frac{{{ m{d}}S}}{{{ m{d}}t}} = frac{{{R_0}Vcos gamma }}{r}$$

(9)

式中, ${R_0}$为地球半径. 另一方面, 飞行器距离中末制导交班点的剩余射程为

$${L_{{ m{togo}}}} = {R_0} cdot arccos left[ {sin phi sin {phi _{ m{f}}} + cos phi cos {phi _{ m{f}}}cos left( {{theta _{ m{f}}} - theta } ight)} ight]$$

(10)

纵平面内预测校正制导的目标是使得飞行器将要飞出的射程$Sleft( sigma
ight)$与剩余射程${L_{{
m{togo}}}}$相等, 即

$$F({sigma _{{ m{opt}}}}) = S({sigma _{{ m{opt}}}}) - {L_{{ m{togo}}}} = 0$$

(11)

式中, ${sigma _{{
m{opt}}}}$为待求解的倾侧角. $Sleft( sigma
ight)$通过对式(9)数值积分得到, 因此需采用迭代算法求得上述方程的解, 一般采用割线法(secant method)

$${left| {{sigma _{{ m{opt}}}}} ight|^{k + 1}} = {left| {{sigma _{{ m{opt}}}}} ight|^k} - frac{{{F^k}}}{{{F^k} - {F^{k{ m{ - 1}}}}}}left( {{{left| {{sigma _{opt}}} ight|}^k} - {{left| {{sigma _{{ m{opt}}}}} ight|}^{k - 1}}} ight)$$

(12)

求解倾侧角的幅值$left| {{sigma _{{
m{opt}}}}}
ight|$.

2.3
倾侧角幅值约束

飞行器在再入段必须满足式(3)的“硬约束”条件, 按照式(12)迭代求解出的倾侧角幅值一般难以满足过程约束, 需对倾侧角幅值加以约束. 将式(2)代入式(3)的约束条件得到在高度?速度(H-V)剖面再入走廊的下边界

$$left. begin{array}{l}H geqslant dfrac{2}{beta }ln left( {dfrac{{{k_Q} ho _0^{0.5}{V^{3.15}}}}{{{{dot Q}_{max }}}}} ight) = {H_{{{dot Q}_{max }}}}left( V ight)H geqslant dfrac{1}{beta }{ m{ln}}left( {dfrac{{sqrt {C_{ m{L}}^2 + C_{ m{D}}^2} { ho _0}{V^2}S}}{{2{n_{max }}m{g_0}}}} ight) = {H_{{n_{max }}}}left( V ight)H geqslant dfrac{1}{beta }{ m{ln}}left( {dfrac{{{ ho _0}{V^2}}}{{2{q_{max }}}}} ight) = {H_{{q_{max }}}}left( V ight)end{array} ight}$$

(13)

式中, ${H_{{{dot Q}_{max }}}}left( V
ight)$, ${H_{{n_{max }}}}left( V
ight)$和${H_{{q_{max }}}}left( V
ight)$分别为热流率、过载和动压约束下飞行器高度的下界.

然而, 在再入飞行过程中, 如果时时刻刻判断高度?速度剖面是否满足再入走廊的边界约束会带来巨大的计算量, 为此将上述再入走廊的约束直接转化为对倾侧角幅值的约束

$$left. begin{array}{l}left| {{sigma _{dot Q}}left( V ight)} ight| ! leqslant ! {cos ^{ - 1}}left[ {left( {g !!-!! dfrac{{{V^2}}}{r}} ight)dfrac{{2m{V^{4.3}}}}{{{C_{ m{L}}}S}}{{left( {dfrac{{{k_Q}}}{{{{dot Q}_{max }}}}} ight)}^2}} ight] !=! left| {{sigma _{{{dot Q}_{max }}}}left( V ight)} ight|left| {{sigma _n}left( V ight)} ight| ! leqslant ! {cos ^{ - 1}}left[ {left( {g !!-!! dfrac{{{V^2}}}{r}} ight)dfrac{{sqrt {1 + {{left( {{{{C_{ m{D}}}}/{{C_{ m{L}}}}}} ight)}^2}} }}{{{g_0}{n_{max }}}}} ight] !=! left| {{sigma _{{n_{max }}}}left( V ight)} ight|left| {{sigma _q}left( V ight)} ight|! leqslant !{cos ^{ - 1}}left[ {left( {g !!-!! dfrac{{{V^2}}}{r}} ight)dfrac{m}{{{C_{ m{L}}}{q_{max }}S}}} ight] !=! left| {{sigma _{{q_{max }}}}left( V ight)} ight|end{array} ight}$$

(14)

式中, $left| {{sigma _{{{dot Q}_{max }}}}left( V
ight)}
ight|$,$left| {{sigma _{{n_{max }}}}left( V
ight)}
ight|$和$left| {{sigma _{{q_{max }}}}left( V
ight)}
ight|$分别为热流率、过载和动压约束下飞行器倾侧角的上界. 即在过程约束下, 倾侧角的最大值为

$$left| {sigma left( V ight)} ight| leqslant min left{ {left| {{sigma _{{{dot Q}_{max }}}}left( V ight)} ight|,left| {{sigma _{{n_{max }}}}left( V ight)} ight|,left| {{sigma _{{q_{max }}}}left( V ight)} ight|} ight}$$

(15)

为进一步抑制再入飞行轨迹的振荡, 尤其是要确保再入后第一个波谷处满足热流率的约束, 在上述倾侧角约束的基础上增加高度变化率的反馈控制, 其目的是为了根据飞行器高度的变化自动调节倾侧角的幅值, 进而实现升力在负重力方向的投影$Lcos sigma $能更好地满足式(4)中的拟平衡滑翔条件, 具体为

$$left| {sigma left( V ight)} ight| = left| {sigma left( V ight)} ight| + kleft( {dot h - {{dot h}_{{ m{ref}}}}} ight)$$

(16)

式中, $dot h$表示当前时刻飞行器高度的变化率; ${dot h_{{
m{ref}}}}$为再入段参考高度变化率, 本文设置${dot h_{{
m{ref}}}} = 0$; $k$为反馈系数.

2.4
倾侧角符号设计

倾侧角符号的设计需通过预测校正横向制导来完成, 倾侧角符号的设计又包含两个方面, 即横向控制量和控制量走廊, 当横向控制量到达走廊边界时, 倾侧角符号反转. 横向控制量可以是横程误差或航向角与视线角误差, 通过设置合适的横程误差或航向角与视线角误差走廊来进行横向制导, 本文选取第二种横向控制量.

飞行器与目标点的视线角可通过球面三角形求得, 其表达式为

$$tan varPhi = frac{{sin left( {{theta _{ m{f}}} - theta } ight)}}{{cos phi tan {phi _{ m{f}}} - sin phi cos left( {{theta _{ m{f}}} - theta } ight)}}$$

(17)

则飞行器航向角与视线角的偏差为

$$Delta psi = psi - varPhi $$

(18)

横向制导律为当航向角与视线角误差超过走廊边界时, 倾侧角反转, 即

$${sigma ^i} = - { m{sign}}left( {{sigma ^{i - 1}}} ight)left| {{sigma _{{ m{opt}}}}} ight|$$

(19)

通过控制倾侧角符号的反转来使得飞行器满足再入终端的经纬度约束.

3.
基于LSTM模型的飞行器再入制导律设计

3.1
解决的问题

在传统的预测校正制导中, 倾侧角的幅值一般基于预测的待飞射程与剩余射程的差, 采用割线法迭代求解倾侧角的幅值. 由于对预测校正制导的实时性要求很高, 所以在纵向制导中每隔固定的周期(一般为50 s, 20 s等量级)校正一次倾侧角的幅值. 而在横向制导中, 需要时刻判断航向角与视线角的误差是否超出走廊边界, 一般每隔0.1 s甚至更小的周期判断一次, 一旦超出走廊则倾侧角的符号反转. 因而, 对于倾侧角这一控制量来说, 其幅值的制导周期是其符号制导周期的上百倍, 存在明显的不匹配. 此外, 由图1(a)可以看出, 预测校正制导每确定一次倾侧角, 需分别在纵向制导和横向制导中对动力学方程进行两次积分, 纵向制导中的积分预测飞行器的待飞射程, 横向制导中的积分是为了确定飞行状态, 进而确定倾侧角的符号, 两次积分过程存在明显的冗余计算.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure1" />



图
1
预测校正制导与基于LSTM模型的再入制导对比



Figure
1.
Comparison of predictor-corrector guidance and LSTM model-based reentry guidance



下载:
全尺寸图片
幻灯片


针对上述预测校正制导中存在的不足, 本文研究基于LSTM模型的飞行器再入制导, 如图1(b)所示, 其核心思想为: 一是不再通过对动力学方程进行积分来预测飞行器的待飞射程和基于割线法校正倾侧角的幅值, 二是将预测校正中“纵向制导确定倾侧角的幅值”和“横向制导确定倾侧角的符号反转”两个过程相融合, 即去除“预测”环节、“校正”环节, 基于飞行器再入段的实时状态信息, 利用LSTM模型实时生成倾侧角, 包括其幅值和符号.

具体为: 一方面, 输入${t_0}$时刻的飞行器状态, 基于LSTM模型输出倾侧角, 本文中制导周期设置为1s, 即下一次在${t_0} + 1$时刻更新倾侧角; 另一方面, 在${t_0}$到${t_0} + 1$这一时间段内, 将${t_0}$时刻输出的倾侧角带入动力学方程(1)进行积分, 动力学方程积分步长为0.1s, 进而得到$left[ {{t_0},{t_0} + 1}
ight]$时间段内${t_0}$, ${t_0} + 0.1$, ${t_0} + 0.2$,···, ${t_0} + 1$各时刻的飞行状态. 以此类推, 在${t_0} + 1$时刻, 基于LSTM模型输出新的倾侧角, 在${t_0} + 1$到${t_0} + 2$这一时间段内, 再将${t_0} + 1$时刻输出的倾侧角代入动力学方程进行积分, 进而得到$left[ {{t_0} + 1,{t_0} + 2}
ight]$时间段内的飞行状态.

该方法的优越性具体体现在以下几个方面:

(1)在计算速度方面, 传统预测校正制导中大量的计算集中在“预测”环节和“校正”环节, 基于LSTM模型的飞行器再入制导, 一方面不再需要纵向制导中对动力学方程的积分来预测待飞射程, 即去除“预测”过程, 大大减小计算量, 提高计算速度; 另一方面, 不再基于割线法迭代求解倾侧角的幅值, 即没有了倾侧角的“校正”过程, 训练完成的LSTM模型具备天然的计算速度快的优势, 模型的输入为飞行器实时的状态信息, 将倾侧角的幅值和符号一并输出.

(2)在倾侧角的制导周期方面, 不存在幅值校正周期和符号反转两个周期, 对倾侧角的制导将只有一个周期, 该周期的大小介于幅值的制导周期和符号的制导周期中间, 从而进一步确保制导系统满足在线制导实时性的要求.

3.2
基于LSTM模型的倾侧角设计

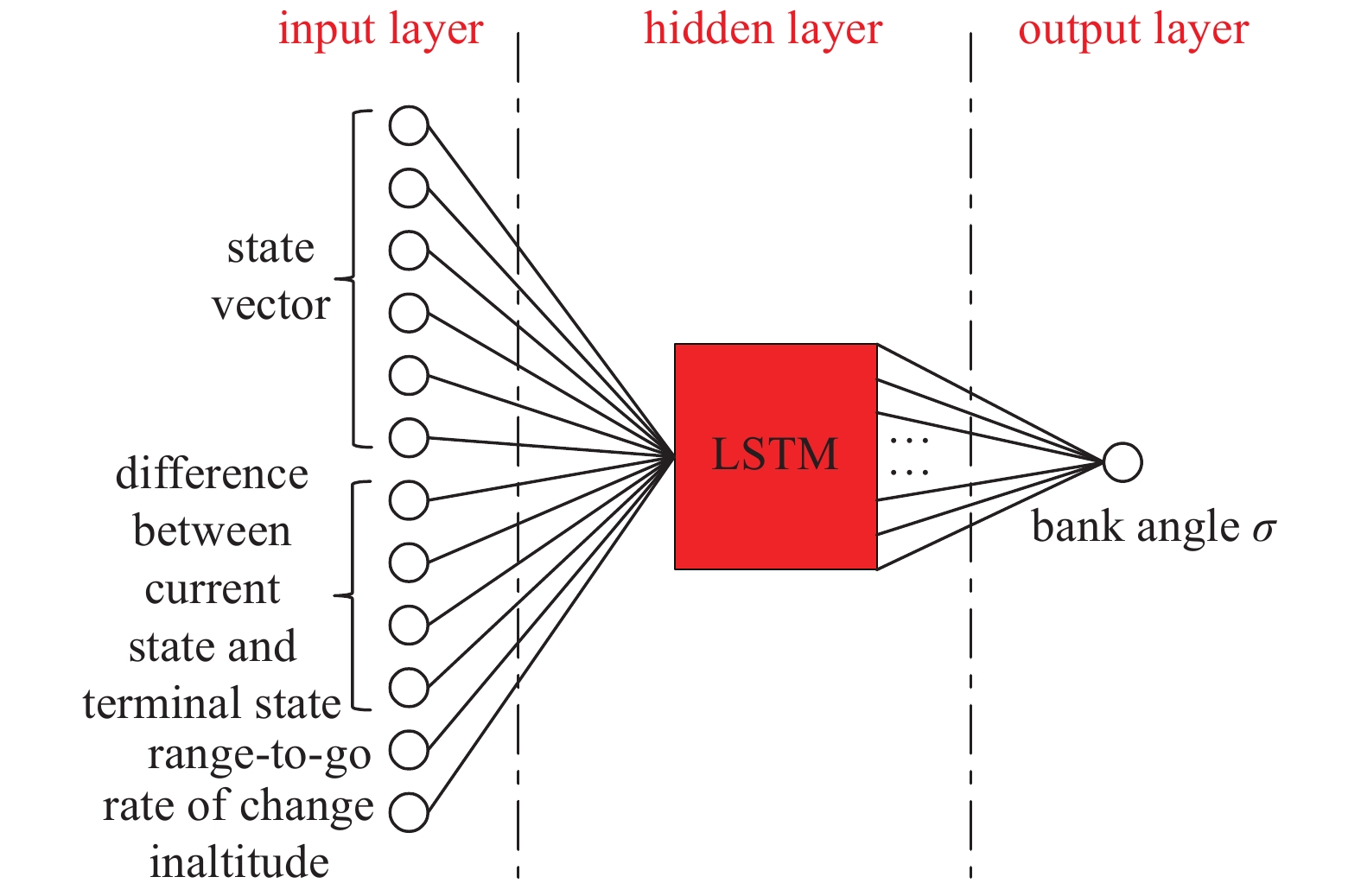
基于LSTM模型实时输出飞行器的倾侧角, 网络模型的结构如图2所示. 其中, 网络的输入为飞行器的实时状态向量, 本文定义状态向量为

$${pmb {s}}(t) = {left[ {r,theta ,phi ,V,gamma ,psi ,Delta r,Delta theta ,Delta phi ,Delta V,{L_{{ m{togo}}}},dot r} ight]^{ m T}}$$

(20)

式中, $Delta r = r - {r_{
m{f}}}$, $Delta theta = theta - {theta _{
m{f}}}$, $Delta phi = phi - {phi _{
m{f}}}$, $Delta V = V - {V_{
m{f}}}$. 隐层为LSTM模型, 其具体结构如图3所示, 隐层输出的节点数为64个, 隐层到输出层是全连接, 输出为倾侧角$sigma $.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
基于LSTM的神经网络模型架构



Figure
2.
Structure diagram of LSTM-based neural network



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
LSTM模型



Figure
3.
LSTM model



下载:
全尺寸图片
幻灯片


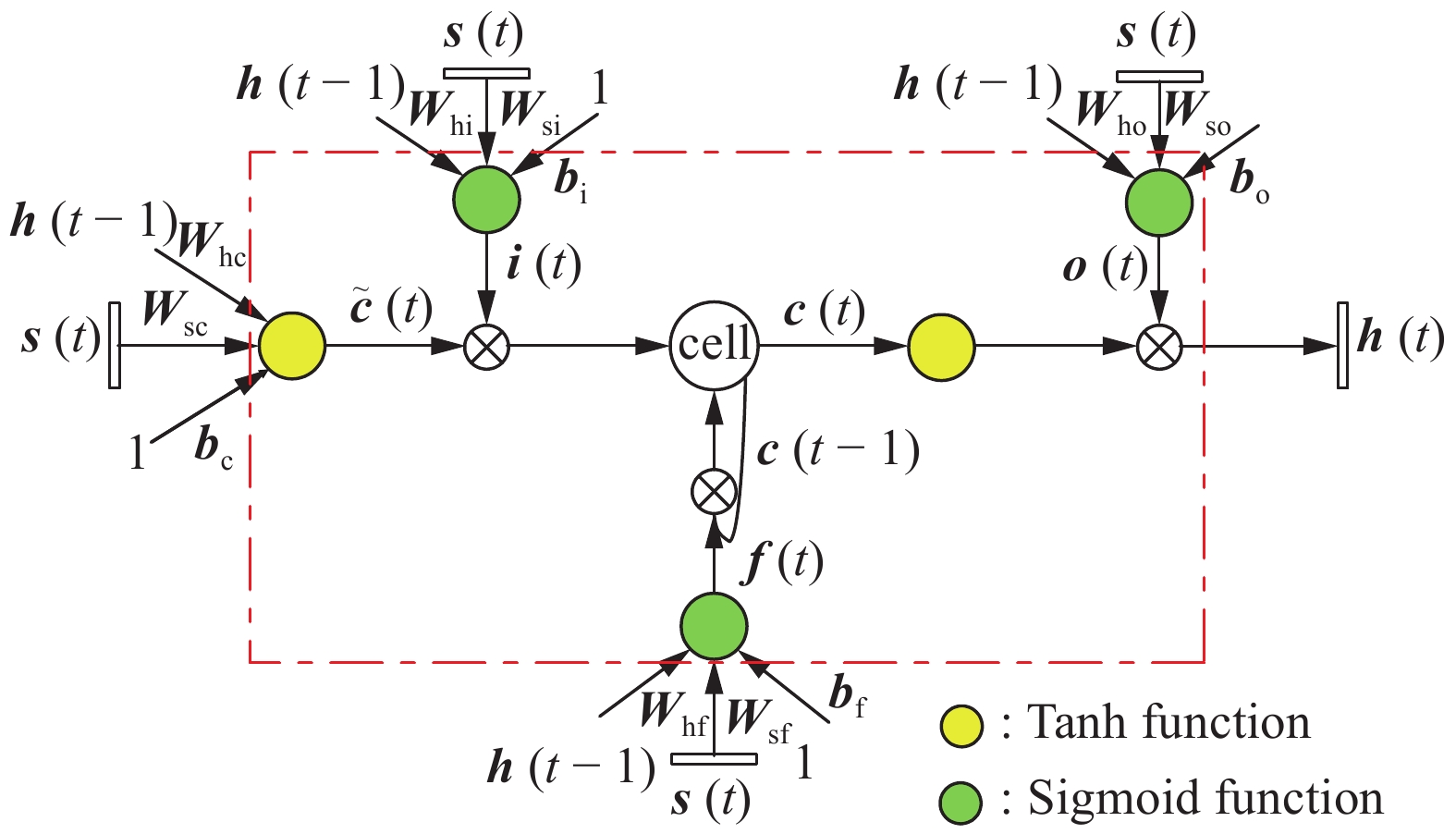
LSTM模型的表达式为

$$left. begin{array}{l} {boldsymbol{tilde c}}(t) = tanh [{{boldsymbol{W}}_{{ m{sc}}}}{boldsymbol{s}}(t) + {{boldsymbol{W}}_{{ m{hc}}}}{boldsymbol{h}}(t - 1) + {{boldsymbol{b}}_{ m{c}}}] {boldsymbol{i}}(t) = sigma [{{boldsymbol{W}}_{{ m{si}}}}{boldsymbol{s}}(t) + {{boldsymbol{W}}_{{ m{hi}}}}{boldsymbol{h}}(t - 1) + {{boldsymbol{b}}_{ m{i}}}] {boldsymbol{f}}(t) = sigma [{{boldsymbol{W}}_{{ m{sf}}}}{boldsymbol{s}}(t) + {{boldsymbol{W}}_{{ m{hf}}}}{boldsymbol{h}}(t - 1) + {{boldsymbol{b}}_{ m{f}}}] {boldsymbol{c}}(t) = {boldsymbol{i}}(t) circ {boldsymbol{tilde c}}(t) + {boldsymbol{f}}(t) circ {boldsymbol{c}}(t - 1) {boldsymbol{o}}(t) = sigma [{{boldsymbol{W}}_{{ m{so}}}}{boldsymbol{s}}(t) + {{boldsymbol{W}}_{{ m{ho}}}}{boldsymbol{h}}(t - 1) + {{boldsymbol{b}}_{ m{o}}}] {boldsymbol{h}}(t) = {boldsymbol{o}}(t) circ tanh [{boldsymbol{c}}(t)] end{array} ight}$$

(21)

其中, ${boldsymbol{tilde c}}(t)$为LSTM模型中输入到记忆单元的值; ${boldsymbol{i}}(t),{boldsymbol{f}}(t),{boldsymbol{o}}(t)$分别为输入门、遗忘门和输出门; ${boldsymbol{c}}(t)$为记忆单元的记忆值; ${boldsymbol{h}}(t)$为LSTM模型的输出. 其中, 输入门${boldsymbol{i}}(t)$控制当前时刻的输入值${boldsymbol{tilde c}}(t)$有多少可以进入记忆单元; 遗忘门${boldsymbol{f}}(t)$决定了记忆单元上一时刻的值${boldsymbol{c}}(t - 1)$有多少被传到当前时刻; 记忆单元当前值${boldsymbol{c}}(t)$是当前输入值${boldsymbol{tilde c}}(t)$与上一时刻记忆值${boldsymbol{c}}(t - 1)$的加权和; 输出门${boldsymbol{o}}(t)$决定了记忆单元中存储的记忆值${boldsymbol{c}}(t)$有多大比例可以被输出. ${pmb {W}}$和${pmb {b}}$ (下标省略)表示待训练的权重矩阵和偏置向量. $tanh ( cdot )$表示双曲正切函数, $sigma ( cdot )$表示Sigmoid函数. $ circ $表示Hadamard积.

选取LSTM模型的根本原因在于飞行器的倾侧角决策过程是一个典型的序贯决策过程. 这是因为在传统的预测校正制导中每一时刻的倾侧角符号不仅取决于当前时刻的状态, 还与上一时刻的倾侧角符号以及上一时刻航向角误差与走廊的关系有关. 若上一时刻航向角误差在走廊内, 当前时刻超出走廊, 则需要反转; 但若上一时刻已经超出走廊, 倾侧角已经反转过一次, 当前时刻还在走廊外, 则无需二次反转. 因而, 飞行器倾侧角的确定不仅需要基于当前时刻的状态信息还需要历史时刻的状态信息. 从智能决策的角度来说, 在决策倾侧角时需考虑飞行器在相邻时刻的状态关系, 而LSTM是解决序贯决策问题的经典模型.

4.
仿真与分析

4.1
LSTM网络模型的训练

LSTM模型的训练分两步, 一是训练样本的生成, 二是网络模型的训练.

4.1.1
训练样本的生成

在训练样本的生成方面, 本文选取美国通用航空飞行器CAV-H为研究对象, 基于传统预测校正制导产生仿真数据, 参数设置如下.

(1)飞行器参数: 质量$m = {
m{907}}{
m{.20;kg}}$, 参考面积$S = {
m{0}}{
m{.4839}};{{
m{m}}^2}$, 过程约束中为最大允许热流率${dot Q_{max }} = $$ 2000;{{{
m{kw}}}/{{{
m{m}}^2}}}$, 最大允许过载${n_{max }} = 3;g$, 最大允许动压${q_{max }} = 100;{
m{kPa}}$.

(2)升力系数${C_{
m{L}}}$和阻力系数${C_{
m{D}}}$与攻角$alpha $和速度$V$的函数关系为

$$left. begin{array}{l} {C_{ m{L}}} = {C_{{ m{L}}0}} + {C_{{ m{L}}1}}alpha + {C_{{ m{L}}2}}{{ m }{ m{e}}^{{C_{{ m{L}}3}}V}} {C_{ m{D}}} = {C_{{ m{D}}0}} + {C_{{ m{D}}1}}{alpha ^2} + {C_{{ m{D}}2}}{{ m{e}}^{{C_{{ m{D}}3}}V}} end{array} ight}$$

(22)

其中, ${C_{{
m{L}}0}} = - 0.235 5$,${C_{{
m{L}}1}} = 2.9451$, ${C_{{
m{L}}2}} = 0.2949$, ${C_{{
m{L}}3}} = $$ - 3.3943 times {10^{ - 4}}$; ${C_{{
m{D}}0}} !=! 0.0234$, ${C_{{
m{D}}1}} !=! 2.3795$, ${C_{{
m{D}}2}} !=! $$ 0.3983$, ${C_{{
m{D}}3}} = - 1.0794 times {10^{ - 3}}$.

(3)中末交班点参数: 高度${h_{
m{f}}} = 23;{
m{km}}$, 经度${theta _{
m{f}}} = {50^ circ }$, 纬度${phi _{
m{f}}} = {3^ circ }$, 速度${V_{
m{f}}} = 1100;{{
m{m}}/{
m{s}}}$.

(4)攻角剖面: 最大攻角${alpha _{max }} = {20^ circ }$, 最大升阻比对应的攻角${alpha _{max L/D}} = {10^ circ }$, 式(7)中可调的速度参数${V_1} = 5000;{{
m{m}}/{
m{s}}}$, ${V_2} = 2500;{{
m{m}}/{
m{s}}}$.

(5)纵向预测校正的周期: 当剩余射程大于500 km时, $T = 50;{
m{s}}$; 当剩余射程小于500 km, 大于200 km时, $T = 15;{
m{s}}$; 当剩余射程小于200 km时, $T = 5;{
m{s}}$.

(6)动力学方程积分步长: 纵向制导的积分步长为1 s, 横向制导的积分步长为0.1 s.

(7)飞行器再入初始点的状态参数见表1.




表
1
飞行器再入初始点的参数范围



Table
1.
Range of initial state parameters



table_type1 ">

Initial state parameters	Range
${h_0}/{ m{km}}$	$left[ {60,75} ight]$
${theta _0}{/(^ circ) }$	$left[ { - {2^ circ },{2^ circ } } ight]$
${phi _0}{/(^ circ) }$	$left[ { - {2^ circ },{2^ circ } } ight]$
${V_0}/({{ m{m}} cdot{ m{ s}}^{-1} })$	$left[ {5500,6200} ight]$
${gamma _0}{/(^ circ) }$	$left[ { - {3^ circ },{3^ circ } } ight]$
${psi _0}{/(^ circ) }$	$left[ { - {3^ circ },{3^ circ } } ight]$

下载:
导出CSV
|显示表格



在上述参数范围内随机设置飞行器的再入初始点参数, 在预测校正制导下可以获得大量的飞行轨迹数据. 本文选取其中1331条飞行轨迹, 每条轨迹约16000个样本点.

4.1.2
模型的训练

将1331条飞行轨迹数据输入图2的基于LSTM的飞行器倾侧角设计模型中, 在训练时目标损失函数(loss function)定义为

$$loss = frac{1}{{2 R S}}sumlimits_{i = 1}^S {sumlimits_{j = 1}^R {{{left( {{sigma _{ij}} - {{hat sigma }_{ij}}} ight)}^2}} } $$

(23)

其中, $S$表示轨迹的数目, $R$表示每一条轨迹的样本点数. 采用SGDM (stochastic gradient descent with momentum)算法^[30], 模型中参数的初始化采用Xavier方法^[31]. 学习率设置为1.0 × 10^?3, 批处理时“batchsize”设置为50, 最大迭代次数(epoch)设置为1000. 除了采用损失函数描述训练效果外, 还采用均方根误差(root mean square error, RMSE)作为定量评价指标, 其定义为

$$RMSE = sqrt {frac{1}{{R cdot S}}sumlimits_{i = 1}^S {sumlimits_{j = 1}^R {{{left( {{sigma _{ij}} - {{hat sigma }_{ij}}} ight)}^2}} } } $$

(24)

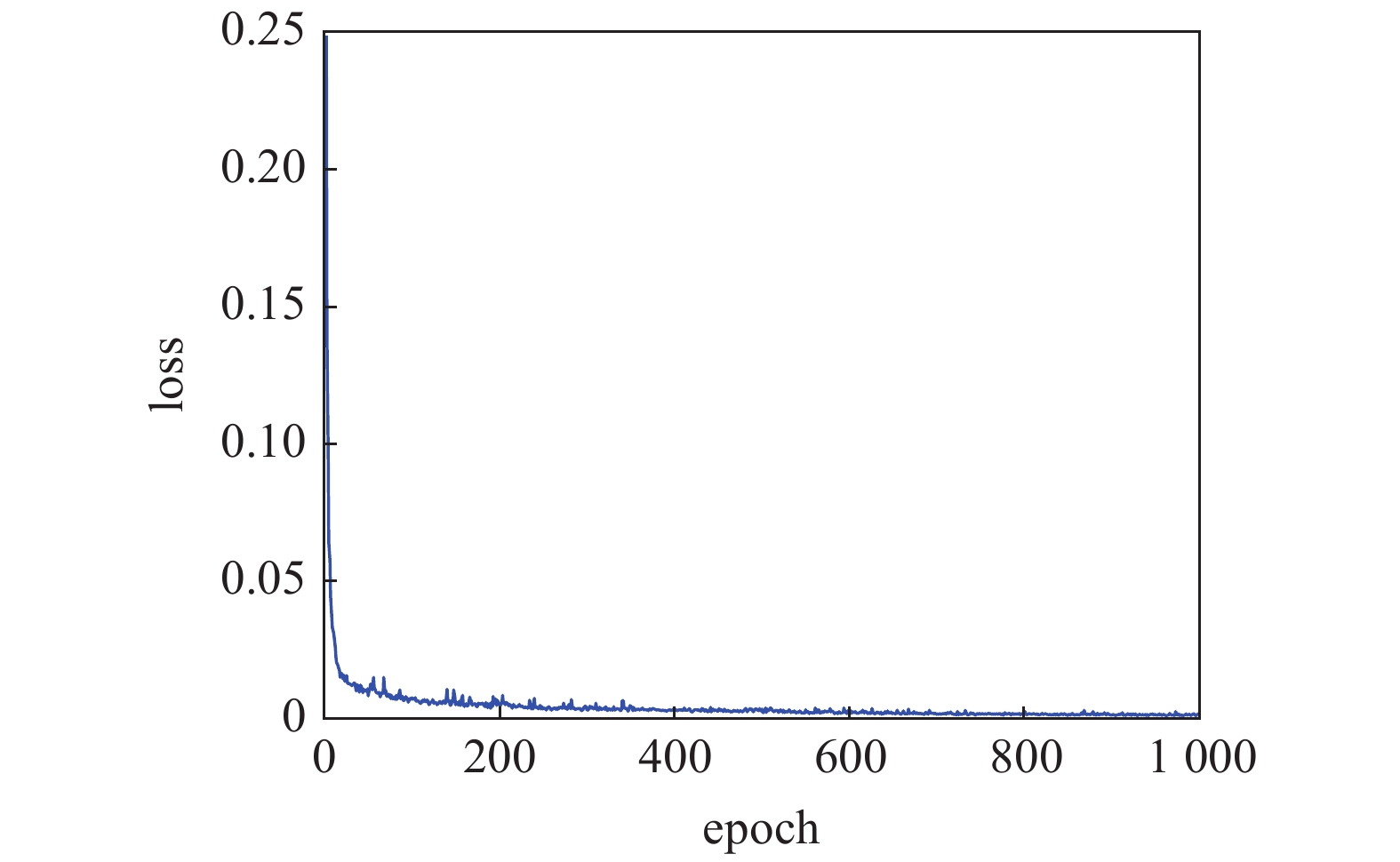
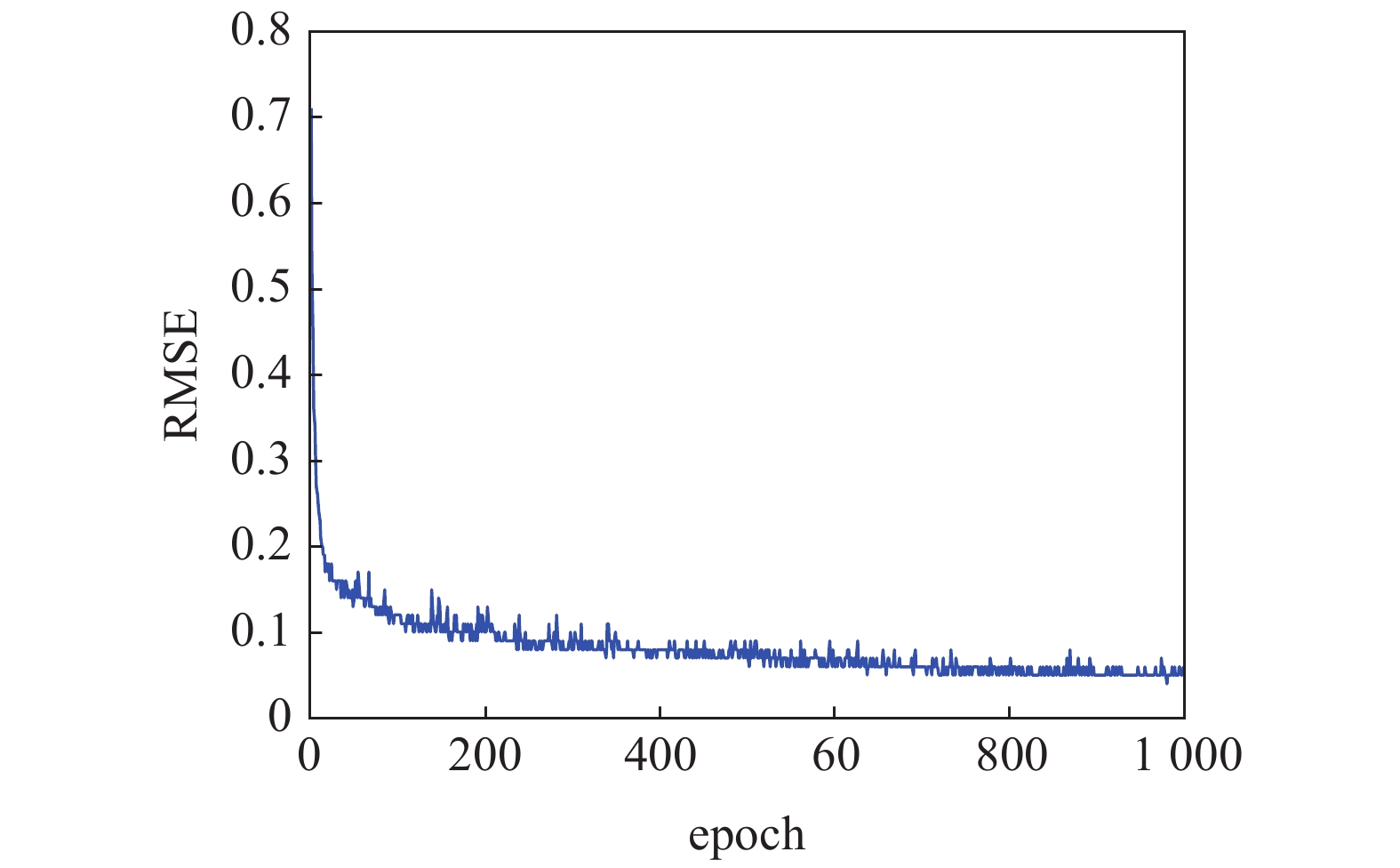
训练效果如图4和图5所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
损失函数随迭代次数的变化曲线



Figure
4.
Loss function-epoch curve



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
均方根误差随迭代次数的变化曲线



Figure
5.
RMSE-epoch curve



下载:
全尺寸图片
幻灯片


由图可以看出目标损失函数和均方根误差随着训练迭代次数的增加逐渐减小且趋于收敛, 表明上述训练参数设置的合理性.

4.2
LSTM网络模型的测试

基于上述训练的LSTM模型进行飞行器再入制导仿真, 并与预测校正制导进行对比, 如图6 ~ 图10所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
高度?速度曲线对比



Figure
6.
Comparison of height-velocity curve



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
横向轨迹曲线对比



Figure
7.
Comparison of horizontal trajectory curve



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
倾侧角?速度曲线对比



Figure
8.
Comparison of bank angle-velocity curve



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
航迹角?时间曲线对比



Figure
9.
Comparison of flight path angle-time curve



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
航向角?时间曲线对比



Figure
10.
Comparison of heading angle-time curve



下载:
全尺寸图片
幻灯片


由图6 ~ 图10可以看出, 两种制导方式下的曲线基本重合, 基于训练的LSTM制导模型, 使得飞行器在满足热流率约束、过载约束和动压约束的前提下, 能够安全可靠地完成既定的飞行任务.

4.3
蒙特·卡罗仿真分析

为验证基于LSTM模型的飞行器再入制导的鲁棒性和对参数偏差的适应性, 本文对飞行器再入初始状态、气动参数进行拉偏仿真分析, 飞行器再入初始状态和气动参数偏差见表2.




表
2
飞行器再入初始状态和气动参数偏差



Table
2.
Initial state error and aerodynamic parameter perturbation



table_type1 ">

Perturbation	Distribution	Error bound
$Delta r/{ m{km}}$	uniform distribution	$ pm 3$
$Delta theta {/(^ circ) }$	uniform distribution	$pm {0.1 }$
$Delta phi {/(^ circ) }$	uniform distribution	$pm {0.1 }$
$Delta V/({{ m{m}}cdot { m{s}}^{-1} })$	uniform distribution	$ pm 100$
$Delta gamma {/(^ circ) }$	uniform distribution	$pm {0.3 }$
$Delta psi {/(^ circ) }$	uniform distribution	$pm {1 }$
$Delta {C_{ m{L}}}/% $	uniform distribution	$ pm 30$
$Delta {C_{ m{D}}}/% $	uniform distribution	$ pm 30$

下载:
导出CSV
|显示表格



在再入初始状态扰动和气动偏差的条件下, 利用训练的LSTM模型进行400组的蒙特·卡罗仿真, 落点经纬度的散布图如图11所示, 并与传统的预测校正制导进行比较. 由图11可以看出, 在满足中末交班点能量约束的前提下, 相比于传统的预测校正制导方法, 基于LSTM的飞行器再入制导的末端状态更加靠近中末交班点, 即更加靠近${theta _{
m{f}}} = {50^ circ }$, ${phi _{
m{f}}} = {3^ circ }$点. 显然, 在初始状态有扰动和气动参数有偏差的情形下, 基于LSTM模型的再入制导方法具有更高的精度, 其原因在于采用LSTM模型输出倾侧角指令时需对输入的飞行器状态向量进行归一化处理, 该过程会降低对状态偏差的敏感性, 加上LSTM神经网络模型具有天然的泛化能力, 因而对于参数的偏差具有更强的鲁棒性.



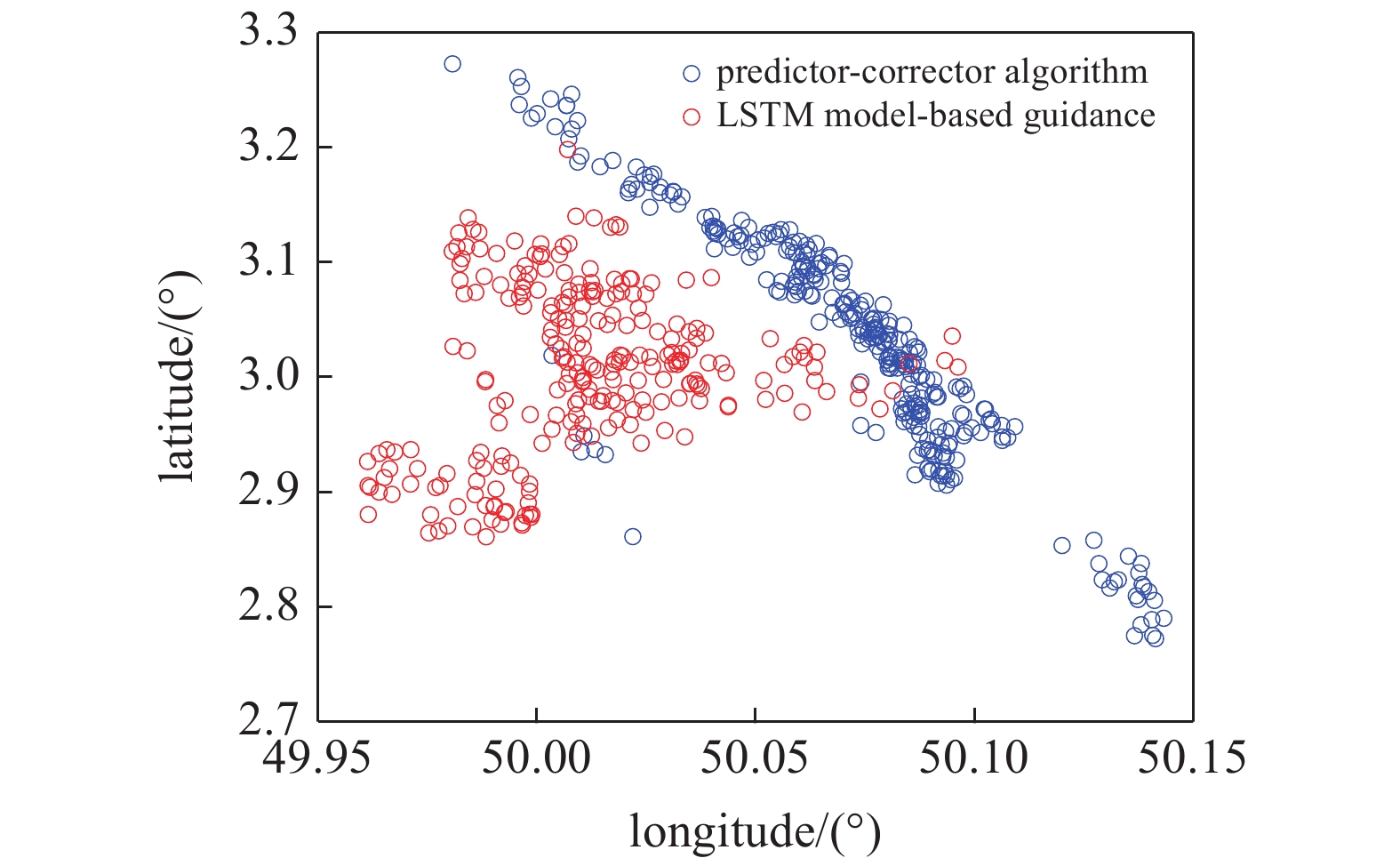onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
初始状态和气动参数扰动下落点经纬度的散布图



Figure
11.
Scatter diagram of longitude and latitude under initial state error and aerodynamic parameter perturbation



下载:
全尺寸图片
幻灯片

4.4
实时性分析

本节进一步分析基于LSTM模型的飞行器再入制导在实时性方面的性能.

在蒙特·卡罗仿真中, 基于LSTM的制导模型完成一次再入段飞行的平均时长为10.18 s, 其具体分布如图12所示, 其中基于LSTM模型生成倾侧角的时长占其中的7.30 s, 龙哥库塔RK-4积分时长占其中的2.63 s.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//20-388-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
计算实时性对比分析



Figure
12.
Comparison of computing time analysis



下载:
全尺寸图片
幻灯片


与之对比, 预测校正制导在蒙特·卡罗仿真中完成一次再入段飞行的平均时长为38.69 s, 其中纵向制导过程占其中的33.97 s, 横向制导过程占其中的4.56 s. 这是因为在纵向制导中, 对动力学方程进行积分的预测过程和基于割线法求解倾侧角的迭代过程计算量较大, 占用的时间较长. 而基于LSTM模型的飞行器再入制导中没有“预测”环节和“积分”环节, 大大减少了计算量, 提高了计算速度. 因而, 在实时性方面, 基于LSTM模型的飞行器再入制导相比于传统预测校正制导具有明显的优势.

5.
结论

本文针对传统预测校正制导中存在的两方面问题, 一是纵向预测中积分计算量大、割线法迭代求解倾侧角幅值难以满足实时性的问题, 二是纵向制导和横向制导中都需要对动力学方程进行积分, 存在明显的冗余计算问题, 提出基于LSTM模型的飞行器智能制导技术, 并基于飞行器的实时状态信息输出倾侧角指令. 该方法的优势体现在两个方面, 一方面不再需要纵向制导中对动力学方程的积分来预测待飞射程, 即去除“预测”过程, 大大减小计算量, 提高计算速度; 另一方面, 不再基于割线法迭代求解倾侧角的幅值, 即去除倾侧角的“校正”过程, 训练完成的LSTM模型具备天然的计算速度快的优势. 此外, 在倾侧角的制导周期方面, 不存在幅值校正周期和符号反转两个周期, 倾侧角的制导将只有一个周期, 从而进一步确保制导系统满足在线制导实时性的要求.

尽管新兴的人工智能技术具有非线性映射能力和实时性方面的天然优势, 但目前的人工智能技术存在难以回避的缺点: 一是, 针对飞行器制导控制任务, 目前的深度学习是纯数据驱动的模式, 需要大量的样本数据来训练神经网络模型, 但在航天领域, 真实的数据往往难以获取, 样本数据不足时容易出现过拟合问题; 二是, 目前的人工智能仍然处于计算智能阶段, 神经网络模型只能在训练样本数据集覆盖的范围内有效, 依然不具备较强的泛化能力, 实际飞行中若出现数据集范围外的情况, 神经网络的性能将难以保证. 制导控制技术与人工智能技术不是简单的替代关系, 制导控制技术可以在关键点上吸纳人工智能技术在记忆、推理、拟合等方面的优势, 两个领域的交叉融合是飞行器智能制导控制领域的热门研究方向.