删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

数字化光处理立体成型技术中吸附力的影响机制

本站小编 Free考研考试/2022-01-01


引言


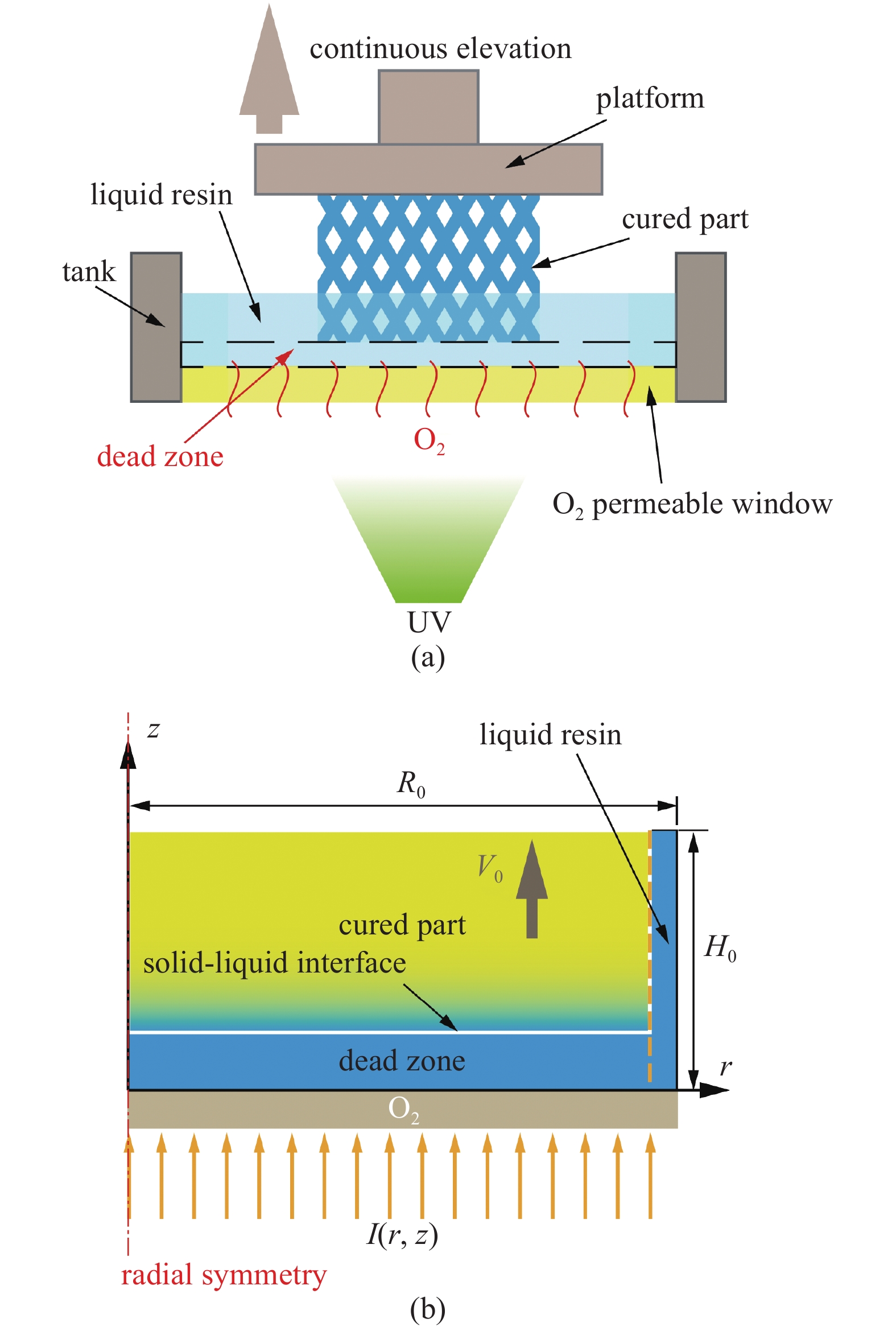
增材制造是一项具有革命意义的新兴制造技术, 被誉为决定未来经济的十二大颠覆技术之一[1], 在工业界与学术界有广泛的应用前景, 如生物医疗[2-5]、航天航空[6-7]、机器人技术[8-9]、智能传感器[10-11]、结构设计[12-13]以及微流控芯片[14-15]等. 数字化光处理(digital light processing, DLP)立体成型技术是树脂光固化增材制造最重要的一类成型方式之一, 与其他方式相比, 其具有较高的成型速度与成型精度[16-17]. DLP成型利用自由基光聚合的原理, 通过逐面曝光、固化、分离再填充的往复循环过程, 层层累加最后形成三维实体, 实现由面至体的成型过程. Tumbleston等[18]基于DLP成型原理提出了CLIP技术, 采用高透氧的特氟龙膜(Teflon AF 2400)作为树脂槽底的透明窗口, 利用氧阻聚的原理, 使已固化成型部分与窗口之间保持一层厚度达数十微米的未固化液膜薄层(dead zone), 从而避免了固化层与窗口的黏连, 实现了高速连续固化成型, 将打印速度进一步提高到每小时百毫米, 其原理如图1(a)所示. 然而, 由于高黏度的树脂导致的液膜薄层的巨大吸附力限制了成型速度的进一步提高, 强行提高速度后液膜将出现空泡并发生破裂, 导致样品缺陷甚至引起打印失败[19-20].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-099-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
(a) DLP成型原理和(b)多物理场模型



Figure
1.
Schematic diagram of (a) DLP 3D printer and (b) multiphysical model



下载:
全尺寸图片
幻灯片


为了提高DLP光固化成型速度, 国内外****从树脂槽成型窗口和打印工艺等方面做了大量研究与改进. Wu等[21]受猪笼草启发对PDMS膜进行表面处理, 获得了超润滑表面并以此作为透明窗口, 降低吸附力从而提高了成型速度至360 mm/h. Walker等[22]利用高速流动的油层将透明窗口与树脂固化区域分隔开, 极大地降低了吸附力, 实现了430 mm/h的固化成型速度. 目前多数研究集中于试验层面, 仅有少量研究从仿真的角度对DLP成型过程进行了机理分析. Wang等[23]搭建了粗粒度分子动力学模型用于模拟CLIP成型过程, 研究了对打印物体成型质量的影响因素, 发现打印物体的成型形状将由单体交联密度、毛细管力及摩擦力的相互作用共同决定. Taki等[24]通过建立了一个考虑自由基聚合反应与氧气分子扩散的成型过程数值模型, 发现垂直提升速度及树脂中光强的衰减程度将影响树脂的交联密度和成型精度. 该模型考虑了连续固化的相变过程, 但没有考虑树脂流动的影响. Wang等[25]忽略了光聚合反应过程, 将死区简单的考虑为平板间的流体运动, 模拟了固化截面尺寸、提升速度等因素的影响. 上述研究中的模型较为简化, 没有全面考虑DLP固化成型中的关键因素的影响, 因而未能揭示液膜薄层区吸附力的物理机制.

本文针对DLP成型过程中的自由基光聚合反应、树脂固化相变以及树脂流动等物理过程, 搭建了多物理场仿真模型并进行数值求解, 研究了DLP打印成型区的演化过程, 对固?液界面形貌及吸附力大小的影响因素进行了模拟分析, 并提出了降低吸附力、提高打印速度的改进措施, 以期为DLP技术的工艺改进与工程应用提供参考.


1.
多物理场模型建立


为了便于研究, 本文以打印半径为R的实心圆柱形状样品为例, 结合DLP打印的成型原理与工作过程, 构建如图1(b)所示的二维轴对称(r, θ, z)简化模型. 整个模型主要针对液膜及紧邻其上方的一部分已固化树脂区域, 圆柱样品中心轴线与z轴重合, 固相区域以恒定速度V0向上提升. 模型的高度为H0, 半径为R0, 受到由下往上的光强分布为 I(z, r)的恒定紫外光照射,固化区域的尺寸即取决于光照范围(要求紫外光照射区域半径R < R0).


1.1
自由基光聚合反应动力学及物质传递


本文采用经典的自由基光聚合反应模型, 主要包括链引发、链增长、链终止等过程, 具体表示为表1所示的5个步骤[26-29]. 首先, 在紫外光(UV)的作用下诱导光引发剂(PI)由基态转变为激发态, 进而分解产生初级自由基($dot {
m{R}}$), 如步骤1所示. 初级自由基($dot {
m{R}}$)进一步进攻体系中的不饱和单体(M)产生单体自由基(${
m{R}}dot{
m{M}}$), 如步骤2所示. 单体自由基(${
m{R}}dot{
m{M}}$)继续与单体(M)作用形成新的链自由基(${
m{R}}{dot{
m{M}}_{{n}}}$), 引起分子链持续增长, 交联密度增大, 如步骤3所示, 链增长速率常数为kp. 最后, 链自由基之间相互反应导致链增长终止(步骤4), 终止速率常数为kt. 此外, 氧气能与自由基反应形成类似于过氧化物的中间体(RMnOO), 抑制其进一步参与聚合反应(步骤5), 反应速率常数为kO.




表
1
自由基光聚合反应动力学模型



Table
1.
Reaction scheme and kinetic model of free radical photopolymerization



table_type1 ">
DescriptionReactionNo.
photoinitiator dissociation${
m{PI}}xrightarrow{{hv}}dot {
m{R}}$		1
primary radical formation$dot {
m{R}} + {
m{M}} to {
m{R}}dot{
m{M}}$		2
propagation reaction${
m{R}}{dot{
m{M}}_{{n}}} + {
m{M}}xrightarrow{{{k_{
m{p}}}}}{
m{R}}{dot{
m{M}}_{{{n}} + 1}}$		3
bimolecular termination${
m{R}}{dot{
m{M}}_{{n}}} + {
m{R}}{dot{
m{M}}_{{m}}}xrightarrow{{{k_{
m{t}}}}}{
m{R}}{{
m{M}}_{{n}}}{{
m{M}}_{{m}}}$		4
oxygen inhibition${
m{R}}{dot{
m{M}}_{{n}}} + {{
m{O}}_{
m{2}}}xrightarrow{{{k_{
m{O}}}}}{
m{R}}{{
m{M}}_{{n}}}{
m{OO}}$		5





下载:
导出CSV
|显示表格



鉴于光引发剂、单体、自由基等物质在树脂中的扩散速率较慢, 远小于氧气, 因此忽略其分子扩散过程, 而只考虑对流传质过程. 初级自由基的生成速率 Ri 与对紫外光的吸收率相关, 可表示为







$${R_{
m{i}}} = varphi varepsilon [{
m{PI}}]I(r,{textit{z}})$$
(1)

式中, φ为量子产率, ε为摩尔吸光系数, [PI]为光引发剂的浓度. 考虑光强分布在树脂中沿轴线方向的衰减过程, 根据朗伯?比尔定律(Beer-Lambert Law)可得







$$Ileft( {r,{textit{z}}}
ight) = {I_0}left( r
ight){{
m{e}}^{ - varepsilon [{
m{PI}}]{textit{z}}}}{
m{ }};;left( {{textit{z}} geqslant 0}
ight)$$
(2)

式中, I0(r) 为树脂下表面所受到的入射光光强, 其沿r方向的分布范围等于拟打印样品的半径R, 即r $leqslant $ R时, I0(r) = I0; r > R 时, I0(r) = 0.

为了简化模型, 将所有的自由基类物质($dot {
m{R}}$, ${
m{R}}dot{
m{M}}$, ${
m{R}}{dot{
m{M}}_{{n}}}$)用$dot {
m{X}}$表示, 由于所有的初级自由基均在步骤1中产生, 因此$dot {
m{X}}$的生成速率仅由该步骤表示[27]. 各物质的传递与消耗可表示为







$$frac{{partial [{
m{PI}}]}}{{partial t}} + {boldsymbol{u}} cdot nabla [{
m{PI}}] = - {R_{
m{i}}}qquadqquadqquadqquadqquad$$
(3)







$$frac{{partial [dot {
m{X}}]}}{{partial t}} + {boldsymbol{u}} cdot nabla [dot {
m{X}}] = {R_{
m{i}}} - {k_{
m{t}}}{[dot {
m{X}}]^2} - {k_{
m{O}}}[dot {
m{X}}][{{
m{O}}_2}]qquad;;$$
(4)







$$frac{{partial [{
m{M}}]}}{{partial t}} + {boldsymbol{u}} cdot nabla [{
m{M}}] = - {k_{
m{p}}}[dot {
m{X}}][{
m{M}}]qquadqquadqquadquad$$
(5)







$$frac{{partial [{{
m{O}}_2}]}}{{partial t}} + {boldsymbol{u}} cdot nabla [{{
m{O}}_2}] = nabla cdot left( {{D_{
m{O}}}nabla [{{
m{O}}_2}]}
ight) - {k_{
m{O}}}[dot {
m{X}}][{{
m{O}}_2}]$$
(6)

式(3)~式(6)中, 只考虑氧气的分子扩散过程, 其扩散系数为DO. [PI], ${{[dot {
m{X}}]}}$, [M], [O2]分别为PI, $dot {
m{X}}$, M, O2的物质的量浓度, u表示对流速度矢量. 式(3) ~ 式(5)中等号左侧第二项为对流项, 与流场分布相关; 等号右侧为反应项, 对应于表1中的5个反应步骤. 而式(6)中除了包括上述二者, 还含有扩散项$nabla$?(DO$nabla$[O2]).


1.2
相分布


随着聚合反应过程的进行, 光敏树脂的黏度将随交联密度的增大而急剧上升, 由液态转变为固态[30]. 常用双键的转化度α来衡量单体分子的交联密度, 此处可通过单体消耗分数来近似表达, 定义为







$$alpha = 1 - frac{{[{
m{M}}]}}{{{{[{
m{M}}]}_0}}}$$
(7)

当转化度α低于临界值αc时, 树脂为液态; 超过αc时则转变为固态. 通过使用阶跃函数H(x)实现对相分布的捕捉







$$lambda = H{
m{(}}alpha {
m{)}}left{ {begin{array}{*{20}{l}} 1 {{
m{mushy}}} 0 end{array}{
m{ }}begin{array}{*{20}{l}} ({alpha leqslant {alpha _{
m{c}}} - Delta alpha /2}) ({{alpha _{
m{c}}} - Delta alpha /2 < alpha < {alpha _{
m{c}}} + Delta alpha /2} ) ({alpha geqslant {alpha _{
m{c}}} + Delta alpha /2} )end{array}}
ight.$$
(8)

其中λ为相分数. 当转化度靠近临界值时, λ从1 (液态)转变为0 (固态). 由于数值突变会引起计算的不稳定性, 并且固?液转变区域即糊状区本应存在厚度, 因此需对其进行光滑过渡, 常采用误差函数进行处理[31]. 此处为了方便, 直接借助COMSOL内置的光滑阶跃函数flc2hs(x, d), 该函数能满足具有连续的二阶导数[32]. 从而式(8)进一步表示为







$$lambda = Hleft( alpha
ight) = 1 - {
m{flc2hs}}left( {alpha - {alpha _{
m{c}}},Delta alpha /2}
ight)$$
(9)

式中, ?α表示过渡段宽度值, 通过对比分析不同取值下的结果差异, 综合实际模型需要, 最终采用?α = 0.05. 为了便于后文分析, 此处定义氧气浓度分数θ以衡量氧浓度变化







$$theta = frac{{[{{
m{O}}_2}]}}{{{{[{{
m{O}}_2}]}_0}}}$$
(10)

式中, [M]0和[O2]0分别为单体与氧气的初始物质的量浓度.


1.3
树脂流动及相变过程


液相区域树脂的运动可视作不可压缩牛顿流体的层流流动, 而固相区域为已成型部分, 将随提升平台以恒定速度V0沿z轴正向运动. 为同时实现树脂在两种状态下的运动, 并同时捕获其相变过程, 在N-S方程中加入体力项S. 由于液膜区域极薄(通常小于100 μm), 重力引起的压强变化将远小于膜内压力分布, 因此忽略重力, 可得[33]







$$
ho left( {frac{{partial {boldsymbol{u}}}}{{partial t}} + {boldsymbol{u}} cdot nabla {boldsymbol{u}}}
ight) = - nabla p + mu {nabla ^2}{boldsymbol{u}} + {boldsymbol{S}}$$
(11)







$${boldsymbol{S}} = A({boldsymbol{u}} - {boldsymbol{V}})qquadqquadqquadqquad;$$
(12)







$$A = - frac{{C{{left( {1 - lambda }
ight)}^2}}}{{{lambda ^3} + q}}qquadqquadqquadquad;$$
(13)

及不可压缩流体连续性方程







$$nabla cdot {boldsymbol{u}} = {boldsymbol{0}}$$
(14)

式中, u为速度矢量, p为压力, V为固相区域的速度矢量, ρ为树脂密度, μ为动力黏度. 在实际成型过程中, 随着单体的转化度的上升, 液态树脂的黏度、密度等性质也会随之改变. 但由于本文重点研究的区域为极薄的树脂液膜层, 其由氧气对反应的抑制作用而产生, 并且液膜内的单体几乎不被消耗, 转化度为0 (见后文分析), 因此液态树脂的黏度、密度等在膜内分布均匀, 故此处将其视作常数. 函数A的值随着液相逐渐转变为固相而从0增大至较大值: 当λ = 1时, 树脂呈液相, A = 0, 式(11)即与S项无关; 当λ = 0时, 树脂呈固相, A为较大值, 为平衡式(11)的左右两侧, 则需u = V, 即以恒定速度V0向z轴正向运动. 其中, q取较小常数以避免分母为0; C为一任意的较大常数以满足A取得较大值, 通常应根据模型具体需要选用不同的取值, 当取值过小时会导致固相区域不能按照预设方向运动而违背实际物理过程, 过大时则会导致数值计算出现收敛性问题. 在反复计算测试之后, 发现当C = 1.2 × 1010 kg/(m3?s), q = 10 × 10?4时能较好的符合实际物理过程, 并获得最优的计算效果.


1.4
边界条件及收敛性分析


液膜区域上方为固相, 速度由S项中参数V指定, 下边界为固定壁面, 采用无滑移边界条件, 而外界液体与大气相通, 边界处相对压力设为零, 初始时刻速度为0, 为静水状态







$${boldsymbol{u}}(r,0,t) = {boldsymbol{0}},;;{
m{ }}{boldsymbol{u}}(r,{textit{z}},0) = {boldsymbol{0}}$$
(15)

整个模型区域树脂受到恒定的紫外光照射, 下边界通过透氧膜与外界氧气接触, 保持恒定氧浓度. 由于树脂槽中的树脂暴露于环境中, 假定其所含氧气的初始平衡浓度值与外界相同, 均为[O2]0. 右边界与树脂槽内未曝光的树脂相通, 各物质浓度均保持初始值平衡值, 上边界采用无通量边界条件, 即







$$left. {begin{array}{*{20}{l}}{[{{
m{O}}_2}] = {{[{{
m{O}}_2}]}_0};;({textit{z}} = 0}){dfrac{{partial [{{
m{O}}_2}]}}{{partial {textit{z}}}} = 0;;({textit{z}} = {H_0}})!!{[{{
m{O}}_2}] = {{[{{
m{O}}_2}]}_0},[{
m{PI}}] = {{[{
m{PI}}]}_0}},{[{
m{M}}] = {{[{
m{M}}]}_0},[mathop {
m{X}}limits^. ] = 0};;(r = {R_0})end{array}}
ight}$$
(16)

式中, [PI]0为光引发剂初始浓度. 与仿真模型相关的各参数取值如表2所示.




表
2
仿真参数



Table
2.
Parameters used in this study



table_type1 ">
ParameterValueUnitsRef.
kp 114.5 m3/(mol·s) [29]
kt 1337 m3/(mol·s) [29]
kO 5 × 105 m3/(mol·s) [29]
DO 1.08 × 10?10 m2/s [29]
H0 300 μm ?
I0 20 mW/cm2 ?
R 450 μm ?
R0 455 μm ?
ε 20 m3/(mol·m) [34]
φ 0.8 ? [35]
V0 5 × 10?2 mm/s ?
αc 0.12 ? [36]
?α 0.05 ? ?
[M]0 4.64 × 103 mol/m3 [28]
[PI]0 54.55 mol/m3 [28]
[O2]0 0.52 mol/m3 ?
μ 0.2 Pa·s [37]
ρ 1080 kg/m3 [38]





下载:
导出CSV
|显示表格



本文搭建的模型形状为规则的矩形, 因此为了减少网格数量并提高计算效率, 均采用结构网格划分. 由于曝光区域边界位置变化梯度大, 因此对右边界进行局部加密; 考虑下边界为壁面, 同时存在由液相至固相的过渡, 因此对该处也进行加密处理. 经过网格独立性验证, 采用270000个单元的结构化网格进行计算分析, 具体划分为nr × nz = 450 × 600, 最小单元尺寸0.09 μm.

上述物理模型通过商业有限元软件COMSOL Multiphysics 5.4进行建模, 采用瞬态求解器进行隐式求解, 计算时长设置为8 s, 整个模拟过程可概述为:

(1)初始时刻均为液态, 流体静止;

(2)受到紫外光照射, 氧气开始消耗, 单体开始转化, 逐渐由液态转变为固态;

(3)转变为固态的区域开始以恒定速度向上提升, 未固化液体被不断填充至空缺部位, 并持续反应, 最终达到稳定状态.


2.
仿真结果


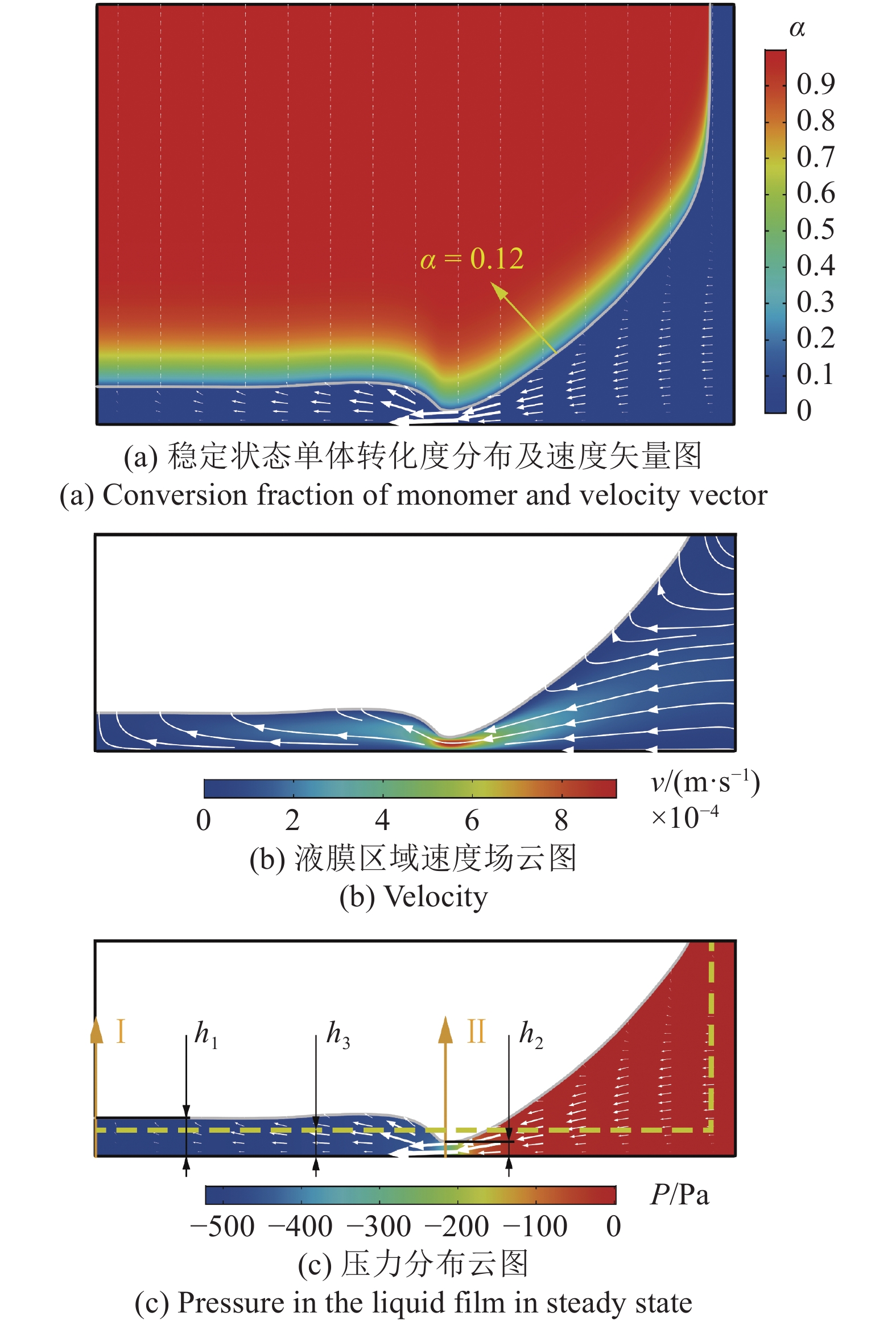
以上模型用来模拟DLP打印成型过程, 至8 s时可视作流场达到稳定, 该时刻固化区域的单体转化度分布以及速度矢量图如图2(a)所示. 灰色实线为临界转化度αc等值线, 根据前文描述此处可将其定义为固?液界面, 呈现出稳定的非均匀波浪衰减形貌, 液膜厚度极小且在边界处波动剧烈, 致使液膜区域出现狭缝段, 由外至内呈现紧缩的特征. 灰色实线以上的区域单体转化度较高, 表现为固相, 以恒定速度V0向z轴正向运动; 其余区域为液相, 液态树脂从液膜外部逐渐流动并填充至液膜内部, 流经狭缝段时流速剧增, 如图2(b)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-099-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
仿真结果



Figure
2.
Simulation result



下载:
全尺寸图片
幻灯片


以往研究中针对DLP成型过程中吸附力的预测模型与经验公式基本都是基于逐层固化过程进行推导的[19, 39-40], 即忽略固化时树脂的流动, 将提升过程近似简化为中间充满黏性液体的极窄间隙的两平板的匀速分离, 吸附力Fs可近似表示为[41-42]







$${F_{
m{s}}} = intlimits_varOmega { - p{
m{d}}varOmega } = frac{{3{text{π}} mu {V_0}{R^4}}}{{2{h^3}}}$$
(17)

式中, p为压力, R为圆柱样品半径, h为液膜厚度, 且满足h $ll $ R.

仿真结果表明, DLP连续成型过程中固?液界面的形貌并不是均匀的平面, 与以往研究中的假设存在差异. 为了探究固?液界面形貌的不同而导致压力分布的变化, 本文对DLP成型过程中液膜区域压力分布进行了分析, 如图2(c)所示. 紧缩段沿径向的压力梯度大, 变化剧烈, 其余位置压力的径向变化趋势相对平缓, 液膜边界压力接近于外界大气压, 越靠近轴线处压力值越大. 由式(17)可知, 对于两圆形平板的匀速分离过程, 其间液体的压力及吸附力均与间隙厚度h的三次方成倒数关系, 即随着h的降低, 压力与吸附力将急剧上升. 而在本模型中, 由于紧缩区域液膜厚度h小于其余区域, 从而导致该处流动阻力较大, 沿径向的压力梯度远高于其余位置.

由于固?液界面形貌较为复杂, 为定量分析液膜整体厚度的变化及影响情况, 定义等效厚度h3(即图2(c)中黄色虚线与下边界之间的距离), 使其满足式(17), 等效于两平板的分离过程, 即F = Fs. 其中, F为本模型所得的吸附力大小, 可通过模型下边界Ω处的压力积分近似表示[39]. 同时, 选取两处关键位置: 中心轴线(Ⅰ)及狭缝区域最薄点(Ⅱ), 如图2(c)中橙色箭头所示, 将其液膜厚度分别定义为h1和h2.

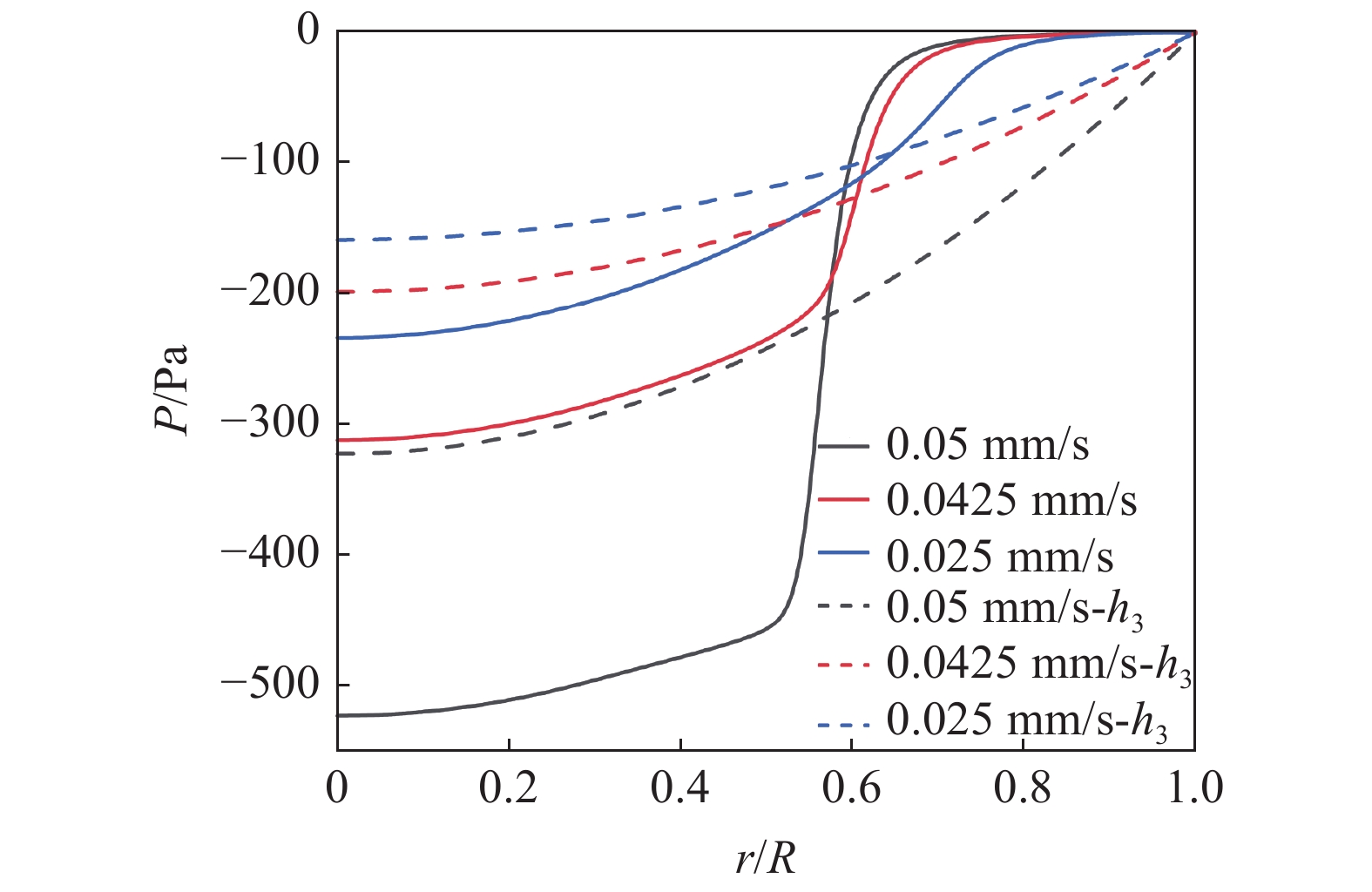
图3为提升速度V0分别为0.025, 0.0425和0.05 mm/s 3种情况下, 模型下边界Ω表面及其对应等效过程沿径向的压力分布. 在保持总吸附力相同时, DLP成型过程的径向压力分布完全不同于已有研究所采用的近似简化模型. 简化模型将该过程视作两平板的匀速分离, 压力分布没有出现突变, 其大小与r2成线性关系. 而本文构建的模型, 因存在狭缝区域而导致的压力出现突增, 且随着速度的增大, 突增区域径向压力梯度增大, 压力增量增大, 与以往研究中所作假设的差异进一步加大. 这是由于在速度较高的情况下, 随着速度的增大, h2逐渐降低, 而h1随之增大, 液膜厚度的不均匀性增大(见后文分析). 因此, 为进一步分析DLP成型过程中吸附力的影响机制, 应主要针对不同因素对固?液界面形貌的影响情况.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-099-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
径向压力分布



Figure
3.
Radial distribution of pressure



下载:
全尺寸图片
幻灯片



3.
分析与讨论



3.1
成型区液膜的演化过程


固?液界面的形貌及液膜厚度会直接影响吸附力的大小, 为探究对吸附力的影响机制, 首先对成型区液膜的演化过程进行分析. 图4为1.5 s, 2.5 s, 3.5 s, 5 s及8 s时刻成型区域的单体转化度分布和氧气浓度分布, 其中白色箭头与红色箭头分别表示对应物质的对流通量与扩散通量. 在本模型中未考虑单体的分子扩散, 因此图4(a)中仅出现对流通量. 由于当单体转化度超过临界值αc后即视为固态(图4(a)中红色区域), 不是本文研究的重点, 故只考虑低转化度部分(α < 0.12).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-099-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
氧气浓度及单体转化度分布随时间的变化



Figure
4.
Variation of the conversion fraction of monomer and oxygen concentration with time



下载:
全尺寸图片
幻灯片


Dendukuri等[27]研究表明, 自由基聚合反应过程中, 当氧气含量消耗至低于临界值θc (趋近于0)后, 单体才开始反应. 将液膜区域氧气浓度高于临界值θc的部分定义为抑制层, 低于θc的部分定义为反应层, 液膜将主要受抑制层厚度的影响. 如图4(a)所示, 液相区域单体转化度总体趋近于0, 而在贴近固?液界面位置出现一段极窄的过渡区域(即反应层). 白色实线表示氧浓度θ = 0.01的等值线, 可见低氧浓度等值线与固?液界面近似重合(即抑制层与液膜近似重合).

图4(b)为不同时刻氧气的浓度分布及其扩散通量与对流通量的矢量图, 灰色实线表示固?液界面. 由式(6)可知, 氧气浓度的变化由对流传质、分子扩散及反应消耗的共同作用导致. 由于沿径向流速较快, 尺度相对较大, 氧气的传递以对流传质为主; 而沿轴向流速较慢, 尺度较小, 分子扩散的作用效果得以体现.

整个过程经历了如图4所示的几个阶段: 首先形成厚度均匀的液膜(1.5 s), 随后出现紧缩形貌(2.5 s)并产生狭缝区域(3.5 s), 然后界面转变为迅速衰减的非均匀波浪形貌(5.0 s), 最终达到稳定状态(8.0 s). 氧气浓度的升高引起液膜增厚, 氧气浓度降低则导致液膜变薄. 该变化过程与氧气的对流传质与分子扩散密切相关, 而对流传质过程受控于流场分布, 固相的提升速度与固?液界面形貌的变化将影响流场分布, 此外形貌的变化取决于氧气的消耗与浓度分布情况. 因此, 对于DLP成型过程, 提升速度、外界氧气浓度、光照强度及截面尺寸等因素都将对打印过程产生影响, 进而引起固?液界面形貌的变化, 并改变液膜区域的压力分布与提升过程中的吸附力大小.


3.2
提升速度的影响


提升速度是DLP成型过程非常关键的一项工艺参数, 与成型质量、成型效率等有着密切的联系. 为了分析其对成型过程的具体影响, 选取并对比了0.0125 ~ 0.05 mm/s之间的不同提升速度, 在20 mW/cm2光强、0.52 mol/m3氧浓度下, 打印直径900 μm实心圆柱样品至稳定状态时, 其固?液界面的形貌、液膜厚度及吸附力大小的变化情况, 如图5(a)与图5(b)所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-099-5.jpg'"
class="figure_img
figure_type2 ccc " id="Figure5" />



图
5
固?液界面形貌及吸附力的影响因素



Figure
5.
Influence factors of profiles of solid-liquid interface and suction force



下载:
全尺寸图片
幻灯片


图5(a)描绘了不同速度下的固?液界面形貌, 可以看出, 随着提升速度的增大, 液膜厚度的不均匀性增大, 振幅增大, 侧面成型精度降低, 狭缝段的位置逐渐向中心轴线移动. 在液膜中心区域, 氧气主要通过沿轴向的分子扩散与沿轴向的对流传质进行物质传递. 分子扩散由浓度梯度驱动, 轴线位置处速度的径向分量为零, 轴向分量随提升速度V0的增大而增大, 因此提高提升速度将引起该位置沿z轴正向的对流通量分量增大, 导致氧浓度升高, 使得液膜厚度增大, 如图5(b)中曲线h1所示, 并且可以观察到厚度与提升速度V0近似成线性关系. 随着V0的增大, 液膜区域的流体径向流速增大, 引起液膜边界区域氧气对流通量增大, 氧浓度升高, 从而使液膜狭缝段向中心移动, 液膜边界增厚, 侧面成型精度降低.

由图5(b)曲线h2可见, 液膜最薄点厚度随着V0的增大存在先略微上升后降低的变化趋势, 这是因为不同的提升速度不仅会改变树脂的填充速度, 同时也会影响固?液界面的形貌, 引起流场分布的变化. 由图5(b)曲线h3可知, 等效厚度在提升速度较低时随V0的增大而增大; 在提升速度较高时随V0的增大而减小. 由式(17)可知, 对于两平板的分离过程, 吸附力与提升速度成线性关系; 而对于DLP成型在高速打印过程中, 随着提升速度的增大, h2逐渐减小, 并导致等效厚度h3的降低, 使吸附力急剧增加, 如图5(b)曲线F所示. 因此, 改变提升速度一方面会直接影响吸附力的大小, 另一方面会因为改变固?液界面形貌而间接导致吸附力的变化.


3.3
氧气浓度与光强的影响


氧气浓度与紫外光光强在聚合反应中具有重要的作用, 将显著的影响反应速率与交联密度. 图5(c)与图5(d)描述了在20 mW/cm2光强下, 以0.05 mm/s的提升速度, 打印直径900 μm实心圆柱样品时, 其固?液界面形貌、液膜厚度与吸附力大小随不同外界氧气浓度[O2]0的变化情况. 随着外界氧气浓度的增大, 扩散进入树脂的氧含量增大, 抑制层增厚, 总体液膜厚度增大, 吸附力得到大幅度下降. 但由于打印过程中由液膜外界通过对流进入液膜区域的树脂氧含量也相应提高, 从而严重影响了成型精度.

图5(e)和图5(f)描述了以0.05 mm/s的提升速度在0.52 mol/m3外界氧气浓度的条件下, 分别以不同的光强进行打印时固?液界面形貌、液膜厚度与吸附力大小的变化情况. 可见, 降低光强同样能增大液膜整体厚度, 降低吸附力, 但同时也将严重影响成型精度. 这是由于降低光强引起自由基的生成速率降低, 链引发、链增长、链终止以及氧气抑制的反应速率均下降, 进而导致固化区域氧气含量增大, 液膜增厚.

不同的样品尺寸、截面形状等参数也会对成型过程中的固?液界面形貌及吸附力等产生影响, 但其取决于打印样品的具体应用需求, 不受工艺过程调控. 此外, 光引发剂的含量、链增长速率常数、链终止速率常数等同样也会影响成型过程, 但其由树脂的材料成分与性质所控制, 不在本文研究范围, 对于以上因素均不做进一步分析.


3.4
吸附力的降低措施


通过调节前文所述的各项参数均能实现对成型过程的调控以降低吸附力. 但由于提高提升速度是工业应用中的一个重要目标, 不能随意调节; 而氧含量的精确控制也难以实现. 因此本节内容提供一种通过控制光强以降低吸附力的思路.

液膜区域的狭缝段增大了树脂流动阻力, 是导致过大吸附力出现的关键因素. 通过整体降低光强的方式能有效增大液膜厚度, 但会显著影响成型精度. 因此此处通过调整光强分布, 针对性地降低狭缝区域的入射光强, 尝试提高狭缝区域的厚度以降低吸附力.

为验证该方法的有效性, 基于前文所述模型, 将均匀分布的入射光强改变为不均匀分布. 狭缝区域分布范围为0.51 < r/R < 0.64, 故将该区域内的紫外光强选择性地衰减至一定值, 其余区域则保持原强度. 分别测试了0.25, 0.5, 0.75, 0.875 4种不同的衰减倍数, 图6(a)中各曲线分别表示采用各衰减倍数时入射光强的径向分布. 图6(b)为不同衰减倍数下达到稳定状态时液膜区域的径向压力分布, 可见其存在相同的变化趋势, 但随着衰减倍数的增大, 狭缝段压力的增量显著降低, 这是由于最薄处液膜厚度得到了有效的提升, 而其余位置厚度未发生明显变化, 同时固?液界面形貌的不均匀性得到了有效改善, 如图6(c)所示. 图6(d)为达到稳定状态时吸附力大小随衰减倍数的变化关系, 可见随着衰减倍数增加, 吸附力迅速减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-099-6.jpg'"
class="figure_img
figure_type2 ccc " id="Figure6" />



图
6
成型过程的改进措施及效果



Figure
6.
Improvement measures and results



下载:
全尺寸图片
幻灯片


当选定区域光强衰减0.875倍时, 最薄处液膜厚度提高了55%, 并且中心轴线位置压力值降低了60%, 吸附力降低了68%. 因此, 通过采用不均匀光强照射, 能有效降低吸附力, 提高成型速度.


4.
结论


通过搭建耦合了自由基光聚合反应动力学、固?液相变及流体流动的多物理场模型, 采用已有文献中的材料属性, 研究了DLP成型过程的物理机理, 分析了成型区树脂液膜在传质、光聚合、固化沉积、氧阻聚等共同作用下的演化过程, 讨论了打印速度、氧气浓度分布、紫外光强等因素对固?液界面形貌以及吸附力的影响, 同时还提出了一种通过调整光强分布降低吸附力的有效措施, 对研究不同类型的树脂光固化增材制造技术具有重要的借鉴意义, 主要结论如下:

(1) 发现固?液界面呈现出稳定的非均匀波浪衰减形貌, 液膜厚度极小且在边界处波动剧烈, 致使压力沿径向出现阶跃式的剧增, 这不同于以往研究中的均匀界面假设.

(2) 成型区树脂液膜的演化与氧气的浓度分布及对流传质与分子扩散过程密切相关, 其厚度分布取决于氧气抑制层厚度分布.

(3) 提升速度、外界氧气浓度及入射光强均会对成型过程产生影响. 在高速打印过程中, 提高打印速度能引起等效厚度的下降, 导致吸附力急剧上升; 提高外界氧浓度、降低光照强度均能有效降低吸附力, 但会显著影响成型精度.

(4) 通过针对性的减弱狭缝段的光照强度能有效的降低吸附力, 改善固?液界面形貌的不均匀性, 提高打印速度.

本文从仿真的角度对DLP成型过程吸附力的产生与影响机制进行了较为深入的分析, 但缺乏定量的实验验证, 仍需进一步开展实验方面的研究. 此外, 虽然提出了一种降低吸附力并提高打印速度有效措施, 但仅仅是提供了一种解决思路, 仍需进一步的实验验证与更深入、更系统的量化研究.

相关话题/过程 物理 物质 计算 技术

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.