引言
近年来, 随着对临近空间战略意义认识的加深, 各航空航天大国发展了众多临近空间飞行器. 为满足长航时、大载荷、高超声速巡航等需求, 这类临近空间飞行器通常整体尺寸较大, 各部件间差异显著, 飞行过程会出现多物理多场耦合、多流区共存的多尺度复杂流动现象, 传统的数值模拟方法如基于宏观连续介质假设的纳维?斯托克斯(N-S)方程、模拟微观分子运动与碰撞的直接模拟蒙特卡洛(DSMC)方法难以满足多尺度一体化模拟需求, 需要研究发展新的模拟手段[1-4]. 本文从介观气体分子速度分布函数满足的方程即玻尔兹曼方程[5-7]出发开展多尺度流动一体化模拟研究.
玻尔兹曼方程作为气体动理学理论的基本方程, 能描述各流域气体流动输运现象, 但它是一个高度非线性的积分?微分方程, 其理论解和直接数值求解均难以实现[7]. 为利用玻尔兹曼方程能统一描述各流域气体流动的特性, 众多****提出了系列替代求解技术, 其中应用最广泛的是模型方程方法, 即用一个相对简单的表达式替换玻尔兹曼方程碰撞积分项[8], 再对简化后的偏微分方程进行求解.
模型方程作为玻尔兹曼方程的近似, 必须满足玻尔兹曼方程的基本属性, 如总和不变量性质、H定理、正确的输运系数等. 第一个也是最著名的模型方程是巴特纳?格罗斯?克鲁克模型[8](BGK模型), 但通过对其进行查普曼?恩斯科(Chapman?Enskog)展开分析得到的普朗特数(Pr)为1, 而单原子气体的Pr约为2/3[9]. 为克服这一缺陷, 国内外****提出了一系列模型方程, 包括椭球统计?BGK (ES-BGK)模型[10-11]、沙克霍夫(Shakhov)模型[12-13]、刘(Liu)模型[14]、贝利(Belyi)模型[15]等, 这些模型方程均假定其碰撞频率与分子速度无关. 此外, 也有****发展了考虑碰撞频率与分子速度相关性的模型方程[16]以及适于多原子气体、考虑热力学非平衡的模型方程[17].
大量数学分析表明[16, 18-20], 上述模型方程均能满足玻尔兹曼方程的基本属性, 且与原始玻尔兹曼方程的碰撞项具有类似的松弛特性, 能保持与纳维?斯托克斯方程、直接模拟蒙特卡洛方法的收敛一致, 因结构简单、贴近跨流域流体物理变化特点、可计算技术针对性强而得到广泛应用[21], 如泰塔雷夫(Titarev)建立了物理空间和速度空间均采用非结构网格的内斯韦塔依(Nesvetay)求解器[22-23], 针对返回式空间飞行器等高马赫数流动与直接模拟蒙特卡洛方法进行了系列对比分析. 李志辉等[24-31]从研究描述各流域均适用的气体分子速度分布函数方程出发, 吸收计算数学指数型积分求解原理, 发展了气体分子运动论离散速度坐标法, 研制经改进的高斯?埃尔米特积分方法等系列离散速度数值积分技术, 消除气体分子速度分布函数对速度空间的连续依赖性, 将玻尔兹曼模型方程化为在各个离散速度坐标点处具有非线性源项的双曲型守恒方程, 基于计算流体力学数值求解技术, 构造直接求解速度分布函数演化更新的气体动理论数值格式和大规模并行计算策略, 建立了气体动理论统一算法(GKUA), 开展了自由分子流到连续流复杂高超声速气动力/热问题大规模并行计算及其在航天工程中的应用研究, 同时对跨流域多体干扰流动问题、跨流域非定常流动问题进行了研究, 获得较好的成功. 徐昆等[32-37]利用上述离散速度坐标法与BGK类型格式相耦合, 发展了统一气体动理学格式(UGKS), 使之适于模拟稀薄流到连续流气体流动问题.
另一方面, 从流动反映的物理现象来看, 当流场中出现非平衡现象时, 某点的速度分布函数已经不再是简单的麦克斯韦平衡态分布, 而是呈现各种形态, 如双峰分布、偏心分布等[38]. 这些分布与当地的气体分子速度、流场宏观速度、温度以及热流矢量、应力张量等宏观输运性质相关, 这从玻尔兹曼方程的查普曼?恩斯科分析解[5, 39]可以看出. 因此在对玻尔兹曼方程碰撞积分进行物理分析、构造碰撞项的模型方程时应同时考虑这些因素, 而常用的玻尔兹曼碰撞积分模型如沙克霍夫模型没有考虑应力张量的影响, ES-BGK模型属于各向异性的类麦克斯韦分布, 没有考虑热流矢量的影响. 当模型方程不能全面反映这些因素时会导致模拟结果出现系统误差, 例如在稀薄过渡流区流动的克努森层内黏性效应占主导, 应考虑应力张量的影响, 沙克霍夫模型与直接模拟蒙特卡洛方法模拟结果存在较大差别[40].
为此, 本文将从玻尔兹曼方程出发, 基于查普曼?恩斯科渐近分析解[9]的数学推导, 构造一种同时考虑热流矢量和应力张量影响、满足玻尔兹曼方程高阶碰撞矩的综合型可计算碰撞模型, 并在数学上分析其基本属性, 建立与玻尔兹曼方程的联系, 给出新模型与现有模型方程的关系, 同时基于碰撞动力学确定该可计算模型碰撞松弛参数表达式. 最后在气体动理论统一算法框架下, 使用该新建玻尔兹曼方程可计算模型, 通过模拟一维激波结构、二维近空间飞行环境平板和多体圆柱干扰流动来验证新模型的有效性和可靠性.
1.
模型方程的构造
玻尔兹曼方程是描述气体分子速度分布函数
ight)$
$$ frac{{partial f}}{{partial t}} + sumlimits_i {{V_i}frac{{partial f}}{{partial {r_i}}}} = Sleft( f ight) = {left( {frac{{partial f}}{{partial t}}} ight)_{ m{col}}} $$  | (1) |
其中,
ight)$
ight)_{
m{col} }} $
在确定速度分布函数
ho $
$$ ho = mn = iiint_{{{mathbb{R}}^3}} {mf{ m{d}} W} $$  | (2) |
$$ ho {U_i} = mn{U_i} = iiint_{{{mathbb{R}}^3}} {m{V_i}f{ m{d}} W} $$  | (3) |
$$ ho {e_{ m{tr}}} = frac{3}{2}n{{{k}}_{ m{B}}}T = iiint_{{{mathbb{R}}^3}} {frac{m}{2}{{left| {boldsymbol{C}} ight|}^2}f{ m{d}} W} $$  | (4) |
$$ {P_{ij}} = iiint_{{{mathbb{R}}^3}} {m{C_i}{C_j}f{ m{d}} W} $$  | (5) |
$$ {q_i} = iiint_{{{mathbb{R}}^3}} {frac{m}{2}{C_i}{{left| {boldsymbol{C}} ight|}^2}f{ m{d}} W} $$  | (6) |
其中,
m{d}}} W = {{
m{d}}} {V_x}{{
m{d}}} {V_y}{{
m{d}}} {V_{textit{z}}}$
m{B}}}$
ight|^2} = {C^2} = C_x^2 + C_y^2 + C_{textit{z}}^2 $
m{tr}}}$
$$ p = n{{{k}}_{ m{B}}}T quadqquad$$  | (7) |
$$ {tau _{ij}} = - left( {{P_{ij}} - {delta _{ij}}p} ight) $$  | (8) |
这里, 符号
气体动理论统一算法所用玻尔兹曼方程可计算模型[24-31]可以写为
$$ frac{{partial f}}{{partial t}} + sumlimits_i {{V_i}frac{{partial f}}{{partial {r_i}}}} = {S_{ m{m}} }left( f ight) = nu left( {{f^{ m{N}} } - f} ight) $$  | (9) |
这里,
m{N}} } $
$$ f_{ m{S}} ^{ m{N}} = {f_{ m{M}} }left[ {1 + left( {1 - Pr} ight)frac{{mdisplaystylesumlimits_i {{C_i}{q_i}} }}{{p{{{k}}_{ m{B}}}T}}left( {frac{{m{C^2}}}{{5{{{k}}_{ m{B}}}T}} - 1} ight)} ight] $$  | (10) |
$$ f_{ m{VVB}}^{ m{N}} = {f_{ m{M}} }left[ {1 + frac{{Pr - 1}}{{Pr}}left( { - msumlimits_{i,j} {frac{{{tau _{ij}}{C_i}{C_j}}}{{2p{{{k}}_{ m{B}}}T}}} } ight)} ight]quad;;; $$  | (11) |
这里
m{M}} }$
$$ {f_{ m{M}} } = frac{n}{{{{left( {2{{text{π}} }{{{k}}_{ m{B}}}T/m} ight)}^{3/2}}}}{{ m{e}} ^{ - frac{{m{C^2}}}{{2{{{k}}_{{ m{B}}}}T}}}} $$  | (12) |
任何一个模型方程都必须满足玻尔兹曼方程碰撞积分的如下3个基本属性[39].
(1)守恒性(质量、动量、能量守恒), 即
$$ iiint_{{{mathbb{R}}^3}} {m{S_{ m{m}} }left( f ight){ m{d}} W} = 0 ;;$$  | (13) |
$$ iiint_{{{mathbb{R}}^3}} {m{V_i}{S_{ m{m}} }left( f ight){ m{d}} W} = 0 $$  | (14) |
$$ iiint_{{{mathbb{R}}^3}} {frac{m}{2}{V^2}{S_{ m{m}} }left( f ight){ m{d}} W} = 0 $$  | (15) |
其中
(2) H定理, 即
$$ Hleft( t ight) = iiint_{{{mathbb{R}}^3}} {fln f{ m{d}} W} $$  | (16) |
$$ frac{partial }{{partial t}}Hleft( t ight) leqslant 0 qquadqquad$$  | (17) |
(3)在平衡态时, 有
m{m}} }left( {{f_{
m{M}} }}
ight) = 0$
此外, 对于单原子气体, 模型方程的查普曼?恩斯科分析得到的普朗特数
为研究构造新的玻尔兹曼方程可计算模型, 首先分析其一阶查普曼?恩斯科分析解[9], 其可以写为
$$ f = {f_{ m{M}} }left[ {1 + varPhi left( {boldsymbol{C}} ight)} ight]qquadqquadqquadqquad $$  | (18) |
$$ begin{split} varPhi left( {boldsymbol{C}} ight) = &left[ {frac{m}{{p{{{k}}_{ m{B}}}T}}left( {frac{{m{C^2}}}{{5{{{k}}_{ m{B}}}T}} - 1} ight)sumlimits_i {{C_i}{q_i}} } ight] - & { msumlimits_{i,j} {frac{{{tau _{ij}}{C_i}{C_j}}}{{2p{{{k}}_{ m{B}}}T}}} }end{split} $$  | (19) |
显然,
ight)$
ight)$
从玻尔兹曼方程的查普曼?恩斯科分析解可以看出, 流场中气体的速度分布函数与局部宏观流动参数如速度、热流、应力等相关, 而沙克霍夫模型没有考虑应力的影响, 贝利模型没有考虑热流的影响. 当流场中局部区域的温度、速度梯度较大即热流和应力影响显著时, 将出现较为严重的非平衡效应, 仅考虑单一因素难以准确模拟复杂非平衡现象. 因此, 可以依据玻尔兹曼方程的查普曼?恩斯科分析解以及常用模型方程的表达式, 构造如下同时考虑热流和应力影响的新型玻尔兹曼方程可计算模型
$$ frac{{partial f}}{{partial t}} + sumlimits_i {{V_i}frac{{partial f}}{{partial {r_i}}}} = {nu ^{ m{N}}}left( {f_{ m{mix}}^{ m{N}} - f} ight) $$  | (20) |
$$ f_{ m{mix}}^{ m{N}} = {f_{ m{M}}}left[ {1 + A cdot {varPhi _{ m{A}} }left( {boldsymbol{C}} ight) + B cdot {varPhi _{ m{B}} }left( {boldsymbol{C}} ight)} ight] $$  | (21) |
$$ {varPhi _{ m{A}} }left( {boldsymbol{C}} ight) = frac{m}{{p{{{k}}_{ m{B}}}T}}left( {frac{{m{C^2}}}{{5{{{k}}_{ m{B}}}T}} - 1} ight)sumlimits_i {{C_i}{q_i}} $$  | (22) |
$$ {varPhi _{ m{B}} }left( {boldsymbol{C}} ight) = - msumlimits_{i,j} {frac{{{tau _{ij}}{C_i}{C_j}}}{{2p{{{k}}_{ m{B}}}T}}} $$  | (23) |
这里, A和B是与分子速度无关的常量,
m{N}}} $
ight)/Pr $
2.
新型玻尔兹曼模型方程的数学分析
在构造玻尔兹曼方程的一个新模型后, 需要对其性质进行分析, 验证其是否满足玻尔兹曼方程碰撞积分项的基本属性.
2.1
守恒性
由于
$$ iiint_{{{mathbb{R}}^3}} {mf_{ m{mix}}^{ m{N}}{ m{d}} W} = ho $$  | (24) |
$$ iiint_{{{mathbb{R}}^3}} {m{V_i}f_{ m{mix}}^{ m{N}}{ m{d}} W} = mn{U_i} = ho {U_i} $$  | (25) |
$$ iiint_{{{mathbb{R}}^3}} {frac{m}{2}{V^2}f_{ m{mix}}^{ m{N}}{ m{d}} W} = frac{{3n{{{k}}_{ m{B}}}T + mn{U^2}}}{2} $$  | (26) |
$$ iiint_{{{mathbb{R}}^3}} {m{C_i}{C_j}f_{ m{mix}}^{ m{N}}{ m{d}} W} = p{delta _{ij}} - B{tau _{ij}} $$  | (27) |
$$ iiint_{{{mathbb{R}}^3}} {m{C_i}{C^2}f_{ m{mix}}^{ m{N}}{ m{d}} W} = 2A{q_i} $$  | (28) |
其中
$$ frac{{partial ho }}{{partial t}} + sumlimits_i {frac{partial }{{partial {r_i}}}left( { ho {U_i}} ight)} = 0 $$  | (29) |
$$ frac{{partial left( { ho {U_i}} ight)}}{{partial t}} + sumlimits_j {frac{partial }{{partial {r_j}}}left( { ho {U_i}{U_j}} ight)} = - frac{{partial p}}{{partial {r_i}}} + sumlimits_j {frac{{partial {tau _{ij}}}}{{partial {r_j}}}} $$  | (30) |
$$begin{split} &frac{partial }{{partial t}} ho left( {{e_{ m{tr}}} + frac{1}{2}{U^2}} ight) + sumlimits_j {frac{partial }{{partial {r_j}}}left[ { ho {U_j}left( {h + frac{1}{2}{U^2}} ight)} ight]}= &qquad { sumlimits_j {frac{partial }{{partial {r_j}}}left[ {sumlimits_k {left( {{tau _{jk}} - {U_k}} ight)} - {q_j}} ight]} } end{split} $$  | (31) |
其中
m{tr}}} + p/
ho $
在平衡态时热流和应力张量均为零, 显然此时当地麦克斯韦分布是模型方程的解.
2.2
查普曼?恩斯科分析
为开展查普曼?恩斯科分析, 首先将新模型方程的无量纲形式写成如下形式
$$ xi left( {frac{{partial hat f}}{{partial hat t}} + sumlimits_i {{{hat V}_i}frac{{partial hat f}}{{partial {{hat r}_i}}}} } ight) = {hat nu ^{ m{N}}}left( {hat f_{ m{mix}}^{ m{N}} - hat f} ight) $$  | (32) |
其中
$$ hat f = {hat f_{ m{M}} }left( {1 + xi {{hat{phi}}_1}} ight) $$  | (33) |
$$ f = {f_{ m{M}} }left( {1 + {phi _1}} ight) $$  | (34) |
经过系列数学运算并回归有量纲量后, 可得
$$ begin{split} &{varphi _1} = A cdot {varPhi _{ m{A}} }left( {boldsymbol{C}} ight) + B cdot {varPhi _{ m{B}} }left( {boldsymbol{C}} ight) - &qquadfrac{1}{{{nu ^{ m{N}} }}}left[ sumlimits_j {{C_j}left( {frac{{m{C^2}}}{{2{{{k}}_{ m{B}}}T}} - frac{5}{2}} ight)frac{{partial T}}{{Tpartial {r_j}}}}+ ight.&qquadleft. frac{m}{{{{{k}}_{ m{B}}}T}}sumlimits_{i,j} {left( {{C_i}{C_j} - frac{{{C^2}}}{3}{delta _{ij}}} ight)frac{{partial {U_i}}}{{partial {r_j}}}} ight] end{split} $$  | (35) |
由于
$$ begin{split} &{tau _{ij}} = - left( {iiint_{{{mathbb{R}}^3}} {m{C_i}{C_j}f{ m{d}} W} - {delta _{ij}}p} ight) =&qquad - iiint_{{{mathbb{R}}^3}} {m{C_i}{C_j}{phi _1}{ m{d}} W} = B{tau _{ij}} + &qquadfrac{{n{{{k}}_{ m{B}}}T}}{{{nu ^{ m{N}}}}}left( {frac{{partial {U_i}}}{{partial {r_j}}} + frac{{partial {U_j}}}{{partial {r_i}}} - frac{2}{3}{delta _{ij}}sumlimits_k {frac{{partial {U_k}}}{{partial {r_k}}}} } ight) end{split}$$  | (36) |
$$ begin{split} &{q_i} = iiint_{{{mathbb{R}}^3}} {frac{m}{2}{C_i}{C^2}f{ m{d}} W} = iiint_{{{mathbb{R}}^3}} {frac{m}{2}{C_i}{C^2}{phi _1}{ m{d}} W} = &qquadA{q_i} - frac{{n{{{k}}_{ m{B}}}T}}{{{nu ^{ m{N}} }}}frac{{5{{{k}}_{ m{B}}}}}{{2m}}frac{{partial T}}{{partial {r_i}}} end{split} $$  | (37) |
则
$$ {tau _{ij}} = frac{{n{{{k}}_{ m{B}}}T}}{{left( {1 - B} ight){nu ^{ m{N}} }}}left( {frac{{partial {U_i}}}{{partial {r_j}}} + frac{{partial {U_j}}}{{partial {r_i}}} - frac{2}{3}{delta _{ij}}sumlimits_k {frac{{partial {U_k}}}{{partial {r_k}}}} } ight) $$  | (38) |
$$ {q_i} = - frac{{n{{{k}}_{ m{B}}}T}}{{{nu ^{ m{N}} }left( {1 - A} ight)}}frac{{5{{{k}}_{ m{B}}}}}{{2m}}frac{{partial T}}{{partial {r_i}}} $$  | (39) |
进而黏性系数
$$ mu = frac{1}{{1 - B}}frac{p}{{{nu ^{ m{N}} }}} $$  | (40) |
$$ kappa = frac{5}{2}frac{{{{{k}}_{ m{B}}}}}{m}frac{p}{{{nu ^{ m{N}} }left( {1 - A} ight)}} = frac{5}{2}frac{{{{{k}}_{ m{B}}}}}{m}frac{{1 - B}}{{1 - A}}mu $$  | (41) |
$$ Pr = frac{{1 - A}}{{1 - B}} $$  | (42) |
可知对于沙克霍夫模型[12],
m{S}}} = p/mu $
ight)/Pr $
m{VVB}}} = Pr cdot p/mu $
2.3
高阶矩分析
为了进一步验证新模型方程在数学上与玻尔兹曼方程的相容性, 这里从麦克斯韦分子满足的玻尔兹曼方程高阶矩进行分析. 由于麦克斯韦分子的特殊性, 即其碰撞积分与相对速度无关, 可以得到对应的高阶矩.
定义碰撞积分项的矩为
$$ Delta Q = iiint_{{{mathbb{R}}^3}} {Q{{left( {frac{{partial f}}{{partial t}}} ight)}_{ m{col}}}{ m{d}} W} $$  | (43) |
这里
$$ Delta {{Q_1}}= Delta left( {{V_i}{V_j}} ight)= frac{p}{mu }frac{{{tau _{ij}}}}{m} $$  | (44) |
$$ Delta{{Q_2}} = Delta left( {{V_i}{V^2}} ight) = frac{{2p}}{mu }left( {sumlimits_j {frac{{{U_j}{tau _{ij}}}}{m}} - frac{{Pr{q_i}}}{m}} ight) $$  | (45) |
对于新模型方程,
$$Delta {{Q_1}} = {nu ^{ m{N}}}left( {1 - B} ight)frac{{{tau _{ij}}}}{m}$$  | (46) |
$$ Delta {{Q_2}} = {nu ^{ m{N}}}left[ {2left( {A - 1} ight)frac{{{q_i}}}{m} + 2left( {1 - B} ight)sumlimits_j {frac{{{U_j}{tau _{ij}}}}{m}} } ight] $$  | (47) |
对比可知
$$ {nu ^{ m{N}}} = frac{{Pr}}{{1 - A}}frac{p}{mu } = frac{1}{{1 - B}}frac{p}{mu } = {nu _{ m{coe}}}frac{p}{mu } $$  | (48) |
该结论与上一节一致, 这进一步证明了新模型方程与玻尔兹曼方程的相容性, 与沙克霍夫模型[12]和贝利模型[15]的一致性.
2.4
H定理的证明
定义[39]
$$ Hleft( t ight) = iiint_{{{mathbb{R}}^3}} {fln f{ m{d}} W} $$  | (49) |
为简单起见, 这里仅考虑
$$ frac{{partial f}}{{partial t}} = {nu ^{ m{N}}}left( {f_{ m{mix}}^{ m{N}} - f} ight) $$  | (50) |
的情况. 则
$$ begin{split} &frac{partial }{{partial t}}Hleft( t ight) = iiint_{{{mathbb{R}}^3}} {frac{{partial f}}{{partial t}}ln f{ m{d}} W} + iiint_{{{mathbb{R}}^3}} {ffrac{{partial ln f}}{{partial t}}{ m{d}} W} = &qquadiiint_{{{mathbb{R}}^3}} {{nu ^{ m{N}} }left( {f_{ m{mix}}^{ m{N}} - f} ight)ln f{ m{d}} W} end{split} $$  | (51) |
即
$$ begin{split} &frac{partial }{{partial t}}Hleft( t ight) = {nu ^{ m{N}} }iiint_{{{mathbb{R}}^3}} {left( {f_{ m{mix}}^{ m{N}} - f} ight)ln frac{f}{{f_{ m{mix}}^{ m{N}}}}{ m{d}} W} +&qquad {nu ^{ m{N}}}iiint_{{{mathbb{R}}^3}} {left( {f_{ m{mix}}^{ m{N}} - f} ight) left[ {ln {f_{ m{M}} } + ln left({1 + varPhi _{ m{mix}}^{ m{N}}} ight)} ight]{ m{d}} W} end{split} $$  | (52) |
其中
m{mix}}^{
m{N}} = left( {1 - dfrac{{Pr}}{{{nu _{
m{coe}}}}}}
ight){varPhi _{
m{A}} }left( {boldsymbol{C}}
ight) + left( {1 - dfrac{1}{{{nu _{
m{coe}}}}}}
ight){varPhi _{
m{B}} }left( {boldsymbol{C}}
ight)$
由于当
$$ ln left( {1 + x} ight) = x - frac{{{x^2}}}{2} + frac{{{x^3}}}{3} - cdots + {left( { - 1} ight)^{l + 1}}frac{{{x^l}}}{l} $$  | (53) |
且从查普曼?恩斯科分析的过程可知分布函数
m{M}} }$
$$ begin{split} &iiint_{{{mathbb{R}}^3}} {f_{ m{mix}}^{ m{N}}ln left( {1 + varPhi _{ m{mix}}^{ m{N}}} ight){ m{d}} W} = iiint_{{{mathbb{R}}^3}} {f_{ m{mix}}^{ m{N}}varPhi _{ m{mix}}^{ m{N}}{ m{d}} W} = &qquadfrac{{2{{left( {1 - Pr/{nu _{ m{coe}}}} ight)}^2}{q^2}}}{{5p{{{k}}_{ m{B}}}T cdot {{{k}}_{ m{B}}}T/m}} + frac{{{{left( {1 - 1/{nu _{ m{coe}}}} ight)}^2}displaystylesumlimits_{i,j} {tau _{ij}^2} }}{{2p{{{k}}_{ m{B}}}T}} end{split} $$  | (54) |
和
$$ begin{split} & iiint_{{{mathbb{R}}^3}} {fln left( {1 + varPhi _{ m{mix}}^{ m{N}}} ight){ m{d}} W} = iiint_{{{mathbb{R}}^3}} {fvarPhi _{ m{mix}}^{ m{N}}{ m{d}} W} = &qquadleft( {1 - frac{{Pr}}{{{nu _{ m{coe}}}}}} ight)frac{{m{q^2}}}{{p{{{k}}_{ m{B}}}T}}frac{2}{{5{{{k}}_{ m{B}}}T}} - left( {1 - frac{1}{{{nu _{ m{coe}}}}}} ight)frac{{displaystylesumlimits_{i,j} {tau _{ij}^2} }}{{2p{{{k}}_{ m{B}}}T}} end{split} $$  | (55) |
合并后, 有
$$ begin{split} &frac{partial }{{partial t}}Hleft( t ight) = {nu ^{ m{N}}}iiint_{{{mathbb{R}}^3}} {left( {f_{ m{mix}}^{ m{N}} - f} ight)ln frac{f}{{f_{ m{mix}}^{ m{N}}}}{ m{d}} W} + &qquad frac{{2m{q^2}{nu ^{ m{N}}}}}{{5p{{{k}}_{ m{B}}}T cdot {{{k}}_{ m{B}}}T}}left[ {{{left( {1 - frac{{Pr}}{{{nu _{ m{coe}}}}}} ight)}^2} - left( {1 - frac{{Pr}}{{{nu _{ m{coe}}}}}} ight)} ight] +&qquad frac{{{nu ^{ m{N}} }}}{{2p{{{k}}_{ m{B}}}T}}left[ {{{left( {1 - frac{1}{{{nu _{ m{coe}}}}}} ight)}^2} + left( {1 - frac{1}{{{nu _{ m{coe}}}}}} ight)} ight]sumlimits_{i,j} {tau _{ij}^2} end{split} $$  | (56) |
由于
m{mix}}^{
m{N}} - f}
ight)$
m{mix}}^{
m{N}}}
ight)$
$$ {nu ^{ m{N}}}iiint_{{{mathbb{R}}^3}} {left( {f_{ m{mix}}^{ m{N}} - f} ight)ln frac{f}{{f_{ m{mix}}^{ m{N}}}}{ m{d}} W} leqslant 0 $$  | (57) |
当
m{mix}}^{
m{N}} = f$
$$ {left( {1 - frac{{Pr}}{{{nu _{ m{coe}}}}}} ight)^2} - left( {1 - frac{{Pr}}{{{nu _{ m{coe}}}}}} ight) leqslant 0 $$  | (58) |
且
$$ {left( {1 - frac{1}{{{nu _{ m{coe}}}}}} ight)^2} + left( {1 - frac{1}{{{nu _{ m{coe}}}}}} ight) leqslant 0 $$  | (59) |
时, 有
ight) leqslant 0$
$$ max left( {Pr,1/2} ight) leqslant {nu _{ m{coe}}} leqslant 1 $$  | (60) |
即当上述不等式成立, 且Kn较小时, 新模型方程满足H定理. 从上面数学分析过程来看,
m{coe}}}$
m{coe}}}$
2.5
碰撞松弛参数的确定
在气体动理学理论中, 根据碰撞间隔理论[39]可以推导出碰撞时间间隔
$$ mu = peta $$  | (61) |
显然, 若将
m{coe}}} $
$$ eta = frac{{4lambda }}{{{{text{π}} }bar C}}{, };;;bar C = sqrt {frac{{8{{{k}}_{ m{B}}}T}}{{{{text{π}} }m}}} $$  | (62) |
表征为分布函数松弛至其初始值的
m{e}}} $
m{e}}} $
此外在直接模拟蒙特卡洛方法中, 对于变径硬球(VHS)模型有[41]
$$ lambda = frac{{2left( {5 - 2omega } ight)left( {7 - 2omega } ight)mu }}{{15sqrt 2 {{text{π}} }n{{left( {m{{{k}}_{ m{B}}}T/{{text{π}} }} ight)}^{1/2}}}} $$  | (63) |
其中,
$$ eta = frac{{4lambda }}{{{{text{π}} }bar C}} = frac{{2left( {5 - 2omega } ight)left( {7 - 2omega } ight)mu }}{{15{{text{π}} }p}} $$  | (64) |
由此可得
$$ {nu _{ m{coe}}} = frac{{15{{text{π}} }}}{{2left( {5 - 2omega } ight)left( {7 - 2omega } ight)}} $$  | (65) |
上述
m{coe}}}$
m{mix}}^{
m{N}}$
m{e}}} $
m{coe}}}$
$$ {nu _{ m{coe}}} = frac{{15{{text{π}} }}}{{2left( {5 - 2omega } ight)left( {7 - 2omega } ight)}}left( {1 - frac{1}{{{ m{e}}} }} ight) $$  | (66) |
对于单原子气体氩气(Ar),
m{coe}}} $
m{coe}}} $
3.
数值分析
3.1
一维激波结构模拟分析
为验证本文新建模型的有效性, 首先模拟了一维激波结构. 设置激波马赫数为
m{s}} } $
图1给出了采用沙克霍夫模型、本文新建模型、贝利模型模拟的激波轮廓线与直接模拟蒙特卡洛方法结果的对比, 分别用“Shakhov” “new model” “VVB”和“DSMC”表示, 其中直接模拟蒙特卡洛方法结果由贝德(Bird)的一维可视化直接模拟(DS1V)代码[41]计算得到,
ho - {
ho _1}}
ight)/left( {{
ho _2} - {
ho _1}}
ight) $
m{s}} } $
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
不同模型模拟的激波轮廓与直接模拟蒙特卡洛方法对比
Figure
1.
Comparison of shock profiles simulated by GKUA with different models and DSMC
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
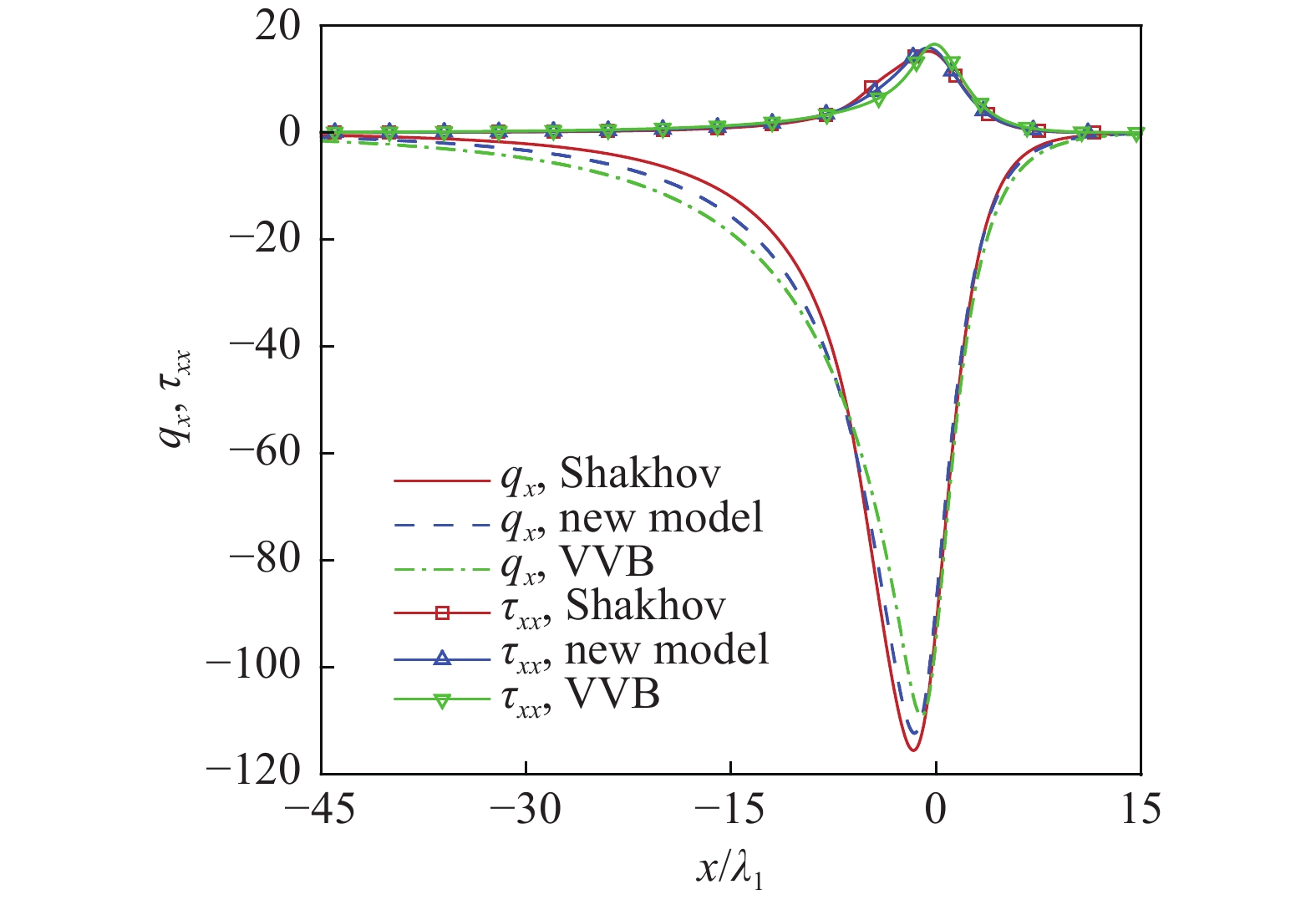
2
不同模型模拟的无量纲热流和切应力对比
Figure
2.
Comparison of non-dimensional heat fluxes and shear stresses simulated by GKUA with different models
下载: 全尺寸图片
幻灯片
3.2
平板绕流模拟分析
为研究新模型方程模拟飞行器再入时在近空间环境黏性效应急剧增加的非平衡流场中黏性应力和热流影响较大的区域流动问题, 首先考察平板绕流. 通常对于这类问题, 在克努森层内越靠近平板前缘, 温度和速度梯度越大, 非平衡效应越显著, 对应的热流和黏性效应影响也越发严重.
来流条件: 马赫数
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
本文模拟的温度云图与直接模拟蒙特卡洛方法结果对比
Figure
3.
Comparison of temperature contours simulated by GKUA with new model and DSMC
下载: 全尺寸图片
幻灯片
图4给出了在
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
Figure
4.
Comparison of pressure and temperature simulated by GKUA with different collision models and DSMC along the direction of y on the section of
下载: 全尺寸图片
幻灯片
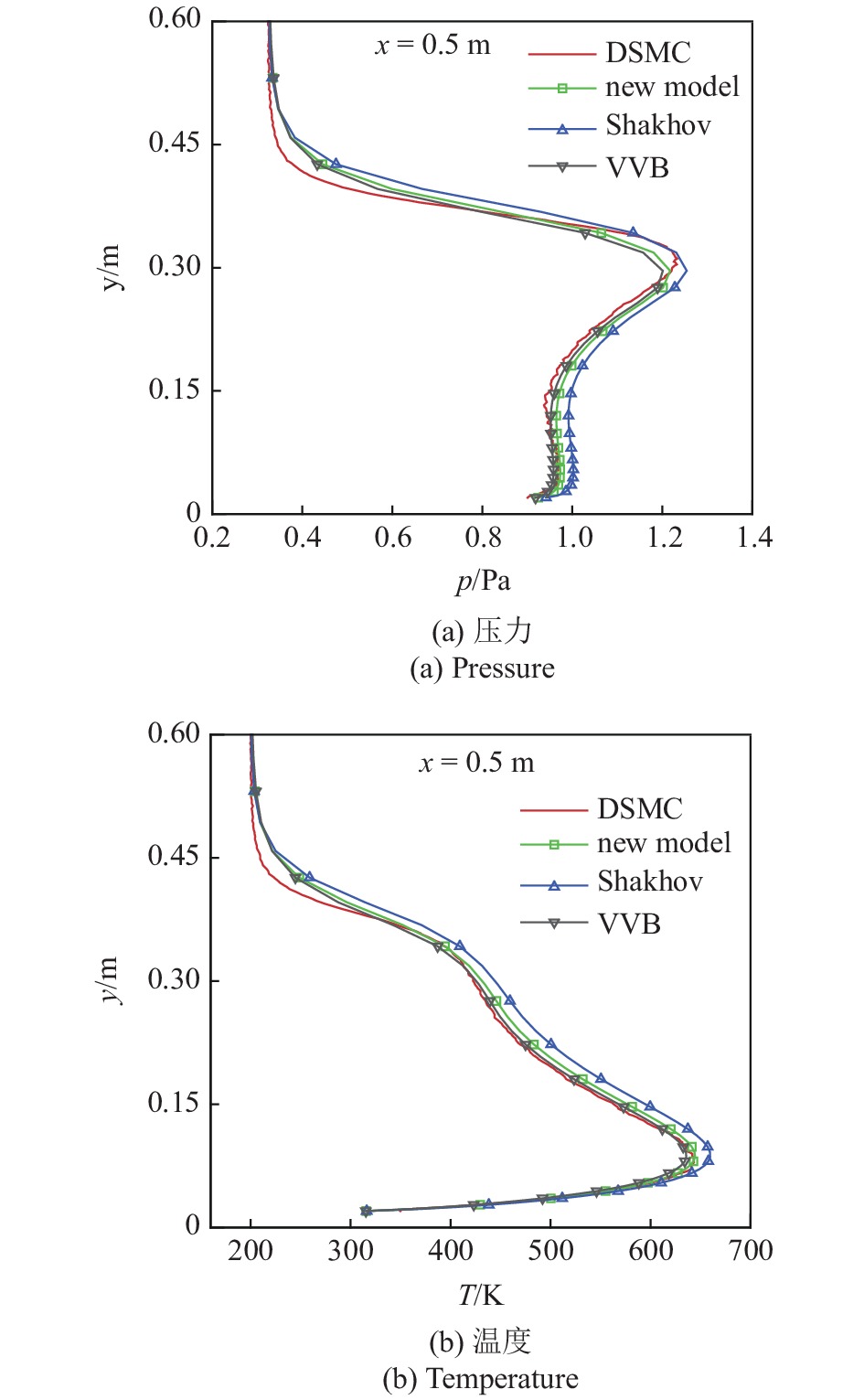
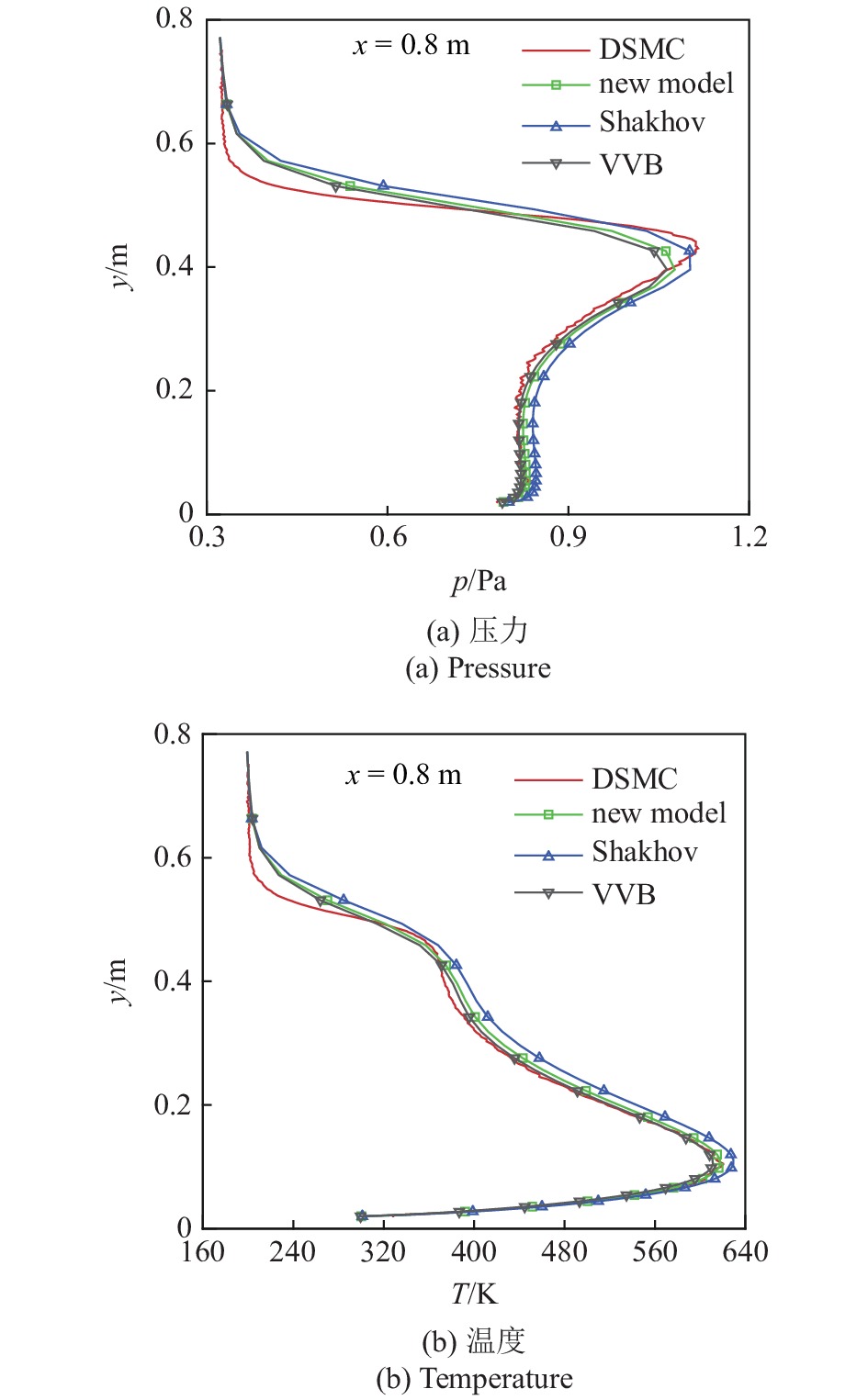
图5和图6分别给出了在
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
Figure
5.
Comparison of pressure and temperature simulated by GKUA with different collision models and DSMC along the direction of y on the section of
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
Figure
6.
Comparison of pressure and temperature simulated by GKUA with different collision models and DSMC along the direction of y on the section of
下载: 全尺寸图片
幻灯片
从图4 ~ 图6可以看出, 由于本文建立的玻尔兹曼方程新模型同时兼顾了流场中应力和热流对气体分子速度分布函数的影响, 整体而言能较好地模拟全域流动. 从统一算法计算
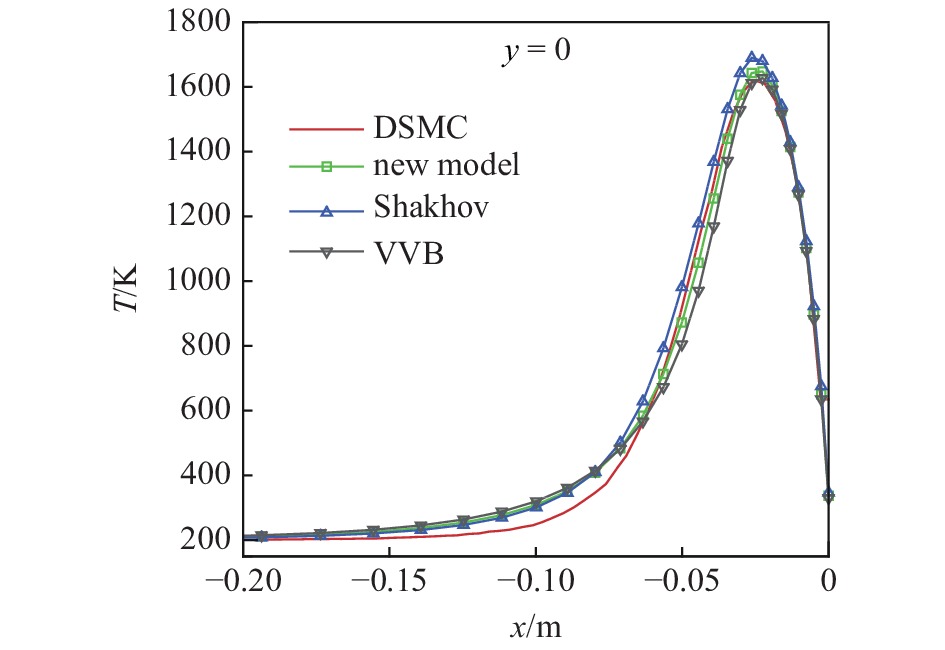
图7给出了驻点线上不同碰撞模型得到的统一算法计算温度分布与直接模拟蒙特卡洛方法模拟值对比. 平板头部压缩激波层是非平衡效应最为严重的区域, 温度梯度和速度梯度均较大. 从图中可以看出, 在近空间飞行环境激波内部, 本文建立的玻尔兹曼方程新模型统一算法计算结果始终与直接模拟蒙特卡洛方法模拟值符合较好. 这进一步说明了需要同时考虑流场中黏性应力和热流对气体分子速度分布函数演化更新的影响. 同时也看出基于玻尔兹曼方程可计算建模统一算法计算结果在驻点激波前部流动趋于近平衡态时温度高于直接模拟蒙特卡洛方法模拟值, 这与一维激波结构中温度轮廓的变化规律类似.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
驻点线上不同碰撞模型统一算法计算的温度分布与直接模拟蒙特卡洛方法模拟值比较
Figure
7.
Comparison of temperature simulated by GKUA with different collision models and DSMC along the stagnation line
下载: 全尺寸图片
幻灯片
3.3
双圆柱干扰流动模拟分析
为验证新建模型统一算法对激波干扰的模拟能力, 这里考察双圆柱干扰流动. 来流条件和计算条件及边界条件与上节一致, 圆柱直径为1 m, 两圆柱圆心间距为4 m. 在该条件下上下两个圆柱的头部脱体激波会相互作用, 形成复杂的激波干扰流动.
图8给出了分别使用3种模型方程的统一算法计算温度分布云图与直接模拟蒙特卡洛方法模拟值的对比. 两圆柱脱体激波相互作用后在
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
3种模型方程计算得到的温度分布云图与直接模拟蒙特卡洛方法结果的对比
Figure
8.
Comparison of temperature contours simulated by GKUA with three collision models and DSMC
下载: 全尺寸图片
幻灯片
表
1
不同模型/方法所得轴向力系数及其偏差与法向力系数
Table
1.
The axial and normal force coefficients by different models and DSMC method and errors between axial force coefficients
table_type1 ">
| Model/Method | Ca | Error/% | Cn |
| DSMC | 1.287 0 | — | 3.82 × 10?4 |
| New model | 1.3458 | 4.57 | 5.76 × 10?3 |
| Shakhov model | 1.3760 | 6.92 | 8.25 × 10?3 |
| Belyi model | 1.3261 | 3.04 | 3.90 × 10?3 |
下载: 导出CSV
|显示表格
图9给出了对称面(即
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//21-104-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
Figure
9.
Comparison of pressure, temperature and velocity simulated by GKUA with different collision models and DSMC along the direction of x on the section of
下载: 全尺寸图片
幻灯片
4.
结论
本文通过分析玻尔兹曼方程的一阶查普曼?恩斯科分析解, 结合沙克霍夫模型和贝利模型构造过程及数学推导与物理分析, 建立了一种同时考虑热流矢量和应力张量影响、满足玻尔兹曼方程高阶碰撞矩的综合可计算碰撞模型, 并在数学上分析了其守恒性、H定理等基本属性, 证明了新模型方程与玻尔兹曼方程的相容性, 给出了新模型与现有模型的关系, 通过碰撞动力学确定了碰撞松弛参数统一表达式. 经过模拟一维激波结构、二维近空间飞行环境平板和多体圆柱干扰流动, 并与直接模拟蒙特卡洛方法及不同碰撞模型方程的统一算法结果对比分析, 得出以下结论:
(1)在稀薄效应显著、非平衡现象突出的流动区域, 热流矢量和应力张量对当地气体分子速度分布函数的影响较大, 在构造碰撞松弛模型时需要同时考虑两者的影响;
(2)在激波捕捉方面, 流场中黏性效应显著的区域沙克霍夫模型结果与直接模拟蒙特卡洛方法模拟值差别较大, 本文新建模型与贝利模型结果接近, 在激波内部本文模型与直接模拟蒙特卡洛方法符合更好, 而在黏性效应较小时仅考虑热流时结果与直接模拟蒙特卡洛方法符合更好, 进一步说需要考虑多参数对分子速度分布函数的综合影响;
(3)本文新建模型的碰撞松弛参数中引入了与自然对数的底
m{e}}} $
