删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

非饱和土半空间Lamb问题及能量传输特性

本站小编 Free考研考试/2022-01-01


引 言


弹性半空间的波动响应一直是弹性动力学领域的研究热点, 其中Lamb问题最具代表性. 随着研究的深入, 不同集中荷载形式(点源和线源、表面和内部等)作用下单相弹性介质的Lamb问题已经取得了比较完备的体系. 近年来, 有关多相多孔介质的Lamb问题逐渐受到人们的重视. 自Biot[1-2]建立了两相介质的波动方程后, 国内外****针对饱和半空间Lamb问题已经取得了一系列研究成果, 主要包括荷载作用于半空间表面[3-5]和半空间内部[6-9]以及层状地基[10-14]等不同方面的动力响应研究. 相对于饱和土, 在工程建设中大量涉及到的是处于地下水位以上的非饱和土体, 而已有研究表明, 介质中孔隙气体的存在对其动力响应行为、弹性波传播特性以及能量传输产生巨大影响, 因此研究非饱和半空间的动力学行为在岩土工程、地震工程等领域有着重要的理论和应用价值.

由于非饱和多孔介质物理力学特性的复杂性, 使得对非饱和半空间Lamb问题及能量传输特性的研究成果较少. 王春玲等[15-17]采用积分变换法和消元法求得了非饱和地基受竖向简谐荷载作用下的稳态响应积分变换解, 但其最终解的形式十分复杂, 不便于应用. 徐明江等[18-20]以三相多孔介质模型为基础, 通过引入双变量本构关系, 采用解析法研究了简谐荷载作用下非饱和土地基的动力响应问题, 给出了积分形式的解答, 但并未考虑颗粒间吸应力对非饱和半空间动力学特征的影响. Zhang等[21]在假定土骨架为多孔弹性连续介质, 且具有均匀性和各向同性的基础上, 通过应用Fiourier展开技术和Hankel积分的方法得到了在内部激励作用下的非饱和土中动态格林函数解, 但上述研究成果均未讨论不同边界条件对非饱和半空间表面的动力学响应特征及能量传输特性的影响规律.

本文在已有研究成果的基础之上, 考虑非饱和土中粒间吸应力的作用, 结合质量守恒方程、动量平衡方程及有效应力原理等基本方程, 运用Helmholtz分解法, 在柱坐标系下建立了非饱和半空间的动力学控制方程. 分别考虑透水(气)和不透水(气)两种边界条件, 对频域内的轴对称问题进行求解, 得到了非饱和半空间表面受到竖向集中简谐荷载作用下的解析解答, 并且通过参数分析讨论了在不同饱和度、不同振动频率以及不同渗透系数下的动力响应特性和能量传输的变化及其影响规律, 以期为不同边界条件下非饱和半空间的表面振动问题提供参考依据.


1.
基本方程


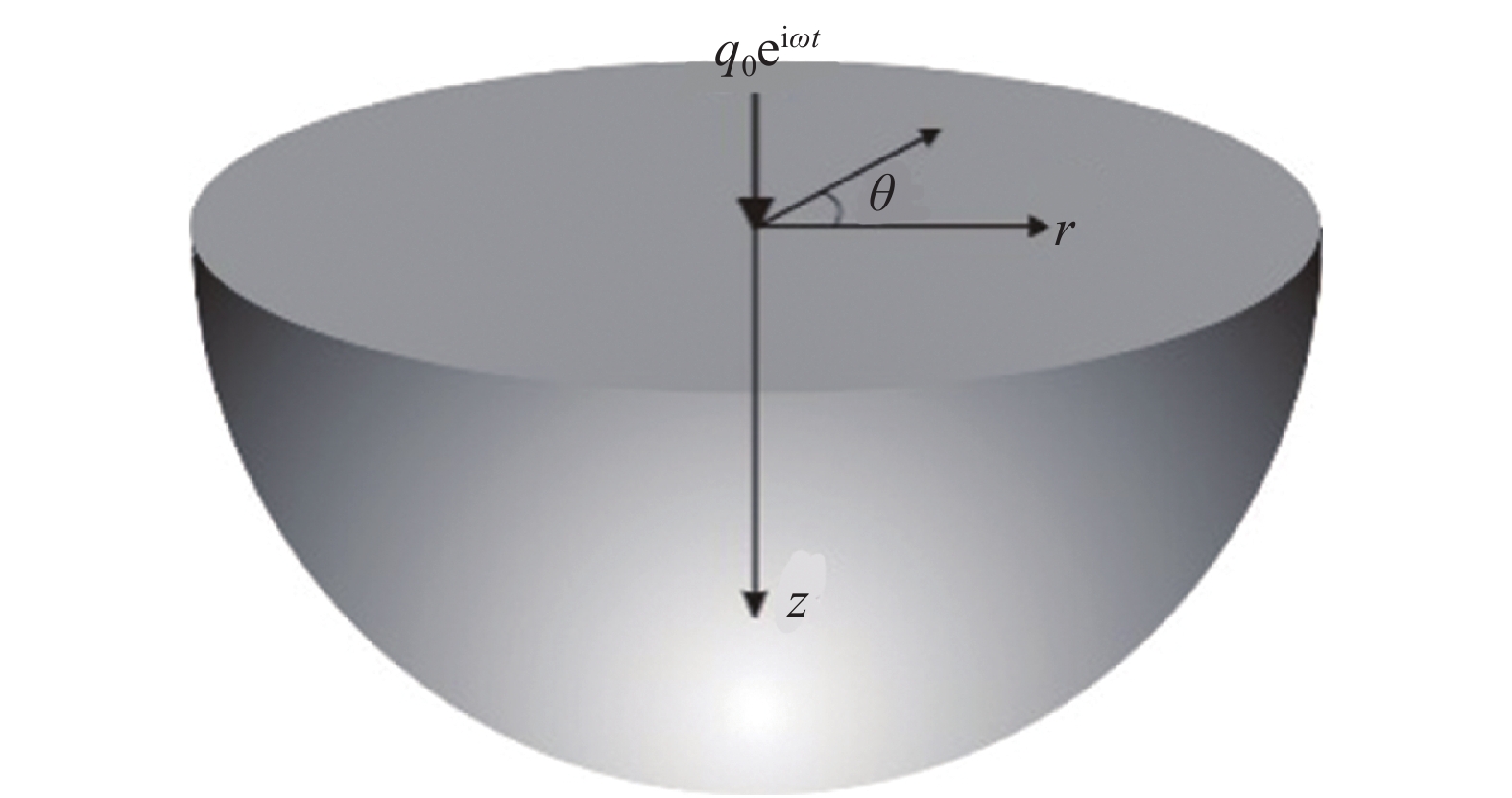
如图1所示的非饱和半空间表面受到频率为ω, 幅度为q0的垂直简谐荷载作用, 考虑轴对称性, 问题的基本方程包括如下6类.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-195-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
半空间计算模型



Figure
1.
Half-space calculation mode



下载:
全尺寸图片
幻灯片


(1) 时域内固体骨架动量平衡方程






$$frac{{partial {sigma _{r}}}}{{partial r}} + frac{{partial {tau _{{r{textit{z}}}}}}}{{partial {textit{z}}}} + frac{1}{r}left( {{sigma _{r}} - {sigma _theta }}
ight) = overline {{
ho _{
m{s}}}} {ddot u_r} + overline {{
ho _{
m{l}}}} {ddot w_r} + overline {{
ho _{
m{a}}}} {ddot v_r}tag{1a}$$






$$frac{{partial {tau _{{r{textit{z}}}}}}}{{partial r}} + frac{{partial {sigma _{textit{z}}}}}{{partial {textit{z}}}} + frac{1}{r}{tau _{{r{textit{z}}}}} = overline {{
ho _{
m{s}}}} {ddot u_{{textit{z}}}} + overline {{
ho _{
m{l}}}} {ddot w_{textit{z}}} + overline {{
ho _{
m{a}}}} {ddot v_{textit{z}}}tag{1b}$$

(2) 时域内孔隙流体运动平衡方程






$$ - frac{{partial {p_{
m{l}}}}}{{partial r}} = {b^{
m{l}}}left( {{{dot w}_r} - {{dot u}_r}}
ight) + {
ho _{
m{l}}}{ddot w_r} tag{2a}$$






$$ - frac{{partial {p_{
m{l}}}}}{{partial {textit{z}}}} = {b^{
m{l}}}left( {{{dot w}_{textit{z}}} - {{dot u}_{textit{z}}}}
ight) + {
ho _{
m{l}}}{ddot w_{textit{z}}} tag{2b}$$






$$ - frac{{partial {p_{
m{a}}}}}{{partial r}} = {b^{
m{a}}}left( {{{dot v}_r} - {{dot u}_r}}
ight) + {
ho _{
m{a}}}{ddot v_r} tag{2c}$$






$$- frac{{partial {p_{
m{a}}}}}{{partial {textit{z}}}} = {b^{
m{a}}}left( {{{dot v}_{textit{z}}} - {{dot u}_{textit{z}}}}
ight) + {
ho _{
m{a}}}{ddot v_{textit{z}}}tag{2d}$$

式(1)和式(2)中, σr, σθ, σz, τrz分别为代表单元体上的总应力和剪应力; ur, uθ, uz分别为径向位移、环向位移和竖向位移; wr, wθ, wz分别为孔隙中液体的径向位移、环向位移和竖向位移; vr, vθ, vz分别为孔隙中气体的径向位移、环向位移和竖向位移; pl和pa分别为孔隙水压力和孔隙气压力; ${bar
ho _{
m{s}}}$, ${bar
ho _{
m{l}}}$和${bar
ho _{
m{a}}}$分别为固相、液相和气相的表观密度.

考虑孔隙中的流体渗透形式符合达西定律, 用固有渗透系数K表征气相和液相的渗透系数kl和ka分别为






$${k_{
m{l}}} = frac{{{
ho _{
m{l}}}g}}{{{eta _{
m{l}}}}}Ktag{3a}$$






$${k_{
m{a}}} = frac{{{
ho _{
m{a}}}g}}{{{eta _{{
m{a}}}}}}Ktag{3b}$$

则式(2a) ~ 式(2d)中系数bl和ba可表示为如下形式






$${b^{
m{l}}} = frac{{n{S_{
m{r}}}{eta _{
m{l}}}}}{K}tag{4a}qquad$$






$${b^{
m{a}}} = frac{{nleft( {1 - {S_{
m{r}}}}
ight){eta _{
m{a}}}}}{K}tag{4b}$$

式中, n为孔隙率; Sr为饱和度; g为重力加速度; ηl和ηa分别为液相和气相的动力黏度系数.

(3) 有效应力原理

有效应力原理是土力学的核心, 目前关于非饱和土中有效应力原理大致可分为单变量理论[22]、双变量理论[23]和复合变量理论[24]. 其中, Lu等[25]在考虑微观颗粒间作用力和有效应力的基础上提出了吸应力表示的有效应力公式







$${sigma '_{ij}} = left( {{sigma _{ij}} - {p_{
m{a}}}{delta _{ij}}}
ight) - {sigma _{
m{s}}}{delta _{ij}}$$
(5)

式中, ${sigma _{
m{s}}} = - left( {{p_{
m{a}}} - {p_{
m{l}}}}
ight){S_{
m{e}}}$表示粒间吸应力, ${S_{
m{e}}}$为有效饱和度, ${S_{
m{e}}} = {{left( {{S_{
m{r}}} - {S_{{
m{w0}}}}}
ight)} / {left( {1 - {S_{{
m{w0}}}}}
ight)}}$, ${S_{{
m{w0}}}}$为残余饱和度. 吸应力表示的有效应力公式是非饱和介质中两相流体压力的函数, 主要受饱和度变化的影响, 消除了Bishop有效应力原理中对参数χ的依赖性.

(4) 质量守衡方程

忽略各相之间的质量交换, 非饱和多孔介质各相的质量守衡方程可描述为[26-28]







$${{partial {{bar
ho }_m}} / {partial t}} + {left( {{{bar
ho }_m}dot u_i^m}
ight)_{,i}} = 0, ;;;;{m = {
m{s}},{
m{l}},{
m{a}}}$$
(6)

式中, ${bar
ho _m}$为非饱和半空间中各相介质的表观密度; $dot u_i^m$为非饱和半空间中各相介质在不同方向上位移的时间导数.

(5) 本构方程

考虑固相颗粒的可压缩性, 弹性各向同性非饱和介质的本构方程为






$$begin{split} {sigma _r} =& left( {lambda + 2mu }
ight)frac{{partial {u_r}}}{{partial r}} + lambda frac{{{u_r}}}{r} + lambda frac{{partial {u_{textit{z}}}}}{{partial {textit{z}}}} - &quadalpha {S_{
m{e}}}{p_{
m{l}}} - alpha left( {1 - {S_{
m{e}}}}
ight){p_{
m{a}}} end{split} tag{7a}$$






$$begin{split} {sigma _theta } = &lambda frac{{partial {u_r}}}{{partial r}} + left( {lambda + 2mu }
ight)frac{{{u_r}}}{r} + lambda frac{{partial {u_{textit{z}}}}}{{partial {textit{z}}}} -&quad alpha {S_{
m{e}}}{p_{
m{l}}} - alpha left( {1 - {S_{
m{e}}}}
ight){p_{
m{a}}} end{split}tag{7b}$$






$$begin{split} {sigma _{textit{z}}} = &lambda frac{{partial {u_r}}}{{partial r}} + lambda frac{{{u_r}}}{r} + left( {lambda + 2mu }
ight)frac{{partial {u_{textit{z}}}}}{{partial {textit{z}}}} -&quad alpha {S_{
m{e}}}{p_{
m{l}}} - alpha left( {1 - {S_{
m{e}}}}
ight){p_{
m{a}}} end{split}tag{7c}$$






$${tau _{r{textit{z}}}} = mu left( {frac{{partial {u_r}}}{{partial {textit{z}}}} + frac{{partial {u_{textit{z}}}}}{{partial r}}}
ight)tag{7d}qquadqquad;;$$

式中,$alpha = 1 - {{{K_{
m{b}}}} / {{K_{
m{s}}}}}$,${K_{
m{s}}}$和${K_{
m{b}}}$分别为固相颗粒以及骨架的体积压缩模量; $lambda $和$mu $为$mathrm{Lame}$常数.

(6) 渗流连续方程






$$begin{split} - {{dot p}_{
m{l}}} = &{a_{11}}left( {frac{{partial {{dot u}_r}}}{{partial r}} + frac{{{{dot u}_r}}}{r} + frac{{partial {{dot u}_{textit{z}}}}}{{partial {textit{z}}}}}
ight) + {a_{12}}left( {frac{{partial {{dot w}_r}}}{{partial r}} + frac{{{{dot w}_r}}}{r} + frac{{partial {{dot w}_{textit{z}}}}}{{partial {textit{z}}}}}
ight) +& {a_{13}}left( {frac{{partial {{dot v}_r}}}{{partial r}} + frac{{{{dot v}_r}}}{r} + frac{{partial {{dot v}_{textit{z}}}}}{{partial {textit{z}}}}}
ight) end{split} tag{8a}$$






$$begin{split} - {{dot p}_{
m{a}}} = &{a_{21}}left( {frac{{partial {{dot u}_r}}}{{partial r}} + frac{{{{dot u}_r}}}{r} + frac{{partial {{dot u}_{textit{z}}}}}{{partial {textit{z}}}}}
ight) + {a_{22}}left( {frac{{partial {{dot w}_r}}}{{partial r}} + frac{{{{dot w}_r}}}{r} + frac{{partial {{dot w}_{textit{z}}}}}{{partial {textit{z}}}}}
ight) +& {a_{23}}left( {frac{{partial {{dot v}_r}}}{{partial r}} + frac{{{{dot v}_r}}}{r} + frac{{partial {{dot v}_{textit{z}}}}}{{partial {textit{z}}}}}
ight) end{split}tag{8b}$$

式中, 系数aij的具体表达式详见附录A. 本构方程(7)和渗流连续方程(8)的具体推导过程分别见附录B和附录C.


2.
问题的求解



2.1
控制方程


考虑简谐荷载作用下各位移分量的形式如下






$${u_r} = {u_r}left( {r,theta,{textit{z}},omega }
ight){{
m{e}}^{{
m{i}}omega t}}tag{9a}$$






$${u_{textit{z}}} = {u_{textit{z}}}left( {r,theta,{textit{z}},omega }
ight){{
m{e}}^{{
m{i}}omega t}}tag{9b}$$






$${w_r} = {w_r}left( {r,theta,{textit{z}},omega }
ight){{
m{e}}^{{
m{i}}omega t}}tag{9c}$$






$${w_{textit{z}}} = {w_{textit{z}}}left( {r,theta,{textit{z}},omega }
ight){{
m{e}}^{{
m{i}}omega t}}tag{9d}$$






$${v_r} = {v_r}left( {r,theta,{textit{z}},omega }
ight){{
m{e}}^{{
m{i}}omega t}}tag{9e}$$






$${v_{textit{z}}} = {v_{textit{z}}}left( {r,theta,{textit{z}},omega }
ight){{
m{e}}^{{
m{i}}omega t}}tag{9f}$$

将式(9)代入孔隙流体运动平衡方程(2)中, 并结合式(1)、式(7)和式(8), 整理后可得频域内非饱和半空间的动力控制方程






$$begin{split}& V_{
m{P}}^2frac{partial }{{partial r}}left( {frac{{partial {u_r}}}{{partial r}} + frac{{{u_r}}}{r} + frac{{partial {u_{textit{z}}}}}{{partial {textit{z}}}}}
ight) + V_{
m{S}}^2frac{partial }{{partial {textit{z}}}}left( {frac{{partial {u_r}}}{{partial {textit{z}}}} - frac{{partial {u_{textit{z}}}}}{{partial r}}}
ight) +&qquad {kappa _1}{omega ^2}{u_r} - {kappa _2}frac{{partial {p_l}}}{{partial r}} - {kappa _3}frac{{partial {p_{
m{a}}}}}{{partial r}} = 0 end{split} tag{10a}$$






$$begin{split}& V_{
m{P}}^2frac{partial }{{partial {textit{z}}}}left( {frac{{partial {u_r}}}{{partial r}} + frac{{{u_r}}}{r} + frac{{partial {u_{textit{z}}}}}{{partial {textit{z}}}}}
ight) + V_{
m{S}}^2frac{partial }{{partial r}}left( {frac{{partial {u_{textit{z}}}}}{{partial r}} - frac{{partial {u_r}}}{{partial {textit{z}}}}}
ight) + &qquad {kappa _1}{omega ^2}{u_{textit{z}}} - {kappa _2}frac{{partial {p_{
m{l}}}}}{{partial {textit{z}}}} - {kappa _3}frac{{partial {p_{
m{a}}}}}{{partial {textit{z}}}} + frac{{V_{
m{S}}^2}}{r}left( {frac{{partial {u_{textit{z}}}}}{{partial r}} - frac{{partial {u_r}}}{{partial {textit{z}}}}}
ight) = 0 end{split} tag{10b}$$






$$begin{split}& - {p_{
m{l}}} = left( {{a_{11}} + {a_{12}}frac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{13}}frac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}
ight)left( {frac{{partial {u_r}}}{{partial r}} + frac{{{u_r}}}{r} + frac{{partial {u_{textit{z}}}}}{{partial {textit{z}}}}}
ight) - &qquadfrac{{{a_{12}}}}{{{theta _1}}}{nabla ^2}{p_{
m{l}}} - frac{{{a_{13}}}}{{{theta _2}}}{nabla ^2}{p_{
m{a}}} end{split}tag{11a}$$






$$begin{split}{l}& - {p_{
m{a}}} = left( {{a_{21}} + {a_{22}}frac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{23}}frac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}
ight)left( {frac{{partial {u_r}}}{{partial r}} + frac{{{u_r}}}{r} + frac{{partial {u_{textit{z}}}}}{{partial {textit{z}}}}}
ight) - &qquadfrac{{{a_{22}}}}{{{theta _1}}}{nabla ^2}{p_{
m{l}}} - frac{{{a_{23}}}}{{{theta _2}}}{nabla ^2}{p_{
m{a}}} end{split}tag{11b}$$

式中 ${theta _1} = {b^{
m{l}}}{
m{i}}omega - {
ho _{
m{l}}}{omega ^2}$,${theta _2} = {b^{
m{a}}}{
m{i}}omega - {
ho _{
m{a}}}{omega ^2}$,${kappa _1} = 1 + dfrac{{{{bar
ho }_{
m{l}}}{b^{
m{l}}}{
m{i}}omega }}{{{{bar
ho }_{
m{s}}}{theta _1}}} + $$ dfrac{{{{bar
ho }_{
m{a}}}{b^{
m{a}}}{
m{i}}omega }}{{{{bar
ho }_{
m{s}}}{theta _2}}}$, ${kappa _2} = dfrac{{{{bar
ho }_{
m{l}}}{omega ^2}}}{{{{bar
ho }_{
m{s}}}{theta _1}}} + dfrac{{alpha {S_{
m{e}}}}}{{{{bar
ho }_{
m{s}}}}}$, ${kappa _3} = dfrac{{{{bar
ho }_{
m{a}}}{omega ^2}}}{{{{bar
ho }_{
m{s}}}{theta _2}}} + dfrac{{alpha left( {1 - {S_{
m{e}}}}
ight)}}{{{{bar
ho }_{
m{s}}}}}$, ${V_{
m{P}}} = $$ sqrt {{{left( {lambda + 2mu }
ight)} / {{{bar
ho }_{
m{s}}}}}}$为纵波波速, ${V_{
m{S}}} = sqrt {{mu / {{{bar
ho }_{
m{s}}}}}}$为横波波速.

根据Helmholtz分解定理, 引入柱坐标系下的两个势函数Φ和Ψ表示ur和uz如下






$${u_r} = frac{{partial varPhi }}{{partial r}} + frac{{{partial ^2}varPsi }}{{partial rpartial {textit{z}}}}tag{12a}qquad$$






$${u_{textit{z}}} = frac{{partial varPhi }}{{partial {textit{z}}}} - frac{{partial varPsi }}{{rpartial r}} - frac{{{partial ^2}varPsi }}{{partial {r^2}}}tag{12b}$$

将式(12a)分别代入式(10a)和式(11)中, 可得







$$V_{
m{P}}^2{nabla ^2}varPhi + {kappa _1}{omega ^2}varPhi = {kappa _2}{p_{
m{l}}} + {kappa _3}{p_{
m{a}}}qquad;;;;;;$$
(13)







$$V_{
m{S}}^2{nabla ^2}varPsi + {kappa _1}{omega ^2}varPsi = 0qquadqquadqquad;;;$$
(14)






$$begin{split} - {p_{
m{l}}} = &left( {{a_{11}} + {a_{12}}frac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{13}}frac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}
ight){nabla ^2}varPhi -& frac{{{a_{12}}}}{{{theta _1}}}{nabla ^2}{p_{
m{l}}} - frac{{{a_{13}}}}{{{theta _2}}}{nabla ^2}{p_{
m{a}}} end{split}tag{15a}$$






$$begin{split} - {p_{
m{a}}} =& left( {{a_{21}} + {a_{22}}frac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{23}}frac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}
ight){nabla ^2}varPhi -& frac{{{a_{22}}}}{{{theta _1}}}{nabla ^2}{p_{
m{l}}} - frac{{{a_{23}}}}{{{theta _2}}}{nabla ^2}{p_{
m{a}}} end{split}tag{15b}$$

考虑到因变量的时间导数同二阶空间导数的乘积与其时间导数同一阶空间导数的乘积相比, 前者是高阶小量[21]. 因此, 利用式(8)可以得到






$${p_{
m{a}}} = dfrac{{{a_{21}} + {a_{22}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{23}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}}{{{a_{11}} + {a_{12}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{13}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}}{p_{
m{l}}}tag{16a}$$






$${p_{
m{l}}} = dfrac{{{a_{11}} + {a_{12}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{13}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}}{{{a_{21}} + {a_{22}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{23}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}}{p_{
m{a}}}tag{16b}$$

将式(16)代入式(13), 可得






$${p_{
m{l}}} = frac{{V_{
m{P}}^2}}{{{h_1}}}{nabla ^2}varPhi + frac{{{kappa _1}{omega ^2}}}{{{h_1}}}varPhitag{17a} $$






$${p_{
m{a}}} = frac{{V_{
m{P}}^2}}{{{h_2}}}{nabla ^2}varPhi + frac{{{kappa _1}{omega ^2}}}{{{h_2}}}varPhi tag{17b}$$

将式(17)代入式(15), 整理后可得







$${nabla ^2}left( {{nabla ^2}varPhi }
ight) + frac{{{H_2}}}{{{H_1}}}{nabla ^2}varPhi + frac{{{H_3}}}{{{H_1}}}varPhi = 0$$
(18)

式中






$$begin{array}{l} {H_1} = dfrac{{{a_{22}} - {a_{12}}}}{{{theta _1}}}dfrac{{V_{
m{P}}^2}}{{{h_1}}} + dfrac{{{a_{23}} - {a_{13}}}}{{{theta _2}}}dfrac{{V_{
m{P}}^2}}{{{h_2}}} {H_2} = dfrac{{{a_{22}} - {a_{12}}}}{{{theta _1}}}dfrac{{{kappa _1}{omega ^2}}}{{{h_1}}} + dfrac{{{a_{23}} - {a_{13}}}}{{{theta _2}}}dfrac{{{kappa _1}{omega ^2}}}{{{h_2}}} + {{a_{21}} - {a_{11}}} + qquad left( {{a_{22}} - {a_{12}}}
ight)dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + left( {{a_{23}} - {a_{13}}}
ight)dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}} + dfrac{{V_{
m{P}}^2}}{{{h_1}}} - dfrac{{V_{
m{P}}^2}}{{{h_2}}} {H_3} = dfrac{{{kappa _1}{omega ^2}}}{{{h_1}}} - dfrac{{{kappa _1}{omega ^2}}}{{{h_2}}} {h_1} = {kappa _2} + {kappa _3}dfrac{{{a_{21}} + {a_{22}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{23}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}}{{{a_{11}} + {a_{12}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{13}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}} {h_2} = {kappa _2}dfrac{{{a_{11}} + {a_{12}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{13}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}}{{{a_{21}} + {a_{22}}dfrac{{{b^{
m{l}}}{
m{i}}omega }}{{{theta _1}}} + {a_{23}}dfrac{{{b^{
m{a}}}{
m{i}}omega }}{{{theta _2}}}}} + {kappa _3} end{array}$$

方程(14)和方程(18)即为以势函数表示的频域内控制方程. 在得到势函数解答的基础上, 可通过基本方程得到各位移分量、应力分量等物理量的解答.


2.2
解析解答


利用分离变量法求解微分方程(14)和(18), 可得






$$begin{split} {varPhi _{11}} =& left[ {{A_{11}}{{
m{I}}_0}left( {{zeta _{11}}r}
ight) + {B_{11}}{{
m{K}}_0}left( {{zeta _{11}}r}
ight)}
ight] cdot&left[ {{C_{11}}sin left( {m{textit{z}}}
ight) + {D_{11}}cos left( {m{textit{z}}}
ight)}
ight]{{
m{e}}^{{
m{i}}omega t}} end{split} tag{19a}$$






$$begin{split} {varPhi _{12}} =& left[ {{A_{12}}{{
m{I}}_0}left( {{zeta _{12}}r}
ight) + {B_{12}}{{
m{K}}_0}left( {{zeta _{12}}r}
ight)}
ight]cdot &left[ {{C_{12}}sin left( {m{textit{z}}}
ight) + {D_{12}}cos left( {m{textit{z}}}
ight)}
ight]{{
m{e}}^{{
m{i}}omega t}} end{split} tag{19b}$$







$$begin{split} varPsi = &left[ {{A_2}{{
m{I}}_0}left( {{zeta _2}r}
ight) + {B_2}{{
m{K}}_0}left( {{zeta _2}r}
ight)}
ight] cdot&left[ {{C_2}sin left( {m{textit{z}}}
ight) + {D_2}cos left( {m{textit{z}}}
ight)}
ight]{{
m{e}}^{{
m{i}}omega t}} end{split} $$
(20)

式中, ${{
m{I}}_0}left( {{zeta _{11}}r}
ight)$, ${{
m{K}}_0}left( {{zeta _{11}}r}
ight)$, ${{
m{I}}_0}left( {{zeta _{12}}r}
ight)$, ${{
m{K}}_0}left( {{zeta _{12}}r}
ight)$, ${{
m{I}}_0}left( {{zeta _2}r}
ight)$, ${{
m{K}}_0}left( {{zeta _2}r}
ight)$分别为第一类和第二类零阶贝塞尔函数;






$$ begin{array}{l} {d_{11}} = dfrac{{{H_2}}}{{{H_1}}},;{d_{12}} = dfrac{{{H_3}}}{{{H_1}}},;{xi _2} = sqrt { - dfrac{{{kappa _1}{omega ^2}}}{{V_S^2}}} xi _{11}^2 = dfrac{{ - {d_{11}} + sqrt {d_{11}^2 - 4{d_{12}}} }}{2},;xi _{12}^2 = dfrac{{ - {d_{11}} - sqrt {d_{11}^2 - 4{d_{12}}} }}{2} {zeta _{11}} = sqrt {xi _{11}^2 + m} ,;{zeta _{12}} = sqrt {xi _{12}^2 + m},;{zeta _2} = sqrt {xi _2^2 + m} end{array}$$

待定系数A, B, C, D由具体的边界条件确定.

考虑如下边界条件







$${sigma _{textit{z}}}left| {_{{textit{z}} = 0;0 leqslant r leqslant {r_0}} = }
ight.{q_0}{{
m{e}}^{{
m{i}}omega t}}$$
(21)







$${tau _{r{textit{z}}}}left| {_{{textit{z}} = 0} = }
ight.0qquadqquad$$
(22)







$$;;;;;;{u_r}left| {_{r,{textit{z}} to infty } = }
ight.{u_{textit{z}}}left| {_{r,{textit{z}} to infty } = }
ight.0$$
(23)

根据边界条件(21) ~ (23)可得







$${A_{11}} = {A_{12}} = {A_2} = {C_{11}} = {C_{12}} = {D_2} = 0$$
(24)







$$m = frac{{left( {2beta - 1}
ight){text{π}} }}{{2{textit{z}}}},;;;beta = 1,2,3,cdots qquadqquad$$
(25)

因此, 对于势函数可重写成以下形式







$$begin{split} {varPhi _m} =& cos left( {m{textit{z}}}
ight)left[ {{B_{11m}}{{
m{K}}_0}left( {{zeta _{11m}}r}
ight)}
ight. + &{left. { {B_{12m}}{{
m{K}}_0}left( {{zeta _{12m}}r}
ight)}
ight]} {{
m{e}}^{{
m{i}}omega t}} end{split} $$
(26)







$${varPsi _m} = sin left( {m{textit{z}}}
ight){B_{2m}}{{
m{K}}_0}left( {{zeta _{2m}}r}
ight){{
m{e}}^{{
m{i}}omega t}}$$
(27)

将式(26)和式(27)代入式(12)和式(17)中, 最终可获得非饱和多孔介质中孔隙压力及位移分量的表达式为






$$begin{split} {p_{{
m{l}}m}} =& sumlimits_{beta = 1}^infty {cos left( {m{textit{z}}}
ight)left[ {{B_{11m}}{{
m{K}}_0}left( {{zeta _{11m}}r}
ight){varsigma _{11m}}}
ight.}+ &{left. { {B_{12m}}{{
m{K}}_0}left( {{zeta _{12m}}r}
ight){varsigma _{12m}}}
ight]frac{{{{
m{e}}^{{
m{i}}omega t}}}}{{{h_1}}}} end{split} tag{28a}qquadquad$$






$$begin{split} {p_{{
m{a}}m}} =& sumlimits_{beta = 1}^infty {cos left( {m{textit{z}}}
ight)left[ {{B_{11m}}{{
m{K}}_0}left( {{zeta _{11m}}r}
ight){varsigma _{11m}}}
ight.}+ &{left. { {B_{12m}}{{
m{K}}_0}left( {{zeta _{12m}}r}
ight){varsigma _{12m}}}
ight]} frac{{{{
m{e}}^{{
m{i}}omega t}}}}{{{h_2}}} end{split} tag{28b}qquadquad$$






$$begin{split} {u_r} = & - {{
m{e}}^{{
m{i}}omega t}}sumlimits_{beta = 1}^infty {cos left( {m{textit{z}}}
ight)left[ {{B_{11m}}{{
m{K}}_1}left( {{zeta _{11m}}r}
ight){zeta _{11m}}}
ight.}+ &{left. { {B_{12m}}{{
m{K}}_1}left( {{zeta _{12m}}r}
ight){zeta _{12m}} + {B_{2m}}{{
m{K}}_1}left( {{zeta _{2m}}r}
ight)m{zeta _{2m}}}
ight]} end{split}tag{29a};;;$$






$$begin{split} {u_{textit{z}}} =& {{
m{e}}^{{
m{i}}omega t}}sumlimits_{beta = 1}^infty {sin left( {m{textit{z}}}
ight)left[ { - {B_{11m}}{{
m{K}}_0}left( {{zeta _{11m}}r}
ight)m}
ight.}- &{left. { {B_{12m}}{{
m{K}}_0}left( {{zeta _{12m}}r}
ight)m + {B_{2m}}{{
m{K}}_0}left( {{zeta _{2m}}r}
ight)zeta _{2m}^2}
ight]} end{split}tag{29b}qquad;$$

将孔隙压力和位移的结果代入本构方程(7)中, 可得各应力分量的表达式为






$$begin{split}& {{sigma }_{r}} = &- sumlimits_{{beta } = 0}^infty {cos left( {{m{textit{z}}}}
ight)left{ {{{B}_{11{m}}}left[ {{eta _{11m}}{{{
m{K}}}_0}left( {{zeta _{11m}}{r}}
ight) - frac{{2{mu }{zeta _{11m}}}}{{r}}{{{
m{K}}}_1}left( {{zeta _{11m}}{r}}
ight)}
ight]}
ight.} + &{{ }{{B}_{12{m}}}left[ {{eta _{12m}}{{{
m{K}}}_0}left( {{zeta _{12m}}{r}}
ight) - frac{{2{mu }{zeta _{12m}}}}{{r}}{{{
m{K}}}_1}left( {{zeta _{12m}}{r}}
ight)}
ight]} + &{left. {{ }{{B}_{2{m}}}{m}left[ {{eta _{2m}}{{{
m{K}}}_0}left( {{zeta _{2m}}{r}}
ight) - frac{{2{mu }{zeta _{2m}}}}{{r}}{{{
m{K}}}_1}left( {{zeta _{2m}}{r}}
ight)}
ight]}
ight}} {{
m{e}}^{{{
m{i}}omega t}}} end{split} tag{30a}$$






$$begin{split} {{sigma }_{{textit{z}}}} =& - {{
m{e}}^{{{
m{i}}omega t}}}sumlimits_{{beta } = 0}^infty {cos left( {{m{textit{z}}}}
ight)left[ {{{B}_{11{m}}}{{eta '_{11m}}}{{{
m{K}}}_0}left( {{zeta _{11m}}{r}}
ight)}
ight.} +&{left. {{ }{{B}_{12{m}}}{{eta '_{12m}}}{{{
m{K}}}_0}left( {{zeta _{12m}}{r}}
ight){ + }{{B}_{2{m}}}{{eta '_{2m}}}{{{
m{K}}}_0}left( {{zeta _{2{
m{m}}}}{r}}
ight)}
ight]} end{split} tag{30b}$$

对于本文所讨论问题的描述, 在非饱和半空间表面(z = 0)分别考虑透水(气)和不透水(气)两种边界条件.

(1) 当半空间表面排水(气)时, 土体表面孔隙气压力和孔隙水压力为0, 即







$${left. {{{p}_{l}}}
ight|_{{{textit{z}} = 0}}} = {left. {{{p}_{a}}}
ight|_{{{textit{z}} = 0}}} = 0$$
(31)

此时, 式(28) ~ 式(30)中各参数分别为






$${B_{11m}} = frac{{{delta _6}}}{{{delta _6}left( {{delta _1} + {delta _0}{delta _2}}
ight) - {delta _3}left( {{delta _4} + {delta _0}{delta _5}}
ight)}}delta qquadqquadqquad$$






$${B_{12m}} = frac{{{delta _0}{delta _6}}}{{{delta _6}left( {{delta _1} + {delta _0}{delta _2}}
ight) - {delta _3}left( {{delta _4} + {delta _0}{delta _5}}
ight)}}deltaqquadqquadqquad$$






$${B_{2m}} = frac{{{delta _4} + {delta _0}{delta _5}}}{{{delta _3}left( {{delta _4} + {delta _0}{delta _5}}
ight) - {delta _6}left( {{delta _1} + {delta _0}{delta _2}}
ight)}}delta qquadqquadqquad;$$






$$delta = frac{{{q_0}}}{{{text{π}} r_0^2}},;{delta _0} = - frac{{{{
m{K}}_0}left( {{zeta _{11m}}r}
ight)left( {zeta _{11m}^2 + {m^2}}
ight)}}{{{{
m{K}}_0}left( {{zeta _{12m}}r}
ight)left( {zeta _{12m}^2 + {m^2}}
ight)}}qquadqquadqquad;$$






$${delta _1} = left[ {{(}{lambda }{ + 2}{mu }{)}{{m}^{2}} + {lambda }zeta _{11m}^2}
ight]{{{
m{K}}}_0}left( {{zeta _{11m}}{{r}_0}}
ight)qquadqquadqquad;;;$$






$${delta _2} = left[ {{(}{lambda }{ + 2}{mu }{)}{{m}^{2}} + {lambda }zeta _{12m}^2}
ight]{{{
m{K}}}_0}left( {{zeta _{12m}}{{r}_0}}
ight)qquadqquadqquad;;;$$






$${delta _3} = - {2}{mmu }zeta _{2m}^2{{{
m{K}}}_0}left( {{zeta _{2m}}{{r}_0}}
ight),;{delta _4} = 2{m}{zeta _{11m}}{{{
m{K}}}_1}left( {{zeta _{11m}}{r}}
ight)qquad$$






$${delta _5} = 2{m}{zeta _{12m}}{{{
m{K}}}_1}left( {{zeta _{12m}}{r}}
ight),;{delta _6} = left( {{{m}^{2}} - zeta _{2m}^2}
ight){zeta _{2m}}{{{
m{K}}}_1}left( {{zeta _{2m}}{r}}
ight);;$$






$${varsigma _{11m}} = {kappa _1}{omega ^2} - V_P^2left( {zeta _{11m}^2 + {m^2}}
ight)qquadqquadqquadqquadqquad$$






$${varsigma _{12m}} = {kappa _1}{omega ^2} - V_P^2left( {zeta _{12m}^2 + {m^2}}
ight)qquadqquadqquad;;;qquad;;;$$






$${eta _{11m}} = {left( {lambda { + 2}{mu }}
ight)zeta _{11m}^2{ + }{lambda }{{m}^{2}}{ + alpha }{{S}_{
m{e}}}frac{{{varsigma _{11m}}}}{{{{h}_{1}}}}{ + alpha }{(1} - {{S}_{
m{e}}}{)}frac{{{varsigma _{11m}}}}{{{{h}_{2}}}}} $$






$${eta _{12m}} = {left( {lambda { + 2}{mu }}
ight)zeta _{12m}^2{ + }{lambda }{{m}^{2}}{ + alpha }{{S}_{
m{e}}}frac{{{varsigma _{12m}}}}{{{{h}_{1}}}}{ + alpha }{(1} - {{S}_{
m{e}}}{)}frac{{{varsigma _{12m}}}}{{{{h}_{2}}}}} ;;$$






$${eta _{2m}} = {left( {{lambda + }{2}{mu }}
ight)zeta _{2m}^2 - {lambda }{zeta _{2m}}} qquadqquadqquadqquadqquadquad$$






$${eta '_{11m}} = {{(}{lambda }{ + 2}{mu }{)}{{m}^{2}} + {lambda }zeta _{11m}^2{ + alpha }{{S}_{
m{e}}}frac{{{varsigma _{11m}}}}{{{{h}_{1}}}} + {alpha }{(1} - {{S}_{
m{e}}}{)}frac{{{varsigma _{11m}}}}{{{{h}_2}}}} $$






$${eta '_{12m}} = {{(}{lambda }{ + 2}{mu }{)}{{m}^{2}} + {lambda }zeta _{12m}^2{ + alpha }{{S}_{
m{e}}}frac{{{varsigma _{12m}}}}{{{{h}_{1}}}} + {alpha }{(1} - {{S}_{
m{e}}}{)}frac{{{varsigma _{12m}}}}{{{{h}_2}}}} $$






$${eta '_{2m}} = - {2}{mmu }zeta _{2m}^2qquadqquadqquadqquadqquadqquadqquadquad$$

(2)当半空间表面不排水(气)时, 土体表面孔隙流体和土骨架之间的相对位移为0, 即







$${boldsymbol u} = {boldsymbol w} = {boldsymbol v}$$
(32)

此时孔隙中流体和土骨架间的位移关系由式(2)得






$${boldsymbol{u}} = {boldsymbol{w}}{ = }frac{{{
m{i}}omega {b^{
m{l}}}{boldsymbol{u}} - nabla {p_{
m{l}}}}}{{{theta _1}}}tag{33a}$$






$${boldsymbol{u}} = {boldsymbol{v}}{ = }frac{{{
m{i}}omega {b^{
m{a}}}{boldsymbol{u}}{boldsymbol{}} - nabla {p_{
m{a}}}}}{{{theta _2}}}tag{33b}$$

此时, 式(28) ~ 式(30)中各参数可表示为






$$begin{split}{B_{11m}} =& left( {{delta' _6} {delta '_8} - {delta '_5} {delta '_9} }
ight)/left{left[ {left( {{delta '_3} {delta '_5} - {delta '_2} {delta' _6} }
ight){delta '_7} + }
ight.
ight.&left.left. {left( {{delta '_1} {delta '_6} - {delta '_3} {delta '_4} }
ight){delta '_8} + left( {{delta '_2} {delta '_4} - {delta '_1} {delta '_5} }
ight){delta '_9} }
ight]{delta ' }
ight}end{split};;;;;;;;;$$






$$begin{split}{B_{12m}} =& left( {{delta '_4} {delta '_9} - {delta '_6} {delta '_7} }
ight)/left{left[ {left( {{delta '_3} {delta '_5} - {delta '_2} {delta '_6} }
ight){delta '_7} + }
ight.
ight.&left.left. {left( {{delta '_1} {delta '_6} - {delta '_3} {delta '_4} }
ight){delta '_8} + left( {{delta '_2} {delta '_4} - {delta '_1} {delta '_5} }
ight){delta '_9} }
ight]{delta ' }
ight}end{split};;;;;;;;;$$






$$begin{split}{B_{2m}} =& left( {{delta '_5} {delta '_7} - {delta '_4} {delta '_8} }
ight)/left{left[ {left( {{delta '_3} {delta '_5} - {delta '_2} {delta '_6} }
ight){delta '_7} + }
ight.
ight.&left.left. {left( {{delta '_1} {delta '_6} - {delta '_3} {delta '_4} }
ight){delta '_8} + left( {{delta '_2} {delta '_4} - {delta '_1} {delta '_5} }
ight){delta '_9} }
ight]{delta ' }
ight}end{split};;;;;;;;;$$






$$;;;;delta ' = delta,;{delta '_1} = {eta '_{11m}}{{{
m{K}}}_0}left( {{zeta _{11m}}{{r}_0}}
ight),;{delta '_2} = {eta '_{12m}}{{{
m{K}}}_0}left( {{zeta _{12m}}{{r}_0}}
ight);;;$$






$${delta '_3} = {eta '_{2m}}{{{
m{K}}}_0}left( {{zeta _{2m}}{{r}_0}}
ight),;{delta '_4} = {delta _4},;{delta '_5} = {delta _5},;{delta '_6} = {delta _6};;;;;;;;$$






$${delta '_7}= frac{{{zeta _{11m}}}}{{{theta _1}}}left( {{varsigma _{11m}} - {{b}^{{
m{l}}}}{{
m{i}}}omega }
ight) - frac{{{zeta _{11m}}}}{{{theta _2}}}left( {{varsigma _{11m}} - {{b}^{{
m{a}}}}{{
m{i}}}omega }
ight)qquad;;$$






$${delta '_8} = frac{{{zeta _{12m}}}}{{{theta _1}}}left( {{varsigma _{12m}} - {{b}^{{
m{l}}}}{{
m{i}}}omega }
ight) - frac{{{zeta _{12m}}}}{{{theta _2}}}left( {{varsigma _{12m}} - {{b}^{{
m{a}}}}{{
m{i}}}omega }
ight)qquad;;$$






$${delta '_9} = {m}{zeta _{2m}}{{
m{i}}}omega left( {frac{{{{b}^{{
m{a}}}}}}{{{theta _2}}} - frac{{{{b}^{
m{l}}}}}{{{theta _1}}}}
ight)qquad;;qquadqquadqquad;;qquad;$$


2.3
能量场特性


通常情况下, 半空间表面单位面积的能量传播情况可由其表面牵引力和质点运动速度的积表示[29]. 因此, 对于本文所考虑的非饱和多孔介质材料, 单位面积上的能量, 可由式(34)表示, 结合两类边界条件(1)和(2)可求得不同透水(气)条件下, 非饱和半空间表面受到简谐荷载作用时能量的传输性质.







$${{{boldsymbol{E}}}_{{boldsymbol{u}}}} = {sigma _{ij}}dot {boldsymbol{u}} + {p_{
m{l}}}dot {boldsymbol{w}} + {p_{
m{a}}}dot {boldsymbol{v}}$$
(34)


3.
解答的有效性验证


在经典Lamb问题的分析研究中, ****们往往采用位移解的形式进行描述. 为验证本文计算结果的准确性, 利用式(29)得出的非饱和半空间表面的竖向位移uz和水平位移ur的解析解答, 同文献[29]在饱和半空间中的计算结果进行对比, 其分析结果十分接近, 说明本文所得结果可以和经典饱和半空间理论很好地衔接, 进一步证明本文计算结果的有效性, 如图2所示.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-195-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
有效性验证



Figure
2.
Validity verification



下载:
全尺寸图片
幻灯片



4.
数值分析与讨论


为讨论不同边界条件下相关参数对非饱和半空间动力响应和能量传输特性的影响规律, 本文将通过数值算例分析在不透水(气)条件、透水(气)条件下土体表面位移及能量变化受到饱和度、振动频率、渗透系数的影响情况. 数值算例中所选取的计算参数如表1所示.




表
1
计算参数[17]



Table
1.
Calculation parameters[17]



table_type1 ">
ParametersValue
λ/MPa12.9
μ/MPa19.4
ρs/(kg?m?3)2700
ρl/(kg?m?3)1000
ρa/(kg?m?3)1.29
Ks/(GPa)36
Kl/(GPa)2.0
Ka/(kPa)100
K/m21 × 10?13
g/(m·s?2)10
q0/kN1
t/s60
αvg/Pa?11 × 10?4
nvg2.0
mvg0.5
n0.6
Sr0.6
Sw00.05
ηl1 × 10?3
ηa1.8 × 10?5





下载:
导出CSV
|显示表格



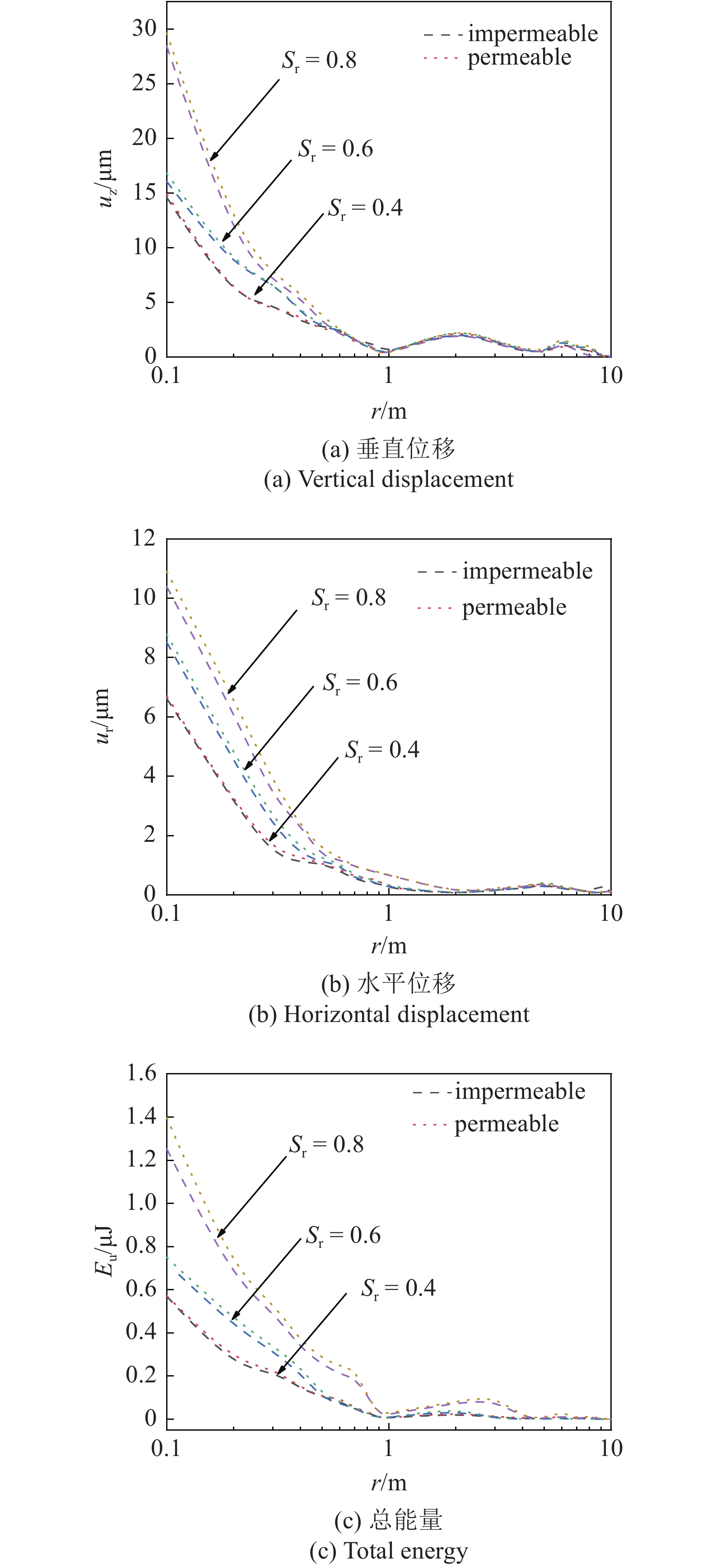
在激振圆频率ω = 1 rad/s时, 图3绘制了非饱和半空间表面处为不透水(气)条件、透水(气)条件时, 饱和度变化对其表面位移及能量传输特性的影响曲线. 由图3可见, 非饱和半空间表面位移幅值会随着饱和度的增大而增大. 这主要是由于随着饱和度的升高, 非饱和介质中基质吸力降低从而引起粒间吸应力降低, 使半空间抵抗外力变形的能力减弱, 导致半空间表面位移幅值会呈现出逐渐增大的趋势. 在不透水(气)条件下, 整体的位移幅值低于透水(气)条件下的位移幅值, 当饱和度较低时, 孔隙内部存在大量气体, 由于气体本身有很强的可压缩性, 因此当饱和度较低时, 两种不同边界条件下的位移幅值相差很小; 当饱和度较高时, 土中孔隙水的含量明显升高, 非饱和介质抵抗变形的能力也会随之提升, 因此当饱和度较高时, 不透水(气)条件下的位移幅值会较为明显的低于透水(气)条件下的位移幅值. 同位移幅值的变化情况类似, 半空间中的能量同样呈现出随着距离振源位置的增大而振荡下降的趋势, 且当表面不透水(气)条件下, 孔隙流体压力占比相对更大, 但由于总应力没有变化, 导致有效应力占比相对较小, 因此在不透水(气)条件下半空间表面受外荷载作用时的总能量值依然小于透水(气)条件下的能量.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-195-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
饱和度对位移和能量的影响曲线



Figure
3.
Influence curve of saturation on displacement and energy



下载:
全尺寸图片
幻灯片


为了分析荷载激振圆频率对非饱和半空间表面位移及能量传输特性的影响, 图4绘出了不同频率下相关物理量的变化曲线. 从图4可以看出, 随着激振频率的逐渐增加, 不论是径向还是竖向位移的幅值均逐渐减小. 因为在荷载振动频率较小时, 透水(气)条件下的地表孔隙水(气)压力更容易消散, 所以在透水(气)和不透水(气)两种不同边界条件下的位移幅值显现出一定的差异, 荷载振动频率较大时的现象与之相反. 且由于施加的外力水平不变, 因此非饱和半空间中的能量变化会呈现出相似的变化趋势.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-195-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
激振频率对位移和能量的影响曲线



Figure
4.
Influence curve of excitation frequency on displacement and energy



下载:
全尺寸图片
幻灯片


在ω = 1 rad/s, 饱和度Sr = 0.6时, 图5给出了固有渗透系数的变化对半空间表面位移幅值和能量传输特性的影响曲线. 由图5可见, 随着固有渗透系数的逐渐降低, 骨架位移也随之减小. 随着距离振源位置的逐渐增加, 位移幅值呈现出振荡下降的现象. 当渗透系数很低时, 两种边界条件的性质趋于一致, 因为在条件(1)的情况下, 表面虽透水(气), 但由于半空间内部的孔隙水(气)压力难以快速消散, 依然会对土骨架产生一定的支持作用, 所以位移幅值会随着渗透系数的降低而呈现出一定的下降趋势. 在不透水(气)条件下, 孔隙流体会持续影响半空间的表面位移, 且孔隙中流体和土骨架之间没有相对位移, 因此不透水(气)边界条件下非饱和半空间表面的位移幅值会略低于透水(气)边界条件下的位移幅值, 且当土骨架位移幅值减小时, 总能量也会呈现出减小的现象, 当渗透系数下降至K < 1 × 10?13 m/s时, 地表位移幅值受渗透系数影响趋于一极限值, 并且随着渗透系数的逐渐降低, 这两种不同边界条件所产生的宏观现象会逐渐趋于一致, 但其差异性将一直存在.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-195-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
渗透系数对位移和能量的影响曲线



Figure
5.
Influence curve of permeability coefficient on displacement and energy



下载:
全尺寸图片
幻灯片



5.
结论


采用Helmholtz分解法, 给出了垂直集中简谐荷载作用下的非饱和土的动力响应解答, 并通过数值算例分析了荷载振动频率、饱和度、渗透系数以及孔隙率对非饱和半空间位移场和能量场的影响规律. 所得结论如下:

(1)激振频率对非饱和半空间表面的动力响应和能量传输特性有着显著的影响, 随着激振频率逐渐增大, 表面位移幅值及总体能量水平均逐渐减小, 且随着距离振源位置的逐渐增加, 位移幅值呈现出振荡减小的现象, 渗透系数越高, 激振频率越小, 该现象越明显.

(2) 表面位移幅值随着饱和度的减小而降低, 并且降低渗透系数也同样会减小位移幅值, 当渗透系数的降低到一定程度时, 位移幅值下降速度放缓, 并逐渐趋于一个极限值.

相关话题/动力 计算 图片 位移 质量

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.