引 言

拟序结构普遍存在于湍流中^[1–3], 并影响湍流的发生、输运与耗散等过程, 对湍流拟序结构的研究、对于理解湍流机理、分析流动相互作用有重要的意义. 从大涡模拟来看, 正确预测湍流拟序结构的关键就在于算法和亚网格尺度(sub-grid-scale, SGS)模型的准确性.

在算法方面, 传统的大涡模拟方法求解网格滤波的控制方程, 并采用SGS模型模化亚网格尺度流动与网格尺度流动之间的相互作用. 虽然近年来部分****利用数值离散的特点, 也发展出不需要添加模型的隐式大涡模拟方法^[4-5], 但为了针对性地讨论应用中亚网格模型的选择问题, 本文仍采用高精度有限差分结合亚网格模型的大涡模拟经典算法, 并讨论SGS模型的性能. 对大涡模拟算法更全面的介绍可以参考Sagaut等^[6]的综述.

目前文献中广泛出现的亚网格尺度模型是经典的常系数Smagorinsky模型(Smagorinsky model, SM), 已有众多文献报道该模型过度耗散了脉动动能^[7-9]. 另一类是基于Germano恒等式和Lilly最小二乘法来动态调整模型系数的动态Smagorinsky模型(dynamic Smagorinsky model, DSM), 这类模型的局限性在于理论上要求在流场均匀的方向上计算平均的模型系数, 而这一平均过程缺少物理上合理的解释, 且造成分布式并行计算中不同处理器之间数据的频繁调用与交换, 降低计算效率. 从计算的角度, 较为理想的模型是局部模型, 计算效率高且能较好地克服SM对湍流黏性估计过高的缺点. Piomelli和Liu^[9]提出了局部动态模型(localized dynamic Smagorinsky model, LDSM), 去除了DSM对流动中需存在各向同性方向的要求, 而是利用流动的历史信息来避免平均过程, 计算效率得到提高. Lenormand等^[10]提出的选择多尺度模型(selective mixed-scale model, SMSM), 在边界层流动^[10]、翼型绕流^[11]和空腔流动^[12]的预测中具有良好应用. 这一模型借助涡矢量方向的变化来判断流动的状态是否发生了转捩, 同时反映湍流的间歇性. Kobayashi等^[13-14]则利用流场中黏性耗散与拟序结构的关联性, 提出了拟序结构模型(coherent-structure Smagorinsky model, CSM), 并应用于各向同性湍流、湍流通道流以及横向射流的计算中, 其模型简单且具有类似于动态模型的性能. Koyabashi^[13]同时改进动能模型, 提出拟序结构动能模型(coherent-structure kinetic-energy model, CKM). 这些局部模型都有望克服传统模型的不足, 但对于预测可压缩喷流中的拟序结构, 目前尚未看到有关它们预测性能的分析与评估的文献.

典型的喷流拟序结构有流向涡、高低速流体间的条带^[15]、剪切层边沿的卷吸流动结构^[16]等, 表现为长时间保持一定形状的大尺度质量团, 且在时间和空间上具有强相关性^[17]. Lumley^[18]最早提出采用本征正交分解(proper orthogonal decomposition, POD)方法提取拟序结构, 且在自由剪切流、分离流、边界层转捩以及湍流通道流中得到广泛的应用. POD方法的目标是针对物理场寻找一组空间正交的基函数, 并按照基函数对物理量方差的贡献排序, 例如对于脉动速度场的研究就是基函数对湍动能的贡献^[19-20]. 本征正交分解的特点使得只需要少量的POD模态就能够提取出流场中能量占主导地位的流动模式. 此外, POD分解的基函数直接由湍流场确定, 不同于傅里叶变换或者小波变换需要人为指定基函数, 因此表征的拟序结构更为客观^[17]. 在POD算法方面, 虽然快照POD算法能够显著减少计算量, 但是有部分高阶模态没有参与计算. 基于矩阵奇异值分解(singular value decomposition, SVD)的经典POD算法包含完整的模态信息, 比快照POD算法对舍入误差的鲁棒性高^[19-20]. 此外数学软件Matlab中提供了SVD的库函数, 也便于编制后处理程序.

本文对亚声速可压缩平行喷流进行大涡模拟. 在验证计算结果的基础上, 研究SM, CKM, SMSM, LDSM和CSM模型的特性, 分析各个模型预测的瞬时涡结构. 同时采用基于SVD的POD分解方法提取喷流拟序结构并分析各模型预测结果的差异, 为可压缩喷流的大涡模拟提供参考.

1.
数值计算与方法

1.1
亚网格尺度模型

控制方程组为Favre质量加权滤波的三维非稳态可压缩N-S方程组^[21]. 方程中的亚网格尺度未知量由亚网格模型给出, 包括亚网格尺度应力${tau _{ij}}$

$$bar ho {tau _{ij}} = overline { ho {{u''}_i}{{u''}_j}} $$

(1)

以及亚网格尺度热通量

$${q_{{ m{sg}}{{ m{s}}_j}}} = - frac{{bar ho {nu _{{ m{sgs}}}}}}{{left( {gamma - 1} ight){{Pr }_{ m{t}}}{{{M}}^2}}}frac{{partial tilde T}}{{partial {x_j}}}$$

(2)

其中$
ho $, $T$, ${{nu _{{
m{sgs}}}}}$以及${u_i}$(i = 1, 2, 3) 分别为密度、温度、模化的亚网格黏性系数以及速度矢量的3个笛卡尔分量. $gamma $是量热完全气体的比热比, 空气取$gamma = 1.4$. M为马赫数, 湍流普朗特数常数${Pr _{
m{t}}} = 1$^[22], 而${u''_i} = {u_i} - {tilde u_i}$, ${tilde u_i} = {{overline {
ho {u_i}} }/{overline
ho }}$, 顶标“-”表示网格滤波, “~”表示Favre质量加权的网格滤波, 所有计算变量均为网格滤波后的变量, 因此除非特殊说明以下省去顶部符号.

Smagorinsky模型(SM)中的亚网格尺度应力为

$${tau _{ij}} = tau _{ij}^a + {tau _{kk}}{{{delta _{ij}}}/3} $$

(3)

其中偏应力部分$tau _{ij}^a$与各向同性部分${tau _{kk}}$的模化为

$$left. {begin{array}{*{20}{l}}{tau _{ij}^a = - underbrace {C_1^2{varDelta ^2}left| {{boldsymbol{S}}left( u ight)} ight|}_{{nu _{{ m{sgs}}}}}{S_{ij}}left( u ight)}{{tau _{kk}} = 4C_1^2{varDelta ^2}{{left| {{boldsymbol{S}}left( u ight)} ight|}^2}}end{array}} ight}$$

(4)

式中, 亚网格黏性系数${nu _{{
m{sgs}}}} = C_1^2{varDelta ^2}left| {{boldsymbol{S}}left( u
ight)}
ight|$, $varDelta$表示网格尺度, $left| {{boldsymbol{S}}left( u
ight)}
ight| = sqrt {{{{S_{ij}}{S_{ij}}}/2}}$是网格尺度的应变率张量${S_{ij}}left( u
ight) = {{partial {u_i}}/{partial {x_j}}} + {{partial {u_j}}/{partial {x_i}}} - 2{{{delta _{ij}}left( {{{partial {u_k}}/{partial {x_k}}}}
ight)}/3}$的模, 对相同的脚标采用求和约定, 其中$i = j$时${delta _{ij}} = 1$, $i ne j$时${delta _{ij}} = 0$. 对于喷流, 取模型系数${C_1} = 0.17$^[23]. ${tau _{kk}}$的模化根据文献[7]的建议得出.

局部动态Smagorinsky模型(LDSM)采用基于Germano恒等式的动态方法, 并利用模型系数的历史信息来局部调整Smagorinsky模型的系数. 该模型根据Germano恒等式导出的应力${L_{ij}} = left(widehat{{{overline {
ho {u_i}}} ;{overline {
ho {u_j}}} /{bar
ho }}}
ight) -$$ {widehat{{bar
ho}{tilde u}_i}};;{widehat{{bar
ho}{{tilde u}_j}}}/{hat{ bar
ho}} $, 与采用SM模型估计的应力${alpha _{ij}} = - {left( {hat varDelta }
ight)^2}left| {{boldsymbol{S}}left( {hat u}
ight)}
ight| cdot $$ {S_{ij}}left( {hat u}
ight)$, $;{beta _{ij}} = - {left( {bar varDelta }
ight)^2}left| {{boldsymbol{S}}left( {tilde u}
ight)}
ight|{S_{ij}}left( {tilde u}
ight)$, 建立式(5)中的关系^[9]

$${cal L}_{ij}^a = - C_2^2{alpha _{ij}} + widehat {C_{ m{t}}^2{beta _{ij}}}$$

(5)

其中$mathcal{L}_{ij}^a = {mathcal{L}_{ij}} - {{{delta _{ij}}{mathcal{L}_{kk}}}/3}$, 顶标 “^”表示测试滤波运算, ${C_{
m{t}}}$为上一时刻的模型系数, 初始值可以根据SM模型取${C_{
m{t}}} = {C_1}$, 当前时刻的模型系数${C_2}$是未知量, 且式(5)对${C_2}$是超定的. ${C_2}$的估计值由式(5)两边取${alpha _{ij}}$的缩并得出^[9], 如式(6)所示. LDSM模型的亚网格尺度应力与亚网格黏性系数通过将式(4)中的$C_1^2$替换为$C_2^2$得出

$$C_2^2 = -sumlimits_{j = 1}^3 {sumlimits_{i = 1}^3 } left( {{cal L}_{ij}^a - widehat {C_{ m{t}}^2{beta _{ij}}}} ight){alpha _{ij}}Bigr/sumlimits_{j = 1}^3 {sumlimits_{i = 1}^3 } left( {{alpha _{ij}}{alpha _{ij}}} ight)$$

(6)

选择多尺度模型(slective mixed-scale model, SMSM)是根据局部涡矢量方向的脉动来调整亚网格黏性系数

$${nu _{{ m{sm}}}} = {C_3}{left| S ight|^alpha }{left( {q_{ m{c}}^2} ight)^{left( {1 - alpha /2} ight)}}{varDelta ^{left( {1 + alpha } ight)}}$$

(7)

其中${C_3} = 0.06$, $alpha $取0.5^[24]. 为了反映湍流的多尺度特性, 引入小尺度脉动的动能$q_{
m{c}}^2 = left( {1/2}
ight){tilde u'_i}{tilde u'_i}$, 其中脉动速度${tilde u'_i} = {tilde u_i} - {hat {tilde u}_i}$. 进一步, 对网格滤波尺度的瞬时涡量$boldsymbol{tilde omega }$进行测试滤波, 得出${hat{ tilde{boldsymbol omega }}}$. $boldsymbol{tilde omega }$和${hat {tilde{boldsymbol omega }}}$两个向量之间的夹角$theta $反映了涡运动的脉动强弱. 对于均匀各向同性湍流, 在夹角$theta $的概率密度函数的峰值位置处有${theta _0} = {20^ circ }$^[24], 据此, 可判断局部流动的状态. 模型引入了选择函数${f_{{{
m{theta }}_0}}}$, 当$theta > $${theta _0}$时, 取${f_{{{
m{theta }}_0}}} = 1$, 表示涡方向在两个滤波尺度上变化较大, 是无规则的完全湍流状态; 否则, 当$theta < {theta _0}$时, 取${f_{{{
m{theta }}_0}}} = {tan left( {theta /2}
ight)/tan left( {{theta _0}/2}
ight)}$, 意味着湍流逐步减弱, 亚网格黏性也应相应减弱, 直到在层流区仅保留分子黏性. 因此, SMSM模型的亚网格黏性系数为

$${v_{{ m{sgs}}}} = {v_{{ m{sm}}}}{f_{{{ m{theta }}_0}}}$$

(8)

拟序结构模型是利用拟序结构与湍流中耗散的相关性来调整亚网格黏性系数${v_{{
m{sgs}}}} = $$ C{varDelta ^2}left| {Sleft( u
ight)}
ight|$, 模型系数$C = {C_4}{left| {{F_{{
m{CS}}}}}
ight|^{3/2}}$中常数${C_4} = 0.05$^[13], ${F_{{
m{CS}}}} = Q/E$为拟序结构函数，其中

$$Q = left( {{A_{ij}}{A_{ij}} - } ight. left. {{B_{ij}}{B_{ij}}} ight)/ 2 + {left( {partial {u_k}/partial {x_k}} ight)^2}/2$$

为速度导数${D_{ij}} = {{partial {u_i}}/{partial {x_j}}}$的第二不变量, 它主要由${D_{ij}}$中反映当地旋转的反对称部分${A_{ij}}$和反映当地变形的对称部分${B_{ij}}$组成, 而$E = {{{{left( {{{partial {u_i}}/{partial {x_j}}}}
ight)}^2}}/2}$为${D_{ij}}$的范数.

其中

$$ {A_{ij}} = {{left( {{{partial {u_j}}/{partial {x_i}}} - {{partial {u_i}}/{partial {x_j}}}} ight)}/2}$$

$${B_{ij}} = {{left( {{{partial {u_j}}/{partial {x_i}}} + {{partial {u_i}}/{partial {x_j}}}} ight)}/2}$$

基于直接数值模拟(direct numerical simulation, DNS), 流场的相关性分析表明, $Q$的绝对值与拟序小尺度涡附近能量耗散的强弱存在关联^[13], 因此$left| {{F_{{
m{CS}}}}}
ight|$反映了流场中黏性与耗散的局部变化, 而$left| {{F_{{
m{CS}}}}}
ight|$的幂次“3/2”是根据不可压缩壁面流动中$C propto {y^3}$, $Q propto {y^2}$以及$E propto $常数(y是壁面的法向)而确定的. 因此, CSM模型的亚网格黏性系数为

$${nu _{{ m{sgs}}}} = {C_4}{left| {{F_{{ m{CS}}}}} ight|^{3/2}}{varDelta ^2}left| {Sleft( u ight)} ight|$$

(9)

拟序结构动能模型是在拟序结构模型的基础上, 在亚网格黏性系数中显式地包含亚网格尺度动能${k_{{
m{sgs}}}}$, 并做量纲调整后得到

$${nu _{{ m{sgs}}}} = {C_5}left| {{F_{{ m{CS}}}}} ight|varDelta sqrt {{k_{{ m{sgs}}}}} $$

(10)

其中，${C_5} = 0.15$, ${k_{{
m{sgs}}}} = {left( {{{tilde u}_i} - {{hat {tilde u}}_i}}
ight)^2}$, ${hat {tilde u}_i}$由显式滤波计算得出^[13].

至此, 可以通过式(2)、式(4)来计算亚网格尺度热通量和亚网格尺度应力. 虽然文献[12]指出亚网格尺度应力中各向同性的部分${tau _{kk}}$相对于热力学压力可以忽略, 但根据Vreman^[7]的建议, 在基于SM的LDSM以及CSM模型中仍然模化${tau _{kk}}$.

1.2
计算对象与数值离散

本文采用Hu等^[22]的亚声速平行喷流为考核算例. 喷流出口雷诺数${{R}}{{{e}}_{
m{J}}} = {D_{
m{J}}}{
ho _infty }{U_{
m{J}}}/{mu _infty }$ $ = 2000$, 马赫数${{{M}}_{
m{J}}} = {U_{
m{J}}}/{c_infty } = 0.9$, 其中${D_{
m{J}}} = 1$、${U_{
m{J}}} = 1$分别为归一化的喷口宽度和喷口速度, 参考值$;{
ho _infty }$, ${mu _infty }$和${c_infty }$分别为来流密度、动力黏度以及环境声速. 计算域与网格划分如图1所示, 流向(x)、横向(y)与展向(z)的尺寸分别为${L_x} times {L_y} times {L_{textit{z}}} = 24 times 15 times 3$, 采用笛卡尔网格进行离散, 对应方向的结点数分别为$181 times 181 times 16$. 为了提高近喷口区域和喷流唇线附近的网格分辨率, 采用双曲正切函数对x和y方向的网格进行拉伸, 而喷流在z方向采用周期边界条件, 划分均匀的网格. 基于Celik等^[25]提出的大涡模拟分辨率指标, 由于课题组前期工作已证明该网格能够分辨湍动喷流中75%以上的湍动能, 考虑到喷流的雷诺数较低, 该计算网格可以满足大涡模拟的网格质量要求^[26].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
计算域与网格(3个方向都每隔3条网格线画一条线)



Figure
1.
Computional domain and the Grid(One in every three lines is shown in each direction)



下载:
全尺寸图片
幻灯片


采用有限差分方法开展数值模拟, 本文的计算源程序以Sandham课题组^[27-28]的(shock-boundary layer interaction, SBLI)代码为基础, 计算精度和可靠性经过了充分的考核验证^{[22, 29]}. 在此基础上, 本文进一步采用OpenMP并行化, 使该代码可用于内存共享式的小型计算工作站.

空间离散的1阶与2阶导数均采用5点4阶中心差分格式计算, 边界点采用Carpenter提出的单侧4阶稳定差分格式^[30], 从而保持空间离散的整体高精度. 为了抑制差分计算引起的非物理振荡, 算法上采用了熵分裂方法, 通过将对流项分裂为守恒形式与非守恒形式的加权求和来实现^[31]. 同时, 在x和y方向的计算边界上, 采用无反射边界条件来抑制非物理振荡波在计算域边界上的反射, 算法上通过保留走出计算域的特征波而将走入计算域的特征波幅值置零来实现^[32]. 在z方向上采用周期边界条件来模拟平行喷流在展向的无限延伸.

时间离散采用低存储显式3阶龙格库塔算法, 这一算法完成3个子时间步的推进仅需要两个存储流场的数组, 对内存资源的消耗低^[21]. 为便于模型特性的研究比较, 时间步长取定值$Delta t = 0.003;075$, 且满足数值稳定性条件$CFL < 1$. 在初始条件方面, 给定喷口平面上流向速度$u$、温度$T$以及压强$p$的形线, 并用喷口平面上的物理量来初始化全场. 喷口的速度分布采用双曲正切函数给定, 并施加伴流速度${U_{{
m{0}}}} =$0.1, 可得

$$left. begin{array}{l}u = 0.45left{ {tanh left[ {10left( {y + 0.5} ight)} ight]} ight.-quad;left. { tanh left[ {10left( {y - 0.5} ight)} ight]} ight} + {U_{{ m{0}}}}{u_{ m{p}}} = 0.33{y^2}left( {4{y^2} - 1} ight){{ m{e}}^{ - 6{y^2}}}sin left( {2{text{π}} {textit{z}}/{L_{textit{z}}}} ight)cos left( {2t} ight){v_{ m{p}}} = 0.4{y^3}{{ m{e}}^{ - 6{y^2}}}sin left( {2{text{π}} {textit{z}}/{L_{textit{z}}}} ight)sin left( {2t} ight)end{array} ight}$$

(11)

式中还包含随时间变化的二维扰动速度$left( {{u_{
m{p}}},{v_{
m{p}}}}
ight)$, 扰动幅值和频率根据线性稳定分析得出, 文献[22]表明这一扰动能够触发湍流. 喷口的温度分布根据Crocco-Busemann温度?速度关系确定

$$T = 1 + 0.5left( {gamma - 1} ight){{M}}_{ m{J}}^2left( {1 - {u}} ight)left({u-U_infty} ight)$$

而喷口的压强取为常数 $p = 1/left( {gamma {{M}}_{
m{J}}^2}
ight)$.

在数值结果方面, 虽然DNS能够准确给出流场结构的信息, 但是DNS对计算资源的消耗量高, 而且流场后处理的数据量大. 以文献[22-33]中提供的DNS数据为基础, 课题组前期工作已开展了计算代码的考核^[34-35]、LES的网格分辨率分析^[26]以及局部模型的研究^{[21, 36]}, 算法的可靠性与模型都已得到验证. 本文在已有工作的基础上, 进一步分析局部模型揭示的喷流拟序结构.

1.3
POD方法

POD方法采用一组正交基函数$psi left( x
ight)$的线性组合来表示物理场$phi left( {x,t}
ight)$, 组合系数为$cleft( t
ight)$, 即

$$ phi left( {x,t} ight) sim displaystylesumlimits_{k = 1}^N {{c_k}left( t ight){psi _k}left( x ight)}$$

所得的基函数也称为POD模态. POD分解的目的是使这种表示的误差在平方平均的意义下最小, 并且在给定误差下最小化表示所需要的模态个数, 从而得到最佳的基函数^[20]. 这组最佳基函数能够最优地表征原物理量的方差, 对于脉动速度场，这种最优是模态反映的湍动能随模态阶数增大而迅速的减小^[19], 脉动速度的第一阶POD模态对湍动能的贡献最大. 详细的理论介绍可参考文献[20].

在计算中, 可对流场的速度分量进行时间采样, 得到关于标量$phi $的N个流场样本, 对于网格点数为$M = {M_x} times {M_y}$的二维样本, 可将每个样本都写成$M times 1$的列向量, 由此得到 $M times N$的样本矩阵

$$mathop {boldsymbol{F}_{M times N}} = left( {begin{array}{*{20}{c}}{{phi _{1,1}}}&{{phi _{1,2}}}& cdots &{{phi _{1,N}}}{{phi _{2,1}}}&{{phi _{2,2}}}& cdots &{{phi _{2,N}}} vdots & vdots & ddots & vdots {{phi _{M,1}}}&{{phi _{M,2}}}& cdots &{{phi _{M,N}}}end{array}} ight),; {M geqslant N} $$

(12)

在离散求解时, 寻找最佳基函数的过程在数学上等价于求样本矩阵F的SVD问题^[20]. 采用Matlab中低存储的“svd( )”库函数计算$boldsymbol{F}$的奇异值分解

$$begin{array}{l}mathop {boldsymbol{F}_{M times N}} = mathop {boldsymbol{varPsi }_{M times N}} mathop {boldsymbol{S}_{N times N}} {mathop {boldsymbol{C}_{N times N}}} ^{ m{T}}end{array}$$

(13)

其中, 左矩阵$boldsymbol{varPsi }$的各列是正交的, $boldsymbol{varPsi } = {left( {{pmbpsi _1},{boldsymbolpsi _2},cdots,{boldsymbolpsi _N}}
ight)}$, 它的第i列${boldsymbolpsi _i}$即为物理场的第i阶POD模态, 右矩阵$boldsymbol{C}$的各列也是正交的, $boldsymbol{C} = {left( {boldsymbol{c}_1,boldsymbol{c}_2,cdots,boldsymbol{c}_N}
ight)}$, 它的第i列$boldsymbol{c}_i$即为模态$boldsymbol{psi} _i$对应的系数, 反映POD模态与时间有关的特征^[19], 而$boldsymbol{S}$为奇异值矩阵, $boldsymbol{S} = {
m{dig}}{left( {{s_1},{s_2},cdots,{s_N}}
ight)}$, $boldsymbol{S}$的对角元为从大到小排列的奇异值${s_i}left( {i = 1,2,cdots,N}
ight)$, 其他矩阵元为零, ${lambda _i} = s_i^2$代表了与第i阶POD模态对应的能量, 且对各阶模态可以定义能量贡献率

$${xi _n} = {{{lambda _n}}Biggr/{sumlimits_{j = 1}^N {{lambda _j}} }}$$

(14)

以及累计能量贡献率

$${eta _n} = {{sumlimits_{i = 1}^n {{lambda _i}} }Biggr/{sumlimits_{j = 1}^N {{lambda _j}} }} $$

(15)

另外, 由于各阶POD模态$boldsymbol{psi} _i$是相互正交的, 所以$lambda $衰减越快, 当前模态所含有的能量相比下一阶模态的差就越大, 当前模态所表征的物理场的相关性就越强.

2.
SGS模型的特性

2.1
平均流场

在分析湍流统计特征时, 为排除初场对统计结果的影响, 取无量纲时间t = 48 ~ 216的流场数据, 对应流体以喷口速度流过2 ~ 9倍的计算域长度, 以计算时间步长$Delta t$为采样间隔, 得到54640个流场样本. 图2以LDSM模型为例, 显示了在唇线上无量纲位置x = 2, 6, 8, 10, 20处的流向脉动速度的功率谱, 谱线具有一段固定的斜率且能观察到惯性区, 反映了湍流的能量级串现象, 也说明流动已经达到了完全湍动状态.



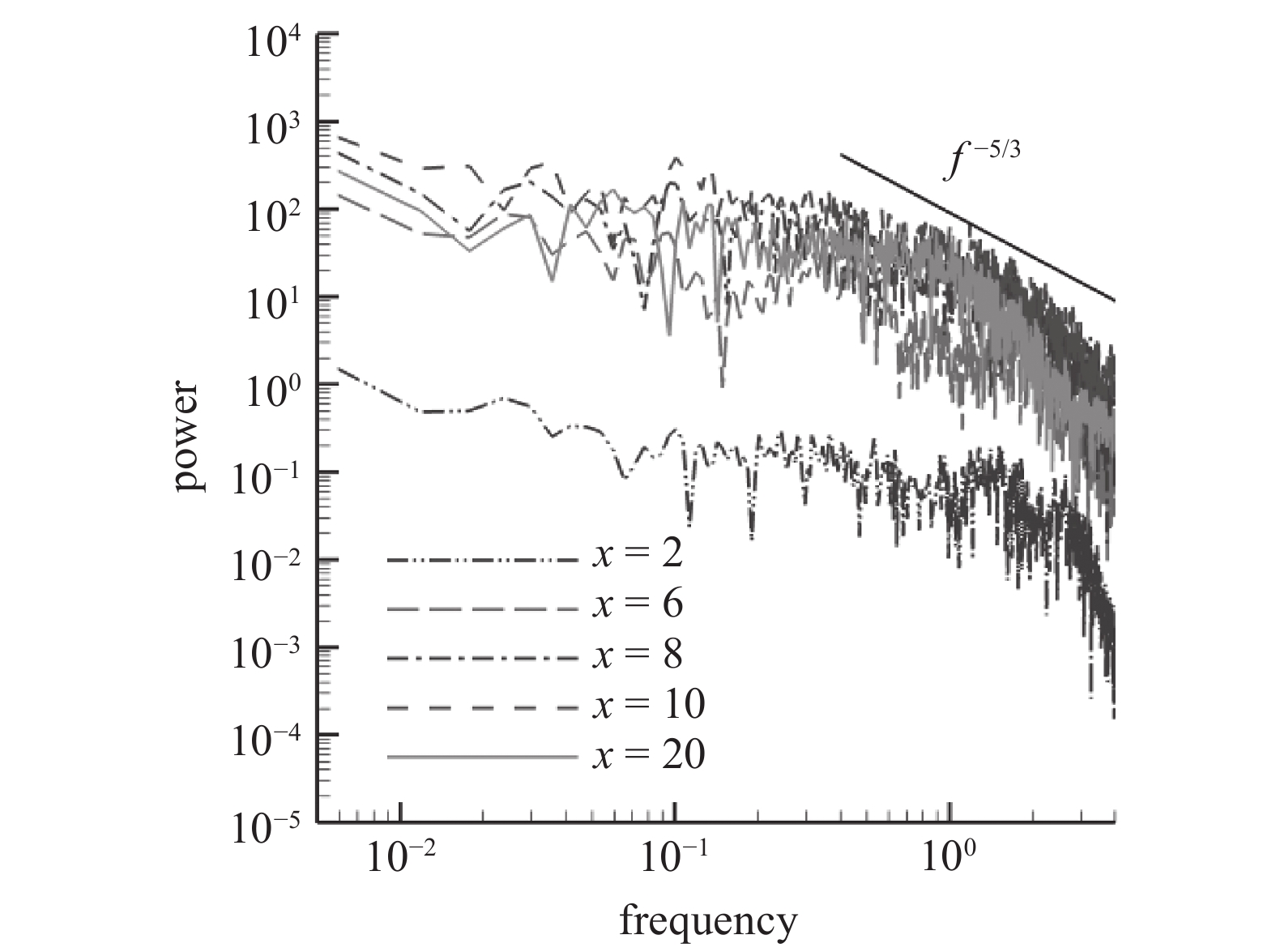onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
LDSM模型预测的脉动速度无量纲功率谱



Figure
2.
Dimensionless power spectra of velocity signals predicted by the LDSM



下载:
全尺寸图片
幻灯片


喷流主流流体与环境流体存在速度差, 形成剪切层. 图3所示为喷流剪切层的发展. 考虑喷流中心线速度${U_{
m{c}}}$与伴流速度${U_0}$, 图3(a)采用速度半值宽${delta _{0.5}}$, 即流向速度$u = $$ 0.5left( {{U_{
m{c}}} + {U_0}}
ight)$时的横向位置y, 显示出剪切层的发展呈现两个线性阶段, 即初期的缓慢增长段与下游的快速增长段, 这对应喷流势流核末端$x approx 6$处的流动转捩现象. 对比5种模型的结果, SM模型预测的剪切层横向发展程度较其他模型大, 表明该模型过度耗散的特点. 图3(b)以LDSM模型为例, 在相似坐标中绘出了喷流不同流向位置的速度形线, 相似坐标的横向位置采用速度半值宽归一化, 平均喷流速度差$leftlangle u
ight
angle - {U_{
m{c}}}$采用主、伴流的速度差$Delta {U_{
m{c}}} = {U_{
m{c}}} - {U_0}$归一化, $leftlangle cdot
ight
angle $表示时间平均. 图3(b)中, 速度形线在入口呈平顶状分布, 而在下游则快速发展为自相似的速度形线, 可以看到$x = 4$时, 自相似形线还没有建立, 但当$x geqslant 8$时, 速度形线与实验喷流^[37–39]的自相似数据点吻合良好, 也验证了计算结果.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
喷流剪切层的发展



Figure
3.
Developments of the jet shear layer



下载:
全尺寸图片
幻灯片


喷流流体与环境流体的强烈掺混伴随着能量的耗散. 对比5种SGS模型的亚网格尺度平均黏性耗散率, 定义为$leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle = leftlangle {
ho {tau _{ij}}partial {u_i}/partial {x_j}}
ight
angle $. 图4为$leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle $在展向中心平面(${textit{z}} = 1.5$)上的分布. 由于喷流入口施加的平均来流条件, 流体喷出后在近喷口区基本为层流状态, 随后在势流核末端($x approx 6$)附近发生流动转捩, 并在下游发展为充分湍流. 图2中, 近喷口的脉动水平比势流核及其下游的区域低1 ~ 2个数量级, 进一步表明来流的层流特征, 此处与湍流脉动相关的亚网格尺度黏性耗散应趋近于零. 但在图4(a)中, SM模型预测的$leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle $在近喷口区内呈两条平行的条带, 表明SM模型对层流扰动敏感, 不能正确反映湍流黏性耗散率的分布区域. 图4(b) ~ 图4(e)分别为CKM, SMSM, LDSM以及CSM的预测结果, 这4种局部模型虽然能够正确地反映近喷口区的$leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle $分布特征, 在转捩区($x = 6 sim 9$)内呈现一对峰值, 但是以CSM模型为参考, CKM, LDSM, SMSM以及SM模型预测的峰值耗散不同, 分别为CSM模型预测值的3.0, 1.8, 1.3和0.9倍. 其中CKM预测的峰值$leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle $接近其他模型的1 ~ 2倍, 稍后分析$leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle $的分布对转捩区内涡结构的影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-4.jpg'"
class="figure_img
figure_type2 ccc " id="Figure4" />



图
4
对比$leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle $在中心平面(${textit{z}} = 1.5$)上的分布



Figure
4.
Comparisons of the distribution of $leftlangle {{varepsilon _{{
m{sgs}}}}}
ight
angle $ in the center plane of the jet (${textit{z}} = 1.5$)



下载:
全尺寸图片
幻灯片

2.2
瞬时流场的涡结构

分析无量纲时间$t = 207$的瞬时流场, 此时喷流以喷口速度流过8倍以上的计算域长度, 已经充分排除初场的影响. 参考Hu等^[22]的部分DNS结果, 以喷流中心线速度$leftlangle u
ight
angle $衰减为0.99时的流向位置得出平均的势流核长度为$x = 6.43$. 图5为$Q = 0.1$的等值面, 图5中红色切片位于Hu等DNS结果^[22]的势流核末端. 在预测流动转捩方面, 图5(c) ~ 图5(e)中, SMSM, LDSM以及CSM模型都能预测大尺度展向涡在平均势流核末端附近的破碎, 以及下游区域内湍流多尺度涡结构的生成. 然而对于SM模型, 图5(a)在切片位置下游仍然能够观察到流向的大尺度涡结构(如图5中箭头所示), 结合图4(a)可知, 湍流中小尺度涡的发展可能受到近喷口过度的亚网格尺度耗散的抑制, 这与文献[7–9]对SM模型过度耗散特点的报道一致. 图5(b)中, CKM模型的预测结果与SM类似, 同样可能由于该模型中局部亚网格尺度耗散较强. 图6为展向涡${omega _{textit{z}}}$的等值面, 同样采用红色切片标记DNS结果^[22]的势流核末端位置. 可以看到, ${omega _{textit{z}}}$的等值面在势流段内呈平行的涡片, 随着流动向下游的发展, ${omega _{textit{z}}}$等值面在势流核末端附近快速卷起, 随后涡结构被拉伸并在下游发展出复杂的三维结构. 图6(a)中, SM模型预测的涡卷起位置位于切片之后, 涡片偏长, 对应图4(a)中近喷口区的不合理耗散, SM模型抑制了流场中展向涡的发展. 图6(b), 图6(d), 图6(e)中, CKM, LDSM以及CSM模型在势流核末端位置附近都能够观察到展向涡的卷起(如图6中箭头标记)以及下游的涡破碎, 但LDSM与CSM模型在切片后预测的小尺度涡结构比CKM模型丰富, 再次表明CKM模型的局部强耗散可对小尺度涡结构产生抑制. 图6(c)中, SMSM预测的涡卷起不显著, 但切片下游的预测结果与LDSM, CSM类似. 相比SM与CKM模型, SMSM, LDSM以及CSM模型更能反映势流核下游展向涡的多尺度特性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
对比$Q = 0.1$的等值面, 采用流向速度着色, 红色切片位置标记了文献[22]中DNS结果的势流核末端: x = 6.43



Figure
5.
Comparisons of the iso-surface of $Q = 0.1$, colored by streamwize velocity. The red slice marks the end of the potential core x = 6.43 of the DNS results in Ref. [22]



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
对比${omega _z}$的等值面, 红色切片位置标记了文献[22]中DNS结果的势流核末端: x = 6.43



Figure
6.
Comparisons of the iso-surface of ${omega _z}$, the red slice marks the end of the potential core x = 6.43 of the DNS results in Ref. [22]



下载:
全尺寸图片
幻灯片

2.3
速度场的POD模态分析

对5种SGS模型的预测结果进行POD分解. 平行喷流主要表现为x-y平面内的二维流动特征, 因此在湍流统计的流场数据中, 截取三维流场的中心平面(${textit{z}} = 1.5$)为样本, 以$10Delta tleft( { = 0.030;75}
ight)$为采样间隔, 得到4685个样本. 针对5种SGS模型, 提取脉动速度分量$u'left( { = u - leftlangle u
ight
angle }
ight)$, $v'left( { = v - leftlangle v
ight
angle }
ight)$和$w'left( { = w - leftlangle w
ight
angle }
ight)$的POD模态. 脉动速度$u'$, $v'$和$w'$的第一阶模态分别对原始脉动速度场的脉动强度: $leftlangle {u'u'}
ight
angle $, $leftlangle {v'v'}
ight
angle $和$leftlangle {w'w'}
ight
angle $的贡献最大, 并在这一意义下脉动速度的第一阶模态与原始脉动速度场最为接近. 图7为流向脉动速度$u'$模态的累计能量贡献率 $eta $, 可以看到, 累计能量贡献率曲线在前200阶内就达到了90%以上, 这200阶模态仅为总模态数的4%, 因此曲线$eta $反映了POD的快速收敛特性. 但5种SGS模型的$eta $具有不同的增长速度, SM模型最快, 而SMSM模型最慢. 脉动速度$v'$与$w'$的$eta $曲线具有与图7相似的快速收敛特征, 因此不再绘出. 图8为脉动速度分量在前20阶模态的能量贡献率衰减曲线$xi $. 可以看到, 5种SGS模型得出的$xi $曲线都在前5阶内迅速衰减, 说明低阶模态占主导且模态表征的流场具有强的相关性. 对比图8中第1阶模态的能量贡献率, 图8(a)中u′模态的衰减曲线显示SM模型的第1阶模态贡献率最高, SMSM模型最低; 图8(b)中横向速度脉动$v'$模态的衰减曲线显示CKM模型的贡献率最高, 而SMSM模型依然排最低; 图8(c)展向速度脉动$w'$模态的衰减曲线中SMSM模型的能量贡献率排序有所提高. 图8表明, 第1阶模态的能量贡献率已经体现出了不同模型之间的差异, 接下来针对第1阶模态展开分析.



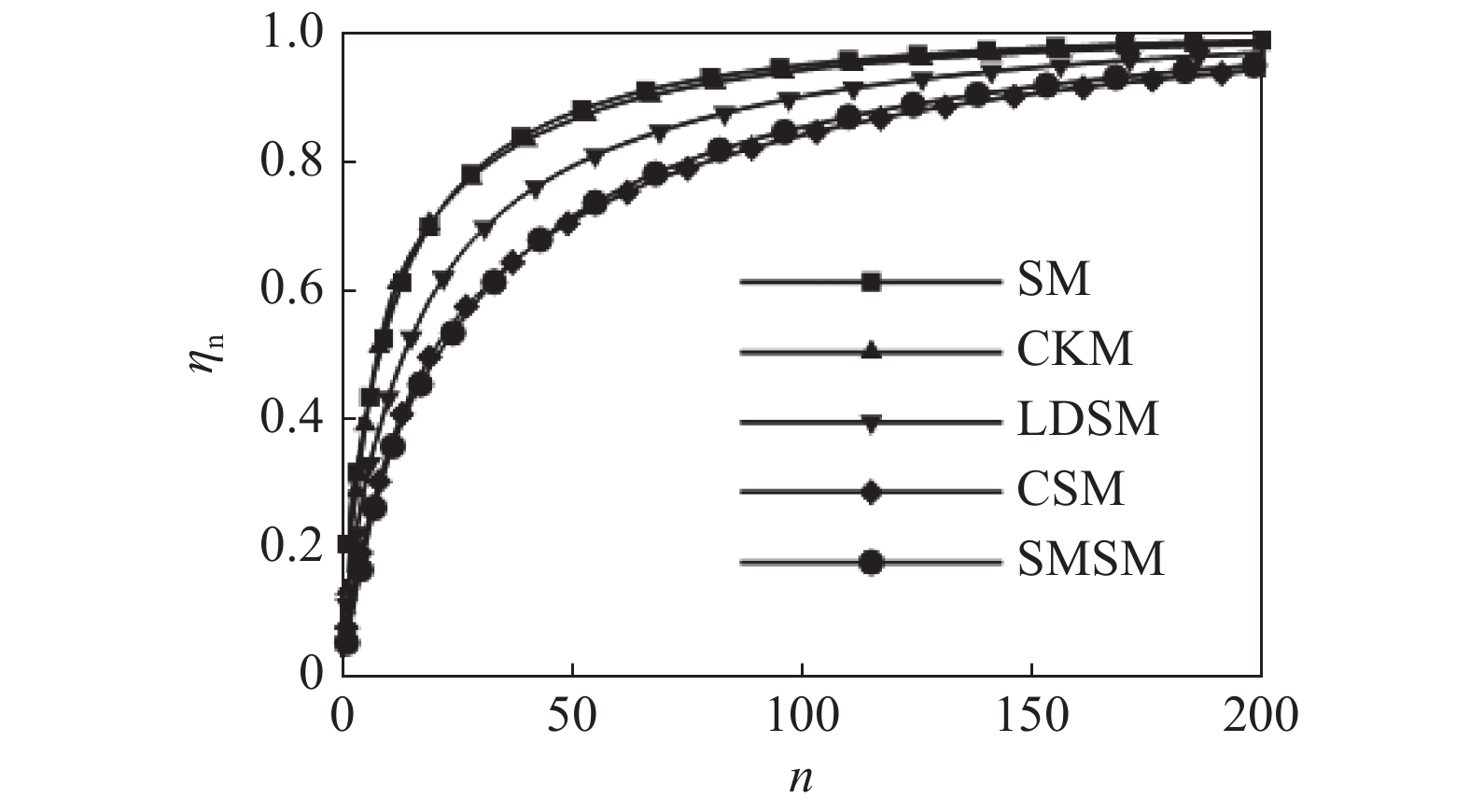onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
$u'$模态的累计能量贡献率的收敛曲线



Figure
7.
Convergency curves of the cumulative energy contribution for the modes of $u'$



下载:
全尺寸图片
幻灯片




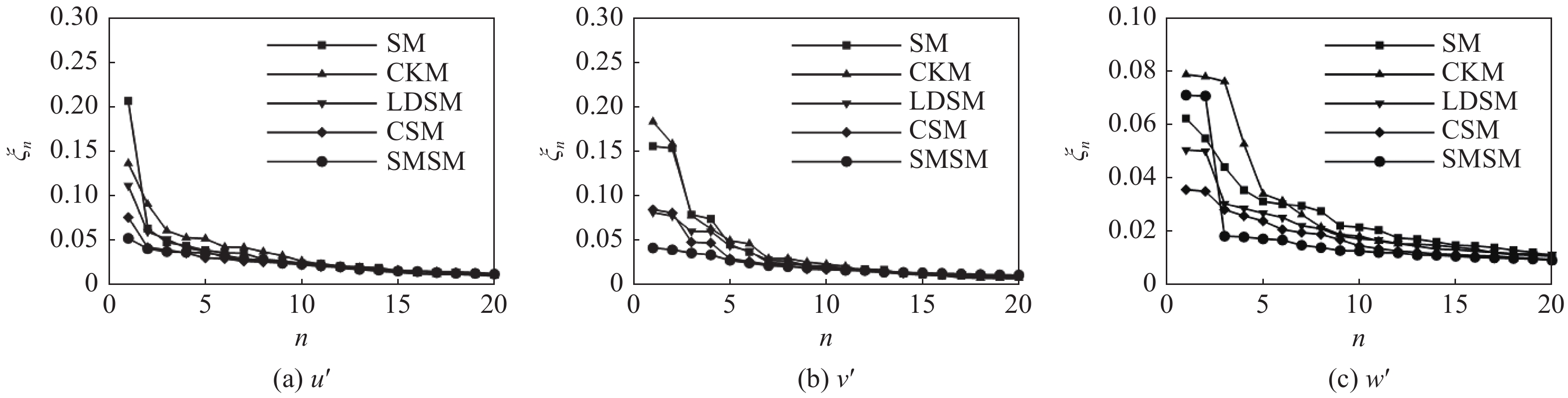onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
脉动速度分量的POD模态的能量贡献率



Figure
8.
Energy contribution rate of POD modes for the fluctuate velocity components



下载:
全尺寸图片
幻灯片


喷流主要表现为流向的动量传递. 对比5种SGS模型预测的流向速度脉动$u'$的第一阶POD模态, 图9显示了模态幅值在中心平面(${textit{z}} = 1.5$)上的分布, 采用接近零的模态幅值等值线$u' = pm 0.003$来显示模态的轮廓. 图9(a)中, SM得到两条沿流向的带状模态, 且在喷流下游$x = 12 sim 24$的范围内一直保持高的模态幅值, 对应图5(a)中大尺度流向涡结构对流场的搅动. 图9(b)中, CKM模型预测的模态也在下游保持沿流向的高幅值带状模态, 在转捩区$left( {x = 6 sim 9}
ight)$内的模态强度呈现一对低谷区, 位置恰好匹配图4(b)中的峰值耗散区位置. 这表明流向速度脉动的POD模态对亚网格尺度的黏性耗散率敏感, 局部的强耗散导致脉动强度$leftlangle {u'u'}
ight
angle $的降低, 从而改变了POD模态的形状. 图9(d)、图9(e)分别为LDSM与CSM模型预测的模态, 两者都沿流向两侧发散开来, 并且在喷流下游呈现分岔或破碎的形态, 模态幅值也逐渐减小, 反映下游的多尺度结构以及脉动能量的逐渐消散. 图9(c)为SMSM模型预测的模态, 模态轮廓在流向上呈断续的条状, 局部的模态幅值低, 这可能与图8(a)中SMSM模型第一阶POD模态的能量贡献率低有关. 而在下游, SMSM的模态呈现与CSM, LDSM模型预测结果相似的分岔形态. 因此, 与SM和CKM模型相比, CSM, LDSM以及SMSM模型都合理地反映了$u'$模态的形态.



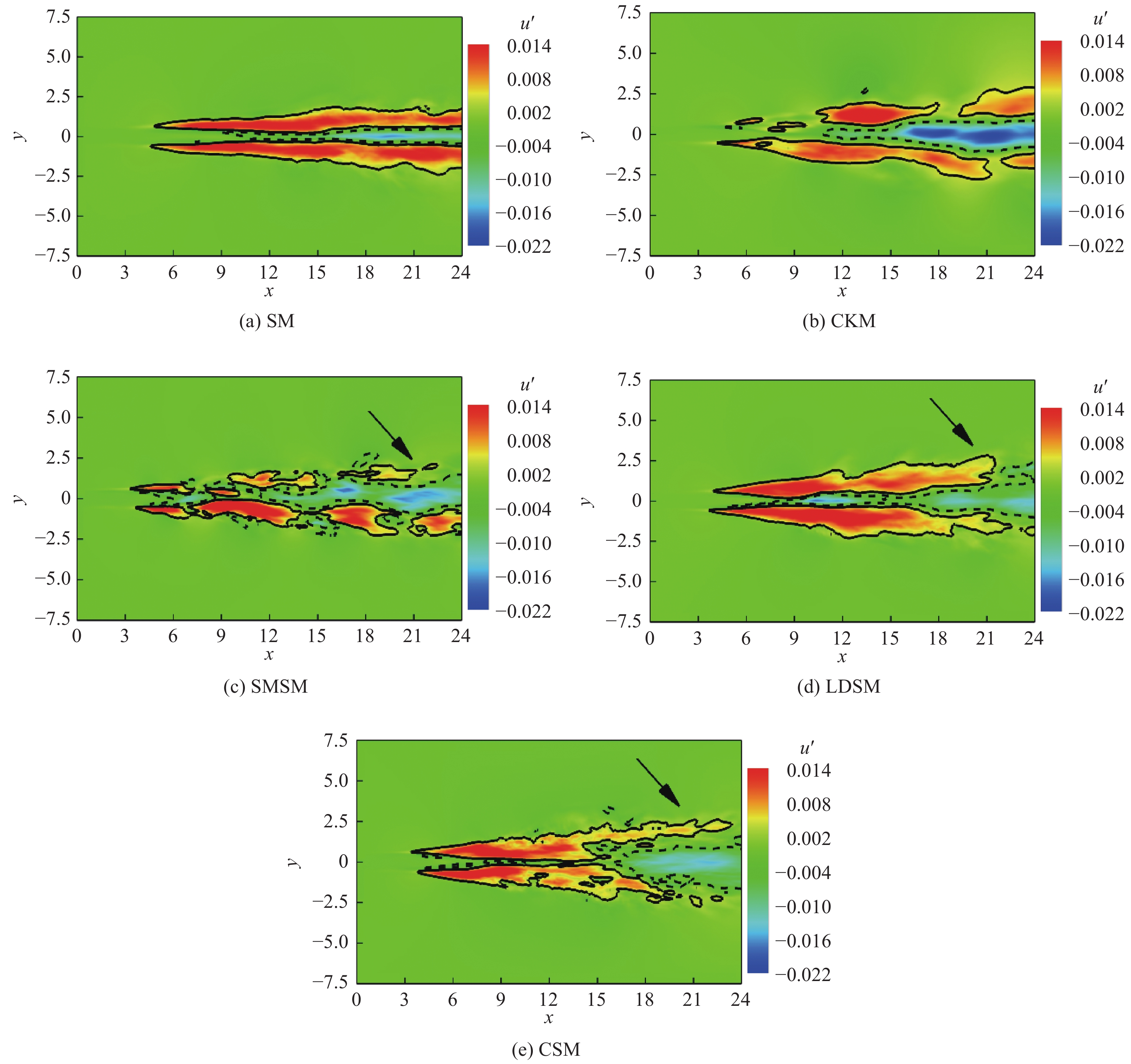onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-9.jpg'"
class="figure_img
figure_type2 ccc " id="Figure9" />



图
9
流向脉动速度$u'$的第一阶POD模态云图, 实、虚等值线分别表示$u' = + 0.003$和$u' = - 0.003$



Figure
9.
Contours of the first-order POD modes of $u'$, with solid contour lines for $u' = + 0.003$ and dashed contour lines for $u' = - 0.003$



下载:
全尺寸图片
幻灯片


图10为横向脉动速度$v'$的第一阶POD模态, 等值线$v' = $±$ 0.003$显示出模态的轮廓. 同时, 图10中采用面内矢量$left( {{boldsymbol{u}}',{boldsymbol{v}}'}
ight)$的POD模态来显示喷流中的流动模式. 观察图10, $v'$的POD模态呈正负相间的肋状, 并沿流向排列. 在肋状模态上下端部的附近, 矢量箭头显示出环形的流动模式, 在喷流上部的红圆标出了逆时针环流, 下部的蓝圆标出了顺时针环流. 环流模式穿过了主流与环境流体, 在圆环的下游侧, 高速的主流流体被送入两侧的低速环境流体中, 而在环流的上游侧, 低速的环境流体被带入主流流体中. 同时, $v'$模态轮廓的横向尺寸也沿着流向逐渐增大. 可见, $left( {{boldsymbol{u}}',{boldsymbol{v}}'}
ight)$的POD模态反映了喷流的流动卷吸现象^[16]. 对比图10(a) ~ 图10(e), SM, SMSM, LDSM以及CSM模型预测的模态都反映了喷流的卷吸现象, 其中SMSM模型预测的旋涡尺度小, 这与图8(a)和图8(b)中的低模态贡献率对应. 而图10(b)中, CKM模型预测的模态基本没有反映该区域内的流动卷吸, 结合图4(b), 脉动速度分量$u'$和$v'$可能受到CKM模型在$x = 6$附近局部的强耗散抑制, 导致未能预测出明显的流动卷吸.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-10.jpg'"
class="figure_img
figure_type2 ccc " id="Figure10" />



图
10
横向脉动速度v'的第一阶POD模态云图与面内矢量$left( {u',v'}
ight)$的第一阶POD模态矢量图(实、虚等值线分别表示 $v' = + 0.003$和$v' = - 0.003$, 红圈标示逆时针环流、蓝圈标示顺时针环流)



Figure
10.
Contours of the first-order POD modes of v' and the in plane vector $left( {u',v'}
ight)$ (Solid contour lines for $v' = + 0.003$ and dashed contour lines for $v' = - 0.003$. Red circle marks counterclockwise circular flow and blue circle indicates clockwise circular flow)



下载:
全尺寸图片
幻灯片


图11为展向脉动速度$w'$的POD模态云图, 等值线$w' = pm 0.003$显示出模态的轮廓. 图11(b) ~ 图11(e)分别为CKM, SMSM, LDSM以及CSM模型预测的结果, $w'$的POD模态在转捩区($x = 3 sim 9$)内呈现规则的脊状排列, 红色表示脉动速度$w'$指向平面外, 蓝色表示脉动速度$w'$指向平面内, 强弱相间的分布反映了$w'$模态对涡结构的展向拉伸, 如图11(f)所示. 图11中的脊状模态显示涡拉伸主要发生在转捩区, 而在下游的模态轮廓呈碎块状, 强度也逐渐减弱, 对应涡结构逐渐发展为三维结构, 展向的拉伸现象不再显著. 图11(a)中, SM模型预测的模态没有反映转捩区内的脊状排列, 在下游呈大团块, 位置与图4(a)中SM模型喷口附近的过度耗散区域相对应. 图11(b)中, CKM模型预测的模态虽然呈现了脊状排列, 但是模态轮廓在下游$x = 21$处仍然呈大尺度块状, 与SM模型的预测结果相似. 相比而言, SMSM,LDSM以及CSM 模型的预测结果则能够合理地反映展向拉伸的流动模式.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-11.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11" />



图
11
展向脉动速度$w'$的第一阶POD模态云图 (续)



Figure
11.
Contours of the first-order POD modes of $w'$, with solid contour lines for $w' = + 0.003$ and dashed contour lines for $w' = - 0.003$ (continued)



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-145-11-1.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11-1" />



11
展向脉动速度$w'$的第一阶POD模态云图



11.
Contours of the first-order POD modes of $w'$, with solid contour lines for $w' = + 0.003$ and dashed contour lines for $w' = - 0.003$



下载:
全尺寸图片
幻灯片


在计算效率方面, 表1对比了5种SGS模型的CPU时间, 以SM模型为基准, LDSM, SMSM, CKM, CSM的计算时间分别为SM模型的: 1.64, 1.28, 1.22和1.00倍, 其中LDSM, SMSM以及CKM模型需要进行滤波运算, 因此需要更多的CPU时间, CSM模型的计算时间最接近SM模型.




表
1
每时间步内每网格点所占用的CPU时间



Table
1.
CPU time per grid point per time step



table_type1 ">

SGS models	LDSM	SMSM	CKM	CSM	SM
CPU time/μs	1748	1371	1300	1065	1064

下载:
导出CSV
|显示表格

3.
结 论

本文开展了亚声速可压缩平行喷流的大涡模拟. 在分析平均流动与耗散的基础上, 针对瞬时涡流以及脉动速度POD模态表征的拟序结构, 对SM, CKM, SMSM, LDSM和CSM, 5种SGS模型的性能进行研究, 得出以下主要结论:

(1) 初步揭示了$u'$模态从流向的带状到下游分岔或破碎形态反映的多尺度特征、$v'$模态沿流向的肋状排列与尺寸增长、矢量$left( {{boldsymbol{u}}',{boldsymbol{v}}'}
ight)$模态的环流模式表征的流动卷吸、以及$w'$模态表征的流场结构在展向上受拉伸的模式.

(2) SMSM, LDSM以及CSM均较好地反映出湍流的多尺度特性, 清晰地分辨了小尺度结构的发展过程. 而SM与CKM模型则未能有效地预测湍流中的小尺度涡结构及部分流场特征模态.

(3) 脉动速度场的POD模态对SGS模型的亚网格尺度耗散敏感, 表现为CKM预测的峰值耗散区对应$u'$模态的低谷区因而环流模式不显著, 以及SM未能反映转捩区内$w'$模态的脊状拉伸模式. SMSM, LDSM和CSM克服了以上模型的不足之处, 其中CSM模型同时兼有计算效率较高的优势.