引 言

因其特有的低模量和能量耗散等“软”的特性以及优异的“小激励大响应”等特征, 多种多样的软材料, 如水凝胶、介电弹性体以及聚甲基氧硅烷等被广泛应用在软机器人、生物医学和柔性电子等各个领域^[1-4]. 近些年, 软材料的力学行为已经成为学术界和工业界广泛关注的热点之一. 在实际应用中, 软材料一般需要粘附于某种基底材料上, 与之共同组成具有特定功能的结构. 如在软机器人设计中, 通过叠加多层软材料制备的层合结构可以制作强韧的气动腔, 为软机器人的移动提供动力^[2]; 柔性电子器件需要紧密贴合在皮肤上以进行稳定的数据采集和传输^[3]等. 在这些应用中, 软材料与不同类型基底之间粘接界面的性能对产品功能的稳定实现起着关键性作用. 一旦界面发生损伤或破坏, 会对粘接结构的完整性以及器件功能的可靠性造成严重损害. 因此, 针对软材料粘接界面破坏行为的研究具有重要的理论指导意义与工程应用价值.

过去几十年, 软材料粘接结构的界面破坏行为已经得到了国际国内****广泛的关注. 一些高质量的综述性文章也陆续发表^[5-8], 如Creton等^[5]针对软材料断裂以及压敏胶粘接界面破坏行为的系统综述, 许巍等^[7]针对粘结界面破坏机理的较为全面的总结, 陈少华等^[8]针对粘附接触力学及薄膜/基底界面力学的系统总结等. 上述综述论文对粘接结构界面力学行为的研究进行了较为深入的总结和评述, 然而研究对象偏重于传统的由金属、塑料等“硬”质材料组成的粘接结构, 较少涉及由具有显著大变形、黏弹性耗散特征的软材料借助软黏合剂等与不同基底构成的粘接结构. 鉴于此, 本文将系统地总结软材料粘接结构界面破坏行为的实验、理论与数值模拟研究, 从软材料粘接结构界面破坏行为的独特性出发, 重点讨论软材料基体的独特力学行为及粘接界面的能量耗散特性对界面破坏的影响, 并基于已有研究进展, 对未来可能的软材料粘接结构界面破坏的研究方向进行展望.

本文内容结构如下: 第1节通过与传统“硬”质粘接结构的对比, 介绍软材料粘接结构界面破坏行为的独特性及其物理来源; 第2节总结软材料粘接结构界面破坏行为的实验研究进展; 第3节在实验表征工作的基础上, 回顾与总结针对软材料粘接结构界面破坏的理论分析方法, 并对已建立的相关理论模型进行总结; 第4节介绍基于内聚力模型(cohesive zone model, CZM)方法的软材料粘接结构界面破坏行为数值模拟分析的相关进展; 第5节基于已有的研究成果, 提出目前研究所面临的挑战, 并对可能的软材料粘接结构界面破坏的未来研究方向和内容进行讨论和展望; 第6节结语.

1.
软材料粘接结构界面破坏的独特性

在粘接结构中, 被粘物与粘接基底之间可借助黏合剂(厚度一般为10 ~ 300 μm^[5])连接或通过化学键/物理相互作用直接连接, 如图1所示. 为避免歧义, 与许巍等^[7]的定义类似, 本文首先规定所讨论的粘接界面泛指被粘物与粘接基底之间所有起到连接作用的界面相, 而非狭义的被粘物与黏合剂/基底之间的界面. 从断裂力学的角度, 粘接界面的破坏可以被看作是一种特殊的具有确定路径的断裂行为. 传统上, 粘接结构的界面破坏行为常使用经典的线弹性断裂力学理论(如Griffith理论等)来描述^[9]. 对线弹性材料组成的粘接结构, 根据Griffith理论, 当界面裂纹扩展单位面积时, 形成新表面所需要的表面能w = U_w ? U_el. 其中, U_w是外部加载功, U_el是材料弹性应变能, w = γ₁ + γ₂ ? γ₁₂为Dupré界面粘附功, γ₁, γ₂分别是两个粘接表面的热力学表面能, γ₁₂为界面能. 界面裂纹扩展的能量释放率可以表示为

$$G = frac{{partial {U_{ m{w}}}}}{{partial A}} - frac{{partial {U_{{ m{el}}}}}}{{partial A}} = w$$

(1)

其中A为粘接面积. 对弹性固体而言, 形成紧密接触的最小要求是单位接触面积黏合剂中储存的弹性应变能不超过Dupré粘附功^[10-12].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
不同粘接结构剥离过程示意图



Figure
1.
Schematic diagram of peeling of different adhesive structures



下载:
全尺寸图片
幻灯片


对于由脆性陶瓷、玻璃或韧性金属、聚碳酸酯等材料通过环氧树脂胶等硬质黏合剂连接组成的粘接结构(即“硬”质粘接结构, 如图1(a)所示), 虽然界面裂纹尖端附近较小的区域内可能出现非弹性/非线性行为, 并可能伴随部分塑性或黏弹性耗散(也称为小尺度屈服^[5]), 但在该区域以外, 界面、被粘物基体材料始终满足线弹性变形规律, 线弹性断裂力学依然能够描述该类界面破坏过程. 此时, 粘附功w可用界面粘接能Γ来替换, Γ包含裂尖局部的塑性或黏弹性耗散, 界面裂纹扩展的能量释放率可以表示为

$$G = frac{{partial {U_{ m{w}}}}}{{partial A}} - frac{{partial {U_{{ m{el}}}}}}{{partial A}} = varGamma $$

(2)

通过压敏胶等软黏合剂连接的, 由“硬”质被粘物与粘接基底组成的粘接结构称为“软界面”粘接结构, 如图1(b)所示. 依据Dahlquist的经验准则^[13], 软黏合剂在1 Hz时储能模量不超过0.1 MPa, 在大变形下的力学响应一般具有显著的非线性特征. 这就使得“软界面”粘接结构在界面破坏过程中, 裂尖可能发生显著钝化, 基于线弹性断裂力学推导的裂尖应力场分布不再适用^[14-16]. 然而, 即使在这种情况下, 如果黏合剂依然保持弹性变形, 塑性或黏弹性耗散仅限于裂尖附近较小(远小于材料宏观尺寸)的区域, 能量方法依然适用. 由于软黏合剂变形过程中分子网络的相互摩擦, 黏弹性耗散十分显著, 这些耗散不仅存在于界面裂纹尖端区域, 也大量发生于块体黏合剂内部. 此时, 传统实验方法所直接获取的界面粘接能($varGamma $可能要比$w$高几个量级)就不再是一个只与材料本征性能有关的参数, 而与结构响应直接相关, 每种具体的加载构型(如剥离角度、剥离速度等)都对应一个特定的表观粘接能^[5].

“软基体”粘接结构是指由高弹体或水凝胶等软材料作为被粘物基体, 通过软黏合剂或直接的化学/物理键与硬/软粘接基底连接组成的粘接结构, 如图1(c)所示. 一般软材料的弹性模量在10³ ~ 10⁷ Pa之间, 具有典型的大变形、非线性甚至黏弹性特性. 基体材料的非线性特征使得基于线弹性假设推导的界面破坏理论, 在描述软材料粘接结构的界面破坏行为时会带来极大误差. 同时, 由于基体的厚度可能远大于黏合剂, 基体的黏弹性耗散也可能远超黏合剂, 对表观粘接能起主控作用, 此时, 只考虑黏合剂能量耗散所建立的一系列理论也就难以准确描述界面破坏行为.

相对于“软界面”粘接结构, “软基体”粘接结构界面破坏问题更加复杂. 首先, 界面与基体都可能具有的大变形、非线性和黏弹性特性对界面破坏的影响难以在实验中进行有效分离, 破坏机理以及性能参数很难得到准确的表征. 另外, 软材料基体与软黏合剂性能对界面破坏可能的耦合影响也进一步提高了破坏机理分析与理论建模的难度.

本文重点关注软黏合剂与软材料基体的非线性与能量耗散特征对软材料粘接结构界面破坏行为的影响, 系统梳理该领域的研究脉络, 并总结现有研究的重要进展, 探讨亟待进一步深入研究的主题, 对未来软材料粘接结构界面破坏方面的研究提出建议.

2.
软材料粘接结构界面破坏的实验研究

源于粘接结构的广泛使用以及粘接界面破坏的普遍发生, 针对粘接结构界面破坏行为的研究已经开展了数十年, 并且得到了长足的发展. 早期研究主要针对具体的粘接结构进行力学行为测试. 在这一阶段, 大量的实验数据得以积累, 后期对界面破坏机理的深入探索又促进了理论分析以及数值模拟工作的蓬勃发展^[7]. 本章对软材料粘接结构界面破坏行为方面的实验研究进行总结.

软材料粘接结构界面性能的强弱一般可用界面粘接能来表征^[5]. 表观界面粘接能可以通过剥离与拉拔两种具有代表性的测试方式得到. 表观界面粘接能的大小不仅决定于被粘物基体、黏合剂的力学性能, 同时也受到加载模式等的影响. 对“软界面”粘接结构, 基体变形较小且一般限于弹性, 粘接能主要由黏合剂性能决定; 对“软基体”粘接结构, 基体变形显著, 并可能伴随大量的能量耗散, 对表观界面粘接能的影响不可忽略. 本章将基于剥离与拉拔两种方式, 介绍上述两种粘接结构界面破坏行为的实验研究进展.

2.1
“软界面”粘接结构界面破坏

对于“软界面”粘接结构, 被粘物基体变形一般限于弹性, 可以通过剥离测试来方便地观察界面稳态破坏过程, 结合稳态剥离力与剥离速率之间的关系, 分析界面稳态破坏机理. 剥离测试是分析软黏合剂稳态破坏过程的理想方法, 通过将黏合剂固接在一个可以弯曲但难以伸长(或伸长很小)的背板上, 以一定的角度和速度将黏合剂与背板同时从刚性基底上剥离(图2(a)), 通过稳态剥离力(图2(b))来计算表观界面粘接能. 由于基体材料的拉伸刚度远大于黏合剂, 其拉伸变形一般可以忽略, 因此, 除极小的剥离角度以外, 能量释放率可以表示为^[17-19]



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
剥离示意图与典型力?位移曲线



Figure
2.
Schematic diagram of peeling and typical force-displacement curve



下载:
全尺寸图片
幻灯片

$$G = frac{F}{b}left( {1 - cos theta } ight)$$

(3)

其中b是背板的宽度, F是稳态剥离力, θ是剥离角度. 对于界面裂纹的稳态扩展行为, 能量释放率就对应了表观界面粘接能. 在实际工程应用中, 界面粘接能多通过90°或180°下的剥离实验测试.

“软界面”粘接结构的表观界面粘接能主要与黏合剂流变学性能、表面相互作用强度、黏合剂几何条件(如厚度)和加载工况(剥离角度)等因素有关. 过去几十年间, ****们借助剥离实验, 对以上因素对“软界面”粘接结构界面破坏行为的影响开展了系统地研究. 通过大量的不同角度与温度下的剥离测试, ****一致发现, 剥离力(与表观界面粘接能等价)随速率和温度变化的实验数据, 可以用与描述黏合剂块体材料线性黏弹性相同的时温等效原理叠加到一条主曲线上^[20-24], 这也表明剥离过程中的能量耗散主要源于黏合剂的线性黏弹性. 随着黏合剂厚度的增大, 界面破坏过程中黏合剂黏弹性耗散增加, 表观界面粘接能随之提高^[25-27]. 随着剥离角度的增加, 界面粘接能逐渐降低^[28-31]. 剥离速率的提高则可能引起界面破坏模式的改变, 随剥离速率的加快, 界面粘接能先逐渐增加至峰值, 之后逐渐下降, 伴随着界面破坏模式由稳态破坏转变为不稳定的黏?滑破坏^[32-34].

虽然剥离测试的实验过程较为简单, 但由于背板与黏合剂变形的耦合, 界面裂纹前缘区域黏合剂的应变分布十分复杂, 难以进行实时观察和表征, 难以分析黏合剂真实的变形与失效机理. 由于表观界面粘接能与黏合剂厚度以及剥离角度都相关^{[25, 34]}, 如果黏合剂真实的变形与失效机理不清楚, 实验所获取的界面粘接能就只能用来进行定性的对比, 无法作为界面性能严格的表征.

界面破坏过程中黏合剂变形与失效机理可通过拉拔测试来分析. 拉拔测试适用于对黏合剂的独立表征, 实验中将圆柱形的平面或半球形压头以一定的速度从黏合剂中匀速拉出(图3(a)), 通过名义应力?应变曲线(图3(b))计算界面粘接能.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
拉拔测试示意图及典型名义应力?名义应变曲线^[5]



Figure
3.
Schematic diagram of probe-tack and typical nominal stress-strain curve^[5]



下载:
全尺寸图片
幻灯片


名义应力?名义应变曲线的形状还可以揭示变形细节, 结合对界面破坏过程的实时观察, 对黏合剂的变形与失效机理进行分析. 如图4(b)所示, 黏合剂与(粗糙)基底材料的粘接面不可避免地存在不同程度的缺陷, 比如界面残留的一些小气泡等. 随着载荷的施加, 这些缺陷逐渐形成空洞并不断扩大. 在后续加载过程中, 由于黏合剂性能的差异, 界面可能有两种不同的破坏机理: (1)界面破坏, 即空洞以裂纹形式沿界面发展; (2)黏合剂块体破坏, 对应内聚破坏, 即空洞沿平行于拉伸应力的方向发展最终形成纤维结构^[35-41].



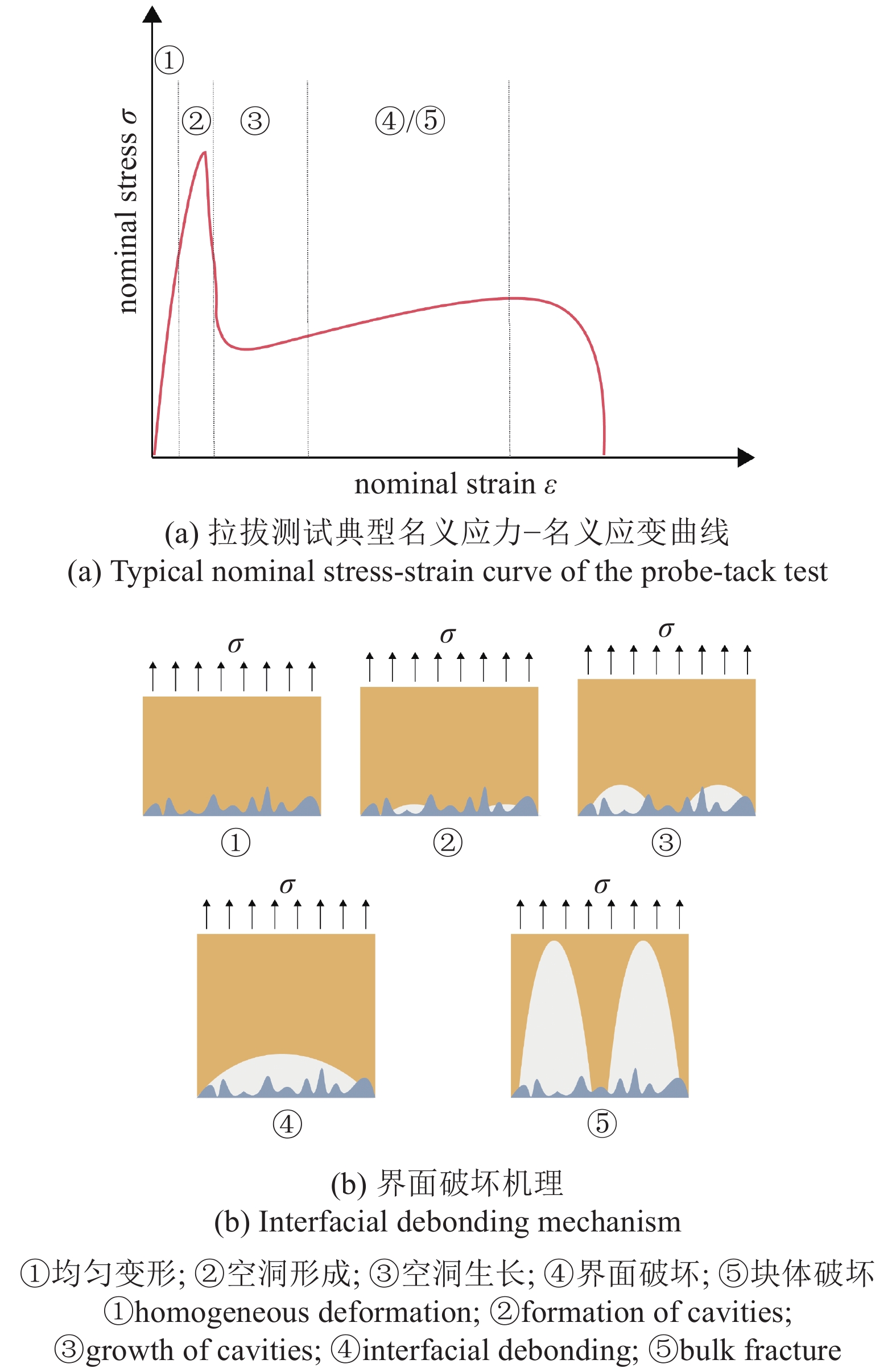onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
拉拔测试典型名义应力?应变曲线及界面破坏机理^[5]



Figure
4.
Typical nominal stress-strain curve of probe-tack test and interfacial debonding mechanism^[5]



下载:
全尺寸图片
幻灯片


假设黏合剂材料的力学性能满足Neo-Hookean形式, 块体破坏与界面破坏机理两者间的转变可用Г/E_a与h_a的关系来定性估计, 其中, E_a与h_a分别为黏合剂的弹性模量与厚度. 对极弱的粘接界面(Г/E_a $ll $ h_a), 初始缺陷处形成的空洞沿界面发展并相互融合形成宏观裂纹, 最终引起黏合剂完全脱离基底材料表面. 对一般的压敏胶材料(Г/E_a < h_a), 空洞首先在块体黏合剂内部发展, 随着界面能量释放率增加到一个较高的临界值(与软材料大变形性能相关), 满足界面裂纹扩展的准则^[36], 黏合剂块体破坏向界面破坏转变. 对高界面强度压敏胶(Г/E_a > h_a), 界面上的任何初始缺陷都倾向于在块体黏合剂中发展, 界面扩展不再发生^[42-43]. 实验也表明, 当块体黏合剂模量较低、黏合剂与基底间界面相互作用较强时, 块体破坏机理更容易发生^[44], 形成的纤维形貌强烈依赖于黏合剂的黏弹性能^[45].

空洞在界面或块体黏合剂内部扩展的不同机理会导致能量耗散的巨大差异. 对黏合剂块体破坏, 围绕空洞的黏合剂材料沿加载方向显著伸长, 会产生大量能量耗散, 且空洞不会融合. 对界面破坏, 多个界面缺陷处萌生的细小裂纹会相互融合, 此时块体黏合剂只发生很小的变形, 能量耗散也较小.

最近, Pandey等^[46]从实验的角度建立了剥离测试与拉拔测试之间的联系: 剥离测试中, 剥离前缘纤维的最大应变、平均应力和界面粘接能分别与拉拔测试中纤维最大应变、平均平台应力与界面粘接能基本一致, 表明黏合剂的黏弹性性能是影响界面粘接的关键因素, 通过一种测试也可以对另一种测试结果进行合理的估计和预测.

对于“软界面”粘接结构, 黏合剂的流变学性能是决定表观界面粘接能的主控因素. 通过对黏合剂的流变学以及宏观断裂机理的分析, 可以对粘接结构界面破坏进行有效的评估. 虽然在有限角度剥离时, 界面的微观失效机理已经通过对剥离前缘纤维区域的实时观察以及拉拔实验得以理解, 但对剪切型(如0°剥离)破坏, 纤维结构是否形成以及具体的形成过程依然难以进行有效的实验观测. 在这方面, 荧光成像技术、同步辐射光源、核磁共振等先进的原位观察技术有望发挥一定的作用. 采用这些技术, 可以对不同类型软材料粘接结构在不同加载模式下的界面破坏行为进行更深入、全面地观测和表征, 系统理解界面破坏的真实物理机理.

2.2
“软基体”粘接结构界面破坏

“软基体”粘接结构的界面破坏主要通过剥离测试进行表征. 通常用于测试界面粘接强度的搭接剪切实验也可以用于“软基体”粘接结构界面粘接能的测试. 搭接剪切实验通过加载曲线的峰值载荷确定界面粘接能. 当采用搭接剪切实验时, 界面粘接能与粘接长度有关, 取决于背板与软材料各自变形对系统总变形的贡献^[47-48]. 与剥离相比, 搭接剪切实验更容易受到预制裂纹制作工艺的影响. 通过预制较长(超过缺陷敏感尺寸)的裂纹, 同时进行预加载使裂纹发生一定扩展之后再进行断裂韧性测试, 可以显著减小数据分散性^[47-49].

剥离过程中剥离力的大小不仅决定于界面性能, 更与基体材料的力学性能紧密相关. 若被粘物基体具有强黏弹性, 其在界面破坏过程中的能量耗散会使得表观界面粘接能显著增加, 甚至引起界面破坏模式的改变.

黏弹性薄膜、胶带在刚性基底上的剥离行为能够直观展现出基体材料的黏弹性性能对剥离行为的影响. 研究表明, 随着剥离速率的提高, 基体的黏弹性耗散逐渐增加, 引起剥离力的提高^{[17, 19]}. 增加基体厚度, 基体刚度随之提高, 剥离力也逐渐增加^[19]. 基底表面粗糙度的增加会通过增加实际接触面积来提高剥离力水平^[19]. 剥离角度与表面粗糙度等因素对剥离力的影响与剥离前缘纤维区域的大小呈正相关^{[19, 50]}.

对于“软基体”粘接结构界面破坏机理的深入分析关键在于理解界面破坏过程中能量耗散的分布情况. 根据Creton等的分析, 聚乙烯醇缩丁醛高弹体在双层刚性基底间进行0°剥离的过程中, 界面裂纹前缘的能量耗散可分为如图5(a)所示4个区域^[51]: 区域①位于界面裂纹尖端局部, 耗散源于界面相互作用的破坏以及高弹体基体的局部非均匀变形; 区域②内高弹体发生快速大变形拉伸, 施加在该区域的大部分外力功均被高弹体黏弹性变形耗散掉; 区域③为变形过渡区, 该区域内高弹体应变率低于快速拉伸区, 存在一定的黏弹性耗散; 区域④内高弹体只发生刚性位移, 不产生黏弹性耗散.



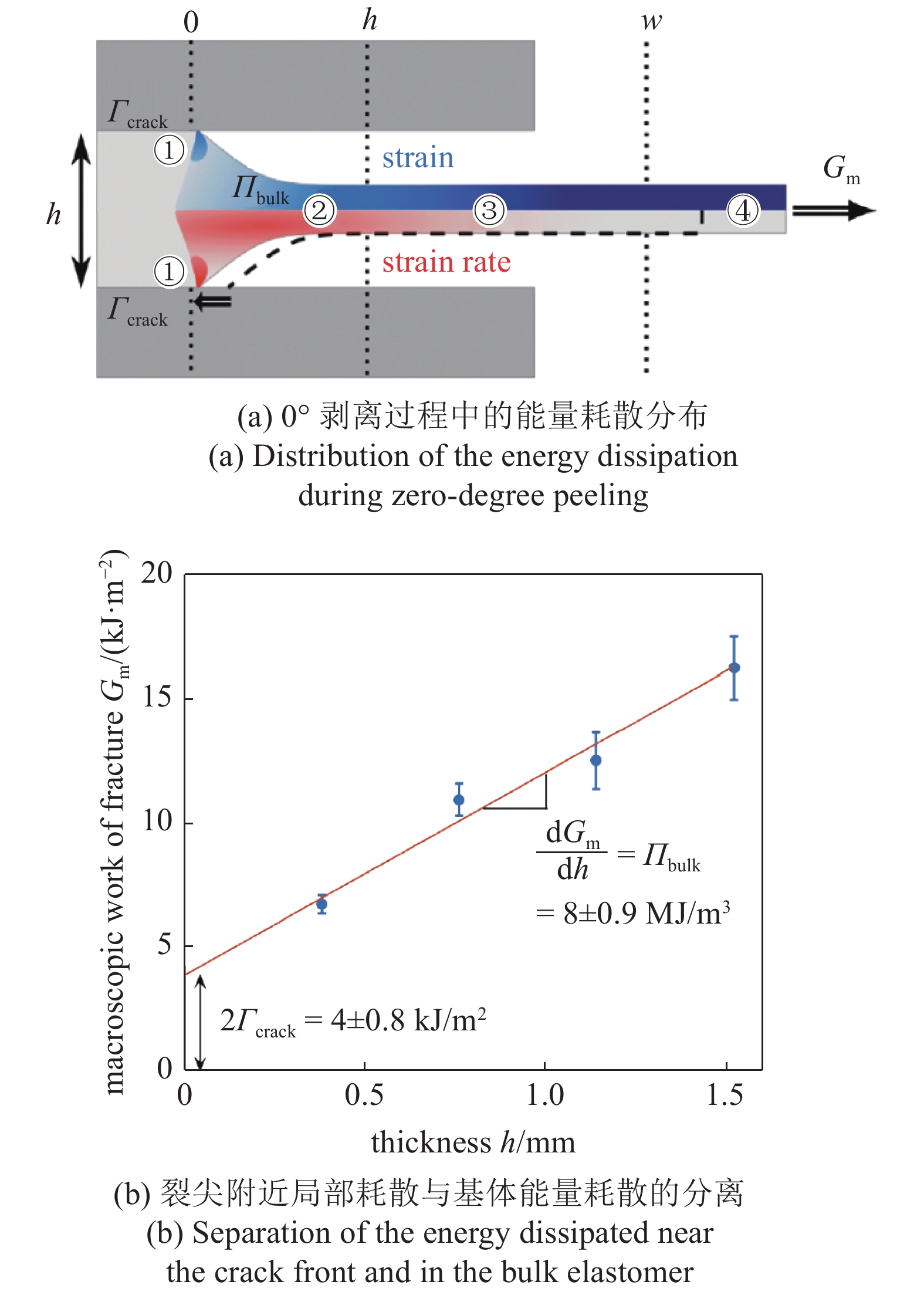onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
“软基体”粘接结构界面0°剥离过程中的能量耗散分布和裂尖附近局部耗散与基体能量耗散的分离^[51]



Figure
5.
Distribution of the energy dissipation during zero degree peeling and separation of the energy dissipated near the crack front and in the bulk elastomer^[51]



下载:
全尺寸图片
幻灯片


在界面0°剥离过程中, 假设外力所做总功完全转化为高弹体的黏弹性耗散与裂尖附近局部耗散两部分. 当逐渐减小高弹体的厚度至接近零, 通过外力总功随高弹体厚度的变化曲线(一般可假设为线性), 可以估算裂尖附近的局部耗散(曲线截距)与高弹体应变能密度(曲线斜率), 如图5(b)所示, 通过该方法可以对裂尖附近局部耗散与高弹体能量耗散进行有效的分离^[51]. 从分析结果可以发现, 此时, 高弹体的黏弹性耗散是决定表观界面粘接能的主控因素.

在对简单加载工况下界面破坏行为的研究基础上, 一些更复杂的加载工况和界面行为对界面破坏的影响也引起了****们的关注. 有实验表明, 界面摩擦引起的能量耗散也对界面破坏影响显著^[52-54]. 在0°剥离情形下, 若剥离后软材料基体与基底间存在较强的界面摩擦, 稳态剥离过程中剥离力可能随着剥离距离的增加而不断提高^[54]. 另外, 在低于界面破坏临界剥离力的恒定载荷作用下, 由于基体材料的黏弹性特征, 界面会发生显著的延迟破坏^[55]. 尤其值得注意的是, 当基体承受低于界面破坏临界伸长的恒定伸长作用时, 界面也可能发生延迟破坏^[56], 此时, 界面裂纹前缘应力随时间的重分配可能是主因. 界面的初始缺陷会对界面粘接的稳定性产生影响, 通过对粘接结构进行适宜的循环预拉伸训练, 可以有效降低界面缺陷的影响, 提高界面破坏的临界能量释放率^[56].

在另外一些“软基体”粘接结构, 比如创可贴或柔性医用元件与人体组织的粘接中, 虽然粘接基底材料(如人体皮肤)并不直接承受外界载荷, 但其典型的软材料特征也是需要考虑的重要因素. 比如在医用胶带的撕脱过程中, 皮肤局部发生较大的变形难以避免, 这对皮肤伤口的愈合是不利的^[57], 系列实验结果也证实皮肤的大变形黏弹性对创可贴在皮肤上的剥离行为影响显著^[57-60]. 通过系统分析剥离角度、速度与个体差异等因素对医用胶带在皮肤表面剥离行为的影响, Plaut等^[58-59]发现90°剥离时, 剥离力随加载率的提高显著增加, 伴随皮肤变形程度的增加; 剥离力随剥离角度的增加逐渐减小, 在 ~150°时达到最低值. 当剥离角为180°时, 皮肤局部非均匀变形减小, 剥离力的率相关性亦不明显. 其他****利用橡胶等材料模拟人体皮肤, 研究医用胶带在皮肤上的剥离行为, 也发现了类似的规律^[60]. 以上结果对医用胶带的合理、可控的撕脱操作提供了很好的指导.

基底材料的黏弹性也可能造成界面破坏模式的改变. Renvoise等^[61-62]对比压敏胶与刚性或黏弹性基底分别组成的粘接结构的界面破坏行为, 发现当黏合剂与刚性基底连接时, 由于黏合剂本身的黏弹性, 随着剥离速率的提高, 界面破坏模式由内聚破坏逐渐演化为黏合剂与基底之间的界面破坏, 并伴随着剥离力的下降; 当速率继续提高, 剥离力继续下降, 界面破坏呈现不稳定的黏?滑破坏形式; 在极快的剥离速率下, 界面破坏转变为黏合剂与弹性背板间的界面破坏. 当黏合剂与黏弹性软基底连接时, 黏合剂与基底间的界面破坏不再发生, 随着剥离速率的不断提高, 界面破坏模式从内聚破坏直接转变为不稳定的黏?滑破坏进而转变为黏合剂与弹性背板间的界面破坏.

此外, 基底材料的黏弹性还会带来界面稳态扩展与瞬态剥离两种模式的分化. Sugizaki等^[63-64]通过实验观察到, 当剥离角度较小、基底材料模量较小且厚度较大时, 界面破坏更倾向于瞬态模式, 剥离速率的提高会进一步促进瞬态剥离的发生. 当剥离角度较大(160° ~ 180°), 由于基底大变形的不稳定性, 稳态破坏逐渐演化为不稳定的黏?滑破坏模式, 引起剥离力的周期性波动.

对于“软基体”粘接结构, 合理分离基体材料与界面性能对界面破坏行为的影响是准确分析其破坏机理的关键. 除了单独对基体材料、界面性能进行性能表征测试, 目前还缺乏有效分离基体与界面黏弹性特性对界面破坏影响的实验手段, 难以进一步为表观界面粘接能的率、温度相关性的分析以及理论建模提供依据.

3.
软材料粘接结构界面破坏的理论分析

对粘接结构界面破坏行为的理论分析, 目前常有两种处理方式: 一是将黏合剂视为一层有厚度的材料, 考虑其弹性、黏弹性等材料性质以及损伤、断裂等力学行为, 建立可描述黏合剂材料在外界载荷下变形与失效过程的力学模型. 这种方式在对拉拔实验中(以及剥离前缘)纤维的伸长与断裂过程进行理论分析时较为方便; 二是用零厚度的内聚力模型来表征界面层, 假设界面粘接层的应力应变场在厚度方向均匀分布, 不同位置的应力应变与厚度无关. 目前, 基于断裂力学的界面破坏模型大多以第二种处理方式为基础.

3.1
“软界面”粘接结构界面破坏

对“软界面”粘接结构界面破坏行为的理论研究大多基于剥离行为. 通过建立稳态剥离力与剥离速率的关系, 直观展现黏合剂流变学性能与大变形特征对剥离行为的影响. 在早期理论分析中, 一般将剥离区域黏合剂假设为一系列相互平行的绳股, 类比剥离前缘经常看到的纤维结构, 数学上用弹性或黏弹性模型来描述^{[34, 65-68]}.

Kaelble首先提出粘接界面剥离理论, 基于能量平衡建立了描述稳态剥离的理论模型. 该模型考虑线性黏弹性的黏合剂, 得到了黏接区域黏合剂层应力分布的解析解: 考虑法向与剪切应力相互独立, 并分别在裂纹前缘产生应力集中, 随着与前缘的距离的增加均呈现指数衰减(如图6所示), 衰减长度与黏合剂厚度成比例, 也与背板和黏合剂的模量比相关, 该理论已经得到了众多实验的验证^{[20, 28, 69-70]}. 根据Kaelble模型, 界面粘接能随黏合剂厚度的增加而增加, 这表明界面粘接能应该包含整个黏合剂层变形的影响, 也暗示了黏合剂的流变学性能比黏合剂与背板/基底间界面性能更重要.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
Kaelble模型界面法向与剪切应力分布^[26-28]



Figure
6.
Normal and shear stress distributions in Kaelble’s model^[26-28]



下载:
全尺寸图片
幻灯片


Gent和Petrich同时考虑黏合剂内聚破坏与界面破坏两种失效机理, 分析了180°剥离行为中黏合剂大变形非线性行为对界面破坏的影响^[21], 指出对两种具有相似线性黏弹性但大变形行为差异明显的黏合剂, 剥离力曲线会显著不同, 该预测也得到了实验验证^[34]. 在实验工作基础上, Derail考虑弹性背板的弯曲以及黏合剂黏弹性, 基于临界伸长的断裂准则建立了剥离行为的理论模型, 发现耗散强烈依赖于内聚区域黏合剂的极限伸长^[22-23].

根据****们的研究, 黏合剂黏弹性会引起界面黏接能显著的剥离速率相关性, 这一关系可以经验性地表示为^[44]

$$varGamma left( v ight) = {varGamma _0}left[ {1 + phi left( {{alpha _{ m{T}}}v} ight)} ight]$$

(4)

其中Г₀是极小裂纹扩展速度下的粘接能阈值, 即界面本征断裂能, ?(α_Tv)是速度相关的耗散因子. 根据目前广泛使用的Lake-Thomas的假设^[71], 本征断裂能对应单位面积断裂面上一层高分子链的断裂所消耗的能量(对于界面破坏机理, Г₀考虑为黏合剂与基底间的界面相互作用). 如果界面只有范德华力, Г₀可以简化为Dupré黏附功w. 对一般的高聚物粘接界面, 分子链可能的跨界面的相互扩散增加了界面相互作用水平, 甚至形成缠结等拓扑结构, 由于扩散分子链的拔出^[72-73]或断裂前强键(比如共价键^[74-75], 氢键或偶极相互组用^[76-77])约束下链的伸长, Г₀可能远大于w. 黏合剂与基底间摩擦所引起的额外剪切对Г₀的贡献, 也可能显著增加剥离力. 这些情况在理论建模时都需要特别考虑.

?(α_Tv)决定于黏合剂的黏弹性性能, 对该性能的准确表征可以用于耗散因子的定量确定. 结合时温等效原理, 还可基于特定工况下的耗散因子对其他温度与加载率下的耗散因子进行定量估计, 进而对界面粘接能的温度与加载率相关性进行预测.

针对拉拔测试中名义应力应变的理论研究也取得了一定进展. 应力应变关系与空洞形成和生长过程的联系是理论建模的重点, 而黏合剂的强黏弹性特征以及有限伸长则是对该过程进行理论建模的难点所在. 早期研究工作中把黏合剂看成弹性固体, 探究固体内部空洞的平衡态结构以及界面较弱时界面空洞的萌生与生长过程^[78]. 然而这些研究并没有得到诸如最大应变、粘接能等重要变量的解析表达. 之后, Takahashi等^[79]结合空洞生长准则, 同时考虑薄黏合剂层的几何限制, 对拉拔过程中的力学响应进行了讨论. Glassmaker等^[80]考虑滑动引起的纤维脱粘, 对界面破坏的最后阶段进行了建模. 最近, Yamaguchi等^[81-82]提出了处理非线性薄膜中局部压力场与块体空洞生长的耦合问题的动态模型, 在后续研究中进一步将Persson模型进行推广, 得到了空洞尺寸演化及各重要力学变量的解析表达式^[83].

3.2
“软基体”粘接结构界面破坏

“软基体”粘接结构的界面破坏行为受界面性能与软材料被粘物基体性能两部分因素的影响, 对其进行的理论分析可建立在线弹性体与刚性基底粘接界面剥离过程的分析基础上.

软材料基体的超弹、黏弹性能对界面破坏的影响在小角度剥离(如0°剥离)时更明显. 根据Ponce等^[54]的分析, 对于单位宽度的线弹性体, 界面破坏模式依赖于粘接长度l与“载荷传递长度”${l_{{
m{lag}}}} = $$ sqrt {(Eh)/({E_{
m{a}}}{h_{
m{a}}})} $相对大小, 其中E, E_a, h和h_a分别为线弹性体与黏合剂的弹性模量和厚度. 若$l < {l_{{
m{lag}}}}$, 当施加的载荷超过界面破坏的临界载荷时, 粘接界面会发生瞬态破坏^[54]. 瞬态破坏的临界载荷可表达成${P_{
m{c}}} = sqrt varGamma cdot sqrt {{A/C}} $, 其中Г, A和$C$分别是界面粘接能, 粘接面积和线弹性体的柔度^[84-86]. 当粘接长度达到或超过${l_{{
m{lag}}}}$, 界面破坏模式变为稳态剥离, 破坏临界载荷不再增加. Kendall^[87-88]考虑稳态剥离过程中外力功完全转化为弹性体的弹性储能与界面粘接能, 建立了稳态剥离的理论模型, 发现剥离力P_c与$sqrt {2EhvarGamma } $成正比, 其中E和h分别是弹性体的弹性模量和厚度. 该结果在实际应用中被广泛用于描述压敏胶的稳态剥离过程. 为了统一瞬态破坏与稳态剥离的描述, Mojdehi等^[89]将瞬态破坏临界载荷的表达式进行了一般化处理, 写成${P_{
m{c}}} sim sqrt varGamma cdot sqrt {{{partial A}/{partial C}}} $, 可同时描述瞬态破坏与稳态剥离行为. 对由软材料基体构成的粘接系统, ${l_{{
m{lag}}}}$一般较小, 稳态剥离是最常见的界面破坏形式.

当界面发生有限角度剥离, 基体的弯曲变形可能会对界面剥离产生影响^[18]. 理论分析发现, 薄膜弯曲刚度对剥离力的影响在剥离初始阶段比较显著, 进入稳态剥离后, 薄膜拉伸弹性能的影响逐渐增加^[90-91]. 如果考虑软材料基体的超弹性, 利用基于线弹性假设的Kendall模型来预测界面的稳态剥离会引入极大的误差, 且误差会随着剥离角度的减小进一步增大^[92-93].

具有黏弹性的软材料从刚性基底上剥离时, 剥离力表现出强烈的速度相关性. Chen等^[17]提出了描述线性黏弹性薄膜从刚性基底上剥离的理论模型, 建立了能量释放率与裂纹扩展速度之间的关系. 基于Chen的理论框架, Peng等^[19]预测了黏弹性薄膜从刚性基底剥离时, 黏弹性能量释放率的剥离速率和角度相关性, 该研究唯象地假设了剥离力的速率依赖性, 而薄膜非线性黏弹性能与剥离力之间的关系尚未明确建立. Huang等^[94]分析了黏弹性体与弹性薄膜粘接界面的破坏过程, 基于对时相关的中性面的解析表达, 计算了与时间相关的界面裂纹扩展的能量释放率, 进而预测了3种不同的界面裂纹扩展状态.

Zhu等^[55]基于能量方法分别建立了黏弹性、超弹性及黏超弹性基体在刚性基底上进行0°剥离的理论模型, 对不同类型粘接结构界面率相关性剥离力与载荷保持下的界面延迟破坏进行了理论预测, 并建立了界面破坏相图. 如图7(a)所示, 由于基体的黏超弹性耗散, 在较高的加载率下, 瞬时剥离力会显著提高. 随着加载率的降低, 瞬时剥离力逐渐趋向于基体完全松弛后的松弛剥离力. 当基体承受瞬时剥离力以下的恒定载荷作用时, 由于基体的黏弹性松弛效应, 界面破坏所需的剥离力逐渐下降, 当降至与施加的载荷相同时, 界面可能会发生延迟破坏. 如图7(b)所示, 基体黏?超弹性越强, 加载率越高, 延迟破坏对应的载荷范围越广.



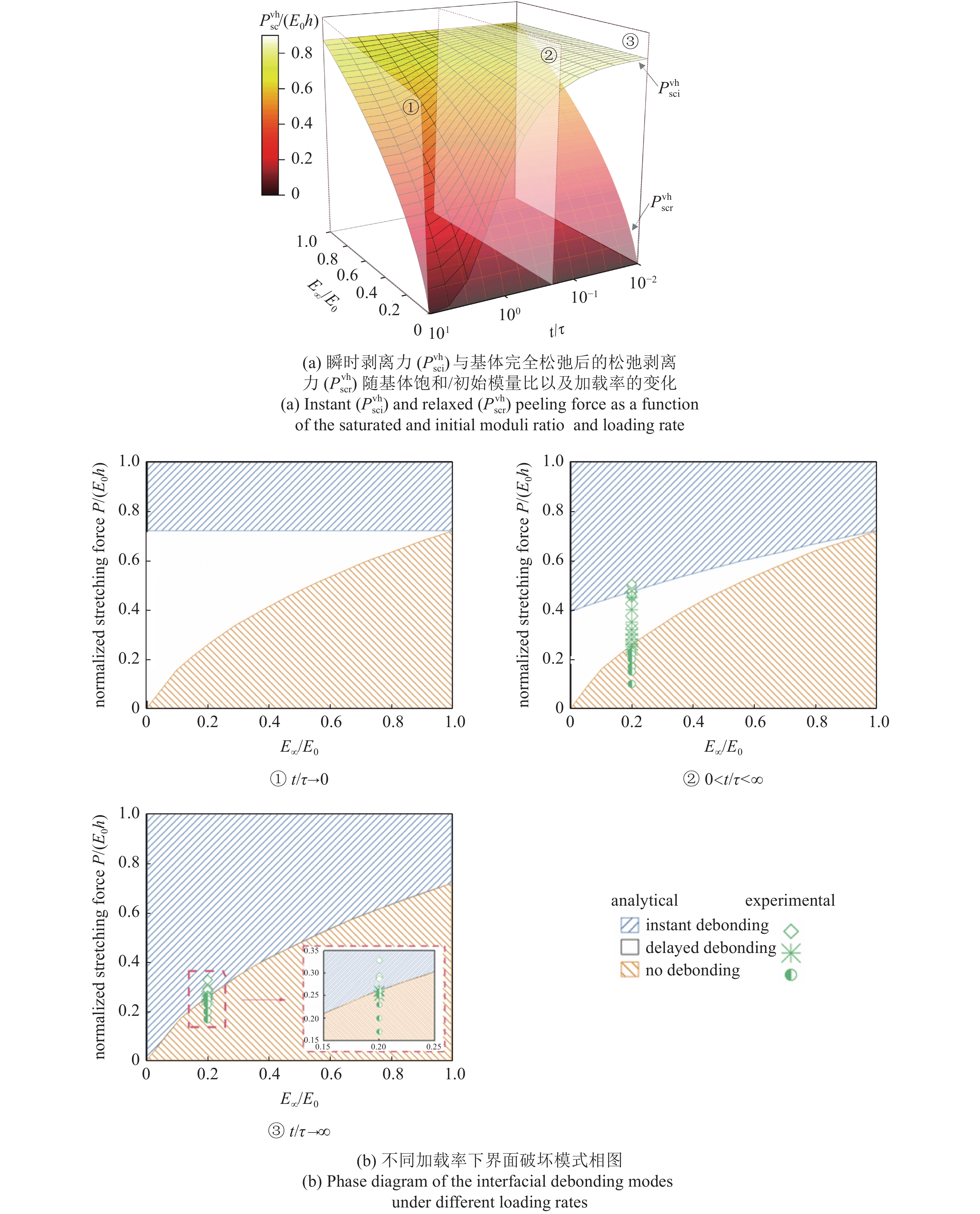onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-7.jpg'"
class="figure_img
figure_type2 ccc " id="Figure7" />



图
7
黏?超弹性被粘物基体在刚性基底上的0°剥离^[55]



Figure
7.
Zero degree peeling of a visco-hyperelastic tape on a rigid substrate^[55]



下载:
全尺寸图片
幻灯片


针对界面与基体性能对界面破坏的耦合影响, Zhao等^[95-96]基于对水凝胶粘接界面破坏的实验与数值模拟研究提出, 表观界面粘接能Г由界面本征断裂能Г₀与水凝胶基体内部的能量耗散Г_D两部分组成, 如图8(a)所示. 基体耗散Г_D会显著提升Г, 而较强的Г₀也会引起界面附近更大范围内基体材料的能量耗散, 进一步促进Г的提升(图8(b)). 此时, Г与Г₀的关系可以表示为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
表观界面粘接能Г与界面本征断裂能Г₀以及水凝胶基体内部的能量耗散Г_D的关系^[96]



Figure
8.
Relation among the apparent adhesion energy Г, the interfacial intrinsic fracture energy Г₀ and bulk energy dissipation Г_D in hydrogel^[96]



下载:
全尺寸图片
幻灯片

$$varGamma = {varGamma _0}left( {frac{1}{{1 - chi h_{max} }}} ight)$$

(5)

其中，χ是无量纲的系数, h_max为基体材料的最大耗散比.

当粘接基底可变形甚至伴随能量耗散, 基底力学性能对剥离行为的影响值得关注. Menga等^[97]研究了弹性薄膜在弹性基底上的V形剥离过程, 考虑基底的弹性应变能, 将Kendall模型进行了推广. 由于剥离过程中部分外力功转化为基底的弹性能, 表观界面粘接能得到一定提升. Afferrante等^[98]针对弹性薄膜在黏弹性基底上的稳态剥离, 基于格林函数方法, 得到了剥离力的解析解, 发现界面稳态剥离只能在某一载荷阈值下发生, 该阈值的存在同时也限制了可实现的界面裂纹扩展速度的范围. 后续研究^[99]还发现, 通过引入多个基底黏弹性特征时间, 可以更有效地调控基底能量耗散, 进而更好地实现对界面破坏模式的有效调控. 在恒定界面粘接能假设下, 针对不同粘接结构界面剥离行为的理论模型如表1所示, 这些模型为多种粘接结构的合理使用和优化设计提供了有力的指导.




表
1
剥离模型总结(恒定界面粘接能)



Table
1.
Summary of the peeling models (constant adhesion energy)



table_type2 ">

Adhesive structure	Theoretical model	Feature	Reference
linear elastic adherend/ rigid substrate	${left( {dfrac{F}{w}} ight)^2}dfrac{1}{{2Et}} + {dfrac{F}{w}}(1 - cos theta ) - gamma = 0$	Considering bending and extension of the adherend	[87]
	$dfrac{F}{w} = sqrt {2Etgamma } $	Steady-state 0° peeling	[88]
	$F = sqrt {{gamma _{ m{s}}}} sqrt {dfrac{A}{C}} $	Catastrophic 0° peeling	[84-85]
	$F = sqrt {{gamma _{ m{s}}}} sqrt {dfrac{{partial A}}{{partial C}}} $	Steady-state and catastrophic 0° peeling	[89]
linear elastic adherend/ linear elastic substrate	$dfrac{F}{w} = sqrt {2gamma dfrac{{{E_2}{t_2}}}{{{E_1}{t_1}}}({E_1}{t_1} + {E_2}{t_2})} $	Steady-state 0° peeling	[87]
hyperelastic adherend/ rigid substrate	$ {dfrac{F}{w}} (lambda - cos theta ) - Uleft( lambda ight) - gamma = 0$	Considering bending and extension of hyperelastic beam	[93]
viscoelastic adherend/ rigid substrate	$G = {G_0}left[ {1 + {{left( {dfrac{v}{{{v_0}}}} ight)}^n}} ight]$	Phenomenological description	[100]
	$G = {dfrac{F}{w}} left( {1 - cos theta + {g_{ m{b}}} + dfrac{F}{{{E_0}A}}{g_{ m{m}}}} ight)$	gb, gm related to the viscoelastic property of the adherend	[37]
	$dfrac{F}{w} = sqrt {2{E_infty }tgamma } sqrt {1 + left( {dfrac{{{E_0}}}{{{E_infty }}} - 1} ight)exp left( { - dfrac{t}{tau }} ight)} $	Steady-state 0° peeling	[55]
visco-hyperelastic adherend/ rigid substrate	$dfrac{F}{w} = {mu ^ * }tleft( { {lambda _{ m{c} } } - {lambda _{ m{c} } }^{ - 2} } ight)$	Steady-state 0° peeling	[55]
linear elastic adherend/ viscoelastic substrate	$hat F(1 - cos theta ) + left[ {dfrac{1}{2} - dfrac{E}{{{E_0}}}{f_{ m{v}}}left( {hat V} ight)} ight]{hat F^2} - hat gamma = 0$	fv related to the visco-hyperelastic property of the substrate	[98]
elastomeric adherend/ elastomeric substrate	$G = {U_{ m{b}}}left( {lambda ''} ight) - {U_{ m{s}}}left( {lambda '} ight) + dfrac{F}{w}left( {lambda ' - lambda ''} ight)$	Ub, Us determined through experiment	[101]

下载:
导出CSV
|显示表格



在现有大部分针对软材料粘接界面破坏的理论研究中, 界面本征断裂能Г₀一般都被认为是恒定的, 然而界面失效的物理本质尚未得到完全的理解, Г₀与加载率、温度等是否相关也存在一定争议. Chaudhury等^[102-103]探索了黏合剂分子链热激活断裂机制引起的界面本征断裂能的率相关性, 建立了界面破坏临界能量释放率模型, 发现断裂能随着分子链拉伸速率的提高而增加, 利用该模型成功描述了聚甲基氧硅烷与玻璃粘接界面的率相关破坏问题. 在后续研究中, 该思想也被推广到高聚物断裂^[104]以及粘接界面的剪切破坏^[56]的描述.

虽然多数“软界面”粘接结构界面破坏的理论研究都是唯象地引入界面粘接能的速度相关性, 但软黏合剂带来的粘接能的率相关性已经得到了普遍的重视, 演化规律也能得到有效的理论描述. 但由于界面本征断裂机制尚不清楚, 界面附近能量耗散机制较为复杂, 同时, 对粘接件基体的大变形黏弹性特性进行简洁的理论描述和准确的解析求解也有较大难度, 目前“软基体”粘接结构界面破坏的理论研究仍远未完善. 此外, 基体与界面能量耗散可能的耦合机制以及缺乏充足的分离实验数据也进一步加大了理论建模与模型验证的难度.

4.
软材料粘接结构界面破坏的数值模拟研究

4.1
界面破坏问题常见的数值模拟方法

对于粘接结构界面破坏问题, 常用的数值模拟方法主要有两类: 一类基于断裂力学, 以虚拟裂纹闭合技术为代表; 另一类基于损伤力学, 以内聚力模型方法为代表.

虚拟裂纹闭合技术是应用最为广泛的模拟裂纹扩展的方法之一^[105-108]. 虚拟裂纹闭合技术假设在裂纹扩展中释放的能量等于将裂纹闭合回到其原始构型所需做的功, 能量释放率通过裂纹尖端处的力和位移信息计算. 虚拟裂纹闭合技术的特点是以独立的能量分量形式计算自相似的裂纹扩展过程. 但是, 裂纹的萌生以及小裂纹的发展是不可被预测的, 并且由于虚拟裂纹闭合技术中能量释放率与特征长度(常与单元网格尺寸相联系)有关, 所以必须依托强大的网格优化技术来描述裂纹扩展过程^[109-110].

内聚力模型方法最早由Dugdale^[111]和Barenblatt^[112]提出, 之后Hillerborg等^[113]引入拉伸强度作为损伤萌生准则, 扩展到描述裂纹从萌生到扩展的过程. 内聚力模型方法认为界面裂纹尖端附近会形成内聚力损伤区域, 该方法的核心就是建立损伤区域界面张开位移与牵引力的关系. 内聚力模型及其参数的确定对于准确描述界面裂纹问题非常关键, 但是大多数模型参数难以简单地通过实验确定^[105]. 与虚拟裂纹闭合技术相比, 内聚力模型方法克服了线弹性的局限性, 在模拟复杂界面裂纹扩展上更具优势. 同时, 内聚力模型对于网格的节点空间坐标信息要求不高, 更易于进行有限元实现^[114]. 此外, 内聚力模型描述裂纹从萌生到扩展的过程是基于显式的损伤机制, 可以跟踪整个扩展过程并能描述局部的材料软化现象. 从描述裂纹问题的完整性, 数值实现的难易程度以及求解过程的计算成本考虑, 针对大多数的界面破坏问题, 内聚力模型相比虚拟裂纹闭合技术更具优势.

最近十几年, 扩展有限元方法^[115]在断裂问题的模拟方面也得到了很好的应用和发展. 扩展有限元方法不需要网格来匹配不连续的几何形状, 可以描述裂纹沿任意路径的扩展, 很好地克服了虚拟裂纹闭合技术和内聚力模型需要预先设定裂纹路径以及要求高质量的网格排布的局限性. 但考虑到大多数粘接界面裂纹扩展路径并非完全任意, 且扩展有限元方法求解难度高, 对非线性问题也有一定的局限性等缺点, 对于粘接结构界面破坏问题, 内聚力模型方法仍是最适合也最常用的方法. 因此, 本文将重点针对基于内聚力模型方法的软材料粘接结构界面破坏问题的模拟工作进行总结和评述.

4.2
基于内聚力模型方法的“软界面”粘接结构界面破坏的模拟分析

内聚力模型方法是否能准确描述界面破坏行为, 首先依赖于内聚力模型的合理性, 同时决定于模型在求解时的收敛性. Alfano等^[116-117]探究了如图9所示的双线性、线性?抛物线、指数和梯形等内聚力本构形式在描述双悬臂梁结构断裂行为时的准确性及计算收敛性, 发现指数形式在计算准确性上表现最佳, 但如果综合考虑模拟的准确性和计算成本, 双线性模型是更为合理的选择. Camanho等^[118]通过对双悬臂梁、缺口弯曲以及混合模式弯曲加载模式下断裂问题的模拟以及与实验结果的对比, 验证了双线性模型在描述I型、II型以及混合型界面破坏问题时都具有较高的准确性. Turon等^[119]基于严格的热力学框架提出了考虑断裂模式混合比的内聚力模型, 由于其易于构建、满足热力学框架并且可基于合理的物理机理和实验现象来描述复杂应力状态下的界面力学响应, 该模型得到广泛的应用和发展^[120-122]. Park等^[123]对基于势函数的内聚力模型进行了详细综述, 特别对各模型描述混合模式界面破坏问题的局限性进行了讨论, 对该类模型的改进方向和未来发展做出了探讨.



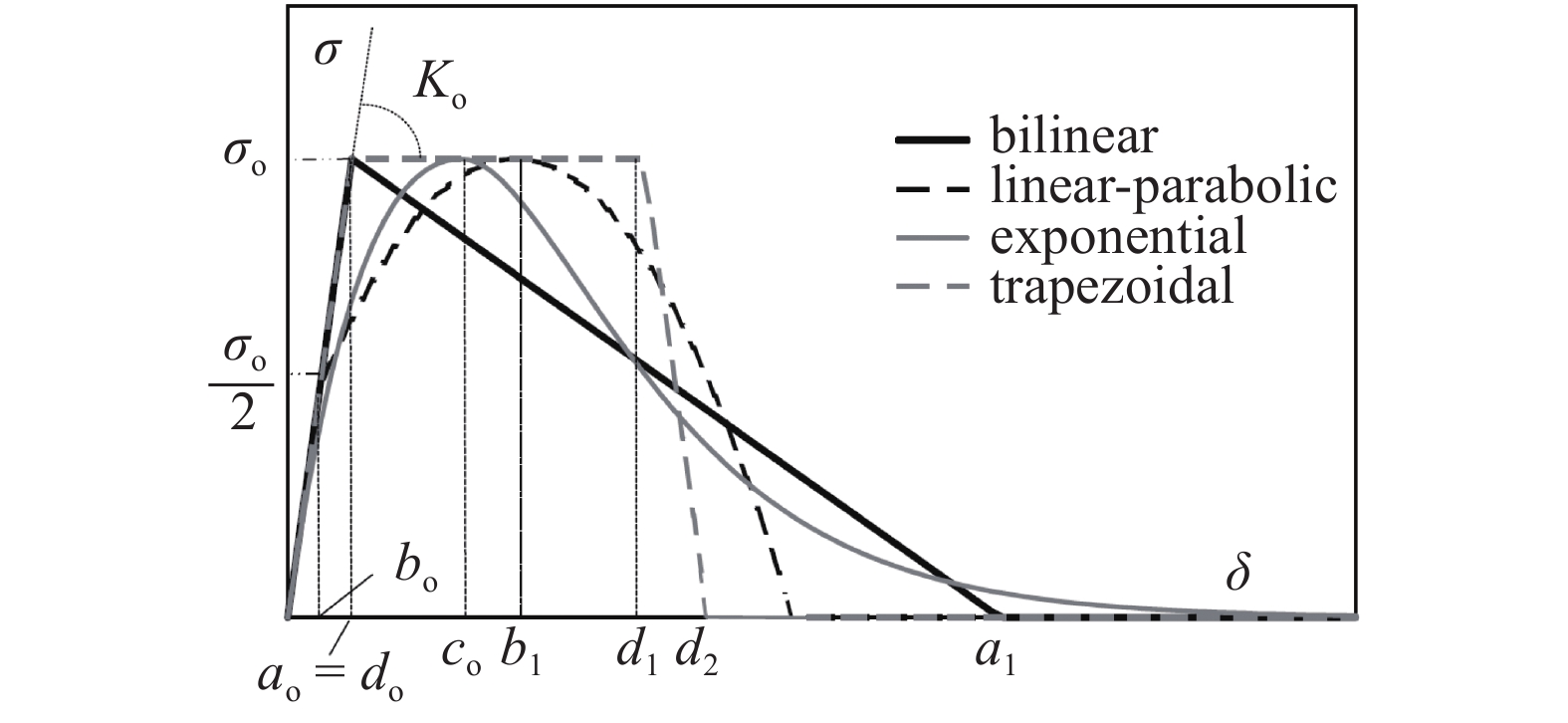onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
经典内聚力本构形式^[117]



Figure
9.
Classic cohesive zone models^[117]



下载:
全尺寸图片
幻灯片


“软界面”粘接结构界面破坏的率相关性是其最显著的特征之一. 由于涉及到界面模型本身的物理机理以及计算效率和收敛性, 如何合理地将率相关性引入界面模型十分重要. 最直接的方法是唯象地将界面内聚能、界面强度或最大张开位移等关键参数表示为与加载率相关的函数, 该方法主要适用于动力学问题, 但主要的困难是参数众多且难以通过实验确定, 对于复杂工况的描述能力有限^[124-126]. 其次, 可在界面损伤的表达式中引入加载率的影响^[127]. 这种方法严格满足热力学框架, 对于较为复杂的加载条件和失效模式都有较好的描述能力, 但由于模型一般较为复杂, 模型的数值实现存在较大难度, 对复杂的材料非线性问题, 模型的适用性也较弱^[128]. 此外, 可将内聚力模型与已有描述实体材料变形行为率相关特性的理论模型相结合来描述界面牵引力与张开位移的率相关行为^[129]: 其中一类是借鉴描述流体^[130]或者高聚物塑性流动^[131]的描述方法, 将界面牵引力表示为与加载率相关的形式, 这种方法一般通过引入反映一定物理机制的内变量来描述界面失效^[131]. 另一类则借鉴经典线性黏弹性模型中的应力应变形式来描述界面牵引力和张开位移的关系^[132-133], 该方法具有描述界面破坏率相关性的能力, 但由于经典黏弹性模型单一特征时间的限制, 使得其仅适用于特定的加载率范围. 这一不足可通过将标准线性黏弹性模型修改为分数阶形式来改进, 可描述的加载率范围可以得到有效扩展(如图10)^[134-135]. Giraldo-Londo?o等^[136]也采用类似的方法对橡胶类材料在较大加载率范围内的混合断裂模式进行了成功的模拟.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
黏弹性内聚力模型对不同加载率下的粘接界面破坏的描述



Figure
10.
Description of interfacial debonding behavior under various loading rates using different viscoelastic CZM models



下载:
全尺寸图片
幻灯片


界面的局部非线性大变形对界面应力状态和破坏模式会产生显著影响. Hui等^[137]对线弹性背板在刚性基底上的0°剥离过程进行了有限元模拟, 界面层采用超弹性的实体单元来描述, 研究发现, 界面层的超弹性性质对“载荷传递长度”的影响不大, 但当变形较大时, 界面层的切向和法向应力数值都非常大, 并且伴随着不可忽略的横向拉伸应力和静水张力(如图11所示). 如考虑有限粘接长度^[138], 界面层的体积应力分量甚至会超过剪切应力, 造成界面空洞的产生继而引发破坏. 此时, 该问题中的界面破坏就不再是单纯的界面II型断裂问题.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//lxxb2021-131-11.jpg'"
class="figure_img
figure_type2 ccc " id="Figure11" />



图
11
0°剥离中超弹性黏合剂/基底间应力分布^[137]



Figure
11.
Stress along the hyperelastic adhesive/substrate interface during 0° peeling^[137]



下载:
全尺寸图片
幻灯片


在内聚力模型研究方面, 目前考虑界面大变形的工作还较少, 考虑到大变形可能产生的网格畸变造成的计算不收敛等问题, 如何在内聚力模型中有效考虑界面大变形进而准确地模拟界面破坏行为还需要更深入地探讨.

4.3
基于内聚力模型方法的“软基体”粘接结构界面破坏的模拟分析

针对“软基体”粘接结构的界面破坏行为, 借助有限元模拟首先可以对理论分析结果进行必要的验证, 此外, 还能够对复杂载荷下结构的界面破坏机理进行分析.

基体超弹性对界面破坏的影响已经在现有的模拟研究中得到一定的考虑, 在此基础上可以进一步讨论加载角度^[139]和速度^[140]的影响. 对于压剪载荷等复杂载荷下的破坏行为^[141], 也能通过模拟的手段得到能量释放速率与裂纹扩展长度的关系, 为理论分析提供验证和指导.

基体的能量耗散特性对界面破坏行为的影响也得到了一定的模拟研究. Seshadri等^[142]采用有限元模拟对黏弹性薄膜与刚性基底粘接结构界面破坏的理论分析结果进行了验证, 证实了不同加载速度下的界面裂纹扩展能量释放率可以通过完全松弛模量与瞬时模量的比值进行描述. Zhang等^[95]采用考虑Mullins效应的超弹性本构模型描述水凝胶的力学行为, 用双线性内聚力模型描述界面性能, 模拟了水凝胶粘接结构的界面破坏, 发现表观界面粘接能与界面内聚能线性相关, 水凝胶基体损伤时的能量耗散对表观界面粘接能的影响可能高于界面内聚能本身(取决于基体厚度). 值得注意的是, 有模拟研究发现, 对于基体材料较厚的情况, 厚度方向上应变率可能发生梯度分布^[143], 这对理论分析建模提出了更高的要求.

由于软材料基体的大变形特征以及基体与界面性能可能的不匹配, 界面破坏过程可能会伴随多种类型的基体或界面失稳现象. 对于弱界面粘接的情况, 刚体与软基体粘接界面在缺陷处的部分脱离会产生周期性的波状界面分离现象^[144-146]. Mukherjee等^[147-149]首先利用有限元研究了波状界面分离现象的形成过程与界面的粘接能和软基体厚度、模量、强度的关系, 之后基于内聚力模型方法模拟了二维情况下柔性板在软材料基底上的剥离行为, 研究了几何约束参数及界面参数对界面破坏的影响, 完善了由界面破坏产生的失稳临界条件.

对于软材料基体与刚性基底强界面粘接的情况, 当软基体内部静水张力达到某临界值, 可能会从缺陷处萌生空洞, 随着载荷的持续施加空洞逐渐生长形成空洞失稳. 若空洞的萌生和生长受到抑制, 可能会造成软基体自身的手指状失稳或与基底粘接界面附近的边缘条状失稳^[150-151]. 软基体内部空洞的形成受到初始缺陷大小和气泡内压的影响^[152-154]. Fu等^[152]结合实验与理论预测了不同缺陷尺寸对空洞形成的影响, 为进一步理解和避免空洞失稳提供了指导. Lin等^{[151, 155]}结合理论与有限元模拟分析了基体几何尺寸对失稳现象的影响, 基体手指状失稳在横向约束作用下会进一步促进空洞失稳, 造成非单调递增的应力应变响应, 通过增加基体刚度可抑制该失稳的发生. Zhong等^[156]发现将连续的粘接层分割为离散的粘接层, 可以有效抑制空洞失稳. 同时, 拉伸加载下非单调的力学响应也可以转变为单调响应, 进而避免“跳跃”失稳的发生. 此外, 粘接层的柔度和延展性以及循环加载下的滞后效应也可以通过合理设计离散粘接层的数量或几何形式来进行调控. 该研究通过简单的方法实现了对复杂失稳现象的有效抑制以及对粘接层力学行为的按需调控, 为实际粘接层以及软粘接接头的设计提供了十分有益的指导.

目前, 对“软基体”粘接结构界面破坏的模拟分析的重点和难点都集中在如何准确地描述“软基体”的黏弹性和大变形两个特性. 已有研究主要针对简单的粘接结构, 讨论部分材料参数和几何参数对界面破坏的影响, 作为理论分析结果的佐证, 缺乏对复杂材料组合粘接结构界面破坏机理的深入分析. 在大变形方面, 虽然已有模拟研究已经对基体非线性大变形进行了一定的考虑, 但针对基体大变形对复杂载荷下界面破坏行为的影响的分析还不够深入, 同时, 界面破坏与基体局部可能产生的非均匀变形之间的耦合影响也值得深入分析. 利用有限元方法的优势, 也可对基体和界面能量耗散对界面破坏的耦合影响进行深度的挖掘, 进而更加全面深入地揭示“软基体”粘接结构界面破坏的机理.

对于软材料粘接结构界面破坏行为的有限元模拟研究, 模拟准确性、收敛性和计算效率是最主要的考虑因素. 目前商用有限元软件中已有的内聚力模型对最简单的“硬”质粘接结构界面破坏行为尚可以进行较为合理的模拟, 但对软材料粘接结构界面破坏行为的模拟则难以准确实现. 大量挑战性的工作还需要开展: 如建立考虑界面大变形黏弹性特征的内聚力模型、确定复杂应力状态下界面损伤萌生或失效的判据以及局部大变形下数值迭代算法的优化等. 这些难题得到合理解决才能够更好地模拟具有强非线性、率相关等复杂特性的软材料粘接结构的界面破坏问题.

5.
挑战与展望

虽然目前软材料粘接结构界面破坏行为的研究已经取得了一定的进展, 但在实验、理论与数值模拟各方面仍面临诸多挑战. 软材料粘接结构界面破坏的实验研究已取得较为丰硕的成果. 基于剥离测试, 能够对不同加载工况和环境条件下的表观界面粘接能进行定量表征, 同时结合剥离前缘的微观观察及拉拔测试, 对界面破坏机理进行分析. 然而, 小角度加载下“软基体”粘接结构界面破坏机理的实验观察与分析尚不充分; 同时, 也缺乏对界面本征断裂能的率、温度相关性的准确的实验表征等. 也源于此, 对软材料基体与界面性能对界面破坏的耦合影响的分析也受到了相应的限制.

在恒定界面粘接能假设下, 基于能量方法的界面破坏理论已得到较为深入的研究, 不同类型软材料粘接结构都已建立了对应的界面破坏理论, 为实际工程应用提供了有力的支持和指导. 然而, 在“软基体”粘接结构界面破坏的理论分析中, 界面粘接能的率、温度相关性还未得到充分的重视. 虽然基于热激活断裂机制的理论模型能够直观地描述界面本征断裂能与分子链拉伸速度的关系, 但界面分子链拉伸速度与宏观加载速度之间存在尺度差异, 界面附近分子链断裂区域范围也尚存争议.

准确高效的数值模拟研究对于软材料粘接结构界面破坏机理的分析至关重要. 现有数值模拟工作多基于内聚力模型方法来分析材料、几何参数对界面破坏行为的影响, 考虑界面粘接能率相关性的内聚力模型多唯象地引入性能参数或损伤变量的率相关性, 较少考虑界面微观破坏机理. 对于疲劳^[157-160]、表面摩擦磨损^[161-165]及长期载荷、位移保持^{[55-56, 166-168]}等复杂加载模式下的软材料粘接结构界面破坏问题, 有限元模拟具有一定的优势, 但目前这些研究还面临着界面损伤萌生及失效准则难以确定等问题, 研究进展较为有限.

面对这些挑战, 目前正在开展的一些更深层次的研究有望在未来针对特定问题在一定程度上给出更进一步的答案, 一些面向应用的研究更是对目前基础研究的成果进行了广泛的探索和利用, 未来也值得关注.

(1) 软材料变形和断裂过程的可视化表征手段. 随着机械化学研究的发展, 近期利用力敏团(mechanophore)进行软材料断裂^[169-172]或界面破坏^[173]过程可视化表征的研究得到迅猛发展. 将力敏团分子嵌入聚合物主链中, 在机械载荷的作用下, 随着力敏团的断裂或构象改变会激活多种光学反应, 例如变色、发出荧光等^[174], 基于此可以实现对微观断裂行为的可视化. 虽然目前定量表征的准确性仍有待提高, 但已有研究依然明确表明: 裂尖分子链的断裂范围远大于Lake-Thomas预测的断裂面附近一排高分子链^[170], 针对不同温度与加载率下的软材料断裂过程的实验表征更是证明软材料黏弹性与本征断裂存在强耦合^[170], 分子链本征断裂在总断裂能中的占比被严重低估. 对于由PSA等软黏合剂组成的粘接结构的界面破坏行为, 对界面黏接能的理论建模需要重新评估发生分子链本征断裂的区域大小以及断裂过程的温度、加载率相关性, 常用的恒定界面粘接能假设应该被修正. 关于机械化学工具在软材料断裂以及其他方面的发展和应用可参考Chen等^[174]的综述文章.

(2) 基于界面破坏机理的异质软材料的强韧粘接策略. 得益于水凝胶材料的飞速发展以及水凝胶粘接结构在科技、工业领域的广泛应用, 基于水凝胶粘接的异质软材料强韧粘接策略已经引起****们的广泛关注. 水凝胶与异质软材料的强韧粘接需要化学、拓扑与力学的协同^[175]: 水凝胶高聚物网络与其他软材料的分子网络之间需要借助化学手段构建共价键或强非共价键等实现强界面相互作用. 合理的界面拓扑的设计, 能够保证界面破坏过程中发生强界面相互作用破坏的同时, 又能尽可能引发粘接基体的非弹性能量耗散. 这些能量耗散可以通过在粘接件基体中引入损伤、相变或黏弹性等力学机制来实现.

水凝胶与异质软材料之间界面的强相互作用与拓扑结构可以通过多种方法来建立. 水凝胶与聚甲基氧硅烷等一般高弹体的界面强粘接可以通过表面改性来实现^{[96, 176]}, 在高弹体表面引入活性基团(可以借助表面引发剂^[177-178]), 使水凝胶前驱体在高弹体表面的固化过程中, 高聚物网络与活性基团间形成共价键或高分子配合物, 进而实现强粘接^{[96, 176]}. 对于已经制备好的水凝胶, 可以在水凝胶与软材料前驱体中加入特定化学物质进行块体改性^[179-181], 使两者在固化过程中自发形成强粘接. 对于不能进行化学改性的生物组织, 可以借助与水凝胶以及生物组织都能形成强键接的桥接高聚物, 建立两者间的强粘接^[182]. 对不含特定功能基团, 不能实现强键接的软材料, 可借助特殊的粘接高聚物, 通过扩散作用分别与水凝胶及软材料形成拓扑缠结网络, 进而实现强粘接^[183-185]. 此外, 针对硬黏合剂由于限制软材料大变形不适用于软材料粘接的问题, 可通过喷雾等方法, 在粘接界面形成离散的微小岛状粘接区域, 在实现强粘接的同时, 岛间软材料依然允许发生大变形^[186].

值得注意的是, 随着墨水直写等3D打印技术的发展, 多种水凝胶与软材料的打印手段相继被提出^[187-189], 打印过程中水凝胶与其他软材料间的强韧粘接对打印结构的完整性及长期稳定性至关重要. 以Liu等^[180]的方法为代表的块体改性方法十分适用于这种多层水凝胶与软材料以任意顺序相互堆叠同时需要界面强粘接的情况. 此外, Yang等^[188]也提出了行之有效的块体改性方法, 能够保证水凝胶与其他软材料间良好的界面粘接性能, 进而保证打印结构的优异力学性能. Zhao等^[189]提出的基于微凝胶的方法能实现水凝胶与多种软材料以及无机固体的强韧粘接, 且是对多种水凝胶都普遍适用的方法, 对3D打印水凝胶更广泛的工程应用具有重要意义. 针对水凝胶的强韧粘接策略, Yang等^[175]给出了详尽的综述.

(3) 按需、可控粘接/脱粘设计. 对于某些应用, 如爬墙机器人, 机械抓手, 医用胶带等, 不仅需要界面能够强韧粘接, 还要求在特定情形下时, 界面能够方便容易地脱开. 因此, 按需、可控脱粘设计也引起了****们广泛的兴趣. 在该领域, 现有研究集中在脱粘临界载荷可强弱转换的可转换粘接方面, 通过对界面附近粘接状态、粘接面积以及界面/基体力学行为的调控, 可以有效实现强、弱粘接的转换, 转换比(强粘接与弱粘接界面破坏临界载荷之比), 可高达10^5[190]. 然而现有转换机制都需要特定的触发激励, 如光、热等^[190], 难以针对所有材料进行广泛推广. 此外, 针对某些应用需要对界面脱粘速度或破坏模式进行调控的更高程度的要求, 目前研究讨论也不够充分. 针对可转换粘接的详细内容可参考Croll等^[190]的综述.

6.
结语

软材料已经在软机器人、生物医学以及柔性电子等各个领域得到广泛应用, 考虑到对以水凝胶为代表的多种软材料的性能调控与功能设计日臻成熟, 未来软材料还会有更加广阔的工程应用前景. 针对软材料粘接结构界面破坏行为的深入研究, 能够为软材料的合理使用与优化设计提供关键的理论支持与工程指导. 本文系统总结了现有软材料粘接结构界面破坏行为的实验、理论与数值模拟研究进展, 重点讨论了界面黏弹性以及软材料基体的大变形能量耗散特性对界面破坏行为的影响. 虽然已有研究已经取得了显著进展, 但在疲劳、表面摩擦等复杂加载下界面的脱粘或失稳机理的实验表征, 基体、界面能量耗散耦合效应的理论描述以及复杂结构在复杂加载下界面脱粘或失稳机理的模拟分析等方面还存在诸多挑战. 真实服役环境下基体与界面可能的老化等行为又会进一步增加研究的复杂性. 同时, 实际工程应用中脱粘, 失稳或老化等不同机理很可能同时发生甚至存在耦合, 这些也都增加了界面破坏行为研究的难度. 然而, 随着对该领域关注的日益增加以及采用不同方法从不同角度切入开展研究的逐步深入, 相信以上难题都会逐步得到解决, 在为软材料粘接结构更为广泛的应用提供有力支撑的同时, 不断推动界面力学学科的发展.