轮对系统的Hopf分岔研究

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

引言

近年来随着高速列车运行速度的提高, 车辆系统的蛇行失稳问题越发突出, 蛇形运动作为车辆系统的固有属性, 严重影响着车辆系统的运行平稳性、乘坐舒适性和安全性^[1], 对车辆系统进行非线性动力学理论方面的研究, 不仅可以从车辆动力学角度更加全面地了解蛇形运动, 而且对车辆系统的设计与参数优化也具有非常重要的意义.

在国外研究中, True^[2]用延续算法求解了非线性车辆系统中的分岔问题. Wagner^[3]将非线性轮轨力分段函数拟合为关于横移量的三次方与五次方的叠加函数, 并用该非线性轮轨函数求解了轮对系统的分岔图, 极大地方便了理论研究非线性轮轨接触对轮对蛇形运动的影响. Zboinski和Dusza^[4-6]研究了车辆系统中悬挂参数、曲线半径、踏面和车轮名义滚动圆半径在曲线轨道上的稳定性. Kim等^[7]建立了31个自由度的车辆系统动力学模型, 通过分岔图研究发现轮对系统的线性临界速度对应亚临界Hopf分岔, 而非线性临界速度对应的是一个鞍结点. Park等^[8]利用分岔理论研究了悬挂参数与轮轨接触关系对车辆系统蛇形运动的影响, 发现轮轨接触关系比悬挂参数更加影响车辆系统的蛇形运动.

在国内研究中, 张卫华等^[9-10]通过研究Poincaré 映射面上不动点的稳定性, 得到了轨道车辆系统的周期解, 并将其结果与滚动振动试验台所得结果进行对比分析, 解释了相关结果出现差异的可能原因. 曾京^[11]针对17个自由度的经典客车模型, 应用QR算法和黄金分割法计算了该客车系统蛇形失稳的临界速度, 并用打靶法对其领域的极限环进行了求解. 张继业等^[12-13]利用Hurwitz行列式得到了平衡点失稳的Hopf分岔代数判据, 极大地方便了车辆系统中寻找Hopf分岔点的过程. 黄世凯^[14]在研究轮对系统陀螺效应的时候, 定义了轮对系统的陀螺力贡献率, 但其并没有从Hopf分岔的角度研究陀螺效应. 董浩等^[15-16]建立了中国高速动车组CRH2和CRH3的转向架和半车车辆系统动力学模型, 采用范式法证明了其在简单轮轨接触关系下均存在亚临界和超临界Hopf分岔, 但并没有建立整车动力学模型, 所以该结论不一定适应整车动力学模型. 高学军等^[17-20]对车辆系统提出了“合成分岔图”, 研究发现车辆系统在拟周期运动后出现混沌现象. 张波等^[21-22]对轮对系统的陀螺效应进行了分析, 对比了考虑陀螺效应与不考虑陀螺效应的分岔图, 研究发现陀螺力不做功, 具有增稳效果. Zeng等^[23]在研究轮对系统的陀螺效应时发现, 轮对系统的陀螺效应关于纵向的分量会降低系统的稳定性, 而关于垂向的分量有助于提高系统的稳定性, 两者的综合作用可以提高车辆系统的临界速度并抑制极限环的幅值. 张婷婷等^[24-25]研究了单轮对系统的Hopf分岔类型及其迁移机理, 但该模型过于简单, 没有考虑陀螺效应和阻尼约束. Ge等^[26]用实测踏面数据修正了轮轨非线性关系, 使用MATCONT求解了修正后的轮对系统的周期解, 但对修正后的轮对系统出现的部分周期解缺少相关理论解释.

目前关于轮对系统非线性动力学的文献中, 缺少同时考虑陀螺效应和退化Hopf分岔理论的研究. 本文在文献[3]的基础上, 研究轮对系统中有、无陀螺效应对单参数下的Hopf分岔类型以及双参数下的退化Hopf分岔的影响.

1.
考虑陀螺效应的轮对模型

1.1
轮对模型建立

轮对系统作为机车车辆里面最简单的系统, 研究轮对系统可以从原理上简单的解释蛇形运动. 如图1所示, 假设轮对系统在直线轨道上做微幅振动, 轮轨之间采用kalker^[27]线性蠕滑模型, 建立考虑陀螺效应、刚度约束和非线性轮轨关系的轮对系统动力学模型.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />

图
1
轮对模型图

Figure
1.
Wheelset model diagram

下载:
全尺寸图片
幻灯片

记$ {boldsymbol{x}}= (y,varphi {)^{text{T}}} $

, 主要影响轮对系统蛇形运动的横移和摇头运动方程为^[3]

$$ {{boldsymbol{M}}} ddot {boldsymbol{x}} + ({boldsymbol{C}} + {boldsymbol{G}})dot {boldsymbol{x}} + {boldsymbol{Kx}} + {boldsymbol{F}}({{boldsymbol{x}}} ) = {{bf{0}}} $$

(1)

其中

$$ {{boldsymbol{M}}} = left[ {begin{array}{*{20}{c}} m&0 0&{{I_z}} end{array}}
ight]; $$

$$begin{split} & {{boldsymbol{C}}} = left[ {begin{array}{*{20}{c}} {dfrac{{2{f_{22}}}}{v}}&0 0&{dfrac{{2({f_{11}}{b^2} + {f_{33}})}}{v}} end{array}}
ight]; ; &{{boldsymbol{G}}} = left[ {begin{array}{*{20}{c}} 0&{dfrac{{2{f_{23}}}}{v} - dfrac{{{I_y}vlambda }}{{{r_0}b}}} {dfrac{{{I_y}vlambda }}{{{r_0}b}} - dfrac{{2{f_{23}}}}{v}}&0 end{array}}
ight]; ;end{split} $$

$$ {{boldsymbol{K}}} = left[ {begin{array}{*{20}{c}} {2{K_y} + dfrac{{Wlambda }}{b}}&{ - 2{f_{22}}} {dfrac{{2{f_{11}}lambda b}}{{{r_0}}}}&{2{f_{23}} + 2{K_x}{l^2} - Wlambda b} end{array}}
ight] $$

$$ {{boldsymbol{F}}} ({{boldsymbol{x}}}) = left[ {begin{array}{*{20}{c}} {F(y)} 0 end{array}}
ight] = left[ {begin{array}{*{20}{c}} {{delta _1}{y^3} + {delta _2}{y^5}} 0 end{array}}
ight]; $$

式中$ m $

, $ {I_z} $

, I_y和$ W $

分别为轮对质量、垂向转动惯量、横向转动惯量和轴重; $ {r_0} $

, $ b $

, $ l $

和$ lambda $

分别为名义滚动圆半径、两滚动圆跨距之半、左右悬挂距离之半和踏面等效锥度; $ {k_x} $

和k_y分别为纵向和横向刚度; $ {f_{11}} $

, $ {f_{22}} $

, $ {f_{23}} $

和$ {f_{{text{3}}3}} $

分别为纵向蠕滑系数、横向蠕滑系数、横向自旋蠕滑系数和自旋蠕滑系数; $ {delta _{text{1}}} $

和$ {delta _{text{2}}} $

为非线性轮轨力系数; $ v $

为轮对运行速度, 以上各参数取值见附录A中表A1.

方程(1)中的矩阵$ {{boldsymbol{G}}} $

为陀螺矩阵^[21], 可以看出影响轮对系统陀螺效应的主要参数是横向自旋蠕滑系数和横向转动惯量. 本文将动力学方程中不考虑横向自旋蠕滑系数和横向转动惯量的轮对系统称为不考虑陀螺效应的轮对系统, 动力学方程中考虑横向自旋蠕滑系数和横向转动惯量的轮对系统称为考虑陀螺效应的轮对系统.

1.2
轮对系统在Hopf分岔点处的线性临界速度表达式推导

令$ {{boldsymbol{Y}}}= (y,dot y,varphi,dot varphi {)^{text{T}}} $

, 方程(1)转化为一阶微分方程组(2), 其平衡点为$ {(y,dot y,varphi,dot varphi )^{text{T}}} = {{text{(0,0,0,0)}}^{text{T}}} $

$$ {dot {boldsymbol{Y}}} = {{boldsymbol{J}}}(v){{boldsymbol{Y}}} + {{boldsymbol{F}}}({{boldsymbol{Y}}}) $$

(2)

其中

$$ {{boldsymbol{J}}}(v) = left[ {begin{array}{*{20}{c}} 0&1&0&0 { - {p_1}}&{ - dfrac{{{p_2}}}{v}}&{{p_2}}&{{f_1}v - dfrac{{{f_2}}}{v}} 0&0&0&1 { - {p_3}}&{gleft(dfrac{{{f_2}}}{v} - {f_1}v
ight)}&{ - s}&{ - dfrac{c}{v}} end{array}}
ight]; $$

$$ {{boldsymbol{F}}}({{boldsymbol{Y}}}){text{ = }}{left[0, - frac{{{delta _1}{y_1}^3 + {delta _2}{y_1}^5}}{m},0,0
ight]^{text{T}}} $$

式中$ {p_1} $

, $ {p_2} $

, $ {p_3} $

, $ {f_1} $

, $ {f_2} $

, $ g $

, $ s $

和$ c $

的具体表达式见附录B中式(B1) ~ 式(B8).

方程(2)的线性部分对应的特征方程如下

$$ det Big[{{boldsymbol{J}}}(v) - e{{boldsymbol{I}}}Big] = 0 $$

(3)

其中$ {{boldsymbol{I}}} $

为四阶单位矩阵.

将方程(3)展开可得

$$ {a_0}{e^4} + {a_1}{e^3} + {a_2}{e^2} + {a_3}e + {a_4} = 0 $$

(4)

其中

$$ begin{array}{l} {a_0} = 1; {a_1} = dfrac{{c + {p_2}}}{v} {a_2} = f_1^2g{v^{text{2}}} + ({p_1} + s - 2{f_1}{f_2}g) + dfrac{{c{p_2} + f_2^2g}}{{{v^{text{2}}}}} {a_3} = ({f_1}g{p_2} + {f_1}{p_3})v + dfrac{{c{p_1} + s{p_2} - {f_2}g{p_2} - {f_2}{p_3}}}{v} {a_4} = {p_1}s + {p_2}{p_3}; end{array} $$

根据Hopf分岔代数判据^[12]可知, 方程(4)的4个特征值中存在一对纯虚根(${e_{1,2}} = pm{text{i}} {omega _0}$

, $ {omega _0} = $

$ sqrt {{a_3}/{a_1}} $

), 且其余两个根的实部均为负数的条件为

$$ left. begin{array}{l} {a_i} > 0; ; ; (i = 0,1, cdots ,4) {varDelta _3} = 0 end{array}
ight} $$

(5)

其中${varDelta _3}$

为Hurwitz行列式.

由方程(5)可知, 当轮对系统的参数满足${a_i} > 0; ; ; (i = 0,1, cdots, 4)$

时, 令${varDelta _3} = 0$

可得关于轮对系统运行速度$ v $

的一元六次方程如下

$$ {b_0}{v^6} + {b_1}{v^4} + {b_2}{v^2} + {b_3} = 0 $$

(6)

其中$ {b_0} $

, $ {b_1} $

, $ {b_2} $

和$ {b_3} $

的具体表达式参见附录B中式(B9) ~ 式(B12).

令$ {v^{text{2}}} = d $

, 由方程(6)可得关于$ x $

的一元三次方程如下

$$ {b_0}{d^3} + {b_1}{d^2} + {b_2}d + {b_3} = 0 $$

(7)

在Hopf分岔点处, 轮对系统有且仅有一个线性临界速度(正实数), 故方程(7)中的一元三次方程的根中必须有且仅有一个正实根, 根据文献[28]中对一元三次方程根的讨论, 令$ A = b_1^2 - 3{b_0}{b_2} $

, $ B = {b_1}{b_2} - $

$ 9{b_0}{b_3} $

, $ C = b_2^2 - 3{b_1}{b_3} $

和$varDelta = {B^2} - 4AC$

, 可得考虑陀螺效应的轮对系统, 在Hopf分岔点处的线性临界速度表达式为

(a) 当$varDelta > 0$

时

$${v_{cr}} = sqrt d = sqrt {frac{{(sqrt[3]{{Y1}} + sqrt[3]{{Y2}}) - {b_1}}}{{3{b_0}}}} $$

(8)

(b) 当$varDelta = 0$

且$ ; ; A = 0 $

时

$$ {v_{cr}} = sqrt d = sqrt { - frac{{{b_1}}}{{3{b_0}}}} $$

(9)

且$ A > 0 $

时

$$ {v_{cr}} = sqrt d = sqrt {max left( {frac{B}{A} - frac{{{b_1}}}{{{b_0}}}, - frac{B}{{2A}}}
ight)} $$

(10)

(d) 当$varDelta < 0;$

且$ A > 0 $

时

$$ {v_{cr}} = sqrt d = sqrt {max left( begin{array}{l} dfrac{{2sqrt A cos dfrac{phi }{3} - {b_1}}}{{3{b_0}}} dfrac{{2sqrt A cos dfrac{{phi + 2{text{π}} }}{3} - {b_1}}}{{3{b_0}}} dfrac{{2sqrt A cos dfrac{{phi + 4{text{π}} }}{3} - {b_1}}}{{3{b_0}}} end{array}
ight)} $$

(11)

其中

$$ Y_1 = - A{b_1} + 1.5{b_0}(B + sqrt varDelta ); $$

$$ Y_{text{2}} = - A{b_1} + 1.5{b_0}(B - sqrt varDelta ) $$

$$ phi = arccos frac{{3{b_0}B - 2A{b_1}}}{{2Asqrt A }} $$

不考虑陀螺效应的轮对系统, 即横向自旋蠕滑系数和横向转动惯量均为零时, 方程(7)中的系数$ {b_0} $

和$ {b_1} $

变为零, $ {b_2} $

和$ {b_3} $

也会分别简化为$ {b_{22}} $

和$ {b_{33}} $

, $ {b_{22}} $

和$ {b_{33}} $

的表达式见附录B中式(B13)和式(B14), 方程(7)简化为一元一次方程

$$ {b_{22}}d + {b_{33}} = 0 $$

(12)

求得不考虑陀螺效应的轮对系统在Hopf分岔点处的线性临界速度表达式为

$$ {v_{cr}} = sqrt d = sqrt { - frac{{{b_{33}}}}{{{b_{22}}}}} $$

(13)

其与文献[24]中是一样的.

取纵向刚度为4 MN/m, 其他参数取值见附录A中表A1, 将参数值代入本文推导的考虑陀螺效应的轮对系统线性临界速度解析表达式(8) ~ 式(11)与不考虑陀螺效应的轮对系统线性临界速度解析表达式(13), 求得考虑陀螺效应的轮对系统在Hopf分岔点处的线性临界速度值为140.5364 m/s, 不考虑陀螺效应的轮对系统在Hopf分岔点处的线性临界速度值为135.4532 m/s.

同理取纵向刚度$ {k_x} $

为4 MN/m, 其他参数取值见附录A中表A1, 对方程(2)的线性部分使用根轨迹法^[11]求解Hopf分岔点处轮对系统的线性临界速度, 即设初速度为$ {v_0} $

, 步长为$ {Delta }v $

和特征值控制精为$ ep $

. 令$ v{text{ = }}{v_0} $

, 计算速度$ v $

对应的方程(2)中$ {{boldsymbol{J}}}(v) $

矩阵的特征值. 然后对每一个速度$ v $

对应下的所有特征值的实部取绝对值, 找出每一个速度$ v $

对应的特征值实部绝对值的最大值$ left| {{R_{max }}}
ight| $

, 若$ left| {{R_{max }}}
ight| leqslant ep $

, 则此时的速度就是轮对系统在Hopf分岔点处的线性临界速度. 若$ left| {{R_{max }}}
ight| > ep $

, 此时当$ {R_{max }} < 0 $

时, 则设$ v{text{ = }}{v_0}{ + Delta }v $

, 当$ {R_{max }} > 0 $

时, 则$ v{text{ = }}{v_0} - {Delta }v $

, 重复以上计算过程, 直到得到满足控制精度$ ep $

的轮对系统Hopf分岔线性速度值为止. 最后求得考虑陀螺效应的轮对系统在Hopf分岔点处的线性临界速度值为140.5364 m/s, 不考虑陀螺效应的轮对在Hopf分岔点处的线性临界速度值为135.4532 m/s.

该结果与本文推导的考虑陀螺效应的轮对系统线性临界速度解析表达式(8) ~ 式(11)与不考虑陀螺效应的轮对系统线性临界速度解析表达式(13)的结果是一样的.

1.3
轮对系统的陀螺效应参数分析

由方程(1)中的陀螺矩阵$ {G} $

可知, 影响轮对系统陀螺效应的主要参数为横向自旋蠕滑系数和横向转动惯量, 假设横向自旋蠕滑系数和横向转动惯量的数值变化不引起轮对系统其他参数的变化.

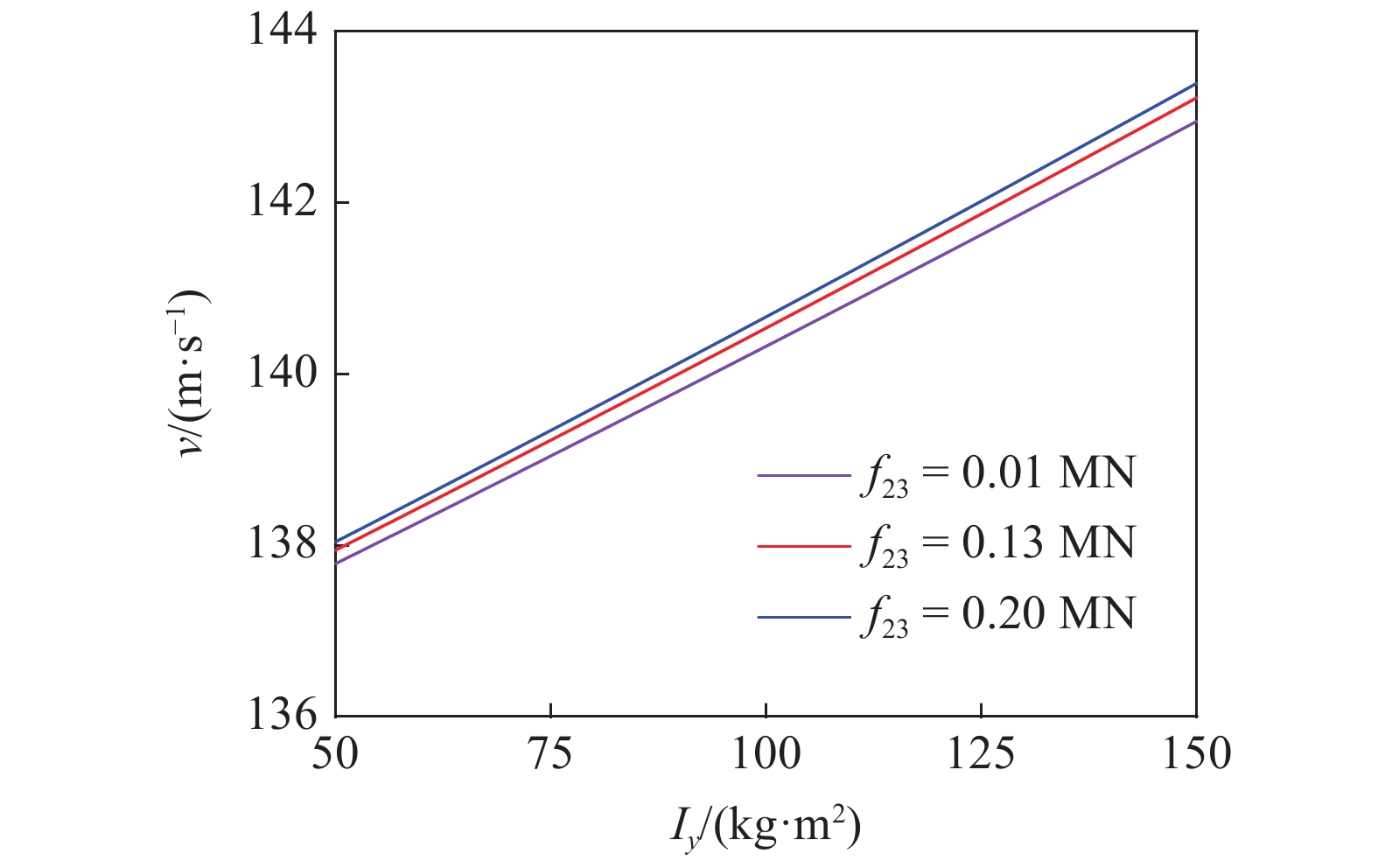
取纵向刚度值为4 MN/m, 横向自旋蠕滑系数分别取0.01 MN, 0.13 MN与0.2 MN, 横向转动惯量的值从50 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

取到150 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

, 其他参数取附录A中表A1, 将其代入式(8) ~ 式(11)中, 得到考虑陀螺效应的轮对系统中, 线性临界速度与横向转动惯量的关系如图2所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />

图
2
轮对系统线性临界速度与横向转动惯量的关系

Figure
2.
The relationship between the linear critical speed of the wheelset system and the lateral moment of inertia

下载:
全尺寸图片
幻灯片

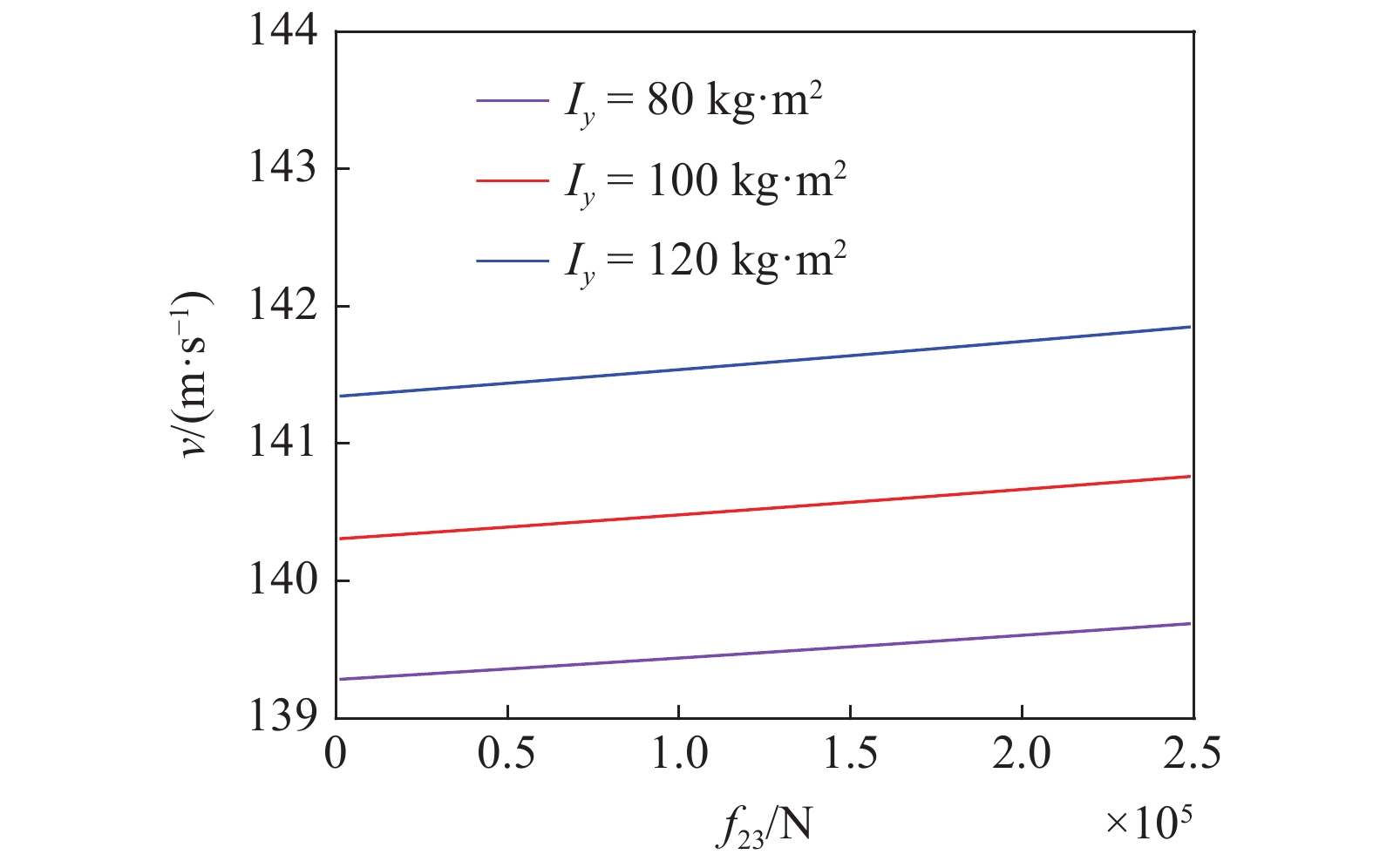
取纵向刚度为4 MN/m, 横向转动惯量分别取80 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

, 100 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

与120 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

, 横向自旋蠕滑系数的值从0.001 MN取到0.25 MN, 其他参数取附录A中表A1, 将其代入式(8) ~ 式(11)中, 得到考虑陀螺效应的轮对系统中, 线性临界速度与横向自旋蠕滑系数的关系如图3所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />

图
3
轮对系统的线性临界速度与横向自旋蠕滑系数关系

Figure
3.
The relationship between the linear critical speed of the wheelset system and the lateral spin-slip coefficient

下载:
全尺寸图片
幻灯片

图2与图3中I_y为轮对系统的横向转动惯量, $ v $

为轮对系统的运行速度, $ {f_{23}} $

为轮对系统的横向自旋蠕滑系数. 由图2可知, 在同一横向自旋蠕滑系数下, 轮对系统的线性临界速度随着横向转动惯量的增大而增大, 该变化趋势比较明显. 在同一横向转动惯量下, 横向自旋蠕滑系数分别为0.01 MN, 0.13 MN与0.2 MN对应的轮对系统的线性临界速度依次增大, 该变化趋势不太明显. 由图3可知, 在同一横向转动惯量下, 轮对系统的线性临界速度随着横向自旋蠕滑系数的增大而增大, 该变化趋势不太明显. 在同一横向自旋蠕滑系数下, 横向转动惯量分别为80 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

, 100 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

与120 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

对应的轮对系统的线性临界速度依次增大, 该变化趋势比较明显.

对比图2与图3可知, 横向转动惯量在轮对系统陀螺效应中起主导作用, 横向自旋蠕滑系数起次要作用.

2.
轮对系统第一、第二Lyapunov系数的求解

为更好地研究轮对系统在Hopf分岔点处的运动形式, 采用分岔理论中的投影法^[29-30]求解轮对系统的第一、第二Lyapunov系数, 从而方便研究轮对系统在单参数下的Hopf分岔类型与双参数下的退化Hopf分岔类型.

2.1
轮对系统第一Lyapunov系数求解

在轮对系统的Hopf分岔点处, 即$ v = {v_{cr}} $

时, 方程(2)中的矩阵$ {{boldsymbol{J}}}(v) $

的特征值中存在一对纯虚根$ pm {omega _0}{text{i}} $

与两个具有负实部的根, 设矩阵$ {{boldsymbol{J}}}(v) $

的特征值为纯虚根时对应的特征向量为$ {{boldsymbol{q}}} = {[{x_1},{x_2},{x_3},{x_4}]^{text{T}}} $

, 满足${{boldsymbol{J}}}(v){{boldsymbol{q}}} = {text{i}}{omega _0}{{boldsymbol{q}}}$

, 其中

$$begin{split} {x_1} = 1;end{split} $$

$$begin{split} {x_2} = {
m{i}}{omega _0}end{split} $$

$$ {x_3} = dfrac{{({p_1} - {omega _0}^2)v + {p_2}{
m{i}}{omega _0}}}{{{p_2}v + ({f_1}{v^2} - {f_2}){
m{i}}{omega _0}}} $$

$$ {x_4} = dfrac{{ - {p_2}{omega _0}^2 + ({p_1} - {omega _0}^2)v{
m{i}}{omega _0}}}{{{p_2}v + ({f_1}{v^2} - {f_2}){
m{i}}{omega _0}}} $$

在轮对系统的Hopf分岔点处, 即$ v = {v_{cr}} $

时, 方程(2)中的矩阵$ {{boldsymbol{J}}}(v) $

的转置矩阵为$ {{{boldsymbol{J}}}^{text{T}}}(v) $

, 该转置矩阵的特征值中存在一对纯虚根$pm {text{i}}{omega _0}$

和两个具有负实部的根, 设矩阵$ {{{boldsymbol{J}}}^{text{T}}}(v) $

的特征值为纯虚根时对应的特征向量为$ {{boldsymbol{p}}} = {[{x_{11}},{x_{22}},{x_{33}},{x_{44}}]^{text{T}}} $

, 满足${{{boldsymbol{J}}}^{text{T}}}(v){{boldsymbol{p}}} = - {text{i}}{omega _0}{{boldsymbol{p}}}$

, 其中

$$ begin{array}{l} {x_{11}} = left(dfrac{{{p_2}}}{v} - {
m{i}}{omega _0}
ight)dfrac{{left({omega _0}^2 - s
ight)v + c{
m{i}}{omega _0}}}{{ - {p_2}v + left({f_1}{v^2} - {f_2}
ight){
m{i}}{omega _0}}} + gleft({f_1}v - dfrac{{{f_2}}}{v}
ight) {x_{22}} = dfrac{{left({omega ^2} - s
ight)v + c{
m{i}}{omega _0}}}{{ - {p_2}v + left({f_1}{v^2} - {f_2}
ight){
m{i}}{omega _0}}} {x_{33}} = dfrac{c}{v} - {
m{i}}{omega _0} + left(dfrac{{{f_2}}}{v} - {f_1}v
ight)dfrac{{left({omega _0}^2 - s
ight)v + c{
m{i}}{omega _0}}}{{ - {p_2}v + left({f_1}{v^2} - {f_2}
ight){
m{i}}{omega _0}}} {x_{44}} = 1 end{array} $$

令$ {{{boldsymbol{p}}}_{text{0}}} = {{boldsymbol{p}}} $

与$ ss = leftlangle {{{boldsymbol{p}},}left. {{boldsymbol{q}}}
ight
angle }
ight. $

, 取${{{boldsymbol{q}}}_0} = {{boldsymbol{q}}}dfrac{1}{{ss}}$

, 此时满足

$$qquadqquadleftlangle {{{{boldsymbol{p}}}_0}}
ight.{,}left. {{{{boldsymbol{q}}}_0}}
ight
angle = 1 $$

(14)

$$ qquadqquadleftlangle {{{{bar {boldsymbol{p}}}}_0}}
ight.{,}left. {{{{boldsymbol{q}}}_0}}
ight
angle = leftlangle {{{{boldsymbol{p}}}_0}}
ight.{,}left. {{{{bar {boldsymbol{q}}}}_0}}
ight
angle = 0 $$

(15)

其中$ {{bar {boldsymbol{p}}}_0} $

与$ {{bar {boldsymbol{q}}}_0} $

分别为$ {{{boldsymbol{p}}}_0} $

和$ {{{boldsymbol{q}}}_0} $

的共轭矩阵, $ leftlangle {}
ight.left. {}
ight
angle $

为内积符号.

从方程(1)中可知非线性轮轨力为关于横移量的三次方和五次方的叠加, 根据投影法^[29-30]求解可得

$$ {c_1} = frac{1}{2}frac{{c{
m{i}}{omega _0} - ({omega _0}^2 - s)v}}{{{p_2}v{text{ + }}({f_1}{v^2} - {f_2}){
m{i}}{omega _0}}}frac{{{text{6}}{delta _1}{{{boldsymbol{q}}}_0}^2(1){{{bar {boldsymbol{q}}}}_0}(1)}}{m} $$

(16)

则第一Lyapunov系数为

$$ {l_1}(0) = frac{{{{{Re}}} {c_1}}}{{{omega _0}}} $$

(17)

当系统在平衡点发生Hopf分岔时, 若第一Lyapunov系数大于零, 系统发生亚临界Hopf分岔. 若第一Lyapunov系数小于零, 系统发生超临界Hopf分岔. 若第一Lyapunov系数等于零, 系统发生退化的Hopf分岔. 故可通过计算轮对系统的第一Lyapunov系数判断系统发生的Hopf分岔类型.

2.2
轮对系统第二Lyapunov系数求解

为研究第一Lyapunov系数等于零时轮对系统在退化Hopf分岔点附近的Bautin分岔形式, 根据投影法^[29-30]求解轮对系统的第二Lyapunov系数, 其中轮对系统对应的投影法中各系数分别如下

$$begin{split} & {{boldsymbol{h}}_{11}} = {{boldsymbol{h}}_{20}} = {{boldsymbol{h}}_{40}} = {{boldsymbol{h}}_{31}} = {{boldsymbol{h}}_{22}} = {[0,0,0,0]^{
m{T}}} & {{boldsymbol{h}}_{30}} = {Big[3{
m{i}}{omega _0}{boldsymbol{I}} - {boldsymbol{J}}(v)Big]^{ - 1}}{[0, - {
m{6}}{delta _1}{{boldsymbol{q}}_0}^3(1)/m,0,0]^{
m{T}}}{kern 1pt} end{split}$$

$$ begin{array}{l}{{boldsymbol{h}}_{21}} ={Big[{
m{i}}{omega _0}{boldsymbol{I}} - {boldsymbol{J}}(v)Big]^{{
m{INV}}}}cdotqquadBig{{[0, - {
m{6}}{delta _1}{{boldsymbol{q}}_0}^2(1){{{bar{boldsymbol q}}}_0}(1)/m,0,0]^{
m{T}}} - 2{c_1}{{boldsymbol{q}}_0}Big}end{array} $$

其中$ {{boldsymbol{I}}} $

是单位矩阵.

将以上各系数代入投影法中, 化简可得

$$ {c_2} = frac{{leftlangle {{{boldsymbol{p}}},{{{Big( 0,{H_1}{text{ + }}{H_2}{text{ + }}{H_3}{text{ + }}{H_4},0,0Big)}^{text{T}}}} }
ight
angle }}{{12}} $$

(18)

其中

$$ {H_1}{text{ = }} - 120{delta _2}{{boldsymbol{q}}}_0^3(1){bar {boldsymbol{q}}}_0^2(1)/m $$

$$ {H_2}{text{ = }} - 6{delta _1}{bar {boldsymbol{q}}}_0^2(1){{{boldsymbol{h}}}_{30}}(1)/m $$

$$ {H_3}{text{ = }} - 18{delta _1}{{boldsymbol{q}}}_0^2(1){{bar {boldsymbol{h}}}_{21}}(1)/m $$

$$begin{split} {H_4}{text{ = }} - 36{delta _1}{{{boldsymbol{q}}}_0}(1){{bar {boldsymbol{q}}}_0}(1){{{boldsymbol{h}}}_{21}}(1)/m end{split}$$

则第二Lyapunov系数表达式为

$$ {l_2}(0) = frac{{{{
m{Re}}} {c_2}}}{{{omega _0}}} $$

(19)

3.
轮对系统的分岔图

3.1
采用打靶法求解轮对系统分岔图

采用打靶法^[11]求解轮对系统的分岔图, 其原理为假设极限环周期为T, 满足$ {{boldsymbol{Y}}}(t + T) = {{boldsymbol{Y}}}(t) $

, 令$ t = Tz $

, 则方程(2)可以被表示为

$$ frac{{{
m{d}}{{boldsymbol{Y}}}}}{{{
m{d}}z}} = T{{boldsymbol{J}}}(v){{boldsymbol{Y}}} + T{{boldsymbol{F}}}({{boldsymbol{Y}}}) $$

(20)

方程(20)满足边界条件$ {{boldsymbol{Y}}}(1) = {{boldsymbol{Y}}}(0) $

, 对方程(20)在区间[0, 1]内积分可以得到$ {{boldsymbol{Y}}}(1) = {{boldsymbol{G}}}({{boldsymbol{Y}}},T,v) $

, 使得其满足

$$ {{boldsymbol{F}}}({{boldsymbol{Y}}},T,v) = {{boldsymbol{G}}}({{boldsymbol{Y}}},T,v) - {{boldsymbol{Y}}} = {boldsymbol{0}} $$

(21)

通过使用得到的轮对系统在Hopf分岔点处的线性临界速度表达式(8) ~ 式(11)与式(13), 参数值代入附录A中表A1, 计算轮对系统Hopf分岔点处的线性临界速度$ {v_{cr}} $

.

取初值分别为$ {T_0} = 2{text{π}} /{omega _0} $

, $ {v_0} = {v_{cr}} $

, $ y = {{y}_{text{0}}} $

, $ dot y = 0 $

, $ varphi = 0 $

和$ dot varphi = 0 $

, 其中, $ {y_0} $

为轮对横移量初始微小扰动, 使用Newton?Raphson迭代法^[31]求解方程(21), 每次使用Newton?Raphson迭代法求解方程(21)的过程中, 都要用变步长欧拉法^[31]在区间[0, 1]内积分求解方程(21), 并判断$ {{boldsymbol{F}}}({{boldsymbol{Y}}},T,v) $

的范数是否满足控制精度, 若满足则得到轮对系统的极限环解(轮对横移量周期解), 然后选取下一极限环的初值为$ {y} = {y_0} + h $

(h为步长)与$ dot y = 0 $

, 其他值取前一极限环的值, 重复循环计算最终可以得到轮对系统的分岔图.

令${boldsymbol{D}} = {{partial {boldsymbol{G}}}}/{{partial {boldsymbol{Y}}}}$

, 当矩阵$ {boldsymbol{D}} $

的特征值最大模小于1时, 极限环稳定, 否则不稳定.

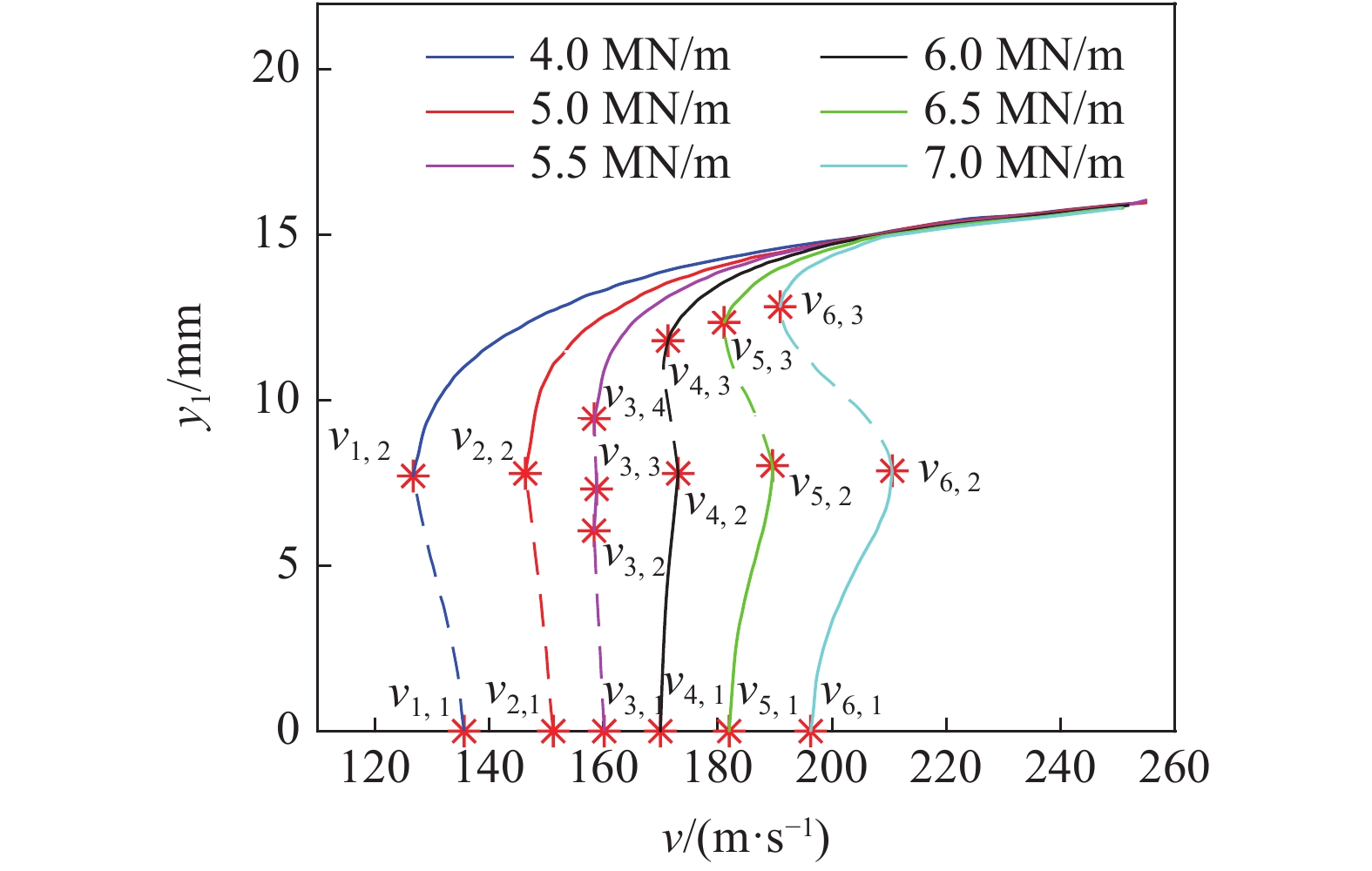
为对比考虑陀螺效应与不考虑陀螺效应对轮对系统分岔图的影响, 取轮对系统的纵向刚度分别为4.0 MN/m, 5.0 MN/m, 5.5 MN/m, 6.0 MN/m, 6.5 MN/m与7.0 MN/m, 其他参数值取附录A中表A1, 采用打靶法^[11]求解出不同纵向刚度值下不考虑陀螺效应与考虑陀螺效应的轮对系统分岔图如下图4与图5所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />

图
4
不同纵向刚度下不考虑陀螺效应的轮对系统分岔图

Figure
4.
The bifurcation diagram of wheelset system without considering the gyroscopic action under different longitudinal stiffness

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />

图
5
不同纵向刚度下考虑陀螺效应的轮对系统分岔图

Figure
5.
The bifurcation diagram of wheelset system considering the gyroscopic action under different longitudinal stiffness

下载:
全尺寸图片
幻灯片

图中$ {y_1} $

表示轮对系统的横移量, $ v $

表示轮对系统的运行速度, 实线表示稳定的极限环, 虚线表示不稳定极限环. ${v_{i,j}};(i = 1,2, cdots ,12;j = 1)$

为轮对系统的线性临界速度, 其余的$ {v_{i,j}} $

为轮对系统的非线性临界速度, 各值见附录A中表A2与表A3.

由方程(17)可得, 图4中不考虑陀螺效应的轮对系统, 纵向刚度依次取4.0 MN/m, 5.0 MN/m, 5.5 MN/m, 6.0 MN/m, 6.5 MN/m与7.0 MN/m时, 分别对应的第一Lyapunov系数依次为0.0515, 0.0238, 0.0108, ?0.0024, ?0.0168与?0.033 6. 图5中考虑陀螺效应的轮对系统, 纵向刚度依次取4.0 MN/m, 5.0 MN/m, 5.5 MN/m, 6.0 MN/m, 6.5 MN/m与7.0 MN/m时, 分别对应的第一Lyapunov系数依次为0.0452, 0.0172, 0.0037, ?0.0103, ?0.0258与?0.044 2. 可知当纵向刚度为4.0 MN/m, 5.0 MN/m, 5.5 MN/m时, 考虑陀螺效应与不考虑陀螺效应的轮对系统第一Lyapunov系数均大于零, 即轮对系统在Hopf分岔点处发生亚临界Hopf分岔. 当纵向刚度为6.0 MN/m, 6.5 MN/m, 7.0 MN/m时, 考虑陀螺效应与不考虑陀螺效应的轮对系统第一Lyapunov系数均小于零, 即轮对系统在Hopf分岔点处发生超临界Hopf分岔.

图4与图5对比可知, 轮对系统的纵向刚度依次取4.0 MN/m, 5.0 MN/m, 5.5 MN/m, 6.0 MN/m, 6.5 MN/m与7.0 MN/m时, 考虑陀螺效应与不考虑陀螺效应的轮对系统均经历了从亚临界Hopf分岔到超临界Hopf分岔的变化, 在轮对系统中, 当纵向刚度值与其他各参数值均已知时, 考虑陀螺效应的线性临界速度和非线性临界速度均高于不考虑陀螺效应的线性临界速度和非线性临界速度, 即在同一纵向刚度值下, 陀螺效应既可以提高轮对系统的线性临界速度, 又可以提高轮对系统的非线性临界速度, 陀螺效应对轮对系统具有增稳效果.

3.2
轮对系统在退化Hopf分岔点处的分岔图

由分岔理论^[29-30]可知, 若在Hopf分岔点处系统满足第一Lyapunov系数为零, 系统发生退化Hopf分岔.

针对轮对系统, 若考虑陀螺效应, 轮对横向转动惯量取100 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

, 横向自旋蠕滑系数取0.13 MN, 其他参数取值见附录A中表A1, 根据第一Lyapunov系数表达式(17)与Hopf分岔点处的线性临界速度表达式(8) ~ 式(11), 得到考虑陀螺效应的轮对系统在退化Hopf分岔点处的纵向刚度与轮对线性临界速度分别为$ {k_{{text{c1}}}} $

与$ {v_{{text{c1}}}} $

$$ left. begin{array}{l} {k_{{text{c1}}}} = {text{5;636;764}}{text{.380;835;N/m}} {v_{{text{c1}}}} = {text{170}}{text{.812;185;m/s}} end{array}
ight} $$

(22)

针对轮对系统, 若不考虑陀螺效应, 轮对系统的横向转动惯量取0 $ {text{kg}} cdot {{text{m}}^{text{2}}} $

, 横向自旋蠕滑系数取0 MN, 其他参数取值见附录A中表A1, 根据第一Lyapunov系数表达式(17)与Hopf分岔点处的线性临界速度表达式(13), 得到不考虑陀螺效应的轮对系统在退化Hopf分岔点处的纵向刚度与轮对线性临界速度分别为$ {k_{{text{c2}}}} $

与$ {v_{{text{c2}}}} $

$$ left. begin{array}{l} {k_{{text{c2}}}} = 5;910;448.522;674;{text{N/m}} {v_{{text{c2}}}} = 168.172;237;{text{m/s}} end{array}
ight} $$

(23)

采用打靶法^[11]分别计算考虑陀螺效应与不考虑陀螺效应的轮对系统在退化Hopf分岔点处的分岔图如下图6所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />

图
6
轮对系统退化Hopf分岔图

Figure
6.
Degenerate Hopf bifurcation diagram of the wheelset system

下载:
全尺寸图片
幻灯片

图中$ {y_1} $

表示轮对系统的横移量, $ v $

表示轮对系统的运行速度, 实线表示稳定的极限环, 虚线表示不稳定极限环. $ {v_{13,1}} $

与$ {v_{14,1}} $

为轮对系统的线性临界速度, 且$ {v_{13,1}} = {v_{{text{c1}}}} $

, $ {v_{14,1}} = {v_{{text{c2}}}} $

, ${v_{i,j}};(i = 13,14;j = 2,3)$

为轮对系统的非线性临界速度, 其值参见附录A中表A4.

由图6可知, 考虑陀螺效应与不考虑陀螺效应的轮对系统在各自的退化Hopf分岔点处, 考虑陀螺效应的线性临界速度与非线性临界速度值均高于不考虑陀螺效应的轮对系统.

4.
轮对系统的退化Hopf分岔形式

4.1
轮对系统在退化Hopf分岔点处的Bautin分岔拓扑形式

当第一Lyapunov系数为零时, 轮对系统发生退化Hopf分岔.

根据文献[30]中对于退化Hopf分岔的讨论可知, 两参数平面系统经过一系列时间尺度变换最终可化简为

$$ dot z = ({mu _1}{text{ + i)}}z + {mu _2}z{left| z
ight|^2} + L(mu )z{left| z
ight|^4} + O({left| z
ight|^6}) $$

(24)

其中, $L(mu ) = {l_2}Big[eta (mu {text{)}}Big]$

. 令$ z = sqrt[{ - 4}]{{left| {L(mu )}
ight|}}u ne 0 $

, $ {beta _1} = {mu _1} $

, $ {beta _2} = {mu _2}/sqrt {left| {L(mu )}
ight|} $

与$ s = L(mu {text{)/}}left| {L(mu )}
ight| $

, 代入方程(24)可得

$$ dot u = ({beta _1}{text{ + i)}}u{text{ + }}{beta _2}u{left| u
ight|^2} + su{left| u
ight|^4} + O({left| u
ight|^6}) $$

(25)

当$ L(mu ) > 0 $

, 即退化Hopf分岔点处的第二Lyapunov系数大于零时, $ s = 1 $

. 当$ L(mu {text{) < }}0 $

, 即退化Hopf分岔点处的第二Lyapunov系数小于零时, $ s = - 1 $

.

由式(19)、式(22)与式(23)可得, 考虑陀螺效应和不考虑陀螺效应的轮对系统在退化Hopf分岔点处的第二Lyapunov系数分别为?0.01478与?0.01463, 均小于零, 结合方程(25)可知, 有、无陀螺效应的轮对系统对应的Bautin分岔^[30]的形式均为

$$ left. begin{array}{l} dot
ho =
ho ({beta _1} + {beta _2}{
ho ^2} + xi {
ho ^4}) dot theta = 1 end{array}
ight} $$

(26)

其中

$$ {beta _1} = frac{{alpha (v,{k_x})}}{{omega (v,{k_x})}}; ; ; ; $$

(27)

$$ {beta _2} = frac{{{l_1}(v,{k_x})}}{{sqrt {left| {{l_2}Big[{v_c}({k_{xc}})Big]}
ight|} }}; ; ; ; ; ; ; $$

(28)

$$ xi = {text{sign}}{l_2}(0) = - 1; ; ; $$

(29)

$$ T = left{ {({beta _1},;{beta _2})|beta _2^2 + 4{beta _1} = 0,;{beta _2} > 0}
ight} $$

(30)

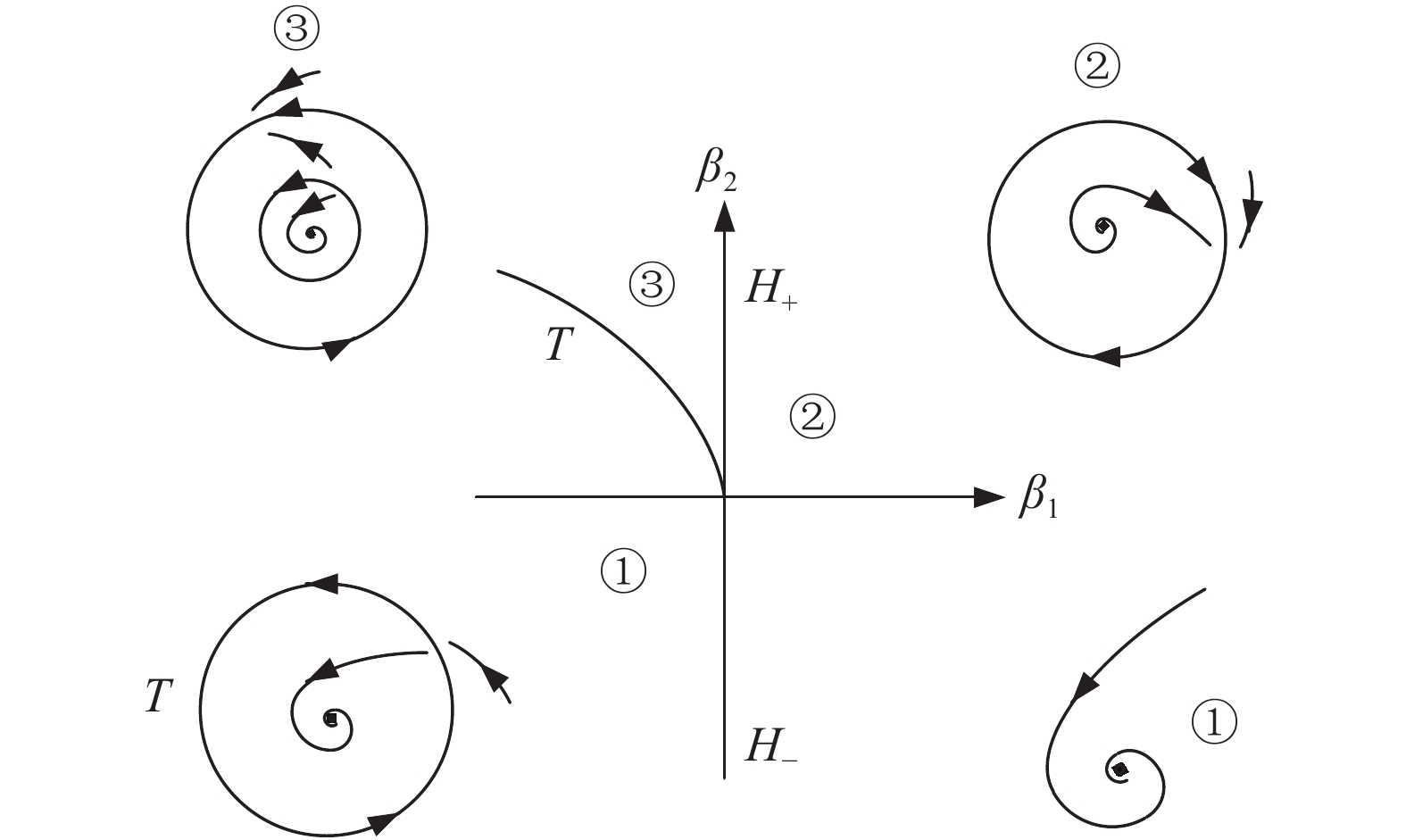
对应的Bautin分岔见图7, 其中$ {H_ - } $

和$ {H_ + } $

分别对应Hopf分岔的第一Lyapunov系数小于0和第一Lyapunov系数大于0.

在图7中绕着Bautin点逆时针方向考察, 从区域①中的点开始, 在该区域里面系统有单个稳定平衡点而没有极限环. 从区域①到区域②穿过Hopf分岔边界$ {H_ - } $

, 出现唯一稳定极限环. 当穿过Hopf分岔边界$ {H_ + } $

进入区域③时, 该稳定的极限环依然存在, 此时平衡点恢复它的稳定性, 同时在第一个环内部额外产生了一个不稳定极限环, 两个具有相反稳定性的环在区域③中存在并在曲线T上相遇消失而留下单个稳定平衡点, 这就走完了一圈.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />

图
7
Bautin分岔图($ xi = - 1 $

)

Figure
7.
Bautin bifurcation diagram ($ xi = - 1 $

)

下载:
全尺寸图片
幻灯片

在图7中每次穿越$ {beta _1} $

轴时系统的第一Lyapunov系数都会出现变号, 若逆时针方向穿越$ {beta _1} $

负半轴, 系统从亚临界Hopf分岔转变为超临界Hopf分岔, 若逆时针穿越$ {beta _1} $

正半轴, 系统从超临界Hopf分岔转变为亚临界Hopf分岔. 这就是系统在双参数下, 由亚临界Hopf分岔到超临界Hopf分岔, 再从超临界Hopf分岔到亚临界Hopf分岔的迁移转化机理.

4.2
轮对系统考虑陀螺效应与不考虑陀螺效应时在退化Hopf分岔点附近的Bautin分岔拓扑图对比

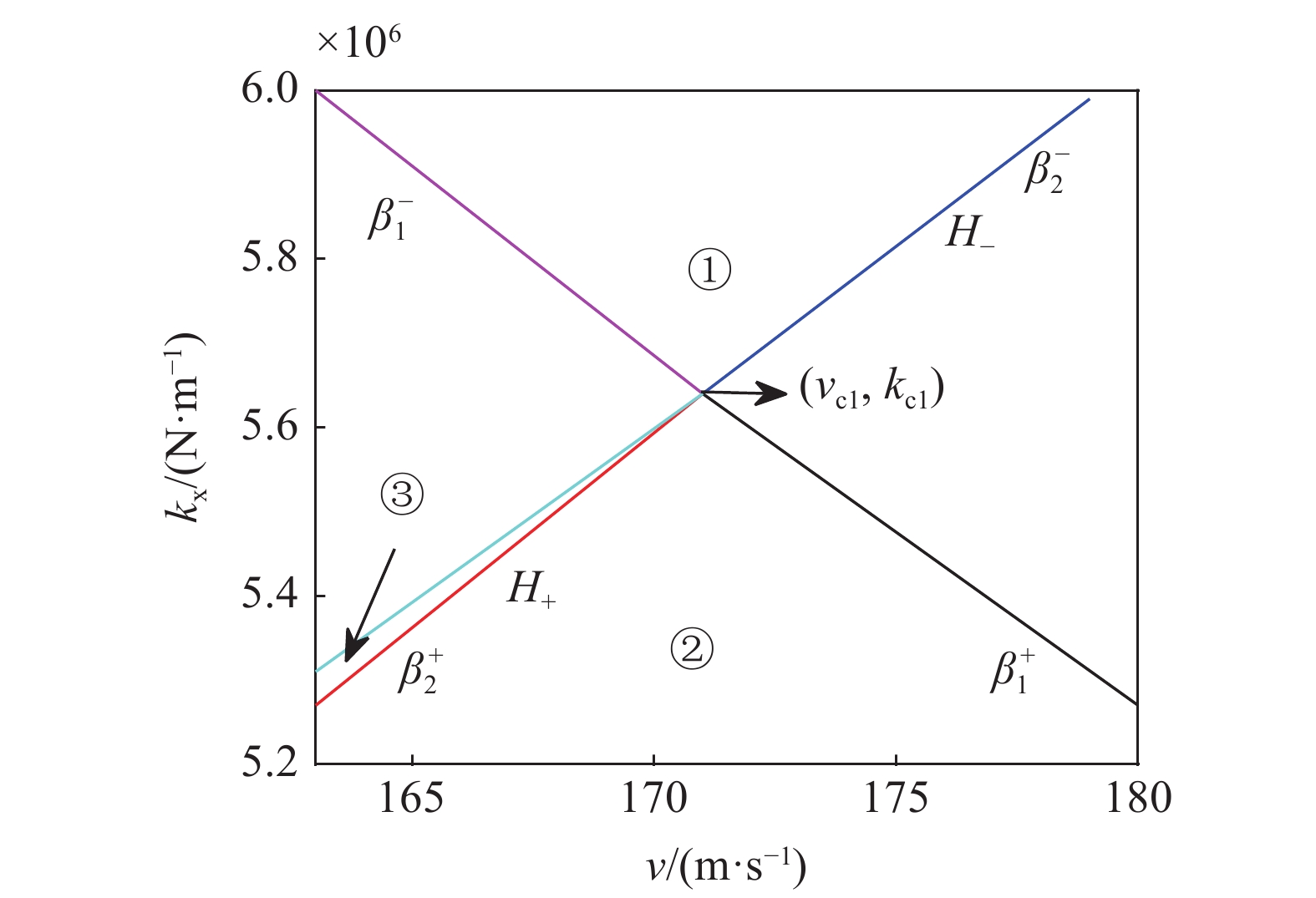
通过式(26) ~ 式(30)中的坐标变化, 得到考虑陀螺效应的轮对系统在运行速度与纵向刚度坐标系下的Bautin分岔拓扑图如图8所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />

图
8
轮对系统考虑陀螺效应时的Bautin分岔拓扑图

Figure
8.
Bautin bifurcation topology diagram of wheelset system when considering gyroscopic action

下载:
全尺寸图片
幻灯片

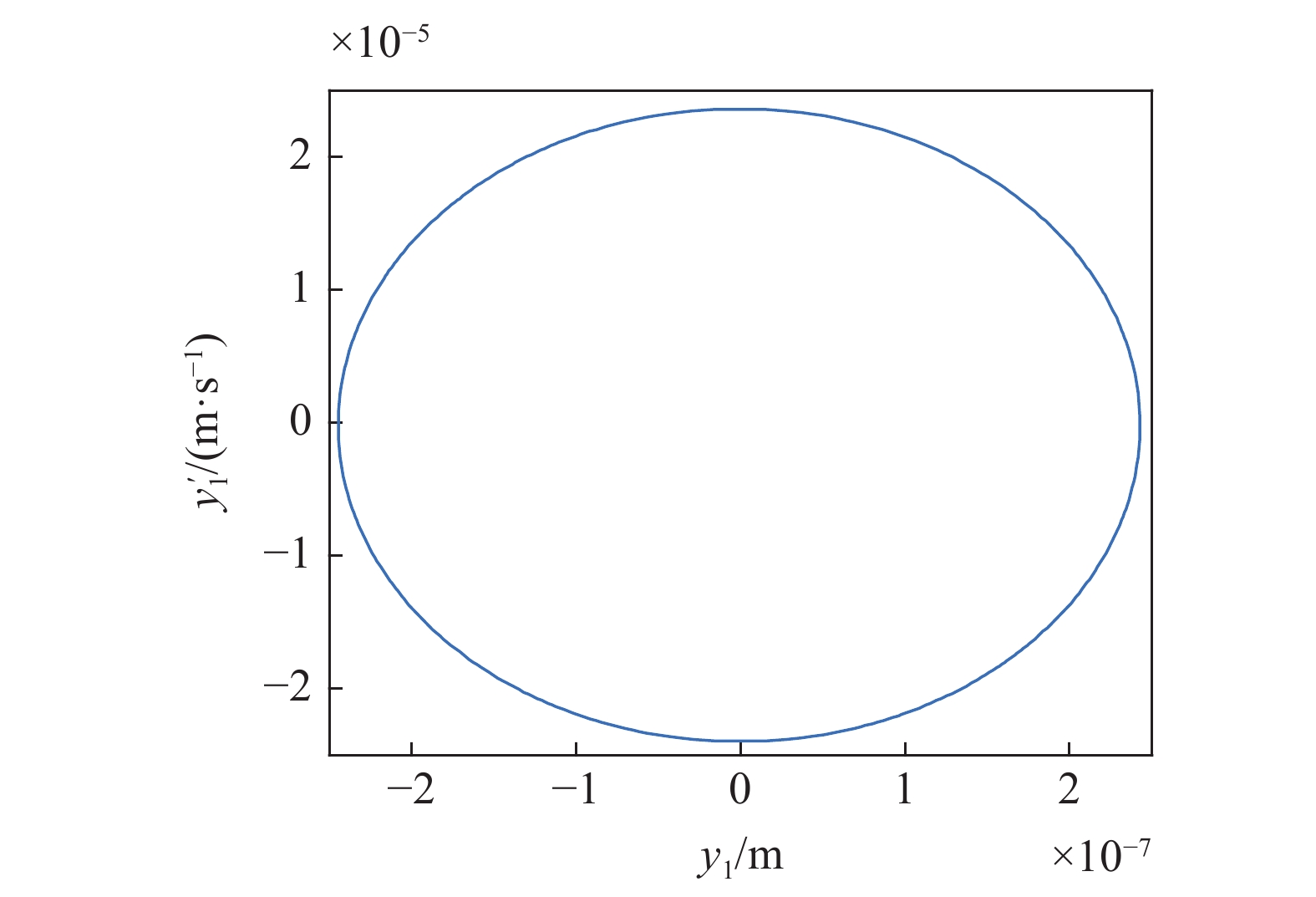
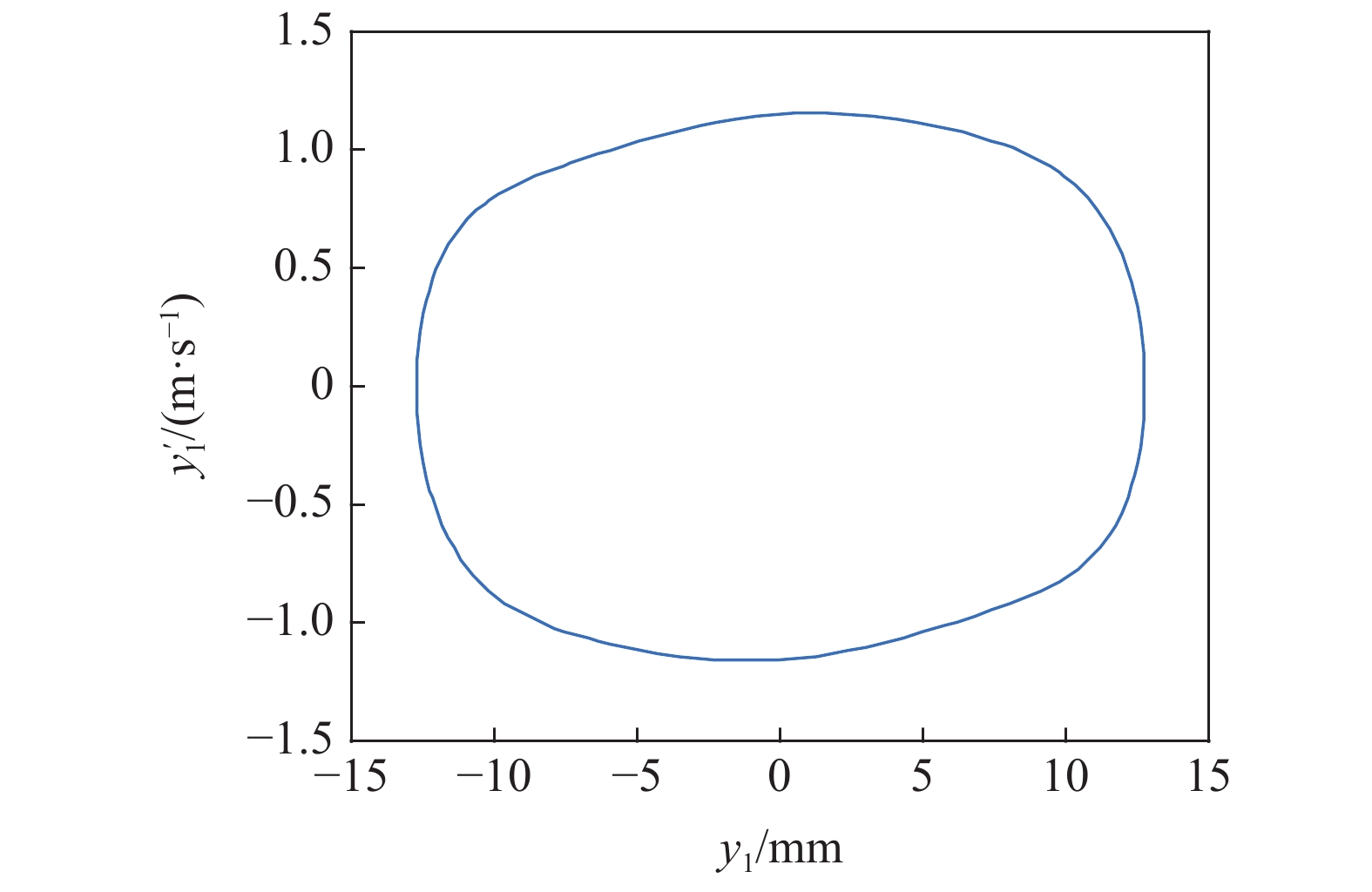
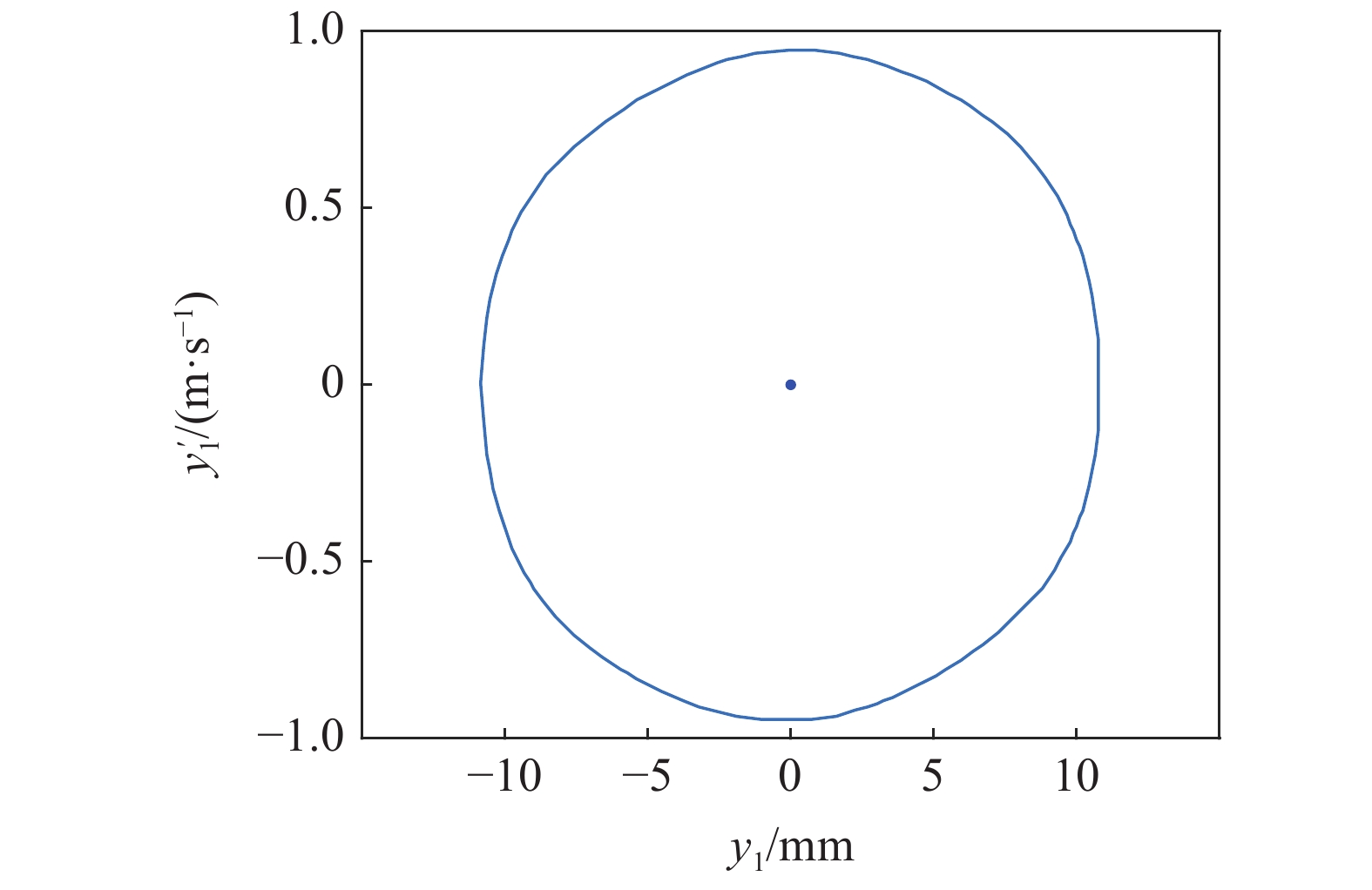
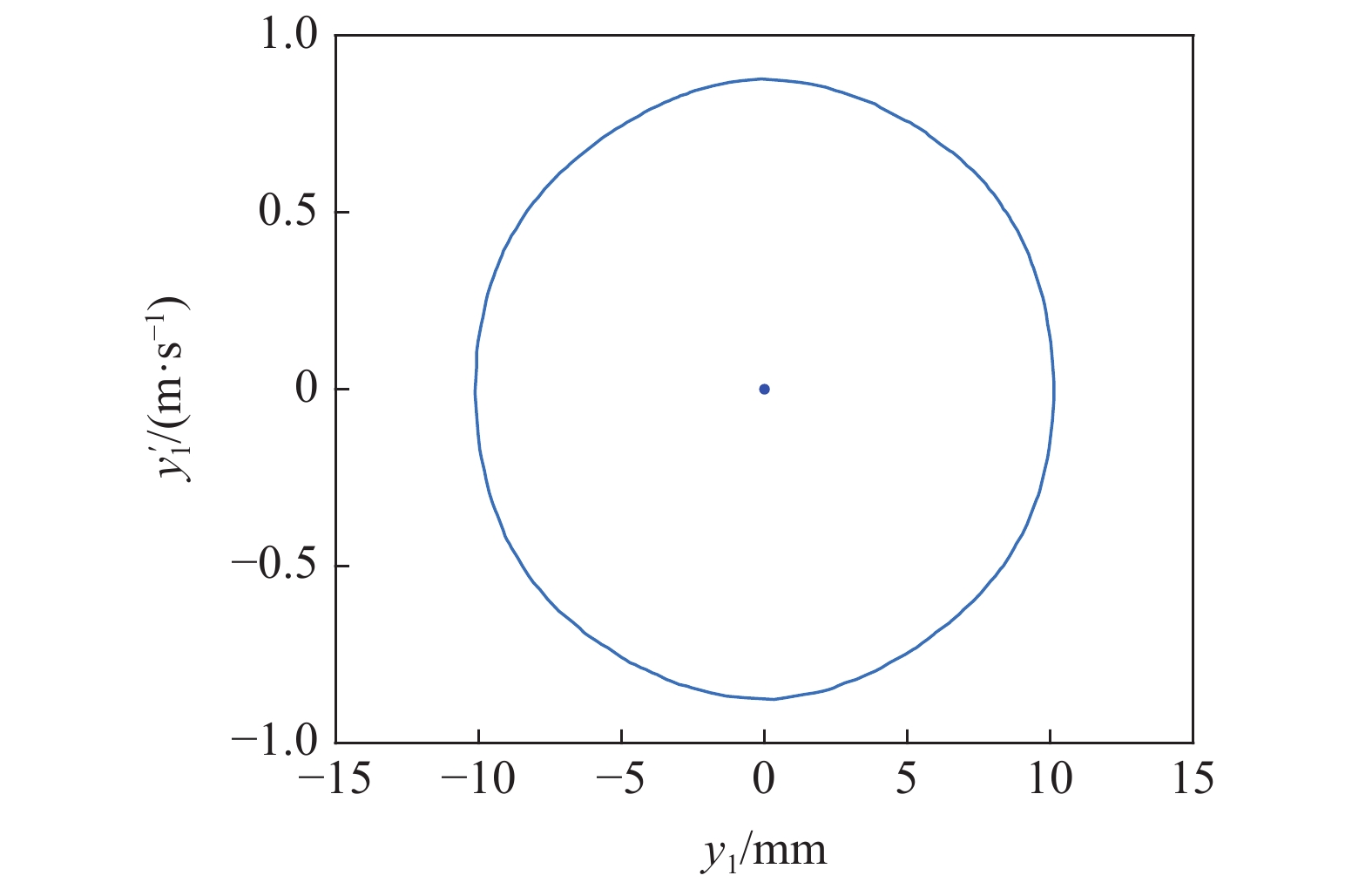
系统中若存在稳定的周期解, 其相图必然存在, 在图8的区域①中取一个点(170 m/s, 5.8 MN/m), 在区域②中取一个点(170 m/s, 5.2 MN/m), 在区域③中取一个点(160 m/s, 5.13 MN/m), 在T 曲线上取一个点(160 m/s, 5544590 N/m), 分别得到对应的相图如图9 ~ 图12所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />

图
9
图8中区域①对应的相图

Figure
9.
Phase diagram corresponding to area ① in Fig 8

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />

图
12
图8中T区域对应的相图

Figure
12.
Phase diagram corresponding to the T region in Fig 8

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />

图
10
图8中区域②对应的相图

Figure
10.
Phase diagram corresponding to area ② in Fig 8

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />

图
11
图8中区域③对应的相图

Figure
11.
Phase diagram corresponding to area ③ in Fig 8

下载:
全尺寸图片
幻灯片

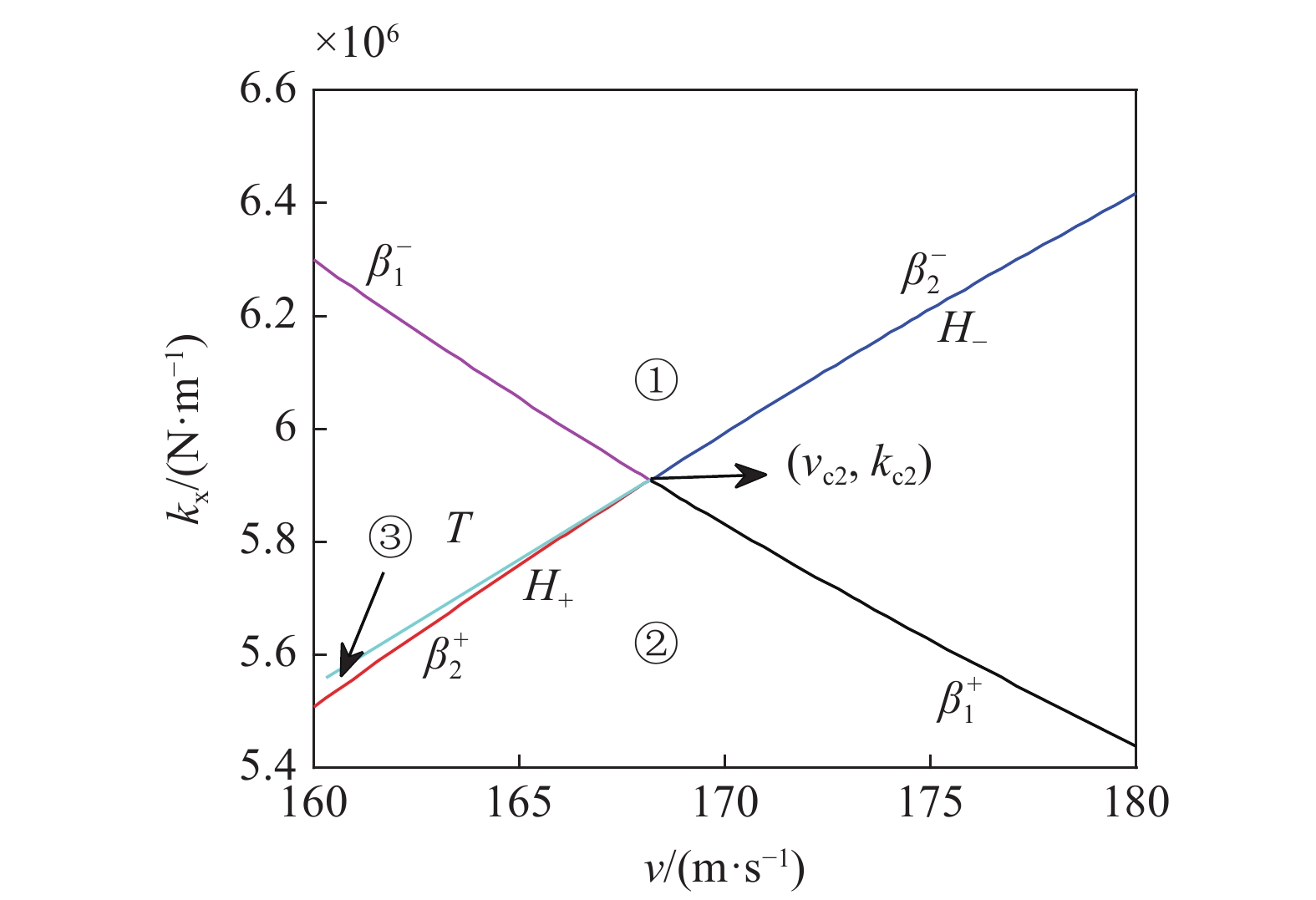
通过式(26) ~ 式(30)中的坐标变化, 得到不考虑陀螺效应的轮对系统在运行速度与纵向刚度坐标系下的Bautin分岔拓扑图如图13所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />

图
13
轮对系统不考虑陀螺效应时的Bautin分岔拓扑图

Figure
13.
Bautin bifurcation topology diagram of wheelset system without considering gyroscopic action

下载:
全尺寸图片
幻灯片

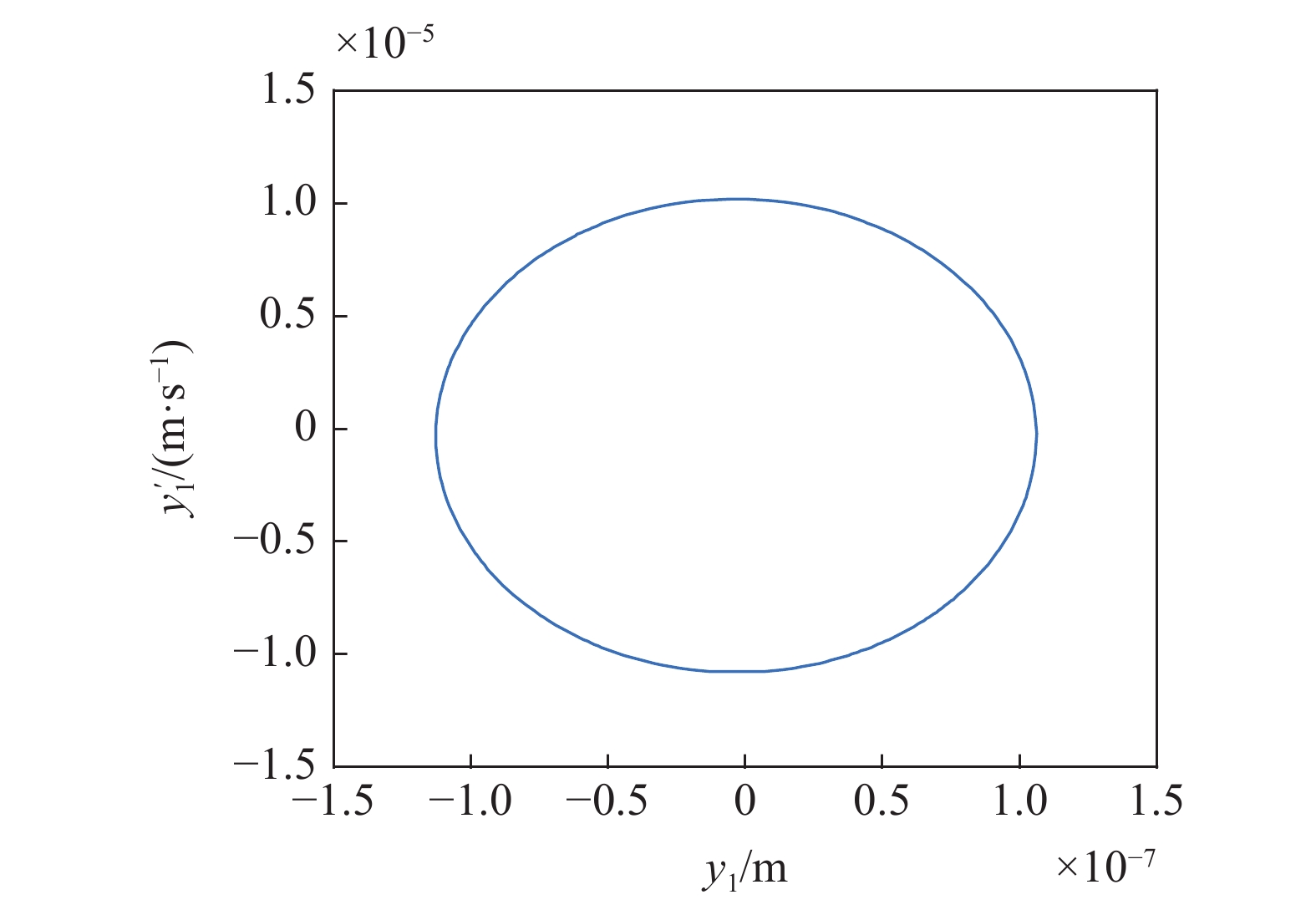
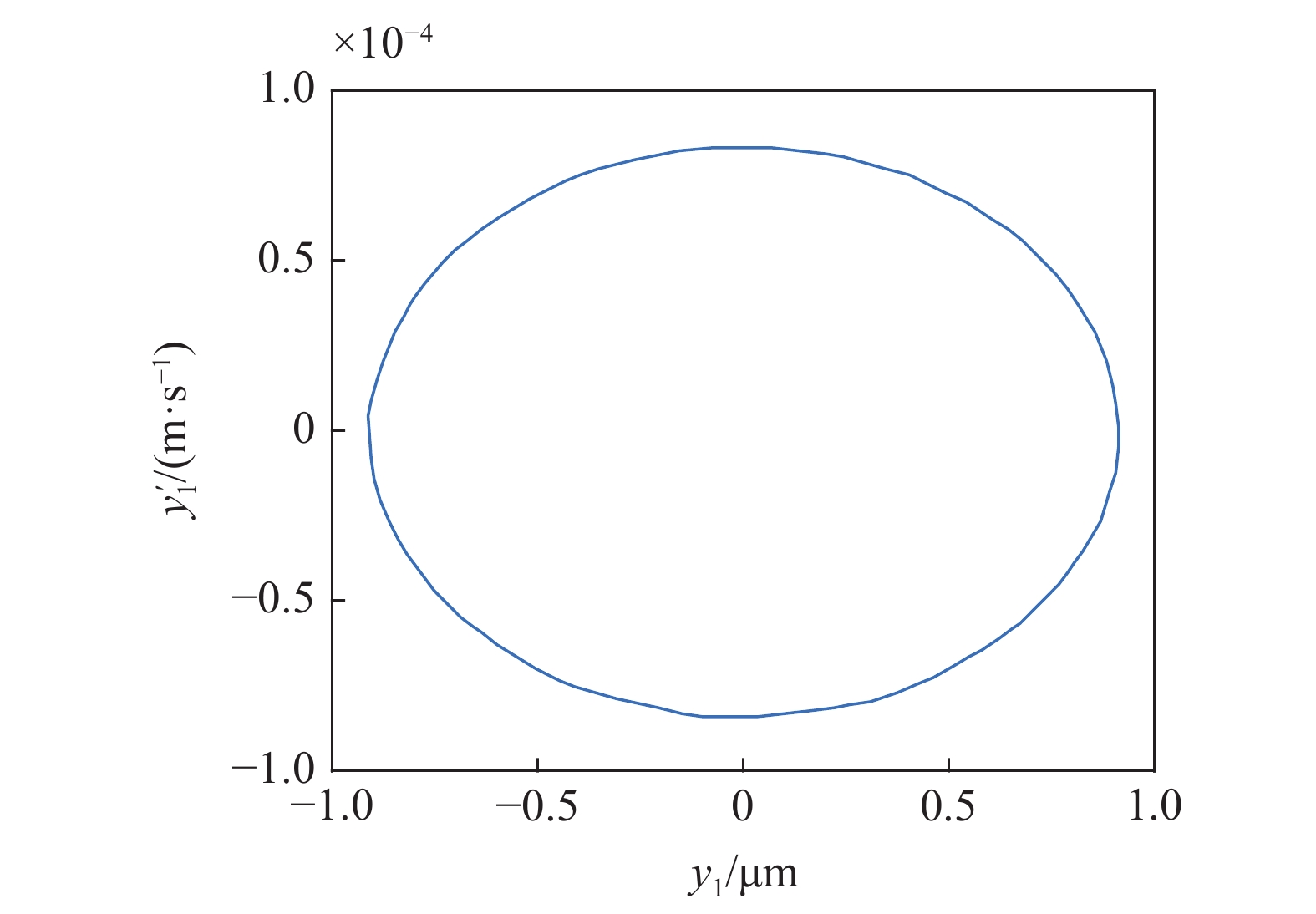
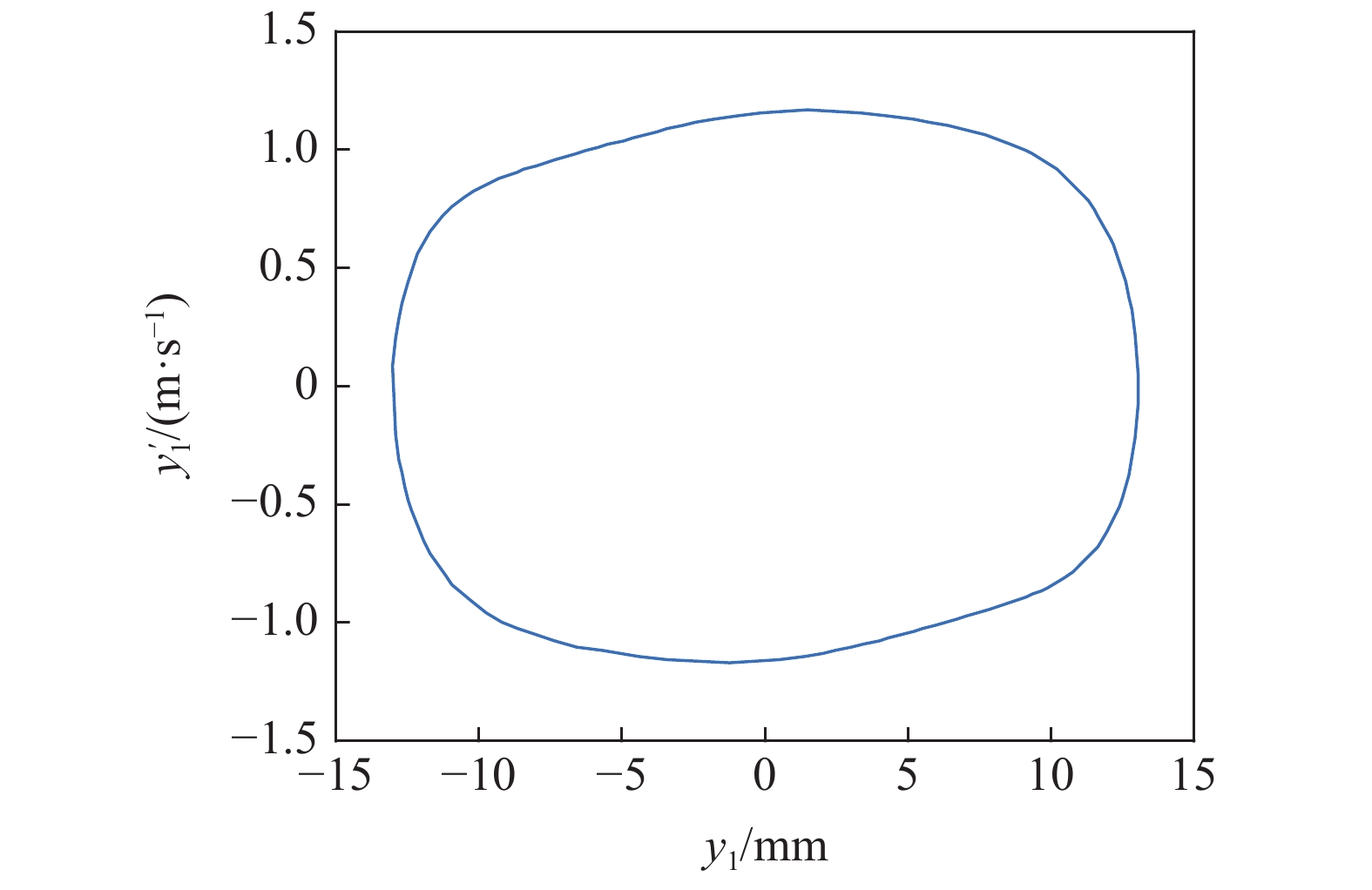
在图13的区域①中取点(170 m/s, 6.5 MN/m), 在区域②中取点(170 m/s, 5.5 MN/m), 在区域③中取点(160 m/s, 5.54 MN/m), 在T 曲线上取点(160.3 m/s, 5558921 N/m), 分别得到对应的相图如图14 ~ 图17所示.

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />

图
14
图9中区域①对应的相图

Figure
14.
Phase diagram corresponding to area ① in Fig 9

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />

图
17
图9中T区域对应的相图

Figure
17.
Phase diagram corresponding to the T region in Fig 9

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />

图
15
图9中区域②对应的相图

Figure
15.
Phase diagram corresponding to area ② in Fig 9

下载:
全尺寸图片
幻灯片

onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-321-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />

图
16
图9中区域③对应的相图

Figure
16.
Phase diagram corresponding to area ③ in Fig 9

下载:
全尺寸图片
幻灯片

图8与图13分别展示了考虑陀螺效应与不考虑陀螺效应的轮对系统在退化Hopf分岔点附近, 依靠双参数(纵向速度和纵向刚度)从亚临界Hopf分岔到超临界Hopf分岔, 再从超临界Hopf分岔到亚临界Hopf分岔的转化过程.

由图9 ~ 图12可知, 考虑陀螺效应的轮对系统, 其在退化Hopf分岔点附近的Bautin分岔拓扑图的区域①中的点具有单个稳定平衡点. 区域②中的点具有单个稳定极限环. 区域③中的点具有单个稳定极限环和单个稳定平衡点, T曲线上只有单个稳定平衡点. 该结论与图7中的理论结果是一致的.

由图14 ~ 图17可知, 不考虑陀螺效应的轮对系统, 其在退化Hopf分岔点附近的Bautin分岔拓扑图的区域①中的点具有单个稳定平衡点. 区域②中的点具有单个稳定极限环. 区域③中的点具有单个稳定极限环和单个稳定平衡点, T曲线上只有单个稳定平衡点. 该结论与图7中的理论结果是一致的.

由图8 ~ 图17可知, 陀螺效应将改变轮对系统的退化Hopf分岔点, 但对于在退化Hopf分岔点附近的Bautin分岔形式影响不大.

5.
结论

本文基于Hopf分岔代数判据、分岔理论和打靶法, 分别得到考虑陀螺效应与不考虑陀螺效的轮对系统Hopf分岔点解析表达式、在不同纵向刚度下的分岔图和在退化Hopf分岔点附近的Bautin分岔拓扑图. 发现影响轮对系统陀螺效应的主要参数是轮对系统的横向转动惯量, 次要参数是轮对系统的横向自旋蠕滑系数. 陀螺效应不仅可以提高轮对系统的线性临界速度, 也可以提高轮对系统的非线性临界速度, 即陀螺效应对轮对系统的运动稳定性具有增稳作用. 陀螺效应会改变轮对系统的退化Hopf分岔点, 但对退化Hopf分岔点附近的Bautin分岔形式影响不大.

附录A

A1
轮对参数表

A1.
Wheelset parameter list

table_type1 ">

Parameter	Value
m/kg	1612
$ {I}_{z}/(text{kg} cdot {text{m}}^{2}) $	881
I_y$ /(text{kg} cdot {text{m}}^{2}) $	100
$ {lambda } $	0.13
$ {{r}_{0}}/{text{m}} $	0.46
$L/{ m{m}}$	1
$b/{ m{m}}$	0.7175
$ {{f}_{{text{11}}}}/{text{MN}} $	13.7
$ {{f}_{{text{22}}}}/{text{MN}} $	11.1
$ {{f}_{{text{23}}}}/{text{MN}} $	0.13
$ {{f}_{{text{33}}}}/{text{MN}} $	0
k_y$/(text{MN} cdot {text{m} }^{{-1} })$	4
$ {W/}{text{kN}} $	112.2
$ {delta _{text{1}}} $	?1.6 × 10¹¹
$ {delta _{text{2}}} $	1.6 × 10¹⁵

下载:
导出CSV
|显示表格

A2
图4中各速度值

A2.
Values of each speed in Fig. 4

table_type1 ">

v/(m·s^?1)	Value
$ {v_{1,1}} $	135.3351
$ {v_{1,2}} $	127.4978
$ {v_{2,1}} $	150.7902
$ {v_{2,2}} $	147.0965
$ {v_{3,1}} $	159.8320
$ {v_{3,2}} $	158.8470
$ {v_{3,3}} $	158.8609
$ {v_{3,4}} $	158.8112
$ {v_{4,1}} $	170.1243
$ {v_{4,2}} $	172.6321
$ {v_{4,3}} $	170.5156
$ {v_{5,1}} $	182.0883
$ {v_{5,2}} $	189.3157
$ {v_{5,3}} $	181.1072
$ {v_{6,1}} $	196.3457
$ {v_{6,2}} $	210.3911
$ {v_{6,3}} $	190.7989

下载:
导出CSV
|显示表格

A3
图5中各速度值

A3.
Values of each speed in Fig. 5

table_type1 ">

v/(m·s^?1)	Value
$ {v_{7,1}} $	140.5364
$ {v_{7,2}} $	133.0938
$ {v_{8,1}} $	157.5975
$ {v_{8,2}} $	155.0780
$ {v_{9,1}} $	167.7721
$ {v_{9,2}} $	167.6546
$ {v_{9,3}} $	168.6460
$ {v_{9,4}} $	167.8276
$ {v_{10,1}} $	179.5391
$ {v_{10,2}} $	184.9333
$ {v_{10,3}} $	179.4192
$ {v_{11,1}} $	193.4721
$ {v_{11,2}} $	205.2436
$ {v_{11,3}} $	189.8764
$ {v_{12,1}} $	210.4280
$ {v_{12,2}} $	231.7092
$ {v_{12,3}} $	199.4705

下载:
导出CSV
|显示表格

A4
图6中各速度值

A4.
Values of each speed in Fig. 6

table_type1 ">

v/(m·s^?1)	Value
$ {v_{13,2}} $	169.9825
$ {v_{13,3}} $	168.5057
$ {v_{14,2}} $	172.7866
$ {v_{14,3}} $	171.1294

下载:
导出CSV
|显示表格

附录B

$$ {p_1} = frac{{2{K_y}b + Wlambda }}{{bm}} tag{B1} $$

$$ {p_2} = frac{{2{f_{22}}}}{m} (B-2) tag{B2}$$

$$ {p_3} = frac{{2b{f_{11}}lambda }}{{I{r_0}}} tag{B3}$$

$$ g = frac{m}{{{I_z}}}tag{B4}$$

$$ {f_1} = frac{{{I_y}lambda }}{{mb{r_0}}} tag{B5} $$

$$ {f_2} = frac{{2{f_{23}}}}{m} tag{B6}$$

$$ s = frac{{2{f_{23}} + 2{k_x}{l^2} - Wlambda b}}{{{I_z}}} tag{B7}$$

$$ c = frac{{2({b^2}{f_{11}} + {f_{33}})}}{{{I_z}}} tag{B8}$$

$$ begin{split}& {b_0} = cf_1^3{g^2}{p_2} + f_1^3{g^2}p_2^2 + cf_1^3g{p_3} +&qquad f_1^3g{p_2}{p_3} - f_1^2{g^2}p_2^2 - 2f_1^2g{p_2}{p_3} - f_1^3p_3^2 end{split} tag{B9}$$

$$ begin{split}&{b_1} = - 3cf_1^2{f_2}{g^2}{p_2} - 3f_1^2{f_2}{g^2}p_2^2 + {c^2}f_1^2g{p_1} - &qquad3cf_1^2{f_2}g{p_3} + cf_1^2g{p_1}{p_2} + cf_1^2g{p_2}s + f_1^2gp_2^2s - &qquad3f_1^2{f_2}g{p_2}{p_3} + 2{f_1}{f_2}{g^2}p_2^2 - c{f_1}g{p_1}{p_2} + &qquadc{f_1}g{p_2}s + 4{f_1}{f_2}g{p_2}{p_3} + {f_1}g{p_1}p_2^2 - &qquad{f_1}gp_2^2s - c{f_1}{p_1}{p_3} + c{f_1}{p_3}s + &qquad2{f_1}{f_2}p_3^2 + {f_1}{p_1}{p_2}{p_3} - {f_1}{p_2}{p_3}send{split}tag{B10}$$

$$begin{split}&{b_2} = 3c{f_1}f_2^2{g^2}{p_2} + 3{f_1}f_2^2{g^2}p_2^2 - 2{c^2}{f_1}{f_2}g{p_1} + &qquad{c^2}{f_1}gp_2^2 + 3c{f_1}f_2^2g{p_3} - 2c{f_1}{f_2}g{p_1}{p_2} - &qquad2c{f_1}{f_2}g{p_2}s + c{f_1}gp_2^3 + 3{f_1}f_2^2g{p_2}{p_3} - &qquad2{f_1}{f_2}gp_2^2s - f_2^2{g^2}p_2^2 + {c^2}{f_1}{p_2}{p_3} + c{f_1}p_2^2{p_3} + &qquadc{f_2}g{p_1}{p_2} - c{f_2}g{p_2}s - 2f_2^2g{p_2}{p_3} - {f_2}g{p_1}p_2^2 + &qquad{f_2}gp_2^2s - {c^2}{p_2}{p_3} + c{f_2}{p_1}{p_3} - c{f_2}{p_3}s + cp_1^2{p_2} - &qquad2c{p_1}{p_2}s - 2cp_2^2{p_3} + c{p_2}{s^2} - f_2^2p_3^2 - &qquad{f_2}{p_1}{p_2}{p_3} + {f_2}{p_2}{p_3}s - p_2^3{p_3}end{split}tag{B11} $$

$$begin{split}&{b_3} = - cf_2^3{g^2}{p_2} - f_2^3{g^2}p_2^2 + {c^2}f_2^2g{p_1} - &qquad{c^2}{f_2}gp_2^2 - cf_2^3g{p_3} + cf_2^2g{p_1}{p_2} + cf_2^2g{p_2}s - &qquadc{f_2}gp_2^3 - f_2^3g{p_2}{p_3} + f_2^2gp_2^2s + {c^3}{p_1}{p_2} - &qquad{c^2}{f_2}{p_2}{p_3} + {c^2}{p_1}p_2^2 + {c^2}p_2^2s - c{f_2}p_2^2{p_3} + cp_2^3send{split} tag{B12}$$

$$ begin{split} &{b_{22}} = - {c^2}{p_2}{p_3} + cp_1^2{p_2} - 2c{p_1}{p_2}s -&qquad 2cp_2^2{p_3} + c{p_2}{s^2} - p_2^3{p_3} end{split}tag{B13}$$

$$ {b_{33}} = {c^3}{p_1}{p_2} + {c^2}{p_1}p_2^2 + {c^2}p_2^2s + cp_2^3s tag{B14}$$