薛淼^*,2), 葛亚威^*, 张正娣^?, 毕勤胜^,**江苏大学土木工程与力学学院, 江苏镇江 212013
^?江苏大学理学院, 江苏镇江 212013

BURSTING OSCILLATIONS AS WELL AS THE CLASSIFICATION IN THE FIELD WITH CODIMENSION-3 FOLD-FOLD-HOPF BIFURCATION¹⁾

Xue Miao^*,2), Ge Yawei^*, Zhang Zhengdi^?, Bi Qinsheng^,**Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, Jiangsu, China
^?Faculty of Science, Jiangsu University, Zhenjiang 212013, Jiangsu, China

通讯作者: 2)毕勤胜, 教授, 主要研究方向: 非线性动力学. E-mail:qbi@ujs.edu.cn

收稿日期:2020-01-15接受日期:2021-03-16网络出版日期:2021-05-19

基金资助:

1)国家自然科学基金资助项目.116232008

Received:2020-01-15Accepted:2021-03-16Online:2021-05-19
作者简介 About authors


摘要
不同尺度耦合系统存在着广泛的工程背景, 通常表现为大幅振荡与微幅振荡交替出现的簇发振荡, 其产生机理一直是当前国内外研究的前沿课题之一. 传统的几何奇异摄动分析方法仅对时域上的两尺度耦合有效, 无法揭示频域上不同尺度之间的相互作用, 同时, 当前相关研究仅针对余维一fold或Hopf分岔展开. 本文针对频域两尺度耦合向量场存在余维三fold-fold-Hopf分岔时的复杂动力特性, 基于包含三阶非线性项以内的该分岔向量场的标准型及其普适开折, 给出相应的分岔集, 从而将双开折参数平面划分为对应于不同行为的子区域. 引入慢变周期激励项取代其中一个开折参数, 随慢变激励项的变化, 会存在两类轨迹访问子区域途径, 产生周期Hopf/LPC, Hopf/LPC/Hopf/LPC, fold/LPC/Hopf/Homoclinic和fold/LPC 4种簇发振荡类型. 在分析过程中, 发现系统轨迹上的真实分岔, 往往与理论上的分岔点之间存在着滞后效应, 这种滞后效应的滞后时间也会随着激励幅值的增大而延长, 因为激励幅值的增大, 会导致轨迹沿相应平衡态运动的惯性增大, 特别是, 当激励幅值增大到一定值后, 会导致轨迹沿某平衡态运动并穿越该区域, 也即相关分岔效应来不及出现, 从而导致振荡形式的改变. 本工作表明, 对于局部分岔下的快慢效应, 通过向量场标准型开折参数的周期扰动, 在一定程度可以对该分岔所导致的所有可能的各种簇发进行归类, 并得到其相应的产生机制.
关键词： 频域两尺度耦合;fold-fold-Hopf分岔;标准型及普适开折;簇发振荡;分岔机制

Abstract
The dynamical systems with the coupling of different scales observed widly in engineering problems often behave in the bursting oscilltions, characterized by the alternations between large-amplitude oscilltations and small-amplitude oscillations, the generation mechanism of which has been one of the hot topics in nonlinear science at home and abroad. The traditional geometric pertubation method can be employed to explore the mechanism of the oscillations only in the systems with two scales in time domain, which can not be directly used to investigate the interaction between different scales in frequency domain. Meanwhile, most of the results are obtained in the vector fields with codimension-1 fold or Hopf bifurcations. Here we focus on the complicated behaviors in the vector field with codimension-3 fold-folfd-Hopf bifurcation when two scales in frequency domain exist. Based on the normal form as well as its universal unfolding with the nonlinear terms up to the third order, all the possible bifurcations are derived, which divide the two unfolding parameter plane into several regions with different dynamics. By introducing a slow-varying periodic excitation instead of one of the unfolding parameters, two types of routes for the tarjectory visiting those regions can be observed, which may result in four classes of bursting oscillations, i.e., periodic Hopf/LPC, Hopf/LPC/Hopf/LPC, fold/LPC/Hopf/Homoclinic and fold/LPC bursting attractors with the variation of the exciting term. It is found that there may exist delay between the locations of the theoretical bifurcation points and the real bifurcation points on the trajectory. The delay may increase with the exciting amplitude, since the inertia of the movement along the equilibrium states may increase. Especiallty, when the exciting amplitude increases to an extent, the trajectory may pass acorss the corresponding regions before the related bifurcation occurs, which leads to the qualitative change of the oscillations. It is shown that, the slow-fast effect with local bifurcations can be investigated by using the periodic perturbation on the unfolding parameters in the normal form of the vector field, which can therefore to present all possible types of bursting patterns as well as the mechanism.
Keywords：coupling of two scales in frequency domain;fold-fold-Hopf bifurcation;normal form and universal unfolding;bursting oscillations;bifurcation mechanism


PDF (5368KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
薛淼, 葛亚威, 张正娣, 毕勤胜. 余维三fold-fold-Hopf分岔下簇发振荡及其分类¹⁾. 力学学报, 2021, 53(5): 1423-1438 DOI:10.6052/0459-1879-21-024
Xue Miao, Ge Yawei, Zhang Zhengdi, Bi Qinsheng. BURSTING OSCILLATIONS AS WELL AS THE CLASSIFICATION IN THE FIELD WITH CODIMENSION-3 FOLD-FOLD-HOPF BIFURCATION¹⁾. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(5): 1423-1438 DOI:10.6052/0459-1879-21-024

引言

不同尺度耦合具有广泛的工程背景, 涉及科学和工程技术的各个领域, 如机翼的颤振^[1]、 绳系卫星中的张弛运动^[2]、 催化反应中的复合模态振荡^[3]、 神经元随机簇放电行为^[4-8]、 忆阻器电路系统混沌振荡^[9-13], 不同尺度耦合的机械系统复杂的响应特性^[14-18]等. 多尺度的耦合往往使系统表现出大幅振荡和微幅振荡交替出现, 这种现象被称为簇发振荡. 不同尺度的耦合, 可以来自时间上的快慢^[19], 也可以来自空间上的大小^[20], 从而在所建立的相应数学模型中, 状态变量或者其某种形式的组合可以分为若干不同的组, 而各组之间随时间变化的速率存在着明显量级上的差异^[21].

不同时间尺度耦合的工作最早可以追溯到van der Pol电路方程中的张弛振动(relaxation oscillation)^[22] , 直到诺贝尔奖获得者Hodgkin和Huxley^[23]建立了两时间尺度神经元(HH)模型, 成功再现了实测中的神经元放电行为, 不同尺度耦合问题逐渐引起重视. 从那时起, 如何处理不同尺度耦合系统的复杂动力学行为一直是困扰****们的课题之一^[24]. 围绕这一问题, 国内外****开展了大量的工作. 由于缺乏有效的分析方法, 早期的相关工作大都是围绕着近似求解开展的, 如准静态法^[25]、 奇异摄动法^[26], 这些方法虽然能够近似描述系统的运动特性, 但是无法解释不同尺度之间的相互作用^[27]. 为此, 基于不变流形等概念, 以Fenichel等^[28]为代表, 建立了几何奇异摄动理论, 其核心思想是将系统分解为两个耦合的快慢子系统, 通过快子系统的主导和慢子系统的调谐在几何结构上的交替, 揭示其复杂运动的产生本质^[29], 但该方法仅能对相关的簇发振荡产生机制给出大致的结果. 随后, 以Rinzel^[30]为代表的****发展了这一理论, 提出了快慢分析法, 利用该方法, 可以将簇发振荡按照两种方式分类, 一是按照其几何结构的分类, 如点$\!-\!$点簇发^[31]、点$\!-\!$环簇发^[32], 二是根据快慢转换的分岔模式分类, 如fold/fold^[33], fold/Hopf和Hopf/LPC^[34]型簇发振荡.

近年来, 基于分岔的分析方法, 成为研究不同耦合系统中的簇发振荡的主要手段, 如Razvan和 Yasaman^[35]探讨了两神经元之间耦合强度对于簇发结构的影响规律, Vo等^[36]分析了反应扩散方程中的多模态吸引子的产生机理, Baldemir等^[37]给出了三维神经元模型中的伪平衡态在沉寂态和激发态转换时的作用, 其他还有电路系统中的簇发振荡等.

需要指出的是, Rinzel^[30]的快慢分析法仅对自治系统也即时域上的两尺度耦合系统有效, 同时, 由于高维和高余维系统的复杂性, 相关工作大都局限在低维耦合系统存在余维一分岔情形, Izhikevich^[38]给出了两快一慢耦合系统可能产生的各种簇发振荡及其机制. 而对于非自治系统, 如周期激励系统, 当激励频率远小于系统的固有频率, 也即存在频域两尺度耦合时, 系统也可能会产生簇发振荡^[39]. 为揭示这类系统的簇发振荡产生机制, 参考几何奇异摄动理论, 提出了频域两尺度快慢分析方法^[40], 并据此得到了诸如周期外激励和周期参数激励下的各种簇发振荡模式及其产生机理^[41-43].

迄今为止, 大部分结果都是针对具体系统存在余维一分岔时得到的, 缺乏系统性. 人们不禁要问, 在不同分岔模式下, 到底存在着哪几种簇发振荡形式, 其产生机制又是什么. 为此, 本文从一类余维三fold-fold-Hopf分岔标准型出发, 以慢变周期激励取得某一开折参数, 分析该慢变激励值访问不同持久集时存在的各种簇发振荡行为及其机制. 需要指出的是, 在此仅考虑一开折参数, 当对3个不同开折参数加以分析, 则可以得到开折参数空间中所有持久集中的行为对簇发振荡结构的影响, 从而可以揭示该分岔点邻域内可能存在的所有簇发振荡模式.

1 频域两尺度快慢分析方法

对于自治快慢耦合系统

(1)$\begin{eqnarray} \label{eq1} \left. \begin{array}{ll} {\rm d}x/{\rm d}t=f\left( {x,y,\mu } \right),& \text{fast subsystem}\\ {\rm d}y/{\rm d}t=\varepsilon g\left( {x,y,\mu } \right),& \text{slow subsystem} \end{array} \right\} \end{eqnarray}$
式中, $x\in R^{M}$, $y\in R^{N}$, $\mu \in R^{K}$, $0<\varepsilon \ll 1$. 传统的快慢分析法, 也即奇异几何摄动分析方法, 是将慢状态变量$y$视为分岔参数, 从而由隐函数定理可得到快子系统随慢变量变化的平衡曲线, 记为$x=\varphi \left( {y,\mu } \right)$, 以及其分岔集, 记为$B\left( {x,y,\mu } \right)=0$. 快子系统的平衡曲线及其吸引子决定耦合系统的主要行为, 包含沉寂态(quiescent state, QS)和激发态(spiking state, SP), 以及沉寂态和激发态之间的分岔连接, 而慢子系统则决定其相应的局部调谐行为^[44]. 通过耦合系统真实轨迹和平衡曲线及其分岔的叠加, 得到其相应的分岔机制^[45]. 而对于非自治系统, 如周期激励系统

(2)$\begin{eqnarray} \label{eq2} {\rm d}x/{\rm d}t=f\left[ {x,\mu ,A\sin \left( {\varOmega t} \right)} \right] \end{eqnarray}$
其中$x\in R^{M}$, $\mu \in R^{K}$, 当周期激励频率远小于系统的固有频率$\omega _{N} $, $\varOmega \ll \omega_{N} $, 也即存在频域上的两尺度耦合时, 同样会产生快慢效应^[46]. 由于不存在明显的快慢子系统, 传统的分析方法不再适用. 为此提出了两种方法, 一是直接法^[47], 引入慢变参数$\theta =\varOmega t$, 也即用代数方程取代微分方程构成慢子系统, 从而得到快子系统为

(3)$\begin{eqnarray} \label{eq3} {\rm d}x/{\rm d}t=f\left[ {x,\mu ,A\sin \left( \theta \right)} \right] \end{eqnarray}$
称为广义自治系统. 另一为间接法^[48], 引入慢变参数$w=A\sin (\varOmega t)$,

构成慢子系统, 从而有广义自治系统

(4)$\begin{eqnarray} \label{eq4} {\rm d}x/{\rm d}t=f\left( {x,\mu ,w} \right) \end{eqnarray}$
构成快子系统. 在具体应用过程中, 直接法需要引入一系列放大图,

而间接法则相对简便一些, 因此, 本文采用间接法. 由广义自治系统可以得到随$w$

变化的平衡曲线及其分岔集, 分别记为

(5)$\begin{eqnarray} \label{eq5} \left. {\begin{array}{ll} f\left( {x,\mu ,w} \right)=0,& \text{equilibrium curve}\\ B\left( {x,\mu ,w} \right)=0,& \text{bifurcation set}\\ \end{array}} \right\} \end{eqnarray}$
为揭示平衡曲线及其分岔集对系统轨迹的影响机制, 引入真实轨迹的转换相图概念^[49], 定义为

(6)$\begin{eqnarray} \label{eq6} \Pi_{G} \equiv \left\{ {\left. {\left( {x,w} \right)} \right|t\in R} \right\}=\left\{ {\left. {\left[ {x,A\sin \left( {\varOmega t} \right)} \right]} \right|t\in R} \right\} \end{eqnarray}$
也即将慢变量$w$视为广义状态变量. 通过平衡曲线及其分岔集和耦合系统轨迹的转换相图的叠加, 揭示各种快慢效应的产生机制.

2 余维三fold-fold-Hopf分岔

分岔的余维数由其算子的补空间的维数决定, 根据向量场标准型理论, Yu等^[50]推导了平衡点Jacobi矩阵存在双零及一对纯虚根特征值时相应分岔的标准型及其普适开折, 其三阶截断的一般形式可以表示为

(7)$\begin{eqnarray} \label{eq7} \left. {\begin{array}{l} {\rm d}x/{\rm d}t=y \\ {\rm d}y/{\rm d}t=\mu_{1} +\mu_{2} x+a_{1} x^{2}+a_{2} xy+ a_{3} x^{3}+\\\qquad a_{4} x^{2}y+a_{5} \left( {u^{2}+v^{2}} \right)+a_{6} x\left( {u^{2}+v^{2}} \right) \\ {\rm d}u/{\rm d}t=\mu_{3} u-\omega v+\left( {c_{1} u+c_{2} v} \right)x+\\\qquad \left( {b_{1} u+b_{2} v} \right)\left( {u^{2}+v^{2}} \right) \\ {\rm d}v/{\rm d}t=\omega u+\mu_{3} v+\left( {c_{1} v-c_{2} u} \right)x+\\\qquad \left( {b_{1} v-b_{2} u} \right)\left( {u^{2}+v^{2}} \right) \\ \end{array}} \right\} \end{eqnarray}$
其中$\mu_{i} \in R$, $i=1,2,3$为普适开折参数. 当所有非线性项不存在退化情形时, 该分岔则可以称为余维三fold-fold-Hopf分岔.

对于双零特征值的Bogdanov-Takens(BT)分岔, 双开折参数平面可以划分为4个不同的区域, 而对于一对纯虚根的Hopf分岔, 单开折参数可以分为两个区间, 不同区域或区间分别对应于不同的动力学行为. 而对于含三开折参数的余维三fold-fold-Hopf分岔而言, 在三开折参数空间上系统的动力学特性要复杂许多^[51]. 从系统(7)中可以看到, 其平衡点$E\left( {x_{0} ,y_{0} ,u_{0} ,v_{0} } \right)$满足

(8)$\begin{eqnarray} \label{eq8} \left. {\begin{array}{l} y_{0} =0 \\ \mu_{1} +\mu_{2} x_{0} +a_{1} x_{0}^{2}+a_{3} x_{0}^{3}+ a_{5} \left( {u_{0}^{2}+v_{0}^{2}} \right)+\\\qquad a_{6} x_{0} \left( {u_{0}^{2}+v_{0}^{2}} \right)=0 \\ \mu_{3} u_{0} -\omega v_{0} +\left( {c_{1} u_{0} +c_{2} v_{0} } \right)x_{0} +\\\qquad \left( {b_{1} u_{0} +b_{2} v_{0} } \right)\left( {u_{0} ^{2}+v_{0}^{2}} \right)=0 \\ \omega u_{0} +\mu_{3} v_{0} +\left( {c_{1} v_{0} -c_{2} u_{0} } \right)x_{0} +\\\qquad \left( {b_{1} v_{0} -b_{2} u_{0} } \right)\left( {u_{0} ^{2}+v_{0}^{2}} \right)=0 \\ \end{array}} \right\} \end{eqnarray}$
从而可得

(9)$\begin{eqnarray} \label{eq9} \left. {\begin{array}{l} \mu_{1} +\mu_{2} x_{0} +a_{1} x_{0}^{2}+a_{3} x_{0}^{3}+ a_{5} \rho_{0} ^{2}+a_{6} x_{0} \rho_{0}^{2}=0 \\ b_{1} \rho_{0}^{2}+\left( {c_{1} x_{0} +\mu_{3} } \right)=0 \\ \end{array}} \right\} \end{eqnarray}$
其中$\rho^{2}=u_{0}^{2} +v_{0}^{2} $. 其相应的特征方程为

(10)$\begin{eqnarray} \label{eq10} (\lambda^{2}+D_{1} \lambda +D_{0} )(\lambda^{2}+G_{1} \lambda +G_{0} )=0 \end{eqnarray}$
其中

(11)$\begin{eqnarray} \label{eq11} \left. {\begin{array}{l} D_{1} =-\left( {a_{2} +a_{4} x_{0} } \right)x_{0} \\ D_{0} =-\left( {\mu_{2} +2a_{1} x_{0} +3a_{3} x_{0}^{2}} \right) \\ G_{1} =-\left( {2\mu_{3} +2c_{1} x_{0} +4b_{1} \rho_{0}^{2}} \right) \\ G_{0} =\Big( \mu_{3}^{2}+\omega^{2}+2c_{1} \mu_{3} x_{0} -2c_{2} \omega x_{0} +\\\qquad c_{1}^{2}x_{0}^{2}+c_{2}^{3}x_{0}^{2}\Big) + \Big[ 4b_{1} \left( {\mu_{3} +c_{1} x_{0} } \right)+\\\qquad 4b_{2} \left( {c_{2} x_{0} -\omega } \right)+ 3b_{1}^{2}\rho _{0}^{2}+3b_{2}^{2}\rho_{0}^{2} \Big]\rho_{0}^{2} \\ \end{array}}\ \ \right\} \end{eqnarray}$
当$D_{0,1} >0$, $G_{0,1} >0$时, 平衡点$E(x_{0} ,y_{0} ,u_{0} ,v_{0} )$稳定.

平衡点可能会通过4种余维一分岔发生失稳. 在分岔集

$\begin{eqnarray*} &&FB_{1} : D_{0} =0\ \ \left( {D_{1} >0,G_{0,1} >0} \right) \\&& FB_{2} : G_{0} =0\ \ \left( {G_{1} >0,D_{0,1} >0} \right) \end{eqnarray*}$

上, 平衡点可能会产生fold分岔, 导致不同平衡点之间的跳跃, 而在分岔集

$\begin{eqnarray*} &&HB_{1} : \quad D_{1} =0\ \ \left( {D_{0} >0,G_{0,1} >0} \right) \\&& HB_{2} : \quad G_{1} =0\ \ \left( {G_{0} >0,D_{0,1} >0} \right) \end{eqnarray*}$

上, 则可能产生超临界Hopf分岔, 导致周期振荡, 其振荡频率分别约为$\omega_{1} =\sqrt {D_{0} } $和$\omega_{2} =\sqrt {G_{0} } $. 而当参数位于两余维一分岔集的相切点上, 则可能产生诸如fold-fold, fold-Hopf, Hopf-Hopf分岔, 同样, 也会存在着更高阶的退化, 导致余维三分岔甚至余维四分岔. 取定参数

(12)$\left.\begin{array}{l}\mu_{3}=0.1, \omega=1.0, a_{1}=1.0, a_{2}=2.0 \\a_{3}=-1.0, \quad a_{4}=-1.0, a_{5}=1.0, a_{6}=-1.0 \\b_{1}=-1.0, \quad b_{2}=-2.0, c_{1}=1.0, \quad c_{2}=2.0\end{array}\right\}$
图1给出了广义自治系统在$(\mu_{1} ,\mu_{2} )$参数平衡上的分岔集.

图1

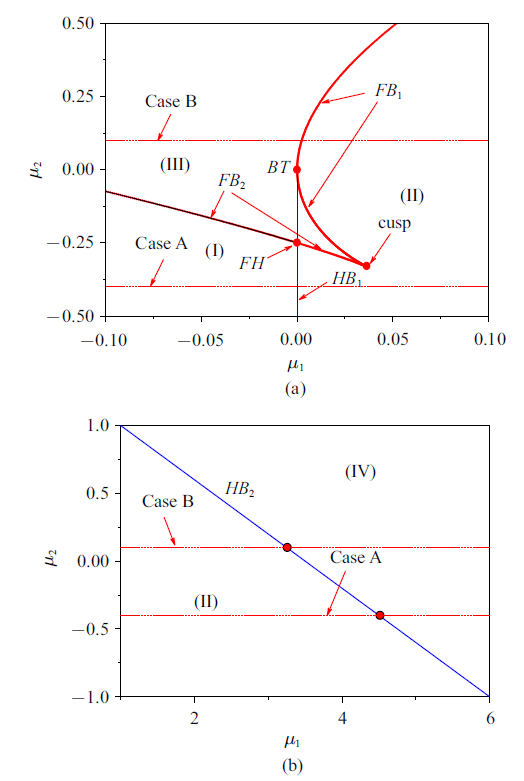
新窗口打开|下载原图ZIP|生成PPT
图1广义自治系统在$(\mu_{1} ,\mu_{2} )$参数平面上的分岔集

Fig.1Bifurcation sets of the generalized autonomous system on the $(\mu_{1} ,\mu_{2} )$ plane



分岔集将参数平面划分为3个区域, 对应于不同的动力学行为. 在区域(I)中系统在$(x,y)$平面上表现为稳定的平衡点, 且在稳定的平衡点局部存在不稳定的极限环, 而在$(u,v)$平面上表现为稳定的极限环. 当参数穿越分岔集$HB_{1} $进入区域(II)时, 稳定的平衡点发生了亚临界Hopf分岔失稳, 且同时不稳定的极限环消失, 系统在$(x,y)$平面上表现为稳定的极限环, 而在$(u,v)$平面上表现为概周期振荡, 也即2-D环面. 当参数穿越分岔集$FB_{1} $进入区域(III)时, 系统表现出两个稳定的平衡点和一个不稳定的平衡点共存. 而当参数从区域(II)穿越分岔集$HB_{2} $进入区域(IV)时, 系统在$(x,y)$平面上表现为稳定的平衡点, 而在$(u,v)$平面上表现为稳定的极限环.

需要指出的是, 在$FB_{1,2} $上, 会产生fold分岔, 导致轨迹趋向$(x,y)$平面上的不同的稳定平衡点, 引起轨迹在不同平衡点之间的跳跃. 另外, 在fold分岔和Hopf分岔曲线的相切点处, 会产生余维二Bogdanov-Takens分岔.

为揭示这些不同区域中的行为对不同尺度耦合系统动力特性的影响, 不失一般性, 让开折参数$\mu_{1} $随时间作缓慢周期变化, 令$\mu_{1} =A\sin \left( {\varOmega t} \right)$, 其中$A$和$\varOmega $分别对应于激励的振幅和频率, 其中令$\varOmega $远小于系统的固有频率. 显然, 此时系统存在着频域上的两尺度耦合.

显然, $\mu_{1} \in [-A,A]$. 随着激励幅值$A$的逐渐增大, 系统轨迹访问$(\mu _{1} ,\mu_{2} )$平面上不同区域的行为仅存在两种可能, 也即

情形一: (I) $\to$ (II) $\to$ (IV);

情形二: (III) $\to$ (II) $\to$ (IV).

因此, 上述两种情形下的簇发振荡即为该分岔向量场标准型截断到三次非线性项时可能的簇发振荡模式.

当然, 也可以取开折参数$\mu_{2} $随时间作缓慢周期变化, 随$A$的变化, 轨迹访问的区域也会发生变化. 在此仅考虑$\mu_{1} $作周期变化.

由频域两尺度分析法, 将$\mu_{1} =A\sin (\varOmega t)$视为慢变参数, 构成慢子系统. 而基于上述分岔分析, 可以得到相应广义自治系统随慢变量变化的平衡曲线和分岔行为.

分别考虑当$\mu_{2} =-0.4$ (情形一)和$\mu_{2} =0.1$ (情形二)两种典型情形下的尺度效应. 图2分别给出了其相应广义自治系统随慢变量$\mu_{1} =A\sin (\varOmega t)$变化的分岔图.

图2

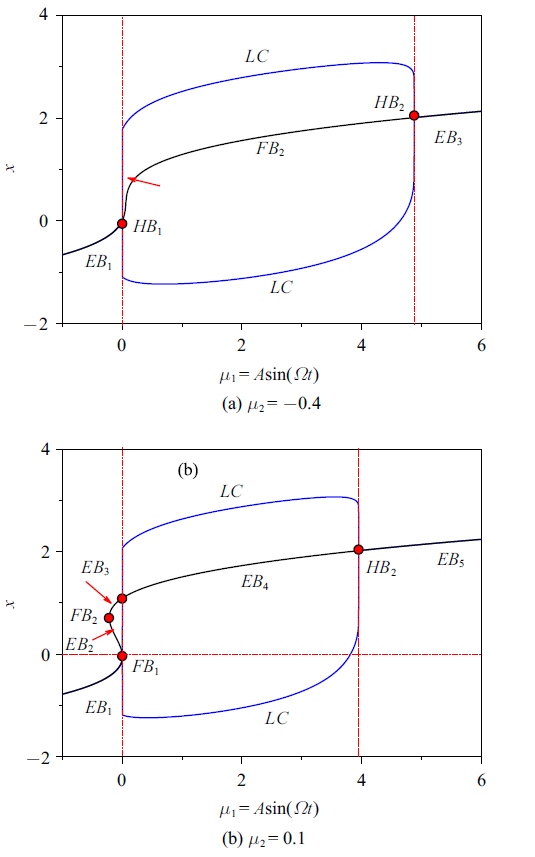
新窗口打开|下载原图ZIP|生成PPT
图2随$\mu_{1} $变化的分岔图

Fig.2Bifurcation diagram with the variation of $\mu_{1} $



从图2可以看出, 两种情形下的分岔图几乎接近, 但其中依然存在着细微的区别. 当$\mu_{2} =-0.4$时, 随着慢变参数$\mu_{1} $的增大, 状态变量$x$沿稳定平衡曲线$EB_{1} $运动, 而在$\mu_{1} \mbox{=0}$附近处, 也即$HB_{1} $点, 穿越亚临界Hopf分岔系统进入周期振荡, 并在$HB_{2} $点分岔值附近, 稳定的极限环消失而稳定于平衡曲线$EB_{3} $. 在平衡曲线上不存在fold分岔(见图2(a)). 需要指出的是, 由本文后续的分析, 稳定极限环$LC$分别在两个亚临界Hopf分岔$HB_{1} $和$HB_{2} $的分岔值附近消失的原因都是由LPC分岔导致稳定的极限环和不稳定的极限环发生碰撞消失.

当$\mu_{2}=0.1$时, 平衡曲线上存在着两fold分岔点$FB_{1,2}$ (见图2(b)), 当慢变参数$\mu_{1} $增大到$\mu_{1}=0$时, 产生fold分岔, 导致周期振荡, 在$HB_{2} $点分岔值附近, 发生LPC分岔导致稳定的极限环和不稳定的极限环碰撞消失而稳定于平衡曲线$EB_{5} $. 需要指出的是, 由本文后续的分析, 稳定的极限环$LC$在fold分岔值附近消失的原因是发生了鞍点同宿分岔.

进一步从$(\mu_{1} ,\mu_{2} )$参数平面上的分岔集看, 当$\mu_{2} =-0.4$时, 慢变参数$\mu_{1} $在$-A$和$+A$之间作周期变化, 系统轨迹可能会进入图1中的区域(I), (II)和(IV), 而$\mu_{2} =0.1$时, 系统轨迹可能会进入图1中的区域(III), (II)和(IV), 从而导致尺度效应的不同.

3 簇发振荡演化及其分岔机制

为分析图1所示分岔集划分的不同区域中的动力学行为对系统尺度效应的影响, 在此分别考虑上述两种情形下随激励幅值增大时系统的动力学行为演化过程.

3.1 情形一: $\mu_{2} =-0.4$

当$\mu_{2} =-0.4$且$A$较小时, 随着慢变参数$\mu_{1} $的变化, 轨迹将周期访问图1中的区域(I)和(II), 使得系统的动力学行为受到两区域中广义自治系统的特性的影响. 图3给出了$A=0.10$时两尺度耦合系统在不同平面上的相图及其相应的时间历程.

图3

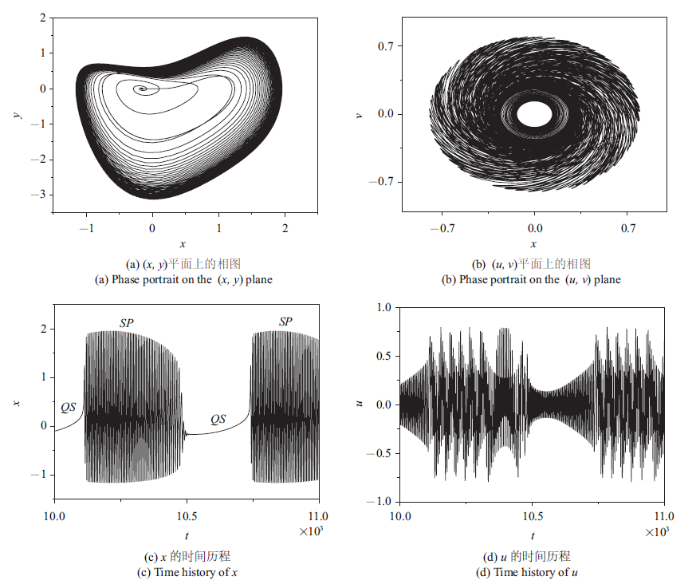
新窗口打开|下载原图ZIP|生成PPT
图3$A=0.10$时的簇发振荡

Fig.3Bursting oscillations for $A=0.10$



从图3可以看出, 系统表现为周期簇发振荡, 每一周期振荡的轨迹可以分为两部分, 分别对应于沉寂态和激发态(见图3(b)). 为分析激发态本质特性, 定义

$\begin{eqnarray*} P=P\{\left. {(x,y,u,v)} \right|t=t_{0} +2N\pi /\varOmega ,N=1,2,\cdots \} \end{eqnarray*}$

图4给出了轨迹在$(u,v)$平面上的Poincaré映射. 从图4中可以发现, 激发态表现为概周期振荡, 进一步的数值计算表明, 其相应的两振荡频率分别近似于区域(I)中$(u,v)$平面上稳定极限环的频率和区域(II)中$\mu _{1} =0.0$附近$(x,y)$平面上稳定的极限环相应频率.

图4

新窗口打开|下载原图ZIP|生成PPT
图4$(u,v)$平面上的Poincaré映射

Fig.4Poincaré map on the $(u,v)$ plane



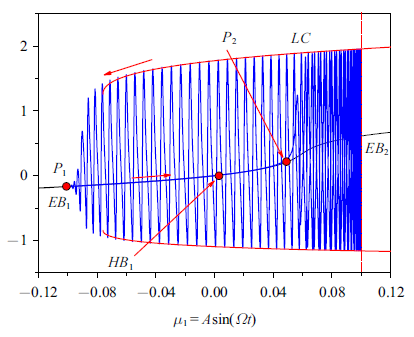
为揭示簇发振荡的产生机制, 图5给出了$(\mu_{1},x)$平面上转换相图和平衡曲线的叠加图. 假设轨迹从$P_{1} $点出发, 对应于$\mu _{1} $取最小值$-0.10$, 轨迹几乎严格沿着稳定平衡曲线$EB_{1}$运动, 表现为沉寂态. 当轨迹运动到亚临界Hopf分岔点$HB_{1}$时, 由于存在慢变过程的影响, 轨迹将穿越该分岔点, 直到$P_{2} $点, 亚临界Hopf分岔的效应才会产生, 使得轨迹快速跳向相应的稳定极限环$LC$, 进入激发态. 需要指出的是在亚临界Hopf分岔点附近, 稳定的平衡点与不稳定的极限环共存, 且不稳定的极限环在亚临界Hopf分岔点$HB_{1}$处消失.

图5

新窗口打开|下载原图ZIP|生成PPT
图5$A=0.1$时转换相图和平衡曲线$(\mu_{1} ,x)$平面上的叠加图

Fig.5Overlap of the transformed phase portrait and equilibrium branches on the $(\mu_{1} ,x)$ plane for $A=0.1$



轨迹很快几乎严格按照稳定极限环振荡. 当慢变参数$\mu_{1} $增大到最大值$0.10$时, 轨迹转向. 极限环的LPC分岔导致稳定的极限环和不稳定的极限环碰撞消失使得轨迹振荡幅值逐渐减小, 最终趋于稳定平衡曲线$EB_{1} $.

当轨迹回到$P_{1} $点时, 完成一个周期的簇发振荡. 从分岔机制上, 该振荡可以称为周期Hopf/LPC簇发, 从几何结构上, 则可以称为周期2-D torus-point簇发.

随着激励幅值的增大, 其转换相图将向左右两边扩展, 而其簇发振荡的模式保持不变. 当激励幅值增加到$A=4.881\,0$时, 在$HB_{2} $点也会产生Hopf分岔, 导致簇发振荡吸引子的定性改变(见图2(a)). 图6给出了$A=8.0$时的簇发振荡吸引子.

图6

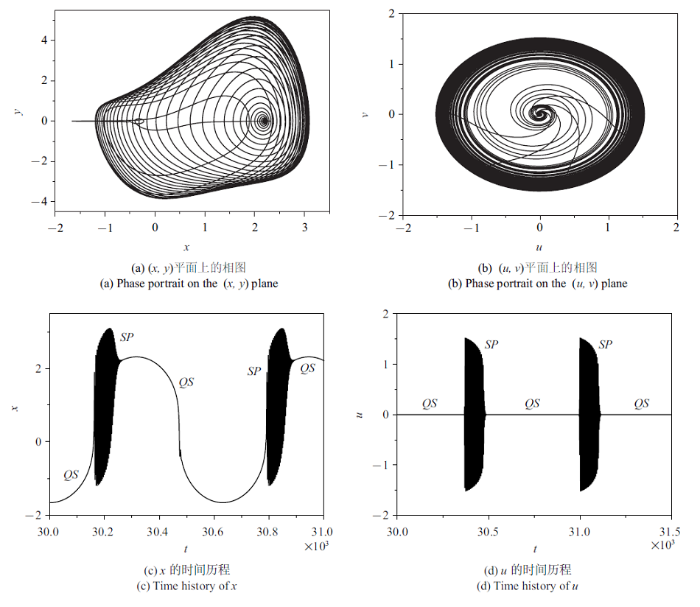
新窗口打开|下载原图ZIP|生成PPT
图6$A=8.0$时的簇发振荡

Fig.6Bursting oscillations for $A=8.0$



从图6可以看出, 系统轨迹同样由Hopf分岔导致在沉寂态和激发态之间转换, 而激发态依然表现为概周期振荡模式(见图7).

图7

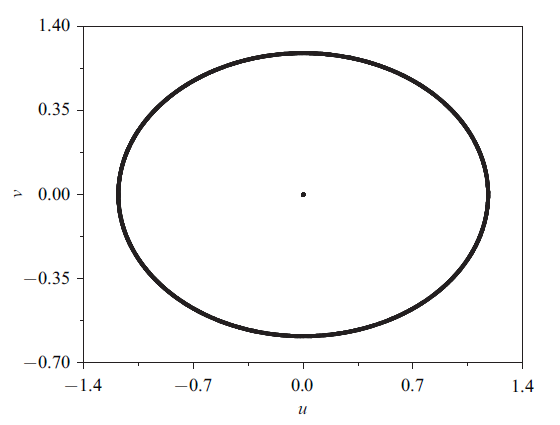新窗口打开|下载原图ZIP|生成PPT
图7$(u,v)$平面上的Poincaré映射

Fig.7Poincaré map on the $(u,v)$ plane



进一步分析可以发现, 在外激励幅值较小时, 沉寂态和激发态之间的转换均由$\mu _{1}=0.0$处亚临界Hopf分岔及其附近的LPC分岔引起, 而当激励幅值较大时, 相应转换由$HB_{1} $和$HB_{2} $两点的亚临界Hopf分岔及其附近的两个LPC分岔引起, 这也可以从其转换相图和平衡曲线的叠加图中得到证实(见图8).

图8

新窗口打开|下载原图ZIP|生成PPT
图8$A=8.0$时转换相图和平衡曲线$(\mu_{1} ,x)$平面上的叠加图

Fig.8Overlap of the transformed phase portrait and equilibrium branches on the $(\mu_{1} ,x)$ plane for $A=8.0$



从$P_{1} $点出发的轨迹几乎严格沿$EB_{1} $运动, 表现为沉寂态. 亚临界Hopf分岔导致轨迹进入激发态, 而LPC分岔则使得轨迹回到沉寂态, 使得轨迹几乎严格地沿稳定平衡曲线$EB_{3} $运动.

簇发振荡的轨迹大致可以分为3部分, 也即分别沿$EB_{1}$和$EB_{3}$的运动和按照稳定的极限环$LC$的振荡, 而由Hopf分岔和LPC分岔相互转换, 因此, 从分岔机制上, 这种振荡可以称为周期Hopf/LPC/ Hopf/LPC簇发振荡, 而从几何结构上则可以称为周期point-torus-point簇发.

由于广义自治系统在区域(I)中为稳定的平衡点, 在(II)中为2-D环面运动, 而在区域(IV)中则又为稳定的平衡点, 当激励幅值较小时, 轨迹会连接区域(I)和(II)中的行为, 而当激励幅值较大时, 轨迹则会表现出3个区域中的不同特性, 从而导致不同的簇发振荡模式, 因此, 当轨迹访问的区域越多, 簇发振荡模式可能会越复杂, 因为其受到更多区域中广义自治系统行为的影响.

3.2 情形二: $\mu_{2} =0.1$

增大参数$\mu_{2} $到$0.1$, 随着外激励幅值的变化, 系统轨迹将可能访问区域(III)、(II)和(IV), 从而导致簇发振荡模式发生定性改变. 图9给出了$A=0.10$时系统的动力学行为.

图9

新窗口打开|下载原图ZIP|生成PPT
图9$A=0.1$时的簇发振荡

Fig.9Bursting oscillations for $A=0.1$



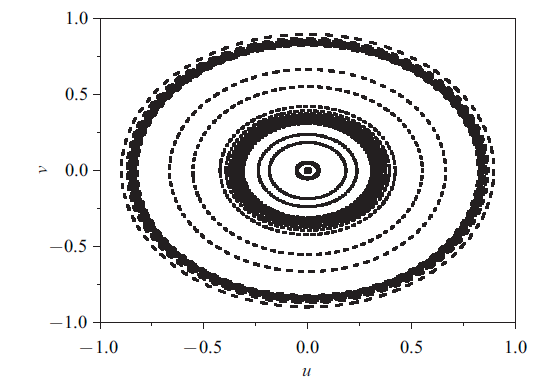
簇发振荡的轨迹大致可以分为两个部分, 分别对应沉寂态和激发态. 定义截面$\varSigma \equiv \{\left. {(x,y,u,v)} \right|x=1.0,\forall t\in R\}$, 图10给出了激发态在截面上的映射, 可以看出激发态表现为概周期振荡模式. 进一步的数值分析可以发现, 两激发态的振荡频率分别近似对应于$(x,y)$平面上由稳定的极限环的频率和$(u,v)$平面上极限环的振荡频率.

图10

新窗口打开|下载原图ZIP|生成PPT
图10$(u,v)$平面上的poincaré映射

Fig.10Poincaré map on the plane $(u,v)$



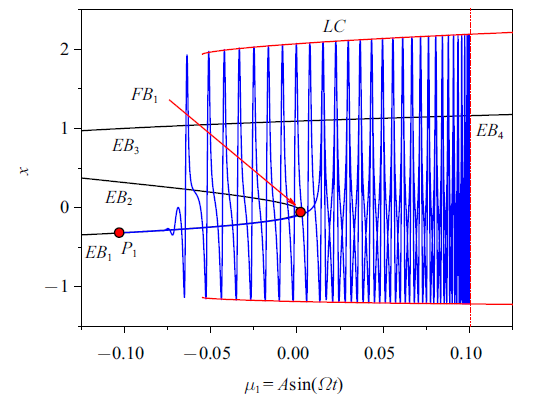
同样, 图11给出了$(\mu_{1} ,x)$平面上的转换相图与平衡曲线的叠加图. 从$P_{1} $点出发的轨迹几乎严格沿稳定平衡曲线$EB_{1} $运动, 表现为沉寂态, 当轨迹运动到分岔点时, 产生Fold分岔, 平衡点失稳导致轨迹跳向稳定极限环$LC$, 产生大幅振荡, 表现为激发态.

图11

新窗口打开|下载原图ZIP|生成PPT
图11$A=0.1$, $\mu_{2} =0.1$时转换相图和平衡曲线在$(\mu_{1},x)$平面上的叠加图

Fig.11Overlap of the transformed phase portrait and equilibrium branches on $(\mu_{1} ,x)$ plane for$A=0.1$, $\mu_{2}=0.1$



轨线几乎严格按照稳定的极限环$LC$振荡, 直到慢变参数$\mu_{1} $达到其最大值$0.10$. 轨迹转而向左, 按照极限环$LC$振荡, 并最终由鞍点同宿分岔导致稳定的极限环$LC$破坏消失, 跳向稳定平衡曲线$EB_{1} $.

类似地, 由分岔机制, 该振荡可以称为周期fold/ Homoclinic簇发振荡.

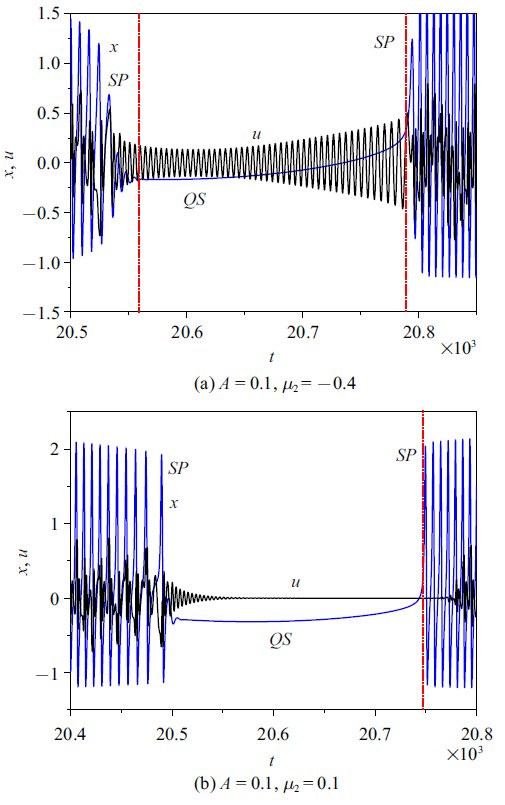
比较$A=0.1$, 而$\mu_{2} $分别取$\mu_{2} =-0.4$和$\mu _{2}=0.1$时的两种簇发振荡, 虽然两吸引子相似, 但本质上是不同的. 在$\mu_{2} =-0.4$时, 随着慢变参数$\mu _{1} $的周期变化, 簇发振荡(见图3)的轨迹访问图1中的区域(I)和区域(II), 当$(\mu_{1} ,\mu_{2} )$位于区域(I)时, 由于此时广义自治系统表现为$(x,y)$平面上的平衡点和$(u,v)$平面上的极限环, 此时轨迹在$(x,y)$平面上将沿稳定平衡曲线$EB_{1} $运动, 而在$(u,v)$平面上则按照相应的极限环振荡, 这也可以从图12中$x$和$u$的时间历程得到证实. 随着$\mu_{1} $的变化在平衡曲线$EB_{1} $产生Hopf分岔, 导致激发态和沉寂态之间的转换. 激发态表现为概周期振荡是因为系统在$(x,y)$平面上表现出稳定的极限环和$(u,v)$平面上的极限环的相互作用, 对应于区域(II)中的2-D环面运动.

图12

新窗口打开|下载原图ZIP|生成PPT
图12$x$和$u$的时间历程

Fig.12Time history of $x$ and $u$



在$\mu_{2} =0.1$时, 随着慢变参数$\mu_{1} $的周期变化, 簇发振荡(见图3)的轨迹访问图1中的区域(III)和区域(II), 当$(\mu_{1} ,\mu_{2} )$位于区域(III)时, 由于此时广义自治系统表现为$(x,y)$和$(u,v)$两子平面上均趋于稳定的平衡点, 此时轨迹在两子平面上均沿稳定平衡曲线运动, 而当$(\mu_{1} ,\mu_{2} )$位于区域(II)时, 轨迹则趋于该域内的稳定环面解, 表现为概周期振荡模式.

在$\mu_{1} =0.0$附近的fold分岔导致从区域(III)到区域(II)中的二维环面振荡, 使得轨迹在沉寂态(平衡点)和激发态(二维环面)之间转换, 这也可以从图12(b)中$x$和$u$的时间历程得到证实.

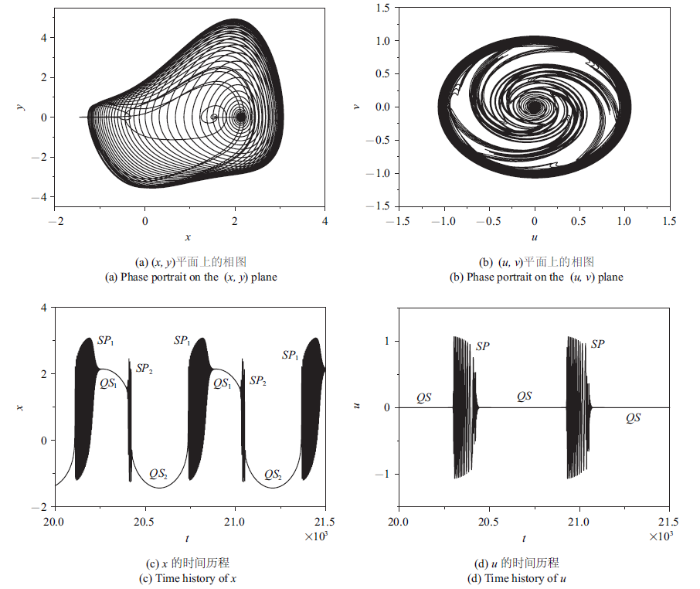
随着外激励幅值的增大, $\mu_{1} $的变化范围也会增大, 一旦穿越图1中的分岔集$HB_{2} $时, 簇发振荡模式会发生定性改变. 图13给出了$A=5.0$时系统的振动特性.

图13

新窗口打开|下载原图ZIP|生成PPT
图13$A=5.0$时的簇发振荡

Fig.13Bursting oscillations for $A=5.0$



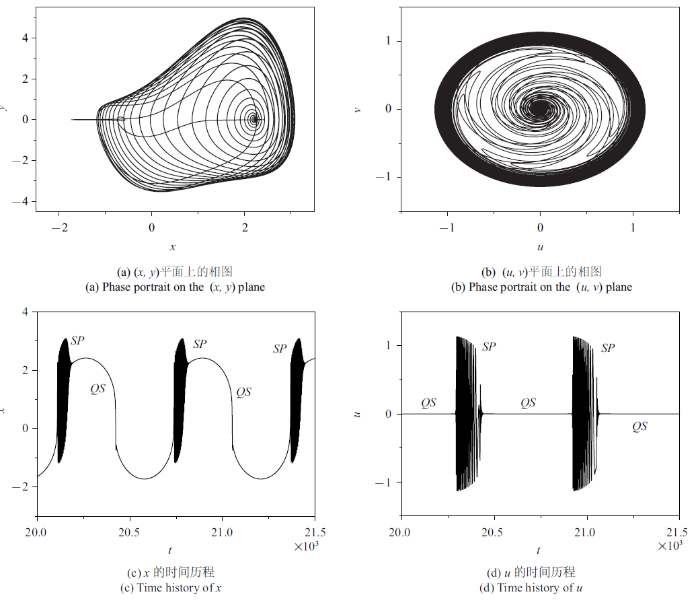
随着$A$的继续增大, 系统的轨迹访问的区域不再发生变化, 而其运动模式却会发生改变. 图14给出了$A=8.0$时的簇发振荡.

图14

新窗口打开|下载原图ZIP|生成PPT
图14$A=8.0$时的簇发振荡

Fig.14Bursting oscillations for $A=8.0$



从图13可以看出, 其簇发振荡分别会出现两种形式的沉寂态和激发态, 记为$QS_{1,2} $和$SP_{1,2} $(见图13(c)). 而随着激励幅值的增大, 激发态$SP_{2} $消失, 如$A=8.0$(见图14(c)).

由于轨迹在图1中的区域(III),(II)和(IV)来回运动, 因此, 三区域中广义自治系统的行为将影响簇发振荡的特性. 不难想象, 在$(x,y)$子平面上, 在(III)和(IV)中, 轨迹趋向其中相应的平衡曲线, 而在(II)中, 轨迹将趋向其中的二维环面解; 在$(u,v)$子平面上, 在(III)中, 轨迹将趋向其中稳定平衡曲线, 在(II)中, 轨迹将趋向其中在$(u,v)$的二维环面解, 而在(IV)中, 轨迹将趋向其中在$(u,v)$子平面上的稳定极限环.

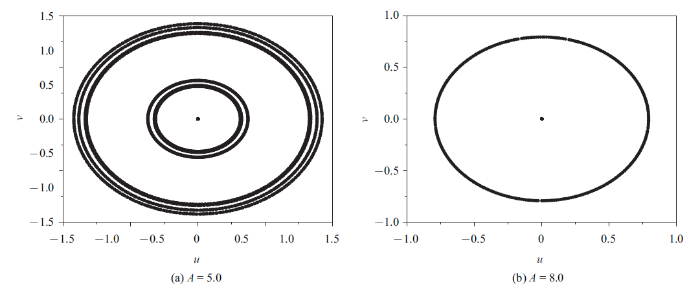
为分析激发态的振动特性, 同样引入截面$\varSigma \equiv \{\left. {(x,y,u,v)} \right|x=1.0,\forall t\in R\}$, 图15给出了$A=5.0$ 和$A=8.0$时Poincaré映射在$(u,v)$平面上的投影, 两种情形下Poincaré映射的投影点均分布于固定圆上, 说明簇发振荡的激发态均表现为概周期特性, 但两种激发态的具体振动特性存在着一定的差别.

图15

新窗口打开|下载原图ZIP|生成PPT
图15$(u,v)$平面上的Poincaré映射

Fig.15Poincaré map on the $(u,v)$ plane



为分析这些差别的产生原因, 转向其转换相图与平衡曲线的叠加图, 见图16.

图16

新窗口打开|下载原图ZIP|生成PPT
图16(a) $A=5.0,\mu_{2} =0.1$时转换相图和平衡曲线$(\mu_{1},x)$平面上的叠加图; (b) (a)图的局部放大图; (c) $A=8.0$, $\mu_{2}=0.1$时转换相图和平衡曲线$(\mu_{1} ,x)$平面上的叠加图; (d) (c)图的局部放大图

Fig.16(a) Overlap of the transformed phase portrait and equilibrium branches on the $(\mu_{1} ,x)$ plane for $A=5.0,\mu_{2} =0.1$; (b) locally enlarged parts in (a); (c) overlap of the transformed phase portrait and equilibrium branches on the $(\mu_{1} ,x)$ plane for $A=8.0,\mu_{2} =0.1$; (d) locally enlarged parts in (c)



在$A=5.0$时, 当轨迹从$P_{1} $点出发, 由于轨迹处在图1中的区域(III)中, 轨迹几乎严格沿其中的稳定平衡曲线$EB_{1} $运动, 表现为沉寂态(见图16(a)). 当慢变参数$\mu_{1} $增大到$\mu_{1} =0.0$时, 轨迹进入区域(II), 由fold分岔导致轨迹跳向2-D环面, 进入激发态(见图16(b)). 当慢变参数$\mu_{1} $增大到$HB_{2} $时, 轨迹进入区域(IV), LPC分岔使得稳定的极限环和不稳定的极限环碰撞消失导致激发态的振荡幅值逐渐减小, 最终轨迹稳定到该域内的平衡曲线.

当轨迹抵达$P_{2} $点后, 随着时间的继续延长, $\mu_{1} $缓慢减小, 轨迹几乎严格沿稳定平衡曲线$EB_{5} $, 当轨迹抵达集$HB_{2} $时, 由于慢变效应, 亚临界Hopf分岔的影响并没有立即出现, 轨迹穿越分岔点, 转而几乎严格沿不稳定平衡曲线$EB_{4} $运动, 直到抵达$P_{3} $点, Hopf分岔的影响才开始出现, 使得轨迹跳向区域(II)中的2-D环面, 产生激发态(见图16(b)).

当慢变参数$\mu_{1} $减少到$\mu_{1} =-0.05$左右时, 轨迹经由鞍点同宿分岔导致极限环消失, 逐渐稳定于该区域内的稳定平衡曲线$EB_{1} $, 转回沉寂态.

当轨迹回到出发点$P_{1} $时, 一周期的簇发振荡过程结束. 从分岔机制上, 该运动模式可以称为周期fold /LPC/Hopf/Homoclinic簇发振荡.

当$A=8.0$时, 轨迹随当慢变参数$\mu_{1} $从$-8.0$增大到$8.0$这半个周期内, 轨迹运动的模式与$A=5.0$时相应段机理完全一样. 而在$\mu_{1} $从$8.0$减小到$-8.0$这半个周期内, 轨迹运动的模式表现出不一样的特性.

从$P_{2} $出发的轨迹, 几乎严格沿稳定平衡曲线$EB_{5} $运动, 穿越分岔点$HB_{2} $, 转而几乎严格沿不平衡曲线$EB_{4} $运动, 再穿越鞍点同宿的分岔值, 沿稳定平衡曲线$EB_{3} $运动. 这一现象的产生, 主要是因为随着$A$的增大, 轨迹沿$EB_{5} $运动的惯性增大, 从而导致两分岔点$HB_{2} $的亚临界Hopf分岔效应还来不及出现, 轨迹已经穿越区域(II).

沿稳定平衡曲线$EB_{3} $运动在$FB_{2} $点由fold分岔跳向平衡曲线$EB_{1} $, 随后抵达$P_{1} $点, 完成一周期的簇发振荡.

同样, 按照轨迹单周期内的分岔行为, 该运动则可以称为周期fold/LPC簇发.

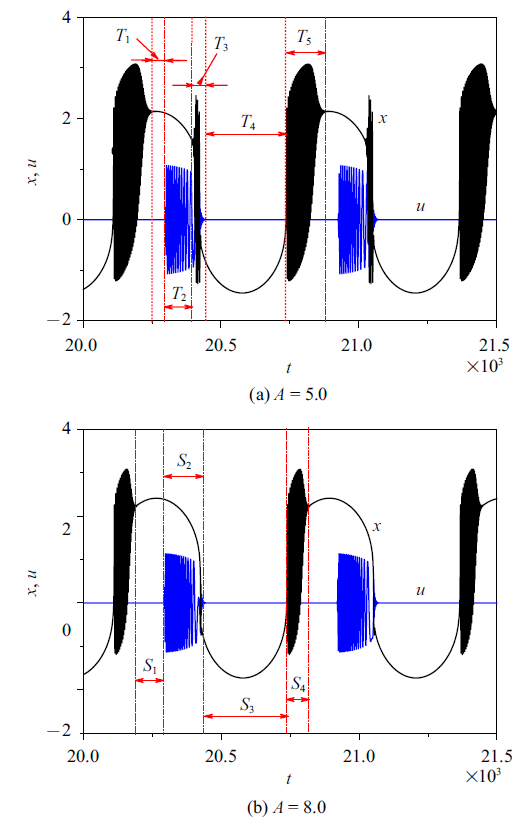
再回到簇发振荡过程中$x$和$u$的时间历程上(见图17)的叠加图, 从图17中可以看出, 当$t\in T_{1} $时, $x$和$u$均沿平衡曲线运动, 当$t\in T_{2} $, 此时轨迹位于区域(IV), $x$沿平衡曲线运动, 而$u$则按照其中的极限环振荡.

图17

新窗口打开|下载原图ZIP|生成PPT
图17$x$和$u$的时间历程的叠加图

Fig.17Overlap of the time history of $x$ and $u$



对于$A=5.0$, 当$t\in T_{3} $时, 轨迹位于区域(II), $x$和$u$均按照其中的2-D 环面运动, 当$t\in T_{4} $, 轨迹位于区域(III), $x$和$u$均沿其中的稳定平衡曲线运动, $t\in T_{5} $, 轨迹位于区域(II), $x$按照其中的2-D 环面振荡, 而$u$则沿其中的稳定平衡曲线运动, $t\in T_{1} $时, $x$和$u$均沿其中的稳定平衡曲线运动, 而当$t\in T_{2} $时,$x$沿稳定平衡曲线运动, $u$按照区域(IV)中的极限环振荡. 而在$A=8.0$时, 当$t\in S_{1} $时, 轨迹位于区域(IV), $x$和$u$均按照稳定平衡曲线运动, $t\in S_{2} $时, $x$沿稳定平衡曲线运动, $u$按照区域(IV)中的极限环振荡. $t\in S_{3} $时, $x$和$u$均沿区域(III)中稳定平衡曲线运动, $t\in S_{4} $时, $x$和$u$均按照(II)中稳定环面运动振荡.

4 结论与讨论

对于不同的余维分岔, 开折参数可以由分岔集划分为不同的区域, 分别对应于不同的动力学行为. 通过引入周期激励项取代某一开折参数, 随着激励幅值的不同, 该周期变化的开折参数会穿越不同的区域, 从而导致相应区域中的行为交替出现. 当激励频率远小于系统的固有频率时, 通常会产生簇发振荡. 定义整个激励项为慢变量, 对于原系统, 也就是某一开折参数会在正负激励幅值之间周期缓慢变化, 从而导致系统轨迹会访问开折参数空间中的不同区域. 这些区域中的各种平衡态及区域边界上的分岔行为会直接影响到簇发振荡的动力特性, 一般而言, 轨迹访问的区域越多, 簇发振荡的行为越复杂.

由于存在着慢过效应, 在快慢耦合系统轨迹上的真实分岔, 往往与理论上的分岔点之间存在着滞后效应, 这种滞后效应的滞后时间也会随之激励幅值的增大而延长, 因为激励幅值的增大, 会导致轨迹沿相应平衡态运动的惯性增大, 特别是, 当激励幅值增加到一定值, 会导致轨迹沿某平衡态运动并穿越该区域, 也即相关分岔效应来不及出现从而导致了不同的簇发振荡类型. 本文采用Izhikevich EM对簇发振荡类型的命名方式, 即采用导致沉寂态和激发态交替转迁的分岔来命名簇发振荡的类型. 然而, 对于沉寂态或激发态过程中发生不会导致转迁行为的某些分岔对簇发振荡模式的影响, 尤其是对实际的物理系统的影响, 需要进一步研究探讨.

本文仅考虑了双开折参数平面上不同区域内运动对系统快慢效应的影响, 对于余维三局部分岔问题, 更一般的情形, 应该考虑三开折参数空间不同子空间中行为的影响, 同时, 本文仅考虑了非线性项的三次截断, 且非线性项不存在退化行为, 当非线项存在退化, 会导致分岔余维数的增大, 而更高次的非线性项的截断会导致平衡态数目及其分岔类型的增加, 使得相应的簇发振荡模式更加丰富.

对于局部分岔下的快慢效应, 通过向量场标准型的开折参数的周期扰动, 在一定程度可以对该分岔所导致的所有可能的各种簇发振荡进行归类, 相关工作尚需进一步深入探讨.

最后, 需要指出的是, 本文仅考虑了余维三fold-fold-Hopf分岔的标准型及其普适开折的理论上的一般形式, 而对于实际系统, 当其平衡态产生该类分岔并存在各种扰动时, 可以将向量场约化为这一标准型及其普适开折, 标准型中的系数和开折参数经过系列推导, 可为表示为实际系统各系数的表达式, 一般情况下, 这些具体表达式可能会非常繁杂.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Mease KD. Multiple time-scales in nonlinear flight mechanics: diagnosis and modeling
Applied Mathematics and Computation, 2005,164:627-648
DOIURL [本文引用: 1]

[2] Leimkuhler B. An efficient multiple time-scale reversible integrator for the gravitational N-body problem
Applied Numerical Mathematics, 2002,43:175-190
DOIURL [本文引用: 1]

[3] Davies ML, Schreiber I, Scott SK. Dynamical behaviour of the Belousov- Zhabotinsky reaction in a field-batch reactor
Chemical Engineering Science, 2004,59:139-148
DOIURL [本文引用: 1]

[4] Bashkirtseva I, Nasyrova V, Ryashko L. Stochastic spiking-bursting excitability and transition to chaos in a discrete-time neuron model
International Journal of Bifurcation and Chaos, 2020,30:2050153
DOIURL [本文引用: 1]

[5] Duan LX, Liang TT, Zhao YQ, et al. Multi-time scale dynamics of mixed depolarization block bursting
Nonlinear Dynamics, 2021,103:1043-1053
DOIURL

[6] Bashkirtseva I, Ryashko L, Slepukhina E. Noise-induced spiking-bursting transition in the neural model with the blue sky catastrophe
Physical Review E Statistical Nonlinear & Soft Matter, 2019,99:062408


[7] Bashkirtseva I, Ryashko L, Slepukhina E. Stochastic generation and deformation of toroidal oscillations in neuron model
International Journal of Bifurcation and Chaos, 2018,28:1850070
DOIURL

[8] Gheouali M, Benzekri T, Lozi R, et al. Geometrical model of spiking and bursting neuron on a mug-shaped branched manifold
International Journal of Bifurcation and Chaos, 2020,30:2030044
DOIURL [本文引用: 1]

[9] Chen M, Qi JW, Wu HG, et al. Bifurcation analyses and hardware experiments for bursting dynamics in non-autonomous memristive FitzHugh-Nagumo circuit
Nonlinear Dynamics, 2020,63:1035-1044
[本文引用: 1]

[10] Chen M, Qi JW, Xu Q, et al. Quasi-period, periodic bursting and bifurcations in memristor-based FitzHugh-Nagumo circuit
AEU-International Journal of Electronics and Communications, 2019,110:152840
DOIURL

[11] Bao H, Zhu D, Liu WB, et al. Memristor synapse-based Morris-Lecar model: Bifurcation analyses and FPGA-based validations for periodic and chaotic bursting/spiking firings
International Journal of Bifurcation and Chaos, 2020,30:2050045
DOIURL

[12] Bao BC, Yang QF, Zhu L, et al. Chaotic bursting dynamics and coexisting multi-stable firing patterns in 3D autonomous M-L model and microcontroller-based validations
International Journal of Bifurcation and Chaos, 2019,29:1950134
DOIURL

[13] Zhou CY, Li ZJ, Xie F, et al. Bursting oscillations in Sprott B system with multi-frequency slow excitations: Two novel ``Hopf/Hopf'' -hysteresis -induced bursting and complex AMB rhythms
Nonlinear Dynamics, 2020,97:2799-2811
DOIURL [本文引用: 1]

[14] Chen ZY, Chen FQ, Zhou LQ. Slow-fast dynamics in the truss core sandwich plate under excitations with high and low frequencies
Applied Mathematical Modelling, 2020,88:382-395
DOIURL [本文引用: 1]

[15] Chen ZY, Chen FQ. Mixed mode oscillations induced by bi-stability and fractal basins in the FGP plate under slow parametric and resonant external excitations
Chaos, Solitons & Fractals, 2020,137:109814
DOIURL

[16] Zhang SH, Zhang HL, Wang C, et al. Bursting oscillations and bifurcation mechanism in a permanent magnet synchronous motor system with external load perturbation
Chaos, Solitons & Fractals, 2020,141:110355
DOIURL

[17] 马新东, 姜文安, 张晓芳 等. 一类三维非线性系统的复杂簇发振荡行为及其机理
力学学报, 2020,52(6):1789-1799


(Ma Xindong, Jiang Wenan, Zhang Xiaofang, et al. Complicated bursting behaviors as well as the mechanism of a three dimensional nonlinear system
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(6):1789-1799 (in Chinese))


[18] Zhang H, Chen DY, Xu BB, et al. The slow-fast dynamical behaviors of a hydro-turbine governing system under periodic excitations
Nonlinear Dynamics, 2017,87:2519-2528
DOIURL [本文引用: 1]

[19] Lashina EA, Chumakova NA, Chumakov GA, et al. Chaotic dynamics in the three-variable kinetic model of CO oxidation on platinum group metals
Chemical Engineering Journal, 2009,154:82-87
DOIURL [本文引用: 1]

[20] Theodosiou C, Sikelis K, Natsiavas S. Periodic steady state response of large scale mechanical models with local nonlinearities
International Journal of Solids and Structures, 2009,46:3565-3576
DOIURL [本文引用: 1]

[21] Surana A, Haller G. Ghost manifolds in slow-fast systems, with applications to unsteady fluid separation
Physica D, 2008,237:1507-1529
DOIURL [本文引用: 1]

[22] Rasmussen A, Wyller J, Vik JO. Relaxation oscillations in spruce- budworm interactions
Nonlinear Analysis: Real World Applications, 2011,12:304-319
DOIURL [本文引用: 1]

[23] Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve
Journal Physiol, 1952,117:500-544
DOIURL [本文引用: 1]

[24] Izhikevich EM. Resonate-and-fire neurons
Neural Networks, 2001,14(6-7):883-894
PMID [本文引用: 1]
We suggest a simple spiking model-resonate-and-fire neuron, which is similar to the integrate-and-fire neuron except that the state variable is complex. The model provides geometric illustrations to many interesting phenomena occurring in biological neurons having subthreshold damped oscillations of membrane potential. For example, such neurons prefer a certain resonant frequency of the input that is nearly equal to their eigenfrequency, they can be excited or inhibited by a doublet (two pulses) depending on its interspike interval, and they can fire in response to an inhibitory input. All these properties could be observed in Hodgkin-Huxley-type models. We use the resonate-and-fire model to illustrate possible sensitivity of biological neurons to the fine temporal structure of the input spike train. Being an analogue of the integrate-and-fire model, the resonate-and-fire model is computationally efficient and suitable for simulations of large networks of spiking neurons.

[25] Verhulst F. Singular perturbation methods for slow-fast dynamics
Nonlinear Dynamics, 2007,50:747-753
DOIURL [本文引用: 1]

[26] Surana A, Haller G. Ghost manifolds in slow-fast systems, with applications to unsteady fluid separation
Physica D, 2008,237:1507-1529
DOIURL [本文引用: 1]

[27] Fujimoto K, Kaneko K. How fast elements can affect slow dynamics
Physica D, 2003,180:1-16
DOIURL [本文引用: 1]

[28] Fenichel N. Geometrical singular perturbation theory for ordinary differential equations
Journal of Differential Equations, 1979,31:53-98
DOIURL [本文引用: 1]

[29] Krupa M, Szmolyan P. Extending geometric singular perturbation theory to non-hyperbolic points-fold and canard points in two dimensions
SIAM Journal on Mathematical Analysis, 2001,33:286-314
DOIURL [本文引用: 1]

[30] Rinzel J. Discussion: Electrical excitability of cells, theory and experiment: Review of the Hodgkin-Huxley foundation and an update
Bulletin of Mathematical Biology, 1990,52:5-23
DOIURL [本文引用: 2]

[31] Rasmussen A, Wyller J, Vik J O. Relaxation oscillations in spruce-budworm interactions
Nonlinear Analysis: Real World and Application, 2011,12:304-319
DOIURL [本文引用: 1]

[32] Opala A, Pieczarka M, Matuszewski M. Theory of relaxation oscillations in exciton-polariton condensates
Physical Review B, 2018,98:195312
DOIURL [本文引用: 1]

[33] Bertram R, Rubin JE. Multi-timescale systems and fast-slow analysis
Mathematical Biosciences: An International Journal, 2017,287:105-121
[本文引用: 1]

[34] Simo H, Woafo P. Bursting oscillations in electromechanical systems
Mechanics Research Communications, 2011,38:537-541
DOIURL [本文引用: 1]

[35] Razvan MR, Yasaman S. Emergence of bursting in two coupled neurons of different types of excitability
Chaos, Solitons and Fractals, 2020,132:109482
DOIURL [本文引用: 1]

[36] Vo T, Bertram R, Kaper TJ. Multi-mode attractors and spatio-temporal canards
Physica D, 2020,411:132544
DOIURL [本文引用: 1]

[37] Baldemir H, Avitabile D, Tsaneva-Atanasova K. Pseudo-plateau bursting and mixed-mode oscillations in a model of developing inner hair cells
Communications in Nonlinear Science and Numerical Simulation, 2020,80:104979
DOIURL [本文引用: 1]

[38] Izhikevich EM. Neural excitability, spiking and bursting
International Journal of Bifurcation and Chaos, 2000,6:1171-1266
[本文引用: 1]

[39] Li XH, Tang JH, Wang YL, et al. Approximate analytical solution in slow-fast system based on modified multi-scale method
Applied Mathematics and Mechanics (English Edition), 2020,41:605-622
DOIURL [本文引用: 1]

[40] Li XH, Hou JY, Chen JF. An analytical method for Mathieu oscillator based on method of variation of parameter
Communications in Nonlinear Science and Numerical Simulation, 2016,37:326-353
DOIURL [本文引用: 1]

[41] Bi QS, Zhang R, Zhang ZD. Bifurcation mechanism of bursting oscillations in parametrically excited dynamical system
Applied Mathematics and Computation, 2014,243:482-491
DOIURL [本文引用: 1]

[42] 张毅, 韩修静, 毕勤胜. 串联式叉型滞后簇发振荡及其动力学行为
力学学报, 2019,51(1):228-236


(Zhang Yi, Han Xiujing, Bi Qinsheng. Series-mode pitchfork-hysteresis bursting oscillations and their dynamical mechanisms
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(1):228-236 (in Chinese))


[43] 魏梦可, 韩修静, 张晓芳 等. 正负双向脉冲式爆炸及其诱导的簇发振荡
力学学报, 2019,51(3):904-911
[本文引用: 1]

(Wei Mengke, Han Xiujing, Zhang Xiaofang, et al. Positive and negative pulse-shaped explosion as well as bursting oscillations induced by it
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):904-911 (in Chinese))
[本文引用: 1]

[44] De S, Balakrishnan J. Burst mechanisms and burst synchronization in a system of coupled type-I and type-II neurons
Communications in Nonlinear Science and Numerical Simulation, 2020,90:105391
DOIURL [本文引用: 1]

[45] Njitacke ZT, Kengne J, Fotsin HB. Coexistence of multiple stable states and bursting oscillations in a 4D hopfeld neural network
Circuits, Systems, and Signal Processing, 2020,39:3424-3444
DOIURL [本文引用: 1]

[46] Bi QS, Ma R, Zhang ZD. Bifurcation mechanism of the bursting oscillations in periodically excited dynamical system with two time scales
Nonlinear Dynamics, 2015,79:101-110
DOIURL [本文引用: 1]

[47] Chen XK, Li SL, Zhang ZD, et al. Relaxation oscillations induced by an order gap between exciting frequency and natural frequency
Science China Technological Sciences, 2017,60:289-298
DOIURL [本文引用: 1]

[48] Han XJ, Xia FB, Ji P, et al. Hopf-bifurcation-delay-induced bursting patterns in a modified circuit system
Communications in Nonlinear Science and Numerical, 2016,36:517-527
DOIURL [本文引用: 1]

[49] Han XJ, Yu Y, Zhang C, et al. Turnover of hysteresis determines novel bursting in Duffing system with multiple-frequency external forcings
International Journal of Non-Linear Mechanics, 2017,89:69-74
DOIURL [本文引用: 1]

[50] Yu P, Zhang W, Bi QS. Vibration analysis on a thin plate with the aid of computation of normal forms
International Journal of Non-Linear Mechanics, 2001,36:597-627
DOIURL [本文引用: 1]

[51] Kuznetsov YA. Elements of Applied Bifurcation Theory. Second edition
New York: Springer-Verlag, 1998
[本文引用: 1]