引 言
随着航天领域的发展, 现代大型柔性航天器往往安装有诸如大型太阳翼等柔性结构, 为了得到可持续的能源, 其尺寸日益增大、结构重量越来越轻, 太阳翼的弹性振动不可避免地与航天器主体平台的运动相互耦合, 这种耦合效应随着太阳翼尺寸的增大显著增强. 此时, 单个太阳能帆板的模态(假设模态)并不能准确反映整个太阳翼在系统中的弹性振动, 这导致采用假设模态离散得到的动力学模型, 在准确性上可能会存在一定的不足. 因此, 大型柔性组合结构的动力学建模与振动响应分析、结构振动控制等问题变得愈加复杂且难以处理[1]. 发展能获取反映系统真实弹性振动的全局模态的解析方法, 将其应用在组合柔性结构的动力学建模, 并此基础上深入开展其振动控制和非线性动态响应的研究, 具有一定的理论意义和工程价值.
航天器大型太阳翼的构成部件为具有无限自由度的柔性体, 无论是对系统的非线性动力学特性进行分析, 还是基于其动力学模型的状态空间进行控制器的设计, 都要对柔性部件的连续位移进行离散, 得到具有有限自由度的常微分方程组的动力学模型[2]. 目前, 比较常用的两种离散方式分别是有限元法[3-5]和模态法[6-7].
有限元法可以离散具有复杂形状的复合柔性结构, 在单元数量足够多的情况下, 有限元模型所得到的结果可以达到较高的精度. 因此, 许多****[8, 9]采用有限元法, 建立系统的有限元模型, 进行动力学特性的分析和研究. Hablani[10-12]通过航天器系统的有限元模型得到结构的整体模态, 并根据模态截断方法采集低阶模态用来离散柔性体. Jin和Wang等[13]和Li等[14]利用ABAQUS软件建立了由柔性杆和薄膜构成的太阳帆航天器的有限元模型, 再利用全局广义坐标得到结构的低阶离散模型. 尽管以上基于有限元模型的方法很容易获取全局模态, 但得到的结果并不是解析的, 难以直接利用这些模态来分析系统的非线性动力学特性和设计振动控制器. 模态综合方法也是一种获取全局模态的途径, 但是这种方法得到的结果是近似且表达式复杂而难以利用[15].
模态法是采用解析的模态函数离散连续系统的动力学方程, 利用Galerkin 截断获得较低维数的模态方程, 从而明显地提高求解系统动力学模型的计算效率, 为非线性动力学特征的分析和控制器的设计提供基础, 这是有限元方法不具备的优点. 模态离散方法的关键在于将连续体位移用模态函数的乘积和与时间有关的模态坐标来描述. Pan 和Liu[16] 通过研究了基于两端自由、简支或悬臂边界的假设模态在柔性多体系统的建模中的计算效率和正确性, 表明采用静定边界条件能取得正确的结果, 而混合静定条件反而会出现较大误差. 在柔性多体系统中, 任意部件的振动都将会引起系统中其他部件的振动. 现有的解析方法在处理大型柔性航天器这样的复杂结构时遭遇到以下困境:
(1)现有解析建模方法仅适用于规则形体, 对于工程中常见的复杂结构, 如何简化与等效;
(2)现有解析方法仅适用于单一结构, 如索、梁、板、壳, 尚无处理组合结构的一般方法;
(3)假设模态法处理组合结构时, 由于各部件之间相互关联, 难以满足所有几何边界条件, 更难以满足力边界条件, 因此合理性和准确性存疑;
(4)模态综合法可用于建立组合结构的动力学模型, 存在一定的缺陷. 如构件较多导致自由度数太大, 使得模型的精度和准确性存在问题.
全局模态概念的提出使得对柔性构件弹性振动耦合效应的准确描述与复杂组合结构解析模态的求取成为可能. 有限元方法是获得复杂结构全局模态的有效途径, 但其数值方法自由度数大、维度高的特点对后续动力学建模和动态响应分析并不友好. 由此可见, 建立系统低维高精度动力学模型的关键在于如何获取系统解析的全局模态. 近年来, 曹登庆等在针对柔性机械臂[17]、多梁铰接结构[18]等细长组合结构的动力学问题的研究中系统地提出了全局模态方法, 这对于大型太阳翼低维高精度动力学模型的建立具有指导和借鉴意义. 袁秋帆等[19]针对中心刚体-单侧大挠性结构构型的航天器, 提出了一种全局模态动力学模型, 推导了非约束模态频率和模态振型. 并基于气浮平台构建了实验系统, 通过实验校验了全局模态动力学模型的准确性. 目前, 对大型太阳翼这类铰链连接多板结构的解析全局模态的求取及其动力学建模方法的研究尚少. 邱志成和姜衡[20]利用有限元软件ANSYS对几种不同的铰链扭转刚度条件下铰接柔性板结构进行了模态分析, 比较了不同铰链刚度对铰接柔性板结构的模态振型和模态频率的影响. Cao等[21]采用自由?自由梁函数作为航天器太阳翼每一块帆板的模态函数, 获得了铰链连接多板结构的解析全局模态, 但其基函数中存在较多三角函数, 降低了计算效率和收敛速度. 基于作者近期的工作[22-23], 本工作以柔性航天器携带的大型太阳翼为背景, 针对铰链连接多板结构的全局固有特性和系统非线性动力学模型的建立展开研究.
当前在对柔性航天器刚柔耦合动力学的研究中, 为了建模便利, 通常都未计及铰链对系统动力学特性的影响, 常采用基于光滑动力学的建模方法. 铰链产生的非线性刚度和阻尼离散地分布于铰接结构各处, 是导致系统模态密集和非线性耦合的主要原因[24]. 对于实际的大型柔性航天器的太阳翼等柔性附件, 运动副间的间隙、摩擦等因素使铰链部件处呈现出很强的非线性动力学特征, 间隙、碰撞和干摩擦等大量复杂非光滑的因素使得可展机构在展开过程中容易引发结构振动和变形, 直接影响航天器姿态运动以及有效载荷的指向稳定度[25]. 张静等[26]针对可展结构中铰链带来的展开后非线性动力学问题, 建立了含铰结构的动力学模型, 分析了铰链对含铰结构非线性动力学特性影响. 何昊南等[27]针对折叠舵面内、外舵铰接处存在的间隙影响开展了地面振动实验和非线性建模方法研究. 虽然袁秋帆等[19]、Wang和Li等[28]****针对带有柔性太阳翼的航天器已经开展了相关地面实验研究, 但目前针对含有铰链的太阳翼, 通过地面振动实验研究铰链间隙、摩擦等非线性因素对系统动力学特性影响的研究仍不充分.
对于非经典边界薄板, 其满足复杂边界条件的模态函数难以直接求解, 故多梁组合结构的全局模态方法不能直接推广应用于多板组合结构的建模. 因此, 本文采用特征正交多项式作为基函数构造翼板的模态函数, 引入拉格朗日乘子描述铰链处的约束条件, 精确获取太阳翼的固有频率和全局模态函数; 针对铰链建模时存在的复杂问题, 采用可变刚度的扭转弹簧等效模型, 考虑铰链非线性刚度及摩擦力矩等因素, 通过全局模态离散得到系统的低维高精度非线性动力学模型, 研究了铰链刚度等结构参数对系统固有特性的影响, 并对太阳翼在周期激励作用下的非线性特性进行分析. 为验证铰接多板结构全局模态动力学建模方法的有效性和准确性, 设计了含柔性铰链太阳翼的地面振动实验系统, 采用锤击法和扫频激励对铰接多板结构进行地面振动测试, 研究铰链非线性因素对其动力学特性的影响. 通过实验结果与理论结果的对比, 验证铰接多板结构全局模态动力学建模方法的有效性和准确性.
1.
铰链连接多板结构动力学建模
1.1
太阳翼全局模态
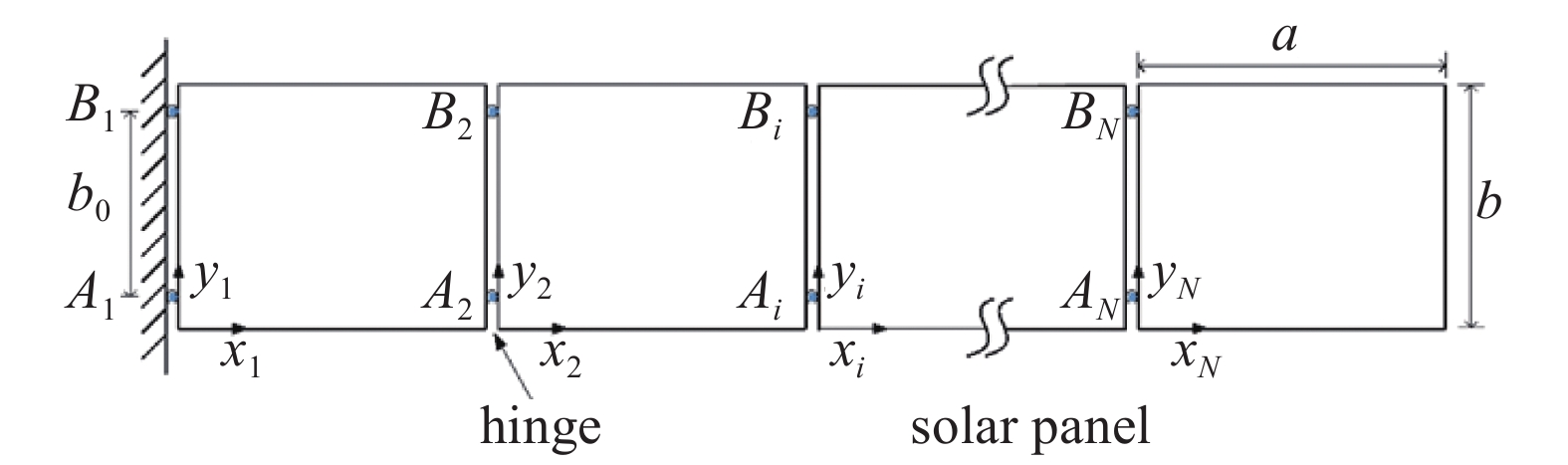
以航天器大型太阳翼为研究背景, 考虑图1所示的铰链连接多板结构, 研究其全局模态的提取方法, 获得铰链连接多板结构的固有频率与全局模态.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
铰链连接多板结构示意图
Figure
1.
Schematic of the solar array
下载: 全尺寸图片
幻灯片
图1中
ight)$
为了方便建模, 对系统作如下假设: (1) 将太阳能电池板的每块板看作是一个各向同性的柔性矩形薄板. (2) 将柔性铰简化为附加扭转弹簧的铰链, 忽略扭转弹簧的质量、尺寸、阻尼和摩擦. 太阳翼处于完全展开状态, 铰链是锁定的. (3) 只考虑系统的横向振动, 忽略面内振动.
由于太阳翼各帆板间的振动相互耦合, 太阳翼任意一点
$${w_i}({x_i},{y_i},t) = {W_i}({x_i},{y_i})sin left( {omega t} ight)$$  | (1) |
其中,
$$T = sumlimits_{i = 1}^N {frac{1}{2} ho h{{int_0^a {int_0^b {left( {frac{{partial {w_i}}}{{partial t}}} ight)} } }^2}{ m{d}} x_i{ m{d}} y_i}$$  | (2) |
$$begin{aligned}[b] {U_{ m{p}}} = &{sumlimits_{i = 1}^N {frac{D}{2}int_0^a {int_0^b {left[ {left( {frac{{{partial ^2}{w_i}}}{{partial {{x_i}^2}}}} ight)} ight.} } } ^2} + 2vfrac{{{partial ^2}{w_i}}}{{partial {{x_i}^2}}}frac{{{partial ^2}{w_i}}}{{partial {{y_i}^2}}} +& {left( {frac{{{partial ^2}{w_i}}}{{partial {{y_i}^2}}}} ight)^2} + 2left( {1 - v} ight)left. {{{left( {frac{{{partial ^2}{w_i}}}{{partial x_ipartial y_i}}} ight)}^2}} ight]{ m{d}} x_i{ m{d}} y_iend{aligned}$$  | (3) |
式中,
ho $
$${U_j} = sumlimits_{i = 1}^N {frac{1}{2}k{{left( {Delta {theta _{Ai}}} ight)}^2}} + sumlimits_{i = 1}^N {frac{1}{2}k{{left( {Delta {theta _{Bi}}} ight)}^2}} $$  | (4) |
式中,
将式(1)代入式(2)和式(3)分别得到太阳翼最大动能Tmax和最大变形势能Umax
$${T_{max }} = sumlimits_{i = 1}^N {frac{1}{2}{omega ^2} ho h{{int_0^a {int_0^b {{{W_i}} } } }^2}{ m{d}} x{ m{d}} y} $$  | (5) |
$$begin{aligned}[b] {U_{{ m{p}}{ _{max }}}} =& {sumlimits_{i = 1}^N {frac{D}{2}int_0^a {int_0^b {left[ {left( {frac{{{partial ^2}{W_i}}}{{partial {x^2}}}} ight)} ight.} } } ^2} + 2vfrac{{{partial ^2}{W_i}}}{{partial {x^2}}}frac{{{partial ^2}{W_i}}}{{partial {y^2}}}+ & {left( {frac{{{partial ^2}{W_i}}}{{partial {y^2}}}} ight)^2} + 2left( {1 - v} ight)left. {{{left( {frac{{{partial ^2}{W_i}}}{{partial xpartial y}}} ight)}^2}} ight]{ m{d}} x{ m{d}} yend{aligned} $$  | (6) |
$${U_{max }} = {U_{{p_{ max }}}} + {U_j}$$  | (7) |
采用特征正交多项式簇作为基函数, 模态函数为其线性组合,
$${W_i}({x_i},{y_i}) = sumlimits_{m = 1}^{{m_t}} {sumlimits_{n = 1}^{{n_t}} {A_{mn}^{left( i ight)}} } varphi _m^{(i)}({x_i})varphi _n^{(i)}({y_i})$$  | (8) |
式中,
ight)}$
根据太阳翼的积分区域和边界条件, 给定满足边界条件的多项式首项, 使用Gram?Schmidt递推算法[29], 可以得到帆板的基函数.
假设铰链与帆板紧固连接, 由几何关系, 铰链的转角
$$Delta {theta _{{A_{,1}}}} = {left. {frac{{partial {W_1}}}{{partial {x_1}}}} ight|_{!!!!{x_1} = 0atop{y_1} = {y_a}}},;;Delta {theta _{{B_{,1}}}} = {left. {frac{{partial {W_1}}}{{partial {x_1}}}} ight|_{!!!!{x_1} = 0atop{y_1} = {y_b}}}qquadquad;;;;;$$  | (9) |
$$Delta {theta _{{A_{,i}}}} = {left. {frac{{partial {W_i}}}{{partial {x_i}}}} ight|_{!!!!{x_i} = 0atop{y_i} = {y_a}}} - {left. {frac{{partial {W_{i - 1}}}}{{partial {x_{i - 1}}}}} ight|_{!!!!{x_{i - 1}} = aatop{y_{i - 1}} = {y_a}}},;;;;{ m{ }}i = 2,3, cdots ,N$$  | (10) |
$$Delta {theta _{{B_{,i}}}} = {left. {frac{{partial {W_i}}}{{partial {x_i}}}} ight|_{!!!!{x_i} = 0atop{y_i} = {y_b}}} - {left. {frac{{partial {W_{i - 1}}}}{{partial {x_{i - 1}}}}} ight|_{!!!!{x_{i - 1}} = aatop{y_{i - 1}} = {y_b}}},;;;;{ m{ }}i = 2,3, cdots ,N$$  | (11) |
式中,
m{ = }}dfrac{{b - {b_0}}}{2}$
由于航天器在轨运行时铰链是锁定的, 且建模时不考虑铰链尺寸, 两翼板间不存在相对位移. 因此, 图1中铰链处的位移关系如下
$$Delta {W_{{A_{,1}}}} = {W_1}left( {0,{y_a}} ight) = 0qquadqquad;;;$$  | (12) |
$$Delta {W_{{B_{,1}}}} = {W_1}left( {0,{y_b}} ight) = 0qquadqquad;;;$$  | (13) |
$$Delta {W_{{A_{,i}}}} = {W_i}left( {0,{y_a}} ight) - {W_{i - 1}}left( {a,{y_a}} ight) = 0$$  | (14) |
$$Delta {W_{{B_{,i}}}} = {W_i}left( {0,{y_b}} ight) - {W_{i - 1}}left( {a,{y_b}} ight) = 0$$  | (15) |
引入Lagrange乘子
m{ }}{lambda _{{B_{,i}}}}$
$$varPi = {U_{max }} - {T_{max }} + sumlimits_{i = 1}^N {{lambda _{{A_{,i}}}}Delta {W_{{A_{,i}}}}} + sumlimits_{i = 1}^N {{lambda _{{B_{,i}}}}Delta {W_{{B_{,i}}}}} $$  | (16) |
根据Rayleigh?Ritz法, 将Lagrange函数对待定系数
ight)}$
$$frac{{partial varPi }}{{partial A_{mn}^{left( i ight)}}} = 0,;;i = 1,2,cdots,Nqquad;;;;;;;$$  | (17) |
$$frac{{partial varPi }}{{partial {lambda _{{A_{,i}}}}}} = 0,;;{ m{ }}frac{{partial varPi }}{{partial {lambda _{{B_{,i}}}}}} = 0,;;i = 1,2,cdots,N$$  | (18) |
据此可导出系统的特征方程如下
$$left( {{boldsymbol{K}} - {omega ^2}{boldsymbol{M}} + {boldsymbol{varLambda }}} ight){boldsymbol{X}} = {boldsymbol{0}}$$  | (19) |
式中,
$${boldsymbol{X}} = {left[ {{boldsymbol{A}}_{}^{left( { m{1}} ight)},;{boldsymbol{A}}_{_{}}^{left( { m{2}} ight)},; cdots ,;{boldsymbol{A}}_{_{}}^{left( N ight)},{{boldsymbol{lambda }}_A},{{boldsymbol{lambda }}_B}} ight]^{ m{T}}};;;;;;;;;$$  |
$${boldsymbol{A}}_{}^{left( i ight)} = left[ {A_{11}^{left( i ight)},{ m{ }}A_{12}^{left( i ight)},{ m{ }} cdots ,A_{1{n_t}}^{left( i ight)},A_{21}^{left( i ight)}, cdots ,{ m{ }}A_{{m_t}{n_t}}^{left( i ight)}} ight]$$  |
$${{boldsymbol{lambda }}_A} = left[ {{lambda _{{A_1}}},{ m{ }}{lambda _{{A_2}}},{ m{ }} cdots ,{ m{ }}{lambda _{{A_N}}}} ight];;;;;;;;;;;;qquadqquad$$  |
$${{boldsymbol{lambda }}_B} = left[ {{lambda _{{B_1}}},{ m{ }}{lambda _{{B_2}}},{ m{ }} cdots ,{ m{ }}{lambda _{{B_N}}}} ight];;;;;;;;;;;;qquadqquad$$  |
矩阵K和M按照一定规则构造, 具体形式可参见文献[23]. 系统固有频率可由特征方程(19)求得, 将固有频率代入式(19)求得特征向量X, 再代入式(8), 则可求得系统的全局模态函数.
1.2
太阳翼非线性动力学模型
利用上节中得到的全局模态, 可建立系统的低维动力学模型. 对于第k阶频率, 系统对应的全局模态可表示为
$${{boldsymbol{varPhi }}_k} = {left[ {{W_{1,k}},{W_{2,k}} cdots ,{W_{N,k}}} ight]^{ m{T}}}$$  | (20) |
定义矢量函数
$${{boldsymbol{W}}_i}left( {{x_i},{y_i}} ight) = left[ {{W_{i,1}}left( {{x_i},{y_i}} ight),{W_{i,2}}left( {{x_i},{y_i}} ight), cdots ,{W_{i,n}}left( {{x_i},{y_i}} ight)} ight]$$  | (21) |
则根据式(1), 第i个帆板的位移表达式为
$$begin{split} {w_i}left( {{x_i},{y_i},t} ight) = &{left[ {{boldsymbol{varPhi }}{boldsymbol{q}}left( t ight)} ight]_i} = {{boldsymbol{W}}_i}left( {{x_i},{y_i}} ight){boldsymbol{q}}left( t ight)= & sumlimits_{k = 1}^n {{W_{i,k}}left( {{x_i},{y_i}} ight){q_k}left( t ight)} end{split} $$  | (22) |
式中,
ight)$
$$left. {begin{array}{*{20}{l}} {{boldsymbol{varPhi }}= left[ {{{boldsymbol{varPhi }}_1},{{boldsymbol{varPhi }}_2}, cdots ,{{boldsymbol{varPhi }}_n}} ight]{ m{ }}} {{ m{ }}{boldsymbol{q}} = {{left[ {{q_1}left( t ight),{q_2}left( t ight),cdots,{q_n}left( t ight)} ight]}^{ m{T}}}} end{array}} ight}$$  | (23) |
铰链被描述为一个带有非线性扭转弹簧和线性阻尼器的单自由度无质量系统. 基于参数辨识方法, 将铰链传递的扭矩表示为状态的函数. 则第i个铰链传递的扭矩可表示为[30]
$$begin{split}M_s = cDelta {dot theta _s} + kDelta {theta _s} + {k_n}{ {Delta {theta _s}} ^3} + mu { m{sign}}Delta {dot theta _s},;;;;s = {A_i},{B_i}end{split}$$  | (24) |
式中,
将式(21)代入系统动能、势能表达式中, 然后利用哈密顿原理并结合式(23)得到如下离散动力学方程
$${{boldsymbol{M}}_{{d}}}{boldsymbol{ddot q}} + {boldsymbol{Cdot q}} + {boldsymbol{mu }}({boldsymbol{dot q}}) + {{boldsymbol{K}}_l}{boldsymbol{q}} + {{boldsymbol{K}}_n}({boldsymbol{q}}) = {boldsymbol{Q}}$$  | (25) |
式中,
质量矩阵
$$begin{split}{{boldsymbol{M}}_{{d}}} = & ho sumlimits_{i = 1}^N {int_0^a {int_{ m{0}}^b {frac{2}{3}{h^3}} frac{{partial {{boldsymbol{W}}}_i^{ m{T}}}}{{partial {x_i}}}frac{{partial {{{boldsymbol{W}}}_i}}}{{partial {x_i}}}{ m{d}}{y_i}{ m{d}}{x_i}} } + & ho sumlimits_{i = 1}^N {int_0^a {int_{ m{0}}^b {frac{2}{3}{h^3}} frac{{partial {{boldsymbol{W}}}_i^{ m{T}}}}{{partial {y_i}}}frac{{partial {{{boldsymbol{W}}}_i}}}{{partial {y_i}}}{ m{d}}{y_i}{ m{d}}{x_i}} } + & ho sumlimits_{i = 1}^N {int_0^a {int_{ m{0}}^b {2h} {{boldsymbol{W}}}_i^{ m{T}}{{{boldsymbol{W}}}_i}{ m{d}}{y_i}{ m{d}}{x_i}} } end{split}$$  | (26) |
线性刚度矩阵
$$begin{split}{{boldsymbol{K}}_l} =& Dsumlimits_{i = 1}^N {int_0^a {int_0^b {frac{{{partial ^2}{boldsymbol{W}}_i^{ m{T}}}}{{partial x_i^2}}frac{{{partial ^2}{{boldsymbol{W}}_i}}}{{partial x_i^2}}} { m{d}}{y_i}{ m{d}}{x_i}} } +& vDsumlimits_{i = 1}^N {int_0^a {int_0^b {frac{{{partial ^2}{boldsymbol{W}}_i^{ m{T}}}}{{partial x_i^2}}frac{{{partial ^2}{{boldsymbol{W}}_i}}}{{partial y_i^2}}} { m{d}}{y_i}{ m{d}}{x_i}} } + & vDsumlimits_{i = 1}^N {int_0^a {int_0^b {frac{{{partial ^2}{boldsymbol{W}}_i^{ m{T}}}}{{partial y_i^2}}frac{{{partial ^2}{{boldsymbol{W}}_i}}}{{partial x_i^2}}} { m{d}}{y_i}{ m{d}}{x_i}} } + & 2left( {1 - v} ight)Dsumlimits_{i = 1}^N {int_0^a {int_0^b {frac{{{partial ^2}{boldsymbol{W}}_i^{ m{T}}}}{{partial {x_i}partial {y_i}}}frac{{{partial ^2}{{boldsymbol{W}}_i}}}{{partial {x_i}partial {y_i}}}} { m{d}}{y_i}{ m{d}}{x_i}} } + & Dsumlimits_{i = 1}^N {int_0^a {int_0^b {frac{{{partial ^2}{boldsymbol{W}}_i^{ m{T}}}}{{partial y_i^2}}frac{{{partial ^2}{{boldsymbol{W}}_i}}}{{partial y_i^2}}} { m{d}}{y_i}{ m{d}}{x_i}} } + & ksumlimits_{i = 1}^N {{{ {Delta {{boldsymbol{varTheta}} _{{A_{i}}}}} }^{ m{T}}}Delta {{boldsymbol{varTheta}} _{{A_{ i}}}}} + ksumlimits_{i = 1}^N {{{ {Delta {{boldsymbol{varTheta}} _{{B_{ i}}}}} }^{ m{T}}}Delta {{boldsymbol{varTheta}} _{{B_{ i}}}}} end{split}$$  | (27) |
$$begin{split} ;;{boldsymbol{mu }}({boldsymbol{dot q}}) =& mu sumlimits_{i = 1}^N {left[ {{ m{sign}}left( {Delta {{boldsymbol{varTheta}} _{{A_i}}}{boldsymbol{dot q}}} ight){{ {Delta {{boldsymbol{varTheta}} _{{A_i}}}} }^{ m{T}}}} ight.} + &left. {{ m{sign}}left( {Delta {{boldsymbol{varTheta}} _{{B_i}}}{boldsymbol{dot q}}} ight){{ {Delta {{boldsymbol{varTheta}} _{{B_i}}}} }^{ m{T}}}} ight]end{split}$$  | (28) |
式中,
ight|_{!!!!{x_1} = 0atop{y_1} = {y_a}}},{
m{ }}Delta {{boldsymbol{varTheta}} _{{B_{,1}}}} = {left. {dfrac{{partial {{{boldsymbol{W}}}_1}}}{{partial {x_1}}}}
ight|_{!!!!{x_1} = 0atop{y_1} = {y_b}}},$
$$Delta {{boldsymbol{varTheta}} _{{A_{,i}}}} = {left. {frac{{partial {{{boldsymbol{W}}}_i}}}{{partial {x_i}}}} ight|_{!!!!{x_i} = 0atop{y_i} = {y_a}}} - {left. {frac{{partial {{{boldsymbol{W}}}_{i - 1}}}}{{partial {x_{i - 1}}}}} ight|_{!!!!{x_{i - 1}} = aatop{y_{i - 1}} = {y_a}}}{ m{ }}$$  | (29) |
$$Delta {{boldsymbol{varTheta}} _{{B_{,i}}}} = {left. {frac{{partial {{{boldsymbol{W}}}_i}}}{{partial {x_i}}}} ight|_{!!!!{x_i} = 0atop{y_i} = {y_b}}} - {left. {frac{{partial {{{boldsymbol{W}}}_{i - 1}}}}{{partial {x_{i - 1}}}}} ight|_{!!!!{x_{i - 1}} = aatop{y_{i - 1}} = {y_b}}}$$  | (30) |
阻尼矩阵
$${boldsymbol{C}} = {kappa _M}{{boldsymbol{M}}_d} + {kappa _K}{{boldsymbol{K}}_p} + c{{boldsymbol{C}}_j}$$  | (31) |
式中,
$${{boldsymbol{K}}_p} = {{boldsymbol{K}}_l} - ksumlimits_{i = 1}^N {{{ {Delta {{boldsymbol{varTheta}} _{{A_{ i}}}}} }^{ m{T}}}Delta {{boldsymbol{varTheta}} _{{A_{ i}}}}} - ksumlimits_{i = 1}^N {{{ {Delta {{boldsymbol{varTheta}} _{{B_{ i}}}}} }^{ m{T}}}Delta {{boldsymbol{varTheta}} _{{B_{ i}}}}} $$  | (32) |
$${{boldsymbol{C}}_j} = sumlimits_{i = 1}^N {{{ {Delta {{boldsymbol{varTheta}} _{{A_{,i}}}}} }^{ m{T}}}Delta {{boldsymbol{varTheta}} _{{A_{,i}}}} + sumlimits_{i = 1}^N {{{ {Delta {{boldsymbol{varTheta}} _{{B_{,i}}}}} }^{ m{T}}}Delta {{boldsymbol{varTheta}} _{{B_{,i}}}}} } ;;;;;;;;;;;;;$$  | (33) |
式(25)中非线性刚度矩阵
$${{boldsymbol{K}}_n}({boldsymbol{q}}) = {k_n}sumlimits_{i = 1}^N {left[ {{{left( {Delta {w_{{A_i}}}} ight)}^3}{{ {Delta {varTheta _{{A_i}}}} }^{ m{T}} } + {{left( {Delta {w_{{B_i}}}} ight)}^3}{{ {Delta {varTheta _{{B_i}}}} }^{ m{T}} }} ight]} $$  | (34) |
式中,
ight|_{!!!!{x_1} = 0atop{y_1} = {y_a}}},;{
m{ }}Delta {w_{{B_{,1}}}} = {left. {dfrac{{partial {w_1}}}{{partial {x_1}}}}
ight|_{!!!!{x_1} = 0atop{y_1} = {y_b}}},$
$$Delta {w_{{A_{,i}}}} = {left. {frac{{partial {w_i}}}{{partial {x_i}}}} ight|_{!!!!{x_i} = 0atop{y_i} = {y_a}}} - {left. {frac{{partial {w_{i - 1}}}}{{partial {x_{i - 1}}}}} ight|_{!!!!{x_{i - 1}} = aatop{y_{i - 1}} = {y_a}}}{ m{ }}$$  | (35) |
$$Delta {w_{{B_{,i}}}} = {left. {frac{{partial {w_i}}}{{partial {x_i}}}} ight|_{!!!!{x_i} = 0atop{y_i} = {y_b}}} - {left. {frac{{partial {w_{i - 1}}}}{{partial {x_{i - 1}}}}} ight|_{!!!!{x_{i - 1}} = aatop{y_{i - 1}} = {y_b}}}$$  | (36) |
2.
地面振动实验
为了验证利用全局模态建立的动力学模型的准确性和合理性, 搭建了如图2所示的铰链连接多板结构实验系统.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
铰链连接多板结构实验平台
Figure
2.
Test platform of the hinged multi-panel structure
下载: 全尺寸图片
幻灯片
采用锤击法对太阳翼结构进行模态测试, 将其结果作为参考依据, 对铰接多板结构全局模态提取方法的合理性进行验证; 通过振动台施加基础激励, 对太阳翼进行动态响应测试, 将实验结果与理论模型计算所得的动态响应进行对比, 对基于全局模态的动力学建模方法的有效性进行验证, 并进一步研究系统的非线性现象.
2.1
实验装置
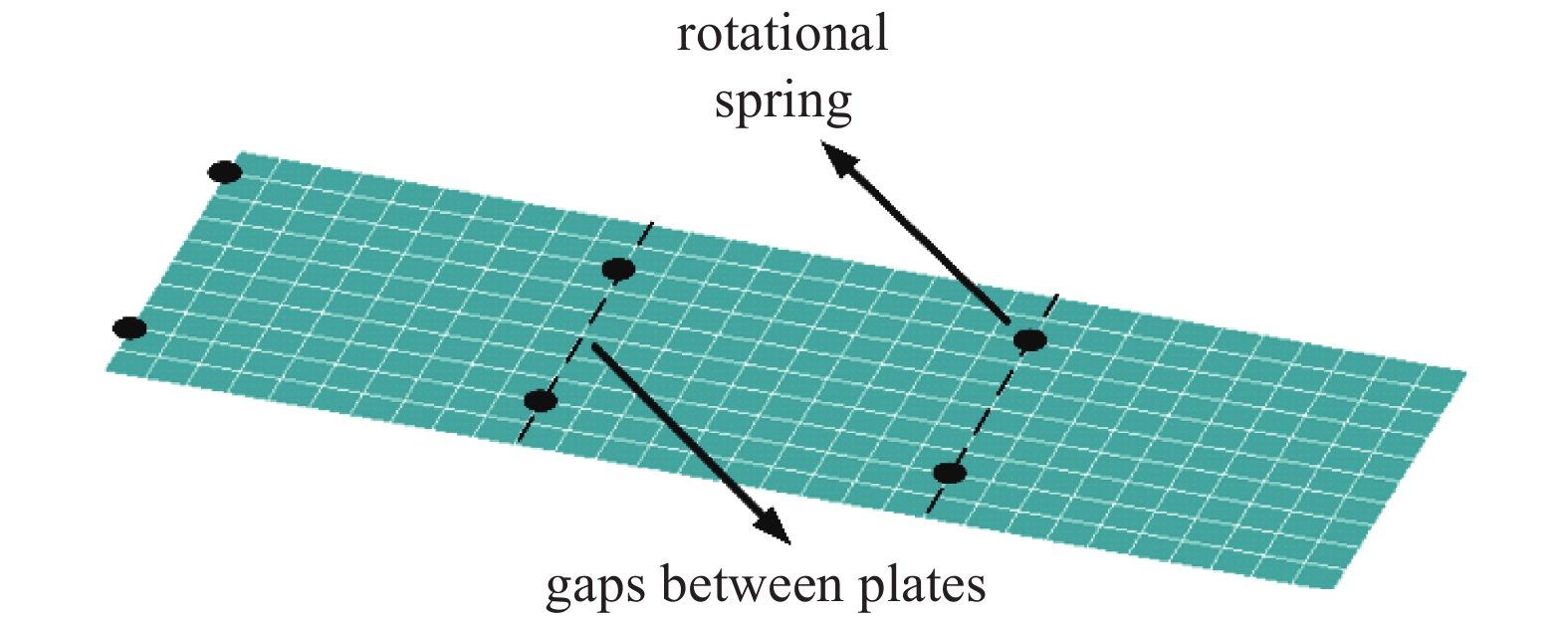
实验平台如图2所示, 太阳翼由三块正方形薄铝板和四个扭转弹簧(图3所示)连接而成. 太阳翼根部通过扭转弹簧连接在夹具(钢板)上, 夹具固定在振动台上.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
扭转弹簧
Figure
3.
Rotational spring
下载: 全尺寸图片
幻灯片
2.2
锤击法模态测试
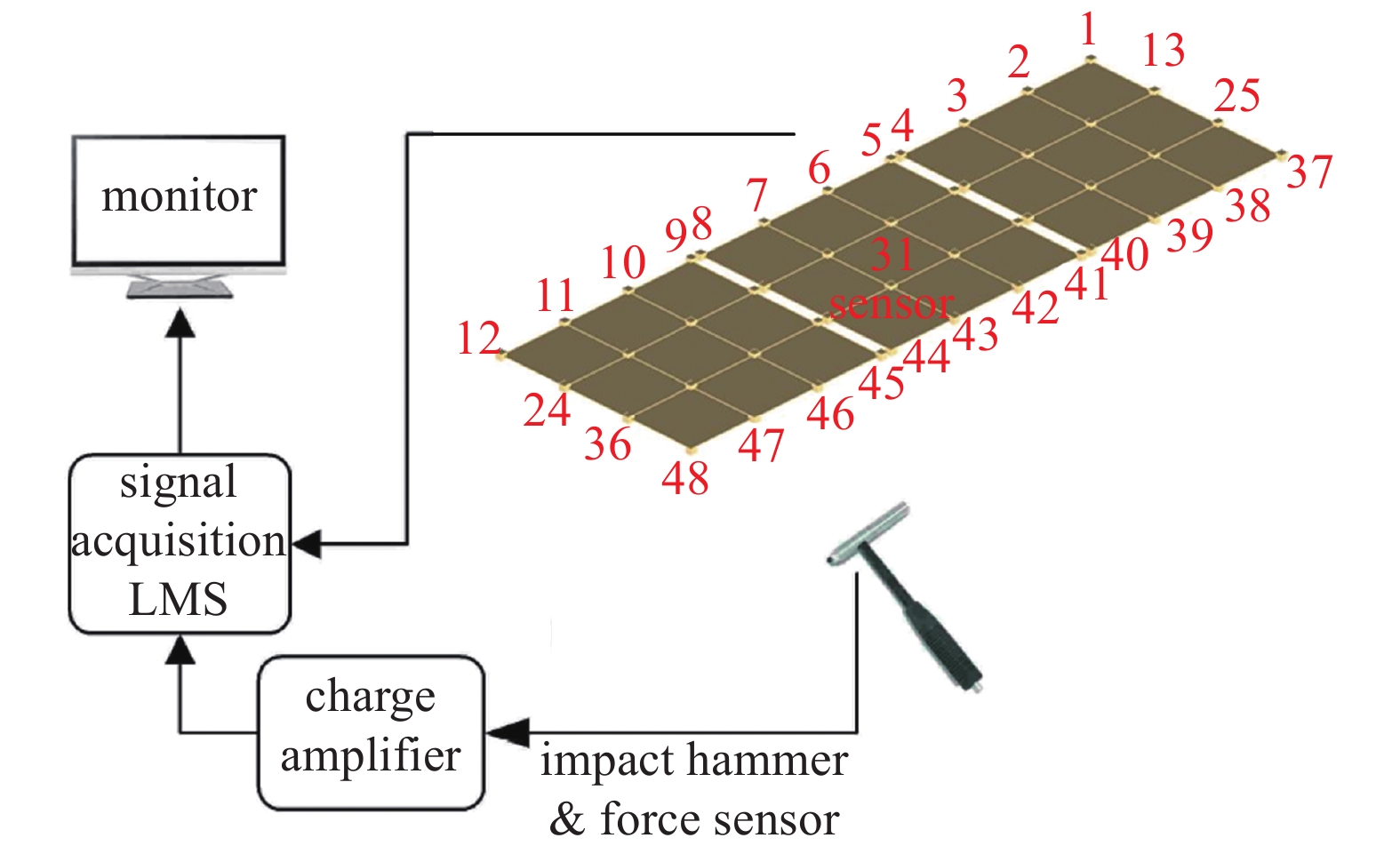
通过锤击法获取太阳翼的模态. 实验系统设置如图4所示, 采用移动力锤锤击、多输入单输出的模态参数识别方法, 即MISO方法来获得结构的模态参数, 固定加速度响应测点(31号点), 力锤依次敲击1?48号点. 加速度传感器型号为SN2066633, 力传感器型号为SN2063818, 锤头选择橡胶头, 加速度传感器粘贴于翼板上. 利用LMS声振测试系统采集和分析激励和响应信号, 可以得到48个频响函数, 利用Polymax方法进行模态识别, 得到系统前4阶模态参数.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
锤击法模态测试
Figure
4.
Experimental setup of hammer test
下载: 全尺寸图片
幻灯片
2.3
太阳翼动态响应测试
太阳翼为铰链处存在摩擦与非线性扭转刚度的非线性结构. 非线性结构的响应对激励量级很敏感, 而锤击法很难控制锤击力度, 所以不宜采用锤击法进行非线性结构的振动实验. 采用振动台进行基础激励, 实验系统如图5所示. 为了得到太阳翼的振动响应, 需要在翼板上粘贴3个加速度传感器, 传感器粘贴位置如图5的红圈所示. 振动台选择位移幅值恒定的正弦扫频激励, 扫频范围为5 ~ 7 Hz (包含第2阶频率), 扫频速度为2 Hz/min. 扫频实验的整个时间历程时长总计为60 s.
在时域内比较了测点1和3在激励幅值恒定为5 mm的加速度响应, 比较了第3测点在激励幅值分别恒定为5 mm, 7 mm的正弦扫频激励下太阳翼的加速度响应.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
振动台激励实验系统
Figure
5.
Experimental setup of vibrator test
下载: 全尺寸图片
幻灯片
3.
结果与讨论
3.1
全局模态验证
通过与有限元模型计算结果和模态实验所得结果进行对比, 验证本文提出的铰接多板结构全局模态求解方法的准确性.
太阳翼有限元模型采用商业软件ANSYS建立. 翼板采用Shell63单元模拟, 连接铰链采用Combine14扭转弹簧单元模拟, 两翼板间铰链连接处的自由度采用Couple命令进行耦合, 以模拟连接处的位移匹配条件. 有限元模型如图6所示. 在计算太阳翼的固有频率和模态时, 有限元模型中的弹簧为线性扭转弹簧, 结构参数如表1所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
太阳翼有限元模型
Figure
6.
Finite element model of the solar array in ANSYS
下载: 全尺寸图片
幻灯片
表
1
太阳翼(铰链连接多板结构)几何参数与材料常数
Table
1.
Geometric parameters and material constants of the solar array (multi-panel structure)
table_type1 ">
| Parameters | Values |
| length of the panel a/m | 0.3 |
| width of the panel b/m | 0.3 |
| thickness of the panel h/m | 0.0015 |
| elastic modulus of the panel E/Pa | 7.0 × 1010 |
| mass density of the panel ${ ho _0}$/(kg·m?3) | 2700 |
| Poisson ratio $v$ | 0.3 |
| position of the joints Ai ${y_a}$/m | 0.04 |
| position of the joints Bi ${y_b}$/m | 0.26 |
| stiffness of the rotation spring k/(${ m{N}} cdot { m{mcdot rad}^{-1}}$) | 35 |
| damping coefficients of panel${kappa _M}$, ${kappa _N}$ | 0.002, 0.001 |
| spring damping coefficients c/(${ m{N}} cdot { m{m cdot ra}}{{ m{d}}^{-3}}$) | 30 |
下载: 导出CSV
|显示表格
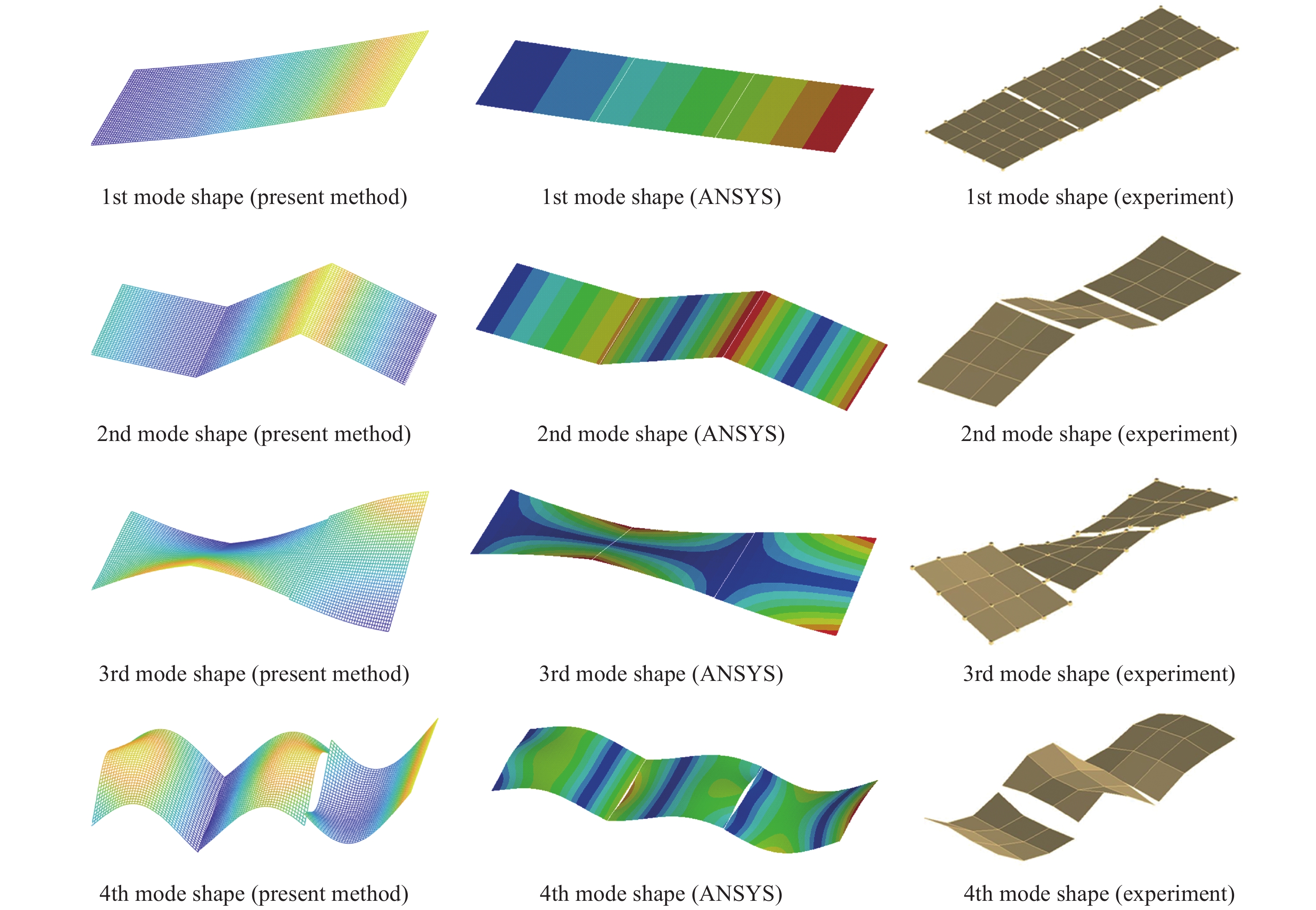
通过全局模态方法推得的特征方程(19)式可得到系统的前4阶频率和振型. 分别将全局模态方法所得频率和有限元方法所得频率与实验结果进行对比, 其相对误差如表2所示, 振型对比结果如图7所示. 由表2前4阶频率的对比结果可以看出全局模态方法计算结果与模态测试结果最大误差小于4.908%, 且其误差小于有限元方法计算结果与实验结果的误差, 说明了全局模态方法的有效性. 因为在该方法的推导过程中没有做任何的近似和省略, 故所得到的固有频率和全局模态是精确的解析解.
表
2
全局模态方法、有限元方法与模型实验的前4阶固有频率对比
Table
2.
Comparison of the first four natural frequencies of the system,
table_type2 ">
| Frequency order | Frequency/Hz | Error/% | Frequency/Hz | Error/% | ||
| Experiment | Proposed method | Experiment | ANSYS | |||
| 1 | 1.077 | 1.025 | 4.828 | 1.077 | 1.007 | 6.500 |
| 2 | 6.262 | 6.194 | 1.086 | 6.262 | 6.070 | 3.066 |
| 3 | 17.013 | 16.178 | 4.908 | 17.013 | 15.914 | 6.460 |
| 4 | 46.827 | 44.814 | 4.299 | 46.827 | 44.849 | 4.224 |
下载: 导出CSV
|显示表格
从图7给出的太阳翼振型可以看出, 太阳翼的低阶模态主要表现为多板结构的刚体模态, 即扭簧的扭转模态. 高阶模态则表现为板的弯或扭以及弯扭耦合特性. 三种方法所得振型可完全对应, 从频率与振型两个方面验证了本文提出的全局模态提取方法的准确性.
采用全局模态方法和模态测试得到不同铰接刚度下太阳翼的前4阶固有频率列于表3, 结果表明, 太阳翼固有频率随着扭转弹簧刚度增加而增大.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-7.jpg'" class="figure_img
figure_type2 ccc " id="Figure7" />
图
7
全局模态方法、有限元方法与模型实验的前4阶振型对比
Figure
7.
Comparison of mode shapes obtained by the global mode method, FEM and experiment
下载: 全尺寸图片
幻灯片
表
3
不同弹簧刚度的前4阶频率
Table
3.
First four natural frequencies with different spring stiffness
table_type2 ">
| Frequency order | k = 35 | k = 350 | |||||
| Experiment | Proposed method | Error/% | Experiment | Proposed method | Error/% | ||
| 1 | 1.077 | 1.025 | 4.828 | 1.189 | 1.133 | 4.710 | |
| 2 | 6.062 | 6.194 | 2.177 | 7.015 | 6.823 | 2.737 | |
| 3 | 17.013 | 16.178 | 4.908 | 18.614 | 17.756 | 4.609 | |
| 4 | 46.877 | 44.814 | 4.401 | 48.191 | 46.291 | 3.943 | |
下载: 导出CSV
|显示表格
3.2
全局模态动力学建模方法验证
上节验证了全局模态求取方法的准确性, 本节将通过动态测试结果与理论计算结果的对比来验证本文非线性动力学模型的正确性.
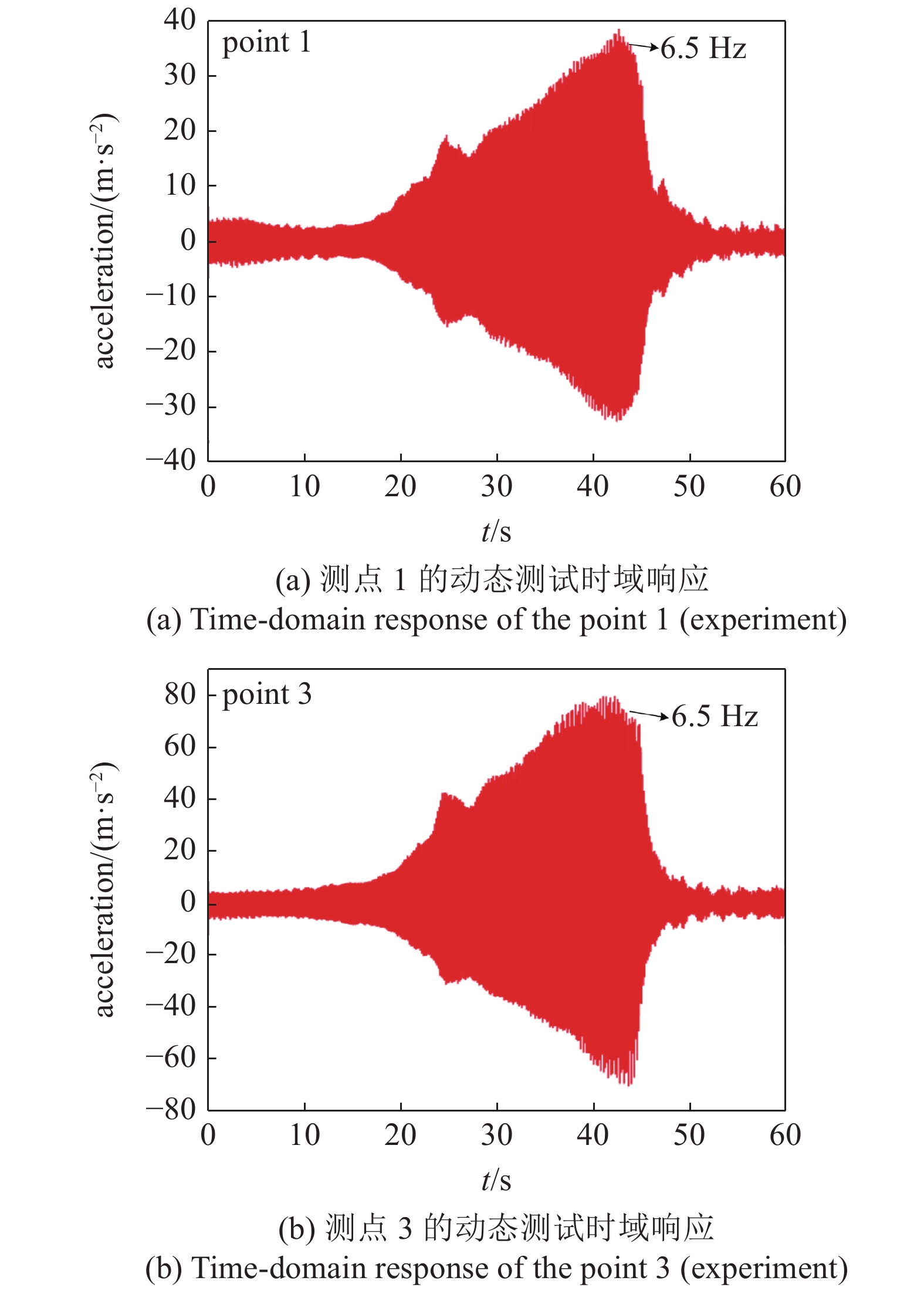
图8给出了太阳翼结构动态响应测试时, 在正弦扫频激励作用下测点1和3的加速度响应.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
测点1和测点3的动态测试时域响应
Figure
8.
Time-domain responses of the dynamic test for point 1 and point 3
下载: 全尺寸图片
幻灯片
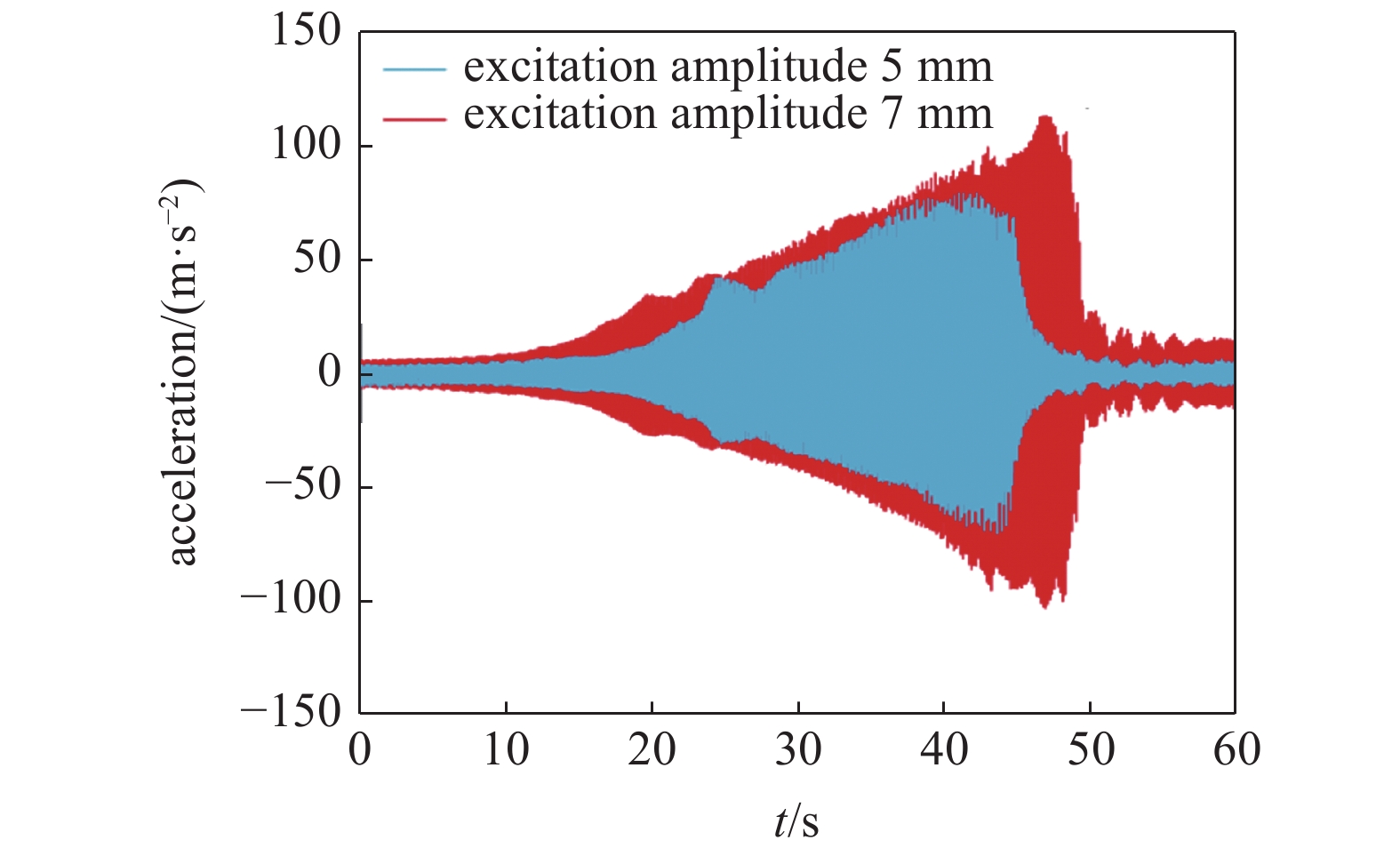
从图8动态响应测试结果可以看出, 在系统第2阶频率(6.062 Hz)附近出现共振区, 与上节全局模态方法与模态测试得到的第2阶频率相对应, 进一步证明了全局模态方法的准确性. 由两个测点的加速度响应可以看出扫频时出现了明显的跳跃现象, 太阳翼非线性特征表现为硬特性, 且越靠近太阳翼自由端的测点响应越大. 图9给出了动态响应测试的激励幅值分别恒定为5 mm和7 mm时, 正弦扫频激励下测点3的时间历程. 从时间历程可以看出随着激励幅值的增大, 非线性现象更加突出, 硬特性特征也更加明显.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
激励幅值为5 mm和7 mm时测点3的动态测试时域响应
Figure
9.
Time-domain response of the dynamic test for the point 3 with excitation amplitude 5 mm and 7 mm
下载: 全尺寸图片
幻灯片
理论计算方面, 在上节中离散非线性动力学模型的基础上, 采用模态截断方法进一步获得满足精度要求的低维动力学模型, 通过式(25)可计算得到基础激励下太阳翼的振动响应. 铰链摩擦力矩
m{N}} cdot {
m{m}}$
在基础激励下, 式(25)中的外激励可以写成
$${boldsymbol{Q}} = - ho hdisplaystylesumlimits_{i = 1}^N {int_0^b {int_0^a {{{boldsymbol{W}}_i}} } A{varOmega ^2}sin left( {varOmega t} ight){ m{d}}{x_i}{ m{d}}{y_i}} $$  | (37) |
式中, A为基础激励幅值,
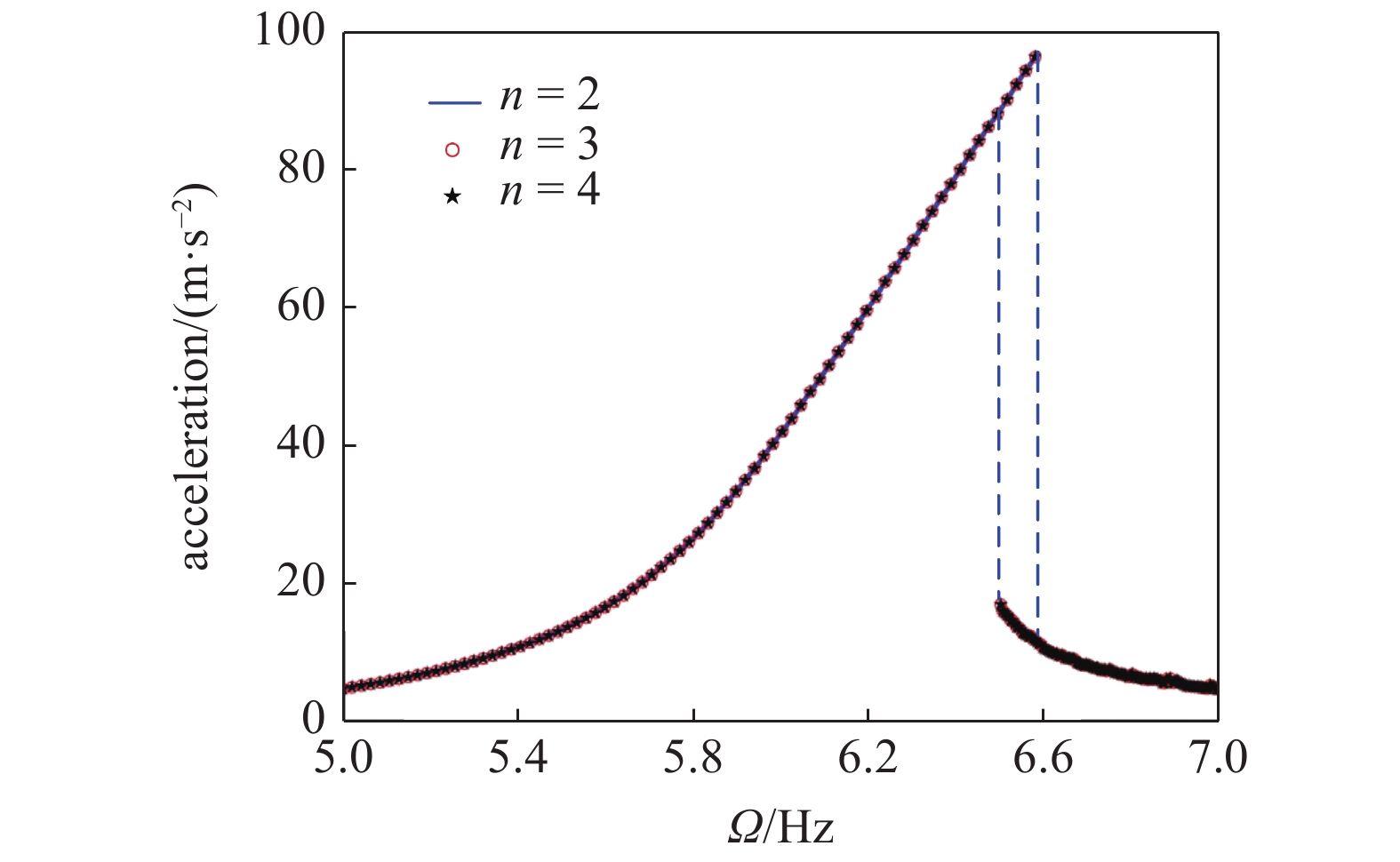
将结构参数与振动台扫频参数带入太阳翼的非线性动力学模型中, 计算得到系统幅频响应曲线. 由于实验扫频激励频带中只包含系统第2阶固有频率, 故此处仅研究系统2阶主共振. 图10为激励幅值为5 mm时测点3的理论仿真结果, 当取系统前2阶、前3阶和前4阶模态对动力学方程进行离散时, 其幅频响应曲线均重合, 故此处仅取前两阶全局模态离散得到的动力学模型便可以准确反映系统非线性动力学特性.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
激励幅值为5 mm时测点3的幅频响应曲线(理论结果, kn = 1200
m{N}} cdot {
m{m/ra}}{{
m{d}}^3}$
Figure
10.
Amplitude?frequency curve of point 3 with excitation amplitude 5 mm (theoretical results, kn = 1200
m{N}} cdot {
m{m/ra}}{{
m{d}}^3}$
下载: 全尺寸图片
幻灯片
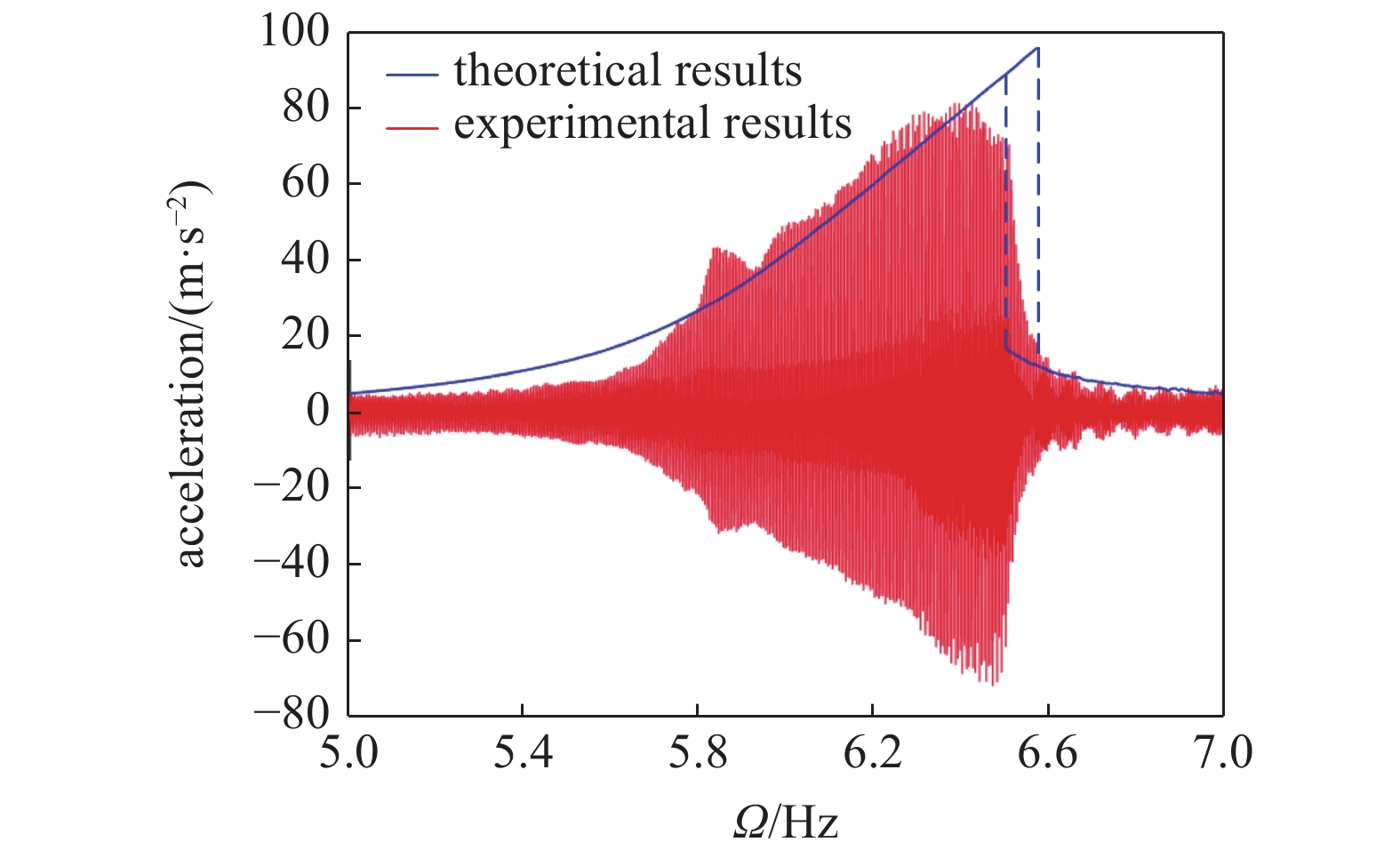
振动台扫频速率设置较小, 故此处可将动态响应测试所得的时域响应的包络线视为系统的幅频响应曲线. 将动态测试时域响应横坐标根据振动台扫频速率与时间换算为频率单位, 所得的响应的包络线即为系统的幅频响应曲线. 图11为激励幅值为5 mm时测点3的实验响应结果与理论计算结果. 为便于对比, 图中将动态测试时域响应横坐标根据振动台扫频速率与时间换算为频率单位, 由图中看出: (1) 低维理论模型可以计算得到动态响应实验中观察到的跳跃现象. (2) 在铰链非线性刚度系数取1200
m{N}} cdot {
m{m/ra}}{{
m{d}}^3}$
m{N}} cdot {
m{m/ra}}{{
m{d}}^3}$
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//lxxb2021-170-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
激励幅值为5 mm时测点3的实验与理论响应对比(kn = 1200
m{N}} cdot {
m{m/ra}}{{
m{d}}^3}$
Figure
11.
Comparison between the experimental and theoretical amplitude-frequency curve of point 3 with excitation amplitude 5 mm (kn = 1200
m{N}} cdot {
m{m/ra}}{{
m{d}}^3}$
下载: 全尺寸图片
幻灯片
4.
结论
本文针对铰链连接多板结构, 提出了获取系统全局模态的一般解析方法, 给出了建立系统低维高精度非线性动力学模型的策略和步骤. 通过特征正交多项式与拉格朗日乘子的引入, 准确地描述了柔性部件的弹性变形以及铰链处的匹配条件, 利用瑞利里兹方法得到系统的频率方程, 据此获取系统的固有频率和反映结构动力学特性的全局模态. 考虑铰链非线性刚度及摩擦力矩等因素, 通过全局模态离散得到系统的低维高精度非线性动力学模型, 研究了太阳翼在周期激励作用下的非线性特性. 开展了太阳翼地面振动实验研究, 采用锤击法获取系统模态, 利用振动台施加正弦扫频激励, 将物理实验结果与理论结果进行对比, 从而验证了全局模态动力学建模方法的合理性与准确性. 通过对仿真结果与实验结果的分析, 得到以下结论:
(1) 太阳翼的低阶模态主要表现为多板结构的刚体模态, 即扭簧的扭转模态. 高阶模态则表现为板的弯曲、扭转以及弯扭耦合特性.
(2) 铰链参数对太阳翼动力学特性影响较大, 其非线性抗扭刚度、摩擦力矩等因素的存在会使太阳翼的动态响应产生跳跃等非线性现象. 随着激励幅值的增大, 非线性现象更加突出, 硬特性特征也更加明显.
通过实验对建模方法合理性与准确性的验证, 得到全局模态动力学建模方法具有以下优点:
(1)解决了多板结构在非经典边界下全局模态解析求解的难题. 所提取的全局模态是反映系统中各个部件弹性振动的真实模态. 此外, 该方法便于分析参数对系统全局模态的影响, 从而可以揭示系统中各个部件之间的振动耦合关系.
(2)对于太阳翼这类复杂的铰接多板结构, 通过全局模态动力学建模方法获得的非线性动力学模型, 具有低维高精度的特点. 仅采用前几阶全局模态离散得到的动力学模型便可以准确反映系统非线性动力学特性, 克服了采用假设模态方法和有限元方法建模时存在的准确性低和自由度数高的问题.
