引言
减阻沟槽作为一种被动的减阻方式因其不消耗能源的特点拥有广泛的应用前景. 减阻沟槽起源于对于海豚表皮的仿生学研究[1], 海豚和鲨鱼表皮存在着微小的, 沿着水流方向排列的沟槽结构. 这些结构与鲨鱼体表的清洁程度和快速游泳能力有较大的关系[2]. 顺流沟槽的研究始于20世纪80年代美国兰利研究所[3-5], 之后科研人员对于不同边界层中的减阻效果和机理进行了大量研究, Walsh等[5-6]和Bechert等[7-8]对于不同截面形状的平行沟槽分别进行了大量模拟和实验, 分别得到了不同截面形状下沟槽的减阻曲线. 对于无量纲间距相同的不同形态的沟槽而言, 其单条沟槽截面积越小, 即越“薄”的沟槽减阻效果越好[9], 但更加不耐用且更易失效. 直线锯齿形沟槽易于加工, 成本较低并且更加耐用, 更加符合生产生活中使用的减阻沟槽形态.
大量实验和模拟数据表明, 对于某一形态的沟槽, 其存在一个有效的减阻范围[8], 这个范围与沟槽的无量纲高度h+和无量纲间距s+有关, GarcíaMayoral和Jiménez[10]使用沟槽截面积的平方根 lg+作为新的特征长度, 以更精确地刻画减阻曲线. 目前关于顺流向沟槽的减阻机理有两个理论: 一是沟槽的表面可以视作一个“虚拟平面”, 沟槽相对于这个“虚拟平面”的表面仍存在一定的突出高度, 这突出结构抑制了沟槽附近的展向脉动[11-13]; 二是沟槽壁面边界层的流向涡结构相对于光滑壁面有所抬升[14-17], 这减小了流向涡同壁间的接触面积和相互作用.
对湍流边界层中的沟槽壁面的研究在之前已有一定的进展, 近年来也有较多的风洞、水洞和水槽中的实验数据和数值模拟结论. 这些文章得到了较为统一的边界层中的统计量分布——即减阻沟槽壁面与光滑平壁面相比, 其黏性底层及缓冲层增厚, 对数律区外移[18-20], 并且相应的雷诺应力和湍流度的强度有所下降, 极值点也有所外移.
液固两相流在日常生产生活中极为常见, 如污水处理、含泥沙的自然水体和颗粒相水力输运等. 在对平壁面液固两相流的研究中, 研究人员发现固体颗粒会影响流场的湍动能. Gore等[21]在关于自由射流和管内流的研究中提出了一个参数O=dp/l, 其中dp为固体粒径, l为湍流积分长度尺度, 实验结果表明在多种流动状况下, 当dp/l > 0.1时, 颗粒的加入会增强湍动能, 反之则会降低湍动能. Noguchi等[22]研究了开口槽流道中的固液两相流. 他们的结果验证了含不同直径颗粒的流场同清水流相比湍流程度得到了减弱或者增强, 该实验说明了临界粒径与Kolmogorov微观尺度相关. 后续的其他实验中也同样提出存在一个分界尺度, 小于该尺度粒径的颗粒会减弱近壁区的湍流强度[23], 而大于该尺度的颗粒会增强近壁区的湍流强度[24-25]. Shokri等[26]研究了大雷诺数下颗粒直径对于液体流动中湍流强度的影响. 实验中使用了不同直径的玻璃珠, 观察到较小的颗粒会造成较强的近壁湍流, 并且高雷诺数下的较轻颗粒具有更加均匀的分布. 其他研究者的实验同样表明颗粒的加入会对相干结构产生抑制[27-28]或促进作用[29], 这些影响与固体颗粒的具体形态有关.
减阻沟槽所适合的工作条件, 譬如管内的流体输运, 飞机和船舶的表面减阻等都不可避免地涉及到两相流. 在这些条件下工作的沟槽其颗粒相尺度大多小于Kolmogorov尺度. 根据已有研究发现, 目前的沟槽研究实验中的流动相大多数集中于清水相和空气相, 而对于含颗粒的液体或含尘气体的研究较少. 对于减阻沟槽应用于被污染的介质或在输运固体颗粒的情况下能否保持减阻尚未得到验证.
本文使用粒子图像测速技术(particles?image?velocimetry,?PIV)对清水和粒子加入后的不同壁面湍流边界层进行研究, 通过对平均速度剖面线, 雷诺应力和湍流度等统计量进行对比, 再进一步使用空间平均局部结构函数, 探讨粒子对不同壁面湍流边界层中拟序结构的影响.
1.
实验设备及参数
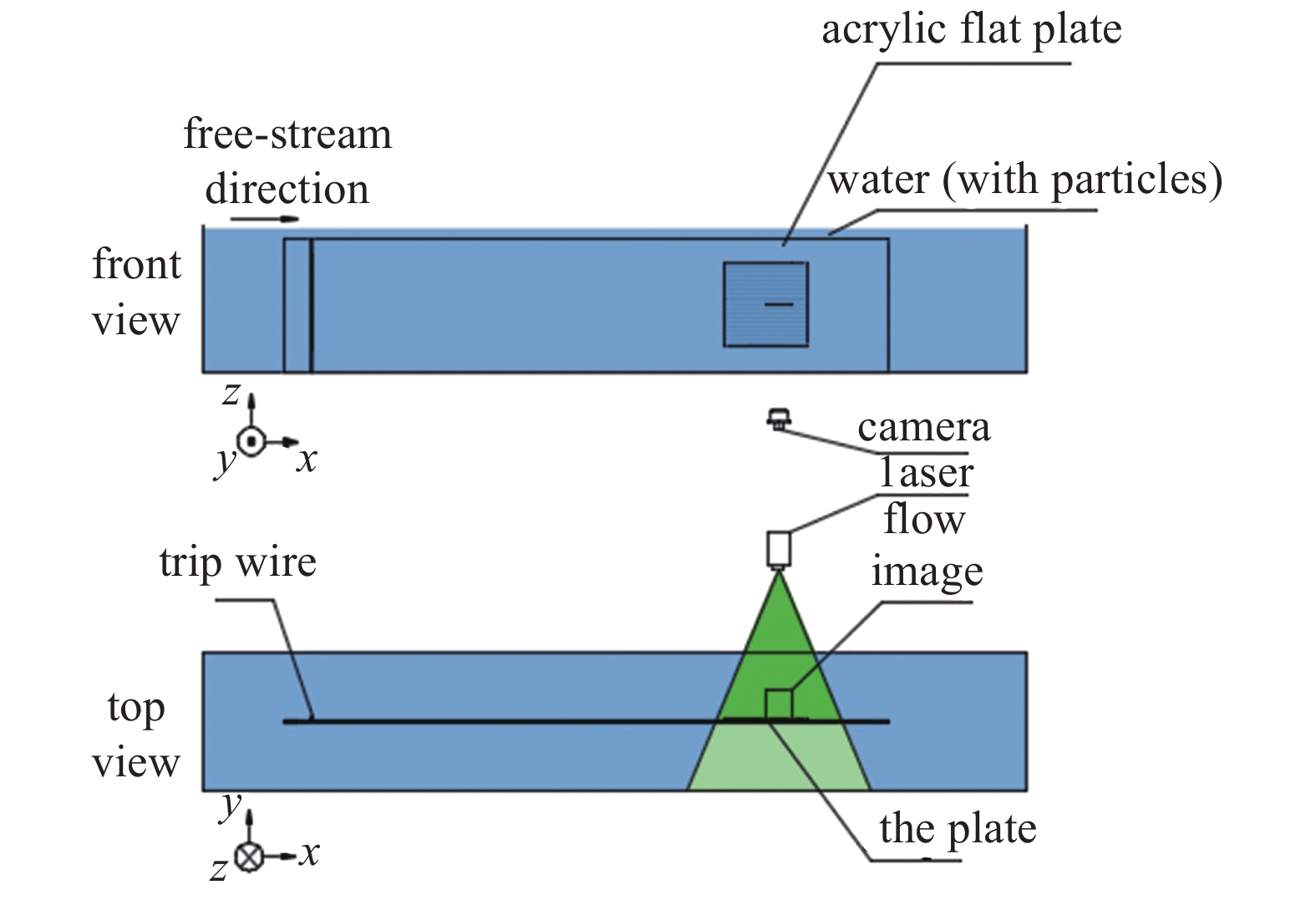
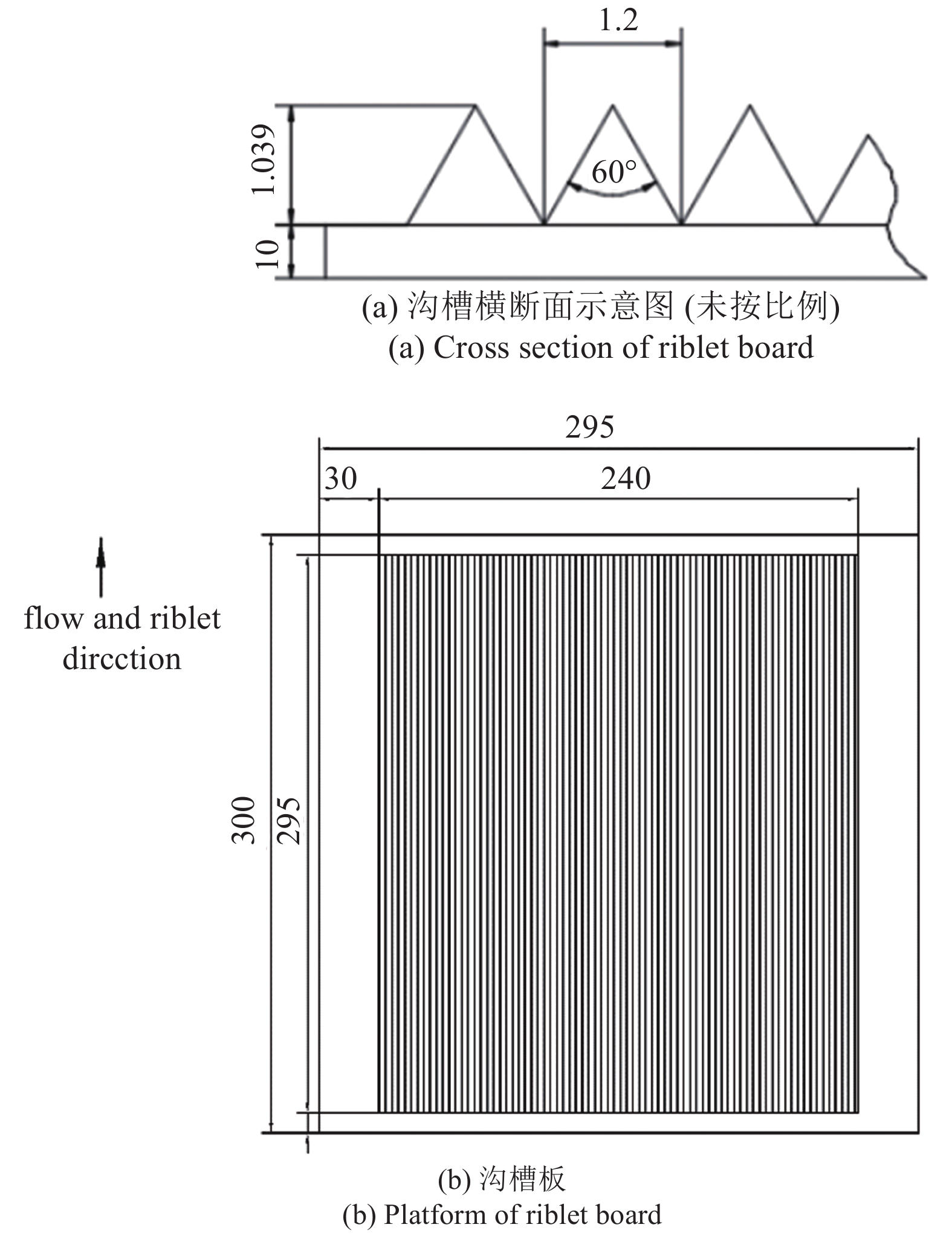
实验在河北工业大学粒子图像测速流体力学实验室中型低速循环水槽中进行, 其背景湍流度小于0.9%. 实验装置如图1所示, 水槽实验段长约2600 mm, 宽500 mm, 高600 mm. 光滑大平板为有机玻璃材质, 长2200 mm, 宽500 mm, 厚15 mm, 前缘进行8∶1椭圆修形. 平板竖直放置在水槽中, 令待测面与水槽侧壁面距离为260 mm. 为获得充分发展的湍流边界层, 在距离平板前缘100 mm处粘贴一条直径为5 mm的绊线. 在距平板前缘1600 mm处有一300 mm × 300 mm的凹槽, 内可嵌平板和沟槽板以进行不同壁面形态的研究, 沟槽板如图2所示. 实验中通过调节动力段轴流泵转速将来流速度U∞调为0.205 m/s和0.280 m/s, 实验环境温度为20 °C, 此时水的密度 ρw = 998 kg/m3, 运动黏性系数 μ = 1.0067 mm2/s, 此时两种工况下的清水相平板的摩擦雷诺数Reτ分别为436.9和489.9. 实验选用15 μm的聚苯乙烯颗粒作为液相的示踪颗粒, 颗粒相选用直径 dp = 155 μm的聚苯乙烯颗粒, 颗粒密度ρp = 1050 kg/m3, 其直径均小于Kolmogorov尺度. 液固质量比为500∶1的液固两相混合液通过泵以2 L/min的流量从距液面深300 mm, 距凹槽前缘2.8 m处注入. 沟槽尺寸如图所示. 实验数据通过德国Lavision公司的PIV系统进行采集. 激光器型号为LPY700, 其双脉冲激光最高频率为100 Hz, 最大能量为100 mJ, 相机为4MX相机(像素为2048 × 2048), 最大采样频率为180 Hz. 本实验中激光器能量为90 mJ, 图像采集模式为双帧双曝, 采集频率为90 Hz, 曝光时间为1000 μs. 对于每个不同工况下的流法向平面进行采集, 样本为8000张, 图像实际视野约为120 mm × 120 mm. 通过系统自带的Davis软件对采集的图像进行互相关处理, 查询窗口大小为32 × 32像素, 重叠率为75%. 得到256 × 256个速度矢量. 注意到第一个有效查询窗口需从壁面开始测量, 本PIV系统不足以精确得到近壁区域, 特别是y+ < 5 (U∞ = 0.205 m/s)和y+ < 8 (U∞ = 0.280 m/s)的位置中的速度场.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
实验装置示意图
Figure
1.
Schematic diagram of the experimental facility
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
沟槽板示意图(单位: mm)
Figure
2.
Schemetic diagram of riblet plate (unit: mm)
下载: 全尺寸图片
幻灯片
实验分为四组: 第一、二组为仅含示踪粒子的清水组, 其中第一组流体流过光滑壁面, 第二组流体流过沟槽壁面; 第三、四组为清水中加入155 μm聚苯乙烯颗粒的两相组, 第三组流体流过光滑壁面, 第四组流体流过沟槽壁面. 对两相流场的处理参考液固双流体模型, 即在数学处理上采用连续介质假设, 按照连续相处理; 而在动力学分析上则考虑颗粒相和流体相之间的耦合作用.
2.
湍流边界层中的统计量分析
2.1
减阻率及平均速度剖面
本实验无法直接对壁面阻力进行测量, 故采用Clauser图法对摩擦速度u*进行拟合[30]. 该方法基于平板湍流边界层的对数律区无量纲速度和法向高度满足对数关系, 通过迭代法得到数值解. 对于光滑壁面, 其速度在对数律区满足
$${u^ + } = frac{1}{kappa }ln {y^ + } + B$$  | (1) |
其中κ为卡门常数, 本文取κ = 0.41.
对于沟槽表面, 其理论零点要低于沟槽槽脊平面, 该方法中y+应替换为测量点坐标y与突出高度hp的和, 同时存在速度偏移项ΔU, 即
$${u^ + } = frac{1}{kappa }ln {y^ + } + B + Delta U$$  | (2) |
对于式(1)和式(2)两侧同时对y取微分后, 均有
$$frac{{Delta u}}{{Delta y}} = frac{{u^*}}{kappa }frac{1}{{y + {h_{ m{p}}}}}$$  | (3) |
通过对式(3)的迭代计算可以得到摩擦速度u*. 定义颗粒雷诺数 Rep = dpup/v, 其中up = gdp(ρ-ρf)/(18μ), 为颗粒沉降系数; 颗粒Stokes数St = τp/τf, 其中τp = ρpdp2/(18μ), 为流体对颗粒的响应时间, τf = v/u*2为流体特征时间; g为重力加速度, ρp为颗粒密度, dp为颗粒直径, ρf为流体密度. μ为流体动力黏度, u*为摩擦速度, 经计算得到颗粒雷诺数为0.100, 在两种自由来流速度下的颗粒斯托克斯数分别为0.123和0.160. 无因次壁面尺度定义为WU = ν/(τ/ρ)0.5其中, τ为壁面摩擦应力, 在两种速度下的沟槽无因次间距s+分别为10.4和14.1, 无因次高度h+分别为9.0和12.2, h/s为0.87. 由文献[8]中图表推算, 0.205 m/s时沟槽处于较优的工作状态, 0.280 m/s的速度下沟槽已越过最优减阻区间, 并且接近失效.
减阻率DR定义为
$$DR = frac{{{tau _{ m{s}}} - {tau _{ m{r}}}}}{{{tau _{ m{s}}}}}$$  | (4) |
其中τs为光滑壁面的摩擦应力, τr为沟槽壁面的摩擦应力, 有
$$tau { m{ = }} ho u^{*2}$$  | (5) |
同样地, 不同工况对于单相平板的减阻率定义为DR*, 其定义为
$$DR^* = frac{{{tau _0} - {tau _{ m{w}}}}}{{{tau _0}}}$$  |
其中τw为工作状况的摩擦应力, τ0面为单相平壁面的摩擦应力. Bechert等[8]提出沟槽壁面存在一虚拟原点, 该原点与沟槽尖端的距离称作突出高度, 这决定了沟槽尖端深入边界层的厚度. Bechert在文章中提出了突出高度的计算方式[8], 对于锯齿形沟槽, 有
$$frac{{{h_{ m{p}}}}}{s} = frac{1}{{2{ m{{text{π}} }}}}left[gamma + 2ln 2 + frac{{ m{{text{π}} }}}{{tan alpha }} - frac{{ m{{text{π}} }}}{alpha } + psi left(1 + frac{alpha }{{ m{{text{π}} }}} ight) ight]$$  |
其中, γ = 0.577 2为欧拉常数, ψ为Digamma函数. 本沟槽顶角为60°, 计算结果为hp = 0.170 7s, s为沟槽槽脊间距. 在两个速度下分别为1.714和2.390个无因次壁面尺度.
从表1中可以看出, 在0.205 m/s的速度下, 两种工况的沟槽壁面均有减阻效果, 并且加入颗粒后, 减阻效果有所提升. 在0.280 m/s的速度下, 清水相的沟槽壁面出现阻力上升的状况, 而两相工况中的沟槽壁面阻力仍然下降.
表
1
不同工况下的减阻效果对比
Table
1.
Drag reduction under different working condition
table_type1 ">
| U∞/(m·s?1) | u*/(m·s?1) | DR/% | DR*/% | |
| clean water smooth wall | 0.205 | 0.0088 | ? | ? |
| clean water riblet wall | 0.205 | 0.0084 | 8.88 | 8.88 |
| particles smooth wall | 0.205 | 0.0086 | ? | 4.49 |
| particles riblet wall | 0.205 | 0.0081 | 11.28 | 15.31 |
| clean water smooth wall | 0.280 | 0.0115 | ? | ? |
| clean water riblet wall | 0.280 | 0.0117 | ?3.51 | ?3.51 |
| particles smooth wall | 0.280 | 0.0115 | ? | 0 |
| particles riblet wall | 0.280 | 0.0112 | 5.43 | 5.43 |
下载: 导出CSV
|显示表格
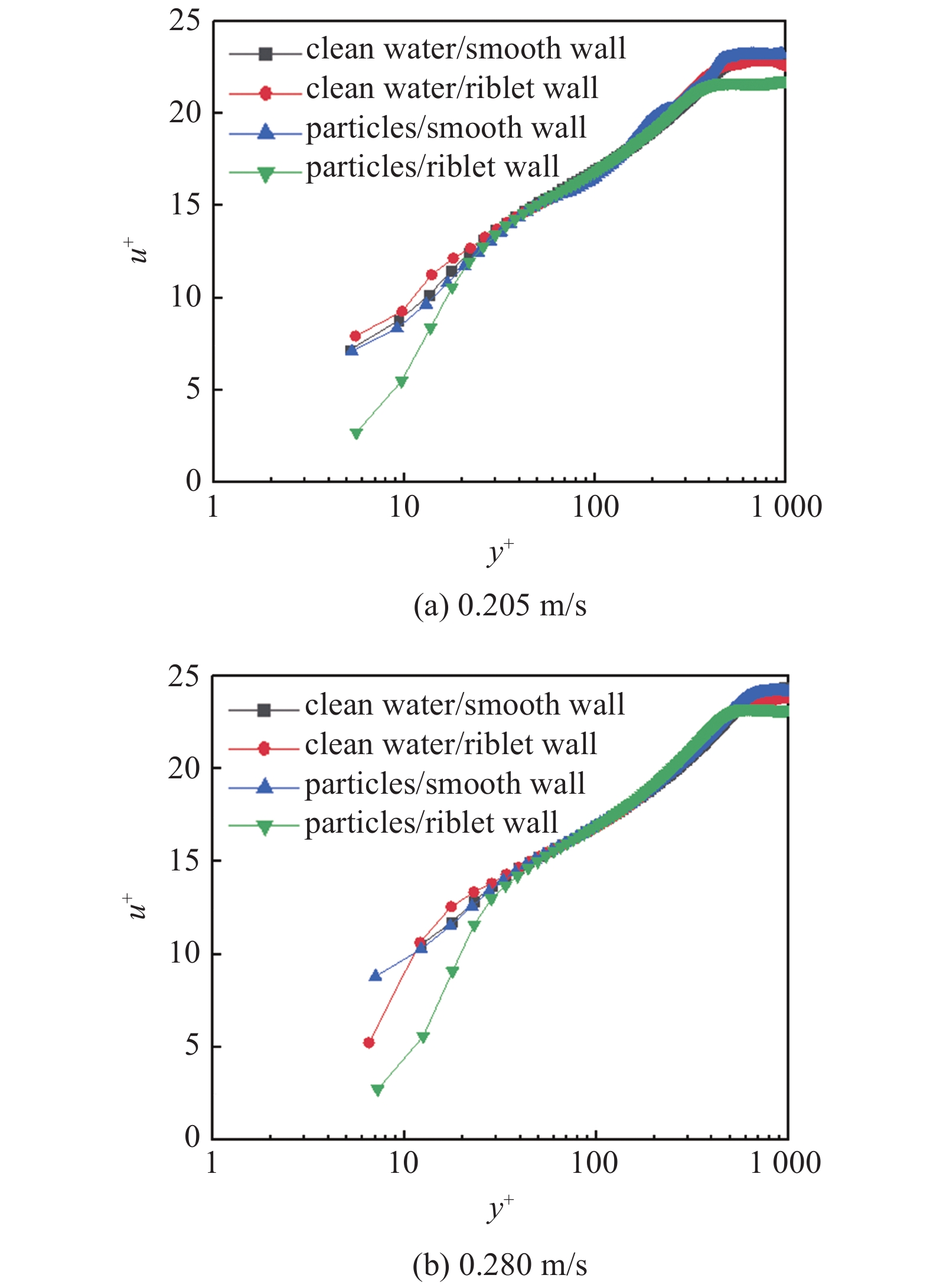
图3为两种速度下不同工况的流向平均速度剖面. 可以看到在清水相工况下, 沟槽壁面的缓冲层厚度略有减小. 而对于两相工况而言, 沟槽壁面的缓冲层均有所增厚, 对数律区外移, 边界层厚度有所增加. 分析可知两相流中颗粒的惯性使近壁面流体的运动更倾向于维持之前的行为, 从而抑制了展向的脉动. 对比两种工况下的光滑?沟槽壁面的流动, 可以看出沟槽壁面更有利于非洁净流体的输运. 并且颗粒的加入对于沟槽壁面的减阻能力有一定程度的提升.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
不同来流速度下流向平均速度剖面
Figure
3.
Streamwise mean velocity profiles at different velocity
下载: 全尺寸图片
幻灯片
2.2
湍流度及雷诺切应力
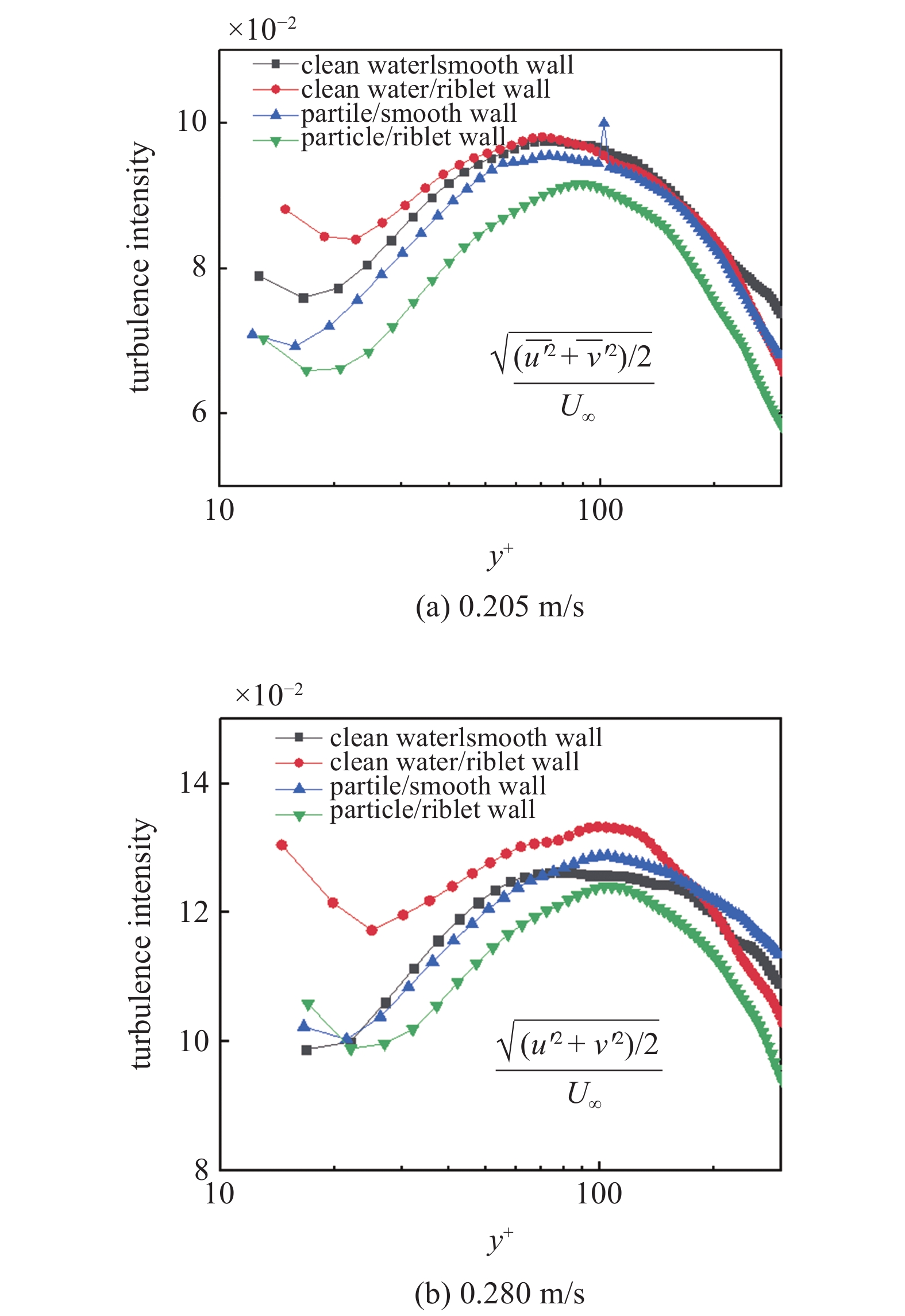
湍流度是衡量流场中湍流强弱的标准. 图4中给出了U∞ = 0.205 m/s和U∞ = 0.280 m/s下平均湍流度的对比. 可以看到, 在0.205 m/s的清水相流场中光滑壁面的湍流度在y+ ≈ 80附近出现峰值, 清水相和含颗粒相沟槽壁面流场的湍流度分布曲线均与光滑壁面类似, 但其峰值内移, 强度近似不变, 这表明沟槽壁面的湍流脉动峰值更加接近壁面. 同清水相沟槽壁面流场相比, 两相沟槽壁面流场的湍流度分布曲线与清水相壁面分布曲线形状类似, 但是其峰值外移, 强度明显下降. 这说明颗粒的加入使得湍流脉动峰值更远离壁面, 并且削弱了流场内部的输运, 湍流脉动得到抑制. 在0.280 m/s的流场中, 可以看到相对光滑壁面而言, 清水相沟槽壁面的湍流度峰值位置几乎不变, 强度有所提高. 这意味着清水相光滑壁面流场中湍流最剧烈的部分对壁面的影响更大; 而两相流场中的沟槽峰值位置亦几乎不变, 但强度降低, 与阻力变化结论吻合.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
不同来流速度下湍流度分布曲线
Figure
4.
Distribution of the turbulence intensity at different velocity
下载: 全尺寸图片
幻灯片
雷诺应力是指在湍流的时间平均运动中, 流体颗粒之间动量交换所产生的附加应力. 雷诺应力越大, 说明流体颗粒动量交换就越大, 流体脉动就越强烈. 图5为不同速度下雷诺应力的对比, 可以看到在0.205 m/s下清水相光滑壁面流场的雷诺应力在y+ ≈ 40附近较为平缓, 其峰值大约在y+ ≈ 30和y+ ≈ 90处. 可观察到两种流动相下的沟槽壁面雷诺应力峰值均有所降低, 并且其峰值同样有所外移. 雷诺应力的降低说明动量交换减弱, 流体脉动被抑制, 是减阻壁面的一个典型特征. 在0.280 m/s的单相工况下可以看到沟槽壁面的雷诺应力峰值仍向外移动, 但峰值相对单相壁面有所增加, 这同平均速度剖面和阻力上升的结果吻合.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
不同来流速度下雷诺切应力分布曲线
Figure
5.
Distribution of the Reynolds shear stress at different velocity
下载: 全尺寸图片
幻灯片
3.
流动中的喷射?扫掠结构检测及其分析
从上文的统计量分析中可以看出, 颗粒的存在加强了沟槽的减阻效果. 但多种工况下颗粒对于沟槽的影响十分类似, 无法推断更加具体的机理上的影响, 故下文从拟序结构的方向进行进一步的分析.
相干结构是湍流边界层研究中的重要对象, 湍流边界层相干结构是指在尺度为边界层厚度的量级空间内流动特征一致或紧密相关的流动, 例如快慢斑、上升流、下扫流和各种涡结构[31]. 对于不可压缩流体, 可以通过对相邻流体微团的相对速度来反映喷射和扫掠运动. 以下使用新象限分裂法和空间局部平均结构函数[32]提取喷射?扫掠行为.
脉动速度沿流向的空间局部平均结构函数为:
$$delta {u_x}(x,l) = {overline {u(x,y)} _{x in [{x_0},{x_0} + l]}} - {overline {u(x,y)} _{x in [{x_0} - l,{x_0}]}}$$  | (6) |
$$delta {v_x}(x,l) = {overline {v(x,y)} _{x in [{x_0},{x_0} + l]}} - {overline {v(x,y)} _{x in [{x_0} - l,{x_0}]}}$$  | (7) |
其中,
基于象限分裂法的壁面湍流相干结构采样如下
$$begin{array}{l} D({x_0},l){ m{ = }} left{ !!!{begin{array}{*{20}{l}} 1!!!!&!!!!!!{({ m{ejection}})},!!!!&!{!!{ m{if}}!!begin{array}{*{20}{c}} {u' < 0& delta {u_x}{{({x_0},l)}^ - } < 0& delta {u_x}{{({x_0},l)}^ + } > 0} {& v' > 0& delta {v_x}{{({x_0},l)}^ - } > 0& delta {v_x}{{({x_0},l)}^ + } < 0} end{array}} { - 1}!!!!&!!!!!!{({ m{sweep}})},!!!!&!!!!{!!{ m{if}}!!begin{array}{*{20}{c}} {u' > 0& delta {u_x}{{({x_0},l)}^ - } > 0& delta {u_x}{{({x_0},l)}^ + } < 0} {& v' < 0& delta {v_x}{{({x_0},l)}^ - } < 0& delta {v_x}{{({x_0},l)}^ + } > 0} end{array}} 0,&{}&{{ m{otherwise}}} end{array}} ight. end{array}$$  | (8) |
其中D(x0,l)为x0处, 湍流尺度为l的检测函数. δux(x0, l)?和δux(x0, l)+是位于x0处的左右邻域. 式(8)体现了喷射和扫掠时流体的运动状况. 在喷射事件中, 低速流体从近壁区被喷射到外层, 局部脉动速度u″ < 0并且达到极小值; v′ > 0并且达到极大值. 在扫掠事件中, 高速流体从外区向壁面下扫, 局部脉动速度u′ > 0并且达到极大值; v′ < 0并且达到极小值.
3.1
喷射和扫掠事件
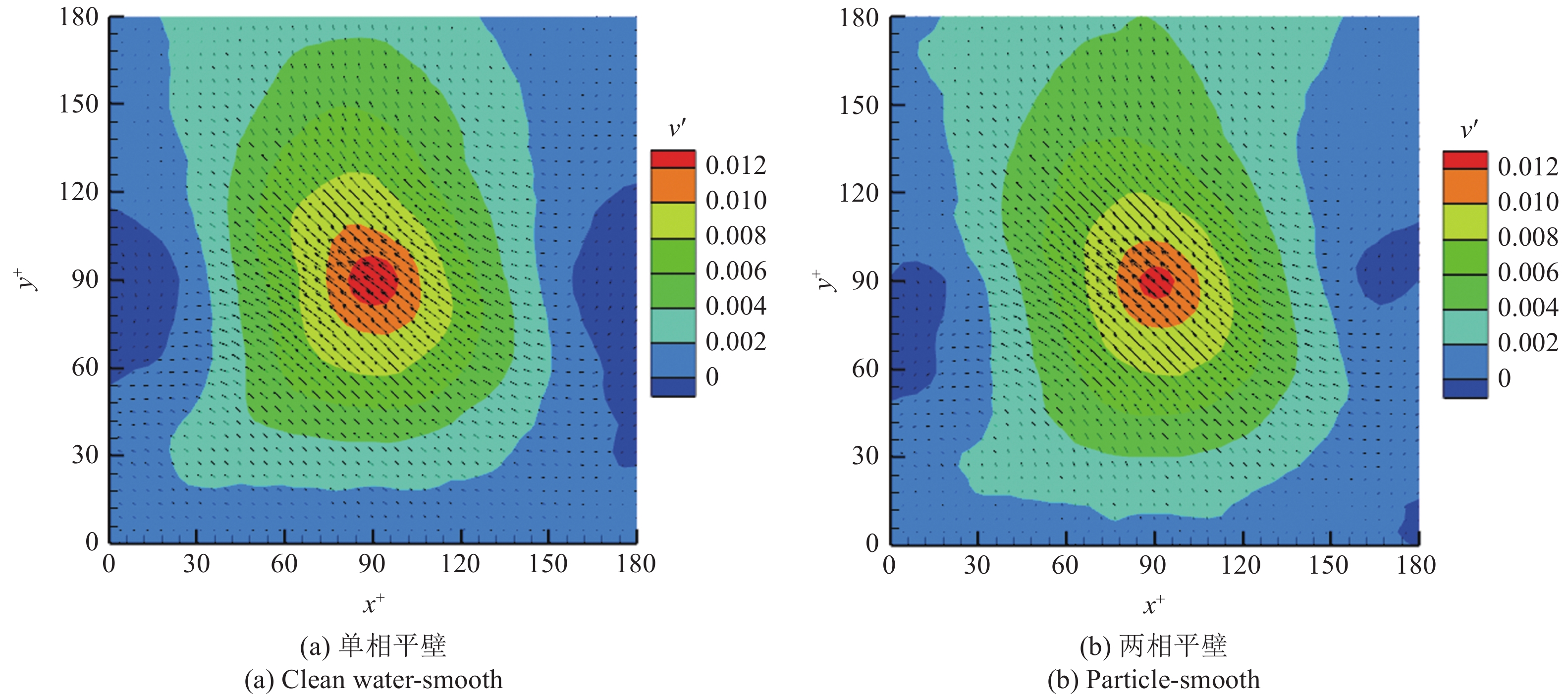
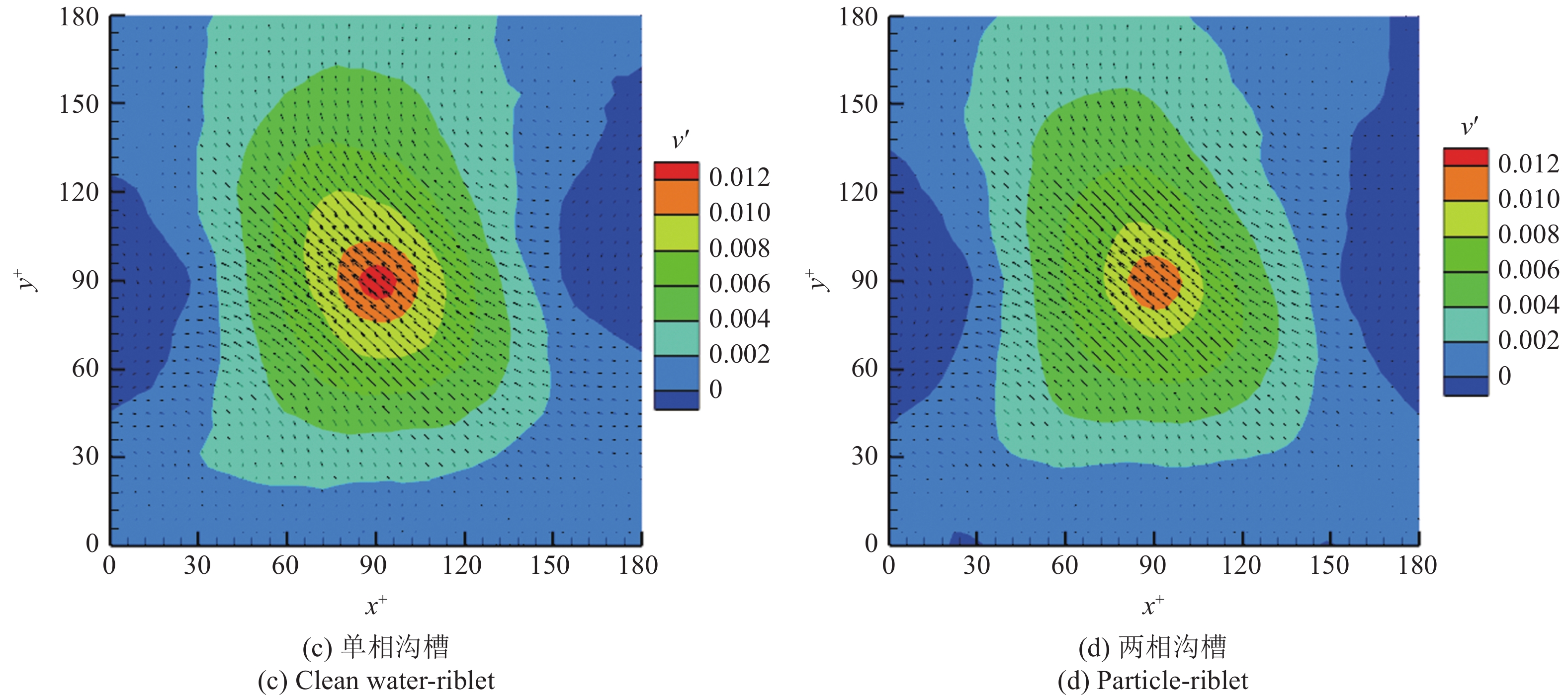
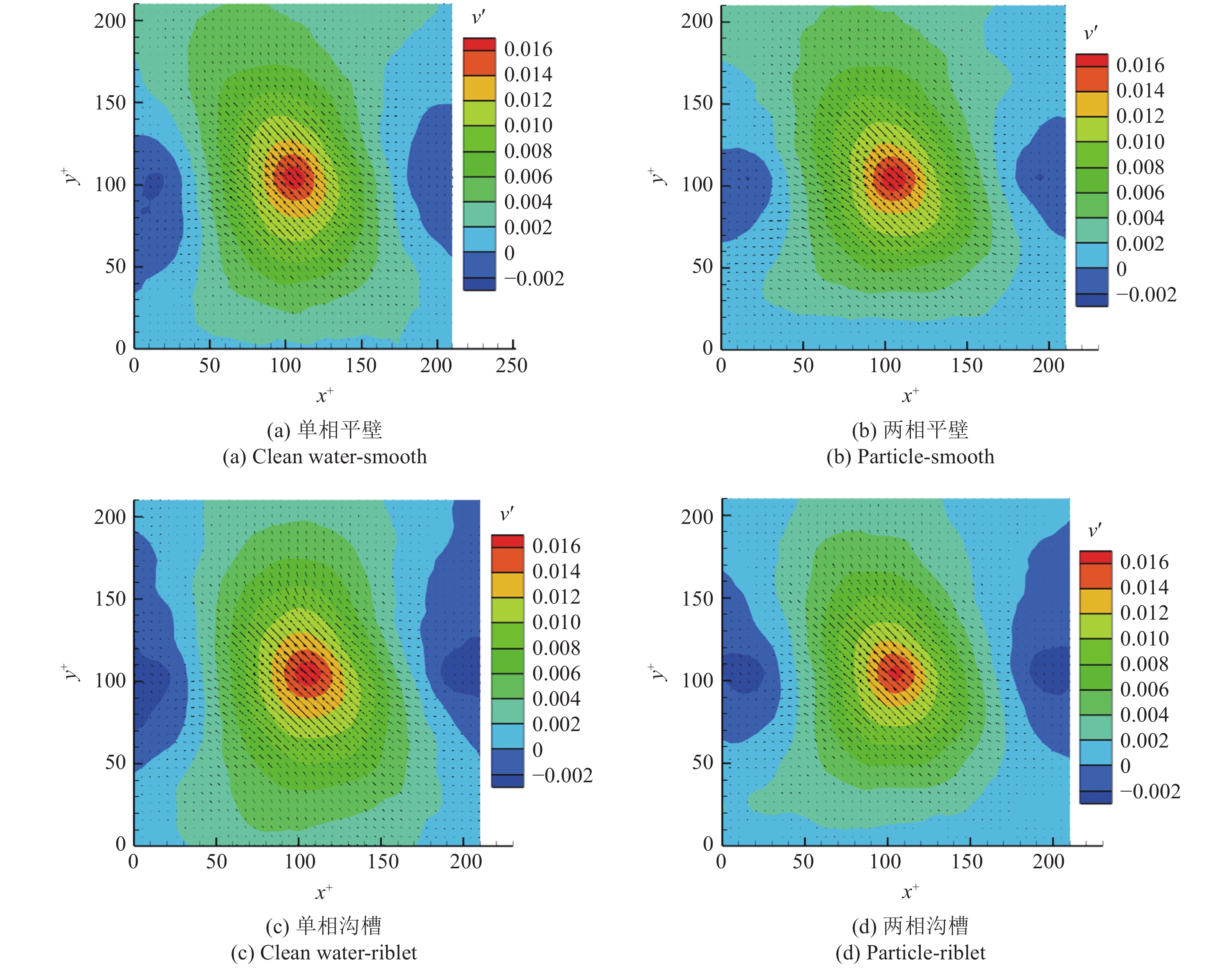
由上文可知, 在速度分别为0.205 m/s和0.280 m/s时, 雷诺应力和综合湍流度的极大值分别在y+ = 90和y+ = 105附近. 图6和图7为0.205 m/s速度下不同工况x-y平面内在无因次法向位置y+ = 90下和0.280 m/s速度下不同工况x-y平面内无因次法向位置y+ = 105下的喷射事件的法向脉动速度二维拓扑结构. 图中横纵坐标分别使用壁面单位WU进行了无量纲化. 除0.280 m/s的单相沟槽外, 可以观察到沟槽壁面下喷射中心流向脉动速度值较大的区域小于同工况下的清水区, 说明沟槽壁面降低了喷射的低速流体和周围流体的速度差, 减小了喷射行为的猝发强度, 也减小了边界层内部之间的动量交换. 并且喷射行为的削弱同样降低了与流向相反的脉动速度. 相对于清水相, 加入颗粒后的流体喷射中心附近的流向脉动速度要小于清水相中的区域, 并且同样可以观察到脉动速度值较大的区域明显减小, 喷射结构被抑制, 这说明颗粒的加入同样降低了边界层内部的动量交换.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-6-1.jpg'" class="figure_img
figure_type2 ccc " id="Figure6-1" />
6
U∞ = 0.205 m/s时不同工况下的喷射法向脉动速度云图
6.
Contours of the normal fluctuating velocity around eject at U∞ = 0.205 m/s
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-6.jpg'" class="figure_img
figure_type2 ccc " id="Figure6" />
图
6
U∞ = 0.205 m/s时不同工况下的喷射法向脉动速度云图(续)
Figure
6.
Contours of the normal fluctuating velocity around eject at U∞ = 0.205 m/s (continued)
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-7.jpg'" class="figure_img
figure_type2 ccc " id="Figure7" />
图
7
U∞ = 0.280 m/s时不同工况下的喷射法向脉动速度云图
Figure
7.
Contours of the normal fluctuating velocity around eject at U∞ = 0.205 m/s
下载: 全尺寸图片
幻灯片
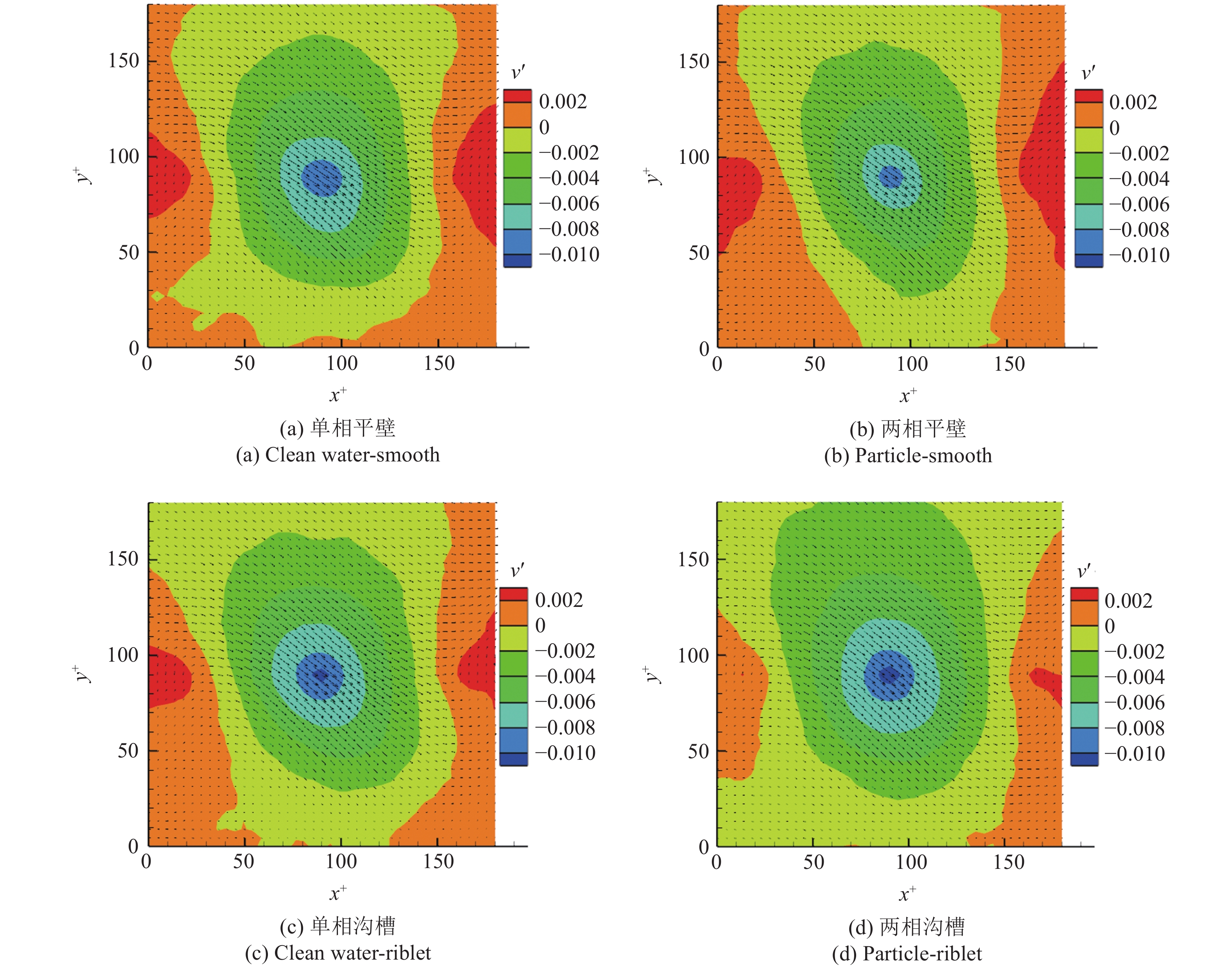
相应地, 图8和图9为0.205 m/s速度下不同工况x-y平面内无因次法向位置y+ = 90下和0.280 m/s速度下不同工况x-y平面内无因次法向位置y+ = 105下的扫掠事件的法向脉动速度二维拓扑结构. 可以看到高速流体在低速流体上部, 并且向壁面下扫. 对两种速度下的不同壁面而言, 颗粒的加入均降低了壁面附近的法向湍动, 降低了壁面附近的扫掠行为的强度, 这是由于颗粒惯性使其在扫掠过程时不易跟随流体接近壁面, 进而使得各层间速度更加均匀, 能量交换有所削弱. 这能够降低输运过程中的阻力. 并且注意到0.280 m/s的两种工况下, 沟槽壁面对扫掠的猝发强度有所强化, 说明当雷诺数较大时, 沟槽的突出结构会增加下扫的高速流体同周围低速流体的速度差异.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-8.jpg'" class="figure_img
figure_type2 ccc " id="Figure8" />
图
8
U∞ = 0.205 m/s时不同工况下的扫掠法向脉动速度云图
Figure
8.
Contours of the normal fluctuating velocity around eject at U∞ = 0.205 m/s
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-9.jpg'" class="figure_img
figure_type2 ccc " id="Figure9" />
图
9
U∞ = 0.280 m/s时不同工况下的喷射法向脉动速度云图
Figure
9.
Contours of the normal fluctuating velocity around eject at U∞ = 0.280 m/s
下载: 全尺寸图片
幻灯片
3.2
扫掠事件数量随法向距离的变化
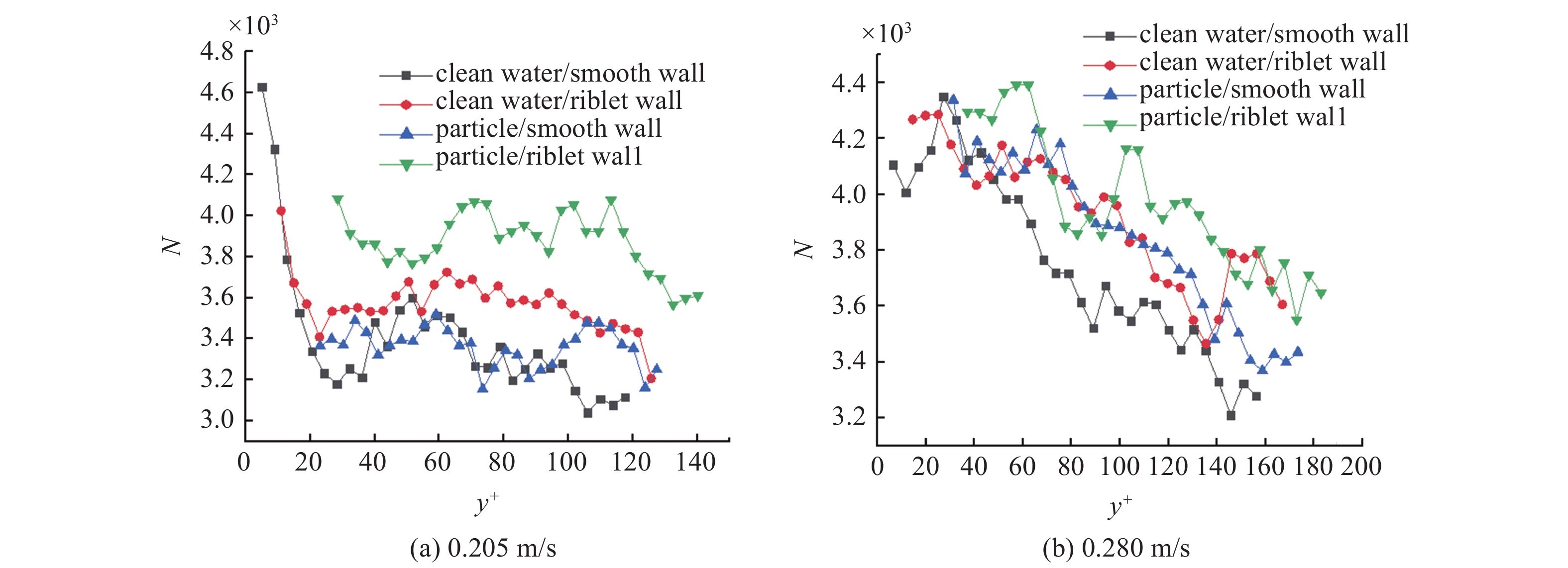
图10为不同速度下扫掠事件发生数量沿法向的分布规律. 可以看到在颗粒加入后沟槽壁面附近的扫掠行为数量均明显增加, 而沟槽和颗粒单独作用时的扫掠行为数量同清水相平板下的数值相差不大. 这是由于两相流中的颗粒将沟槽诱导出的流向涡破碎成了小涡, 从而导致涡诱发出的扫掠事件数目增加. 并且在0.280 m/s下扫掠行为的数量均随着法向距离的增加而减少.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-149-10.jpg'" class="figure_img
figure_type2 ccc " id="Figure10" />
图
10
不同来流速度下扫掠数目沿法向分布规律
Figure
10.
Distributions of the number of sweep along normal-wall positions
下载: 全尺寸图片
幻灯片
4.
结论
本文利用粒子图像测速技术分别对清水相工况和液固两相工况下的平板及沟槽板湍流边界层瞬时速度场进行测量, 得到了平均速度剖面、雷诺应力和湍流度等统计量, 提取分析了8种工况条件下喷射?扫掠结构和流向/法向脉动速度的二维拓扑结构, 得到了以下结论:
(1)在对数律区中, 颗粒组的无量纲速度均略大于清水组, 雷诺切应力有所降低, 湍流度有所减弱;
(2)对于沟槽而言, 无论其实际处于减阻还是增阻状态, 颗粒的加入均会降低沟槽壁面附近对数律区中的湍流强度, 与沟槽的减阻产生协同效应, 并且令失效的沟槽重新产生减阻效果;
(3)颗粒对喷射?扫掠两种行为产生的影响类似, 而这种影响同壁面类型无关. 对于两种行为而言, 颗粒的加入会降低其猝发事件强度. 从而可以降低壁面附近的法向脉动强度, 降低流体与壁面的相互作用, 提升沟槽的减阻能力.
